Abstract
Dynamic objects present a major challenge for visual simultaneous localization and mapping (Visual SLAM), as feature measurements originating from moving regions can corrupt camera pose estimation and lead to inaccurate maps. In this paper, we propose a lightweight, semantic-free front-end enhancement for ORB-SLAM that detects and suppresses dynamic features using optical flow geometry. The key idea is to estimate a global motion direction point (MDP) from optical flow vectors and to classify feature points based on their angular consistency with the camera-induced motion field. Unlike magnitude-based flow filtering, the proposed strategy exploits the geometric consistency of optical flow with respect to a motion direction point, providing robustness not only to depth variation and camera speed changes but also to different camera motion patterns, including pure translation and pure rotation. The method is integrated into the ORB-SLAM front-end without modifying the back-end optimization or cost function. Experiments on public dynamic-scene datasets demonstrate that the proposed approach reduces absolute trajectory error by up to approximately 45% compared to baseline ORB-SLAM, while maintaining real-time performance on a CPU-only platform. These results indicate that reliable dynamic feature suppression can be achieved without semantic priors or deep learning models.
1. Introduction
Simultaneous localization and mapping (SLAM) is a fundamental technology in computer vision and robotics that allows a robot or device to construct a map of an unknown environment while simultaneously estimating its own movement route. SLAM has been widely applied in various fields, such as autonomous vehicles [1], robotics [2], and surveying in hazardous environments [3]. The basic principle of SLAM involves detecting the robot’s motion by sequentially processing sensory data from the surrounding environment and concurrently building a map of that environment. The most notable of the various sensors used as information acquisition tools is the camera. Among the various sensors used for data acquisition, cameras stand out due to the rich visual information they provide. Consequently, SLAM research has increasingly shifted toward Visual SLAM (VSLAM).
VSLAM methods match successive image frames using reference points on the images. Some VSLAM methods, such as LSD-SLAM [4], DTAM [5], and DSO [6], utilize changes in pixel density on the image. Categorized as direct methods, these are sensitive to lighting changes and are more suitable for low-textured scenes. On the other hand, in feature-based methods, reference points are matched using key points. Feature-based methods are more frequently used in VSLAM systems. Feature points are local landmarks in images that can be distinctive, such as corners, edges, and textures. Popular feature extraction methods such as Speeded-Up Robust Features (SURF) [7], Scale-Invariant Feature Transform (SIFT) [8], and Oriented FAST and Rotated BRIEF (ORB) [9] obtain recognizable pixel groups on the image more robustly. These feature points can be matched in images with different poses. In this way, these points are used as reference points to calculate the pose change in consecutive image frames.
Theoretically, many challenges in VSLAM have been addressed, particularly in static environments. Notable methods such as ORB-SLAM [10], ORB-SLAM2 [11], ORB-SLAM3 [12], PTAM [13], and LSD-SLAM [4] perform robustly in static environments. However, when keypoints are taken from moving objects, traditional SLAM systems suffer from pose estimation errors, leading to inaccurate maps with accumulative drift [14]. Distinguishing between static and dynamic features in a scene remains a significant challenge and forms the core of the dynamic SLAM problem.
Several solutions have been proposed to overcome the dynamic SLAM problem. One category involves the use of specialized sensors, such as RGB-D cameras, which provide depth information with embedded IR modules [15]. However, their limited range makes them suitable only for small indoor environments. There are also proposed methods with tools such as IMU sensors [16]. However, they have disadvantages such as cost and mobility. Low cost, ease of use, and portability make the monocular camera one of the most commonly employed sensors in VSLAM studies. Our study focuses on using RGB images captured by a monocular camera. Another prominent category includes deep learning-based methods [17,18,19], which typically rely on semantic segmentation or object detection. While effective, these methods often demand high computational resources, making them less practical for real-time applications [20]. Moreover, such methods require prior knowledge of object classes and may fail to detect unexpected moving entities. Hence, there is strong motivation to develop a lightweight, non-learning-based algorithm that does not rely on object recognition—one that is more generally applicable across diverse dynamic scenarios.
In this study, we propose an optical flow-based method for efficiently detecting and suppressing dynamic feature points in VSLAM. The proposed approach operates on monocular RGB images and is therefore applicable to a wide range of robotic platforms equipped with standard cameras. The method analyzes the geometric consistency of optical flow vectors to distinguish motions induced by the camera from those originating from independently moving objects. The proposed strategy is integrated into the front-end of ORB-SLAM, where dynamic features are filtered prior to pose estimation, allowing camera trajectories to be estimated using predominantly static scene information without modifying the back-end optimization or cost function. Experiments conducted on the TUM RGB-D dataset [21] demonstrate both accurate detection of dynamic regions and noticeable improvements in trajectory estimation performance in dynamic environments. Furthermore, as the proposed method avoids deep learning models and semantic inference, it introduces only limited computational overhead and does not require GPU acceleration, making it suitable for real-time operation on resource-constrained robotic systems.
The principal contributions of this study can be summarized as follows:
- We propose an optical flow-based dynamic feature filtering method that exploits motion-consistent angular relationships to distinguish feature points associated with moving objects from those induced by camera motion.
- We integrate the proposed method into the front-end of the ORB-SLAM system, enabling more robust trajectory estimation in dynamic environments without modifying the original back-end optimization or cost function.
2. Related Works
Numerous methods have been proposed to handle the dynamic SLAM problem. Approaches using visual input can broadly be classified into two main categories: semantic-based methods and geometric-based methods. Semantic SLAM methods are widely studied as a solution for dynamic environments. These methods typically leverage deep learning techniques—such as object detection and semantic segmentation—to identify moving objects in the scene. Unlike traditional SLAM systems, which rely heavily on static feature points, semantic methods improve localization accuracy by excluding dynamic elements. For instance, Yu et al. [22] perform object detection by including SegNet [23] in ORB-SLAM2 [11]. Focusing on people in the image, this method excludes feature objects belonging to moving people. Yuan et al. [24] perform Mask R-CNN moving object prediction by performing instance object segmentation. RDS-SLAM [25] assigns probability values to moving objects using semantic segmentation. Bescos et al. [18] detect objects using R-CNN. Then they examine them with multi-view geometry to detect moving objects accurately. Peng et al. [26] use a depth clustering algorithm using semantic segmentation. It makes determinations about the movements of objects according to the depth information it estimates. Liu et al. [27] propose a method based on object tracking. Features of the dynamic object mask are detected. YGC-SLAM [28] detects the movement of the objects according to the geometric changes it detects using YOLOv5 and k-means algorithm.
Geometric-based methods, on the other hand, rely on visual cues without the need for object semantics. These techniques detect motion by analyzing inconsistencies in the spatial structure or pixel-level geometry between frames. Scona et al. [29] generate a depth map and assign a moving probability to each cluster of objects. Reference [30] generates a dynamic map by calculating the triangulation consistency. It removes the regions that it labels as moving. Kim et al. [31] use a nonparametric model to estimate the background to reduce the effect of moving objects. Dai et al. [32] estimate stable points by examining the correlations between map points and points corresponding to image edges. Alcantarilla et al. [33] detect and remove moving objects with their method based on dense scene flow. Cheng et al. [34] detect moving objects using optical flow. It finds feature points of moving objects depending on whether the flow lengths are above a certain threshold value. DVO SLAM [35] uses color and depth information to create a 3D density map.
Despite the extensive research on dynamic VSLAM, several limitations remain in existing approaches. Semantic-based methods rely on prior object knowledge and often require deep learning models, which introduce considerable computational overhead and limit real-time applicability on resource-constrained platforms. Optical flow-based approaches provide a lightweight alternative; however, many existing methods primarily depend on flow magnitude or residual thresholds to identify dynamic regions. Such magnitude-based criteria are highly sensitive to scene depth variations and camera velocity, making them difficult to generalize across different environments. For instance, the method proposed by Cheng et al. [34] employs flow length thresholds to detect moving objects, which can misclassify distant static points or nearby slow-moving objects. In contrast, the approach proposed in this work exploits the geometric consistency of optical flow directions with respect to a global motion direction point, enabling a motion-consistent angular analysis that remains robust under different camera motion patterns, including pure translation and pure rotation. By focusing on angular coherence rather than flow magnitude and integrating the method into the front-end of ORB-SLAM, the proposed approach addresses dynamic feature contamination without relying on semantic information or modifying the underlying optimization framework.
3. Methodology
In this section, we present a dynamic VSLAM framework that leverages optical flow to detect and filter moving objects in dynamic scenes. The primary goal of the proposed approach is to improve camera pose estimation accuracy by isolating static scene elements that are influenced only by camera motion. The framework follows a structured pipeline consisting of initial pose estimation, extraction of optical flow vectors, motion direction point (MDP) detection, identification of dynamic feature points, and refined pose estimation using only static features.
The proposed system is a feature-based VSLAM method that utilizes ORB keypoints as landmarks in monocular RGB image frames. Optical flow is computed sparsely at the detected ORB keypoint locations to maintain full compatibility with the feature-based SLAM pipeline and to limit computational overhead. For each frame, a global motion direction point is estimated to represent the dominant camera-induced motion pattern in the image plane. Feature points whose optical flow vectors exhibit angular inconsistencies with respect to this global motion pattern are classified as dynamic and excluded from subsequent pose estimation. The overall structure of the proposed approach is illustrated in Figure 1.
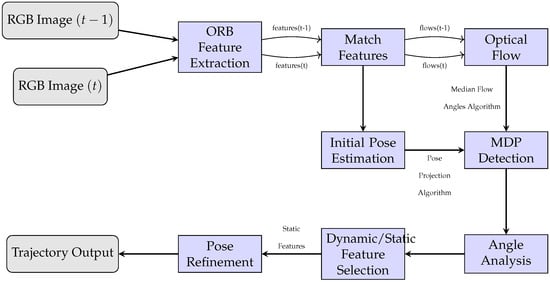
Figure 1.
Flowchart of the proposed method.
From a system integration perspective, the proposed method operates as a front-end enhancement to ORB-SLAM and focuses on suppressing dynamic feature points prior to camera pose estimation. The remaining motion-consistent feature points are subsequently passed to the standard ORB-SLAM tracking and back-end optimization modules without any modification to the original back-end, ensuring seamless integration while improving robustness in dynamic environments.
3.1. Problem Definition
Digital images are obtained by projecting a 3D scene onto a 2D image plane, where depth information is inherently lost. As a result, computers cannot directly infer perspective information from 2D images. In computer vision, various image transformation models are employed to analyze depth and motion, with perspective projection being the most commonly used. The perspective projection model is shown in Figure 2, and the corresponding mathematical formulation, widely used in VSLAM, is given by
where is the projection matrix of the pose transformation in the image, X, Y, Z are the locations of points in the real world plane, and u and v are the pixel coordinates of points in the digital image. consists of the pose matrix containing the camera internal parameters and the camera pose information.
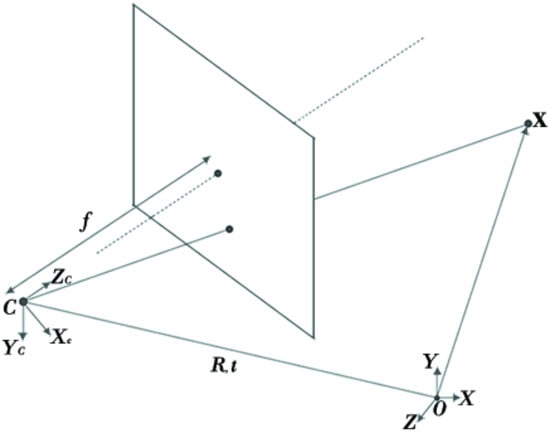
Figure 2.
Perspective projection model. The dashed line represents the light hitting the camera’s focal point.
3.2. Two-View Geometry
The triangular plane made by the projections of a point in the real world on two different images is singular. This plane is called the epipolar plane [36]. The components of the pose that change between the two images are the rotation matrix and the translation vector . and are the pixel positions of the point in the images. The constraint equation provided by the singular epipolar plane is expressed as follows:
where and are matrices expressing the camera’s internal parameters. The unknown variables in the equation are the pose components and . To calculate these variables, and hence the camera pose change, at least 12 feature points must be matched since the projection matrix has 12 elements [37]. To match the same point in two different images, we use ORB, a feature extraction method that does not affect the changes in the image. In order to obtain the correct pose change by using the epipolar geometry shown in Figure 3, the matched points must be in the same real position for both images. The main problem here is to determine whether the objects from which the feature points are obtained are moving.
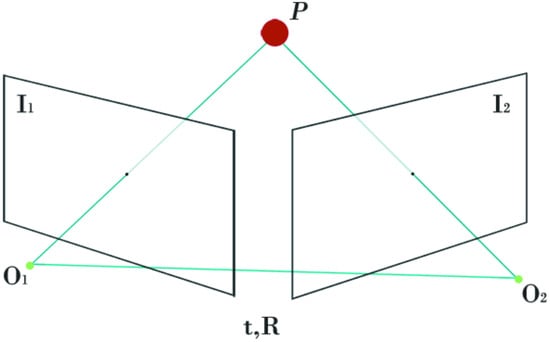
Figure 3.
Epipolar geometry.
3.3. Optical Flow
Optical flow is a vector representing the pattern resulting from the motion of moving pixel groups within an image sequence. Estimation of horizontal and vertical speeds of pixel groups within an image due to camera or object motion is performed by optical flow. A digital image is expressed with horizontal and vertical pixel positions and time variables I(). In the Lucas–Kanade optical flow method [38], when a consecutive image frame is expressed as I(), assuming that the gray level value remains constant, the equation can be expressed as follows:
Using the Taylor linear formulation, Equation (3) can be rewritten as the following linear partial derivative formulation:
where , , and denote the spatial derivatives of the gray level values of pixels, while vectors u and v denote the optical flows between consecutive image frames.
The optical flow method is a useful method for estimating camera movements or object movements. However, in general use, it provides information about movement in cases where either the camera is moving and the objects are stable or the camera is stable and the objects are moving. In the VSLAM problem, both the camera and the objects are moving. To detect moving objects together with the camera movement, we use the optical flow method for cases where the objects are mostly stable and the moving objects are statistically in the minority. For this purpose, we examine the camera movement model and talk about the concept of the motion direction point.
3.4. Motion Direction Point
The motion direction point (MDP) is the projection of the general direction of the camera movement on the image. The general distributions of the flow vectors provide information about the camera movement. In Full Rotation (FR) movements, where the flow vectors extend in the same direction, the MDP is on the image boundary. In Full Translation (FT) cases, where the flow vectors extend to a point on the image, the motion direction point is in the image and the flow vectors point to the MDP. Determination of MDP with flow vectors for camera motion models is shown in Figure 4. Since the motion models are different, it will not be useful to use the angles of the flow vectors. Therefore, the useful parameter related to the camera movement will be the MDP. Using the relationship between the general distributions of the flow vectors and the camera movement, we select the outlier flow vectors and label them as moving objects. We propose two different algorithms to detect the MDP.
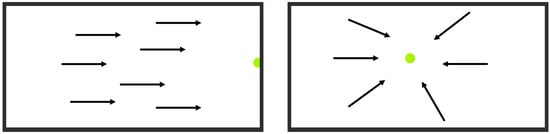
Figure 4.
Camera motion models. The arrows represent flow vectors, and the green dot represents the MDP point.
3.4.1. Pose Projection Algorithm
Let us express the position of the MDP on the digital image with K = (). In the algorithm that we propose to detect the K point, we utilize the pose information that we obtain by using all flow vectors that belong to moving and stable feature points. The matrix, which expresses the pose angle between consecutive images, consists of the , , and angles it has in the x, y, and z axes. In the case of an FT motion, the K is expected to be near the image center. According to the magnitudes of the angles that the motion has in the x and y axes, the camera motion direction point K = () moves away from the image center. Distances of the K point from the center increase horizontally and vertically according to the magnitudes of the angles in the mentioned axes. Certain threshold angle values correspond to the horizontal and vertical image boundaries of the and points. The algorithm that detects the K point by utilizing the linear distributions of these threshold values is given Algorithm 1: follows:
| Algorithm 1: Pose Projection algorithm | |
| 1: | if then |
| 2: | () or () |
| 3: | else |
| 4: | = |
| 5: | end if |
| 6: | if then |
| 7: | () or () |
| 8: | else |
| 9: | = |
| 10: | end if |
In this algorithm, represents the threshold angle value at which the rotation angle on the z axis coincides with the horizontal position of the point on the right and left edges of the image frame, while represents the threshold angle value at which the vertical position coincides with the lower and upper limits of the image frame. These threshold values determine the positions of the camera movement direction point on the image, as shown in Figure 5. Threshold values vary according to image dimensions and camera focal length.
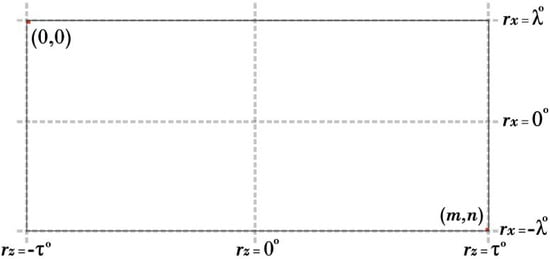
Figure 5.
Pose projection algorithm illustration.
In this study, and are determined empirically for the camera used in the TUM RGB-D dataset and are kept fixed across all experiments. Specifically, was selected from the range and from the range based on preliminary experiments evaluating stability and classification consistency. A geometric derivation of these thresholds based on camera intrinsics (focal length and image size) is possible; however, in this work we adopt an empirical calibration strategy to maintain simplicity and robustness.
3.4.2. Median Flow Angles Algorithm
In the algorithm that we propose to detect the K point, we estimate the angles that all flow vectors make with the candidate K point by evaluating them. According to the motion model, the flow vectors should have a natural direction distribution. In cases where the z axis component of the displacement vector is positive, the angle that the flow vectors will make with the K point should be close to . On the other hand, when is negative, this angle should be close to . In order to detect the most suitable K point, we find the median S of the angle values between the flow vectors and the candidate K point as follows:
Trying all pixel locations in the image as a candidate K point will give the most accurate result. However, this is inefficient in terms of processing load. Instead, it is more practical to try the K point within certain slices starting from the starting point of the image. As the lengths of these slices increase, a point farther from the ideal K point will be detected. Determining an optimal step range will vary depending on the computer structure used and processing priorities.
3.5. Detection of Moving Objects
Feature points are classified as static or dynamic based on the angular relationship between their optical flow vectors and the motion direction point . For static scene points, the observed optical flow is induced solely by camera motion and is therefore geometrically consistent with the direction defined by . As a result, the angle between the optical flow vector and the vector pointing toward remains close to either or , depending on the direction of camera translation.
Specifically, when the camera undergoes forward translational motion (), optical flow vectors of static points tend to point toward the motion direction point, resulting in angles close to . Conversely, during backward motion (), the flow vectors diverge from , yielding angles close to . In contrast, feature points belonging to independently moving objects exhibit additional motion components, causing their optical flow vectors to deviate from this global motion pattern and produce angles that fall outside the expected range for static points.
We denote by the angle between each optical flow vector and the vector pointing toward the motion direction point . Based on this formulation, feature points are classified as follows:
where i denotes the feature point index, represents the angular threshold, and and denote the sets of dynamic and static feature points, respectively. Rather than using a fixed threshold for all feature points, we adapt the threshold based on the spatial distance between each flow vector and the motion direction point . This adaptation accounts for the fact that flow vectors aligned with the same global motion may still exhibit small angular variations depending on their image location.
Accordingly, a distance-dependent angular tolerance is introduced, and the effective threshold for each feature point is defined as
where denotes the pixel distance between the ith feature point and , and l is the diagonal length of the image in pixels. The cosine function provides a smooth and bounded adjustment of the threshold, allowing a slightly higher tolerance for points closer to the motion direction point while preventing excessive relaxation for distant points. This formulation yields a more robust separation between static and dynamic feature points.
3.6. Design Rationale
The design choices of the proposed method are guided by the objective of achieving robust dynamic feature suppression while maintaining real-time performance and broad applicability across monocular platforms. Optical flow is selected as the primary motion cue because it provides direct, frame-to-frame motion information without requiring scene reconstruction or prior semantic knowledge.
Rather than relying on flow magnitude, which is highly sensitive to depth variations and camera speed, the proposed approach exploits the angular consistency of flow vectors with respect to the motion direction point (MDP). This choice enables reliable discrimination between camera-induced motion and independently moving objects, even when their motion magnitudes are similar. The motion direction point is introduced to represent the dominant global motion pattern caused by camera translation in the image plane. By formulating the classification problem in terms of angular deviation from this global motion model, the method avoids the need for object-level segmentation or learning-based motion priors.
The use of an adaptive angular threshold further improves robustness by accounting for the spatial relationship between feature points and the MDP, where angular sensitivity naturally increases near the motion center. Finally, the proposed algorithm is implemented as a front-end enhancement to ORB-SLAM to ensure compatibility with a widely adopted feature-based SLAM pipeline while preserving real-time performance without relying on computationally expensive deep learning components.
4. Experiments
In this section, we demonstrate the performance of our proposed method using the public TUM RGB-D dataset. Initially, we distinguish the flow vectors of dynamic feature points. We detected the K-point using our two different proposed MDP detection algorithms. These two algorithms have several advantages over each other. The Pose Projection algorithm is more advantageous in terms of processing speed. Because it uses pose information directly rather than calculating the average angle values of all flow vectors with the candidate K-point, the computational overhead is lower. However, the Median Flow Angles algorithm provides more accurate location determination by directly determining the K point based on the direction of the flow vectors. The pose error of the Pose Projection algorithm is particularly high when the number of dynamic feature points is large, and this increases the error. We obtained our experimental results based on the K-points detected using the Median Flow Angles algorithm.
Our experimental results primarily reflect the distinction between dynamic and static points. Then, we perform pose estimations using only the feature points we labeled as static. We integrate our proposed method with the ORB-SLAM algorithm and compare the trajectory results. All experiments were conducted on an HP Pavilion 15 laptop equipped with an Intel Core i5 CPU running at 2.4 GHz and 16 GB of RAM. No dedicated GPU was used during the experiments. The proposed method was implemented in MATLAB R2023a. All experiments were conducted offline using monocular RGB image sequences from the TUM RGB-D dataset.
4.1. Evaluations of Dynamic Feature Points Detection
Figure 6 presents example visual results obtained from three different video sequences, each represented by four sample image pairs. In each pair, the top image illustrates the optical flow vectors along with the detected K point, which is highlighted using a yellow circular marker, while the bottom image depicts the feature points labeled as either static or dynamic. Dynamic points are indicated in green, while static points are shown in red. It can be seen that feature vectors belonging to moving people are generally labeled as dynamic. Feature points belonging to people who were expected to be moving but were not were successfully labeled as static. While semantic methods typically label feature vectors belonging to objects expected to be moving entirely dynamically, we can see that our proposed method successfully detects features belonging to objects that are actually moving. We also succeeded in accurately dynamically labeling feature points belonging to moving chairs. This allows us to successfully label objects based on whether they are moving or not, without resorting to object recognition. Sudden changes in the environment, such as the abrupt appearance of moving objects, are also handled by the proposed method. As illustrated in Figure 6, in the fr3/w/rpy sequence (first row), a person suddenly enters the scene, causing an abrupt change in the observed motion pattern. Although such abrupt events may cause transient misclassifications in the immediately following frame, the angle-based consistency check enables the system to quickly adapt, and stable static/dynamic separation is typically recovered within a few frames.

Figure 6.
Optical flow vectors of feature points, K point representing MDP, and static/dynamic labeled feature points.
We used a binary classification method to quantitatively evaluate dynamic or static point detections. We count feature points in images as static/dynamic and true/false as follows:
- TP (true positive): Green-labeled dynamic feature points.
- FP (false positive): Green-labeled static feature points.
- TN (true negative): Red-labeled static feature points.
- FN (false negative): Red-labeled dynamic feature points.
To compute the quantitative evaluation metrics (TP, FP, TN, FN), ground-truth dynamic and static labels for feature points are required. Since the TUM RGB-D dataset does not provide per-feature motion annotations, ground-truth labels were generated manually for evaluation purposes. Specifically, for each evaluated sequence, feature points were visually inspected and labeled as static or dynamic based on their association with moving objects observed in the image frames (e.g., humans or independently moving entities) and their consistency across consecutive frames. Feature points consistently attached to the background structure were labeled as static, while those located on moving objects were labeled as dynamic. For each dataset sequence, manual annotations were performed on 40 representative image frames, with feature points labeled consistently across all sequences by the authors. This manual labeling process was applied only for quantitative evaluation and was not used at any stage of the proposed algorithm. Although manual annotation is time-consuming, it provides a reliable reference for assessing the correctness of dynamic feature detection in the absence of publicly available per-feature ground truth.
We calculated the detection of dynamic and static points with some quantitative metrics. We measured the detection of dynamic and static points using numerical metrics: accuracy (Ac), precision (Pr), True Positive Rate (TPR), and True Negative Rate (TNR). Ac indicates the percentage of all predictions that were correct. Pr indicates the accuracy rate of positive predictions. TPR indicates the rate of correct prediction of true positives. TNR indicates the rate of correct prediction of true negatives. These metrics are calculated as follows:
Quantitative results for three different test sequences are shown in Table 1. Both the example images in Figure 6 and the numerical results in the table demonstrate that we can distinguish dynamic feature points with high accuracy. Feature points on moving people are detected dynamically in images of movement. Feature points on still bodies and limbs are also often labeled as static. Dynamic feature points are detected not only in human movements but also in inanimate objects. However, some false detections are also possible. These errors are largely due to optical flow calculations.

Table 1.
Numerical performance values of dynamic feature point detection.
4.2. Integration to ORB-SLAM
In this section, we evaluate the integration of our proposed method into the ORB-SLAM algorithm. With the detection of dynamic feature points, we can now perform pose estimation using only static feature points. We test the ORB-SLAM method both without and with our proposed method. Figure 7 shows the trajectories generated for the three different video sequences. In the left column, the plots generated without applying the proposed method are highlighted with the label ’without’. The figures in the right column are plots obtained using our proposed method and are indicated with the label ’with’. The ground truth is shown with the blue line. The estimated trajectories are shown with the red line. The green lines represent the differences between the actual and estimated positions.
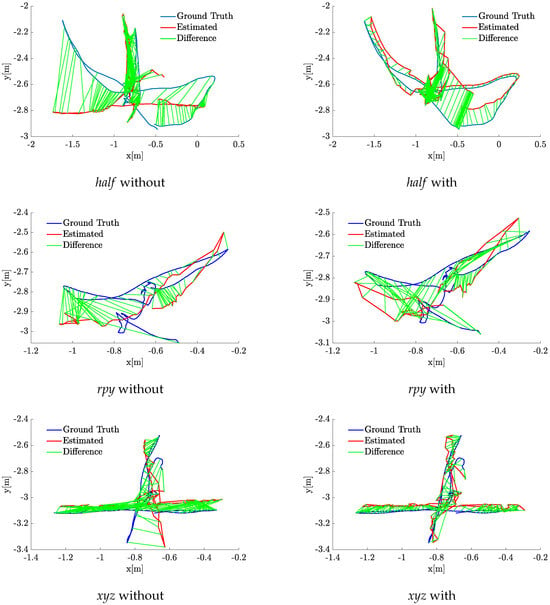
Figure 7.
Output trajectories with and without proposed method in meters.
Visual results on trajectories show that integrating our proposed method into ORB-SLAM reduces the error in dynamic environments. To present a quantitative evaluation of the improvement, we discuss the concepts of absolute trajectory error (ATE) and Rotational Pose Error (RPE). ATE represents vectorial pose changes, while RPE represents angle changes between poses. We calculate the Root Mean Square Error (RMSE) and standard deviation (SD) to determine the error values by comparing the obtained trajectory outputs with the ground truth. Table 2 shows the ATE results. An improvement is observed in RMSE and SD values for all sequences with the proposed method. Although direct access to the internal cost function of ORB-SLAM is not available, the effect of dynamic feature suppression on the optimization process is indirectly reflected in standard trajectory-level metrics such as ATE. Since ORB-SLAM minimizes reprojection error through nonlinear optimization, improvements in ATE indicate a reduction in the underlying optimization cost. The consistent decrease in ATE across dynamic sequences therefore demonstrates the positive impact of the proposed front-end filtering on the SLAM cost minimization process.

Table 2.
ATE results in meters. The better results are highlighted in bold.
Table 3 shows the Rotational Pose Errors (RPEs) in terms of deg/s using our proposed method. We examine the amount of error in the angle values of the poses estimated between consecutive key frames. Improvements in RMSE and SD values are observed with our proposed method.

Table 3.
RPE results in deg/s. The better results are highlighted in bold.
Table 2 and Table 3 show the ATE and RPE results obtained with and without our proposed method. Better values are marked in bold. For all three sequences, the ORB-SLAM method provided better trajectory estimation in dynamic environments. The ATE results comparing our proposed method with other methods are shown in Table 4.

Table 4.
ATE comparison with other methods. The best results are highlighted in bold.
Table 4 summarizes the overall performance of the proposed method. Although RDS-SLAM [25] achieves higher accuracy in the half and xyz sequences, it relies on semantic information to explicitly label dynamic objects. In contrast, the proposed method is purely geometry-based and does not require semantic segmentation or object-level motion labels. These different design choices reflect a trade-off between accuracy and reliance on high-level semantic priors. A comprehensive evaluation across a broader range of dynamic object types and motion patterns is left as future work.
4.3. Robustness to Image Noise
To analyze the robustness of the proposed method against disturbances in the optical channel, we evaluate its performance under additive image noise. Gaussian noise with zero mean and different standard deviations is injected into the input images, and the dynamic feature detection performance is re-evaluated using the same evaluation protocol. The experiments are conducted on the same set of manually annotated frames used in the quantitative analysis to ensure consistency. Both quantitative and qualitative results are reported.
Table 5 reports the classification performance under increasing noise levels. While a gradual decrease in accuracy and precision is observed as the noise level increases, the proposed method maintains stable performance under moderate noise.

Table 5.
Effect of Gaussian image noise on dynamic feature point detection accuracy.
Figure 8 provides a qualitative illustration of the effect of Gaussian noise on dynamic feature point detection. The same image frame is shown with noise levels of , 10, and 15, where static and dynamic feature points are marked in red and green, respectively. Despite increased noise, most dynamic regions are consistently identified, although some misclassifications appear at higher noise levels.

Figure 8.
Effect of Gaussian noise on dynamic feature point detection. Static and dynamic feature points are shown in red and green, respectively. The same image frame is used in all cases to isolate the effect of noise.
4.4. Effect of Camera Speed Variation
Camera speed has a direct influence on the magnitude of optical flow vectors, which may degrade the performance of methods that rely solely on flow magnitude thresholds. In contrast, the proposed approach primarily exploits the angular consistency between optical flow vectors and the motion direction point (MDP), rather than their absolute magnitudes. As a result, variations in camera speed mainly affect the length of flow vectors, while their directional relationship with the MDP remains largely preserved for static scene points.
Experimental results across different TUM sequences implicitly include variations in camera motion speed, such as slow translational motion in the half sequence and more aggressive motion in the xyz and rpy sequences. Despite these variations, the proposed method maintains stable dynamic feature suppression and trajectory estimation performance, indicating robustness to camera speed changes.
These observations support the claim that the proposed angle-based formulation is less sensitive to speed variations compared to magnitude-based optical flow filtering approaches, making it suitable for real-world scenarios involving non-uniform camera motion.
4.5. Failure Case Analysis
Although the proposed method demonstrates robust performance in dynamic environments, certain failure cases can be observed. First, inaccuracies in optical flow estimation, particularly under low-texture regions or strong image noise, may lead to incorrect angular measurements and cause misclassification of static feature points as dynamic. This effect becomes more pronounced when Gaussian noise is added to the input images, as discussed in the noise robustness analysis.
Second, sudden environmental changes, such as the abrupt appearance of a moving person in the scene (see Figure 6, fr3/w/rpy sequence), may temporarily disturb the global motion pattern. In such cases, feature points located near the motion direction point are more sensitive to small flow deviations, which can result in false dynamic detections in a limited number of frames.
Finally, combined camera rotation and translation can introduce complex optical flow fields that deviate from the ideal radial model assumed by the proposed angle-based criterion. While the method remains effective in most practical scenarios, extreme rotational motions may reduce the separability between static and dynamic flow vectors.
These failure cases highlight the inherent limitations of geometry-based dynamic feature detection methods and motivate future work on adaptive thresholding and the integration of complementary motion cues.
5. Conclusions
In this study, we proposed a lightweight and geometry-based method for detecting dynamic feature points to improve VSLAM performance in dynamic environments. The proposed approach relies solely on optical flow information extracted from monocular RGB images and does not require semantic segmentation, depth sensors, or learning-based models. As a result, it offers a computationally efficient and cost-effective alternative suitable for real-time robotic applications. The method was integrated into the ORB-SLAM framework and evaluated on multiple dynamic sequences from the TUM RGB-D dataset. Quantitative results demonstrate consistent improvements in trajectory estimation accuracy when dynamic feature points are filtered. Specifically, the proposed method achieved relative reductions in ATE RMSE of approximately 45% on the fr3/w/half sequence, 37% on fr3/w/rpy, and 37% on fr3/w/xyz compared to the baseline system without dynamic feature filtering. These results confirm that removing motion-inconsistent feature points using optical flow significantly enhances SLAM robustness in the presence of dynamic objects. Additional experiments further showed that the proposed method maintains stable performance under moderate image noise and sudden changes in the scene, indicating robustness to practical visual disturbances commonly encountered in real-world environments. All parameters were kept fixed across sequences, and no per-scene tuning was applied, demonstrating consistent behavior under varying motion patterns. Despite these promising results, the proposed method has certain limitations. In particular, reliably identifying feature points belonging to objects that move in the same direction as the camera remains challenging, as such motion can produce optical flow patterns similar to those of static background points. Addressing this ambiguity while preserving the monocular and geometry-based nature of the approach constitutes an important direction for future work. Further improvements may be achieved by incorporating additional motion constraints or temporal consistency cues to better handle complex and highly correlated motion scenarios. In addition, while the evaluation was conducted on standard indoor benchmark sequences, extending the experimental validation to larger-scale and more diverse environments remains an important direction for future work. Overall, this work demonstrates that optical flow-based dynamic feature filtering can serve as an effective and efficient mechanism for improving VSLAM performance in dynamic environments, offering a practical alternative to computationally intensive learning-based approaches.
Author Contributions
Conceptualization, S.D. and F.A.; methodology, S.D.; software, S.D.; validation, F.A. and S.D.; formal analysis, S.D.; investigation, F.A.; resources, S.D.; data curation, S.D.; writing—original draft preparation, S.D.; writing—review and editing, S.D.; visualization, S.D.; supervision, F.A.; project administration, F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. The TUM RGB-D dataset used in this work is openly available at: https://vision.in.tum.de/data/datasets/rgbd-dataset (accessed on 27 November 2025).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; the collection, analysis, or interpretation of data; the writing of the manuscript; or the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| SLAM | Simultaneous Localization and Mapping |
| VSLAM | Visual Simultaneous Localization and Mapping |
| ORB | Oriented FAST and Rotated BRIEF |
| RGB | Red Green Blue |
| MDP | Motion Direction Point |
| TP | True Positive |
| FP | False Positive |
| TN | True Negative |
| FN | False Negative |
| Ac | Accuracy |
| Pr | Precision |
| TPR | True Positive Rate |
| TNR | True Negative Rate |
| ATE | Absolute Trajectory Error |
| RPE | Relative Pose Error |
| FT | Full Translation |
| FR | Full Rotation |
References
- Zheng, S.; Wang, J.; Rizos, C.; Ding, W.; El-Mowafy, A. Simultaneous localization and mapping (slam) for autonomous driving: Concept and analysis. Remote Sens. 2023, 15, 1156. [Google Scholar] [CrossRef]
- Alqobali, R.; Alshmrani, M.; Alnasser, R.; Rashidi, A.; Alhmiedat, T.; Alia, O.M. A survey on robot semantic navigation systems for indoor environments. Appl. Sci. 2023, 14, 89. [Google Scholar] [CrossRef]
- Ebadi, K.; Bernreiter, L.; Biggie, H.; Catt, G.; Chang, Y.; Chatterjee, A.; Denniston, C.E.; Deschênes, S.P.; Harlow, K.; Khattak, S.; et al. Present and future of slam in extreme underground environments. arXiv 2022, arXiv:2208.01787. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 834–849. [Google Scholar]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2320–2327. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Bay, H. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2564–2571. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 225–234. [Google Scholar]
- Saputra, M.R.U.; Markham, A.; Trigoni, N. Visual SLAM and structure from motion in dynamic environments: A survey. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Endres, F.; Hess, J.; Engelhard, N.; Sturm, J.; Cremers, D.; Burgard, W. An evaluation of the RGB-D SLAM system. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1691–1696. [Google Scholar]
- Karam, S.; Lehtola, V.; Vosselman, G. Simple loop closing for continuous 6DOF LIDAR&IMU graph SLAM with planar features for indoor environments. ISPRS J. Photogramm. Remote Sens. 2021, 181, 413–426. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, Q.; Tang, Y.; Liu, S.; Han, H. Blitz-SLAM: A semantic SLAM in dynamic environments. Pattern Recognit. 2022, 121, 108225. [Google Scholar] [CrossRef]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Qiu, X.; Rong, Z.; Zou, X. Dynamic-SLAM: Semantic monocular visual localization and mapping based on deep learning in dynamic environment. Robot. Auton. Syst. 2019, 117, 1–16. [Google Scholar] [CrossRef]
- Bescos, B.; Campos, C.; Tardós, J.D.; Neira, J. DynaSLAM II: Tightly-coupled multi-object tracking and SLAM. IEEE Robot. Autom. Lett. 2021, 6, 5191–5198. [Google Scholar] [CrossRef]
- Engelhard, N.; Endres, F.; Hess, J.; Sturm, J.; Burgard, W. Real-time 3D visual SLAM with a hand-held camera. In Proceedings of the RGB-D Workshop on 3D Perception in Robotics at the European Robotics Forum, Vasteras, Sweden, 8 April 2011. [Google Scholar]
- Yu, C.; Liu, Z.; Liu, X.J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A semantic visual SLAM towards dynamic environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1168–1174. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, S. Sad-slam: A visual slam based on semantic and depth information. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; IEEE: Piscataway, NJ, USA, 2020; pp. 4930–4935. [Google Scholar]
- Liu, Y.; Miura, J. RDS-SLAM: Real-time dynamic SLAM using semantic segmentation methods. IEEE Access 2021, 9, 23772–23785. [Google Scholar] [CrossRef]
- Peng, Y.; Xv, R.; Lu, W.; Wu, X.; Xv, Y.; Wu, Y.; Chen, Q. A high-precision dynamic RGB-D SLAM algorithm for environments with potential semantic segmentation network failures. Measurement 2025, 256, 118090. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Pan, W. Dynamic RGB-D SLAM based on static probability and observation number. IEEE Trans. Instrum. Meas. 2021, 70, 8503411. [Google Scholar] [CrossRef]
- Zhang, J.; Ke, F.; Tang, Q.; Yu, W.; Zhang, M. YGC-SLAM: A visual SLAM based on improved YOLOv5 and geometric constraints for dynamic indoor environments. Virtual Real. Intell. Hardw. 2025, 7, 62–82. [Google Scholar] [CrossRef]
- Scona, R.; Jaimez, M.; Petillot, Y.R.; Fallon, M.; Cremers, D. Staticfusion: Background reconstruction for dense rgb-d slam in dynamic environments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3849–3856. [Google Scholar]
- Zou, D.; Tan, P. Coslam: Collaborative visual slam in dynamic environments. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 354–366. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, J.H. Effective background model-based RGB-D dense visual odometry in a dynamic environment. IEEE Trans. Robot. 2016, 32, 1565–1573. [Google Scholar] [CrossRef]
- Dai, W.; Zhang, Y.; Li, P.; Fang, Z.; Scherer, S. Rgb-d slam in dynamic environments using point correlations. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 373–389. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Yebes, J.J.; Almazán, J.; Bergasa, L.M. On combining visual SLAM and dense scene flow to increase the robustness of localization and mapping in dynamic environments. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1290–1297. [Google Scholar]
- Cheng, J.; Sun, Y.; Meng, M.Q.H. Improving monocular visual SLAM in dynamic environments: An optical-flow-based approach. Adv. Robot. 2019, 33, 576–589. [Google Scholar] [CrossRef]
- Kerl, C.; Sturm, J.; Cremers, D. Dense visual SLAM for RGB-D cameras. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2100–2106. [Google Scholar]
- Xu, G.; Zhang, Z. Epipolar Geometry in Stereo, Motion and Object Recognition: A Unified Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 6. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.