Lattice-Based Group Signature with VLR for Anonymous Medical Service Evaluation System

Abstract

The medical industry has made significant advancements in recent years. However, the lack of accountability in medical management has resulted in systemic deficiencies, which have adversely affected patient trust and contributed to an increase in medical disputes. As a result, there is a growing emphasis on managing the quality of medical services, particularly in enhancing patient experience. To address these challenges, we propose a new system for evaluating health services. This system will allow patients to anonymously rate the services they receive while also providing doctors the opportunity to appeal specific reviews. The hospital handles the evaluations and appeals through the management of the cloud platform. We propose a new scheme to assist the work of the platform, which is a lattice-based group signature with verifier-local revocation (VLR-GS). Most of the work on VLR-GS has focused on the random oracle model (ROM) or using non-interactive zero-knowledge proofs (NIZKs). Our construction is anonymous and traceable in the standard model under the hardness of the learning with errors problem and short integer solution problem. Furthermore, theoretically analyzing it has practical significance in both security and efficiency. In conclusion, the proposed scheme establishes a secure and privacy-oriented platform for an anonymous medical service evaluation system, with the goal of fostering patient trust and improving hospital service quality within the healthcare sector.

1. Introduction

The World Health Organization (WHO) has made the improvement of healthcare quality a global priority, urging countries around the world to take active measures to continuously improve the quality of medical services [1]. Quality is essential to healthcare operations and serves as the fundamental standard for testing and measuring medical service work. In 1986, the United States introduced the concept of “patient-centered”, to provide quality medical services. This approach aims to create an environment that prioritizes the needs of patients and their families as much as possible. In addition, countries such as the United Kingdom, Switzerland, Sweden, and Germany have conducted patient experience surveys. These surveys are valuable tools for government oversight and help guide patient choices in healthcare facilities. Management of medical service quality includes all components that influence healthcare quality, such as planning, organization, coordination, and service assurance. This is critical for effective hospital management and is an important symbol of scientific management. The quality and management of medical services are completed through the evaluation of patients. Management has become an important work that modern hospitals must do to improve and improve the quality of medical services. However, due to the lack of medical management, medical deficiencies have been caused, patient trust has been reduced, and medical disputes have intensified.

To solve these problems and address privacy concerns, this article designs an anonymous medical service evaluation system for patients. The system is built on a cloud platform and emphasizes a “patient-centered” approach. Its design prioritizes safety, fosters a positive service culture, streamlines the service process, enhances the service environment, and maintains cost control. In this system, as Figure 1, patients make appointments on a cloud platform. After describing your condition to the doctor, the doctor returns the diagnosis. Patients who have completed the consultation on the same day will be anonymously evaluated as a group and uploaded to the cloud platform through a secure channel. Doctors can also appeal questionable reviews. The hospital utilizes a cloud platform to manage patient evaluations and gather feedback from doctors, then revokes malicious or erroneous evaluations of medical services. The system ensures the quality of medical services and helps improve the level of medical and health technology.

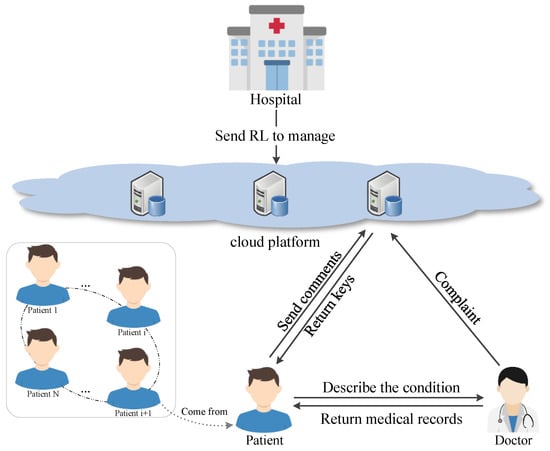
Figure 1. System model diagram.

Actively use cloud computing technology to optimize the service process, improve the long-term mechanism to resolve medical disputes, and build a harmonious doctor–patient relationship. For this threat, we propose a novel VLR-GS scheme to improve the performance of the system’s cloud platform. Group signature is a type of cryptographic tool that enables group users to sign messages anonymously while ensuring traceability. “Who the signature came from” is secret, but the manager might use some information to find out who, if necessary, thus demonstrating the responsibility of the group members for the signature.

Many group signatures based on number theory assumptions exhibit significant vulnerabilities when confronted with the capabilities of quantum computers. In contrast, lattice-based GS schemes have gradually gained attention because of their immunity to quantum adversaries, high computational efficiency, and provable security. The first such scheme was constructed through the pioneering work of Gordon et al. [2]. The emergence of lattice-based cryptography signifies a compelling alternative to the traditional, which excels in simple algebraic operations and a strong mathematical foundation. It demands exponential time for quantum adversaries to breach, positioning it as a formidable choice for secure communication and data protection, even in the worst case.

In multi-user signature systems, being able to revoke membership is crucial for blocking signatures from members who have misbehaved or voluntarily left the group. For large-scale groups, the VLR mechanism is considered to be more flexible. Figure 2 illustrates the specific flow. It involves maintaining a revocation list (RL) containing tokens for revoked users. The list is regularly updated and only provided to the verifier. According to the list RL, the verifier can test the signature’s legitimacy. If unsuccessful, the verifier rejects the signature.

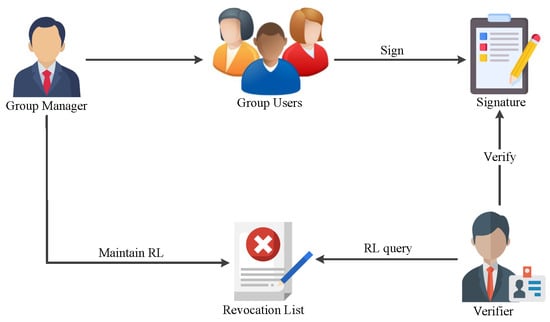
Figure 2. The VLR mechanism.

1.1. Contribution

Our major contribution is threefold, which are as follows:

(1)

The quality management of medical services is the eternal theme of health work. The medical service evaluation system we propose enhances traditional management approaches. Patients can upload their evaluations to the cloud platform after consultation in this system. Hospitals can then use this platform to analyze patient data for improved management. When doctors have questions about reviews, hospitals can utilize the platform to assist.

(2)

To assist the platform to work better, we propose a novel scheme, which is a lattice-based VLR-GS. With this scheme, patients become part of a group that includes patients who have completed their care within a specific day and can anonymously evaluate their experiences. As a group manager, the hospital can verify and manage user-generated reviews. If any review is found to be illegitimate or malicious, appropriate actions can be taken. In addition, doctors can file complaints, and, if necessary, the hospital can use the group private key to identify the reviewer.

(3)

We instantiate the GS scheme into a concrete construction, using the framework of [3]. This scheme can be proven secure on the SIS and LWE problems, and we demonstrated that the scheme in the standard model (SM) ensures anonymity and unforgeability. And through proper analysis, our scheme performs well in the same type of scheme theoretically. This approach balances security with its efficiency.

1.2. Related Work

The initial security model presented by [4] outlines an anonymous static group signature. Their research demonstrated that trapdoor permutations are sufficient for constructing GS schemes, as these permutations imply NIZKs [5,6,7]. And [5] addresses two open problems related to NIZKs. Furthermore, their results also indicate that group signatures can be constructed from factoring-based assumptions. Moreover, Camenisch and Groth [8] established that one-way function (OWF) and NIZKs imply group signature schemes. Most current works, such as [9,10,11], construct group signature schemes with the help of NIZKs.

Gordon et al. [2] were the first to propose a lattice-based GS in ROM. The scheme was built upon [4] and further integrated zero-knowledge proof and lattice. However, this scheme had large key sizes and signatures. Several works [12,13,14,15,16] have proposed simpler and more efficient solutions. The majority of lattice-based schemes have been developed using two primary methods. The first method involves utilizing one access structure and knowledge argument, as identified in [13,14,17,18]. Despite extensive development, there are still no NIZKs specifically designed for GS in the standard model. The second method involves an ABS scheme with distinct properties utilized to build the GS scheme, as demonstrated in [3]. This method has the advantage of being more suitable for a lattice. The previous post-quantum security GS with a forward security scheme was established by Ling et al. [19] from the lattice in ROM and followed the classical framework, so it was proved using NIZKs. Through the framework of [3], ref. [20] realizes the first lattice FS-GS in SM, and its public key and signature length are linearly related to the number of users. Ref. [21] uses the Bonsai tree and proposes the first lattice-based fully dynamic GS scheme without NIZKs based on [3].

The mechanism of VLR for group signatures, originally formalized by Boneh and Shacham [22], provides signers with the benefit of not constantly updating information about revoked users, making it practical for large user populations. This concept has been further explored and expanded upon by [23,24,25,26,27]. Most existing VLR-GS schemes use bilinear maps and will become vulnerable once quantum computers are developed. The lattice-based VLR-GS was proposed in the work of [28], making it the first scheme to be considered quantum-resistant. Subsequently, many schemes were proposed, such as [18,29,30,31].

1.3. Outline of the Article

In Section 1, we review the related works, and in Section 2, we introduce the relevant notations and definitions. Section 3 presents a new VLR-GS scheme designed for the medical service evaluation system, along with its security proofs. Section 4.1 offers a detailed overview of the lattice-based construction of this scheme, which will serve as the foundation for our comparative analysis in Section 4.2. Finally, in the conclusion, we summarize the main points of the text and suggest potential directions for future research.

2. Preliminaries

Notations. We say that $\kappa$ denotes the main security parameter throughout this scheme, while the maximum number of members $N=2^l=poly\left(\kappa \right)$. If matrix $\mathbf{A}\in {\mathbb{R}}^{n\times m}$ and $\mathbf{B}\in {\mathbb{R}}^{n\times m^{\prime }}$ denotes the concatenation as $\left[\mathbf{A}\Vert \mathbf{B}\right]\in {\mathbb{R}}^{n(m+m^{\prime })}$. Then $\parallel ·\parallel$ denotes the euclidean norm $l_2$, and ${\parallel ·\parallel }_{\infty }$ denotes the infinity norm $l_{\infty }$. Table 1 lists other symbols.

Table 1. Notations.

Notation	Definition
q	Prime number
$\mathbb{Z}$	Set of integers
$\mathbb{R}$	Set of real numbers
$\mathbf{a},\mathbf{b}$	Vectors
$\mathbf{A},\mathbf{B}$	Matrices
$\stackrel{\$}{\leftarrow }$	Sampling uniformly at random
$loge$	Logarithm of e with base 2
$\mathcal{O}$, $\tilde{\mathcal{O}}$	Asymptotic notations
$\mathcal{M}$	The message space
$\mathsf{\Sigma }$	The signature
F	Circuit family

2.1. Lattice

This section we introduce some facts on lattices that are needed [32,33].

Definition 1. 

For positive integers $n,m,q\ge 2$, a randomly chosen matrix $\mathbf{A}$ from ${\mathbb{Z}}_q^{n\times m}$, a lattice known as the m-dimensional q-ary orthogonal lattice, can be characterized:

$${\mathsf{\Lambda }}_q^{\perp }\left(\mathit{A}\right)=\{\mathbf{e}\in {\mathbb{Z}}^m\mid \mathit{A}·\mathit{e}\equiv 0modq\}$$

For a positive scale parameter s, a vector $\mathbf{c}$∈${\mathbb{R}}^m$, and a given point c in the m-dimensional real space ${\mathbb{R}}^m$, the Gaussian function ${\rho }_{s,c}\left(\mathbf{e}\right)$, the discrete Gaussian distribution, can be rephrased:

$$D_{\mathsf{\Lambda },s,c}={\displaystyle \frac{{\rho }_{s,c}\left(\mathbf{e}\right)}{{\sum }_{\mathbf{e}\in \mathsf{\Lambda }}{\rho }_{s,c}\left(\mathbf{e}\right)}},\forall \mathbf{e}\in {\mathbb{Z}}^m$$

2.1.1. Hard Problems

We recall two assumptions of SIS and LWE. Their definition is from the work of [32,34]:

Definition 2 (The SIS Assumption).

Given a modulus q, assume a matrix $\mathbf{A}$∈${\mathbb{Z}}_q^{n\times m}$, which lacks full column rank modulo q. Additionally, a positive real number β is provided. Find the minimum non-zero integer solution $\mathit{x}$ to the modular q homogeneous linear equation system, $\mathit{Ax}=\mathbf{0}(modq)$, such that $\left|\right|\mathbf{x}\left|\right|\le \beta$.

Definition 3 (The LWE Assumption).

Here, we define the LWE problem in the following manner. First, randomly select a vector $\mathit{s}$∈${\mathbb{Z}}_q^n$, a random distribution χ over $\mathbb{Z}$. Let ${\mathit{A}}_{\mathit{s},\chi }$ denote a distribution generated by selecting $\mathit{A}$∈${\mathbb{Z}}_q^{n\times m}$ uniformly at random, then outputting $(\mathit{A},{\mathit{A}}^T\mathit{s}+\mathit{e}modq)$, where $\mathit{e}$$\stackrel{\$}{\leftarrow }$${\chi }^m$.

What can already be confirmed for SIS is that the problems are equally difficult as a certain worst-case problem, which means that with a nonnegligible probability, solving the $\mathrm{SIS}(n,m,q,\beta )$ problem is as challenging as solving the ${\mathrm{GapSVP}}_{\gamma }$ and ${\mathrm{SIVP}}_{\gamma }$ problems, with high probability in the worst-case situation. Regarding LWE, it follows that there exists an efficient sampleable $\beta$-bounded distribution $\chi$ such that the ${\mathrm{LWE}}_{n,q,\chi }$ problem is as challenging as the ${\mathrm{SIVP}}_{\gamma }$ problem.

2.1.2. Trapdoor

Hereafter, assume SampZ($\gamma$) is a sampling algorithm designed for discrete Gaussian distribution over $\mathbb{Z}$, with $\gamma$ greater than zero.

Definition 4 (Trapdoor).

Given a matrix $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$. For all $\mathbf{V}\in {\mathbb{Z}}_q^{n\times m_0}$, We designate ${\mathbf{A}}_{\gamma }^{-1}\left(\mathbf{V}\right)$ to be the distribution of $\mathbf{SampZ}{\left(\gamma \right)}^{m\times m_0}$ under the condition that $\mathbf{A}·{\mathbf{A}}_{\gamma }^{-1}\left(\mathbf{V}\right)=\mathbf{V}$. For any $\mathbf{V}$, a γ-trapdoor for $\mathbf{A}$ is a trapdoor that samples from ${\mathbf{A}}_{\gamma }^{-1}\left(\mathbf{V}\right)$ in polynomial time and denote this trapdoor by ${\mathbf{A}}_{\gamma }^{-1}$.

Here, we require a special gadget matrix $\mathbf{G}\in {\mathbb{Z}}_q^{n\times m}$, which is constructed by padding ${\mathbf{I}}_n\otimes (1,2,4,...,2^{⌈logq⌉})$ with additional zero columns. Many research studies have confirmed the validity of these properties [32,35,36,37,38].

Lemma 1 (Trapdoor Properties).

These properties are demonstrated by lattice trapdoors:

• If ${\mathbf{A}}_{\gamma }^{-1}$ is known, ${\mathbf{A}}_{{\gamma }^{\prime }}^{-1}$ can be obtained for any ${\gamma }^{\prime }\ge \gamma$.
• If ${\mathbf{A}}_{\gamma }^{-1}$ is known, ${[\mathbf{A} \Vert \mathbf{B}]}_{\gamma }^{-1}$ and ${[\mathbf{B} \Vert \mathbf{A}]}_{\gamma }^{-1}$ can be obtained.
• For $\mathbf{A}\in {\mathbb{Z}}_q^{n\times m}$ and $\mathbf{R}\in {\mathbb{Z}}^{m\times m}$, ${[\mathbf{AR}+\mathbf{G} \Vert \mathbf{A}]}_{\gamma }^{-1}$ can be obtained for $\gamma =m·{\parallel \mathbf{R}\parallel }_{\infty }·\omega \left(\sqrt{logm}\right)$.
• The statistical closeness of the distributions is shown to hold for any $\gamma \ge {\gamma }_0$:

  $$(\mathbf{A},{\mathbf{A}}_{\gamma }^{-1},\mathbf{U},\mathbf{V})\stackrel{\mathrm{stat}}{\approx }(\mathbf{A},{\mathbf{A}}_{\gamma }^{-1},{\mathbf{U}}^{\prime },{\mathbf{V}}^{\prime })$$
  In the above, $\mathbf{U}\stackrel{\$}{\leftarrow }\mathbf{SampZ}{\left(\gamma \right)}^{m\times m^{\prime }}$ and ${\mathbf{V}}^{\prime }\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{n\times m^{\prime }}$.

2.2. Fully Homomorphic Computation

We also introduce a pair of deterministic algorithms: $\mathbf{PubEval}$ and $\mathbf{TrapEval}$.

Lemma 2 (Fully Homomorphic Computation).

The algorithms exist and possess these important facts [39]:

• $\mathbf{PubEval}(\overrightarrow{\mathbf{B}},F)\to {\mathbf{B}}_F$: The algorithm takes as input a vector $\overrightarrow{\mathbf{B}}=[{\mathbf{B}}_1\parallel {\mathbf{B}}_2\parallel$ $\cdots \parallel {\mathbf{B}}_k]\in {\mathbb{Z}}_q^{n\times mk}$ and a circuit $F:{\{0,1\}}^k\to \{0,1\}$, then gets a matrix ${\mathbf{B}}_F\in {\mathbb{Z}}_q^{n\times m}$.
• $\mathbf{TrapEval}(\overrightarrow{R},F,x)\to {\mathbf{R}}_{F,x}$: The algorithm accepts a vector $\overrightarrow{\mathbf{R}}=[{\mathbf{R}}_1\parallel \cdots$ $\parallel {\mathbf{R}}_k]\in {\mathbb{Z}}_q^{n\times mk}$ which $\parallel {\mathbf{R}}_i{\parallel }_{\infty }\le \delta$, a circuit F, and a binary vector $x\in {\{0,1\}}^k$, it outputs a matrix ${\mathbf{R}}_{F,x}\in {\mathbb{Z}}_q^{n\times m}$. In particular, we have $\mathbf{PubEval}(\mathbf{A}\overrightarrow{\mathbf{R}}+x\otimes \mathbf{G})=\mathbf{A}{\mathbf{R}}_{F,x}+F\left(x\right)\mathbf{G}$, where $x\otimes \mathbf{G}=[x_1\mathbf{G}\parallel x_2\mathbf{G}\parallel$ $\cdots \parallel x_k\mathbf{G}]$.

2.3. One-Time Signatures

This section presents the lattice-based OTS constructions from chameleon hash functions built on preimage samplable (trapdoor) functions. Consider $H=(Gen,h,h^{-1})$ as the chameleon hash functions family and let $T_{e{k}_0,e{k}_1}:{\mathcal{Y}}_{ek}\to {\mathcal{M}}^{\prime }\subseteq {\mathcal{M}}_{e{k}_1}$ as a target collision-resistant function and $(e{k}_0,e{k}_1)$ as evaluation keys.

• $\mathrm{OTS}.\mathrm{KeyGen}\left(1^{\kappa }\right)$: Perform the following steps to generate $(ovk,osk)$:

  (1)

  Sample two pairs of matrices ${\mathbf{B}}_i\in {\mathbb{Z}}_q^{n\times m_1}$ and ${\mathbf{K}}_i\in {\mathbb{Z}}_q^{n\times m_2}$, where $i\in \{0,1\}$. Then, define $e{k}_i=({\mathbf{B}}_i,{\mathbf{K}}_i)$, and the trapdoor $t{d}_i\subset {\mathsf{\Lambda }}^{\perp }\left({\mathbf{K}}_i\right)$ is a short basis for the lattice whose parity-check matrix is ${\mathbf{K}}_i$.

  (2)

  Sample ${\mathbf{r}}_s^0$ and ${\mathbf{r}}_s^1$ from a discrete Gaussian over ${\mathbb{Z}}_q^{m_2}$.

  (3)

  Calculate $({\mathbf{z}}_0,{\mathbf{z}}_1)$, where ${\mathbf{z}}_0=h(e{k}_0,m_f,{\mathbf{r}}_s^0)={\mathbf{B}}_0·m_f+{\mathbf{K}}_0·{\mathbf{r}}_s^0$ and ${\mathbf{z}}_1=T_{e{k}_1,e{k}_0}\left(h(e{k}_1,m_f,{\mathbf{r}}_s^1)\right)=T_{e{k}_1,e{k}_0}({\mathbf{B}}_1·m_f+{\mathbf{K}}_1·{\mathbf{r}}_s^1)$. In this context, $m_f$ represents an arbitrary message in ${\mathcal{M}}_{e{k}_1}$, which may differ among signers.

  (4)

  Output $(ovk,osk)$, where $ovk=(e{k}_0,e{k}_1,{\mathbf{z}}_0)$ and $osk=(t{d}_0,t{d}_1,{\mathbf{r}}_0^s,{\mathbf{r}}_1^s,{\mathbf{z}}_1)$.

• $\mathrm{OTS}.\mathrm{Sign}(osk,m)$: Upon receiving m, computes the signature $\sigma =(h^{-1}(t{d}_1,m_f,r_s^1,m),$ $h^{-1}(t{d}_0,mf,r_s^0,z_1))=(\mathbf{r},{\mathbf{r}}^{\prime })$. The calculation process is as follows:

  (1)

  Sample $\mathbf{t}\in {\mathbb{Z}}^{m_2}$ such that ${\mathbf{K}}_1\mathbf{t}=h(e{k}_1,m_f,{\mathbf{r}}_s^1)-{\mathbf{B}}_1·m$. Then sample $\mathbf{v}$ using $SampD(t{d}_1,s,-\mathbf{t})$. We have $\mathbf{r}=\mathbf{t}+\mathbf{v}$.

  (2)

  Sample ${\mathbf{t}}^{\prime }\in {\mathbb{Z}}^{m_2}$ such that ${\mathbf{K}}_0{\mathbf{t}}^{\prime }=h(e{k}_0,m_f,{\mathbf{r}}_s^0)-{\mathbf{B}}_1·{\mathbf{z}}_1={\mathbf{z}}_0-{\mathbf{B}}_1·{\mathbf{z}}_1$. Then sample ${\mathbf{v}}^{\prime }$ using $SampD(t{d}_0,s,-{\mathbf{t}}^{\prime })$. We have ${\mathbf{r}}^{\prime }={\mathbf{t}}^{\prime }+{\mathbf{v}}^{\prime }$ and $h(e{k}_0,{\mathbf{z}}_1,{\mathbf{r}}^{\prime })=h(e{k}_0,m_f,{\mathbf{r}}_s^0)={\mathbf{z}}_0$.

• $\mathrm{OTS}.\mathrm{Vrfy}(ovk,m,\sigma )$: Given the input $(m,\sigma )$, accept if the condition

  $$h(e{k}_0,T_{e{k}_1,e{k}_0}\left(h(e{k}_1,m,\mathbf{r})\right),{\mathbf{r}}^{\prime })={\mathbf{z}}_0$$

  is satisfied, which is $h(e{k}_0,{\mathbf{z}}_1,{\mathbf{r}}^{\prime })={\mathbf{z}}_0$. Otherwise, reject.

It should be emphasized that the OTS scheme satisfies the SUF-CMA security, this concrete proof from [40].

2.4. VLR-GS

The definition in this section is based on Boneh and Shacham [22]. A VLR-GS includes the following algorithms:

• $\mathrm{VLR}.\mathrm{Setup}(1^n,1^N)\to (mpk,msk)$: Input the security parameter n, group size N. Then outputs the manager’s keys $(mpk,msk)$.
• $\mathrm{VLR}.\mathrm{KeyGen}(mpk,msk,i)\to (usk,grt)$: The group manager uses $(mpk,msk))$ to generate group public key $gpk$, user’s secret keys ${\left\{us{k}_i\right\}}_{i\in \left[N\right]}$ and revocation tokens ${\left\{gr{t}_i\right\}}_{i\in \left[N\right]}$. Note, the manager transmits $(us{k}_i,gr{t}_i)$ to user i in confidence.
• $\mathrm{VLR}.\mathrm{Sign}(mpk,us{k}_i,M)\to \mathsf{\Sigma }$: The signing algorithm works with $mpk$, ${gsk}_i$, and message M. Finally, the user gets their own signature $\mathsf{\Sigma }$.
• $\mathrm{VLR}.\mathrm{Vrfy}(mpk,\mathrm{RL},M,\mathsf{\Sigma })\to \top /\perp$: As given in the $mpk$, the revocation list (RL) is along with message–signature pairs $(M,\mathsf{\Sigma })$. Finally, outputs a result ⊤, which means that the signature is valid. Otherwise outputs ⊥.

The VLR-GS scheme is required to meet correctness, anonymity, and traceability.

Correctness: For the above scheme, we need to prove that the correctly generated signature $\mathsf{\Sigma }$ passes the verification algorithm. For all $mpk$ outputted by $\mathrm{VLR}.\mathrm{Setup}$ and $us{k}_i$, $gr{t}_i$ outputted by $\mathrm{VLR}.\mathrm{KeyGen}$, pairs $(M,\mathsf{\Sigma })$, we have

$$\mathrm{VLR}.\mathrm{Vrfy}(mpk,\mathrm{RL},M,\mathrm{VLR}.\mathrm{Sign}(mpk,us{k}_i,M))=\top \iff gr{t}_i\notin \mathrm{RL}$$

It should be emphasized that this scheme satisfies selfless anonymity and traceability, as shown by this concrete proof from [31].

3. VLR-GS for Medical Service Evaluation System

Focusing on the challenges currently existing schemes face, this article introduces an innovative lattice-based VLR-GS scheme designed to resist quantum attacks for a medical service evaluation system with a cloud platform.

3.1. Definition of the Scheme

Here, we give a generic definition from an OTS in Section 2.3 with strong unforgeability, an OWF scheme with the underlying hard problem, and a secret key encryption scheme $\mathrm{SKE}=(\mathrm{SKE}.\mathrm{Setup},\mathrm{SKE}.\mathrm{KeyGen},\mathrm{SKE}.\mathrm{Enc},\mathrm{SKE}.\mathrm{Dec})$ and indexed ABS scheme requested in [3]. We need this ABS scheme $\mathrm{ABS}=(\mathrm{ABS}.\mathrm{Setup},\mathrm{ABS}.\mathrm{KeyGen},\mathrm{ABS}.\mathrm{Sign},\mathrm{ABS}.\mathrm{Vrfy})$ that can handle the function class ${\left\{C_{\kappa }\right\}}_{\kappa }$, which serves to hardwire $ovk$ to $\mathbf{ct}$ and $\mathbf{g}$. See the circuit design in Figure 3.

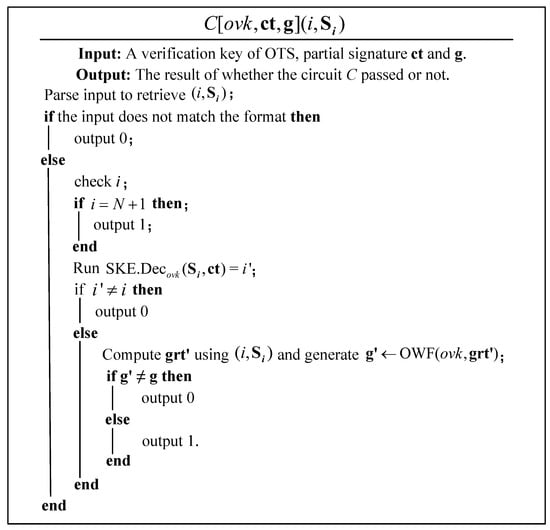
Figure 3. The design of the circuit.

The general construction of the VLR-GS scheme for the system is as follows:

• $\mathbf{Setup}(1^{\kappa },1^N)$: Input the security parameters, run $pp\leftarrow \mathrm{SKE}.\mathrm{Setup}\left(1^{\kappa }\right)$, $\left(mpk,msk\right)\leftarrow \mathrm{ABS}.\mathrm{Setup}\left(1^{\kappa },1^N\right)$. Output the public parameters $pp$ and the group manager’s keys $\left(mpk,msk\right)$.
• $\mathbf{KeyGen}\left(mpk,msk,i\right)$: For group member i, group manager runs:

  1.

  Compute ${\mathbf{S}}_i\leftarrow \mathrm{SKE}.\mathrm{KeyGen}\left(pp\right)$ and ${\mathbf{sk}}_i\leftarrow \mathrm{ABS}.\mathrm{KeyGen}(mpk,msk,i)$.

  2.

  Generate the revocation token ${\mathbf{grt}}_i$ using ${\mathbf{S}}_i$.

  Finally, group manager securely transmits ${usk}_i:=({\mathbf{S}}_i,{\mathbf{sk}}_i)$ and ${\mathbf{grt}}_i$ to user over secure channels.
• $\mathbf{Sign}\left(mpk,M,{usk}_i\right)$: Before signing message M, parse ${usk}_i\to \left({\mathbf{S}}_i,{\mathbf{sk}}_i\right)$ and sample $\left(ovk,osk\right)\leftarrow \mathrm{OTS}.\mathrm{KeyGen}\left(1^{\kappa }\right)$. Compute $\mathbf{ct}\leftarrow \mathrm{SKE}.{\mathrm{Enc}}_{ovk}\left({\mathbf{S}}_i,i\right)$, then generate $\mathbf{g}\leftarrow \mathrm{OWF}(ovk,{\mathbf{grt}}_i)$. Next, sample ${\sigma }_1\leftarrow \mathrm{ABS}.\mathrm{Sign}(mpk,{\mathbf{sk}}_i,M,C)$. Given ${\sigma }_1$ and run ${\sigma }_2\leftarrow \mathrm{OTS}.\mathrm{Sign}(osk,M \Vert {\sigma }_1)$. Finally, the user outputs $\mathsf{\Sigma }:=(ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$.
• $\mathbf{Vrfy}\left(mpk,\mathrm{RL},M,\mathsf{\Sigma }\right)$: Firstly, parse $\mathsf{\Sigma }\to (ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$ and validate $\mathbf{g}$ using RL. Then verify whether the given $\mathsf{\Sigma }$ is valid on M using $\mathrm{ABS}.\mathrm{Vrfy}$ and $\mathrm{OTS}.\mathrm{Vrfy}$.

The above ABS scheme is no-signing-query unforgeability, then it can be transformed into a new ${\mathrm{ABS}}^{\prime }$ that ensures co-selective unforgeability, following in [3].

The design of the system mainly focuses on “patient-centered”, and this scheme could significantly enhance the functionality of the evaluation platform. After a consultation, users have the opportunity to rate the doctor and the consultation process anonymously, ensuring their information remains confidential. This reflects the anonymity of the scheme. Hospitals, acting as administrators, can utilize the VLR feature of the solution to revoke access for users who post inappropriate comments. This reflects the revocable feature. Doctors have the ability to challenge questionable reviews, and hospitals can employ traceability to identify the individuals who left these reviews, thereby safeguarding the rights and interests of doctors. This reflects the traceability.

3.2. Security Analysis

The scheme meets the group signature security requirements set forth in [4].

3.2.1. Correctness

For the scheme in Section 3.1, we first need to prove that correctly generated $\mathsf{\Sigma }:=(ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$ passes $\mathbf{Vrfy}$. For ${\left\{{usk}_i\right\}}_{i\in \left[N\right]}$, ${\left\{{\mathbf{grt}}_i\right\}}_{i\in \left[N\right]}$ and group public key $mpk$ by $\mathbf{KeyGen}$, we have $\mathbf{Vrfy}(mpk,\mathrm{RL},M,\mathbf{Sign}(mpk,M,{usk}_i,{\mathbf{grt}}_i))=\top$. We can confirm the correctness of $\mathrm{OTS}$ by observing that $\mathrm{OTS}.\mathrm{Vrfy}(ovk,M \Vert {\sigma }_1,{\sigma }_2)=\top$. Additionally, $\mathrm{ABS}.\mathrm{Vrfy}(mpk,M,C,{\sigma }_1)=\top$ is supported by $C[ovk,\mathbf{ct},\mathbf{g}]=1$, which stems out of the correctness of SKE and OWF.

3.2.2. Anonymity

We demonstrate anonymity through a series of theorems.

Theorem 1. 

Suppose $\mathrm{ABS}$ offers privacy and unforgeability, $\mathrm{SKE}$ ensures IND-CCA security and key robustness, $\mathrm{OWF}$ (underlying LWE problem) is hard, and $\mathrm{OTS}$ provides strong unforgeability. In that case, the VLR-GS achieves selfless anonymity.

Proof of Theorem 1. 

We prove using a series of corresponding games between the challenger and $\mathcal{A}$, where ${\mathbf{G}}_0$ is the original game and the value of $coin$ is chosen by the challenger. Let $\mathrm{Pr}\left[{\mathbf{G}}_i\right]$ denote the probability of $\mathcal{A}$ winning the game in ${\mathbf{G}}_i$, and ${\mathsf{\Sigma }}^{\ast }=\left({ovk}^{\ast },{\mathbf{ct}}^{\ast },{\mathbf{g}}^{\ast },{\sigma }_1^{\ast },{\sigma }_2^{\ast }\right)$ as the challenge signature.

${\mathbf{G}}_0$:

We define ${\mathbf{G}}_0$ as the original game between adversary $\mathcal{A}$:

1.

The challenger executes $\mathbf{Setup}$ and $\mathbf{KeyGen}$ to acquire $(mpk,us{k}_i,{\mathbf{grt}}_i)$ for $i\in \left[N\right]$. Then sends $mpk$ to $\mathcal{A}$.

2.

If $\mathcal{A}$ queries about M from member i, response $\mathsf{\Sigma }=\left(ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2\right)$. For corruption queries, return $us{k}_i$. For revocation queries, return ${\mathbf{grt}}_i$.

3.

$\mathcal{A}$ sends $M^{\ast }$ and $(i_0^{\ast }$, $i_1^{\ast })$ such that they never asked for their secret keys and tokens before.

4.

The challenger selects secret $coin\leftarrow \left\{0,1\right\}$, then returns ${\mathsf{\Sigma }}^{\ast }=\mathbf{Sign}(mpk,{usk}_{i_{coin}^{\ast }},M^{\ast })$ to $\mathcal{A}$ .

5.

$\mathcal{A}$ makes queries as before. But $\mathcal{A}$ is not allowed to inquire about $us{k}_i$ and ${\mathbf{grt}}_i$ for $(i_0^{\ast }$, $i_1^{\ast })$.

6.

Finally, $\mathcal{A}$ outputs ${coin}^{\prime }$ as its guess.

The probability of $\mathcal{A}$ wins is $|\mathrm{Pr}\left[{\mathbf{G}}_0\right]-{\displaystyle \frac{1}{2}}|$.

${\mathbf{G}}_1$:

In this game, after running the $\mathbf{Setup}(1^{\kappa },1^N)$, the challenger runs $\mathbf{KeyGen}$ to obtain ${\mathbf{sk}}_{N+1}$. Then, all signatures generated by the challenger utilizing ${\mathbf{sk}}_{N+1}$. Note $\left|\mathrm{Pr}\left[{\mathbf{G}}_0\right]-\mathrm{Pr}\left[{\mathbf{G}}_1\right]\right|=\mathrm{negl}\left(\kappa \right)$.

${\mathbf{G}}_2$:

In ${\mathbf{G}}_2$, we alter how the challenge query responses. If $\mathcal{A}$ queries $M^{\ast }$ and $coin=1$, the challenger maintains the same execution style. If $coin=0$, the challenger runs $\left(ov{k}^{\ast },os{k}^{\ast }\right)\leftarrow \mathrm{OTS}.\mathrm{KeyGen}\left(1^{\kappa }\right)$ and computes ${\mathbf{ct}}^{\ast }\stackrel{\$}{\leftarrow }\mathrm{SKE}.\mathrm{Samp}\left(pp\right)$. We define $\mathrm{SKE}.\mathrm{Samp}$ as the pseudorandom sampling algorithm that is related to $\mathrm{SKE}$. Next, it runs ${\mathbf{g}}^{\ast }\leftarrow \mathrm{OWF}(ov{k}^{\ast },{\mathbf{grt}}_{i_0^{\ast }})$. Then, it runs ${\sigma }_1^{\ast }\leftarrow \mathrm{ABS}.\mathrm{Sign}\left(mpk,{\mathbf{sk}}_{N+1},C\right)$, also ${\sigma }_2^{\ast }\leftarrow \mathrm{OTS}.\mathrm{Sign}\left({osk}^{\ast },M^{\ast }\Vert {\sigma }_1^{\ast }\right)$. After that, note $\left|\mathrm{Pr}\left[{\mathbf{G}}_1\right]-\mathrm{Pr}\left[{\mathbf{G}}_2\right]\right|=\mathrm{negl}\left(\kappa \right)$.

${\mathbf{G}}_3$:

We incorporate a further refinement to the method by which the challenge query addresses. When querying for $M^{\ast }$, ${\mathbf{ct}}^{\ast }\stackrel{\$}{\leftarrow }\mathrm{SKE}.\mathrm{Samp}\left(pp\right)$ by the challenger is conducted independently of $coin$. After that, we have $\left|\mathrm{Pr}\left[{\mathbf{G}}_2\right]-\mathrm{Pr}\left[{\mathbf{G}}_3\right]\right|=\mathrm{negl}\left(\kappa \right)$.

${\mathbf{G}}_4$:

In ${\mathbf{G}}_4$, we alter how the challenge query responses. If $\mathcal{A}$ queries $M^{\ast }$ and $coin=1$, the challenger maintains the same execution style. If $coin=0$, the challenger runs $\left(ov{k}^{\ast },os{k}^{\ast }\right)\leftarrow \mathrm{OTS}.\mathrm{KeyGen}\left(1^{\kappa }\right)$ and computes ${\mathbf{ct}}^{\ast }\stackrel{\$}{\leftarrow }\mathrm{SKE}.\mathrm{Samp}\left(pp\right)$. Next, runs ${\mathbf{g}}^{\ast }\leftarrow \mathrm{OWF}\left(ov{k}^{\ast },{\mathbf{grt}}_i\right)$ for $i\in \left[N\right]\setminus \left\{i_{coin}^{\ast }\right\}$. Then, it runs ${\sigma }_1^{\ast }\leftarrow \mathrm{ABS}.\mathrm{Sign}\left(mpk,{\mathbf{sk}}_{N+1},C\right)$, also ${\sigma }_2^{\ast }\leftarrow \mathrm{OTS}.\mathrm{Sign}\left({osk}^{\ast },M^{\ast }\Vert {\sigma }_1^{\ast }\right)$. Finally, it returns ${\mathsf{\Sigma }}^{\ast }$ to $\mathcal{A}$. After that, note $\left|\mathrm{Pr}\left[{\mathbf{G}}_3\right]-\mathrm{Pr}\left[{\mathbf{G}}_4\right]\right|=\mathrm{negl}\left(\kappa \right)$.

${\mathbf{G}}_5$:

For ${\mathbf{G}}_5$, we are redefining the process for addressing the challenge query. Once $\mathcal{A}$ submits the challenge query for $M^{\ast }$, the generation process of ${\mathbf{g}}^{\ast }\leftarrow \mathrm{OWF}\left(ov{k}^{\ast },{\mathbf{grt}}_i\right)$ by the challenger is conducted independently of $coin$. Note that $\left|\mathrm{Pr}\left[{\mathbf{G}}_4\right]-\mathrm{Pr}\left[{\mathbf{G}}_5\right]\right|=\mathrm{negl}\left(\kappa \right)$.

In ${\mathbf{G}}_5$, this challenge signature ${\mathsf{\Sigma }}^{\ast }$ is sampled without the $coin$ value, the probability $\mathrm{Pr}\left[{\mathbf{G}}_5\right]={\displaystyle \frac{1}{2}}$. Based on these indistinguishable games, we obtain $\left|\mathrm{Pr}\left[{\mathbf{G}}_0\right]-{\displaystyle \frac{1}{2}}\right|$ is negligible. This concludes the proof. □

3.2.3. Traceability

Theorem 2. 

If ABS is co-selective unforgeable, SKE exhibits robustness, and the underlying LWE problem of OWF is difficult, then this GS has full traceability.

Proof of Theorem 2. 

Suppose there is an adversary $\mathcal{A}$ who successfully makes a forgery $(M^{\ast },{RL}^{\ast },{\mathsf{\Sigma }}^{\ast })$, yet this forgery such that $\mathbf{Vrfy}\left(mpk,\mathrm{RL},M,\mathsf{\Sigma }\right)=\top$ and the implicit algorithm may either encounter failures or trace back to a user who is not part of the set $\mathcal{T}\setminus {RL}^{\ast }$. We define each of the above two cases as $C_1$ and $C_2$, and the events outlined represent collectively exhaustive scenarios about the occurrence of a forgery. So we need to prove the probability of $C_1$ and $C_2$ winning is negligible.

Lemma 3. 

If ABS is co-selective unforgeable, note that $\mathrm{Pr}\left[C_1\right]=negl\left(\kappa \right)$.

Proof of Lemma 3. 

To avoid contradiction, assume that the probability $\mathrm{Pr}\left[C_1\right]$ is non-negligible. We subsequently construct a new adversary, referred to as $\mathcal{B}$, that can break the co-selective unforgeability in a comparable probability. The following outlines the procedure:

1.

The challenger sends $1^{\kappa }$ to $\mathcal{B}$.

2.

$\mathcal{B}$ runs $pp\leftarrow \mathrm{SKE}.\mathrm{Setup}\left(1^{\kappa }\right)$ and ${\mathbf{S}}_i\leftarrow \mathrm{SKE}.\mathrm{KeyGen}\left(pp\right)$ for $i\in \left[N\right]$. Then, transmit $1^N$, ${\left\{{\mathbf{S}}_i\right\}}_{i\in \left[N\right]}$ to the challenger.

3.

The challenger calculates and transmits $mpk$ and ${\left\{{usk}_i,{\mathbf{grt}}_i\right\}}_{i\in \left[N\right]}$ to $\mathcal{B}$.

4.

$\mathcal{B}$ transfers $mpk$ to $\mathcal{A}$ and keeps $({usk}_i,{\mathbf{grt}}_i)$ secretly.

5.

$\mathcal{A}$ makes queries during the game. In this process, $\mathcal{B}$ has $\left\{{usk}_i\right\}$ to handle all queries without querying the challenger.

• Signing queries: When $\mathcal{A}$ queries $(M,C,i)$, $\mathcal{B}$ runs $\mathbf{Sign}$, then transmits the signature to $\mathcal{A}$.
• Corruption queries: The corruption set, referred to as $\mathcal{T}$, is defined as an empty set. When $\mathcal{A}$ queries information about i, $\mathcal{B}$ adds the index to the set $\mathcal{T}$, then outputs ${usk}_i$.

6.

Finally, $\mathcal{A}$ outputs a forgery ${\mathsf{\Sigma }}^{\ast }$ with the corresponding message and ${\mathrm{RL}}^{\ast }$.

If $\mathbf{Vrfy}\left(mpk,{\mathrm{RL}}^{\ast },M^{\ast },{\mathsf{\Sigma }}^{\ast }\right)=\top$ and the implicit tracing algorithm fails, $\mathcal{B}$ makes $(M^{\ast },{\sigma }_1^{\ast },C[ov{k}^{\ast },{\mathbf{ct}}^{\ast },{\mathbf{g}}^{\ast }])$ as forgery; else, $\mathcal{B}$ aborts.

We note that as long as $C_1$ happens, $\mathcal{B}$ will win. We note that $\mathcal{B}$ made no signing queries, so $\mathcal{B}$ wins with negligible probability. □

Lemma 4. 

If ABS is co-selective unforgeable, SKE exhibits key robustness, and the problem underlying OWF is hard, note that $\mathrm{Pr}\left[C_2\right]=negl\left(\kappa \right)$.

Proof of Lemma 4. 

To avoid contradiction, assume that the probability $\mathrm{Pr}\left[C_1\right]$ is non-negligible. We construct a new adversary, called $\mathcal{B}$, that can break ABS with non-negligible probability. The following outlines the procedure for $\mathcal{B}$:

1.

The challenger sends $1^{\kappa }$ to $\mathcal{B}$.

2.

$\mathcal{B}$ chooses its guess $j^{\ast }$, runs $pp\leftarrow \mathrm{SKE}.\mathrm{Setup}\left(1^{\kappa }\right)$ and ${\mathbf{S}}_i\leftarrow \mathrm{SKE}.\mathrm{KeyGen}\left(pp\right)$ for $i\in \left[N\right]$. Then, it generates the revocation token ${\mathbf{grt}}_i$ using ${\mathbf{S}}_i$ and transmits $1^N$, ${\left\{{\mathbf{S}}_i\right\}}_{i\in \left[N\right]\setminus \left\{j^{\ast }\right\}}$ and $\mathcal{S}=\left[N\right]\setminus \left\{j^{\ast }\right\}$ to the challenger.

3.

The challenger calculates and transmits $mpk$ and ${\left\{{usk}_i,{\mathbf{grt}}_i\right\}}_{i\in \left[N\right]\setminus \left\{j^{\ast }\right\}}$ to $\mathcal{B}$.

4.

$\mathcal{B}$ transfers $mpk$ to $\mathcal{A}$ and keeps ${({usk}_i,,{\mathbf{grt}}_i)}_{i\in \left[N\right]\setminus \left\{j^{\ast }\right\}}$ secretly.

5.

$\mathcal{A}$ conducts two queries during the game. In this process, $\mathcal{B}$ has $\left\{{usk}_i\right\}$ to handle all queries without querying the challenger. The difference is that if $i=j^{\ast }$, $\mathcal{B}$ runs $\mathrm{OTS}.\mathrm{KeyGen}$. Then, it calculates $\mathbf{ct}$ and $\mathbf{g}$ using $(us{k}_{j^{\ast }},{\mathbf{grt}}_{j^{\ast }})$. Later, $\mathcal{A}$ queries for $(M,C,j^{\ast })$ to the challenger, who transmits ${\sigma }_1$ to $\mathcal{B}$. After that, $\mathcal{B}$ computes ${\sigma }_2$. Finally, returns $\mathsf{\Sigma }=(ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$ to $\mathcal{A}$.

6.

Finally, $\mathcal{A}$ output a forgery ${\mathsf{\Sigma }}^{\ast }$ with the corresponding message and ${\mathrm{RL}}^{\ast }$.

It aborts if $\mathrm{OWF}(ovk,{\mathbf{grt}}_{i\in \left[N\right]\setminus \left\{j^{\ast }\right\}})={\mathbf{g}}^{\ast }$ or $\left|\left\{i\in \left[N\right]:\mathrm{SKE}.{\mathrm{Dec}}_{{ovk}^{\ast }}({\mathbf{S}}_i,{\mathbf{ct}}^{\ast })\ne \perp \right\}\right|\ne 1$; else, $\mathcal{B}$ gets $(M^{\ast },C[ov{k}^{\ast },{\mathbf{ct}}^{\ast },{\mathbf{g}}^{\ast }],{\sigma }_1^{\ast })$. If also either of $\mathbf{Vrfy}\left(mpk,{\mathrm{RL}}^{\ast },M^{\ast },{\mathsf{\Sigma }}^{\ast }\right)=\perp$ or $\mathrm{SKE}.{\mathrm{Dec}}_{{ovk}^{\ast }}({\mathbf{S}}_{i^{\ast }},{\mathbf{ct}}^{\ast })=i^{\ast }\ne j^{\ast }$ does hold, then $\mathcal{B}$ aborts.

As long as $C_2$ happens, $\mathcal{B}$ will win. Firstly, note that $\mathrm{ABS}.\mathrm{Vrfy}$ can pass by the result of $\mathbf{Vrfy}$ is ⊤. And $\mathcal{B}$ has made no prohibited key query, that is to say, $C[ov{k}^{\ast },{\mathbf{ct}}^{\ast },{\mathbf{g}}^{\ast }]=0$ causes $\mathrm{SKE}.{\mathrm{Dec}}_{{ovk}^{\ast }}({\mathbf{S}}_{i^{\ast }},{\mathbf{ct}}^{\ast })\ne \perp$ and the LWE problem behind OWF. Then, $\mathcal{B}$ never takes prohibited signing queries. Remember that $\mathcal{B}$ has exclusively performed signing queries for $(M,C[ovk,\mathbf{ct},\mathbf{g}],i^{\ast })$. Once $\mathcal{A}$ wins, we have $(M^{\ast },C[ov{k}^{\ast },{\mathbf{ct}}^{\ast },{\mathbf{g}}^{\ast }])\ne (M,C[ovk,\mathbf{ct},\mathbf{g}])$. This concludes the proof. □

We demonstrate that cases $C_0$ and $C_1$ are collectively exhaustive for a successful forgery with negligible probability, which means that the above scheme is traceable. □

4. Lattice-Based VLR-GS Construction in the Standard Model

As demonstrated in this section, we introduce a new lattice-based VLR-GS construction in SM without NIZKs. We represent each user’s identity in binary as a string, denoted as $i\in {\{0,1\}}^k$. Based on n, we will fix other parameters as outlined below:

• $\gamma$ is required to be large enough so that $\gamma >{\gamma }_0\sqrt{n}·2^{\mathcal{O}\left(d_{\mathcal{F}}\right)}$.
• Dimension $m=\Omega \left(nlogq\right)$ and ${\gamma }_0=\omega \left(\sqrt{nlogqlogm}\right)$ from trapdoor properties.
• $\beta ⩾\gamma m·\omega \left(\sqrt{logm}\right)$ so that $R_{\left(i\right)}^F$ can be extended to ${[{\mathbf{A}}_0 \Vert {\mathbf{A}}_{\left(1\right)}^F \Vert \cdots \Vert {\mathbf{A}}_{\left(N\right)}^F]}_{\beta }^{-1}$ by Lemma 1, and ${\beta }_{\mathrm{SIS}}>Nnm\beta \gamma$.
• $\mathrm{SIS}$ is hard and $q>{\beta }_{\mathrm{SIS}}·\sqrt{n}·\omega \left(logn\right)$.
• $\mu \ge \sqrt{n}\omega (logn)$ and $\mu$-bounded distribution $\mathcal{X}$ makes $\mathrm{LWE}(n,q,\mathcal{X})$ hard to solve.

4.1. Construction of the Scheme

To illustrate easily, we omit the subscript of the message space collection ${\left\{{\mathcal{M}}_{\kappa }\right\}}_{\kappa \in \mathbb{N}}$ and just write $\mathcal{M}$. The construction of the scheme is specified as follows:

• $\mathbf{Setup}(1^{\kappa },1^N)$: Take $\kappa$ and N as the inputs, then get public parameters $pp=(n,m,k,\beta ,\gamma ,{\gamma }_0,\mu ,q)$. The algorithm proceeds as follows:
  • Pick a random vector $\mathbf{u}\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^n$ and run $\left({\mathbf{A}}_0,{\mathbf{A}}_{{\gamma }_0}^{-1}\right)\leftarrow \mathbf{TrapGen}\left(1^m,1^n,q\right)$ such that ${\mathbf{A}}_0\in {\mathbb{Z}}_q^{n\times m}$.
  • Sample randomly $Nk$ matrices ${\mathbf{A}}_i^j\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{n\times m}$ for $i\in \left[N\right]$ and $j\in \left[k\right]$, then define the matrix ${\overrightarrow{\mathbf{A}}}_{\left(i\right)}=[{\mathbf{A}}_i^1\mid \cdots \mid {\mathbf{A}}_i^k]$.
  Finally, the algorithm outputs $mpk=({\mathbf{A}}_0,{\left\{{\overrightarrow{\mathbf{A}}}_{\left(i\right)}\right\}}_{i\in \left[N\right]},\mathbf{u})$, and $msk={\mathbf{A}}_{{\gamma }_0}^{-1}$.
• $\mathbf{KeyGen}\left(mpk,msk,i\right)$: For group user $i\in \left[N\right]$, the group manager performs the following to generate group member’s token ${\mathbf{grt}}_i$ and signing key ${usk}_i$:
  • Sample ${\mathbf{S}}_0\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{n\times m}$ and ${\mathbf{S}}_1\stackrel{\$}{\leftarrow }{\mathbb{Z}}_q^{n\times k}$ and define ${\mathbf{S}}_i:=({\mathbf{S}}_0,{\mathbf{S}}_1)$.
  • Compute ${\mathbf{grt}}_i={\mathbf{S}}_1·i\in {\mathbb{Z}}_q^n$, where $i\in {\left\{0,1\right\}}^k$.
  • Compute ${\overrightarrow{\mathbf{R}}}_{\left(i\right)}\leftarrow {\mathbf{A}}_{{\gamma }_0}^{-1}[{\overrightarrow{\mathbf{A}}}_{\left(i\right)}-i\otimes \mathbf{G}]$ and define ${usk}_i=({\mathbf{S}}_i,{\overrightarrow{\mathbf{R}}}_{\left(i\right)})$. Note that ${\overrightarrow{\mathbf{A}}}_{\left(i\right)}={\mathbf{A}}_0{\overrightarrow{\mathbf{R}}}_{\left(i\right)}+i\otimes \mathbf{G}$.
  Finally, it sends $({usk}_i,{\mathbf{grt}}_i)$ to user i over secure channels.
• $\mathbf{Sign}\left(mpk,\mathbf{m},{usk}_i,{\mathbf{grt}}_i\right)$: Given $mpk=({\mathbf{A}}_0,{\left\{{\overrightarrow{\mathbf{A}}}_{\left(i\right)}\right\}}_{i\in \left[N\right]},\mathbf{u})$, message $\mathbf{m}\in \mathcal{M}$, a group member’s signing key ${usk}_i=({\mathbf{S}}_i,{\overrightarrow{\mathbf{R}}}_{\left(i\right)})$ and revocation token ${\mathbf{grt}}_i$, the signer runs this algorithm:
  • Generate $\left(e{k}_d,t{d}_d\right)\leftarrow \mathbf{TrapGen}(1^m,1^n,q)$ and $e{k}_d=({\mathbf{B}}_d,{\mathbf{K}}_d)$, where ${\mathbf{K}}_d\in {\mathbb{Z}}_q^{n\times m}$ and ${\mathbf{B}}_d\in {\mathbb{Z}}_q^{n\times m(N+2)}$ for $d\in \left\{0,1\right\}$. Sample ${\mathbf{r}}_0\in {\mathbb{Z}}_q^{m(N+2)}$ and ${\mathbf{r}}_1\in {\mathbb{Z}}_q^m$. Compute ${\mathbf{z}}_0=h({ek}_0,m_{ek},{\mathbf{r}}_0)$ and ${\mathbf{z}}_1=T_{{ek}_1,{ek}_0}\left(h({ek}_1,m_{ek},{\mathbf{r}}_1)\right)$. Finally, define $ovk=(e{k}_0,e{k}_1,{\mathbf{z}}_0)$ and $osk=(t{d}_0,t{d}_1,{\mathbf{r}}_0,{\mathbf{r}}_1,{\mathbf{z}}_1)$.
  • Sample ${\mathbf{x}}_0\leftarrow SampZ{\left(3\sqrt{n}\right)}^m$ and ${\mathbf{x}}_1\leftarrow SampZ{\left(3\sqrt{n}\right)}^k$. Next, compute ${\mathbf{ct}}_0^T:={{\mathbf{z}}_0}^T{\mathbf{S}}_0+{\mathbf{x}}_0^T$ and ${\mathbf{ct}}_1^T:={{\mathbf{z}}_0}^T{\mathbf{S}}_1+{\mathbf{x}}_1^T+⌈q/2⌉·i^T$. Thus it outputs $\mathbf{ct}:=\left({\mathbf{ct}}_0,{\mathbf{ct}}_1\right)$.
  • Compute $\mathbf{g}={\mathbf{K}}_0^T·{\mathbf{grt}}_i+\mathbf{e}modq$, where $\mathbf{e}\leftarrow {\mathcal{X}}^m$. Note that ${∥\mathbf{e}∥}_{\infty }\le \mu$ with overwhelming probability and output $\mathbf{g}$.
  • Output 0 if $\mathbf{m}\notin \mathcal{M}$, $F\notin \mathcal{F}$, $F\left(i\right)=0$ and $C[ovk,\mathbf{ct},\mathbf{g}]=0$. Otherwise, compute ${\mathbf{A}}_{\left(i\right)}^F=\mathbf{PubEval}({\overrightarrow{\mathbf{A}}}_{\left(i\right)},F)$ and ${\mathbf{R}}_{\left(i\right)}^F=\mathbf{TrapEval}({\overrightarrow{\mathbf{R}}}_{\left(i\right)},F,i)$ such that ${∥{\mathbf{R}}_{\left(i\right)}^F∥}_{\infty }\le \gamma$. It then computes ${[{\mathbf{A}}_0\Vert {\mathbf{A}}_{\left(i\right)}^F]}_{\beta }^{-1}$ and further computes ${\left[{\mathbf{A}}_0\Vert {\mathbf{A}}_{\left(1\right)}^F\Vert \cdots \Vert {\mathbf{A}}_{\left(N\right)}^F\right]}_{\beta }^{-1}$ from ${[{\mathbf{A}}_0\Vert {\mathbf{A}}_{\left(i\right)}^F]}_{\beta }^{-1}$. Finally it outputs ${\sigma }_1\leftarrow {\left[{\mathbf{A}}_0\Vert {\mathbf{A}}_{\left(1\right)}^F\Vert \cdots \Vert {\mathbf{A}}_{\left(N\right)}^F\right]}_{\beta }^{-1}\left(\mathbf{u}\right)$ and ${\sigma }_1\in {\mathbb{Z}}^{m(N+1)}$.
  • Given $osk$, signature ${\sigma }_1$ and message $\mathbf{m}\in {\mathbb{Z}}^m$, then compute ${\sigma }_2=(\mathbf{r},{\mathbf{r}}^{\prime })$, where $\mathbf{r}=h^{-1}({td}_1,m_{ek},{\mathbf{r}}_1,\mathbf{m}\Vert {\sigma }_1)\in {\mathbb{Z}}_q^m$ and ${\mathbf{r}}^{\prime }=h^{-1}({td}_0,m_{ek},{\mathbf{r}}_0,{\mathbf{z}}_1)\in {\mathbb{Z}}_q^m$.
  Finally, it outputs $\mathsf{\Sigma }=(ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$.
• $\mathbf{Vrfy}\left(mpk,\mathrm{RL},\mathbf{m},\mathsf{\Sigma }\right)$: Given $mpk$, message $\mathbf{m}$, the signature $\mathsf{\Sigma }$, and a set of tokens $\mathbf{v}$ in RL that are to be revoked, the verifier performs the steps below. First, parse $\mathsf{\Sigma }\to (ovk,\mathbf{ct},\mathbf{g},{\sigma }_1,{\sigma }_2)$, and there are three Conditions needed to check:
  • Condition 1:
    For each token in $\mathrm{RL}$, compute ${\mathbf{e}}_i^{\prime }=\mathbf{g}-{\mathbf{K}}_0^T·\mathbf{v}modq$. If there exists i such that ${∥{\mathbf{e}}_i^{\prime }∥}_{\infty }\le \beta$, returns 0; else, checks Condition 2.
  • Condition 2:
    It outputs 0 if $F\notin \mathcal{F}$, $C=0$, or ${\sigma }_1\notin {\mathbb{Z}}^{m(N+1)}$. Otherwise, it first computes ${\mathbf{A}}_{\left(i\right)}^F=\mathbf{PubEval}({\overrightarrow{\mathbf{A}}}_{\left(i\right)},F)$, then checks whether $\left[{\mathbf{A}}_0\Vert {\mathbf{A}}_{\left(1\right)}^F\Vert \cdots \Vert {\mathbf{A}}_{\left(N\right)}^F\right]·{\sigma }_1=\mathbf{u}$ and $∥{\sigma }_1∥\le \sqrt{n}\beta$. If one of the two is not satisfied, then output 0; else, check Condition 3.
  • Condition 3:
    Given the public key $ovk=(e{k}_0,e{k}_1,{\mathbf{z}}_0)$ and ${\sigma }_1$, ${\sigma }_2$. It checks whether ${\mathbf{z}}_0=h({ek}_0,{\mathbf{r}}^{\prime },T_{{ek}_1,{ek}_0}\left(h({ek}_1,\mathbf{m}\Vert {\sigma }_1,\mathbf{r})\right))$. If they hold, output 1.

If and only if all of these conditions are met, the verification algorithm outputs 1 (accept); in contrast, when any of them are unsatisfied, it outputs 0 (reject).

4.2. Comparisons and Analysis

Here, we compare the above scheme in detail with earlier lattice-based GS schemes as presented in Table 2. In our scheme, the bit size of ${usk}_i=({\mathbf{S}}_i,{\overrightarrow{\mathbf{R}}}_{\left(i\right)})$ is $\mathcal{O}(nmlogq+nklogq+m\times mklogq)=\tilde{\mathcal{O}}(n^{2}logN)$. And $mpk$ has $({\mathbf{A}}_0,\left\{{\overrightarrow{\mathbf{A}}}_{\left(i\right)}\right\},\mathbf{u})$ of bit size $\mathcal{O}(nmlogq+N(n·mlogN)logq+nlogq)=\tilde{\mathcal{O}}\left(n^{2}N\right)$. The signature $\mathsf{\Sigma }$ is $\tilde{\mathcal{O}}\left(n^{2}N\right)$.

Table 2. Comparison of existing lattice-based GS schemes.

Scheme	$\left|\mathit{mpk}\right|$	$\left|{\mathit{usk}}_{\mathit{i}}\right|$	$\left|\mathbf{\Sigma }\right|$	Problem	Model	VLR
[2]	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	$\tilde{\mathcal{O}}\left(n^2\right)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	LWE	ROM	×
[12]	$\tilde{\mathcal{O}}\left(n^2\right)$	$\tilde{\mathcal{O}}\left(n^2\right)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	LWE	ROM	×
[41]	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}(nlogN)$	$\tilde{\mathcal{O}}(nlogN)$	ISIS	ROM	×
[31]	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}(nlogN)$	$\tilde{\mathcal{O}}(nlogN)$	ISIS	ROM	√
[19]	$\tilde{\mathcal{O}}(nlogN)$	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}\left(n^2{log}^{2}N\right)$	SIS LWE	ROM	×
[17]	$\tilde{\mathcal{O}}\left(n^2\right)$	$\tilde{\mathcal{O}}\left(n\right)$	$\tilde{\mathcal{O}}(nlogN)$	LWE	ROM	√
[27]	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}(nlogN)$	$\tilde{\mathcal{O}}(nlogN)$	SIS LWE	ROM	√
[18]	$\tilde{\mathcal{O}}\left(n^2\right)$	$\tilde{\mathcal{O}}\left(n\right)$	$\tilde{\mathcal{O}}(nlogN)$	SIS LWE	ROM	√
[3]	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	SIS LWE	SM	×
[20]	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}(nlogN)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	SIS LWE	SM	×
[21]	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	$\tilde{\mathcal{O}}\left(N\right)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	SIS LWE	SM	×
Ours	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	$\tilde{\mathcal{O}}(n^{2}logN)$	$\tilde{\mathcal{O}}\left(n^{2}N\right)$	SIS LWE	SM	√

After the above theoretical comparison in Table 2, we make a more detailed comparison of lattice-based group signature schemes in SM, and these three schemes utilize ABS instead of NIZKs. Because of the same group signature construction, the gap between the efficiency of the three is very small. That’s why we focus on the communication cost. We set the parameters as follows: $n=\tilde{\mathcal{O}}\left(\kappa \right)$ = 8, $m=n^{1.1}$, $q=2^{32}$ according to [3]. And then we consider the theoretical sizes of these schemes when the group number is $N=2^3,2^4,2^5,2^6,2^7$.

The three articles are based on the framework of [3] in Table 3. Ref. [20] proposes a lattice-based GS with forward security, which has a larger secret key size than the proposed one. Ref. [21] uses the Bonsai tree structure to propose a new GS scheme with a larger $mpk$ and $us{k}_i$. We construct this scheme shown in Section 4. The size of $\mathsf{\Sigma }$ is similar to [21], and the other two are significantly smaller than [20,21]. In Figure 4, the performance of our scheme is more clearly represented by a line chart.

Table 3. Comparison of three schemes in SM in terms of $mpk$, $usk$ and $\mathsf{\Sigma }$.

Schemes	Sizes (KB)	$\mathit{N}=2^3$	$\mathit{N}=2^4$	$\mathit{N}=2^5$	$\mathit{N}=2^6$	$\mathit{N}=2^7$
[20]	$mpk$	139.25	185.56	231.88	278.19	324.50
	$usk$	3.33	3.37	3.40	3.44	3.47
	$\mathsf{\Sigma }$	30.98	36.30	46.61	66.93	107.25
[21]	$mpk$	10.34	25.34	60.34	140.34	320.34
	$usk$	2.00	2.41	2.83	3.26	3.69
	$\mathsf{\Sigma }$	7.39	12.70	23.33	44.59	87.09
Our scheme	$mpk$	7.84	20.34	50.34	120.34	280.34
	$usk$	1.58	2.00	2.42	2.84	3.27
	$\mathsf{\Sigma }$	7.43	12.74	23.37	44.63	87.13

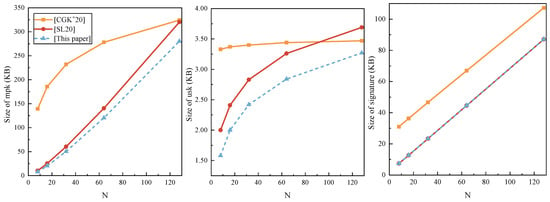
Figure 4. Comparison of schemes in SM.

In our theoretical analysis, although our scheme performs averagely in all comparisons, as shown in Table 2, the proposed scheme compared with others under SM is considered positive in Table 3 and Figure 4.

5. Conclusions

The medical service evaluation system we propose enhances traditional management approaches. To help the cloud platform work better, we propose a new scheme, which is a lattice-based VLR-GS. With this scheme, patients as part of a group can anonymously evaluate their experiences. The hospital can verify and manage the reviews uploaded by users. If any review is found to be illegitimate or malicious, appropriate actions can be taken. In addition, doctors can complain, and if necessary, the hospital can identify the reviewer. We instantiate the GS scheme for this system into a concrete construction. This scheme is proven secure under SIS and LWE problems, and we demonstrate that the scheme ensures anonymity and unforgeability. Such a scheme in SM is designed to take into account the balance between efficiency and security. And our scheme performs well in the same type of scheme. In the future, we need to find ways to enhance efficiency without compromising security.