Maximizing Energy Efficiency of UAV-Assisted RF-Powered Networks with Quality-of-Service Constraints

Abstract

In this paper, we investigate a UAV-assisted wireless powered communication network (WPCN) where UAVs act as access points (APs) to periodically serve a group of ground sensor nodes (SNs). Unlike fixed APs in traditional WPCNs, UAV-assisted WPCNs can leverage UAV mobility to maximize system throughput by optimizing the UAV trajectory and wireless resource allocation. However, due to the limited data buffer capacity of the SNs, UAVs may fail to provide timely services, leading to data overflow. Therefore, UAVs must offer efficient and timely services to the SNs. Our objective was to maximize the total energy efficiency of all ground SNs by jointly optimizing UAV transmit power, downlink (DL) wireless energy transfer (WET) time, uplink (UL) wireless information transfer (WIT) time, and SN transmit power under minimal quality-of-service (QoS) constraints. However, the formulated optimization problem is non-convex and difficult to solve directly. To address this, we applied fractional programming theory to transform the non-convex problem into a tractable form. Subsequently, a block coordinate descent-based algorithm was proposed to obtain a near-optimal resource allocation scheme. Extensive simulation results show that our proposed method achieved significantly better performance in terms of system throughput and energy efficiency compared to other benchmark solutions.

1. Introduction

The Internet of Things (IoT), designed to meet massive device connectivity needs, has greatly benefited from the profound revolution driven by the development of fifth-generation communication technology [1]. To support energy-self-sufficient IoT operations, Wireless Power Transfer (WPT) has emerged as a promising technology, capable of providing sustainable and controllable energy to low-power devices via radio frequency (RF) radiation [2]. Compared with near-field WPT, far-field RF-based WPT operates over longer distances and can simultaneously charge multiple wireless devices (WDs), even in mobile and dense scenarios. A key application is the Wireless Powered Communication Network (WPCN), which enables dedicated wireless charging and information collection for massive IoT devices, enhancing the operational range and throughput over traditional backscatter systems. However, in conventional WPCNs, Access Points (APs) are deployed at fixed locations, which limits their adaptability and coverage once installed [3,4,5]. Moreover, UAV-assisted WPCNs are key for 6G, as they leverage the upper midband spectrum (6–100 GHz) [6]—this spectrum offers large bandwidth (100 s of MHz) for high-throughput IoT but suffers from severe path loss. UAVs mitigate this via LoS channels, while outage-based technologies [7] ensure reliability in dynamic 6G environments.

This fixed infrastructure presents significant challenges, especially given the explosive growth in data demand from WDs in remote or emergency-stricken areas. RF signals suffer from severe propagation loss, leading to low end-to-end WPT efficiency as the distance between APs and WDs increases. Consequently, traditional WPCNs face the “double near-far” problem [3]: distant WDs not only receive less energy but must also compensate for greater path loss during Wireless Information Transfer (WIT), resulting in very low data rates [8,9,10].

As a prominent robotic platform, the Unmanned Aerial Vehicle (UAV) has attracted extensive research interest due to its flexible deployment, high probability of establishing Line-of-Sight (LoS) channels with ground WDs, and controllable mobility [9,11]. Integrating UAVs into WPCNs, where they act as mobile APs, is a key component of future sixth-generation (6G) networks [12,13,14,15]. In this paradigm, a UAV first charges a group of WDs via downlink RF WPT, after which the WDs use the harvested energy to transmit their information to the UAV in the uplink. However, this approach introduces its own challenges. Given the UAV’s limited onboard energy, the efficient allocation of communication resources and the design of optimal flight trajectories to complete tasks in an energy-efficient manner have become critical research problems. Existing literature on UAV-assisted WPCNs has primarily focused on objectives such as minimizing energy consumption [16,17], minimizing mission completion time [18], or maximizing energy efficiency [19]. However, another practical issue is data overflow, which can occur if the UAV fails to provide timely service to WDs with limited data buffers. Providing timely service is complicated by the time-varying nature of wireless channels, making it difficult to guarantee deterministic delay bounds. To address this, Effective Capacity offers a powerful framework for providing statistical Quality-of-Service (QoS) guarantees for delay-sensitive applications [20,21,22,23]. Therefore, our objective in this paper was to maximize the total effective capacity of all WDs. We achieved this by jointly optimizing the time allocation for UAV downlink WPT and uplink WIT, the UAV’s transmit power, and the WDs’ transmit powers, all while satisfying the statistical QoS requirements of each WD.

The remainder of the paper is organized as follows. Section 2 summarizes the related work on the proposed method, while Section 3 introduces the framework of the proposed UAV-assisted wireless charging communication network. Section 4 analyzes and solves the optimization problem. Finally, Section 5 concludes this paper.

2. Related Works

There have been several studies on the position optimization of UAV-BS. For instance, in [24,25], the authors proposed that UAVs act as aerial base stations flying at a fixed altitude to serve multiple users. However, these two works overlooked the fact that adjusting the altitude could enhance channel power gains, thereby improving communication performance. In [26], to maximize the number of covered users, the authors proposed an optimal algorithm for placing the UAV-BS under a minimum transmit power constraint. In [27], the authors optimized the 3D positioning of the UAV-BS to improve secure transmission performance at the physical layer. In [28], the UAV-BS is equipped with a directional antenna, which can cover most users through 3D position adjustment.

Nonetheless, numerous works [3,29,30,31] have focused on network throughput optimization. Specifically, the authors in [6] jointly optimized resource allocation and trajectory design to maximize system throughput. In [29], the authors maximized system throughput through the joint optimization of UAV trajectory design, reflection coefficients, and time allocation. The authors in [30] maximized the total uplink and downlink capacity by jointly optimizing UAV trajectories, downlink/uplink user scheduling, and uplink transmit power. However, these works [6,29,30] ignored the impact of service delay on data transmission. In [31], the authors, by jointly optimizing resource allocation and UAV trajectory, maximized the minimum average downlink throughput among all users while satisfying delay constraints. The authors of [3] maximized the minimum total throughput of delay-tolerant users by jointly optimizing UAV trajectory, power allocation, and bandwidth allocation of the backhaul link while ensuring the QoS of latency-sensitive users. Nevertheless, those works [3,31] did not consider the influence of the time-varying characteristics of wireless fading channels on transmission delay. In [32], the authors achieved the maximization of effective capacity by optimizing power allocation under different QoS constraints in the downlink of UAV-BS. However, they neglected the impact of the UAV-BS’s 3D position on effective capacity.

3. System Model

3.1. System Description

In this section, we discuss a hybrid multiple access system where UAVs assist in power supply. As shown in Figure 1, the system consists of one UAV and $KM$ SNs, among which SNs are divided into $K$ regions. K-Clustering is essential for practical implementation and adapting to bandwidth constraints in heterogeneous networks, which single-cluster NOMA cannot address effectively. Each region contains $M$ nodes, with $S{N}_{k,m}(k\in \mathsf{\Phi }\triangleq \{1,...,K\},m\in \mathsf{\Omega }\triangleq \{1,...,M\})$ denoting the $k-\mathrm{th}$ node in the $m-\mathrm{th}$ region, and all network devices are equipped with only a single antenna. It is assumed that the predefined position of node $S{N}_{k,m}$ on the ground in the 3D Cartesian coordinate system is $q_{k,m}=[x_{k,m},y_{k,m}]$, and the positions of the nodes are a priori known to the UAV. The initial position of the UAV is given as $(x_0,y_0,z_0)$, where $q_0=(x_0,y_0)$. It is assumed that the UAVs hover in the air, and the distance between the UAV and node is [33]:

$$d_{k,n}=\sqrt{{\parallel q_0-q_{k,m}\parallel }^2+z_0^2}$$

(1)

$\parallel \cdot \parallel$ represents Euclidean norms.

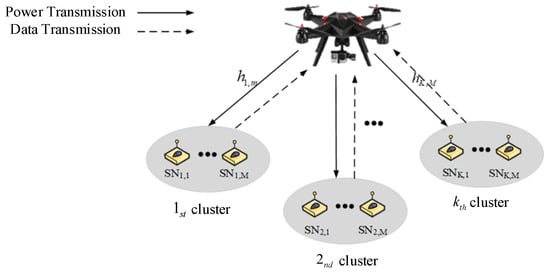
Figure 1. UAV-assisted WPCN system.

3.2. Mathematical Model

To satisfy the data requirements of the ground SNs while minimizing system-wide energy consumption, it is crucial for the UAV to jointly optimize its 3D position and the allocation of communication resources. Accordingly, this section is dedicated to solving the energy efficiency (EE) maximization problem. We begin by formulating the overall system EE, which results in a non-convex fractional programming problem. To tackle the non-convexity, we leveraged Dinkelbach’s method, a classic fractional programming technique, to transform the problem into a more tractable, subtractive form. To manage the receiving complexity at the UAV, we proposed a hybrid multiple access scheme where time-division multiple access (TDMA) is used for inter-region communication and non-orthogonal multiple access (NOMA) is used for intra-region communication. Finally, we developed an iterative algorithm based on block coordinate descent (BCD) to efficiently solve the transformed problem and find a high-quality resource allocation solution.

For the CSI acquisitions, the UAV broadcasts a pilot signal at the start of each frame (duration = 5 ms, <coherence time). Each SN estimates its instantaneous CSI $h_{k,i}$ and feeds back the statistical distribution $(\mathbb{E}[{\mid h_{k,i}\mid }^2]=1)$ instead of instantaneous values. The UAV uses the CSI to optimize resource allocation.

Each region k is allocated ${\tau }_k$, so ${\displaystyle \sum _{k=1}^K{\tau }_k}\le T_{\mathrm{total}}-{\tau }_d$. For $S{N}_i$ in region k, SIC decodes signals in order of increasing index. The SINR for $i$ is:

$${\mathrm{SIN}\mathrm{R}}_{k,i}={\displaystyle \frac{P_{k,i}{G}_{k,i}}{{\displaystyle \sum _{j=i+1}^M{P}_{k,j}}{G}_{k,j}+{\sigma }^2}}$$

(2)

The throughput is calculated as $R_{k,i}={\tau }_k{\log }_2(1+{\mathrm{SIN}\mathrm{R}}_{k,i})$ with the finite-block length correction. The unified channel model considering path loss + small-scale Rayleigh fading is: $G_{k,i}={\beta }_0{d}_{k,i}^{-\alpha }\cdot {\mid h_{k,i}\mid }^2$. Hybrid LoS/NLoS Channel Model: The channel gain is

$$G_{k,i}=\left\{\begin{array}{ll}{\beta }_0{d}_{k,i}^{-{\alpha }_{\mathrm{LoS}}}\cdot {\mid h_{k,i}\mid }^2\hfill & \mathrm{LoS}\mathrm{probability}{p}_{\mathrm{LoS}},\hfill \\ {\beta }_0{d}_{k,i}^{-{\alpha }_{\mathrm{NLoS}}}\cdot {\mid h_{k,i}\mid }^2\hfill & \mathrm{NLoS}\mathrm{probability}1-p_{\mathrm{LoS}},\hfill \end{array}\right.$$

(3)

where $(p_{\mathrm{LoS}}={\displaystyle \frac{1}{1+a\exp (-b(\theta -a))}})$ (LoS probability model, $(a=0.1,b={10}^{°})$, $\theta$ is the elevation angle). ${\alpha }_{\mathrm{LoS}}=2.2$, ${\alpha }_{\mathrm{NLoS}}=3.8$ are the path loss exponents for urban areas.

Figure 2 depicts the operational system flow. In the downlink, to provide energy to all SNs, a duration ${\tau }_0$ is allocated to the UAV to broadcast energy signals. In other words, UAVs transmit wireless power to their surrounding SNs within a specified time frame to enable SNs to harvest energy, and the number of SNs does not affect the UAV’s energy transmission. The energy harvested by the $k-\mathrm{th}$ node in the $m-\mathrm{th}$ region is:

$$E_{k,m}=\eta {\tau }_0{P}_0{G}_{k,m},k\in \mathsf{\Phi },m\in \mathsf{\Omega }$$

(4)

where the UAV transmitting power is denoted by $P(P_0\le P_{\max })$, the maximum transmitting power is $P_{\max }$, and the energy conversion efficiency is $\eta (0\le \eta \le 1)$.

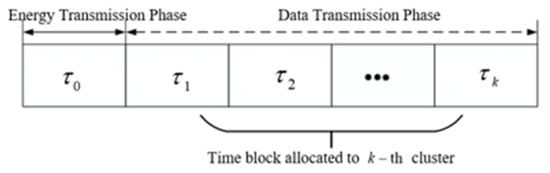
Figure 2. Time allocation diagram for energy transmission phase and data transmission phase.

$E_{\mathrm{WET}}$ represents the energy consumption in the downlink, which consists of two components: the loss incurred during signal propagation and the total energy consumed by the UAV’s circuit system during transmission. Therefore, $E_{\mathrm{WET}}$ can be expressed as the sum of these two energy consumptions:

$$E_{\mathrm{WET}}=P_0{\tau }_0-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M{E}_{k,m}}+P_E{\tau }_0}$$

(5)

where $P_0{\tau }_0-{\displaystyle {\sum }_{k=1}^K{\displaystyle {\sum }_{m=1}^M{E}_{k,m}}}$ represents the energy loss caused by wireless signals during propagation. $P_E$ denotes the constant circuit power consumption of the UAV during transmission. $P_E{\tau }_0$ stands for all the energy consumed by the UAV’s circuit system in the downlink.

In the uplink transmission, the TDMA is adopted between two regions to transmit signals to the UAV orthogonally. ${\tau }_k$ denotes the data transmission time in the $k-\mathrm{th}$ region, and the total transmission time of the $K+1-\mathrm{th}$ block is not able to exceed $T_{\max }$, which is formed as:

$${\tau }_0+{\displaystyle \sum _{k=1}^K{\tau }_k}\le T_{\max }$$

(6)

In each region, there are $M$ nodes that adopt the NOMA technology to achieve simultaneous data transmission. Therefore, when UAVs receive signals from the $k-\mathrm{th}$ region, they receive data transmitted by multiple SNs in that region simultaneously. The signal from the SNs in the $k-\mathrm{th}$ region is:

$$y_k={\displaystyle \sum _{m=1}^M{h}_{k,m}}{x}_{k,m}+n_k$$

(7)

In Equation (5), within the $k-\mathrm{th}$ region, $x_{k,m}$ represents the signal sent by the $m-\mathrm{th}$ SN to the UAV. $n_k$ denotes the additive white Gaussian noise with the noise power of ${\sigma }^2$. The UAV uses serial interference cancellation (SIC) for intra-region NOMA, with the following steps for region k (containing SNs form 1 to M): the decoding order was organized so that SNs were decoded in increasing order of their indices (1→2→…→M). This order was chosen because SNs with smaller indices have weaker channel gains (per K-Means clustering, which groups SNs by channel gain), ensuring that SIC prioritizes weaker signals (reducing near-far imbalance). The interference cancellation is when decoding $SN_1$, treating signals from SNs 2–M as interference. Then, compute SINR using Equation (5) and decode $R_{k,1}$. To decode $S{N}_2$, subtract the decoded signal of SN 1 from the received signal, then treat SNs 3–M as interference. When decoding $R_{k,2}$, repeat the above process until all SNs in the region are decoded. If the decoding of SN $i$ fails (BER $>{10}^{-5}$), the UAV discards $R_{k,i}$ and proceeds to $S{N}_{i+1}$.

The energy consumed by a node during data transmission will not exceed its collected energy, since the energy required for the node to transmit data derives from the energy harvested in the first phase. Therefore, the following equation can be obtained:

$$E_{k,m}=P_{k,m}{\tau }_k+P_{C_{k,m}}{\tau }_k,k\in \mathsf{\Phi },m\in \mathsf{\Omega }$$

(8)

where $P_{C_{k,m}}$ is the constant circuit power consumption of the SN terminal, and $P_{C_{k,m}}{\tau }_k$ is the energy consumed by the circuit of node $S{N}_{k,m}$.

$E_{\mathrm{WIT}}$ represents the total energy consumption in the uplink, which consists of the energy consumed by all SNs across $K$ regions. The energy consumed by the nodes in the $k-\mathrm{th}$ region during transmission phase can be expressed by Equation (9):

$$E_{{\mathrm{WIT}}_k}={\displaystyle \sum _{m=1}^M(P_{k,m}}{\tau }_k+P_{C_{k,m}}{\tau }_k),k\in \mathsf{\Phi },m\in \mathsf{\Omega }$$

(9)

Therefore, during the wireless transmission phase, the total energy consumed by SNs across all regions can be expressed as follows:

$$E_{\mathrm{WIT}}={\displaystyle \sum _{k=1}^K{E}_{{\mathrm{WIT}}_k}}={\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M(P_{k,m}}{\tau }_k+P_{C_{k,m}}{\tau }_k)}$$

(10)

The energy consumption of UAV-assisted wireless powered communication networks consists of two components: the energy consumed in the downlink and that in the uplink. Therefore, the total energy consumption of the entire system $E_{\mathrm{sum}}$ can be expressed as the following formula:

$$E_{\mathrm{sum}}=E_{\mathrm{WIT}}+E_{\mathrm{WET}}$$

(11)

In this scenario, the UAVs adopted the successive interference cancellation method to decode the information of SNs in the $k-\mathrm{th}$ region. We assumed that the throughput of $M$ nodes in the $k-\mathrm{th}$ region was the sum of the achievable rates of all nodes in the system. In the NOMA system, the total uplink throughput remains unaffected regardless of the decoding order. Thus, the decoding order of node information can be determined according to the increasing order of node indices. When decoding the information of the first node, it will be interfered with by signals from other nodes, and when decoding the information of the second node, signals from other nodes will interfere with the decoding process of the first node, and so on. Therefore, the throughput of a node in the $k-\mathrm{th}$ region, measured in $\mathrm{bits}/\mathrm{Hz}$, is expressed as:

$$R_{k,m}={\tau }_k{\log }_2(1+{\displaystyle \frac{P_{k,m}{G}_{k,m}}{{\displaystyle \sum _{i=m+1}^M{P}_{k,i}{G}_{k,i}+{\sigma }^2}}})$$

(12)

The achievable rate per unit bandwidth of nodes in the $k-\mathrm{th}$ region can be expressed as:

$$R_{k,M}={\tau }_k{\log }_2(1+{\displaystyle \frac{P_{k,M}{G}_{k,M}}{{\sigma }^2}})$$

(13)

Therefore, throughput per unit bandwidth of nodes in the $k-\mathrm{th}$ region can be expressed as:

$$\begin{array}{ll}{R}_k& ={\displaystyle \sum _{m=1}^M{R}_{k,m}}\\ & ={\tau }_k{\displaystyle \sum _{m=1}^{M-1}[{\log }_2(1+\frac{P_{k,m}{G}_{k,m}}{{\displaystyle \sum _{i=m+1}^M{P}_{k,i}{G}_{k,i}+{\sigma }^2}})]}+{\tau }_k{\log }_2(1+{\displaystyle \frac{P_{k,M}{G}_{k,M}}{{\sigma }^2}})\\ & ={\tau }_k{\displaystyle \sum _{m=1}^{M-1}[{\log }_2({\displaystyle \sum _{i=m}^M{P}_{k,i}{G}_{k,i}+{\sigma }^2)-{\log }_2({\displaystyle \sum _{i=m+1}^M{P}_{k,i}{G}_{k,i}+{\sigma }^2})}]}\\ & \hspace{1em}+{\tau }_k[{\log }_2(P_{k,M}{G}_{k,M}+{\sigma }^2)-{\log }_2({\sigma }^2)]\\ & ={\tau }_k{\log }_2(1+{\displaystyle \sum _{m=1}^M{P}_{k,m}{\gamma }_{k,m}})\end{array}$$

(14)

where ${\gamma }_{k,m}=G_{k,m}/{\sigma }^2,k\in \mathsf{\Phi },m\in \mathsf{\Omega }$.

The throughput of the entire network is the sum of the achievable rates of each node across all regions:

$$R_{\mathrm{sum}}={\displaystyle \sum _{k=1}^K{R}_k}={\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1+{\displaystyle \sum _{m=1}^M{P}_{k,m}}{\gamma }_{k,m})}$$

(15)

The energy efficiency of the system refers to the ratio of the total energy required to the number of tasks completed by the system, i.e., $EE=R_{\mathrm{sum}}/E_{\mathrm{sum}}$. In this paper, considering that the UAVs’ transmitting power and SNs’ power were constrained, and the sum of the uplink and downlink transmission durations remained constant, these parameters were jointly optimized to improve the system’s energy efficiency under certain conditions. The energy efficiency maximization problem is thereby described as follows:

$$\begin{gathered} \begin{array}{l}{\max }_{{\tau }_0,\left\{{\tau }_k\right\},P_0,\left\{P_{k,m}\right\}}{\displaystyle \frac{{\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1+{\displaystyle \sum _{m=1}^M{P}_{k,m}}{\gamma }_{k,m})}}{P_0{\tau }_0(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E{\tau }_0+{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M(P_{k,m}{\tau }_k+P_{C_{k,m}}{\tau }_k)}}}}\end{array} \\ \begin{array}{cc}\hfill s.t.C1:& {\tau }_0+{\displaystyle \sum _{k=1}^K{\tau }_k}\le T_{\max }\hfill \\ \hfill C2:& P_0\le P_{\max }\hfill \\ \hfill C3:& P_{k,m}{\tau }_k+P_{C_{k,m}}{\tau }_k\le \eta P_0{\tau }_0{G}_{k,m},\forall k\in \mathsf{\Phi },\forall m\in \mathsf{\Omega }\hfill \\ \hfill C4:& {\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1+{\displaystyle \sum _{m=1}^M{P}_{k,m}{\gamma }_{k,m}})}\ge R_{\min }\hfill \\ \hfill C5:& ({\tau }_k{\log }_2\left(1+{\mathrm{SIN}\mathrm{R}}_{k,i}\right)\ge {\displaystyle \frac{{\theta }_{k,i}}{1-e^{-{\theta }_{k,i}{\Gamma }_{k,i}}}})\hfill \\ \hfill C6:& P_{k,i}\le {\displaystyle \frac{\eta P_{\max }{G}_{k,i}{\tau }_d-P_{c,k,i}{\tau }_k}{{\tau }_k}}\hfill \\ \hfill C7:& {\tau }_0\ge 0,{\tau }_k\ge 0,P_{k,m}\ge 0,\forall k\in \mathsf{\Phi },\forall m\in \mathsf{\Omega }\hfill \end{array} \end{gathered}$$

(16)

It can be seen from Problem (16) that C1 is a time limit, and C2 restricts the maximum allowable transmitting power of UAVs in the downlink to $P_{\max }$. C3 is an energy consumption constraint, and it clearly states that in the uplink transmissions, the energy harvested by each regional SN during the energy transmission phase is the upper limit of its available energy, and the energy consumed by the SN during operation cannot exceed this upper limit. C4 is a quality constraint, which specifies that the minimum throughput of the system is a constant, denoted by $R_{\min }$. C5 is effective capacity constraint. ${\theta }_{k,i}$ is the delay exponent (larger $\theta$ = stricter delay QoS) and ${\Gamma }_{k,i}$ is the minimum throughput requirement.

4. Problem Analysis

The objective function of Problem (14) has a fractional structure and involves coupled optimization variables, making Problem (14) non-convex. However, traditional optimization methods are not directly applicable. To address this problem more effectively, two lemmas were introduced and proven in this section.

Lemma 1.

If the system adopts the optimal resource allocation strategy, all nodes can fully consume the energy they have harvested, i.e.,

$$P_{k,m}{\tau }_k+P_{C_{k,m}}{\tau }_k=\eta P_0{\tau }_0{G}_{k,m}$$

(17)

Proof. 

The proof of Lemma 1 employs the reduction to absurdity. Suppose $\{{\tau }_0^{*},\{{\tau }_k^{*}\},P_0^{*},\{P_{k,m}^{*}\left\}\right\}$ is the optimal solution to Problem (16) and $P_{k,m}^{*}{\tau }_k^{*}+P_{C_{k,m}}{\tau }_k^{*}<\eta P_0^{*}{\tau }_0^{*}{h}_{k,m}$ is the satisfied condition of optimal solution. Meanwhile, the optimal solution for energy efficiency is $E{E}^{*}$. A feasible solution can be constructed as $\{{\tilde{\tau }}_0,\{{\tilde{\tau }}_k\},{\tilde{P}}_0,\{{\tilde{P}}_{k,m}\left\}\right\}$, such that ${\tilde{P}}_0=P_0^{*}$, ${\tilde{\tau }}_k={\tau }_k^{*}$ and ${\tilde{P}}_{k,m}=P_{k,m}^{*}$, so the optimal value of the optimal energy efficiency is $\widetilde{EE}$. Since $P_{k,m}^{*}{\tau }_k^{*}+P_{C_{k,m}}{\tau }_k^{*}<\eta P_0^{*}{\tau }_0^{*}{h}_{k,m}$, in the feasible solution, the energy harvesting time of the SN’s ${\tilde{\tau }}_0$ can be shortened, enabling the SN to utilize all the energy it has harvested during information and data transmission, that is, ${\tilde{\tau }}_0=\lambda {\tau }_0^{*}(0<\lambda <1)$, and ${\tilde{P}}_{k,m}{\tilde{\tau }}_k+P_{C_{k,m}}{\tilde{\tau }}_k=\eta {\tilde{P}}_0{\tilde{\tau }}_0{h}_{k,m}$ is also satisfied, where $\lambda$ denotes the proportion of the reduction in energy transmission time to the total energy transmission time. Both solutions above satisfy the constraints C1~C5. Therefore, the feasible solution can be expressed as $\{\lambda {\tau }_0^{*},\{{\tau }_k^{*}\},P_0^{*},\{P_{k,m}^{*}\left\}\right\}$, which is then substituted into the objective function of Problem (14), yielding:

$$\widetilde{EE}={\displaystyle \frac{{\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1+{\displaystyle \sum _{m=1}^M{P}_{k,m}}{\gamma }_{k,m})}}{P_0^{*}(\lambda {\tau }_0^{*})(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E(\lambda {\tau }_0^{*})+{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M(P_{k,m}^{*}{\tau }_k^{*}+P_{C_{k,m}}{\tau }_k^{*})}}}}$$

(18)

Suppose there exists a resource allocation strategy so that all nodes can retain a portion of their available energy during transmission. However, according to the condition $0<\lambda <1$, this leads to a contradiction with the assumed resource allocation strategy. Therefore, when maximizing energy efficiency, all nodes will fully consume the energy they have harvested during transmission.

Unlike traditional energy efficiency optimization problems that assume full energy consumption a priori, Lemma 1 proves that full energy consumption $E_{k,i}^{\mathrm{harvested}}=E_{k,i}^{\mathrm{consumed}}$ is a necessary condition for the optimal solution of Problem (17) in our system. In this system, all sensor nodes (SNs) use the energy supplied by the UAV for information transmission. If energy remains in a node’s battery after completing data transmission, the UAV only needs to transfer less energy to that node, thereby improving the overall system energy efficiency. □

Lemma 2.

If the system makes optimal decisions on resource allocation, the UAV will transmit signals at maximum power to achieve the best communication performance. That is, under this strategy, the UAV needs to utilize its available energy resources as much as possible to maximize the energy efficiency of the entire system, i.e., $P_0=P_{\max }$.

Proof. 

Suppose $\{{\tau }_0^{*},\{{\tau }_k^{*}\},P_0^{*},\{P_{k,m}^{*}\left\}\right\}$ is the optimal solution to Problems (4)–(14), and $P_0^{*}<P_{\max }$ is the satisfied condition in the optimal solution. Meanwhile, $E_0^{*}\triangleq P_0^{*}{\tau }_0^{*}$ represents the total energy transmitted by the UAV, and $E{E}^{*}$ is the optimal energy efficiency under this condition. $\{{\tilde{\tau }}_0,\{{\tilde{\tau }}_k\},{\tilde{P}}_0,\{{\tilde{P}}_{k,m}\left\}\right\}$ is a further constructed feasible solution, with ${\tilde{\tau }}_k={\tau }_k^{*}$, ${\tilde{P}}_0=P_0^{*}$, ${\tilde{P}}_{k,m}=P_{k,m}^{*}$, and $E_0^{*}={\tilde{P}}_0{\tilde{\tau }}_0$ being the conditions satisfied by this feasible solution, and $\widetilde{EE}$ denotes the optimal value of energy efficiency. It can be known from the optimal solution that ${\tilde{P}}_0=P_{\max }>P_0^{*}$, and according to the given conditions of the problem, the energy harvesting time in the optimal solution is shorter than that in the feasible solution, i.e., ${\tilde{\tau }}_0<{\tau }_0^{*}$, holds. Both sets of solutions satisfy the constraints C1~C5. When substituting them into the objective function, it can be found that the first two terms in the denominator of the objective function satisfy the following relationship:

$${\tilde{P}}_0{\tilde{\tau }}_0(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E{\tilde{\tau }}_0<P_0^{*}{\tau }_0^{*}(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E{\tau }_0^{*}$$

(19)

To maximize energy efficiency, the UAV transmits energy information at $P_{\max }$, in which case $E{E}^{*}<\widetilde{EE}$ is obtained. However, this contradicts the assumption that $\{{\tau }_0^{*},\{{\tau }_k^{*}\},P_0^{*},\{P_{k,m}^{*}\left\}\right\}$ is the optimal solution to Problem (16). This indicates that the UAV always selects the maximum transmit power when sending energy information to maximize energy efficiency. □

According to Lemma 1 and Lemma 2, to maximize energy efficiency, it is only necessary to optimize variables such as ${\tau }_0$, $\left\{{\tau }_k\right\}$, and $\left\{P_{k,m}\right\}$. To further simplify the objective function, $P_{k,m}=\eta P_0{\tau }_0{h}_{k,m}/{\tau }_k-P_{C_{k,m}}$ and $P_0=P_{\max }$ can be substituted into the objective function of Problem (15) for solution transformation. Problem (16) can be equivalently expressed as:

$$\begin{gathered} \begin{array}{l}{\max }_{{\tau }_0,\left\{{\tau }_m\right\}}{\displaystyle \frac{{\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1-{\displaystyle \sum _{m=1}^M{P}_{C_{k,m}}{\gamma }_{k,m}}+{\displaystyle \sum _{m=1}^M\eta P_{\max }{h}_{k,m}{\gamma }_{k,m}\frac{{\tau }_0}{{\tau }_k}})}}{P_{\max }{\tau }_0(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E{\tau }_0+{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M(\eta {\tau }_0{P}_{\max }{h}_{k,m})}}}}\end{array} \\ \begin{array}{cc}\hfill s.t.C1:& {\tau }_0+{\displaystyle \sum _{k=1}^K{\tau }_k}\le T_{\max }\hfill \\ \hfill C2:& {\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1-{\displaystyle \sum _{m=1}^M{P}_{C_{k,m}}{\gamma }_{k,m}}+{\displaystyle \sum _{m=1}^M\eta P_{\max }{h}_{k,m}{\gamma }_{k,m}\frac{{\tau }_0}{{\tau }_k}})\ge R_{\min }}\hfill \\ \hfill C3:& {\tau }_0\ge 0,{\tau }_m\ge 0,\forall k\in \mathsf{\Phi },\forall m\in \mathsf{\Omega }\hfill \end{array} \end{gathered}$$

(20)

Although the transformed Problem (19) is more manageable than the original Problem (14), it remains a non-convex problem and thus cannot be easily solved using methods such as nonlinear fractional programming. For the sake of generality, this paper assumed that the maximum energy efficiency achievable in Problem (20) is denoted as $q^{*}$, which is expressed by the following formula:

$$q^{*}={\max }_{{\tau }_0,\left\{{\tau }_k\right\},\left\{P_{k,m}\right\}}{\displaystyle \frac{R_{sum}(\{{\tau }_k\},\{P_{k,m}\})}{E_{sum}({\tau }_0,\{{\tau }_k\},\{P_{k,m}\})}}$$

(21)

The objective function of Problem (18) can be equivalently transformed into a subtractive form. Thus the transformed Problem (18) can be equivalently converted into the following form:

$$\begin{gathered} \begin{array}{l}{\max }_{{\tau }_0,\left\{{\tau }_k\right\}}{\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1-1-{\displaystyle \sum _{m=1}^M{P}_{C_{k,m}}{\gamma }_{k,m}}+{\displaystyle \sum _{m=1}^M\eta P_{\max }{h}_{k,m}{\gamma }_{k,m}\frac{{\tau }_0}{{\tau }_k}})}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-q[{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M(\eta {\tau }_0{P}_{\max }{G}_{k,m})}}+P_{\max }{\tau }_0(1-{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{m=1}^M\eta G_{k,m}}})+P_E{\tau }_0]\end{array} \\ \begin{array}{cc}\hfill \hspace{1em}s.t.C1:& {\tau }_0+{\displaystyle \sum _{k=1}^K{\tau }_k}\le T_{\max }\hfill \\ \hfill C2:& {\displaystyle \sum _{k=1}^K{\tau }_k{\log }_2(1-{\displaystyle \sum _{m=1}^M{P}_{C_{k,m}}{\gamma }_{k,m}}+{\displaystyle \sum _{m=1}^M\eta P_{\max }{G}_{k,m}{\gamma }_{k,m}\frac{{\tau }_0}{{\tau }_k}})\ge R_{\min }}\hfill \\ \hfill C3:& {\tau }_0\ge 0,{\tau }_m\ge 0,\forall k\in \mathsf{\Phi },\forall m\in \mathsf{\Omega }\hfill \end{array} \end{gathered}$$

(22)

By assigning a specific value to $q$, Problem (22) can be determined to be a convex problem. This is because when $q$ is fixed, the first term of the objective function (22) is a concave function, which can also be referred to as a convex-down function. The second and third terms of the objective function (22) are linear functions, whose graphs are straight lines with constant slopes and intercepts. To solve the optimal value of this standard convex optimization problem, the interior point method is employed.

As shown in Algorithm 1, in this paper, we adopted the iterative descent of the block coordinate (IDBC) algorithm to solve the optimal value $q^{*}$. The specific solution steps are organized as follows. First, we initialized the number of iterations, UAV transmit power, error precision, minimum system network throughput requirement, and the value of $q$; in each iteration, first assign a value to $q$, then solve Problem (21) to find the optimal energy efficiency under this value. Next, update the value of $q$ according to Equation (19), and then use Problem (20) to update $q$ until it converges. The optimal solution of energy efficiency $EE$ is achieved when $q^{*}$ reaches its maximum value, which also means that the optimal solution of energy efficiency can be obtained by finding the maximum value of variable $q^{*}$. Therefore, this algorithm iteratively updates the value of $q$ to gradually increase the maximum energy efficiency and obtain the optimal solution.

Algorithm 1: Iterative Descent of Block Coordinate

Input: iterations $n=0$, UAV transmitting power $P_{\max }$, error precision $\xi$, minimum system network throughput requirement $R_{\min }$, $q^{(0)}$; Output: Optimal value $E{E}^{*}$

While $\left|q_{(n)}-q_{(n-1)}\right|>\xi$, do: 1:   $n=n+1$;

2:   Given $q^{(n)}$, solve (4)–(20) through interior point method to derive the uplink and downlink time allocation strategy ${{\tau }_0}^{(n)}$, $\left\{{{\tau }_k}^{(n)}\right\}$;

3:    From Lemma 1 and Lemma 2, derive UAV and SN transmitting power $\{{P_0}^{(n)},\{{P_{k,m}}^{(n)}\left\}\right\}$;

4:    From ${{\tau }_0}^{(n)}$, $\left\{{{\tau }_k}^{(n)}\right\}$ and $\{{P_0}^{(n)},\{{P_{k,m}}^{(n)}\left\}\right\}$, calculate $R_{sum}^{(n)}(\{{\tau }_k^{(n)}\},\{P_{k,m}^{(n)}\})$;

5:    From ${{\tau }_0}^{(n)}$, $\left\{{{\tau }_k}^{(n)}\right\}$ and $\{{P_0}^{(n)},\{{P_k}^{(n)}\left\}\right\}$, calculate $E_{sum}^{(n)}({\tau }_0^{(n)},\{{\tau }_k^{(n)}\},\{P_{k,m}^{(n)}\})$; 6:    If $\left|q_{(n)}-q_{(n-1)}\right|\le \xi$, do: 7:   Optimal value $E{E}^{*}$ is derived. Optimal resource allocation strategy is ${{\tau }_0}^{(n)}$, $\left\{{{\tau }_k}^{(n)}\right\}$, $\{{P_0}^{(n)},\{{P_{k,m}}^{(n)}\left\}\right\}$. 8:    Else, do:

$q^{(n)}$ is updated calculate $q^{(n)}={\displaystyle \frac{R_{sum}^{(n)}(\{{\tau }_k^{(n)}\},\{P_{k,m}^{(n)}\})}{E_{sum}^{(n)}({\tau }_0^{(n)},\{{\tau }_k^{(n)}\},\{P_{k,m}^{(n)}\})}}$,

5. Simulation Results

In this section, we evaluate the performance of the proposed iterative descent of the block coordinate (IDBC) algorithm through simulations. To demonstrate the superior performance of the proposed algorithm, we compared the performance with other benchmark strategies—fixed time allocation strategy (FTAS) and throughput maximization strategy (TMS). In FTAS, the power allocation scheme was derived from Lemma 1 and Lemma 2, with the downlink time fixed at ${\tau }_0=T_{\max }/2$, and the uplink time evenly allocated as ${\tau }_k=(1-{\tau }_0)/K$. Meanwhile, the goal of TMS is to find the maximum value of network throughput $R_{sum}={\displaystyle {\sum }_{k=1}^K{\tau }_k{\log }_2(1+{\displaystyle {\sum }_{m=1}^M{P}_{k,m}{\gamma }_{k,m}})}$, and its power allocation scheme corresponds with that of the FTAS, both adopting the interior-point method to acquire the optimal time allocation under its own strategy. In summary, we compared the effects of different strategies through extensive simulations and verified the effectiveness of the proposed algorithm based on the experimental results.

In the simulation, we set up 10 nodes, and divided them into 5 regions, where each region contained 2 nodes, i.e., $K=5,M=2$ SNs were randomly distributed in a 200 m × 200 m area (consistent with urban/suburban IoT deployments), with the UAV hovering at 100 m, 100 m, and 50 m. The distance between the UAV and SNs ranged from 30 m to 150 m (instead of being equal), reflecting real-world spatial heterogeneity. The channel power gain of the wireless uplink/downlink is denoted as $h_{k,m}={10}^{-3}{\rho }_{k,m}^2{d}_{m,n}^{-\alpha }$, wherein $d_{m,n}$ represents the distance from the UAV to node $S{N}_{k,m}$. The path loss factor describes the Rayleigh fading phenomenon occurring in small scales, and in our simulation, its parameters were set as $\alpha =2.2$, with the exponential random variable ${\rho }_{k,m}^2$ having a mean value of 1. We set the system bandwidth as 180 kHz. The noise power spectral density was −170 dBm/Hz, and noise power was set as ${\sigma }^2=-117\mathrm{dBm}$. UAV maxima transmit power was set as $P_{\max }=40\mathrm{dBm}$. The circuit power consumption of UAV was 10 $\mathrm{mW}$, and the circuit power consumption of a node terminal was 0.05 $\mathrm{mW}$. The maximum transmission time $T_{\max }=1\mathrm{s}$ represents the time required for the $K+1_{th}$ blocks to transmit, and the minimum rate requirement of the node is $R_{\min }=100\mathrm{bits}/\mathrm{Hz}$. The iteration convergence threshold was set to $\xi =0.0001$.

In terms of evaluation metrics, average energy efficiency was calculated through the averaging of energy efficiencies from randomly selected 100 samples under random channel conditions, with the unit of bits/Joule/Hz. The unit of average network efficiency has the unit of bits/Joule/Hz.

As depicted in Figure 3, under varying maximum transmit powers of the UAV, the three distinct strategies exhibited different average energy efficiencies. From the blue-marked lines, we can see that in the IDBC scheme, the average energy efficiency increased as the transmit power of the UAV increased. However, after reaching a certain power threshold, around 25 ${\mathrm{dB}}_{\mathrm{m}}$, the energy efficiency slowed down its increasing trend and gradually reached a stable state. This is because after exceeding a certain point, increasing the transmit power only resulted in a rise in energy consumption rate, whereas the collection rate remained constrained. Nevertheless, the energy efficiency exhibited by the other two comparative algorithms demonstrated a slightly different pattern that it first increased with the transmitting power, within a certain range, and after some point, it started to decrease instead. To explain this, we use the TMS scheme as an example. The TMS scheme’s primary objective is to improve system throughput. Thus, when the system throughput reaches the current system capacity, the throughput is not increasing any longer while the energy consumption keeps going up, resulting in a decrease in system energy efficiency after that. This is similar to the FTAS scheme, in which the primary goal is fixed-time allocation. Overall, among the three schemes, our proposed IDBC achieved the optimal performance in terms of average energy efficiency.

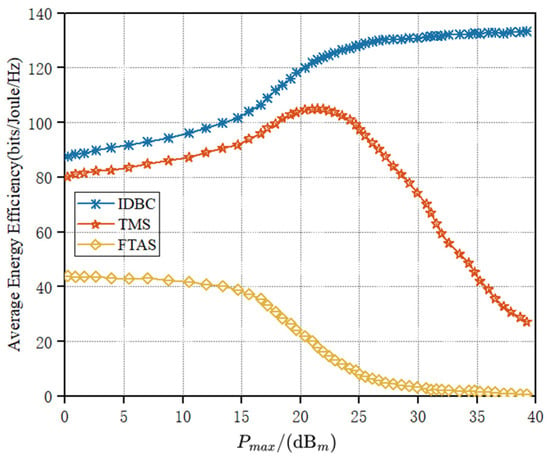
Figure 3. UAV transmitting power versus average energy efficiency.

As depicted in Figure 4, under different maximum transmit powers of the UAV, the three algorithms exhibited different performances in terms of the average network throughput. From a general view of the figure, it can be observed that the average network throughput improved with the increase in transmit power, and this is because increasing transmit power leads to an improvement in the energy harvesting rate, thereby enhancing the average network throughput of the system. Since all three schemes operated under the same energy constraints and time constraints, and therefore under the same conditions, the average network throughput improved with the increase in the UAV’s transmit power. This phenomenon indicates that within a certain power range, increasing the transmit power can improve the system performance in terms of network throughput. Among the comparison schemes, the average throughput performance obtained by the TMS was superior to the IDBC.

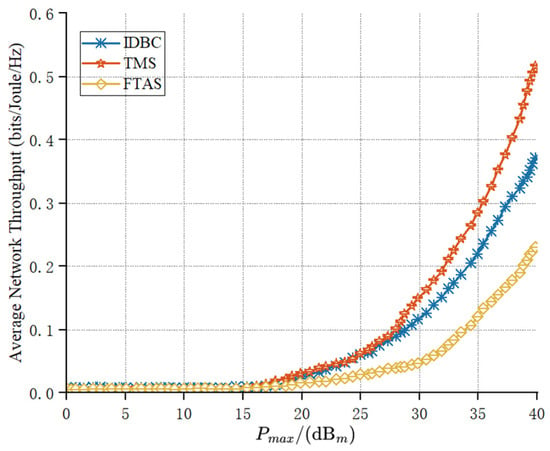
Figure 4. UAV transmitting power versus average network throughput.

Figure 5 illustrates the relationship between the average energy efficiency and the distance from nodes to the UAV ($P_{\max }=15\mathrm{dBm}$) among the three compared algorithms. As observed from the drawn curves, the average energy efficiency of the system gradually decreases as the distance between the nodes and the UAV increases. The main reason is that a shorter distance results in better channel gain, thereby enabling more efficient energy utilization, whereas a greater distance between nodes and the UAV leads to increased energy loss during transmission. Optimally deploying node positions allows nodes to harvest more energy for information and data transmission, thereby improving system throughput and energy efficiency, which is an essential aspect in practical network design. Furthermore, Figure 5 shows that our proposed IDBC scheme exhibited the optimal performance in terms of energy efficiency performance.

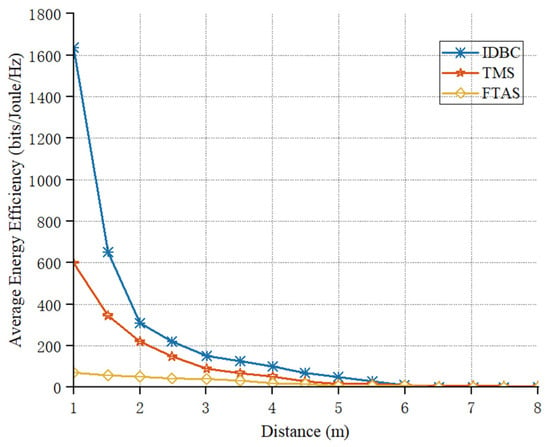
Figure 5. Distance from base station to nodes versus average energy efficiency.

As depicted in Figure 6, the average energy efficiency varied under different path loss factors across the three different comparison schemes ($P_{\max }=15\mathrm{dBm}$, $d_m=3\mathrm{m}$). It can be observed that there is a clear relationship between path loss factors and average energy efficiency. As the path loss factor increased, the average system energy efficiency decreased rapidly. This is because the greater path loss factor indicates greater resistance or loss encountered during signal transmission, which reduces the energy received by the UAV. As a result, it lowers the average energy efficiency of the system and fails to meet the energy requirements for system operation. Therefore, reducing the path loss effects in wireless communication environment is one of the most important means to improve system energy efficiency. Furthermore, it can be observed that the FTAS scheme exhibited a slower downward trend compared to the other two algorithms.

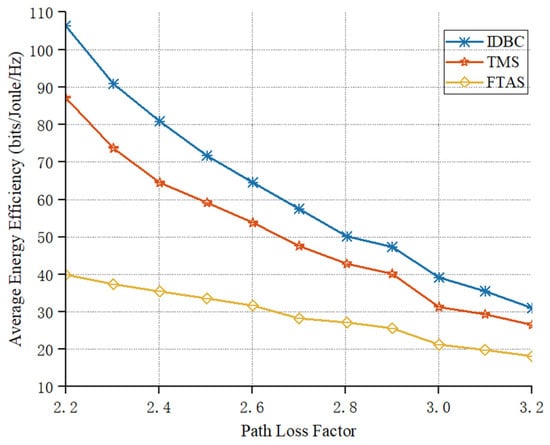
Figure 6. Path loss factor versus average energy efficiency.

6. Conclusions

In this paper, we investigated a resource allocation scheme for a UAV-BS to serve a group of users with heterogeneous delay-constrained QoS requirements in the downlink across diverse environments. Specifically, we formulated a resource allocation problem that aimed to maximize the total energy efficiency of all users by jointly optimizing the UAV’s energy and data transmission time, its transmission power, and the users’ transmission power. To solve this problem, we proposed a fractional programming approach combined with a block coordinate descent algorithm. Numerical simulation results demonstrated that the proposed algorithm significantly outperformed benchmark schemes in terms of overall energy efficiency. As for our future research direction, UAVs in power grid IoT face EMI from high-voltage equipment. This can degrade the channel quality (e.g., increase fading variance by 20%) and disrupt SIC decoding. Our future work will integrate EMI-aware channel models (e.g., Rician fading with EMI-induced noise) into the optimization framework. In addition, we will also consider how to avoid interference caused by external factors in this model for robustness, such as UAV gimbal/motor systems generating electromagnetic noise that degrades the onboard sensor performance. Our future work will integrate both interference mitigation and robust optimization.