Multiple Attention Group Event Recommendation with Fine-Grained Features

Abstract

Event-based social network is a novel platform where users establish social relationships and realize interest matching through participation in offline events. However, event recommendation faces severe challenges, including extreme data sparsity due to the short life cycles of events, and the dynamic interplay between individual and group preferences on fine-grained features. Existing methods ignore the users’ diverse and personalized preferences across different event features such as venue and organizer. We first conduct a data analysis to argue that not only do users themselves have different preferences for different features, but more importantly, these preferences dynamically influence the behavior of different groups they belong to. Therefore, in this work, we propose a novel Multiple Attention Group Event Recommendation (MAGER) framework based on Neural Collaborative Filtering to address these challenges. MAGER first employs fine-grained feature attention to generate personalized event representations, and then dynamically aggregates member preferences and influences through a group-level attention mechanism. More importantly, a heterogeneous attention structure integrates these learning modules, enabling generation of more accurate representations of event, users, and groups. We conduct extensive experiments on three-real world datasets, the experimental results show that MAGER achieves substantial improvements in user and group recommendations effectiveness compared to baselines in terms of HR@K and NDCG@K. Specifically, HR@5 improvement of 3.63–13.07%; NDCG@K improvement of 5.63–18.55% for user recommendation, and HR@5 improvement of 2.05–19.02%; NDCG@K improvement of 2.51–36.12% for group recommendation on three dataset.

1. Introduction

1.1. Research Background

Event-based Social Networks (EBSNs) as a novel social network, such as Douban-Event (http://beijing.douban.com/, accessed on 23 November 2025) and Meetup (http://www.meetup.com/, accessed on 23 November 2025), gradually attracting the increasing attention of academia [1] and industry [2,3,4,5]. Unlike traditional social networks, users on EBSN participation in offline or online events, users not only establish social relationships in the network, but also realize interest matching and offline interaction by participating in various events. Event has the characteristics of a short life cycle and a strong timeliness, so it is usually necessary to recommend appropriate events to users before the event starts, so as to ensure that users make participation decisions in a limited time [6,7]. However, event often do not accumulate enough history interaction before recommendation, which makes the event recommendation face a serious sparse interaction problem, which seriously affects the performance of recommender systems in EBSN scenarios.

1.2. Analysis of Existing Problems

In event recommendation scenario, previous studies mainly focus on how to exploit the event context features to alleviate the data sparsity problem. For example, Du et al. [6], Liao et al. [8], and Wang et al. [9] both propose methods to model event features using multidimensional context information, which improve the recommendation effect to a certain extent. Furthermore, Macedo et al. [10] propose a multi-context learn-to-rank framework, which comprehensively considers the user’s social relationship, event content, and time preference characteristics, and improves the accuracy of recommendation. Du et al. [11] utilize the intrinsic correlation between the event organizer and the event content to recommend event for group, which alleviates the problem of feature sparsity caused by the insufficient information of the event text. Specific features can effectively alleviate the sparse interaction problem, and improving the interpretability of the recommendation [12]. However, they still adopt a feature stacking strategy on the individual level, ignoring the personalized preferences of users on fine-grained features from the group view.

Intuitively, users have different degree preferences for different features such as venue, time, etc. Take an instance, as shown in Figure 1a, user2 prefers to participate in events at daytime but prefers outdoor events over indoor ones. And user3 prefers the event on weekends but has a greater preference for indoor. The difference in one feature may have a significant impact on the user’s behavior. This phenomenon shows that the exploiting of fine-grained feature plays a non-negligible role in accurately capturing user interests and their behavior patterns. Considering this challenge, Lai et al. [13] calculate user’s preference scores separately for different features of target event, such as proposing a soft spatial constraint to compute spatiotemporal preference scores. However, these preference scores from various features are simply linearly superimposed and separately computed user preferences across different features, there is a lack of a concise strategy that effectively unifies user preferences across multiple features. More important, users’ different preferences for fine-grained features have a decisive influence in group decision, as shown in Figure 1b, users’ preference for fine-grained features is a decisive factor in group behavior.

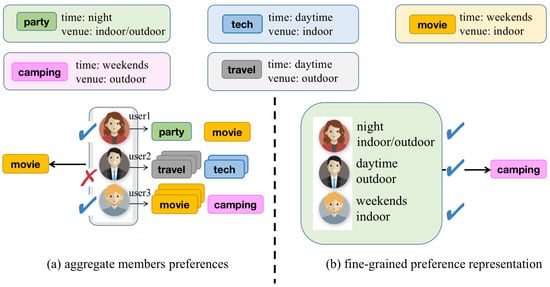
Figure 1. A case: the influence of a user’s interest under event features on their group.

Unlike simple aggregation methods based on historical interactions, such as AGREE [14], which only measure the preferences of members at the user–item interaction level, this consideration can help the group discover events that better align with the group consensus intentions, enhancing group satisfaction. In the group recommendation problem, the interests of group members are different, and their influence on the group behavior is also different. Some studies [15,16] start trying to use the deep method based to modeling group behavior. For example, the ConsRec [17] uses hypergraph learning to reduce the complexity of the aggregation process. However, these methods often ignore the importance of fine-grained features under sparse interactions problem, we argue that such coarse-grained strategies are ineffective to learning member preference and result in the imprecise for group representation.

1.3. Solutions and Advantages

To formalize the significance of fine-grained features for event recommendation, we present the sparse interaction situation between user/group and event, as well as between user/group and fine-grained features in a quantitative manner. We calculate the sparsity of user/group–event interactions and user/group–feature interactions in the Douban-Event and Meetup datasets. The results are shown in Table 1. For each dataset, we randomly select 1000 users and 1000 groups and compute their proportion of interaction with events and each fine-grained feature. Here, the variables $o,v,w,h$ represent the organizer, venue, week, and hour features, respectively, as defined in Section 3. From the results in Table 1, we observe that in the Douban-Event, $f_e$ is the smallest, indicating that user–event interactions are the sparsest, while $f_o, f_v, f_w, f_h$ are relatively larger, meaning that user/group interactions with each feature are denser. By contrast, in the Meetup, $f_o$ is smaller than $f_e$ because many of the events attended by a user/group are organized by the same organizer, which leads to a very low $f_o$ values.

Table 1. The proportion of interaction with events and the proportion of interaction with each features with randomly an User and a Group in Douban-Event Beijing dataset (the $f_e$ is the proportion of the number of events that user/group has participated in to the total number of events, and the $f_o$ is the proportion of the number of organizer that user/group has participated in to the total number of organizers, etc.).

Object	Douban-Event Beijing
	${\mathit{f}}_{\mathit{e}}$	${\mathit{f}}_{\mathit{o}}$	${\mathit{f}}_{\mathit{v}}$	${\mathit{f}}_{\mathit{w}}$	${\mathit{f}}_{\mathit{h}}$
User	0.0053	0.0108	0.0073	0.5736	0.0498
Group	0.0025	0.0088	0.0035	0.4286	0.0417
Object	Meetup Phoeix
	${\mathit{f}}_{\mathit{e}}$	${\mathit{f}}_{\mathit{o}}$	${\mathit{f}}_{\mathit{v}}$	${\mathit{f}}_{\mathit{w}}$	${\mathit{f}}_{\mathit{h}}$
User	0.0067	0.0022	0.0505	0.8740	0.5226
Group	0.0073	0.0020	0.0507	1.0000	0.5417

In summary, user/group interactions with fine-grained features are denser and beneficial for event recommendation, making the mining of fine-grained features crucial. Therefore, this paper aims to address the problem of extreme sparsity of user/group event by exploiting the user/group preferences for fine-grained features of event, proposing a multiple attention based group recommendation framework. Specifically, the two key challenges are as follows: I. The problem of extreme sparsity of user/group-event, since events often have short life cycles in EBSNs, making it difficult to accumulate historical feedback. II. The lack of a member-level fine-grained feature fusion framework with group-oriented, where insufficient exploration of users’ diverse preferences for event features leads to neglecting the impact of members’ dynamic fine-grained preferences on group decision-making.

1.4. Main Work and Structure

In this paper, we propose a multiple attention mechanism that initially obtains personalized event representation through fine-grained feature modeling, followed by aggregation at the group-level based on member influence to derive precise group preference representation. Building upon this foundation, we present a group event recommendation framework named MAGER (Multi-level Attention Group Event Recommendation). Inspired by Neural Collaborative Filtering, this framework aims to simultaneously capture interaction information between event and user/group. Specifically, the MAGER framework first generates the initial user embedding by using a mechanism based on time decay. Subsequently, we obtain event embeddings through a fine-grained feature attention across different features, and an attention module further integrates members’ event preferences with their influence within the group to generate the aggregated group representation. This hierarchical attention mechanism not only effectively addresses challenges caused by sparse interaction data in event recommendation but also enables precise capture of user preferences at the feature-level, thereby providing a more nuanced basis for group decision-making.

The main contributions of this work can be summarized as follows:

• We conduct data analysis to demonstrate that user/group interactions with fine-grained features are denser than the interactions with events, which helps alleviate the recommendation accuracy degradation. Furthermore, we explore how different members’ diverse preferences for features influence the behavior of different groups.
• We first propose a group recommendation framework that integrates fine-grained feature attention with member weight attention, capable of capturing both personalized interests of group members and their relative influence within the group.
• To address the challenges of sparse textual content and insufficient interactions, we design a fine-grained feature attention module that extracts users’ latent interest features from multiple features.
• We conduct extensive experiments on three real-world EBSN datasets, the results show that MAGER framework has significant improvements in both recommendation effectiveness and efficiency compare with state-of-the-art methods.

The remaining sections of this paper are organized as follows: Section 2 introduces related work including reviews the research of event recommendations in EBSNs and group recommendation. Section 3 is problem definition that formalizes the task of our work and introduces all parameters used in our model. Section 4 gives a data analysis case. Section 5 provides a detailed description of our proposed MAGER framework. Section 6 reports experimental results and corresponding analyses. Section 7 discusses this paper.

2. Related Work

2.1. Event Recommendation in EBSNs

Event recommendation in EBSNs has emerged as a critical research area, addressing challenges such as cold-start, data sparsity. Existing studies propose diverse methodologies to enhance recommendation accuracy by leveraging multi-dimensional contextual and advanced machine learning techniques [12,18]. One prominent approach integrates multiple contextual signals to address the cold-start problem, Macedo et al. [10] combine content, collaborative, social, location, and temporal signals to rank events, demonstrating superior performance. Lai et al. [13] further distinguished preference factors from spatial–temporal constraints, using factorization machine to model user decisions under implicit feedback. Liu et al. [19] unify interactions among users, events, groups, and locations into a pairwise matrix factorization framework. These methods highlight the importance of multi-source contextual data in mitigating the transient nature of events.

Representation learning and graph-based models have gained traction for their ability to model heterogeneous relationships [20,21]. Zhang et al. [18] employ a denoising framework to attenuate noise in contextual features, enhancing robustness against data sparsity. Liu et al. [22] refine embeddings by propagating information through a user-event-intent graph, addressing feature sparsity via contextual intent nodes. Jiang et al. [23] extract semantic features from meta-graphs using convolutional networks and attention mechanisms, revealing latent user-event preferences. These works underscore the potential of graph structures in capturing complex entity interactions.

Social influences are increasingly recognized as vital factors. Taking into account the influence of adjacent event and users, Sun et al. [24] propose a social event matching method based on graph neural networks, designing an affinity calculation model to predict the affinity between users and new events, while considering the bilateral constraints extracted from user and event attributes. Liang et al. [25] introduce a prefiltering algorithm to balance global satisfaction and individual fairness, addressing biases in group recommendations. Additionally, taking into account the significance of the organizer, TrinhHuy et al. [26] estimate the scale of the participants for the event organizers, classifying the participants based on K-means clustering and trained a classification model using the constructed dataset to predict the scale of the new event. Han et al. [12] distinguish organizer roles and dynamic influence patterns, modeling their impact on user preferences through topic models.

2.2. Group Recommendation

Group recommendation focuses on providing items that meet the collective preferences of multiple users. Recent studies tackle challenges like data sparsity and dynamic group behaviors using graph models and attention. Li et al. [27] model user preferences by connecting sequences and dynamic group partner influences through dynamic graph structures. Liang et al. [28] enhance fuzzy preference profiling by representing user–group–item interactions as heterogeneous graphs, achieving robust performance in incomplete data scenarios. After they propose a hierarchical attention network for cross-domain group recommendation [29], transferring knowledge from data-rich domains to sparse target domains via adversarial learning. Huang et al. [30] propose a two-tower group recommendation framework that leverages similar-user features and multi-scale contrastive learning to more effectively model user–group interactions in EBSNs. The topic model has also attracted attention in the group recommendation task, Du et al. [11] propose a topic model based to alleviates cold-start issues by modeling organizer–content correlations.

Graph-based models dominate group recommendation research due to their ability to capture complex relationships. Liao et al. [31] integrate explicit and implicit information via multi-head attention on dual user-event graphs. Deng et al. [32] further incorporate users’ long- and short-term preferences using graph attention networks, fusing temporal dynamics with heterogeneous attributes for richer group representations. For occasional groups with limited interaction data, Guo et al. [33] employ hypergraph embedding to exploit group overlaps and user–user interactions, enhancing representation learning through hierarchical hyperedge embedding. Hypergraph convolution based recommendation models have been developed. Zhao et al. [34] disentangle member–item interactions via a masked autoencoder, mitigating noise through degree-sensitive masking and disentangled hypergraph convolutions. Wu et al. [17] explore group consensus through multi-view learning, utilizing hypergraph convolution for efficient aggregation. Attention mechanism-based methods, Yin et al. [35] leverage attention mechanisms and bipartite graph embeddings to model users’ global and local social influences, adapting weights dynamically across groups. Huang et al. [36] enhance group semantic features via multi-attention networks, integrating co-occurrence, social, and descriptive attributes to refine preference learning.

To conduct a more detailed comparison, we select some representative methods of group recommendation and compared them with MAGER to further highlight our novelty and differences, as shown in Table 2. Firstly, we can observe that group recommendation methods always aggregate member preference to generate group representation. The difference lies in the different network architectures designed, such as CVTM using a probabilistic generation model, HyperGroup using a graph convolutional network, while our MAGER utilizes a neural collaborative filtering architecture. Its advantage lies in the simple structure, stable training, and suitability for sparse data, etc. Secondly, we can observe that these comparison methods do not aggregate member preferences from fine-grained features perspective. For example, VTGAE [18] uses event spatiotemporal features, but only concatenates these features to generate event embeddings. This is also the way most methods handle item features. This method ignores the variability of users or groups’ preferences for different features. In summary, MAGER not only aggregates fine-grained features, member preferences, and group-level preferences for features, but more importantly, it forms a dependency relationship among the three attention modules, enabling it to capture the dynamic preferences of users and groups at different features. This is significantly different from other general co-attention networks.

Table 2. Comparison different methods. “agg.” denotes that the aggregation. “dynamic preference” denotes the initial embedding of user or group. Note: ✓: used; ✗: not used.

Methods	Aggregation Type	Member Agg.	Item-Level Feature Agg.	Feature Agg. for Individual	Dynamic Preference
CVTM [11]	Probability distribution	✓	✗	✓	✗
GBGCN [37]	GCN based propagation	✓	✗	✓	✗
AGREE [14]	Attention mechanism	✓	✗	✗	✗
Hyper Group [33]	Hypergraph represen.	✓	✗	✓	✗
ConsRec [17]	Hypergraph represen.	✓	✗	✓	✗
GroupIM [38]	MI Max. attention	✓	✗	✗	✗
GroupAV [39]	Attentive variation	✓	✗	✓	✗
DHMAE [34]	Hypergraph & atten.	✓	✗	✗	✗
MAGER	Attention mechanism	✓	✓	✓	✓

3. Problem Definition

We use a boldface capital letter to denote a matrix (e.g., X), a boldface lowercase letter to denote a vector (e.g., u), a capital squiggle letter to denote a set (e.g., $\mathcal{G}$), a capital letter to denote a amount (e.g., M), and a lowercase letter to denote a scalar (e.g., g). The notations of our model MAGER are shown in Table 3.

Table 3. Notations of MAGER parameters.

Notations	Description
$g,u,e$	a group, a user, a event
$v,o$	venue of event, organizer of event
$w,h$	day of week of event starting time, hour of day of event starting time
$\mathcal{G},\mathcal{U},\mathcal{E}$	groups set, users set, events set
$g_k,u_i,e_j$	the k-th group, the i-th user, the j-th event
$u_{k,m}$	the m-th member of k-th group
$\mathbf{X}$	group–event interaction matrix
$\mathbf{Y}$	user–event interaction matrix
$x_{gj}$	the interaction of the g-th group to the j-th event
$y_{ij}$	the interaction of the i-th user to the j-th event

A group set is represented as $\mathcal{G}=\{g_1,\dots ,g_K\}$, a event set is represented as $\mathcal{E}=\{e_1,\dots ,e_J\}$, and a user set is represented as $\mathcal{U}=\{u_1,\dots ,u_I\}$. Suppose that a group $g_k$ has M members, i.e., $g_k=\{u_1,\dots ,u_M\}$, and an event $e_j$ has four features: organizer $o_j$, venue $v_j$, day of week $w_j$ and hour of day $h_j$. Specifically, the organizer is an initiator of event, the venue is the location of event, and the starting time of the event is regarded as a two-dimensional time pattern, consisting of “week” and “hour”. Therefore, we define an event participation record as:

An Event Participation Record. When a user participates in an event, we can create an event participation record $(u,e,w,h,v,o)$. And when a group participates in an event, we can create an event participation record $(g,e,w,h,v,o)$. The w and h form a two-dimensional coordinate that event e started, which means the time pattern hour of day h and day of week w.

There are two participation interaction forms: user–event and group–event. We use X to denote group–event interaction matrix, i.e., $\mathbf{X}={\left[x_{gj}\right]}_{K\times J}$, where $\mathbf{X}(g,j)=1$ indicates group $g_k$ has participated in event $e_j$, and create a participation record $x_{gj}=(g,e,w,h,v,o)$. We use Y to denote user–event interaction matrix, i.e., $\mathbf{Y}={\left[y_{ij}\right]}_{I\times J}$, where $\mathbf{Y}(i,j)=1$ indicates user $u_i$ has participated in event $e_j$, and create a participation record $y_{ij}=(u,e,w,h,v,o)$. Our task is to recommend a rank event list to a group or a user, that is, to achieve both group recommendation task and personalized recommendation task. Formally, it is written as follows:

Input: User set $\mathcal{U}$, Group set $\mathcal{G}$, Event set $\mathcal{E}$, user–event interaction $\mathbf{Y}$, group–event interaction $\mathbf{X}$.

Output: A function $f_u:\mathcal{E}\to \mathcal{R}$, a function $f_g:\mathcal{E}\to \mathcal{R}$, which means to map an event to a real score for each user or each group.

4. Data Analysis and Motivation

The previous studies ignore the impact of users’ personalized preferences for fine-grained features of item on group decision-making. For instance, various aggregation-based methods such as AGREE [14], ConsRec [17] and PGR-PM [40] merely learn members’ dynamic preferences toward items. We argue that not only do users themselves have different preferences for different fine-grained features, but also these preferences dynamically influence the behavior of the different groups they belong to. For example, a student may personally prefer attending events on weekends, with their family group to frequently engage in weekend events, while their social group may only focus on party-related events without considering time constraints. It may be known that the student has high weight in their family group, and the decisions of the family group follow their preferences. However, when the student is in the social group, their time preference no longer exists; rather, they align with the will of the social group. This indicates that the student’s preferences for the fine-grained features change dynamically depending on the different groups they are in.

To elaborate further, we conduct a case study: a distribution chart is used to quantify the heterogeneity of individual preferences in terms of fine-grained features. Specifically, we randomly select a user and we statistically analysis the distribution of their fine-grained preferences for the events they participated in, as shown in Figure 2. A total of 18 events were participated, which were held by 10 different organizers, held at 7 different venues, and distributed across 3 different weeks, all scheduled within the same hour of the day. From the distribution of these features, it is evident that the user exhibits distinct preferences toward event features. For example, the user shows diverse preferences with respect to organizers, whereas their preference for the hour feature is highly concentrated.

Figure 2. The distribution of user preferences for fine-grained features of event.

Moreover, we demonstrate that there are significant differences in the attention weights that individual users assign to the features of the event when they participate in different groups. (1) We show the changes in a single user’s preference for specific features across different groups, as shown in Figure 3a. We select the same user and randomly identified two groups he had participated in, namely group 1 and group 2. We select the features that this user interacted with most frequently, such as organizer o_86, venue v_124, week w_0, and hour h_18, and calculate the frequency of participate for these features in group 1 and group 2. Here, the total number event participated in by group 1 and group 2 was 10 times each. It can be seen that group 1 has no preference for the o_86 and v_124 features, and group 2 has no preference for the o_86 feature. This proves that a single user’s preference for fine-grained features will significantly change as he moves between different groups. (2) We present the heat map of the attention weights for the event features when group 1 and group 2 participate in the same event. As shown in Figure 3b, we can observe that there is a significant difference in the attention weights given to the features by group 1 and group 2.

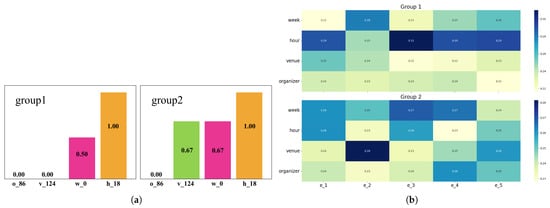
Figure 3. The distribution of attention weights that a single user assigns to the different features when participating in different groups. (a) user preference for features across groups; (b) weight heatmap of features for groups.

These findings again prove our motivation: users not only exhibit dynamic preferences for fine-grained features but also that these preferences further influence the decision-making of their groups.

5. Methodology

The differences between our MAGER and the general co-attention network as shown in Figure 4. The novelty of MAGER lies first in the use of multi-attention cross-feature to capture the fine-grained features of events, rather than simply aggregating through MLP. Secondly, MAGER includes dual-layer attentions on both user side and group side, while most general co-attention networks only contain a single-layer user–item attention. Most importantly, the attention calculation of MAGER relies on the candidate event context, rather than statically weighting members or historical behaviors. Specifically, the overall architecture of our model MAGER as shown in Figure 5, which illustrates the recommendation tasks in this paper, i.e., recommend well-pleasing events for groups or users. Specifically, the MAGER is divided into three components. The first one is Multiple Attention Group Representation Learning, the second is Neural Collaborative Filtering for modeling group–event interactions and user–event interactions, and the third is Recommendation and Optimization for learning model parameters. In the first component, we design three attention modules: the first one is obtaining the event representation ${\mathbf{e}}_j$ by using fine-grained features (such as $o_j,v_j,w_j,h_j$); the second is generating the group $g_k$’s aggregated preference embedding ${\mathbf{g}}_{k,j}^a$ based on the preferences of members; the third is obtaining the event representation at the group-level ${\mathbf{e}}_j^{g_k}$ by using fine-grained features.

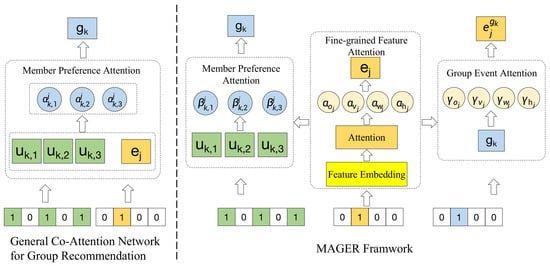
Figure 4. The comparison between the general co-attention network for group recommendation and the MAGER framework.

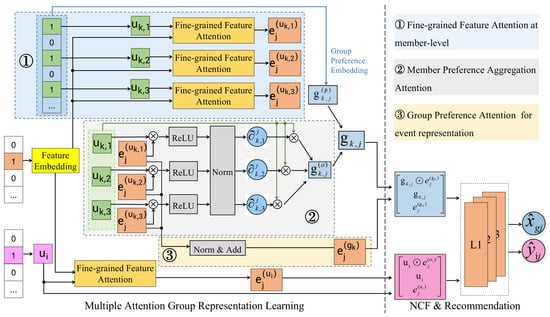
Figure 5. The framework of MAGER.

Furthermore, to generate the initial embeddings of users, we take into account the real-world scenario and that the interests of users and groups change over time, so we design a mechanism based on time decay to generate the dynamic preference representations of users. We assume that the historical interaction sequence of user u is ${\mathcal{H}}_u={\left\{(e_i,t_i)\right\}}_{i=1}^n$, where $e_i$ represents an interactive event and $t_i$ is the timestamp. The influence of the interaction term decreases with the passage of time. Therefore, we define the time decay weight as follows:

$${\sigma }_i=exp(-\tau (t_{now}-t_i))$$

(1)

where $\tau >0$ denotes the attenuation rate. Then the user’s dynamic preference embedding is

$${\mathbf{u}}_t={\displaystyle \frac{{\sum }_{i\in {\mathcal{H}}_u}{\sigma }_i{\mathbf{e}}_j}{{\sum }_{i\in {\mathcal{H}}_u}}}$$

(2)

where ${\mathbf{e}}_j$ is an event embedding that user u interacts with which is obtained based on “Fine-grained Attention” module. The dynamic user preference embedding is used to generate the group aggregated preference representation.

5.1. Multiple Attention Group Representation Learning

In this section, we introduce the significant module of our framework: Multiple Attention Group Representation Learning module that consists of three attention structures: (1) fine-grained feature-based attention event representation that first aims to learn event representation based on event features and target user by attentive mechanism; (2) member of group embedding aggregation that aims to estimate group preference on an event by a aggregate function; (3) group representation and group attention event representation which obtains final group embedding and corresponding event embedding. This three-level hierarchical attention structure, combined with the joint modeling of user- and group-level recommendations, is unique to our framework and specifically addresses the challenges in EBSNs.

5.1.1. Fine-Grained Feature-Based Attention for Event Representation

In EBSN scenarios, different users may have varying preferences for different features of event. Therefore, when modeling event representations, simply averaging or performing weighted summation of all features may fail to adequately capture users’ personalized preferences. To address this, we introduce a feature-based attention mechanism in this module to learn refined event representations, thereby better modeling users’ preference weights for different event features.

In this module, we learn event representation based on different features and target user. We propose a method to weight sum the embedding of different features, in which the weight parameters present the influence of each feature in deciding user behavior preference on event. To have an intuition for when a feature of event appears more in the preference behavior of a user, it should have more weight in the event representation. We assume event $e_j$ has four fine-grained features ${\mathcal{F}}_{e_j}=\{o_j,v_j,w_j,h_j\}$, each feature’s embedding vector are ${\mathbf{f}}_j^o$, ${\mathbf{f}}_j^v$, ${\mathbf{f}}_j^w$, ${\mathbf{f}}_j^h$, respectively. Assign an independent attention head to each feature $At{t}_{{\mathcal{F}}_{e_j}}$ as follows:

$${\mathbf{z}}_{o_j}=At{t}_{{\mathcal{F}}_{e_j}}\left({\mathbf{f}}_j^o\right)$$

(3)

$${\mathbf{z}}_{v_j}=At{t}_{{\mathcal{F}}_{e_j}}\left({\mathbf{f}}_j^v\right)$$

(4)

$${\mathbf{z}}_{w_j}=At{t}_{{\mathcal{F}}_{e_j}}\left({\mathbf{f}}_j^w\right)$$

(5)

$${\mathbf{z}}_{h_j}=At{t}_{{\mathcal{F}}_{e_j}}\left({\mathbf{f}}_j^h\right)$$

(6)

then influence weights of each feature are obtained through feature-level attention, taking the organizer feature as an example, the formula is as follow:

$${\alpha }_{o_j}={\displaystyle \frac{exp\left({\mathbf{q}}^{T}tanh\left({\mathbf{W}}_1{\mathbf{z}}_{o_j}\right)\right)}{{\sum }_{{\mathcal{F}}_{e_j}}exp\left({\mathbf{q}}^{T}tanh\left({\mathbf{W}}_1{\mathbf{z}}_{{\mathcal{F}}_{e_j}}\right)\right)}}$$

(7)

where the ${\mathbf{W}}_1$ is a learnable weight matrix, the $\mathbf{q}$ is a learnable vector. Then the final event representation is as follows:

$${\mathbf{e}}_j={\alpha }_{o_j}{\mathbf{z}}_{o_j}+{\alpha }_{v_j}{\mathbf{z}}_{v_j}+{\alpha }_{w_j}{\mathbf{z}}_{w_j}+{\alpha }_{h_j}{\mathbf{z}}_{h_j}$$

(8)

5.1.2. Member of Group Embedding Aggregation

After learning the feature-based attentive event representation, we further introduce a group representation module to integrate the interest features of group members and generate the final group embedding representation. Since group recommendations differ from personalized recommendations, a group consists of multiple members who may exhibit varying interests in the same event; thus, how to effectively aggregating members’ interest is a critical challenge in group recommendation task. Inspired by [14], we use a neural attention network to highlight the influence of members of group on target event for aggregating member embedding vector. In this module, each group $g_k=\{u_1,\dots ,u_{M_k}\}$, where the embedding representation of each member $u_{k,m}$ is derived through attention weighted computation with the target event. Subsequently, we assign a weight to each member in the group to measure their influence on the target event. The final group embedding representation is then generated by performing a weighted summation of the members’ embedding representations based on these weights.

Specifically, our goal is to learn a member-level attention weight to quantify the influence of member $u_{k,m}$ in the group $g_k$. This weight holistically considers both the member’s personal interest preferences and their social influence within the group. For instance, in social network, certain members (e.g., opinion leader) exert greater influence on group event decision, and thus their weights should be higher. Based on this, we define the group embedding representation as follows:

$${\mathbf{g}}_{t,k,j}^a=\sum _{m=1}^{M_k}{\beta }_{u_{k,m}}{\mathbf{u}}_{t,k,m}$$

(9)

where ${\mathbf{g}}_{t,k}^a$ is an aggregate dynamic preference representation of group $g_k$. ${\mathbf{u}}_{t,k,m}$ denotes dynamic preference embedding of member. $M_k$ denotes the number of members of group $g_k$. We use the ${\mathbf{e}}_j^{u_{k,m}}$ was obtained by “Fine-grained Features Attention” module to compute the influence weight of member $u_{k,m}$. Then the attention weight ${\beta }_{u_{k,m}}$ of each member as follows:

$${\beta }_{u_{k,m}}={\displaystyle \frac{exp({\mathbf{v}}^{T}tanh({\mathbf{W}}_2[{\mathbf{u}}_{t,k,m}\left|\right|{\mathbf{e}}_j^{u_{k,m}}]))}{{\sum }_{m=1}^{M_k}exp({\mathbf{v}}^{T}tanh({\mathbf{W}}_2[{\mathbf{u}}_{t,k,m}\left|\right|{\mathbf{e}}_j^{u_{k,m}}]))}}$$

(10)

where ${\mathbf{W}}_2$ is a learnable weight matrix, and the $\mathbf{v}$ is a learnable vector. $\left|\right|$ denotes concatenation operate.

5.1.3. Group Representation and Group-Attention Event Representation

Besides the group embedding vector derived from member embedding aggregation, the group own preference embedding cannot be ignored. In some scenarios, a group’s event decision is influenced not only by the individual interests of its members but also by the group’s consensus preferences, particularly when members have a common purpose. For instance, a group formed by a reading enthusiast and a travel enthusiast might ultimately choose to watch a movie together. In such cases, relying solely on individual member preferences may fail to capture the group’s holistic intent. Thus, for group recommendation tasks, we propose integrating both the member-aggregated embedding and the group consensus preference embedding into the final group representation. The group consensus preference embedding, denoted as ${\mathbf{g}}_{t,k,j}^p$, can be learned from group–event historical interactions. Like the user dynamic preference embedding, the group consensus preference embedding is also calculated based on a time decay mechanism as follows:

$${\mathbf{g}}_{t,k}^p={\displaystyle \frac{{\sum }_{i\in {\mathcal{H}}_g}{\rho }_i{\mathbf{e}}_j}{{\sum }_{i\in {\mathcal{H}}_g}}}$$

(11)

where ${\mathcal{H}}_g=\left\{{(e_i,t_i)}_{i=1}^n\right\}$ denotes the historical interaction sequence of group $g_k$, ${\rho }_i$ denotes the time decay weight, and the ${\mathbf{e}}_j$ is an event embedding that group $g_k$ interacted with which is obtained based on “Fine-grained Feature Attention” module. Therefore, we define the final group embedding as follows:

$${\mathbf{g}}_{t,k,j}={\mathbf{g}}_{t,k,j}^a+{\mathbf{g}}_{t,k,j}^p$$

(12)

where the ${\mathbf{g}}_{t,k,j}^a$ is the group’s dynamic aggregation representation obtained in the above section by aggregating the members’ embedding.

After modeling the aggregation of member interests and modeling the group consensus preferences, we further generate the event representation for group $g_k$ to better characterize the group consensus interest in different event. To achieve this, we introduce a “Norm and Add” (Normalization and Weighted Summation) module to integrate personalized event embeddings of group members and produce the final group event representation. Specifically, we first utilize the “fine-grained feature attention” module to obtain event embeddings for each member. These embeddings capture the degree of preference each member holds for various event features. However, since different members exert varying levels of influence in group decision-making, we further normalize these member-specific event representations and assign appropriate weights to ensure that the final group event representation effectively reflects the collective preference trend of the group. Thus the event representation for group $g_k$ is as follows:

$${\mathbf{e}}_j^{g_k}=\sum _{{\mathcal{F}}_{e_j}}{\gamma }_{{\mathcal{F}}_{e_j}}{\mathbf{z}}_{{\mathcal{F}}_{e_j}}$$

(13)

where the ${\mathbf{e}}_j^{g_k}$ is the event embedding for group $g_k$. ${\mathbf{z}}_{{\mathcal{F}}_{e_j}}$ denotes feature embedding of event $e_j$. Then the weight ${\gamma }_{{\mathcal{F}}_{e_j}}$ of each feature is as follows:

$${\gamma }_{{\mathcal{F}}_{e_j}}={\displaystyle \frac{exp\left({\mathbf{g}}_{k,j}^T{\mathbf{W}}_{\mathbf{3}}{\mathbf{z}}_{{\mathcal{F}}_{e_j}}\right)}{{\sum }_{{\mathcal{F}}_{e_j}}exp\left({\mathbf{g}}_{k,j}^T{\mathbf{W}}_{\mathbf{3}}{\mathbf{z}}_{{\mathcal{F}}_{e_j}}\right)}}$$

(14)

where ${\mathbf{W}}_{\mathbf{3}}$ is a learnable weight matrix, and the ${\mathbf{g}}_{k,j}$ is the final group representation. We can predict the group preferences after obtaining the final group representations and the corresponding event representations.

5.2. Interaction Learning with Neural Collaborative Filtering

We adopt Neural Collaborative Filtering (NCF) to model the interaction information between group–event and user–event. NCF is a deep-learning-based approach that learns complex interaction relationships between users/groups and target event through nonlinear transformations and Multi-Layer Perceptrons (MLP), thereby enhancing recommendation accuracy. Specifically, for each group–event interaction pair $(g_k,e_j)$, we first obtain the embedding representations of group $g_k$ and event $e_j$ via a representation learning module, which can be acquired from a pre-trained embedding layer. Subsequently, the obtained group and event embeddings are fed into a pooling layer to further learn interaction relationships. The output embedding vectors of the pooling layer for user and group are as follows:

$${\mathbf{h}}_0^g=f_{pooling}({\mathbf{g}}_{k,j}\odot {\mathbf{e}}_j^{\left(g_k\right)},{\mathbf{g}}_{k,j},{\mathbf{e}}_j^{\left(g_k\right)})$$

(15)

$${\mathbf{h}}_0^u=f_{pooling}({\mathbf{u}}_i\odot {\mathbf{e}}_j^{\left(u_i\right)},{\mathbf{u}}_i,{\mathbf{e}}_j^{\left(u_i\right)})$$

(16)

where include two recommendation tasks: group recommendation and user recommendation.

After the pooling layer, we feed the interaction representation into a fully connected layer to further learn the complex relationships between users/groups and events and compute the final prediction score. The primary role of the fully connected layer is to perform nonlinear transformations, enhancing the model’s expressive capacity. Specifically, for the target group $g_k$ and target user $u_i$, we construct independent fully connected neural networks, obtaining the final hidden representation through layer-wise computations. The outputs of neurons in the L-th layer are defined as follows:

$${\mathbf{h}}_l^g=ReLU({\mathbf{W}}_l^g{\mathbf{h}}_{l-1}^g+{\mathbf{b}}_l^g)$$

(17)

$${\mathbf{h}}_l^u=ReLU({\mathbf{W}}_l^u{\mathbf{h}}_{l-1}^u+{\mathbf{b}}_l^u)$$

(18)

where the ${\mathbf{W}}_l$ is the weight matrix of the l-th layer, mapping input features to the hidden space. ${\mathbf{b}}_l$ is the bias vector of the l-th layer, enhancing the model’s learning capacity. The ReLU activation function introduces nonlinearity, empowering the model with stronger expressive capabilities. After obtaining the hidden representation of the final layer, we compute the final recommendation scores using a single-layer linear transformation. The predicted score ${\widehat{x}}_{gj}$ for target group $g_k$ on event $e_j$ and the predicted score ${\widehat{y}}_{ij}$ for target user $u_i$ on event $e_j$ are calculated as follows:

$${\widehat{x}}_{gj}={\mathbf{w}}_g^T{\mathbf{h}}_l^g$$

(19)

$${\widehat{y}}_{ij}={\mathbf{w}}_u^T{\mathbf{h}}_l^u$$

(20)

where the ${\mathbf{w}}_g$ is the weight parameter of prediction layer of group recommendation, the ${\mathbf{w}}_u$ is the weight parameter of prediction layer of user recommendation.

5.3. Recommendation and Optimization

We adopt the Regression-based Pairwise Loss (RPL) [41] as the optimization objective to learn model parameters and jointly model group–event and user–event interactions. The core idea of this loss function is to optimize the preference ranking of users or groups across different events through pairwise comparisons, enabling the model to better capture the true interests of users or groups. To ensure effective learning of group preferences, we define the group-event loss function as follows:

$$Los{s}_{group}=\sum _{(g,j,j^{\prime })\in D_g}{({\widehat{x}}_{gj}-{\widehat{x}}_{g{j}^{\prime }}-1)}^2$$

(21)

where $D_g$ denotes the group–event interaction data in the training set for group g. The triplet $(g,j,j^{\prime })$ indicates that group g has interacted with event j but not with event $j^{\prime }$. Here ${\widehat{x}}_{gj}$ and ${\widehat{x}}_{g{j}^{\prime }}$ represent the model’s predicted preference scores of group g for event j and event $j^{\prime }$, respectively. The objective of this loss function is to ensure that the predicted score for the interacted event j is higher than that for the non-interacted event $j^{\prime }$, i.e., ${\widehat{x}}_{gj}>{\widehat{x}}_{g{j}^{\prime }}$. The optimization aims to minimize the squared error of ${\widehat{x}}_{gj}-{\widehat{x}}_{g{j}^{\prime }}-1$, thereby enforcing a margin of approximately 1 between the predicted scores to enhance the model’s discriminative capability.

Similarly, for the user–event recommendation task, we apply the same optimization strategy, defined as follows:

$$Los{s}_{user}=\sum _{(u,j,j^{\prime })\in D_u}{({\widehat{y}}_{uj}-{\widehat{y}}_{u{j}^{\prime }}-1)}^2$$

(22)

By maintaining a reasonable margin between scores, i.e., ${\widehat{y}}_{uj}-{\widehat{y}}_{u{j}^{\prime }}\approx 1$, the model effectively learns the user’s true preferences. To optimize the model, we employ Stochastic Gradient Descent (SGD) to minimize the combined losses $Los{s}_{group}$ and $Los{s}_{user}$.

In recommendation tasks, another widely used pairwise learning method is Bayesian Personalized Ranking (BPR) [42]. However, BPR suffers from a potential issue in multi-layer models: its loss can be reduced simply by scaling up the hidden weights, leading to a trivial solution and necessitating strict $L_2$ regularization to constrain the parameters. In contrast, the regression-based pairwise loss (RPL) directly enforces a fixed margin between positive and negative samples (i.e., ${\widehat{r}}_{ij}-{\widehat{r}}_{is}=1$), which prevents such trivial solutions and enables stable optimization without additional regularization. This property makes the loss particularly suitable for integration with our fine-grained attention mechanism, as it provides clearer and more robust optimization signals for the model.

6. Experiments

6.1. Data Preparation

Experiments are conducted on three real-world datasets: the Meetup dataset [10], Douban-Event dataset [11] and Yelp dataset (https://www.kaggle.com/datasets/yelp-dataset/yelp-dataset, accessed on 23 November 2025), which are popular in EBSNs. The basic statistics of these datasets as shown in Table 4. For these datasets, we collect event data from 1 January 2015 to 31 December 2016, including participants, start time, venue, and organizers of each event. Since these datasets lack group information, we generate synthetic groups based on the following condition: users who participated in the same event at the same time and location more than three times. We define group recommendation task as that recommend events to ephemeral groups of users. Notably, we generated groups of different sizes (ranging from 2 to 6) to validate the effectiveness of method across different group sizes.

Table 4. Basic statistics of Douban-Event and Meetup Datasets. Note: # denotes number of.

Datasets	Douban-Event		Meetup		Yelp
	Shanghai	Beijing	Phoenix	Chicago
#Users	687	3532	6998	3748	87,483
#Events	1001	3154	27,644	23,430	149,843
#Groups (each size)	1000	1000	1000	1000	1000
#Groups Interactions	27,899	70,733	573,359	293,888	1,732,381
#Users Interactions	5714	115,889	474,897	203,433	1,375,841
#Venue	453	2074	4734	3894	-
#Organizers	103	454	984	715	-
Sparsity of groups interactions	97.21%	97.76%	97.93%	99.75%	98.95%
Sparsity of users interactions	99.17%	98.96%	99.75%	99.77%	99.88%

6.2. Experimental Methods

6.2.1. Evaluation Methods

We employ HR (Hit Ratio) and NDCG (Normalized Discounted Cumulative Gain) metrics to evaluate the Top-N (N = 5, 10, 15, 20) recommendation performance of our model and baseline methods. HR measures whether the testing event is ranked in the Top-N list. The formula for HR is as follows:

$$HR@N={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}hit\left(i\right)$$

(23)

NDCG evaluates the ranking quality of recommended event by considering their positions in the list. NDCG is the normalized version of DCG, which discounts the contribution of lower-ranked events (later positions have smaller gains). The formula for DCG is as follows:

$$DCG=\sum _{i=1}^m{\displaystyle \frac{re{l}_i}{{log}_2(i+1)}}$$

(24)

where $re{l}_i$ is the graded relevance of the event at position i. If the event in recommendation list at i appears in the test set $re{l}_i=1$, otherwise $re{l}_i=0$.

For the dataset split, we employ the time-aware validation method [43] to evaluate our model MAGER and the baseline methods. Given a user profile, which is a collection of participation records, to rank participation records according to the corresponding timestamps. The earlier 70% records are selected as the training set, and the recent 30% records are used as the test set.

6.2.2. Baselines

To justify the effectiveness of our model, we compare our model MAGER with the following state-of-the-art baselines:

STARec [43] proposes a latest time-aware model, which distinguishes between user social preferences and individual interests, explicitly depicting the inconsistency between social preferences and actual decisions.

CVTM [11] proposes a group recommendation model based on topic model, which finds the correlation of content information and the venue.

GBGCN [37] addresses the group-buying recommendation problem in social e-commerce and constructs directed heterogeneous graphs to integrate user-initiated, participation behaviors, and social network data.

AGREE [14] introduces a model that dynamically adapts group member weights through attention mechanism to address preference aggregation in group recommendation, integrating NCF to capture group–item interactions.

HyperGroup [33] uses hierarchical hyperedge embedding and graph neural networks to enhance group representation learning through user–user interactions and hypergraph-based group similarity.

ConsRec [17] addresses consensus learning through multi-view (member-level aggregation, item-level tastes, and group-level preferences) fusion and employs a hypergraph neural network for member interest aggregation.

GroupIM [38] proposes a novel framework that addresses group interaction sparsity through data-driven regularization strategies, leveraging user preference covariance and contextual relevance.

GroupAV [39] introduces a multi-view attentive variational network for group recommendation that employs Variational AutoEncoder (VAE) and density-based preference modeling to address user interest drift.

DHMAE [34] integrates a disentangled hypergraph neural network with a graph masked autoencoder to eliminate reliance on data augmentation and address noise by reconstructing masked node/hyperedge features.

6.3. Experimental Result and Analysis

6.3.1. Effectiveness of MAGER

We compare the performance of MAGER with baselines in top-N user/group recommendation on Douban-Event, Meetup and Yelp datasets, as shown in Table 5, Table 6, Table 7, Table 8 and Table 9. We show the results of HR@N and NDCG@N metrics. To support the significance of our improvements, we report the performance improvements using statistical tests. Using t tests, as shown in Table 10, we report the different in HR and NDCG for MAGER and baselines on Shanghai and Phoenix datasets. Our method achieve statistical significance, where p-values < 0.01 over all baselines for group recommendation in two datasets.

Table 5. Recommendation performance of MAGER and baselines for Group/User Recommendation on HR and NDCG metrics on Douban-Event Shanghai dataset (bold: best; underline: runner-up).

Methods	Douban-Event Shanghai
	User Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.3603	0.3915	0.4578	0.4993	0.2183	0.2514	0.2783	0.2905
CVTM	0.0756	0.1028	0.1154	0.1285	0.0707	0.0854	0.0978	0.1085
GBGCN	0.1165	0.1899	0.2287	0.2684	0.0835	0.1002	0.1198	0.1273
AGREE	0.1096	0.1765	0.2263	0.2526	0.0749	0.0921	0.1032	0.1174
GroupIM	0.1013	0.1704	0.2118	0.2347	0.0716	0.0912	0.1011	0.1114
Hyper Group	0.3034	0.3264	0.3785	0.4033	0.1723	0.2003	0.2345	0.2648
DHMAE	0.3184	0.3384	0.3903	0.4302	0.1893	0.2235	0.2398	0.2804
ConsRec	0.3305	0.3523	0.4006	0.4354	0.2004	0.2345	0.2604	0.2945
GroupAV	0.3443	0.3745	0.4484	0.4932	0.2143	0.2445	0.2884	0.3132
MAGER	0.4074	0.4290	0.4765	0.5297	0.2588	0.2895	0.3270	0.3477
Methods	Group Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.2039	0.2582	0.3173	0.3692	0.1718	0.1937	0.2026	0.2088
CVTM	0.1234	0.1832	0.2546	0.3123	0.1332	0.1458	0.1584	0.1734
GBGCN	0.2398	0.3234	0.3774	0.4142	0.2445	0.2591	0.2753	0.2904
AGREE	0.2279	0.3138	0.3613	0.4004	0.2160	0.2253	0.2362	0.2508
GroupIM	0.1983	0.3098	0.3545	0.3989	0.1545	0.1743	0.1983	0.2181
Hyper Group	0.3304	0.3834	0.4353	0.4834	0.2538	0.3013	0.3354	0.3638
DHMAE	0.3604	0.4134	0.4734	0.5143	0.2819	0.3399	0.3667	0.3942
ConsRec	0.3485	0.3932	0.4602	0.4995	0.2843	0.3445	0.3684	0.3832
GroupAV	0.3843	0.4445	0.5184	0.5732	0.2803	0.3412	0.3884	0.4132
MAGER	0.4574	0.5013	0.5945	0.6529	0.3870	0.4205	0.4484	0.4729

Table 6. Recommendation performance of MAGER and baselines for Group/User Recommendation on HR and NDCG metrics on Douban-Event Beijing dataset (bold: best; underline: runner-up).

Methods	Douban-Event Beijing
	User Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.3619	0.4024	0.4699	0.5173	0.2083	0.2173	0.2394	0.2476
CVTM	0.0904	0.1254	0.1597	0.2045	0.0844	0.1036	0.1165	0.1165
GBGCN	0.1514	0.2216	0.2548	0.2911	0.1249	0.1310	0.1356	0.1356
AGREE	0.1404	0.2054	0.2478	0.2741	0.1104	0.1254	0.1276	0.1298
GroupIM	0.1356	0.1954	0.2365	0.2622	0.1043	0.1143	0.1176	0.1205
Hyper Group	0.3201	0.3465	0.3856	0.4167	0.1903	0.2143	0.2216	0.2365
DHMAE	0.3274	0.3565	0.4036	0.4572	0.2054	0.2154	0.2476	0.2935
ConsRec	0.3565	0.3754	0.4238	0.4738	0.2265	0.2265	0.2726	0.2965
GroupAV	0.3505	0.3931	0.4682	0.4971	0.2115	0.2403	0.2813	0.3008
MAGER	0.4084	0.4306	0.5177	0.5423	0.2495	0.2704	0.3098	0.3252
Methods	Group Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.2028	0.2743	0.3254	0.3683	0.1683	0.1804	0.1915	0.2035
CVTM	0.1743	0.2265	0.2894	0.3154	0.1832	0.1904	0.2055	0.2055
GBGCN	0.2743	0.3474	0.3903	0.4454	0.2904	0.3057	0.3211	0.3365
AGREE	0.2584	0.3294	0.3804	0.4213	0.2636	0.2847	0.3041	0.3154
GroupIM	0.2035	0.3132	0.3715	0.4054	0.1843	0.1933	0.2155	0.2322
Hyper Group	0.3584	0.3747	0.4148	0.2894	0.3101	0.3544	0.3747	0.3890
DHMAE	0.4052	0.4276	0.4978	0.5305	0.3045	0.3365	0.3705	0.3911
ConsRec	0.3843	0.4065	0.4762	0.5182	0.3184	0.3689	0.3941	0.4165
GroupAV	0.4243	0.4583	0.5042	0.5549	0.3144	0.3594	0.3748	0.3926
MAGER	0.4655	0.5243	0.5993	0.6793	0.3832	0.4105	0.4223	0.4223

Table 7. Recommendation performance of MAGER and baselines for Group/User Recommendation on HR and NDCG metrics on Meetup Phoenix dataset (bold: best; underline: runner-up).

Methods	Meetup Phoenix
	User Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.4216	0.4694	0.5246	0.6102	0.3498	0.3942	0.4353	0.4394
CVTM	0.2056	0.2328	0.3054	0.3543	0.2707	0.2999	0.3478	0.4034
GBGCN	0.3765	0.4239	0.5137	0.5837	0.3215	0.3732	0.4298	0.4985
AGREE	0.3796	0.4325	0.5193	0.6002	0.3249	0.3801	0.4332	0.5023
GroupIM	0.2113	0.2404	0.3118	0.3784	0.3116	0.3412	0.4011	0.4533
Hyper Group	0.3934	0.4584	0.5385	0.6022	0.3473	0.3903	0.4645	0.5114
DHMAE	0.4021	0.4603	0.5432	0.6097	0.3542	0.4082	0.4665	0.5174
ConsRec	0.4295	0.4779	0.5686	0.6144	0.3634	0.3815	0.4274	0.4293
GroupAV	0.4143	0.4645	0.5354	0.6032	0.3543	0.3745	0.4084	0.4132
MAGER	0.4474	0.5070	0.6195	0.6633	0.4098	0.4235	0.4770	0.5041
Methods	Group Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.3694	0.4238	0.4715	0.5172	0.3247	0.3982	0.4301	0.4428
CVTM	0.3734	0.4332	0.4746	0.5345	0.3432	0.4058	0.4584	0.4985
GBGCN	0.4398	0.5234	0.5774	0.6234	0.4345	0.4791	0.5053	0.5274
AGREE	0.4979	0.5408	0.5913	0.6321	0.4560	0.4953	0.5302	0.5506
GroupIM	0.4373	0.4998	0.5445	0.5987	0.4245	0.4643	0.5003	0.5142
Hyper Group	0.5364	0.5814	0.6453	0.6843	0.4738	0.5013	0.5304	0.5543
DHMAE	0.5503	0.5925	0.6784	0.7043	0.4896	0.5204	0.5490	0.5643
ConsRec	0.5484	0.5834	0.6634	0.6975	0.4843	0.5145	0.5404	0.5602
GroupAV	0.5543	0.6045	0.6884	0.7132	0.5043	0.5445	0.5884	0.6032
MAGER	0.5874	0.6313	0.7045	0.7343	0.5380	0.5705	0.6184	0.6402

Table 8. Recommendation performance of MAGER and baselines for Group/User Recommendation on HR and NDCG metrics on Meetup Chicago dataset (bold: best; underline: runner-up).

Methods	Meetup Chicago
	User Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.4093	0.4382	0.5016	0.5937	0.3302	0.3749	0.4136	0.4216
CVTM	0.1804	0.2214	0.2548	0.3482	0.2983	0.3166	0.3606	0.3852
GBGCN	0.3345	0.4052	0.4862	0.5725	0.3188	0.3504	0.3733	0.3962
AGREE	0.3481	0.4194	0.4954	0.5743	0.3276	0.3587	0.3905	0.4149
GroupIM	0.1946	0.2276	0.2691	0.3658	0.3132	0.3365	0.3852	0.4065
Hyper Group	0.3605	0.4365	0.5062	0.5747	0.3365	0.3752	0.4173	0.4561
DHMAE	0.3847	0.4502	0.5135	0.5929	0.3641	0.3845	0.4265	0.4587
ConsRec	0.4102	0.4595	0.5172	0.6043	0.3605	0.3713	0.3785	0.3785
GroupAV	0.4100	0.4493	0.4927	0.5803	0.3565	0.3658	0.3852	0.3953
MAGER	0.4304	0.4957	0.5743	0.6552	0.3954	0.4043	0.4154	0.4464
Methods	Group Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.3375	0.3874	0.4282	0.4759	0.3129	0.3684	0.3924	0.4187
CVTM	0.3542	0.3945	0.4532	0.5105	0.3304	0.3537	0.4055	0.4177
GBGCN	0.4054	0.4337	0.4619	0.5376	0.3631	0.3743	0.3822	0.4025
AGREE	0.4294	0.4529	0.4899	0.5542	0.3904	0.4122	0.4187	0.4265
GroupIM	0.4024	0.4304	0.4538	0.5194	0.3525	0.3691	0.3699	0.3847
Hyper Group	0.4815	0.5277	0.5859	0.6412	0.4755	0.4836	0.4911	0.5155
DHMAE	0.5104	0.5385	0.5932	0.6778	0.4622	0.4816	0.5031	0.5229
ConsRec	0.5022	0.5293	0.5743	0.6404	0.4303	0.4562	0.4691	0.4805
GroupAV	0.5135	0.5532	0.6133	0.6796	0.4802	0.5032	0.5248	0.5316
MAGER	0.5694	0.6204	0.6733	0.7107	0.5032	0.5254	0.5402	0.5622

Table 9. Recommendation performance of MAGER and baselines for Group/User Recommendation on HR and NDCG metrics on Yelp dataset (bold: best; underline: runner-up).

Methods	Yelp
	User Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.3284	0.3594	0.3938	0.4237	0.2793	0.3026	0.3193	0.3216
CVTM	0.2983	0.3364	0.3472	0.3644	0.2074	0.2153	0.2266	0.2266
GBGCN	0.1561	0.1893	0.2235	0.2590	0.1783	0.1892	0.1973	0.2189
AGREE	0.3483	0.3628	0.3972	0.4274	0.2917	0.3055	0.3185	0.3303
GroupIM	0.1874	0.2089	0.2316	0.2539	0.1643	0.1716	0.1864	0.1875
Hyper Group	0.3183	0.3337	0.3704	0.4116	0.2784	0.2911	0.2974	0.3065
DHMAE	0.3384	0.3526	0.3874	0.4125	0.2906	0.3189	0.3284	0.3284
ConsRec	0.3494	0.3703	0.4018	0.4383	0.2984	0.3093	0.3288	0.3428
GroupAV	0.3178	0.3302	0.3673	0.3974	0.2673	0.2864	0.2918	0.3107
MAGER	0.3621	0.3912	0.4229	0.4607	0.3152	0.3294	0.3519	0.3862
Methods	Group Recommendation
	HR@5	HR@10	HR@15	HR@20	N@5	N@10	N@15	N@20
STARec	0.2583	0.2934	0.3542	0.3827	0.2105	0.2384	0.2794	0.2815
CVTM	0.3287	0.3514	0.3853	0.4073	0.2153	0.2389	0.2403	0.2433
GBGCN	0.1273	0.1472	0.2084	0.2463	0.1284	0.1489	0.1565	0.1592
AGREE	0.3807	0.4093	0.4389	0.4716	0.3308	0.3427	0.3526	0.3680
GroupIM	0.2084	0.2355	0.2618	0.2893	0.1703	0.1823	0.1987	0.2099
Hyper Group	0.3609	0.3983	0.4325	0.4692	0.3391	0.3426	0.3582	0.3597
DHMAE	0.3804	0.4083	0.4327	0.4620	0.3271	0.3398	0.3406	0.3511
ConsRec	0.3814	0.4183	0.4408	0.4766	0.3428	0.3524	0.3682	0.3778
GroupAV	0.3483	0.3867	0.4007	0.4285	0.2284	0.2356	0.2414	0.2506
MAGER	0.3892	0.4294	0.4427	0.4803	0.3514	0.3589	0.3709	0.3812

Table 10. p-Values of all the t-tests over top@5 to top@20 carried out to compare the performance of all baselines.

Methods	Datasets
	Shanghai (User Recommendation)						Phoenix (User Recommendation)
	HR			NDCG			HR			NDCG
	M	SD	p-Value	M	SD	p-Value	M	SD	p-Value	M	SD	p-Value
STARec	0.43	0.06	0.0113	0.26	0.03	0.0147	0.51	0.08	0.039	0.40	0.04	0.0095
CVTM	0.11	0.02	0.00025	0.09	0.02	0.00041	0.27	0.07	0.0004	0.33	0.05	0.0006
GBGCN	0.20	0.06	0.00018	0.11	0.02	0.00056	0.47	0.09	0.0015	0.41	0.07	0.0066
AGREE	0.19	0.06	0.00016	0.10	0.02	0.00047	0.48	0.09	0.0034	0.41	0.08	0.0082
GroupIM	0.18	0.06	0.00015	0.09	0.02	0.00043	0.29	0.07	0.0004	0.38	0.06	0.0043
Hyper Group	0.35	0.05	0.00045	0.22	0.04	0.0031	0.50	0.09	0.0043	0.43	0.07	0.0190
DHMAE	0.37	0.05	6.8 $\times {10}^{-5}$	0.23	0.04	0.0023	0.50	0.09	0.0055	0.44	0.07	0.0319
ConsRec	0.38	0.05	0.00036	0.25	0.04	0.0074	0.52	0.08	0.0185	0.40	0.03	0.0055
GroupAV	0.42	0.07	0.0109	0.27	0.04	0.0181	0.50	0.08	0.0172	0.39	0.04	0.0057
MAGER	0.46	0.05	-	0.31	0.04	-	0.56	0.09	-	0.45	0.04	-
Methods	Shanghai (Group Recommendation)						Phoenix (Group Recommendation)
	HR			NDCG			HR			NDCG
	M	SD	p-Value	M	SD	p-Value	M	SD	p-Value	M	SD	p-Value
STARec	0.29	0.07	0.00082	0.19	0.02	0.000066	0.45	0.06	0.0001	0.40	0.05	0.0001
CVTM	0.22	0.08	0.00033	0.15	0.17	0.000035	0.45	0.07	0.0001	0.43	0.07	0.0006
GBGCN	0.34	0.08	0.00179	0.27	0.02	0.00027	0.54	0.08	0.0008	0.49	0.04	0.0003
AGREE	0.33	0.07	0.00138	0.23	0.02	0.00012	0.57	0.06	0.0004	0.51	0.04	0.0001
GroupIM	0.32	0.08	0.00138	0.19	0.03	0.000095	0.52	0.07	0.0002	0.48	0.04	0.0001
Hyper Group	0.41	0.07	0.00245	0.31	0.05	0.00187	0.62	0.07	0.00017	0.51	0.04	0.001
DHMAE	0.44	0.06	0.00572	0.35	0.05	0.00416	0.63	0.07	0.0015	0.53	0.03	0.0031
ConsRec	0.43	0.06	0.00451	0.35	0.05	0.00329	0.62	0.07	0.0005	0.53	0.03	0.0024
GroupAV	0.48	0.08	0.00703	0.36	0.06	0.00757	0.64	0.07	0.0071	0.56	0.04	0.0009
MAGER	0.55	0.09	-	0.43	0.04	-	0.07	0.07	-	0.59	0.05	-

Recommendation on Douban-Event. From these results, as shown in Table 5 and Table 6, we can observe the following: (1) In user recommendation task, MAGER consistently and significantly outperforms all baselines, and MAGER provides such as 13.07% on HR@5 and 18.55% on NDCG@5 improvement over STARec on Shanghai. And MAGER provides such as 12.85% on HR@5 improvement over STARec and 17.97% on NDCG@5 improvement over GroupAV on Beijing. (2) In group recommendation task, MAGER also consistently and significantly outperforms all baselines, and MAGER provides such as 19.02% on HR@5 improvement over GroupAV and 36.12% on NDCG@5 improvement over ConsRec on Shanghai. And MAGER provides such as 9.71% on HR@5 improvement over GroupAV and 20.35% on NDCG@5 improvement over ConsRec on Beijing. (3) Both Agree and ConsRec are aggregation-based methods, but ConsRec demonstrates significantly superior performance compared to AGREE. The possible reason from the denser group–event interactions in the Douban-Event, as shown in Table 4, which enables ConsRec to achieve better recommendation effectiveness. (4) GroupIM is a contrastive learning-based method, which often generate contrastive views by adopting random strategies, which impairs the performance of this method. And CVTM and GBGCN both are a method that does not use member aggregation strategy, which cannot improve the effectiveness of group recommendation. (5) GroupAV achieves the best results among all baselines for group recommendation, the possible reason is that GroupAV learns group preferences from multiple views. However, MAGER still outperforms GroupAV. since MAGER not only exploiting the multi-view preferences of the group, also to learn the preferences of members and groups for fine-grained features. This is very helpful in the EBSNs scenario, as using only event ID embeddings would significantly reduce the recommendation effect. (6) STARec performs the best in user recommendation. The main reason is that STARec models rich contextual information, such as location, time, and social relationships, which are highly applicable in EBSNs. Another important reason is that STARec is latest time-aware related, which is in line with the EBSN scenario and can capture dynamic user/group preferences.

Recommendation on Meetup. From these results, as shown in Table 7 and Table 8, we can observe that (1) In user recommendation task, MAGER consistently and significantly outperforms all baselines, and MAGER provides such as 4.17% on HR@5 and 12.77% on NDCG@5 improvement over ConsRec on Phoenix. And MAGER provides such as 4.92% on HR@5 improvement over ConsRec and 8.60% on NDCG@5 improvement over DHMAE on Chicago. (2) In group recommendation task, MAGER also consistently and significantly outperforms all baselines, and MAGER provides such as 5.97% on HR@5 and 6.68% on NDCG@5 improvement over GroupAV on Phoenix. And MAGER provides such as 10.89% on HR@5 and 4.79% on NDCG@5 improvement over GroupAV on Chicago. (3) CVTM has better performance of recommendation than Douban-Event, and the possible reason is that there are more event text information in Meetup that can be mined. (4) ConsRec is better than DHMAE in user recommendation and worse than DHMAE in group recommendation, on both datasets, showing the effectiveness of the hypergraph-based method (DHMAE) over the aggregation-based method (ConsRec) on group recommendation.

Recommendation on Yelp. From these results, as shown in Table 9, we can observe that (1) In User Recommendation task, MAGER consistently and significantly outperforms all baselines, and MAGER provides such as 3.63% on HR@5 and 5.63% on NDCG@5 over ConsRec. (2) In Group Recommendation task, MAGER consistently and significantly outperforms all baselines, and MAGER provides such as 2.05% on HR@5 and 2.51% on NDCG@5 over ConsRec. (3) On the Yelp dataset, the ConsRec method outperforms all other baselines, probably because ConsRec focuses primarily on preference consistency among group members. Since the businesses in the Yelp dataset mainly consist of shopping centers, restaurants, and hotels, they align better with the consistent member preferences modeled by ConsRec. (4) AGREE shows significantly better performance compared to the Douban-Event and Meetup datasets. A possible reason is that only venue and time features are available in Yelp, while the absence of more features (e.g., organizer) greatly diminishes the advantage of MAGER. Nevertheless, the fine-grained feature attention method still outperforms the simple concatenation way.

6.3.2. Contribution of Different Components

We conduct two types of ablation studies. The first one is to compare the contributions of different features of event to the recommendation performance of our MAGER and to compare different feature fusion methods. The second is to compare the influence of different attention component on our model MAGER.

(1) We first employ the Leave-One-Feature-Out method [13] to evaluate the impact of different event features on the MAGER’s recommendation performance. This method removes single features in turn and observes changes in recommendation performance to quantify their importance. The experimental results, as shown in Table 11, Table 12 and Table 13, reveal the following observation: The organizer feature has the most significant influence on the recommendations, indicating that organizer plays a critical role in modeling group/user preferences. This is likely because users tend to follow events hosted by specific organizers (e.g., familiar communities, institutions, or individuals), which strongly influences their participation decisions.

Table 11. The performance of different MAGER variants on Douban-Event dataset (bold: best; underline: runner-up).

Variants	Shanghai				Beijing
	Group		User		Group		User
	H@10	N@10	H@10	N@10	H@10	N@10	H@10	N@10
LeaveOrganizerOut	0.2084	0.1232	0.1334	0.0785	0.2305	0.1046	0.1794	0.0755
LeaveVenueOut	0.4295	0.3023	0.3184	0.2144	0.4331	0.2998	0.3509	0.2100
LeaveTimeOut	0.4853	0.3784	0.3745	0.2774	0.4903	0.3771	0.4069	0.2534
Ave.FeatureEmb.	0.2657	0.1434	0.1543	0.0933	0.2845	0.1308	0.1846	0.0898
Concat.FeatureEmb.	0.3929	0.2814	0.3003	0.1968	0.4188	0.2784	0.3483	0.2084
NoFeatures	0.1983	0.1203	0.1238	0.0773	0.2105	0.0978	0.1693	0.0738
MAGER-Static	0.4683	0.3594	0.3589	0.2714	0.4648	0.3482	0.3646	0.2258
MAGER	0.5013	0.4205	0.4290	0.2895	0.5243	0.4105	0.4306	0.2704

Table 12. The performance of different MAGER variants on Meetup dataset (bold: best; underline: runner-up).

Variants	Phoenix				Chicago
	Group		User		Group		User
	H@10	N@10	H@10	N@10	H@10	N@10	H@10	N@10
LeaveOrganizerOut	0.2564	0.2134	0.1739	0.1398	0.2495	0.2065	0.1495	0.1384
LeaveVenueOut	0.5234	0.4777	0.4095	0.3575	0.5093	0.4487	0.3784	0.3506
LeaveTimeOut	0.5784	0.5233	0.4564	0.4002	0.5711	0.5184	0.4453	0.3991
Ave.FeatureEmb.	0.3045	0.2782	0.1903	0.1616	0.2847	0.2755	0.1793	0.1610
Concat.FeatureEmb.	0.4877	0.4081	0.3974	0.2978	0.4394	0.3908	0.3565	0.3076
NoFeatures	0.2387	0.2108	0.1594	0.1285	0.2408	0.1976	0.1473	0.1193
MAGER-Static	0.5183	0.4278	0.3874	0.3394	0.4592	0.3984	0.3495	0.3163
MAGER	0.6313	0.5705	0.5070	0.4235	0.6204	0.5254	0.4957	0.4043

Table 13. The performance of different MAGER variants on Yelp dataset (bold: best; underline: runner-up).

Variants	Group		User
	HR@10	NDCG@10	HR@10	NDCG@10
LeaveVenueOut	0.2972	0.2301	0.2133	0.1965
LeaveTimeOut	0.3663	0.2581	0.2387	0.2007
Ave.FeatureEmbedding	0.2732	0.2298	0.2012	0.1883
Concat.FeatureEmbedding	0.4138	0.3492	0.3852	0.3177
NoFeatures	0.2583	0.2104	0.1983	0.1896
MAGER-Static	0.3974	0.2896	0.3084	0.2451
MAGER	0.4294	0.3589	0.3912	0.3294

In addition, the AverageFeatureEmbedding variant, ConcatenateFeatureEmbedding variant, and NoFeatures variant are designed to evaluate the effectiveness of our proposed fine-grained feature attention method. The results show that the performance of the Concat.FeatureEmbedding method is the best. This is because the concatenate method retains complete feature information and performs better in nonlinear models (such as NCF). And the NoFeatures variant uses only the event ID embedding and has the poorest performance, which indicates the significance of fine-grained features. To verify the significance of the dynamic update mechanism, we design the MAGER-Static variant that uses static group and user embeddings. The results demonstrate that the dynamic update mechanism is helpful in improving the MAGER performance.

(2) There are mainly three key attention components: one is the Fine-grained Feature Attention for event representation (FFA), the second is the Member Aggregation Attention for group preference representation (MAA), and the third is the Group Preference Attention for event representation (GPA). From the result of Table 14, we can observe that the performance of the model without GPA (w/o GPA) is the best, indicating that the GPA component has the least impact on MAGER. When MAGER model is performing group recommendation, it needs to generate group representations and corresponding event representations. Since the representation of event requires the participation of the target user, the GPA component is constructed when generating event representations. In the w/o GPA, we generate event presentations using a simple ConcatenateFeatureEmbedding method, but in the user recommendation, the event representation still uses the FFA component to generate. From the results, it can be seen that removing the GPA component has a relatively small impact on the effect, and the effect remains unchanged for the user recommendation task. However, the performance of the w/o MAA is the worst, which indicates that for MAGER model, the attention dynamic aggregation of the preference of group members is the most important. Note that the w/o MAA uses the average member preference method to aggregate the group members’ preferences. Finally, we design a variant of NoMultiAttention, i.e., Ave.Feature and Ave.Member, which means that all the three attention modules of MAGER have been removed and replaced by simple averaging operation. Specifically, averaging feature embeddings, averaging member preference embeddings, and averaging feature embeddings for group preference. The results show that the performance of Ave.Feature and Ave.Member is much worse than that of MAGER and even worse than removing a single attention, this proves our multi-attention structure is effective.

Table 14. The influence of attention component for MAGER (bold: best; underline: runner-up).

Variants	Shanghai				Phoenix
	Group		User		Group		User
	H@10	N@10	H@10	N@10	H@10	N@10	H@10	N@10
w/o FFA	0.3929	0.2814	0.3003	0.1968	0.4877	0.4081	0.3974	0.2978
w/o MAA	0.3827	0.2805	0.4290	0.2895	0.4712	0.4053	0.5070	0.4235
w/o GPA	0.4348	0.3326	0.4290	0.2895	0.5413	0.4529	0.5070	0.4235
Ave.Feature & Ave.Member	0.2027	0.1285	0.1385	0.0953	0.2518	0.1998	0.1671	0.1265
MAGER	0.5013	0.4205	0.4290	0.2895	0.6313	0.5705	0.5070	0.4235

6.3.3. Sensitivity to Data Sparsity

To investigate the performance of our MAGER under data sparsity, we conduct a comparative experiment on sparse training datasets from Douban-Event Shanghai and Meetup Phoenix. The sparse training datasets are obtained by randomly reducing the original training data by ratios ranging from 5% to 20% in increments of 5, while keeping the testing datasets unchanged [43]. Notably, if a user’s interaction data was completely removed during preprocessing, their testing data will be remove. We only report the results with 20% less training data. As shown in Table 15, we observe that the performance of all methods degradation with sparser training sets. Nevertheless, MAGER consistently achieves the best performance in both group and user recommendation, which confirms the effectiveness under sparse data.

Table 15. Sensitivity to data sparsity of MAGER (for 20% less training data).

Methods	Shanghai				Phoenix
	Group		User		Group		User
	H@10	N@10	H@10	N@10	H@10	N@10	H@10	N@10
CVTM	0.1832	0.1458	0.1028	0.0854	0.4332	0.4058	0.2328	0.2999
CVTM-	0.1789	0.1423	0.1006	0.0814	0.4295	0.4007	0.2285	0.2980
GBGCN	0.3234	0.2591	0.1899	0.1002	0.5234	0.4791	0.4239	0.3732
GBGCN-	0.3072	0.2473	0.1746	0.0984	0.5083	0.4629	0.4100	0.3582
AGREE	0.3138	0.2253	0.1765	0.0921	0.5408	0.4953	0.4325	0.3801
AGREE-	0.2974	0.2084	0.1575	0.0883	0.5327	0.4852	0.4267	0.3687
GroupIM	0.3098	0.1743	0.1704	0.0912	0.4998	0.4643	0.2404	0.3412
GroupIM-	0.3005	0.1643	0.1649	0.0874	0.4913	0.4583	0.2309	0.3326
HyperGroup	0.3834	0.3013	0.3264	0.2003	0.5814	0.5013	0.4584	0.3903
HyperGroup-	0.3525	0.2876	0.3082	0.1869	0.5498	0.4973	0.4329	0.3762
DHMAE	0.4134	0.3399	0.3384	0.2235	0.5925	0.5204	0.4603	0.4082
DHMAE-	0.4085	0.3311	0.3254	0.2174	0.5904	0.5156	0.4539	0.4061
ConsRec	0.3932	0.3445	0.3523	0.2345	0.5834	0.5145	0.4779	0.3815
ConsRec-	0.3664	0.3264	0.3395	0.2201	0.5771	0.4982	0.4628	0.3792
GroupAV	0.4445	0.3412	0.3745	0.2445	0.6045	0.5445	0.4645	0.3745
GroupAC-	0.4392	0.3352	0.3697	0.2414	0.6019	0.5389	0.4529	0.3716
MAGER	0.5013	0.4205	0.4290	0.2895	0.6313	0.5705	0.5070	0.4235
MAGER-	0.4943	0.4201	0.4207	0.2821	0.6245	0.5648	0.4983	0.4176

6.3.4. Influence of Different Embedding Sizes

Figure 6 presents the impact of varying embedding sizes on the group recommendation performance of the MAGER method on Douban-Event Shanghai and Meetup Phoenix datasets, with HR@10 metric. Experimental results demonstrate that an embedding size of 128 achieves the most stable convergence behavior and the highest final performance across all evaluation metrics. In contrast, embedding sizes of 32 and 64 allow for relatively rapid initial convergence but exhibit limited performance improvements during later training stages, ultimately reaching levels comparable to the 128 setting. This suggests that while smaller embeddings enable the proposed attention-based neural collaborative filtering to quickly capture group-level participation preferences, they lack sufficient representational capacity for finer-grained preference modeling. Notably, when the embedding size is increased to 256, the performance metrics during training remain significantly lower compared to the 128 embedding size. This degradation indicates that excessively large embeddings introduce redundancy and noise, impairing both convergence efficiency and preference representation quality, thereby leading to suboptimal recommendation outcomes. These findings highlight the importance of carefully tuning the embedding size to balance model expressiveness and generalization ability.

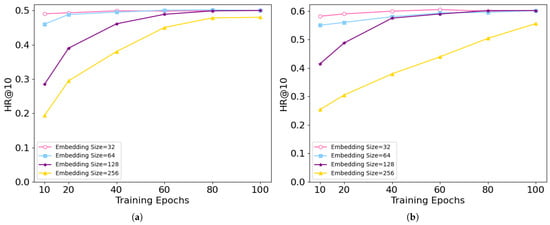
Figure 6. The performance of MAGER for different embedding size on Douban-Event Shanghai and Meetup Phoenix datasets for group recommendation task. (a) Douban-Event Shanghai; (b) Meetup Phoenix.

6.3.5. Influence of Group Size

The performance of various group recommendation methods under different group sizes is illustrated in Figure 7 on the Douban-Event and Meetup datasets respectively. The experimental results reveal minimal differences in recommendation performance across different methods and group sizes. The possible reasons are as follows: (1) The method of group formation plays a crucial role in these results. In our experimental data, groups were created by selecting users with similar interests, leading to strong preference homogeneity among group members. This characteristic ensures stable collective preferences regardless of variations in group size, thus minimizing fluctuations in performance for each method. (2) The relatively small size of the groups used in the experiment also had an impact on this result. Due to the limited size of the groups, the influence on the recommendation model was also restricted. However, significantly expanding the group size (for example, increasing to more than 10 people) might introduce greater diversity in group preferences, which could potentially exacerbate the performance differences between different methods. For instance, a larger group might experience more conflicts of interest among its members, making the collective preference prediction more complex and affecting the quality of the recommendations. (3) From the trends of the lines in Figure 7, we can observe that for HR@10, when the group size = 6, the performance of almost all methods experiences a slight decline. One possible reason is that HR measures the proportion of hits in the recommendation list, and as the group size increases, individual member interests become more diverse, making it more difficult for the recommendation list to satisfy all members simultaneously. For instance, when the group size = 2, it only needs to cover the interests of two members, whereas for a size = 6, it must satisfy six members at once, leading to a lower hit rate.

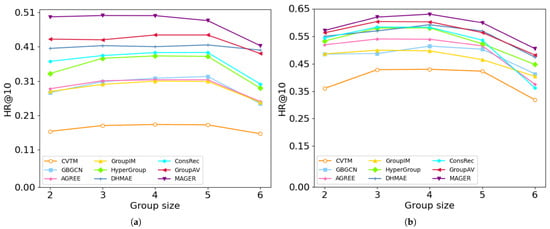
Figure 7. The performance of MAGER for different size of groups for group recommendation task. (a) Douban-Event Shanghai; (b) Meetup Phoenix.

6.3.6. Efficiency Study

We evaluate the efficiency of our MAGER by comparing the total running time (training plus testing) with all baselines on two datasets, as shown in Figure 8, which shows the HR@5 and running time (seconds/minutes). We conduct the experiments on GPU machines of Nvidia Tesla V100 with 32 GB memory. We can observe that our MAGER performs relatively efficiently on both of the two different datasets, but MAGER still has the best recommendation accuracy compared to baselines. Shanghai and Phoenix are two datasets of different sizes. The model MAGER perform nearly well in terms of efficiency on both datasets of these two sizes.

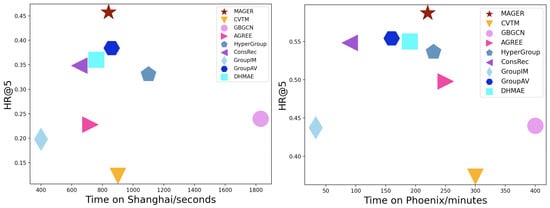
Figure 8. Efficiency study.

7. Discussion

In this work, we propose MAGER, a group event recommendation framework based on multiple attention mechanisms, which effectively captures user and group preferences at the fine-grained feature level through a heterogeneous attentions structure. Experiments on three real-world datasets demonstrate that MAGER significantly outperforms existing methods in both group and user recommendation tasks, validating the importance of feature-level attention and heterogeneous attentions structure in modeling dynamic group preferences.

7.1. Theoretical and Practical Implications

This work demonstrates that the Fine-grained Feature Attention (FFA) module plays a crucial role in capturing user and group preferences in EBSNs. A key theoretical insight revealed by our empirical analysis is that among all event features, the organizer exhibits the most dominant influence on both user and group behaviors. This finding indicates that users tend to rely heavily on organizer credibility when selecting events, which substantially shapes group preferences. Therefore, future EBSN recommendation models should avoid treating all features uniformly and instead explicitly differentiate the contributions of individual features, especially organizer-related signals, when modeling user and group decisions. This insight enhances our theoretical understanding of how fine-grained features affect group preferences in EBSNs scenarios. From a practical perspective, MAGER demonstrates robust performance under sparse interaction, which are common in real-world platforms such as Douban-Event and Meetup where new events emerge frequently and user interaction histories are limited. By accurately learning feature-level preferences, even when user histories are short, MAGER improves recommendation quality in dynamic and data sparse. This highlights the practical value of incorporating feature-aware attention mechanisms in EBSN recommenders, particularly in platforms characterized by fast-evolving event life cycles. Overall, this study provides both theoretical insights into feature-specific preference modeling and practical evidence of adaptability to sparse and dynamic social settings.

7.2. Limitations

Despite its advantages, MAGER has several limitations. First, MAGER does not explicitly capture latent correlations among different features, which may reduce the richness of event representations. Second, our experiments are conducted on two structurally similar EBSNs, and thus further validation is needed on more heterogeneous platforms. Third, although the hierarchical attention design improves performance, its computational cost increases with the number of event features, which may limit scalability in large-scale applications. More importantly, the use of synthetic groups constitutes a key limitation. In this study, groups are generated by clustering users who have participated in the same event more than three times. As shown in Section 6.3.5, this construction method leads to strong preference homogeneity among group members, which in turn results in minimal performance variation across different group sizes. This homogeneity, in turn, minimized performance fluctuations across different group sizes, potentially masking the true challenges of modeling dynamic group preferences. Future work should therefore explore more realistic or dynamic group formation mechanisms to better reflect real-world group behaviors and to more rigorously evaluate the model’s capability in handling preference diversity.

7.3. Future Work

Future work could explore more diverse group construction methods, such as forming groups based on social or geographical criteria with minimal overlap in historical activities, to evaluate the model’s robustness under preference conflicts and low-consistency conditions. Additionally, introducing a cross-feature attention mechanism to explicitly model correlations between features, e.g., organizer and venue, and incorporating this information into NCF could further enrich event representations. Finally, applying MAGER to a wider range of heterogeneous EBSN platforms and integrating multi-modal event features would help validate its generalizability and practical applicability.