Bifurcation and Firing Behavior Analysis of the Tabu Learning Neuron with FPGA Implementation

Abstract

Neuronal firing behaviors are fundamental to brain information processing, and their abnormalities are closely associated with neurological disorders. This study conducts a comprehensive bifurcation and firing-behavior analysis of an improved Tabu Learning neuron model using a semi-analytical discrete implicit mapping framework. First, a discrete implicit mapping is constructed for the Tabu Learning neuron, enabling high-precision localization of stable and unstable periodic orbits within chaotic regimes and overcoming the limitations of conventional time-domain integration. Second, an eigenvalue-centered analysis is used to classify bifurcation types and stability, summarized in explicit bifurcation tables that reveal self-similar offset bifurcation routes, coexisting periodic and chaotic attractors, and chaotic bubbling firing patterns. Third, the proposed neuron model and its discrete mapping are implemented on an FPGA platform, where hardware experiments faithfully reproduce the analytically predicted stable and unstable motions, thereby tightly linking theoretical analysis and digital neuromorphic hardware. Overall, this work establishes a unified analytical–numerical–hardware framework for exploring complex neuronal dynamics and provides a potential basis for neuromodulation strategies and neuromorphic computing system design.

1. Introduction

Biological neurons, the most basic anatomical and functional units of the brain, transmit information through energy absorption, integration, transformation, and release [1]. These processes enable organisms to perform advanced functions such as information processing and retrieval [2], cognition [3], and memory formation [4]. When neurons interact through synaptic coupling or respond to external current stimulation, they collectively form a bio-nervous system capable of reproducing the firing dynamics of the brain [5]. In 1952, Hodgkin and Huxley revealed that the exchange of potassium and sodium ions generates electrical energy, leading to the development of the Hodgkin-Huxley (H-H) model to describe the membrane behavior of a giant axon [6]. Since then, various refined neuron models have been established, including the FitzHugh-Nagumo (FHN) model [7] and the Morris-Lecar (ML) model, which simulates the barnacle muscle fiber [8]. Drawing inspiration from these foundational works, numerous artificial neuron models have been initiated or innovated to better represent biological information processing. A key contribution was made by Beyer and Ogier, who pioneered the integration of tabu search into neural networks to solve optimization problems [9]. The subsequent period saw the proposal of several discrete neuron formulations, ranging from the Izhikevich model [10] and the Chialvo neuron [11,12] to the Hindmarsh-Rose model [13].

Among these models, the Tabu Learning neuron is particularly suitable for the present study. First, it introduces an additional state variable that encodes an activity-dependent tabu memory, implementing dynamical negative feedback on recently visited states. This mechanism naturally produces rich multistable and history-dependent firing patterns that are difficult to obtain in classical two-variable models such as FHN or ML, while retaining a relatively low dimensionality that is convenient for analysis. Second, the Tabu Learning framework originates from optimization theory, where the tabu memory helps escape local minima. In a neuronal context, this gives rise to complex energy landscapes with coexisting attractors and intricate transition routes, offering a compact platform for exploring how memory-like modulation shapes firing dynamics. Third, the simple two-dimensional structure of the Tabu Learning neuron, together with its sinusoidal activation, is highly amenable to FPGA implementation, enabling a direct link between bifurcation analysis, semi-analytical discrete mapping, and real-time neuromorphic experiments.

The nonlinear nature of neurons and neural networks gives rise to diverse dynamics, such as bursting and spiking, under the influence of electromagnetic fields or memristive elements [14,15]. For example, an HR neuron model driven by constrained electromagnetic fields was used to explore chaotic dynamics and the coexistence of periodic and hidden bursting behaviors [16,17]. Other work investigated a Hindmarsh–Rose model subjected to external electromagnetic radiation, where a piecewise memristor produced multiple hidden attractors with complex scroll structures. In parallel, recent experiments have shown that commercial memristor devices can be directly embedded into analog oscillator circuits, e.g., by replacing passive resistors in relaxation and Wien-bridge oscillators, to study how real memristive elements modify system dynamics [18,19]. These results indicate that memristors are not only of theoretical interest but are also becoming commercially accessible components for practical nonlinear and neuromorphic circuits. Detailed analyses of attraction basins and time series in such systems have revealed diverse firing dynamics, including spiking, bursting, and transitional patterns. Recently, a Tabu Learning single-neuron model with a nonlinear activation function was proposed, and diverse firing behaviors such as spiking, bursting, and bistable activities were analyzed using phase portraits and cross-sectional methods [20]. A Tabu neuron model influenced by electromagnetic fields and external current further exhibited bistability and anti-monotonic transitions through bifurcation diagrams, phase trajectories, and attraction basins [21].

Despite the abovementioned advances, existing research indicates that investigations of neuronal and neural network dynamics have predominantly relied on traditional numerical simulations to explore complex behaviors such as firing patterns [22], extreme multistability [23], and antimonotonic phenomena [24]. Although numerical simulations play a vital role in exploring the dynamic characteristics of neural systems, they have certain limitations. Specifically, the intricate transitions and the associated bifurcation structures in various models are often difficult to capture analytically, as computational errors accumulate through recursive and iterative calculations in traditional numerical approaches. Such analytical insights can help elucidate the underlying mechanisms of certain neurological conditions. Disorders like periodic paralysis [25], Alzheimer’s disease [26], and Parkinson’s disease [27] may be closely related to the abnormal dynamic behaviors revealed in these neuron models. At the same time, the discrete mapping approach offers an effective means to improve computational accuracy, enabling analytical exploration of bifurcation mechanisms in nonlinear dynamical systems. Luo [28] first introduced this approach, which has since been employed to conduct semi-analytical analyses of chaotic transitions in multiple nonlinear systems. Related studies have revealed diverse bifurcation trees featuring coexisting stable and unstable periodic behaviors [29,30,31].

Compared with the above studies, this work makes several distinct advances. First, whereas previous Tabu Learning neuron models mainly relied on conventional numerical simulations to investigate firing patterns under different external stimuli [20,21], we construct a semi-analytical discrete implicit mapping that enables high-precision localization of stable and unstable periodic orbits and rigorous identification of their bifurcation boundaries. Second, in contrast to earlier applications of the discrete mapping technique that focused primarily on non-neuronal chaotic systems such as electronic circuits and mechanical oscillators [28,29,30,31], we extend this framework to a biologically inspired single-neuron model with sinusoidal excitation and reveal self-similar offset bifurcation routes, coexisting attractors, and chaotic bubbling phenomena. Third, beyond model-level analysis, we implement the proposed neuron and its discrete mapping on an FPGA platform, providing hardware evidence that bridges high-precision dynamical predictions and digital neuromorphic realizations. As summarized in Table 1, most existing works either provide detailed numerical or semi-analytical studies without hardware verification or focus on hardware-oriented neuron realizations without explicitly tracking unstable periodic orbits. In contrast, the present work combines a semi-analytical discrete implicit mapping framework with an FPGA-based digital implementation of the improved Tabu Learning neuron, accurately identifying stable and unstable periodic motions in the analytical domain and reproducing the corresponding firing behaviors on hardware.

Table 1. Comparison of representative related works and the present study.

Category	Representative Works	Main Advantages	Limitations Relative to This Work
Classical neuron models with numerical analysis	HH, FHN, ML, HR, and related neuron models with numerical studies of firing/bifurcations [9,10,11,12,13]	Rich spiking/bursting and nonlinear dynamics	Unstable periodic orbits in chaos not explicitly located
Tabu Learning neuron models with numerical analysis	Single-neuron and field-driven Tabu Learning neuron models analyzed via phase portraits and bifurcation diagrams [20,21]	Diverse firing patterns and coexistence in Tabu Learning neuron	Use conventional numerical integration; unstable periodic motions not systematically captured
Discrete implicit mapping analyses	Discrete implicit mapping and related semi-analytical methods for nonlinear oscillators and chaotic systems [29,30,31]	Accurately locate stable/unstable periodic orbits and bifurcations	Mainly treat generic nonlinear systems, not neuron models; no FPGA neuron implementation or firing-behavior validation
FPGA-based neuron implementations	FPGA implementations of spiking neurons and neuromorphic circuits [32]	Provide real-time/high-throughput neuromorphic hardware	Typically use standard numerical schemes; unstable periodic motion structures rarely analyzed on hardware
This work	Improved Tabu Learning neuron with discrete implicit mapping and FPGA realization	Semi-analytical framework + FPGA circuit that reproduces stable and unstable periodic motions	Currently focuses on a single neuron; extension to multi-neuron/network-level FPGA implementations left for future work

Motivated by these considerations, this study analyzes the bifurcation evolution of an improved Tabu Learning neuronal system and identifies periodic patterns as well as chaotic bubbling phenomena through two-parameter bifurcation diagrams. The influence of external current stimulation on system stability and bifurcation characteristics is systematically examined. In addition, a digital neuron circuit is implemented on an FPGA platform to simulate the neuronal firing behaviors and to experimentally validate the theoretical predictions. The integration of analytical modeling and hardware implementation enhances both the accuracy and reliability of the findings, thereby providing a solid basis for further exploration of neuromorphic systems and neural dynamics.

In addition to digital implementations, many studies have explored analog and mixed-signal realizations of neuron models using standard CMOS technology [32,33,34]. Such designs can offer low-power, compact circuits suitable for large-scale integration, but they are often sensitive to process, voltage, and temperature variations, and it is difficult to precisely control and measure unstable periodic orbits embedded in chaos. In contrast, FPGA-based realizations operate in a fully digital domain, allowing the neuron dynamics to be implemented as a finite-state machine that iteratively evaluates the discrete implicit mapping with well-defined fixed-point precision.

The remainder of this paper is organized as follows. Section 2 introduces the Tabu Learning neuron model and the discretization method. Section 3 presents the bifurcation evolution and firing behavior analysis. Section 4 describes the FPGA-based digital circuit experiments. Section 5 concludes the study with a summary and future perspectives.

2. Model Formulation and Analysis

2.1. Formulation of the Tabu Learning Single-Neuron Model

The dynamics of the non-autonomous Tabu Learning single-neuron model are governed by a two-dimensional nonlinear function, expressed in a simplified form as:

$$\left\{\begin{array}{l}\dot{x}=-ax+bf(x)+y+I\\ \dot{y}=-cy-df(x)\end{array}\right.$$

(1)

where $a$, $b$, $c$, and $d$ represent four positive parameters, while $x$ and $y$ denote the neuron’s firing state variable and the Tabu Learning state variable, respectively. In this paper, the external stimulus applied to the system is denoted as:

$$I=A\sin (\omega t)$$

(2)

where $A$ and $\omega$ represent the amplitude and frequency of the external stimulating current. Typically embodied by a bounded nonlinear function, the activation function is employed to mimic the firing behavior of the neuron. The periodicity of the external stimulating current can induce chaotic firing behavior in the neuron. The expression of the sin-like activation function used here is:

$$f\left(x\right)=\sin \left(\lambda x\right)$$

(3)

From a numerical viewpoint, Equation (1) defines a non-autonomous initial value problem (IVP) of the form $\dot{z}\left(t\right)=F\left(z\left(t\right),t\right),z\left(t_0\right)=z_0$, where $z\left(t\right)={\left(x\left(t\right),y\left(t\right)\right)}^T$ and the explicit time dependence arises from the sinusoidal forcing term. Since the right-hand side $F$ is smooth and the system parameters considered in this work do not lead to stiffness, standard one-step Runge–Kutta methods are appropriate for reproducing the dynamical behavior of the non-autonomous Tabu learning single-neuron model. For direct time-domain simulations and for generating reference trajectories in the bifurcation diagrams, we adopt the classical fourth-order Runge–Kutta (RK4) scheme with a fixed step size $h$, which provides a good compromise between accuracy and computational cost. The step size is chosen such that it resolves both the intrinsic time scale of the neuron and the period of the external stimulus, and step-size refinement tests (halving and quartering $h$) yield visually indistinguishable phase portraits and bifurcation diagrams, indicating that the numerical results are well converged for the chosen $h$.

In addition to this conventional explicit integration, we introduce in Section 2.2 a semi-analytical discrete implicit mapping constructed over one forcing period. While RK4 is well-suited for capturing the global time evolution and long transients of the IVP, the discrete implicit mapping is particularly advantageous for accurately localizing unstable periodic orbits embedded in chaotic regimes and for performing eigenvalue-based bifurcation analysis. In this sense, the mapping method can be viewed as a high-precision complement to standard numerical integration for the non-autonomous Tabu learning neuron.

Extending these findings that link parameter modulation to multi-scroll attractors in the Tabu Learning model, our investigation delves into the coexistence of multiple firing patterns, with a systematic analysis of their dynamic features in the time domains.

2.2. Semi-Analytical Model

To improve the computational accuracy of the neuronal system and to mitigate the iterative computation errors inherent in conventional numerical methods, this study employs a discrete implicit mapping approach for the analysis of neuronal dynamics. Considering a sufficiently small time interval $t\in [t_{k+1}-t_k]$, the Tabu Learning single-neuron model is discretized using the midpoint scheme. Accordingly, the mapping $P_k\left(\left\{k\in 1,2,3,\dots \right\}\right)$ is defined as follows:

$$P_k:x_k\to x_{k+1}\Rightarrow x_{k+1}=P_k{x}_k$$

(4)

where $x_k={\left(x_k,y_k\right)}^T$ represents the discrete nodes. The equations obtained via the discrete mapping method are given as follows:

$$\begin{array}{l}{x}_{k+1}=x_k+h\left(-a{\displaystyle \frac{x_{k+1}+x_k}{2}}+b\sin \left(\lambda {\displaystyle \frac{x_{k+1}+x_k}{2}}\right)+{\displaystyle \frac{y_{k+1}+y_k}{2}}+A\sin \left(\omega t_{k/2}\right)\right)\\ y_{k+1}=y_k+h\left(-c{\displaystyle \frac{y_{k+1}+y_k}{2}}-d\sin \left(\lambda {\displaystyle \frac{x_{k+1}+x_k}{2}}\right)\right)\end{array}$$

(5)

The corresponding algebraic equations are:

$$\begin{array}{l}{g}_{1,k+1}=x_{k+1}-x_k-h\left(-a{\displaystyle \frac{x_{k+1}+x_k}{2}}+b\sin \left(\lambda {\displaystyle \frac{x_{k+1}+x_k}{2}}\right)+{\displaystyle \frac{y_{k+1}+y_k}{2}}+A\sin \left(\omega t_{k/2}\right)\right)=0\\ g_{2,k+1}=y_{k+1}-y_k-h\left(-c{\displaystyle \frac{y_{k+1}+y_k}{2}}-d\sin \left(\lambda {\displaystyle \frac{x_{k+1}+x_k}{2}}\right)\right)=0\end{array}$$

(6)

The perturbation variation $\Delta x_N$ can be expressed as:

$$\Delta x_N=DP\Delta x_1=D{P}_N·D{P}_{N-1}·\cdots ·D{P}_2·D{P}_1·\Delta x_1$$

(7)

Governing the period-1 motion of the Tabu Learning single-neuron model, the associated Jacobian matrix is given by:

$$DP={{\displaystyle \prod _{k=1}^N\left[\frac{\partial x_{k+1}}{\partial x_k}\right]}}_{(x_k^{\ast },x_{k+1}^{\ast })}$$

(8)

The stability and bifurcation types of the period-1 motion are assessed from the characteristic equation:

$$\left|DP-\lambda I_{2\times 2}\right|=0$$

(9)

Within the framework of the discrete implicit mapping method, the stability of the period-1 motion is governed by its eigenvalues, as follows:

(1)

When $\left|{\lambda }_i\right|<1 \left(i=1,2\right)$, the period-1 motion is stable.

(2)

When $\left|{\lambda }_i\right|>1 \left(i=1,2\right)$, the period-1 motion is unstable.

(3)

When $\left|{\lambda }_i\right|=1$ and $\left|{\lambda }_j\right|<1 \left(i,j\in \left\{1,2\right\}\right)$, the period-1 motion reaches the bifurcation boundary.

At the bifurcation boundary, the bifurcation type of the period-1 motion is determined as follows:

(1)

If ${\lambda }_i=1$ and $\left|{\lambda }_j\right|<1\left(i,j\in \left\{1,2\right\},i\ne j\right)$, the period-1 motion undergoes a saddle-node bifurcation.

(2)

If ${\lambda }_i=-1$ and $\left|{\lambda }_j\right|<1\left(i,j\in \left\{1,2\right\},i\ne j\right)$, the period-1 motion undergoes a period-doubling bifurcation.

The analytical procedure for determining stability and bifurcation types, as previously outlined for period-1 motion, is readily applied to the general period-m case.

It is worth commenting on the sensitivity of the proposed mapping method to the choice of the time step. In the present framework, the discrete implicit mapping is constructed by integrating the continuous-time Tabu Learning neuron over one forcing period with a fixed sampling interval $h$. Therefore, the mapping should be regarded as a numerical Poincaré map associated with a given $h$: for sufficiently small step sizes, the truncation error introduced by the underlying time discretization is negligible compared with the characteristic amplitude of the state variables, and the fixed points and eigenvalues of the map converge as $h$ is refined. In practice, we have verified that halving or quartering the time step around the nominal value used in this paper leads to visually indistinguishable phase portraits and bifurcation diagrams, while the changes in the eigenvalues of the localized periodic orbits remain within a very small fraction of their magnitude. Only when the time step is increased to values comparable to the fastest intrinsic time scale of the neuron dynamics do noticeable deviations appear. Consequently, the step size adopted in this study represents a compromise between accuracy and computational efficiency, and all reported bifurcation structures and orbit classifications have been checked to be robust with respect to moderate variations of $h$.

3. Dynamic Analysis

3.1. Bifurcation Evolution

This section adopts the discrete implicit mapping method to elucidate the chaotic routes and dynamic behaviors of the Tabu Learning neuron system. Numerical simulations are implemented in Microsoft Visual C++ to achieve high computational efficiency and accuracy. Additionally, the bifurcation evolution process is systematically illustrated, and both the types and locations of bifurcations are identified through eigenvalue analysis.

The computational accuracy of the discrete implicit mapping method was set to $o\left(h^3\right)<{10}^{-9}$, with the time step set to $h=T/N<{10}^{-3}$, where $T=2\pi /\omega$, and $N$ represents the number of discrete points within each period. The initial conditions of the system are chosen as $\left(x\left(0\right),y\left(0\right)\right)=\left(0,0\right)$. Subsequently, the corresponding two-parameter diagrams are generated under the following system parameter settings. Specifically, Figure 1a illustrates $b=3.7$, $c=0.1$, $d=2.2$, $\lambda =1$, $\omega =2\pi \cdot 0.09$, while Figure 1b depicts $a=0.7$, $b=3.7$, $c=0.1$, $\lambda =1$, $\omega =2\pi \cdot 0.09$.

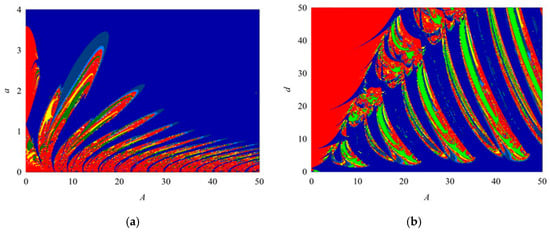
Figure 1. Two-parameter mapping diagrams: (a) Mapping related to parameters $A$ and $a$; (b) Mapping related to parameters $A$ and $d$.

Figure 1a shows the two-parameter diagram for parameters $A$ and $a$, with their value ranges of $\left[0,50\right]$ and $\left[0,4\right]$, respectively. Moreover, Figure 1b presents the two-parameter diagram for parameters $A$ and $d$, where both of them vary within $\left[0,50\right]$. In both diagrams, blue shades (from dark to light) represent period-1, period-2, and period-4 motions, green corresponds to period-3, yellow indicates period-5, and red signifies chaotic behavior. The Tabu Learning neuron system displays a rich variety of dynamic behaviors across different parameter regions.

Importantly, the system exhibits distinct self-similar offset characteristics resulting from the use of $f\left(x\right)=\sin \left(\lambda x\right)$ as the activation function. Here, “self-similar offset” means that the main bifurcation structures and coexistence windows appear as a series of nearly identical copies that are shifted in both the parameter space and the state space. Owing to the $2\pi$-periodicity and odd symmetry of the sinusoidal activation, trajectories that differ by an approximate phase shift $2k\pi /\lambda \left(k\in Z\right)$ experience almost the same effective feedback, so the system generates multiple dynamically equivalent attractors and basins that are translated versions of each other. This mechanism gives rise to the banded, stream-like arrangement of colored regions in the two-parameter diagrams of Figure 1 and to the alternating red–blue stripes observed in the basins of attraction in Figure 2, thereby visually manifesting the self-similar offset characteristics of the Tabu Learning neuron system.

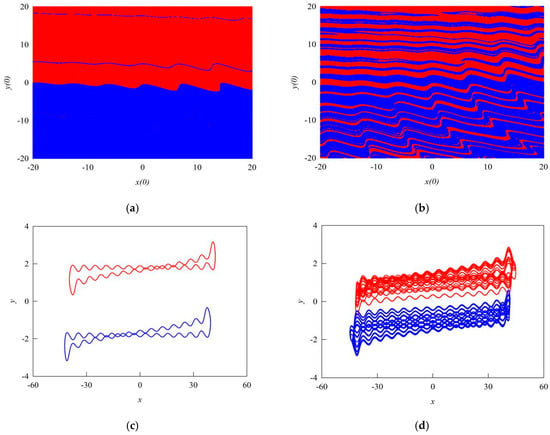
Figure 2. Coexisting basins of attraction and corresponding phase trajectories in the $x(0)$–$y(0)$ parameter plane: (a) basin for period-1 motion; (b) basin in the chaotic region; (c) Phase trajectory of the coexisting period-1 motions, (d) Phase trajectory in the coexisting chaotic region.

Figure 2 depicts the basins of attraction at points $A=37$ and $A=39$ corresponding to the numerical bifurcation diagram in Figure 3a, with system parameters identical to those used in Figure 3a. Specifically, Figure 2a presents the basin of attraction for period-1 motion at $A=37$, where the initial conditions $x(0)$ and $y(0)$ both vary within $\left[-20,20\right]$. Figure 2b illustrates the basin of attraction in the chaotic region at $A=39$, using the same initial condition range for both variables.

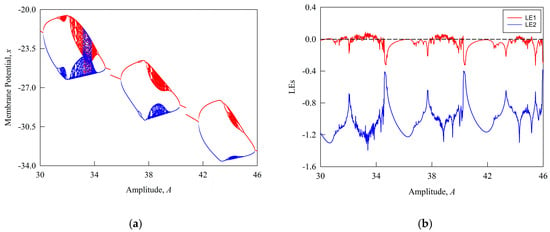
Figure 3. Global bifurcation diagram and Lyapunov exponent spectrum under the influence of the external stimulus current amplitude $A$: (a) Global coexisting bifurcation diagram via numerical method versus $A$; (b) Corresponding Lyapunov exponent spectrum versus $A$.

Figure 2 exhibits a characteristic “stream-like” pattern with alternating red and blue regions in the basins of attraction. This intricate structure visually reveals the system’s extreme sensitivity to initial conditions, as even minute variations in the initial values can lead to markedly divergent trajectories. Specifically, initial conditions located within the red region guide the system trajectory to converge onto the red periodic orbit, whereas those within the blue region evolve strictly along the blue trajectory. Such an alternating distribution not only indicates the coexistence of multiple stable periodic attractors but also implies potential transitions between different basins of attraction. Collectively, these features strongly reflect the complex dynamical organization and coexistence characteristics inherent in the system’s phase space.

Figure 3a presents the global numerical bifurcation diagram, and Figure 3b displays the corresponding Lyapunov exponent (LE) spectrum. The system parameters used in Figure 3a are set as $a=0.7$, $b=3.7$, $c=0.1$, $d=2.2$, $\lambda =1$, $\omega =2\pi \cdot 0.09$. The red trajectory corresponds to the initial condition $\left(x\left(0\right),y\left(0\right)\right)=\left(0,0\right)$ at $A=37$, whereas the blue trajectory corresponds to $\left(x\left(0\right),y\left(0\right)\right)=\left(-20,-20\right)$ at $A=31$, with the control parameter $A$ varying within the range $\left[30,46\right]$. As shown in Figure 3b, the LE spectrum exhibits strong agreement with the bifurcation diagram, thereby providing mutual validation for the numerical analysis. In particular, regions with the largest positive exponents correspond precisely to the chaotic domains in the bifurcation diagram, while regions with the largest negative exponents align with stable periodic motions. Together, these observations further confirm the presence of self-similar offset characteristics and reveal two distinct types of coexistence phenomena within the system, highlighting the rich and intricate dynamical behaviors of the constructed Tabu Learning neuron model.

A comparative analysis of bifurcation diagrams, generated by the traditional Runge–Kutta algorithm and the discrete implicit mapping method in Figure 4, highlights the advantages of the latter. In the figures, bifurcation points are marked by gray dashed lines and labeled as “PD” for period-doubling and “PB” for pitchfork bifurcations. As illustrated in the results, solid black lines represent stable periodic motions, whereas short red dashed lines correspond to unstable periodic motions, thereby providing a clear distinction between stability states in the system’s dynamic evolution.

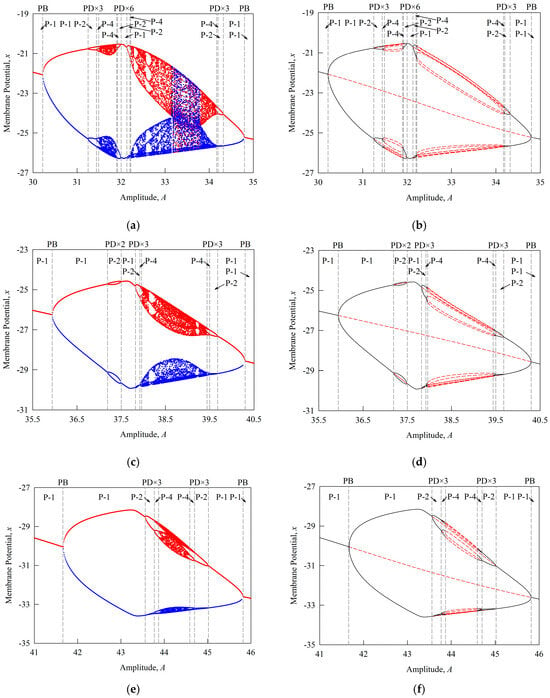
Figure 4. Local coexisting bifurcation diagrams under the influence of the external stimulus current amplitude $A$: (a) Numerical local coexisting bifurcation diagram for $A\in \left(30,35\right)$; (b) Analytical local coexisting bifurcation diagram for $A\in \left(30,35\right)$; (c) Numerical local coexisting bifurcation diagram for $A\in \left(35.5,40.5\right)$; (d) Analytical local coexisting bifurcation diagram for $A\in \left(35.5,40.5\right)$; (e) Numerical local coexisting bifurcation diagram for $A\in \left(41,46\right)$; (f) Analytical local coexisting bifurcation diagram for $A\in \left(41,46\right)$.

Figure 4a,c,e show the bifurcation diagrams obtained using conventional numerical methods, illustrating the system’s nonlinear dynamic responses under variations in the external stimulus current amplitude $A$. In comparison, Figure 4b,d,f present the corresponding bifurcation structures computed through the discrete implicit mapping method, which clearly reveal the evolution of both stable and unstable regions under the same parameter variations. Additionally, Figure 5 provides an enlarged view of Figure 4b, distinctly exposing bifurcation pathways that cannot be detected by conventional numerical approaches. Evidently, the discrete implicit mapping method not only identifies unstable periodic orbits with high accuracy after the system enters the chaotic regime but also captures subtle turning points in dynamic behavior within chaotic regions, including chaotic crises and transient chaos boundaries. By contrast, traditional numerical methods primarily depict the transition into chaos, yet show limited precision in characterizing the intricate internal dynamics within chaotic domains.

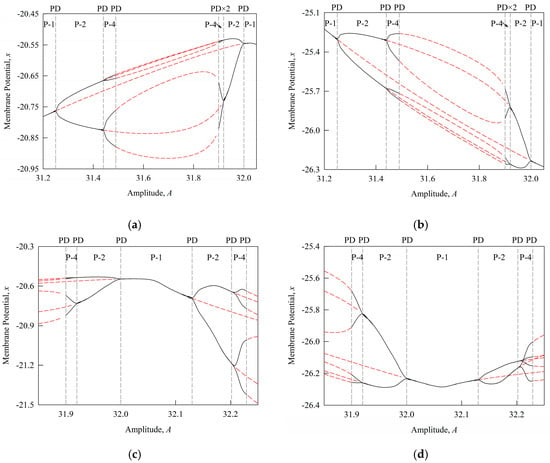
Figure 5. Local coexisting bifurcation diagrams under the influence of the external stimulus current amplitude $A$: (a) Analytical local coexisting bifurcation diagram for $A\in \left(31.2,32.05\right)$; (b) Analytical local coexisting bifurcation diagram for $A\in \left(31.2,32.05\right)$; (c) Analytical local coexisting bifurcation diagram for $A\in \left(31.85,32.25\right)$; (d) Analytical local coexisting bifurcation diagram for $A\in \left(31.85,32.25\right)$.

Further analysis reveals that the Tabu Learning neuron system exhibits intricate coexistence and symmetric behaviors, particularly in the vicinity of pitchfork (PB) and period-doubling (PD) bifurcation points, where the stability of periodic motions undergoes pronounced transitions. A noteworthy phenomenon observed in this system is that period-doubling bifurcations consistently occur in pairs. Each forward period-doubling bifurcation is accompanied by a corresponding reverse bifurcation, which can lead to the annihilation of periodic solutions or to changes in their stability. This paired PD bifurcation behavior underscores the distinctive nonlinear dynamic structure of the system.

Table 2, Table 3 and Table 4 systematically summarize the bifurcation types, locations, and stability states of periodic motions (“S” for stable and “U” for unstable) in the Tabu Learning neuron system across different parameter intervals. Together, these results provide detailed quantitative evidence for characterizing the system’s complex dynamical patterns and bifurcation characteristics under variations in the external stimulus current amplitude $A$.

Table 2. Bifurcation types and stability of periodic motions in the Tabu Learning neuron (Part 1).

Period-m	$\mathit{A}$	Left Bifurcation	Right Bifurcation	Stability
Common P-1	(30.00, 30.22)	-	PB	S
	(30.22, 34.80)	PB	PB	U
	(34.80, 35.00)	PB	-	S
Coexisting P-1	(30.22, 31.25)	PB	PD	S
	(31.25, 32.00)	PD	PD	U
	(32.00, 32.13)	PD	PD	S
	(32.13, 34.32)	PD	PD	U
	(34.32, 34.80)	PD	PB	S
Coexisting P-2	(31.25, 31.44)	PD	PD	S
	(31.44, 31.92)	PD	PD	U
	(31.92, 32.00)	PD	PD	S
	(32.13, 32.20)	PD	PD	S
	(32.20, 34.20)	PD	PD	U
	(34.20, 34.32)	PD	PD	S
Coexisting P-4	(31.44, 31.49)	PD	PD	S
	(31.49, 31.90)	PD	PD	U
	(31.90, 31.92)	PD	PD	S
	(32.20, 32.22)	PD	PD	S
	(32.22, 34.17)	PD	PD	U
	(34.17, 34.20)	PD	PD	S

Table 3. Bifurcation types and stability of periodic motions in the Tabu Learning neuron (Part 2).

Period-m	$\mathit{A}$	Left Bifurcation	Right Bifurcation	Stability
Common P-1	(35.50, 35.94)	-	PB	S
	(35.94, 40.30)	PB	PB	U
	(40.30, 40.50)	PB	-	S
Coexisting P-1	(35.94, 37.19)	PB	PD	S
	(37.19, 37.50)	PD	PD	U
	(37.50, 37.82)	PD	PD	S
	(37.82, 39.68)	PD	PD	U
	(39.68, 40.30)	PD	PB	S
Coexisting P-2	(37.19, 37.50)	PD	PD	S
	(37.82, 37.92)	PD	PD	S
	(37.92, 39.50)	PD	PD	U
	(39.50, 39.68)	PD	PD	S
Coexisting P-4	(37.92, 37.96)	PB	PD	S
	(37.96, 39.44)	PD	PD	U
	(39.44, 39.50)	PD	PD	S

Table 4. Bifurcation types and stability of periodic motions in the Tabu Learning neuron (Part 3).

Period-m	$\mathit{A}$	Left Bifurcation	Right Bifurcation	Stability
Common P-1	(41.00, 41.60)	-	PB	S
	(41.60, 45.82)	PB	PB	U
	(45.82, 46.00)	PB	-	S
Coexisting P-1	(41.60, 43.56)	PB	PD	S
	(43.56, 45.02)	PD	PD	U
	(45.02, 45.82)	PD	PB	S
Coexisting P-2	(43.56, 43.77)	PD	PD	S
	(43.77, 44.70)	PD	PD	U
	(44.70, 45.02)	PD	PD	S
Coexisting P-4	(43.77, 43.87)	PD	PD	S
	(43.87, 44.59)	PD	PD	U
	(44.59, 44.70)	PD	PD	S

In this work, the main bifurcation types associated with the Tabu learning neuron can be interpreted in the standard framework of discrete-time dynamical systems. For a periodic orbit of the discrete implicit mapping, the eigenvalues of the corresponding monodromy matrix lie inside the unit circle for a stable orbit and on or outside the unit circle for an unstable one. A saddle-node (SN) bifurcation occurs when a real eigenvalue crosses $+1$, leading to the creation or annihilation of a pair of period-$m$ orbits and corresponding to the appearance or disappearance of a firing pattern at the edges of a periodic window. A period-doubling (PD) bifurcation is characterized by a real eigenvalue crossing $-1$, which gives rise to a period-$2m$ orbit and, in the neuronal context, marks the transition from tonic spiking to multi-spike or bursting-like responses through a PD cascade. When a complex-conjugate pair of eigenvalues crosses the unit circle, a Neimark–Sacker (NS) bifurcation (also referred to as a secondary Hopf bifurcation) may occur, leading to quasi-periodic firing on invariant closed curves. This eigenvalue-based classification is consistent with the evolution of phase trajectories and time-domain waveforms shown, where tonic periodic spiking, multi-periodic patterns, and chaotic bursting behaviors emerge as the control parameter $A$ is varied. Similar bifurcation mechanisms underlying transitions between regular spiking, bursting, and chaotic firing have been reported in classical neuron models and nonlinear oscillators [28,29,30], which further supports the use of eigenvalue analysis and discrete mapping techniques for revealing diverse firing patterns in the proposed Tabu learning neuron.

To further elucidate the decisive role of eigenvalues in determining bifurcation types and the stability of periodic motions, Figure 6 presents the global eigenvalue distributions under variations in the external stimulus current amplitude. In addition, Figure 6a,b, Figure 6c,d, and Figure 6e,f correspond to the parameter ranges shown in Figure 4b, Figure 4d, and Figure 4f, respectively, illustrating the variations in the real parts and moduli of the eigenvalues. In each subfigure, solid black lines represent the eigenvalue trajectories associated with stable periodic motions, whereas red dashed lines denote those corresponding to unstable periodic motions. As shown in the figure, the real part of the eigenvalue, Re(λ), directly determines the stability of an orbit, while the modulus, |λ|, serves as the key criterion for evaluating the stability of the discrete implicit mapping system.

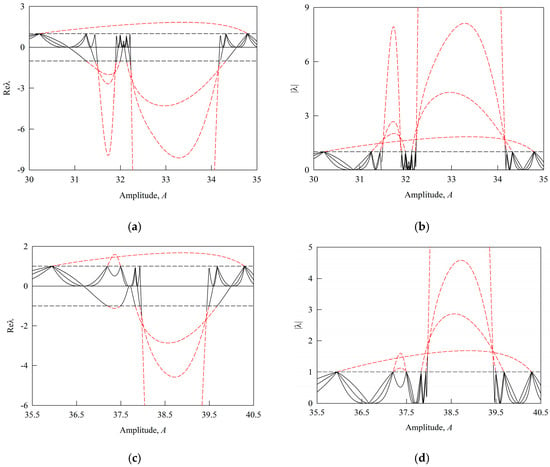
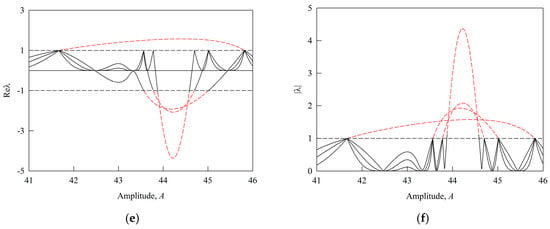
Figure 6. Local coexisting bifurcation diagrams under the influence of the external stimulus current amplitude $A$: (a) Numerical local coexisting bifurcation diagram for $A\in \left(30,35\right)$; (b) Analytical local coexisting bifurcation diagram for $A\in \left(30,35\right)$; (c) Numerical local coexisting bifurcation diagram for $A\in \left(35.5,40.5\right)$; (d) Analytical local coexisting bifurcation diagram for $A\in \left(35.5,40.5\right)$; (e) Numerical local coexisting bifurcation diagram for $A\in \left(41,46\right)$; (f) Analytical local coexisting bifurcation diagram for $A\in \left(41,46\right)$.

Stable periodic motion (S) occurs when all eigenvalues have moduli less than unity (|λ| < 1), as indicated by the black trajectories lying entirely below the |λ| = 1 threshold in Figure 6b,d,f. This condition implies that perturbations decay over time, allowing the system to maintain its original periodic orbit. Unstable periodic motion (U) is identified when |λ| > 1 for any eigenvalue. This is visually confirmed in Figure 6b,d,f by the red trajectory segments that exceed the |λ| = 1 boundary. In this case, perturbations are amplified, resulting in orbital instability. Additionally, a period-doubling bifurcation (PD) occurs precisely when one eigenvalue attains a modulus equal to unity (|λ|=1) while all others remain less than one. At this critical juncture, the originally stable periodic orbit undergoes a loss of stability and bifurcates into a new stable orbit whose period is twice the original. As illustrated in Figure 6, this critical eigenvalue behavior, characterized by the crossing of the |λ| = 1 boundary, exhibits strong agreement with the bifurcation types (PD, PB) observed in the bifurcation diagrams and with the corresponding stability transitions (S↔U) summarized in Table 1, Table 2 and Table 3. Such consistency provides robust validation for the analytical accuracy of the discrete implicit mapping method. Overall, the global eigenvalue diagrams establish a clear and quantitative correspondence between eigenvalue dynamics and macroscopic bifurcation behavior, as well as the stability of periodic motions. These findings offer valuable insights into the complex dynamical mechanisms of the Tabu Learning neuron system under varying excitation conditions and lay a solid theoretical foundation for its further investigation and optimization.

3.2. Firing Behaviors

Neuronal information processing depends on variations in action potentials, commonly referred to as firing activity. Periodic discharges generally manifest in two primary forms: spiking and bursting. Specifically, spiking is characterized by rapid fluctuations in membrane potential, representing a transition toward a large-amplitude limit cycle, whereas bursting consists of alternating phases of quiescence and high-frequency firing. It has been widely reported that abnormalities in the combination or regulation of these firing patterns are closely associated with the onset and progression of various neurological disorders.

This study examines the firing dynamics of the Tabu Learning neuron under external stimuli using the discrete implicit mapping method, with additional verification through numerical simulations. Under specific stimulus current conditions, the system exhibits stable periodic firing, as illustrated in Figure 7, where the phase trajectory forms a closed loop and the corresponding time-domain waveform displays regular oscillations. The strong consistency between the numerical and analytical results confirms the effectiveness of the proposed method and establishes a reliable foundation for understanding the intrinsic dynamical properties of the system.

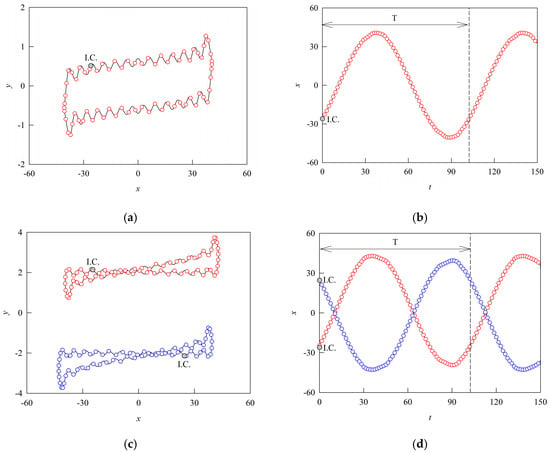
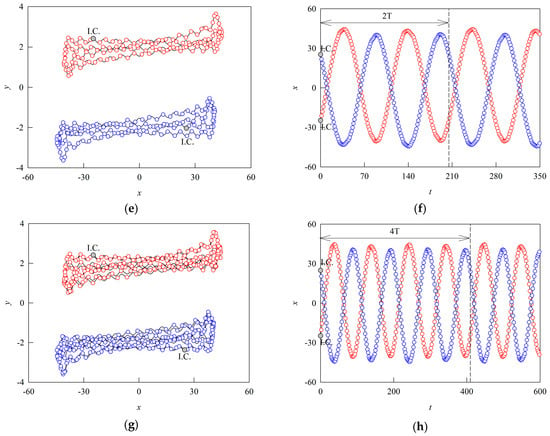
Figure 7. Stable Common Periodic Firing: (a) Phase trajectory of stable common period-1 firing; (b) Time-domain waveform of stable common period-1 firing; (c) Phase trajectory of stable coexisting period-1 firing; (d) Time-domain waveform of stable coexisting period-1 firing; (e) Phase trajectory of stable coexisting period-2 firing; (f) Time-domain waveform of stable coexisting period-2 firing; (g) Phase trajectory of stable coexisting period-4 firing; (h) Time-domain waveform of stable coexisting period-4 firing.

Further investigation reveals that the system exhibits multiple stable periodic firing regimes under different parameter conditions. As depicted in Figure 7a,b, a typical period-1 spiking pattern is observed, where the phase trajectory forms a single closed loop corresponding to repetitive spikes in the time-domain waveform. In addition, the analytical results (small red-edged circles) show excellent concordance with the numerical solutions (solid black lines), confirming the robustness of the proposed method. Furthermore, by appropriately tuning the parameters, the analytical approach successfully predicts a variety of stable coexisting periodic firing patterns, all of which are validated through numerical simulations. Specifically, Figure 7c,d displays two distinct coexisting period-1 orbits, Figure 7e,f shows two intertwined loops in the phase trajectory corresponding to alternating spike morphologies in the time domain, and Figure 7g,h presents a more complex configuration with four loops and a corresponding period-4 spike sequence, reflecting the system’s highly organized nonlinear dynamics.

A comprehensive examination of the phase trajectories and time-domain waveforms in Figure 7 reveals multiple stable firing regimes and their intricate dynamical features under external current stimulation, thereby providing critical insights into the underlying firing mechanisms of the Tabu Learning neuron.

As variations in the stimulus drive the system into a chaotic regime, the neuronal firing becomes highly complex, characterized by recurrent transitions among multiple unstable periodic orbits. Specifically, Figure 8 illustrates three representative unstable periodic motions predicted by the discrete implicit mapping method, accompanied by numerical validation. In the figure, red-edged circles denote analytically obtained unstable periodic orbits, solid black lines correspond to numerical solutions over the same period initialized with analytical conditions, and gray lines depict extended-time numerical simulations used for comparison.

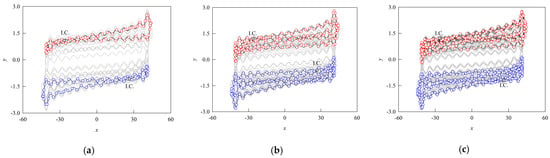
Figure 8. Phase trajectories of unstable periodic motions: (a) unstable coexisting period-1 motion; (b) unstable coexisting period-2 motion; (c) unstable coexisting period-4 motion.

Initially, the numerical solutions exhibit excellent agreement with the analytical results. The numerical solution eventually diverges into chaos, following a progressive deviation from the original unstable orbit that stems from accumulated iterative errors over time. This result attests to the critical dependence of unstable orbits on initial conditions and exposes a fundamental limitation in conducting long-term numerical analysis. In contrast, the discrete implicit mapping method, which is inherently free from iterative errors, directly and accurately reconstructs the entire unstable periodic orbit and preserves consistency even over extended durations. This capability underscores a fundamental advantage of the proposed approach. Furthermore, the density distribution of red circles along the orbit intuitively reflects the instantaneous velocity of motion, thereby providing valuable indicators for analyzing the underlying fast-slow dynamics in neuronal firing.

This study demonstrates that under external stimulus currents, the single Tabu Learning neuron system exhibits a wide range of dynamical behaviors, encompassing multiple stable periodic firing patterns and densely distributed unstable periodic orbits within chaotic regimes. A systematic comparative analysis further confirms the accuracy and reliability of the discrete implicit mapping method in predicting both stable and unstable periodic orbits. In particular, for unstable periodic orbits that are notoriously difficult to capture and sustain using conventional numerical approaches, the proposed analytical framework exhibits distinct advantages by yielding precise initial conditions and complete orbital information. Consequently, this method provides a robust theoretical foundation and a novel analytical perspective for the in-depth exploration of complex nonlinear dynamics in neuronal systems, with special relevance to the generation mechanisms and evolutionary pathways of unstable firing modes associated with neuropathological phenomena.

4. Hardware Implementation of the Digital Circuit

This work presents an FPGA-based digital realization of the Tabu Learning neuron system. The hardware design is developed and verified in the ModelSim simulation environment. The implementation proceeds from the modular construction and functional programming of the core hardware blocks, followed by full system integration and bitstream generation on the Vivado 2018.2 platform. The initial conditions and control parameters are configured within the design environment according to the IEEE-754 single-precision floating-point standard, ensuring that the circuit operates strictly in accordance with the predefined specifications. The overall hardware architecture is organized into four principal modules—top_tabu, RK_tabu, value_intermediate, and change_DA—which cooperate to perform real-time computation and dynamical analysis of the neuron model.

Numerical integration is carried out using the fourth-order Runge–Kutta (RK4) method, applied to the discrete neuron equations in (1). The arithmetic operations in RK4 are implemented by instantiating optimized FPGA IP cores for addition and multiplication, thereby improving both computational throughput and numerical accuracy. The sine function is realized as a dedicated IP core based on an on-chip RAM structure. In the sine module, the input variable $x$ is first scaled by a multiplier and converted into an integer address, which is then used to access a 64-bit wide RAM. The higher 32 bits store the precomputed coefficient $k_l$, and the lower 32 bits store $c_l$, enabling fast table-lookup evaluation of the sinusoidal nonlinearity. Intermediate iteration variables and buffer data are computed and stored in the value_intermediate module, while the change_DA module drives an AN9796 digital-to-analog converter to output analog signals. In this way, the dynamic behavior of the Tabu Learning neuron can be monitored in real time using an oscilloscope. In addition, several works have specifically addressed the efficient implementation of trigonometric functions, such as sine, on FPGAs using CORDIC, LUT, or hybrid schemes [35], which can be readily integrated into neuron and oscillator circuits.

Simulation and hardware testing confirm that each state update can be completed well within a single sampling interval, so that the proposed Tabu Learning neuron circuit operates in real time with respect to the discretization step adopted in the bifurcation and firing-behavior analysis. In addition, the overall resource utilization on the target FPGA still leaves sufficient headroom to accommodate future extensions, such as multi-neuron network implementations or the integration of additional monitoring and control logic.

The hardware configuration is illustrated in Figure 9. As shown in Figure 10, the phase trajectories and corresponding time-domain waveforms of the stable common period-1, coexisting period-1, period-2, and period-4 motions are presented, whereas Figure 11 depicts the unstable coexisting period-1, period-2, and period-4 motions. These experimental observations consistently validate the accuracy and operational stability of the FPGA-based hardware implementation, thereby establishing a solid foundation for subsequent research and system-level optimization.

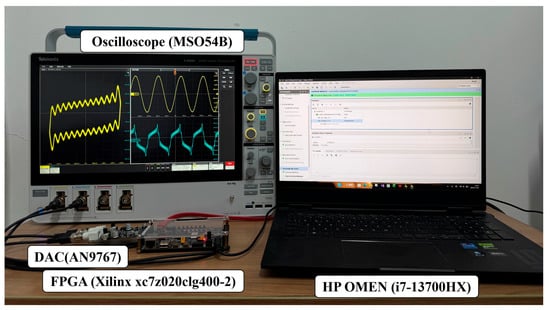
Figure 9. Hardware Setup.

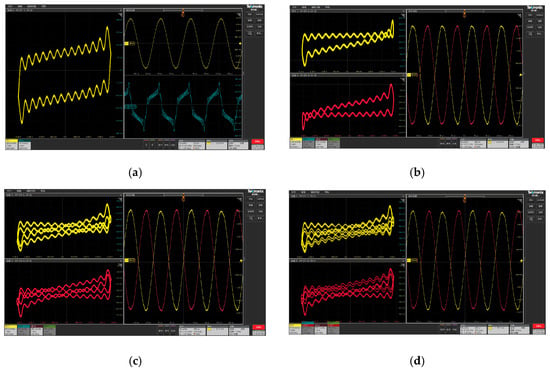
Figure 10. Experimental Results of Phase Trajectories and Time-Domain Waveforms Observed via Oscilloscope: (a) Stable Common Period-1 Motion; (b) Stable Coexisting Period-1 Motion; (c) Stable Coexisting Period-2 Motion; (d) Stable Coexisting Period-4 Motion.

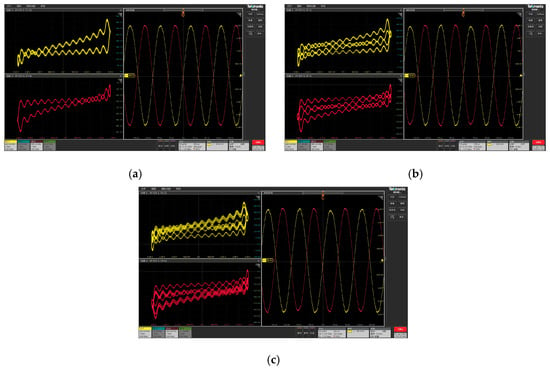
Figure 11. Experimental Results of Phase Trajectories and Time-Domain Waveforms Observed via Oscilloscope: (a) Unstable Coexisting Period-1 Motion; (b) Unstable Coexisting Period-2 Motion; (c) Unstable Coexisting Period-4 Motion.

5. Conclusions

This study systematically investigates the Tabu Learning neuron system using both conventional numerical techniques and a discrete implicit mapping approach. By modulating the amplitude of the external stimulus current, a series of self-similar bifurcation pathways is uncovered, thereby revealing the system’s hierarchical transition patterns across three distinct parameter regions. Through the discrete implicit mapping method, unstable periodic motions embedded within chaotic regimes are accurately detected, and their corresponding periods and bifurcation types are quantitatively characterized via eigenvalue analysis. In addition, phase trajectories and time-domain waveforms are employed to elucidate the temporal firing dynamics of the neuron. Furthermore, the FPGA-based hardware implementation successfully reproduces both stable and unstable periodic motions, thereby validating the theoretical predictions. Overall, these findings not only strengthen the reliability of the analytical modeling framework but also establish a practical experimental platform that bridges theoretical nonlinear dynamics with real-time neuromorphic system research.