Communication-Constrained UAV Pickup and Delivery for Continuous Operations

Abstract

This paper investigates a communication-constrained unmanned aerial vehicle (UAV) pickup and delivery system for continuous multi-period operations. To ensure real-time control updates between UAVs and the ground server, a minimum communication rate requirement is imposed throughout each mission. The objective is to minimize the average mission completion time of multiple rotary-wing UAVs while satisfying mobility, payload, safety, and communication constraints. The resulting mixed-integer nonlinear programming problem, involving binary pickup/drop-off decisions, trajectories, and variable time-slot durations, is mathematically intractable. To address this, a successive convex approximation framework combined with a penalty convex–concave procedure is developed, enabling iterative convex reformulation and convergence to a near-optimal binary-feasible solution. Simulation results demonstrate that the proposed algorithm efficiently generates collision-free trajectories and adaptive flight paths that maintain reliable communication links, outperforming baseline strategies in terms of completion time and coordination efficiency under communication constraints.

1. Introduction

The rapid evolution of lightweight materials, high-density batteries, and compact sensors has transformed unmanned aerial vehicles (UAVs) from specialized tools into versatile platforms for civilian and industrial use [1,2]. Among their diverse applications, ranging from aerial inspection and environmental observation to public safety, UAV-assisted logistics has attracted particular attention due to its potential to enable fast, flexible, and low-cost parcel delivery. Global logistics operators have already begun incorporating autonomous UAVs into last-mile distribution networks to alleviate congestion and reduce human labor costs. However, as UAV delivery networks expand, maintaining reliable wireless connectivity between UAVs and ground control stations becomes essential for real-time command updates, safety monitoring, and operational continuity [3,4,5,6]. Consequently, modern UAV delivery systems must account not only for flight efficiency but also for communication reliability, which critically influences their feasibility and performance in dynamic and large-scale environments.

Building on these advances, extensive research has been devoted to UAV-assisted wireless communication systems that exploit UAV mobility and line-of-sight (LoS) channel advantages to enhance connectivity and efficiency [7,8,9,10,11,12,13,14]. Early study [7] initiated this direction by formulating energy-minimization frameworks for rotary-wing UAV communication, highlighting the trade-off between propulsion energy and transmission performance. Subsequent works [8,9] extended this perspective by jointly optimizing UAV trajectories and operation times to minimize mission completion delay under energy constraints, laying the groundwork for energy-efficient UAV-assisted networking. More recent studies have incorporated the energy harvesting capability, enabling sustainable operation of UAV communication systems [10,11,12]. Furthermore, another line of research has explored UAV-enabled secure communication, where cooperative or dual-UAV schemes are employed to mitigate eavesdropping threats and strengthen information security [13,14].

Following the extensive progress in UAV-assisted wireless communications, attention has increasingly shifted toward leveraging UAVs for efficient and autonomous logistics operations [15,16,17,18,19,20]. In particular, UAV-enabled parcel delivery has become a vibrant research area, aiming to enhance delivery efficiency, reduce operational costs, and ensure system reliability. Early study [15] conceptualized UAV-based delivery as an extension of vehicle routing, developing formulations that balance delivery time and operational cost under resource constraints. Moreover, refs. [16,17] incorporated stochastic task dynamics and three-dimensional (3D) trajectory optimization to manage uncertainty in task arrivals, payload limits, and scheduling dependencies. As UAV fleets expanded, several representative studies explored different aspects of cooperative multi-UAV delivery. In particular, ref. [18] examined swarm-oriented UAV delivery frameworks, assessing their operational performance and scalability across different logistics models. In addition, ref. [19] proposed a distributed and adaptive coordination algorithm for formation-based UAV missions, allowing each UAV to make localized routing decisions while preserving global coherence and avoiding inter-vehicle interference in dynamic environments. Meanwhile, ref. [20] explored the routing and scheduling problem for multiple UAVs with varying payload capacities and uncertain delays, introducing a hybrid genetic and simulated annealing approach to achieve computational efficiency and solution robustness.

Although UAV communication and delivery have been extensively studied, continuous multi-mission UAV logistics that explicitly incorporate communication constraints remain largely unexplored. Most existing studies assume perfect connectivity and thus overlook that meeting a minimum communication rate often compels UAVs to alter their trajectories, delay service actions, or reschedule tasks. By explicitly modeling this rate-driven coupling, our framework captures operational behaviors that prior work inherently misses. To address this limitation, this study presents the first unified optimization framework that jointly captures the key operational constraints of persistent UAV logistics, including communication-rate requirements, pickup/drop-off sequencing, payload limitations, inter-UAV safety separation, and time-slot allocation, within a single coupled formulation. The resulting mixed-integer nonlinear programming (MINLP) model integrates UAV mobility, service-zone constraints, binary mission decisions, and communication feasibility in a unified manner that has not been jointly considered in prior UAV logistics or communication studies.

To cope with the inherent nonconvexity of this coupled MINLP, we develop a customized successive convex approximation (SCA)–penalty convex–concave procedure (PCCP) iterative convexification algorithm that simultaneously addresses these operational constraints and the associated nonconvex geometric and communication-rate expressions. The proposed method constructs convex surrogates for these heterogeneous constraints and iteratively refines them while steering the relaxed binary variables toward feasible near-integer values through penalized components. This yields an efficient solution procedure with polynomial computational complexity and ensures stable convergence of the overall optimization framework. The resulting algorithm enables UAVs to proactively adjust their trajectories and service timing in response to communication requirements, uncovering operational patterns, such as intentional detours toward the server to satisfy rate feasibility, that cannot be captured by existing approaches. Simulation results verify that the proposed framework consistently outperforms baseline delivery strategies and quantify the performance degradation induced by communication rate constraints through comparison with a communication-free upper bound. These findings highlight that explicitly incorporating connectivity requirements is crucial for robust and scalable continuous UAV logistics.

The remainder of this paper is organized as follows. Section 2 presents the system model and problem formulation for the communication-constrained UAV pickup and delivery system. Section 3 details the proposed optimization framework, and Section 4 provides simulation results and performance analyses under various system parameters. Finally, Section 5 concludes the paper with key insights.

2. System Model and Problem Statement

Figure 1 illustrates a communication-constrained UAV pickup and delivery system. A total of M rotary-wing UAVs depart from their respective origins ${\mathbf{c}}_m^{\mathrm{org}}$, pick up K items, deliver them to predefined delivery zones, and finally return to their destinations ${\mathbf{c}}_m^{\mathrm{dst}}$. In Figure 1, the black circle labeled with number k denotes the pickup location of item k, while the red circle labeled with number k represents the delivery zone of item k. Each item $k\in \mathcal{K}=\{1,2,\dots ,K\}$ has a weight $w_k$. The flight duration of UAV $m\in \mathcal{M}=\{1,2,\dots ,M\}$ is denoted by $T_m$, which is divided into N variable-length time slots ${\delta }_m\left[n\right]\ge 0$ satisfying $T_m={\sum }_{n=1}^N{\delta }_m\left[n\right]$. While N is fixed, ${\delta }_m\left[n\right]$ is an optimization variable [17].

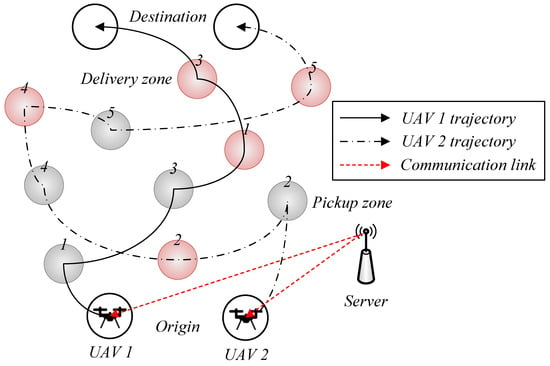
Figure 1. System model of communication-constrained UAV pickup and delivery systems.

At time slot $n\in \mathcal{N}=\{1,2,\dots ,N\}$, the 3D position of UAV m is given by ${\mathbf{c}}_m\left[n\right]=({\mathbf{q}}_m\left[n\right],z_m\left[n\right])$, where ${\mathbf{q}}_m\left[n\right]=(x_m\left[n\right],y_m\left[n\right])$ and $z_m\left[n\right]$ denote its horizontal and vertical coordinates, respectively. Each UAV’s movement is limited by the maximum speed $V_{\max }$, ensuring that the travel distance in slot n does not exceed $V_{\max }{\delta }_m\left[n\right]$. To avoid in-air collisions, the distance between any two UAVs must remain greater than the minimum safety distance $d_{\min }$. Accordingly, the UAV mobility constraints are expressed as

$$\begin{array}{cc}\hfill & {\mathbf{c}}_m\left[0\right]={\mathbf{c}}_m^{\mathrm{org}},{\mathbf{c}}_m\left[N\right]={\mathbf{c}}_m^{\mathrm{dst}},\forall m,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_m[n-1]\parallel \le V_{\max }{\delta }_m\left[n\right],\forall m,n,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_{m^{\prime }}{\left[n\right]\parallel }^2\ge d_{\min }^2,\forall m\ne m^{\prime },n.\hfill \end{array}$$

(3)

Let ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$ be binary variables indicating the pickup and drop-off operations of UAV m for item k at time slot n, respectively. Specifically, ${\alpha }_{m,k}\left[n\right]=1$ if item k is picked up by UAV m during slot n, and ${\beta }_{m,k}\left[n\right]=1$ if it is dropped off; otherwise, both are 0. Each UAV has a maximum payload capacity $W_{\max }$, and its total carried weight at slot n, denoted by $W_m\left[n\right]$, must satisfy $W_m\left[n\right]\le W_{\max }$. Accordingly, the pickup and drop-off constraints are formulated as

$$\begin{array}{cc}\hfill & \{{\alpha }_{m,k}\left[n\right],{\beta }_{m,k}\left[n\right]\}\in \{0,1\},\forall m,k,n,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{m=1}^M\sum _{n=1}^N{\alpha }_{m,k}\left[n\right]\le 1,\forall k,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \sum _{m=1}^M\sum _{n=1}^N{\beta }_{m,k}\left[n\right]\le 1,\forall k,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \sum _{k=1}^K({\alpha }_{m,k}\left[n\right]+{\beta }_{m,k}\left[n\right])\le 1,\forall m,n,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \sum _{j=2}^n{\beta }_{m,k}\left[j\right]\le \sum _{j=1}^{n-1}{\alpha }_{m,k}\left[j\right],\forall m,k,n\ne 1,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & W_m\left[n\right]=\sum _{k=1}^K{w}_k\left(\sum _{j=1}^n{\alpha }_{m,k}\left[j\right]-\sum _{j=1}^n{\beta }_{m,k}\left[j\right]\right)\le W_{\max },\forall m,n,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \sum _{m=1}^M\sum _{k=1}^K\sum _{n=1}^N{\beta }_{m,k}\left[n\right]\ge K.\hfill \end{array}$$

(10)

Constraints (5) and (6) ensure that each item is picked up and delivered by at most one UAV, whereas (7) limits each UAV to a single pickup or drop-off operation per time slot. In addition, constraint (8) guarantees that every item is picked up prior to its delivery, and (10) represents the mission completion condition, which ensures that all items are successfully delivered.

Each UAV operates at a fixed altitude H, and descending below H is allowed only during item pickup or drop-off operations. Accordingly, the altitude constraint is expressed as

$$\begin{array}{c}\hfill \left(1-\sum _{k=1}^K\left({\alpha }_{m,k}\left[n\right]+{\beta }_{m,k}\left[n\right]\right)\right)H\le z_m\left[n\right]\le H,\forall m,n.\end{array}$$

(11)

To perform item pickup or drop-off, the UAV must operate within the designated service zone of each item. For item k, the pickup zone is defined as a circular area centered at ${\widehat{\mathbf{c}}}_k=({\widehat{\mathbf{q}}}_k,{\widehat{z}}_k)$ with radius ${\widehat{R}}_k$, while the drop-off zone is defined as a circular area centered at ${\check{\mathbf{c}}}_k=({\check{\mathbf{q}}}_k,{\check{z}}_k)$ with radius ${\check{R}}_k$. These zones represent the spatial tolerances that allow UAVs to safely approach and execute pickup and drop-off operations. The UAV is required to remain within each corresponding zone not only at the moment of pickup or drop-off but also during the associated descent and ascent phases. Accordingly, the spatial constraints can be expressed as

$$\begin{array}{cc}\hfill & {\alpha }_{m,k}\left[n\right]{\parallel {\mathbf{c}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k\parallel }^2\le {\widehat{R}}_k^2,\forall m,k,n\ne N,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & {\alpha }_{m,k}\left[n\right]{\parallel {\mathbf{q}}_m\left[j\right]-{\widehat{\mathbf{q}}}_k\parallel }^2\le {\widehat{R}}_k^2,\forall m,k,n\ne N,j\in \{n-1,n+1\},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\beta }_{m,k}\left[n\right]{\parallel {\mathbf{c}}_m\left[n\right]-{\check{\mathbf{c}}}_k\parallel }^2\le {\check{R}}_k^2,\forall m,k,n\ne N,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\beta }_{m,k}\left[n\right]{\parallel {\mathbf{q}}_m\left[j\right]-{\check{\mathbf{q}}}_k\parallel }^2\le {\check{R}}_k^2,\forall m,k,n\ne N,j\in \{n-1,n+1\}.\hfill \end{array}$$

(15)

These spatial constraints (13) and (15) are necessary to maintain consistency with the altitude condition in (11), which permits the UAV to descend below H only while performing item pickup or drop-off operations. Without these constraints, the UAV might start descending prematurely during flight toward a pickup or delivery site, thereby violating the prescribed altitude range and potentially compromising flight safety.

For continuous multi-period operation, each UAV must receive the control and trajectory information for the next operation cycle from the server during the current one. To enable this information exchange, a reliable communication link between the server, located at ${\mathbf{c}}_S$, and UAV m is required. Assuming the LoS propagation model [10,11,12,13,14], the channel power gain between the server and UAV m at time slot n is defined as

$$\begin{array}{c}\hfill h_m\left[n\right]={\displaystyle \frac{{\mu }_0}{\parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_S{\parallel }^2}},\forall m,n,\end{array}$$

(16)

where ${\mu }_0$ denotes the average channel power gain at a reference distance of 1 m. Subsequently, the achievable rate between the server and UAV m at time slot n can be expressed as

$$\begin{array}{cc}\hfill r_m\left[n\right]& ={\delta }_m\left[n\right]{log}_2\left(1+{\displaystyle \frac{h_m\left[n\right]p_{\mathrm{tx}}}{{\sigma }^2}}\right)\hfill \\ \hfill & ={\delta }_m\left[n\right]{log}_2\left(1+{\displaystyle \frac{{\mu }_0{p}_{\mathrm{tx}}}{{\sigma }^2{\parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_S\parallel }^2}}\right),\hfill \end{array}$$

(17)

where $p_{\mathrm{tx}}$ denotes the constant transmit power of the server, and ${\sigma }^2$ is the noise power. To ensure reliable data exchange for successive operation cycles, a minimum rate requirement is imposed as

$$\begin{array}{c}\hfill r_m\left[n\right]\ge r_{\min },\forall m,n,\end{array}$$

(18)

where $r_{\min }$ is the minimum required rate.

In this study, we aim to minimize the average mission completion time of all UAVs while ensuring the communication requirement. The optimization is jointly performed over the pickup and drop-off assignment variables ($\mathit{\alpha }\triangleq \{{\alpha }_{m,k}\left[n\right],\forall m,k,n\}$ and $\mathit{\beta }\triangleq \{{\beta }_{m,k}\left[n\right],\forall m,k,n\}$), the UAV trajectories ($\mathit{c}\triangleq \{{\mathbf{c}}_m\left[n\right],\forall m,n\}$), and the slot durations ($\mathit{\delta }\triangleq \{{\delta }_m\left[n\right],\forall m,n\}$), which can be formulated as

$$\begin{array}{cc}\hfill \mathbf{\left(}\mathbf{P}\mathbf{1}\mathbf{\right)}\mathbf{:}\underset{\mathit{\alpha },\mathit{\beta },\mathit{c},\mathit{\delta }}{min}& {\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{\delta }_m\left[n\right]}{M}}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \left(1\right)\text{–}\left(15\right),\left(18\right).\hfill \end{array}$$

Notably, we model communication feasibility via a minimum communication-rate requirement between each UAV and the server. This choice provides a simple yet effective way to capture how geometry-dependent channel quality influences UAV trajectory and scheduling decisions within our optimization framework. However, problem (P1) is the MINLP problem because the decision variables $\mathit{\alpha }$ and $\mathit{\beta }$ are binary, as defined in (4), and constraints (3), (12)–(15), and (18) are nonconvex with respect to their associated optimization variables. Consequently, obtaining a globally optimal solution in closed form is mathematically intractable.

3. Proposed Algorithm

To overcome the nonconvexity inherent in problem (P1), an iterative convexification framework based on the SCA and PCCP methods is employed. Through this approach, the original nonconvex problem is reformulated into a convex problem that can be efficiently solved using standard optimization tools such as CVX [21]. Furthermore, the binary decision variables in $\mathit{\alpha }$ and $\mathit{\beta }$ are relaxed to continuous values, and the PCCP is integrated to preserve their binary nature throughout the optimization process. By repeating these convex reformulations, a computationally efficient algorithm capable of yielding near-optimal solutions is obtained.

As an initial step, the nonconvex constraint in (3) is convexified. The left-hand side (LHS) of (3) is convex with respect to $\parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_{m^{\prime }}\left[n\right]\parallel$, and any convex function can be lower-bounded by its first-order Taylor expansion at a given point [22]. Accordingly, the constraint is replaced with the following conservative linear form:

$$\begin{array}{cc}\hfill \parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_{m^{\prime }}{\left[n\right]\parallel }^2& \ge 2{({\tilde{\mathbf{c}}}_m\left[n\right]-{\tilde{\mathbf{c}}}_{m^{\prime }}\left[n\right])}^T({\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_{m^{\prime }}\left[n\right])-{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\tilde{\mathbf{c}}}_{m^{\prime }}\left[n\right]\parallel }^2\hfill \\ \hfill & \ge d_{\min }^2,\forall m\ne m^{\prime },n,\hfill \end{array}$$

(19)

where ${\tilde{\mathbf{c}}}_m\left[n\right]$ denotes the 3D position of UAV m at time slot n obtained from the previous SCA iteration.

To handle the binary variables ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$ in (4), they can be equivalently represented as

$$\begin{array}{cc}\hfill & \{{\alpha }_{m,k}\left[n\right],{\beta }_{m,k}\left[n\right]\}\in [0,1],\forall m,k,n,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & {\alpha }_{m,k}\left[n\right](1-{\alpha }_{m,k}\left[n\right])\le 0,\forall m,k,n,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\beta }_{m,k}\left[n\right](1-{\beta }_{m,k}\left[n\right])\le 0,\forall m,k,n.\hfill \end{array}$$

(22)

Here, ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$ are relaxed to continuous variables in (20), while their binary nature is enforced by the additional nonlinear constraints (21) and (22). However, these constraints are nonconvex and result in a tightly restricted feasible region for ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$, making the problem challenging to solve directly.

Since the LHS of (21) and (22) is concave with respect to ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$, respectively, and any concave function can be upper-bounded by its first-order Taylor expansion [22], the PCCP [23] is applied with nonnegative slack variables ${\rho }_{m,k}\left[n\right]\ge 0$ and ${\tau }_{m,k}\left[n\right]\ge 0$. This allows ${\alpha }_{m,k}\left[n\right]$ and ${\beta }_{m,k}\left[n\right]$ to be efficiently updated while expanding the feasible search space during optimization. Accordingly, constraints (21) and (22) are replaced with the following convex surrogate forms:

$$\begin{array}{c}\hfill {\left({\tilde{\alpha }}_{m,k}\left[n\right]\right)}^2+{\alpha }_{m,k}\left[n\right](1-2{\tilde{\alpha }}_{m,k}\left[n\right])\le {\rho }_{m,k}\left[n\right],\forall m,k,n,\end{array}$$

(23)

$$\begin{array}{c}\hfill {\left({\tilde{\beta }}_{m,k}\left[n\right]\right)}^2+{\beta }_{m,k}\left[n\right](1-2{\tilde{\beta }}_{m,k}\left[n\right])\le {\tau }_{m,k}\left[n\right],\forall m,k,n,\end{array}$$

(24)

where ${\tilde{\alpha }}_{m,k}\left[n\right]$ and ${\tilde{\beta }}_{m,k}\left[n\right]$ denote the pickup and drop-off indicators of UAV m for item k at time slot n obtained from the previous SCA iteration.

To address the nonconvexity of constraint (12), it is reformulated as the following alternative expression:

$$\begin{array}{c}\hfill {\alpha }_{m,k}\left[n\right]\le {\displaystyle \frac{{\widehat{R}}_k^2+\epsilon }{\parallel {\mathbf{c}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k{\parallel }^2+\epsilon }},\end{array}$$

(25)

where $\epsilon >0$ is a constant introduced to avoid division by zero. While (25) is still nonconvex, the right-hand side (RHS) is convex in $\parallel {\mathbf{c}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k{\parallel }^2+\epsilon$. Thus, by applying a first-order approximation at a local point ${\tilde{\mathbf{c}}}_m\left[n\right]$, a convex lower-bound representation can be derived as follows:

$$\begin{array}{c}\hfill {\alpha }_{m,k}\left[n\right]\le {\displaystyle \frac{{\widehat{R}}_k^2+\epsilon }{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k{\parallel }^2+\epsilon }}-{\displaystyle \frac{{\widehat{R}}_k^2+\epsilon }{(\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k{{\parallel }^2+\epsilon )}^2}}\left(\parallel {\mathbf{c}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k{\parallel }^2-{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\widehat{\mathbf{c}}}_k\parallel }^2\right),\forall m,k,n\ne N.\end{array}$$

(26)

Similarly, constraints (13)–(15) can be handled using the same convexification procedure as that applied to (25).

$$\begin{array}{cc}\hfill & {\alpha }_{m,k}\left[n\right]\le {\displaystyle \frac{{\widehat{R}}_k^2+\epsilon }{\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\widehat{\mathbf{q}}}_k{\parallel }^2+\epsilon }}-{\displaystyle \frac{{\widehat{R}}_k^2+\epsilon }{(\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\widehat{\mathbf{q}}}_k{{\parallel }^2+\epsilon )}^2}}\left(\parallel {\mathbf{q}}_m\left[j\right]-{\widehat{\mathbf{q}}}_k{\parallel }^2-{\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\widehat{\mathbf{q}}}_k\parallel }^2\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \forall m,k,n\ne N,j\in \{n-1,n+1\},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & {\beta }_{m,k}\left[n\right]\le {\displaystyle \frac{{\check{R}}_k^2+\epsilon }{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\check{\mathbf{c}}}_k{\parallel }^2+\epsilon }}-{\displaystyle \frac{{\check{R}}_k^2+\epsilon }{(\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\check{\mathbf{c}}}_k{{\parallel }^2+\epsilon )}^2}}\left(\parallel {\mathbf{c}}_m\left[n\right]-{\check{\mathbf{c}}}_k{\parallel }^2-{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\check{\mathbf{c}}}_k\parallel }^2\right),\forall m,k,n\ne N,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\beta }_{m,k}\left[n\right]\le {\displaystyle \frac{{\check{R}}_k^2+\epsilon }{\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\check{\mathbf{q}}}_k{\parallel }^2+\epsilon }}-{\displaystyle \frac{{\check{R}}_k^2+\epsilon }{(\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\check{\mathbf{q}}}_k{{\parallel }^2+\epsilon )}^2}}\left(\parallel {\mathbf{q}}_m\left[j\right]-{\check{\mathbf{q}}}_k{\parallel }^2-{\parallel {\tilde{\mathbf{q}}}_m\left[j\right]-{\check{\mathbf{q}}}_k\parallel }^2\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \forall m,k,n\ne N,j\in \{n-1,n+1\},\hfill \end{array}$$

(29)

where ${\tilde{\mathbf{q}}}_m\left[j\right]$ denotes the horizontal position of UAV m at time slot j obtained from the previous SCA iteration.

To convexify constraint (18), we exploit the convexity of $r_m\left[n\right]$ with respect to $\parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_S{\parallel }^2$. Accordingly, the lower bound of $r_m\left[n\right]$ can be obtained via its first-order Taylor expansion around the previous iteration point ${\tilde{\mathbf{c}}}_m\left[n\right]$, yielding

$$\begin{array}{cc}\hfill r_m\left[n\right]& \ge {\delta }_m\left[n\right]\left(-{\tilde{A}}_m\left[n\right](\parallel {\mathbf{c}}_m\left[n\right]-{\mathbf{c}}_S{\parallel }^2-\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\mathbf{c}}_S{\parallel }^2)+{log}_2\left(1+{\displaystyle \frac{{\mu }_0{p}_{\mathrm{tx}}}{{\sigma }^2{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\mathbf{c}}_S\parallel }^2}}\right)\right)\hfill \\ \hfill & \triangleq {\delta }_m\left[n\right]{\overline{r}}_m\left[n\right],\hfill \end{array}$$

(30)

where ${\tilde{A}}_m\left[n\right]$ is represented by

$$\begin{array}{c}\hfill {\tilde{A}}_m\left[n\right]={\displaystyle \frac{{log}_2\left(e\right){\mu }_0{p}_{\mathrm{tx}}}{{\mu }_0{p}_{\mathrm{tx}}\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\mathbf{c}}_S{\parallel }^2+{\sigma }^2{\parallel {\tilde{\mathbf{c}}}_m\left[n\right]-{\mathbf{c}}_S\parallel }^4}}.\end{array}$$

(31)

Substituting the approximated lower bound ${\overline{r}}_m\left[n\right]$ into (18) leads to the following convex reformulation:

$$\begin{array}{c}\hfill {\overline{r}}_m\left[n\right]\ge {\displaystyle \frac{r_{\min }}{{\delta }_m\left[n\right]}},\forall m,n.\end{array}$$

(32)

Based on the relaxed constraints, the original problem (P1) can be converted into the following convex optimization problem:

$$\begin{array}{cc}\hfill \mathbf{\left(}\mathbf{P}\mathbf{2}\mathbf{\right)}\mathbf{:}\underset{\mathit{\alpha },\mathit{\beta },\mathit{c},\mathit{\delta },\mathit{\rho },\mathit{\tau }}{min}& {\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{\delta }_m\left[n\right]}{M}}+\nu \mathcal{P}(\mathit{\rho },\mathit{\tau })\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \left(1\right),\left(2\right),\left(5\right)\text{–}\left(11\right),\left(19\right),\left(20\right),\left(23\right),\left(24\right),\left(26\right)\text{–}\left(29\right),\left(32\right),\hfill \end{array}$$

where $\mathit{\rho }\triangleq \{{\mathit{\rho }}_{m,k}\left[n\right],\forall m,k,n\}$, $\mathit{\tau }\triangleq \{{\mathit{\tau }}_{m,k}\left[n\right],\forall m,k,n\}$, and the penalty function is defined as $\mathcal{P}(\mathit{\rho },\mathit{\tau })={\sum }_{m=1}^M{\sum }_{k=1}^K{\sum }_{n=1}^N({\rho }_{m,k}\left[n\right]+{\tau }_{m,k}\left[n\right])$. The term $\mathcal{P}(\mathit{\rho },\mathit{\tau })$ penalizes violations of the binary nature of the pickup and drop-off indicators. The weighting parameter $\nu >0$ controls the trade-off between the main objective and the penalty term in problem (P2). For relatively small values of $\nu$, the optimizer emphasizes minimizing the primary objective, which may result in nonzero slack variables $(\mathit{\rho },\mathit{\tau })$ and thus relaxed indicator values. As $\nu$ gradually increases, the influence of the penalty term strengthens, progressively shrinking $(\mathit{\rho },\mathit{\tau })$ toward zero and enforcing near-binary solutions for $(\mathit{\alpha },\mathit{\beta })$. Through this continuation process, the optimization asymptotically converges to a binary-feasible solution while maintaining numerical stability [23]. The overall optimization framework is summarized in Algorithm 1. Specifically, in the PCCP step, the slack variables $\mathit{\rho }$ and $\mathit{\tau }$ are initialized to one and treated solely as optimization variables in Problem (P2), where their values are directly determined by the convex solver at each iteration. The penalty parameter is initialized at ${\nu }^{\left(0\right)}=10$ and updated geometrically as ${\nu }^{\left(r\right)}=\gamma {\nu }^{(r-1)}$ with $\gamma =1.2$ until a maximum value of ${10}^5$ is reached. This gradual penalty escalation progressively suppresses the slack variables, guiding the relaxed binary variables toward their discrete counterparts while maintaining numerical stability. Following the PCCP principles in [24], this update schedule ensures that the violation measure $\mathcal{P}(\mathit{\rho },\mathit{\tau })$ decreases across iterations and converges to zero, leading the algorithm to a stationary point of Problem (P2).

Algorithm 1 Proposed Algorithm

1:$$Set $r=0$ and initialize $\mathit{\alpha }$, $\mathit{\beta }$, $\mathit{c}$, $\mathit{\delta }$, $\mathit{\rho }$, $\mathit{\tau }$, $\nu$, ${\nu }_{\max }$, and $\gamma >1$ 2:$$Calculate ${\eta }^{\left(r\right)}={\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{\delta }_m\left[n\right]}{M}}$ based on these initial values 3:$$repeat 4:$$$r\leftarrow r+1$ 5:$$${\eta }^{\mathrm{old}}\leftarrow {\eta }^{(r-1)}$ 6:$$Find $\{{\mathit{\alpha }}^{\left(r\right)},{\mathit{\beta }}^{\left(r\right)},{\mathit{c}}^{\left(r\right)},{\mathit{\delta }}^{\left(r\right)},{\mathit{\rho }}^{\left(r\right)},{\mathit{\tau }}^{\left(r\right)}\}$ by solving $\mathbf{\left(}\mathbf{P}\mathbf{2}\mathbf{\right)}$ for $\{{\mathit{\alpha }}^{(r-1)},{\mathit{\beta }}^{(r-1)},{\mathit{c}}^{(r-1)},{\mathit{\delta }}^{(r-1)},{\mathit{\rho }}^{(r-1)},{\mathit{\tau }}^{(r-1)}\}$ 7:$$Update ${\nu }^{\left(r\right)}=min\{\gamma {\nu }^{(r-1)},{\nu }_{\max }\}$ 8:$$Calculate ${\eta }^{\left(r\right)}={\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{\delta }_m^{\left(r\right)}\left[n\right]}{M}}+{\nu }^{\left(r\right)}\mathcal{P}({\mathit{\rho }}^{\left(r\right)},{\mathit{\tau }}^{\left(r\right)})$ 9:$$until $|{\eta }^{\left(r\right)}-{\eta }^{\mathrm{old}}| \le ϵ$.

Based on the standard worst-case complexity of interior-point methods [22,25], the computational complexity of the proposed algorithm can be approximated as $O\left({\left(MKN\right)}^{3.5}Ilog(1/ϵ)\right)$, where I denotes the number of SCA iterations required for convergence. This indicates that the overall procedure scales polynomially with the problem dimension $MKN$, exhibiting a complexity order of $3.5$. Such polynomial growth ensures that the proposed framework remains computationally practical and suitable for real-time applications [26].

4. Performance Evaluation and Discussion

In the performance evaluation, pickup and delivery zones are uniformly distributed while the server is fixed at [500, −500, 0] m within a 1000 m × 1000 m area. The default simulation parameters are given in Table 1 [10,11,12]. The proposed scheme is then compared with an upper bound and two baseline schemes.

Table 1. Parameter Setup.

Description	Value
Number of UAVs	M = 1
Number of items	K = 6
Number of time slots	N = 125
Maximum flight speed	$V_{\max }$ = 30 m/s
Altitude	H = 20 m
Safety threshold	$d_{\min }$ = 10 m
Maximum payload capacity	$W_{\max }$ = 40 kg
Tolerance for pickup and drop-off zones	${\widehat{\mathcal{R}}}_k$ = ${\check{\mathcal{R}}}_k$ = 1 m, $\forall k$
Minimum required rate	$r_{\min }$ = 4 bits/Hz
Average channel power gain	${\mu }_0$ = −30 dB
Noise power	${\sigma }^2$ = −70 dBm
Transmit power of server	$p_{\mathrm{tx}}$ = 30 dBm
Penalty parameters	$\{{\nu }^0,{\nu }_{\max },\gamma \}$ = $\{10,{10}^5,1.2\}$
Convergence threshold	$ϵ$ = 0.1

• Proposed scheme: The UAV strategies are optimized by Algorithm 1.
• Upper bound: The UAV strategies are optimized by Algorithm 1 without considering communication constraints.
• Baseline 1 scheme: The UAVs repeatedly pick up as many items as their weight limit allows, deliver them to the corresponding destinations, and continue this process until all items are served.
• Baseline 2 scheme: The UAVs pick up one item and immediately deliver it to its destination, following the order of the nearest location from their current positions and repeating this process for all items.
• Baseline 3 scheme [27]: The pickup–drop-off sequence is kept identical to that of the proposed scheme, while the flight paths are generated using a rapidly exploring random tree star (RRT*) algorithm executed for 2 × 10⁴ sampling iterations.

Note that for Baseline 1 and 2 schemes, each rule imposes a constraint on how the pickup–drop-off sequence may be formed, rather than fixing the sequence explicitly. Within the set of sequences permitted by each rule, the pickup–drop-off order, UAV trajectories, and slot durations are jointly optimized by Algorithm 1 under identical problem constraints, ensuring a fair and reproducible comparison with the proposed method.

Figure 2 presents the trajectory and resource allocation of the proposed scheme. In Figure 2a, when the communication constraint is not imposed (i.e., $r_{\min }$ = 0 bits/Hz), representing the upper-bound case, the UAV focuses solely on minimizing the total mission completion time. To achieve this, it forms nearly straight flight paths while still satisfying the pickup–delivery precedence constraint, meaning that for each item, the UAV must visit the pickup zone before the corresponding delivery zone. In this unconstrained case, the trajectory becomes time-efficient and direct, since the UAV is not required to maintain a certain communication rate with the server and therefore can move freely without detours toward the communication coverage region. In Figure 2b, when the communication constraint is set to $r_{\min }$ = 4 bits/Hz, the UAV trajectory bends toward the server, as indicated by the red path. This behavior arises because satisfying the communication constraint (32) requires either approaching the server to enhance spectral efficiency ${\overline{r}}_m\left[n\right]$ or prolonging the time slot duration ${\delta }_m\left[n\right]$ to the achievable rate. However, increasing ${\delta }_m\left[n\right]$ directly enlarges the overall mission completion time, which contradicts the optimization objective. Consequently, the UAV moves closer to the server to increase spectral efficiency instead of extending the slot duration, resulting in a curved trajectory toward the communication link. As shown in Figure 2c, when the UAV bends its trajectory toward the server to meet the communication constraint, the corresponding slot durations ${\delta }_m\left[n\right]$,shown in red, remain relatively small to minimize the overall mission completion time. In addition, when flying along straight segments where communication is sufficient, the UAV extends ${\delta }_m\left[n\right]$ to travel at the maximum allowable speed, thereby further reducing the mission completion time. In Figure 2d, the bars represent the altitude levels of the pickup and delivery zones. It can be observed that the UAV descends within the allowable tolerance of ${\widehat{\mathcal{R}}}_k$ = ${\check{\mathcal{R}}}_k$ = 1 m to perform the corresponding operations, during which the pickup and drop-off indicators are activated to 1, confirming the successful execution of each task. As illustrated in Figure 2e,f, which show the horizontal trajectories when the number of UAVs is M = 2, the absence or presence of the communication constraint leads to distinct flight behaviors. When the constraint is not imposed, each UAV follows a nearly straight path to minimize the total mission time. In contrast, when the communication constraint is active, both UAVs bend their trajectories toward the server to satisfy the required rate condition, exhibiting a similar tendency to the single-UAV case.

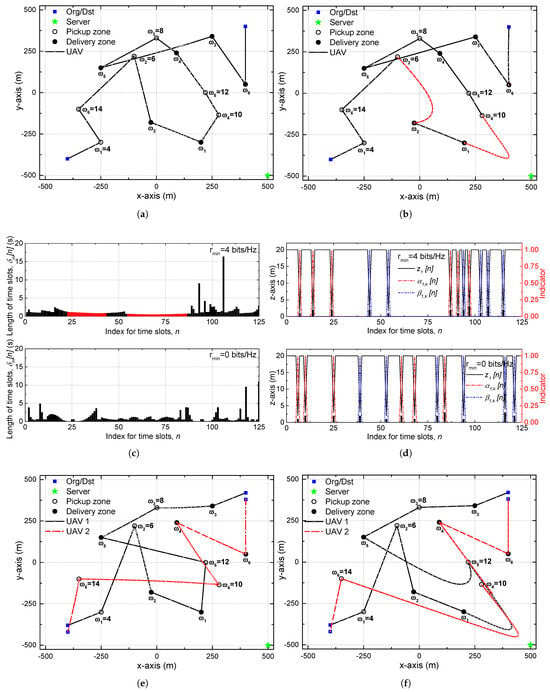
Figure 2. Trajectory and resource allocation of proposed scheme. (a) Horizontal trajectory when $r_{\min }$ = 0 bits/Hz. (b) Horizontal trajectory when $r_{\min }$ = 4 bits/Hz. Horizontal trajectory when $r_{\min }$ = 4 bits/Hz. (c) Length of time slots. (d) Vertical trajectory and pickup/drop-off indicator. (e) Horizontal trajectory when $r_{\min }$ = 0 bits/Hz and M = 2. (f) Horizontal trajectory when $r_{\min }$ = 4 bits/Hz and M = 2.

Figure 3 compares the average mission completion times ($\eta ={\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{\delta }_m\left[n\right]}{M}}$) of different schemes under various system parameters. As shown in Figure 3a, as $r_{\min }$ increases, the UAV is required to satisfy stricter communication constraints, which forces it to deviate from straight paths and form curved trajectories toward the server. This detour behavior leads to less efficient routes, thereby increasing the overall mission completion time $\eta$ for all schemes except the upper bound, which ignores communication constraints. Baseline 1 achieves better performance than Baseline 2 because it collects multiple items within its payload capacity before performing deliveries, allowing more effective path planning and reducing redundant trips between pickup and delivery zones. In contrast, Baseline 2 immediately delivers each item after pickup, resulting in frequent back-and-forth movements and longer total flight time. Baseline 3 shows the strongest performance among the baselines, as its sampling-based exploration generates more efficient trajectories and avoids many of the inefficient routes produced by heuristic scheduling. The proposed scheme further improves upon these approaches by jointly optimizing both the service strategy and the communication-constrained trajectories. Finally, the gap between the proposed scheme and the upper bound quantifies the performance degradation caused by the communication constraint, highlighting its impact on overall system efficiency.

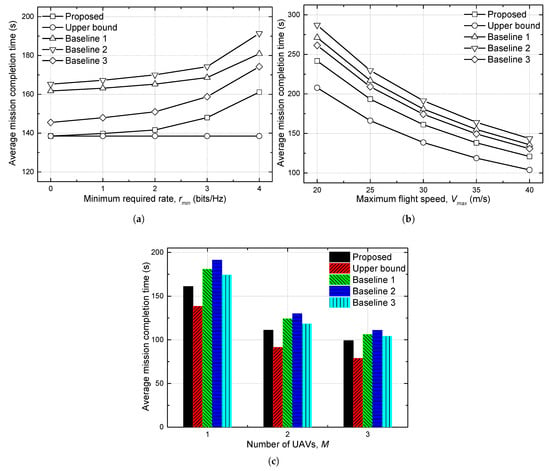
Figure 3. Performance comparisons. (a) $\eta$ versus $r_{\min }$. (b) $\eta$ versus $V_{\max }$. (c) $\eta$ versus M.

As shown in Figure 3b, increasing the maximum flight speed $V_{\max }$ enables the UAV to travel faster, thereby achieving shorter mission completion times across all schemes. Moreover, as depicted in Figure 3c, increasing the number of UAVs M leads to a reduction in $\eta$, since the same set of items can be distributed among more UAVs, effectively reducing each UAV’s workload. Notably, as M increases, the performance gap between the proposed scheme and the baselines becomes smaller because load balancing among multiple UAVs allows even heuristic approaches to form relatively efficient routes without explicit optimization. Nevertheless, the proposed scheme consistently outperforms the baselines, demonstrating its superior coordination capability and robustness in multi-UAV operations under communication constraints.

5. Conclusions

This study presented an optimization framework for UAV-enabled pickup and delivery operations under continuous communication constraints. By formulating the problem as the MINLP and addressing its nonconvex structure through SCA and PCCP-based iterative convexification, the proposed algorithm achieved efficient coordination among multiple UAVs while maintaining reliable connectivity with the ground server. The analysis revealed that communication constraints significantly affect the UAVs’ flight paths, often inducing trajectory deviations toward the server to satisfy minimum data-rate requirements. Through comparison with the upper-bound case without communication constraints, the study quantitatively revealed the impact of the communication requirement on overall system efficiency. Furthermore, the proposed framework consistently outperformed baselines, showing robustness and scalability with polynomial-time complexity suitable for real-time operation.