NCS-BWO Algorithm for Permanent Magnet Synchronous Motor Parameter Identification

Abstract

To address the problems of low identification accuracy, poor global search capability, and susceptibility to local optima in permanent magnet synchronous motor (PMSM) parameter identification, this paper proposes a hybrid niching clonal selection black widow optimization (NCS-BWO) algorithm. This algorithm combines the exploitation capability of black widow optimization (BWO) with the exploration capability of the clonal selection algorithm (CSA). First, a niching strategy called nearest-better clustering (NBC) is used to generate sub-populations, incorporating a cluster size optimization mechanism to ensure a balanced population distribution. Subsequently, adaptive Gaussian mutation and elite differential evolution (DE) mutation operators are introduced during the CSA hypermutation stage. Finally, the high-quality population resulting from the niching clonal selection algorithm (NCSA) serves as the initial population for the BWO. The effectiveness of the NCS-BWO algorithm was validated using six benchmark test functions, and its performance was compared with that of six other algorithms. Furthermore, a full-rank discrete model of the PMSM was established, and the NCS-BWO algorithm was applied for parameter identification. Both the simulation and experimental results demonstrate that the proposed NCS-BWO algorithm achieves superior accuracy in PMSM parameter identification.

1. Introduction

Permanent magnet synchronous motors (PMSMs) offer numerous advantages, including simple structure, excellent controllability, and high power density. They have garnered widespread attention and have been extensively applied in major industrial sectors [1,2]. However, PMSM parameters are susceptible to environmental effects. For instance, temperature variations can cause changes in the stator resistance and flux linkage, and magnetic saturation may cause changes in the stator inductance, leading to degraded performance in PMSM drive systems [3,4]. Therefore, obtaining precise motor parameters and mathematical models is crucial for improving the control performance of PMSMs [5,6,7].

PMSM parameter identification can be categorized as offline or online. Offline identification methods primarily encompass experimental measurements and finite element analysis, which are widely applied in controller and motor designs. Reference [8] employed a sinusoidal current control strategy with harmonic voltage injection to reduce unnecessary harmonic losses. It identified magnetic flux by detecting the back electromotive force, achieving good identification accuracy but identifying fewer parameters. Reference [9] proposed an offline parameter self-learning method with error-estimation compensation, which utilized a finite element approach to design the PMSM parameter identification system. While this method enables motor parameter acquisition, it presents challenges due to the complexity of data collection. Offline parameter identification fails to reflect parameter variations during actual motor operation, and is unsuitable for applications that require continuous operation. Online identification methods, by acquiring real-time motor operating data and combining estimation algorithms, enable accurate, real-time parameter estimation and enhance system control performance with strong real-time capability and adaptability [10].

Online PMSM parameter identification methods include recursive least squares (RLS) [11], extended Kalman filter (EKF) [12], model reference adaptive system (MRAS) [13,14], and intelligent algorithms [15]. Reference [16] combined RLS with current derivative methods to overcome the rank deficiency issue, thereby enabling the identification of all PMSM electrical parameters under steady-state conditions. Reference [17] proposed a filtering algorithm with a dynamic forgetting factor; however, it could only identify the stator resistance and inductance. The EKF was employed for parameter estimation in [18,19,20], its design complexity and high sensitivity to noise often result in low identification accuracy. References [21,22] utilized MRAS for parameter identification, but the adaptive design is intricate. Traditional online identification methods face challenges in terms of convergence speed, robustness, or implementation complexity.

In recent years, metaheuristic algorithms have achieved remarkable efficacy in PMSM parameter identification, owing to their computational simplicity, strong optimization capabilities, and straightforward principles. Reference [23] proposed an enhanced raccoon optimization algorithm (EROA) that improved the resistance identification accuracy but exhibited low accuracy in stator inductance and magnetic flux identification. Reference [24] proposed an improved fuzzy particle swarm optimization (PSO) algorithm. While retaining the single-population PSO framework, this approach still struggles to maintain stable subpopulations and simultaneously locate multiple extreme points. Reference [25] introduced a chaotic inertial weight decay strategy into the particle swarm optimization algorithm, improving the identification accuracy and speed, but increasing the algorithmic complexity.

To further enhance algorithmic performance, the hybrid intelligent optimization algorithm has gradually emerged as a research hotspot. By integrating different optimization strategies, these algorithms effectively balance exploration and exploitation capabilities, demonstrating significant advantages in solving complex problems. For instance, the hybrid fireworks grey wolf optimizer (FWGWO) algorithm proposed in [26] combined the exploitation capability of the grey wolf optimizer (GWO) with the exploration capability of the fireworks algorithm (FWA) through an adaptive balance coefficient, showing excellent performance in benchmark function tests, though its applicability in real-world dynamic environments requires further validation. Reference [27] integrated the invasive weed optimization (IWO) algorithm with cuckoo search (CS), which significantly improved performance, but the resulting algorithm’s parameter sensitivity remains to be optimized. Reference [28] integrated the global exploration ability of the artificial bee colony (ABC) algorithm with the local exploitation ability of the genetic algorithm (GA), and its performance is superior to other hybrid algorithms. However, this hybrid approach relies heavily on empirical parameter tuning, and its scalability for multi-objective optimization problems needs further exploration. While these studies have achieved progress in their respective fields, they commonly face challenges such as weak adaptability to dynamic environments and complex parameter tuning.

Peña-Delgado et al. proposed the black widow optimization (BWO) algorithm in 2020, which was inspired by the unique mating behavior of black widow spiders [29]. This algorithm primarily simulates the distinctive reproductive behavior of the spider, featuring a simple structure and rapid optimization speed [30,31,32]. It can achieve satisfactory results under conditions of low population size and few iterations. However, the BWO algorithm exhibits a weak global search capability, making it prone to becoming trapped in local optima. The clonal selection algorithm (CSA) is a branch of immune algorithms. Owing to its strong search capabilities, CSA has been widely applied in numerous fields [33,34]. However, the CSA suffers from insufficient local search ability and slow convergence speed.

To address these limitations, this paper proposes a niching clonal selection black widow optimization (NCS-BWO) algorithm. First, a niching method called nearest-better clustering (NBC) is employed to divide the initial population into several clusters, and a cluster size optimization mechanism is incorporated to ensure an even distribution. Each cluster evolves independently using the CSA. Subsequently, during the hypermutation phase of CSA, an adaptive Gaussian mutation operator and an elite differential evolution (DE) mutation operator are introduced to enhance the exploratory performance. Finally, the results of niching clonal selection algorithm (NCSA) are used as the initial population of BWO, thereby allowing the BWO algorithm to start from an initial population that is closer to the optimal one than the randomly generated initial population. By integrating NCSA and BWO, the NCS-BWO achieves a proper balance between exploration and exploitation. Furthermore, the simulation model and experimental platform for PMSM based on vector control were established. Both simulation and experimental results verify the superiority of the proposed NCS-BWO algorithm in PMSM parameter identification.

2. PMSM Mathematical Model

The PMSM is a complex nonlinear system characterized by strong coupling and multiple variables. To facilitate analysis, PMSM modeling typically ignores disturbances such as core eddy currents, magnetic saturation effects, harmonics, and hysteresis losses. In the dq-axis rotating coordinate system, the voltage equations for the PMSM can be expressed as follows:

$$\left\{\begin{array}{l}{u}_d=R_s{i}_d+L_d{\displaystyle \frac{d{i}_d}{dt}}-{\omega }_e{L}_q{i}_q\\ u_q=R_s{i}_q+L_q{\displaystyle \frac{d{i}_q}{dt}}+{\omega }_e{L}_d{i}_d+{\omega }_e{\psi }_f,\end{array}\right.$$

(1)

where i_d and i_q are the dq-axis currents, u_d and u_q represent the dq-axis voltages, ω_e represents the electrical angular velocity, R_s denotes the stator resistance, L_d represents the d-axis inductance, L_q represents the q-axis inductance, and ψ_f denotes the permanent magnet flux linkage.

When the PMSM operates stably at a constant speed under vector control, the influences of i_d and i_q are negligible, which is approximated as

$$\left\{\begin{array}{l}{\displaystyle \frac{d{i}_d}{dt}}=0\\ {\displaystyle \frac{d{i}_q}{dt}}=0\end{array}\right.$$

(2)

.

Equation (1) can be simplified as

$$\left\{\begin{array}{l}{u}_d=R_s{i}_d-{\omega }_e{L}_q{i}_q\\ u_q=R_s{i}_q+{\omega }_e{L}_d{i}_d+{\omega }_e{\psi }_f.\end{array}\right.$$

(3)

To facilitate parameter estimation, Equation (3) needs to be discretized as follows:

$$\left\{\begin{array}{l}{u}_d\left(k\right)=-{\omega }_e\left(k\right)L_q{i}_q\left(k\right)\\ u_q\left(k\right)=R_{\mathrm{s}}{i}_q\left(k\right)+{\omega }_e\left(k\right){\psi }_f,\end{array}\right.$$

(4)

where u_d(k) and u_q(k) denote the data collected at time step k.

This study primarily investigates parameter identification for surface-mounted PMSMs, assuming equal dq-axis inductances, that is, L_d = L_q = L_s. To identify motor parameters, an identification model must be constructed. The parameters that require simultaneous identification of the PMSM are R_s, L_s, and ψ_f. However, the rank of (4) is two, it is not possible to directly obtain the values for all parameters simultaneously. To address this problem, when the PMSM operates under steady-state conditions, a negative d-axis current for flux-weakening is injected, in addition to the conventional i_d = 0 vector control strategy, thereby achieving a full-rank mode [35]. The timing diagram of the d-axis current injection and data acquisition is shown in Figure 1, both Data1 and Data2 contain complete sampling data of i_d = 0 and i_d = −2.

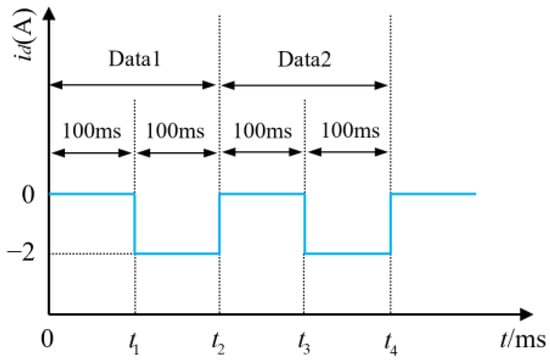
Figure 1. Data acquisition sequence diagram.

The same amount of data is collected under i_d = 0 and i_d = −2, and the fourth-order identification model is obtained as follows:

$$\left\{\begin{array}{l}{u}_{d0}(k)=-{\widehat{L}}_s{\omega }_{e0}(k)i_{q0}(k)\\ u_{q0}(k)={\widehat{R}}_s{i}_{q0}(k)+{\widehat{\psi }}_f{\omega }_{e0}(k)\\ u_{d1}(k)={\widehat{R}}_s{i}_{d1}(k)-{\widehat{L}}_s{\omega }_{e1}(k)i_{q1}(k)\\ u_{q1}(k)={\widehat{R}}_s{i}_{q1}(k)+{\widehat{L}}_s{\omega }_{e1}(k)i_{d1}(k)+{\widehat{\psi }}_f{\omega }_{e1}(k),\end{array}\right.$$

(5)

Where $u_{d0}\left(k\right)$ and $u_{q0}\left(k\right)$ denote the data collected at time step k under the control strategy i_d = 0. $u_{d1}\left(k\right)$ and $u_{q1}\left(k\right)$ represent data collected at time step k under control strategy i_d = −2. ${\widehat{R}}_{\mathrm{s}}$, ${\widehat{L}}_s$, and ${\widehat{\psi }}_f$ are the parameter identification results of the algorithm.

3. Algorithm Improvement

3.1. BWO Algorithm

The black widow optimization (BWO) algorithm simulates the linear and spiral movements of black widow spiders within their webs. The position update formula for the black widow spider is

$$X_i(t+1)=\left\{\begin{array}{l}{X}_{best}-m{X}_{r1}(t), \mathrm{rand}\left(\right)\le 0.3 \\ X_{best}-\cos (2\pi \beta \left)X_i\right(t), \mathrm{otherwise},\end{array}\right.$$

(6)

where t denotes the current iteration count, X_i (t + 1) and X_i (t) represent the positions of the i-th individual before and after its update, respectively. X_best denotes the current optimal individual position, X_r1 is the position of the randomly selected r₁-th individual, with i ≠ r₁. m is a random float in [0.4, 0.9], and β is a random float in [−1, 1].

Sex pheromones are crucial in the mating behavior of black widow spiders. The hunger level of female spiders can be reflected through sex pheromone secretion, with well-nourished females producing more sex pheromones and male spiders being attracted to females with higher pheromone secretion. The sex pheromone rate value is defined as follows:

$$pheromone(i)={\displaystyle \frac{fitnes{s}_{\max }-fitness(i)}{fitnes{s}_{\max }-fitnes{s}_{\min }}},$$

(7)

where fitness(i) denotes the fitness value of the i-th black widow spider, fitness_max and fitness_min represent the maximum and minimum fitness values, respectively.

Females with low pheromone levels are considered hungry and cannibalistic. As a result, they are excluded from the mating process and replaced by other individuals in the population. For spiders with pheromone rates of less than or equal to 0.3, the position update formula is as follows:

$$X_i(t)=X_{best}+{\displaystyle \frac{1}{2}}\left[X_{r2}\left(t\right)-{(-1)}^{\rho }{X}_{r3}\left(t\right)\right],$$

(8)

where X_i(t) represents the position of the female spider with the low pheromone value to be updated, r₂ and r₃ correspond to random integers selected between 1 and the maximum population value., with r₂ ≠ r₃. X_r2 and X_r3 denote the r₂-th and r₃-th individuals selected from the population, respectively, and ρ is a randomly generated binary number, ρ ∈ {0, 1}.

3.2. NCS-BWO Algorithm Design

The classic BWO exhibits weak global search capabilities and a tendency to converge to suboptimal solutions, thus failing to meet the high-precision requirement for PMSM parameter identification. To address this, this study proposes a hybrid NCS-BWO algorithm to improve its global search ability and escape local optima.

3.2.1. NCSA

The clonal selection algorithm (CSA) originates from clonal selection theory in biological immune systems. The underlying theory posits that when an antigen invades, B cells in the immune system recognize it and undergo cloning and mutation. Similarly to other immune algorithms, CSA first randomly generates a population of antibodies, each corresponding to a candidate solution. The antibodies are then matched to the antigen. Based on the degree of matching, antibodies with strong adaptability are selected for replication and mutation to generate mature antibodies. After re-evaluation and selection, the next-generation population is obtained.

The classic CSA exhibits population homogeneity after iterations, leading to insufficient diversity when transitioning to the global search phase of the BWO. Therefore, this study integrates a niching strategy called nearest-better clustering (NBC) with CSA to form a niching clonal selection algorithm (NCSA). The niching method typically divides the entire population into several subpopulations, either explicitly or implicitly. Ideally, each subpopulation tracks an optimal solution until it converges. Compared with other niching methods, NBC offers significant advantages: it is adaptable to different problems and requires setting only one parameter. An excessive number of parameters complicates the algorithm and makes it difficult to handle [36]. The NBC strategy performs adaptive partitioning based on individual fitness and distance, dividing the population into multiple clusters to enhance the diversity during optimization. The specific steps are as follows:

Step 1: The population is partitioned into multiple clusters, with the best individual within each cluster designated as the seed, denoted as X_seed.

Step 2: Calculate the Euclidean distance between pairs of individuals.

Step 3: Excluding the best individual, the nearest-better neighbor X_near,i of each individual X_i is identified based on the Euclidean distance and an edge to be created between them.

Step 4: Delete edges exceeding the threshold length. The threshold is expressed as follows:

$$\phi =\lambda \times l_{mean},$$

(9)

where φ is the threshold, λ is a control parameter and l_mean is the average distance of all edges. Each connected component corresponds to a cluster.

3.2.2. Cluster Size Optimization Mechanism

This study incorporates a cluster size optimization mechanism into the NBC strategy, which regulates the number of antibodies within each cluster. An excessively large cluster not only diminishes the number of individuals in other clusters, but also increases the computational overhead, thereby degrading algorithmic performance. Therefore, to achieve a balanced antibody distribution across clusters, a cluster-size optimization mechanism is employed. The cluster size is controlled by the parameter n_max, and the disadvantageous individual removal operator d_min is employed. The specific procedure is as follows:

Step 1: The number of antibodies in each cluster is calculated. If the number exceeds n_max, the top n_max individuals are retained and the number of removed individuals is recorded.

Step 2: If the total number of antibodies removed in Step1 is less than d_min, then the worst antibody from each cluster is iteratively removed until the total number of removals reaches d_min.

Step 3: Replace all antibodies removed in Step 1 and Step2 with newly generated random antibodies.

3.2.3. Adaptive Gaussian Mutation and Elite DE Mutation Strategy

In this study, an adaptive Gaussian mutation operator and an elite DE mutation operator are introduced into the hypermutation phase of CSA. The variable step size of the Gaussian mutation is correlated with the maximum distance of each cluster to enhance its adaptability across different clusters. Meanwhile, an elite DE mutation operator, which mimics the DE mutation mechanism, is introduced to enhance the convergence capability of the clusters.

The Gaussian mutation modifies the original position using a random number following a normal distribution with the mean μ and the variance σ. The probability density function of the Gaussian distribution is

$$f(x)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}\exp \left(-{\displaystyle \frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}\right).$$

(10)

This study employs the standard Gaussian probability density function, where μ and σ are set to 0 and 1, respectively. Gaussian mutation is used to update the individuals within the cluster.

$$S_{ij}=X_{ij}+\alpha \cdot Gaussian(0,1),$$

(11)

where X_ij and S_ij denote the positions of the i-th individuals in the j-th dimension before and after Gaussian mutation, respectively. α represents the step size factor, and Gaussian(0,1) is a random variable that follows a Gaussian distribution. This study combines the weight coefficient α with the coverage distance of the cluster, where the coverage distance is the maximum distance between antibodies within a cluster. During the initial clustering phases, the substantial coverage distance results in a large α value, inducing strong perturbations and facilitating significant antibody displacements for extensive global exploration. As the iterations proceed, the cluster radius decreases, leading to a reduction in α and finer movements conducive to localized refinement. The coefficient α is defined as follows:

$$\alpha ={\displaystyle \frac{1}{2}}\times {\displaystyle \frac{c_r}{\sqrt{D}}},$$

(12)

where c_r is the coverage distance of cluster c, and D is the dimension of the fitness function.

To guide the antibodies toward the optimal individual and ensure robust optimization capability, an elite DE mutation operator is employed.

$$S_{ij}=X_{ij}+0.5\times (X_{seed,j}-X_{ij}),$$

(13)

where X_seed,j denotes the position of the optimal individual in the j-th dimension of each cluster.

The position of the seed antibody remains unaltered throughout the hypermutation process. The clones of the remaining antibodies undergo adaptive Gaussian or elite DE mutations, with each mutation type applied with an equal probability of 50%. Finally, each antibody in the population is compared with its corresponding mutated clone and the superior antibody is selected for the next generation.

$$X_i(t+1)=\left\{\begin{array}{l}{S}_i^{best}\left(t) , f\right(S_i^{best}(t\left)\right)>f(X_i(t\left)\right)\\ X_i(t) ,\mathrm{otherwise}\end{array}\right.,$$

(14)

where $S_i^{best}$ denotes the optimal mutated clone of the i-th antibody.

3.3. Sensitivity Analysis of Algorithm Parameters

According to reference [37], the value of the control parameter λ significantly influences the performance of the algorithm. An increase in λ leads to a reduction in the number of clusters, whereas decreasing its value results in a greater number of clusters. As indicated in references [38,39], the parameter n_max serves to restrict the number of antibodies within each cluster. An excessive number of antibodies in a cluster not only fails to significantly improve solution quality but also degrades algorithmic performance. In this study, a parameter sensitivity analysis was conducted using the penalized function. Each parameter was run 20 times under different value conditions, and the average value was taken as the result. Table 1 summarizes the relationship between the parameter settings and the corresponding fitness values. The expression of the penalized function is as follows:

$$\begin{array}{ll}f\left(x\right)& =0{.1\{\sin }^2(3\pi x_1)+{\displaystyle {\sum }_{i=1}^n{(x_i-1)}^2[}1+{\sin }^2(3\pi x_i+1)]+{(x_n-1)}^2[1+{\sin }^2(2\pi x_n)]\}\\ & +{\displaystyle {\sum }_{i=1}^{n}u(x_i,5,100,4)},x_i\in \left[-5,5\right]\end{array}$$

(15)

$$u(x_i,a,k,m)=\left\{\begin{array}{l}k{(x_i-a)}^m , x_i>a,\\ 0 , -a<x_i<a,\\ k{(-x_i-a)}^m , x_i<-a.\end{array}\right.$$

(16)

Table 1. Relationship between the fitness function and λ, n_max.

λ	nmax
	5	10	20	25
1	2.91 × 10−27	4.34 × 10−27	1.22 × 10−27	9.45 × 10−27
1.5	3.78 × 10−28	2.32 × 10−28	2.32 × 10−27	1.05 × 10−28
2	7.83 × 10−29	3.23 × 10−29	2.98 × 10−28	7.22 × 10−27
2.5	5.1 × 10−27	5.62 × 10−27	9.33 × 10−28	2.83 × 10−27

Table 1 shows that λ and n_max have the minimum fitness function when they are 2 and 10.

3.4. Algorithm Performance Evaluation

To facilitate the reproduction of the proposed NCS-BWO algorithm, the key parameters used in this study are summarized in Table 2. These parameter values were determined through the sensitivity analysis and were used in all subsequent benchmark tests and PMSM identification experiments.

Table 2. Key parameters of the NCS-BWO algorithm.

Parameter	Symbol	Value
NBC threshold	λ	2
Max cluster Size	nmax	10
Min removal	dmin	10
Clone number	nc	2
Population size	pop	100
NCSA iterations	N1	10
BWO iterations	N2	190

To validate the superiority of the proposed NCS-BWO algorithm, a comprehensive performance evaluation was performed, comparing its optimization performance with eight other algorithms, including NCSA, BWO, CSA, genetic algorithm (GA), particle swarm optimization (PSO), whale optimization algorithm (WOA), greylag goose optimization (GGO), and black-winged kite algorithm (BKA) using six benchmark test functions from the CEC2005 benchmark set. The specific details of these functions are listed in Table 3, which includes two unimodal functions (F₁ and F₂), two multimodal functions (F₃ and F₄), and two fixed-dimensional multimodal functions (F₅ and F₆). The constant values required for the computation of F₆ are provided in Table 4.

Table 3. Benchmark function.

Function	Dimensionality	Range	Best Value
$F_1={\displaystyle {\sum }_{i=1}^n\left|x_i\right|}+{\displaystyle {\prod }_{i=1}^n\left|x_i\right|}$	30	[−10, 10]	0
$F_2={{\displaystyle {\sum }_{i=1}^n\left({\displaystyle {\sum }_{j=1}^i{x}_j}\right)}}^2$	30	[−100, 100]	0
$F_3={\displaystyle {\sum }_{i=1}^n\left[x_i^2-10\cos (2\pi x_i)+10\right]}$	30	[−5.12, 5.12]	0
$F_4=-20\exp (-0.2\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{x_i}^2}})-\exp ({\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\cos 2}\pi x_i)+20+\mathrm{e}$	30	[−32, 32]	0
$F_5={\left[{\displaystyle \frac{1}{500}}+{\displaystyle {\sum }_{j=1}^{25}\frac{1}{j+{\displaystyle {\sum }_{i=1}^2{\left(x_i-a_{ij}\right)}^6}}}\right]}^{-1}$$\left(a_{ij}\right)=\left(\begin{array}{llllllllll}-32 & -16 & 0 & 16 & 32 & -32 & \cdots & 0& 16& 32\\ -32 & -32 & -32 & -32 & -32 & -16 & \cdots & 32& 32& 32\end{array}\right)$	2	[−65.536, 65.536]	0.998
$F_6=-{\displaystyle {\sum }_{i=1}^4{c}_i\exp }\left[-{\displaystyle {\sum }_{j=1}^6{a}_{ij}{\left(x_i-p_{ij}\right)}^2}\right]$	6	[0, 1]	−3.32

Table 4. Constant values for benchmark function F₆.

i	aij,j = 1	aij,j = 2	aij,j = 3	ci	pij,j = 1	pij,j = 2	pij,j = 3
1	3	10	30	1	0.3689	0.1170	0.2673
2	0.1	10	35	1.2	0.4699	0.4387	0.747
3	3	10	30	3	0.1091	0.8732	0.5547
4	0.1	10	35	3.2	0.03815	0.5743	0.8828

Table 5 presents the results of the nine algorithms on six benchmark functions, with each algorithm independently executed 20 times, and the mean and standard deviation values serving as the evaluation criterion. Table 5 indicates that the NCS-BWO demonstrates the best optimization performance across all test functions. In the F₁ and F₂ benchmark tests, NCS-BWO achieves the smallest optimization values. Although NCSA ranks second, it still outperforms the other algorithms. For multimodal function F₃, all algorithms except GA and PSO converge near the optimal. In the fixed-dimensional multimodal function F₆, NCS-BWO achieves superior optimization results compared with the other six algorithms. At the end of Table 5, two relatively advanced algorithms, GGO and BKA, are presented. Under the same conditions, the solution ability of NCS-BWO is superior to these two advanced algorithms, indicating that the algorithm proposed in this paper effectively improves the performance of the original algorithm.

Table 5. Optimization results of various algorithms based on six test functions.

Function		NCS-BWO	NCSA	BWO	CSA	GA	PSO	WOA	GGO	BKA
F1	Mean	5.83 × 10−288	3.38 × 10−216	1.89 × 10−122	1.39 × 10−62	0.242	1.223	9.99 × 10−31	1.31 × 10−22	1.04 × 10−50
	Std	0.468	0.524	0.537	2.026	8.377	20.765	8.068	6.454	2.516
F2	Mean	0	9.86 × 10−215	1.04 × 10−121	9.65 × 10−59	0.013	0.968	6.22 × 10−14	3.27 × 10−17	2.72 × 10−50
	Std	0.144	0.162	0.248	4.081	8.114	8.877	9.648	5.625	5.436
F3	Mean	0	0	0	0	42.026	110.679	0	0	0
	Std	5.470	6.495	10.017	21.130	75.006	58.003	59.442	46.774	39.908
F4	Mean	4.44 × 10−16	4.44 × 10−16	4.44 × 10−16	4.44 × 10−16	8.566	1.686	1.47 × 10−14	4.44 × 10−16	4.44 × 10−16
	Std	0.186	0.580	0.298	1.070	3.182	2.103	2.326	2.617	1.712
F5	Mean	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998	0.998
	Std	4.79 × 10−4	4.85 × 10−4	0.263	0.162	0.531	0.230	0.640	0.420	14.371
F6	Mean	−3.322	−3.31147	−3.19915	−3.20309	−2.65133	−3.322	−3.2094	−3.1373	−3.1999
	Std	0.037	0.043	0.005	0.041	1.25 × 10−14	0.099	0.039	0.102	0.063

The convergence curves of the nine algorithms are plotted in Figure 2 to observe their convergence speeds. It can be intuitively observed from Figure 2 that the NCS-BWO algorithm demonstrates a fast convergence rate and strong optimization capability, which is evident across all test functions. As shown in Figure 2a,b, corresponding to F₁ and F₂, both PSO and GA exhibit relatively poor optimization performance, whereas the other algorithms show better overall performance, with NCS-BWO achieving the highest convergence accuracy. For the benchmark function tests F₃, F₄, and F₅, shown in Figure 2c–e, most algorithms converge near the optimal value, but NCS-BWO converges the fastest. Regarding the benchmark function test F₆, as depicted in Figure 2f, BWO tends to become trapped in local optima, whereas NCS-BWO and NCSA converge near the optimal value, with NCS-BWO achieving the fastest convergence speed. As shown above, NCS-BWO effectively enhances global search capabilities through the NCSA. It also leverages the rapid optimization capabilities of BWO to achieve fast convergence and high accuracy. The NCS-BWO algorithm demonstrates significant advantages in terms of global search accuracy, convergence speed, and stability, validating its effectiveness and superiority in complex optimization problems.

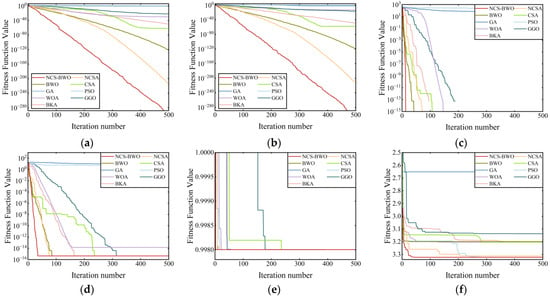
Figure 2. Convergence curves of the nine algorithms on six benchmark test functions: (a) F₁; (b) F₂; (c) F₃; (d) F₄; (e) F₅; (f) F₆.

4. PMSM Parameter Identification Design Based on NCS-BWO

4.1. Principles of PMSM Parameter Identification

The multi-parameter identification problem for the PMSM can be transformed into a system optimization problem. The procedure essentially involves comparing the identification model with the actual system to compute fitness values. The NCS-BWO algorithm is then employed to iteratively refine the parameters by screening these fitness values until a minimum is achieved. Finally, output the required recognition parameter values. Parameter identification actually involves constructing an appropriate fitness function, enabling the algorithm to obtain optimal motor parameters in the vector control system. Figure 3 illustrates the principle of PMSM parameter identification.

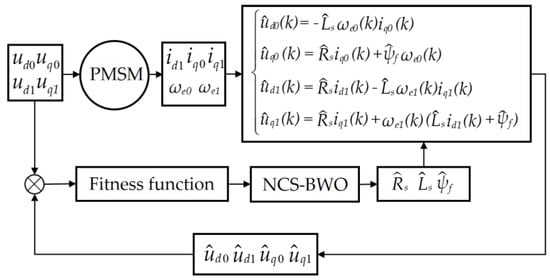
Figure 3. Schematic of PMSM parameter identification.

The fitness function in Figure 3 is defined as follows:

$$\begin{array}{ll}F({\widehat{R}}_{\mathrm{s}},{\widehat{L}}_s,{\widehat{\psi }}_f)=& {\lambda }_1{(u_{d0}(k)-{\widehat{u}}_{d0}(k))}^2\\ & +{\lambda }_2{(u_{q0}(k)-{\widehat{u}}_{q0}(k))}^2\\ & +{\lambda }_3{(u_{d1}(k)-{\widehat{u}}_{d1}(k))}^2\\ & +{\lambda }_4{(u_{q1}(k)-{\widehat{u}}_{q1}(k))}^2,\end{array}$$

(17)

where λ₁, λ₂, λ₃, and λ₄ denote the weighting factors of the fitness function. When the fitness values are equal, the weight distribution influences identification accuracy. $u_{d0}$ and $u_{q0}$ are the motor dq-axis voltage measurement values under the control of i_d = 0. ${\widehat{u}}_{d0}$ and ${\widehat{u}}_{q0}$ are the corresponding estimated values obtained from the collected data through the algorithm under the control of i_d = 0. $u_{d1}$ and $u_{q1}$ are the measured values of the motor dq-axis voltage when i_d = −2. ${\widehat{u}}_{d1}$ and ${\widehat{u}}_{q1}$ are the corresponding estimated values obtained from the collected data through the algorithm when i_d = −2. $\{{\widehat{R}}_{\mathrm{s}},{\widehat{L}}_s,{\widehat{\psi }}_f\}$ is the parameter identification results of the algorithm.

4.2. Steps for PMSM Parameter Identification Using NCS-BWO

Step 1: Collect motor data under modes i_d = 0 and i_d = −2, including the dq-axis current, voltage, and electrical angular velocity.

Step 2: The algorithm iteration times and population size are set, and the initial population is randomly generated.

Step 3: The fitness of each antibody within the population is calculated using (17).

Step 4: The NBC strategy is employed to partition the population into multiple clusters.

Step 5: Apply the cluster size optimization mechanism to each cluster.

Step 6: Clone antibodies within each cluster.

Step 7: The positions of the seeds in the antibodies remains unchanged. The clones of the remaining antibodies undergo a Gaussian mutation using (11) or a DE mutation using (13). The mutation probabilities for both types are equal.

Step 8: Compare each antibody in the current population with its corresponding mutated clones using (14), selecting the better one to form the next-generation population.

Step 9: Set BWO’s initial population to the set of best solutions accumulated by NCSA, and the current optimal individual is recorded.

Step 10: Update all black widow spiders in the current population using (6).

Step 11: Perform sex pheromone analysis on all individuals using (7). Update individuals with sex pheromone values less than or equal to 0.3 using (8).

Step 12: The fitness values of all the individuals are calculated for the updated population. Evaluate each individual’s fitness value, and compare the fitness of the current optimal individual with the historical best fitness. If the current individual’s fitness exceeds the historical best, it is updated as the new optimal value and this optimal individual is saved; otherwise, it retains the original historical best value.

Step 13: Check whether the current iteration count is less than the set maximum iteration count. If the maximum iteration count is reached, output the historical optimal value and the optimal individual; otherwise, proceed to Step 10 and repeat the above process.

Figure 4 shows the flowchart of the NCS-BWO algorithm for PMSM parameter identification.

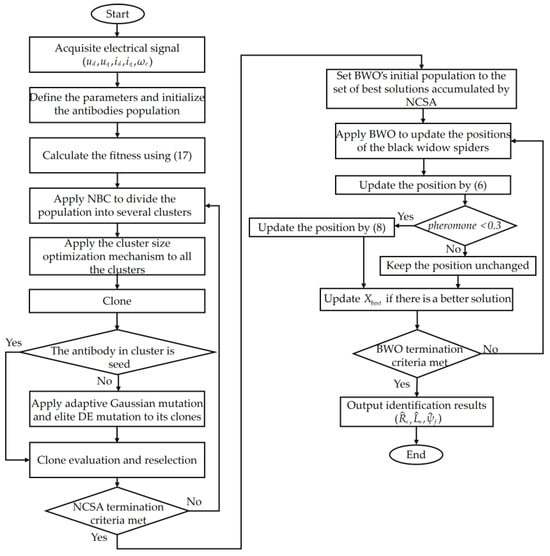
Figure 4. Flowchart of PMSM parameter identification based on NCS-BWO algorithm.

5. Simulation and Experimental Analysis

5.1. Simulation Analysis

A simulation model of the PMSM vector control system was established using Matlab/Simulink to validate the performance advantages of the NCS-BWO algorithm for PMSM parameter identification, as shown in Figure 5. The simulation configuration is for the motor to operate at the rated speed and rated torque. A search space spanning from 0 to 2 was defined for the identification of stator resistance, flux linkage, and stator inductance to evaluate the algorithm’s optimization performance. Relevant motor parameters are listed in Table 6.

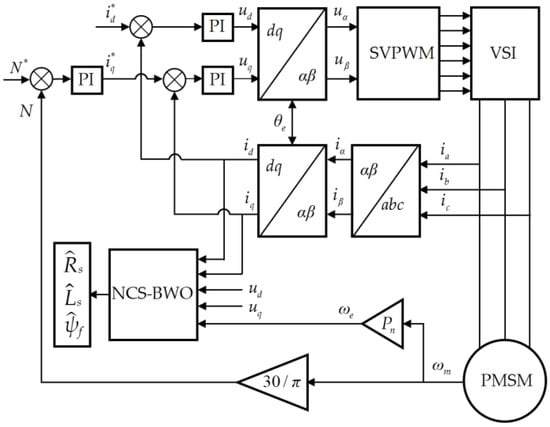
Figure 5. Vector control system block diagram.

Table 6. PMSM parameters.

Parameters	Value
Rs (Ω)	0.89
Ls (mH)	0.62
ψf (Wb)	0.0164
Pole Pairs	4
DC link voltage (V)	24
Rated power (W)	64
Rated speed (rpm)	3000
Rated torque (N·m)	0.2
Switching frequency (kHz)	10

The simulation duration was set to 0.4 s. Table 7 summarizes the parameter configurations for the nine algorithms under comparison. Specifically, λ represents the threshold control parameter, n_max denotes the maximum number of antibodies within a single cluster, d_min is the individual removal operator, n_c refers to the number of clones, pop indicates the population size, N₁ is the number of iterations of NCSA, N₂ is the number of iterations of the BWO algorithm. N is the total number of iterations. P_m and P_c correspond to the mutation rate and crossover rate, W represents the inertia weight, C₁ and C₂ denote the individual and social learning factors, respectively, and b defines the spiral coefficient.

Table 7. Parameter settings for the nine algorithms.

Algorithm	Parameter Settings
NCS-BWO	λ = 2; nmax = 10; dmin = 10; nc = 2; pop = 100; N1 = 10; N2 = 190
NCSA	λ = 2; nmax = 10; dmin = 10; nc = 2; pop = 100; N = 200
BWO	pop = 100; N = 200
CSA	nc = 2; Pm = 0.5; pop = 100; N = 200
GA	Pc = 0.8; Pm = 0.1; pop = 100; N = 200
PSO	W = 0.8; C1 = C2 = 1; pop = 100; N = 200
WOA	b = 1; pop = 100; N = 200
GGO	b = 1; pop = 100; N = 200
BKA	pop = 100; N = 200

To validate the effectiveness of the NCS-BWO algorithm, a comparative study was conducted by applying the NCSA, BWO, CSA, PSO, GA, WOA, GGO, and BKA algorithms to PMSM parameter identification simulations. Each algorithm was independently executed 20 times to ensure statistical reliability, with the average of the outcomes adopted as the final result. A summary of the identification results and their corresponding errors is provided in Table 8, where F represents the average fitness convergence value, with lower values denoting greater accuracy in the identified parameters. The parameter identification and the fitness function curves are presented in Figure 6.

Table 8. Comparison of simulation results for seven parameters of identification algorithms.

Parameter		NCS-BWO	NCSA	BWO	CSA	GA	PSO	WOA	GGO	BKA
Rs	Value (Ω)	0.8902	0.8890	0.8812	0.8739	0.9200	0.8397	0.9122	0.8790	0.8929
	Error (%)	0.02	0.11	0.99	1.81	3.37	5.65	2.49	1.24	0.33
Ls	Value (mH)	0.6195	0.6193	0.6272	0.602	0.7023	0.5754	0.6383	0.6338	0.6118
	Error (%)	0.09	0.11	1.16	2.90	13.27	7.19	2.96	2.23	1.32
ψf	Value (Wb)	0.016399	0.01636	0.016477	0.016520	0.016107	0.016058	0.016095	0.016343	0.01645
	Error (%)	0.01	0.24	0.47	0.73	1.79	2.08	1.86	0.35	0.31
F	Value	5.96 × 10−08	8.77 × 10−07	1.52 × 10−04	1.97 × 10−04	1.99 × 10−02	1.37 × 10−02	7.08 × 10−04	7.57 × 10−05	1.36 × 10−05

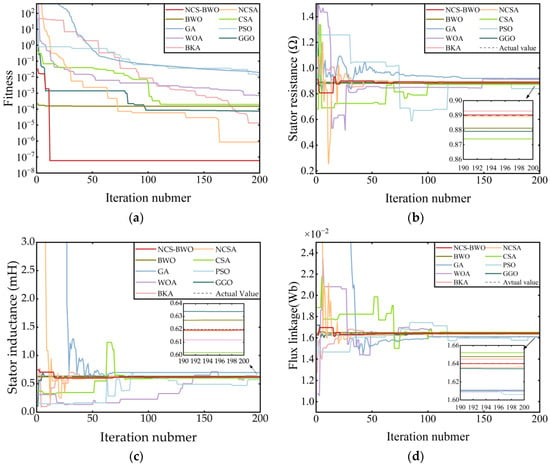
Figure 6. Parameter identification curves of PMSM using nine algorithms in the simulation environment: (a) fitness function; (b) stator resistance; (c) stator inductance; (d) flux linkage.

According to the data in Table 8, it can be observed that NCS-BWO achieves the highest identification accuracy, with all parameter identification errors below 0.1%. The NCS-BWO exhibits the lowest average fitness value among the nine algorithms, confirming its superior performance in PMSM parameter identification. At the end of Table 8, two advanced algorithms, GGO and BKA, are introduced to compare their performance with that of NCS-BWO. Under the same conditions, the performance of NCS-BWO is superior to these two advanced algorithms, indicating that the algorithm proposed in this paper significantly improves the performance of the original algorithm.

Owing to the high degree of nonlinearity in the mathematical model of the PMSM, the designed fitness function exhibits multiple extrema points. This leads to significant fluctuations or poor convergence in the parameter identification results, posing a substantial challenge to the search capability and convergence of the algorithm. Figure 6 demonstrates that NCS-BWO, NCSA, BWO, CSA, WOA, GGO, and BKA exhibit superior optimization capabilities, whereas GA and PSO yield unsatisfactory stator resistance identification results that fail to satisfy the requirements. Although NCS-BWO and BWO exhibit similar convergence speeds, BWO is more prone to local optima. Despite achieving an accuracy comparable to that of NCS-BWO, NCSA exhibits a slower convergence. NCS-BWO employs a niching clonal selection strategy to enhance the global search capability while inheriting BWO’s rapid convergence property, enabling swift and smooth convergence toward real values.

5.2. Experimental Analysis

To further validate the PMSM parameter identification effectiveness of the NCS-BWO algorithm in practice, an experimental hardware platform for the motor drive control system was constructed, as shown in Figure 7. This device consists of two identical PMSMs of model 42JSF630AS-1000, driven by BOOSTXL-DRV8305 inverter modules. Among the two PMSMs, one functions as the controlled object, while the other applies the load torque. The control algorithm was developed in MATLAB/Simulink(R2023a), converted into C code, and subsequently downloaded to the TMS320F28379D digital signal processor on the control board using Code Composer Studio (v12.0.0), where PWM switching is implemented at 10 kHz. An incremental encoder with 2500 PPR is used for rotor position sensing. Through digital 4X decoding, the final feedback resolution is enhanced to 10,000 CPR for precise position and speed estimation. The motor parameters are as follows: stator resistance R_s = 0.89 Ω, stator inductance L_s = 0.62 mH, number of pole pairs n_p = 4, flux linkage ψ_f = 0.0164 Wb, viscous damping coefficient B_m = 3.5 × 10⁻⁴ N·m·s/rad, and rotor inertia J_m = 2.8 × 10⁻⁶ kg·m².

Figure 7. Experiment platform.

Experimental procedure: After the motor reached steady-state operation, a weak d-axis negative d-axis current was injected. Motor data, including the voltage, current, and electrical angular velocity, were then sampled. Data were acquired via sensors, underwent coordinate transformation through the DSP controller, and were transmitted to the host computer via the CAN bus to perform parameter identification of the motor system. Figure 8 depicts the parameter identification and fitness function curves, and Table 9 summarizes the identification results and errors.

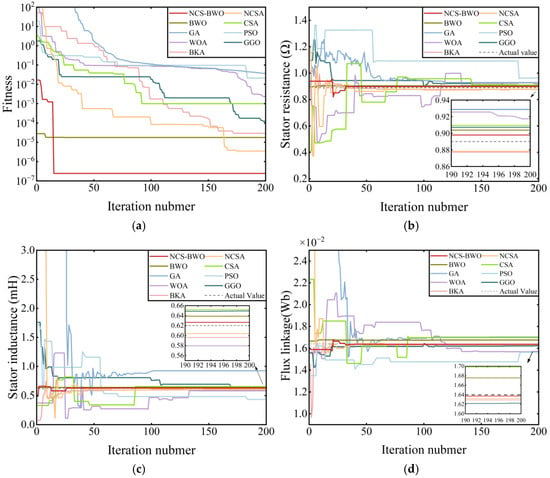
Figure 8. Parameter identification curves of PMSM using the nine algorithms in the physical motor environment: (a) fitness function; (b) stator resistance; (c) stator inductance; (d) flux linkage.

Table 9. Comparison of experimental results for seven parameters of identification algorithms.

Parameter		NCS-BWO	NCSA	BWO	CSA	GA	PSO	WOA	GGO	BKA
Rs	Value (Ω)	0.8979	0.8784	0.9038	0.9095	0.9287	0.9629	0.9175	0.9072	0.8772
	Error (%)	0.89	1.31	1.55	2.19	4.35	8.19	3.09	1.93	1.44
Ls	Value (mH)	0.6267	0.604	0.6389	0.652	0.9246	0.4343	0.5795	0.6492	0.5962
	Error (%)	1.08	2.58	3.05	5.16	49.13	29.96	6.53	4.71	3.83
ψf	Value (Wb)	0.01637	0.01632	0.01675	0.01698	0.01703	0.01562	0.01571	0.01622	0.01629
	Error (%)	0.16	0.47	2.16	3.55	3.86	4.73	4.18	1.08	0.65
F	Value	2.43 × 10−7	3.51 × 10−6	1.77 × 10−5	9.99 × 10−4	3.72 × 10−2	2.10 × 10−2	2.36 × 10−3	1.22 × 10−4	2.92 × 10−5

Figure 8a shows the average fitness convergence curves for the nine identification algorithms: NCS-BWO, NCSA, BWO, CSA, GA, PSO, WOA, GGO, and BKA. The performance of these algorithms can be evaluated by observing their convergence speed and accuracy after stabilization. As shown in Figure 8a, the NCS-BWO algorithm demonstrates superior convergence accuracy by arriving at the minimal fitness value. Although the BWO algorithm exhibits the fastest convergence rate, it produces relatively large errors after iteration completion. The slow convergence rate of NCS-BWO during the initial iteration phase is designed to prevent becoming stuck in local optima. NCSA achieves convergence accuracy comparable to that of NCS-BWO after iteration completion; however, NCS-BWO demonstrates faster convergence speed and greater stability.

Owing to external environmental interference and limitations in sensor accuracy, the motor parameter identification results exhibited larger errors compared to the simulation outcomes. Figure 8b–d present the identification curves for stator resistance, stator inductance, and magnetic flux, respectively. The PSO and GA demonstrate large and fluctuating errors in parameter identification, indicating a poor performance. Although the WOA produces smaller errors, it suffers from poor stability. Despite the CSA and BWO show better stability, their errors still fall short of those of NCSA and NCS-BWO. Both the NCSA and NCS-BWO achieve identification errors below 1.7%. The NCSA converge slowly and exhibits significant fluctuations during the identification of the stator resistance parameter. As advanced algorithms, GGO and BKA outperform conventional algorithms in terms of convergence speed and accuracy, yet their overall performance still falls short of NCS-BWO. The NCS-BWO algorithm exhibits minimal fluctuations, converges rapidly, and produces identification values closest to the true values, validating its capability to find optimal solutions.

The parameter identification results and errors are presented in Table 9. As indicated by the average fitness values and error values in Table 9, the NCS-BWO algorithm attains superior identification accuracy, with respective errors of 0.89%, 1.08%, and 0.16%. The proposed hybrid NCS-BWO algorithm combines the advantages of NCSA and BWO, demonstrating strong exploration and exploitation capabilities. It outperforms the other eight algorithms in terms of computational capability, meeting the requirements for high performance and high precision in control systems.

5.3. Analysis of Computational Efficiency

In the above experiments, each algorithm was run 20 times, and the average execution time of the nine algorithms was calculated. To compare the computational workload of the nine algorithms, this study considered factors such as the number of algorithm iterations, and population size. Under the condition of keeping these factors consistent, the computational workload of the algorithm can be reflected by the execution time. This is illustrated in Table 10.

Table 10. Comparison of the execution time of the nine algorithms.

Algorithm	Running Time (s)
NCS-BWO	0.4823
NCSA	1.3859
BWO	0.3754
CSA	0.7202
GA	0.6523
PSO	0.5602
WOA	0.6234
GGO	0.5477
BKA	0.5150

We compared the running time of nine algorithms with 200 iterations and a population size of 100. Table 10 shows that the running time of the NCS-BWO and BWO algorithms is significantly less than that of the other seven algorithms. The NCSA has the longest running time because the NBC strategy requires calculating the distance between each individual and its adjacent individuals, which greatly increases the computational load. The NCS-BWO only requires several iterations of NCSA and the obtained high-quality population is used as the initial population of the BWO. This hybrid algorithm maintains rapidity, as shown in Table 10, even though it increases the computational complexity of the algorithm.

6. Conclusions

This study proposes a hybrid NCS-BWO algorithm for PMSM parameter identification. The hybrid algorithm first employs NCSA to enhance global search capability, utilizing a nearest-better clustering strategy to partition the population and incorporating adaptive Gaussian and elite DE mutations to enrich population diversity. The NCSA outcomes are then used as the initial population of BWO, and leverage the rapid convergence of BWO to refine the solution accuracy. The simulations and experiments demonstrate that the NCS-BWO algorithm can identify the stator resistance, stator inductance, and flux linkage of the PMSM. Comparisons with the parameter identification results of NCSA, BWO, CSA, and other algorithms demonstrate that the NCS-BWO algorithm offers advantages such as high accuracy and a fast convergence speed. The identification errors for stator resistance, inductance, and flux linkage are 0.89%, 1.06%, and 0.16%, respectively.

In summary, this paper holds significant importance in PMSM state detection, fault diagnosis, robust control, and other applications. The inherent adaptability of intelligent algorithms has broadened the applicability of parameter identification techniques. Future research will be dedicated to enhancing the practicality and generalizability of the proposed approach. This will involve streamlining the mathematical models, optimizing algorithmic efficiency, and pursuing applications in various contexts.