A Robust Image Watermarking Scheme via Two-Stage Training and Differentiable JPEG Compression

Abstract

Digital image watermarking is a vital tool for copyright protection and content authentication. However, most existing methods perform well only under single noise types, while real-world applications often involve composite noises with multiple distortions, leading to poor robustness. To address this issue, we propose a robust image watermarking scheme. To improve performance under combined noise conditions, a two-stage training strategy is introduced: in the first stage, noise intensity increases gradually to stabilize training; in the second stage, mixed strong noises are applied to enhance generalization against complex attacks. Specifically, a strength-balanced watermark optimization algorithm is employed during the testing stage to improve visual quality while maintaining strong robustness. Furthermore, to improve robustness against JPEG compression, we adopt a differentiable fine-grained JPEG module that accurately simulates real compression and enables gradient backpropagation during training. Experimental results demonstrate the superiority of the proposed method under various single and combined distortions. Under noise-free conditions, it achieves 0% bit error rate and 53.55 dB PSNR. Under composite distortions, our scheme maintains a low average BER of 2.40% and a PSNR of 42.70 dB.

1. Introduction

With the explosive growth of digital content, protecting intellectual property rights and ensuring the integrity of information have become particularly important [1,2]. The image-blind watermarking technique serves as a key tool, offering robust copyright protection and verification for digital images with high imperceptibility [3,4]. However, with the diversification of multimedia applications and technological advances, traditional watermarking schemes gradually show their limitations, especially in dealing with combined noise conditions and maintaining balance between robustness and imperceptibility [5].

Traditional digital watermarking schemes are usually divided into pixel and frequency domain schemes. The pixel domain-based schemes perform the watermark-embedding process by adjusting the pixel data of the image, through processes such as pixel value adjustment, pixel block shifting, and pixel feature encoding [6,7,8,9]. These schemes are favored for their good imperceptibility, but exhibit low robustness against various attacks. In contrast, frequency domain-based schemes perform the watermarked embedding process by adjusting the coefficients in the transform domain of the image, through processes such as DCT coefficient adjustment [10,11], and DWT coefficient modification [12,13]. These schemes improve attack resistance at the expense of imperceptibility.

The swift progress in deep learning has led researchers to adopt it in the field of digital watermarking, resulting in numerous innovative schemes [14,15,16,17,18]. These schemes mainly focus on improving models [19], training strategies [20], and noise layer design [21] to enhance model performance. However, these models tend to perform poorly under combined noise conditions. This is because various types of noise require more additional watermark residual information to maintain a high decoding rate, thereby reducing imperceptibility of the watermark image.

In deep learning models, the noise layer is essential for enabling the model to effectively learn various noise features and withstand different types of distortions. Consequently, it is important to identify functions that accurately model real-world noise. For most of the differentiable digital distortions, researchers have proposed relevant mathematical functions to improve robustness of the model under such distortions, while JPEG compression presents a challenge because it involves non-differentiable operations such as quantization and cropping [22]. As a result, existing models exhibit a low watermark-decoding rate under JPEG compression distortion, failing to meet practical application standards for watermark decoding.

Following the research and analysis presented above, we can summarize the limitations and challenges faced by current image-watermarking schemes: existing schemes fail to effectively balance watermark imperceptibility and robustness under combined noise conditions. Moreover, since JPEG compression involves non-differentiable operations, it restricts the model’s ability to learn noise distribution [23]. Consequently, most models exhibit poor robustness against JPEG compression, limiting their practical application. To address the above issues, we propose a novel two-stage training scheme for model training. In the testing phase, we introduce a strength-balanced watermarking optimization algorithm, enabling the model to achieve an optimal trade-off between watermarking imperceptibility and robustness under combined noise conditions. To enhance the model’s robustness against JPEG compression, we introduce a differentiable fine-grained JPEG compression module, closely mimicking real JPEG compression. Experimental results demonstrate superior outcomes compared to previous schemes.

In summary, the main contributions of this paper include the following three aspects:

•

A novel two-stage watermarking model-training strategy is proposed, which effectively ensure the robustness of watermarking under combined noise conditions.

•

The strength-balanced watermarking optimization algorithm is proposed to optimize imperceptibility and robustness of watermarks in the testing phase.

•

A differentiable JPEG compression module is introduced to enhance the model’s robustness against JPEG compression distortions.

The remainder of this paper is organized as follows: Section 2 provides a brief review of related work. Section 3 details the proposed scheme. Section 4 outlines the experimental setup, evaluation metrics, and details of the experiment results. Finally, Section 5 presents the conclusion of our study.

2. Related Work

2.1. Image Watermarking Based on Deep Learning

The deep learning-based watermarking model was first proposed by Kandi et al. [24] in 2017. By employing autoencoder convolutional neural networks (CNNs), it brings better imperceptibility and robustness than traditional schemes. HiDDeN [14] was the first paper introducing adversarial networks to image-blind watermarking. It was also the first end-to-end scheme using neural networks. The end-to-end framework enables joint learning of encoder and decoder, but training both modules makes it challenging to optimize the trade-off between watermark robustness and imperceptibility. Liu et al. [20] proposed the TSDL training strategy. The scheme consists of two phases: noise-free end-to-end adversary training stage and noise-aware decoder-only training stage. This scheme effectively counters black-box noise. However, further improvements are required in terms of watermark robustness and imperceptibility under combined noise conditions. Table 1 compares representative deep watermarking methods along several critical dimensions, including robustness to single and composite distortions, imperceptibility, use of differentiable JPEG approximation, training strategy, and generalization capability. The comparison underscores limitations of existing frameworks in jointly addressing practical challenges such as strong mixed noise and non-differentiable transformations. Motivated by these schemes, we design a novel two-stage training strategy. By using different noise strengths with loss functions for training in different stages, robustness and imperceptibility of watermarked images can be significantly improved.

Table 1. Comparison of existing deep image watermarking methods across key features including robustness, imperceptibility, differentiable JPEG use, and training strategy.

Features	HiDDeN	MBRS	Adaptor
Robustness to single distortions	Moderate	Good	Good
Robustness to composite distortions	Poor	Moderate	Moderate
Imperceptibility	Good	Good	Good
Differentiable JPEG modeling	JPEG-SS	JPEG-Combined	JPEG-Combined
Training strategy	Single-stage	Single-stage	Two-stage

2.2. Strength Factor

Strength factor was explored by several scholars within the realm of deep learning-based watermarking schemes. Redmark [18] and TSDL [20] employed the strength factor to control robustness and imperceptibility of watermarking, yet overall enhancement was limited without significant improvements. MBRS [21] used the strength factor during testing to adjust PSNR values for different models, enabling a clearer comparison of watermark-decoding rates. However, in-depth exploration of strength factor remains insufficient. Later, the Adoptor scheme [25] proposed an adaptive strength factor training strategy that introduces a novel loss function during the training phase, aiming to ensure high watermark-decoding rates while maximizing PSNR and SSIM values for each image. Nevertheless, this scheme necessitates retraining model for different datasets, thereby lacking generalizability. To address this limitation, we propose a strength-balanced watermarking optimization algorithm to generate watermarked images with high imperceptibility against various types and intensities of distortions.

2.3. JPEG Simulations

Among various types of distortions faced by watermarking, existing deep learning schemes cannot effectively measure watermarking performance under JPEG compression [23]. This limitation arises because rounding and truncation operations inherent in JPEG compression are non-differentiable. Consequently, scholars have proposed several schemes. HiDDeN [14] introduced JPEG-Mask and JPEG-Drop schemes as alternatives to actual JPEG compression. The two-stage training scheme proposed by TSDL [20] represents an improvement over simulation schemes. However, since only decoder is trained in the second stage, information loss after compression occurs, affecting final performance. MBRS [21] proposes a training strategy that combines real and simulated JPEG compression and has achieved significant results. However, when trained jointly with other noises, robustness of MBRS [21] against JPEG compression decreases because adding other noises distorts the original combined training mechanism. To address these challenges, this paper introduces a refined JPEG compression function module, which is integrated into the noise layer for direct application during training, similar to other differentiable noise types.

3. Methodology

3.1. Model Architecture

The overall architecture of our model is shown in Figure 1. It consists of four parts. (1) Encoder: The encoder contains parameters ${\theta }_{en}$, the inputs are original image $I_{ori}\in {\mathbb{R}}^{C\times H\times W}$ and original watermark $W_{ori}\in {\{0,1\}}^L$, and output is residual image $I_{res}$; thus, watermarked image $I_{enc}$ is obtained as follows:

$$I_{enc}=I_{ori}+I_{res}$$

(1)

(2) Noise layer: A joint noise layer is constructed by fitting a mathematical function to various noises. The input to the noise layer is watermarked image $I_{enc}$ and output is noise image $I_{noi}$. (3) Decoder: The decoder, also with parameters ${\theta }_{de}$, takes noisy image $I_{noi}$ as input and outputs decoded watermark $W_{rec}$. (4) Adversary: The adversary has parameters ${\theta }_{di}$ to differentiate between the original image $I_{ori}$ and watermarked image $I_{enc}$. The main function of adversary is to distinguish the difference between watermarked image $I_{enc}$ and original image $I_{ori}$, so as to further improve the encoder’s ability to fuse features of the watermark and original image, and thus improve the quality of the watermarked image.

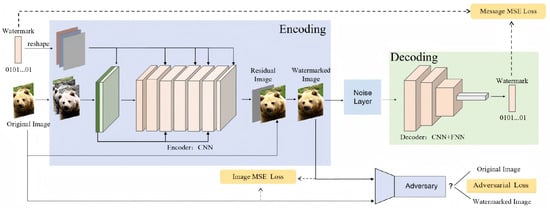
Figure 1. Overall framework of our scheme. The framework has four modules: (1) encoder, (2) decoder, (3) noise layer, and (4) adversary.

Encoder. Encoder architecture of our model is shown in the left figure of Figure 2. The encoder E is a network trained with parameters ${\theta }_{en}$ to embed the watermark into the original image. The watermark $W_{ori}$ is expanded redundantly into a form of $3\times H\times W$, matching the dimensions of original image. Then, this extended watermark is concatenated with cover image to generate a residual image $I_{res}$. This residual image is then added to the cover image to produce the watermarked image. The encoder consists of seven convolutional layers. To capture features from both the watermark and cover image at multiple levels, outputs from layers 2, 4, 5, and 7 are concatenated with the watermarked image, respectively, while outputs from convolutional layers 3 and 6 are spliced with the original encoded image. Utilizing these multi-level convolutional mappings allows for more efficient learning of the watermark pattern. An MSE loss function is applied during training of the encoder, aimed at minimizing the difference between the watermarked image and original image.

$$L_{E_1}=MSE(I_{ori},I_{enc})=MSE(I_{ori},E({\theta }_{en},I_{ori},W_{ori}))$$

(2)

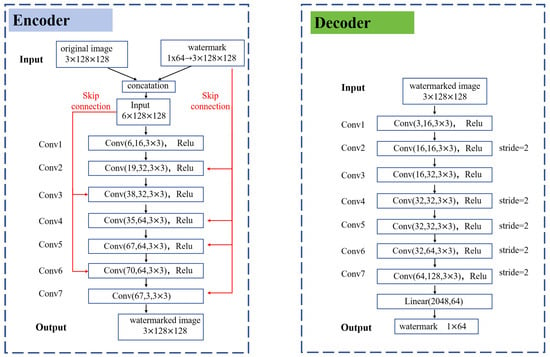
Figure 2. Detailed structure diagram of encoder and decoder; both encoder and decoder consist of seven convolutional blocks. Symmetric skip connections in the encoder allow the encoder to fuse multi-scale features.

Decoder. The decoder D with parameters ${\theta }_{de}$ is trained to extract the watermark from a noise image $I_{noi}$. As shown in the right figure of Figure 2, the main structure of the decoder is similar to the encoder, using seven convolutional layers and one fully connected layer. To ensure the final output has the same structure as the original watermark $W_{ori}$, the stride sizes of Conv1 and Conv3 are set to the default value of 1, whereas the stride sizes of remaining layers are set to 2 for reducing feature tensor size. After Conv7, a flatten operation is performed on remaining neurons, and then a dense layer is used to output a one-dimensional tensor which has the same size as $W_{ori}$. We also applied MSE loss function to train the decoder, to minimize the difference between recovered watermark $W_{rec}$ and original watermark $W_{ori}$, aiming to make each bit same.

$$L_{De}=MSE(W_{rec},W_{ori})=MSE(W_{ori},D({\theta }_{de},I_{noi}))$$

(3)

Adversary. In our scheme, the adversary consists of three layers of $3\times 3$ convolutional layers followed by a pooling layer for classification. The adversary is utilized to predict whether an image contains watermark information. It is trained by minimizing the following loss function. Update parameters ${\theta }_{di}$ to minimize

$$L_A=log(1-A({\theta }_{di},E({\theta }_{En},I_{ori},W_{ori})))+log\left(A({\theta }_{di},I_{ori})\right)$$

(4)

And update parameters ${\theta }_{En}$ to minimize

$$I_{E_2}=log\left(A({\theta }_{di},I_{enc})\right)=log\left(A({\theta }_{di},E({\theta }_{En},I_{ori},W_{ori}))\right)$$

(5)

Noise layer. The noise layer is a crucial component of the model for achieving robustness. Common differentiable noises, such as crop, Gaussian filtering (GF), Gaussian noise (GN), resize, and salt and pepper (S&P) noise can be directly modeled using existing mathematical functions. However, for non-differentiable noise types like JPEG compression, existing fitting functions are not particularly effective. To address this issue, we introduce a refined JPEG compression function module designed in Reich et al. [26]. To the best of our knowledge, this is the first application of this scheme in the field of watermarking. This JPEG compression module performs differentiable processing on quantization, rounding down, truncation, and other operations, making it directly applicable for training deep learning models under highly fitting real JPEG compression. Specifically, for differentiable quantization, the JPEG compression module uses polynomial approximation proposed by Shin et al. [27] to approximate quantization operation using the rounding function.

$$x=\lfloor x\rfloor +{\left(x-\lfloor x\rfloor \right)}^3$$

(6)

In the quantization step, a given JPEG quality Q is mapped to a scale factor s. The scaling factor s is calculated as follows:

$$s\left(Q\right)=\left\{\begin{array}{cc}{\displaystyle \frac{5000}{Q}}\hfill & Q<50\hfill \\ 200-2\ast Q\hfill & Q\ge 50\hfill \end{array}\right.$$

(7)

Since scaling factor s and the corresponding quantization table need to be stored as integers, a differentiable scale floor function is necessary. The JPEG compression module utilizes polynomial rounding to approximate downward rounding function, offering advantages over alternative schemes.

$$s=\lfloor s-0.5\rfloor +{(s-0.5-\lfloor s-0.5\rfloor )}^3$$

(8)

For differentiable quantization table (QT) clipping, the JPEG compression module employs a differentiable clipping technique to constrain values within an appropriate range.

$$clip\left(x\right)=\left\{\begin{array}{cc}0+0.001\ast (x-0)\hfill & \mathrm{if}x<0\hfill \\ x\hfill & \mathrm{if}x\in [0,255]\hfill \\ 255+0.001\ast (x-255)\hfill & \mathrm{if}x>255\hfill \end{array}\right.$$

(9)

3.2. Model Training and Testing Strategy

The scheme employed in our scheme comprises three steps: two training stages and a testing stage for adaptive control of watermarking performance through strength factor adjustment. During training, the method learns to generate residual images that are robust to various high-intensity distortions. At test time, a strength-balanced watermarking optimization algorithm is applied to adaptively produce high-quality watermarked images under diverse noise conditions. The entire process of model training and testing strategy is shown in Figure 3.

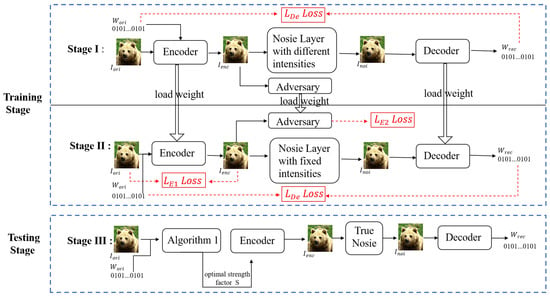
Figure 3. Two-stage training and adaptive testing framework for robust watermarking. Stage I stabilizes feature learning under variable distortions, while Stage II refines imperceptibility and robustness via multi-loss optimization; Stage III applies strength-balanced embedding at inference time.

In the first training stage, the model is trained under various strong noise distortion conditions. To enhance stability and accelerate training speed, only the loss function of the decoder is utilized in this phase, as represented by the following equation.

$$L_1={\lambda }_D{L}_{De}$$

(10)

At the same time, to improve robustness of the model under combined noise conditions, we choose to train a single model that can withstand a variety of noises, rather than training separate models for each type of noise. The noise layer $N_{pool}$ we used is shown as follows. When training the model, the watermarked image is randomly distorted by one of the noises in the noise pool $N_{pool}$ before decoding, which ensures that the model has good robustness to various types of noises. By covering such aggressive distortions early in training, the model learns generalized robustness across diverse attack scenarios.

$$\begin{array}{cc}\hfill N_{pool}& =\{Identity\left(\right),Crop\left(p_c\right),S\&P\left(p_p\right),Cropout\left(p_o\right),GN\left(\delta \right),\hfill \\ \hfill & GF\left(\sigma \right),Resize\left(p_r\right),Dropout\left(p_d\right),JPEG\left(Q\right)\}\hfill \end{array}$$

(11)

As shown in corresponding variables in Table 2, during the training process, the model randomly selects different types of noises with varying intensities each time. Consequently, the model learns generalized features under diverse noise conditions. The first stage of training is designed to enable the decoder to efficiently learn robust features for various types of noise.

Table 2. The parameter settings of the noise pool in different training stages.

Parameter	${\mathit{p}}_{\mathit{c}}$	${\mathit{p}}_{\mathit{p}}$	${\mathit{p}}_{\mathit{o}}$	$\mathit{\delta }$
First stage value	$(0,50\%]$	$(0,10\%]$	$(0,50\%]$	$(0,10\%]$
Second stage value	$3.5\%$	$10\%$	$10\%$	$10\%$
Parameter	$\mathit{\sigma }$	${\mathit{p}}_{\mathit{r}}$	${\mathit{p}}_{\mathit{d}}$	$\mathit{Q}$
First stage value	$[2,25]$	$(0,1]$	$(0,50\%]$	$[10,50]$
Second stage value	2	$50\%$	$30\%$	10

In the second stage, building upon the robust decoder obtained from the first stage of training, the model is further trained using all the loss functions. This ensures that the model benefits from both initial robustness and optimization across all parameters.

$$L_2={\lambda }_E{L}_{E_1}+{\lambda }_D{L}_{De}+{\lambda }_A{L}_{E_2}$$

(12)

Our focus shifts toward enhancing imperceptibility while preserving robustness. To achieve this balance, we fix distortion parameters to moderate levels—representative of realistic but less extreme perturbations. This design choice enables the model to prioritize perceptual quality without sacrificing resilience under practical conditions. And the training is continued using a fixed medium intensity noise as shown in Table 2. This training strategy improves the quality of watermarked images while maintaining robustness of the watermark.

While both our method and TSDL [20] adopt a staged training paradigm, their objectives and design philosophies are different. TSDL [20] first prioritizes generating high-fidelity watermarked images and only subsequently incorporates robustness considerations. In contrast, our staged design is a targeted technical strategy to achieve strong resilience against composite distortions. The first stage directly optimizes for robustness by exposing the model to increasingly severe synthetic noise and differentiable approximations of common attacks, thereby learning distortion-invariant watermark representations early in training. The second stage focus shifts toward enhancing imperceptibility while preserving robustness.

In the testing phase, to further improve the quality of watermarked image, we designed a strength-balanced watermarking optimization algorithm to measure the quality of watermarked image and decoding accuracy; the algorithm process is shown in Algorithm 1. The core principle behind our algorithm is that since watermarked image $I_{enc}$ is derived from direct addition of original image $I_{ori}$ and residual image $I_{res}$, robustness and imperceptibility of the watermark are mainly influenced by residual image. Therefore, we use strength factor S to adjust the weight of residual image during the testing phase. The relationship can be represented as follows:

$$I_{enc}=I_{ori}+I_{res}\ast S$$

(13)

By adjusting S, we aim to identify an optimal value in different noise conditions that ensures watermark imperceptibility while maintaining an acceptable decoding loss rate. In our implementation, the strength-balancing algorithm adopts a sequential search strategy: it starts from small watermark strength and incrementally increases S by a fixed step until either the extracted watermark achieves the target bit error rate or the maximum number of attempts is reached. This design ensures deterministic runtime—for each image, the algorithm performs at most iterations, which in our experiments is set to 50. The strength factor S is bounded within $(0,1]$ and optimized independently for each test image. Starting from $S=0.01$, we iteratively enhance S until the extracted watermark satisfies a target BER threshold, thus achieving the best possible visual quality while preserving robustness.

Algorithm 1 Method of the Strength-Balanced Watermarking Optimization

Input:  Original images $I_{ori}$, watermarks $W_{ori}$, error_rate Output:  BER, PSNR, SSIM, optimal strength factor S   1: Initialize parameters:   2:    $S\leftarrow 0.01$   3:    $step\_size\leftarrow 0.02$   4:    $max\_attempts\leftarrow 50$   5:    $optimal\_S\leftarrow S$   6:    $attempt\leftarrow 0$   7: while$attempt<max\_attempts$do   8:     Encode $W_{ori}$ into $I_{ori}$ with strength S → Generate $I_{enc}$ and $W_{rec}$   9:     Compute $PSNR$ and $SSIM$ between $I_{ori}$ and $I_{enc}$ 10:       Compute $BER$ between $W_{ori}$ and $W_{rec}$ 11:       if $BER<error\_rate$ then 12:          $optimal\_S\leftarrow S$ 13:          $S\leftarrow S+step\_size$ 14:          $attempt\leftarrow attempt+1$ 15:     else 16:         Break loop 17:     end if 18: end while 19: Output $optimal\_S$, corresponding $BER$, $PSNR$, $SSIM$

4. Experiments

To validate effectiveness of the proposed scheme, this section provides a detailed introduction to the experimental process and results. The content encompasses five main parts: First, we describe the datasets and explain how we chose the evaluation metrics. Second, we detail the experimental steps, including model training and testing setups. Third, we analyze the scheme’s performance in terms of watermark invisibility and robustness. Fourth, we compare our scheme with state-of-the-art schemes to show its advantages. Finally, ablation experiments verify the effectiveness of our refined JPEG compression module and explain why our model is simple yet effective.

4.1. Datasets and Evaluation Metrics

Datasets. Similar to other schemes, we randomly selected 10,000 natural images from the COCO dataset [28] as the training set and an additional 1000 images as the validation set. We used 5000 COCO datasets [28] different from the training and validation sets as the test set. To better demonstrate the scheme’s generalization ability, we randomly selected 1000 images from the Mini-ImageNet [29] dataset of different categories as the test set. The evaluation will be based on the average performance metrics reported on the test set.

Metrics. To evaluate the performance of our scheme, we use a series of quantitative metrics. The robustness of watermarks measured by the bit error ratio (BER), which refers to the error between original watermark $M_{ori}$ and extracted watermark $M_{rec}$. The imperceptibility of watermarked images $I_{enc}$ is measured by Signal-to-Noise Ratio (PSNR) and Structural Similarity (SSIM).

$$\begin{array}{cc}\hfill BER(\%)& =\left({\displaystyle \frac{1}{L}}\times \sum _{k=1}^L|M_{ori}-M_{rec}|\right)\times 100\%\hfill \end{array}$$

(14)

$$\begin{array}{c}\hfill PSNR(I_{ori},I_{enc})=20\times {log}_{10}{\displaystyle \frac{\mathrm{MAX}(I_{ori},I_{enc})-1}{\mathrm{MSE}(I_{ori},I_{enc})}}\end{array}$$

(15)

$$\begin{array}{c}\hfill SSIM(I_{ori},I_{enc})={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}}\end{array}$$

(16)

where $MAX\left(\right)$ is the maximum pixel value of test image, and $MSE\left(\right)$ refers to the Mean Squared Error. $u_x$, ${\sigma }_x^2$, ${\sigma }_{xy}$ refer to the average, variances, and covariance of images, respectively. $C_1$ and $C_2$ are two constants to prevent unstable results. For better result presentation, we adopt the average strength factor S obtained from the test set as the final result. In the comparison table with other scheme, the best-performing values are highlighted in bold.

Baseline. Our baselines for comparison are HiDDeN [14], MBRS [21], Adaptor [25], and MCFN [30]. Their works all use convolutional neural networks as the model framework and use strength factors to control the experimental results. HiDDeN [14] and MBRS [21] opened the source code of their model. We are unable to achieve the best performance they reported. Adaptor [25] and MCFN [30] are not yet open-source. So to respect their reported results, we directly use the results published in MCFN [30]. Following standard practice in deep image watermarking above, we report mean BER and PSNR over the entire test set. All baselines are evaluated under identical distortion settings to ensure fair comparison.

4.2. Implementation Details

The model training in this scheme is divided into two stages. During training and testing, all images are uniformly resized to $128\times 128$. To maintain consistency with other schemes, we randomly embed $L=64$ bits of information into each image. The entire training process is conducted on NVIDIA GeForce RTX 3090.

In the first stage, the initial learning rate is set to $1\times {10}^{-3}$, with a batch size 32, and the weight factor ${\lambda }_D$ is 10. These parameters were set based on the HiDDeN [14]. Additionally, the learning rate is automatically halved every 20 epochs to ensure rapid convergence in the early training stages and more precise learning of watermark robustness features. In the second stage, the initial learning rate is set to $1\times {10}^{-4}$ and a reduced batch size 8, weight factor ${\lambda }_E$ is 6.18, ${\lambda }_D$ is 10, and ${\lambda }_A$ is 0.001.

Both stages involve training for 100 epochs and employ the Adam optimizer with default hyperparameters. For the noise layer, we use a randomly mixed high-intensity noise layer, as described earlier. This scheme aims to enhance the model’s resistance to various distortions by exposing it to different noises, thereby improving the robustness in practical applications.

4.3. Imperceptibility and Robustness Tests

We evaluate the imperceptibility and robustness of our scheme using a model trained under combined noise conditions. Extensive tests were conducted with varying noise intensities, and Figure 4 shows visual quality results of each noise. Each column shows test results for each specific noise, and the name of noise and noise intensity are shown in the first row. The next two rows are original image $I_{ori}$ and watermarked image $I_{enc}$. We can find that images $I_{ori}$ and $I_{enc}$ are almost indistinguishable visually, which shows that our model has good invisibility. The bottom row shows noise image $I_{noi}$ attacked by a specific noise.

Figure 4. Visual comparisons of the experimental results under different traditional noises. Each column corresponds to a type of noise. Top: original image $I_{ori}$; middle: encoded image $I_{enc}$; bottom: noisy image $I_{noi}$.

Table 3 shows quantitative results for robustness and imperceptibility of our blind-watermarking scheme under various single distortions on 1000 Mini-ImageNet images. The metrics include BER, PSNR, SSIM, and a strength factor S which collectively assess both the fidelity of the watermarked image and the accuracy of watermark extraction.

Table 3. Results of robustness and imperceptibility against one single distortion under 1000 images in Mini-ImageNet dataset.

Noise	Factor	Combined
		BER (%)	PSNR (dB)	SSIM	S
Identity	-	0.0	53.55	0.995	0.064
Dropout	p = 30%	0.0	44.14	0.968	0.192
GF	$\delta$ = 0.01	0.0	43.72	0.966	0.186
Resize	p = 50%	0.0	48.15	0.985	0.121
S&P	p = 10%	0.0	39.13	0.921	0.317
GN	$\sigma$ = 25	4.16	41.49	0.947	0.247
Cropout	p = 50%	7.80	45.50	0.973	0.169
Crop	p = 50%	7.26	45.90	0.975	0.154
RealJPEG	Q = 50	0.01	36.61	0.888	0.434
Average	-	2.40	42.70	0.953	0.227

In the Identity case, our scheme achieves a PSNR value of 53.55 and a BER of less than 0.01%, which demonstrates the high imperceptibility and robustness of the scheme. Under different types of noise, the performance varies due to their distinct impacts on image structure and frequency content. Overall, the average performance across all distortions shows a BER of 2.40%, PSNR of 42.70 dB, SSIM of 0.953, and S of 0.227, demonstrating consistent and superior performance compared to state-of-the-art schemes under diverse attack scenarios.

Table 4 shows the robustness and imperceptibility results of our watermarking scheme under two types of combined noise distortions, tested on 1000 images from the Mini-ImageNet [29] dataset. Each row represents a different combination of noise attacks, such as SP followed by Crop, or JPEG compression combined with GF. The PSNR values for all test cases are above 30 dB, which means the watermarked image remains visually very close to the original image, even after multiple distortions. The BER values are kept below 5%, showing that the watermark can still be accurately extracted under complex attack conditions. These results show that our scheme is effective under both single and real-world combined distortions, where multiple attacks occur sequentially. This makes our scheme more practical and reliable for real applications.

Table 4. The robustness and imperceptibility results of two types of combined noise across 1000 images in the Mini-ImageNet dataset. The meaning of ‘SP(0.1) + Crop(0.5)’ is that the watermarked image is first processed by SP(0.1) and then processed by Crop(0.5) to obtain a noisy image containing two types of distortions.

Noise (Factor)	Combined
	BER (%)	PSNR (dB)	SSIM	S
SP(0.1) + Crop(0.5)	3.92	33.14	0.808	0.638
SP(0.1) + RealJpeg(50)	4.11	32.62	0.80	0.68
RealJpeg(50) + GF(2)	5.00	31.69	0.78	0.758
RealJpeg(50) + Crop(0.5)	4.45	32.82	0.805	0.667
RealJpeg(50) + Resize(0.5)	4.29	35.33	0.87	0.508
GN(0.01) + Crop(0.5)	3.56	39.89	0.931	0.291

4.4. Comparison with the State of the Arts

We compare our scheme with several state-of-the-art watermarking schemes, including HiDDeN [14], MBRS [21], and Adaptor [25], which also use strength factors to balance imperceptibility and robustness. To fully evaluate the performance of our scheme, we conduct extensive experiments on 5000 images from the COCO [28] dataset under different noise types and intensities. We adopt commonly used noise from prior watermarking studies. These noises are categorized into two types: differentiable and non-differentiable. Differentiable noise includes Crop, Dropout, and Gaussian noise. Non-differentiable noise includes JPEG compression.

4.4.1. Testing of Differentiable Noise

Differentiable noise can be categorized into geometric noise and non-geometric noise. Crop noise is one of the most common geometric distortions, where part of the image is removed. This can seriously affect watermark extraction because the embedded watermark may be partially or completely lost. In our experiments, we test three crop ratios R of 0.3, 0.5, and 0.7, meaning that 9%, 25%, and 49% of the watermarked image is kept, respectively. As shown in Table 5, when $R=0.7$, our scheme achieves a BER of only 0.02%, while HiDDeN [14], MBRS [21], and Adaptor [25] have BERs of 15.8%, 9.0%, and 0.86%, respectively. This shows that our scheme can still recover the watermark accurately even when a large portion of the image is cropped. At the same time, our PSNR value reaches 43.52 dB, which is higher than all other schemes, indicating better visual quality.

Table 5. Comparison of experimental results for different crop ratios under 5000 images in COCO dataset.

Crop	R = 0.3				R = 0.5				R = 0.7
Metric	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$
HiDDeN	31.46%	0.921	34.24	1	24.5%	0.943	35.77	1	15.8%	0.950	37.56	1
MBRS	25.6%	0.943	37.36	1	10.5%	0.946	37.69	1	0.90%	0.963	40.40	1
Adaptor	24.7%	0.945	37.56	1.08	10.4%	0.968	40.86	0.97	0.86%	0.972	41.92	0.91
Ours	16.2%	0.965	44.12	0.18	7.26%	0.975	45.90	0.15	0.025%	0.959	43.52	0.21

Even at smaller crop ratios like $R=0.3$, our scheme maintains a low BER and high PSNR, outperforming others.

In non-geometric noise, we choose Gaussian noise and Dropout for comparative evaluation. These noises affect the pixel values directly and can reduce both image quality and watermark extraction accuracy.

Gaussian noise adds random noise to each pixel, which affects the signal strength of the watermark. We test three noise levels: ${\sigma }^2$ of $0.001$, $0.005$, and $0.010$. From Table 6, at ${\sigma }^2$ of $0.010$, our scheme maintains a BER of 0.00% and a PSNR of 43.54 dB, outperforming others. Even at high noise levels, our watermark remains fully recoverable.

Table 6. Comparison of experimental results of Gaussian noise under different ${\sigma }^2$ under 5000 images in COCO dataset.

Gaussian Noise	${\mathit{\sigma }}^2=0.001$				${\mathit{\sigma }}^2=0.005$				${\mathit{\sigma }}^2=0.010$
Metric	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$
HiDDeN	23.2%	0.910	34.60	1	28.1%	0.930	33.47	1	30.3%	0.908	32.86	1
MBRS	0.031%	0.957	41.08	1	0.052%	0.923	38.03	1	0.10%	0.911	37.25	1
Adaptor	0.016%	0.970	43.56	0.77	0.052%	0.937	39.30	0.84	0.084%	0.924	38.63	0.91
Ours	0.00%	0.990	49.68	0.09	0.00%	0.978	45.86	0.14	0.00%	0.965	43.54	0.19

Dropout noise randomly removes pixels from the image, which may destroy part of the embedded watermark. In our experiments, we test three dropout ratios R of 0.3, 0.5, and 0.7. As shown in Table 7, when $R=0.7$, our scheme achieves a BER of 0.00%, while HiDDeN [14] has a BER of 23.5%, MBRS [21] is 0.0051%, and Adaptor [25] is 0.0050%. This shows that our scheme can still recover the watermark perfectly even when 70% of the pixels are removed. At the same time, our PSNR reaches 50.33 dB, which is higher than all other schemes, indicating excellent visual quality.

Table 7. Comparison of experimental results of dropout at different ratios under 5000 images in COCO dataset.

Dropout	R = 0.3				R = 0.5				R = 0.7
Metric	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$
HiDDeN	40.60%	0.937	34.82	1	26.1%	0.923	34.69	1	23.5%	0.902	32.58	1
MBRS	0.0052%	0.961	41.39	1	0.0021%	0.977	44.45	1	0.00051%	0.983	46.64	1
Adaptor	0.0052%	0.971	43.20	0.87	0.0018%	0.988	48.47	0.79	0.00050%	0.993	48.89	0.76
Ours	0.00%	0.967	43.68	0.20	0.00%	0.984	47.63	0.13	0.00%	0.991	50.33	0.09

This improvement comes from our proposed strength-balanced optimization algorithm, which dynamically adjusts the watermark strength during testing. It ensures strong robustness without sacrificing image quality. These results demonstrate that our scheme is more effective than existing approaches in handling geometric distortions, especially under severe cropping conditions.

4.4.2. Testing of Non-Differentiable Noise

JPEG compression is a common non-differentiable distortion that reduces image quality by removing high-frequency details. This can damage the watermark signal, especially when the compression quality is low. In our experiments, we test three JPEG quality factors Q of 30, 50, and 70. Lower values mean stronger compression and more loss of image information.

As shown in Table 8, at $Q=30$, our scheme achieves a BER of 0.041%, which is much lower than HiDDeN [14] (39.8%) and MBRS [21] (0.61%), showing strong robustness even under heavy compression. At $Q=70$, our BER drops to 0.001%, indicating nearly perfect watermark recovery. In addition, our PSNR values are slightly lower than those of Adaptor [25] and MBRS [21], but still above 37 dB, meaning the visual quality remains good. For example, at $Q=50$, our PSNR is 36.16 dB, close to Adaptor’s [25], while maintaining a very low BER.

Table 8. Robustness and imperceptibility test results for JPEG compression under 5000 images in COCO dataset.

JPEG	Q = 30				Q = 50				Q = 70
Metirc	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$	BER	SSIM	PSNR	$\mathit{S}$
HiDDeN	39.8%	0.877	32.57	1	35.2%	0.858	31.00	1	33.4%	0.862	31.65	1
MBRS	0.61%	0.937	35.14	1	0.031%	0.947	36.41	1	0.044%	0.947	38.14	1
Adaptor	0.51%	0.953	37.63	0.87	0.016%	0.963	38.42	0.76	0.037%	0.970	40.96	0.74
Ours	0.041%	0.853	34.71	0.53	0.018%	0.882	36.16	0.45	0.001%	0.899	37.18	0.41

4.4.3. Testing of Combined Noise

To fairly evaluate the performance of our scheme compared with other schemes, we use the same dataset as MCFN [30] and randomly selected 5000 images as the test set for the experiment at combined noise condition. Table 9 shows values of each metric for each scheme under different noises, and our scheme not only achieves a higher PSNR than other schemes but also excels in robustness tests.

Table 9. Results of robustness and imperceptibility compared with different models under 5000 images in COCO dataset.

Models	Metrics	Noise
		GN $\mathit{\delta }$ = 0.05	GF $\mathit{\sigma }=\mathbf{2}$	S&P $\mathit{p}=\mathbf{1}\%$	Dropout $\mathit{p}=\mathbf{70}\%$	Crop $\mathit{p}=\mathbf{70}\%$	JPEG $\mathit{Q}=\mathbf{50}$
HiDDeN	PSNR(dB)	29.92	33.49	34.90	35.04	38.68	30.99
	SSIM	0.902	0.919	0.943	0.930	0.965	0.858
	BER(%)	22.0	12.0	28.0	22.0	21.0	35.2
MBRS	PSNR(dB)	33.19	42.78	42.73	41.6	39.59	31.08
	SSIM	0.832	0.973	0.973	0.975	0.956	0.832
	BER(%)	0.0063	0.0035	0.0016	0.013	0.98	0.0022
Adapor	PSNR(dB)	34.8	45.37	44.15	44.53	41.92	31.15
	SSIM	0.873	0.984	0.981	0.982	0.972	0.841
	BER(%)	0.0034	0.0030	0.0016	0.011	0.86	0.0024
MCFN	PSNR(dB)	35.15	47.67	48.27	49.75	47.79	31.56
	SSIM	0.919	0.991	0.986	0.990	0.993	0.848
	BER(%)	0.0022	0.0024	0.00014	0.00062	0.047	0.001
Ours	PSNR(dB)	37.55	45.14	46.78	50.80	48.46	36.31
	SSIM	0.902	0.974	0.982	0.992	0.987	0.884
	BER(%)	0.0	0.0	0.0	0.0	0.0	0.00006

To further illustrate the performance of our scheme, we provide a detailed analysis based on the results shown in Table 9. Under Dropout ($p=70\%$), our scheme achieves a PSNR of 50.80 dB, which is higher than HiDDeN [14] (35.04 dB), MBRS [21] (41.6 dB), Adaptor [25] (44.53 dB), and MCFN [30] (49.75 dB). Similarly, under Crop ($p=70\%$), our scheme maintains a high PSNR of 48.46 dB, outperforming all other schemes. In terms of JPEG compression ($Q=50$), our scheme achieves a PSNR of 36.31 dB, which is significantly higher than other schemes. Notably, our scheme also achieves the lowest bit error rate (BER) across all noise types. This comprehensive evaluation confirms that our scheme not only enhances the quality of watermarked images but also ensures robust watermarking under various types of noise conditions.

4.5. Ablation Experiments

To further validate our idea, we will conduct ablation experiments, targeting to independently validate the two-stage training strategy, network architecture design, and differentiable JPEG compression module.

4.5.1. Two-Stage Training Strategy

The two-stage training strategy is introduced to improve model robustness under strong and mixed noise conditions. To verify its necessity, we train the same network using only a single stage with the combined $L_2$ total loss, without the initial pre-training phase. Under this setting, the watermark decoding rate during training stabilizes around 50%. This poor performance suggests that model struggles to simultaneously learn robustness against multiple strong distortions when all losses are applied from the beginning. The conflicting gradients from different loss terms hinder stable convergence. In contrast, our two-stage approach first stabilizes feature learning in the pre-training stage, then enhances robustness in the fine-tuning stage, leading to significantly better generalization.

4.5.2. Network Architecture Design

We evaluate the impact of network architecture by replacing our lightweight design with the more complex model used in MBRS [21]. During the training stage, the MBRS [21] model performs well on the training set with a BER of 0, while the BER on validation set is as high as 20%, indicating that model is not able to effectively learn the mixed noise features, leading to overfitting of model. Excessive model complexity may be the cause of the problem. MBRS contains a large number of attention modules which tend to focus more on feature extraction from the original image. In contrast, our scheme uses only a combination of convolutional and watermarked embeddings, allowing the model to focus more on the learning of residual image, which can help model converge and achieve better results.

4.5.3. Differentiable JPEG Compression Module

To verify the advantage of the JPEG differentiable compression layer used in our scheme, we replace its original mixed training scheme with our noise layer based on the MBRS [21] scheme. We also compare with the scheme JPEG-SS used in the model HiDDeN [14], and the experimental results obtained are shown in Table 10. The experimental results show that our scheme can be closer to the real JPEG compression and obtain better results in the robustness test. This is because our module more closely simulates the actual quantization and rounding operations in standard JPEG encoding, while still allowing gradient approximation for training. As a result, the model becomes more resilient to JPEG compression noise.

Table 10. Comparison among MBRS, JPEG-SS, and the differentiable JPEG compression of our scheme.

	Q = 90		Q = 50		Q = 30
	BER	PSNR	BER	PSNR	BER	PSNR
JPEG-SS	0.00%	36.31	0.01%	36.31	1.63%	36.32
MBRS	0.00%	44.44	0.55%	40.77	4.04%	40.76
Ours	0.00%	44.57	0.00%	39.52	4.44%	39.52

5. Discussion

Our approach delivers strong robustness and visual quality under a wide range of common image degradations, but several limitations warrant discussion. As shown in Table 11, since the same encoder–decoder architecture is shared between Stage 1 and Stage 2, the total number of parameters in our model is the sum of the parameters used across both stages, amounting to 0.84 M. The overall computational complexity is 3.98G FLOPs, corresponding to the full two-stage inference pipeline. Although our model architecture is lightweight, with fewer parameters and lower FLOPs than other baselines, the sequential training process approximately doubles the total training time compared to single-stage approaches. At inference time, an additional latency arises from our adaptive strength calibration, which tailors watermark intensity to each input image to balance detectability and imperceptibility. Though this step is key to consistent performance across diverse content, it may be prohibitive in latency-sensitive applications. Future efforts could replace this iterative search with a learned predictor to retain benefits while improving speed.

Table 11. Comparison of model parameters, FLOPs, and inference time under 5000 images in COCO dataset.

Model	HiDDeN	MBRS	Ours (Stage 1)	Ours (Stage 2)	Ours (Stage 1 + Stage 2)
Params(M)	0.45	20.81	0.42	0.42	0.84
FLOPs(G)	7.39	15.15	1.99	1.99	3.98
Time(s)	117.63	205.99	-	-	507.47

Generalization behavior also reveals both strengths and boundaries. Evaluations on the ImageNet [29] dataset show performance comparable to that on in-domain benchmarks, suggesting the model captures transferable features rather than overfitting to specific textures or structures. This resilience is likely reinforced by the aggressive and varied distortion augmentation used during the first training stage. Nevertheless, like most data-driven watermarking schemes, our method assumes the test-time distortions resemble those seen during training. It handles mild, low-intensity unseen perturbations reasonably well but struggles when confronted with unseen distortion. These limitations define the current boundary of our method’s applicability.

For large-scale datasets, the per-image adaptive strength optimization in our inference pipeline introduces non-negligible latency. As demonstrated in Table 11, our method incurs higher inference latency than baseline approaches due to the per-image adaptive strength optimization, especially under severe distortions that require more iterations. While this component is critical for robustness, it limits scalability on large datasets. Future work will explore efficient alternatives to reduce runtime without compromising performance.

From a practical standpoint, our scheme is well-suited for copyright protection and content provenance tracking in digital media distribution. By ensuring reliable watermark recovery even after common editing operations, it enables creators and platforms to verify ownership or trace unauthorized reuse. Moreover, the core principles of our framework can offer a reference design which can be adapted to video watermarking.

6. Conclusions

In this paper, in order to further improve robustness and imperceptibility of watermarking in combined noise conditions, we propose a two-phase training strategy aimed at obtaining a model with high robustness to multiple types of noise. In the testing phase, we employ a strength-balanced watermarking optimization algorithm to further improve imperceptibility of watermarking while ensuring high robustness. Moreover, to enhance the robustness of existing schemes to JPEG compression, we introduce a fine-grained JPEG compression module. Experimental results show that our scheme outperforms other existing schemes and demonstrates significant practical value. Specifically, the scheme allows selection of optimal strength factors based on the application scenarios to achieve best performance. In future studies, we will continue to optimize the algorithm to improve its efficiency and extend application scenarios of this scheme so that it can work effectively in more complex distortion conditions, such as print-and-scan or print-and-shoot scenarios.