Abstract
As artificial intelligence continues to push into real-time, edge-based and resource-constrained environments, there is an urgent need for novel, hardware-efficient computational models. In this study, we present and validate a neuromorphic computing architecture based on resonant-tunnelling diodes (RTDs), which exhibit the nonlinear characteristics ideal for physical reservoir computing (RC). We theoretically formulate and numerically implement an RTD-based RC system and demonstrate its effectiveness on two image recognition benchmarks: handwritten digit classification and object recognition using the Fruit-360 dataset. Our results show that this circuit-level architecture delivers promising performance while adhering to the principles of next-generation RC, eliminating random connectivity in favour of a deterministic nonlinear transformation of input signals.
1. Introduction
Machine learning-based image recognition has become a cornerstone technology in scientific research [], healthcare [], defence [], agriculture [] and industry [,]. By enabling computers to identify and classify visual data with high accuracy, these systems are transforming how we interpret complex patterns from diagnosing medical conditions in radiology [] to guiding autonomous vehicles [] and enhancing satellite imagery analysis [].
At its core, this technology learns from large datasets of images, gradually improving its ability to detect subtle features that might be missed by the human eye. Typically, an image recognition system consists of a scanner that converts real-world images and objects into digital form and a machine vision subsystem that learns from datasets of these digital images to infer the identity of previously unseen scanned inputs [].
The recognition part of such a system is mostly delegated to software running on a digital computer. Typically, the computer must have considerable computational power to store and process information. While using a high-performance workstation is not an issue in a stationary context, such as a research laboratory server room or data centre, this solution is not suitable for autonomous systems, especially airborne drones, where power supply capacity, weight and cost are critical constraints [,].
While it is technically possible to replace the software and digital computer with electronic [,,] or optical [] neural networks, a more viable solution may lie in a hybrid approach. In this method, certain functions of the neural network, such as the nodes and their associated activation functions, are replaced by electronic components or circuits []. This neuromorphic approach, which uses brain-inspired principles to design circuits capable of performing computational tasks with significantly greater power efficiency than conventional computers [,,], would still rely on a reasonably fast and low-power digital computer for data processing. However, it would be more efficient overall due to the implementation of neurons as electronic circuits [,].
This approach is particularly well suited to physical (hardware) reservoir computing (RC), a branch of neuromorphic computing that employs the intrinsic dynamics of physical systems to perform efficient computation [,,,]. In particular, RC systems have proven effective for processing highly nonlinear and chaotic time-series datasets. A key advantage of RC is its low training cost, as it typically requires minimal training data and relies only on linear optimisation of the readout layer []. However, conventional RC models depend on randomly initialised weight matrices to define neuron connectivity and input mapping, which often requires careful tuning. To address this challenge, recent research has shown a mathematical equivalence between RC and nonlinear vector auto-regression (NVAR), a formulation that eliminates the need for random matrices, reduces hyperparameter complexity and offers improved interpretability [,]. This development is referred to as next-generation reservoir computing.
RC systems can also be implemented using a diverse range of physical platforms, including electronic [,], optical [] and mechanical systems []. Among these, electronic systems are particularly promising, as they can be realised in mixed-signal or fully analogue form [,]. Moreover, large-scale implementations are feasible through printed electronics, enabling the physical circuitry to emulate the structure and connectivity of software-based neural networks [].
In this paper, we theoretically investigate a novel algorithmic approach to an electronics-based physical RC system as a step toward practical neuromorphic computing. The proposed system exploits the intrinsic physical nonlinearity of tunnel diodes—specifically, resonant tunnelling diodes (RTDs), which have been identified as promising candidates for neuromorphic applications [,,]—to realise the reservoir layer. This eliminates the need for computationally intensive software-defined transformations or input masking typically employed in conventional algorithmic RC frameworks. Focusing on the machine learning aspects of the proposed algorithm, we evaluate its computational performance and discuss its energy efficiency in comparison with a state-of-the-art convolutional neural network (CNN) model implemented in software on a high-performance workstation computer.
RTDs are chosen as the core element of the reservoir layer due to their inherent nonlinear dynamics and ultrafast temporal response. Their characteristic negative differential resistance (NDR), arising from quantum tunnelling through a double-barrier quantum well, enables the generation of excitable, multistable, and oscillatory behaviours at low voltages and high frequencies. Such dynamics is particularly well-suited for reservoir computing and adjacent concepts, as a single RTD can produce rich, high-dimensional temporal patterns that effectively map input signals into a nonlinear feature space [,]. Relative to other nonlinear electronic components, RTDs offer a combination of strong nonlinearity, compactness, and high-speed operation, along with a high peak-to-valley current ratio and reliable dynamical behaviour. This makes them ideal for constructing efficient, scalable, and tunable physical reservoirs capable of complex temporal processing without requiring large networks of conventional active elements.
Specifically, we explore the image recognition performance of a physical RC architecture, where an array of parallel RTDs exhibits nonlinear current–voltage () behaviour (Figure 1). This nonlinear response naturally induces the rich spatiotemporal dynamics required for high-dimensional input projection []. The system operates in a purely feedforward configuration (Figure 2), using the inherent characteristics of the diodes to perform dynamic state mapping, thus enabling efficient analogue computation without recurrent feedback or complex signal preprocessing. We also highlight that the RC architecture developed in this paper serves as a hardware counterpart to the next-generation RC algorithm [], eliminating the need for random matrices and the computationally expensive operations associated with them in traditional RC models []. The computational performance of the proposed RTD-based RC system improves as we controllably increase the nonlinearity of the response of individual RTDs.
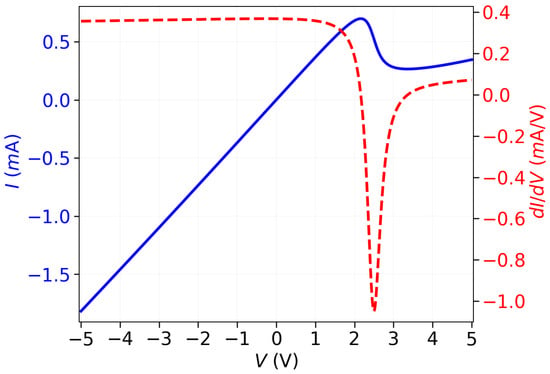
Figure 1.
characteristic (the blue curve) and NDR (the red dashed curve) of the model RTD employed in this study.
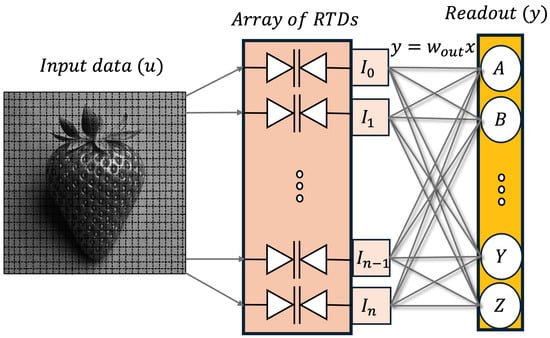
Figure 2.
Schematic illustration of the proposed RTD-based RC architecture. An array of RTDs serves as a computational reservoir that facilitates, by virtue of the nonlinear characteristics of the diodes, the transformation of low-dimensional input signals into high-dimensional representations. The reservoir output (the currents , , produced by each diode) is processed using a linear readout mechanism.
2. Resonant-Tunnelling Diode as a Computational Reservoir
A tunnel (Esaki) diode is a type of heavily doped junction semiconductor device whose characteristic exhibits a region of negative differential resistance (NDR) due to quantum mechanical tunnelling [,]. While resonant-tunnelling diodes (RTDs) differ in structure—instead of using a heavily doped junction they typically involve quantum well structures with double barriers—they share key physical principles with Esaki diodes, most notably quantum tunnelling and the resulting nonlinear transport phenomena [,,,]. Therefore, while this study employs a theoretical model developed specifically for RTDs [,], the underlying discussion is, in principle, applicable to other classes of quantum electron devices that explore the effect of quantum tunnelling. Indeed, what is important for the mainstream discussion in this present work is the fact that a voltage-dependent tunnelling behaviour of the diode gives rise to highly nonlinear responses, where the diode’s resistance varies dynamically with the applied signal [].
It is also instructive to comment on the suitability of RTDs as elements of an RC system. While the algorithmic RC architecture and its modifications are well established and understood [], the debate over the suitability of different physical systems for RC purposes remains ongoing, primarily because virtually any nonlinear dynamical physical system can, in principle, serve as a reservoir, although not all such systems yield efficient computational performance [,,].
Apart from their suitability for broader applications in neuromorphic computing [,,], RTDs (more specifically, their characteristics) can, in principle, mathematically substitute standard activation functions, potentially yielding improved overall model performance [,]. (The same holds true for the quantum tunnelling effect model, which is relevant to the operation of an RTD []). However, in the computational scheme proposed in this work, RTDs substitute the computationally demanding, nonlinear signal processing component of the reservoir computing algorithm with the physical—albeit numerically simulated in this study—response of RTDs (a hardware implementation of an array of RTDs is technologically viable [,]). As a result, the RTD-based RC system promises to be more energy-efficient while delivering robust computational performance, thereby fulfilling one of the main goals of physical reservoir computing [,,,].
The I − V characteristic of an RTD can be approximated by the expression []
where the individual components are defined as
The parameters are given by , , and , where q denotes the electron charge, is Boltzmann’s constant, T is the temperature, V is the voltage, and a, b, c, d, , and are system-specific parameters. In this study, we adopt the values K, A, V, V, V, , , and A [].
We note that the coefficients in Equation (1) are fitting parameters of the model, which can be associated with specific physical quantities relevant to semiconductor physics []. As discussed in the cited paper, Equation (1) most accurately reproduces the correct lineshape of the characteristics of typical RTD devices. This accuracy is achieved by allowing the fitting parameters to vary beyond values with strict physical meaning. Alternative models of the large-signal dynamics of RTDs also exist [] and may be employed in place of Equation (1) when analysing more specialised RTD devices.
The characteristic of the RTD calculated using Equation (1) has three distinct regions: two segments where the differential resistance is positive, separated by a central region exhibiting NDR (approximately within the interval in Figure 1). The term in Equation (1) governs the low-voltage behaviour, producing both the initial positive differential resistance and the NDR region. However, this term does not capture the resurgence of current at higher voltages. In turn, the term , dominant at elevated voltages, accounts for this second region of positive differential resistance [].
3. Reservoir Computing Model
Figure 2 presents a schematic diagram of the proposed RC system architecture. At its core, the nonlinear characteristic of RTDs is exploited as the primary nonlinear element. A parallel array of RTDs constitutes the reservoir layer, with each diode contributing to the nonlinear transformation of the input signals, as explained below.
The RTD-based RC system processes grayscale images by converting them into electric voltage signals. To this end, each input image is first transformed into a binary format and then normalised to align with the diode’s operating voltage range, . It is worth noting that, from the perspective of neural network algorithms, the operating voltage range from −5 V to 0 is treated analogously to the response of the standard ReLU activation function and its variants []. For positive inputs, the ReLU output depends linearly on the input, while for strictly negative inputs, the output is zero. When Equation (1) is used as an activation function, it provides computationally equivalent functionality, with the key distinction being that the nonlinearity arises from the specific physical mechanisms governing the operation of the RTD.
The image processing procedure used by us is conducted row-wise: each horizontal row of pixels in the image is encoded into a sequence of voltage pulses applied to a corresponding RTD in the array. Thus, for an image of size pixels, the reservoir comprises n RTDs, each receiving a pulse train of length m that represents the pixel intensities of its row. For example, with standard MNIST images of pixels, the system utilises 28 diodes, each driven by a 28-element voltage pulse sequence. The values , , of the output current produced by each diode are treated as the dynamic reservoir states [], which form a high-dimensional embedding of the input and used to train a linear readout (Figure 2).
Furthermore, each image is associated with a one-hot encoded label vector, where the elements corresponding to the true class is set to 1 and all others to 0. For example, the digit ‘1’ in the MNIST dataset and the fruit ‘Apricot’ in the Fruit-360 dataset both correspond to class index 1 and are encoded as .
The image recognition procedure begins with the aforementioned pixel-to-voltage encoding, followed by the application of these voltage sequences to the RTD array. For each input image, the dynamic responses from the diodes are assembled into a reservoir state matrix , where k is the number of samples and j is the dimensionality of the reservoir output. The corresponding label vectors form the output matrix , where s is the number of classes.
As the next step, the output weights are computed by applying ridge regression to minimise the mean squared error between predicted and target outputs as []
where is the regularisation parameter and is the identity matrix.
As a part of the testing procedure, the reservoir states for unseen inputs, , are processed through the trained readout layer as
The classification is done by selecting the index corresponding to the maximum value in the predicted output vector .
The proposed RTD-based RC architecture is advantageous compared with the traditional RC algorithm []. For example, it eliminates the need for mask matrices, delay lines, virtual nodes and feedback terms that are often present in standard RC system implementations []. The only tuning required by the RTD-based RC system is the proper configuration of the pixel-to-voltage mapping function, aim to ensure that sufficient nonlinearity is present in the system’s response.
4. Results and Discussion
To theoretically evaluate the performance of the RTD-based RC system, the equations of the RTD model and the equations of the RC model presented above were implemented as a software package in Python 3. The resulting software was tested on two benchmark image recognition datasets: the standard MNIST and Fruit-360 []. The well-known MNIST dataset contains 60,000 grayscale images of handwritten digits from 0 to 9, each ones sized pixels. The Fruit-360 dataset includes 10,000 grayscale images representing 15 fruit classes, resized to pixels. Both datasets were split into 70% training and 30% testing subsets.
All numerical experiments were conducted using a 64-bit workstation computer powered by an Apple M3 Max CPU and equipped with 128 GB of unified memory. The input images were shuffled prior to training and testing to ensure unbiased results. The voltage mapping range applied to the RTD array was optimised and set to V.
Furthermore, the performance of the RTD system was evaluated using a k-fold cross-validation approach (). The dataset was randomly partitioned into k subsets; in each iteration, one subset was used for testing while the remaining subsets were used for training. The reported accuracy represents the mean performance across all folds, ensuring a statistically robust evaluation of model generalisation.
Figure 3a shows the training accuracy and training loss as functions of the number of epochs for the RTD reservoir trained on the MNIST dataset. The model is observed to converge after 30 epochs, achieving an accuracy of 92.5% and a loss of 0.26, indicating effective learning. Figure 3b shows the confusion matrix—which illustrates the distribution of predicted versus actual classifications and highlights the performance of the model across individual digit classes—where the majority of samples are correctly classified, particularly for digits ‘1’, ‘0’ and ‘7’. We can observe that misclassifications are minimal and primarily occur between visually similar digits, such as ‘4’ and ‘9’, suggesting the potential benefit of more sophisticated feature extraction or improved temporal encoding (see, e.g., Refs. [,] for further relevant discussion).
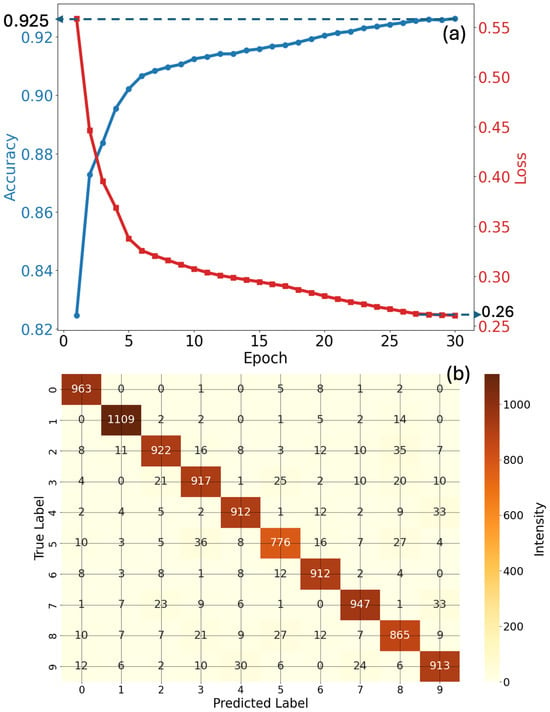
Figure 3.
Evaluation of the RTD-based RC system trained on the MNIST dataset: (a) training performance over epochs showing accuracy and loss, and (b) confusion matrix illustrating classification accuracy across digit classes.
Figure 4 summarises the performance of the RTD-based RC system on the Fruit-360 dataset, which contains visually distinct classes of fruits. The RC system achieves a final accuracy of 99.1% after 30 training epochs. As shown in Figure 4a, the accuracy increases rapidly while the loss declines consistently to a final value of approximately 0.046, indicating fast convergence and minimal overfitting [].
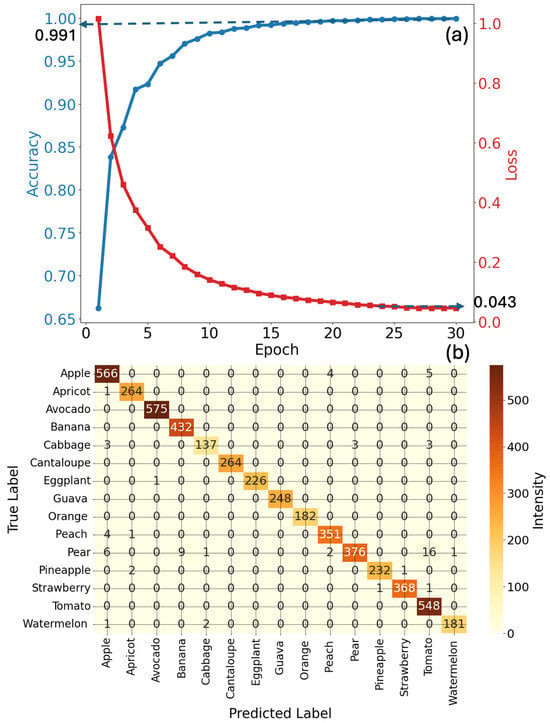
Figure 4.
Evaluation of the RTD-based RC system trained on the Fruit-360 dataset: (a) training performance (accuracy and loss) over epochs, and (b) confusion matrix showing classification accuracy across fruit classes.
The confusion matrix in Figure 4b shows near-perfect classification across all 15 fruit categories. Notably, the classes ‘Apple’, ‘Avocado’ and ‘Strawberry’ exhibit perfect or near-perfect accuracy, showcasing the strong discriminative ability of the model in classifying natural images with high inter-class variability.
The superior performance of the RC system on the Fruit-360 dataset compared to the MNIST handwritten digits dataset can be attributed to the greater size, complexity and variability of the images in the Fruit-360 dataset. Indeed, Fruit-360 comprises thousands of images spanning a diverse set of fruit classes, each with unique textures and shapes. This richness in visual features enables the RC system to exploit its computational ability more effectively. In contrast, MNIST contain a large number of images of only ten digit classes, with comparatively low intra-class variability and limited feature complexity. As a result, the ability of the RC system to do nonlinear transformations and temporal encoding may be underutilised on MNIST.
As a next step, to evaluate the impact of the nonlinearity of the response of RTDs on the training dynamics of the RC system, numerical experiments were conducted using a small subset of the Fruit-360 dataset by setting different voltage limits ranging from 0.5 V to 5 V. Figure 5 illustrates how varying influences the training accuracy. The results clearly show that a higher leads to better accuracy. In particular, using lower values of (e.g., 0.5 V) restricts the input voltage range, resulting in the reservoir operating mostly within the linear region of the characteristic. This limits the dynamic transformation capability of the reservoir and, therefore, yields poorer accuracy of approximately 80% (an explanation of the operation of a reservoir using a linear activation function can be found in Ref. []). However, as increases to 4–5 V, the reservoir accesses a richer nonlinear operating regime, enabling more expressive mappings and more effective temporal feature encoding [,]. As shown in Figure 5, this significantly enhances performance, with final accuracies approaching or exceeding 95%, which further confirms the critical role of nonlinearity in the reservoir’s computational power.
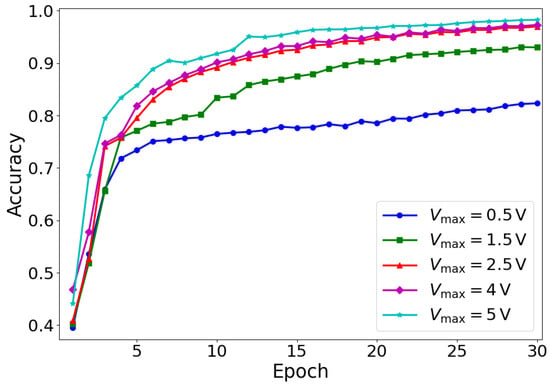
Figure 5.
Training accuracy as a function of epochs for increasing values of . Raising results in an increase in the strength of nonlinearity, thereby improving classification accuracy.
5. Connection to the Next-Generation Reservoir Computing Framework
The observed increase in accuracy with increasing can be understood in light of the following comparison between the operation of the RTD-based RC and the principles underlying the next-generation RC framework [] discussed in at the beginning of this paper.
Recall that a traditional algorithmic RC system [,] uses a reservoir composed of randomly connected nodes. In Ref. [], an alternative RC algorithm was introduced in which the state matrix of the traditional RC system is replaced by a matrix , composed of future states corresponding to the current and time-delayed discrete input data points and their nonlinear functionals. This newly constructed state matrix is then used to calculate , thereby avoiding certain computationally intensive steps associated with traditional RC systems.
Furthermore, based on the results presented in Ref. [], it has been demonstrated that this computational scheme not only circumvents the use of randomly generated neural connection matrices but is also equivalent to, and in some cases more efficient than, the traditional RC algorithm. This approach is called next-generation reservoir computing [,].
The nonlinear component of the future states can be defined as an arbitrary nonlinear function of the input signal. In Ref. [], accurate forecasts were achieved using polynomial functions, with the key insight that only a few low-order polynomial terms were sufficient to obtain reliable results. A similar finding was reported in Ref. [] within the context of quantum RC systems, where the authors applied a nonlinear transformation to the input data and demonstrated that subsequent processing steps typical of traditional RC algorithms were no longer necessary.
The nonlinear transformation of the input data implemented in the RTD-based RC system proposed in this work can be illustrated by applying a sinusoidal wave to one of the diodes in the RTD array shown in Figure 2. (Such an approach was approbated in the previous works Refs. [,]. The choice of the frequency of the sinusoidal wave is immaterial in this scenario; however, it is well established that typical RTDs operate at frequencies of several hundred gigahertz, i.e., the results obtained with our model are expected to remain valid at much higher frequencies). We then compute the Fourier spectra of both input sinusoidal wave and output signal produced the diode, and present them in Figure 6.
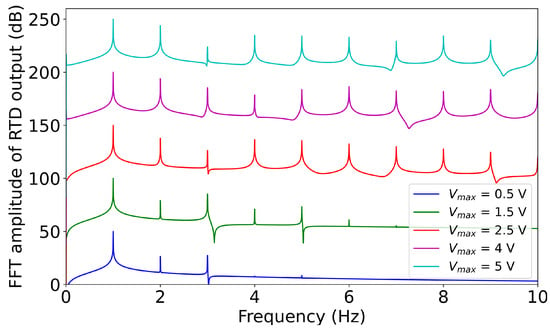
Figure 6.
Fourier transform spectra of the outputs of the RTD excited by a test input sinusoidal signal. Compared with the single-frequency spectrum of the input sinusoidal signal, the RTD output is enriched by higher-order harmonics generated through nonlinear processes. The number of harmonics, and thus the strength of the nonlinear response, increases with the amplitude of the input signal, as controlled by . For illustration, each spectrum is vertically shifted by 50 dB.
The spectrum of the RTD output reveals not only the fundamental frequency peak at 1 Hz but also additional peaks corresponding to the second, third, fourth and so on higher-order harmonics. We can see that the number of harmonics increases as the control voltage amplitude is increased. In contrast, the spectrum of the input sinusoidal wave contains only a single peak at 1 Hz. This result demonstrates that the RTD effectively performs a nonlinear transformation of the input, effectively representing it as a polynomial-like function and thereby enriching the reservoir’s feature space in a next generation RC system fashion.
This result helps explain the differences between the accuracy-vs-epochs curves shown in Figure 5. The most pronounced increase in accuracy is observed when increases from 0.5 V to 1.5 V. Spectral analysis reveals that this change results in the emergence of significant fourth and fifth nonlinear harmonics in the output spectrum in Figure 6. (The colour markings of the lines in Figure 5 and Figure 6 are consistent, allowing for a direct comparison between the classification accuracy trends and the spectral content of the RTD outputs at corresponding values of ). A similar trend occurs when reaches 2.5 V, where the fourth, fifth and sixth harmonics become prominent and comparable in amplitude to the second and third harmonics.
This observation highlights the advantage of retaining multiple nonlinear terms in the next generation RC framework. However, while retaining additional nonlinear terms beyond quadratic and cubic typically incurs increased computational cost in algorithmic implementations of the next-generation scheme, the RTD-based approach allows up to ten nonlinear terms to be retained simply by increasing , with only a modest rise in the system’s overall energy consumption.
6. Temperature Dependence of the Model Accuracy
We examined how temperature variations affect the performance of an RTD-based reservoir in image recognition tasks, using the Fruit-360 dataset for evaluation. The analysis was conducted with a fixed maximum bias voltage of V and a temperature range of 250–400 K. It is worth noting that the upper limit of the temperature range considered in this analysis exceeds the typical operational temperature of electronic devices incorporating RTDs [,]. Nevertheless, a broader range was deliberately examined to enable a more comprehensive investigation of the temperature dependence.
Figure 7a shows the evolution of recognition accuracy over 30 training epochs for different temperatures. While the accuracy converges rapidly in all cases, small differences can be observed between curves corresponding to different temperatures, reflecting subtle temperature-induced variations in the reservoir states.
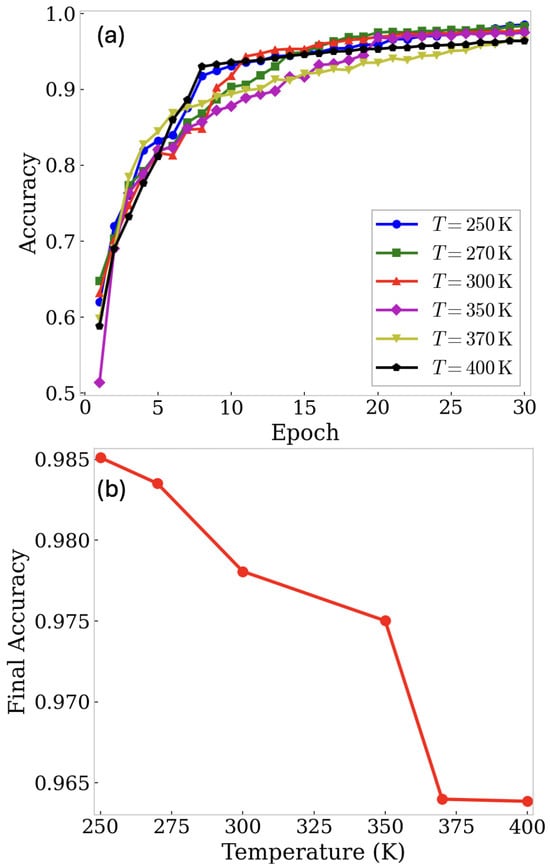
Figure 7.
(a) Recognition accuracy versus training epochs for different temperatures (250 K to 400 K). Accuracy converges rapidly in all cases, with only minor variations due to temperature-induced changes in the reservoir states. (b) Final recognition accuracy as a function of temperature. Accuracy decreases slightly from 0.985 at 250 K to 0.965 at 400 K, corresponding to a modest reduction of approximately 2%, highlighting the robustness of the RTD-based reservoir to moderate thermal variations.
Figure 7b presents the final accuracy as a function of temperature. The results indicate a modest decline from 0.985 at the lowest temperature to 0.965 at the highest, corresponding to a decrease of approximately 2%. This small reduction is consistent with the fact that temperature primarily affects the amplitude of the tunnelling current rather than the shape of the NDR region. Consequently, the nonlinear dynamics necessary for effective reservoir computing are largely preserved, resulting in only minor performance degradation.
Despite the limited impact observed, even small thermal fluctuations can influence the reproducibility of device states. Therefore, temperature stabilisation remains important in practical applications. Implementing thermal management and bias compensation strategies can further enhance robustness, ensuring consistent and reliable performance of TD-based reservoirs under varying environmental conditions.
7. Energy Consumption Analysis
In this section, we estimate the energy consumption of a potential hardware prototype of the proposed RTD-based system. Following prior work in this area [], we compare its performance against a state-of-the-art convolutional neural network (CNN) implemented in Python 3.1 using the PyTorch 2.7 machine learning library. The network consisted of a conventional sequence of convolutional, nonlinear activation, pooling and fully connected layers [], as is standard in contemporary classification algorithms. The model was trained on the benchmark datasets used in the previous sections. The training used mini-batch optimisation and cross-entropy loss, and inference followed the standard feed-forward evaluation to produce class probabilities.
The benchmark computer used to run the CNN model is a Mac Studio M2 Ultra workstation with a 20-core CPU. When idle, this system consumes approximately 10 W of electric power, increasing to over 200 W under maximum computational load []. Using custom software that implements the CNN model, we estimated the workstation’s energy consumption based on processor type and workload intensity. Upon initialisation, the software employs Python’s os library to query the system for CPU specifications and retrieves the predefined power consumption profiles for idle and fully active states []. The algorithm then estimates the average power draw by interpolating between these two operating points according to a parameter that represents the computational workload.
To estimate the electrical power consumption of the RTD-based system, we consider an array of 100 RTDs for simplicity and assume that each RTD element draws approximately 1.0 mW of power [,]. Thus, the total electrical power consumption of the array is about 0.1 W, which we take as a lower realistic bound. Yet, to account for potential inefficiencies in the design of the RTD circuit, we also consider 1.0 W as an exaggerated upper bound. Assuming typical inference durations in the range of 10 ms to 10 s, the estimated energy per run lies between 1 mJ and 10 J.
The complete RTD-based prototype may also includes supporting electronics such as analog-to-digital (ADC) and digital-to-analog (DAC) converters, amplifiers and control units. Although these components are only tentatively identified as important and included in our preliminary circuit design, we assume that the supporting electronics consume approximately 10 times more energy than the RTD core itself, as is typical for early-stage hardware implementations. Greater integration, for example through FPGA- or microcontroller-based system-on-chip designs, is expected to significantly reduce overall power consumption in future design iterations.
Thus, using an electricity cost of 0.30 USD per kWh (i.e., approximately USD/J), for the complete RTD-based prototype estimated computation cost per run will range from about USD to USD . These values were obtained using the total energy per run figure-of-merit, including the energy consumed by the supporting electronics, as per the top two rows of Table 1.

Table 1.
Comparison of a 100-element RTD-based system and a CNN model for Fruit-360 dataset detection (per single inference/run).
As shown in Table 1, a single run of the CNN model consumes approximately 5 J of energy, compared with about 110 J for the RTD-based system. However, the 110 J value represents an absolute upper-bound estimate, with most of the energy attributed to the supporting electronics rather than the RTD core itself, as indicated in the second row of the table. This value can be reduced by considering our realistic lower-bound energy consumption estimate and through the use of more advanced supporting electronic modules.
In contrast, the energy consumption of the CNN model is determined by the total power drawn by the workstation computer and cannot be significantly reduced without hardware modification. Moreover, even after a CNN computation is completed, the workstation continues to consume considerable power because the operating system and background software processes required to access the model and its associated data remain active. Owing to the complexity of this situation, this continuous background power consumption is not included in our analysis.
The cost of a single CNN inference is approximately USD 4.17 × 10−7, about 20 times higher than the upper-bound cost of the RTD-based system. Nevertheless, our calculations indicate that this cost could be reduced by up to four orders of magnitude if the supporting electronics was implemented on an advanced integrated circuit.
Finally, we estimate that the CNN model exhibits ‘very high’ repeatability of output results, whereas the RTD-based system is expected to demonstrate ‘high’ repeatability. In fact, while the CNN model is implemented as software that produces highly consistent results, minor temperature drift may affect computational stability of the RTD-based system, indicating that additional temperature stabilisation measures could be required.
Thus, while it may be argued that a state-of-the-art CNN system can achieve high-accuracy results in a conventional manner, the RTD-based system offers distinct advantages. It is potentially less expensive and more energy efficient, and can be directly implemented in autonomous platforms such as airborne drones []. Even if the cost of a workstation is modest, its substantial power consumption and weight make it unsuitable for onboard deployment in drones designed for extended flight durations. In contrast, the RTD-based system provides a promising solution to this limitation.
8. Conclusions
In this work, we have explored the potential of resonant-tunnelling diodes as nonlinear physical elements for reservoir computing applications. We have demonstrated that the characteristic nonlinearity of the diodes can effectively substitute conventional reservoir computing algorithms relying on traditional machine learning activation functions, thereby enabling efficient and robust classification of MNIST and Fruit-360 image datasets. Through numerical experiments, we have shown that resonant-tunnelling diode-based reservoirs can achieve high classification accuracy on these benchmark datasets, with performance strongly influenced by the degree of nonlinearity and dynamic range of the diode response.
We have also suggested the technological viability of hardware implementations involving arrays of resonant-tunnelling diodes, indicating their low power consumption, high-speed operation and compatibility with existing semiconductor technologies. Hence, we argue that resonant-tunnelling diodes offer a promising physical substrate for energy- and computationally efficient reservoir computing systems, especially in scenarios where compact, high-throughput and low-latency computation is desired.
Future work will focus on experimental realisation of resonant-tunnelling diode-based reservoir systems, integration with temporal encoding schemes and exploration of hybrid architectures involving quantum tunnelling effects and emerging device platforms such as spiking-neuron integrated circuits [].
Author Contributions
Conceptualisation, writing, editing, and discussion: A.H.A., H.A.-G. and I.S.M.; methodology, software, and validation: A.H.A. All authors discussed the presentation of the results, reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated and presented by us are included within the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | convolutional neural network |
| CPU | central processing unit |
| MNIST | Modified National Institute of Standards and Technology database |
| NDR | negative differential resistance |
| NMSE | normalized mean squared error |
| NVAR | nonlinear vector auto-regression |
| RC | reservoir computing |
| RTD | resonant-tunnelling diode |
| ReLU | rectified linear unit |
References
- Krenn, M.; Pollice, R.; Guo, S.Y.; Aldeghi, M.; Cervera-Lierta, A.; Friederich, P.; dos Passos Gomes, G.; Häse, F.; Jinich, A.; Nigam, A.; et al. On scientific understanding with artificial intelligence. Nat. Rev. Phys. 2022, 4, 761–769. [Google Scholar] [CrossRef] [PubMed]
- Najjar, R. Redefining Radiology: A Review of Artificial Intelligence Integration in Medical Imaging. Diagnostics 2023, 13, 2760. [Google Scholar] [CrossRef] [PubMed]
- Alcántara Suárez, E.J.; Monzon Baeza, V. Evaluating the role of machine learning in defense applications and industry. Mach. Learn. Knowl. Extr. 2023, 5, 1557–1569. [Google Scholar] [CrossRef]
- Dhanush, G.; Khatri, N.; Kumar, S.; Shukla, P.K. A comprehensive review of machine vision systems and artificial intelligence algorithms for the detection and harvesting of agricultural produce. Sci. Afr. 2023, 21, e01798. [Google Scholar] [CrossRef]
- Zhang, L.; Jia, X.; Chang, Q.; Liu, X.; Zhang, Z.; Cao, Y.; Liu, J.; Yang, Y. The development of machine vision and its applications in different industries: A review. Mechan. Eng. Adv. 2024, 2, 1746. [Google Scholar] [CrossRef]
- Qiu, C.; Tang, H.; Yang, Y.; Wan, X.; Xu, X.; Lin, S.; Lin, Z.; Meng, M.; Zha, C. Machine vision-based autonomous road hazard avoidance system for self-driving vehicles. Sci. Rep. 2024, 14, 12178. [Google Scholar] [CrossRef]
- Rolf, E.; Proctor, J.; Carleton, T.; Bolliger, I.; Shankar, V.; Ishihara, M.; Recht, B.; Hsiang, S. A generalizable and accessible approach to machine learning with global satellite imagery. Nat. Commun. 2021, 12, 4392. [Google Scholar] [CrossRef]
- Tcho, I.W.; Kim, W.G.; Choi, Y.K. A self-powered character recognition device based on a triboelectric nanogenerator. Nano Energy 2020, 70, 104534. [Google Scholar] [CrossRef]
- Katkuri, A.V.R.; Madan, H.; Khatri, N.; Abdul-Qawy, A.S.H.; Patnaik, K.S. Autonomous UAV navigation using deep learning-based computer vision frameworks: A systematic literature review. Array 2024, 23, 100361. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, R.; Zhang, Y.; Feroskhan, M. Vision-based learning for drones: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 15601–15621. [Google Scholar] [CrossRef] [PubMed]
- Graf, H.P.; Jackel, L.D. Analog electronic neural network circuits. IEEE Circuits Devices Mag. 1989, 5, 44–49. [Google Scholar] [CrossRef]
- Yang, L.; Zeng, Z.; Shi, X. A memristor-based neural network circuit with synchronous weight adjustment. Neurocomputing 2019, 363, 114–124. [Google Scholar] [CrossRef]
- Fu, T.; Zhang, J.; Sun, R.; Huang, Y.; Xu, W.; Yang, S.; Zhu, Z.; Chen, H. Optical neural networks: Progress and challenges. Light Sci. Appl. 2024, 13, 263. [Google Scholar] [CrossRef]
- Akter, S.; Haider, M.R. mTanh: A low-cost inkjet-printed vanishing gradient tolerant activation function. J. Low Power Electron. 2025, 15, 27. [Google Scholar] [CrossRef]
- Schuman, C.D.; Kulkarni, S.R.; Parsa, M.; Mitchell, J.P.; Date, P.; Kay, B. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2022, 2, 10–19. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, B.; Tang, J.; Yao, P.; Yu, S.; Chang, M.F.; Yoo, H.J.; Qian, H.; Wu, H. Neuro-inspired computing chips. Nat. Electron. 2020, 3, 371–382. [Google Scholar] [CrossRef]
- Kudithipudi, D.; Schuman, C.; Vineyard, C.M.; Pandit, T.; Merkel, C.; Kubendran, R.; Aimone, J.B.; Orchard, G.; Mayr, C.; Benosman, R.; et al. Neuromorphic computing at scale. Nature 2025, 637, 801–812. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, G.; Yamane, T.; Héroux, J.B.; Nakane, R.; Kanazawa, N.; Takeda, S.; Numata, H.; Nakano, D.; Hirose, A. Recent advances in physical reservoir computing: A review. Neural Newt. 2019, 115, 100–123. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K. Physical reservoir computing–an introductory perspective. Jpn. J. Appl. Phys. 2020, 59, 060501. [Google Scholar] [CrossRef]
- Maksymov, I.S. Analogue and physical reservoir computing using water waves: Applications in power engineering and beyond. Energies 2023, 16, 5366. [Google Scholar] [CrossRef]
- Abbas, A.H.; Maksymov, I.S. Reservoir computing using measurement-controlled quantum dynamics. Electronics 2024, 13, 1164. [Google Scholar] [CrossRef]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Gauthier, D.J.; Bollt, E.; Griffith, A.; Barbosa, W.A.S. Next generation reservoir computing. Nat. Commun. 2021, 12, 5564. [Google Scholar] [CrossRef]
- Bollt, E. On explaining the surprising success of reservoir computing forecaster of chaos? The universal machine learning dynamical system with contrast to VAR and DMD. Chaos 2021, 31, 013108. [Google Scholar] [CrossRef]
- Liang, X.; Tang, J.; Zhong, Y.; Gao, B.; Qian, H.; Wu, H. Physical reservoir computing with emerging electronics. Nat. Electron. 2024, 7, 193–206. [Google Scholar] [CrossRef]
- Abbas, A.H.; Abdel-Ghani, H.; Maksymov, I.S. Edge-of-Chaos and Chaotic Dynamics in Resistor-Inductor-Diode-Based Reservoir Computing. IEEE Access 2025, 13, 18191–18199. [Google Scholar] [CrossRef]
- Chembo, Y.K. Machine learning based on reservoir computing with time-delayed optoelectronic and photonic systems. Chaos 2020, 30, 013111. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.H.; Abdel-Ghani, H.; Maksymov, I.S. Classical and quantum physical reservoir computing for onboard artificial intelligence systems: A perspective. Dynamics 2024, 4, 643–670. [Google Scholar] [CrossRef]
- Yan, M.; Huang, C.; Bienstman, P.; Tino, P.; Lin, W.; Sun, J. Emerging opportunities and challenges for the future of reservoir computing. Nat. Commun. 2024, 15, 2056. [Google Scholar] [CrossRef]
- Gardner, S.D.; Haider, M.R. An inkjet-printed artificial neuron for physical reservoir computing. IEEE J. Flex. Electron. 2022, 1, 185–193. [Google Scholar] [CrossRef]
- Ortega-Piwonka, I.; Piro, O.; Figueiredo, J.; Romeira, B.; Javaloyes, J. Bursting and excitability in neuromorphic resonant tunneling diodes. Phys. Rev. Appl. 2021, 15, 034017. [Google Scholar] [CrossRef]
- Ortega-Piwonka, I.; Teruel, A.E.; Prohens, R.; Vich, C.; Javaloyes, J. Simplified description of dynamics in neuromorphic resonant tunneling diodes. Chaos 2021, 31, 113128. [Google Scholar] [CrossRef]
- Romeira, B.; Adão, R.; Nieder, J.B.; Al-Taai, Q.; Zhang, W.; Hadfield, R.H.; Wasige, E.; Hejda, M.; Hurtado, A.; Malysheva, E.; et al. Brain-inspired nanophotonic spike computing: Challenges and prospects. Neuromorph. Comput. Eng. 2023, 3, 033001. [Google Scholar] [CrossRef]
- Sattari-Esfahlan, S.M.; Ilatikhameneh, H.; Fouladi-Oskouei, J. Fermi velocity modulation induced low-bias negative differential resistance in graphene double barrier resonant tunneling diode. Ann. Phys. 2021, 533, 2100121. [Google Scholar] [CrossRef]
- Bisquert, J.; Fenollosa, R.; Cordero, A.; Torregrosa, J.R. Bifurcation and frequency properties of s-type neuronic oscillators. J. Phys. Chem. Lett. 2025, 16, 3616–3631. [Google Scholar] [CrossRef]
- Esaki, L. New phenomenon in narrow germanium p − n junctions. Phys. Rev. 1958, 109, 603–604. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chang, L.L.; Esaki, L.; Tsu, R. Resonant tunneling in semiconductor double barriers. Appl. Phys. Lett. 1974, 12, 593–595. [Google Scholar] [CrossRef]
- Sun, J.P.; Haddad, G.; Mazumder, P.; Schulman, J.N. Resonant tunneling diodes: Models and properties. Proc. IEEE 1998, 86, 641–660. [Google Scholar] [CrossRef]
- Jin, Y. Tunnel Field-Effect Transistor and Applications. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2008. [Google Scholar]
- Stepney, S. Physical reservoir computing: A tutorial. Nat. Comput. 2024, 23, 665–685. [Google Scholar] [CrossRef]
- te Vrugt, M. An introduction to reservoir computing. arXiv 2024, arXiv:2412.13212. [Google Scholar] [CrossRef]
- Nakajima, M.; Zhang, Y.; Inoue, K.; Kuniyoshi, Y.; Hashimoto, T.; Nakajima, K. Reservoir direct feedback alignment: Deep learning by physical dynamics. Commun. Phys. 2024, 7, 411. [Google Scholar] [CrossRef]
- McNaughton, J.; Abbas, A.H.; Maksymov, I.S. Neuromorphic Quantum Neural Networks with Tunnel-Diode Activation Functions. arXiv 2025, arXiv:2503.04978. [Google Scholar] [CrossRef]
- Abbas, A.H. TunnElQNN: A Hybrid Quantum-classical Neural Network for Efficient Learning. arXiv 2025, arXiv:2505.00933. [Google Scholar] [CrossRef]
- Maksimovic, M.; Maksymov, I.S. Transforming neural networks into quantum-cognitive models: A research tutorial with novel applications. Technologies 2025, 13, 183. [Google Scholar] [CrossRef]
- Kempisty, J.J.; Hirschman, K.D.; Kurinec, S.K.; Jin, N.; Chung, S.Y.; Berger, P.R.; Thompson, P.E. Integration of silicon-based tunnel diodes with CMOS: An RIT-OSU-NRL-NSF effort. In Proceedings of the Fourteenth Biennial University/Government/Industry Microelectronics Symposium (Cat. No.01CH37197), Richmond, VA, USA, 20–22 June 2001; pp. 74–77. [Google Scholar] [CrossRef]
- Schulman, J.N.; De Los Santos, H.J.; Chow, D.H. Physics-based RTD current-voltage equation. IEEE Electron Device Lett. 1996, 17, 220–222. [Google Scholar] [CrossRef]
- Ourednik, P.; Picco, G.; Tuan Nguyen, D.; Spudat, C.; Feiginov, M. Large-signal dynamics of resonant-tunneling diodes. J. Appl. Phys. 2023, 133, 014501. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Muresan, H.; Oltean, M. Fruit recognition from images using deep learning. Acta Univ. Sapientiae Inform. 2018, 10, 26–42. [Google Scholar] [CrossRef]
- Maksimovic, M.; Maksymov, I.S. Quantum-cognitive neural networks: Assessing confidence and uncertainty with human decision-making simulations. Big Data Cogn. Comput. 2025, 9, 12. [Google Scholar] [CrossRef]
- Aliferis, C.; Simon, G. Overfitting, Underfitting and General Model Overconfidence and Under-Performance Pitfalls and Best Practices in Machine Learning and AI. In Artificial Intelligence and Machine Learning in Health Care and Medical Sciences: Best Practices and Pitfalls; Simon, G.J., Aliferis, C., Eds.; Springer International Publishing: Cham, Switzerland, 2024; pp. 477–524. [Google Scholar] [CrossRef]
- Jaeger, H. Short Term Memory in Echo State Networks; GMD Report 152; German National Research Center for Information Technology: St. Augustin, Germany, 2001. [Google Scholar]
- Wang, H.; Hu, J.; Baek, Y.; Tsuchiyama, K.; Joly, M.; Liu, Q.; Gigan, S. Optical next generation reservoir computing with complex media. In Proceedings of the AI and Optical Data Sciences VI; Notomi, M., Zhou, T., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2025; Volume 13375, p. 1337508. [Google Scholar] [CrossRef]
- Govia, L.C.G.; Ribeill, G.J.; Rowlands, G.E.; Ohki, T.A. Nonlinear input transformations are ubiquitous in quantum reservoir computing. Neuromorph. Comput. Eng. 2022, 2, 014008. [Google Scholar] [CrossRef]
- Trouvain, N.; Pedrelli, L.; Dinh, T.T.; Hinaut, X. ReservoirPy: An Efficient and User-Friendly Library to Design Echo State Networks. In Proceedings of the ICANN 2020—29th International Conference on Artificial Neural Networks, Bratislava, Slovakia, 15 September 2020. [Google Scholar]
- Maksymov, I.S. Physical reservoir computing enabled by solitary waves and biologically inspired nonlinear transformation of input data. Dynamics 2024, 4, 119–134. [Google Scholar] [CrossRef]
- Bar-Joseph, I.; Gedalyahu, Y.; Yacoby, A.; Woodward, T.K.; Chemla, D.S.; Sivco, D.L.; Cho, A.Y. Temperature dependence of the resonant-tunneling process in a double-barrier diode. Phys. Rev. B 1991, 44, 8361–8364. [Google Scholar] [CrossRef] [PubMed]
- Pfenning, A.; Hartmann, F.; Rebello Sousa Dias, M.; Castelano, L.K.; Süßmeier, C.; Langer, F.; Höfling, S.; Kamp, M.; Marques, G.E.; Worschech, L.; et al. Nanothermometer Based on Resonant Tunneling Diodes: From Cryogenic to Room Temperatures. ACS Nano 2015, 9, 6271–6277. [Google Scholar] [CrossRef]
- Abdel-Ghani, H.; Abbas, A.H.; Maksymov, I.S. Reservoir computing with a single oscillating gas bubble: Emphasizing the chaotic regime. AppliedMath 2025, 5, 101. [Google Scholar] [CrossRef]
- Apple Inc. Mac Mini (2018)—Technical Specifications. Apple Support, 2020. Available online: https://support.apple.com/en-hk/111912 (accessed on 15 March 2024).
- Hejda, M.; Alanis, J.A.; Ortega-Piwonka, I.; Lourenço, J.; Figueiredo, J.; Javaloyes, J.; Romeira, B.; Hurtado, A. Resonant tunneling diode nano-optoelectronic excitable nodes for neuromorphic spike-based information processing. Phys. Rev. Appl. 2022, 17, 024072. [Google Scholar] [CrossRef]
- Spudat, C.; Ourednik, P.; Picco, G.; Nguyen, D.T.; Feiginov, M. Limitations of output power and efficiency of simple resonant-tunneling-diode oscillators. IEEE Trans. Terahertz Sci. Technol. 2023, 13, 82–92. [Google Scholar] [CrossRef]
- Owen-Newns, D.; Robertson, J.; Donati, G.; Figueiredo, J.; Wasige, E.; Ludge, K.; Romeira, B.; Hurtado, A. Neuromorphic Photonic Processing and Memory with Spiking Resonant Tunnelling Diode Neurons and Neural Networks. arXiv 2025, arXiv:2507.20866. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).