Multicast Covert Communication in PA-Assisted ISAC Systems

Abstract

A covert communication scheme is designed for pinching antenna (PA)-enabled integrated sensing and communication (ISAC) systems. The base station (BS) emits sensing signals to detect the potential eavesdropper while opportunistically performing covert multicast transmissions. To enhance covertness, the inherent power uncertainty of the sensing signals is exploited to confuse eavesdroppers, thereby creating protective coverage for the legitimate transmission. For the considered systems, we design an alternating optimization framework to iteratively optimize the baseband, beamforming, and PA positionson the two waveguides, in which successive convex approximation and particle swarm optimization methods are introduced. Simulated results confirm that the proposed scheme achieves the highest covert communication rates with different numbers of multicast users compared to benchmark methods. Furthermore, increasing the transmit power and the number of PAs can further improve the covertness performance.

1. Introduction

To address the requirements of new applications such as autonomous driving and the metaverse, Integrated Sensing and Communications (ISAC) has become a prominent research topic [1]. In ISAC systems, wireless communications and radar sensing share the same spectrum and hardware infrastructure, enabling more efficient and cost-effective system designs [2].

Because of the openness and broadcasting nature of ISAC systems, confidential information encoded in the waveform is vulnerable to interception and eavesdropping. This risk is particularly prominent when the sensing target is a malicious node that may eavesdrop on legitimate transmissions. There has been some research studying covert communication [3] in ISAC, ensuring an extremely low interception probability [4,5,6,7,8,9] and hiding communications behavior, which naturally prevents confidential information from being intercepted. Reference [4] proposes a covert beamforming design framework to maximize the mutual information of radar, ensuring covert transmission. Reference [5] exploits dual-functional artificial noise with diverse power to confuse the eavesdropper and sense the targets simultaneously. The authors of [6] maximized the minimum data rate achievable by legitimate users, with constraints on the total transmit power, covert communication requirements for multiple wardens, and a minimum SNR threshold for each target to be detected. Reference [7] employs a reconfigurable intelligent surface (RIS) technique to dynamically control the wireless propagation environment by adjusting the incoming signals, thereby enhancing desired signals and suppressing unwanted reflections to improve covert communication performance. The authors of [8] proposed an active RIS-assisted covert communication system based on NOMA-ISAC and enhanced the covert rate through joint optimization of both transmission and reflection beamforming. Additionally, reference [9] proposes a joint beamforming and Unmanned Aerial Vehicle (UAV) trajectory design to enhance covertness in an ISAC system.

An enabling technique such as the use of Pinching Antennas (PAs) [10,11,12] is introduced in an ISAC system. The deposition of dielectric particles at designated locations on a dielectric waveguide enables the activation of PAs to generate controlled electromagnetic radiation fields, thereby defining specific communication zones [13]. These advantages of PAs have motivated some works to explore PA system (PASS) integrated with ISAC [14,15,16,17]. Reference [14] derives the Cramér–Rao Lower Bound (CRLB) for PASS-ISAC systems, demonstrating significant CRLB reduction compared to traditional systems. Reference [15] addresses the joint optimization of the communication rate and radar performance by developing a maximum-entropy reinforcement learning technique. Reference [16] maximizes sensing power under communication constraints for systems with single-transmit and single-receive waveguides. Reference [17] further characterizes the performance boundary using communication and sensing rates as metrics.

These pioneering works show the superiority of integrating PAs with ISAC for high-efficiency transmission. Additionally, the potential of PAs to enhance transmission security has gradually drawn attention. As shown in Table 1, a small number of studies have begun to use PAs to achieve physical-layer security (PLS) [18,19,20] and covert communication (CC) [21] in a system without ISAC. However, PA-enabled ISAC covert communications remain a research gap. Unlike PLS [18,19,20], we noticed that the integration of PAs and ISAC will bring about the dual promotion of covert communications: On the one hand, unlike PLS, which safeguards communication security at the information level, covert communication ensures that communication signals remain undetected at the signal level. This fundamental distinction leads to differences in optimization objectives, performance metrics, and other key aspects when designing PA systems [22,23]. On the other hand, the integration of PAs and ISAC will bring about the dual promotion on covert communications: (1) ISAC leverages its sensing capability to provide eavesdropper location information, thereby facilitating covert beamforming. Meanwhile, PAs can be dynamically repositioned to increase echo signal energy, further improving covert communication effectiveness. (2) PAs can move along the waveguide over tens of meters, enabling repositioning to the nearest receiver and creating reliable Line-of-Sight (LoS) links. (3) PAs significantly reduce both system complexity and implementation costs compared to relay- or UAV-assisted covert communication. PAs eliminate the need for predefined relay protocols, complex trajectory planning, and expensive hardware, relying instead on low-cost dielectric waveguides and power amplifiers.

Table 1. Comparison of related works.

References	PA	ISAC	PLS	CC	Brief Introduction
[4,5,6,7,8,9]		🗸		🗸	See the second paragraph.
[18,19,20]	🗸		🗸		Maximize the secrecy rate [18] and weighted secrecy sum rate [19] by optimizing positions and baseband beamforming. Engage the pre-installed pinching antennas and implement coordinated amplitude and phase adjustments to enhance the data rate [20].
[21]	🗸			🗸	Investigate optimization of PA positions with power budget and beamforming to maximize covert rate.
[24]		🗸	🗸		Design the beamformer for an ISAC system, jointly improving the sensing accuracy and communication secrecy rate.

Motivated by the aforementioned observation, we focus on leveraging these advantages for covert communication. We investigate a waveguide multiplexing-based PA-assisted ISAC multicast covert communication system design. In this system, the BS is connected to two dielectric waveguides, transmitting both multicast communication signals and sensing signals to detect the eavesdropper while exploiting the power uncertainty of sensing signals to further confuse the eavesdropper. The main innovations and research contributions are summarized as follows:

• A waveguide multiplexing-based PA-assisted ISAC multicast covert communication system is proposed, where the BS connects to two dielectric waveguides, each embedded with multiple pinching antennas (PAs). Beyond transmitting multicast signals, the BS simultaneously emits sensing signals to detect a potential eavesdropper. The sensing signal also serves as artificial noise to interfere with the eavesdropper. Furthermore, the inherent power uncertainty of sensing signals is exploited to confuse the eavesdropper, thereby enhancing the covertness for legitimate users.
• Considering the eavesdropper adaptive detection threshold adjustment, we derive the minimum detection error probability (DEP). We formulate the problem in terms of maximizing the lowest achievable covert rate to guarantee a minimum quality of service for every user while satisfying both sensing illumination power requirements and covertness constraints, and an alternating optimization (AO) algorithm is designed, which iteratively optimizes the baseband beamforming through successive convex approximation (SCA) and PA positions on both waveguides through particle swarm optimization (PSO) methods.
• Simulated results show that the covert communication rate declines as the number of users increases; however, the proposed approach achieves the highest covert communication rates compared to benchmark schemes. When the sensing illumination power requirement increases, more BS power is allocated to sensing, leading to reduced covert communication rates.

2. System Model

As illustrated in Figure 1, we consider the covert communications in a PA-assisted ISAC system, where a BS multicasts to M single-antenna legitimate users while sensing an illegitimate eavesdropper. The BS is linked to two dielectric waveguides, each of length L, with one waveguide dedicated to the communication signal and the other to sending the sensing signal. Each waveguide is outfitted with N pinching antennas, represented by the set expressed as $N=\{1,\dots ,N\}$. For the p-th waveguide, the location of the n-th pinching antenna is formulated as ${\psi }_{p,n}=\left(t_{p,n},y_p,d\right),p\in \left\{1,2\right\}$ in a three-dimensional coordinate system, where $p=1$ corresponds waveguide 1 and $p=2$ corresponds to waveguide 2. The coordinate of the m-th communication user is ${\psi }_{c,m}=(t_{c,m},y_{c,m},0)$. Similarly, the eavesdropper is located at ${\psi }_w=(t_w,y_w,0)$. The BS intends to transmit covert information to the legitimate single-antenna users through downlink transmission in the presence of the eavesdropper. In addition to this legitimate transmission, the single-antenna eavesdropper aims to detect the covert transmission activities.

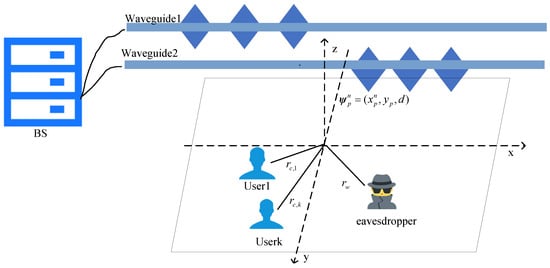
Figure 1. PA-assisted ISAC multicast covert communication system.

As illustrated in Figure 2, the sensing signal not only detects the eavesdropper but also acts as the shelter to create uncertainty at the eavesdropper. The transmit power of the sensing signal ($P_r$) is uniformly distributed over the interval of $[P_{\mathrm{r},\min },P_{\mathrm{r},\max }]$, i.e.,

$$f_{P_r}={\displaystyle \frac{1}{P_{r,max}-P_{r,min}}},P_{r,min}\le P_r\le P_{r,max}$$

(1)

where $P_{r,min}$ and $P_{r,max}$ correspond to the minimum and the maximum of the sensing signal’s total transmit power. We assume the eavesdropper knows the distribution of $P_r$ but cannot obtain its instantaneous power value. This ambiguity prevents the eavesdropper from distinguishing whether fluctuations in received signal power originate from active covert transmissions or natural variations in $P_r$. Besides assisting in covert signal transmission between the BS and legitimate users (ensuring low detection probability at the eavesdropper), the sensing signal also serves to enhance sensing functionality.

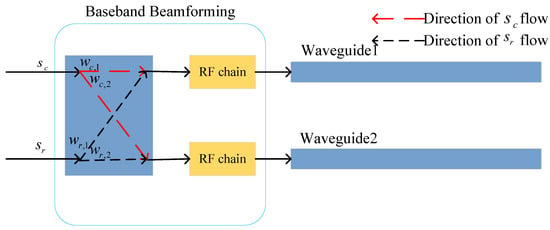
Figure 2. PA-assisted ISAC multicast covert communication architecture based on waveguide multiplexing.

2.1. Transmission Scheme

Let $s_c\in C$ denote the multicast communication, where $E\left[\right|s_c{|}^2]=1$. The precoded signal can be expressed as $w_c={[w_{c,1},w_{c,2}]}^T\in C^{2\times 1}$. The precoded symbol is then up-converted through the radio frequency (RF) chain and introduced to the waveguide at position ${\alpha }_p$. In the p-th waveguide, the controllable intra-waveguide phase shift for the input signal at N PAs is denoted by

$$g\left(t_p\right)=\left[\sqrt{{\alpha }_1}{e}^{-j\theta \left(t_{p,1}\right)}\sqrt{{\alpha }_2}{e}^{-j\theta \left(t_{p,2}\right)}\cdots \sqrt{{\alpha }_N}{e}^{-j\theta \left(t_{p,N}\right)}\right]\in {\mathbb{C}}^{N\times 1},$$

(2)

where $\sqrt{{\alpha }_n}$ represents the power-scaling factor of the n-th PA. To simplify the analysis, we assume equal power allocation among N PAs, i.e., $\sqrt{{\alpha }_n}=\sqrt{{\displaystyle \frac{{\alpha }_s}{N}}},\forall n\in \mathcal{N}$, where ${\alpha }_s$ denotes the radiation coefficient of PAs. The phase shift introduced to the n-th PA by feed point ${\alpha }_p$ can be given by

$$\theta \left(t_{p,n}\right)=2\pi {\displaystyle \frac{\parallel {\alpha }_{p,0}-{\alpha }_{p,n}\parallel }{{\lambda }_g}}={\kappa }_s\parallel t_{p,n}\parallel ,$$

(3)

where ${\lambda }_g$ refers the guided wavelength in the waveguide, ${\kappa }_g={\displaystyle \frac{2\pi }{{\lambda }_g}}$ denotes the guided wavenumber, ${\lambda }_g={\displaystyle \frac{\lambda }{n_{\mathrm{eff}}}}$ represents the guided wavelength, and $n_{\mathrm{eff}}$ denotes the effective refractive index of the waveguide [9]. The channel responses within the two waveguides can be modeled as follows:

$$G\left(T\right)=\left[\begin{array}{cc}g\left(t_1\right)& 0\\ 0& g\left(t_2\right)\end{array}\right]$$

(4)

For the considered high-frequency regime, the LoS-dominant model is widely used to approximate the the free-space channel. Let $h_{p,m}\left(t_n\right)\in C^{N\times 1}$ denote the channel vector between the p-th waveguide and user m. The resultant free-space channel vector is given by

$$h_m\left(T\right)={\left[h_{1,m}\left(t_1\right),h_{2,m}\left(t_2\right)\right]}^T,$$

(5)

where each element is expressed as follows:

$${\left[h_{p,m}\left(t_p\right)\right]}_n={\displaystyle \frac{\sqrt{\eta }}{D_m\left(t_{p,n}\right)}}exp\left(-j{k}_c{D}_m\left(t_{p,n}\right)\right)$$

(6)

where $\eta ={\displaystyle \frac{c^2}{16{\pi }^2{f}_c^2}}$, c is the speed of light, with $f_c$ as the carrier frequency and $\kappa ={\displaystyle \frac{2\pi }{\lambda }}$ as the free-space wavenumber. Moreover, $D_m\left(t_{p,n}\right)=\parallel {\alpha }_{p,n}-{\psi }_{c,m}\parallel$ denotes the Euclidean distance from the n-th PA on the p-th waveguide to user m. The BS transmits sensing signals to confuse the eavesdropper when detecting covert data transmission. The sensing signal is defined as $s_r\left(k\right)$, which satisfies $\parallel s_r{\left(k\right)\parallel }^2=1$, where $k\in \{1,\cdots ,K\}$ represents the symbol index. Let ${\mathcal{H}}_0$ denote the hypothesis that the BS is not transmitting private data to the communication users and ${\mathcal{H}}_1$ denote the hypothesis that covert transmission is ongoing. Under ${\mathcal{H}}_0$, the BS transmits only the sensing signal ($s_r\left(k\right)$) with the normalized covariance matrix ($w_r=E\left[s_r\left(k\right)s_r^H\left(k\right)\right]\ge 0$) to the eavesdropper, aiming to both sense the target and confuse the eavesdropper. Under ${\mathcal{H}}_1$, in addition to $s_r\left(k\right)$, the BS transmits the covert communication signal ($w_c{s}_c\left(k\right)$) to the legitimate users. We use $w_c$ to denote the corresponding transmit beamforming vector. We assume that the sensing signal is independent of the information symbols ($s_c\left(k\right)$). Therefore, from the eavesdropper’s perspective, the transmitted signal is

$$x\left(k\right)=\left\{\begin{array}{cc}{w}_r{s}_r\left(k\right),\hfill & H_0\hfill \\ w_c{s}_c\left(k\right)+P_r{w}_r{s}_r\left(k\right),\hfill & H_1\hfill \end{array}\right..$$

(7)

2.2. Covert Communications

During covert communication, under ${\mathcal{H}}_1$, the received signal at communication user m is

$$y_m=h_m^{H}G\left(T\right)(w_c{s}_c\left(k\right)+P_r{w}_r{s}_r\left(k\right))+n_m\left(k\right),$$

(8)

where $n_m\left(k\right)$ represents additive white Gaussian noise (AWGN) affecting user m with zero mean and variance (${\sigma }_m^2$). Since $P_r$ follows a uniform distribution, $E\left[P_r\right]={\displaystyle \frac{P_{min}+P_{max}}{2}}$. Thus, the covert communication rate at user m is

$$R_{c,m}={log}_2\left(1+{\displaystyle \frac{|h_m^{H}G\left(T\right)w_c{|}^2}{E\left[P_r\right]{\left|h_m^{H}G\left(T\right)w_r\right|}^2+{\sigma }_m^2}}\right).$$

(9)

Under ${\mathcal{H}}_0$, the signal received by the communication user is given by

$$y_m=h_m^{H}G\left(T\right)P_r{w}_r{s}_r\left(k\right)+n_m\left(k\right).$$

(10)

Although under ${\mathcal{H}}_0$, the received signal is irreducible noise, due to the randomness of $P_r$, this noise can actually be exploited to assist in covert communication between the BS and users and simultaneously sense communication users, reducing overhead without CSI feedback.

On the other hand, the eavesdropper attempts to detect covert communication by a Neyman–Pearson test of the received signal ($y_w\left(k\right)$). The received signal at the eavesdropper is expressed as follows:

$$y_w=\left\{\begin{array}{cc}{h}_w^{H}G\left(T\right)P_r{w}_r{s}_r\left(k\right)+n_w\left(k\right),\hfill & H_0\hfill \\ h_w^{H}G\left(T\right)(w_c{s}_c\left(k\right)+P_r{w}_r{s}_r\left(k\right))+n_w\left(k\right),\hfill & H_1,\hfill \end{array}\right.$$

(11)

where $n_w\left(k\right)$ is AWGN at the eavesdropper with zero mean and variance (${\sigma }_w^2$). The eavesdropper uses the average received power (i.e., $\zeta ={\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{\left|y_w\left[k\right]\right|}^2$) as the test statistic with the following decision rule:

$$\xi \underset{D}{\stackrel{p}{\gtrless }}\Gamma$$

(12)

where $\Gamma >0$ is the detection threshold and ${\mathcal{D}}_1$ and ${\mathcal{D}}_0$ represent the binary decisions favoring ${\mathcal{H}}_1$ and ${\mathcal{H}}_0$, respectively. For $K\to +\infty$, the average received power at the eavesdropper is given by

$$\zeta =\left\{\begin{array}{cc}{P}_r{\left|h_w^{H}G\left(T\right)w_r\right|}^2+{\sigma }_w^2,\hfill & {\mathcal{H}}_0\hfill \\ |h_w^{H}G\left(T\right)w_c{|}^2+P_r{\left|h_w^{H}G\left(T\right)w_r\right|}^2+{\sigma }_w^2,\hfill & {\mathcal{H}}_1\hfill \end{array}\right..$$

(13)

The detection error probability ($\xi$) at the eavesdropper is expressed as follows:

$$\xi =P_{\mathrm{FA}}+P_{\mathrm{MD}}$$

(14)

where $\xi \in [0,1]$ represents the total error probability and $P_{\mathrm{MD}}=Pr\left({\mathcal{D}}_0\right|{\mathcal{H}}_1)$ is the missed detection probability. Furthermore, $P_{\mathrm{FA}}=Pr\left({\mathcal{D}}_1\right|{\mathcal{H}}_0)$ is the false-alarm probability.

$$\begin{array}{cc}\hfill P_{\mathrm{FA}}& =Pr(P_r{\rho }_1+{\sigma }_w^2>\Gamma )\hfill \\ \hfill & =\left\{\begin{array}{cc}1,\hfill & \Gamma \le P_{r,min}{\rho }_1+{\sigma }_w^2\hfill \\ 1-{\displaystyle \frac{\Gamma -{\sigma }_w^2-{\rho }_1{P}_{r,min}}{{\rho }_1(P_{r,max}-P_{r,min})}},\hfill & P_{r,min}{\rho }_1+{\sigma }_w^2\le \Gamma \le P_{r,max}{\rho }_1+{\sigma }_w^2\hfill \\ 0,\hfill & \Gamma \ge P_{r,max}{\rho }_1+{\sigma }_w^2\hfill \end{array}\right.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill P_{\mathrm{MD}}& =Pr(P_r{\rho }_1+{\rho }_2+{\sigma }_w^2<\Gamma )\hfill \\ \hfill & =\left\{\begin{array}{cc}0,\hfill & \Gamma \le P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2\hfill \\ {\displaystyle \frac{\Gamma -{\sigma }_w^2-{\rho }_2-P_{r,min}{\rho }_1}{{\rho }_1(P_{r,max}-P_{r,min})}},\hfill & P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2\le \Gamma \le P_{r,max}{\rho }_1+{\rho }_2+{\sigma }_w^2\hfill \\ 1,\hfill & \Gamma \ge P_{r,max}{\rho }_1+{\rho }_2+{\sigma }_w^2\hfill \end{array}\right.\hfill \end{array}$$

(16)

where ${\rho }_1={\left|h_w^{H}G\left(T\right)w_r\right|}^2$, ${\rho }_2={\left|h_w^{H}G\left(T\right)w_c\right|}^2$. When $P_{r,max}{\rho }_1+{\sigma }_w^2<P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2$, the minimum value of $\xi$ is $\xi =0$. In this case, covert communication cannot be achieved. When $P_{r,max}{\rho }_1+{\sigma }_w^2>P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2$, the eavesdropper’s DEP is given by

$$\xi =\left\{\begin{array}{cc}1,\hfill & \Gamma \le P_{2,min}{\rho }_1+{\sigma }_w^2\hfill \\ 1-{\displaystyle \frac{\Gamma -{\sigma }_w^2-{\rho }_1{P}_{2,min}}{{\rho }_1(P_{2,max}-P_{2,min})}},\hfill & P_{2,min}{\rho }_1+{\rho }_2+{\sigma }_w^2\ge \Gamma \ge P_{2,min}{\rho }_1+{\sigma }_w^2\hfill \\ 1-{\displaystyle \frac{{\rho }_2}{{\rho }_1(P_{2,max}-P_{2,min})}},\hfill & P_{2,max}{\rho }_1+{\sigma }_w^2\ge \Gamma \ge P_{2,min}{\rho }_1+{\rho }_2+{\sigma }_w^2\hfill \\ {\displaystyle \frac{\Gamma -{\sigma }_w^2-{\rho }_2-P_{2,min}{\rho }_1}{{\rho }_1(P_{2,max}-P_{2,min})}},\hfill & P_{2,max}{\rho }_1+{\rho }_2+{\sigma }_w^2\ge \Gamma \ge P_{2,max}{\rho }_1+{\sigma }_w^2\hfill \\ 1,\hfill & \Gamma \ge P_{2,max}{\rho }_1+{\rho }_2+{\sigma }_w^2\hfill \end{array}\right..$$

(17)

When $\Gamma \le P_{2,min}{\rho }_1+{\rho }_2+{\sigma }_w^2$, ${\displaystyle \frac{d\xi }{d\Gamma }}=-1$, so $\xi$ is a monotonically decreasing function. When $\Gamma \ge P_{2,max}{\rho }_1+{\sigma }_w^2$, ${\displaystyle \frac{d\xi }{d\Gamma }}=1$, so $\xi$ is a monotonically increasing function. Therefore, when $\Gamma$ lies in the interval of $[P_{2,min}{\rho }_1+{\rho }_2+{\sigma }_w^2,P_{2,max}{\rho }_1+{\sigma }_w^2]$, DEP is the minimum, i.e.,

$${\xi }^{*}=1-{\displaystyle \frac{{\rho }_2}{{\rho }_1(P_{2,max}-P_{2,min})}}$$

(18)

It should be noted that to realize covert communication, the covertness constraint condition ($P_{r,max}{\rho }_1+{\sigma }_w^2>P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2$) must be satisfied. The covertness constraint conditions of ${\xi }^{*}\ge 1-\epsilon$ and $P_{r,max}{\rho }_1+{\sigma }_w^2>P_{r,min}{\rho }_1+{\rho }_2+{\sigma }_w^2$ can be respectively derived as follows:

$$P_{r,min}|h_w^{H}G\left(T\right)w_r{|}^2+|h_w^{H}G\left(T\right)w_c{|}^2\le P_{r,max}{|h_w^{H}G\left(T\right)w_r|}^2$$

(19)

$$|h_w^{H}G\left(T\right)w_c{|}^2+|h_w^{H}G\left(T\right)w_r{|}^2{P}_{r,min}\le \epsilon {|h_w^{H}G\left(T\right)w_r|}^2{P}_{r,max}$$

(20)

The left-hand sides of inequalities (19) and (20) are equal, while the right-hand side of inequality (20) is the right-hand side of inequality (19) multiplied by an additional $\epsilon$. Due to $\epsilon \in [0,1]$, if inequality (20) holds, inequality (19) must necessarily hold; thus, inequality (19) can be omitted.

2.3. Sensing Metric

We use illumination power [16] as a performance metric. Since the sensing signal follows a uniform distribution, the expected received illumination power at the target is given by

$$\mathbb{E}\left[P_{\mathrm{s}}\right]={\displaystyle \frac{P_{min}+P_{max}}{2}}{\left|h_w^{H}G\left(T\right)w_r\right|}^2.$$

(21)

3. Problem Formulation and Solution

In covert communication, BS maximizes the minimum covert communication rate among all multicast users while hiding legitimate transmissions from the eavesdropper by increasing its total error probability. The optimization problem can be formulated as follows:

$$\underset{t_1,t_2,W_c,W_r}{max}\underset{m}{min}{R}_{c,m}$$

(22a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\mathbb{E}\left[P_s\right]\ge {\gamma }^s\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\left(20\right)\hfill \end{array}$$

(22c)

$$\begin{array}{cc}\hfill & \mathrm{tr}\left(W_c\right)\le P_{max}-P_{r,max}\hfill \end{array}$$

(22d)

$$\begin{array}{cc}\hfill & \mathrm{tr}\left(W_r\right)\le 1\hfill \end{array}$$

(22e)

$$\begin{array}{cc}\hfill & |t_{p,n}-t_{p,n-1}|>{\Delta }_{min},n\in \mathcal{N},p\in \{1,2\}\hfill \end{array}$$

(22f)

$$\begin{array}{cc}\hfill & -L/2\le t_{p,n}\le L/2,n\in \mathcal{N},p\in \{1,2\}\hfill \end{array}$$

(22g)

$$\begin{array}{cc}\hfill & \mathrm{rank}\left(W_c\right)=1\hfill \end{array}$$

(22h)

$$\begin{array}{cc}\hfill & \mathrm{rank}\left(W_r\right)=1\hfill \end{array}$$

(22i)

where $W_c=w_c{w}_c^H\in C^{2\times 2}$, $W_r=w_r{w}_r^H\in C^{2\times 2}$, and $P_{max}$ represents the total power budget. The power constraint (22d) ensures the total power budget. (22c) is the covertness constraint, with $ϵ\in [0,1]$ typically set to a small value to guarantee transmission covertness. (22b) represents the sensing illumination power constraint. (22e) is the normalization constraint for the sensing signal beamforming matrix. (22f) specifies the minimum spacing (${\Delta }_{min}=\lambda /2$) between adjacent PAs. (22g) defines the feasible region for PA positions on the waveguide. (22h) and (22i) are the rank-1 constraints.

The difficulty in solving problem (22) is the joint optimization of baseband beamforming variables and PA positions, which is tightly coupled and complex. To overcome this challenge, we design an alternating optimization framework to decouple the original problem into two subproblems. An iterative procedure is employed to solve these subproblems successively, utilizing both PSO and SCA techniques.

3.1. Pinching Antenna Position Optimization

Given fixed $\mathbf{w}$ and $\mathbf{v}$, the original problem (22) can be transformed into the following form:

$$\underset{t_1,t_2}{max}\underset{m}{min}{R}_{c,m}$$

(23a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\left(22\mathrm{b}\right),\left(22\mathrm{c}\right)\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\left(22\mathrm{f}\right),\left(22\mathrm{g}\right)\hfill \end{array}$$

(23c)

We employ the PSO algorithm to address this challenging problem. First, we introduce a particle swarm comprising q individuals. The position of the n-th PA along waveguide 1 (waveguide 2) is given by $t_{i,n},n\le N$($t_{i,N+n}$), as shown below:

$$T_i^{\left(0\right)}={\left[t_{i,1}^{\left(0\right)},\cdots ,t_{i,N}^{\left(0\right)},t_{i,N+1}^{\left(0\right)},\cdots ,t_{i,2N}^{\left(0\right)}\right]}^T$$

(24)

To comply with constraint (22g), all initial values ($t_{i,n}^{\left(0\right)}$) are set within the interval of $\left[-{\displaystyle \frac{L}{2}},{\displaystyle \frac{L}{2}}\right]$. Accordingly, the initial velocity is defined as follows:

$$V_i^{\left(0\right)}={\left[v_{i,1}^{\left(0\right)},v_{i,2}^{\left(0\right)},\cdots ,v_{i,N}^{\left(0\right)},v_{i,N+1}^{\left(0\right)},\cdots ,v_{i,2N}^{\left(0\right)}\right]}^T$$

(25)

Following [25], the i-th particle updates its position according to its own historical best position ($T_{i,p}$) and the global best position of the entire swarm ($T_g$). The equation for iterative updates is formulated as follows:

$$V_i^{(l+1)}=\alpha V_i^{\left(l\right)}+c_1{\beta }_1(T_{i,p}-T_i^{\left(l\right)})+c_2{\beta }_2(T_g-T_i^{\left(l\right)})$$

(26)

$$T_i^{(l+1)}=T_i^{\left(l\right)}+T_i^{(l+1)},$$

(27)

where l represents the iteration index and $\alpha$ represents the inertia weight, which balances global and local search. A higher $\alpha$ promotes exploration at the expense of individual refinement, while a lower value has the converse effect. To improve performance, $\alpha$ decreases linearly during within the range of $[{\alpha }_{min},{\alpha }_{max}],{\alpha }_{max}=0.9,{\alpha }_{min}=0.1$, with the update step size expressed as ${\displaystyle \frac{({\alpha }_{max}-{\alpha }_{min})}{l_{max}}}$. Coefficients $c_1$ and $c_2$ are learning factors. Random variables ${\beta }_1$ and ${\beta }_2$ are distributed between 0 and 1, introducing randomness to enhance search diversity and prevent premature convergence. After each position update, a boundary check ensures particles remain within $\left[-{\displaystyle \frac{L}{2}},{\displaystyle \frac{L}{2}}\right]$, ensuring continuous satisfaction of constraint (22f).

The fitness evaluation for each particle during every iteration is performed using the unconstrained problem (23). Given the position ($T_i$), the minimum user secrecy rate can be derived from (9) and denoted as $R_{c,min}\left(T_i\right)$. In addition, to ensure the constraints of problem (23), the penalty coefficient ($\alpha >0$) is introduced into the fitness function, which is updated as follows:

$$F\left(T_i\right)=R_{c,min}\left(T_i\right)-\mu P\left(T_i\right)$$

(28)

where $\mu P\left(T_i\right)$ is the penalty term; $\mu$ is the penalty factor; and $P\left(T_i\right)$ is used to count the total number of times that the current PA position violates the constraints of problem (23), as given by the following formula:

$$\begin{array}{cc}\hfill P\left(T_i\right)=& \sum _{n=2}^N\mathbb{I}(t_{i,n}-t_{i,n-1}<\Delta )+\sum _{n=N+2}^{2N}\mathbb{I}(t_{i,n}-t_{i,n-1}<\Delta )+\mathbb{I}({\left|h_w^{H}G\left(T\right)w_c\right|}^2\hfill \\ & +{\left|h_w^{H}G\left(T\right)w_r\right|}^2{P}_{r,min}>\epsilon {\left|h_w^{H}G\left(T\right)w_r\right|}^2{P}_{r,max})+\mathbb{I}(P_s<{\gamma }^s)\hfill \end{array}$$

(29)

where k denotes the indicator function. If the condition inside the parentheses holds, it is equal to 1; otherwise, it is equal to 0. As the fitness of each particle is evaluated, both their individual and collective best positions undergo iterative refinement until convergence is achieved.

3.2. Baseband Beamforming Optimization

Given the PA positions, the original problem degenerates into a traditional beamforming problem. At this time, this sub-problem is expressed as a semidefinite programming (SDP) problem:

$$\underset{W_c,W_r}{max}\underset{m}{min}{R}_{c,m}$$

(30a)

$$\mathrm{s}.\mathrm{t}.tr\left(h_w^H\left(T\right)G\left(T\right)W_r\right)\ge {\gamma }^s$$

(30b)

$$\begin{array}{c}tr\left(h_v^H\left(T\right)G\left(T\right)W_c\right)+tr\left(h_w^H\left(T\right)G\left(T\right)W_r\right)P_{r,min}\hfill \\ \le \epsilon ·tr\left(h_w^H\left(T\right)G\left(T\right)W_r\right)P_{r,max}\hfill \end{array}$$

(30c)

$$tr\left(W_c\right)\le P_{max}-P_{r,max}$$

(30d)

$$tr\left(W_r\right)\le 1$$

(30e)

$$\mathrm{s}.\mathrm{t}.\left(22\mathrm{h}\right),\left(22\mathrm{i}\right)$$

(30f)

To solve problem (30), we introduce an auxiliary variable and restate the problem as follows:

$$\underset{W_c,W_r,\gamma }{max}\gamma$$

(31a)

$$\mathrm{s}.\mathrm{t}.R_{c,m}\ge \gamma ,\forall m$$

(31b)

$$\mathrm{s}.\mathrm{t}.\left(30\mathrm{b}\right),\left(30\mathrm{c}\right),\left(30\mathrm{d}\right),\left(30\mathrm{e}\right),\left(30\mathrm{f}\right)$$

(31c)

where $\gamma$ denotes the minimum covert communication rate among all multicast users. By relaxing problem (31) through the omission of the rank-one constraints, we can directly solve it while ensuring the solution’s alignment with the original problem [26]. The proof is provided in Appendix A. Applying the SCA method to $W_r$, the local point obtained at the j-th iteration is given by

$$\begin{array}{cc}\hfill & {log}_2\left(1+{\displaystyle \frac{|h_m^{H}G\left(T\right)w_c{|}^2}{E\left[P_r\right]{\left|h_m^{H}G\left(T\right)w_r\right|}^2+{\sigma }_m^2}}\right)={log}_2\left(|h_m^{H}G\left(T\right)w_c{|}^2+E\left[P_r\right]{\left|h_m^{H}G\left(T\right)w_r\right|}^2+{\sigma }_m^2\right)\hfill \\ \hfill & -{log}_2\left(E\left[P_r\right]{\left|h_m^{H}G\left(T\right)w_r\right|}^2+{\sigma }_m^2\right)={log}_2\left(tr\left[h_m^H\left(T\right)G\left(T\right)W_c\right]+tr\left[h_m^H\left(T\right)G\left(T\right)W_r\right]+{\sigma }_m^2\right)\hfill \\ \hfill & -{log}_2\left(tr\left[h_m^H\left(T\right)G\left(T\right)W_r\right]+{\sigma }_m^2\right)-{\displaystyle \frac{tr\left[h_m^H\left(T\right)G\left(T\right)\left(W_r-W_r^{\left(j\right)}\right)\right]}{\left(tr\left(h_m^H\left(T\right)G\left(T\right)W_r\right)+{\sigma }_m^2\right)ln\left(2\right)}}={\tilde{R}}_{c,m}\hfill \end{array}$$

(32)

Problem (31) can be transformed into the following form:

$$\begin{array}{cc}\hfill \underset{W_c,W_r,\gamma }{max}& \gamma \hfill \end{array}$$

(33a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& {\tilde{R}}_{c,m}\ge \gamma ,\forall m\hfill \end{array}$$

(33b)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.\left(30\mathrm{b}\right),\left(30\mathrm{c}\right),\left(30\mathrm{d}\right),\left(30\mathrm{e}\right)\hfill \end{array}$$

(33c)

Now, problem (33) can be directly solved by CVX.

Convergence: In problem (23), the objective value is non-decreasing due to the retention of globally optimal positions. Similarly, the SCA applied to problem (30) ensures a non-decreasing objective across iterations. Given that problem (22) is a constrained optimization with an upper-bounded objective function, the sequence of objective values generated by the algorithm is guaranteed to converge, leading to eventual termination.

Complexity: The computational cost has two components. The PSO stage requires $\mathcal{O}\left(L_{max}IM\right)$ operations, where $L_{max}$ denotes the maximum iteration count, I is the population size, and M is the number of waveguides. Meanwhile, solving problem (33) demands $\mathcal{O}\left(I{N}^{3.5}\right)$ computations, with I being the number of SCA iterations. Thus, the computational complexity amounts to $\mathcal{O}(L_{max}IM+J{N}^{3.5})$ [27].

4. Numerical Result

We evaluate the performance of the proposed PA-assisted ISAC multicast covert communication system in this section. We consider a three-dimensional topological network setting. The length of the two dielectrics is 5 m. The carrier frequency is $f_c=28$ GHz. The height of the waveguide is $d=30$ m, ${\sigma }_c^2=-90$ dBm. ${\eta }_{eff}=1.4$. $P_{max}=20w$. The y-axis coordinates of the two waveguides are $y_1=0.25$ and $y_2=-0.25$. Additionally, we consider (Hybrid Beamforming (HB) [28,29] and Fully Digital Beamforming (FDB)) [30,31] benchmark schemes:

(1) HB: This configuration employs a base station with two radio frequency (RF) chains positioned at [−L/2, 0, d]. Each RF chain is connected to N conventional antennas. Covert transmission is realized by leveraging sensing signals in conjunction with hybrid beamforming techniques.

(2) FDB: The BS is equipped with $2N$ RF chains, along with $2N$ antennas, each matched to one RF chain placed at [−L/2, 0, d]. By incorporating a sensing signal and adopting a fully digital beamforming architecture, the covert performance is effectively enhanced.

Figure 3 demonstrates the convergence of the proposed scheme. It can be observed that all schemes converge to a stable covert rate, ensuring overall convergence in solving the joint optimization problem constructed in this paper. Additionally, a larger covert constraint factor and a greater number of antennas enhance covert performance. This is because a larger covert constraint factor results in a looser covert constraint and more antennas provide more degrees of freedom.

Algorithm 1: Two-Stage Alternating Optimization Algorithm.

1   Randomly initialize particle swarm $\{T_i^{\left(0\right)},V_i^{\left(0\right)}\}$, beamforming matrix $W_r^{\left(j\right)}$. Introduce auxiliary variables $\{W_c,W_r,T,\gamma \}$. Set simulation parameters $c_1=1.5,c_2=1.5,\mu =50,L_{max}=500$. Randomly initialize $W_r=W_r^{\left(0\right)}$, $T=T_g$. 2   Repeat: 3       Given $\{W_c,W_r\}$, solve Problem (23) using PSO. Randomly initialize $\{T_i^{\left(0\right)},V_i^{\left(0\right)}\}$. Set $T_g=T$, $l=1$. 4       Repeat: 5           Update $\alpha ={\alpha }_{max}-{\displaystyle \frac{({\alpha }_{max}-{\alpha }_{min})l}{L_{max}}}$ 6           Repeat: 7                Update $V_i^{(l+1)},T_i^{(l+1)}$ via (26) and (27). Evaluate $F\left(T_i^{\left(j\right)}\right)$ via (28). Update $T_{i,p}$ and $T_g$ according to $F\left(T_i^{\left(j\right)}\right)$, $i\leftarrow i+1$. 8           Until: $i>I$ 9           $l\leftarrow l+1$. 10       Until: $l>L_{max}$ 11       Let $T=T_g$, solve Problem (33) via SCA. Set $W_r=W_r^{\left(0\right)}$, $j=1$. Set convergence criterion ${\epsilon }_0$. 12       Repeat: 13          Given $W_r^{(j-1)}$, iteratively solve Problem (33) to update $W_r^{\left(j\right)}$, $W_c$ and $j\leftarrow j+1$. 14       Until: Objective function (33a) converges with precision ${\epsilon }_0={10}^{-3}$. 15       Update $W_c$ and $W_r$. 16    Until: Objective function (22a) converges with precision ${\epsilon }_1={10}^{-3}$.

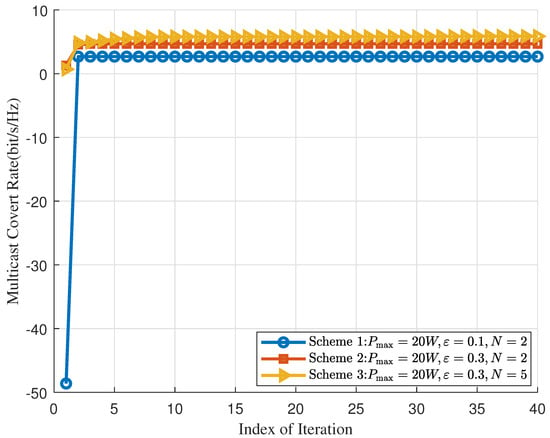
Figure 3. Convergence behavior of the Algorithm 1.

Figure 4 shows the impact of transmit power on multicast covert rates. Both PASS and the two benchmark schemes exhibit increasing multicast covert rates as the base station’s total power increases. Under all conditions, PA significantly outperforms benchmark schemes due to the strong LoS link, with this performance gain becoming more pronounced as transmit power rises. In comparison with conventional antenna architectures, PASS achieves remarkable gains, owing to its advantages in combating large-scale path loss. Our proposed method achieves the highest covert communication rate. This outcome is anticipated, as the PASS framework effectively harnesses the reconfigurability of PAs to enhance system performance while fully exploiting the advanced signal processing capabilities available at the baseband, thereby yielding superior covert communication rates. FDB consistently surpasses HB, indicating that it provides an excellent balance between performance and system complexity. The physical advantages of FDB over HB lie in two key aspects. Firstly, FDB has more RF chains than HB. This gives FDB considerably more beamforming degrees of freedom for more flexible and precise signal manipulation. Secondly, FDB performs fully digital beamforming, enabling high-precision amplitude and phase control in the digital domain, whereas HB’s hybrid architecture involves analog components with limited precision. These features allow FDB to achieve better covert performance through more accurate signal shaping and power distribution.

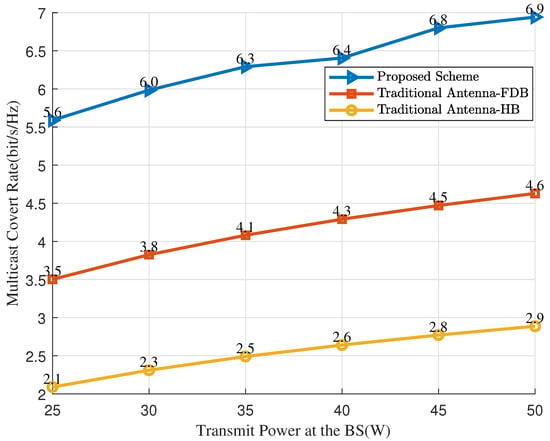
Figure 4. The multicast covert rate versus the transmit power.

Figure 5 illustrates the relationship between the covert communication rate and the number of PAs. The covert rate improves with increasing N. This enhancement occurs because a larger N offers extra degrees of freedom to enhance covert performance. However, the distance between the PAs and the communication users is observed to increase with the height of the dielectric waveguide, consequently reducing the covert communication rate as height increases.

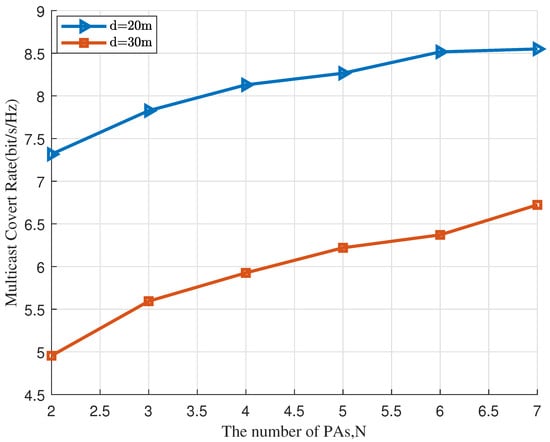
Figure 5. The multicast covert rate versus the number of PAs (N).

Figure 6 shows the relationship between the covert constraint and the covert rate. As $\epsilon$ increases, the covert constraint relaxes, and the covert rate increases monotonically. Compared to conventional antenna systems, PASS achieves significant performance gains by leveraging the mobility advantages of its antenna architecture. Among all benchmark schemes, the method proposed in this work attains the highest covert communication rate.

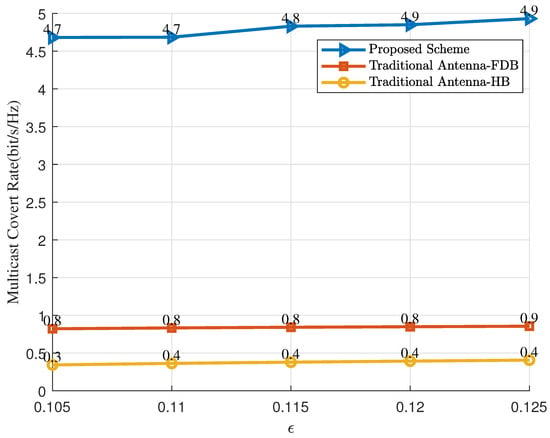
Figure 6. The multicast covert rate versus the covert communication constraint ($\epsilon$).

Figure 7 illustrates the relationship between the number of users and the multicast covert communication rate. The performance of all schemes decreases as the number of users increases. More users have to share limited system resources, and the main beam has to be widened to cover more dispersed user locations, resulting in a reduction in directional gain. However, the proposed scheme outperforms the comparative schemes, as the PAs provide an additional passive beamforming dimension, which, combined with the active beamforming at the base station, enables more precise beam control. As the number of users continues to increase, the beam becomes very wide, and the rate of decline slows down. At this point, further increasing the number of users causes the minimum rate to gradually approach a convergent lower bound.

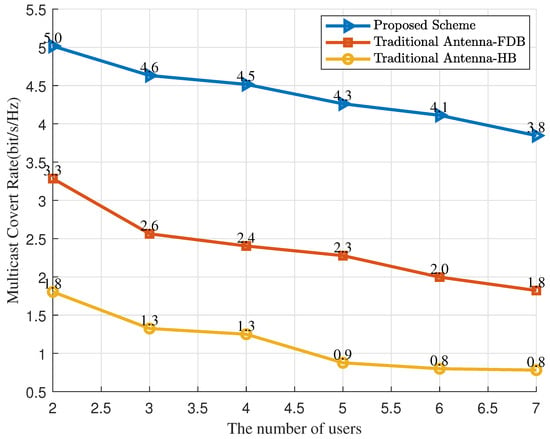
Figure 7. The multicast covert rate versus the number of users.

5. Conclusions

We proposed a PA-assisted ISAC covert communication system with waveguide multiplexing, in which the uncertainty of sensing signal power is utilized to confuse the eavesdropper to further enhance the system’s covertness. For the considered system, we maximize the minimum covert communication rate among all multicast users through joint optimization of baseband beamforming variables and PA positions. To solve the non-convex problem, we first designed an AO framework; then, the SCA and PSO methods were employed to iteratively optimize the baseband beamforming and the positions of the parasitic antennas on the two waveguides. The simulation results showed that the proposed scheme achieved an average performance improvement of 368% for HB and 204% for FDB. Furthermore, increasing transmit power and the number of PAs can further improve the covertness performance.