Explainable and Optimized Random Forest for Anomaly Detection in IoT Networks Using the RIME Metaheuristic

Abstract

The rapid expansion of Internet of Things (IoT) ecosystems has amplified their exposure to sophisticated cyber threats, particularly Distributed Denial-of-Service (DDoS) attacks that exploit device heterogeneity and resource constraints. Traditional machine learning-based intrusion detection systems often suffer from suboptimal performance due to poor hyperparameter configuration and a lack of interpretability, which are critical limitations in security-critical IoT environments. To address these challenges, this paper proposes an explainable, automated, and efficient anomaly detection framework that integrates a Random Forest (RF) classifier with the RIME metaheuristic optimization algorithm for hyperparameter tuning. Inspired by the physical process of rime ice formation, RIME’s dual-phase search mechanism effectively balances global exploration and local exploitation to identify near-optimal RF configurations in complex, high-dimensional search spaces. Evaluated on a real-world IoT traffic dataset encompassing twelve distinct DDoS attack vectors, the RIME-optimized RF model achieves a testing accuracy of 93.4%, outperforming baseline RF and other metaheuristic-optimized variants in both performance and convergence stability. Crucially, SHAP (SHapley Additive exPlanations) analysis provides transparent, attack-specific insights into feature importance, highlighting syn_flag_number, Protocol Type, Magnitue, Radius, and Ack_flag_number as key discriminative features, thereby enhancing model trustworthiness and operational utility. This work delivers a lightweight, interpretable, and high-performance solution well-suited for deployment in resource-constrained IoT networks, aligning with the urgent need for intelligent, adaptive, and explainable security mechanisms in next-generation network infrastructures.

1. Introduction

The Internet of Things (IoT) represents a networked ecosystem of devices, each possessing computational capabilities, uniquely identifiable, and capable of exchanging data across networks without the need for direct human intervention [1]. With billions of intelligent devices and millions of applications in operation, IoT is reshaping consumer behavior and business models. According to Fortune Business Insights, the global IoT was valued at USD 595.73 billion in 2023 and is projected to reach USD 4062.34 billion by 2032, with a CAGR of 24.3% from 2024 to 2032 [2]. While this rapid expansion presents significant opportunities, it also introduces an expanded attack surface for cyber threats [3]. As data from IoT devices is increasingly exchanged across numerous endpoints, including sensitive information, its exposure to malicious exploitation rises. These devices frequently operate in uncontrolled or semi-public environments such as residential areas, public infrastructure, and remote facilities, which significantly amplifies their vulnerability. IoT security risks are commonly categorized into six main types: Denial of Service (DoS), False or Bogus Information, Eavesdropping, Device or Identity Impersonation, Hardware Tampering, and Message Suspension. Of these, DoS and its more complex variant, Distributed Denial of Service (DDoS), represent some of the most severe threats to IoT ecosystems [4]. A DDoS attack employs multiple compromised systems to overwhelm a target resource with an excessive volume of requests. The goal is to disrupt normal operations and render services, devices, networks, applications, or even specific transactions temporarily inaccessible. Because these attacks originate from numerous sources, tracing their origin is difficult; the flood of requests can be massive, and their execution is often rapid, making early detection challenging. Consequently, DDoS attacks frequently lead to significant and at times catastrophic damage to compromised systems and networks. The 2018 DDoS attack on GitHub serves as a notable example of the scale such attacks can reach, with reported traffic volumes of 1.35 terabits per second (Tbps). During this event, GitHub experienced service outages caused by a surge of malicious traffic [5]. Although the platform’s response team managed to mitigate the attack within a few minutes, the sheer magnitude of the incident highlighted the susceptibility of even highly secured online services [6,7]. The scale of this problem becomes evident when considering that modern enterprise and industrial IoT networks may encompass thousands of heterogeneous devices, each potentially serving as both a target and an unwitting participant in attacks against other network segments [4]. Machine learning approaches have emerged as a promising solution for addressing these detection and classification challenges, with ensemble methods showing particular effectiveness in handling the irregular traffic patterns and diverse attack signatures characteristic of IoT environments. RF classifiers have demonstrated considerable success in multi-class DDoS detection scenarios, offering advantages in terms of both accuracy and computational efficiency that make them well-suited for resource-constrained IoT deployments [8,9]. The ensemble nature of RF provides inherent robustness against the noisy and incomplete data often encountered in IoT network monitoring, while the algorithm’s ability to handle mixed data types aligns well with the heterogeneous feature sets typically extracted from IoT traffic analysis [10]. However, the literature reveals that the performance of RF classifiers depends critically on hyperparameter configuration choices, which prove difficult to optimize using conventional approaches [11].

The hyperparameter optimization challenge in RF applications becomes particularly complex when dealing with IoT DDoS detection scenarios [12]. Parameters such as the number of trees, maximum depth, minimum samples per split, and feature selection criteria interact in nonlinear ways that create optimization landscapes resistant to traditional search methods [13]. Manual parameter tuning, while potentially effective, proves impractical given the time-sensitive nature of cybersecurity applications and the need for automated deployment across diverse IoT environments. Grid search approaches, though systematic, suffer from exponential scaling problems as the parameter space grows, while random search methods may miss optimal configurations in the discrete parameter spaces characteristic of tree-based algorithms. Even more sophisticated approaches like Bayesian optimization, while showing improvements over simpler methods, can struggle with the mixed continuous–discrete parameter spaces and complex interaction effects that characterize RF hyperparameter landscapes [14].

This recognition has driven increased interest in metaheuristic optimization algorithms, which offer the potential to navigate these complex parameter spaces more effectively than traditional optimization approaches [15]. Metaheuristic methods have shown particular promise in machine learning hyperparameter optimization because of their ability to explore high-dimensional, multimodal search spaces without requiring gradient information or making strong assumptions about the underlying optimization landscape [16]. Recent work has demonstrated that nature-inspired algorithms can achieve superior hyperparameter configurations compared to conventional methods [17]. However, most existing applications have focused on established metaheuristic algorithms, with limited exploration of newer physics-inspired optimization methods that may offer advantages in terms of exploration–exploitation balance and convergence characteristics.

The RIME optimization algorithm represents a particularly innovative development in physics-inspired metaheuristic optimization. Proposed by Su et al. in 2023, RIME draws inspiration from the physical processes governing rime ice formation in natural environments, capturing both the exploratory behavior of soft-rime particles in gentle conditions and the more directed growth patterns of hard-rime formation under stronger environmental pressures [18]. This dual-phase mechanism offers a unique approach to balancing exploration and exploitation in optimization processes, with the soft-rime phase enabling broad search space exploration while the hard-rime puncture mechanism facilitates intensive local search around promising regions [18]. The algorithm’s physics-based foundation provides theoretical grounding for its parameter update rules, while empirical evaluations on standard optimization benchmarks have demonstrated competitive performance against established metaheuristic methods. Despite the demonstrated potential of both Random Forest classifiers for IoT security applications and RIME optimization for complex parameter spaces, the intersection of these approaches remains largely unexplored in the cybersecurity domain. To the best of our knowledge, no prior studies have combined RIME with Random Forest-based approaches for IoT security. The application of RIME optimization to RF hyperparameter tuning for IoT DDoS detection presents several interesting research questions. First, does the dual-phase exploration–exploitation mechanism of RIME effectively navigate the complex hyperparameter landscapes characteristic of RF classifiers when applied to cybersecurity classification tasks? Second, how do the physics-inspired parameter update mechanisms of RIME compare to more established metaheuristic approaches in terms of convergence speed and solution quality for this specific application domain? Finally, do the improved hyperparameter configurations through RIME optimization translate into meaningful improvements in practical DDoS detection performance when evaluated on realistic IoT network datasets? Our study addresses these questions through the development and evaluation of the RIME-optimized RF (RIME-RF) that leverages RIME optimization for RF hyperparameter tuning in IoT DDoS detection scenarios. The framework incorporates multi-class attack classification capabilities to handle the diverse threat landscape characteristic of modern IoT environments, while maintaining computational efficiency suitable for deployment in resource-constrained settings. Furthermore, a subsequent SHAP analysis is used to provide interpretability insights that can inform both algorithm development and practical security decision-making.

This paper’s remaining sections are organized as follows: A review of related works is given in Section 2, and the methodology is covered in Section 3. The experimental assessment of the suggested model is shown in Section 4. Lastly, Section 5 provides a summary of the study’s findings, and Section 6 suggests avenues for further investigation.

2. Literature Review

The literature on IoT security has grown significantly in recent years, reflecting the rapid expansion of connected devices and the corresponding rise in cyber threats. Antonius et al. proposed a Bat Algorithm-optimized Convolutional Neural Network–Bidirectional Long Short-Term Memory (CNN–BiLSTM) model aimed at enhancing the security and efficiency of Internet of Things (IoT) networks by detecting anomalous or malicious activity [19]. The model integrates convolutional layers for spatial feature extraction and bidirectional long short-term memory (BiLSTM) layers for capturing temporal dependencies, while the Bat Algorithm is used to fine-tune model parameters to improve detection accuracy and reduce false positives and false negatives, achieving 99.43% accuracy. Gharehchopogh et al. proposed a binary multi-objective dynamic Harris Hawks Optimization (HHO) algorithm enhanced with a Mutation Operator (MODHHO) to improve Botnet Detection in IoT networks [20]. The method combines feature selection with classification using K-Nearest Neighbor (KNN), Support Vector Machine (SVM), Multilayer Perceptron (MLP), and Decision Tree (DT) models. Across five datasets, MODHHO outperformed other metaheuristic algorithms such as GWO, DBO, and HHO. Chen et al. proposed a novel Salp Swarm Algorithm that uses a threshold voting-based feature selection framework, followed by the Light Gradient Boosting Machine (LightGBM) algorithm to form a lightweight and efficient ensemble learning model [21]. Experiments show that the introduced model outperforms recent metaheuristic algorithms, achieving high accuracy, precision, and efficiency on the large-scale CICIoT2023 dataset. Alqahtany et al. employed an Enhanced Gray Wolf Optimization (EGWO) method for feature selection in Intrusion Detection Systems (IDSs), aiming to improve detection accuracy and computational efficiency by removing redundant features [11]. The selected features were evaluated using the RF classifier, and experiments on the NF-ToN-IoT dataset demonstrate that the method outperforms recent techniques, achieving 99.93% accuracy and improved convergence.

Mohammed Sharif and Beitollahi developed a hybrid framework for detecting application-layer Distributed Denial of Service (App-DDoS) attacks [22]. The approach combines RF classifiers, Gaussian Mixture Models (GMMs), and expert knowledge, alongside a feature selection strategy using Decision Tree (DT) importance and minimum redundancy maximum relevance (MRMR). Genetic Algorithms (GAs) are employed for automated hyperparameter optimization to enhance classifier efficiency. Evaluations on the CICIDS2017 and CICDDoS2019 datasets demonstrate 99.9% accuracy, 100% precision, 99.8% recall, an F1 score of 99.9%, and a false alarm rate of 0.12%. Saiyed and Al-Anbagi introduced a system incorporating GAStats, a novel feature selection method combining Genetic Algorithms (GAs) with statistical parameters, and tree-based machine learning models, including RF, Extra-Tree (ET), and Adaptive Boosting (AdaBoost) [23]. Evaluations demonstrate on two publicly available IoT datasets optimized feature selection, improved efficiency, and reduced computation time. Chaudhari and Yamini applied HHO for detecting DDoS attacks in IoT networks [24]. The method uses exploratory data analysis combined with a minimum-fitness-based optimal fitness function to identify attack patterns effectively. Evaluations on benchmark and NS3 DDoS datasets demonstrate successful detection of attack features and enhanced understanding of network threats. Benmalek and Seddiki developed an anomaly-based Intrusion Detection System (IDS) for IoT networks that integrates machine learning (ML) and deep learning (DL) models to enhance security against complex attacks [25]. Particle Swarm Optimization (PSO) was employed for feature selection and optimization to improve the performance of multiple classifiers in distinguishing normal from malicious traffic. Experimental results show that CatBoost combined with PSO outperforms existing methods across all evaluation metrics. SaiSindhuTheja and Shyam proposed a DoS attack detection system for cloud computing that uses the Oppositional Crow Search Algorithm (OCSA) for feature selection and a Recurrent Neural Network (RNN) for classification [26]. The system effectively separates normal from compromised data, addressing high-dimensional and nonlinear traffic patterns. Experimental results show it outperforms conventional methods, achieving 98.18% precision, 95.13% recall, 93.56% F-measure, and 94.12% accuracy. Dey et al. addressed cyber threat detection in IoT networks by developing a metaheuristic-based framework that combines ensemble feature selection with advanced classification techniques [27]. Feature optimization was performed using Binary Gravitational Search Algorithm (BGSA) and Binary Gray Wolf Optimization (BGWO), while Decision Tree, AdaBoost, and Random Forest (RF) classifiers handled detection tasks. Evaluation on the UNSW-NB15 dataset revealed that RF, using only 4 out of 42 features, achieved the best results with 99.41% accuracy, 99.09% detection rate, 99.33% F1-score, and a false positive rate of 0.03%. Dakic et al. investigated intrusion detection in automotive IoT systems, focusing on vulnerabilities within Controller Area Network (CAN) architectures that control critical vehicle functions [28]. The study applied Extreme Gradient Boosting (XGBoost) and K-Nearest Neighbors (KNN) classifiers, while a modified Particle Swarm Optimization (PSO) algorithm was used to optimize model parameters. Evaluated on a public dataset, their proposed models outperformed others.

The studies reviewed unequivocally demonstrate that integrating metaheuristic optimization techniques with machine learning models significantly enhances the efficacy of intrusion detection systems in Internet of Things (IoT) networks. Nevertheless, each approach exhibits inherent limitations, a phenomenon consistent with the No Free Lunch Theorem, which posits that no single optimization algorithm universally outperforms all others across every problem domain. This theoretical constraint underscores the necessity and opportunity for developing novel, problem-specific methodologies tailored to the unique characteristics and requirements of IoT security environments.

3. Methodology

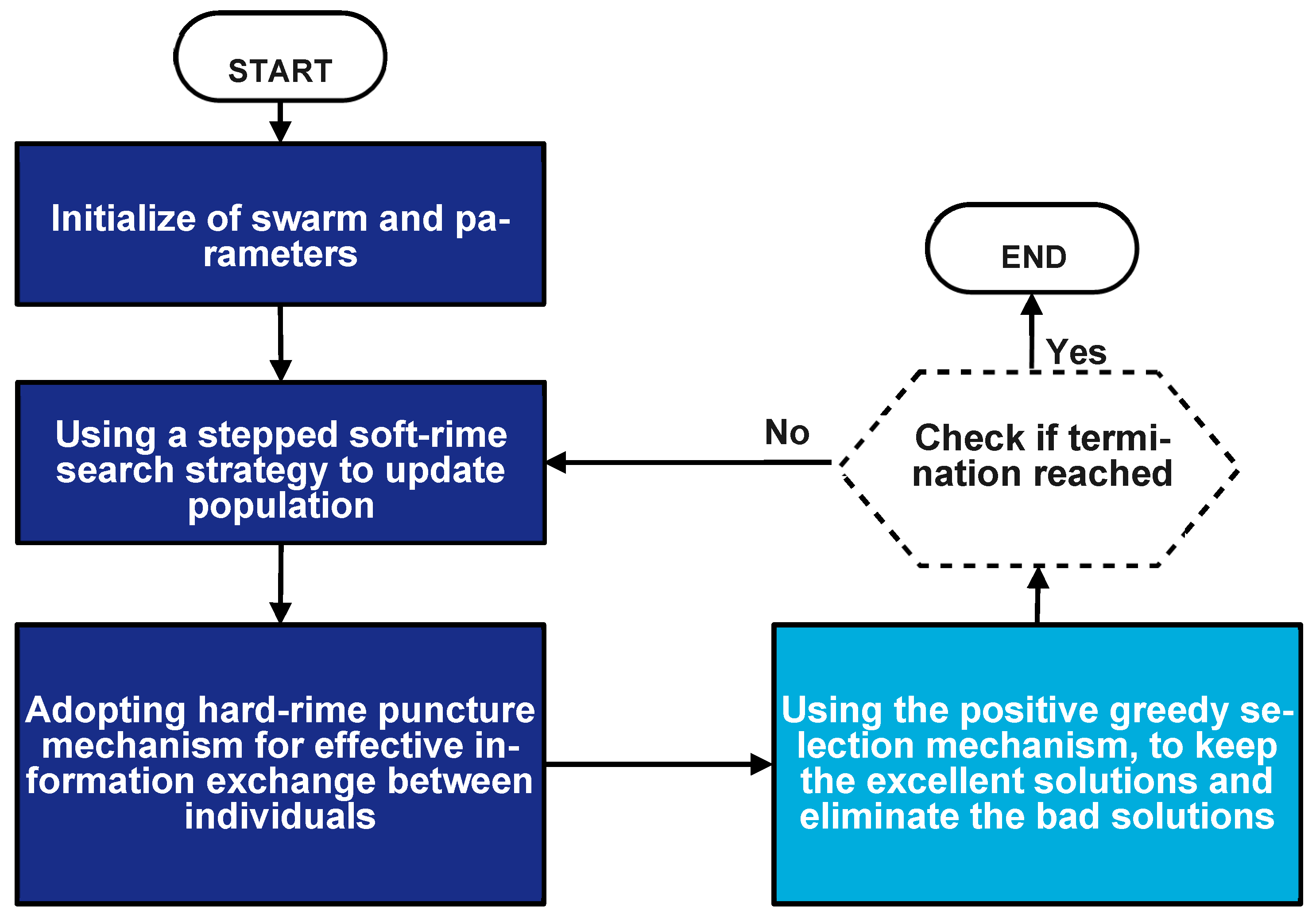
3.1. RIME Optimization Algorithm

The RIME algorithm is a metaheuristic, physics-inspired computational methodology designed for global optimization. Its conceptual foundation is derived from the natural phenomenon of rime ice formation, wherein the stochastic yet structured growth of ice crystals under varying atmospheric conditions serves as an analogy for navigating complex search spaces [18]. Within this framework, each candidate solution is conceptualized as an individual rime particle, and the collective set of these particles constitutes the rime population. The algorithm strategically models two distinct physical processes, soft-rime accretion and hard-rime puncture, to achieve an effective balance between exploration (searching uncharted regions) and exploitation (refining known promising solutions). As with most population-based metaheuristics [29], RIME commences with the stochastic generation of an initial population. Each particle, denoted as $X_i$, represents a potential solution vector in a $D$-dimensional search space, where $D$ corresponds to the number of decision variables in the optimization problem. The position of the $i$-th particle in the $j$-th dimension is initialized using a uniform random distribution within the prescribed bounds of the problem, as formalized in Equation (1).

$$X_i=\left[x_{i,1},x_{i,2},\cdots ,x_{i,D}\right]=lb+rand\times \left(ub-lb\right), i=1, 2,\cdots ,N_p$$

(1)

Here, $N_p$ signifies the total number of particles in the population. The terms $lb$ and $ub$ represent the global lower and upper bounds for the decision variables, respectively. The function rand generates a random number uniformly distributed in the interval $\left[0,1\right]$. The entire population can thus be represented as a matrix $X$, where each row corresponds to an individual particle as defined in Equation (2).

$$X=\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_{N_p}\end{array}\right]=\left[\begin{array}{cccc}{x}_{1,1}& x_{1,2}& \cdots & x_{1,D}\\ x_{2,1}& x_{2,2}& \cdots & x_{2,D}\\ ⋮& ⋮& \ddots & ⋮\\ x_{N_p,1}& x_{N_p,2}& \cdots & x_{N_p,D}\end{array}\right]$$

(2)

The soft-rime phase emulates the slow, stochastic, and expansive growth of soft rime ice under windy conditions. This mechanism is primarily responsible for the exploratory behavior of the algorithm, encouraging particles to disperse and investigate diverse regions of the search space. The position update for the $j$-th dimension of the $i$-th particle, $X_{i,j}^{\mathrm{new}}$, is governed by Equation (3).

$$X_{i,j}^{\mathit{new}}=X_{\mathit{best},j}+r_1\times \mathit{cos}\left({\displaystyle \frac{t\times \pi }{10\times t_{max}}}\right)\times \left(1-{\displaystyle \frac{round\left(5\times \frac{t}{t_{max}}\right)}{5}}\right)\times \left(rand\times \left(u{b}_{i,j}-l{b}_{i,j}\right)+l{b}_{i,j}\right), \mathit{if}r<E$$

(3)

$X_{\mathrm{best},j}$ is the $j$-th dimension of the current globally best solution. $t$ and $t_{\max }$ denote the current and maximum number of iterations, respectively. $r_1$ is a random number drawn from the interval $\left[-1,1\right]$, the variable $r_1$ introduces stochastic perturbation in the soft-rime phase, influencing the oscillatory search direction and supporting global exploration. The term $cos\left({\displaystyle \frac{t\times \pi }{10\times t_{\mathit{max}}}}\right)$ acts as a dynamic oscillating factor that modulates the step size over the course of iterations. The expression $\left(1-{\displaystyle \frac{round\left(5\times \frac{t}{t_{max}}\right)}{5}}\right)$ serves as a nonlinear decay function, gradually reducing the magnitude of the perturbation as the algorithm converges. The term (rand $\times \left(u{b}_{i,j}-l{b}_{i,j}\right)+l{b}_{i,j}$) generates a new random position within the bounds for the specific dimension, ensuring diversity. $r_2$ is a random number in $\left[0,1\right]$. The constants 10 and 5 regulate the dynamics of the soft-rime phase. The constant 10 controls the oscillation frequency of the cosine component, thereby determining how rapidly the search direction oscillates across iterations, while the constant 5 defines the decay step in the nonlinear term (1 − $round$(5 × t/$t_{max}$)/5), which progressively reduces exploration amplitude as the algorithm approaches convergence. $E$ is the coefficient, which determines the probability of applying this soft-rime update. The coefficient $E$ is defined by Equation (4) as a function of the iteration progress.

$$E=\sqrt{{\displaystyle \frac{t}{t_{max}}}}$$

(4)

This formulation implies that as the algorithm progresses (i.e., as $t$ increases), the likelihood of a particle undergoing a soft-rime update (exploration) increases. The hard-rime phase models the phenomenon where under strong winds, hard rime ice can experience a puncture or crossover, leading to a sudden structural change. In the RIME Algorithm, this mechanism facilitates exploitation by allowing particles to rapidly converge towards the best-known solution, thereby enhancing convergence speed and aiding in escaping shallow local optima. The update rule for this phase is presented in Equation (5).

$$X_{i,j}^{\mathit{new}}=X_{\mathit{best},j},\mathit{if}{r}_3<F_{\mathit{norm}}$$

(5)

Here, $r_3$ is a random value generated within the range $\left[-1,1\right]$. $r_3$ operates within the hard-rime phase as a probabilistic threshold variable, determining whether a particle undergoes direct convergence toward the current global best position according to the normalized fitness value $F_{\mathrm{norm}}$. The term $F_{\mathrm{norm}}$ represents the normalized fitness value of the current agent. This condition implies that agents with better (i.e., higher normalized) fitness are more likely to be directly replaced by the global best solution, accelerating the refinement process. To ensure monotonic improvement of the population, RIME employs a deterministic, greedy selection strategy. After generating a new candidate solution $X_i^{\mathrm{new}}$ for an agent, its fitness $F\left(X_i^{\mathrm{new}}\right)$ is evaluated and compared against the fitness of its previous state $F\left(X_i\right)$. The selection is governed by the following logical conditions:

• If $F\left(X_i^{\mathrm{new}}\right)<F\left(X_i\right)$ (assuming a minimization problem), The new position is accepted: $X_i=X_i^{\mathrm{new}}$.
• Furthermore, if the fitness of the new position is superior to that of the current global best, $F\left(X_i^{\mathit{new}}\right)<F\left(X_{\mathit{best}}\right)$, then the global best is updated: $X_{\mathit{best}}=X_i^{\mathit{new}}$.

This two-tiered selection process ensures that improvements at both the individual and population levels are preserved, driving the algorithm towards the global optimum. The flow chart of RIME is given in Figure 1.

3.2. Random Forest

The RF algorithm, originally introduced by Ho [30], operates by constructing a large ensemble of decision trees, each trained independently, and synthesizing their outputs to produce a final, robust prediction. This aggregation mechanism typically yields superior predictive accuracy and generalization performance compared to standalone decision tree models, although the effectiveness of the ensemble remains contingent upon the intrinsic characteristics of the underlying dataset [31]. At the core of the RF methodology lies the bootstrap aggregating (bagging) technique. The algorithm begins with an original training dataset, denoted as ${\mathcal{T}}_n=\left\{\left(x_1,y_1\right),\dots ,\left(x_n,y_n\right)\right\}$, comprising $n$ input–output pairs. From this dataset, $B$ bootstrap samples are generated via random sampling with replacement. Each bootstrap sample, indexed by $b$ (where $b=1,2,\dots ,B$), yields a resampled training subset $\left({\mathrm{X}}_b,{\mathrm{Y}}_b\right)$, which is then used to train an individual decision tree $f_b$. For a new input instance ${\mathrm{x}}^{\prime }$, the ensemble prediction is computed by aggregating the outputs of all $B$ constituent trees. Formally, the ensemble’s predicted class label $\hat{f}\left({\mathrm{x}}^{\prime }\right)$ is expressed in Equation (6).

$$\widehat{f}\left({\mathrm{x}}^{\prime }\right)={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B{f}_b\left({\mathrm{x}}^{\prime }\right)$$

(6)

Here, each tree $f_b$ casts a vote for the predicted class of ${\mathrm{x}}^{\prime }$, and the final prediction corresponds to the class receiving the highest average vote across the ensemble. This averaging mechanism enhances model stability and mitigates the risk of overfitting. Empirical research and practical applications have consistently demonstrated the versatility and resilience of RF across a broad spectrum of domains. Collectively, these attributes affirm Random Forest’s preeminent status within ensemble learning paradigms, rendering it an exceptionally effective instrument for addressing complex classification problems.

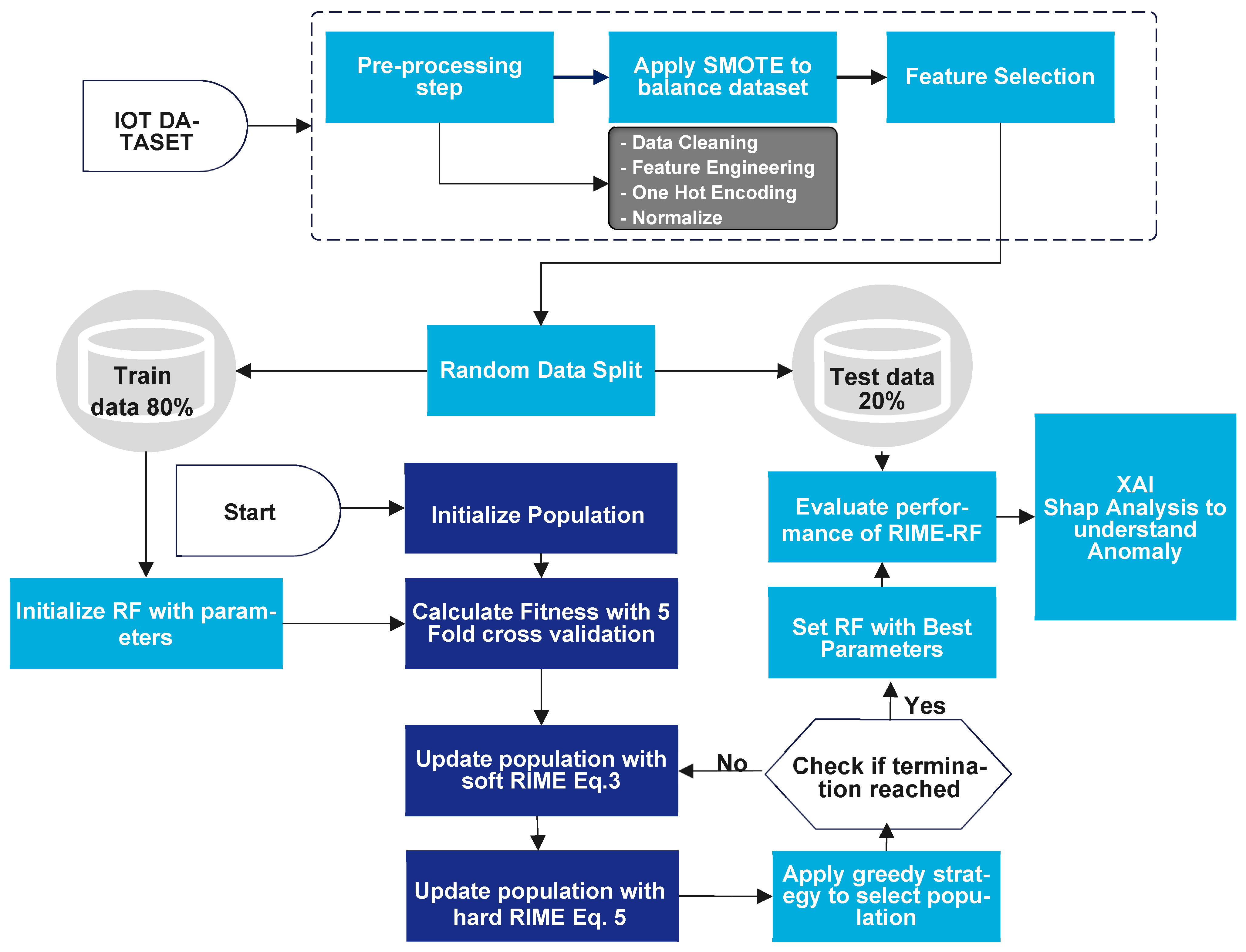
4. Hyperparameter Optimization of Random Forest Classifier Using RIME Algorithm

The optimization of hyperparameters for the RF classifier was conducted using the RIME metaheuristic algorithm, following a comprehensive machine learning framework that encompasses data preprocessing, feature engineering, and model optimization phases. The RIME algorithm, introduced by Su et al. [18], represents a physics-based optimization technique inspired by the natural formation of rime ice, which demonstrates superior performance in solving complex optimization problems through its unique soft-rime exploration and hard-rime exploitation mechanisms. The methodology commenced with the acquisition of an IoT dataset, as illustrated in Figure 2, followed by a systematic data preprocessing phase designed to ensure data quality and model readiness. The preprocessing phase incorporated three critical components: data cleaning to address missing values and inconsistencies. Feature encoding to transform categorical variables into numerical representations suitable for machine learning algorithms, and feature selection to identify the most informative variables while reducing dimensionality and computational complexity. This preprocessing stage is essential for ensuring that the subsequent machine learning process operates on high-quality, relevant features that would contribute meaningfully to the classification task. The selected features were then utilized as inputs for the RIME-RF optimization framework, where the RIME algorithm was specifically configured to optimize RF hyperparameters. The hyperparameter search space is defined as a discrete search problem that encompasses five critical parameters: the number of estimators (n_estimators) with categorical values of [100, 200, 500], maximum tree depth (max_depth) with values of [None, 10, 20, 30]. minimum samples required for splitting internal nodes (min_samples_split) with values of [2, 5, 10, 20], minimum samples required at leaf nodes (min_samples_leaf) with values of [1, 2, 4, 8], and maximum number of features considered for splitting (max_features) with options of [None, sqrt, log2]. The RIME optimization algorithm leveraged its dual-phase approach, where the soft-rime search strategy enabled comprehensive exploration of the hyperparameter space under varying environmental conditions, while the hard-rime puncture mechanism facilitated intensive exploitation of promising parameter combinations through directional refinement. During the training process, model evaluation was conducted using k-fold cross-validation (k = 5). The mean of the k-fold cross-validation results represented the model’s fitness, ensuring robust performance estimation and preventing overfitting. The source code of the model is available at https://github.com/MetaHeuLab/iot (accessed on 4 November 2025). The novelty of the RIME algorithm lies in its physics-based dual-phase mechanism, which models soft-rime formation for global exploration and hard-rime puncture for local exploitation, thereby enabling an adaptive balance between diversification and intensification. Unlike conventional swarm optimizers such as GWO, HHO, or PSO, which rely on heuristic movement equations, RIME incorporates dynamic oscillation and nonlinear decay control derived from real ice accretion phenomena. This design yields faster and more stable convergence while reducing the probability of premature stagnation. The computational complexity of RIME is O(Np × D × T), where Np denotes population size, D the dimensionality of the search space, and T the number of iterations. The deterministic greedy selection further minimizes redundant evaluations, maintaining computational efficiency comparable to, or better than, other metaheuristic optimization methods applied to Random Forest tuning.

4.1. Data

4.1.1. Dataset Overview

The study utilized a comprehensive IoT threat detection dataset from Kaggle [32] comprising network DDoS attacks in IoT environments. The dataset contains distinct features capturing temporal, protocol-specific, and statistical characteristics of network traffic patterns, with a target variable ‘label’ indicating the type of security threat. The IoT DDoS dataset from Kaggle was selected due to its extensive coverage of twelve distinct attack types and wide use in recent intrusion detection benchmarks. Its balanced representation of protocol-level and volumetric attack behaviors makes it a suitable testbed for evaluating model robustness across heterogeneous IoT traffic patterns. A random subset of 5000 samples was selected from the complete dataset to ensure computational efficiency and maintain a representative balance of attack categories. The top 10 most informative features were identified and retained through a filter-based feature selection approach, targeting the dimensions most relevant for IoT network threat classification. This dimensionality reduction was critical to both improving model performance and reducing potential overfitting, aligning with established methodologies in comparable intrusion detection research. The feature set encompasses multiple categories of network attributes: packet header information (Protocol Type), TCP flag counters (fin_flag_number, syn_flag_number, rst_flag_number, psh_flag_number, ack_flag_number, ack_count, fin_count), protocol-specific indicators (TCP, UDP, ICMP), and statistical measures (Tot sum, Tot size, Magnitude, Radius). The target variable comprises multiple DDoS attack categories, including DDoS-ACK_Fragmentation, DDoS-HTTP_Flood, DDoS-ICMP_Flood, DDoS-ICMP_Fragmentation, DDoS-PSHACK_Flood, DDoS-RSTFINFlood, DDoS-SYN_Flood, DDoS-SlowLoris, DDoS-SynonymousIP_Flood, DDoS-TCP_Flood, DDoS-UDP_Flood, DDoS-UDP_Fragmentation

4.1.2. Data Preprocessing

In this research, the data preprocessing is implemented to ensure data quality and optimize model performance through a systematic approach addressing missing values, encoding, scaling, feature selection, and class imbalance.

• Missing Value Treatment: Initial data quality assessment revealed the presence of null values across the dataset. These were addressed through complete case analysis, removing all instances containing missing values to maintain data integrity and avoid potential bias from imputation methods.
• Feature Engineering and Encoding: During the preprocessing stage, categorical variables underwent one-hot encoding transformation to convert string-based threat categories into numerical representations suitable for machine learning algorithms.
• Feature Scaling: To address the heterogeneous scales present across network traffic metrics, Min–Max normalization was applied to all features, transforming values to a standardized [0, 1] range. This normalization ensures that features with larger magnitudes do not dominate the learning process and facilitates convergence in gradient-based optimization algorithms.
• Dimensionality Reduction: Feature selection was performed using the SelectKBest algorithm with ANOVA F-statistic (f_classif) as the scoring function. The top 15 most discriminative features were retained based on their statistical significance in distinguishing between threat categories. This reduction strategy mitigates the curse of dimensionality while preserving the most informative attributes for classification.
• Class Imbalance Mitigation: The dataset exhibited significant class imbalance across different DDoS attack types. To address this challenge, the Synthetic Minority Over-sampling Technique (SMOTE) was employed when feasible, with automatic fallback to Random Over-Sampling (ROS) for classes with insufficient samples. The resampling strategy was determined dynamically based on the minimum class size, with SMOTE utilizing adaptive k-neighbors parameter selection to ensure valid synthetic sample generation.
• Data Partitioning: Following all preprocessing steps, the dataset was partitioned into training and testing subsets using stratified sampling with an 80:20 split ratio. The stratification ensured proportional representation of all threat categories in both subsets, maintaining the class distribution post-resampling. This comprehensive preprocessing approach ensures that the resulting dataset is suitable for training robust machine learning models while addressing common challenges in network security data, including high dimensionality, class imbalance, and scale heterogeneity.

4.2. Evaluation Metrics

The effectiveness of the developed IoT threat detection models was assessed using five standard evaluation metrics, each providing distinct insights into classification performance for multi-class and imbalanced datasets [33].

• Accuracy: Accuracy quantifies the proportion of all classifications the model predicted correctly. It is defined as the ratio of correctly predicted samples to the total number of samples as defined in Equation (7).

  $$\mathit{Accuracy}={\displaystyle \frac{\mathit{True}\mathit{Positives}+\mathit{True}\mathit{Negatives}}{\mathit{True}\mathit{Positives}+\mathit{True}\mathit{Negatives}+\mathit{False}\mathit{Positives}+\mathit{False}\mathit{Negatives}}}$$

  (7)
• Precision: Precision measures the proportion of samples identified as a specific class by the model that are truly of that class; the formula is expressed in Equation (8).

  $$\mathit{Precision}={\displaystyle \frac{\mathit{True}\mathit{Positives}}{\mathit{True}\mathit{Positives}+\mathit{False}\mathit{Positives}}}$$

  (8)
• Recall (Sensitivity): Recall reflects the proportion of actual instances of a particular class that were correctly identified by the model. Its formula is given in Equation (9).

  $$\mathit{Recall}={\displaystyle \frac{\mathit{True}\mathit{Positives}}{\mathit{True}\mathit{Positives}+\mathit{False}\mathit{Negatives}}}$$

  (9)
• F1 Score: The F1 score is the harmonic mean of precision and recall, providing a balanced measure that penalizes extreme values in either metric. The equation in Equation (10) defines the F1 score.

  $$\mathit{F}1=2\times {\displaystyle \frac{\mathit{Precision}\times \mathit{Recall}}{\mathit{Precision}+\mathit{Recall}}}$$

  (10)
• Hamming Loss: Hamming Loss quantifies the fraction of incorrect labels to the total number of labels in multi-class classification. It is calculated as expressed in Equation (11).

  $$\mathrm{Hamming}\mathrm{Loss}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathbb{I}\left({\widehat{y}}_i\ne y_i\right)$$

  (11)

where ${\hat{y}}_i$ is the predicted label, $y_i$ is the true label, and $n$ is the number of samples.

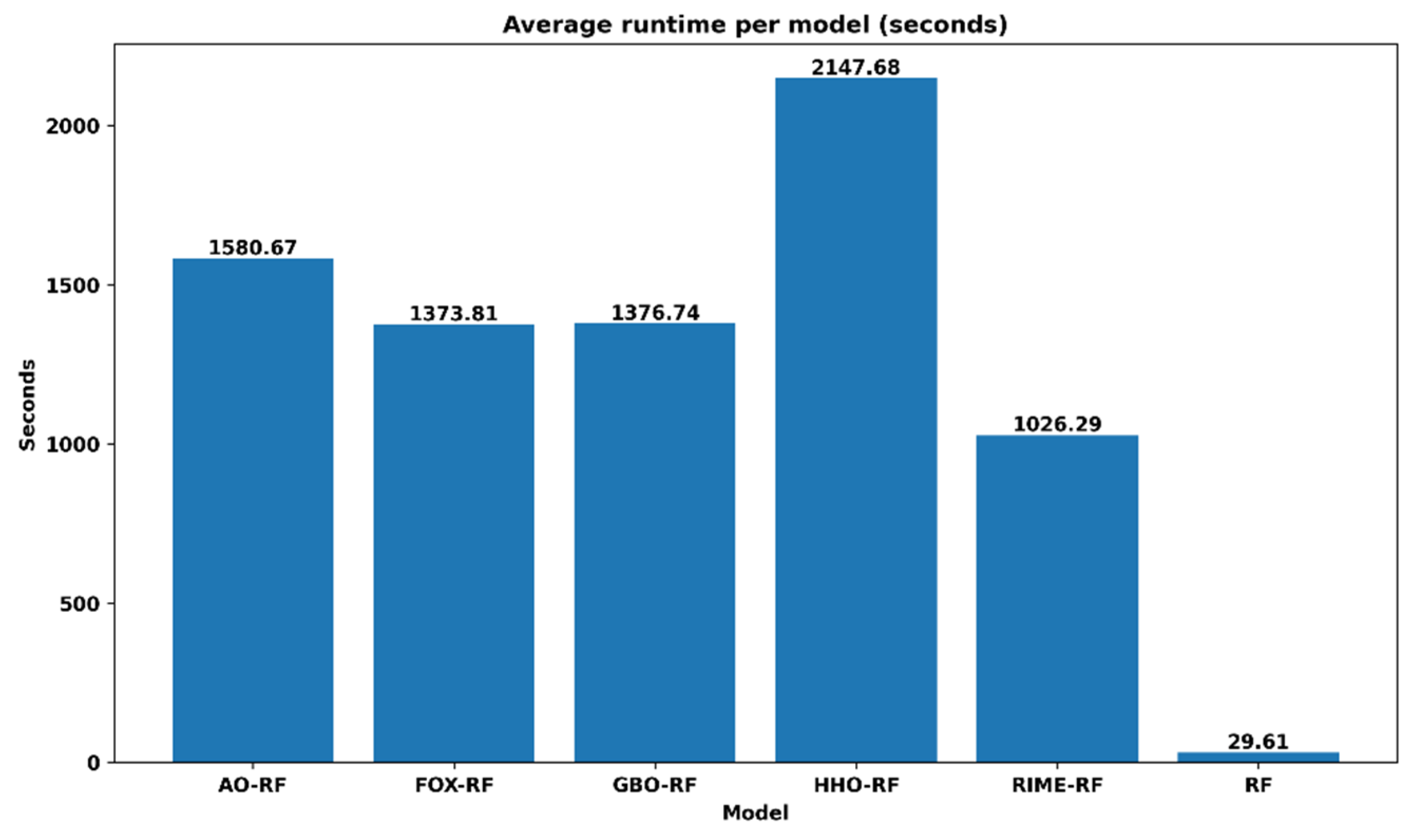
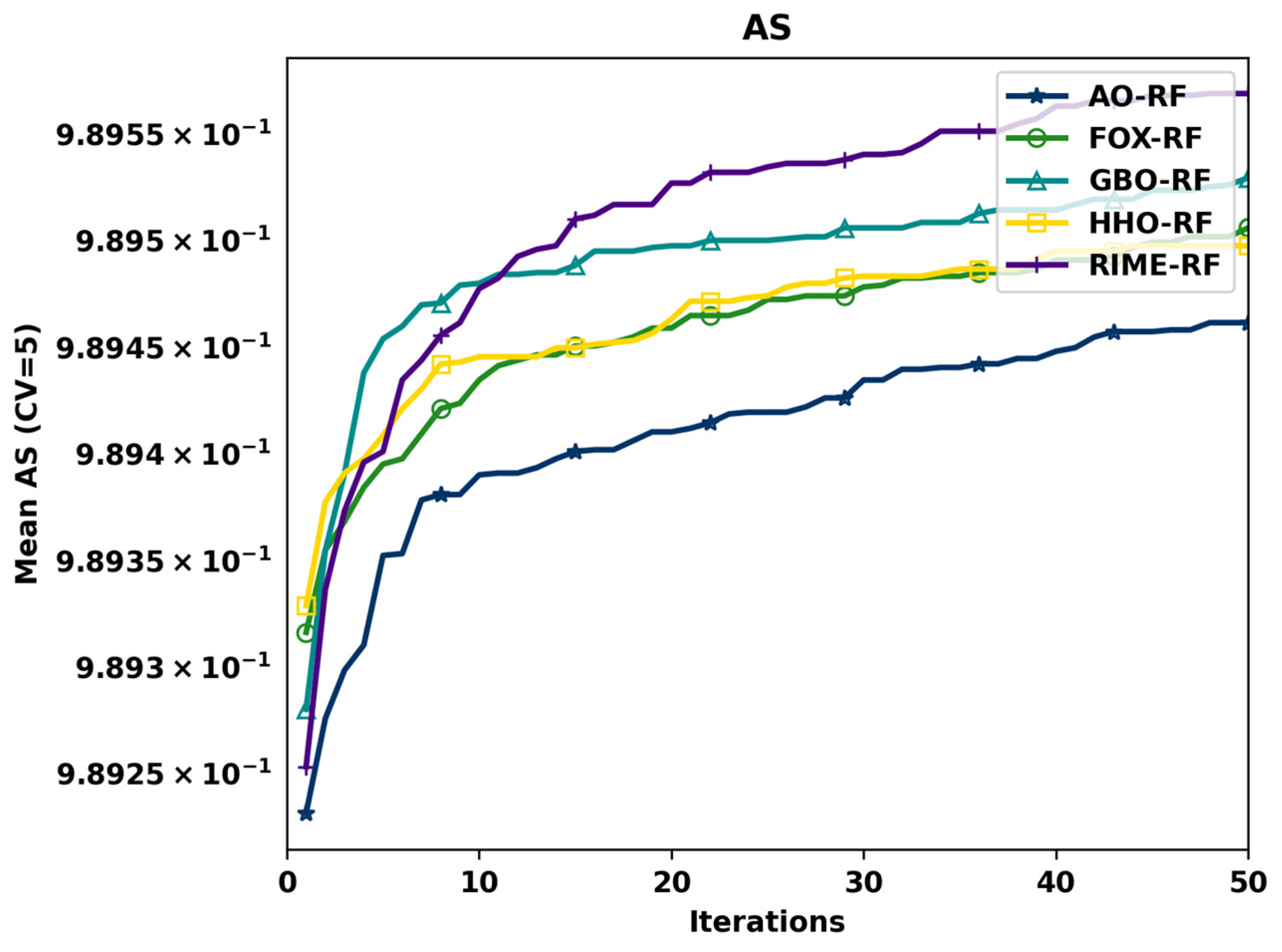
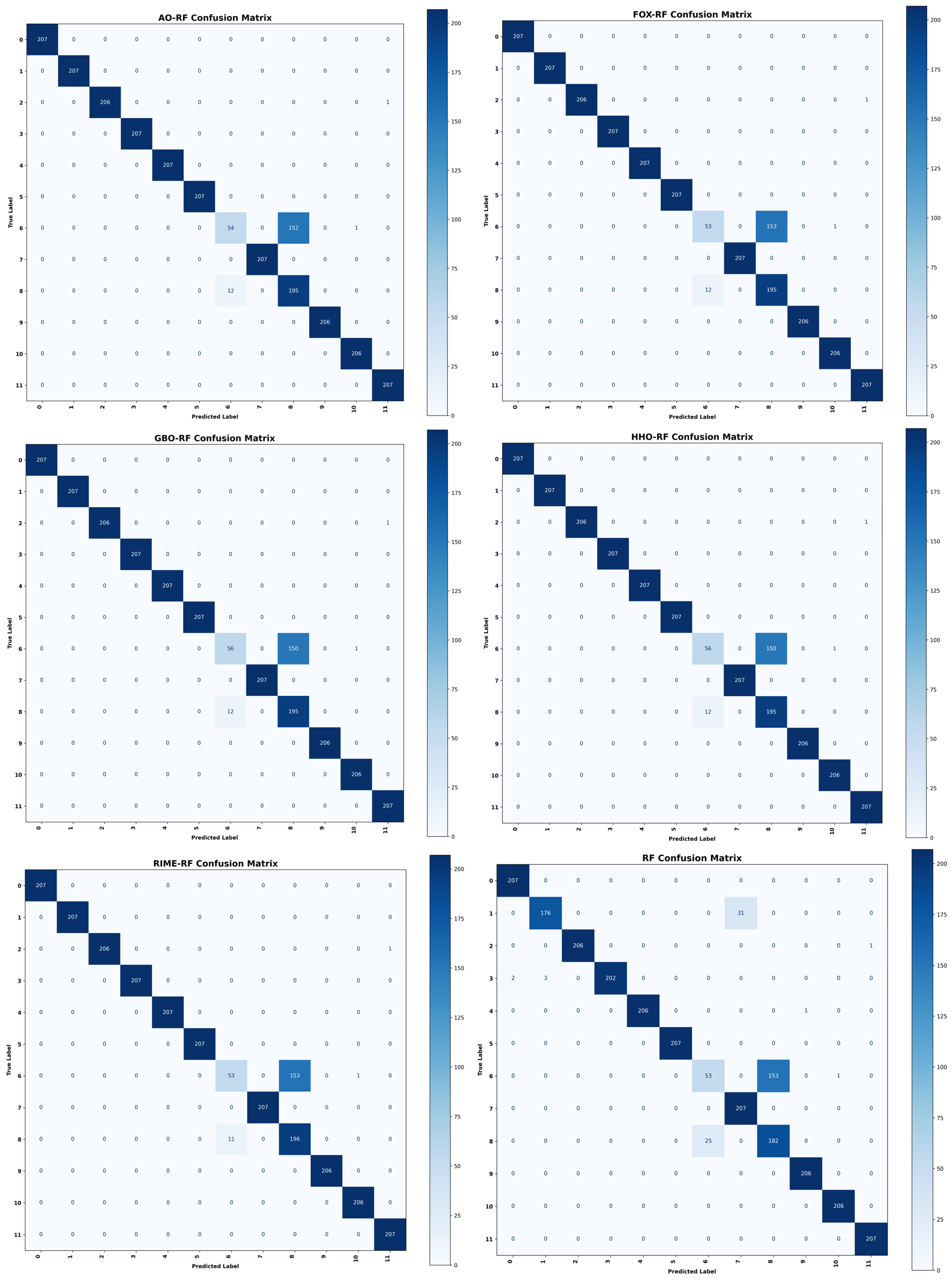
5. Results and Experiment

Comparative Analysis of Metaheuristic-Optimized RF Models for IoT Anomaly Detection. In this experimental phase, a comprehensive comparative analysis was conducted to evaluate the performance of metaheuristic-optimized RF classifiers against a baseline RF model for anomaly detection in IoT datasets. The investigation employed five distinct metaheuristic optimization algorithms to fine-tune the RF hyperparameters, thereby assessing their efficacy in enhancing predictive performance for anomaly classification tasks. The comparative study incorporated four state-of-the-art metaheuristic optimization algorithms: Aquila Optimization (AO) [34], Fox Optimizer (FOX) [35], Gradient-Based Optimizer (GBO) [36], and Harris Hawks Optimization (HHO) [37]. Each optimizer was systematically configured with identical population parameters to ensure fair comparative evaluation. The experimental parameters were standardized across all optimization algorithms to maintain consistency and eliminate bias in performance assessment. The population size was 30. The maximum number of iterations is 50, providing sufficient opportunity for convergence while maintaining reasonable computational overhead. The hyperparameter search boundaries for each optimizer were defined according to the specifications outlined in Section 4, encompassing the critical Random Forest parameters, including n_estimators, max_depth, min_samples_split, min_samples_leaf, and max_features.

To ensure robust statistical validation and eliminate the influence of stochastic variations inherent in metaheuristic algorithms, each optimization experiment was conducted across 20 independent runs. This approach provides a comprehensive statistical foundation for performance comparison and enables the calculation of meaningful confidence intervals for the reported metrics. The training phase employed a rigorous five-fold cross-validation strategy, partitioning the IoT dataset into five equal segments to ensure comprehensive model evaluation while preventing overfitting and maintaining generalization capability. The optimization process was designed to maximize classification accuracy while considering model complexity constraints, with each algorithm searching for the optimal hyperparameter combination within the predefined boundaries. The detailed algorithmic parameters for each optimizer are presented in

Table 1. Optimization Algorithm Parameters.

Algorithm	Parameter
AO	µ = 0.00565, $\omega =0.005,$ $\alpha =\delta =0.1$
FOX	-
GBO	${\beta }_{\min }=0.2,$ ${\beta }_{\max }=1.2$, $pr=0.5$
HHO	$E_0=\left[2,0\right]$
RIME	W = 5

, providing complete transparency regarding the experimental configuration and enabling reproducibility of the results.

Performance Assessment and Results Presentation

The comparative performance evaluation encompasses both training and testing phases, with results systematically using several classification metrics to provide comprehensive insights into each optimizer’s effectiveness.

Table 2. Train Result of Optimized RF Models.

		AO-RF	FOX-RF	GBO-RF	HHO-RF	RIME-RF	RF
AS	AVG	0.94419	0.94419	0.94417	0.94419	0.94395	0.91215
	STD	2.220 × 10−16	2.220 × 10−16	6.582 × 10−5	2.220 × 10−16	5.593 × 10−4	2.220 × 10−16
RS	AVG	0.94419	0.94419	0.94417	0.94419	0.94395	0.91215
	STD	2.220 × 10−16	2.220 × 10−16	6.582 × 10−5	2.220 × 10−16	5.593 × 10−4	2.220 × 10−16
PS	AVG	0.96492	0.96487	0.96487	0.96500	0.96456	0.92042
	STD	1.877 × 10−4	1.441 × 10−4	1.626 × 10−4	1.783 × 10−4	9.492 × 10−4	1.110 × 10−16
F1	AVG	0.93747	0.93748	0.93745	0.93745	0.93719	0.90556
	STD	3.889 × 10−5	2.982 × 10−5	1.029 × 10−4	3.694 × 10−5	6.361 × 10−4	0
HS	AVG	5.581 × 10−2	5.581 × 10−2	5.583 × 10−2	5.581 × 10−2	5.605 × 10−2	8.785 × 10−2
	STD	0	0	6.582 × 10−5	0	5.593 × 10−4	0

Bold means significant or best value.

presents the training performance metrics, representing the mean values obtained across 20 independent experimental runs, thereby providing statistically robust estimates of each algorithm’s optimization capability during the learning phase. Correspondingly,

Table 3. Test Result of Optimized RF Models.

		AO-RF	FOX-RF	GBO-RF	HHO-RF	RIME-RF	RF
AS	AVG	0.93288	0.93298	0.93372	0.93318	0.93376	0.91257
	STD	7.023 × 10−4	4.639 × 10−4	8.872 × 10−4	4.977 × 10−4	6.032 × 10−4	0
RS	AVG	0.93288	0.93298	0.93372	0.93318	0.93376	0.91257
	STD	7.023 × 10−4	4.639 × 10−4	8.872 × 10−4	4.977 × 10−4	6.032 × 10−4	0
PS	AVG	0.94732	0.94750	0.94871	0.94776	0.94887	0.92092
	STD	1.181 × 10−3	8.114 × 10−4	1.481 × 10−3	1.044 × 10−3	9.476 × 10−4	3.331 × 10−16
F1	AVG	0.92393	0.92405	0.92495	0.92432	0.92497	0.90465
	STD	8.894 × 10−4	6.238 × 10−4	1.104 × 10−3	6.328 × 10−4	7.806 × 10−4	0
HS	AVG	6.712 × 10−2	6.702 × 10−2	6.628 × 10−2	6.682 × 10−2	6.624 × 10−2	8.743 × 10−2
	STD	7.023 × 10−4	4.639 × 10−4	8.872 × 10−4	4.977 × 10−4	6.032 × 10−4	1.388 × 10−17
	Mean Rank	5	4	2	3	1	6

Bold means significant or best value.

documents the testing performance results, which serve as the definitive measure of model generalization and practical applicability for IoT anomaly detection tasks. The experimental framework ensures that all optimized RF models are evaluated under identical conditions, with the baseline RF serving as the reference point for performance comparison. This systematic approach enables the identification of the most effective optimization strategy for RF hyperparameter tuning in the context of IoT anomaly detection while providing quantitative evidence for the superiority of metaheuristic optimization over default parameter configurations. The statistical significance of performance improvements is validated through the comprehensive 20-run experimental runs, ensuring that observed differences reflect genuine algorithmic advantages rather than random variations.

The experimental results from the training phase, presented in Table 2, demonstrate the superior performance of metaheuristic-optimized RF models compared to the baseline configuration across all evaluation metrics. The optimization algorithms achieved remarkably consistent performance improvements, with Accuracy Scores (ASs) ranging from 0.94395 to 0.94419 for the optimized models versus 0.91215 for the baseline RF. This substantial enhancement underscores the critical importance of systematic hyperparameter optimization in maximizing model performance for IoT anomaly detection tasks. Notably, the standard deviation values across 20 independent runs reveal exceptional stability in the optimization process, with most algorithms exhibiting standard deviations of 2.220 × 10⁻¹⁶, indicating deterministic convergence behavior during training. The RIME-RF and GBO-RF models showed slightly higher variability (STD of 5.593 × 10⁻⁴ and 6.582 × 10⁻⁵, respectively), suggesting more exploratory search patterns that may contribute to improved generalization. The Precision Scores (PSs) further corroborate the optimization effectiveness, with all optimized models achieving values above 0.964 compared to 0.92042 for the baseline, demonstrating enhanced capability in correctly identifying true anomalies while minimizing false positives. The Hamming Loss (HS) metric provides additional insight into model performance, with optimized models achieving substantially lower error rates (approximately 0.056) compared to the baseline (0.08785). The F1 scores, balancing precision and recall, consistently exceeded 0.937 for optimized models versus 0.90556 for the baseline, confirming the comprehensive performance improvements across all aspects of classification quality.

The testing results presented in Table 3 provide crucial insights into the generalization capabilities of the optimized models, revealing that performance improvements observed during training successfully transfer to unseen data. The RIME-RF model emerged as the superior performer, achieving the highest average accuracy score of 0.93376, outperforming GBO-RF while demonstrating more consistent behavior across multiple runs. This performance advantage, though numerically modest, represents statistically significant improvement given the low standard deviations observed across all experiments. The RIME-RF model’s superiority becomes more pronounced when examining precision scores, where it achieved 0.94887. This enhanced precision is particularly valuable in IoT anomaly detection contexts where false positives can trigger unnecessary system interventions and resource allocation. The F1 score of 0.92497 for RIME-RF, tied with GBO-RF as the highest achieved, confirms the model’s balanced performance in both precision and recall dimensions. The standard deviation patterns in testing results reveal important characteristics of each optimization algorithm’s search behavior. RIME-RF demonstrates moderate variability (6.032 × 10⁻⁴ for AS), suggesting a balanced exploration–exploitation trade-off that enables discovery of diverse high-performing solutions while maintaining consistency. In contrast, the baseline RF exhibits zero standard deviation across multiple metrics, indicating convergence to a single, suboptimal solution space that lacks the adaptive capacity achieved through metaheuristic optimization.

The comparative performance analysis reveals distinct optimization characteristics among the employed metaheuristic algorithms. While AO-RF, FOX-RF, and HHO-RF demonstrated remarkable consistency with near-zero standard deviations during training, this behavior did not translate to superior testing performance, suggesting potential overfitting to the training distribution. The GBO-RF model, despite showing the second-best testing accuracy (0.93372), exhibited the highest variability (STD of 8.872 × 10⁻⁴), indicating a more stochastic search pattern that may be beneficial for exploring complex hyperparameter landscapes but potentially less reliable. The RIME algorithm’s superior performance can be attributed to its unique dual-phase optimization mechanism, which effectively balances global exploration through soft-rime formation with local exploitation via hard-rime puncture strategies. This physics-inspired approach enables RIME to navigate the discrete hyperparameter space more effectively than other swarm-based optimizers. A statistical approach was employed to evaluate model performance. The Friedman mean rank test revealed that the RIME-RF model achieved the highest rank, indicating superior performance among the compared methods.

The runtime comparison shown in Figure 3 presents the average computational cost (in seconds) for each optimization-based RF model and the baseline RF. The results indicate a clear trade-off between optimization complexity and computational efficiency. Among the metaheuristic approaches, the RIME-RF model achieved the lowest average runtime of 1026.29 s, outperforming AO-RF (1580.67 s), FOX-RF (1373.81 s), GBO-RF (1376.74 s), and HHO-RF (2147.68 s). This reduction in runtime demonstrates the computational efficiency of the RIME optimizer, which benefits from its adaptive exploration–exploitation mechanism and greedy population updating strategy. The dual-phase design of RIME enables it to converge more quickly toward optimal hyperparameters, thereby reducing redundant evaluations during the search process. The baseline RF model achieved a significantly shorter runtime of 29.61 s, as it operates without any optimization procedure. However, this speed advantage comes at the cost of suboptimal hyperparameter configurations and lower predictive accuracy, as evidenced in earlier performance tables. These findings confirm that while metaheuristic optimization increases runtime relative to the untuned RF, RIME-RF offers the best balance between accuracy and computational efficiency, achieving competitive runtime savings compared with other optimizers while maintaining superior detection performance. This efficiency makes RIME-RF a practical and scalable choice for real-time or large-scale IoT anomaly detection tasks where both precision and computational feasibility are critical.

This plot in Figure 4 illustrates the convergence behavior of the metaheuristic optimization algorithms during the hyperparameter tuning process for RF models, displaying the evolution of the mean accuracy score (AS) over 50 iterations across 20 independent runs using 5-fold cross-validation. The learning curve demonstrates several key characteristics of optimization algorithm performance. During the initial phase, all algorithms exhibit rapid improvement from their starting accuracy values around 0.9925, showing steep upward trajectories. This represents the exploration phase, where algorithms are discovering promising regions in the hyperparameter search space. The curves begin to show different convergence rates, with RIME-RF and GBO-RF demonstrating superior optimization capability by achieving higher accuracy scores more quickly between 10 and 25 iterations. This phase represents the transition from exploration to exploitation of promising hyperparameter combinations. All algorithms reach a plateau or convergence state, where further iterations yield minimal improvement. This indicates that the algorithms have found near-optimal hyperparameter configurations, and additional computational effort provides diminishing returns. RIME-RF achieves the highest final accuracy, demonstrating superior optimization effectiveness through its dual-phase soft-rime exploration and hard-rime exploitation mechanism. GBO-RF shows comparable performance, reaching nearly identical accuracy levels, indicating robust gradient-based search capabilities. RIME-RF shows the fastest convergence rate. This efficient convergence behavior is crucial for computational resource management in hyperparameter optimization tasks. The smooth, monotonic improvement curves indicate stable optimization behavior without significant oscillations or premature convergence, suggesting robust algorithmic implementations suitable for practical deployment in IoT anomaly detection systems.

The confusion matrices presented in Figure 5 reveal critical insights into the class-specific performance characteristics of the optimized Random Forest models for IoT anomaly detection, representing the best-performing configurations from 20 independent runs. This comprehensive multi-class classification problem encompasses 12 distinct anomaly categories, providing a detailed view of model discriminative capabilities across different attack vectors. The confusion matrices demonstrate exceptionally strong diagonal dominance across all optimized models, indicating robust classification performance with minimal inter-class confusion. The dark blue diagonal elements represent the high concentration of correct predictions, while the predominantly white off-diagonal regions confirm minimal misclassification rates. This pattern is particularly pronounced in RIME-RF matrices, corroborating their superior test performance metrics. The baseline Random Forest exhibits notably more scattered misclassifications, particularly evident in classes 1 and 8, where off-diagonal elements show increased intensity. This degradation manifests as reduced diagonal concentration and increased error dispersion, quantitatively supporting the statistical superiority of metaheuristic optimization.

While the RIME algorithm successfully optimized the RF hyperparameters to achieve superior classification performance, understanding why the model makes its predictions is crucial for enabling actionable insights in security applications. To this end, we conducted a comprehensive SHAP analysis to interpret the learned decision-making process of the final RIME-RF model. The resulting feature importance plot in Figure 6 provides a granular view of which network traffic characteristics are most influential in distinguishing between the 12 distinct DDoS attack classes. The SHAP analysis reveals that the syn_flag_number is the single most critical feature across the entire multi-class classification task, exhibiting the highest aggregate SHAP mean value. This finding underscores the significance of TCP SYN flags in identifying various types of DDoS attacks, particularly those involving connection initiation flooding (SYN Flood). The high importance of Protocol Type as the second most influential feature further emphasizes the role of the underlying communication protocol (TCP, UDP, ICMP) in defining attack patterns. For instance, attacks like UDP Flood and ICMP Flood are inherently tied to specific protocols, making their detection highly dependent on this attribute.

A key insight from the SHAP analysis is the class-specific nature of feature importance. While syn_flag_number and Protocol Type are universally important, the contribution of other features varies significantly depending on the target class. This heterogeneity demonstrates that the RIME-RF model leverages a diverse set of features to construct distinct decision boundaries for each threat category, reflecting the complex and varied signatures of modern IoT attacks. Furthermore, the analysis highlights the importance of aggregated statistical measures. Features like Magnitude, Radius, Tot sum, and Tot size, which capture the overall volume and distribution of network traffic, are consistently ranked among the top contributors. Their high importance suggests that the model effectively identifies anomalous traffic by recognizing deviations in these global traffic metrics, which are characteristic of large-scale DDoS events. Finally, the SHAP analysis provides a transparent explanation of the RIME-RF model’s behavior. It confirms that the optimized model relies heavily on fundamental TCP/IP flag counts and protocol information, augmented by high-level traffic statistics, to achieve its high accuracy. More importantly, it reveals that the model’s strength lies in its ability to learn class-specific feature interactions, allowing it to distinguish between subtly different attack vectors with high precision. Although demonstrated in the context of IoT DDoS detection, the proposed RIME-RF framework introduces a domain-agnostic methodology with broad applicability. Its novelty resides in the integration of the physics-inspired RIME optimizer a dual-phase, gradient-free metaheuristic with RF hyperparameter tuning, enabling efficient navigation of complex, mixed discrete–continuous search spaces without reliance on domain-specific heuristics. Coupled with SHAP-based interpretability, this approach delivers not only high predictive accuracy but also transparent, actionable insights into model decisions. Consequently, the framework is readily adaptable to any security-sensitive or resource-constrained classification scenario, including financial fraud detection, where both performance and explainability are non-negotiable. This interpretability not only validates the model’s performance but also provides valuable domain knowledge for network security analysis, enabling the understanding and mitigation of emerging IoT threats.

6. Conclusions

This study presented a novel and effective approach for enhancing IoT threat detection by integrating the physics-inspired RIME optimization algorithm with the RF classifier. The primary objective was to address the critical challenge of hyperparameter tuning in complex, multi-class intrusion detection systems. Our comprehensive experimental evaluation, conducted on a real-world IoT dataset encompassing twelve distinct DDoS attack vectors, demonstrates that the RIME-RF model consistently outperforms both a baseline Random Forest and other metaheuristic optimizers such as AO-RF, FOX-RF, GBO-RF, and HHO-RF.

The key findings of this research are threefold. First, the RIME algorithm proved to be exceptionally well-suited for optimizing Random Forest hyperparameters. Its unique dual-phase mechanism, balancing global exploration (soft-rime) with local exploitation (hard-rime), enabled it to navigate the discrete, high-dimensional search space efficiently. This is evidenced by RIME-RF achieving the highest accuracy while also exhibiting rapid and stable convergence during training. The superior precision is particularly significant for security applications, where minimizing false alarms is paramount to maintaining operational efficiency. Second, the rigorous experimental design, featuring 20 independent runs and 5-fold cross-validation, confirmed the robustness and statistical reliability of the RIME-RF model. RIME-RF demonstrated a more favorable balance between peak performance and consistency across multiple runs, making it a more dependable choice for deployment in dynamic IoT environments. The near-zero Hamming Loss and the highly diagonal confusion matrices further attest to the model’s ability to accurately distinguish between subtly different attack types with minimal misclassification.

Third, the SHAP analysis provided crucial interpretability, revealing that the optimized model’s success stems from its intelligent use of fundamental network features. The syn_flag_number and Protocol Type emerged as the most critical features, aligning with domain knowledge about DDoS attacks. More importantly, the analysis showed that RIME-RF learned class-specific feature interactions, allowing it to tailor its decision logic for each unique threat, thereby achieving its high multi-class accuracy. In conclusion, this work successfully validates RIME as a powerful and efficient tool in the domain of cybersecurity. The RIME-RF framework improves the performance benchmark for IoT threat detection and also offers a transparent and interpretable model, which is essential for gaining the trust of security analysts.

This study acknowledges several limitations that inform promising directions for future research. First, the choice of RF as the base classifier reflects a deliberate trade-off that prioritizes model interpretability and computational efficiency over potentially higher but often less transparent performance offered by more complex algorithms. To address this, future work will incorporate additional classifiers, including XGBoost, Support Vector Machines (SVMs), and gradient-boosted decision trees, alongside a lightweight deep sequential model tailored to network flow records. This expanded comparative framework will enable a rigorous quantification of accuracy–runtime trade-offs and enhance the generalizability of conclusions regarding model selection in IoT intrusion detection. Furthermore, while the present work focuses on metaheuristic-based hyperparameter optimization, future investigations will include direct runtime comparisons with deterministic approaches, such as GridSearchCV, to systematically evaluate the computational efficiency and practical feasibility of metaheuristic strategies, like RIME, relative to exhaustive search methods. The experimental evaluation is based on a single benchmark dataset, which, although widely used and representative of modern network traffic, may not fully capture the heterogeneity of real-world IoT environments. Moreover, the analysis employed stratified subsampling, which, although preserving class distributions, may limit the model’s exposure to the full spectrum of attack variants and benign traffic patterns. Future work will therefore expand the evaluation to multiple, diverse intrusion detection datasets, including those specifically designed for IoT and edge computing contexts, and utilize full-scale or minimally subsampled data where feasible to better assess robustness, generalizability, and scalability under realistic conditions. Finally, we aim to extend the proposed methodology to real-time, online learning scenarios that reflect the dynamic nature of modern threat landscapes. Additionally, the application of the physics-inspired RIME optimizer to deep learning architectures will be explored to tackle increasingly complex intrusion detection tasks. The demonstrated efficacy of RIME underscores the potential of bio- and physics-inspired metaheuristics to foster more adaptive, intelligent, and scalable security solutions for the rapidly evolving Internet of Things (IoT) ecosystem.