Draughts: A Decentralized Jump-Based System for Interactive Anonymous Communication ^†

Abstract

Across a diverse landscape of anonymity designs, the dominant paradigms—onion routing (e.g., Tor) and mix networks (e.g., Loopix)—carry intrinsic constraints: long-lived circuits invite traffic correlation, and mixnets often rely on a network-wide state, making it hard to reconcile anonymity and scalability. This paper presents Draughts, a fully decentralized system in which each packet follows an independent and dynamically determined transmission path. Built upon Jump routing, Draughts introduces three key innovations: (i) replacing global state $O\left(N\right)$ with local two-hop neighborhood knowledge $O\left(k^2\right)$; (ii) supporting anonymous replies to enable real-time bidirectional communication; and (iii) proposing a path-length control mechanism that balances anonymity and transmission efficiency. Evaluation results show that Draughts achieves strong sender anonymity, resists predecessor and traffic analysis attacks, and reduces receiver buffer maintenance overhead, achieving a favorable trade-off between anonymity and performance.

1. Introduction

The protection of communication metadata—such as identities and timestamps—represents a crucial frontier in privacy, as its leakage can reveal sensitive social and behavioral patterns even when content is encrypted [1,2]. Despite providing strong content confidentiality, mainstream encrypted platforms like Signal remain vulnerable to metadata analysis [3]. Therefore, anonymous communication systems are essential to address this critical gap in modern privacy infrastructure.

We argue that modern anonymous communication systems should meet three key requirements:

• Anonymous reply: Real-world applications often involve interactive processes—such as browsing, chatting, voting, and complaint submission—requiring initiators to receive responses without revealing their identities.
• Decentralization: Dependence on high-privilege directory servers or global network state introduces trust and scalability issues, as well as potential single points of failure.
• Resistance to traffic analysis: Advanced pattern-recognition techniques can exploit subtle correlations in traffic to de-anonymize users, particularly in systems with deterministic paths or insufficient cover.

The dominant paradigm in anonymous communication relies on onion-style multi-layer encryption, yet this approach faces practical limitations. Its deterministic decryption order forces the entire forwarding path to be determined prior to packet transmission—either via long-lived circuits (e.g., Tor [4]) or via global network knowledge as in mixnets (e.g., Loopix [5,6]). Circuit-based designs reuse fixed paths to reduce path-construction overhead, but recurring patterns render such systems vulnerable to sophisticated traffic analysis attacks [7,8,9]. In contrast, mixnets allow per-packet independent paths (e.g., Sphinx [10]) but depend on global network knowledge, creating scalability and trust bottlenecks.

Hop-by-hop routing (also called random walk) provides an alternative in which the packet’s transmission path is not predetermined by the sender but is dynamically decided by relays—whether to select the next hop or terminate forwarding—thereby supporting decentralization and per-packet independence. However, early schemes such as Crowds [11] exposed packet content to intermediate nodes and relied on directory services to maintain candidate next hops, limiting anonymity and precluding receiver concealment. Jump routing [12], which employs commutative encryption [13,14] (satisfying $E_{k_2}\left(E_{k_1}\left(m\right)\right)=E_{k_1}\left(E_{k_2}\left(m\right)\right)$) to enable packets to remain doubly encrypted while being re-encrypted and decrypted along the path, solved the plaintext exposure problem but still relied on a centralized management server with global visibility and lacked support for anonymous replies.

When each packet follows an independent path, traffic patterns are disrupted, which naturally enhances resistance to traffic analysis. However, when a group of ordered packets must be delivered, the one with the longest path may delay the entire group, causing the receiver’s buffer to continuously grow and degrading transmission performance [15,16]. A natural approach is to attach a variable to each packet that influences relay forwarding decisions to expedite delivery when necessary. Yet the inclusion of such a field inherently risks leaking information, potentially undermining anonymity.

To overcome these challenges, we present Draughts, a decentralized jump-based anonymous communication system with built-in support for anonymous replies. Draughts requires each node to maintain only local neighbor information (up to two hops), thereby eliminating the need for global state. It supports per-packet independent paths to mitigate traffic analysis, provides real-time anonymous replies without revealing initiator identities, and introduces a path-length control algorithm to balance anonymity and transmission performance.

Contributions. This work makes the following contributions:

• We propose Draughts, a jump-based anonymous communication design that eliminates global-state dependence by rethinking inter-node structures and extending commutative-encryption jump routing to support anonymous replies.
• We introduce a chaotic iterative path-length control (CIPLC), which ensures unpredictable hop counts while enabling fast convergence of the iterative process.
• We construct a predecessor attack model that estimates sender probability distributions and measure anonymity using normalized Shannon entropy, demonstrating Draughts’s resilience under local active attacks.
• We develop a traffic analysis attack model that predicts sender distributions from potential initiators and quantify anonymity via cross-entropy metrics, showing Draughts’s resistance to global passive attacks.
• We evaluate Draughts’s transmission performance by analyzing packet latency statistics, out-of-order (OOD) rates for flows of different sizes, and flow completion time (FCT), validating that Draughts achieves a balanced trade-off between anonymity and performance.

This article is an extended version of our conference paper Draughts [17]. Beyond the original design, we introduce the CIPLC, conduct more comprehensive transport-performance experiments (latency, out-of-order rates across flow sizes, and flow completion time), and re-evaluate system anonymity under strengthened predecessor and global traffic-analysis models.

The remainder of this paper is organized as follows: Section 2 reviews related work, including paradigms of anonymous networks, principles and limitations of jump routing, and path-length control algorithms in hop-by-hop routing. Section 3 details the design of Draughts, including network structure, anonymous reply routing, path-length control, and packet format and processing. Section 4 presents attack models for predecessor and traffic analysis attacks and evaluates Draughts’s resistance. Section 5 analyzes transmission performance from the perspectives of latency, packet reordering, and FCT. Finally, Section 6 concludes the paper.

2. Related Work

This section reviews existing anonymous communication paradigms, the design of jump routing, and techniques for controlling path length in hop-by-hop routing. We summarize their key mechanisms, strengths, and limitations to highlight the motivation for our proposed Draughts system.

2.1. Classification of Anonymous Network Paradigms

In recent years, many anonymous communication systems have been proposed. From a core mechanism perspective, the main implementation approaches are based on onion routing, mixnets, Private Information Retrieval (PIR) systems, dead-drop data exchange, and hop-by-hop routing. These mechanisms are not entirely independent and often appear in combination. At the same time, each approach often corresponds to different routing methods: broadcast/multicast, source routing, or hop-by-hop routing [18].

Onion Routing. The most representative systems are Tor and I2P [19]. Since its inception, Tor has been the most popular anonymous communication system, capable of providing real-time, scalable communication services. However, its fixed routing leads to obvious traffic patterns, making it difficult to guarantee anonymity, especially against near-global passive adversaries equipped with machine learning and other AI techniques [20,21,22,23].

Torsk [24] uses a Distributed Hash Table (DHT) to replace directory servers for circuit extension, improving scalability and achieving full decentralization.

HORNET [25], based on the Sphinx format, stores all relay information onion-encrypted in the message header, so that relay nodes no longer need to maintain circuit state information, and data is no longer transmitted as a stream. Each packet can have a completely independent path. The problem, however, is that the sender relies on a large amount of relay node state, which must be periodically downloaded from directory servers.

Compared to Tor, I2P achieves full decentralization. The sender uses a DHT approach to build multiple onion-like tunnels. Packets are sent from the sender’s outbound tunnel, enter the receiver’s inbound tunnel, and are finally delivered to the receiver. Although I2P uses different tunnels for traffic, its essence is still a fixed transmission path, which cannot withstand traffic analysis attacks.

It is clear that within the onion routing paradigm, it is fundamentally difficult to simultaneously achieve traffic analysis resistance, decentralization, and high scalability.

Mixnets. A mixnet can be viewed as combining layered onion routing with packet obfuscation based on active delays. Due to multiple rounds of mixing, traffic patterns are largely eliminated, and mixnets perform well against traffic analysis attacks, regaining attention in recent years. The most representative work is Loopix. Although nodes are still grouped, they no longer share keys. The sender randomly selects a path for each packet and transmits it in the Sphinx format. Additionally, Loopix introduces loopback and dummy-drop traffic to approximate a Poisson process, further strengthening its resistance to traffic analysis. However, Loopix is an asynchronous system and cannot support real-time communication. It also suffers from the same scalability limitations as HORNET. Furthermore, Nym supplements Loopix with Single-Use Reply Blocks (SURBs) [26] to support anonymous reply.

LARMix [27] argues that paths in Loopix can be further optimized to reduce transmission delay. LARMix++ [28] replaces Loopix’s layered architecture with free routing, achieving load balancing for each mix node and further reducing delay.

Although many works continue to improve Loopix, the reliance on global state still causes scalability bottlenecks, and these systems depend on centralized directory servers [29,30]. Moreover, the asynchronous design limits practical deployment.

PIR. PIR applies to anonymous database retrieval. Users hide their true query position using a mask vector, retrieve and reconstruct the target message from multiple replicas, and thus achieve receiver anonymity by obtaining the message without revealing the query intent. Riposte applies PIR in reverse to achieve sender anonymity [31].

Riffle [32] combines a mixnet and PIR. Servers act as both mix nodes and PIR replicas. Data is encrypted, shuffled, and submitted to a main server, which broadcasts to all servers. The main server performs PIR retrieval for the receiver and returns the result. Riffle achieves both sender and receiver anonymity.

In practice, real-time communication using PIR is nearly impossible, but PIR is advantageous for database-style uploading and downloading. Moreover, such systems are difficult to decentralize.

Dead Drops. Communicating parties place or retrieve data at a pre-agreed location to achieve asynchronous information exchange. Vuvuzela [33] also incorporates mixnet-style shuffling: all data is mixed before reaching the server. Users first negotiate a dead-drop ID known only to them and then exchange messages in the corresponding region on the server. Vuvuzela exhibits strong scalability but remains centralized.

DAENet [34] is a P2P architecture built on DHT. In each round, communicating parties select a node as a dead-drop point for message exchange and use Intel SGX to ensure trusted mixing and protocol execution. DAENet achieves decentralization and good scalability, but as the user base grows, DHT routing causes path length and delay to increase significantly. Together with its asynchronous model, communication efficiency is reduced.

Hop-by-Hop Routing. This is also known as random walk. The initiator selects only the first relay node, which then selects the second, and so on, until the message reaches its destination. Crowds is an early anonymous web-browsing tool but relies on a centralized management server. Random forwarding occurs only for the first packet; subsequent requests follow the same path, and responses return along that path. All intermediate nodes can observe traffic in plaintext and see receiver addresses, breaking receiver anonymity. Furthermore, its design is too simple to provide decentralization, scalability, or traffic analysis resistance.

Rumor Riding [35] proposes encrypting the request packet and letting the key and ciphertext perform separate random walks in a P2P network. When they meet, the ciphertext is decrypted and forwarded to the receiver. This mechanism cannot guarantee success for every request and requires nodes to cache large amounts of data. However, intermediate nodes no longer observe plaintext traffic, and the system is decentralized.

Jump routing employs commutative encryption to alternately re-encrypt and decrypt packets, protecting the receiver’s identity so that only the final relay learns it. In contrast to Rumor Riding, which cannot guarantee delivery, Jump routing ensures that packets reliably reach their destinations.

Our prior conference version of Draughts [17] presented a jump-based design with built-in anonymous replies. The present journal article rethinks path-length control and significantly extends evaluation.

2.2. Jump Routing

Jump routing uses commutative encryption to secure traffic and receiver identity, with intermediate nodes selecting the next-next hop rather than the direct next hop. Each intermediate node determines its next-next hop, meaning its own next hop is selected by the previous node. When the path extension is determined to end, the packet is routed to the next hop, which then forwards it to the receiver. Leveraging commutative encryption, the two layers of encryption on a packet can be decrypted in any order. Through continuous re-encryption and decryption, the path is dynamically extended, ensuring two layers of encryption remain until the final stage. Only the last two hops perform decryption without additional re-encryption. This design allows intermediate nodes to know only partial path information, achieving an effect similar to onion routing.

The commutative encryption algorithm is realized in two steps. First, a shared key K is generated based on the Diffie-Hellman (DH) key exchange. Then, K is expanded into a keystream $\left\{k_i\right\}$ using AES in counter mode (AES-CTR). The encryption and decryption of a plaintext sequence $\left\{m_i\right\}$ are performed by bitwise XOR with the keystream:

$$c_i=m_i\oplus k_i,m_i=c_i\oplus k_i.$$

Since XOR satisfies commutativity and associativity, applying different keystreams $\left\{k_i\right\}$ and $\left\{k_i^{\prime }\right\}$ in arbitrary order yields the same result:

$$(m_i\oplus k_i)\oplus k_i^{\prime }=(m_i\oplus k_i^{\prime })\oplus k_i,$$

and performing an even number of XOR operations with distinct keystreams always recovers the original message.

Figure 1 illustrates its routing and encryption process. Despite these strengths in traffic security and path anonymity, Jump routing has clear limitations: it does not support decentralization, high scalability, or anonymous reply.

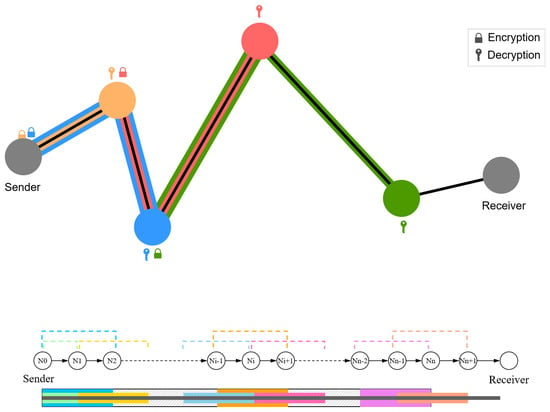
Figure 1. Routing and Encryption Process of Jump Routing.

2.3. Path-Length Control in Hop-by-Hop Routing

In hop-by-hop routing, a packet’s transmission path is not fixed. In systems where all packets of a flow follow the same path, this only scales overall latency without causing packet reordering. However, systems with independent per-packet paths benefit from traffic analysis resistance but face performance degradation: when ordered packets are delivered, the receiver must wait for the slowest packet before processing.

Muñoz-Gea et al. [36] proposed the ADU (Always Down-or-Up) algorithm, which iteratively selects forwarding ranges based on a random variable $u\in [1, M]$. Depending on which sub-interval u falls into, the algorithm constrains the next iteration to an “Always Down” or “Always Up” mode or allows either, thereby controlling path length while preserving anonymity.

Danezis et al. proposed D-Crowds [37], where the sender samples an initial path length from a distribution D as a time-to-live (TTL) value and sends the message with this TTL to a random node. Each intermediate node decrements TTL and forwards the packet until TTL reaches zero, at which point it delivers to the destination. However, TTL inherently reveals hop-count information. If an attacker observes TTL changes and knows D, they may infer path length and sender identity, weakening anonymity.

Although these studies have advanced path-length control, they require additional packet fields and largely assume traditional predecessor attack models, overlooking the potential anonymity risks introduced by such parameters.

3. Draughts Design

This section details the network architecture, routing algorithm, and packet format and processing of Draughts. Symbols used in this paper are summarized in Table 1.

Table 1. Summary of notation.

Symbol	Description
CUR	Current node
NH	Next hop node
NNH	Next-next hop node
PH	Previous hop node
PPH	Previous-previous hop node
SAddr	Sender address
RAddr	Receiver address
${\mathrm{ID}}_{\mathrm{i}}$	Unique identifier of node i

3.1. Threat Model and Goals

3.1.1. Goals

Xia [12] has already addressed receiver anonymity in hop-by-hop routing under Jump routing and proposed a message-based routing architecture that can effectively obfuscate traffic features and strengthen resistance to traffic-analysis attacks. However, as a system, Jump routing is not yet complete: it depends on a global view, does not support anonymous replies, and suffers from severe packet reordering. In Jump routing, when selecting the next-next hop, a node chooses from the global set of nodes, which requires every node to know global state. In addition, Jump routing does not support anonymous replies and only provides one-way anonymous communication. If a requester expects a response from the responder, the requester must reveal its identity so the responder can initiate a new transmission. This disclosure is inappropriate in scenarios such as voting or whistle blowing.

The goal of Draughtsis, drawing on Jump routing, to propose an anonymous communication system that fits real-world needs. It should have the following properties:

• Decentralization achieved by avoiding reliance on a global view;
• Support for anonymous replies to enable anonymous interaction and feedback;
• Mitigation of receiver-side reordering to reduce communication cost.

3.1.2. Threat Model

From a routing standpoint, Draughts adopts a hop-by-hop paradigm and features per-packet path independence; accordingly, this paper primarily considers two classical adversaries.

Predecessor-style adversary: Following Crowds [11], this local active adversary can fully control a node, including its keys. The adversarial node infers the sender by assuming that its predecessor on the path is the sender with the highest probability. Draughts still uses hop-by-hop forwarding, but introduces per-packet path-control parameters that expose a packet’s relative position along its path. We therefore extend the predecessor model: the adversary can derive the current hop number from these fields and estimate a probability distribution over the sender’s identity. See Section 4.1 for details.

Global traffic-analysis adversary: Following Loopix [5], this global active adversary monitors the network topology and, for each node, the timing and counts of incoming and outgoing packets. Suppose two potential senders transmit to the same receiver with identical traffic patterns. The adversary maintains a probability tag for each packet before and after every forwarding event and evaluates predictions upon delivery at the receiver. Our refinements strengthen the temporal causality of the probability tagging, and we use cross-entropy—whose physical meaning here is clearer—as the evaluation metric. See Section 4.2.

3.2. Draughts Architecture

Draughts implements two-hop randomized forwarding: at each hop the CUR forwards to the NH and independently selects the NNH using only neighbor and neighbor-of-neighbor state, thereby avoiding any global directory.

By contrast, the original Jump design also requires each node to determine its NNH but assumes that all nodes can obtain a network-wide directory of nodes that support randomized forwarding—either via a centralized server or via broadcast/multicast synchronization. This assumption limits scalability and contradicts the goal of operating without a global view.

Per-hop operation is purely local. The node at hop i (i.e., $\mathrm{CUR}={\mathrm{Node}}_i$) reads $\mathrm{NH}={\mathrm{Node}}_{i+1}$ from the packet header (chosen by ${\mathrm{Node}}_{i-1}$), and then samples $\mathrm{NNH}={\mathrm{Node}}_{i+2}$ uniformly at random from the neighbor set of NH using its locally maintained neighbor-of-neighbor view. It writes this NNH into the packet for the next hop and forwards the packet to NH. Thus NH is always a direct neighbor of CUR, and NNH is always a direct neighbor of NH.

For example, consider Figure 2. Suppose $\mathrm{CUR}={\mathrm{Node}}_{35}$ receives a packet from $\mathrm{PH}={\mathrm{Node}}_{21}$ whose header already specifies $\mathrm{NH}={\mathrm{Node}}_{33}$; PH previously drew $\mathrm{NNH}={\mathrm{Node}}_{33}$ from ${\mathrm{Node}}_{35}$’s neighbor set $\{25, 33, 2\}$. Node 35 now performs the analogous step for the next hop: using its neighbor-of-neighbor state, it samples a new NNH from the neighbor set of $\mathrm{NH}={\mathrm{Node}}_{33}$ (e.g., from $\{14, 29\}$ choose 14), writes that NNH into the packet, and forwards the packet to $\mathrm{NH}={\mathrm{Node}}_{33}$.

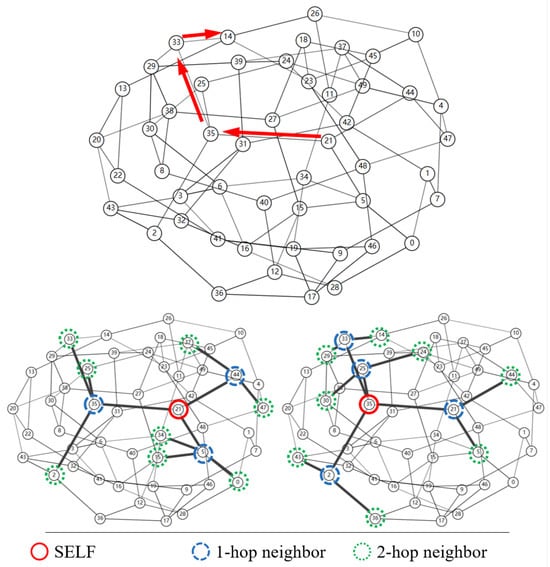
Figure 2. Draughts architecture and topology, with a packet-forwarding example.

This design is decentralized—no node requires a global view. The per-node state reduces from $O\left(N\right)$ to $O\left(k^2\right)$, where k is the average node degree.

3.3. Draughts Routing

Draughts routing builds upon the principles of Jump routing, as shown in Figure 3.

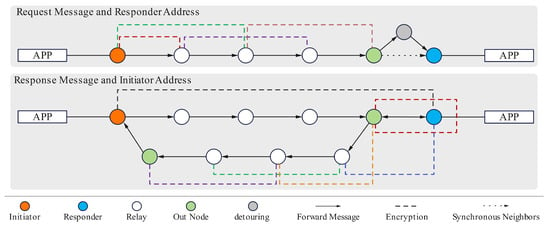
Figure 3. Draughts routing with anonymous replies. The dashed line between two nodes indicates encryption with their shared key.

The routing process starts with the initiator’s identity being commutatively encrypted using a shared key between the initiator and responder. When the packet reaches the last hop, this encrypted field is re-encrypted using a temporary key generated by the last hop. Upon receiving the packet, the responder decrypts this field and re-encrypts it using a temporary shared key with the NNH to encode recipient information for the response packet. Finally, the last hop on the return path fully decrypts the field and forwards the response to the initiator.

Draughts introduces several key design improvements over the original Jump protocol to enhance routing efficiency and anonymity:

• CIPLC: Instead of using a fixed forwarding probability, each intermediate node calculates the forwarding probability using the forwarding parameter $x_f$ carried in the packet. This mechanism controls path length without revealing explicit hop counts, balancing anonymity and delivery efficiency (Section 3.4).
• Localized NNH selection: The NNH is chosen only from the direct neighbors of the NH rather than the global network. This reduces global search overhead while maintaining anonymity.
• Double encryption of initiator information: Initiator data is encrypted first with a temporary key established during initialization and then with a temporary key from the last hop. Upon decryption by the responder, it is re-encrypted for the return path, ensuring confidentiality throughout bidirectional anonymous communication.
• Last-hop neighbor synchronization: The last hop designates itself as the NNH, serving as the entry point for the response phase. Its neighbor data is synchronized to the receiver to enable proper response routing.

To further reduce metadata correlation, a lightweight relay is introduced between the last hop and receiver. This relay does not perform encryption/decryption or routing decisions; it simply forwards the packet. Additionally, link encryption is applied to state information packets before reaching the receiver, and the receiver’s public key for link encryption is included in the original plaintext packet.

3.4. Chaotic Iterative Path-Length Control

Traditional random walk methods decide whether to continue forwarding based on a biased coin with fixed probability $p_f$. This creates a wide and long-tailed distribution of path lengths, which can cause high packet reordering and poor throughput in message-based communication.

CIPLC addresses this by introducing a chaotic iterative function to generate a forwarding parameter x, from which $p_f$ is derived. The function exhibits early-stage randomness and late-stage rapid convergence, ensuring hop counts are unpredictable yet statistically bounded. This improves packet-level delivery efficiency while preserving anonymity, since neither explicit hop counts nor probabilities are revealed.

The iterative function $f\left(x\right)$ and probability function $g\left(x\right)$ are

$$x_{i+1}=f\left(x_i\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{when}{x}_i=0\hfill \\ \left|a·x_i·cos\left({\displaystyle \frac{1}{x_i}}\right)·(1+b·r)\right|\hfill & \mathrm{when}{x}_i\ne 0\hfill \end{array}\right.$$

(1)

where $a,b$ are parameters, and $r\in (-1, 1)$ is uniform random noise.

$$P_f=g\left(x\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{when}\left|x\right|\le \epsilon \hfill \\ 2·\mathrm{sigmoid}\left(\right|c·x\left|\right)-1\hfill & \mathrm{when}\left|x\right|>\epsilon \hfill \end{array}\right.$$

(2)

where c is a parameter and $\mathrm{sigmoid}\left(t\right)=1/(1+e^{-t})$.

Figure 4 shows how x evolves (a) and how $p_f$ is derived (b).

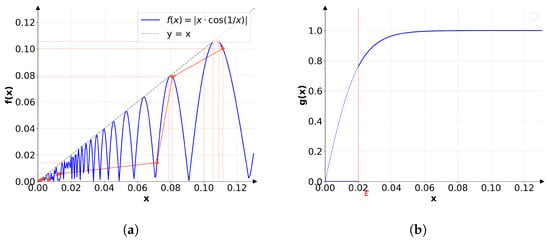
Figure 4. Illustration of the CIPLC algorithm. (a) Convergent iterative function $f\left(x\right)$ with iteration example; (b) Piecewise mapping function $g\left(x\right)$ from x to $P_f$.

We evaluate anonymity enhancement in Section 4.1 and performance benefits in Section 5.

3.5. Packet Format and Processing

Draughts packets are constructed from end-to-end encrypted data. Only next-hop and next-next-hop information is included, unlike Sphinx packets which contain complete path data. All packets are padded to equal length to mitigate traffic analysis.

The packet structure (Figure 5) represents the Draughts data format built upon UDP.

Figure 5. Draughts packet structure.

Intermediate node processing is summarized in Algorithm 1.

Algorithm 1 Draughts Intermediate Node Forwarding Process

Require:  Received Draughts data packet 1: Decrypt header parameters 2: if$I{D}_{NNH}\ne \mathrm{Null}$ then 3:    if $C_{RAddr}$ verification succeeds then 4:        $NextHop\leftarrow$ Receiver 5:    else if CIPLC algorithm result indicates Extend path then 6:        Decrypt $C_{data}$ and $C_{RAddr}$ 7:        $NextHop\leftarrow$ NNH node 8:        Update $I{D}_{NNH}$ with a new value {assign a new NNH for subsequent hops} 9:        Encrypt $C_{data}$ and $C_{RAddr}$ 10:    else 11:        Decrypt $C_{data}$ and $C_{RAddr}$ 12:        $I{D}_{NNH}\leftarrow \mathrm{Null}$ 13:    end if 14: else 15:    Decrypt $C_{data}$ and $C_{RAddr}$ 16:    $I{D}_{NNH}\leftarrow$ self 17:    Encrypt $C_{SAddr}$ 18:    Synchronize neighbor table to receiver 19:    $NextHop\leftarrow$ any neighbor node 20: end if 21: Encrypt header parameters 22: Transmit packet to $NextHop$

The responder restores plaintext from $C_{data}$ and, if a reply is required, performs re-decryption/re-encryption of the sender field before forwarding.

4. Anonymity Evaluation

This section evaluates the anonymity of Draughts under two classical attack models: the predecessor attack and the traffic-analysis attack. In the predecessor-attack setting, the adversary controls a local node and is assumed to know the global network topology. By decrypting and observing the forwarding parameter x (generated by CIPLC) embedded in intercepted packets, the attacker attempts to infer the sender’s identity. We quantify the adversary’s uncertainty—i.e., the attacker’s residual inability to pinpoint the true sender given all observations—using normalized Shannon entropy over the posterior distribution of candidate senders; higher values (closer to 1) indicate that the sender is nearly indistinguishable among all candidates (stronger anonymity), whereas lower values (closer to 0) indicate that the attacker can identify the sender with high

In the traffic-analysis scenario, the adversary does not compromise any network nodes and cannot access packet payloads or control parameters. Instead, it possesses knowledge of the global topology and complete traffic information, including the arrival and departure of packets at each node. Using this information, the attacker correlates input and output packets to estimate the posterior distribution over two potential senders. The estimation accuracy is measured using cross-entropy, where higher values reflect stronger resistance to traffic analysis.

4.1. Predecessor Attack

In this work, the predecessor attack is modeled as a probabilistic inference problem, where the adversary aims to identify the true sender of a message within the network. The adversary is assumed to have the following capabilities:

• Knowledge of the global network topology;
• Full knowledge of the path-length control algorithm (CIPLC) and its model parameters;
• Ability to observe the forwarding parameter x contained in each packet traversing a node under its control.

Unlike a global adversary, the attacker here is local and does not collude with other malicious nodes. The adversary uses the observed parameter x to infer the posterior probability that each node is the sender. Specifically, for each packet, the attacker computes the hop-length probability distribution

$$P(H_i\mid x),i=1,2,\dots ,H_{max},$$

(3)

where $H_i$ denotes the event that the sender is i hops away from the observed node and x is the forwarding parameter carried by the packet.

Using $P(H_i\mid x)$ and the known network topology, the adversary distributes this probability mass across candidate nodes. The resulting probability assignment over all nodes forms a sender probability distribution

$$p=\{p_1,p_2,\dots ,p_n\},\sum _{j=1}^n{p}_j=1,$$

(4)

where $p_j$ represents the inferred probability that node j is the true sender.

To quantify anonymity, we adopt the normalized Shannon entropy:

$$H_{\mathrm{norm}}={\displaystyle \frac{-{\sum }_{j=1}^n{p}_j{log}_2{p}_j}{{log}_{2}n}},$$

(5)

where $H_{\mathrm{norm}}\in [0, 1]$; values closer to 1 indicate higher uncertainty for the adversary, hence stronger anonymity.

Experiments are conducted on a network of $n=3000$ nodes, each maintaining 3 to 5 neighbors, with link delays uniformly sampled from $[150, 300]$ ms. We compare the proposed CIPLC algorithm with two baseline path-length control schemes:

• Traditional fixed-probability decrement;
• ADU (Always-Down-or-Up) algorithm.

Each scheme is evaluated under multiple parameter settings to explore the trade-off between anonymity (entropy) and average path length. A scatter plot of mean path length versus mean entropy illustrates comparative performance (see Figure 6).

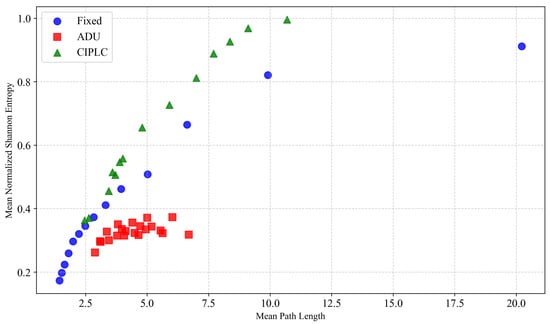
Figure 6. Comparison of average path length and entropy across different path-length control algorithms.

The results indicate that the ADU algorithm yields lower entropy than both the fixed-probability scheme and the proposed CIPLC. This is because ADU mainly optimizes the variance of path lengths (see Section 5 for detailed path-length distribution analysis) while neglecting the anonymity loss caused by the explicit control parameter.

In contrast to the baseline scheme with fixed forwarding probability (i.e., no path-length control information), CIPLC introduces the forwarding parameter x without reducing anonymity and can even achieve slightly higher entropy. This improvement is principled: under the same observation model, CIPLC induces a more uniform sender-probability assignment p than a fixed-probability walk; by Equation (5), greater uniformity of p increases the normalized entropy $H_{norm}$, thereby strengthening anonymity while still allowing explicit control over path length and preserving packet-level efficiency.

4.2. Traffic Analysis Attack

We consider an attacker who has identified two candidate senders $S_1,S_2$ that each emit packets to receiver R at a constant rate. The attacker tags observed packets and maintains, at each node, reception times $t_i$ and prior sender probabilities $P(S_k\mid i)$. Forwarding delay is modeled as a deterministic queuing term plus a stochastic processing term; the total forwarding time for packet i is therefore $T_i\sim \mathcal{N}(t_i+t_p,{\sigma }^2)$, where $t_p$ and ${\sigma }^2$ are the mean and variance of processing delay (the attacker is assumed to have estimated queue lengths, processing rates, and $t_p,\sigma$).

At observation time $\delta$ the attacker sees an outgoing packet and computes the posterior that it originated from sender $S_k$ by Bayes’ rule:

$$P(S_k\mid \delta )={\displaystyle \frac{{\sum }_{i}P(S_k\mid i)f_{T_i}\left(\delta \right)}{{\sum }_i{f}_{T_i}\left(\delta \right)}},f_{T_i}\left(\delta \right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp\left(-{\displaystyle \frac{{(\delta -(t_i+t_p))}^2}{2{\sigma }^2}}\right).$$

This gives an online re-tagging rule the attacker can apply.

We measure attacker accuracy using cross-entropy

$$H(P,Q)=-\sum _{x}P\left(x\right)logQ\left(x\right),$$

where P is the true sender distribution and Q is the attacker estimate. In the two-sender testbed a packet from $S_1$ has $P\left(S_1\right)=1,P\left(S_2\right)=0$ (and vice versa).

Figure 7 illustrates the re-tagging principle: (top) impulses of prior sender probabilities at reception times $t_i$; (middle) forwarding-delay densities $f_{T_i}(·)$; (bottom) Bayes-updated posteriors $P(S_1\mid \delta )$, $P(S_2\mid \delta )$ for a packet forwarded at $\delta$. The example shows how temporal uncertainty and multiple candidate arrivals combine to produce probabilistic re-tagging.

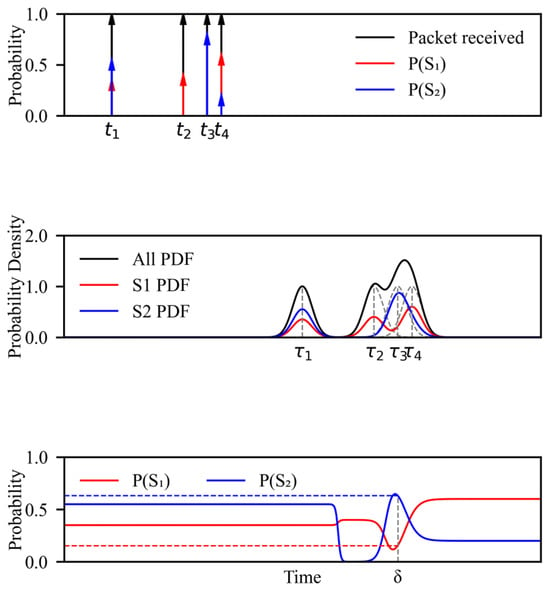
Figure 7. Principle example: re-tagging of an outgoing packet’s sender probability using arrival times and forwarding-delay distributions.

We ran grouped experiments to evaluate attacker cross-entropy under varying local neighbor counts and user populations. Results quantify the trade-off between per-node state and anonymity, and compare Draughts with Jump and Tor under identical background traffic. Figure 8 shows cross-entropy versus neighbor count (neighbor ranges near $[4, 5]$ or $[5, 6]$ yield low cross-entropy while limiting state). Figure 9 compares cross-entropy across systems as user count varies; more users increase cross-entropy (background noise), and Draughts/Jump outperform Tor under the same load.

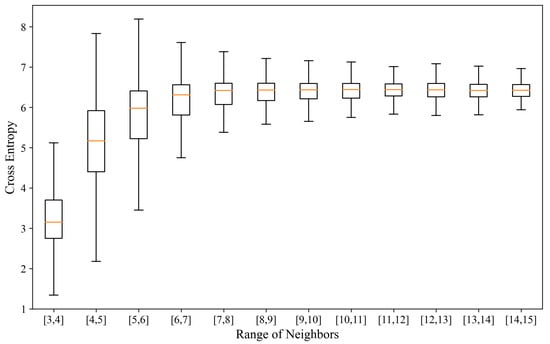
Figure 8. Experimental result: cross-entropy under different local neighbor counts in Draughts.

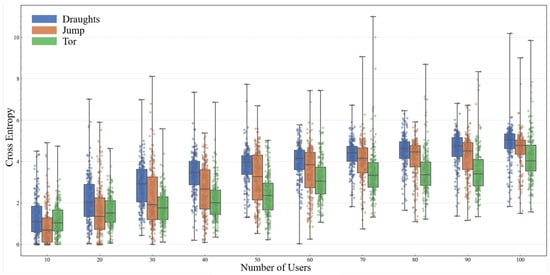
Figure 9. Experimental result: comparison of cross-entropy across Draughts, Jump, and Tor as the number of participating users varies.

In summary, compact local neighbor selection combined with randomized path-length control and probabilistic mixing substantially reduces the effectiveness of predecessor and traffic-analysis attacks while keeping per-node state manageable.

5. Performance Evaluation

In anonymous communication systems based on the random walk paradigm, packet path lengths are not fixed (unlike Tor). Classical forwarding schemes with fixed probabilities often suffer from a prominent long-tail effect in path-length distribution, leading to excessive delays for a subset of packets and potential missed delivery deadlines.

This section focuses on evaluating the transmission performance of Draughts, with an emphasis on how different path-length control algorithms impact network behavior. Three core metrics are assessed: (i) transmission delay, (ii) OOD rate, and (iii) FCT. Three forwarding strategies are compared: a fixed forwarding probability scheme (Fixed), the Always-Down-or-Up (ADU) scheme, and the proposed CIPLC algorithm.

To ensure consistent and rigorous experimental conditions, we configured the network with 3000 nodes, where each node has 4 to 6 neighbors, and the link delay between any two adjacent nodes is randomly distributed within the range of 100 ms to 300 ms. For each of the three algorithms (Fixed, ADU, CIPLC), we tested multiple groups of parameters to control the termination of random walks: each node independently makes a decision for every packet—either continuing the random walk or terminating the forwarding process.

5.1. Transmission Delay Analysis

We conducted grouped experiments for each algorithm and its corresponding parameter combinations. After the system entered a stable operating state, we intercepted 1000 consecutive packets from each group to analyze their delay distribution, and plotted the cumulative distribution functions (CDFs) of packet delay, as shown in Figure 10.

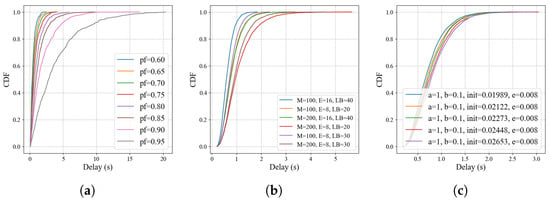
Figure 10. CDF of packet delay for the three algorithms: (a) Fixed, (b) ADU, and (c) CIPLC.

For the Fixed algorithm, we tested fixed forwarding probabilities ($p_f$) ranging from 0.6 to 0.95 (with an increment of 0.05). A packet is forwarded to another node with probability $p_f$, and the random walk is terminated with the complementary probability. As illustrated in Figure 10a, $p_f$ directly governs both path length and delay distribution: a smaller $p_f$ results in shorter path lengths and more concentrated delays, while a larger $p_f$ extends path lengths and worsens delay inhomogeneity. Specifically, as $p_f$ increases, the average delay rises, and the long-tail effect becomes increasingly severe. For instance, when $p_f=0.9$, 80% of packets reach the receiver within 3.18 s, but the slowest packet experiences a delay of up to 16.45 s—this extreme gap between typical and maximum delays highlights the poor delay stability of the Fixed algorithm under high $p_f$ settings.

For the ADU algorithm, which uses parameters M, e, and $LB$ to control random walk termination, a random number u is regenerated in each forwarding step to determine the next action: if u falls within [1, e] or [M-e, M], the random walk terminates; if u falls within [e, $LB$], the next u is restricted to the interval [1, u]; if u falls within [M-$LB$, M], the next u is restricted to [u, M]; and if u falls within [LB, M-$LB$], u is randomly selected from [1, M] without restriction. From the delay CDF in Figure 10b, it is evident that ADU’s delay distribution is significantly more concentrated than that of the Fixed algorithm. This performance advantage arises from ADU’s active termination mechanisms: a larger $e/M$ ratio (i.e., the ratio of e to M) increases the probability of u falling into the termination intervals [1, e] or [M-e, M], accelerating walk termination and reducing path hops; similarly, a larger $LB$ makes it easier for subsequent u values to approach the boundary, further promoting rapid termination. These mechanisms effectively reduce the occurrence of extremely long paths, thereby mitigating the long-tail effect in delay distribution.

For the CIPLC algorithm, we set the parameter $a=1.0$ for all test groups to enhance the randomness of iterations, where b represents the range of each perturbation applied during iterations, and $ϵ$ denotes the threshold for terminating the random walk. As reflected in Figure 10c, CIPLC exhibits a delay distribution that is comparable to ADU in terms of concentration. Its strong performance stems from rapid convergence: while the initial value of the iteration and its proximity to the asymptote of the iteration function $f\left(x\right)$ affect the number of iterations, the applied perturbations ensure that once an iteration approaches the horizontal axis, the process converges quickly and terminates forwarding. This rapid transition from random iteration to convergence avoids overly long paths, resulting in tightly clustered delay distributions.

To further compare the delay distribution characteristics across all algorithms and parameter combinations, we sorted all test groups by their median path length and plotted the transmission delay distribution as a boxplot (Figure 11). As observed from the figure, all algorithms exhibit increased delay dispersion as the average path length increases—this is an inherent trend in random walk-based systems, as longer paths introduce more uncertainty in cumulative delay. However, when different algorithms have similar average path lengths, both ADU and CIPLC demonstrate significantly better delay control: their delay variances are much smaller than that of the Fixed algorithm, which confirms the superiority of ADU and CIPLC in suppressing delay inhomogeneity.

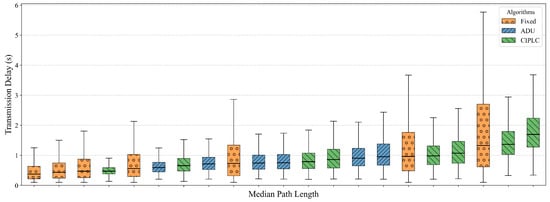
Figure 11. Transmission delay distribution across algorithms and parameters, ordered by median path length.

5.2. Out-of-Order Analysis

Random walk routing inherently leads to packet reordering at the receiver, particularly when each packet in a data flow is transmitted independently and dynamically. Unlike fixed-path routing (e.g., Tor), where packets follow consistent paths and arrive in predictable order, random walk systems allow each packet to take distinct routes—this results in significant differences in arrival times for sequentially sent packets, laying the foundation for reordering issues.

Such reordering imposes critical challenges on the receiver, following a mechanism analogous to the buffer logic in TCP. When transmitting a complete data flow, the receiver cannot deliver packets to the upper layer immediately upon arrival: if a packet with a smaller sequence number (i.e., an earlier-sent packet) is missing, all subsequent packets that arrive in advance must be temporarily stored in a buffer. Only after the missing earlier packet arrives can the receiver sort the buffered packets and deliver them in the correct order. Severe reordering will force the receiver to maintain larger buffers to avoid packet loss due to overflow, but maintaining oversized buffers for each individual flow incurs substantial resource overhead, which is often impractical in real-world deployment.

To quantify packet reordering and its impact on receiver resources, we define the OOD metric as the maximum buffer size required by the receiver to ensure in-order packet delivery. Specifically, this metric represents the largest number of out-of-order packets that must be held in the receiver’s buffer at any moment before the receiver can resume delivering packets in sequence. This definition directly reflects the buffer pressure each path-length control algorithm imposes on the receiver, enabling intuitive and quantitative comparison of algorithm performance.

We conducted continuous packet emission experiments under different flow sizes (i.e., different numbers of packets per data flow). For each flow size and each combination of algorithm parameters, we recorded the maximum buffer size required by the receiver to maintain in-order delivery, and summarized the OOD results in Figure 12.

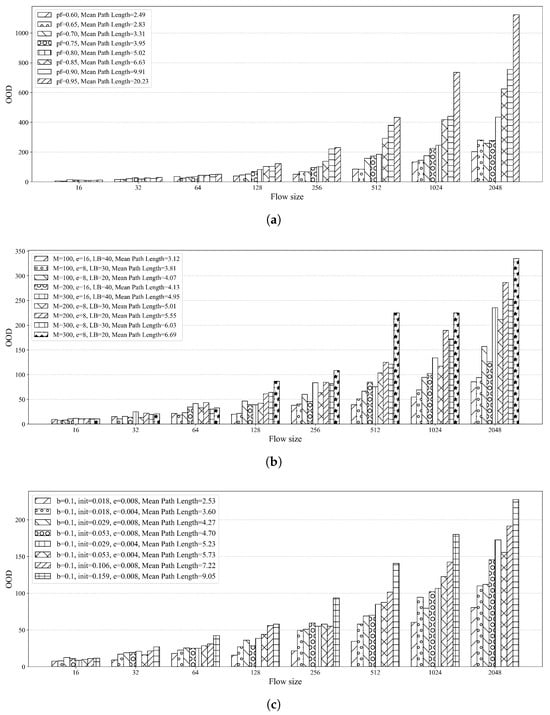
Figure 12. OOD rate (maximum buffer size required) under different flow sizes for the three algorithms: (a) Fixed, (b) ADU, and (c) CIPLC.

From the OOD results, a key trend emerges regarding the relationship between flow size and buffer requirements: as the flow size increases, the maximum buffer size required by the receiver also increases. This trend is consistent with intuition—more packets in a flow create more opportunities for packet reordering, thus demanding a larger buffer to accommodate out-of-order packets. Notably, however, the growth of OOD is not proportional to the growth of flow size. When the flow size doubles (e.g., from 256 packets to 512 packets, or from 512 packets to 1024 packets), the OOD value only increases slightly. The underlying reason lies in the fact that the severity of reordering in a data flow is ultimately determined by the maximum transmission delay of any packet in that flow, which is a characteristic determined by the algorithm’s parameters rather than the flow size itself. Even if the flow size doubles, the longest transmission time of a single packet (governed by the algorithm’s path-length control logic) remains unchanged, thereby bounding the maximum number of out-of-order packets and preventing OOD from growing exponentially with flow size.

The OOD performance of the three algorithms further aligns with the transmission delay distribution results presented in Section 5.1. The Fixed algorithm, which exhibits the most dispersed delay distribution (i.e., the largest gap between the fastest and slowest packet delays), leads to severe packet reordering, forcing the receiver to maintain the largest buffer size. In contrast, ADU and CIPLC both feature more concentrated delay distributions, which significantly reduce the time gaps between the arrival of sequential packets. This reduction in arrival time variance minimizes packet reordering, thereby lowering the buffer size required at the receiver.

A concrete experimental case with consistent comparison conditions (flow size = 512 packets, similar average path lengths across algorithms) further illustrates this advantage. For the Fixed algorithm (configured with $p_f=0.75$, average path length = 3.95 hops), the OOD value reaches 182.5. For the ADU algorithm (configured with $M=100$, $e=8$, $LB=20$, average path length = 4.13 hops), the OOD value is 69.5. For the CIPLC algorithm (configured with $b=0.1$, $x_0=0.029$, $ϵ=0.008$, average path length = 4.24 hops), the OOD value is 64.5. Under this scenario, the OOD values of ADU and CIPLC are only approximately one-third of that of the Fixed algorithm, meaning the receiver’s buffer overhead for this data flow is reduced to roughly one-third of the overhead required when using the Fixed algorithm—representing a substantial improvement in resource efficiency for the receiver.

5.3. Flow Completion Time Analysis

FCT is a key user-centric metric for end-to-end data transmission efficiency, defined as the time from the sender’s transmission of the first packet in a flow to the receiver’s successful reception of all packets. Notably, the last received packet is not necessarily the last sent one, due to packet reordering (analyzed in Section 5.2).

To clarify factors influencing FCT in random walk-based anonymous systems, we use an analytical decomposition model:

$$\mathrm{FCT}\approx T_{\mathrm{avg}}+T_{\mathrm{cont}}+T_{\mathrm{ood}}$$

(6)

Here, $T_{\mathrm{avg}}$ is the mean packet transmission delay, which has a linear correlation with the algorithm’s average path length (validated in Section 5.1) and is determined by algorithm parameters. $T_{\mathrm{cont}}$ is the continuous packet transmission time, dependent on flow size N (number of packets) and the sender’s fixed transmission rate R—under constant R, $T_{\mathrm{cont}}$ increases linearly with N. $T_{\mathrm{ood}}$ is the OOD waiting time, introduced when the receiver waits for delayed out-of-order packets to confirm flow completion, and is linked to the reordering severity analyzed earlier.

The contribution of each component to FCT varies with N. For small N, $T_{\mathrm{cont}}$ is negligible, so FCT is dominated by $T_{\mathrm{avg}}$ and $T_{\mathrm{ood}}$. This makes FCT highly dependent on algorithm performance, with ADU and CIPLC outperforming the Fixed algorithm due to smaller $T_{\mathrm{avg}}$ and $T_{\mathrm{ood}}$. For large N, $T_{\mathrm{cont}}$ becomes dominant (far exceeding $T_{\mathrm{avg}}$), reducing the impact of $T_{\mathrm{avg}}$ and narrowing FCT gaps between algorithms—though $T_{\mathrm{ood}}$ still causes minor differences.

Figure 13 shows FCT across different N under fixed R. To ensure fair comparison, we selected parameter configurations with average path length $\approx 4$ for all algorithms, and their FCT contrast is presented in Figure 14. Key results include: when $N=16$ (smallest tested flow), Fixed’s FCT is nearly twice that of ADU and CIPLC (the largest gap observed); for other small N (e.g., 64, 128), Fixed’s FCT remains higher but the gap is <2-fold; as N increases (e.g., 512, 1024), FCT differences shrink, yet Fixed still has slightly larger FCT—attributed to its larger $T_{\mathrm{ood}}$ from severe reordering (Section 5.2).

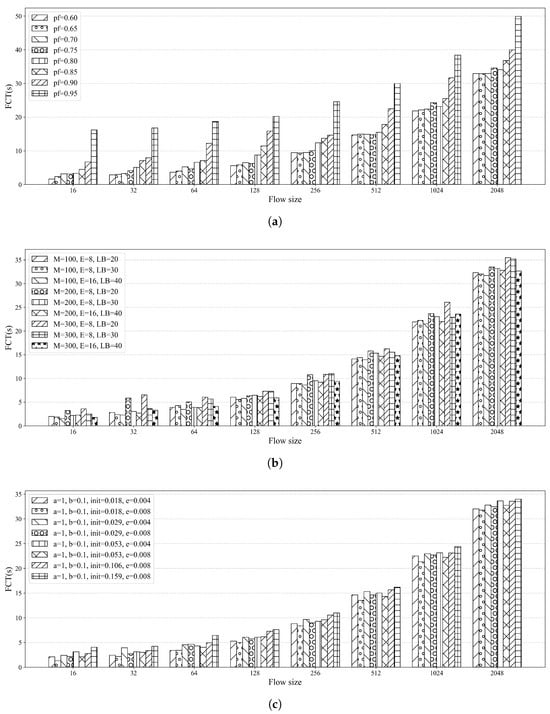
Figure 13. FCT under different flow sizes N for three algorithms: (a) Fixed, (b) ADU, (c) CIPLC.

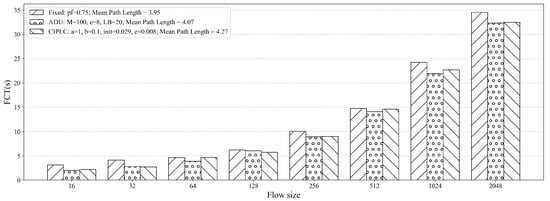
Figure 14. FCT comparison across N under matched mean path length (≈4) for three algorithms.

5.4. Discussion

Anonymous communication systems inherently face a critical trade-off between anonymity preservation and transmission performance: systems with strong resistance to traffic analysis and predecessor attacks often suffer from high latency or packet reordering, while performance-optimized designs may compromise anonymity via explicit parameter leakage. Experimental results of the three path-length control algorithms (Fixed, ADU, CIPLC) clarify this trade-off and guide practical deployment parameters for Draughts.

First, in terms of anonymity (Section 4.1 and Figure 6), both CIPLC and the Fixed scheme achieve significantly higher normalized Shannon entropy than ADU. ADU optimizes path-length variance but introduces explicit control parameters (e.g., M, e, $LB$), leaking path information and weakening resistance to predecessor attacks. CIPLC uses chaotic iterative functions to generate forwarding parameters (x), avoiding hop-count/probability leakage and preserving anonymity comparable to the Fixed scheme—even slightly enhancing entropy in some configurations.

In terms of transmission performance (Section 5.1, Section 5.2 and Section 5.3), CIPLC and ADU outperform the Fixed scheme markedly. The core limitation of the Fixed scheme lies in its long-tail delay distribution (Figure 10a): this inhomogeneity leads to significant packet reordering (OOD), which forces the receiver to maintain excessively large buffers to avoid out-of-order-induced packet loss—imposing heavy resource overhead that is impractical for large-scale or real-time deployment. ADU addresses this via active path termination mechanisms, concentrating delay distributions to reduce OOD and buffer demands; CIPLC aligns with this performance advantage through chaotic iteration, ensuring rapid path convergence without sacrificing randomness. Critically, CIPLC is the only algorithm that matches ADU’s low OOD and controlled delay while retaining the Fixed scheme’s high anonymity.

6. Conclusions

This paper presented Draughts, an anonymous communication system based on the hop-by-hop routing paradigm. Each node only needs to maintain neighbor information within two hops, a feature that eliminates reliance on a global view, making the system fully decentralized and highly scalable. Each data packet has an independent and dynamic transmission path, significantly weakening traffic characteristics and providing strong resistance to traffic analysis attacks. We extended the Jump routing mechanism to support anonymous reply functionality, enabling interactive and feedback-driven communication that better suits real-world needs, such as anonymous voting and reporting. Furthermore, we proposed CIPLC, which balances the anonymity and transmission performance of systems with per-packet independent transmission.

Future work will focus on the detection of malicious nodes among neighbors, large-scale deployment, adaptive parameter optimization, and integration with real-world network stacks to further enhance the system’s robustness and practicality.