It Is Simple to Program with Spiking Neurons

Abstract

Neural and synaptic models that are relatively biologically accurate are easy to use to run efficient and distributed programs. The mechanism described in this paper uses these models to develop cell assemblies with a small number of neurons that persist indefinitely unless stopped. These in turn can be used to implement finite state automata and many other useful components, including cognitive maps and natural language parsers. These components support the development of, among other things, agents in virtual environments. Two spiking neuron agents are described, both able to run using either a standard neural simulator or using neuromorphic hardware. Examples of their behavior are described touching the individual spike level. The component model supports step-wise development, and the example of extending the cognitive mapping mechanism from the simple agent to the full agent is described. Spiking nets support parallelism, use on neuromorphic platforms, and engineering and exploration of multiple subsystems, which in turn can help explore the neural basis of cognitive phenomena. Relationships between these spiking nets and biology are discussed. The code is available to ease reuse by other researchers.

1. Introduction

It is simple to write programs with spiking neurons. Biological brains are made of neurons that communicate, to a large extent, via spikes. Neuroscientists have developed many types of models of these neurons and many simulators for them. A different group, including engineers, has developed neuromorphic hardware that can run neural simulations or emulations very efficiently. It has been shown that simulated and emulated neurons are Turing complete. While there is immense interest in machine learning networks that are inspired by neurons and growing interest in spiking networks for machine learning, there has been less work in processing with neurons. However, using binary cell assemblies (see Section 2), it is simple to develop finite state automata (FSA) with spiking neural networks. These automata can then be used to develop a wide range of programs.

This paper is largely the result of work done on the Human Brain Project (HBP) for Neuromorphic Embodied Agents that Learn (NEAL). The basic idea of NEAL was to build packages that would enable easy development of agents in spiking neurons. The paper initially describes the concept of cell assemblies and how a simple version, binary cell assemblies, can be easily implemented in spiking neurons (Section 2).

As it is easy to develop systems in spiking neurons, code is made available that simplifies the task. The paper then briefly describes the basic neural model, simulator and code (Section 3). Next there is a description of how any FSA can be readily implemented with binary CAs (Section 4), and a description of several other packages: timers, regular grammar parsers, regular grammar generators, planning systems, and cognitive mapping systems (Section 5). Then two novel agents, based entirely on spiking neurons, in a virtual environment (Section 6), are described. This is followed by a section on engineering with neurons (Section 7), a discussion (Section 8), and a conclusion (Section 9).

2. Cell Assemblies

The basic unit of computation in the brain and larger nervous system is the neuron. Neurons are connected by electrical and unidirectional chemical synapses [1]. Like many systems, these are often modeled computationally.

One of the basic concepts of neuropsychology is the cell assembly (CA) [2]. There is significant biological evidence for CAs [3,4], and they are widely used by the community [5]. The theory states that among other things, a semantic memory is represented by a CA, which is a group of neurons with high mutual synaptic strength. Developing that synaptic strength, via Hebbian learning, is the formation of a long-term memory. When the neurons in the CA start to fire at a sufficiently high rate, they cause other neurons in the CA to begin to fire. This leads to CA ignition, a cascade of firing that enables the CA to continue to fire persistently without stimulation from outside the CA. This persistent firing CA is the neural basis of a psychological short-term memory with the psychological memory active as long as the neurons in the CA fire. While the actual topology of an actual biological CA is unclear [6], it is relatively simple to make simulated binary CAs from spiking neurons.

A binary CA is a theoretical construct that works in simulation. It can consist of a small number of neurons with high mutual synaptic strength. If the neurons are all fired at once, they will each stimulate each other, cause the others to fire again, and the CA will continue to fire indefinitely. While this is readily simulated, it is probably biologically inaccurate and at least most biological CAs are not isomorphic to this structure.

The topology that is used in the simulations in this system has 10 leaky integrate-and-fire neurons per CA and is shown in Figure 1. Eight neurons have excitatory synapses to the other nine. The remaining two have inhibitory synapses to the other eight. When the excitatory eight fire, the energy takes some time to travel over the synapses, and the eight neurons continue to fire every 5 ms. in 1 ms. timestep simulations. If extra excitation arrives, causing the eight to fire more rapidly, these cause the two inhibitory neurons to fire, which causes the excitatory neurons to slow down. It is a quite stable system. The CA is called binary because it is either on (firing) or off (not firing).

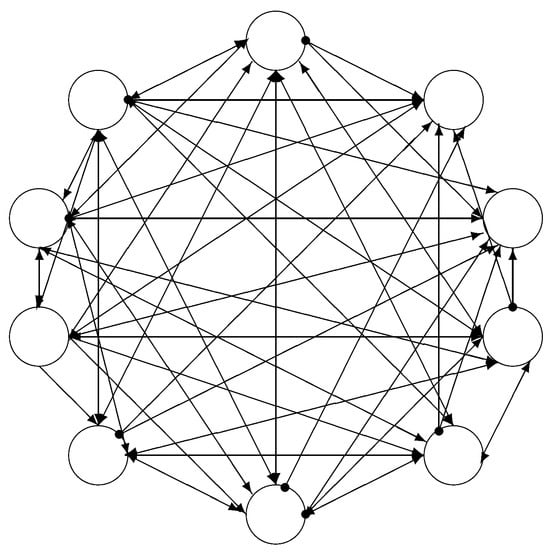
Figure 1. The topology of the binary CA used in NEAL. There are eight excitatory neurons and two inhibitory neurons, all represented by hollow circles. The arrows represent excitatory synapses, and the lines capped with small filled circles are inhibitory synapses.

Other topologies, aside from the 10-neuron topology described here, will work; in earlier systems only five excitatory neurons were used, but the inhibitory neurons added extra stability. Other neural models will work. Initially, they were developed with neurons with adaptation, and pairs of sets fired in an alternating manner so that adaptation did not grow. Binary CAs have even been implemented on asynchronous neuromorphic hardware [7]. They are not particularly biologically plausible (the authors are unaware of any set of 10 neurons so configured in an actual biological brain), but they are a sound mechanism for developing programs.

3. PyNN, Nest and Parameters

The simulations that are described below are based on a widely used leaky integrate and fire neural model [8]. The activation is the current voltage $V_M$. Equation (1) describes the change in voltage, $V_M$ is the membrane potential and $C_M$ is the membrane capacitance. The four currents are the leak current, the currents from excitatory and inhibitory synapses, and the input current (from some external source, which is generally not used in NEAL). The variable currents are governed by Equations (2)–(4). In Equations (2) and (3) $E_{Ex}^{rev}$ and $E_{In}^{rev}$ are the reversal potentials; excitation and inhibition change, respectively, slow as the voltage approaches these reversal potentials. In Equation (4), $V_{rest}$ is the resting potential of the neuron, and ${\tau }_M$ is the leak constant.

$${\displaystyle \frac{d{V}_M}{dt}}={\displaystyle \frac{(-I_{Leak}-I_{Ex}^{syn}-I_{In}^{syn}+I_{Ext})}{C_M}}$$

(1)

$$I_{Exc}^{syn}=G_{Ex}\times (V_M-E_{Ex}^{rev})$$

(2)

$$I_{Inh}^{syn}=G_{In}\times (V_M-E_{In}^{rev})$$

(3)

$$I_{Leak}={\displaystyle \frac{C_M(V_M-V_{rest})}{{\tau }_M}}$$

(4)

$$G_{Ex}\left(t\right)=k_{Ex}\times t\times e^{-{\displaystyle \frac{t}{{\tau }_{Ex}^{syn}}}}$$

(5)

$$G_{In}\left(t\right)=k_{In}\times t\times e^{-{\displaystyle \frac{t}{{\tau }_{In}^{syn}}}}$$

(6)

In Equations (5) and (6), $G_{Ex}$ and $G_{In}$ are the conductance in $\mathrm{m}\mathrm{S}/\mathrm{c}{\mathrm{m}}^2$ to scale the post-synaptic potential amplitudes used in Equations (2) and (3). t is the duration of the time step. The constant $k_{Ex}$ and $k_{In}$ are chosen so that $G_{Ex}\left({\tau }_{Ex}^{syn}\right)=1$ and $G_{In}\left({\tau }_{In}^{syn}\right)=1$. The ${\tau }_{Ex}^{syn}$ and the ${\tau }_{In}^{syn}$ are the decay rate of excitatory and inhibitory synaptic current.

When the voltage reaches the threshold, there is a spike, and the voltage is reset. No current is transferred during the refractory period ${\tau }_{refract}$.

One of the goals of the HBP was to build large simulations, and to have different groups work together on these simulations. One mechanism to encourage this was to make use of common middleware, PyNN [9] (version 0.12.3), a python based library for specifying neural topologies, and interactions. This could be run through different neural simulators, so the same code would run in different simulators with just a switch.

The code below runs in Nest [10] (version 3.7.0) and on SpiNNaker neuromorphic hardware [11]. One of the key parameters in simulators is the time step. All of the code uses a 1 ms. time step as it was an early prerequisite for SpiNNaker, though that has now changed.

Additionally, one component, the cognitive map (see Section 5) uses spike timing dependent plasticity to learn. STDP is a Hebbian learning rule that has a well-supported biological basis [12]. These are provided in Nest and SpiNNaker and are part of the synapse model in PyNN.

The code can be found on https://cwa.mdx.ac.uk/NEAL/simpleProgramming.html (accessed 6 November 2025).

4. CAs and Finite State Automata

A finite state automata (FSA) is a simple theoretical concept that is widely used in computer science [13]. One version of the system is based around a finite number of states and a finite alphabet of inputs. A particular automaton is always in one state and moves to another state on an input from the alphabet. In the recognition mode, the system starts in a particular state, the start state. As it consumes inputs, elements of the alphabet, it transitions through other states one for each input. If the automaton is in a state that is an accepting state when the last input is consumed, the input was a member of that automaton’s language. Any regular language can be recognized, or generated by an FSA. FSAs are widely used, for example, as the basis of simple video game agents, and for tokenization in compilers.

FSAs can be readily implemented in spiking neurons using binary CAs. Each state is represented by a CA. Each item of the input alphabet is represented by a CA. The system is started by igniting the CA that represents the start state. On a transition, both alphabet item CA and current state are firing. Either alone is insufficient to fire neurons in another CA, but together they cause that next state CA to ignite. The next state, CA, in turn inhibits the prior CA and the alphabet CA, so they stop firing, and the system has transitioned states.

This does not quite take care of all deterministic FSAs. There is a problem with a state that transits to itself for, for example, Kleene Plus; that is if a state transits to itself on an input there is a problem with the CA based system because the state both inhibits the alphabet entry and the pre-state, which is itself. This can be accounted for by an intermediate state that is activated, inhibiting both predecessors, and then slides back to the original state shortly thereafter using excitatory synapses. In practice this is rarely used, but it can be implemented using automatic FSA translation, or timers to keep the exact FSA.

It is well known that any non-deterministic FSA can be mechanically converted to a deterministic FSA [13]. This means that empty transitions and transitions to multiple states on a single alphabet presentation can be ignored.

5. FSAs, Timers, Parsers, Generators, Planners, and Cognitive Maps

Special neural components have been developed that can be easily used for new tasks. The parser is based solely on the state machine class, but the others contain novel spiking neuron topology beyond the state machines. Python classes, using pyNN, are used for the components. These can be subclassed for particular applications.

The full CA based NEAL system can also be used to generate timers. These are akin to synfire chains [14]. One state fires and activates another and the second stops the first. A timer component is provided in the code with several variants. Some are self terminating, and some are cyclic. An addition of an extra element in the chain makes the timer persist for longer. In the agents in Section 6, timers are used in the planning and cognitive mapping components.

Four components for particular types of tasks have been developed as base classes in python. The two obvious components are the natural language parser, and the generator. Both are regular grammars but work for any regular grammar. The parser provides populations of words and states, with the words being the elements of the alphabet. To parse a sentence, the universal parsing start state is turned on, then the words are presented. Typically, the final states are used as a signal to another component, for instance to set a goal in planning. In the provided NEAL package, there is an API to create a parser for a particular grammar using a text file. Note that aside from during transitions, only neurons from a CA representing one state of the parser are firing at any given time. As the simulators, neuromorphic systems, and indeed biological brains find neural firing expensive, large grammars are not particularly slower than smaller ones.

The two agents described in Section 6 each have an input language. The simple agent has 13 input sentences and the full agent 22. The simple agent has 34 states and 21 unique input words, each represented by a CA. The full agent’s parser has 84 states and 23 input words. Regular grammars can account for all sentences, but they are not as efficient or psycholinguistically accurate as context free parsers.

The generator is similar to the parser though it produces strings from an alphabet. There are CAs for each state, but only one neuron for each alphabet member. When the alphabet member spikes, it turns off the prior state and moves on. The single neuron spike can be used by another system (e.g., a CABot4 agent) to generate the sentence. A particular generator can be specified by a text file that describes the sentences to be generated. It does allow for embedded phrases but is still regular.

The planning system was inspired by Maes [15]. It is a system composed of separate items for goals, modules, facts and actions. Each item has an activation level and is similar to an interactive activation system [16]. Theoretically, each goal, module and fact item is also similar to a CA that can have varying levels of activation. When each level of activation is managed by a new state, it can be readily implemented with a state machine, and made more flexible with timers. Typically, in these systems facts come from the environment, actions may influence the environment, and the goals can be set from the environment (usually via the parser). These things can also be changed by other internal systems as is done in the CABot4 agents.

The planners for the two agents are identical and are relatively simple. The planning system can be used to approximate interactive activation theory [16] to an arbitrary degree of precision.

The cognitive map component is based around a number of discrete places and a number of objects. Each object can be bound to a place using STDP. The only plastic synapses are between objects and places, with none between objects. An FSA is used to manage the process of binding, unbinding and retrieving queries about the contents of the places or the position of the objects. Timers are also used to manage the correct binding times and query times. When binding, a CA for an object and a place are ignited, and the binding signal is sent to the automata. This then moves through the process of turning on the binding objects and places long enough for STDP to sufficiently strengthen the synapses so that presenting an object will activate (or retrieve) its place and vice versa. Unbinding has been added at the cost of a large timer (see Section 6.3).

6. CABot4

This section has a description of two versions of the Cell Assembly roBot version 4 (CABot4). These agents use a parser, generator, planner and cognitive map components. The agents are based in a virtual environment that has discrete positions.

The environment is a simple window, implemented in python and tcl/tk, that supports text input and output and is connected with the agent. It keeps track of the rooms and objects, which are also stored by the agent in the cognitive map. The user can type things into an input window. For example, the simplest four commands are to turn right or left or move forward or backward. This command sentence is sent to the agent, which then parses the sentence. This sets a goal in the planner that results in an action. The agent then sends this action back to the environment, which modifies the agent’s orientation or position. Communication between the agent and the environment is via spikes.

6.1. Simple CABot4 Construction

The agent communicates with the environment in both Nest and SpiNNaker. In Nest communication is slightly more complicated and uses text files. The environment is in a loop and each time through the loop it checks to see if the agent has sent a command. The agent needs to run for a few simulated ms., then checks for input and output. Input is queried from the spikes of particular neurons, and input causes particular neurons to spike. For example, when the user types in the command Move forward. the environment appends this (with the current time step) to the words.txt file. When the time step is reached by the agent, it turns on the particular neurons associated with the start state and the words, starting the parser, then turning the words on in sequence. When the agent’s planning actions generate a spike on the forward action, this is caught, and appended (with the current time step) to the actions.txt file. Timing also needs to be aligned with the environment setting its time to the most recent action. The environment tends to run ahead.

In SpiNNaker, communication is much simpler, as there is a facility for direct spike injection, and reading spikes at runtime. As timing is more closely aligned, it is also much more efficient.

A slightly more complex command is Move left. Its associated goal turns on the turn left action followed, timer delayed, by a forward.

Commands such as Where is the apple? do not use the planner. They activate the cognitive map, which in turn activates the generator. It responds with something like It is in room 2. In both CABot4 systems there are four locations (rooms 1 to 4) and two objects (an apple and a banana). Their location can be specified at start-up.

The agent manages the communication between the different components. Of course, all of the communication is with neural firing, spikes.

6.2. Simple CABot4 Results

The simple agent consists of 2034 neurons, 550 in the parser, 399 in the planner, 360 in the generator, and 770 in the cognitive map. An example run is shown in Figure 2. Each dot represents a spike by a neuron at a particular time step.

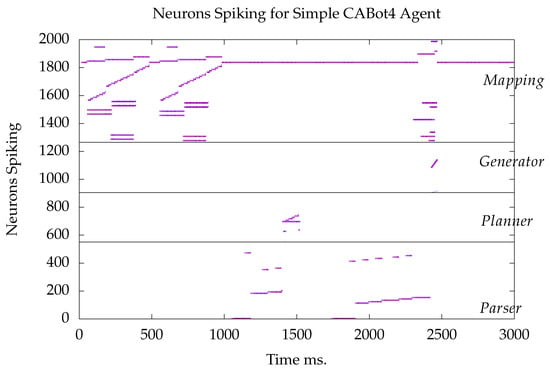
Figure 2. A rastergram for a run of the simple CABot4 agent. The black horizontal lines mark the boundaries of the subsystems. The spikes represent the behavior when the apple and banana are initially placed in rooms 1 and 2, respectively, followed by the command Move left., and the query Where is the apple?

As the dots are very close together both horizontally and vertically, they often look like lines. An active binary CA is typically eight neurons firing every 5 ms. If it remains active for a long time it looks like a line. For example, the start state of the cognitive map automaton population contains the neurons numbered from 1834 to 1843. There is a long line from 984 ms. to 2334 ms. where this state is continuously firing.

The user submitted two commands from the environment. The first is to Move left., and the second is Where is the apple?

Initially, the cognitive map automaton is started, and the automaton runs throughout the simulation. The agent is set up to bind two objects to two places, and this starts at 50 ms, but once done the map returns to the start state. Eventually, when the query Where is the apple? is submitted at 1760 ms., the map changes state to retrieve the answer and then returns to the start state. The bottom stripes in the cognitive mapping section of the figure are the bound object and place cells. The two short stripes around 2400 ms. are the apple CA (the longer) and the room 2 CA that is ignited from the apple CA via the plastic synapses.

The bottom section of Figure 2 has the parse states and parse words. Both user commands begin by starting the initial parse state. The words above the states cause the transitions of states. For the first command Move left., a goal is set in the planner. When the goal is met, the parser is stopped. An action is produced that is sent to the environment to update the agent’s position. Here the parser goes to a final state at 1301 ms. and that state switches on the goal move left in the planner. That goal comes on at 1402 ms, switching off its associated parsing final state. That goal starts an neuron 664 and is a short horizontal line from 1402 to 1522 ms. The diagonal line is a series of module CAs, and the two lower dots are actions that are handled by the environment.

The second user input is the query Where is the apple?, which is parsed. This then interacts with the cognitive map to retrieve the answer, which signals the generator to generate the sentence It is in room 2. The generator is the neurons between 904 and 1263. The spikes from the generator’s words are sent to the environment, which is displayed to the user.

6.3. Full CABot4 Construction

The overall mechanism of building components allows a useful degree of compartmentalization. The use of PyNN supports use on a laptop with no additional hardware using Nest and the use of a larger number of neurons in real time on SpiNNaker. Nest can also be used on supercomputers.

The simple CABot4 agent is based on slightly updated code from the NEAL project from the HBP. The code has been updated to, for example, use Python 3, and newer versions of Nest and the SpiNNaker software. The simple agent was implemented for this paper, but it largely used old components.

There was however a problem with the cognitive mapping component. Once a place and an object are bound, via STDP, they cannot be unbound. The new version of the component allows a pair to be unbound. As STDP increases the weight of at least one of a pair of synapses from neuron A to neuron B or from neuron B to neuron A when both fire at roughly the same time, unbinding is relatively complex. In the modified cognitive mapping system, it is done when individually bound neurons (8 from each CA), are activated by a timer in a relatively precise manner. This takes about 13 s of simulation time to decouple the place and object.

This timer contains over 2500 neurons, so the new agent uses more than twice as many neurons as the simple CABot4 agent. This means that the simulation slowed markedly on the Nest version on laptops; on a typical machine, a simulated second took about a minute. Fortunately, the use of a single SpiNNaker board supports hundreds of thousands of neurons in real time. So, on SpiNNaker, the CABot4 agent actually works quite efficiently to explore the environment, set and unset bindings, and ask about what is bound. All of the commands from the simple agent work in the new agent. New commands were also added to the parser to put a particular object in a room, or remove it (to bind and unbind objects with rooms). Similarly, the generator was also extended to say nothing was in a room or an object was not in any room.

6.4. Full CABot4 Results

An example run of the full CABot4 agent is shown in Figure 3. This comes from the SpiNNaker version of the system. Unlike the simple agent, binding is explicitly specified by the user.

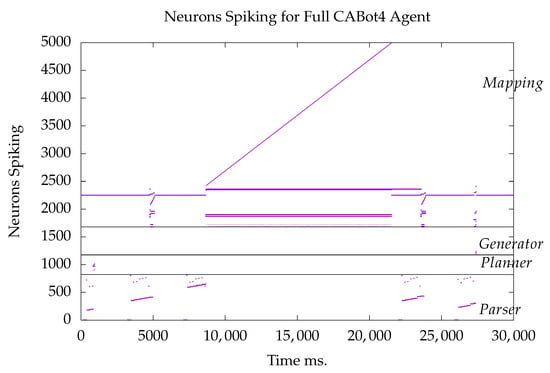
Figure 3. A rastergram for a run of the full CABot4 system. The spikes represent the behavior when the commands, Move left., Put the apple in room 1., Remove the apple from room 1., Put the apple in room 2., and What room is the apple in? are given in sequence with some time between commands. The black horizontal lines mark the boundaries of the subsystems.

In Figure 3, the user has specified five commands. The first is the simple Move left. command. In the full agent, the parsing neurons are from 0 to 819, and the command can be seen in the first second along with the response in the planning neurons, which are from 820 to 1146.

The next command is to Put the apple in room 1. in the third second. That command causes the cognitive mapping neurons (at the top) to fire, binding the first object, the apple, to the first place, room 1. The automaton that manages the cognitive map is active throughout the run around the 2200 neurons. This is more or less identical to the binding execution at the beginning of the simple CABot4 Figure 2, though only one room object pair are bound.

The command Remove apple from room 1. is given at 8 s. Once it is parsed it starts the unbinding process in the cognitive map. This is supported by the active CA for room 1 and apple in non-binding neurons, the two upper stripes of activation below the automaton. The timer runs for the duration, the long, steeply sloping line. This turns on the appropriate binding neurons in room 1 and apple CAs, the lower wobbly line. It is wobbly because only one neuron in either of the binding CAs is active at a time. This is sufficient to reduce the synaptic weight between each of the 16 bound neurons so that the ignition of one CA does not cause the other to ignite. They are unbound.

There has been conjecture that once bound, no bound pair of neurons can be unbound by Hebbian learning [17]. Here is an example that shows it can be done, though it is carefully engineered. It is also worth noting that the very long timer might be replaced by two smaller timers, where the first advances the second in a sort of embedded loop.

The fourth command (about 22 s) is Put the apple in room 2., which causes the first object, the apple, to be bound to the second place, room 2. This is then confirmed by the final user query.

What room is the apple in? is processed starting near 26 s. This command interacts with the cognitive map and the generator to give the answer It is in room 2. This is done by a small number of generator neurons that each fire once, a very simple chain.

7. Parallelism and Engineering with Neurons

Section 2, Section 3, Section 4, Section 5 and Section 6 have given a method to develop systems in spiking neurons, example classes, and example agents that run on standard computers and on SpiNNaker. Section 7.1 describes a method to develop similar systems with other neural models and other neuromorphic platforms. Section 7.2 discusses parallelism, and ways to extend NEAL and NEAL-like systems.

7.1. Other Neuromorphic Platforms

Note that NEAL has taken advantage of the regularity of Nest and SpiNNaker simulation of neurons. That is, given the same system and inputs, the network will behave identically each time it is run. This can simplify system development, as most errors are reproducible. SpiNNaker processing is on ARM chips, a von Neumann architecture. One board has 768 chips and the billion neuron system, accessible remotely, has a million chips. this means that neurons are still simulated on SpiNNaker and it is reasonably simple to change neural and synaptic models on the same system. Randomness can be introduced into neural models, but processing is generally regular.

On the other hand, it is likely that biology is more stochastic, with neurons changing behavior. Of course, the neural models used are capable of taking advantage of stochastic behavior, and CA models can account for that by redundancy. Binary CAs were emulated on the BrainScaleS neuromorphic system [7]. Unlike SpiNNaker, this platform is quite stochastic with neurons and synapses behaving much less regularly. BrainScaleS neural model is prespecified, but it does emulate neural behavior 10,000 times faster than real time. None the less, the basic FSA mechanism, worked on BrainScaleS, and should work on many different neuron types and neuromorphic platforms.

The key is the robustness of the binary CA structure. Above, a 10 neuron structure, with eight excitatory and two inhibitory neurons was used. With a given input, each neuron behaves the same, but if the neurons have variance, the stability of the overall group behavior can increase with the number of neurons.

Note that reverberate and fire neurons (e.g., [18]) are difficult to use with the current FSA mechanism. A reverberate and fire neuron can be caused to fire when it is inhibited a great deal. The FSA mechanism above depends on a great deal of inhibition making the basic system difficult to use for reverberate and fire neurons.

On the other hand, earlier versions of the system used adaptive neurons [19], and binary CAs can be implemented relatively easily with these, and fire persistently indefinitely. This was done by making a binary CA out of two sets of neurons that fire in alternating steps so that adaptation is avoided. A ring of sets of neurons could be used if necessary.

7.2. Parallelism and Extending NEAL

What are the benefits of engineering, for instance, an agent in spiking neurons? While there are long-term benefits of helping to understand the brain and cognition, there is the immediate benefit of parallelism exploited by parallel hardware. There is also the software engineering benefit of a single communication mechanism, spikes.

The CABot4 agents use four separate FSAs, but there is really no limit to the number of FSAs that can be used simultaneously in a spiking neural system. In NEAL, there are a small number of neurons per CA and neurons can be expensive to simulate, even in neuromorphic hardware. Thus a small CA supports more functionality, in this context, by being more efficient. So, on the billion neuron SpiNNaker machine in Manchester, 100 million states could be simulated in parallel in real time. If each FSA had 90 states and an alphabet of ten, a million FSAs could run simultaneously.

Parallelism is not limited to FSAs, but is at the neural level. Aside from input and output (via spikes), each neuron behaves largely independently of other neurons.

The NEAL components use FSAs, but neurons are not limited to implementing FSAs. An earlier version of this work developed a context free parser in spiking neurons that bound semantic items for a short time with short term potentiation [20]. Another earlier version of the system processed visual input, but this used thousands of neurons. Indeed, there is a vast suite of calculation that has been done with spiking neurons. Eliasmith [21] has developed large models that are based around vector processing with spiking neurons. Balanced networks [22] can implement dynamical variables, which are readily used for robots. It is far from clear how biological brains do calculations, but spiking nets can calculate in many ways, and these nets can be readily integrated with a NEAL based system.

FSAs can be used as scaffolding for these systems. A simple version of a component can be developed with FSAs and then an improved version can be used with extra mechanisms, or indeed no FSAs at all.

A great deal of communication in the brain is between neurons with chemical synapses. When a neuron spikes, it emits neurotransmitters that are received by a small number of other neurons. It is simple to develop a component in isolation, and provide an API that communicates with spikes. The four components described in Section 5, natural language parsing and generation, planning, and cognitive mapping, were all developed in isolation and communicate (both internally and externally) with spikes. The enhancement of the simple agent to the full agent (Section 6) shows the modification of the cognitive mapping component and the extension of the particular natural language parsing and generation components.

Indeed, there is no need for each neuron to be of the same type, so dozens of neural models can be supported simultaneously. Different components could use different neural models, and be developed independently. Different versions of components could be compared for efficiency, effectiveness and biological accuracy. Different agents could be assembled from these components for different tasks and for comparison on the same task. Many neuromorphic systems work only on specific neural models, but again, different neuromorphic systems could be combined, and integrated with standard simulated systems, like Nest. They can all communicate with spikes.

8. Discussion and Future Work

The authors propose that following the human model is the best way to get to full-fledged, Turing test passing AI. That means being embodied, and following psychological, and neural models. In this paper, the agents are embodied [23] in a simple virtual environment, though work has been done elsewhere with spiking neurons and cell assembly based physical robots. While it is difficult to make bodies, it is relatively easy to simulate them in virtual environments. This brief discussion centers on progress on this task in NEAL.

8.1. Discussion: Current Behavior

The CABot4 spiking agents say something about the spiking neural behavior. The framework has been used to develop relatively sophisticated agents that perform complex tasks. It can also be used to explore biological behavior, and a single system can be used for both. One difficulty is that it takes a lot of neurons to generate behavior. However, a mouse has much less than a billion neurons, and behaves. So, it can theoretically be simulated on the large SpiNNaker machine in real time.

Parallel hardware architectures, such as neuromorphic systems, can support real time performance of systems using large numbers of neurons. More sophisticated agents can be built with more neurons, as is shown by the difference between the simple and full CABot4 agents. These large neural systems can then be used to drive agents embodied in both physical and virtual environments.

NEAL components have also been used in systems that are not agents. For example, they have been used to support several neurocognitive models. These can then be used in new agents that are accurate, both psychologically and neurally, on a particular neurocognitive task. While it is likely that there are a vast number of neural solutions to a particular task, showing a particular solution is important.

The binary CA model can be used repeatedly to cover a range of tasks. If the particular CA systems are kept separate, or largely separate, these new systems can be developed in isolation, and relatively easily combined, as has been done in developing the CABot4 agents. As mentioned in Section 6, time to run the simulation increases rapidly in Nest, but not in SpiNNaker below a threshold, typically 768,000 neurons per SpiNNaker board. Time to load the topology and download spike data after the simulation does increase. Environments are managed separately, but more complex environments can be used to explore more complicated agent behavior.

While it is useful to explore the behavior of human brains, it is also useful to explore other mammals and other animals such as birds to understand brain functioning. There is evidence [24] of CAs in mice, and they have much smaller brains. Understanding mouse CA behavior should be very useful. It is likely that much mouse neural processing is similar to human neural processing.

Growing discovery of neural functionality can be supported by exploration of function by simulation. Particular functions can be explored with simulated neurons, and NEAL can be used as scaffolding for this function. For example, a structure for associative memory could be simulated, and this could interact with the language component via a NEAL parser. This can be used to explore basic spiking neuron functionality, brain circuit functionality, and neuro-psychological functionality.

The binary CA model is not particularly biologically accurate, but there is substantial evidence for CAs in biological brains. More flexible CAs could be explored and introduced for new components, or indeed to replace existing binary CA systems. These could also involve many different types of neurons and plasticity. More complex neural models can be more expensive to simulate, but can also lead to more biologically accurate systems. In SpiNNaker, more complex models can be used along with simpler models, but the number of complex neurons simulated on a particular core will be reduced.

Biologically, it is difficult to measure the spiking behavior of 10,000 neurons or more [25]. However, unlike the full biological systems, but like other simulations, spike trains from NEAL simulations can readily be evaluated. Models of particular psychological tasks, implemented in a spiking net, can be compared to neurobiological studies of animals performing the same task. For instance, Zipser et al.’s [26] short term memory task could be implemented in spiking neurons. The performance of particular neurons could match the neurons they recorded.

8.2. Future Work

Future work using NEAL includes context free grammar parsing, recurrent network machine learning, and developmental psychological models with long-lasting agents. The authors are currently working on bringing the context free natural language parsing model [20] into the NEAL framework. It still needs memory activation to replace a stack, but this is only needed in relatively rare constructs. Hopefully, episodic memory and associative memory components can be added to improve the range of neurolinguistic phenomena the model supports.

Of course, the big win from neural networks is learning. The cognitive mapping component uses learning, but it is restricted to a small finite number of pairs of components. It is currently unclear how the brain uses its neurons to learn. CA based systems have already implemented reinforcement learning with Hebbian learning [27]. Some good work is being done with spiking nets and STDP for categorization (for example [28]) but performance is below gradient descent methods. Moreover it is not clear how biological networks learn the topology that enables them to behave as they do. The highly recurrent nature of the topology, unlike most modern connectionist learning systems, is probably necessary to efficiently learn to behave effectively in dynamic environments. Using recurrent structures, the authors hope to include machine learning tasks into NEAL based agents. Hopefully, this will address catastrophic forgetting problems.

On the other hand, spiking nets can be used as a replacement for standard deep net technology that is less expensive in terms of electricity. The problem is that deep nets are typically implemented in neurons with differentiable continuously valued output, and the gradient descent on the error function can calculated. With spikes, it is difficult to calculate the gradient, and thus spiking versions typically perform worse than those that are continuously valued. One attempt to address this problem [29] has made significant progress. This work focuses on the time to first spike of the target neuron, and realizes a spiking system with a low spike rate, which is more electrically efficient. This work could be integrated into the NEAL framework with both Nest and SpiNNaker. Both would develop two systems, one for training and one for use. The training system would use Stanojevic et al.’s [29] learning rule, and the other system would have static synapses. New synaptic and neural models can readily be integrated into Nest, SpiNNaker and NEAL. A complication can arise with calculating the error. In Nest, this could be done between training epochs and the error injected back into the training mechanism, similar to the way the Nest agents run for a few ms. then interact with the environment. This is more difficult in SpiNNaker, but can probably be managed. Another mechanism would be to calculate the error in neurons. The PyNN python class that built these neural topologies to implement these mathematics could form its own component.

Developmental psychological issues may also be addressed with structural plasticity. Agents that exist for long periods of time (months) in relatively complex environments can be used to explore problems such as the frame problem. NEAL controlled robots may be used for physical environments. This could include structural plasticity, which could also be aligned with biological evidence of early biological topological formation.

The approach used in the CABots can integrate this work, but it is focused on actual behavior. One way to gauge the success of a CABot4 agent is to evaluate its external behavior, its movement and natural language answers. The work reported above and most other simulated spiking network research is based around unidirectional chemical synapses. The use of gap junctions [30] is worth exploring, and could easily be incorporated into the NEAL framework. This could be particularly useful to integrate with balance networks [22] as most current simulations make use of biologically unrealistic fast transmission. That could then be used to control a robot. Also one of the advantages of SpiNNaker is that boards can be used on mobile robots as a controller.

Note that one group has proposed an algebra to make use of CAs [31], but if one chooses to develop systems with spiking neurons using CAs, the binary CA mechanism is much simpler. While the basic code that is provided can be used with existing simulators, the concept is also simple. So, it is simple to make one’s own binary CA model, and then use that as a basis to develop spiking network systems. Of course, implementing Papadimitriou et al.’s [31] work in NEAL is an option.

There are many simulations of biological neurons, both individually, and in groups. For example, one project [32] simulates several hundred thousand cortical neurons. It uses accurate models of neurons and an accurate topology. When run, the neurons spike like neurons in the cortex, following several known behaviors. The simulations run on supercomputers much slower than real time, and the neurons do not actually perform a task. Replacing these models with simpler models and larger time steps may enable duplication on, for instance, the billion neuron SpiNNaker machine. Getting the cortical model to perform another task would be a step toward more biologically accurate computation.

9. Conclusions

As the Human Brain Project has ended, research needs to move forward with small groups. The authors encourage people to use NEAL itself and the PyNN framework, and are happy to discuss this with potential collaborators. If anyone makes a component, please share it.

This paper has shown that the NEAL framework is functional and extendable. It can be used to implement spiking networks that control agents in both Nest and SpiNNaker, and that component can be reused in other systems. Using NEAL, it is simple to program with spiking neurons.

Neuromorphic computation has been proposed as an answer to the computational load of LLMs and other deep nets. Spiking nets certainly can be used for these tasks. However, the limits of deep nets are obvious, and raise the truly fascinating questions involved in understanding how brains work. In silico spiking net models, and indeed NEAL, can help address these questions.