Abstract
This paper studies the pilot design for compressed sensing (CS)-based sparse channel estimation in multi-input–multi-output orthogonal frequency division multiplexing (MIMO-OFDM) systems. To improve the performance of estimating multiple jointly sparse channels, based on the assumption that the modulus of the pilot symbol at each pilot carrier position is equal to a constant, the pilot is currently allocated by means of lowering the sensing matrix’s total coherence (TC). However, according to the block compressed sensing (BCS) theory, the recovery ability of the sensing matrix is determined by the block coherence (BC) and subblock coherence (SC), which should be as small as possible. Therefore, we propose a novel scheme, which designs the pilot by simultaneously minimizing the TC, BC, and SC of the sensing matrix to improve the channel estimation accuracy. We first formulate the jointly sparse channel estimation as a block sparse signal recovery problem, and the pilot allocation problem is comprised of allocating the pilot index for each transmitter and allocating the pilot symbol at each carrier. Then, we derive the error bound of BCS-based channel estimation, where the pilot symbols bear any value. Finally, a novel sequential joint criterion design (SJCD) method is proposed to design pilots with a joint criterion, where the pilot pattern and pilot power are designed by BC and TC, respectively. Simulation results show that, compared with existing algorithms, the proposed algorithm can achieve a better channel estimation performance in terms of normalized mean square error (NMSE) and bit error rate (BER).
1. Introduction
Traditional channel estimation methods estimate all channel coefficients whose values are considered nonzero, and the associated channel estimation error is high. Extensive works have shown that wireless channels exhibit sparsity [1,2,3]. Most values on the sampling tap of the channel are zero or near zero while the length of the discrete channel is large, and the number of taps with significant values is small. That is, the channel can be modeled as a sparse signal, and sparse channels can be estimated by compressed sensing. Therefore, the sparsity can be used as a priori information to improve the channel estimation accuracy and achieve a better channel estimation accuracy than traditional methods with a small overhead. Orthogonal frequency division multiplexing (OFDM) is a key technology for sixth-generation communications such as smart metasurfaces since it combats inter-symbol interference by adding a cyclic prefix at the beginning and has high spectral efficiency [4,5,6,7]. For MIMO-OFDM systems whose number of pilot carriers has a linear relationship with the number of transmitting antennas, compressed sensing-based channel estimation can reduce the overhead and improve the spectral efficiency. Compressed sensing, which is capable of exploiting the inherent sparsity of signals, has been widely used to acquire channels with fewer pilot overheads in comparison with conventional methods [8,9,10]. It is well known that the evenly distributed pilot pattern is optimal for traditional channel estimation methods such as maximum likelihood estimation, maximum a posteriori estimation, etc. Nevertheless, an equally spaced pilot distribution is not optimal for estimating channels by means of CS theory [2,11,12]. According to the CS theory, the sensing matrix that better satisfies the restricted isometry property (RIP) can guarantee successful sparse recovery with a high probability [1,13,14]. However, checking if the RIP is met by a matrix is prohibitively high-cost. Alternatively, one can evaluate the sensing matrix based on the mutual coherence (MC), which is equivalent to RIP and easy to compute [15,16].
According to CS, the smaller the MC, the more accurate the sparse recovery. Therefore, a lot of research efforts have been devoted to minimizing the MC of the sensing matrix to enable sparse recovery with a low error bound. In CS-based orthogonal frequency division multiplexing (OFDM) channel estimation, a sensing matrix is determined by a pilot, and hence one can design the pilot to minimize the MC of the sensing matrix in order to improve the channel estimation performance. Pilot pattern design is investigated based on the MC for the OFDM system in [17,18,19,20,21], where the power of each pilot symbol is assumed to be equal. A scheme using modified discrete stochastic approximation to allocate the pilot index position is proposed in [17]. Ref. [18] derives that the set forming the cyclic different set (CDS) is the optimum pilot carrier index. In addition, a scheme using discrete stochastic approximation is introduced to allocate the pilot pattern. Nevertheless, only when the pilot carrier number and the carrier number are unique paired values does CDS exist. A tree-based backward pilot generation is proposed in [22]. Ref. [19] formulates the pilot design problem as an optimal column selection problem, and a novel technique employing cross-entropy optimization with constraints is put forward to generate an optimum pilot allocation. Ref. [20] presents three pilot design schemes to obtain a near-optimal pilot pattern, and simulation results verify the effectiveness of the proposed methods. Ref. [23] introduces a new estimation of distribution algorithm to allocate the pilot carrier positions.
For MIMO-OFDM systems, ref. [24,25] propose a genetic algorithm-based method to optimize the pilot pattern, to minimize the MC of the sensing matrix. Based on the distributed compressed sensing (DCS) theory, a genetic algorithm-based method of optimizing the pilot locations is presented in [25]. Ref. [26] studies the co-sparsity of channels in massive multi-input–multi-output systems, and joint estimating channels are conducted by the presented block sparse model. Ref. [15] proposes a joint allocation of pilot carrier index and pilot symbol, where pilot carrier indices and pilot symbols are sequentially designed by minimizing the MC of the sensing matrix. In [20], a search scheme that minimizes the MC of the sensing associated with each transmitting antenna is proposed for MIMO-OFDM assuming the modulus of pilot symbols is the same. Allocating pilots for MIMO-OFDM systems with superposed pilots is investigated, and two pilot design methods are proposed in [27] in which the pilot power and pilot pattern are jointly designed based on the MC. Since MIMO-OFDM systems are usually equipped with co-located antennas, channels between different transmit-and-receive antenna pairs have a common support but different nonzero coefficients, namely joint sparsity [28]. For channels with joint sparsity, which can be employed in DCS or BCS-based sparse recovery, it is verified that BCS-based sparse channel recovery with block orthogonal matching pursuit (BOMP) is equivalent to DCS-based sparse channel recovery with simultaneous orthogonal matching pursuit in [25]. Ref. [25] designs pilot patterns for DCS-based channel estimation with the TC, which better reflects the average effect of the sensing matrix on the reconstruction algorithms [29,30]. In [31], a generalized shift invariance property is used to allocate the pilot indices where the values of the MC of all pilot sets are the same. Ref. [32] allocates pilot indices of different transmitters based on the identical multi-set intersection property. However, ref. [25] designs the pilot assuming that the pilot values are equal, which is not optimal from the point of view of minimizing the TC or MC. Additionally, pilot design based on the TC may yield a resulting sensing matrix with a large MC and vice versa. The works aimed at designing the pilot based on different criteria are summarized in Table 1.

Table 1.
Comparison of pilot design methods for MIMO-OFDM.
In a nutshell, either MC or TC is employed to allocate the pilots in the aforementioned works. However, CS theory shows that a smaller TC as well as a smaller MC simultaneously guarantee a lower sparse recovery error bound compared with that with a small TC or MC alone [25,29]. Therefore, the pilot is jointly designed with TC and MC for an OFDM system in [33], where the pilot pattern is designed by minimizing MC, and the pilot power is designed by minimizing TC. As a consequence, a sensing matrix better meeting TC, BC, as well as SC simultaneously improves the sparse recovery accuracy. On the one hand, for MIMO-OFDM systems with co-sparse channels, we hope to further reduce the overhead to improve the spectral efficiency. However, to the best of the authors’ knowledge, no paper has studied how to design pilots using multiple criteria for evaluating the sensing matrix to improve the channel estimation performance. This inspires us to solve the problem of optimizing the pilot using multiple sensing matrix evaluation methods for MIMO-OFDM channel estimation.
Our research differs from existing studies. First, unlike MIMO-OFDM systems based on compressed sensing, where pilots are designed separately for each antenna, the sensing matrix based on block compressed sensing theory is a composite sensing matrix composed of matrices corresponding to the pilots for each transmitting antenna. Therefore, pilot design requires the concurrent design of multiple pilots, and we propose a novel algorithm realizing simultaneous design for multiple transmitting antennas. Second, no known papers have proposed designing pilots using multiple criteria. We propose a novel scheme that designs patterns based on block compressed sensing theory and allocates pilot symbols based on TC. Third, no papers have mathematically modeled pilot symbol design based on TC for MIMO-OFDM systems. This paper models this problem as a constrained mathematical optimization problem and solves it using the optimization software. Furthermore, we derive a lower bound on the channel estimation performance based on block compressed sensing theory. Finally, a novel design scheme is presented, which enables the use of multiple criteria for allocating pilot carriers and pilot symbols.
To the best of the authors’ knowledge, no works study pilot design to minimize the TC, BC, and SC of the sensing matrix simultaneously for joint sparse channel estimation in MIMO-OFDM systems. Based on compressed sensing theory, this paper proposes a scheme for allocating MIMO-OFDM pilots using multiple sensing matrix evaluation criteria and establishes a mathematical model for simultaneously allocating pilot symbols of multiple transmitters in a MIMO-OFDM system. Based on the channel estimation mathematical model and block compressed sensing theory, the relationship between block coherence of the sensing matrix and MC of the submatrices that constitute the sensing matrix, as well as the lower bound on the channel estimation performance of MIMO-OFDM systems, is derived. Finally, a novel pilot design method is proposed to implement pilot design using multiple evaluation criteria. When a certain number of pilots is used, sparse sampling and signal reconstruction using the sensing matrix generated by the proposed method can achieve a smaller channel estimation mean square error. In other words, the proposed pilot design method can reduce the number of pilots and improve spectral efficiency of the MIMO-OFDM system. Therefore, it has important theoretical and practical value in guiding the design of pilots for channel estimation in practical MIMO-OFDM systems. This study provides a novel method for designing pilots using multiple criteria for evaluating the sensing matrix. Compared with existing methods, the system using the pilot designed in this paper can achieve a better channel estimation performance, and our work advances the technique of block compressed sensing-based sparse MIMO-OFDM channel estimation. Furthermore, the numerical simulation results also verify the effectiveness of the method proposed in this paper.
Compared with the existing methods, we face the following three challenges in allocating pilots for MIMO-OFDM systems using multiple criteria. First, because existing pilot design schemes are all based on a single criterion, there is no referable implementation solution in the known literature on how to use multiple criteria to allocate pilots for MIMO-OFDM systems. This is the first challenge of this paper. Second, because the sensing matrix is a composite matrix composed of partial Fourier transform matrices corresponding to different antennas, multiple pilot symbols need to be designed simultaneously. As a consequence, the means to efficiently allocate pilot index positions for multiple antennas at the same time is the second challenge of this paper. Third, when designing pilot symbols on pilot carriers, an approach to mathematically model the simultaneous design of pilot symbols for multiple antennas is not available in the literature. This is the third challenge encountered in this paper. Exploring the mathematical modeling of pilot symbol allocation and the pilot design implementation method are the key issues studied in this paper and also its important contributions.
In this paper, the problem of allocating pilots is investigated by jointly minimizing the TC, BC, and SC of the sensing matrix for MIMO-OFDM systems, where the channels exhibit joint sparsity. We first formulate the jointly sparse channel estimate as a block sparse recovery problem and the allocating pilots as a multiple-objective optimization problem. The pilot design is decomposed into allocating a discrete carrier index optimization as well as the continuous pilot symbol optimization. Then, we derive the error bound of the BCS-based channel estimation. Finally, a novel allocation scheme is put forward to design pilots based on the BC and TC simultaneously, where allocating pilot symbols by means of the TC is formulated as a constrained second-order cone programming (SOCP) problem.
It is found that the scheme of designing pilots using multiple criteria is feasible. All pilot design schemes in the existing literature design pilots based on a single criterion, which is actually based on either MC or TC. The sensing matrix corresponding to the pilot optimized by MC has a large value of TC, and vice versa. A sensing matrix with a large MC or TC value will degrade the accuracy of signal reconstruction. Unlike existing methods that design pilots via a single criterion, we use multiple criteria to design pilots simultaneously. The proposed method can suppress the BC and TC of the sensing matrix. The sensing matrix determined by the designed pilot will not have a relatively large BC and TC. Our research improves the accuracy of sparse channel estimation of MIMO-OFDM systems. The effectiveness of the suggested approach evaluated by NMSE and BER has been validated by simulation results. More explicitly, the contributions of this article are as follows:
- A pilot design architecture, which minimizes TC, BC, and SC of the sensing matrix, is proposed for MIMO-OFDM systems. In view of the SC equaling zero, this architecture first designs the pilot pattern based on the BC, and then it designs the pilot power based on the TC. As a result, both BC and TC of the designed sensing matrix are decreased.
- Based on the BCS, we formulate the pilot power design problem as a multi-objective optimization problem with multiple constraints. Then, based on the definition of BC, we derive the relationship between MC and BC in the BCS-based MIMO-OFDM channel estimation model and the error bound for the BCS-based channel estimation method.
- A novel SJCD algorithm is proposed to design pilots for MIMO-OFDM systems. The SJCD method first designs the pilot pattern based on the BC and then the pilot value based on the TC. In the procedure of the pilot pattern design, only the pilot pattern for the transmitter with the largest BC is optimized, which effectively reduces the computational complexity. It is shown in numerical simulation that the channel estimation method employing the SJCD algorithm performs the best.
Notations: Vector are represented by boldface lowercase letters. represents the complex modulus. and are the norm and Frobenius norm, respectively. Matrices are denoted by uppercase letters. , , and denote the i-th row, the i-th column, and the (i,j)-th entry of , respectively. , , , , and are a matrix normalizing each column of to one, a matrix with the (i,j)-th entry equaling , an identity matrix, an all-zero matrix, and an all-one matrix, respectively. is the spectrum norm of , where is the largest eigenvalue of the matrix involved. and are the transpose and conjugate transpose, respectively. denotes the inner product.
2. Block Compressed Sensing, System Model, and Problem Formulation
2.1. Block Compressed Sensing
2.1.1. Block Sparsity
For signals with a block structure, the literature [34] proposes the BCS theory, which employs the inherent block structure of signals to improve the sparse recovery performance. Consider a sparse signal of size , and assume that the signal is obtained by the sensing matrix of size according to (1),
where is the noise.
A block sparse signal can be considered as the signal obtained by cascading block signals as (2)
where represents the l-th block of , and the size of each block is . Similar to (2), the matrix can be regarded as a cascade of subblocks , of size and denoted by
where is a vector of size .
Define
where is an indicator function that counts the number of nonzero subblocks in the vector . If has at most nonzero blocks, that is, , the sparse signal is called a block sparse signal with the block sparsity . When , the block sparse signal becomes a traditional sparse signal. The nonzero coefficients of the block sparse signal are located only in the nonzero blocks.
2.1.2. Block Coherence and Subblock Coherence
After obtaining the sampled vector of the block sparse signal using Equation (1), in order to recover the original block sparse signal, we need to reconstruct the original signal using the measured value vector and the sensing matrix . Because traditional sparse signal reconstruction algorithms do not employ the block sparsity of the signal during the sparse signal reconstruction process, sparse block signals can be recovered with a high probability by methods such as block matching pursuit, block orthogonal matching pursuit (BOMP), or the mixed -optimization program. It is shown in [35] that BOMP yields perfect recovery if satisfies appropriate block restricted isometry propert (BRIP). However, computing BRIP is an NP-hard problem, and it is impossible to evaluate whether a matrix satisfies BRIP in a finite time. Therefore, the literature [34] uses BC and SC to evaluate the sensing matrix.
BC is defined as
where , the BC describes the global characteristics of the sensing matrix, and the local characteristics of the sensing matrix are evaluated by the SC, which is defined as
is a normalized matrix by columns. When , we have .
It is shown in [34] that the smaller the BC and SC of the sensing matrix, the more accurate the sparse signal reconstructed by the BOMP algorithm. Therefore, the goal of pilot design is to ensure that the sensing matrix determined by the designed pilot has a small BC and SC.
2.2. System Model and Problem Formulation
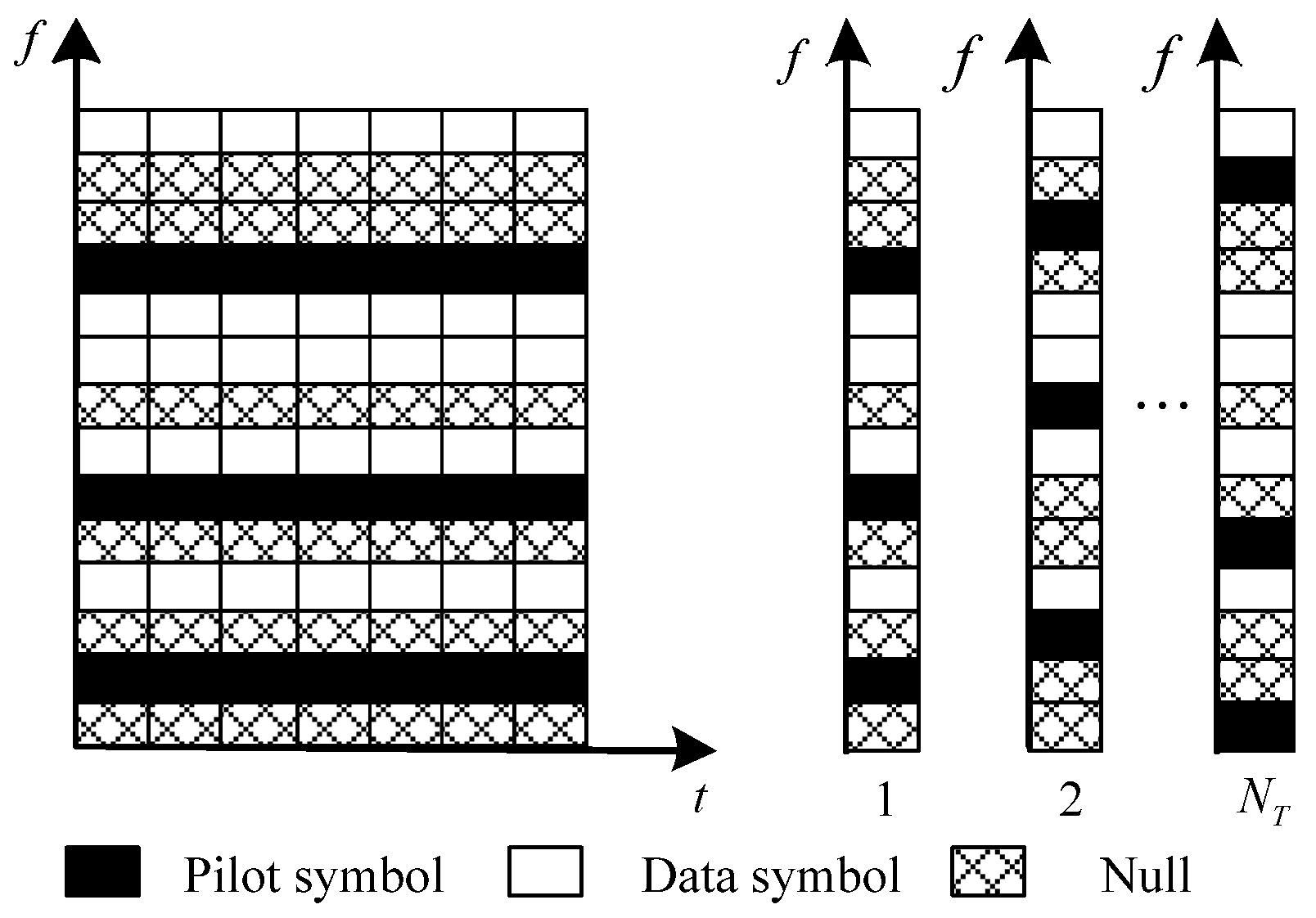
Consider a MIMO-OFDM system with transmitting antennas and receiver antennas. Assume that an OFDM symbol consists of subcarriers in which subcarriers are preserved for carrying pilot symbols. Denote all available index sets and the pilot index set, namely the pilot pattern of the transmitting antenna, by , , , , , respectively. Let , denote the symbols transmitted at the -th transmitting antenna, where , at the subcarrier set are pilot symbols. The pilot carrier index sets of each antenna in the MIMO-OFDM system are orthogonal to each other; that is, the carrier index sets in the frequency domain do not overlap. Each transmitter employs comb-type pilots, as shown in Figure 1, i.e., .
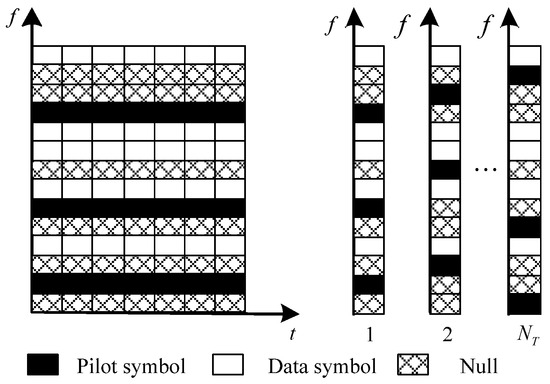
Figure 1.
Frequency-domain orthogonal pilot pattern.
Assume that the channel between the transmitter and receiver is a frequency-selective fading channel, and the multipath delays are in integral numbers of sampling. The channel is modeled as
is the discrete channel sampling length, and is the complex gain of the l-th tap. The channel is K-sparse if the number of nonzero items in is K and .
Suppose that the cyclic prefix of OFDM is no less than L. The parallel data and pilots are modulated using inverse discrete Fourier transform, and the modulated signal is transmitted through the wireless channels. After sampling and the discrete Fourier transform, the received pilot symbol vector denoted by at the receiver from the transmitter is
where is a diagonal matrix with pilot symbols on its main diagonal, and is the pilot index set of the -th transmitter. The channel between the transmitter and the receiver is represented as , which is the time-domain sparse signal with the maximum length and nonzero factors. is the additive white Gaussian noise. is a partial Fourier transformation matrix formed by extracting a full Fourier transformation matrix with rows indexed by and the first columns.
We consider a MIMO-OFDM system in which the channel exhibits joint sparsity, which means that the position of the nonzero fading factors of
is the common set
while the coefficients of each
are distinct.
We denote , and is given by
Concatenating all received pilot symbols from transmitters at the receiver gives
Denote by a permutation matrix
, , , where
is the
column of
and
satisfies
.
We concatenate
into a column vector, giving
where
,
,
,
is a block sparse signal with
blocks of each size
and
nonzero blocks, and
is the sensing matrix with
of size
given by
Equation (11) is a BCS sampling method, and can be reconstructed with block sparse recovery algorithms [29]. According to the BCS, is the sensing matrix, and we aim to optimize by the pilot design. The global properties and local properties of the sensing matrix are evaluated by the BC and SC, respectively. The BC of is
. Subblock coherence is
where is a matrix with normalized columns. Denote by
Because only entries on the diagonal of the are nonzero and the entries on the main diagonal are all column vectors, the columns of are orthogonal to each other. As a consequence, any two different columns of the matrix are orthogonal to each other and . The research in this article exploits orthogonal comb-type pilots; that is, the index sets of pilot carriers of different transmitters do not overlap. Therefore, always holds if the MIMO-OFDM system uses the comb-type pilots. It is shown that the smaller the BC and SC, the more accurate the sparse recovery [25]. In essence, both are generalizations of the MC, which is defined as
where .
Since the MC only measures the worst incoherence between any two distinct columns [36] and the TC quantifies the average recovery behavior of the sensing matrix, [25] minimizes the TC defined in the Equation (19) by designing pilot patterns
In this paper, instead of minimizing TC alone, we design pilots by minimizing the BC, SC, and TC simultaneously, as shown in Equation (20) for improving the BCS-based sparse channel estimation performance. Equation (20) is a multi-objective optimization problem, and the pilot power as well as the pilot pattern of each transmitting antenna need to be solved.
3. Proposed Method
3.1. Analysis of Block Coherence and Error Bound
For BCS-based sparse channel estimation, we first give the following Theorem 1, which shows that the BC is equivalent to the MC for the sensing matrix .
Theorem 1.
In Equation (11), the BC of is .
Proof of Theorem 1.
Define that , is the column of , and is the matrix by normalizing each column of to one. According to the definition of the BC, we have
□
Then the error bound for the sparse recovery with the BOMP is given in Theorem 2.
Theorem 2.
Denote by a block sparse channel of size with K nonzero blocks, is the i-th block of size , the estimate of
is
, is the smallest nonzero value of , , is the additive white Gaussian noise, and is the SC of the sensing matrix . For some constant , if (22) holds,
and then the sparse recovery error of BCS with BOMP is bounded by
Proof of Theorem 2.
According to [37], a block signal of at most nonzero blocks satisfies
where is the size of each block of the block signal, and is the dimension of the block signal. For some constant , the sparse recovery error of the BOMP is bounded by
We have , , , and since columns of are orthogonal. We can obtain Equations (22) and (23) by substituting , , and into Equations (24) and (25), respectively. □
3.2. Pilot Design with Joint Criterion
Pilot carrier positions and pilot symbols are two degrees of freedom, and henceforth two degrees of freedom can be assigned to two criteria, respectively, in allocating pilots. In order to minimize the TC, BC, and SC of the sensing matrix, we first allocate the pilot index with the BC and then allocate the pilot power with the TC since the SC equals zero. In the procedure of pilot pattern design with the BC, we optimize with the MC instead of optimizing with the BC since Equation (21) shows that is equivalent to . Equations (18) and (19) indicate that we only need to optimize , whereas and are determined by the pilot pattern vector and the pilot power vector .
It is noted that there are distinct entries in . We then devise the pilot symbol of the transmitter with the constraint that the sum of squares of the Frobenius norm of the pilot symbol vector is [27], and to avoid the pilot power that is too small or too large, where represents the minimum of , and where the maximum value of is [15]. Then, Equation (20) can be reformulated as
Equation (26) is a constrained multiple-objective optimization problem. As the maximum inner product of any pair of columns in equals the MC and each entry of takes values from a discrete and limited integer set , assuming pilot values are equal, we first obtain with the MC by solving
Then, given , we obtain by solving
Given a , the moduli of entries located on the main diagonals of are the same because of the periodicity of base , and the off-diagonal has entries. Note that is a symmetric matrix. Hence, (28) can be formulated as
where is a block diagonal matrix given by
where , and . Equation (29) can be cast as
Equation (32) is an SOCP problem, and the associated pilot power can be uniquely determined by solving Equation (32) with optimization software.
3.3. Pilot Design Scheme
To devise the pilot based on the MC and TC, we initially allocate the pilot indices of all transmitters according to the MC. Next, the TC is used to allocate the pilot symbols. Unlike the single-input–single-output orthogonal frequency-division multiplexing (SISO-OFDM) system, the MIMO-OFDM system has multiple antennas and must ensure that the pilots of each antenna are mutually orthogonal. Therefore, we cascade the pilots of transmitting antennas to form as follows.
The consecutive elements from to are the pilot pattern of the antenna. When optimizing the , we replace with all available pilot index positions one by one, thus achieving pilot patterns without duplicate indexes.
It is shown in Equation (21) that the MC of is determined by the matrix with the largest MC. Therefore, the index of the transmitting antenna corresponding to the sensing matrix with the largest MC can be found first, and then we optimize each entry of the associated pilot index set. Specifically, denote that , , and then we only optimize elements from to . Otherwise, assuming each entry of is replaced one by one, it will result in invalid pilot index replacements.
Now, we elaborate the proposed SJCD, which is an adaption of Algorithm 2 in [20], to allocate the pilot with the two criteria simultaneously. Firstly, initialize the number of transmitters, receivers, outer iterations, inner iterations, and pilot subcarriers as ,, , , and , respectively. Initialize ,, , and , where , , , and are used for storing pilot power vectors, values of the TC, the output pilot patterns, and the available index set, respectively. There are iterations in SJCD. The outer iteration is conducted times, and the inner iterations are conducted times. At first, SJCD carries out outer iterations. In the iteration of the outer loop, we randomly generate a pilot pattern with entries and set . Then, the algorithm executes the inner iterations. The inner iteration is ended while to avoid an invalid iteration since is the same as the iteration result . Otherwise, we update . Since is a block diagonal matrix and , we optimize consecutive entries of in the inner iteration. We first obtain and then in turn update elements from to of . To be specific, replace with each element of once. Then, we compute the MC with respect to each element of and pick out the index meeting
After iterations, we calculate the pilot power by solving Equation (32) and store in , as shown in line 15 of Algorithm 1. Then, assign the value of to . After assigning the value of to , end the iteration. After iterations of the outer loop, we obtain index sets preserved in every row of and the associated square of modulus of each pilot symbols preserved in every row of , respectively.
Then, the index of the smallest value in the vector is obtained. As a consequence, the corresponding pilot index set and pilot powers are achieved. The pilot pattern and the pilot power of each subcarrier of the transmitter are and , respectively. The detailed procedure of SJCD is summarized in Algorithm 1.
| Algorithm 1 Sequential Joint Criterion Design (SJCD) |
 |
The computational complexity of the SJCD mainly depends on solving the pilot pattern in line 11 and the pilot powers in line 15. In line 11, operations are carried out to pick out the best index. Therefore, the total complexity of the inner iterations equals . The complexity of solving the SOCP in line 15 is [30] and hence the total complexity is . The complexities of MMC and MTC are and , respectively, where and denote generations and individuals, respectively. Compared with MMC and MTC, the SJCD needs to compute an SOCP problem with multiple constraints and solve the discrete pilot index sets. Therefore, the SJCD has a higher complexity.
4. Simulation Result
We consider a MIMO-OFDM system, setting system parameters to , , and . The maximum channel length is , where nonzero taps are uniformly and randomly distributed in , and the fading taps satisfy . We compare four methods: (1) Extension Scheme 1 in [20]. We also allocate the pilot symbol by means of the MC according to [15] since the equal pilot powers are not optimal. We call this method the minimizing MC (MMC) method. (2) Genetic algorithm (GA) in [25]. We call this method the minimizing TC (MTC) method. In GA, the number of generations, the number of individuals, the generation gap, the crossover probability, and the mutation probability are 5000, 100, 0.9, 0.7, and 0.6, respectively. (3) Proposed SJCD. (4) Randomly generated pilot patterns, denoted by random, with pilot powers being . In MMC and SJCD, we set , , , , and . For fair comparison, the data symbol is modulated with binary phase shift keying and normalized to in the four methods. Since the common sparsity is considered, nonzero channel taps of different channels are the same and randomly placed among L taps. The channel gain of each path is independent and identically distributed. The mean of the channel gain is zero and the associated variance is one. The runtime of SJCD is 37.89 s and 227.15 s for and , respectively. The solver used in this paper is the Mosek and the program is conducted on a computer with Intel Core i5-3210M CPU and 12 GB RAM.
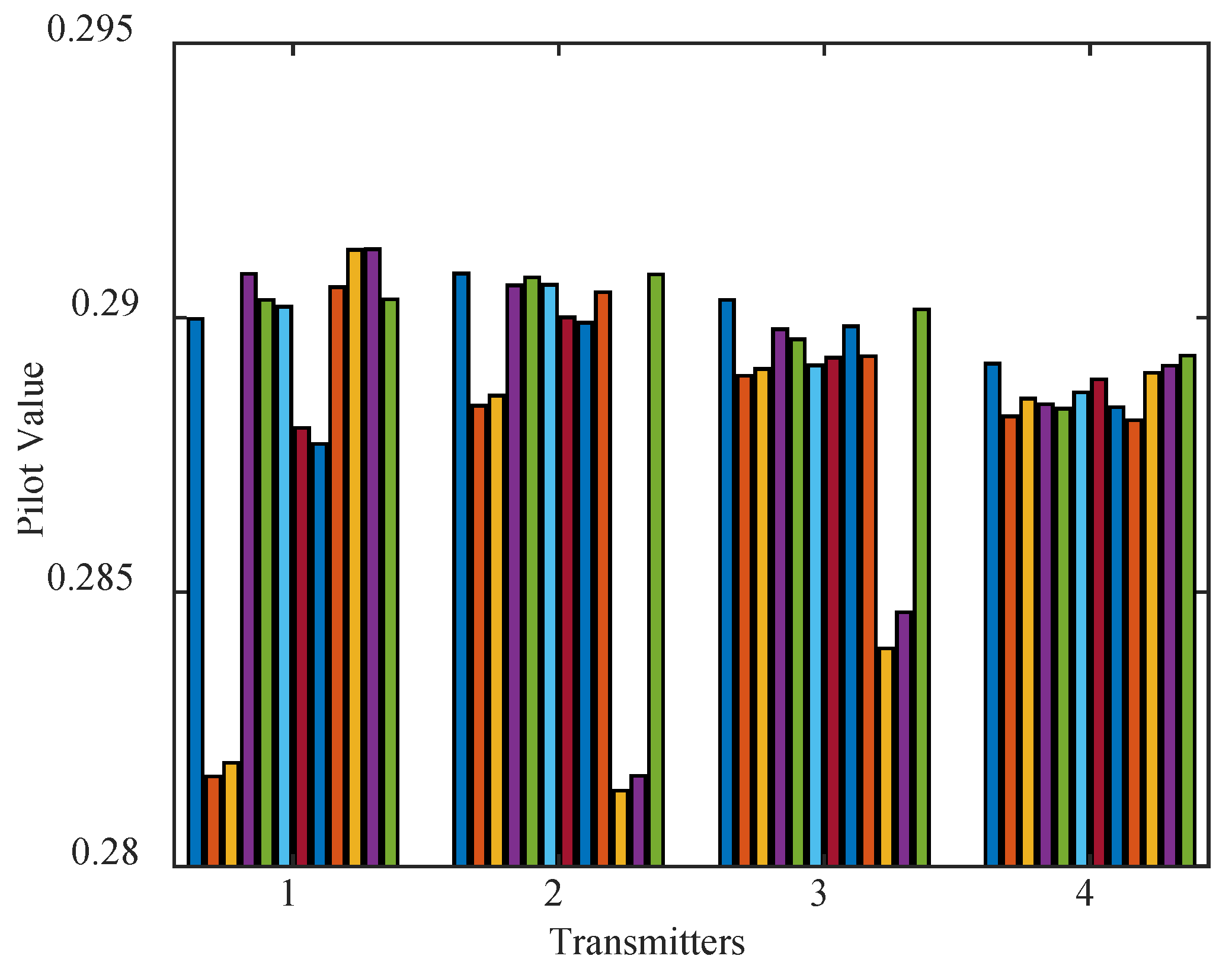
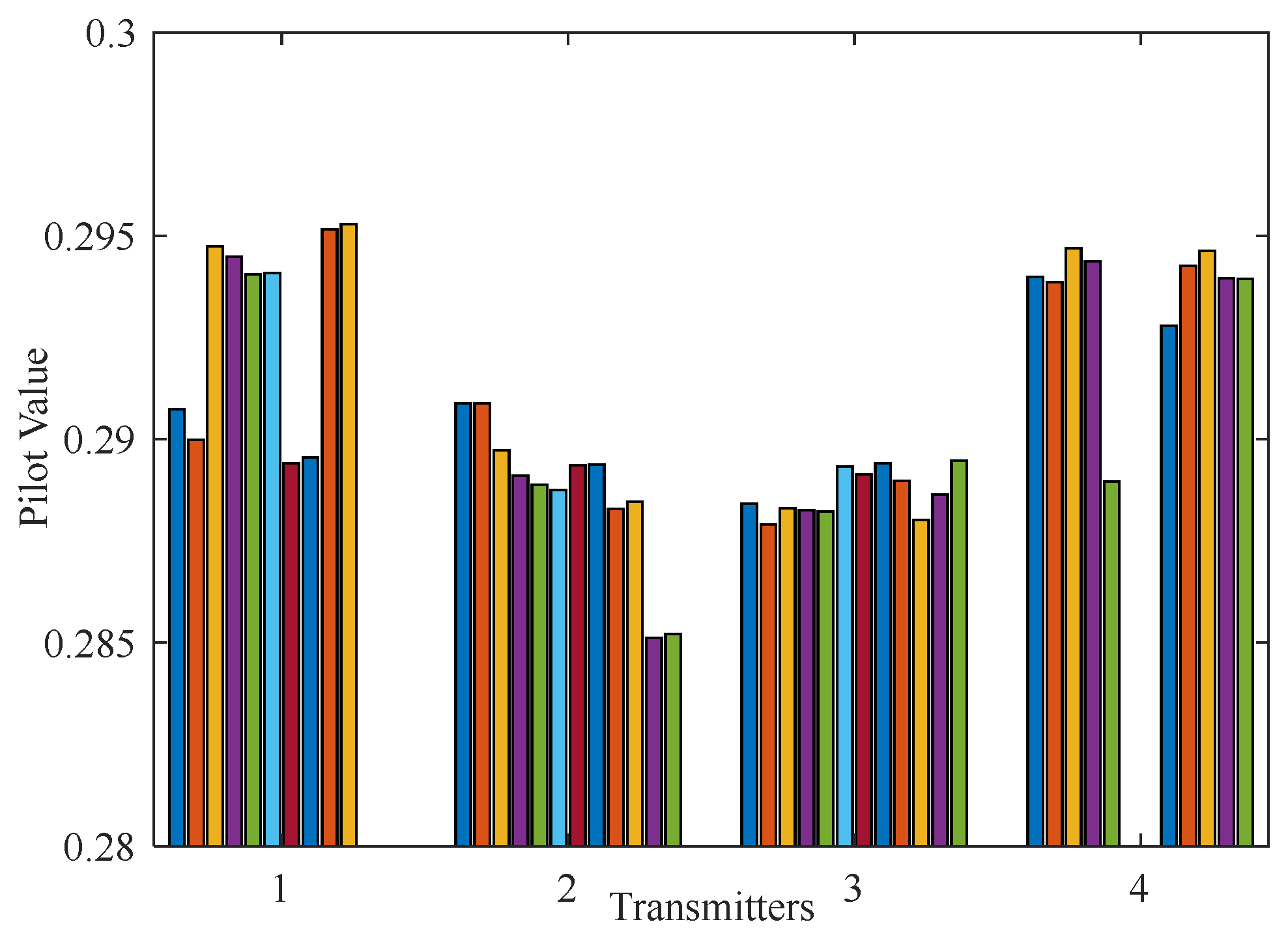
First, pilots are constructed using the four methods. When the total number of OFDM carriers is N = 512 and N = 256, the MC and TC of the sensing matrix corresponding to the pilots designed by the four methods are shown in Table 2 and Table 3, respectively. The pilot amplitudes on the pilot carriers of each transmitting antenna designed by the SJCD method are shown in Figure 2 and Figure 3. In Figure 2 and Figure 3, each bar with color represents distinct pilot carrier positions, and the height of bars denotes the value at pilot carrier positions. Since the MMC method minimizes MC, the MC of the sensing matrix corresponding to the pilot constructed by the MMC method is the smallest. The optimization goal of the MTC method is to minimize the TC of the sensing matrix. As shown in Table 2, the TC of the sensing matrix associated with the pilot pattern designed by the MTC method is the smallest among all methods. Since the SJCD optimized the sensing matrix using two criteria, the MC of the sensing matrix corresponding to the pilot designed by the SJCD is greater than that designed by the MMC method, and the TC is greater than that designed by the MTC method. However, the value of TC achieved by MMC is large, and the MTC method yields a sensing matrix with a large MC. The pilot designed by the SJCD avoids the sensing matrix with the large MC and TC. Table 2 shows that the MC of the pilot designed by the SJCD method is only 0.0209 greater than that of the pilot designed by the MMC, but the associated TC is 0.9415 less than that of the MMC. The TC associated with the SJCD method is only 0.1829 greater than the TC of the sensing matrix corresponding to the pilots designed by the MTC method, but the associated MC is 0.3671 less than that of the MTC method. As a consequence, the SJCD is a good tradeoff between the MMC and MTC and avoids the associated sensing matrix bearing a too large TC or MC. We can draw the same conclusion as Table 3.

Table 2.
MC and TC with respect to different schemes .

Table 3.
MC and TC with respect to different schemes, .
Figure 2.
Pilot value on each pilot subcarrier of each transmitter, .
Figure 3.
Pilot value on each pilot subcarrier of each transmitter, .
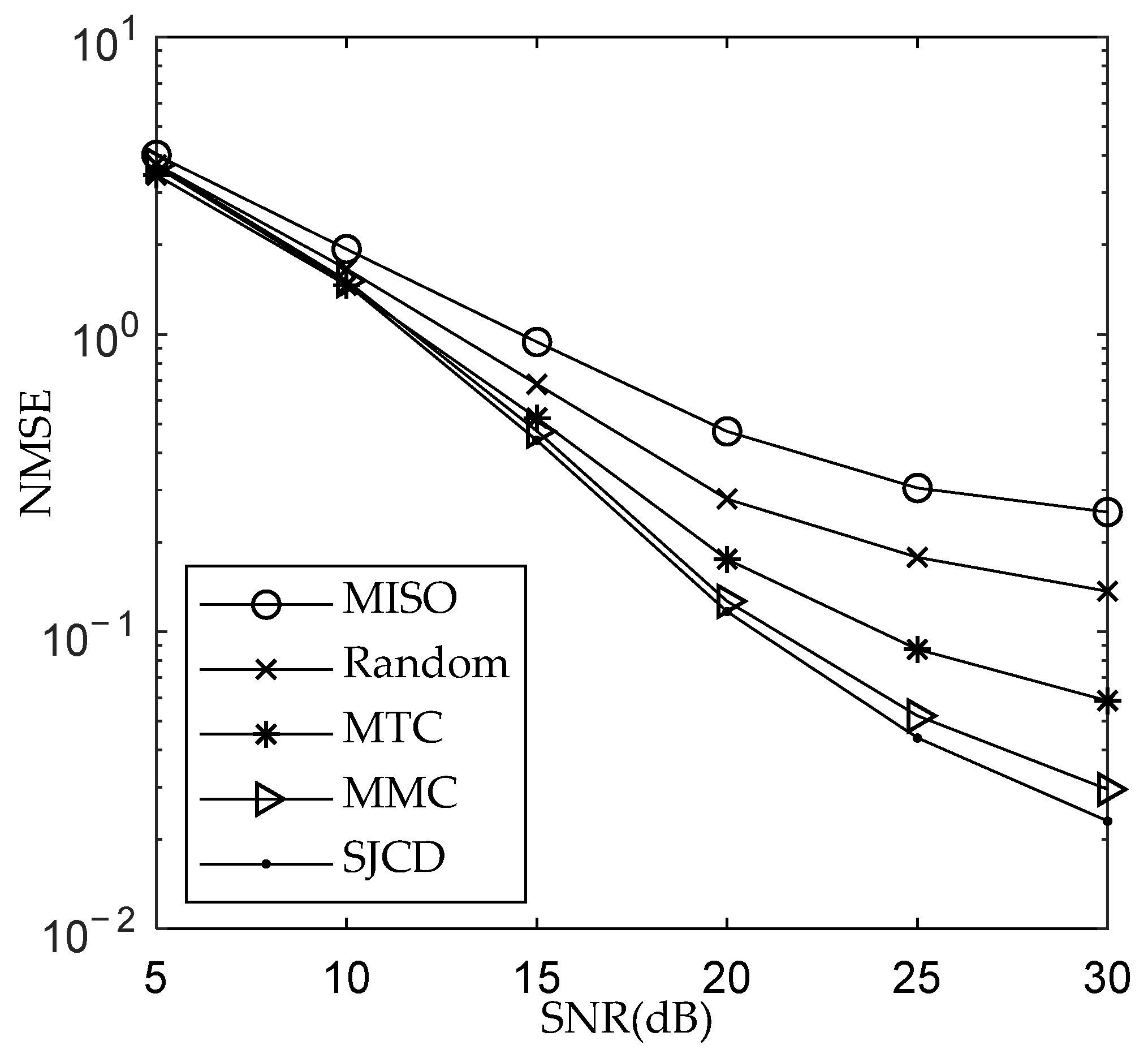
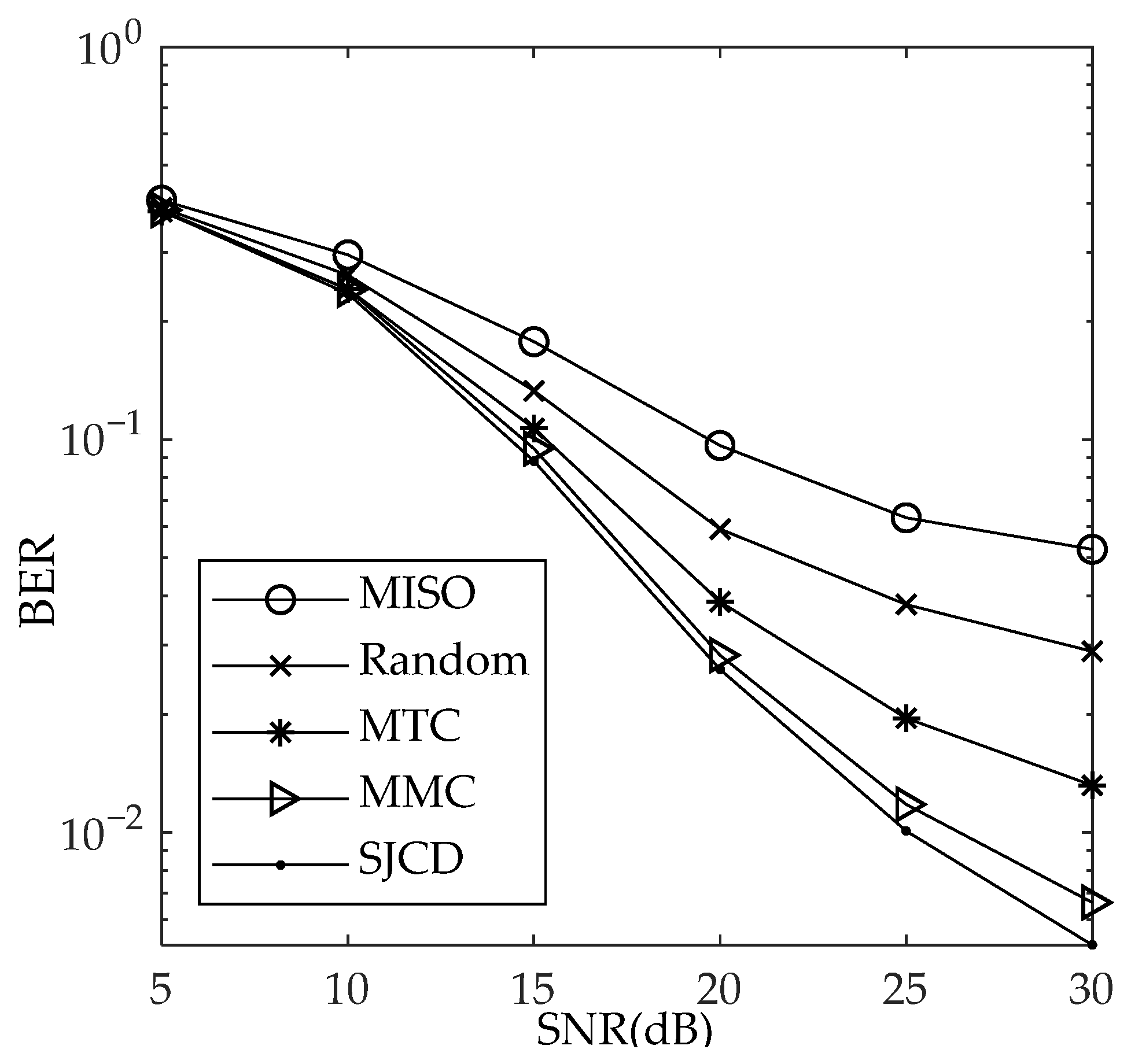
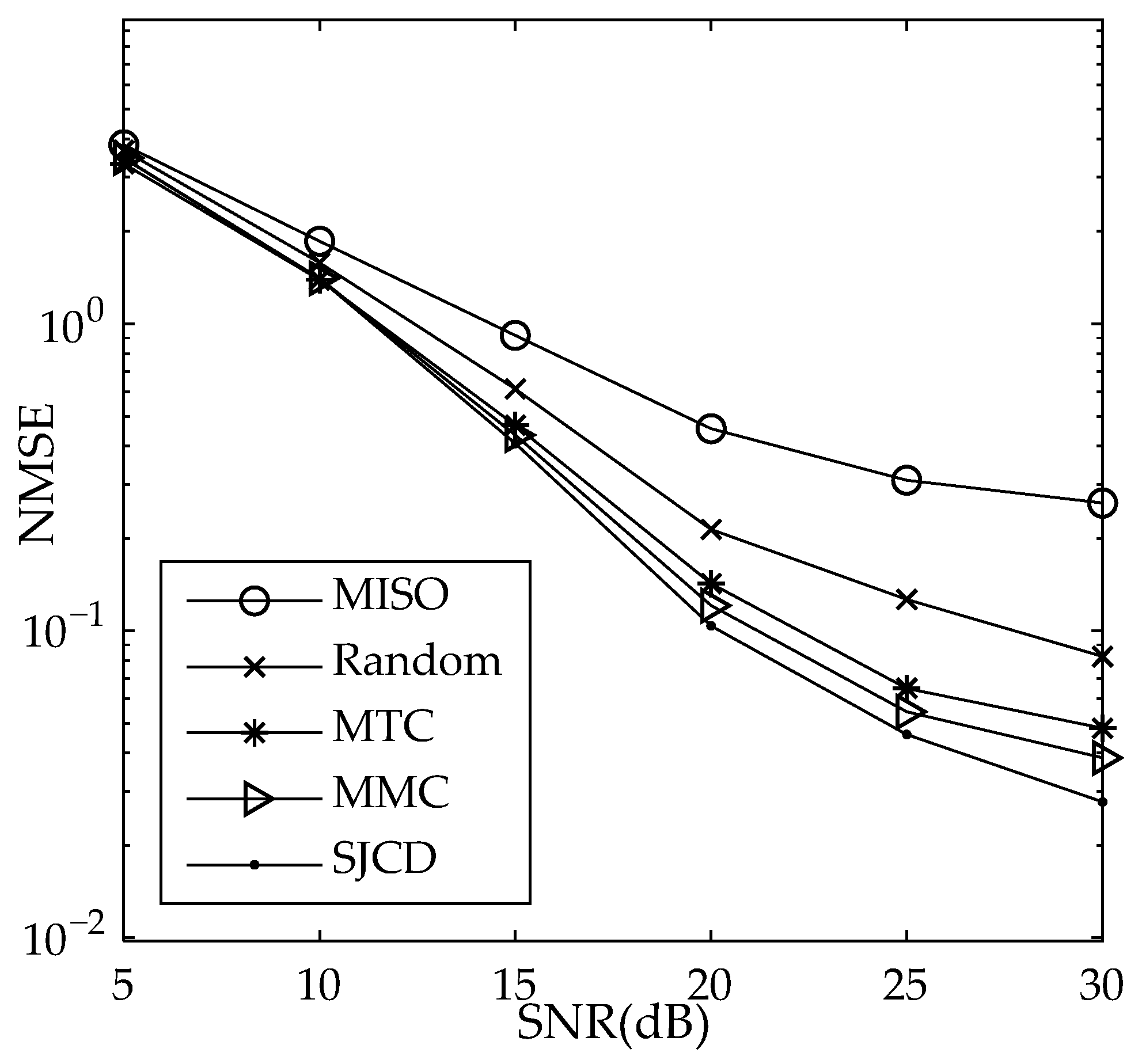
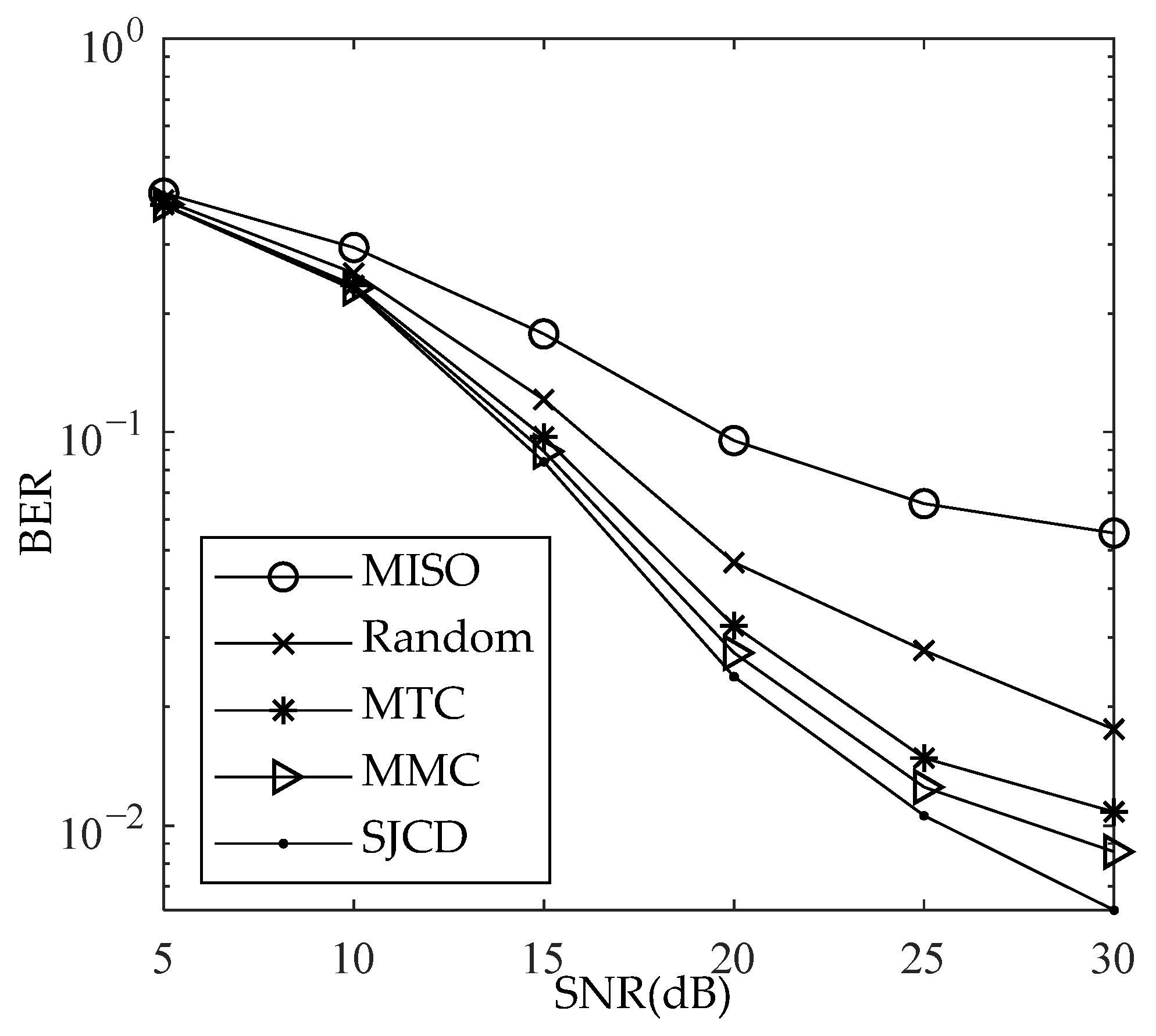
We perform 2000 channel estimation simulations for the MIMO-OFDM system. In each simulation, the nonzero positions of each sparse channel are randomly distributed in [1, 80], and the coefficients on the nonzero taps are random variables, which are i.i.d. complex Gaussian distributed with zero mean and unit variance. In 2000 simulations, we fixedly use the pilots in Table 2 and Table 3 for channel estimation. We take the average of NMSE and BER of 2000 simulations and plot it for each SNR. We use binary phase shift keying for data modulation and zero-forcing for data detection in simulations. In addition, pilot powers are not normalized in the four methods. Figure 4 and Figure 5 give the simulation results of NMSE versus the signal-to-noise ratio (SNR) and BER versus SNR for N = 512, respectively. Figure 6 and Figure 7 give the simulation results of NMSE versus SNR and BER versus SNR for N = 256, respectively. The BOMP is used for sparse signal recovery. In addition, we also simulate a multiple-input–single-output (MISO) channel estimation using pilots obtained by the SJCD as a comparison, in which each receiver simultaneously estimates jointly sparse channels. For simplicity, we assume that there is no data superposition in data subcarriers and zero-forcing is used to demodulate data.
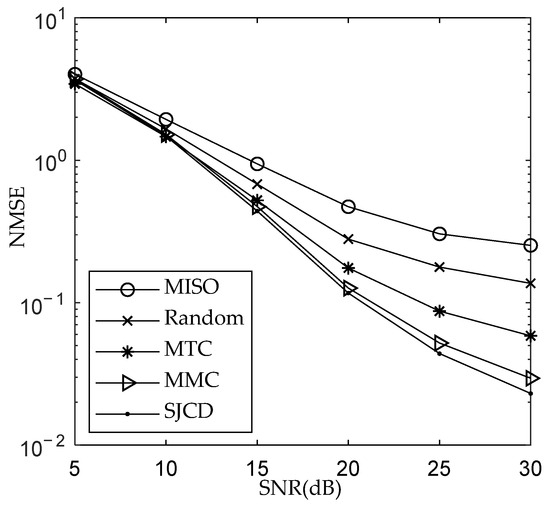
Figure 4.
NMSE plots of different pilot design methods, .
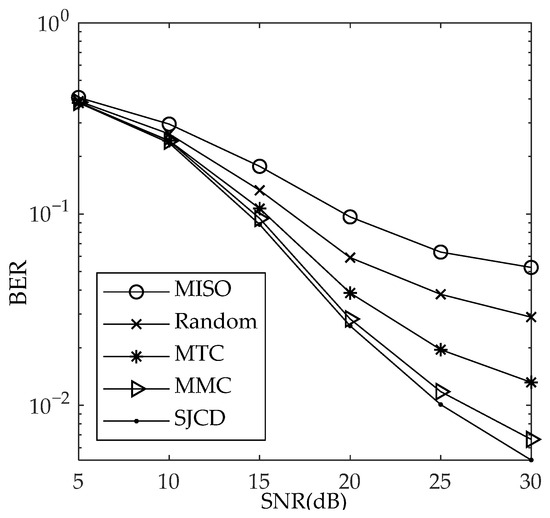
Figure 5.
BER plots of different pilot design methods, .
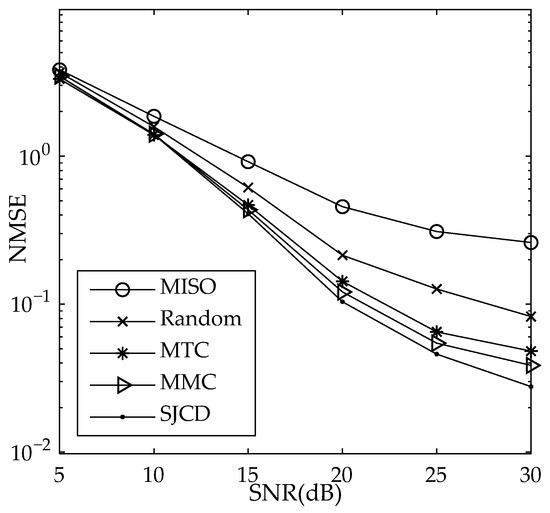
Figure 6.
NMSE plots of different pilot design methods, .
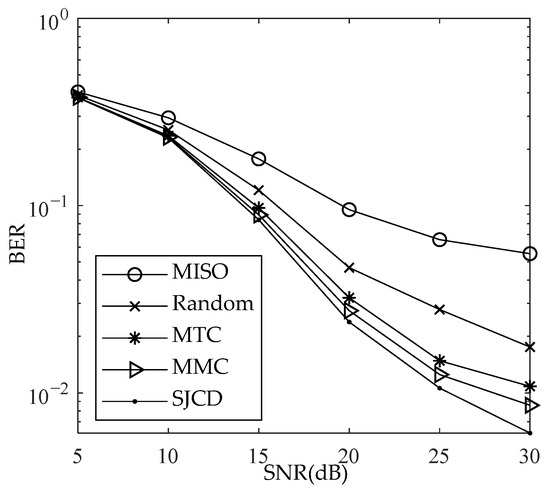
Figure 7.
BER plots of different pilot design methods, .
Figure 4 shows that the NMSE of the MTC scheme is 3 dB higher than that of the MMC scheme at 30 dB SNR. This is because the sensing matrix determined by the pilots obtained by MTC has a large MC, which leads to the performance degradation. For MIMO-OFDM systems with block-sparse channels, the BOMP algorithm exploits the channel’s co-sparsity to recover the channel and accurately identify the locations of nonzero coefficients. Therefore, the correlation between any two columns of the sensing matrix determined by the pilots obtained by the MMC algorithm is lower than that obtained by the MTC, resulting in a lower NMSE for the MMC scheme. The NMSE of the SJCD method is 1.7 dB, 4.78 dB, and 7.64 dB smaller than the NMSE of the MMC, MTC, and random methods at 30 dB SNR, respectively. The SJCD method has the smallest NMSE. This is because the SJCD method avoids large correlations between the two distinct columns of the sensing matrix and enables the sensing matrix to bear the better average recovery ability in the sparse signal recovery owing to a small TC. Furthermore, as the SNR increases, the performance gap between the SJCD and other methods enlarges. The reason is that the sensing matrix corresponding to the MMC or MTC method has a larger TC or MC, respectively. A larger TC or MC leads to a decrease in the average sparse channel estimation performance of the MIMO-OFDM system. Compared with the MISO method, the NMSE of the pilots designed by the MTC, MMC, and SJCD methods is 5.4 dB, 8.4 dB, and 10 dB smaller than the NMSE of the pilots designed by the MISO at 30 dB SNR, respectively, because the MTC, MMC, and SJCD jointly estimate channels, while the MISO jointly estimates only channels. Equation (21) shows that the greater the number of jointly estimated channels, the smaller the BC. The increase in the number of jointly estimated channels is more conducive to enabling the BCS recovery algorithms to accurately identify the nonzero blocks to improve the accuracy of the sparse signal reconstruction. Therefore, the channel estimation NMSE and BER of the MISO method are greater than those of the other three methods. Figure 5 shows that the SJCD outperforms other methods from the perspective of BER at 30 dB SNR.
For , Figure 6 shows that the NMSE of the SJCD is 1.43 dB and 2.4 dB smaller than that of MMC and MTC, respectively. Figure 7 shows that the SJCD achieves the smallest BER compared with other methods. The suggested approach is validated by simulation results and is superior to the other schemes from the perspective of the NMSE and BER.
5. Conclusions
In this paper, we investigate the pilot design of the BCS-based sparse channel estimation and propose a novel pilot design scheme that minimizes the TC, BC, and SC of the sensing matrix simultaneously. We first formulate the channel estimation of jointly sparse channels as a BCS sparse signal recovery problem and allocate pilot symbols as a multiple-objective optimization problem. Then, we derive the error bound of the BCS-based sparse channel estimation and the relationship between the MC and BC of the sensing matrix of the sparse channel estimation model in MIMO-OFDM systems. In addition, we propose a novel SJCD algorithm to design pilots with a joint criterion, in which the pilot pattern and pilot power are designed with the objective of minimizing the BC and TC, respectively. Simulation results validate the effectiveness of the proposed method in terms of NMSE and BER.
Author Contributions
Conceptualization, S.X. and A.T.; Methodology, S.X.; Software, S.X. and W.Y.; Validation, Y.W.; Investigation, C.S.; Data Curation, S.W.; Writing—Original Draft, S.X. and J.C.; Writing—Review and Editing, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Natural Science Foundation of Shandong Province, China (Grant No. ZR2022QF127).
Data Availability Statement
Data are contained within the article. The original contributions presented in this paper are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Shenyang Xiao, Yongjing Wei, Chao Sun, Shihao Wang, Anqi Tian, Shengrun Mi and Junming Cao were employed by the State Grid Shandong Information & Telecommunication Company. Author Weili Yue was employed by the State Grid Jinan Power Supply Company. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Duarte, M.F.; Eldar, Y.C. Structured compressed sensing: From theory to applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Li, T.; Wang, X.; Li, D.; Jian, Y. Sparse channel estimation with distorted signals for UWB OFDM systems. IEEE Wirel. Commun. Lett. 2023, 12, 620–624. [Google Scholar] [CrossRef]
- Cai, J.; He, X.Y.; Wang, H.; Song, R.F. Deterministic pilot design for structured sparse channel estimation in MISO systems. Wirel. Netw. 2019, 26, 2609–2621. [Google Scholar] [CrossRef]
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Abdulhussain, S.H.; Eissa, M.R.; Baidhani, A.A.; Noordin, N.K. 6G Wireless Communications Networks: A Comprehensive Survey. IEEE Access 2021, 9, 148191–148243. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, C.; Ni, W.; Ng, D.W.K. Reconfigurable Intelligent Surface-Aided Energy-Efficient Mobile Edge Computing in OFDM Systems. IEEE Commun. Lett. 2025, 29, 1446–1450. [Google Scholar] [CrossRef]
- Li, J.X.; Jana, A.; Yuan, Y.Y.; Zhang, K.; Burokur, S.N.; Genevet, P. Exploiting hidden singularity on the surface of the Poincaré sphere. Nat. Commun. 2025, 16, 5953. [Google Scholar] [CrossRef]
- Chen, X.Q.; Zhang, L.; Zheng, Y.N.; Liu, S.; Huang, Z.R.; Liang, J.C.; Di Renzo, M.; Galdi, V.; Cui, T.J. Integrated sensing and communication based on space-time-coding metasurfaces. Nat. Commun. 2025, 16, 1836. [Google Scholar] [CrossRef]
- Abdallah, A.; Celik, A.; Mansour, M.M.; Eltawil, A.M. RIS-Aided mmWave MIMO channel estimation using deep learning and compressive sensing. IEEE Trans. Wirel. Commun. 2023, 22, 3503–3521. [Google Scholar] [CrossRef]
- He, R.; Ai, B.; Wang, G.; Yang, M.; Huang, C.; Zhong, Z. Wireless channel sparsity: Measurement, analysis, and exploitation in estimation. IEEE Wirel. Commun. 2021, 28, 113–119. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, P.; Fang, J.; Li, H. Compressed channel estimation for IRS-Assisted millimeter wave OFDM systems: A low-rank tensor decomposition-based approach. IEEE Wirel. Commun. Lett. 2022, 11, 1258–1262. [Google Scholar] [CrossRef]
- Li, T.; Li, D.; Yi, X.; Jian, Y. A sparse channel estimation scheme combined with distorted signal detection for UWB OFDM systems. IEEE Wirel. Commun. Lett. 2022, 11, 1438–1442. [Google Scholar] [CrossRef]
- Salari, S.; Chan, F. Joint CFO and channel estimation in OFDM systems using sparse Bayesian learning. IEEE Commun. Lett. 2021, 25, 166–170. [Google Scholar] [CrossRef]
- Candes, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Xiao, Z.; Cao, S.; Zhu, L.; Liu, Y.; Ning, B.; Xia, X.G.; Zhang, R. Channel estimation for movable antenna communication systems: A framework based on compressed sensing. IEEE Trans. Wirel. Commun. 2024, 23, 11814–11830. [Google Scholar] [CrossRef]
- Qi, C.H.; Wu, L.N.; Huang, Y.M.; Nallanathan, A. Joint design of pilot power and pilot pattern for sparse cognitive radio systems. IEEE Trans. Veh. Technol. 2015, 64, 5384–5390. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- Qi, C.H.; Wu, L.N. Optimized pilot placement for sparse channel estimation in OFDM systems. IEEE Signal. Process. Lett. 2011, 18, 749–752. [Google Scholar] [CrossRef]
- Qi, C.H.; Wu, L.N. A study of deterministic pilot allocation for sparse channel estimation in OFDM systems. IEEE Commun. Lett. 2012, 16, 742–744. [Google Scholar] [CrossRef]
- Qi, C.H.; Yue, G.S.; Wu, L.N.; Nallanathan, A. Pilot design for sparse channel estimation in OFDM-based cognitive radio systems. IEEE Trans. Veh. Technol. 2014, 63, 982–987. [Google Scholar] [CrossRef]
- Qi, C.H.; Yue, G.S.; Wu, L.N.; Huang, Y.M. Pilot design schemes for sparse channel estimation in OFDM systems. IEEE Trans. Veh. Technol. 2015, 64, 1493–1505. [Google Scholar]
- He, X.Y.; Song, R.F.; Zhu, W.P. Optimal pilot pattern design for compressed sensing-based sparse channel estimation in OFDM systems. Circuits Syst. Signal Process. 2012, 31, 1379–1395. [Google Scholar] [CrossRef]
- Qi, C.H.; Wu, L.N. Tree-based backward pilot generation for sparse channel estimation. Electron. Lett. 2012, 48, 501–503. [Google Scholar] [CrossRef]
- Wang, H.; Guo, Q.; Zhang, G.X.; Li, G.X. Pilot pattern optimization for sparse channel estimation in OFDM systems. IEEE Commun. Lett. 2015, 19, 1233–1236. [Google Scholar] [CrossRef]
- He, X.Y.; Song, R.F.; Zhu, W.P. Pilot allocation for sparse channel estimation in MIMO-OFDM systems. IEEE Trans. Circuits Syst. II-Express Briefs 2013, 60, 612–616. [Google Scholar] [CrossRef]
- He, X.Y.; Song, R.F.; Zhu, W.P. Pilot allocation for distributed compressed sensing based sparse channel estimation in MIMO-OFDM systems. IEEE Trans. Veh. Technol. 2016, 65, 2990–3004. [Google Scholar] [CrossRef]
- Qi, C.H.; Wu, L.N. Uplink channel estimation for massive MIMO systems exploring joint channel sparsity. Electron. Lett. 2014, 50, 1770–1772. [Google Scholar] [CrossRef]
- Mohammadian, R.; Amini, A.; Khalaj, B.H. Deterministic pilot design for sparse channel estimation in MISO/Multi-user OFDM systems. IEEE Trans. Wirel. Commun. 2017, 16, 129–140. [Google Scholar] [CrossRef]
- Gong, B.; Lin, G.; Qin, Q.; Ren, X.; Chen, W. Block distributed compressive sensing based doubly selective channel estimation and pilot design for large-scale MIMO systems. IEEE Trans. Veh. Technol. 2017, 66, 9149–9161. [Google Scholar] [CrossRef]
- Zelnik-Manor, L.; Rosenblum, K.; Eldar, Y.C. Sensing matrix optimization for block-sparse decoding. IEEE Trans. Signal Process. 2011, 59, 4300–4312. [Google Scholar] [CrossRef]
- Uwaechia, A.N.; Mayhuddin, N.M. Spectrum-efficient distributed compressed sensing based channel estimation for OFDM systems over doubly selective channels. IEEE Access 2019, 7, 35072–35088. [Google Scholar] [CrossRef]
- Xiao, S.Y.; Jin, Z.G.; Su, Y.S. Pilot design for sparse MIMO-OFDM channel estimation with generalized shift invariance property. AEU Int. J. Electron. C. 2018, 96, 48–57. [Google Scholar] [CrossRef]
- Zhou, Y.; Gu, Z.; Wang, S.K.; Yang, Y.; Fan, P.Z. Non-Uniform Pilot Pattern Design for Sparse Channel Estimation in MIMO-OFDM Systems. IEEE T. Veh. Technol. 2025, 74, 3039–3051. [Google Scholar] [CrossRef]
- Shenyang, X.; Zhigang, J.; Ye, C.; Yun, L.; Yishan, S. Joint mutual coherence and total coherence pilot design for OFDM channel estimation. IEEE Access 2019, 7, 144536–144547. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Bölcskei, H. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Mishali, M. Robust recovery of signals from a structured union of subspaces. IEEE Trans. Inf. Theory 2009, 55, 5302–5316. [Google Scholar] [CrossRef]
- Elad, M. Optimized projections for compressed sensing. IEEE Trans. Signal Process. 2007, 55, 5695–5702. [Google Scholar] [CrossRef]
- Ben-Haim, Z.; Eldar, Y.C. Near-oracle performance of greedy block-sparse estimation techniques from noisy measurements. IEEE J. Sel. Top. Signal. Process. 2011, 5, 1032–1047. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).