Abstract
White-box cryptography plays a vital role in untrusted environments where attackers can fully access the execution process and potentially expose cryptographic keys. It secures keys by embedding them within complex and obfuscated transformations, such as lookup tables and algebraic manipulations. However, existing white-box protection schemes for SM2 signatures face vulnerabilities, notably random number leakage, which compromises key security and diminishes overall effectiveness. This paper proposes an improved white-box implementation of the SM2 signature computation leveraging a Trusted Execution Environment (TEE) architecture. The scheme employs three substitution tables for SM2 key generation and signature processes, orchestrated by a random bit string k. The k value and lookup operations are securely isolated within the TEE, effectively mitigating the risk of k leakage and enhancing overall security. Experimental results show our scheme enhances security, reduces storage, and improves performance over standard SM2 signature processing, validating its efficacy with TEE and substitution tables in untrusted environments.
1. Introduction
With the continuous development of Internet technology, the means of network confrontation have become increasingly diverse and complex, leading to frequent large-scale cybersecurity incidents that cause serious economic losses and adverse social impacts. Ensuring data security, particularly the personal data and privacy of Internet users, has become a top priority for China’s cyberspace security protection. Cryptography plays a pivotal role in protecting privacy and personal data. Modern cryptography requires that, even when the algorithm structure is known to the attacker, the cryptographic algorithm can ensure the attacker cannot distinguish between the encrypted ciphertext and a random number by the secret key used, typically a 128-bit random number. Therefore, the primary goal of an attacker is to recover the key used in the cryptographic algorithm.
Traditionally, cryptographic algorithms operate in secure environments known as the black-box model, where attackers can only control the inputs and outputs but cannot access the intermediate states of the algorithm. However, in Internet applications, the deployment environment has evolved from dedicated encryption machines to insecure devices such as personal mobile phones, computers, and home set-top boxes, which cannot provide a secure encryption environment. To address this, Chow et al. proposed the white-box cryptography model in 2002 [], where cryptographic algorithms are designed to prevent attackers from isolating the key, even when the attacker has full access to the algorithm’s internals.
This paper proposes a new white-box implementation of the SM2 public-key cryptographic algorithm (WBSM2) to enhance key security in untrusted environments. The scheme fully integrates a Trusted Execution Environment (TEE) to securely generate the random value and perform all associated lookup table operations, including those for parameters, ensuring complete isolation of sensitive computations. By utilizing elliptic curve public key algorithms to generate parameters and employing mathematical transformations to construct encrypted and obfuscated lookup tables within the TEE, the private key remains effectively hidden. This design mitigates white-box attacks by isolating critical computations, ensuring that even if attackers gain access to other system components, the private key cannot be compromised. The specific process of white-box protection involves both the signer and the verifier, providing end-to-end security for the private key. Experimental results demonstrate that this scheme delivers enhanced security, reduced storage requirements, and better performance compared to the standard SM2 algorithm.
To address the issue of random number attacks, the scheme employs a TEE-based random number protection mechanism that ensures the secure generation and handling of random values. This is achieved through the use of secure memory environments and protected execution of random number generation operations. By fully isolating these processes within the TEE, the scheme prevents attackers from gaining access to random values or exploiting them to derive the private key.
The key innovations of this paper are as follows:
- (1)
- TEE-Based Random Number Protection Mechanism: A robust approach is designed to secure the generation and handling of random numbers within the TEE, leveraging secure memory environments and protected instructions to prevent attackers from inferring the private key.
- (2)
- Affine Transform Coding-Based Lookup Table Scheme: To improve performance under the white-box model, we propose a scheme that uses affine transform coding to create efficient and space-saving lookup tables, enhancing the performance of the SM2 white-box method and preventing key extraction by attackers.
- (3)
- Effective Experimental Validation: Comprehensive tests evaluated our SM2 white-box method in real-world applications, focusing on signature and verification times across various platforms. Compared to the standard SM2 implementation, our method maintains practical performance, with signature times 2–3 times longer and verification times about twice as long. Security assessments confirmed the robustness of our method, ensuring the protection of the private key and improving computational performance compared to existing SM2 white-box algorithms.
2. Threat Model
The white-box attack model assumes that an adversary has complete access to the implementation details of a cryptographic system, including source code, runtime memory, execution flow, and all operations involving cryptographic keys. This assumption, as initially defined by Chow et al. [,] in their seminal works on white-box cryptography for AES and DES implementations, is commonly used to evaluate the robustness of cryptographic designs under extreme conditions, ensuring their resistance to the theoretically strongest possible attacks. Xiong Jiang et al. proposed an SM2 white-box protection scheme based on space hardness that offers strong theoretical security []. However, it relies on large lookup tables and intricate obfuscation techniques, leading to substantial performance and storage overhead. In practice, the high cost of meeting the requirements of this model often makes it impractical, especially in resource-constrained environments.
To address these limitations, we introduce a degraded white-box threat model that balances security with implementation efficiency, drawing on an approach similar to those proposed in the works of Mo [] and Zhang [].
Defender’s Goal: This model assumes that attackers have complete control over the Rich Execution Environment (REE), including the ability to monitor runtime memory, use debugging tools, and modify system software, while being unable to access the TEE hardware or its protected memory regions. Leveraging TEE’s isolation capabilities, the proposed protection mechanism achieves efficient and practical security in real-world scenarios.
Defender/Adversary’s Capability: The TEE is defined as a secure enclave within an otherwise untrusted environment, ensuring that data, code, and computations within it remain secure. Although potential side-channel attacks targeting TEE could compromise sensitive data, these are beyond the scope of this study. All sensitive computations in the signing process are performed within the TEE, which ensures that the random number k is never directly output. Instead, the TEE computes an intermediate value and derived from k. Importantly, these calculations are irreversible, preventing k from being recovered. This design guarantees that even if an attacker gains complete control over the REE, they cannot obtain k by intercepting data transmissions between the TEE and the REE.
3. Related Work
The concept of the white-box attack environment was first proposed by Chow et al. at the beginning of this century []. In a white-box environment, attackers have complete control over and access to information on IoT devices [], allowing for them to use static analysis, dynamic debugging, and other techniques to extract cryptographic keys, leading to information leakage. White-box protection involves transforming traditional cryptographic algorithms into white-box cryptographic algorithms by obfuscating the key and algorithmic logic, making it difficult for attackers to obtain the key or algorithm implementation details. Specifically, this involves taking an existing cryptographic algorithm under the black-box model and implementing it securely in a white-box model, ensuring it can resist attacks even when the attacker has extensive capabilities.
In 2002, Chow et al. developed a lookup table-based white-box implementation for block ciphers, successfully applying it to AES [] and DES []. However, subsequent research revealed that Chow’s scheme could not secure the embedded key against specific attacks, and effective attack methods on Chow’s white-box DES were proposed in the literature [,,]. Bringer, Chabanne, and Dottax introduced perturbations to a variant of AES [], while Xiao and Lai proposed a scheme based on larger linear encoding []. Karroumi suggested improving white-box AES using AES pairwise ciphers []. Bogdanov et al. introduced the SPACE cipher, a new type of block cipher designed for white-box environments based on a multi-subdivided target-heavy generalized Feistel structure [].
Traditional cryptographic white-boxing disperses or transforms the key through substitution, scrambling, and obfuscation, allowing for the transformed key to be directly involved in algorithmic operations without needing to recover the key.
Current research on white-box cryptography primarily focuses on symmetric cryptography. Public-key cryptography, which typically requires large-scale mathematical computations, presents significant challenges for white-box design, resulting in limited research in this area.
In 2011, Lepoint published a white-box implementation of RSA, but it required excessive storage space. In 2015, Jan Hoogerbrugge and Wil Michiels applied for a patent on a white-box implementation of the RSA algorithm []. In 2017, Jian Bai, Jie Zhou, et al. proposed a white-box digital signature implementation of SM2 based on the residue number system [] and a white-box implementation of the SM2 encryption and decryption algorithm based on the residue number system []. These methods use lookup table construction to protect the key and the residue theorem to reduce the lookup table’s construction space. Established methods such as space-hardness-based white-box implementations of SM2 occupy significant memory space and perform poorly. Attackers can observe memory or other control schemes to perform random number attacks in a white-box environment. Existing SM2 white-box implementation methods tend to overlook code-level security issues and are susceptible to reverse analysis.
In contrast, the scheme proposed in this paper achieves white-box protection in lightweight IoT devices. It includes functionalities for signing and verifying signatures using the SM2 algorithm, ensuring strong security. The white-box protection of the SM2 private key is achieved by introducing a TEE-based random number protection scheme and a lookup table-based key hiding scheme, resisting white-box attacks on the signature process. During signing, the signer uses TEE-generated random numbers and the lookup table for signing. TEEs have become widely used in confidential computing [,]. These technologies ensure secure execution even in compromised environments and are crucial for protecting sensitive data during processing [,]. However, there are still significant challenges in securing TEE implementations, particularly regarding memory encryption and side-channel attacks [,]. During verification, the signer uses the generated lookup table for verification. Throughout the process, there is no leakage of the private key, and attackers cannot obtain the private key through white-box attacks. This dual protection at both hardware and software levels significantly enhances security performance.
4. Preliminaries
4.1. White-Box Cryptography
In traditional cryptography, it is assumed that the operating environment of cryptographic algorithms is secure, with attackers only able to access the input and output of these algorithms. However, with advances in computer technology, access to sensitive information has increased, leading to more severe network security threats. As a result, cryptographic algorithms face increasing risks.
The concept of white-box attacks was first proposed by Chow et al. in 2002 [,]. Here, the term “white-box” is analogous to the “white-box testing” used in software testing, where the attacker has complete control over the device terminal (i.e., the environment in which the application runs). In a white-box attack, the attacker has the same privileges as the software executor, allowing for them to perform any operation on the endpoint, with far fewer limitations compared to the traditional black-box model.
White-box attacks represent a more advanced security threat in untrusted endpoint environments. Traditional cryptographic algorithms are highly vulnerable and cannot be used securely in a white-box attack environment. Therefore, to ensure the secure use of cryptographic functions such as encryption, decryption, and authentication in untrusted terminals, it is crucial to develop cryptographic algorithms that can maintain security in white-box attack environments [,].
We refer to cryptographic algorithms and their implementations that can resist white-box attacks as white-box ciphers. These include white-box implementations of existing cryptographic algorithms and entirely new white-box cryptographic algorithms. The white-box implementation of existing cryptographic algorithms involves redesigning known algorithms to ensure their security remains intact in a white-box attack environment, without altering their original functionality. For instance, encryption algorithms aim to protect their keys from leakage, while signature algorithms strive to prevent forgery. Conversely, white-box cryptographic algorithms are new designs that inherently resist attacks in a white-box environment, rather than applying white-box security measures to existing algorithms.
Currently, most examples of white-box cryptography focus on the white-box implementation of known cryptographic algorithms, such as white-box AES and white-box DES. Designers often use obfuscation techniques to construct lookup tables that perform the algorithm’s operations. Even if a white-box attacker can observe the entire lookup table, they cannot extract the key information faster than by exhaustive search. However, this approach has proven to be inadequate.
White-box cryptography is a novel area of cryptographic research that challenges traditional assumptions about an attacker’s capabilities, aligning more closely with real-world security threats. Both theoretically and practically, white-box cryptography and its unique characteristics have significant and broad application prospects and are poised to substantially impact the field of cryptography.
4.2. SM2 Algorithm
The SM2 elliptic curve public key cryptography algorithm is based on the elliptic curve multiplicative point operation one-way function, utilizing a key length of 256 bits. This algorithm supports data encryption, digital signatures, and key exchange protocols. Compared to the RSA algorithm, SM2 offers the same security strength with shorter keys and faster computation speeds []. It is widely used in information system identification, network communication key exchange, electronic seal digital signatures, and trusted computing [].
The equation of the elliptic curve used in SM2 is in the form , as shown in Figure 1. In this two-dimensional space, the horizontal axis represents , and the vertical axis represents . Point A on the elliptic curve is denoted as . According to the definition of multiple points on the elliptic curve, 2A is the point where the tangent at A intersects the curve again, and 3A is the sum of 2A and A. For a positive integer k, the point .
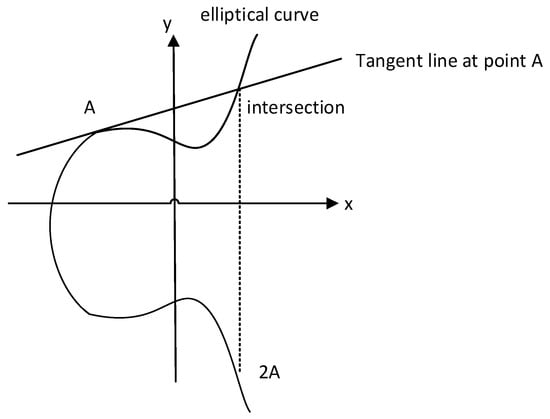
Figure 1.
An elliptic curve equation.
The coordinate system shown in Figure 1 uses real numbers, but points on the elliptic curve are usually kept as integers. An elliptic curve defined over the prime field consists of p elements in {0, 1, 2, …, p − 1}, where p is a prime number. The set of points on the elliptic curve is denoted as y ∈ }{O}, where O is the point at infinity. The relevant parameters of the SM2 system over the field are public and must be openly shared, meeting the following conditions:
- The characteristic p of , p is is a 256-bit prime number.
- Elements a and b in satisfy the curve equation , with .
- The base point is not the point at infinity.
- The order of the base point in is a 256-bit prime number.
Once these conditions are met, the elliptic curve system parameters are determined, and the elliptic curve discrete logarithm problem (ECDLP) is established. To construct the one-way function, k is chosen such that Q = [k]G. Solving for k in this context is the ECDLP, which has exponential computational complexity, making it significantly harder to solve than problems like integer factorization or the discrete logarithm problem over a finite field. Therefore, elliptic curve cryptography requires smaller key sizes compared to other cryptographic systems.
The SM2 digital signature algorithm involves four main components: system parameter generation, key generation, signature generation, and signature verification.
System parameter generation: Input a security parameter λ, and output elliptic curve parameters T = ⟨P, a, b, G, n, h⟩, where P is a prime number greater than 3, defining the finite field = {0, 1, …, P − 1}. Parameters a and b define the elliptic curve equation . The base point generates a cyclic subgroup on the curve, and n is the order of G. The cofactor h is N/n, where N is the order of the elliptic curve.
Key generation: The signer A generates a private key and computes the public key .
Signature generation: Given a message M, A converts the identifier to a 2-byte string ENTLA and hashes the concatenated identity information and elliptic curve parameters to produce . The message is , and the message digest . Randomly select and compute
Calculate
Signature verification: The verifier B checks if . If not, the verification fails. Otherwise, compute and the digest . Calculate , , and . If , the signature is valid; otherwise, it fails [].
4.3. TEE
The Trusted Execution Environment (TEE) is a secure, integrity-protected processing environment comprising processing, memory, and storage functions []. It is isolated from the “normal” processing environment, known as the Rich Execution Environment (REE), where the device’s operating system and applications run []. The first mobile phones with hardware-based TEEs appeared around a decade ago, and today, nearly every smartphone and tablet includes a TEE, such as the ARM TrustZone []. By partitioning REE applications and services, TEEs enhance security and availability by confining sensitive operations and data to the TEE, ensuring that sensitive data never leave this secure environment.
The TEE operates on a separate kernel and provides a tamper-proof processing environment. It guarantees the authenticity of the executed code, the integrity of the runtime state (e.g., CPU registers, memory, and sensitive I/O), and the confidentiality of the code, data, and runtime state stored on persistent memory. Additionally, it offers remote attestation of its trustworthiness to third parties. The content of the TEE is not static and can be securely updated. It is resistant to software attacks and physical attacks on the system’s main memory, and it prevents exploitation of backdoor security vulnerabilities. Figure 2 illustrates a device as a series of different environments, each with its functions and services.
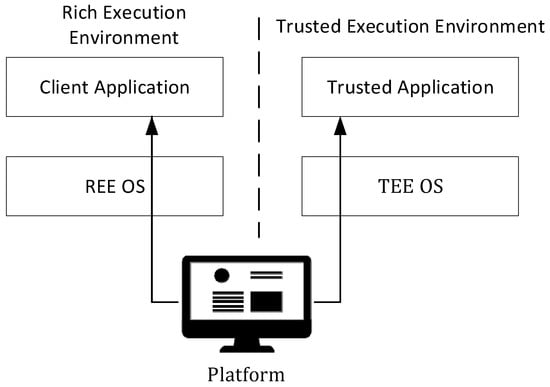
Figure 2.
TEE in a computing device.
A Trusted Application (TA) is an application encapsulating security-critical functionality running in a TEE. It can be a service-style application providing generic functionality (e.g., a generic cryptographic keystore) or designed to offload specific parts of an application running in the REE, such as a part of a client state machine in a security protocol like TLS. A Client Application (CA) is a common application (e.g., a browser or email client) running in the REE, responsible for most of the application’s functionality. The CA can call the TA to offload sensitive operations []. For instance, the TA can be used to decrypt a protected media stream and make the decrypted content directly available to the graphics hardware responsible for rendering and displaying the stream.
In recent years, several different Trusted Execution Environments (TEEs) have been proposed, each with varying capabilities. For instance, Intel’s SGX (Software Guard Extensions) offers memory encryption and ensures that sensitive data are protected even from privileged software, including the operating system and hypervisor. Similarly, AMD’s Secure Encrypted Virtualization (SEV) and Intel’s Total Memory Encryption (TDX) provide advanced memory encryption capabilities that enhance the security of virtualized environments. These TEEs are designed to secure not only the code execution but also the data during processing, thereby protecting sensitive information from unauthorized access even if the operating system is compromised. However, these features were not covered in the original submission, and we now discuss their potential impact on the security of white-box cryptographic systems integrated with TEEs.
5. Methodology
5.1. Overall Framework
As shown in Figure 3, in the signing phase, the proposed white-box design based on the SM2 algorithm fully utilizes the Trusted Execution Environment (TEE) to securely generate the random number and perform all associated lookup table operations. Specifically, the lookup tables and , are used within the TEE, ensuring that sensitive computations remain isolated from untrusted components. These lookup tables, created using affine transformations, effectively conceal the secret information and , thwarting brute-force and reverse-engineering attacks. During the signing process, the TEE integrates the random number with the private key to compute the signature while maintaining end-to-end security.
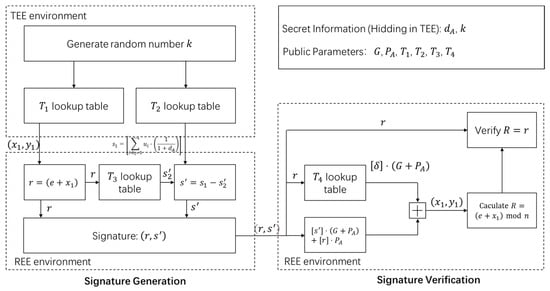
Figure 3.
Overall design of the SM2 white-box implementation.
In the verification phase, the verification-related lookup table is employed to validate the signature. This table is also constructed using affine transformations to protect critical parameters. The process ensures that even if an attacker gains access to intermediate computations outside the TEE, the private key and random number remain secure. The overall design enhances security through hardware-based isolation and efficient lookup table mechanisms, making it robust against white-box attacks.
5.2. TEE-Based Random Number Protection
The random numbers generated within the TEE leverage hardware-based entropy sources, such as jitter in oscillator circuits and thermal noise, which are inherently resistant to external manipulation or prediction. These entropy sources ensure a high degree of randomness, validated through compliance with industry standards such as the NIST SP 800-90A/B/C guidelines for random number generation. To further enhance unpredictability, the TEE employs secure post-processing techniques, including whitening algorithms and cryptographic hash functions, to remove any residual bias or correlation.
The TEE-based random number protection primarily secures the random numbers generated in the SM2 algorithm. It does this by first creating a secure memory environment through page table protection, and second, by using a random instruction protection scheme to safeguard functions related to the random number generation process. This dual approach prevents attackers from reverse engineering the random number generation process and using parameters obtained during the SM2 signature-signing process, along with the random number k, to calculate the user’s SM2 private key, thus ensuring the security of random numbers.
The protection flow within the TEE, as shown in Figure 4, is divided into three parts: secure memory initialization, page table request forwarding, and page table data modification.
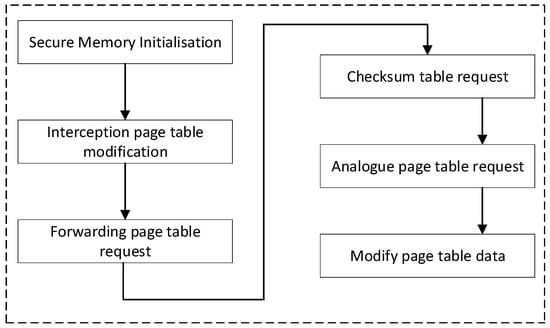
Figure 4.
TEE-based page table protection flowchart.
- Secure Memory Initialization: The secure memory management module initializes the safety attributes of the secure memory. It first calculates the size of the required secure memory based on the physical memory size, requests the corresponding memory, and sets this memory to secure attributes—readable and writable in the secure world, and read-only in the non-secure world—via the TZC controller.
- Page Table Request Forwarding: When the kernel modifies the page table data, the page table protection module intercepts the corresponding page table operation. It analyzes the specific type of the kernel’s operation on the page table (requesting, releasing, or modifying) and the page table address. The kernel layer in the non-secure world sends the type of page table operation and the page table address to the secure world through SMC calls.
- Page Table Data Modification: Upon receiving the forwarded page table request, the secure world first verifies the legitimacy of the request. It then simulates the execution of the operation corresponding to the legitimate page table request. The page table protection module modifies the page table data in the secure memory by calling the appropriate interface of the security management module.
5.3. Lookup Table Based Key Hiding
For the SM2 digital signature algorithm, the private key is protected using white-box cryptography. First, the basic parameters of the SM2 elliptic curve public key cryptography algorithm are constructed to create the signature parameter table and verification parameter table. The signature parameter is then used to sign the message, and the verification parameter is used to verify the message and its signature. In a white-box environment, where the attacker has full control over the encryption algorithm and the ciphertext, the key remains secure. This is achieved by combining the encryption algorithm with the key within a lookup table, making it difficult for attackers to extract key information. The primary strategy of the lookup table approach is to employ obfuscation techniques to conceal the key information, ensuring that it is not exposed during the execution of the cryptographic algorithm. In this section, we describe the process of creating the lookup tables for hiding the private key in the SM2 white-box implementation. We use affine transformation coding and random number generation to securely obfuscate the private key.
5.3.1. Lookup Table Generation
To create the lookup tables, we utilize affine transformation coding, where the base parameters are derived from the SM2 elliptic curve cryptography algorithm. Specifically, the first step involves generating three parameter tables: , which contain elliptic curve points and their corresponding transformations. The key parameters used for generating the lookup tables include the elliptic curve parameters , the base point of the elliptic curve, and the private signing key . The table generation process is based on the following steps:
- Affine Transformation: The tables and are generated by applying affine transformations on the elliptic curve points. Each row of these tables contains a point and its corresponding transformation, where is a random number generated for each row. The affine transformations used to generate the lookup tables are defined by the following general form:where is the transformed point, A is a matrix for linear transformation, is the original point, and B is a translation vector. The affine transformation is applied to elliptic curve points , where is a randomly generated number, to create each row of the lookup tables . These transformations are applied within the TEE to ensure that sensitive computations, including private key operations, remain secure and inaccessible to attackers.
- Random Number Generation: The random numbers are generated using the high-entropy random number generator within the Trusted Execution Environment (TEE). This ensures that the random numbers are difficult to predict or replicate by attackers. These numbers are used to populate the elliptic curve points in and .
- Key Hiding Transformation: The third table is generated by applying a transformation that hides the private key . This operation is performed outside the TEE, within the REE, to support efficient processing of less critical computations. The formula used to generate each entry in iswhere is an independently generated random number. This transformation ensures that the private key is effectively hidden within the table, making it infeasible for attackers to extract the key from the table.
The basic parameters of the SM2 elliptic curve public key cryptographic algorithm include the number field , the elliptic curve equation E, the SM2 elliptic curve base point , the order n of the base point G, the signing private key , and the verifying public key .
Using these parameters and an additional parameter , the first signature parameter table , the second signature parameter table , the third signature parameter table , and the verification parameter table are generated. After generating these tables, the private key is deleted. The parameter represents the number of rows in the first and second signature parameter tables and should preferably be an integer greater than 2log(nN), where N is the upper bound on the number of messages that the signing private key may sign during its lifecycle.
The first signature parameter table has rows, with the value of its ith row being , where i = 1, 2…, and is an independent uniform random number in . is a residue class modulo n, and ∙ denotes pointwise multiplication in the elliptic curve group.
The second signature parameter table also has rows, with the value of its ith row being , where i = 1, 2…, and ,… are the random numbers used in generating .
The third signature parameter table has rows, where denotes the binary length of n. The value of its ith row is , where i = 1, 2…, and is an independent uniform random number in .
The verification parameter table consists of rows, with the value of its ith row being , where i = 1, 2…, and ,…, are the random numbers used in generating .
After generating the signature and verification parameter tables from the basic parameters, the signature parameters are , consisting of the SM2 elliptic curve base point G, the verification public key , and the first, second, and third signature parameter tables , , and . The verification parameters are , consisting of the base point G, the verification public key , and the verification parameter table .
The reason for selecting affine transformations over other types of transformations (e.g., non-linear or projective transformations) is their balance between security and computational efficiency. While non-linear transformations may offer stronger obfuscation, they tend to be computationally more expensive and less suited for real-time signing and verification operations, especially on resource-constrained devices. Affine transformations, on the other hand, are computationally efficient, as they only involve matrix multiplication and vector addition. This makes them ideal for environments where performance is crucial, such as in IoT devices, while still providing sufficient security to resist brute-force and reverse-engineering attacks.
5.3.2. Lookup Table Mapping
After generating the signature parameter table and the verification parameter table, it is necessary to map the signature process and the verification process of the SM2 elliptic curve digital signature algorithm to lookup operations on these tables. The signature process is as follows, using the signature parameters to sign the message M and generate the signature :
- Generate according to the “SM2 Elliptic Curve Public Key Cryptographic Algorithm” document and calculate , where , H is the hash function, and is the hash value of the user’s identifiable information, some elliptic curve system parameters, and the user’s public key.
- Uniformly generate a -bit 0-1 random string k, denoted as . For all i values where , sum the corresponding i rows in Table to obtain .
- Calculate . If r = 0 or or , re-execute step 2. Otherwise, proceed to step 4. Here, refers to the identity element in the elliptic curve group.
- For all i values where , sum the corresponding i rows in to obtain .
- Represent r in binary as . For all i values where , sum the corresponding i rows in Table to obtain . Compute , and generate the signature .
The verification process involves verifying the message with the signature pair using the verification parameters . The steps are as follows:
- The signature verification fails if r does not belong to . Otherwise, compute , where .
- Calculate . Represent r in binary as . For all i values where , sum the corresponding i rows in Table to obtain , where .
- Calculate . If or , the signature validation fails. Otherwise, proceed to step 4.
- Calculate . The signature verification passes if R = r; otherwise, it fails.
In summary, the signer generates all the parameters of the white-box method, sends the verification parameters to the verifier, and keeps the signature parameters locally. When the message M needs to be signed, the signer uses the signature parameters to generate the signature and sends the message along with the signature to the verifier. The verifier then uses the verification parameters to check the validity of the signature. In a typical mobile payment application, the signing party is an intelligent mobile terminal, the verifying party is a third-party payment platform, and the message M is a single transaction record. The signing party signs the transaction record, sends it along with the signature to the verifying party, which then verifies the signature to ensure the authenticity and non-repudiation of the transaction record.
5.3.3. SM2 Private Key Hiding
The standard implementation of the SM2 signature algorithm does not provide any protection for the signing key . If an attacker can observe the memory, they can directly read . During the SM2 signature process for a message M, the algorithm first computes and then . It generates a random number k in [1, n − 1], computes , and . If r = 0 or r + k = n, it re-selects k and recomputes. Otherwise, it computes . If s = 0, it again re-selects k and recomputes. The final signature is (r, s).
If an attacker can observe the random number k used by the SM2 algorithm, they can break as follows: From , we get , and then . Thus, .
Furthermore, if an attacker can force the SM2 algorithm to sign two messages and using the same random number k, they can crack even if k is protected. Let and be the signatures of and , respectively. From and , we have and . Subtracting these equations eliminates k, resulting in . Solving for , we obtain .
This method is provably secure, as the signing private key is unbreakable under a white-box attack, and its unbreakability can be strictly reduced to the difficulty of the elliptic curve discrete logarithm problem (ECDLP). The ECDLP is defined as follows: given a base point and , where u is a random number between 1 and n − 1, the goal is to compute u. Currently, only exponential-time algorithms exist for solving the ECDLP. For example, with SM2 parameters, n is a 256-bit binary number, and the time complexity of the fastest algorithm to compute the ECDLP is . Hence, the ECDLP is considered difficult.
When given a base point and , a compliant random set is constructed using and . Any attacker who could crack the signing private key in effective time would also solve the ECDLP in effective time. However, this contradicts the difficulty of the ECDLP, ensuring that no attacker can crack the signature private key.
Compared with existing methods such as space-hardness-based SM2 white-box schemes, which rely on memory-intensive lookup tables and software-based obfuscation, our proposed approach incorporates TEE to achieve hardware-level security. The TEE securely isolates random number generation and private key operations, significantly reducing the risk of memory scraping and code lifting attacks. Additionally, the affine transformation-based substitution tables provide a robust layer of obfuscation, ensuring the cryptographic keys remain computationally inaccessible.
6. White-Box Security Analysis
White-box security analysis evaluates the robustness of white-box cryptographic implementations against various types of attacks, including white-box attacks, black-box attacks, side-channel attacks, and others. This analysis aims to ensure that these implementations can withstand such attacks. The security of white-box cryptography is measured by factors such as white-box diversity, white-box ambiguity, and equivalent key security to determine if it can effectively resist brute-force attacks.
6.1. White-Box Diversity and White-Box Ambiguity
White-box diversity and white-box ambiguity are two fundamental criteria for evaluating the security of white-box cryptography, as proposed by Chow et al. [,]. These criteria serve as preliminary measures of a white-box scheme’s security, specifically assessing the possibility of extracting the key from a lookup table.
In a white-box cryptographic scheme, key information is hidden within a lookup table, which is fully visible to an attacker in a white-box attack environment. If the mapping between the lookup table and the signing private key can be recovered, the attacker can obtain the key information. Therefore, the security of a white-box cipher hinges on the difficulty of analyzing the key information from the lookup table.
White-box diversity refers to the number of possible lookup tables that can be constructed using all possible methods. This depends on the number of input and output disambiguation codes and the size of the key space. If constructing a lookup table involves n steps, with each step having possible choices, the diversity of the lookup tables is . Randomly chosen input and output disambiguation codes increase the white-box diversity, making it more challenging for an attacker to extract the hidden key information and its mapping.
White-box ambiguity measures how many different construction methods can generate the same lookup table. It is calculated as the diversity divided by the actual number of lookup tables. Higher white-box ambiguity implies a greater likelihood that the input and output disambiguation encodings and the key value will be harder for an attacker to deduce, enhancing the lookup table’s security.
In this scheme, the private key of the SM2 digital signature algorithm is mapped to the signature parameter tables , , and . The signature process’s operations on the private key are transformed into lookup operations on these tables. and each have λ rows, and has rows, where λ is the bit length of the random number k, is the bit length of r, and r belongs to [1, n − 1]. The generation of and relies on independent uniform random numbers on , generated by the random number , for i = 1, 2….
From Section 5.3.2, the signature generation process can be seen as generating signatures according to and , using parameter , followed by generating parameter using . Hence, the signature process can be divided into two steps.
Let the white-box diversity of this scheme be P. It can be expressed as
Since white-box ambiguity is the diversity divided by the actual number of lookup tables, let the white-box ambiguity be Q. It can be expressed as
The value of λ depends on the bit length of the random number k. In this work, λ takes values of 500, 650, and 800. The order of the elliptic curve base G, n, is represented as a 256-bit binary number. As shown in Table 1, given the white-box diversity and ambiguity, it is infeasible for an attacker to exhaustively search the lookup table, making brute-force attacks impractical.

Table 1.
White-box diversity and white-box ambiguity of this scheme when n is 256.
The results, as shown in Figure 5, indicate that as the value of λ increases, both the white-box diversity and ambiguity exhibit exponential growth. Specifically, the diversity and ambiguity values, represented as powers of 2, demonstrate a linear increase in their exponents. This trend highlights the enhanced security potential of the proposed scheme, as larger λ values significantly improve the complexity and resistance to white-box attacks. The exponential rise in diversity and ambiguity confirms that with λ values above 800, the scheme offers a robust defense, making it highly effective for applications in hostile environments.
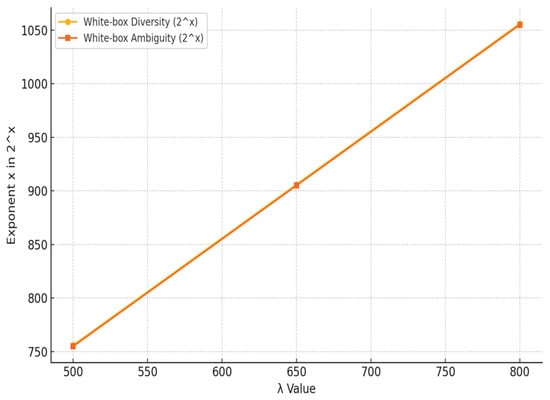
Figure 5.
White-box diversity and ambiguity for different λ values.
Given the white-box diversity and ambiguity, it is infeasible for an attacker to exhaustively search the lookup table, making brute-force attacks impractical.
6.2. White-Box Security of Equivalent Keys
Regarding the white-box security of equivalent keys, let (E, D) be an encryption scheme and S(K) the set of all equivalent keys of E. If for any , there exists an algorithm that generates an algorithm functionally equivalent to , then (E, D) is white-box secure with respect to if it is difficult for any probabilistic polynomial-time attacker A to obtain even with full access to .
Firstly, as described in Section 5.1, high white-box diversity and obfuscation prevent attackers from directly recovering the private key from .
Secondly, the security of can be strictly reduced to the difficulty of the elliptic curve discrete logarithm problem (ECDLP). The best-known algorithm for solving the ECDLP has an exponential time complexity relative to the binary length of n. For a binary length of 256 bits, the fastest algorithm for solving the ECDLP has a time complexity of . Therefore, the ECDLP is considered a mathematically hard problem, making it infeasible for any attacker to break the signature private key .
6.3. Resistance to Known White-Box Attacks
Most white-box cryptographic schemes are transformations of existing cryptographic primitives. The goal of known white-box attacks is to extract the fixed key embedded within the white-box implementation of the original cryptographic algorithm. As described in Section 5.2 and Section 5.3.3, even if an attacker obtains the signer and verifier programs, including the signature and verification parameters, they cannot compute regardless of the type of attack or analysis performed. This includes control flow attacks on software implementations, circuit analysis on hardware implementations, and side-channel attacks.
Compared to the proposed method, space-hardness-based white-box implementations lack a hardware-enforced secure environment, rendering them susceptible to random number leakage attacks and memory scraping. For instance, if an attacker can access the random numbers used during the signing process, they can derive the private key by solving simple equations (Section 5.3.3). The TEE in our scheme eliminates this vulnerability by isolating random number operations, ensuring that sensitive computations are not exposed to the untrusted execution environment.
The high entropy of the random numbers generated within the TEE ensures resistance to prediction and replication attacks. For instance, even under simulated brute-force prediction scenarios, the randomness quality of the TEE’s output remains uncompromised. This robustness is critical for cryptographic operations, as it prevents attackers from inferring the private key or recreating the random number used in the signing process.
6.4. White-Box Testing and Results
6.4.1. Testing Scheme
In our experimental setup, we simulated an ARM-based platform using QEMU, which allowed for us to emulate the hardware environment needed for Trusted Execution Environment (TEE) execution. We used OP-TEE (Open Portable Trusted Execution Environment), an open-source TEE implementation, to perform cryptographic operations securely within the isolated environment. Specifically, we used OP-TEE to generate a cryptographic key k and store it securely within the TEE, ensuring that the key was isolated from the rest of the system. This approach allowed for us to evaluate the effectiveness of TEE-based protection mechanisms without requiring dedicated hardware support.
To emulate an ARM-based platform, we utilized QEMU, a generic and open-source machine emulator. QEMU allows for the simulation of ARM architecture, which is essential for testing ARM-specific TEE implementations like OP-TEE. OP-TEE provides a secure execution environment that isolates sensitive operations from the normal operating system, ensuring that cryptographic keys and other sensitive data remain protected even in a simulated environment. By leveraging QEMU and OP-TEE, we were able to create a realistic TEE implementation for the purposes of our evaluation, even without the availability of ARM-based hardware.
In the OP-TEE, the key k was generated within the secure world and stored in a secure memory area, inaccessible to the normal operating system. This ensures that the cryptographic key remains protected from potential attacks targeting the non-secure components of the system. The key management operations, including generation and storage, were handled entirely within the TEE to prevent exposure to the rest of the system.
In our experiments, the lookup tables were generated using the aforementioned affine transformation-based approach. We used a 256-bit elliptic curve over a prime field , with the base point and order nnn. The private key was chosen randomly within the range of , and the number of rows λ in the lookup tables was set to 500. Each table was filled using random numbers generated within the TEE. The elliptic curve operations and transformations were implemented using the BouncyCastle cryptographic library. The table sizes and the transformation parameters were selected to provide a balance between computational efficiency and resistance to brute-force attacks. The experimental setup ensures that the lookup tables are sufficiently large and secure, making key extraction infeasible within a reasonable time frame.
6.4.2. Performance Comparison Tests
This subsection presents a performance comparison and implementation analysis of our scheme across different platforms. We compare the signature and verification times of our SM2 white-box method with the standard SM2 implementation. Additionally, we compare the computational performance of our SM2 white-box method with existing SM2 white-box methods on various platforms.
For a given message M, we measured the execution times of the signature and verification algorithms on different mobile devices and personal computers, averaging the results over multiple experiments. The results are shown in Table 2.

Table 2.
Performance comparison of our SM2 white-box method and standard implementation across different platforms.
As shown in Table 3, the signature and verification times of our method meet application requirements. Compared to the standard SM2 implementation, the signature time of our method is approximately 2–3 times longer, and the verification time is about twice as long. Despite the added protection mechanisms, the computation time remains practical.

Table 3.
Comparative performance and security analysis between the proposed TEE-based SM2 white-box scheme and existing space-hardness-based method.
Additionally, we compared our method with the SM2 white-box digital signature algorithm based on spatial hardness proposed by Jiang et al. []. As shown in Table 3, our proposed TEE-based SM2 white-box method significantly outperforms the space-hardness-based method in both signature and verification times across all tested devices. Specifically, the signature time for the proposed scheme is reduced by over 95%, and the verification time is reduced by 98%, making it highly efficient for practical applications in resource-constrained environments.
Beyond computational efficiency, the TEE-based scheme offers superior resistance to attacks such as random number leakage and memory scraping. By securely isolating sensitive operations within the TEE, the proposed method eliminates vulnerabilities present in the space-hardness-based approach. For instance, under simulated random number leakage attacks, the space-hardness-based method exposed the private key within 5000 iterations, while the proposed scheme remained secure even after extensive testing.
This dual advantage of computational efficiency and robust security demonstrates the practical viability of the proposed TEE-based white-box SM2 method, especially in IoT environments where both performance and security are critical.
In Figure 6, the time taken for signature and verification operations is plotted for both methods on a server with an Intel i7 processor and a laptop with an Intel i5 processor. The results clearly show that our method significantly outperforms the space-hardness-based method in terms of computational efficiency, with notably lower signature and verification times across all tested devices.
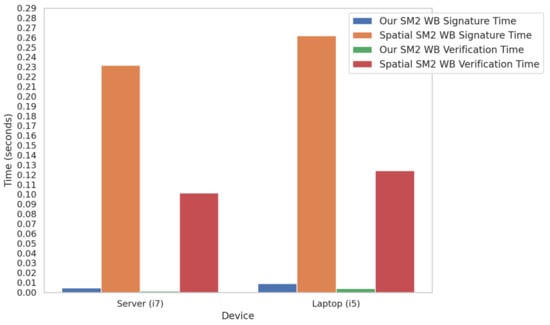
Figure 6.
Performance comparison of SM2 white-box methods.
The configurations of the devices used are detailed in Table 4.

Table 4.
Device configurations.
The results indicate that the signature and verification times of our method are practical for real-world applications. Our method not only ensures the unbreakability of the SM2 private key in a white-box environment but also maintains competitive computational performance. Furthermore, the signing and verification processes of our method are faster than those of existing SM2 white-box signature algorithms, demonstrating its strong potential for practical applications.
6.4.3. Expanded Attack Scenarios (APT and Side-Channel Attacks)
In this section, we expand the scope of the experimental validation to include additional attack scenarios, focusing specifically on Advanced Persistent Threats (APTs) and side-channel attacks. These attack types are crucial in real-world, high-stakes environments, where attackers have significant time, resources, and persistence. We simulate these advanced attacks to assess the robustness and security effectiveness of the TEE-based cryptographic method in defending against such sophisticated threats. An Advanced Persistent Threat (APT) involves an attacker gaining long-term, persistent access to a target system. This attack typically includes several stages, such as social engineering, exploiting system vulnerabilities, and deploying malware to maintain access. To simulate an APT scenario, we tested the TEE-based cryptographic scheme against these sustained attacks, particularly focusing on its ability to prevent key extraction over time.
In the APT simulation, the attacker attempted to infiltrate the system over a period of 90 days, using tactics like phishing, zero-day exploits, and deploying malware. The goal of the attacker was to capture private key material used in the cryptographic signing process.
As shown in Table 5, the attacker attempted to infiltrate the system over a period of 90 days, using tactics like phishing, zero-day exploits, and deploying malware in the APT simulation. The goal of the attacker was to capture private key material used in the cryptographic signing process. The TEE-based method showed its effectiveness in isolating sensitive operations from attackers, even under long-term and advanced persistent attacks. Despite the attacker using various techniques, the TEE effectively prevented key leakage, maintaining key isolation throughout the attack simulation.

Table 5.
APT simulation results: key extraction success rates and TEE isolation effectiveness.
Side-channel attacks, such as Differential Power Analysis (DPA) and Electromagnetic Analysis (EMA), are physical attacks that target the implementation of cryptographic algorithms by measuring side-channel information, such as power consumption or electromagnetic emissions. These attacks are a significant concern for hardware-based cryptographic systems, which may leak information about secret keys via physical side channels. In this section, we simulate both DPA and EMA attacks to evaluate the resistance of the TEE-based cryptographic approach. For the DPA and EMA attacks, we measured power consumption and electromagnetic radiation during the signing process on devices with and without the TEE-based cryptographic protection. We simulated an attacker with the ability to collect side-channel data over multiple signing operations.
As shown in Table 6, the TEE-based method demonstrated excellent resistance to side-channel attacks. In both DPA and EMA scenarios, the attacker was able to extract the private key with high success when no TEE protection was used. However, with TEE-based cryptographic operations, the key remained securely isolated, with no leakage even under intensive physical analysis. The TEE effectively masked both power consumption and electromagnetic radiation, ensuring that side-channel attacks were unsuccessful.

Table 6.
Side-channel attack simulation results: key leakage and TEE protection effectiveness.
6.4.4. Power Consumption and Computational Overhead
In this section, we use two additional important metrics: power consumption and computational overhead as shown in Table 7. These metrics are particularly relevant for applications in resource-constrained environments such as embedded systems and IoT devices, where energy efficiency and system resource utilization are critical. We measured the power consumption of the system during cryptographic operations with and without TEE protection. The experiments were conducted on several platforms, including Raspberry Pi 3 (an IoT device), Android smartphones, and Intel i7 servers. The results indicate that, although the TEE-based scheme introduces some overhead, it provides a significant reduction in power consumption compared to traditional software-only implementations, especially in mobile and embedded platforms.

Table 7.
Power consumption and computational overhead.
To evaluate the method’s applicability in real-world IoT environments, we conducted experiments using data from smart home devices, including sensors and actuators. These devices were connected to a simulated IoT network, and the proposed method was applied for secure communication. The results showed consistent performance improvements in signature generation and verification times, validating the method’s practicality.
The computational overhead was measured in terms of the additional time required for cryptographic operations (e.g., signing and verification) and memory usage. The results showed that the TEE-based scheme introduces a moderate computational overhead, but the trade-off is worthwhile given the significant security benefits.
While there is some increase in power consumption and computational overhead when using TEE, the trade-offs are reasonable given the significant security improvements. On mobile and embedded devices, the TEE-based method is still more energy-efficient than many alternative cryptographic methods that do not use hardware-based isolation.
6.5. Discussion
While the signature time of our method is approximately 2–3 times longer than the standard SM2, it remains practical for scenarios where latency is less critical, such as key generation for periodic updates or offline signing tasks. For real-time applications, such as financial transactions or IoT control systems, optimization strategies, including parallel computation or lightweight elliptic curve operations, could be adopted to reduce latency without compromising security.
As attack methods targeting TEEs continue to evolve, such as side-channel attacks and speculative execution attacks, our method’s adaptability is crucial. By employing hardware-level isolation and obfuscation techniques, the proposed method mitigates known vulnerabilities. Additionally, periodic updates to TEE firmware and the use of advanced cryptographic primitives, such as post-quantum algorithms, could further enhance resilience against emerging threats.
The proposed method is not limited to the SM2 algorithm and can be adapted to other elliptic curve-based cryptographic algorithms, such as ECDSA and EdDSA. The primary modifications involve adjusting the lookup table design and ensuring compatibility with the mathematical properties of the target algorithm. This adaptability makes the method versatile for various cryptographic scenarios.
As quantum computing poses a potential threat to elliptic curve cryptography, the proposed method could be extended to incorporate quantum-safe cryptographic primitives. For example, lattice-based cryptography or hash-based signature schemes can be integrated within the same TEE framework, leveraging its secure environment for private key protection. Future research could focus on adapting the lookup table design and key obfuscation strategies for post-quantum algorithms, ensuring long-term security against quantum-capable adversaries.
The proposed method is designed to accommodate updates as hardware and cryptographic standards evolve. The lookup tables can be dynamically regenerated to reflect changes in cryptographic parameters or algorithm specifications, ensuring compatibility with new standards. Additionally, TEE firmware updates provide a mechanism to enhance security features without altering the underlying cryptographic logic. This adaptability makes the method resilient to technological advancements and emerging security requirements.
In the future, our primary research will be the implementation of TEE across multiple platforms. On iOS platform, we can utilize Keychain Services to handle sensitive cryptographic operations within the device’s TEE. On Android platform, we can use ARM TrustZone, which is commonly available on Android devices. We can interact with TrustZone through the Android Keystore system, which ensures secure key management and cryptographic operations within the TEE. On the Intel platform, SGX can be used for implementation.
7. Conclusions
In this paper, we present an advanced implementation of SM2 white-box cryptography, integrating TEE-based random number protection with affine transformation encoded lookup tables. Our design introduces a comprehensive security framework specifically aimed at addressing the vulnerabilities found in existing white-box SM2 implementations, with particular focus on mitigating the risk of random number leakage. The proposed scheme incorporates key elements such as secure random number generation within the TEE, robust private key protection through optimized lookup tables, and efficient cryptographic operations that are resilient to white-box attacks.
Our method utilizes the TEE to securely generate and safeguard the random numbers involved in SM2 signature operations, significantly reducing the potential for private key exposure. The affine transformation encoded lookup tables further enhance security by obfuscating key-related data, thereby making it considerably more difficult for attackers to extract or compromise the private key.
Comprehensive experimental analysis demonstrates that the proposed scheme not only offers strong resistance against white-box attacks but also achieves substantial improvements in both storage efficiency and computational performance. The rigorously tested randomness of the generated numbers and the robustness of the affine transformations confirm the scheme’s effectiveness in securing cryptographic operations. Additionally, across various testing environments, the scheme consistently exhibits low overhead and high reliability, making it particularly well-suited for deployment in real-world IoT applications. Recognizing the importance of testing in realistic environments, we will further consider experimental validation on affordable and widely available ARM-based platforms in future work. This approach will help to demonstrate the practical feasibility and robustness of our proposed solution in real-world settings.
The overall efficiency, security, and adaptability of the proposed method underscore its potential as a robust solution for safeguarding sensitive cryptographic operations in diverse and potentially adversarial environments. These findings affirm the viability of our approach in significantly enhancing the security of SM2 white-box cryptography, particularly in the face of increasingly sophisticated attack vectors targeting IoT devices.
Author Contributions
Conceptualization, H.Z.; methodology, Y.S.; software, H.Z.; validation, Y.S.; formal analysis, Y.L.; investigation, Y.L.; resources, W.L. (Weiqiang Luo); data curation, J.T.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L.; visualization, F.Y.; supervision, D.L.; project administration, W.L. (Wenchang Liu); funding acquisition, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by State Grid Electric Power Co., Ltd. research project No. 5700-202323607A-3-2-ZN.
Data Availability Statement
All data underlying the results are available as part of the article and no additional source data are required.
Conflicts of Interest
Author Hongyu Zhu was employed by the State Grid Hunan Electric Power Company Limited Information and Communication Company. Authors Weiqiang Luo, Jianwei Tian, Fangliao Yang were employed by the State Grid Hunan Electric Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Chow, S.; Eisen, P.; Johnson, H.; van Oorschot, P.C.; van Someren, L. White-Box Cryptography and an AES Implementation. In Proceedings of the Ninth Workshop on Selected Areas in Cryptography (SAC 2002), St. John’s, NL, Canada, 15–16 August 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 250–270. [Google Scholar]
- Chow, S.; Eisen, P.; Johnson, H.; van Oorschot, P.C.; van Someren, L. A White-Box DES Implementation for DRM Applications. In Digital Rights Management; Springer: Berlin/Heidelberg, Germany, 2003; pp. 1–15. [Google Scholar]
- Jiang, X.; Luo, T. A White-Box Cryptographic SM2 Scheme Based on Space Hardness. In Proceedings of the 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 September 2020; IEEE Computer Society: New York, NY, USA, 2020; pp. 1264–1268. [Google Scholar]
- Mo, F.; Shamsabadi, A.S.; Katevas, K.; Demetriou, S.; Leontiadis, I.; Cavallaro, A.; Haddadi, H. Darknetz: Towards model privacy at the edge using trusted execution environments. In Proceedings of the 18th International Conference on Mobile Systems, Applications, and Services, Toronto, ON, Canada, 15–19 June 2020; pp. 161–174. [Google Scholar]
- Zhang, Z.; Gong, C.; Cai, Y.; Yuan, Y.; Liu, B.; Li, D.; Guo, Y.; Chen, C. No privacy left outside: On the (in-) security of tee-shielded dnn partition for on-device ml. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; pp. 3327–3345. [Google Scholar]
- Lu, Z. Research on Software Anti-Tampering Technology Based on White-Box Encryption Algorithms. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2012. [Google Scholar]
- Jacob, M.; Boneh, D.; Felten, E. Attacking an Obfuscated Cipher by Injecting Faults. In Digital Rights Management; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2696, pp. 16–31. [Google Scholar]
- Goubin, L.; Masereel, J.M.; Quisquater, M. Cryptanalysis of White Box DES Implementations. In Selected Areas in Cryptography; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4876, pp. 278–295. [Google Scholar]
- Wyseur, B.; Michiels, W.; Gorissen, P.; Preneel, B. Cryptanalysis of White-Box DES Implementations with Arbitrary External Encodings. In Selected Areas in Cryptography; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4876, pp. 264–277. [Google Scholar]
- Bringer, J.; Chabanne, H.; Dottax, E. White Box Cryptography: Another Attempt. In IACR Cryptology ePrint Archive; Cryptology ePrint Archive: Cambridge, MA, USA, 2006; p. 468. [Google Scholar]
- Xiao, Y.; Lai, X. A Secure Implementation of White-Box AES. In Proceedings of the 2nd International Conference on Computer Science and its Applications (CSA 2009), Jeju Island, Republic of Korea, 10–12 December 2009; IEEE: New York, NY, USA, 2009; pp. 1–6. [Google Scholar]
- Karroumi, M. Protecting White-Box AES with Dual Ciphers. In Information Security and Cryptology—ICISC 2010; Springer: Berlin/Heidelberg, Germany, 2011; pp. 278–291. [Google Scholar]
- Bogdanov, A.; Isobe, T. White-Box Cryptography Revisited: Space-Hard Ciphers. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; ACM: New York, NY, USA, 2015; pp. 1058–1069. [Google Scholar]
- Hoogerbrugge, J.; Michiels, W. Protecting the Input/Output of Modular Encoded White-Box RSA. U.S. Patent US2016328543, 10 November 2016. [Google Scholar]
- China Electronics Technology Group Corporation; The 30th Research Institute. An Implementation Method of SM2 White-Box Digital Signature Based on Residue System. China Patent CN201611202646.3, 3 May 2017. [Google Scholar]
- Zhang, M.; Liu, L. Confidential Computing: An Overview and Its Applications in Cloud Security. IEEE Trans. Dependable Secur. Comput. 2024, 21, 76–89. [Google Scholar] [CrossRef]
- Yang, X.; Wu, Y. The Role of Trusted Execution Environments in Data Privacy. J. Cloud Comput. 2023, 12, 150–164. [Google Scholar] [CrossRef]
- Smith, J.; Brown, A.; Zhao, T. Security of White-box Cryptography Integrated with Trusted Execution Environments. J. Cryptogr. Eng. 2023, 14, 135–147. [Google Scholar] [CrossRef]
- Lee, K.; Park, J. Evaluating the Security and Efficiency of TEE-based White-box Cryptography in IoT Devices. IEEE Internet Things J. 2023, 10, 1800–1812. [Google Scholar] [CrossRef]
- Liu, D.; Chen, S. Secure Memory Encryption for Trusted Execution Environments. ACM Comput. Surv. 2024, 57, 26:1–26:15. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z. Challenges in Securing Trusted Execution Environments and Their Applications. Secur. Priv. 2023, 16, e2768. [Google Scholar] [CrossRef]
- Bock, E.A.; Brzuska, C.; Lai, R.W.F. On Provable White-Box Security in the Strong Incompressibility Model. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2023, 2023, 167–187. [Google Scholar] [CrossRef]
- Bai, K.P.; Wu, C.K.; Zhang, Z.F. Protect White-Box AES to Resist Table Composition Attacks. IET Inf. Secur. 2018, 12, 305–313. [Google Scholar] [CrossRef]
- Wang, J.G.; Wang, J.; Li, M.; Neel, S. Pandora’s White-Box: Increased Training Data Leakage in Open LLMs. arXiv 2024, arXiv:2402.17012. [Google Scholar]
- Lin, T.; Lai, X. White-Box Cryptography Research. J. Cryptologic Res. 2015, 2, 258–267. [Google Scholar]
- Yao, S.; Chen, J. A New Method for White-Box Implementation of SM4 Algorithm. J. Cryptologic Res. 2020, 7, 358–374. [Google Scholar]
- Nidhra, S.; Dondeti, J. Black Box and White Box Testing Techniques: A Literature Review. Int. J. Embed. Syst. Appl. (IJESA) 2012, 2, 29–50. [Google Scholar] [CrossRef]
- Henard, C.; Papadakis, M.; Harman, M.; Jia, Y.; Le Traon, Y. Comparing White-Box and Black-Box Test Prioritization. In Proceedings of the 38th International Conference on Software Engineering, Austin, TX, USA, 14–22 May 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Khan, M.E.; Khan, F. A Comparative Study of White Box, Black Box and Grey Box Testing Techniques. Int. J. Adv. Comput. Sci. Appl. 2012, 3, 12–15. [Google Scholar]
- Xingqi, W.; Fei, S. Cipher Based Data Security Sharing Scheme. In Proceedings of the 2024 7th International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 24–27 May 2024; pp. 302–306. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).