Abstract
With the increasing demand for implementing deep-learning models on devices on resource-constrained devices, the development of power-efficient neural networks has become imperative. This paper introduces HADQ-Net, a novel framework for optimizing deep convolutional neural networks (CNNs) through Quantization-Aware Training (QAT). By compressing 32-bit floating-point (FP32) precision weights and activation values to lower bit-widths, HADQ-Net significantly reduces memory footprint and computational complexity while maintaining high accuracy. We propose adaptive quantization limits based on the statistical properties of each layer or channel, coupled with normalization techniques, to enhance quantization efficiency and accuracy. The framework includes algorithms for QAT, quantized convolution, and quantized inference, enabling efficient deployment of deep CNN models on edge devices. Extensive experiments across tasks such as super-resolution, classification, object detection, and semantic segmentation demonstrate the trade-offs between accuracy, model size, and computational efficiency under various quantization levels. Our results highlight the superiority of QAT over post-training quantization methods and underscore the impact of quantization types on model performance. HADQ-Net achieves significant reductions in memory footprint, computational complexity, and energy consumption, making it ideal for resource-constrained environments without sacrificing performance.
1. Introduction
In recent years, the advancement of artificial intelligence (AI) and deep-learning technologies has catalyzed groundbreaking advancements across various domains, ranging from computer vision and natural language processing to robotics, healthcare, and, especially, Generative AI [1]. The key enablers of this AI revolution are deep convolutional neural networks (CNNs), which have demonstrated exceptional capabilities in tasks such as image recognition, object detection, semantic segmentation, and more. However, the widespread adoption of deep CNNs in real-world applications is often hindered by challenges related to computational complexity, memory requirements, and energy efficiency [2]. These challenges are particularly pronounced in resource-constrained environments, such as edge devices and embedded systems.
To optimize or compress the convolutional neural networks (CNNs) for deployment on hardware accelerators such as FPGAs, DPUs, GPUs, TPUs, etc., several key methodologies and techniques have been explored. These include efficient model architectures, pruning, knowledge distillation, parameter sharing, compression techniques, and quantization [3].
One of the primary strategies to optimize CNNs is quantization, a process that involves reducing the precision of network parameters, such as weights and activations, from higher bit-widths (e.g., 32-bit floating-point) to lower bit-widths (e.g., fixed-point or integer representations). Quantization enables model size reduction and faster inference without altering the model architecture. Quantizing neural network parameters significantly reduces memory footprint, storage requirements, and computational complexity, enabling efficient deployment on resource-constrained hardware accelerators such as FPGAs, DPUs, GPUs, and TPUs. However, traditional quantization methods often suffer from accuracy degradation, particularly when using low-precision representations. This accuracy–performance trade-off hinders the full potential of quantized neural networks in real-world applications. To address this challenge, recent research has focused on developing advanced quantization techniques that preserve model accuracy while leveraging the benefits of low-precision representations.
In this work, our main motivation is to create a framework for quantizing any CNN for deployment on desired hardware accelerators or edge devices. This paper introduces a novel approach for power-efficient and hardware-adaptable deep convolutional neural network translation based on Quantization Aware Training (QAT). QAT is a systematic approach that incorporates quantization considerations during training, enabling neural network parameters to be optimized for performance under low-precision representations. By leveraging QAT, our proposed methodology aims to achieve superior accuracy retention while enabling efficient deployment of deep CNNs on resource-constrained hardware accelerators.
The increasing demand for efficient and scalable machine-learning solutions has driven the development of hardware-adaptable systems capable of supporting diverse computational requirements [4]. Modern hardware architectures (e.g., GPUs and TPUs) are now designed to handle low-bit processing, with multiplier sizes supporting integer precision levels such as INT4 and INT8, and even extending to extremely low-bit operations like 1-bit, 2-bit, and 3-bit precision. These advancements enable significant improvements in energy efficiency and computational speed, particularly for resource-constrained devices [2]. Furthermore, hardware support for mixed-precision processing, whether applied per tensor or per channel, allows for optimized performance by dynamically balancing precision and computational load [5,6]. Additionally, reduced parameter storage requirements in these systems facilitate the deployment of larger and more complex models without compromising efficiency. This study explores the implications of these hardware capabilities for machine-learning applications, highlighting their potential to enable scalable, power-efficient [7], and high-performance solutions across a wide range of use cases.
Benchmarking machine-learning studies on widely recognized datasets and various models is crucial for evaluating performance and scalability. In this study, most evaluations were conducted on the CIFAR-100, a subset of ImageNet, Hymenoptera, Berkeley Segmentation, and coco-2017 datasets. A range of models, from efficient small networks to larger architectures like ResNet152 and YOLOv7, were used to demonstrate the scalability and effectiveness of the proposed method. Additionally, while Quantization-Aware Training (QAT) introduces significant training overhead [8], achieving accuracy improvements with low-bit precision (e.g., 2-bit or 3-bit representations) is particularly important for power-efficient and resource-constrained devices. Computational efficiency is critical in such scenarios [7,9].
The paper presents a comprehensive overview of the proposed methodology, including the underlying principles of Quantization-Aware Training (QAT), adaptive limit value determination, normalization technique, and algorithmic frameworks for quantized convolution and inference processes. Additionally, experimental results and observations are provided to demonstrate the effectiveness of the proposed HADQ-Net framework across various tasks, including image super-resolution, classification, object detection, and semantic segmentation.
Overall, the contributions of this work include the development of a robust and adaptable framework for quantized deep CNN deployment, addressing the challenges of power efficiency, hardware adaptability, and accuracy retention in resource-constrained environments. Through empirical evaluations and comparative analyses, we demonstrate the potential of our approach to enable the widespread deployment of deep-learning models in real-world edge computing scenarios. This paves the way for transformative applications in AI-driven technologies.
2. Literature Review
With the rise of edge computing and the Internet of Things (IoT) [10], there is a growing demand for deploying deep-learning models on edge devices with limited computational resources. Optimizing or compressing CNNs for deployment on such devices requires careful consideration of factors such as power efficiency, model size, and inference speed [2,7].
Apart from quantization, various model compression techniques have been proposed to reduce the size and enable efficient deployment of neural network models. However, in this work, we aimed to retain the original network architecture while ensuring efficient deployment to hardware accelerators. Given these constraints, quantization emerges as the most critical component among compression methods. Quantization, though widely used in machine learning today, was originally developed in the field of information theory and has been extensively studied over the past century, particularly in digital signal processing [11]. It is a fundamental technique for reducing the memory footprint and computational complexity of neural networks, making them suitable for resource-constrained hardware platforms. Various quantization methods have been proposed in the literature [11,12], mapping high-precision floating-point parameters to lower-precision fixed-point or integer representations while striving to maintain model accuracy [13].
There are two primary methods to quantize a network: Quantization-Aware Training (QAT) and Post-Training Quantization (PTQ) [12,14]. First, QAT incorporates quantization effects into the optimization process by simulating quantization during training. In simulated quantization, the model parameters are stored with reduced precision, while the computations are carried out using floating-point arithmetic [15,16,17]. By fine-tuning model parameters under quantization constraints, QAT enables the model to learn robust representations that are resilient to precision limitations, thereby improving inference accuracy when deployed on low-power hardware [4,18,19,20]. QAT is important to achieve higher accuracy during inference, as it models quantization errors during training to match quantization effects during the inference [8]. Secondly, PTQ, on the other hand, quantizes a pre-trained floating-point network without retraining, reducing computational costs while preserving accuracy as much as possible [12,15,20]. While PTQ is simpler and more efficient, QAT generally yields higher accuracy, particularly for lower bit-widths, when sufficient training data are available [14,15].
The distribution of quantization intervals is an important part of the quantization process, as it directly impacts both accuracy and computational cost. Uniform quantization, a straightforward approach, divides the dynamic range of parameters into evenly spaced intervals, mapping each parameter to the nearest representable value within those intervals [4,16,21]. In contrast, non-uniform quantization techniques allocate more bits to parameters that have a greater influence on model accuracy [14,22]. Techniques such as logarithmic quantization and adaptive quantization dynamically adjust quantization levels based on the distribution of parameter values [23]. While uniform quantization is simple and easy to implement, it may cause more accuracy degradation compared to non-uniform methods [24]. However, due to its lower computational complexity and reduced overhead, uniform quantization remains the preferred approach for many practical applications.
Range calculation is also a crucial step in the quantization process. During inference, the weight range can be determined statically since weights remain constant. However, for activation, we can determine the range statically or dynamically. In static quantization, the range is determined beforehand during inference. While this approach is computationally efficient, it may lead to lower accuracy. In dynamic quantization, the range is calculated in real time for each activation during inference [25]. Although this method introduces higher computational overhead, it generally results in improved accuracy [26].
Determining the scope of the quantization range is also another important stage. In layer-wise or per-layer quantization, the quantization range for weights or activations is determined based on all filter weights or activations within a layer. In contrast, in channel-wise or per-channel quantization, the quantization range is determined separately for each weight or activation channel [5,27,28]. Channel-wise quantization achieves higher accuracy than layer-wise or per-tensor quantization, although with increased computational overhead [6].
Many networks constrain network weights or activations to binary (1-bit) [28,29,30] or ternary (2-bit) [14,31,32] representations. Binary and ternary operations provide an effective way to enhance the efficiency of deep-learning models. These operations leverage bit-wise arithmetic, resulting in significant speed improvements compared to higher-precision formats like FP32 and INT8. By using fewer bits to represent weights and activations, binary and ternary quantization significantly reduces memory usage and computational requirements. To achieve higher accuracy, other multi-bit quantization methods have been explored [14,21,27]. Multi-bit techniques enable a balance between resource usage and accuracy. INT8 models achieve accuracy levels comparable to full-precision (FP32) models. However, quantization below 8-bit often leads to significant accuracy loss, requiring careful handling [17,22].
Quantization can be categorized into fixed-precision quantization and mixed-precision quantization (1-bit to 8-bit), based on the bit-width of different layers [14]. The former applies a uniform bit-width across the entire network, whereas the latter allows for varying bit-widths for each channel or layer [33,34,35]. In mixed precision, the objective is to maintain higher precision for layers that are more sensitive and computationally critical while using low-precision quantization for layers that are less sensitive and less critical [22,36,37]. Recently, DNN hardware accelerators have begun to support mixed precision; however, finding the optimal bit-width for each layer remains a challenging task. This requires detailed analysis and involves a trade-off between accuracy and highly constrained hardware resources, including memory, computation area, throughput, latency, and energy [20].
Hardware-aware quantization techniques take into account the characteristics and constraints of the target hardware platform during quantization, such as on-chip memory, bandwidth, cache hierarchy, latency, energy [2], and storage [11,22,37]. By optimizing quantization parameters, such as bit-widths, scaling factors, and ranges, for specific hardware architectures, these techniques aim to maximize inference performance while minimizing resource utilization, either automatically or through the expertise of domain specialists.
Network initialization is also critical for the QAT process. It is common and recommended practice in the literature to start from a pre-trained FP32 model [12,15,17]. This approach not only improves accuracy but also reduces the number of required iterations.
In summary, the background information in this field covers a wide range of quantization techniques, model compression methods, and deployment strategies tailored for hardware accelerators and edge devices. By leveraging these techniques, researchers aim to bridge the gap between deep-learning theory and practical deployment, enabling efficient and scalable inference in real-world applications.
Related Work
Quantization of deep neural networks (DNNs) has become a key technique for deploying models on resource-constrained hardware, particularly due to its potential to significantly reduce memory usage and computational complexity. Early quantization methods primarily applied uniform, fixed bit-width quantization across all layers, without accounting for the varying sensitivity of different layers to precision loss. This often led to noticeable drops in accuracy, particularly in deeper or more complex architectures.
To address this, recent studies have explored mixed-precision quantization and its integration with neural architecture search. Wu et al. [38] introduced a differentiable neural architecture search (DNAS) framework for assigning different bit-widths to different layers, optimizing quantization under an accuracy-efficiency trade-off. Building upon this idea, methods such as HMQ [39] and multi-bit co-training [40] have proposed search-based strategies to identify optimal bit configurations using Gumbel-Softmax estimators or Monte Carlo sampling guided by accuracy predictors.
Another major area of research focuses on binarization and extremely low-bit quantization. Courbariaux et al. [41] pioneered binary networks with weights constrained to two values. However, such networks have limited performance when applied to large-scale datasets like ImageNet. Subsequent works such as those by Wang et al. [42], Ding et al. [43], and Hou et al. [44] introduced loss-aware binarization methods using second-order approximations, such as diagonal Hessian-based proximal Newton updates, to improve training stability and inference robustness.
Activation quantization has also received significant attention. Choi et al. [26] proposed PACT, a learnable clipping-based approach that optimizes activation ranges during training. Despite its effectiveness, PACT suffers from inaccurate gradient estimation at the clipping boundary. To improve gradient flow, DSQ [45] used a differentiable soft quantization function based on tanh, while LSQ [46] and LSQ+ [47] introduced learnable quantization step sizes and differentiable zero points for precise gradient-based optimization.
Further enhancements include adaptive quantization strategies based on the statistical properties of weights. Techniques such as Spatial Shift Per-Point Quantization (SSPQ) [48] and PROFIT [49] aimed to stabilize activation patterns and maintain model accuracy at extremely low precisions. However, the trade-off between quantization granularity and computational overhead remains a central challenge.
In the context of outlier sensitivity, several works have addressed the adverse effects of large weight magnitudes on quantization resolution. Cai et al. [50] and Jung et al. [51] introduced weight normalization and clipping threshold optimization techniques, respectively, to compress the dynamic range. However, these approaches often require retraining and may suffer from information loss due to aggressive clipping. Zhao et al. [52] attempted to avoid retraining by duplicating outlier channels at inference time (OCS), though this method struggles at ≤4-bit precision. Distribution-aware quantization methods, such as DFQ [53], improved upon uniform scaling by minimizing inter-channel weight discrepancies without data access, though they too lacked granularity in targeting individual outliers.
In hardware-oriented quantization, uniform quantization remains the most popular due to its simplicity and compatibility with fixed-point hardware. Still, it fails to exploit the non-Gaussian nature of real-world weight distributions. Non-uniform schemes, such as PoT [54] and IPoT [55,56,57], use power-based quantization to better match weight sparsity and distribution characteristics. These methods offer high energy efficiency but require statistical weight distribution knowledge, which may not always be feasible in real-time embedded applications.
Recently, distribution-aware and adaptive quantization approaches have emerged to mitigate the shortcomings of fixed quantization strategies. Channel-wise and group-wise quantization methods [58,59] have demonstrated improvements in domains such as super-resolution and generative modeling. Furthermore, EdgeQAT [60] employed entropy and distribution metrics to guide quantization-aware training for edge-friendly language models.
Representative quantization methods such as DoReFa-Net [28], PACT [26], DSQ [45], LSQ [46], and LSQ+ [47] continue to form the basis for low-bit DNN deployment. While non-uniform quantization methods like QIL [51], POT [54,61], APOT [56], and LQ-Net [21] offer improved task performance through data-aware interval learning and logarithmic encoding, they often entail additional computational cost and hardware complexity.
Inspired by these advancements, our work proposes a quantization framework that we aim to enhance model robustness and computational efficiency while preserving inference accuracy, particularly in edge deployment scenarios.
While recent advances in network quantization have made significant strides in efficiency, critical gaps remain in achieving practical deployment on resource-constrained devices. Prior studies often overlook the compounded trade-offs between accuracy, latency, and hardware compatibility, particularly for widely used architectures. Our work addresses these limitations by proposing a uniform quantization framework that optimizes three key dimensions: computational overhead (inference through fast integer operations), dynamic activation quantization (preserving accuracy via layer-wise or channel-wise precision adaptation), and scalability (supporting both fixed- and mixed-precision modes with minimal tuning). Unlike existing methods that force a choice between low-bit efficiency and multi-bit accuracy, our approach is flexible for channel-wise and layer-wise strategies, bridging the theoretical advantages of dynamic quantization with the practical demands of edge deployment. This balance of low-latency execution, minimal resource consumption, and plug-and-play compatibility with widely used standard networks positions our method as a versatile solution for real-world edge devices or TinyML applications.
3. Proposed Method
In this study, we investigated the QAT method to quantize the neural networks. By leveraging the availability of training data, the QAT method provides better accuracy and more optimized networks in terms of bit-widths. For the distribution of quantization intervals, the uniform quantization method was employed. This approach was chosen because we aim to develop networks that are as efficient as possible for deployment on resource-constrained devices. To achieve higher accuracy, dynamic quantization was applied to activations during inference. Given the trade-off between accuracy and computational complexity, both layer-wise and channel-wise quantization were evaluated. Additionally, the accuracy of low-bit and multi-bit quantization was thoroughly analyzed. Furthermore, fixed and mixed precision quantization techniques were investigated.
At first glance, the focus may appear to be primarily on the training step. However, the main goal is to enhance the inference process efficiently, with a focus on hardware-aware optimization. For example, gradients and errors were not quantized during backpropagation. Instead, the Straight Through Estimator (STE) was employed to approximate the gradients [46,62].
For maximum power and resource optimization, all the weights and activations were quantized. However, for simplicity, the quantization of the bias term was omitted as its impact on accuracy and resource usage is negligible.
3.1. Proposed Quantization Aware Training Methodology
To compress FP32 precision weights and activation values in neural networks, quantization is required to reduce the bit-width.
For the uniform quantization method, given the bit-width b, the FP32 activation value or weight x in the range (, ) and s is the scale factor, the uniform quantization process [11,17] can be defined as:
The dequantization process [11,17] is given by:
To optimize the quantized weights and activation values, it is important to understand their behavior. To achieve this, many CNN networks were analyzed. First, the weight distributions were examined. The histogram of the weights in a CNN layer is shown in Figure 1. It was observed that the histogram exhibits a symmetric shape, resembling a Gaussian distribution.
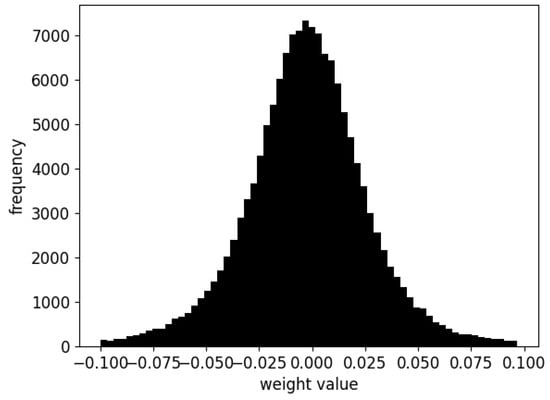
Figure 1.
Histogram of the weights.
Secondly, activation values were analyzed in Figure 2. It was observed that their histogram has a quasi-Gaussian shape, resembling a Gaussian distribution; however, the negative values in the distribution are clamped to zero.
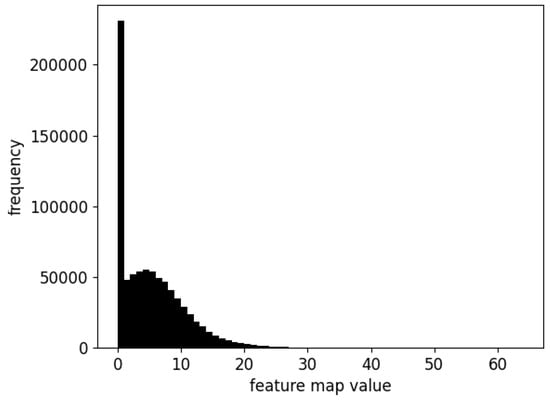
Figure 2.
Histogram of the activation values.
Based on these findings, and consistent with non-uniform quantization approaches, it was observed that the most important values are located around zero. Their importance decreases as the values deviate further from zero. This is because the frequency of usage for these values decreases as they move away from zero. Therefore, if the maximum value is limited to a fixed number, the accuracy decreases very slightly. This creates an advantageous situation in the context of quantization. In uniform quantization, the same bin size is allocated to all quantized values. However, by reducing the peak-to-peak range, the step size becomes narrower. As a result, quantization error decreases.
A fixed limit value is insufficient to achieve optimal accuracy. Instead, it should be adaptively adjusted for each layer or channel. Therefore, an adaptive limit value is proposed, determined using the mean and standard deviation. In addition to the adaptive limit adjustment, normalization further improves accuracy. Here, values are normalized based on the absolute maximum of the clipped weights and activation values.
3.2. Architecture and Design Overview
Experimental measurements were used to identify the most effective upper and lower clipping limits as:
and
respectively. Using these limits, the clamped weight or activation values are computed. Further accuracy improvements are obtained by normalizing the weight or activation values using:
where all values (val) are divided by the absolute maximum of the corresponding weight or activation values. Normalization can be performed either at the layer or channel level, depending on the quantization strategy.
3.3. Algorithm Overview
Algorithm 1 presents a comprehensive methodology for quantizing 32-bit floating-point weights or feature maps (activation tensors), a critical step in optimizing convolutional neural networks (CNNs) for deployment in resource-constrained environments. The algorithm systematically calculates statistics such as mean and standard deviation, ensuring robustness and stability in the quantization process. By employing clamping, the algorithm effectively restricts extreme values, thereby mitigating the impact of outliers on the quantization outcome. The normalization step further enhances the process by scaling values to fit within the desired range, enabling a smooth transition to quantized representations. Using a carefully calculated scale factor, the algorithm quantizes normalized values into a finite set of levels, achieving lower precision while preserving essential information for inference tasks. This comprehensive approach reduces memory footprint and computational complexity while ensuring minimal accuracy loss, enabling efficient deployment of CNN models on edge devices for a wide range of real-world applications.
Figure 3 presents a flowchart of Algorithm 1, outlining the step-by-step quantization process for weight or feature map tensors at a specified bit-width. The algorithm starts by computing key parameters required for subsequent operations. This visual representation highlights the systematic approach to optimizing CNN models for efficient deployment in resource-constrained environments.
| Algorithm 1 Quantization Process |
| Input: W_F: 32-bit floating point weight or feature map tensor N: Quantization bit-width clamp_factor: 2 Output: W_F_quantized: quantized CNN weights or feature map values S: scale factor of the quantization process 1: num_of_levels = 2^N 2: dynamic_range = 2 3: mean = mean(W_F) 4: std = standard_deviation(W_F) 5: clamp_min = mean − (clamp_factor * std) 6: clamp_max = mean + (clamp_factor * std) 7: W_F_clamped = clamp(W_F, clamp_min, clamp_max) 8: W_F_normalized = W_F_clamped/max(|W_F_clamped|) + 1 9: S = dynamic_range/num_of_levels 10: W_F_quantized = round(W_F_normalized/S) |
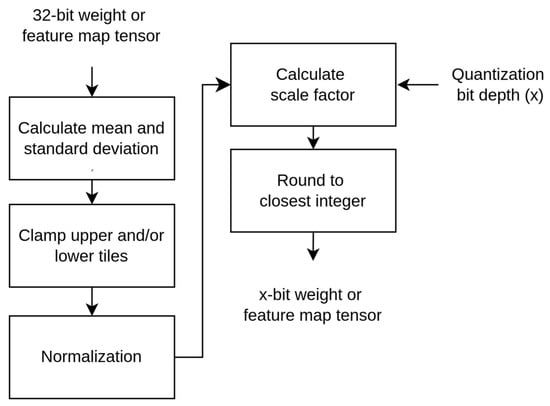
Figure 3.
Quantization flowchart.
Algorithm 2 presents our quantized convolution procedure for the training stage, a critical operation in deploying deep-learning models on resource-constrained platforms. By reducing the precision of weight and feature map tensors to a specified bit-width, the algorithm minimizes memory usage and computational overhead. After quantization, tensors are dequantized using scale factors computed during the process, ensuring compatibility for convolution operations. The convolution step incorporates parameters such as stride, padding, dilation, and groups to generate output feature maps. This framework enables efficient inference on low-power hardware while maintaining reasonable accuracy, making it ideal for edge computing and embedded systems.
| Algorithm 2 Quantized Convolution for Training Stage |
| Input: W: weight tensor F: feature map tensor stride padding dilation groups bias bit_depth_w: quantization bit-width for weights bit_depth_f: quantization bit-width for feature map Output: F_out: output feature map 1: W_quant, S = quantization(W, bit_depth_w) 2: F_quant, S = quantization(F, bit_depth_f) 3: W_dequant = W_quant * S 4: F_dequant = F_quant * S 5: F_out = conv2d(F_dequant, W_dequant, bias, stride, padding, dilation, groups) |
Figure 4 illustrates the flowchart of Algorithm 2, detailing the steps involved in quantized convolution for the training stage. The process optimizes deep-learning models for deployment in resource-constrained environments through a sequence of critical operations. The algorithm incorporates bias addition to introduce learnable offsets, enhancing model flexibility. Additionally, the Rectified Linear Unit (ReLU) activation function is applied to introduce non-linearity, improving the model’s expressive power. By integrating quantization and convolution efficiently, Algorithm 2 enables deep-learning models to achieve a balance between computational efficiency and predictive accuracy, making it well-suited for edge devices.
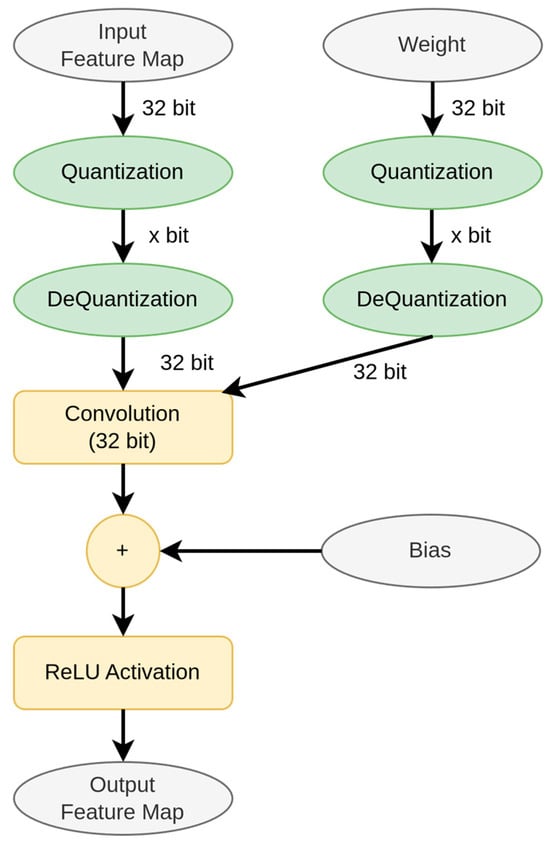
Figure 4.
Quantized Convolution for Training Stage.
Algorithm 3, Quantization-Aware Training (QAT), provides a systematic framework for training deep convolutional neural networks (CNNs) while accounting for the effects of quantization. By integrating quantization into the training process, the algorithm optimizes the model’s parameters for low-precision representations, which is critical for deployment on resource-constrained devices. During each epoch, the algorithm iteratively performs forward and backward propagation, incorporating quantized convolutions at each layer to simulate quantization effects during inference. This approach enables the model to learn robust representations resilient to the precision limitations imposed by quantization, ultimately producing a quantized CNN capable of efficient inference without sacrificing predictive accuracy. By carefully considering quantization effects during training, Algorithm 3 enables deep-learning practitioners to develop models tailored for deployment in real-world edge computing scenarios with limited computational resources.
| Algorithm 3 Quantization Aware Training |
| Input: Dataset and labels Deep CNN network Quantization bit-widths (per layer or per channel) Training parameters Output: Quantized deep CNN network 1: weight initialization 2: for each epoch do 3: Forward process: 4: for each layer do 5: Quantized Convolution 6: end for 7: Compute the loss 8: Backward process: 9: Gradient of the loss function 10: Update the weights 11: Update the parameters 12: end for |
Algorithm 4, Quantized Inference, presents an efficient method for deploying quantized deep convolutional neural networks (CNNs) on resource-constrained devices. By leveraging quantization techniques, the algorithm optimizes the model parameters for reduced-precision representations, ensuring efficient inference while preserving predictive accuracy. The inference process follows a layer-wise approach, where each layer undergoes forward propagation with quantized feature maps and weights, maintaining consistency with the training scheme. Convolutional operations with quantized tensors enhance computational efficiency, while ReLU activation introduces non-linearity to improve model expressiveness. The final output corresponds to task-specific inference results, such as image super-resolution, classification, object detection, or semantic segmentation. Overall, Algorithm 4 enables seamless deployment of quantized deep CNNs, empowering edge devices to perform complex inference tasks with minimal computational overhead.
| Algorithm 4 Quantized Inference |
| Input: F: feature maps W_quant: quantized to x bits Quantized deep CNN network Output: results (super-resolution, classification, detection, segmentation etc.) 1: for each layer do 2: Forward process: 3: F_quant = quantization(F, bit_depth_f) 4: F_conv = convolution(F_quant, W_quant) 5: F = ReLU(F_conv + bias) 6: end for 7: results |
Figure 5 illustrates the flowchart of quantized inference convolution, a crucial step in deploying deep convolutional neural networks (CNNs) on resource-constrained platforms. This process involves online feature map quantization and convolution operations using quantized weights and feature maps, where both inputs are represented with reduced precision to conserve memory and computational resources. Despite reduced precision, quantized inference convolution preserves the essential properties of standard convolution, effectively extracting features while maintaining compatibility with the quantized model parameters. By integrating quantization into the inference process, CNNs can achieve efficient computation on edge devices without significant accuracy degradation. This makes real-world deployment feasible for deep-learning applications on hardware with limited computational capabilities.
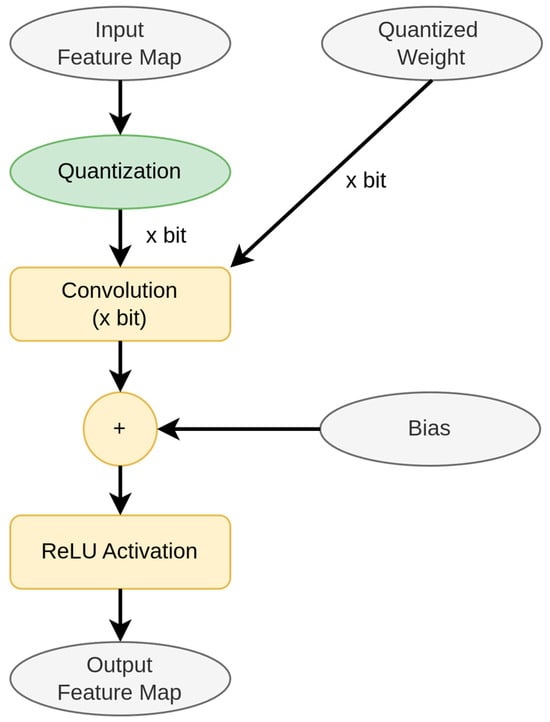
Figure 5.
Quantized inference.
Figure 6 illustrates the end-to-end deployment process of deep-learning models on resource-constrained devices. The workflow begins with a high-precision (32-bit) trained model, optimized for maximum accuracy. Through Quantization-Aware Training (QAT), model parameters are fine-tuned while incorporating quantization effects, enabling deployment at reduced precision (‘x-bit’) without significant accuracy loss. The quantized model is then optimized for efficient inference, where convolution operations utilize quantized weights and activations, ensuring faster and resource-efficient processing. This is crucial for real-world edge applications. Finally, the model output represents predictions tailored to the specific task, such as classification, object detection, or image super-resolution.
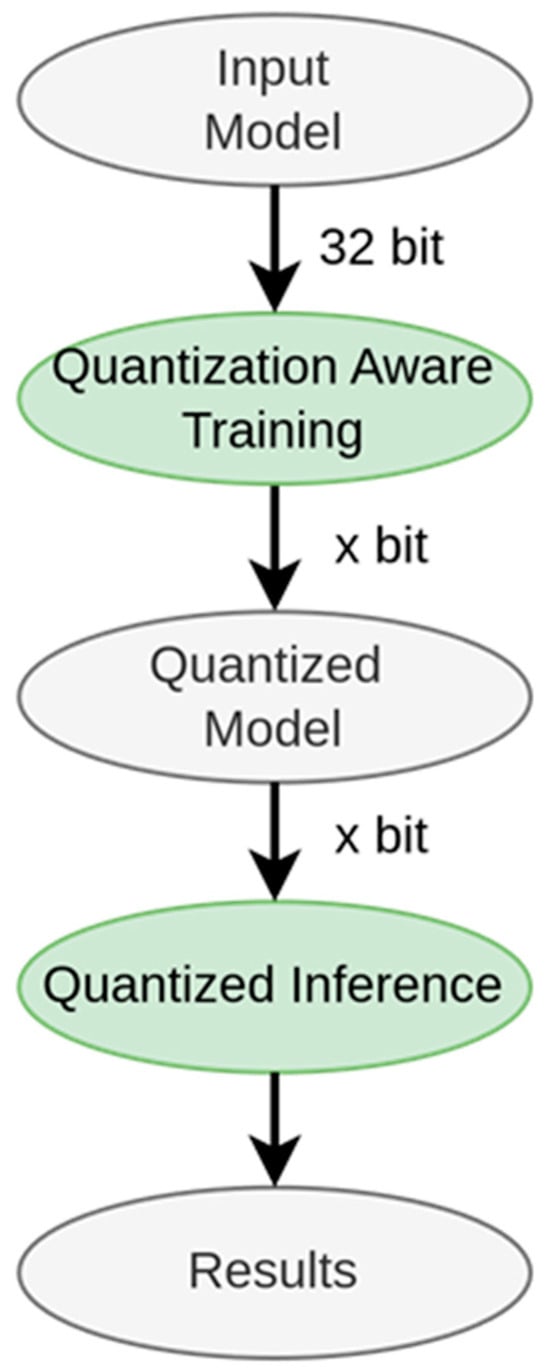
Figure 6.
Overall flowchart.
Through this iterative process of optimization and quantization, deep-learning models can be effectively deployed in resource-constrained environments without sacrificing performance.
3.4. Deep Convolutional Neural Networks
The algorithms, spanning various deep convolutional neural network (CNN) architectures, including those tailored for super-resolution, classification, detection, and segmentation tasks, have demonstrated remarkable success when deployed with low bit-widths. By optimizing models for quantized inference using techniques such as Quantization-Aware Training (QAT), the algorithms effectively balance computational efficiency with task-specific performance. In super-resolution tasks, which aim to enhance image resolution, the algorithms efficiently process high-dimensional data using reduced-precision representations, achieving impressive results. Similarly, in classification tasks, where models categorize inputs into predefined classes, the algorithms maintain high accuracy even with lower bit-widths. For object detection and semantic segmentation tasks, which require accurate identification of objects and their boundaries, the algorithms demonstrate robust performance by leveraging quantized inference for real-time processing on edge devices. These successful outcomes underscore the effectiveness of the algorithms in enabling deep CNNs to operate efficiently across a diverse range of tasks while meeting the constraints of resource-constrained environments.
4. Experimental Results and Discussion
The primary objective of this study is to develop quantized neural network models and evaluate their performances across different quantization scenarios. Since quantization-aware training (QAT) necessitates retraining, we conducted our experiments using an NVIDIA GeForce RTX 3090 Ti GPU (24 GB memory) with PyTorch (https://pytorch.org/ (accessed on 27 August 2025)), implementing software-based emulation of resource-constrained environments. This approach enabled efficient development and preliminary evaluation of our quantization framework prior to hardware deployment. While our current results focus on training outcomes, comprehensive inference performance metrics will require implementation on dedicated edge computing platforms as a future work. To ensure statistical reliability, all networks were trained multiple times.
4.1. Train-Test Benchmark Results
The experimental results presented in this section showcase the performance of various quantization methods across different tasks and bit-width configurations. Overall, these results underscore the importance of carefully selecting and fine-tuning quantization methods to strike a balance between accuracy, model size, and computational efficiency in real-world applications, particularly for deployment on resource-constrained devices.
The experimental setup uses a pre-trained ResNet18 model, trained with 32-bit floating-point precision on the CIFAR-100 dataset and achieving a typical accuracy of 0.926. For quantization experiments, the CIFAR-100 dataset serves as a basis for evaluating the performance of quantization methods on ResNet18. The goal is to assess how well the model retains its accuracy when quantized to lower bit-width representations, enabling deployment on resource-constrained devices. Quantizing the pre-trained ResNet18 model and evaluating its performance on the CIFAR-100 dataset allows us to gain insights into the crucial trade-offs among accuracy, computational efficiency, and model size for real-world deployment scenarios.
Recent research has predominantly emphasized large-scale GPU implementations, which often incur significant computational overhead through techniques like non-uniform quantization. This focus stems from prioritizing accuracy gains over computational efficiency. However, for edge device inference, the critical metrics shift to computational efficiency, latency, and power consumption. Consequently, contemporary edge computing studies continue to employ established low-bit quantization methods like DoReFa-Net and PACT as benchmark standards [63,64,65,66], with these approaches remaining prevalent in actual edge deployments.
Table 1 presents comparative results between DoReFa-Net, PACT, and our proposed method (labeled “Ours (HADQ-Net)”). Accuracy values are reported for various combinations of weight and activation bit-widths, ranging from 1-bit to 8-bit. As observed, the proposed method achieves higher accuracy levels, particularly at higher bit-widths, while maintaining competitive accuracy even at lower bit precision.

Table 1.
Accuracy comparison with widely known low-bit quantization methods.
Table 2 highlights the superior performance of Quantization-Aware Training (QAT) compared to Post-Training Quantization (PTQ). Accuracy values are reported for different combinations of weight and activation bit-widths ranging from 1-bit to 8-bit.

Table 2.
Accuracy comparison of QAT and PTQ methods for HADQ-Net.
As observed, QAT consistently outperforms PTQ across all bit-width configurations, demonstrating that incorporating quantization effects during training results in superior accuracy retention compared to post-training quantization methods.
Table 3 highlights the impact of mixing weight bit-widths on total weight size while maintaining acceptable accuracy levels. The size of fixed precision weights and mixed precision weights is reported in megabytes (MB) for the last four convolutional layers, with a bit-width of 2 bits for both weights and activations. Additionally, accuracy values for both fixed precision and mixed precision quantization methods are provided. As observed, the mixed precision approach reduces weight size while maintaining acceptable accuracy levels compared to the fixed precision approach across various bit-width configurations.

Table 3.
Accuracy and the total weight size for fixed and mixed precision quantization methods using HADQ-Net.
The comparison between fixed precision and mixed precision quantization methods provides insightful results. Despite a smaller weight size of 3.27 MB, the mixed precision approach achieves a higher accuracy of 0.823, compared to the fixed precision accuracy of 0.797 with a weight size of 3.93 MB. This demonstrates the effectiveness of mixed precision quantization in optimizing model parameters, improving performance without compromising accuracy. By judiciously leveraging lower precision representations, mixed precision quantization offers a compelling solution for deploying deep-learning models on resource-constrained devices with limited memory and computational resources.
In Table 4, “Per Tensor QAT” and “Per Channel QAT” represent quantization approaches applied per tensor and per channel, respectively. Accuracy values are reported for various combinations of weight and activation bit-widths, ranging from 1-bit to 8-bit. As observed, the Per Channel QAT method achieves higher accuracy compared to Per Tensor QAT for bit-widths greater than 2, albeit at the cost of increased computational complexity. This indicates that per-channel quantization leads to better accuracy retention, likely due to preserving more fine-grained information during the quantization process.

Table 4.
Per tensor vs. per channel QAT (HADQ-Net).
Table 5 reports the parameter sizes (in MB) for various weight and activation bit-width combinations ranging from 1-bit to 8-bit, along with the 32-bit floating-point (FP32) precision. As expected, parameter size increases with bit-width, with the largest size observed for FP32 precision. This highlights the trade-off between model size and precision, where lower-bit representations significantly reduce memory requirements, making them ideal for resource-constrained environments.

Table 5.
Parameter sizes vs. Bit-width using HADQ-Net.
4.2. Super-Resolution
Table 6 presents a comparison of average PSNR (Peak Signal-to-Noise Ratio) values across various super-resolution methods and bit-width configurations, including 32-bit floating point precision. PSNR is a widely used metric for assessing image reconstruction quality, where higher values indicate better image fidelity. The comparison includes methods such as FSRCNN-S, SubPixelCNN, FSRCNN, SRCNN, SRGAN, and VDSR. As observed, PSNR generally increases with bit-width, suggesting that higher precision representations lead to better image quality. Notably, SRGAN lacks PSNR values for all bit-widths due to its unique characteristics. Overall, Table 6 provides key insights into the performance of different super-resolution techniques under various precision constraints, aiding in the selection of the most suitable method for specific applications.

Table 6.
Average PSNR vs. Bit-width using HADQ-Net.
4.3. Classification
Table 7 presents a comparative analysis of classification accuracy across various neural network architectures under different bit-width configurations, including 32-bit floating point precision. The accuracy values reflect the proportion of correctly classified samples, offering insights into the impact of quantization on model performance. Overall, higher bit widths generally result in improved accuracy, emphasizing the importance of precision in model representation.

Table 7.
Classification accuracy vs. Bit-width using HADQ-Net.
ResNet18 maintains consistently high accuracy across different bit-widths. ResNet50 and ResNet152 exhibit notable performance gains with increased precision. DenseNet121 demonstrates stable accuracy across varying bit-widths. EfficientNet shows substantial improvements as bit-width increases. These findings highlight the trade-offs between precision and classification accuracy, aiding in the optimal selection of bit-widths for deployment in real-world applications where computational constraints must be balanced with performance requirements.
EfficientNet demonstrates lower relative accuracy compared to other architectures while exhibiting an unusually steep accuracy improvement between 6-bit and 7-bit quantization (0.790 → 0.960). To eliminate potential hyperparameter influences, we rigorously repeated all experiments five times with different random seeds. Considering EfficientNet’s MBConv block architecture—which combines depthwise separable convolutions with squeeze-excitation layers—we propose that uniform 6-bit quantization fails to properly preserve the network’s dynamic range. This suggests that a carefully optimized mixed-precision quantization strategy, accounting for the MBConv structure’s unique characteristics, could yield better results.
In Table 7, which evaluates classification accuracy across various neural network architectures under different bit-width configurations, it is important to note that the dataset used is a small subset of ImageNet. This subset includes a limited number of images and classes compared to the full ImageNet dataset, which contains millions of images across thousands of classes. Despite its smaller scale, this subset remains a valuable benchmark for evaluating neural network models, offering insights into their classification capabilities under different quantization levels. While results from smaller datasets may not fully reflect real-world performance, they provide a practical assessment of model behavior in resource-constrained scenarios with limited data availability.
4.4. Detection
Table 8 compares the mean Average Precision (mAP) of various object detection methods across different bit-width configurations, including 32-bit floating point precision. mAP measures the accuracy of bounding box predictions, with higher values indicating better detection performance. The table highlights the impact of quantization on detection accuracy. Faster R-CNN consistently achieves high mAP values across all bit-widths, showcasing its robustness in object detection. YOLOv7 shows greater variability in mAP, with notable improvements at higher bit widths. These findings illustrate the trade-offs between precision and detection performance, offering practical insights for selecting optimal quantization levels in real-world object detection applications, where computational efficiency must be balanced with accuracy.

Table 8.
Detection mAP vs. Bit-width using HADQ-Net.
4.5. Segmentation
Table 9 compares the Average Precision (AP) of the Mask R-CNN model for semantic segmentation across different bit-width configurations, including 32-bit floating point (FP32) precision. AP is measured at different IoU (Intersection over Union) thresholds: 0.50:0.95 (comprehensive assessment), 0.50 (loose match), and 0.75 (strict match). Higher AP values indicate better segmentation performance and mask accuracy. Segmentation AP varies with quantization levels, with generally higher accuracy at higher bit-widths. Despite lower precision, the model maintains competitive AP values across different IoU thresholds, highlighting Mask R-CNN’s resilience to quantization effects. These findings provide valuable insights into the trade-offs between model precision and segmentation accuracy, helping optimize bit-width selection for real-world applications where efficiency and accuracy must be balanced.

Table 9.
Segmentation AP@IoU vs. Bit-width using HADQ-Net.
In future research, quantization techniques can be further explored for various hardware accelerator platforms, including FPGAs, GPUs, TPUs, and DPUs [67]. Recently, GPUs, DPUs, and TPUs have begun to support INT4 matrix operations, enabling the development of highly efficient applications. Given their flexibility and parallel processing capabilities, FPGAs present an excellent opportunity for further optimization. In low-bit quantization scenarios, replacing multiplication operations with approximate computing methods can be highly beneficial. This approach can further reduce resource usage, power consumption, and overall latency while maintaining accuracy. By leveraging approximate multipliers or bit-wise operations, significant efficiency gains can be achieved, making quantized models more suitable for deployment on resource-constrained hardware. Taking this work further, the HADQ-Net framework can be used to implement any network architecture on an ASIC chip, enabling real-time applications with optimized performance and efficiency.
HADQ-Net significantly optimizes memory bandwidth, power consumption, and latency through its efficient quantization framework. By reducing the precision of weights and activations from FP32 to lower bit-widths (e.g., INT8, INT4, or even 1–3 bits), the model drastically decreases the memory footprint, enabling faster data transfer and reduced memory bandwidth requirements. This is particularly beneficial for hardware accelerators with limited on-chip memory. Additionally, lower precision computations reduce power consumption, as fewer bits are processed during arithmetic operations, leading to more energy-efficient inference. Furthermore, the quantized operations, such as quantized convolution, minimize computational complexity, resulting in lower latency and faster inference times. By leveraging adaptive quantization limits and normalization techniques, HADQ-Net ensures that these optimizations do not compromise accuracy, making it an ideal solution for deploying deep-learning models on resource-constrained edge devices.
5. Conclusions
In this study, we explored how to obtain efficient and scalable machine-learning models. Modern hardware architectures, supporting low-bit processing (e.g., INT4, INT8, and even 1, 2, and 3-bit precision), have shown significant improvements in energy efficiency and computational speed, particularly for resource-constrained devices. The integration of mixed-precision processing, whether applied per tensor or per channel, has further optimized performance by dynamically balancing precision and computational load. Additionally, we demonstrated that optimizing networks for efficiency leads to a reduction in memory and storage requirements, making deployment more feasible on embedded and edge devices. These findings highlight the crucial role of hardware adaptability in meeting the increasing demands of modern machine learning applications.
In conclusion, HADQ-Net presents a comprehensive exploration of power-efficient and hardware-adaptable deep convolutional neural network (CNN) translation, focusing on quantization-aware training (QAT) for hardware accelerators. Through detailed analysis and experimentation, we have demonstrated the performance of various quantization methods, including uniform quantization, parameterized clipping activation (PACT), and hardware-aware automated quantization (HAQ), in compressing FP32 precision weights and activation values to lower bit-widths. Our proposed adaptive limit value and normalization techniques have shown promising results in enhancing model accuracy while minimizing quantization errors. Additionally, the release of our HADQ-Net quantization framework on GitHub enables broader accessibility and facilitates the custom implementation of quantized convolution layers, streamlining deployment on low-power edge devices. By optimizing convolution operations for reduced-precision representations and integrating quantization directly into training, we achieved significant improvements in model efficiency without sacrificing predictive accuracy. These findings pave the way for the efficient deployment of deep-learning models in resource-constrained environments, offering practical solutions for real-world applications such as super-resolution, classification, detection, segmentation, and beyond.
In this study, we evaluated the proposed method on widely recognized datasets, including CIFAR-100, ImageNet Object Localization, Hymenoptera, Berkeley Segmentation, and coco-2017, using a diverse range of models, from efficient small networks to larger architectures such as ResNet152 and YOLOv7. The results demonstrate the method’s scalability and robustness across different model sizes and complexities. However, the Quantization-Aware Training (QAT) approach, while effective, introduces significant training overhead, which remains a challenge for practical deployment. Despite this, our findings highlight the importance of achieving accuracy improvements at low bit depths, such as 2 or 3 bits, particularly for power-efficient and resource-constrained devices. Future work will focus on extending the evaluation to the full ImageNet dataset and exploring optimizations to reduce the training overhead of QAT, further enhancing its applicability to real-world scenarios.
Through continuous refinement and innovation in quantization techniques, we aim to further advance deep learning and enhance the capabilities of edge devices, enabling them to perform complex inference tasks with minimal computational overhead. As part of our future work, we plan to quantize a complex neural network and deploy it on FPGA hardware, evaluating its efficiency, accuracy, and resource utilization. This implementation will provide deeper insights into the real-world performance of quantized models on reconfigurable hardware platforms.
6. Patents
This research has been legally protected through a filed patent application, ensuring exclusive rights to these scientific advancements.
Author Contributions
Design, C.U.O.; validation, C.U.O.; formal analysis, C.U.O.; investigation, C.U.O. and M.E.Y.; resources, C.U.O. and M.E.Y.; data curation, C.U.O.; writing—original draft preparation, C.U.O.; writing—review and editing, C.U.O. and M.E.Y.; supervision, M.E.Y.; project administration, M.E.Y.; funding acquisition, C.U.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Aselsan Inc.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available in the following publicly accessible repositories: CIFAR-100 dataset: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 27 August 2025); ImageNet Object Localization dataset: https://www.kaggle.com/c/imagenet-object-localization-challenge/data (accessed on 27 August 2025); Hymenoptera dataset: https://www.kaggle.com/datasets/thedatasith/hymenoptera (accessed on 27 August 2025); Berkeley Segmentation dataset: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/ (accessed on 27 August 2025); coco-2017 dataset: https://cocodataset.org/#download (accessed on 27 August 2025). The proposed framework and experimental results will be available on GitHub after the publication: https://github.com/can-ugur/HADQ-Net (accessed on 27 August 2025).
Conflicts of Interest
Authors Can Uğur Oflamaz and Müştak Erhan YALÇIN declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| QAT | Quantization Aware Training |
| PTQ | Post Training Quantization |
| FPGA | Field Programmable Gate Array |
| DPU | Deep Learning Processor Unit |
| GPU | Graphics Processing Unit |
| TPU | Tensor Processing Unit |
| IoT | Internet of Things |
| DNN | Deep Neural Network |
| STE | Straight Through Estimator |
| ReLU | Rectified Linear Unit |
| PSNR | Peak Signal-to-Noise Ratio |
| mAP | mean Average Precision |
| IoU | Intersection over Union |
| AP | Average Precision |
References
- Wu, T.; He, S.; Liu, J.; Sun, S.; Liu, K.; Han, Q.-L.; Tang, Y. A Brief Overview of ChatGPT: The History, Status Quo and Potential Future Development. IEEE/CAA J. Autom. Sin. 2023, 10, 1122–1136. [Google Scholar] [CrossRef]
- Sharma, S.; Kang, B.; Kidambi, N.V.; Mukhopadhyay, S. HamQ: Hamming Weight-based Energy Aware Quantization for Analog Compute-In-Memory Accelerator in Intelligent Sensors. IEEE Sens. J. 2024, 25, 7798–7808. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.-H.; Yang, T.-J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Qin, H. Hardware-friendly Deep Learning by Network Quantization and Binarization. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI-21), Montreal, QC, Canada, 19–26 August 2021; pp. 4911–4912. [Google Scholar]
- Chen, P.; Liu, J.; Zhuang, B.; Tan, M.; Shen, C. AQD: Towards Accurate Quantized Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 104–113. [Google Scholar]
- Huang, Q.; Wang, D.; Dong, Z.; Gao, Y.; Cai, Y.; Li, T.; Wu, B.; Keutzer, K.; Wawrzynek, J. Codenet: Efficient deployment of input-adaptive object detection on embedded fpgas. In Proceedings of the ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, New York, NY, USA, 28 February–2 March 2021; pp. 206–216. [Google Scholar]
- Wang, Z.; Luo, T.; Goh, R.S.M.; Zhou, J.T. EDCompress: Energy-Aware Model Compression for Dataflows. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 208–220. [Google Scholar] [CrossRef]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengi, Y. Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations. J. Mach. Learn. Res. 2016, 18, 6869–6898. [Google Scholar]
- Ateya, A.A.; Soliman, N.F.; Alkanhel, R.; Alhussan, A.A.; Muthanna, A.; Koucheryavy, A. Lightweight Deep Learning-Based Model for Traffic Prediction in Fog-Enabled Dense Deployed IoT Networks. J. Electr. Eng. Technol. 2023, 18, 2275–2285. [Google Scholar] [CrossRef]
- Gholami, A.; Kim, S.; Dong, Z.; Yao, Z.; Mahoney, M.W.; Keutzer, K. A Survey of Quantization Methods for Efficient Neural Network Inference. arXiv 2021, arXiv:2103.13630. [Google Scholar] [CrossRef]
- Nagel, M.; Fournarakis, M.; Amjad, R.A.; Bondarenko, Y.; van Baalen, M.; Blankevoort, T. A White Paper on Neural Network Quantization. arXiv 2021, arXiv:2106.08295. [Google Scholar] [CrossRef]
- Wu, S.; Li, G.; Chen, F.; Shi, L. Training and Inference with Integers in Deep Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Xu, W.; Li, F.; Jiang, Y.; Yong, A.; He, X.; Wang, P.; Cheng, J. Improving Extreme Low-Bit Quantization With Soft Threshold. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 1549–1563. [Google Scholar] [CrossRef]
- Wu, H.; Judd, P.; Zhang, X.; Isaev, M.; Micikevicius, P. Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation. arXiv 2020, arXiv:2004.09602. [Google Scholar] [CrossRef]
- Novkin, R.; Klemme, F.; Amrouch, H. Approximation- and Quantization-Aware Training for Graph Neural Networks. IEEE Trans. Comput. 2024, 73, 599–612. [Google Scholar] [CrossRef]
- Krishnamoorthi, R. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar] [CrossRef]
- Kwasniewska, A.; Szankin, M.; Ozga, M.; Wolfe, J.; Das, A.; Zajac, A.; Ruminski, J.; Rad, P. Deep Learning Optimization for Edge Devices: Analysis of Training Quantization Parameters. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Lisbon, Portugal, 14–17 October 2019; pp. 96–101. [Google Scholar]
- Zhen, K.; Nguyen, H.D.; Chinta, R.; Susanj, N.; Mouchtaris, A.; Afzal, T.; Rastrow, A. Sub-8-Bit Quantization Aware Training for 8-Bit Neural Network Accelerator with On-Device Speech Recognition. In Proceedings of the IEEE Spoken Language Technology Workshop (SLT), Doha, Qatar, 9–12 January 2022; pp. 3033–3037. [Google Scholar]
- Lee, H.; Lee, N.; Lee, S. A Method of Deep Learning Model Optimization for Image Classification on Edge Device. Sensors 2022, 22, 7344. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 373–390. [Google Scholar]
- Choukroun, Y.; Kravchik, E.; Yang, F.; Kisilev, P. Low-bit Quantization of Neural Networks for Efficient Inference. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 3009–3018. [Google Scholar]
- Choi, J.; Venkataramani, S.; Srinivasan, V.; Gopalakrishnan, K.; Wang, Z.; Chuang, P. Accurate and Efficient 2-bit Quantized Neural Networks. In Proceedings of the 2nd SysML Conference, Palo Alto, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Cai, Z.; He, X.; Sun, J.; Vasconcelos, N. Deep learning with low precision by half-wave Gaussian quantization. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5406–5414. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient Inference Engine on Compressed Deep Neural Network. ACM SIGARCH Comput. Archit. News 2016, 44, 243–254. [Google Scholar] [CrossRef]
- Choi, J.; Wang, Z.; Venkataramani, S.; I-Jen Chuang, P.; Srinivasan, V.; Gopalakrishnan, K. PACT: Parameterized Clipping Activation for Quantized Neural Networks. arXiv 2018, arXiv:1805.06085. [Google Scholar] [CrossRef]
- Qu, Z.; Zhou, Z.; Cheng, Y.; Thiele, L. Adaptive Loss-Aware Quantization for Multi-Bit Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7988–7997. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients. arXiv 2018, arXiv:1606.06160. [Google Scholar] [CrossRef]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; pp. 525–542. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Liu, B.; Li, F.; Wang, X.; Zhang, B.; Yan, J. Ternary Weight Networks. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, A.; Yao, A.; Wang, K.; Chen, Y. Explicit Loss-Error-Aware Quantization for Low-Bit Deep Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9426–9435. [Google Scholar] [CrossRef]
- Dong, Z.; Yao, Z.; Gholami, A.; Mahoney, M.W.; Keutzer, K. HAWQ: Hessian aware quantization of neural networks with mixed-precision. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 293–302. [Google Scholar]
- Yang, L.; Jin, Q. FracBits: Mixed precision quantization via fractional bit-widths. Proc. AAAI Conf. Artif. Intell. 2021, 35, 10612–10620. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Kim, H.; Lee, H.-J. Layer-specific optimization for mixed data flow with mixed precision in FPGA design for CNN-based object detectors. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 2450–2464. [Google Scholar] [CrossRef]
- Tailor, S.A.; Fernandez-Marques, J.; Lane, N.D. Degree-Quant: Quantization-Aware Training for Graph Neural Networks. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020. [Google Scholar]
- Wang, K.; Liu, Z.; Lin, Y.; Lin, J.; Han, S. HAQ: Hardware-Aware Automated Quantization with Mixed Precision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8604–8612. [Google Scholar]
- Wu, B.; Wang, Y.; Zhang, P.; Tian, Y.; Vajda, P.; Keutzer, K. Mixed precision quantization of ConvNets via differentiable neural architecture search. arXiv 2018, arXiv:1812.00090. [Google Scholar] [CrossRef]
- Habi, H.V.; Jennings, R.H.; Netzer, A. HMQ: Hardware friendly mixed precision quantization block for CNNs. In Proceedings of the 16th European Conference Computer Visiom (ECCV), Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 448–463. [Google Scholar]
- Xu, K.; Feng, Q.; Zhang, X.; Wang, D. MultiQuant: Training once for multi-bit quantization of neural networks. In Proceedings of the 31st International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022; pp. 3629–3635. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J. BinaryConnect: Training deep neural networks with binary weights during propagations. Proc. Adv. Neural Inf. Process. Syst. 2015, 28, 3123–3131. [Google Scholar]
- Wang, P.; He, X.; Li, G.; Zhao, T.; Cheng, J. Sparsity-inducing binarized neural networks. Proc. AAAI Conf. Artif. Intell. 2020, 34, 12192–12199. [Google Scholar] [CrossRef]
- Ding, R.; Chin, T.-W.; Liu, Z.; Marculescu, D. Regularizing activation distribution for training binarized deep networks. In Proceedings of the IEEE/CVF Conference, Compututer Vision Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11400–11409. [Google Scholar]
- Hou, L.; Yao, Q.; Kwok, J.T. Loss-aware binarization of deep networks. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–10. [Google Scholar]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable soft quantization: Bridging full-precision and low-bit neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision(ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4851–4860. [Google Scholar]
- Esser, S.K.; McKinstry, J.L.; Bablani, D.; Appuswamy, R.; Modha, D.S. Learned step size quantization. arXiv 2019, arXiv:1902.08153. [Google Scholar] [CrossRef]
- Bhalgat, Y.; Lee, J.; Nagel, M.; Blankevoort, T.; Kwak, N. LSQ+: Improving low-bit quantization through learnable offsets and better initialization. In Proceedings of the IEEE/CVF Conference Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 2978–2985. [Google Scholar]
- Kim, E.; Lee, K.-H.; Sung, W.-K. Optimizing spatial shift pointwise quantization. IEEE Access 2021, 9, 68008–68016. [Google Scholar] [CrossRef]
- Park, E.; Yoo, S. PROFIT: A novel training method for sub-4-bit MobileNet models. Proc. Eur. Conf. Comput. Vis. 2020, 12351, 430–446. [Google Scholar] [CrossRef]
- Cai, W.; Li, W. Weight normalization based quantization for deep neural network compression. arXiv 2019, arXiv:1907.00593. [Google Scholar] [CrossRef]
- Jung, S.; Son, C.; Lee, S.; Son, J.; Han, J.; Kwak, Y.; Choi, C. Learning to quantize deep networks by optimizing quantization intervals with task loss. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4350–4359. [Google Scholar]
- Zhao, R.; Hu, Y.; Dotzel, J.; De Sa, C.; Zhang, Z. Improving neural network quantization without retraining using outlier channel splitting. arXiv 2019, arXiv:1901.09504. [Google Scholar] [CrossRef]
- Nagel, M.; Baalen, M.V.; Blankevoort, T.; Welling, M. Data-free quantization through weight equalization and bias correction. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1325–1334. [Google Scholar]
- Wess, M.; Dinakarrao, S.M.P.; Jantsch, A. Weighted quantization-regularization in DNNs for weight memory minimization toward HW implementation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2929–2939. [Google Scholar] [CrossRef]
- Choi, J.; Yoo, J. Performance evaluation of stochastic quantization methods for compressing the deep neural network model. J. Inst. Control Robot. Syst. 2019, 25, 775–781. [Google Scholar] [CrossRef]
- Li, Y.; Dong, X.; Wang, W. Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks. arXiv 2019, arXiv:1909.13144. [Google Scholar]
- Liu, Z.; Cheng, K.T.; Huang, D.; Xing, E.P.; Shen, Z. Nonuniform-to-uniform quantization: Towards accurate quantization via generalized straight-through estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 4942–4952. [Google Scholar]
- Hong, C.; Kim, H.; Baik, S.; Oh, J.; Lee, K. DAQ: Channel-wise distribution-aware quantization for deep image super-resolution networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2675–2684. [Google Scholar]
- Ryu, H.; Park, N.; Shim, H. DGQ: Distribution-aware group quantization for text-to-image diffusion models. arXiv 2025, arXiv:2501.04304. [Google Scholar]
- Shen, X.; Kong, Z.; Yang, C.; Han, Z.; Lu, L.; Dong, P.; Lyu, C.; Li, C.; Guo, X.; Shu, Z.; et al. EdgeQAT: Entropy and distribution guided quantization-aware training for the acceleration of lightweight LLMs on the edge. arXiv 2024, arXiv:2402.10787. [Google Scholar]
- Miyashita, D.; Lee, E.H.; Murmann, B. Convolutional neural networks using logarithmic data representation. arXiv 2016, arXiv:1603.01025. [Google Scholar] [CrossRef]
- Bengio, Y.; Leonard, N.; Courville, A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv 2013, arXiv:1308.3432. [Google Scholar] [CrossRef]
- Wu, D.; Wang, Y.; Fei, Y.; Gao, G. A Novel Mixed-Precision Quantization Approach for CNNs. IEEE Access 2025, 13, 49309–49319. [Google Scholar] [CrossRef]
- Zhao, W.; Yin, S.; Bai, C.; Wang, Z.; Yu, B. BAQE: Backend-Adaptive DNN Deployment via Synchronous Bayesian Quantization and Hardware Configuration Exploration. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2025, 44, 1394–1405. [Google Scholar] [CrossRef]
- Yoo, J.; Ban, G. Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization. Sensors 2025, 25, 2918. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Yu, Z.; Liu, X.; Yang, J.; Xiao, R.; Wang, T.; Tang, C.; Lv, J. Precision Neural Network Quantization via Learnable Adaptive Modules. arXiv 2025, arXiv:2504.17263. [Google Scholar] [CrossRef]
- Emani, M.; Xie, Z.; Raskar, S.; Sastry, V.; Arnold, W.; Wilson, B.; Thakur, R.; Vishwanath, V.; Liu, Z.; Papka, M.E.; et al. A Comprehensive Evaluation of Novel AI Accelerators for Deep Learning Workloads. In Proceedings of the IEEE/ACM International Workshop on Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS), Dallas, TX, USA, 13–18 November 2022; pp. 13–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).