Research on Generalized Average Modeling and Characteristic Harmonic Frequency Configuration Strategy for PWM Inverter Using Modelica
Abstract
1. Introduction
2. Generalized Average Modeling of PWM Inverters
2.1. Generalized Average Theory
2.2. Complete Process of Generalized Averaging for PWM Inverters
3. Modelica-Based Implementation of the Generalized Average Model
3.1. Interface for GAM Library
3.2. Passive Components for GAM Library
3.3. Inverter Components for GAM Library
4. Characteristic Harmonic Frequency Configuration Strategy for GAM
5. Simulation Case Verification
5.1. Case1: One-Phase Full-Bridge PWM Inverter
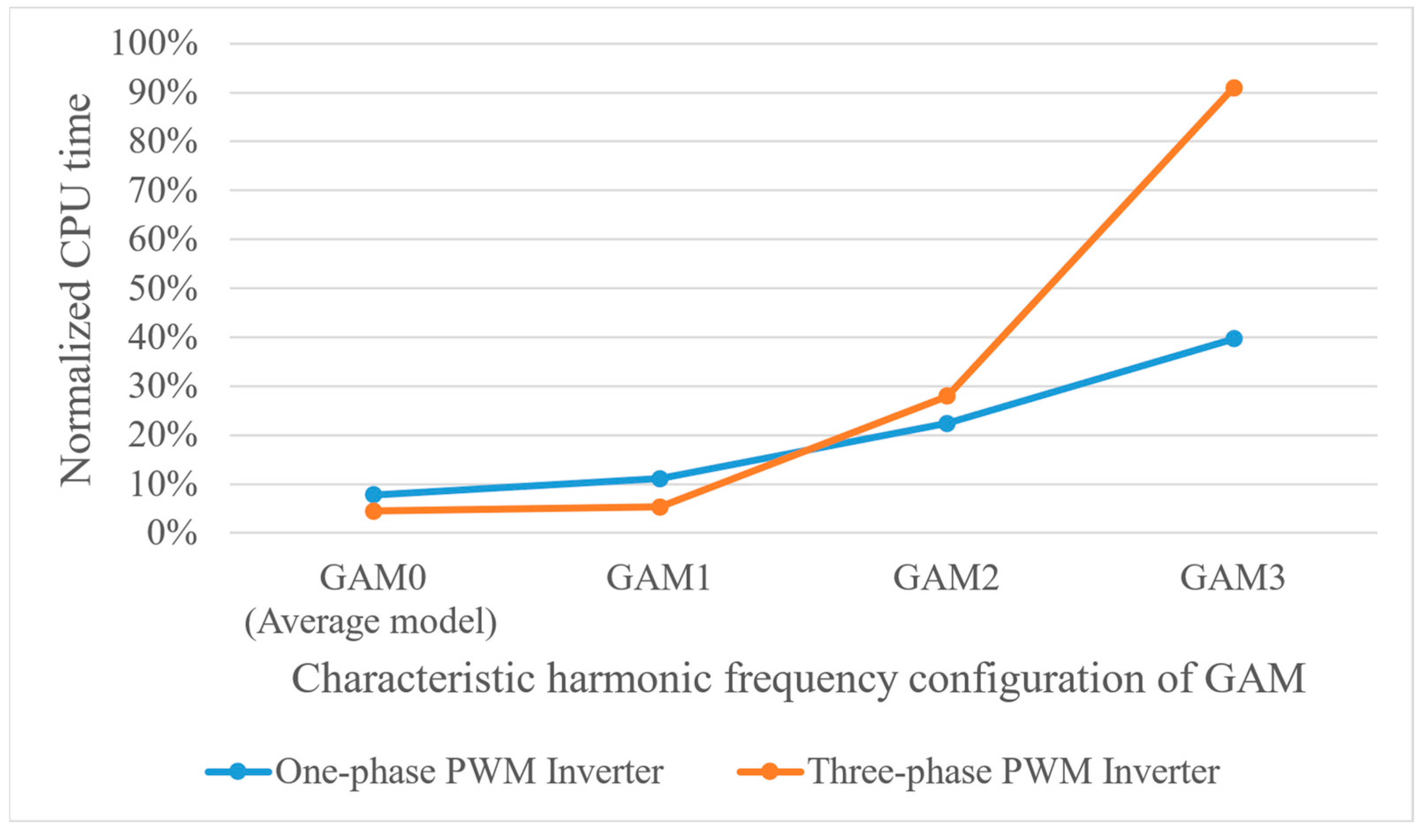
- The detailed model explicitly represents the switching actions of semiconductor devices, which forces the solver to take microsecond-level steps in order to capture high-frequency transitions. This greatly increases the computational burden. In contrast, GAM replaces the switching actions with frequency-domain representations, thereby eliminating the need to resolve high-frequency switching transients. This allows the solver to take larger integration steps, resulting in significantly shorter simulation times.
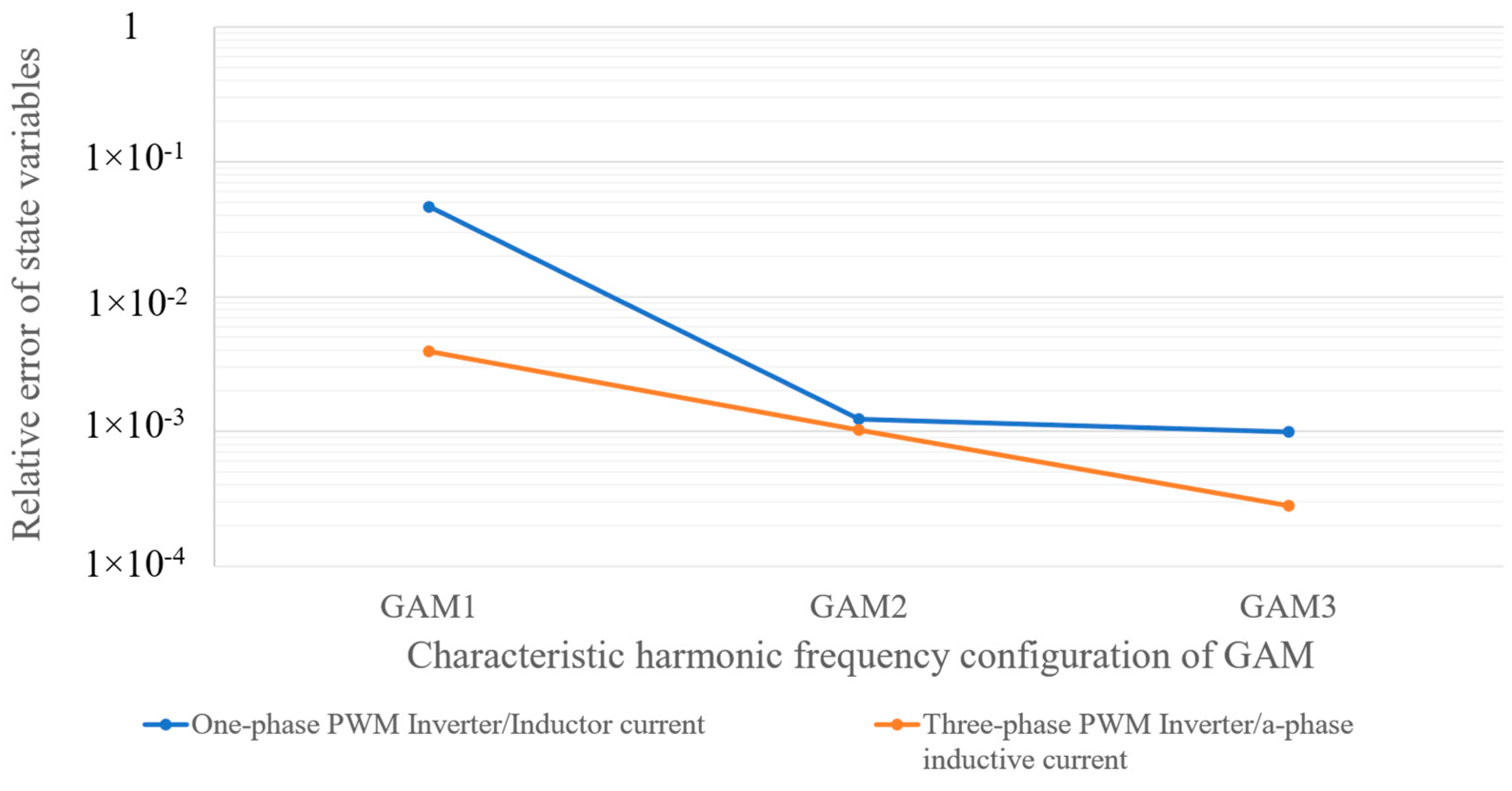
- The frequency configuration adopted by GAM1 only considers a modulation wave frequency of 60 Hz. Essentially, this resembles the average model, reflecting only the fundamental frequency response characteristics of the PWM inverter. The simulated state variable curves exhibit fewer harmonic features. However, since GAM1 is modeled under the mapping rules derived in Section 2.2, it requires additional calculations for frequency coupling matrices compared to directly using average state variables. Consequently, the model solution process consumes more computational time than the average model.
- The frequency configuration adopted by GAM2 is based on GAM1, taking into account the carrier frequency of 10 kHz and the sideband frequency of 10 kHz ± 2 × 60 Hz. Therefore, the state variable curves obtained from the simulation can reflect more characteristic harmonics, and the model has high accuracy and fast computing speed.
- The frequency configuration adopted by GAM3 is based on GAM2 but further considers the sideband frequencies near twice the carrier frequency, namely 2 × 10 kHz ± 60 Hz and 2 × 10 kHz ± 3 × 60 Hz. Therefore, this simulation model provides the highest model accuracy. However, since the frequency configuration of GAM3 provides the most characteristic harmonic frequencies, the model calculation speed is inferior to that of GAM2.
- It is also observed that when the load resistance increases (from 2 Ω to 5 Ω in the step-change case), the fundamental current amplitude decreases as expected, but the model accuracy of the average model and GAMs compared to the detailed model was not significantly affected relative to before the load transformation. This suggests that the accuracy of the GAM approach is robust with respect to load variations.
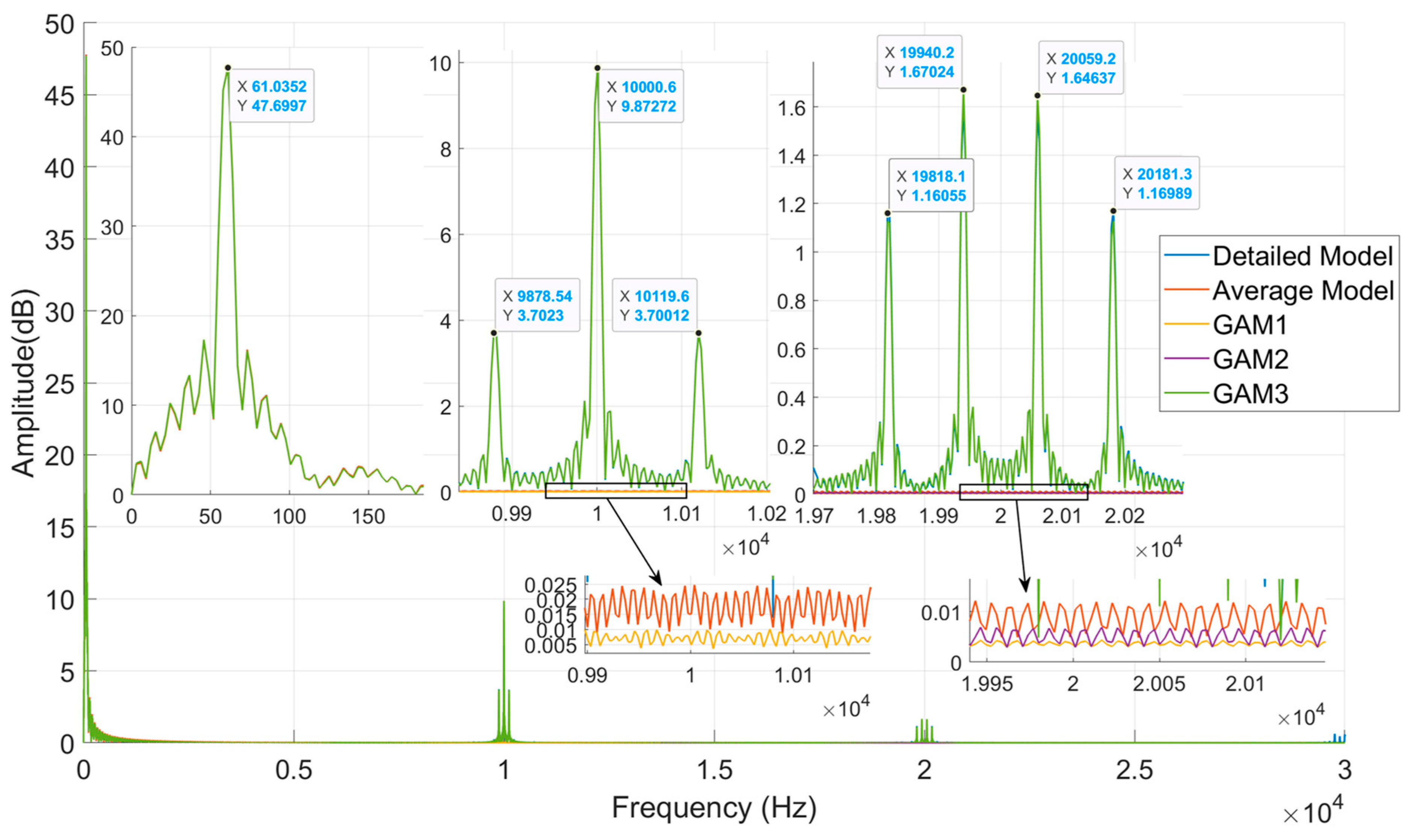
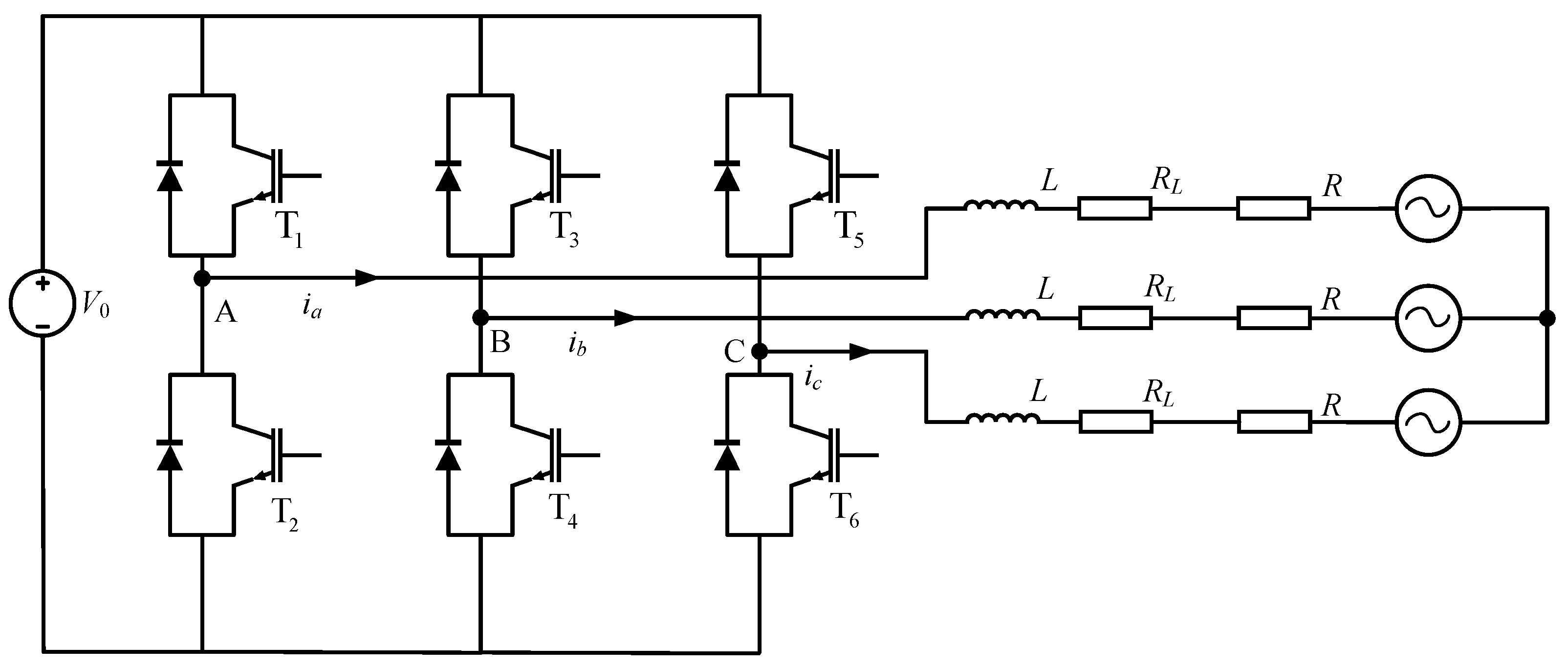
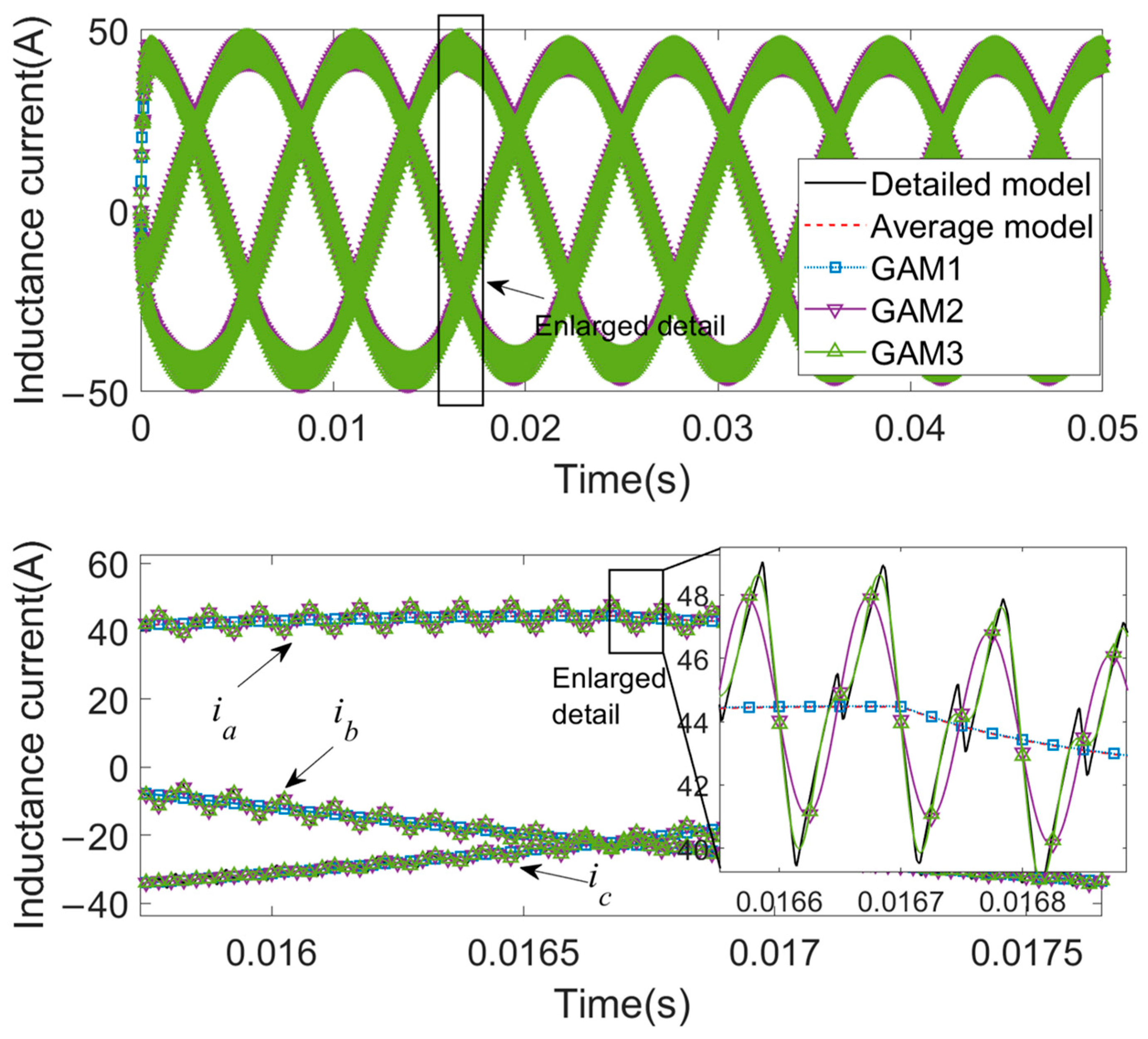
5.2. Case2: Three-Phase PWM Inverter
- The GAM1 model contains the fewest characteristic harmonic frequencies and has the accuracy closest to the average value model;
- GAM2 and GAM3 consider higher-order characteristic harmonics, resulting in higher model accuracy;
- The GAM3 model considers a larger number of characteristic harmonic frequencies, resulting in increased computational complexity, with simulation CPU time nearly matching that of the detailed model.
5.3. Calculation Speed Analysis of PWM Inverter GAM
5.4. Error Boundary Analysis of PWM Inverter GAM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GAM | Generalized average model |
| PWM | Pulse width modulation |
Appendix A
| Parameter | Description | Value |
|---|---|---|
| Input voltage | 220 V | |
| LC filter capacitor | 8 μF | |
| Inductance internal resistance | 0.05 Ω | |
| LC filter inductor | 0.276 mH | |
| Initial load resistance | 2 Ω | |
| Load resistance step time | 16.7 ms | |
| Final load resistance | 5 Ω | |
| Modulation phase | 1 rad | |
| Modulated amplitude value | 0.9 | |
| Modulation frequency | 60 Hz | |
| Switching frequency | 10 kHz |
| Parameter | Description | Value |
|---|---|---|
| Input voltage | 220 V | |
| Inductance internal resistance | 0.05 Ω | |
| LC filter inductor | 0.276 mH | |
| Load resistance | 2.2 Ω | |
| Modulated wave step time | 16.7 ms | |
| Initial modulated wave signal | ||
| Final modulated wave signal | ||
| Modulation frequency | 60 Hz | |
| Switching frequency | 10 kHz |
References
- Liu, J.W.; Li, X.B.; Liu, X.O. Distributed power access and energy storage configuration in active distribution network. Power Gener. Technol. 2022, 43, 476. [Google Scholar] [CrossRef]
- Qian, Y.W.; Tian, H.; Liu, C.; Tian, X.; Zhou, X.; Daim, J. Droop Control Strategy of Distributed Photovoltaic Reactive Power Considering Probability Distribution. Power Gener. Technol. 2024, 45, 273. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Blaabjerg, F. Power electronics: The enabling technology for renewable energy integration. CSEE J. Power Energy Syst. 2021, 8, 39–52. [Google Scholar] [CrossRef]
- Lunardi, A.; Lourenço, L.F.N.; Munkhchuluun, E.; Meegahapola, L.; Filho, A.J.S. Grid-connected power converters: An overview of control strategies for renewable energy. Energies 2022, 15, 4151. [Google Scholar] [CrossRef]
- Affam, A.; Buswig, Y.M.; Othman, A.-K.B.H.; Bin Julai, N.; Qays, O. A review of multiple input DC-DC converter topologies linked with hybrid electric vehicles and renewable energy systems. Renew. Sustain. Energy Rev. 2021, 135, 110186. [Google Scholar] [CrossRef]
- Khalilzadeh, M.; Vaez-Zadeh, S.; Rodriguez, J.; Heydari, R. Model-free predictive control of motor drives and power converters: A review. IEEE Access 2021, 9, 105733–105747. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, X.; Zhang, W.; Zeng, Y. An integrated power converter-based brushless DC motor drive system. IEEE Trans. Power Electron. 2022, 37, 8322–8332. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.; Kant, P. Assessment of multi-phase conversion and modified pwm strategy for power converters of medium-voltage induction motors drive. IEEE Trans. Ind. Appl. 2023, 59, 3458–3469. [Google Scholar] [CrossRef]
- Jagadeesh, I.; Indragandhi, V. Comparative study of DC-DC converters for solar PV with microgrid applications. Energies 2022, 15, 7569. [Google Scholar] [CrossRef]
- Li, P.; Guo, T.; Li, Y.; Han, X.; Wang, P.; Li, X.; Wang, Z. An adaptive coordinated optimal control method for parallel bidirectional power converters in AC/DC hybrid microgrid. Int. J. Electr. Power Energy Syst. 2021, 126, 106596. [Google Scholar] [CrossRef]
- Yan, D.; Yang, C.; Hang, L.; He, Y.; Luo, P.; Shen, L.; Zeng, P. Review of general modeling approaches of power converters. Chin. J. Electr. Eng. 2021, 7, 27–36. [Google Scholar] [CrossRef]
- Chalangar, H.; Ould-Bachir, T.; Sheshyekani, K.; Mahseredjian, J. Methods for the accurate real-time simulation of high-frequency power converters. IEEE Trans. Ind. Electron. 2021, 69, 9613–9623. [Google Scholar] [CrossRef]
- Surya, S.; Arjun, M.N. Mathematical modeling of power electronic converters. SN Comput. Sci. 2021, 2, 267. [Google Scholar] [CrossRef]
- Voperian, V. Simplified analysis of pwm converters using model of pwm switch, part i: Continuous conduction mode. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 490–505. [Google Scholar] [CrossRef]
- Basso, C.P. Switch-Mode Power Supplies. In Spice Simulations and Practical Designs; McGraw-Hill Education Ltd.: New York, NY, USA, 2008. [Google Scholar]
- Ben-Yaakov, S. Average simulation of PWM converters by direct implementation of behavioural relationships. Int. J. Electron. 1994, 77, 731–746. [Google Scholar] [CrossRef]
- Górecki, P. Electrothermal Averaged Model of a Diode–IGBT Switch for a Fast Analysis of DC–DC Converters. IEEE Trans. Power Electron. 2022, 37, 13003–13013. [Google Scholar] [CrossRef]
- Sarnago, H.; Lucia, O.; Mediano, A.; Burdio, J.M. Analytical model of the half-bridge series resonant inverter for improved power conversion efficiency and performance. IEEE Trans. Power Electron. 2014, 30, 4128–4143. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, Z.; Cheng, M. Modeling, analysis, and design of multifunction grid-interfaced inverters with output LCL filter. IEEE Trans. Power Electron. 2013, 29, 3830–3839. [Google Scholar] [CrossRef]
- Kroutikova, N.; Hernandez-Aramburo, C.; Green, T. State-space model of grid-connected inverters under current control mode. IET Electr. Power Appl. 2007, 1, 329–338. [Google Scholar] [CrossRef]
- Motwani, J.K.; Xue, Y.; Nazari, A.; Dong, D.; Cvetkovic, I.; Boroyevich, D. Modeling of power electronics systems and PWM modulators in harmonic-state space. IEEE Open J. Power Electron. 2022, 3, 689–704. [Google Scholar] [CrossRef]
- Moreno-Font, V.; El Aroudi, A.; Calvente, J.; Giral, R.; Benadero, L. Dynamics and stability issues of a single-inductor dual-switching DC–DC converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 415–426. [Google Scholar] [CrossRef]
- Rajakumari, R.F.; Ramkumar, M.S. Design considerations and performance analysis based on ripple factors and switching loss for converter techniques. Mater. Today Proc. 2021, 37, 2681–2686. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Y.; Liu, C.-C.; Gao, H. Piecewise average-value model of PWM converters with applications to large-signal transient simulations. IEEE Trans. Power Electron. 2015, 31, 1304–1321. [Google Scholar] [CrossRef]
- Alrajhi, H. A Generalized State Space Average Model for Parallel DC-to-DC Converters. Comput. Syst. Sci. Eng. 2022, 41, 717–734. [Google Scholar] [CrossRef]
- Behjati, H.; Niu, L.; Davoudi, A.; Chapman, P.L. Alternative time-invariant multi-frequency modeling of PWM DC-DC converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3069–3079. [Google Scholar] [CrossRef]
- Caliskan, V.; Verghese, O.; Stankovic, A. Multifrequency averaging of DC/DC converters. IEEE Trans. Power Electron. 1999, 14, 124–133. [Google Scholar] [CrossRef]
- Liao, Z.; Stansby, P.; Li, G.; Moreno, E.C. High-capacity wave energy conversion by multi-float, multi-pto, control and prediction: Generalized state-space modelling with linear optimal control and arbitrary headings. IEEE Trans. Sustain. Energy 2021, 12, 2123–2131. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. Kimball. Generalized average modeling of dual active bridge DC–DC converter. IEEE Trans. Power Electron. 2011, 27, 2078–2084. [Google Scholar] [CrossRef]
- Liu, X.; Cramer, A.M.; Pan, F. Cramer, and Fei Pan. Generalized average method for time-invariant modeling of inverters. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 64, 740–751. [Google Scholar] [CrossRef]
- Wang, L.; Deng, X.; Han, P.; Qi, X.; Wu, X.; Li, M.; Xu, H. Electromagnetic transient modeling and simulation of power converters based on a piecewise generalized state space averaging method. IEEE Access 2019, 7, 12241–12251. [Google Scholar] [CrossRef]
- Sanders, S.; Noworolski, J.; Liu, X.; Verghese, G. Generalized averaging method for power conversion circuits. IEEE Trans. Power Electron. 1991, 6, 251–259. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
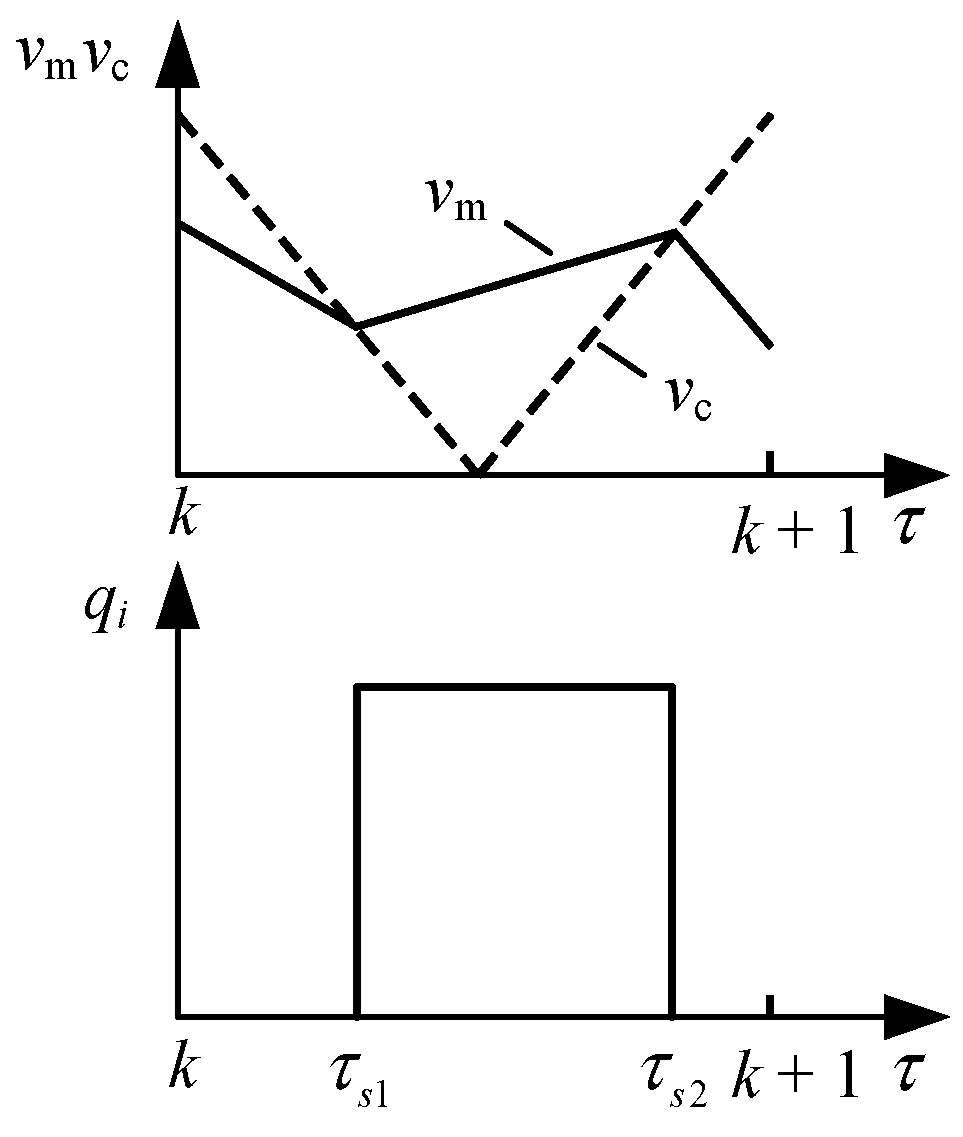
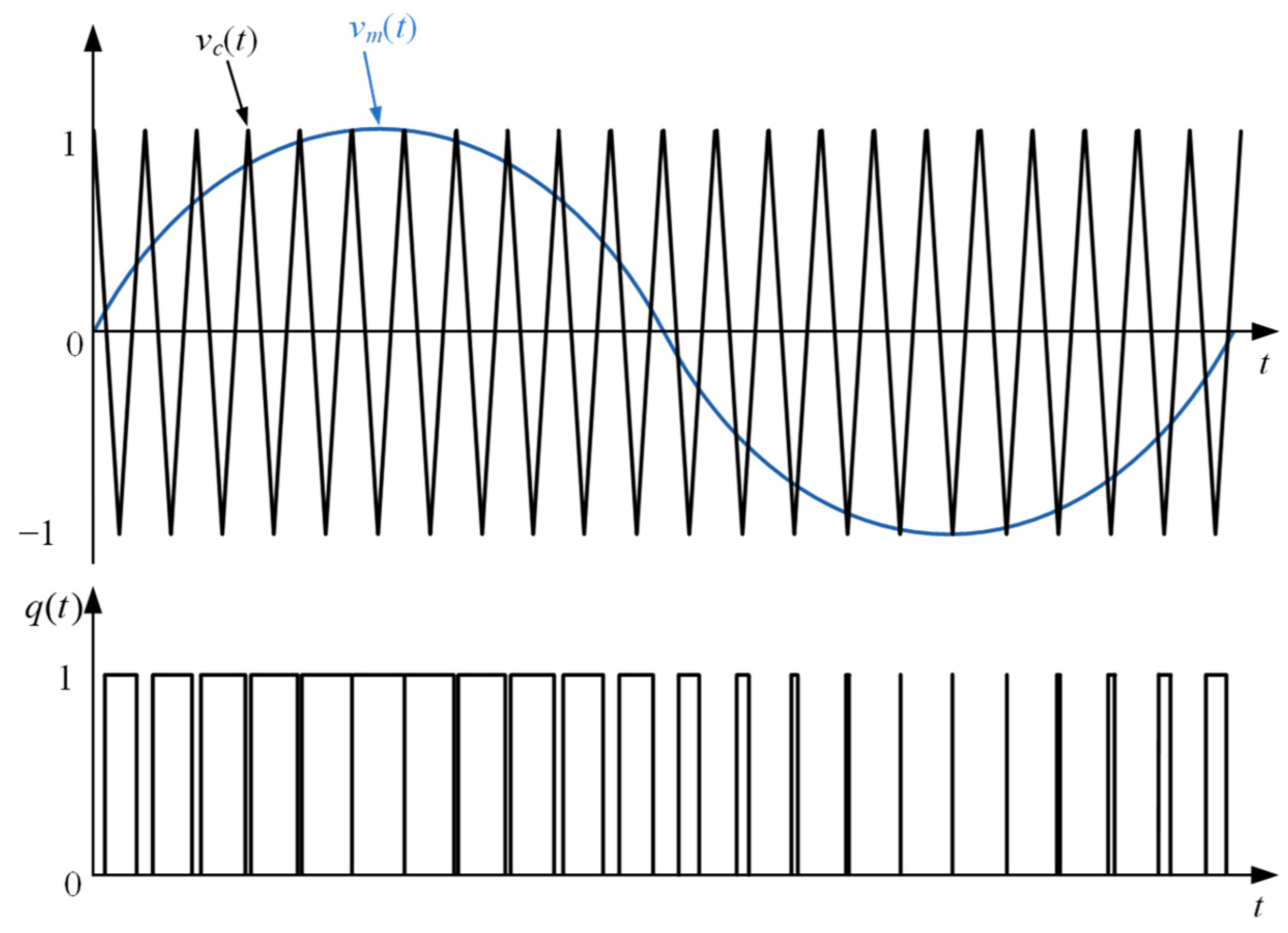


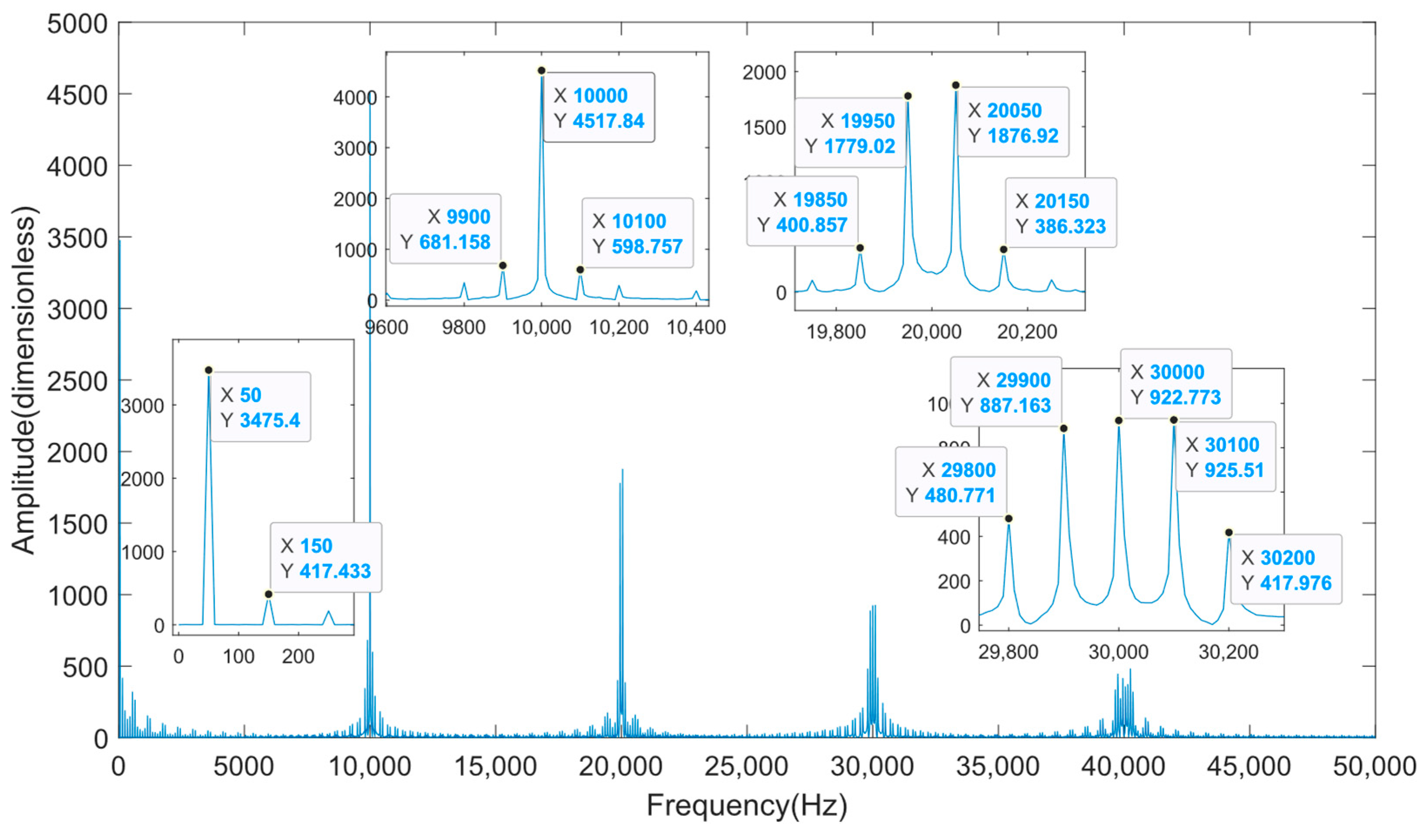
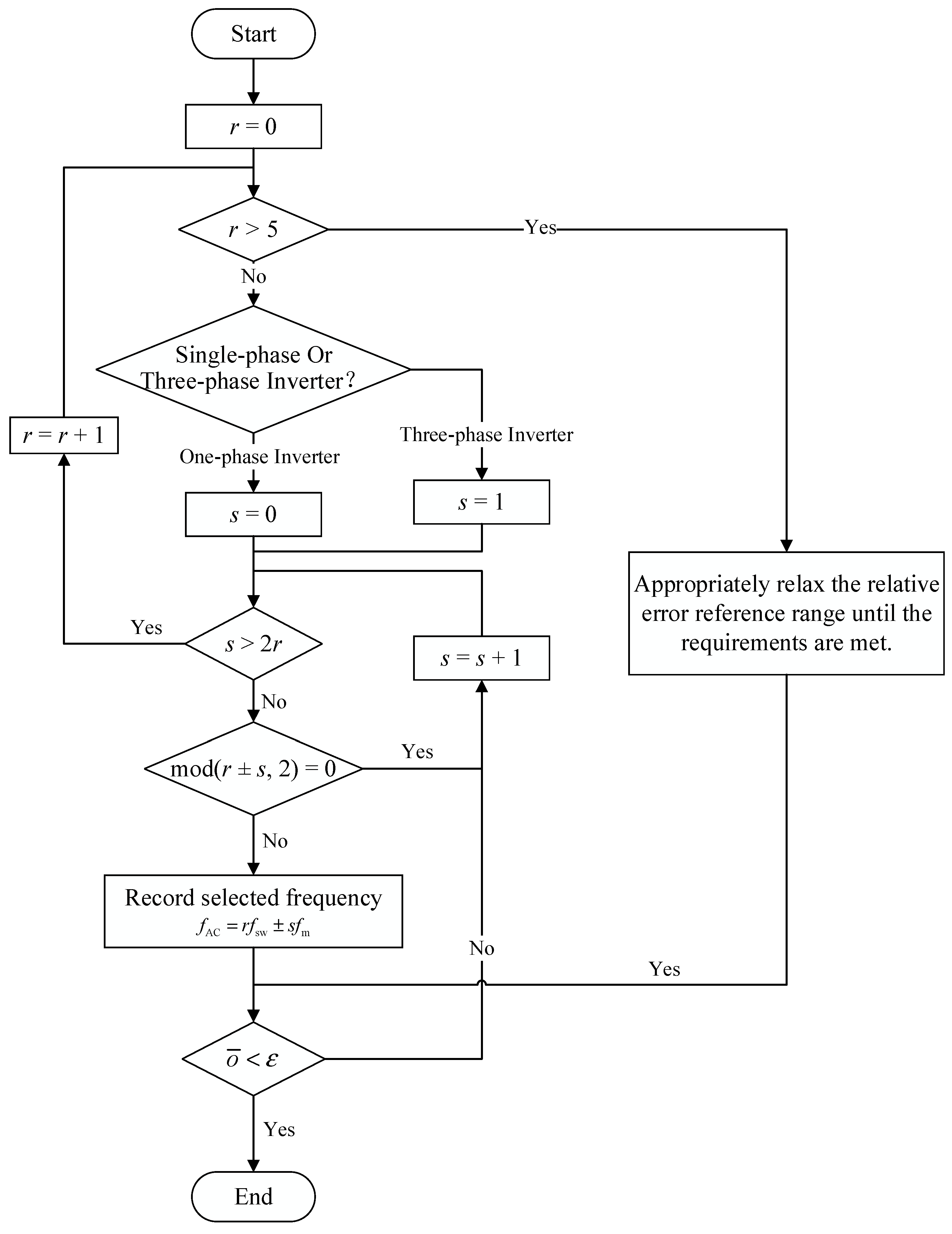



| Mapping Rules | Description | Example |
|---|---|---|
| Mapping rules for time domain state variables on GAM | ||
| Mapping rules for time domain state variable derivatives on GAM | ||
| Mapping rules for time domain switching functions on GAM | ||
| Mapping rules for the product terms of time-domain switching functions and input variables (containing only DC components) on GAM | ||
| Mapping rules for time-domain switch functions and product terms with input variables (including higher harmonic terms) on GAM |
| Simulation Model | Frequency Configuration |
|---|---|
| GAM 1 | 60 Hz |
| GAM 2 | 60 Hz, 10 kHz, 10 kHz ± 2 × 60 Hz |
| GAM 3 | 60 Hz, 10 kHz, 10 kHz ± 2 × 60 Hz, 2 × 10 kHz ± 60 Hz, 2 × 10 kHz ± 3 × 60 Hz |
| Simulation Model | Model Accuracy (Relative Error of State Variables) | CPU Simulation Time (Simulation Time 5 s) | |||
|---|---|---|---|---|---|
| Inductor Current | Capacitor Voltage | ||||
| Detailed model | 20.010 s | ||||
| Average model | 0.04640 | 0.01071 | 1.553 s | ||
| GAM 1 | 0.04640 | 0.01071 | 2.216 s | ||
| GAM 2 | 0.001233 | 2.234 × 10−4 | 4.475 s | ||
| GAM 3 | 9.916 × 10−4 | 2.968 × 10−5 | 7.938 s | ||
| Simulation Model | Frequency Configuration |
|---|---|
| GAM 1 | 60 Hz |
| GAM 2 | 60 Hz, 10 kHz ± 2 × 60 Hz |
| GAM 3 | 60 Hz, 10 kHz ± 2 × 60 Hz, 2 × 10 kHz ± 60 Hz, 2 × 10 kHz ± 3 × 60 Hz |
| Simulation Model | Model Accuracy (Relative Error of State Variables) | CPU Simulation Time (Simulation Time 0.1 s) | ||||
|---|---|---|---|---|---|---|
| a-Phase Inductive Current | b-Phase Inductive Current | c-Phase Inductive Current | ||||
| Detailed model | 1.227 s | |||||
| Average model | 0.003931 | 0.003931 | 0.003909 | 0.055 s | ||
| GAM 1 | 0.003930 | 0.003911 | 0.003909 | 0.065 s | ||
| GAM 2 | 0.001025 | 0.001020 | 0.001020 | 0.343 s | ||
| GAM 3 | 2.811 × 10−4 | 2.797 × 10−4 | 2.796 × 10−4 | 1.116 s | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Chen, L.; Ding, J.; Liu, X. Research on Generalized Average Modeling and Characteristic Harmonic Frequency Configuration Strategy for PWM Inverter Using Modelica. Electronics 2025, 14, 3685. https://doi.org/10.3390/electronics14183685
Sun Z, Chen L, Ding J, Liu X. Research on Generalized Average Modeling and Characteristic Harmonic Frequency Configuration Strategy for PWM Inverter Using Modelica. Electronics. 2025; 14(18):3685. https://doi.org/10.3390/electronics14183685
Chicago/Turabian StyleSun, Zhaoxuan, Liping Chen, Jianwan Ding, and Xiaoyan Liu. 2025. "Research on Generalized Average Modeling and Characteristic Harmonic Frequency Configuration Strategy for PWM Inverter Using Modelica" Electronics 14, no. 18: 3685. https://doi.org/10.3390/electronics14183685
APA StyleSun, Z., Chen, L., Ding, J., & Liu, X. (2025). Research on Generalized Average Modeling and Characteristic Harmonic Frequency Configuration Strategy for PWM Inverter Using Modelica. Electronics, 14(18), 3685. https://doi.org/10.3390/electronics14183685





