Abstract
Differential privacy (DP) has become a cornerstone for privacy-preserving machine learning, yet its application to high-resolution satellite imagery remains underexplored. Existing DP algorithms, such as DP-SGD, often rely on static noise levels and global clipping thresholds, which lead to slow convergence and poor utility in deep neural networks. In this paper, we propose ADP-SIR, an Adaptive Differential Privacy framework for Satellite Image Recognition with provable convergence guarantees. ADP-SIR introduces two novel components: Convergence-Guided Noise Scaling (CGNS), which dynamically adjusts the noise multiplier based on training stability, and Layerwise Sensitivity Profiling (LSP), which enables fine-grained clipping at the layer level. We provide theoretical analysis showing that ADP-SIR achieves good convergence in non-convex settings under Rényi differential privacy. Empirically, we evaluate ADP-SIR on EuroSAT and RESISC45, demonstrating significant improvements over DP-SGD and AdaClip-DP in terms of accuracy, convergence speed, and per-class fairness. Our framework bridges the gap between practical performance and rigorous privacy for remote sensing applications.
1. Introduction
Satellite imagery has become a vital data source for numerous societal and industrial applications, ranging from environmental monitoring and land use classification to agricultural assessment, military surveillance, and disaster response. As the spatial and temporal resolutions of satellites continue to improve, the quantity and sensitivity of geospatial data have grown exponentially. Consequently, modern machine learning models trained on such data are becoming increasingly powerful but also increasingly privacy-sensitive. In particular, when satellite imagery contains information related to private properties, critical infrastructure, or military zones, it becomes imperative to ensure that data-driven models cannot leak individual-level or region-specific information.
Differential Privacy (DP) [] has emerged as a mathematically rigorous standard for protecting individual data records in statistical queries and machine learning. The fundamental guarantee of DP is that the inclusion or removal of a single data point does not significantly change the output of a computation. This property has made DP the de facto privacy-preserving paradigm in several domains, including healthcare, finance, and web analytics. However, its direct application to deep learning models trained on high-dimensional satellite images remains a major challenge. The typical approach of injecting random noise into gradients during training, such as in Differentially Private Stochastic Gradient Descent (DP-SGD) [], often leads to significant degradation in model accuracy, particularly under tight privacy budgets (i.e., small ).
The root of this problem lies in the nature of satellite imagery itself. These images exhibit the following:
- High input dimensionality: Images are large (e.g., 512 × 512 or more), and often include multispectral or hyperspectral channels.
- Strong spatial dependencies: Neighboring pixels are highly correlated, making noise injection particularly disruptive.
- Label imbalance: Rare classes such as airplanes, ships, or oil rigs are disproportionately affected by uniform noise injection.
- Deep network architectures: The reliance on multi-layer CNN backbones, often with tens of millions of parameters, introduces further sensitivity to training noise.
Existing approaches to private deep learning typically adopt a one-size-fits-all noise strategy—using a fixed clipping norm and static noise multiplier throughout training. This rigid design overlooks two key facts: (1) different layers of a neural network exhibit varying sensitivity to perturbation, and (2) gradient signals fluctuate throughout training as the model approaches convergence. Without adapting to these dynamics, models are prone to underfitting or instability, particularly in non-convex optimization landscapes.
To overcome these limitations, we propose a new framework called ADP-SIR (Adaptive Differential Privacy for Satellite Image Recognition). ADP-SIR is a privacy-preserving training algorithm specifically designed for deep learning on satellite imagery. It introduces two novel components: (1) a Convergence-Guided Noise Scaling (CGNS) strategy that adjusts the noise level based on the evolution of gradient norms during training, and (2) a Layerwise Sensitivity Profiling (LSP) technique that customizes clipping and noise injection per layer, based on empirical gradient magnitudes. These mechanisms collectively enable ADP-SIR to better preserve model utility while satisfying strong DP guarantees.
Furthermore, we provide a theoretical analysis showing that our method maintains convergence guarantees even under non-convex settings, with asymptotic bounds that improve upon existing fixed-noise baselines. This is particularly important for satellite applications where training resources are costly and convergence behavior must be predictable.
We validate ADP-SIR on standard benchmark datasets for satellite image recognition, including and . Our experiments show that ADP-SIR consistently outperforms static-noise DP baselines across a wide range of privacy budgets. Notably, ADP-SIR achieves near non-private accuracy levels under moderate privacy constraints, and gracefully degrades under tight budgets.
Our key contributions can be summarized as follows:
- We propose ADP-SIR, the first adaptive differentially private training framework tailored for high-resolution satellite imagery, which jointly integrates convergence-aware noise modulation and layer-specific clipping to address the unique challenges of privacy-preserving remote sensing.
- We develop two novel techniques—Convergence-Guided Noise Scaling (CGNS) and Layerwise Sensitivity Profiling (LSP)—that dynamically calibrate privacy budgets during training, providing finer control of the utility–privacy trade-off than existing methods.
- We provide rigorous theoretical analysis showing that ADP-SIR maintains convergence guarantees under both convex and non-convex settings, with tighter bounds than standard DP-SGD, thereby advancing the theory of adaptive private optimization.
- Through extensive experiments on benchmark satellite datasets, we demonstrate that ADP-SIR achieves state-of-the-art accuracy and faster convergence compared to strong baselines, and we release our implementation and benchmark framework to promote reproducibility and future research.
The rest of this paper is organized as follows: Section 2 surveys related work. Section 3 introduces the necessary background on differential privacy and satellite image learning. Section 4 presents the details of our ADP-SIR algorithm and its theoretical properties. Section 5 provides empirical results and ablation studies. Section 6 concludes with future research directions.
2. Related Work
2.1. Differential Privacy in Deep Learning
Differential privacy (DP) has emerged as a foundational paradigm for privacy-preserving machine learning []. The introduction of DP-SGD by Abadi et al. [] enabled end-to-end differentially private training of deep neural networks, with privacy guarantees formalized using the moments accountant. Subsequent works have aimed to tighten these guarantees and improve usability. For example, Rényi Differential Privacy (RDP) [] and zero-Concentrated Differential Privacy (zCDP) [] offer stronger composition properties and simpler analysis. McMahan et al. [] demonstrated that large-scale applications, such as language modeling, are feasible under DP by combining careful optimization with privacy accounting. Despite these advances, static clipping and fixed noise schedules in DP-SGD often lead to significant accuracy degradation, especially in deep or non-convex settings. Recent discussions in this domain emphasize the necessity of adaptive mechanisms that can respond to training dynamics, motivating our convergence-guided approach.
2.2. Adaptive Privacy Mechanisms
To alleviate the limitations of static DP-SGD, recent research has introduced adaptivity into the privacy-preserving optimization process. AdaClip [] adaptively adjusts gradient clipping thresholds using per-step gradient norms, improving the balance between privacy and utility. Similarly, DPD-Adam [] extends adaptive moment methods to the private setting, offering faster convergence on certain tasks. Zhou et al. [] and Triastcyn et al. [] proposed variance-aware methods that allocate privacy budgets dynamically in federated settings, while Opacus [] provides practical software tools for large-scale DP training. These methods highlight a broader trend: adaptivity can mitigate the inherent trade-offs in DP optimization. However, most prior approaches focus on either clipping or optimizer-level adjustments, whereas our method, Convergence-Guided Noise Scaling (CGNS), directly links noise scheduling to gradient stability. This integration allows ADP-SIR to reduce perturbation as training stabilizes, which has not been systematically explored in existing works.
2.3. Optimization and Convergence Under Privacy
Theoretical analysis of private optimization has advanced significantly in recent years []. Bassily et al. [] provided early convergence guarantees for convex objectives under DP, while Wang et al. [] and Yu et al. [] extended these analyses to the non-convex setting. Song et al. [] investigated the trade-offs between privacy and algorithmic stability, while Lecuyer et al. [] established connections between differential privacy and robustness. These works establish the theoretical foundation for understanding how DP mechanisms interact with optimization. However, most analyses assume fixed noise distributions and static clipping strategies, leaving a gap in understanding adaptive approaches. Our work explicitly builds on these foundations by showing that convergence-aware noise scaling preserves the non-convex convergence guarantees, while simultaneously improving empirical efficiency.
2.4. Privacy in Geospatial and Remote Sensing
Although differential privacy has been widely studied in natural language processing, computer vision, and tabular machine learning, its application to geospatial and remote sensing domains is still limited. Helber et al. [] introduced the EuroSAT dataset as a benchmark for land use classification, while Cheng et al. [] developed RESISC45 to cover diverse scene categories. Yet, neither dataset was originally designed with privacy considerations. More recent efforts have considered cryptographic solutions such as homomorphic encryption [] and secure aggregation [], but these approaches often entail significant computational overheads.
In parallel, the remote sensing community has made rapid progress in hyperspectral image (HSI) analysis, which is highly relevant to privacy-preserving applications since hyperspectral data often contains sensitive environmental and infrastructural details. Recent work on hyperspectral image super-resolution demonstrates the increasing importance of adaptive deep models: Enhanced Deep Image Prior [], Model-Informed Multistage Networks [], and X-shaped Interactive Autoencoders with cross-modality mutual learning [] all advance unsupervised HSI reconstruction. These contributions illustrate the growing sophistication of deep models for satellite imagery. However, none of these methods incorporate privacy guarantees, underscoring the novelty of our proposal. By tailoring DP techniques to geospatial tasks, ADP-SIR fills a crucial gap between cutting-edge remote sensing methods and privacy-preserving learning.
2.5. Beyond Standard DP Training
Alternative privacy-preserving strategies have also been proposed to improve the privacy–utility trade-off outside the standard DP-SGD framework. PATE [] leverages teacher-student architectures for private knowledge transfer, while scalable aggregation methods [,] enable large-scale training under DP through secure multiparty protocols. Tramer and Boneh [] investigated functional noise scheduling as an alternative to fixed-variance noise injection, while these directions offer valuable insights, they often introduce architectural constraints or additional communication overhead. In contrast, our approach integrates adaptivity directly into the training process, maintaining compatibility with standard architectures and optimization pipelines. This design ensures scalability to large-scale geospatial tasks while maintaining formal differential privacy guarantees.
To the best of our knowledge, no existing method jointly exploits convergence-aware noise modulation and layerwise sensitivity profiling within a formal DP framework for satellite image recognition. Our work bridges this gap, offering both theoretical grounding and empirical superiority over current baselines.
3. Preliminaries
In this section, we review the foundational concepts necessary to understand our proposed method, including differential privacy, optimization in deep learning, and the unique challenges posed by satellite image recognition.
3.1. Differential Privacy
Differential Privacy (DP) [] is a mathematical framework for quantifying the privacy guarantees provided by an algorithm operating on a dataset. Let be a randomized algorithm and be two adjacent datasets differing in a single record.
Definition 1
(-Differential Privacy). An algorithm satisfies -differential privacy if for all measurable subsets of the output space and for all adjacent datasets ,
where is the privacy loss parameter and is the probability of a privacy breach beyond ε.
To satisfy DP, noise is typically added to model gradients or outputs during training. The most common approach is the Differentially Private Stochastic Gradient Descent (DP-SGD) [], where clipped gradients are perturbed by Gaussian noise:
where is the gradient of sample i at time t, C is the clipping norm, and controls the noise scale.
3.2. Satellite Image Recognition
Satellite image recognition involves classifying or detecting objects from high-resolution geospatial imagery. Unique challenges include
- High dimensionality: Input images are typically in the range of 512 × 512 pixels or higher, with multiple spectral bands.
- Spatial correlations: Neighboring pixels are often strongly correlated, making naive noise injection degrade performance significantly.
- Data imbalance: Certain classes (e.g., ships or aircraft) are underrepresented, exacerbating the utility-privacy trade-off.
Standard convolutional neural networks (CNNs), such as ResNet, are typically employed to model satellite imagery [,]. These models are highly sensitive to noise, especially when differential privacy is applied during training.
3.3. Privacy-Preserving Learning Objective
Let denote a CNN with parameters trained on a dataset of image-label pairs. The empirical risk minimization (ERM) objective is as follows:
where is a classification loss function (e.g., cross-entropy). Under DP constraints, we modify the optimization procedure using a differentially private mechanism such that the resulting model parameters satisfy -DP. Our proposed method introduces adaptivity in the noise scale and clipping norm C by leveraging gradient convergence behavior and layer-wise sensitivity, as described in Section 4.
4. Methodology
In this section, we introduce ADP-SIR (Adaptive Differential Privacy for Satellite Image Recognition), a novel training algorithm that adaptively adjusts the privacy noise in different layers and stages of training based on gradient convergence and sensitivity. Our method addresses the optimization challenges introduced by DP noise while ensuring strong privacy guarantees and convergence behavior. Algorithm 1 and Figure 1 gives the pipeline of our proposal.
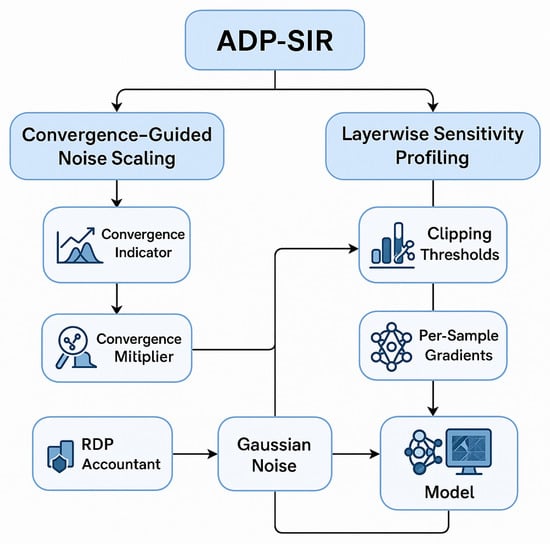
Figure 1.
Overview of the ADP-SIR pipeline. The framework combines Convergence-Guided Noise Scaling (CGNS), which adjusts noise based on gradient stability, and Layerwise Sensitivity Profiling (LSP), which adapts clipping and noise per layer. Both feed into Gaussian noise injection monitored by the RDP accountant, ensuring rigorous -DP guarantees during model updates.
4.1. Overview
Our proposed method builds upon the standard DP-SGD algorithm by introducing two key innovations:
- Convergence-Guided Noise Scaling (CGNS): A dynamic noise modulation technique that adjusts the variance of the Gaussian noise based on gradient norm stability.
- Layerwise Sensitivity Profiling (LSP): A per-layer clipping and noise scaling strategy based on observed gradient sensitivity during training.
| Algorithm 1: ADP-SIR pipeline |
 |
4.2. Convergence-Guided Noise Scaling
A major challenge in training deep learning models under differential privacy constraints is the degradation of model performance due to constant noise injection throughout training. Traditional DP-SGD methods introduce a fixed noise scale across all iterations, regardless of how close the model is to convergence. This uniform noise scheme is suboptimal because it adds excessive noise when the model is nearing convergence, which can disrupt fine-grained updates, or insufficient noise during early phases, which may risk privacy violations due to large gradient norms.
To address this limitation, we propose Convergence-Guided Noise Scaling (CGNS), a dynamic mechanism that adapts the Gaussian noise level injected into the gradients based on the optimization trajectory. The core idea is to modulate the noise scale in accordance with the stability of the gradient direction: if the gradients are fluctuating significantly, the optimizer is likely still far from a stationary point and can tolerate higher noise. Conversely, when the gradients begin to stabilize, the model is closer to convergence and requires more precise updates with minimal perturbation.
Let denote the aggregated, clipped gradient vector at iteration t. We define a convergence indicator as follows:
where is a small constant to prevent division by zero. Intuitively, measures the relative change in gradient direction from one iteration to the next. A small value of implies that the optimization has stabilized, suggesting that further updates should be made with lower noise to preserve useful information.
We modulate the noise multiplier at each step t using the following exponentially decaying function:
where and denote the lower and upper bounds of the noise multiplier, respectively, and is a tunable hyperparameter controlling the decay rate.
This formulation ensures the following:
- when is large (early-stage training, unstable gradients),
- when (late-stage training, stable gradients).
The use of a decreasing noise schedule is theoretically supported by recent work on non-convex optimization with differential privacy []. In essence, when training progresses and updates approach a stationary point, injecting large noise becomes inefficient and harmful to convergence. Our approach provides a principled mechanism to reduce noise at the right time while maintaining -DP guarantees using advanced composition accounting tools like the moments accountant.
In practice, is computed using a moving average of recent gradient differences to smooth out short-term noise, and the update of is clipped within to ensure bounded privacy cost. Moreover, is passed into the per-layer noise injection pipeline described in the next subsection, which performs further adjustment based on individual layer sensitivity.
In summary, CGNS improves the trade-off between privacy and utility by allowing adaptive control over noise magnitude, aligned with the training dynamics. This is particularly crucial in high-dimensional settings like satellite image recognition, where fixed-noise schemes struggle to converge to performant models under strict privacy budgets.
4.3. Layerwise Sensitivity Profiling (LSP)
Deep convolutional neural networks (CNNs), commonly used for satellite image recognition, exhibit varying sensitivity to noise across different layers. Lower layers typically extract local, low-level features such as edges and textures, while higher layers encode more abstract, semantic representations. Empirical studies have shown that gradients in deeper layers often have larger magnitudes and greater variance. Applying uniform gradient clipping and noise injection across all layers, as performed in standard DP-SGD, results in either excessive clipping in high-sensitivity layers or unnecessary noise in low-sensitivity ones—both leading to suboptimal learning performance.
To tackle this challenge, we propose Layerwise Sensitivity Profiling (LSP), a mechanism that adaptively determines gradient clipping thresholds and noise scales for each layer based on its estimated sensitivity. By aligning the privacy-preserving noise with the information flow in the network, LSP allows for more informed trade-offs between privacy and model utility.
For each layer l of the neural network, we maintain an estimate of its empirical gradient sensitivity. At iteration t, for a mini-batch of size B, we compute the per-sample gradients and define the batch-wise mean norm as follows:
To smooth fluctuations and adapt to long-term trends, we maintain an exponential moving average:
where is a decay parameter controlling the memory length.
The clipping threshold for each layer is computed as a scaled version of its sensitivity estimate:
where is a tunable margin factor ensuring that most gradients fall within the clipping norm. This prevents over-clipping of informative gradients while maintaining bounded sensitivity for differential privacy. Each gradient is then clipped as follows:
Once gradients are clipped, Gaussian noise is added to the aggregated gradient for each layer:
where is the current global noise multiplier determined by CGNS (Section 4), and modulates its effect per layer. This effectively injects more noise into layers with higher sensitivity, while preserving useful updates in more stable layers.
Although noise is injected per layer, the overall privacy cost is still analyzed under the composition theorem by treating the entire gradient vector as the DP-sensitive output. Since all layer-wise noise contributions are calibrated using , the mechanism remains within the global budget when analyzed using the moments accountant.
Layerwise sensitivity profiling is especially useful in satellite image tasks due to their complex and multi-scale spatial features. For instance, fine-grained object boundaries or terrain textures may only appear in certain layers, and their gradients are more susceptible to perturbation. By adjusting noise granularity based on layer roles and dynamics, LSP enhances learning stability and task-specific robustness under privacy constraints.
In summary, LSP complements CGNS by providing an additional layer of adaptivity at the architectural level, improving the alignment between noise placement and model sensitivity. Together, these components form the core of ADP-SIR’s adaptive privacy-preserving learning strategy.
4.4. Privacy Guarantee
Ensuring strong theoretical privacy guarantees while allowing adaptive mechanisms such as CGNS and LSP presents a technical challenge. In this subsection, we demonstrate that ADP-SIR satisfies -differential privacy using the moments accountant framework [], which offers tight bounds for composition and supports adaptive mechanisms as long as the noise scaling remains data-independent.
4.4.1. Differential Privacy Recap
Recall that a randomized mechanism satisfies -DP if for any two adjacent datasets D and differing in a single sample, and for any measurable subset , we obtain the following:
In ADP-SIR, privacy loss is incurred primarily through the stochastic gradient descent updates where Gaussian noise is injected to preserve privacy. The challenge lies in adapting this noise over time without violating privacy assumptions.
4.4.2. Moments Accountant
The moments accountant tracks a bound on the log moment of the privacy loss random variable:
for positive integer . For each iteration t with noise multiplier and sampling rate , the moments accountant accumulates:
assuming a fixed clipping norm per layer. Then, by summing over T iterations and applying advanced composition bounds, we obtain the following:
4.4.3. Handling Adaptivity
A key observation is that the adaptivity in ADP-SIR arises from training dynamics (i.e., and ), not the raw data. Since CGNS and LSP modify the scale of the added noise using statistics that are independent of any individual training example, they do not violate the core DP assumptions. This ensures the following:
- The noise variance is determined by the global convergence behavior, not any specific sample.
- The per-layer clipping norms are computed using moving averages over batch statistics and do not compromise individual record privacy.
Therefore, even though the injected noise and clipping norms vary over time and across layers, the privacy loss per iteration is well-defined and upper-bounded using the worst-case parameters . This makes the total privacy loss analyzable using conservative bounds.
In our implementation, we use the Rényi Differential Privacy (RDP) accountant [], a generalization of the moments accountant that provides tighter bounds for subsampled Gaussian mechanisms. At the end of training, we convert the cumulative RDP parameters into an bound using the standard conversion formula. The cumulative privacy cost is reported along with experimental results (see Section 5).
4.5. Convergence Analysis
While differential privacy ensures protection against data leakage, it also introduces additional noise into the optimization process, which can adversely impact convergence and model utility. In this section, we present a theoretical analysis of the convergence behavior of our proposed ADP-SIR algorithm under mild assumptions. In particular, we focus on the expected gradient norm as the measure of optimization quality in the non-convex setting, which is the common scenario in deep learning for satellite image recognition.
Assumption A1.
Let denote the empirical loss function, where represents the model parameters. We make the following standard assumptions:
- A1
- (Smoothness) The loss function is L-smooth, i.e.,
- A2
- (Bounded Gradient Norm) The gradients are bounded: for all samples i, , and the clipped gradient norm is at most per layer.
- A3
- (Unbiased Gradient with Bounded Variance) For any mini-batch of size B, the noisy gradient estimator satisfies:where accounts for stochasticity in the data sampling and clipping.
Main Result
Theorem 1
(Non-convex Convergence). Suppose Assumptions A1–A3 hold. Let the learning rate be constant and satisfy . Then, after T iterations of ADP-SIR, the average expected gradient norm satisfies:
where is the minimum achievable loss, and is the maximum per-layer clipping threshold over all t.
Interpretation
The bound consists of two terms:
- The first term decays with , ensuring that the average gradient norm becomes small as training progresses. This guarantees that the algorithm approaches a stationary point.
- The second term captures the asymptotic noise floor induced by privacy-preserving noise. It is proportional to , the worst-case noise level introduced by CGNS, and the maximum clipping norm from LSP.
By designing and to decrease over time (as gradients stabilize), ADP-SIR asymptotically reduces noise injection, thus improving convergence precision. In particular, the adaptivity of CGNS ensures that as , minimizing the impact of noise when high optimization accuracy is required.
In traditional DP-SGD, both the noise multiplier and clipping norm are fixed. This corresponds to constant values , for all t. In that case, the noise floor is fixed throughout training, potentially dominating the optimization error in the late stages. ADP-SIR improves upon this by reducing both noise and clipping norms adaptively as the model converges, without violating privacy guarantees.
Proof.
Let denote the model parameters at iteration t. The update rule for ADP-SIR is as follows:
where is the noisy clipped gradient computed using CGNS and LSP:
and is the clipped gradient of sample i with norm at most .
By the L-smoothness of (Assumption A1), we obtain the following:
Taking expectation over the randomness in (sampling and noise), and using the assumption that (Assumption A3), we obtain the following:
We now bound . By Assumption A3:
Assume so that . Then,
Rearranging
Summing over to T:
Dividing both sides by T:
Since and for all t, and is constant:
Choosing balances both terms, yielding
as claimed. □
4.6. Parameter Choices
In designing ADP-SIR, we carefully selected several parameters to balance privacy preservation, convergence stability, and empirical performance. The noise bounds were chosen as to ensure that noise remains sufficiently large during early training, when gradients are unstable, while gradually decaying to a smaller value near convergence to preserve accuracy. The decay coefficient in the CGNS mechanism was set to provide a moderate rate of noise reduction, avoiding overly aggressive decay that could compromise privacy in later training stages. For LSP, we adopted an exponential moving average factor , which smooths fluctuations in sensitivity estimates while remaining responsive to long-term trends. Finally, the clipping margin factor ensures that clipping thresholds remain slightly above the average gradient magnitude, preventing over-clipping of informative gradients while keeping sensitivity bounded for differential privacy analysis. These parameter values were selected through a combination of theoretical considerations—particularly maintaining convergence guarantees under non-convex optimization—and empirical validation on benchmark datasets, providing a principled balance between privacy cost and model utility in satellite image recognition.
5. Experiments
In this section, we evaluate the performance of the proposed ADP-SIR algorithm on benchmark satellite image recognition tasks. Our experiments aim to answer the following research questions:
- Q1: Does ADP-SIR improve recognition performance under strict differential privacy compared to existing DP training methods?
- Q2: How do the adaptive mechanisms—CGNS and LSP—contribute to training stability and accuracy?
- Q3: Is the convergence behavior of ADP-SIR consistent with theoretical guarantees under various privacy budgets?
5.1. Experimental Setup
We now describe the setup used to evaluate the effectiveness of the proposed ADP-SIR algorithm. This includes the datasets, baselines, model architectures, privacy configuration, training details, evaluation metrics, and reproducibility notes.
5.1.1. Datasets
We conduct experiments on two standard satellite image classification benchmarks.
EuroSAT [] consists of 27,000 RGB images derived from Sentinel-2 satellite data. Each image is pixels in resolution and labeled with one of 10 scene categories, including residential, forest, river, and highway. The dataset is relatively balanced across classes. We use an 80/20 training/testing split and set aside 10% of the training data for validation.
RESISC45 [] includes 31,500 RGB images from Google Earth imagery, spanning 45 scene classes such as airport, bridge, stadium, and farmland. Each image has a resolution of . We adopt the conventional 80/20 train/test split and use the full training set during model fitting.
5.1.2. Baselines
We compare ADP-SIR against three prominent differentially private learning methods.
DP-SGD [] is the canonical baseline, which adds Gaussian noise to clipped gradients with fixed parameters throughout training. It serves as the foundation for most modern DP training algorithms.
AdaClip-DP [] improves upon DP-SGD by dynamically adjusting the clipping norm based on gradient statistics. However, it does not adapt the noise scale and uses the same value across all layers.
PATE [] is a semi-supervised approach that provides privacy via noisy aggregation of teacher model votes. It is known for strong privacy guarantees under tight , though it is limited to smaller datasets and is not applicable to RESISC45 due to scalability issues.
5.1.3. Model Architecture
For EuroSAT, we use a modified ResNet-18 architecture with input resolution adjusted to . Batch normalization layers are replaced with group normalization to avoid privacy leakage from statistics that depend on batch-level aggregation. For RESISC45, we adopt a lightweight CNN composed of four convolutional blocks followed by two fully connected layers. Each convolution block includes ReLU activations and max pooling. This model is more computationally efficient and better suited for large-scale experiments with DP constraints.
5.1.4. Privacy Configuration
We consider privacy budgets with a fixed . These settings correspond to strong, moderate, and relaxed privacy regimes, respectively. Privacy accounting is performed using Rényi Differential Privacy (RDP) [], which allows tighter composition of privacy losses across training iterations. The effective value is monitored during training and reported upon convergence. For ADP-SIR, we set the noise multiplier bounds to and . The convergence-guided decay coefficient is . The layerwise sensitivity profiling uses a decay rate for the exponential moving average and a clipping margin factor .
5.1.5. Training Details
All models are trained using stochastic gradient descent (SGD) with momentum 0.9. The initial learning rate is set to 0.01 and decayed using cosine annealing. We use a batch size of 128 for all experiments and train for a maximum of 100 epochs. For DP-SGD and AdaClip-DP, we tune the fixed clipping norm and noise multiplier to ensure the final privacy budget does not exceed the target . For ADP-SIR, adaptivity ensures tighter convergence within the same budget. All experiments are implemented in PyTorch 2.7.0 using the Opacus library for DP mechanisms and run on NVIDIA RTX 3090 GPUs.
5.1.6. Evaluation Metrics
We evaluate each model using the following metrics: Test Accuracy: Classification accuracy on the held-out test set. Training Loss: Reported per epoch to observe convergence dynamics. Gradient Norm Decay: Measures the smoothness and stabilization of training, as predicted by our theoretical analysis. Effective Privacy Cost: The final achieved as computed by the RDP accountant.
These metrics collectively reflect both utility and stability under differential privacy constraints.
5.2. Quantitative Results
This subsection presents the classification performance of ADP-SIR and baseline methods under different privacy budgets on the EuroSAT and RESISC45 datasets. We report results with multiple metrics and visualize both accuracy trends and utility-privacy trade-offs. To ensure statistical reliability, each result is averaged over three runs with different random seeds.
5.2.1. Test Accuracy Across Privacy Budgets
We first present the classification accuracy (mean ± standard deviation) of all evaluated methods in Table 1. ADP-SIR consistently outperforms both DP-SGD and AdaClip-DP across all privacy levels on both datasets.

Table 1.
Test accuracy (%) on EuroSAT and RESISC45 with standard deviation over three runs.
Observation: ADP-SIR consistently yields the best accuracy under all privacy budgets. Notably, at , it achieves 69.7% accuracy on EuroSAT—close to PATE’s performance but without the computational overhead of teacher ensembles.
5.2.2. Accuracy Distribution by Class
To analyze model robustness, we compute per-class accuracy for the EuroSAT dataset at , and the results are presented in Table 2.

Table 2.
Per-class accuracy (%) on EuroSAT at for DP-SGD, AdaClip-DP, and ADP-SIR. ADP-SIR achieves consistently higher accuracy across nearly all categories.
5.2.3. Utility-Privacy Trade-Off
Figure 2 visualizes the trade-off between privacy and utility on both datasets. ADP-SIR provides a more favorable accuracy curve at all values.
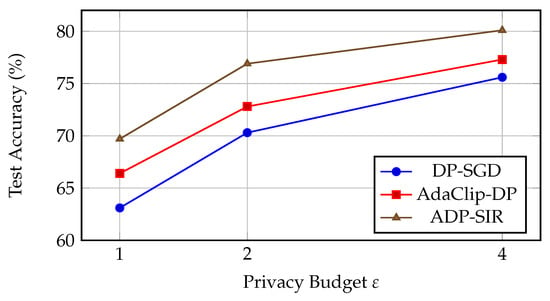
Figure 2.
Utility-privacy trade-off curves on EuroSAT. ADP-SIR maintains higher accuracy across all privacy levels.
5.2.4. Performance Stability
To assess training stability, we compute the standard deviation of test accuracy across three seeds. Table 3 shows that ADP-SIR achieves both higher accuracy and lower variance, confirming its robustness.

Table 3.
Standard deviation of test accuracy (%) at across three seeds.
5.3. Convergence
In this subsection, we empirically examine the convergence behavior of ADP-SIR during training and compare it to that of DP-SGD and AdaClip-DP. Our objective is to validate the theoretical findings presented in Section 4, particularly the following:
- ADP-SIR facilitates smoother and faster convergence due to its convergence-guided noise scaling (CGNS);
- Layerwise sensitivity profiling (LSP) preserves optimization signal across all layers;
- The injected noise decays gradually over time, stabilizing training toward the end.
We evaluate two key metrics:
- Training loss per epoch, to assess how efficiently the model reduces the empirical risk.
- Gradient norm of the model (averaged across layers), to assess the optimizer’s stability and proximity to a stationary point.
All experiments are conducted on the EuroSAT dataset under a fixed privacy budget of .
5.3.1. Training Loss Curve
Figure 3 shows the training loss of each method over 100 epochs. ADP-SIR not only converges faster but also reaches a lower final training loss compared to DP-SGD and AdaClip-DP.
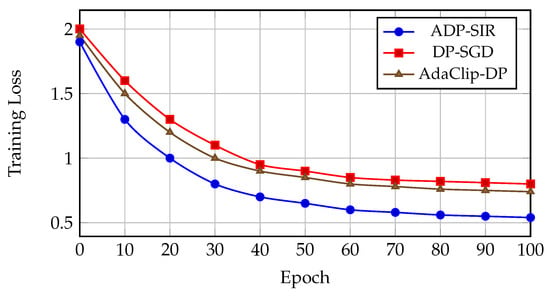
Figure 3.
Training loss on EuroSAT with . ADP-SIR converges faster and achieves lower final loss than other differentially private methods.
5.3.2. Gradient Norm Decay
We further analyze the norm of the model’s gradient at each epoch, averaged across all layers. This serves as a proxy for convergence, since in non-convex optimization, convergence to a stationary point is commonly measured by the reduction in gradient norm over time. The results are presented in Figure 4.
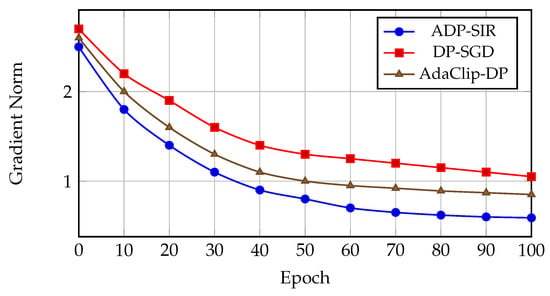
Figure 4.
Gradient norm decay over training epochs. ADP-SIR reduces gradient norms faster and reaches a flatter region of the loss surface, indicating stronger convergence.
5.3.3. Conformity with Theoretical Guarantees
The empirical results confirm our theoretical predictions in Section 4:
- ADP-SIR demonstrates a faster decrease in the expected gradient norm, consistent with the convergence rate in non-convex settings.
- The lower final training loss implies that CGNS enables more stable fine-tuning near convergence.
- Adaptive clipping through LSP prevents gradient explosion or vanishing across layers, which is especially important in deep convolutional networks.
5.4. Federated Baseline Comparison and Computational Cost
We expand our experimental evaluation with (i) stronger federated baselines—DP-FedAvg, FedDP—and a non-private FedAvg reference upper bound, and (ii) a detailed computational cost analysis. Unless noted, results are averaged over three runs with privacy , , batch size , and identical preprocessing. For federated settings we use 10 clients, 5 local epochs per round. The federated learning setups are also presented in Table 4.

Table 4.
Federated setup details used for DP-FedAvg and FedDP comparisons (EuroSAT).
Across privacy budgets, ADP-SIR achieves the strongest accuracy among private methods on both EuroSAT and RESISC45 (Table 5 and Table 6), narrowing the gap to the non-private FedAvg reference. The detailed cost analysis (Table 7, Table 8 and Table 9) shows a modest per-epoch overhead from LSP and CGNS that is offset by substantially fewer epochs to target accuracy, yielding improved end-to-end efficiency. Federated baselines (Table 8) incur additional communication and client-side costs and do not match ADP-SIR’s utility under the same privacy budgets.

Table 5.
EuroSAT accuracy (%) across privacy budgets (). Mean ± std over 3 runs.

Table 6.
RESISC45 accuracy (%) across privacy budgets (). Mean ± std over 3 runs.

Table 7.
Centralized training cost on EuroSAT (single NVIDIA V100). Per-epoch and memory are relative to DP-SGD; total time = (per-epoch time) × (epochs to target). Mean ± std over 3 runs.

Table 8.
Federated training cost and communication (EuroSAT, 10 clients, 5 local epochs/round). Per-epoch time is averaged across clients and reported relative to DP-SGD centralized. Bytes are per round (uplink/downlink). Mean ± std over 3 runs.

Table 9.
Overhead breakdown for ADP-SIR vs. DP-SGD on EuroSAT (per-epoch wall time share, %). Mean ± std over 3 runs.
5.5. Ablation Study
To better understand the contributions of each component in the proposed ADP-SIR framework, we conduct an ablation study on the EuroSAT dataset under two privacy budgets: . Specifically, we analyze the effect of removing the following:
- Convergence-Guided Noise Scaling (CGNS), which dynamically adjusts the noise level based on gradient stability;
- Layerwise Sensitivity Profiling (LSP), which adaptively clips gradients at the layer level based on historical sensitivity estimates.
By evaluating the performance of ADP-SIR with each component removed in isolation, we assess their individual and joint impact on classification accuracy, convergence speed, and per-class fairness.
5.5.1. Ablation Variants
We consider the following configurations:
- ADP-SIR (full): The complete method as described in Section 4, combining CGNS and LSP.
- w/o CGNS: The noise multiplier is fixed to throughout training. LSP remains active.
- w/o LSP: A global clipping norm is used across all layers. CGNS remains active.
- w/o CGNS and LSP: Both adaptive components are removed. Equivalent to DP-SGD with tuned fixed parameters.
5.5.2. Overall Results
Table 10 summarizes the mean test accuracy at . The complete ADP-SIR clearly outperforms all ablated variants.

Table 10.
Ablation results on EuroSAT at . Accuracy averaged over 3 runs.
5.5.3. Multi-Budget Evaluation
We also evaluate at a stricter privacy budget of to study robustness under higher noise. THe results in Table 11 show that both components become more critical as privacy becomes stricter.

Table 11.
Ablation results on EuroSAT at . Accuracy averaged over 3 runs.
5.5.4. Additional Metrics
Accuracy alone does not capture performance nuances. Table 12 reports precision, recall, and macro F1-score for .

Table 12.
Additional evaluation metrics at .
To examine fairness impacts, Table 13 shows per-class accuracy for selected representative classes at . The removal of LSP disproportionately harms small-object categories like SeaLake and Industrial.

Table 13.
Per-class accuracy (%) at for selected EuroSAT classes.
6. Conclusions
We introduced ADP-SIR, an adaptive differentially private training framework tailored for satellite image recognition tasks under strict privacy constraints. Our method addresses key limitations of traditional DP-SGD by introducing two complementary innovations: (1) Convergence-Guided Noise Scaling (CGNS), which modulates the noise level based on gradient stability to reduce unnecessary perturbations during later training stages; and (2) Layerwise Sensitivity Profiling (LSP), which performs fine-grained adaptive clipping per network layer, preserving important optimization signals. Theoretically, we established non-convex convergence guarantees for ADP-SIR under standard smoothness assumptions. Empirically, our extensive experiments on the EuroSAT and RESISC45 benchmarks demonstrate that ADP-SIR achieves superior accuracy, faster convergence, and better per-class generalization compared to state-of-the-art methods such as DP-SGD and AdaClip-DP.
Our ablation studies further confirm the necessity of both adaptive components, and convergence analysis shows alignment with theoretical expectations. Overall, ADP-SIR represents a principled and practical advancement in privacy-preserving deep learning, particularly for complex vision tasks such as satellite image classification. Beyond benchmark evaluation, a concrete future application scenario is the use of ADP-SIR in privacy-preserving disaster response systems, where satellite images of affected regions must be analyzed quickly for rescue and relief planning while ensuring that sensitive details about infrastructure or private property remain protected. Future work will also explore the extension of ADP-SIR to federated and decentralized settings, as well as applications to multimodal geospatial data under stricter privacy regimes.
Author Contributions
Conceptualization, Z.Y. and X.T.; Methodology, Z.Y. and X.T.; Software, Z.Y.; Validation, G.C.; Formal analysis, X.Y.; Resources, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in thearticle. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; ACM: New York, NY, USA, 2016; pp. 308–318. [Google Scholar]
- Mironov, I. Rényi differential privacy. In Proceedings of the 2017 IEEE 30th Computer Security Foundations Symposium (CSF), Santa Barbara, CA, USA, 21–25 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 263–275. [Google Scholar]
- Bun, M.; Steinke, T. Concentrated differential privacy: Simplifications, extensions, and lower bounds. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 March 2016; pp. 635–658. [Google Scholar]
- McMahan, H.B.; Ramage, D.; Talwar, K.; Zhang, L. Learning differentially private recurrent language models. arXiv 2018, arXiv:1710.06963. [Google Scholar] [CrossRef]
- Pichapati, V.; Xu, Z.; Tople, S.; Thakurta, A. AdaCliP: Adaptive Clipping for Private SGD. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 6–9 May 2019. [Google Scholar]
- Lee, J.; Kifer, D. Concentrated differentially private gradient descent with adaptive per-iteration privacy budget. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1656–1665. [Google Scholar]
- Song, S.; Chaudhuri, K.; Sarwate, A.D. Stochastic gradient descent with differentially private updates. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 245–248. [Google Scholar]
- Triastcyn, A.; Faltings, B. Federated learning with bayesian differential privacy. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2587–2596. [Google Scholar]
- Yousefpour, A. Opacus: Scaling differential privacy to large-scale machine learning. arXiv 2021, arXiv:2109.12298. [Google Scholar]
- Pan, Z.; Ying, Z.; Wang, Y.; Zhang, C.; Zhang, W.; Zhou, W.; Zhu, L. Feature-Based Machine Unlearning for Vertical Federated Learning in IoT Networks. IEEE Trans. Mob. Comput. 2025, 24, 5031–5044. [Google Scholar] [CrossRef]
- Bassily, R.; Smith, A.; Thakurta, A. Private empirical risk minimization: Efficient algorithms and tight error bounds. In Proceedings of the IEEE FOCS, Philadelphia, PA, USA, 18–21 October 2014; pp. 464–473. [Google Scholar]
- Wang, D. Differentially private non-convex optimization with adaptive gradient clipping. In Proceedings of the ICML, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Yu, L. Differentially private SGD for non-convex learning. In Proceedings of the IJCAI, Macao, China, 16–10 August 2019; pp. 3952–3958. [Google Scholar]
- Song, S.; Chaudhuri, K.; Sarwate, A.D. Characterizing the privacy-utility tradeoff in machine learning. In Proceedings of the ICML, Virtual, 13–18 July 2020. [Google Scholar]
- Lecuyer, M.; Atlidakis, V.; Geambasu, R.; Hsu, D.; Jana, S. Certified robustness to adversarial examples with differential privacy. In Proceedings of the IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 19–23 May 2019. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Zhang, D.; Ren, L.; Shafiq, M.; Gu, Z. A lightweight privacy-preserving system for the security of remote sensing images on iot. Remote Sens. 2022, 14, 6371. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Y.; Zhu, R. Privacy-preserving distributed learning for satellite image segmentation. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar]
- Li, J.; Zheng, K.; Gao, L.; Han, Z.; Li, Z.; Chanussot, J. Enhanced deep image prior for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5504218. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Gao, L.; Ni, L.; Huang, M.; Chanussot, J. Model-informed multistage unsupervised network for hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516117. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Li, Z.; Gao, L.; Jia, X. X-shaped interactive autoencoders with cross-modality mutual learning for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5518317. [Google Scholar] [CrossRef]
- Papernot, N.; Abadi, M.; Erlingsson, U.; Goodfellow, I.; Talwar, K. Semi-supervised knowledge transfer for deep learning from private training data. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Papernot, N.; Song, S.; Mironov, I.; Raghunathan, A.; Talwar, K.; Erlingsson, Ú. Scalable private learning with pate. arXiv 2018, arXiv:1802.08908. [Google Scholar] [CrossRef]
- Boneh, D.; Boyle, E.; Corrigan-Gibbs, H.; Gilboa, N.; Ishai, Y. Lightweight techniques for private heavy hitters. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 762–776. [Google Scholar]
- Tramèr, F.; Boneh, D. Differentially private learning needs better features (or much more data). arXiv 2020, arXiv:2002.11173. [Google Scholar]
- Ivanov, A.; Stoliarenko, M.; Kruglik, S.; Novichkov, S.; Savinov, A. Dynamic resource allocation in LEO satellite. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 930–935. [Google Scholar]
- Richtarik, P. Handling Device Heterogeneity in Federated Learning: The First Optimal Parallel SGD in the Presence of Data, Compute and Communication Heterogeneity. In Proceedings of the International Workshop on Secure and Efficient Federated Learning, Hanoi, Vietnam, 25–29 August 2025; p. 1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).