Abstract
This paper proposes a novel multimodal emotion recognition framework, termed Sparse Alignment and Liquid-Mamba (SALM), which effectively integrates the complementary strengths of Mamba networks and Liquid Neural Networks (LNNs). To capture neural dynamics, high-resolution EEG spectrograms are generated via Short-Time Fourier Transform (STFT), while heatmap features from facial images, videos, speech, and text are extracted and aligned through entropy-regularized Sinkhorn and Greenkhorn optimal transport algorithms. These aligned representations are fused to mitigate semantic disparities across modalities. The proposed SALM model leverages sparse alignment for efficient cross-modal mapping and employs the Liquid-Mamba architecture to construct a robust and generalizable classifier. Extensive experiments on benchmark datasets demonstrate that SALM consistently outperforms state-of-the-art methods in both classification accuracy and generalization ability.
1. Introduction
Multimodal Emotion Recognition (MER) leverages facial expressions, speech, EEG, and text to understand emotions. In real-world scenarios, discrepancies in semantics and statistical distributions across modalities remain a key challenge; for example, sarcasm may be evident in vocal tone yet ambiguous in text, while subtle facial cues such as smirks can contradict spoken words.
Recent MER research has increasingly focused on bridging these modality gaps through semantic alignment and structural correspondence modeling. Optimal Transport (OT) methods such as Sinkhorn [] and Greenkhorn [] have shown strong performance in aligning heterogeneous features under noisy, imbalanced conditions, particularly for high-dimensional EEG spectrograms and video frames. Building on this, graph-based strategies (e.g., heterogeneous graph attention networks) further capture fine-grained associations between facial action units and emotion-related text, enabling richer cross-modal context integration.
However, even with improved alignment, MER faces three persistent challenges: modeling long-range dependencies across asynchronous signals; extracting discriminative, high-resolution EEG features while suppressing modality-specific noise; and designing fusion mechanisms that avoid overfitting and generalize well in high-dimensional spaces. To tackle these issues, recent studies have progressively introduced more sophisticated sequence modeling architectures. Esernet [] uses Swin Transformer to boost speech emotion recognition by improving temporal sensitivity over CNNs. Transifc [] applies invariant cue-aware feature concentration for image classification, aligning modality-invariant signals. Mmatrans [] enhances transformers with muscle movement-aware attention for facial expression recognition. These works show a trend from basic feature fusion to modality alignment and context-aware temporal modeling, which informs our approach. Fuzzy clustering [] in MER can model uncertainty to enable soft alignment across modalities, while also facilitating time-series modeling of dynamic emotional variations [].
Driven by recent advances, we propose a unified MER framework that integrates Mamba [] and Liquid Neural Networks (LNNs) [] with sparsity-aware fusion and OT-based semantic-temporal alignment. Mamba’s selective state-space model (using the SS2D module) captures long-range dependencies in spatiotemporal data (e.g., EEG spectrograms, facial videos). Our design also features a selective scanning convolution paired with an LNN-enhanced state-space module (SS-Conv-LNN-SSM) that combines local convolutional feature extraction, LNN adaptability for short-term dynamics, and state-space long-term dependency capture to retain key multimodal cues while reducing redundancies. LNNs further adapt to short-term variations, effectively capturing transient emotional signals like micro-expressions and vocal prosody in complex, asynchronous conditions.
Our framework tackles three key challenges in multimodal emotion recognition: (1) preserving fine-grained modality-specific cues through high-resolution selective scanning convolutions, (2) capturing transient emotional dynamics via Liquid Neural Networks, and (3) extending temporal dependencies using Mamba’s state-space mechanisms. Crucially, an entropy-regularized sparse alignment module is jointly optimized with the multi-timescale sequence modeling, effectively coupling optimal transport-based cross-modal alignment with multi-scale temporal reasoning. This design mitigates semantic drift and temporal asynchrony, enabling more robust and precise emotion recognition.
The contributions of this work are summarized as follows:
- We introduce a unified MER framework that employs Sinkhorn and Greenkhorn optimal transport to generate structure-preserving, semantically aligned EEG, visual, auditory, and textual representations.
- Our fusion architecture merges Mamba’s long-range temporal modeling with LNN’s fine-grained adaptability for robust, efficient multimodal integration.
- Extensive benchmarks show our framework outperforms state-of-the-art baselines in accuracy, robustness, and generalization under imbalanced, semantically ambiguous conditions.
2. Related Work
Multimodal Emotion Recognition (MER) fuses text, speech, facial expressions, and EEG to infer emotions. A key challenge is aligning these asynchronous, diverse modalities with varying sampling rates, structures, and noise levels. Existing studies have explored a variety of solutions, including graph-based modeling, Optimal Transport (OT)-based alignment, and entropy-regularized Sinkhorn-based optimization.
Graph-based approaches model inter-modal relationships through structured topologies. For example, HetEmotionNet [] employs a dual-stream heterogeneous graph recurrent neural network, integrating Graph Transformer Networks (to address modality heterogeneity), Graph Convolutional Networks (to capture inter-modal correlations), and Gated Recurrent Units (to model temporal dependencies). This combination enables spatial–temporal–spectral feature modeling, while extensions with dynamic graphs and temporal transformers further capture emotional evolution over time. Recent graph-based MER research has further advanced contextual and relational modeling in conversations. Ai et al. [] proposed DER-GCN to jointly capture dialog and event relations via a weighted multi-relationship graph and self-supervised masked graph autoencoders. Wang et al. [] introduced DEDNet, which disentangles inter-speaker and intra-speaker dependencies through relational subgraph interaction, enabling dynamic dependency tracking. Shi et al. [] designed IMDNet, a speaker-centric graph with attribute embeddings and utterance distance attention, reducing cross-speaker interference. Lu et al. [] further extended this line by constructing HyperCRM, a hypergraph-based contextual modeling framework that employs multi-stage hypergraph convolution to capture long-range dependencies. These works collectively demonstrate the effectiveness of graph and hypergraph structures for multimodal conversation-level emotion recognition.
OT-based methods tackle distributional discrepancies between modalities. Unlike dense attention, Graph OT (GOT) [] treats alignment as a graph matching problem using Wasserstein and Gromov–Wasserstein distances, producing sparse and interpretable transport plans. Recent advances employ OT regularizers [], hierarchical OT [] with ADMM solvers, and Sinkhorn regularization to improve semantic coherence and scalability. For instance, CMOT [] uses token-level OT between speech and text for richer embeddings, while Sinkhorn distance accelerates convergence in multimodal fusion. In computer vision, OT-based alignment has been combined with structure-aware encoding, e.g., TransSil [] using silhouette cues, EHPE [] applying skeleton-based Gaussian encoding, and DSR-Net [] introducing rollback queries for temporal consistency. Beyond dialog data, recent physiological-signal-driven MER frameworks also highlight the role of effective fusion and augmentation. Li et al. [] introduced a ConvNeXt-attention fusion model combined with a conditional self-attention GAN for multimodal physiological data augmentation, alleviating data scarcity. Xu et al. [] proposed HCSFNet, a hierarchical cross-modal spatial fusion network integrating EEG and video features with coordinated attention, spatial pyramid pooling, and self-distillation, achieving state-of-the-art results on DEAP. These works emphasize cross-modal spatial alignment and data enrichment as complementary to OT-based distributional alignment.
Sinkhorn-based refinements extend OT alignment with improved computational feasibility and robustness. For spatial–geometric alignment tasks, e.g., EEG–vision fusion, Sinkhorn-based metrics maintain topological consistency [], inspiring manifold-based interpretations of EEG spectrograms and visual embeddings. Dynamic OT formulations [] address temporal variability in affective signals, while low-rank Sinkhorn approximations [] and entropic OT with contrastive learning [] scale to large datasets. Other variants integrate Gaussian Mixture Models [], multi-marginal transport, and multimodal transformers for semantic separation. Robust Sinkhorn variants further improve alignment under domain shifts and data imbalance. For example, Wang et al. [] extend Talagrand’s inequality via the Entropy Power Inequality for domain-variant MER, while Liu et al. [] propose Bilateral Scaled Sinkhorn Distance with attention and multi-scale pooling for few-shot generalization. Selective Kernel Attention with unbalanced Sinkhorn distances [] addresses class imbalance, and in speech–text fusion, Lu et al. [] integrate Sinkhorn into Transformer-based architectures without auxiliary language models.
Despite these advances, several gaps remain: (1) Most OT-based frameworks focus on static or shallow temporal modeling, struggling with asynchronous or non-stationary modalities (e.g., EEG vs. video). (2) Real-time performance in latency-sensitive applications, such as mobile affective computing and human–robot interaction, is rarely addressed. (3) The integration of OT-based alignment with adaptive, multi-timescale temporal modeling for physiological signal-based MER remains largely unexplored, particularly under constraints of computational efficiency. We propose an entropy-regularized sparse alignment and multi-timescale temporal model. EEG, speech, visual, and text features are aligned into a shared semantic space using Sinkhorn/Greenkhorn solvers, while high-resolution EEG is maintained via STFT. Pretrained encoders (ViT, CLIP, Wav2Vec2, VideoMAE) ensure modality robustness, and a hierarchical temporal model combining Mamba’s long-range state-space and Liquid Neural Networks’ local flexibility captures global transitions and transient cues. Finally, a sparsity-aware fusion module integrates features, reducing redundancy and enabling real-time deployment.
3. Method: Sparse Alignment and Liquid-Mamba (SALM) Architecture
As illustrated in Figure 1, Sparse Alignment and Liquid-Mamba (SALM) is composed of three core components: modality-specific encoding to transform raw data into heatmap representations; cross-modal alignment using Sinkhorn-Greenkhorn-based optimal transport; semantic-level fusion through a sparse integration mechanism; and classification utilizing a hybrid Liquid Neural Network (LNN) and Mamba backbone. The architecture is designed to facilitate effective interaction across heterogeneous modalities, enhancing both the accuracy and generalization of emotion recognition in dynamic and naturalistic contexts.
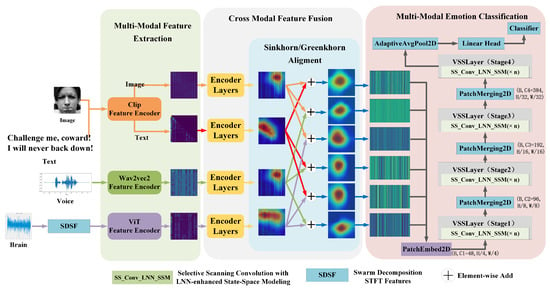
Figure 1.
Overview of the proposed Sparse Alignment and Liquid-Mamba (SALM) architecture.
3.1. Representation: Encoding Modalities into Heatmap Features
Multimodal seeks to project different input modalities into a unified feature space. In SALM, all modality inputs—ranging from visual and auditory data to physiological signals and textual content—are transformed into attention-based heatmap features. This representation unification enables more effective downstream alignment and fusion processes. As shown in Figure 1, each modality is transformed into a heatmap representation. Video uses VideoMAE [] to extract spatiotemporal maps capturing motion and facial cues. EEG signals are converted via STFT into spectrogram-style heatmaps. Text and image features are extracted using CLIP [] and projected onto spatial grids for cross-modal alignment. Speech employs Wav2Vec2 [] to generate spectro-temporal maps capturing acoustic cues, while images use a Vision Transformer (ViT) for high-resolution attention maps. Despite differing output shapes, all representations are normalized and resized to a common resolution for alignment.
3.2. Cross-Modal Alignment and Fusion via Optimal Transport-Augmented Self-Attention
Effective multimodal fusion encounters two challenges: semantic heterogeneity from modality-specific structures (e.g., speech vs. image) and unbalanced classification performance due to uneven data distributions and modality reliability.
3.2.1. Sinkhorn-Based Entropy-Regularized Heatmap Alignment
To align modality-specific features with divergent statistical and spatial structures, we adopt the Sinkhorn algorithm, which solves the entropy-regularized optimal transport (OT) problem in a differentiable manner. Given source and target modality feature maps and , where m and n are spatial token counts and d is the feature dimension, the cost matrix is computed as:
We then define the regularized optimal transport objective as
where is the transport matrix, denotes the set of joint distributions with marginals and , is the regularization coefficient, and is the entropy. Sinkhorn’s iterative matrix-scaling updates produce soft alignments that are differentiable and semantically meaningful.
3.2.2. Greenkhorn Acceleration for Efficient Transport Alignment
Although the Sinkhorn algorithm is effective, its computational overhead grows quadratically with token counts. To mitigate this, we incorporate the Greenkhorn algorithm, a greedy variant that performs coordinate-wise updates to accelerate convergence, while the optimization objective remains the same as Equation (2).
Greenkhorn iteratively selects the most violated marginal constraint—either a row or column—and updates only that slice of :
This greedy update strategy significantly reduces runtime and memory cost, making it suitable for real-time fusion in large-scale multimodal systems. Despite being approximate, Greenkhorn often matches Sinkhorn’s performance in aligning modality-specific semantic regions.
3.2.3. Optimal Transport-Augmented Attention Fusion
Once the modalities are aligned via Sinkhorn or Greenkhorn, we apply a self-attention-based fusion mechanism. We introduce modality-specific reliability weights derived from pretrained accuracies to reweight the query, key, and value projections:
where and are normalized to reflect modality reliability and class imbalance. Cross-attention output is computed as
Dual-attention enables bi-directional feature exchange, capturing modality-specific nuances while maintaining global consistency. Optimal transport aligns semantically matched features to improve performance on imbalanced or noisy modalities. Combining Sinkhorn/Greenkhorn-based alignment with reliability-weighted self-attention fusion resolves semantic misalignment and classification imbalance, fostering robust multimodal learning in real-world affective computing.
As shown in Figure 2, varying the regularization coefficient in the Sinkhorn alignment impacts the smoothness of the transport plan. Notably, Greenkhorn achieves similar alignment quality with significantly fewer iterations, validating its use in resource-constrained systems.
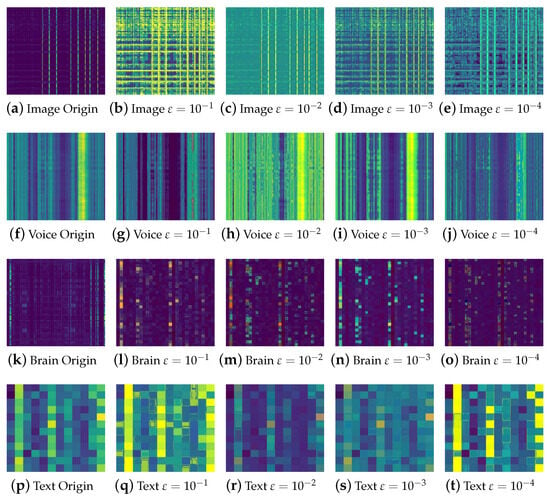
Figure 2.
As the entropic regularization coefficient varies in Sinkhorn alignment, the smoothness of the heatmap’s transport matrix also changes across different modalities, including images, speech, brain signals, and text.
4. Mamba-LNN Fusion Architecture for Multimodal Emotion Modeling
We propose SS-Conv-LNN-SSM as shown in Figure 3, a novel neural fusion architecture for robust multimodal integration (EEG, speech, image, text). It uses entropy-regularized heatmap alignment, attention-based fusion, and dynamic temporal modeling to efficiently integrate spatial and temporal features. The architecture combines a selective scanning mechanism for spatial dependencies with a Liquid Neural Network for adaptive temporal processing—modeling spatial relationships via state-space methods and convolution and simulating long-range dynamics inspired by neuronal potentials. With Sinkhorn/Greenkhorn alignment and QKV-based fusion ensuring semantic correspondence and cross-modal interaction, SS-Conv-LNN-SSM enhances temporal coherence, adaptability, and feature propagation against irregularity, asymmetry, and noise. Its dual-branch structure merges convolutional precision with biological temporal dynamics, with LNN modules offering variable temporal sensitivity and Mamba modules capturing long-range dependencies for stability. This framework supports applications in affective computing and multimodal mental health monitoring.
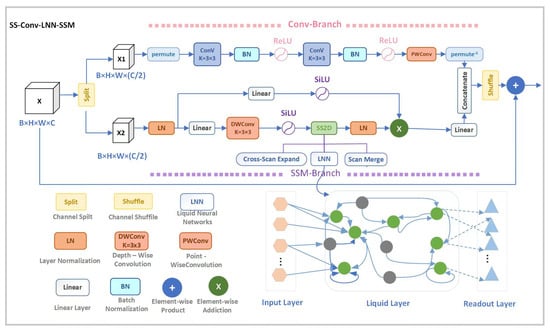
Figure 3.
The architecture of SS-Conv-LNN-SSM.
4.1. Two-Dimensional Selective Scanning Module (SS2D)
Inspired by VMamba, SS2D models global directional dependencies in 2D feature maps (e.g., aligned attention heatmaps) after Sinkhorn-based optimal transport. It scans inputs in multiple directions using state-space dynamics to enhance spatial coherence in multimodal fusion.
4.1.1. Cross-Scan Expansion
Given aligned modality-specific feature maps , four directional sequences are extracted. These sequences are passed through directional Mamba-style State-Space Models (S6 blocks), which maintain a balance between recurrent memory and feedforward processing. Given an input feature map , four directional sequences , , are formed:
4.1.2. Directional State-Space Modeling (S6 Block)
Each directional sequence is processed using a state-space model inspired by Mamba. Let denote the input and the previous hidden state.
The output is reshaped back to the 2D spatial domain. This enables efficient long-range context modeling while preserving direction-sensitive patterns, essential for interpreting structural differences between modalities (e.g., temporal EEG vs. spatial vision maps).
4.1.3. Scan Merge
Directional outputs are merged into the original spatial layout
The final aggregated output is
4.2. SS-Conv-LNN-SSM: Local-Global Feature Fusion
To integrate fine-grained spatial encoding and dynamic temporal adaptation, we extend SS2D with a dual-branch fusion structure: (1) a local convolutional encoder and (2) a global temporal branch using LNNs.
4.2.1. Branch Decomposition
Given the input , we split it along the channel dimension
Local Convolutional Branch
Local spatial patterns are extracted via convolution. The processing flow is:
where is the output of the local branch, BN denotes batch normalization, and PWConv denotes point-wise convolution.
Global Liquid Neural Network (LNN) Branch
The global branch models temporal evolution using a Liquid Neural Network (LNN). For each spatial position and time t, the input is , and the hidden state evolves as:
where is a learnable time constant, is the integration step size (default 1), and is a learnable recurrent weight matrix.
The full LNN processing pipeline is:
where ⊙ denotes element-wise multiplication. The output represents the global temporal features.
4.2.2. Fusion and Output Projection
The outputs from both branches are fused and projected as
where ⊕ is residual addition, is channel-wise concatenation and shuffling, g is a linear projection layer. This operation integrates the local convolutional branch , which encodes fine-grained spatial features, with the global LNN branch , which models temporal dynamics and long-range dependencies. The residual connection preserves the original input information, promoting stable feature propagation and effective joint encoding of spatial and temporal patterns.
By combining Sinkhorn-Greenkhorn alignment, Mamba scanning, and LNN-based temporal modeling, the framework ensures semantic-spatial consistency, captures long-range dependencies, and adapts dynamically to spatiotemporal variations. This integration enhances robustness, scalability, and feature integrity, making the architecture suitable for tasks such as multimodal emotion recognition and affective computing.
5. Experimental Results and Discussion
The SALM framework is validated through five experiments on the CMU-MOSEI, MER, MELD, IEMOCAP and RPPG datasets, demonstrating its effectiveness in multimodal sentiment analysis, emotion classification with tri- and quadri-modal fusion, conversational emotion recognition, and rPPG signal detection.
5.1. Multimodal Emotion Recognition on CMU-MOSEI
The CMU-MOSEI dataset [] benchmarks multimodal sentiment and emotion analysis with 2928 video clips labeled with emotion categories. This study extracts four modalities—video, image, text, and speech—using VideoMAE for video and transformer encoders for text and speech. The features are temporally aligned and fused to create robust multimodal representations. The dataset is imbalanced: happiness has over 12,000 instances, while fear has about 1900. Additionally, modality accuracy varies—video achieves 0.89 for positive emotions versus text (0.39) and speech (0.16); for neutral emotions, speech leads at 0.82 compared to video (0.29) and text (0.59). Advanced multimodal fusion is needed to balance these differences.
The SALM framework is evaluated using five metrics: Acc-7, Acc-2, F1-score, MAE, and Corr. Acc-7 assesses fine-grained emotion classification, Acc-2 measures binary sentiment, the F1-score balances precision and recall for imbalanced classes, MAE quantifies average error, and Corr gauges the linear correlation strength between predictions and actual values. As shown in Table 1, the SALM model achieves state-of-the-art performance on CMU-MOSEI, notably improving Acc-7 (64.3%), Acc-2 (86.6%), and F1-score (86.6%)—surpassing all baseline models. In terms of MAE and Corr, SALM remains competitive, with an MAE of 0.613 and a Pearson correlation of 0.773. These results confirm SALM’s strong capability in modeling complex cross-modal interactions and achieving accurate emotion prediction across diverse emotional states. Sinkhorn alignment improves cross-modal consistency by reducing semantic misalignment, while Greenkhorn speeds convergence via sparse transport mappings. Combined with a Liquid-Mamba backbone, SALM achieves high accuracy and computational efficiency for real-world affective computing.

Table 1.
Comparison with baselines on CMU-MOSEI (%). ↑ indicates that higher values are better; ↓ indicates that lower values are better.
5.2. Ablation Study
We conduct an ablation study on the CMU-MOSEI dataset to evaluate SALM’s core components: Sinkhorn Fusion (S), Greenkhorn Fusion (G), and Liquid-Mamba (L). Performance is measured under seven-class and two-class settings using accuracy, F1-score, MAE, and Pearson correlation (see Table 2).

Table 2.
Ablation study on CMU-MOSEI. “S”: Sinkhorn Fusion, “G”: Greenkhorn Fusion, “L”: Liquid-Mamba module.Symbols √ and × indicate whether the module is enabled or disabled, respectively. ↑ indicates that higher values are better; ↓ indicates that lower values are better.
Ablation study results reveal that retaining Greenkhorn Fusion while removing Sinkhorn Fusion achieves a seven-class classification accuracy of 72.5%, an F1-score of 71.3%, a Pearson correlation of 0.685, and an MAE of 0.779, indicating that Greenkhorn Fusion provides superior cross-modal alignment compared to Sinkhorn Fusion. Conversely, retaining Sinkhorn Fusion while excluding Greenkhorn Fusion reduces classification accuracy to 64.3%, lowers the F1-score to 63.6%, and decreases the correlation to 0.576. Further removal of both fusion modules—leaving only the Liquid-Mamba module—degrades performance to 61.3% accuracy, a 61.3% F1-score, and a correlation of 0.580, demonstrating that relying solely on the Liquid-Mamba module cannot adequately compensate for the lack of effective cross-modal alignment.
Table 3 presents the effect of varying the entropic regularization coefficient on model performance for the CMU-MOSEI dataset. The results indicate that achieves the highest accuracy (64.30%) and F1 score (63.60%), with relatively low MAE (1.0570) and a moderate correlation (0.5760). Increasing to the range 0.3–0.7 leads to a marked decline in classification accuracy (by approximately 9–13%) and correlation, suggesting that excessive smoothing diminishes feature discriminability. At , accuracy drops by about 16% compared with the optimal setting, and the correlation sharply decreases to 0.1035, indicating significant degradation in predictive alignment with ground truth. These findings highlight that small values preserve feature separability, whereas overly strong regularization can suppress discriminative cues and severely impair classification performance.

Table 3.
Impact of different Sinkhorn coefficients on model performance for the CMU-MOSEI Dataset. ↑ indicates that higher values are better; ↓ indicates that lower values are better.
The influence of the time constant in the LNN module is summarized in Table 4. Across the range , accuracy and F1 remain highly stable (63.70–64.30% and 62.30–63.60%, respectively), while MAE and correlation exhibit only minor fluctuations. The highest correlation (0.578) occurs at , suggesting that longer temporal integration marginally improves temporal consistency without compromising classification performance. This stability indicates that the LNN module is robust to variations in , simplifying hyperparameter tuning and enhancing adaptability to datasets with heterogeneous temporal dynamics.

Table 4.
Impact of different LNN coefficients on model performance for the CMU-MOSEI Dataset. ↑ indicates that higher values are better; ↓ indicates that lower values are better.
Overall, exerts a pronounced influence on classification accuracy, with optimal performance near . In contrast, shows low sensitivity within the tested range, confirming the LNN module’s suitability for scenarios requiring resilience to diverse temporal properties.
5.3. Experimental Analysis of Multimodal Emotion Recognition (MER)
We evaluate three cross-modal fusion strategies—unaligned, Sinkhorn-based optimal transport (OT), and Greenkhorn-based sparse OT—using F1-score, validation accuracy, mean absolute error (MAE), and Pearson correlation coefficient. All fusion outputs are classified using the Mamba-LNN architecture. The results for the quadri-modal three-class MER task are presented in Table 5.

Table 5.
Performance comparison of different alignment strategies on the quadri-modality three-class MER task. ↑ indicates that higher values are better; ↓ indicates that lower values are better.
Among unimodal inputs, EEG achieves the highest performance with an F1-score of 0.7706 and an accuracy of 76.37%, confirming its effectiveness in capturing emotion-related neural activity. In contrast, voice, image, and text modalities perform significantly worse, with text yielding only 0.2294 F1 and 28.10% accuracy, highlighting its limitations in coarse-grained emotional distinctions.
The unaligned fusion model, which directly concatenates features without alignment, attains an F1-score of 0.6 and an accuracy of 63.60%. These modest results reveal that direct fusion fails to resolve semantic inconsistencies and distribution mismatches across modalities.
Introducing Sinkhorn-based OT alignment substantially improves performance: the F1-score increases to 0.7642, accuracy to 77.04%, MAE decreases to 0.2851, and the correlation coefficient rises to 0.6456. These gains indicate that soft probabilistic alignment reduces semantic drift and promotes better cross-modal consistency.
Greenkhorn alignment achieves the best results across all metrics, with an F1-score of 0.8761, accuracy of 87.69%, MAE of 0.1543, and correlation of 0.8091. Its sparse scaling and efficient convergence mechanisms enable effective alignment of high-dimensional modality features, resulting in superior classification performance and robust training stability.
To evaluate generalization, we further tested the model on a more challenging tri-modality seven-class MER task (Table 6). In this fine-grained scenario, the image modality leads among unimodal inputs with an F1-score of 0.5832 and accuracy of 58.20%. Text performs worst again, confirming its inadequacy in distinguishing nuanced emotional categories.

Table 6.
Performance comparison of different alignment strategies on the tri-modality seven-class MER task. ↑ indicates that higher values are better; ↓ indicates that lower values are better.
The unaligned fusion approach marginally improves accuracy to 46.63% and the F1-score to 0.4664, but the improvement is limited, indicating that label granularity exacerbates misalignment issues. Interestingly, Sinkhorn alignment underperforms in this setting, dropping to 38.80% accuracy and a 0.3818 F1-score, suggesting that its element-wise matching may become unstable in high-dimensional, high-class tasks due to inter-class overlap and semantic ambiguity.
In contrast, Greenkhorn alignment delivers the most robust performance in this task as well, achieving an F1-score of 0.6022, an accuracy of 60.30%, and notable reductions in MAE and increases in correlation. This affirms Greenkhorn’s capacity to handle complex multimodal interactions under fine-grained classification, owing to its efficient sparse updates and better convergence behavior.
As illustrated in Figure 4a, EEG outperforms other modalities in the quadri-modal three-class MER task, achieving 76% accuracy, while text lags far behind at 23%. Unaligned fusion remains suboptimal due to cross-modal feature discrepancies. Incorporating Sinkhorn alignment improves accuracy to 76%, while Greenkhorn alignment significantly boosts it to 88%, outperforming both unimodal baselines and other fusion strategies. This highlights Greenkhorn’s superior ability to reconcile diverse feature spaces and maintain semantic consistency.
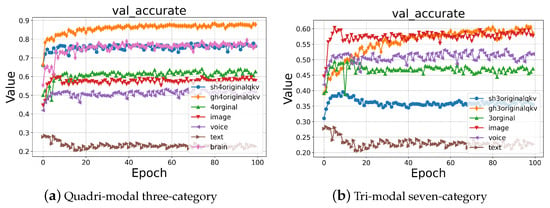
Figure 4.
SALM on MER.
In the more demanding tri-modal seven-class task (Figure 4b), unaligned fusion reaches 60% accuracy, suggesting that naïve integration can still benefit from complementarity, but its gains are limited by alignment errors. Greenkhorn achieves the same 60% accuracy, but with more stable convergence and a higher F1-score, making it a more reliable choice. In contrast, Sinkhorn alignment drops drastically to 35% accuracy, reflecting its limited robustness in high-dimensional, high-class settings.
These results demonstrate that cross-modal alignment is essential. In the tri-class setting, Greenkhorn improves accuracy by over 24% and F1-score by 27.6% compared to unaligned fusion, effectively mitigating modality mismatch and boosting classification robustness. Its sparse optimization offers scalable, stable alignment suitable for complex multimodal emotion recognition tasks. Additionally, the Mamba-LNN classifier, when coupled with Greenkhorn, shows excellent generalization to sequential inputs and effectively captures temporal dynamics and modality heterogeneity, further enhancing system performance under real-world conditions.
5.4. Multi-Modal Emotion Recognition on MELD
In the third experiment, we evaluate our model on MELD, a dataset from the EmotionLines corpus featuring multi-turn dialogues from Friends. It contains 1433 segments and approximately 13,000 utterances labeled into seven emotion categories and three sentiment classes (positive, negative, and neutral). The task is challenging due to multiple speakers, varying emotional intensities, and multimodal inputs (text, audio, and visual).
Table 7 shows our multimodal emotion framework surpassing baselines in both three-class (77.33% F1) and seven-class (67.13% F1) tasks, setting a new state-of-the-art on MELD. Our model outperforms baselines (RoBERTa DialogueRNN: 72.14%/63.61%, COSMIC: 73.20%/65.21%) with improvements of +5.19% (three-class) and +1.92% (seven-class), effectively capturing subtle emotional variations and cross-modal context. Our model excels by incorporating spatiotemporal dependencies and cross-modal alignment to better understand emotions in multi-turn, multi-speaker conversations. Consistent gains in both three-class and seven-class classifications show its robust generalization. These results support its effectiveness for real-world affective computing, such as empathetic virtual agents, emotion-aware dialogue systems, and human–AI interactions, demonstrating its potential in complex, multimodal environments.

Table 7.
Comparison with baselines on MELD’s 3-class and 7-class emotion recognition (%).
5.5. Multi-Modal Emotion Recognition on IEMOCAP
IEMOCAP is a widely recognized benchmark for speech emotion recognition, comprising approximately 12 h of recordings split into five sessions. Each session features a dyadic conversation between one male and one female actor, involving a total of ten actors from USC’s School of Dramatic Arts. The dataset encompasses nine emotion categories: anger, happiness, excitement, sadness, frustration, fear, surprise, other, and neutral. Given the inherent class imbalance, unweighted accuracy (UA)—the average accuracy across all classes—is adopted as the primary evaluation metric, while weighted accuracy (WA) is reported as a complementary measure.
As shown in Table 8, the proposed method achieves a WA of 79.2% and a UA of 75.3%, surpassing all baseline systems on the IEMOCAP benchmark. Compared with the widely adopted Attention Pooling [], our model yields absolute gains of 7.45 percentage points in WA and 7.44 percentage points in UA, indicating substantial improvements in both overall accuracy and class-balanced performance. Relative to the co-attention-based CA-MSER [], our framework achieves notable gains of 9.4 percentage points in WA and 4.45 percentage points in UA, underscoring the effectiveness of the proposed cross-modal fusion with entropy-regularized sparse alignment and timescale temporal modeling. Furthermore, the consistently higher UA compared to recurrent architectures (BiGRU) and hybrid designs (CNN-LSTM) demonstrates superior robustness against class imbalance, a persistent challenge in IEMOCAP. These results collectively validate that our approach not only advances state-of-the-art performance but also delivers balanced and reliable emotion recognition across diverse categories in multimodal settings.

Table 8.
Comparison with existing SER results on the IEMOCAP dataset.
5.6. Multimodal Physiological Signals Integrating rPPG and EEG
We built a dataset by collecting rPPG signals from a smartwatch under diverse, real-life conditions. Participants watched audiovisual stimuli to evoke seven emotions—happiness, sadness, anger, contempt, disgust, fear, and surprise—and completed a three-class task (positive, negative, and neutral) based on daily life contexts. For example, study focus was labeled neutral/mildly positive; distraction, neutral/mildly negative; physical activity, positive arousal; and public speaking or work stress, negative. We improved emotion recognition by fusing rPPG signals and EEG data [], comparing three approaches: Original (unaligned data), Sinkhorn Fusion (using Sinkhorn-based optimal transport), and Greenkhorn Fusion (using Greenkhorn optimization).
Figure 5a shows all models improved accuracy early in training. Sinkhorn and Greenkhorn Fusions converged faster than the unaligned baseline, and after 20 epochs, they outperformed it. Greenkhorn Fusion reached a slightly higher peak accuracy and was more stable. All models rapidly reduced loss initially and then stabilized as shown in Figure 5b. Although the original model achieved a competitive final loss, Greenkhorn fusion converged more stably with lower average loss in later epochs, enhancing both classification performance and training robustness. These results show that optimal transport-based alignment—especially Greenkhorn Fusion—improves accuracy and stability in multimodal emotion recognition systems using rPPG and EEG, yielding more reliable emotion detection for wearable applications.
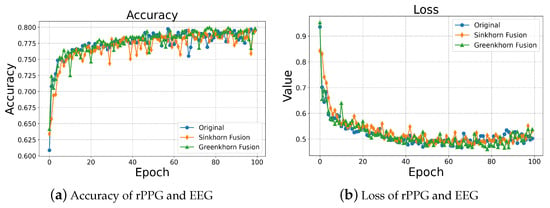
Figure 5.
Multimodal physiological signals integrating rPPG and EEG.
6. Efficiency Evaluation Across Models
To evaluate the practical deployment potential of the proposed Mamba-LNN-Greenkhorn model, we conducted a comprehensive comparison of inference speed, computational complexity, and parameter count across multiple state-of-the-art models. Table 9 summarizes the results.

Table 9.
Comparison of inference speed, computational complexity, and parameter count across different models.
As shown in Table 9, Mamba-LNN-Greenkhorn achieves the fastest inference speed of 1.15 ms per sample, outperforming models such as GLIFCVT and MViT (both 1.3 ms) and nearly doubling the speed of BEiT and ViT (2.5 ms). This efficiency renders it suitable for real-time deployment in latency-sensitive applications, including human–computer interaction, affective computing, and healthcare systems, where rapid response is critical. In terms of computational complexity, Mamba-LNN-Greenkhorn requires only 1.18 GFLOPs, substantially lower than large-scale models such as BEiT and ViT (16.86 GFLOPs) and even lower than GLIFCVT (3.71 GFLOPs). The reduced complexity enables deployment on edge devices and mobile platforms with limited computational resources while minimizing power consumption without sacrificing processing efficiency. Moreover, the parameter count of Mamba-LNN-Greenkhorn is only 8.9 M, considerably smaller than BEiT/ViT (85 M) and ConvNeXt-V2/SwinViT (27 M). The compact architecture reduces memory and bandwidth requirements, facilitates lightweight training and inference, and ensures scalability for real-world applications where storage and transmission resources are constrained. Overall, the combination of ultra-fast inference, low computational complexity, and compact parameterization demonstrates that Mamba-LNN-Greenkhorn is highly suitable for practical deployment in real-time, resource-constrained, and user-facing systems, providing both efficiency and usability without compromising recognition performance.
7. Discussion
In our experiments, we employed the AdamW optimizer with an initial learning rate range of –, a weight decay of , and a batch size of 64. The learning rate was scheduled using the CosineAnnealingWarmRestarts strategy with parameters and . Each model was trained for 100 epochs, and the SS-Conv-LNN-SSM backbone was configured with depths of and feature dimensions of . To mitigate overfitting, we adopted the following regularization strategies:
- Dropout with a rate of applied to both the classifier and LiquidCell1D.
- DropPath, linearly increased from 0.2 to 0.3 across SS-Conv-LNN-SSM blocks.
- Weight decay employed as L2 regularization.
- Data augmentation during training, including Resize(256) → RandomCrop(224), RandomHorizontalFlip (p = 0.5), RandomRotation (±15°), and ColorJitter; validation utilized only resizing and normalization.
- Gradient clipping with a threshold of max_norm = 1.0.
- Adaptive learning rate decay implemented via ReduceLROnPlateau (factor = 0.5, patience = 5).
For statistical robustness, we repeated each experiment several times with different random seeds and reported mean ± standard deviation and 95% confidence intervals. On the rPPG+EEG dataset, the proposed model achieved F1 = (95% CI: 0.770–0.813), MAE = (95% CI: 0.253–0.287), Corr = (95% CI: 0.617–0.664), and accuracy = (95% CI: 0.789–0.805). Paired t-tests against baselines showed medium-to-large effect sizes (e.g., ), confirming that the performance gains are statistically stable and significant.
The Sinkhorn algorithm employs entropic regularization for smoothing discrete optimal transport (OT) problems. In high dimensions, a fixed oversmooths the transport plan, dispersing mass over many low-probability matches and weakening key signals. Greenkhorn outperforms Sinkhorn for multimodal alignment. Greenkhorn adapts by selectively updating the row or column with the largest error, concentrating on critical semantic correspondences rather than uniformly updating all entries. This targeted approach yields sharper, sparser alignment maps with fewer iterations, especially when small regularization is needed. Additionally, by prioritizing imbalanced or noisy rows/columns, Greenkhorn reduces the adverse effects of weak modalities, resulting in more robust gradients and better downstream performance. In the coarse-grained three-class task, emotions are labeled as positive, negative, and neutral, providing clear cues for multimodal fusion and accuracy. In contrast, the fine-grained seven-class task distinguishes nuanced emotions (e.g., anger, disgust, sadness, and fear), leading to overlapping signals that complicate alignment and increase noise and imbalance. Although SALM excels in multimodal emotion recognition, its reliance on EEG spectrograms, facial, speech, and text heatmaps—and the extensive entropy-regularized OT alignment required—creates bottlenecks in training time and memory for large datasets. Additionally, Liquid-Mamba struggles with non-grid data. Future work aims to enhance SALM’s efficiency and adaptability for real-time, resource-constrained environments through memory optimization by developing efficient OT alignment to reduce memory overhead; adaptive scanning by creating techniques for irregular non-grid data; and enhanced interpretability by improving model transparency using visualization and attention heatmaps.
8. Conclusions
This study proposes the SALM multimodal emotion recognition framework, which integrates Mamba and Liquid Neural Networks via a sparsity-aware fusion architecture. EEG spectrograms are extracted with STFT, while features from facial images, videos, speech, and text are aligned using Sinkhorn and Greenkhorn optimal transport. Mamba’s sequence modeling and LNN’s adaptability combine to enhance accuracy and resilience to noise. SALM offers dynamic cross-modality adaptation and effective long-range dependency modeling, though high OT matrix memory usage and Mamba’s directional scanning on non-grid data need further research. Future work will focus on memory-efficient OT alignment, adaptive scanning for irregular structures, and improved interpretability.
Author Contributions
Conceptualization, G.C., D.Z. and W.Y.; Methodology, G.C., Y.L., D.Z. and W.Y.; Software, G.C., Y.L., Z.M. and C.X.; Validation, Y.L., Z.M. and C.X.; Formal analysis, G.C., D.Z. and W.Y.; Investigation, G.C., Y.L., D.Z., W.Y., Z.M. and C.X.; Resources, Y.L., D.Z., W.Y., Z.M. and C.X.; Data curation, Y.L., W.Y., Z.M. and C.X.; Writing—original draft, G.C. and Y.L.; Writing—review & editing, D.Z.; Visualization, Y.L., Z.M. and C.X.; Supervision, D.Z. and W.Y.; Project administration, G.C. and D.Z.; Funding acquisition, G.C., D.Z. and W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62173353); the Special Project in Key Fields of Guangdong Province Universities and Colleges (2023ZDZX4040 and 2021ZDZX1062); The Guangzhou Municipal Science and Technology Program Project (Key R&D Program) (No.: 2025B04J0005); The Guangzhou Intelligent Education Technology Collaborative Innovation Center Construction Project (No.: 2023B04J0004). Digital Quality Course Construction Project: Software Engineering Online Offline Blended Course (PX-117251592). The authors would like to express their sincere gratitude to Zemin Zhong, Shijin Lin, Zhuoxian Qian and Xinyi Ye for their valuable assistance in conducting the experiments for this study.
Data Availability Statement
The data presented in this study are openly available in Zenodo at DOI 10.5281/zenodo.16525211.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, Q.; Zhang, M.; Tang, Y.; Huang, Z. Att-Sinkhorn: Multimodal Alignment with Sinkhorn-based Deep Attention Architecture. In Proceedings of the 2023 28th International Conference on Automation and Computing (ICAC), Birmingham, UK, 30 August–1 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, J.; Yang, D.; Wei, K. Improved Complexity Analysis of the Sinkhorn and Greenkhorn Algorithms for Optimal Transport. arXiv 2023, arXiv:2305.14939. [Google Scholar] [CrossRef]
- Liu, T.; Wang, M.; Yang, B.; Liu, H.; Yi, S. ESERNet: Learning spectrogram structure relationship for effective speech emotion recognition with swin transformer in classroom discourse analysis. Neurocomputing 2025, 612, 128711. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, C.; Deng, Y.; Xie, B.; Liu, T.; Li, Y.F. TransIFC: Invariant Cues-Aware Feature Concentration Learning for Efficient Fine-Grained Bird Image Classification. IEEE Trans. Multimed. 2025, 27, 1677–1690. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, Q.; Zhang, C.; Zhu, J.; Liu, T.; Zhang, Z.; Li, Y.F. MMATrans: Muscle Movement Aware Representation Learning for Facial Expression Recognition via Transformers. IEEE Trans. Ind. Inform. 2024, 20, 13753–13764. [Google Scholar] [CrossRef]
- Zhan, J.; Cai, M.; Li, Q. Fuzzy clustering-based three-way asynchronous consensus for identifying manipulative and herd behaviors. IEEE Trans. Fuzzy Syst. 2025. Early Access. [Google Scholar] [CrossRef]
- Zhu, C.; Ma, X.; Ding, W.; Pedrycz, W.; Zhan, J. Long-term prediction model for fuzzy granular time series based on trend filter decomposition and ensemble learning. IEEE Trans. Cybern. 2025. Early Access. [Google Scholar] [CrossRef]
- Yue, Y.; Li, Z. Medmamba: Vision mamba for medical image classification. arXiv 2024, arXiv:2403.03849. [Google Scholar] [CrossRef]
- Ayoub, O.; Andreoletti, D.; Knapińska, A.; Goścień, R.; Lechowicz, P.; Leidi, T.; Giordano, S.; Rottondi, C.; Walkowiak, K. Liquid Neural Network-based Adaptive Learning vs. Incremental Learning for Link Load Prediction amid Concept Drift due to Network Failures. arXiv 2024, arXiv:2404.05304. [Google Scholar] [CrossRef]
- Jia, Z.; Lin, Y.; Wang, J.; Feng, Z.; Xie, X.; Chen, C. HetEmotionNet: Two-Stream Heterogeneous Graph Recurrent Neural Network for Multi-modal Emotion Recognition. arXiv 2021, arXiv:abs/2108.03354. Available online: https://arxiv.org/abs/2108.03354 (accessed on 10 September 2025).
- Ai, W.; Shou, Y.; Meng, T.; Li, K. DER-GCN: Dialog and Event Relation-Aware Graph Convolutional Neural Network for Multimodal Dialog Emotion Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4908–4921. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Liu, K.; Wu, W.; Hu, F.; Yu, H.; Wang, G. Dynamic Emotion-Dependent Network With Relational Subgraph Interaction for Multimodal Emotion Recognition. IEEE Trans. Affect. Comput. 2025, 16, 712–725. [Google Scholar] [CrossRef]
- Shi, W.; Chen, X.; Yao, B.; Wen, Y.; Sheng, B. Identity and Modality Attributes Driven Multimodal Fusion Networks for Emotion Recognition in Conversations. IEEE Trans. Multimed. 2025, 27, 4361–4371. [Google Scholar] [CrossRef]
- Lu, N.; Han, Z.; Tan, Z. A Hypergraph Based Contextual Relationship Modeling Method for Multimodal Emotion Recognition in Conversation. IEEE Trans. Multimed. 2025, 27, 2243–2255. [Google Scholar] [CrossRef]
- Chen, L.; Gan, Z.; Cheng, Y.; Li, L.; Carin, L.; Liu, J. Graph Optimal Transport for Cross-Domain Alignment. arXiv 2020, arXiv:2006.14744. [Google Scholar] [CrossRef]
- Yuan, S.; Bai, K.; Chen, L.; Zhang, Y.; Tao, C.; Li, C.; Wang, G.; Henao, R.; Carin, L. Weakly supervised cross-domain alignment with optimal transport. arXiv 2020, arXiv:2008.06597. [Google Scholar] [CrossRef]
- Lee, J.; Dabagia, M.; Dyer, E.L.; Rozell, C.J. Hierarchical Optimal Transport for Multimodal Distribution Alignment. arXiv 2019, arXiv:1906.11768. [Google Scholar] [CrossRef]
- Zhou, Y.; Fang, Q.; Feng, Y. CMOT: Cross-modal Mixup via Optimal Transport for Speech Translation. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Toronto, ON, Canada, 9–14 July 2023; Rogers, A., Boyd-Graber, J., Okazaki, N., Eds.; ACL: Austin, TX, USA, 2023; pp. 7873–7887. [Google Scholar] [CrossRef]
- Liu, H.; Song, Y.; Liu, T.; Chen, L.; Zhang, Z.; Yang, X.; Xiong, N.N. TransSIL: A Silhouette Cue-Aware Image Classification Framework for Bird Ecological Monitoring Systems. IEEE Internet Things J. 2025. Early Access. [Google Scholar] [CrossRef]
- Liu, H.; Liu, T.; Chen, Y.; Zhang, Z.; Li, Y.F. EHPE: Skeleton Cues-Based Gaussian Coordinate Encoding for Efficient Human Pose Estimation. IEEE Trans. Multimed. 2024, 26, 8464–8475. [Google Scholar] [CrossRef]
- Deng, Y.; Ma, J.; Wu, Z.; Wang, W.; Liu, H. DSR-Net: Distinct selective rollback queries for road cracks detection with detection transformer. Digit. Signal Process. 2025, 164, 105266. [Google Scholar] [CrossRef]
- Li, A.; Wu, M.; Ouyang, R.; Wang, Y.; Li, F.; Lv, Z. A Multimodal-Driven Fusion Data Augmentation Framework for Emotion Recognition. IEEE Trans. Artif. Intell. 2025, 6, 2083–2097. [Google Scholar] [CrossRef]
- Xu, M.; Shi, T.; Zhang, H.; Liu, Z.; He, X. A Hierarchical Cross-Modal Spatial Fusion Network for Multimodal Emotion Recognition. IEEE Trans. Artif. Intell. 2025, 6, 1429–1438. [Google Scholar] [CrossRef]
- Lin, X.; Wei, X.; Zhao, S.; Li, Y. Vascular Skeleton Deformation Evaluation Based on the Metric of Sinkhorn Distance. In Proceedings of the 2024 IEEE International Symposium on Biomedical Imaging (ISBI), Athens, Greece, 27–30 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Peyré, G.; Cuturi, M. Computational Optimal Transport: With Applications to Data Science. Found. Trends Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- He, L.; Zhang, H. Large-Scale Graph Sinkhorn Distance Approximation for Resource-Constrained Devices. IEEE Trans. Consum. Electron. 2024, 70, 2960–2969. [Google Scholar] [CrossRef]
- Gossi, F.; Pati, P.; Chouvardas, P.; Martinelli, A.L.; Kruithof-de Julio, M.; Rapsomaniki, M.A. Matching single cells across modalities with contrastive learning and optimal transport. Briefings Bioinform. 2023, 24, bbad130. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Xing, S.; Li, S.; Zhao, Y.; Tu, Z. DecAlign: Hierarchical Cross-Modal Alignment for Decoupled Multimodal Representation Learning. arXiv 2025, arXiv:cs.CV/2503.11892. [Google Scholar]
- Wang, S.; Stavrou, P.A.; Skoglund, M. Generalized Talagrand Inequality for Sinkhorn Distance using Entropy Power Inequality. In Proceedings of the 2021 IEEE Information Theory Workshop (ITW), Kanazawa, Japan, 17–21 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Wang, X.; Yamada, M.; Yang, Y. Bilaterally Normalized Scale-Consistent Sinkhorn Distance for Few-Shot Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11475–11485. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Rahman, H.A. DeepSD: Sinkhorn Distance Calculated by Different Methods for Few-Shot Learning. In Proceedings of the 2025 7th International Conference on Software Engineering and Computer Science (CSECS), Taicang, China, 21–23 March 2025; pp. 1–9. [Google Scholar] [CrossRef]
- Lu, X.; Shen, P.; Tsao, Y.; Kawai, H. Hierarchical Cross-Modality Knowledge Transfer with Sinkhorn Attention for CTC-Based ASR. In Proceedings of the ICASSP 2024 - 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 13116–13120. [Google Scholar] [CrossRef]
- Tong, Z.; Song, Y.; Wang, J.; Wang, L. VideoMAE: Masked Autoencoders are Data-Efficient Learners for Self-Supervised Video Pre-Training. arXiv 2022, arXiv:cs.CV/2203.12602. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Baevski, A.; Zhou, H.; Mohamed, A.; Auli, M. wav2vec 2.0: A Framework for Self-Supervised Learning of Speech Representations. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, BC, Canada, 6–12 December 2020; 2020; Volume 33, pp. 12449–12460. [Google Scholar]
- Bagher Zadeh, A.; Liang, P.P.; Poria, S.; Cambria, E.; Morency, L.P. Multimodal Language Analysis in the Wild: CMU-MOSEI Dataset and Interpretable Dynamic Fusion Graph. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018; Gurevych, I., Miyao, Y., Eds.; ACL: Austin, TX, USA, 2018; pp. 2236–2246. [Google Scholar] [CrossRef]
- Zadeh, A.; Chen, M.; Poria, S.; Cambria, E.; Morency, L.P. Tensor Fusion Network for Multimodal Sentiment Analysis. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017. [Google Scholar]
- Liu, Z.; Shen, Y.; Lakshminarasimhan, V.B.; Liang, P.P.; Zadeh, A.B.; Morency, L.P. Efficient Low-rank Multimodal Fusion With Modality-Specific Factors. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018; pp. 2247–2256. [Google Scholar]
- Zadeh, A.; Liang, P.P.; Mazumder, N.; Poria, S.; Cambria, E.; Morency, L.P. Memory fusion network for multi-view sequential learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Wang, Y.; Shen, Y.; Liu, Z.; Liang, P.; Zadeh, A.; Morency, L.P. Words Can Shift: Dynamically Adjusting Word Representations Using Nonverbal Behaviors. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 7216–7223. [Google Scholar]
- Tsai, Y.H.H.; Bai, S.; Liang, P.P.; Kolter, J.Z.; Morency, L.P.; Salakhutdinov, R. Multimodal transformer for unaligned multimodal language sequences. In Proceedings of the conference. Association for Computational Linguistics, Meeting, NIH Public Access, Florence, Italy, 28 July–2 August 2019; Volume 2019, p. 6558. [Google Scholar]
- Tsai, Y.H.H.; Ma, M.Q.; Yang, M.; Salakhutdinov, R.; Morency, L.P. Multimodal routing: Improving local and global interpretability of multimodal language analysis. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, NIH Public Access, Virtual, 8–12 November 2020; Volume 2020, p. 1823. [Google Scholar]
- Li, Q.; Gkoumas, D.; Lioma, C.; Melucci, M. Quantum-inspired multimodal fusion for video sentiment analysis. Inf. Fusion 2021, 65, 58–71. [Google Scholar] [CrossRef]
- Zhu, A.; Hu, M.; Wang, X.; Yang, J.; Tang, Y.; An, N. Multimodal Invariant Sentiment Representation Learning. In Proceedings of the Findings of the Association for Computational Linguistics, Vienna, Austria, 14–18 July 2025; Che, W., Nabende, J., Shutova, E., Pilehvar, M.T., Eds.; ACL: Austin, TX, USA, 2025; pp. 14743–14755. [Google Scholar] [CrossRef]
- Rahman, W.; Hasan, K.; Lee, S.; Zadeh, A.A.B.; Mao, C.; Morency, L.P.; Hoque, E. Integrating Multimodal Information in Large Pretrained Transformers. In Proceedings of the Meeting of the Association for Computational Linguistics, Virtual, 5–10 July 2020. [Google Scholar]
- Yuan, Z.; Li, W.; Xu, H.; Yu, W. Transformer-based Feature Reconstruction Network for Robust Multimodal Sentiment Analysis. In Proceedings of the the 29th ACM International Conference on Multimedia, Virtual, 20–24 October 2021; pp. 4400–4407. [Google Scholar]
- Mai, S.; Zeng, Y.; Hu, H. Multimodal Information Bottleneck: Learning Minimal Sufficient Unimodal and Multimodal Representations. IEEE Trans. Multimed. 2023, 25, 4121–4134. [Google Scholar] [CrossRef]
- Rong, L.; Ding, Y.; Wang, M.; El Saddik, A.; Hossain, M.S. A Multi-Modal ELMo Model for Image Sentiment Recognition of Consumer Data. IEEE Trans. Consum. Electron. 2024, 70, 3697–3708. [Google Scholar] [CrossRef]
- Chlapanis, O.S.; Paraskevopoulos, G.; Potamianos, A. Adapted multimodal bert with layer-wise fusion for sentiment analysis. In Proceedings of the ICASSP 2023–2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Zhang, J.; Wu, X.; Huang, C. AdaMoW: Multimodal sentiment analysis based on adaptive modality-specific weight fusion network. IEEE Access 2023, 11, 48410–48420. [Google Scholar] [CrossRef]
- Lin, R.; Hu, H. Dynamically shifting multimodal representations via hybrid-modal attention for multimodal sentiment analysis. IEEE Trans. Multimed. 2024, 26, 2740–2755. [Google Scholar] [CrossRef]
- Huang, J.; Ji, Y.; Qin, Z.; Yang, Y.; Shen, H.T. Dominant SIngle-Modal Supplementary Fusion (SIMSUF) For Multimodal Sentiment Analysis. IEEE Trans. Multimed. 2024, 26, 8383–8394. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, G.; Zhou, X.; Kim, J.Y.; Zhu, H.; Deng, L. Deep tensor evidence fusion network for sentiment classification. IEEE Trans. Comput. Soc. Syst. 2024, 11, 4605–4613. [Google Scholar] [CrossRef]
- Zhi, Y.; Li, J.; Wang, H.; Chen, J.; Wei, W. A Multimodal Sentiment Analysis Method based on Fuzzy Attention Fusion. IEEE Trans. Fuzzy Syst. 2024, 32, 5886–5898. [Google Scholar] [CrossRef]
- Hu, R.; Yi, J.; Chen, L.; Jin, Z. Graph Reconstruction Attention Fusion Network for Multimodal Sentiment Analysis. IEEE Trans. Ind. Inform. 2025, 21, 297–306. [Google Scholar] [CrossRef]
- Xin, F.; Gong, W.; Shi, T.; Zhong, J.; Li, K.; Gonzàlez, J. Gated Fusion Network with Progressive Modality Enhancement for Sentiment Analysis. IEEE Access 2024, 12, 165810–165821. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Y.; Liu, S.; Tang, B. Shared-private memory networks for multimodal sentiment analysis. IEEE Trans. Affect. Comput. 2022, 14, 2889–2900. [Google Scholar] [CrossRef]
- Mai, S.; Zeng, Y.; Zheng, S.; Hu, H. Hybrid contrastive learning of tri-modal representation for multimodal sentiment analysis. IEEE Trans. Affect. Comput. 2022, 14, 2276–2289. [Google Scholar] [CrossRef]
- Sun, L.; Lian, Z.; Liu, B.; Tao, J. Efficient multimodal transformer with dual-level feature restoration for robust multimodal sentiment analysis. IEEE Trans. Affect. Comput. 2023, 15, 309–325. [Google Scholar] [CrossRef]
- Yao, M.; Hu, J.; Zhou, Z.; Yuan, L.; Tian, Y.; Xu, B.; Li, G. Spike-driven transformer. Adv. Neural Inf. Process. Syst. 2024, 36, 64043–64058. [Google Scholar]
- Iakymchuk, T.; Rosado-Muñoz, A.; Guerrero-Martínez, J.F.; Bataller-Mompeán, M.; Francés-Víllora, J.V. Simplified spiking neural network architecture and STDP learning algorithm applied to image classification. EURASIP J. Image Video Process. 2015, 2015, 4. [Google Scholar] [CrossRef]
- Prasanna, Y.L.; Tarakaram, Y.; Mounika, Y.; Palaniswamy, S.; Vekkot, S. Comparative Deep Network Analysis of Speech Emotion Recognition Models using Data Augmentation. In Proceedings of the 2022 International Conference on Disruptive Technologies for Multi-Disciplinary Research and Applications (CENTCON), Bengaluru, India, 22–23 December 2022; Volume 2, pp. 185–190. [Google Scholar]
- Zhong, P.; Wang, D.; Miao, C. Knowledge-enriched transformer for emotion detection in textual conversations. arXiv 2019, arXiv:1909.10681. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, L.; Sun, C.; Li, S.; Zhu, Q.; Zhou, G. Modeling both Context-and Speaker-Sensitive Dependence for Emotion Detection in Multi-speaker Conversations. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 5415–5421. [Google Scholar]
- Majumder, N.; Poria, S.; Hazarika, D.; Mihalcea, R.; Gelbukh, A.; Cambria, E. Dialoguernn: An attentive rnn for emotion detection in conversations. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 6818–6825. [Google Scholar]
- Shi, Y.; Sun, X. Transformer-Based Potential Emotional Relation Mining Network for Emotion Recognition in Conversation. In Proceedings of the National Conference on Man-Machine Speech Communication, Hefei, China, 15–18 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 238–251. [Google Scholar]
- Makhmudov, F.; Kultimuratov, A.; Cho, Y.I. Enhancing Multimodal Emotion Recognition through Attention Mechanisms in BERT and CNN Architectures. Appl. Sci. 2024, 14, 4199. [Google Scholar] [CrossRef]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Hazarika, D.; Poria, S.; Zadeh, A.; Cambria, E.; Morency, L.P.; Zimmermann, R. Conversational memory network for emotion recognition in dyadic dialogue videos. In Proceedings of the conference. Association for Computational Linguistics, North American Chapter, New Orleans, LA, USA, 1–6 June 2018; Volume 2018, p. 2122. [Google Scholar]
- Mower, E.; Matarić, M.J.; Narayanan, S. A Framework for Automatic Human Emotion Classification Using Emotion Profiles. IEEE Trans. Audio, Speech, Lang. Process. 2011, 19, 1057–1070. [Google Scholar] [CrossRef]
- Zou, H.; Si, Y.; Chen, C.; Rajan, D.; Chng, E.S. Speech Emotion Recognition with Co-Attention based Multi-level Acoustic Information. arXiv 2022, arXiv:cs.SD/2203.15326. [Google Scholar]
- Zhao, Z.; Bao, Z.; Zhang, Z.; Cummins, N.; Wang, H.; Schuller, B.W. Attention-Enhanced Connectionist Temporal Classification for Discrete Speech Emotion Recognition. In Proceedings of the Interspeech, Graz, Austria, 15–19 September 2019; pp. 206–210. [Google Scholar] [CrossRef]
- Tarantino, L.; Garner, P.N.; Lazaridis, A. Self-Attention for Speech Emotion Recognition. In Proceedings of the Interspeech, Graz, Austria, 15–19 September 2019; pp. 2578–2582. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, H.; Zou, J. HGFM: A Hierarchical Grained and Feature Model for Acoustic Emotion Recognition. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 6499–6503. [Google Scholar]
- Nediyanchath, A.; Paramasivam, P.; Yenigalla, P. Multi-Head Attention for Speech Emotion Recognition with Auxiliary Learning of Gender Recognition. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 7179–7183. [Google Scholar]
- Feng, H.; Ueno, S.; Kawahara, T. End-to-End Speech Emotion Recognition Combined with Acoustic-to-Word ASR Model. In Proceedings of the Interspeech, Virtual, 25–29 October 2020; pp. 501–505. [Google Scholar]
- Wang, Y.; Huang, J.; Zhao, Z.; Lan, H.; Zhang, X. Speech Emotion Recognition Using Multi-Scale Global–Local Representation Learning with Feature Pyramid Network. Appl. Sci. 2024, 14, 11494. [Google Scholar] [CrossRef]
- Chowanda, A.; Iswanto, I.A.; Andangsari, E.W. Exploring deep learning algorithm to model emotions recognition from speech. Procedia Computer Science 2023, 216, 706–713. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, H.; Guan, W. Speech Emotion Recognition Using Cascaded Attention Network with Joint Loss for Discrimination of Confusions. Mach. Intell. Res. 2023, 20, 595–604. [Google Scholar] [CrossRef]
- Moine, C.L.; Obin, N.; Roebel, A. Speaker Attentive Speech Emotion Recognition. In Proceedings of the Interspeech, Brno, Czech Republic, 30 August–3 September 2021; pp. 2866–2870. [Google Scholar] [CrossRef]
- Chen, G.; Qian, Z.; Zhang, D.; Qiu, S.; Zhou, R. Enhancing Robustness Against Adversarial Attacks in Multimodal Emotion Recognition With Spiking Transformers. IEEE Access 2025, 13, 34584–34597. [Google Scholar] [CrossRef]
- Bao, H.; Dong, L.; Piao, S.; Wei, F. BEiT: BERT Pre-Training of Image Transformers. In Proceedings of the ICLR 2022, Virtual, 25–29 April 2022. [Google Scholar]
- Woo, S.; Debnath, S.; Hu, R.; Chen, X.; Liu, Z.; Kweon, I.S.; Xie, S. ConvNeXt V2: Co-Designing and Scaling ConvNets with Masked Autoencoders. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Piscataway, NJ, USA, 18–22 June 2023; pp. 16133–16142. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; An kumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. In Proceedings of the 35th International Conference on Neural Information Processing Systems (NeurIPS), Red Hook, NY, USA, 6–14 December 2021; p. 924. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Piscataway, NJ, USA, 11–17 October 2021; pp. 9992–10002. [Google Scholar]
- Wu, B.; Xu, C.; Dai, X.; Wan, A.; Zhang, P.; Yan, Z.; Tomizuka, M.; Gonzalez, J.; Keutzer, K.; Vajda, P. Visual Transformers: Token-Based Image Representation and Processing for Computer Vision. arXiv 2020, arXiv:2006.03677. [Google Scholar] [CrossRef]
- Li, H.; Sui, M.; Zhao, F.; Zha, Z.; Wu, F. MVT: Mask Vision Transformer for Facial Expression Recognition in the Wild. arXiv 2021, arXiv:2106.04520. [Google Scholar] [CrossRef]
- Xue, F.; Wang, Q.; Guo, G. TransFER: Learning Relation-Aware Facial Expression Representations with Transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Piscataway, NJ, USA, 11–17 October 2021; pp. 3581–3590. [Google Scholar]
- Wen, Z.; Lin, W.; Wang, T.; Xu, G. Distract Your Attention: Multi-Head Cross Attention Network for Facial Expression Recognition. Biomimetics 2023, 8, 199. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Qian, Z.; Qiu, S.; Zhang, D.; Zhou, R. A Gated Leaky Integrate-and-Fire Spiking Neural Network Based on Attention Mechanism for Multi-modal Emotion Recognition. Digit. Signal Process. 2025, 165, 105322. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).