Optimizing SPHINCS+ for Low-Power Devices

Abstract

Different optimization techniques for the SHAKE variant of SPHINCS+ are explored on an FPGA with the means to find a power-efficient model for resource-constrained devices. This work explores multiple hashing implementations, such as registering inputs and directly feeding data to hashing units, as well as different variations in hashing permutations per clock cycle. The design is evaluated based on resource requirements, the signature generation rate, and both static and active power consumption. This design shows a decrease in energy consumed per signature by 20% to 30% compared to other state-of-the-art SPHINCS+ implementations, while only using 12–14k lookup tables (LUTs), depending on the SPHINCS+ variant. Moreover, an amendment is proposed to the SPHINCS+ specification that allows for decreased processing time and memory consumption while maintaining the security level and non-deterministic properties. This is accomplished by rearranging the inputs in the random oracle model.

1. Introduction

Quantum computing (QC) is faster than traditional digital computing in a variety of spaces, ranging from cosmology to physics and genomic analysis. This is due to three properties unique to quantum computing. One of these properties, superposition, unlike binary-encoded computing, allows a quantum bit to concurrently exist in multiple states. Secondly, quantum entanglement is the correlation between two or more qubits. This is when the state of one qubit directly influences the state of two or more other qubits, regardless of the physical distance between them. Thirdly, interference is also leveraged by quantum computing, or the wave-like nature of quantum particles, in which subatomic particles influence themselves and other particles while in a state of superposition.

Researchers are still finding applications where QC can improve processing time over digital computers. However, not all opportunities provided by quantum computing enhance society. In fact, QC can be implemented to directly attack modern data security. There are two algorithms available to QC that directly undermine the security promises granted by modern cryptographic methods.

The first of these algorithms, Grover’s unsorted database search, reduces the time complexity for a database search from $O\left(N\right)$ to $O\left(\sqrt{N}\right)$ [1]. This is carried out by starting with a superposition of all possible search states. We then amplify the amplitude of the state containing the item we are searching for by iteratively applying the quantum Grover operator. Grover’s algorithm is particularly powerful in finding a cryptographic key. For example, when applied to the Advanced Encryption Standard (AES) 128, Grover’s algorithm can take approximately $2^{64}$ quantum AES queries, compared to the $2^{127}$ classical queries required for a brute-force search [2].

The second algorithm by Peter Shor is designed to quickly solve factorization of large numbers and discrete logarithms [3]. On a classical computer, the method for fast factorization is the generalized number field sieve, which has a time complexity of $O\left(e^{\left(1.9log{\left(N\right)}^{1/3}\right)}\left(log{\left(log\left(N\right)\right)}^{2/3}\right)\right)$ [4]. Alternatively, Shor’s algorithm can factor large numbers in $O\left(log{\left(N\right)}^3\right)$ time [5]. This is a significant speedup, especially when applied to large numbers with more than 2000 bits. Shor’s algorithm is considered to be more impactful than Grover’s algorithm, as it can be applied to asymmetric cryptographic methods such as the Rivest–Shamir–Adleman (RSA) algorithm and elliptic curve cryptography (ECC).

These two quantum algorithms threaten modern data security, which impacts all corners of society. If modern cryptographic methods, such as RSA and AES, were to be broken, things such as financial information, military intelligence, satellite communications, and medical data are all at risk of being exposed. A quantum computer capable of breaking today’s standards is referred to as a cryptographically relevant quantum computer (CRQC).

Luckily, at the time of this writing, a CRQC is not yet in existence. To best estimate the timeline for the availability of a CRQC, the quantum threat timeline report from the Global Risk Institute weighs expert opinions from both academic and professional institutions. The 2024 report illustrates that current industry experts believe a CRQC will be realistically available within the next 15 years [6].

Unfortunately, there are some pitfalls that go with this prediction. The first is that this timeline assumes that novel algorithms more powerful than Grover’s and Shor’s will not be developed. Researchers are actively evaluating new methods for attacking security and improving currently known algorithms [7,8,9], and it is difficult to predict when a quantum algorithm may be released that can offer further speedup in cracking modern cryptography.

The second pitfall is that one may assume that for the next 15 years, their data are safe from quantum attacks. However, data are still vulnerable to harvest-now, attack-later attacks. Once encrypted data are stored in a database, they can be broken into when a CRQC is available to the entity that harvested the data. This is an issue for data with a lifetime that exceeds the 15-year prediction, such as medical and financial records.

For this reason, it is essential that we migrate to quantum-safe cryptography, known as post-quantum cryptography (PQC), as soon as possible. At the time of this writing, the National Institute of Standards and Technology (NIST) has accepted four PQC standards, with three of them published [10]. The three published standards include one key-encapsulation mechanism, CRYSTALS-Kyber, published by NIST as ML-KEM [11]. The two other published standards are signature methods, with one being CRYSTALS-Dilithium, published under ML- DSA by NIST [12], and SPHINCS+, published under SLH-DSA by NIST [13].

While improvements in quantum resilience can be achieved through these algorithms, a greater cost (in both time complexity and power consumption) is incurred compared to conventional encryption methods such as AES and RSA. For this reason, it is imperative that new methods, utilizing both hardware and software, be explored to reduce the time to execute an algorithm and the associated power consumption.

1.1. IoT Security

One form of technology that is either of the lowest priority for security or overlooked altogether is the Internet of things (IoT) devices. These pieces of technology come in various forms, ranging from wearables to remote sensors, medical implants, and smartphones and tablets. It was estimated that there were over 125 billion IoT devices in 2023 [14].

These devices, by definition, are connected to the Internet, often through a wide-area network (WAN), wireless local area network (WLAN), or local area network (LAN). Further, as these devices are typically battery-powered, they are resource-constrained to save on energy usage and reduce their form factor. These two properties combined make them the perfect target for an adversary to break into a network [15,16].

The lack of resource availability makes transitioning IoT devices to the PQC era a daunting task. This is especially true since decreasing resources leads to an increase in run-time, and therefore, power consumption. Further methods must be introduced to address this need and secure IoT devices, and, in turn, other connected devices in a network [17].

1.2. Contributions

With the means to address the need for a low-power PQC solution, we design an exhaustive implementation for SPHINCS+ that aims to balance power consumption and execution time for resource-constrained devices. Within our design, we propose an amendment to the SPHINCS+ specification that will allow for the reduction in memory overhead. Further, we evaluate the following new methods that are yet to be tested on SPHINCS+:

• Parallelizing hash functions, with configurable rounds between clock cycles;
• Multiple implementations of SHAKE-256 and its impact on performance;
• An Advanced Extensible Interface (AXI) Stream-compliant plain-text input and ciphertext output.

The rest of the paper is organized as follows: Section 2 covers the current state-of-the-art works in PQC. In Section 3, we provide the necessary background for understanding SPHINCS+. Section 4 describes our implementation methods. Section 5 discusses our proposed amendment to SPHINCS+. In Section 6, we evaluate the impact of our design. Finally, Section 7 concludes the paper.

2. Background

When evaluating PQC signature algorithms, there are three possible directions to follow if one wants to abide by the NIST certifications: CRYSTALS-Dilithium, Falcon, and SPHINCS+. Further, a hardware design could optimize one of these three algorithms for either low power, low area, high throughput, or a balance between two or more of these properties.

Designs pertaining to IoT will typically focus on power optimization, as lower power usage directly correlates with longer battery life. Another, but lesser, priority is area optimization. Since IoT devices are often presented as either sensors or wearables, minimizing the form factor is also important. We evaluate current state-of-the-art PQC implementations that focus on these two areas. Within this section, we compare the state-of-the-art implementations for the three NIST-approved digital signature algorithms, with a focus on power and area reduction.

Despite being different algorithms, the three signature schemes can all be classified by a general security level of 1–5. For each level, the security of a PQC algorithm is defined by the computational resources required of a quantum computer to break the algorithm, relative to the classical resources required to break modern cryptography. These varying levels of security are defined as follows:

• Level 1: The algorithm is as secure as AES-128 is against classical brute-force attacks. This is suitable for applications with low security requirements, or where there is only a need for short-term data protection, such as firmware updates and basic communication between IoT devices and the cloud.
• Level 2: An attacker would need quantum resources equivalent to the classical resources required to identify a collision in SHA-256. This is a moderate increase in security over Level 1. Algorithms with this security level could be applied to non-critical personal data, such as basic health metrics.
• Level 3: The algorithm is as difficult to break using a quantum computer as AES-192 is using classical methods. This security level is targeted towards applications requiring a middle-to-long-term level of security. Level 3 security can be applied to ensure the secure communication of operational data, like performance metrics, in industrial IoT (IIoT) factory environments.
• Level 4: Someone looking to break this level of security would require computational resources similar to a classical computer looking to identify a collision in SHA-384. This level offers a security guarantee suitable for more sensitive data. Level 4 can be utilized in IoT gateways, protecting control signals for critical infrastructure.
• Level 5: This level of algorithm has a quantum security level equivalent to AES-256, resisting classical attacks. This provides the highest level of security assurances and is suitable for critical infrastructure or highly sensitive data. This security level would be expected in infrastructure such as nuclear power plants or defense systems, where security is the highest priority.

The security requirements for each application are up to the developers to decide, as higher levels of security will lead to more resource requirements, larger signatures, higher power consumption, and prolonged signature generation time. As we illustrate later in this section, these tradeoffs and the varying impact from increased security are both algorithm- and design-dependent.

Further, we can compare each of the three algorithms by evaluating the standardized public and private key sizes, signature sizes, and run-time in clock cycles. The three algorithms were selected in part because they each optimize a unique aspect of signature generation. For example, SPHINCS+ has the smallest key size; Falcon has the smallest signature size; and finally, Dilithium has the fastest run-time. We summarize key and signature size in

Table 1. Key and signature generation time for the three NIST-approved digital signature algorithms. The SPHINCS+ statistics are for the SHAKE-256 variant. More options are available for each algorithm, and these can be found in their respective standardization documents.

Digital Signature	Security	PK	SK	Signature
Algorithm	Level	B	B	B
Dilithium 2	1	1312	2528	2420
Dilithium 5	5	2592	4864	4595
Falcon 512	1	897	1271	690
Falcon 1024	5	1793	2305	1330
SPHINCS+ 128 small	1	32	64	7856
SPHINCS+ 192 small	3	32	64	16,224
SPHINCS+ 256 small	5	64	128	29,792
SPHINCS+ 128 fast	1	32	64	17,088
SPHINCS+ 192 fast	3	32	64	35,664
SPHINCS+ 256 fast	5	64	128	49,856

, while run-time is presented in

Table 2. Comparison of the run-time for each of the variants for the three NIST-approved digital signature algorithms. The SPHINCS+ statistics are for the SHAKE-256 variant. More options are available for each algorithm, and these can be found in their respective standardization documents.

Digital Signature	Security	Key Gen	Sign	Verify
Algorithm	Level	Cycles	Cycles	Cycles
Dilithium 2	1	1.4 M	6.2 M	1.5 M
Dilithium 5	5	3.1 M	8.5 M	3.8 M
Falcon 512	1	198 M	38 M	0.47 M
Falcon 1024	5	481 M	83 M	0.98 M
SPHINCS+ 128 small	1	616 M	4.7 B	4.8 M
SPHINCS+ 192 small	1	893 M	8.1 B	6.5 M
SPHINCS+ 256 small	5	594 B	7.1 B	10 M
SPHINCS+ 128 fast	1	9.7 M	240 M	13 M
SPHINCS+ 192 fast	1	14.2 M	387 M	20 M
SPHINCS+ 256 fast	5	37 M	764 M	20 M

.

2.1. CRYSTALS-Dilithium

Dilithium, from the CRYSTALS package, is one of three NIST-certified signature algorithms. Dilithium is based on the modular learning with errors (M-LWE) problem. Given the algorithm’s reliance on modular arithmetic, the numerical theoretical transform (NTT), and linear algebra, it is difficult to minimize the number of digital signal processors (DSPs) in the design without significantly hindering performance. This is due to DSPs being able to handle complex arithmetic faster than logic gates, at the expense of higher power requirements.

In [18], Wu et al. attempted to tackle a low-area Field Programmable Gate Array (FPGA) implementation of Dilithium. Their design supports NIST security levels 2, 3, and 5, with each requiring at least 15 block RAM (BRAM), 8 DSPs, and 20k–29k lookup tables (LUTs) depending on the security level. They were able to reduce their overall memory footprint by calculating the A polynomial matrix on the fly, which removed the requirement to store the entire polynomial in memory. Further, they optimized their design for throughput by implementing subcomponents that were each capable of processing up to four coefficients in parallel.

Another Dilithium implementation by Zhao et al. utilized segmented pipelining to reduce the memory footprint of the design while increasing throughput at the expense of increased gate count [19]. They also experimented with the number of NTT modules used in the design and impact on throughput. While they tried to balance area and throughput, their design resulted in the use of 11 BRAMS, 10 DSPs, and 30k LUTs.

In one additional design for Dilithium, Wang et al. [20] were able to perform the entirety of Dilithium with a 21K LUT count, providing up to Level 5 security. Their hardware architecture utilized similar amounts of DSPs and BRAM, with 10 and 28, respectively. They were able to achieve these numbers by leveraging the on-board ARM processor on a Zync-7000 for packing and unpacking both keys and signatures at the beginning and end of the signing process.

2.2. Falcon

The fast Fourier lattice-based compact signatures of NTRU or Falcon were designed to be a compact signature scheme, with the smallest signature size out of all the NIST-approved signature algorithms. At the time of this writing, Falcon is approved by NIST, but the formal Federal Information Processing Standard (FIPS) has yet to be released.

The benefit of a small signature, however, comes with a significant caveat. In order to minimize signature size while maintaining a significant level of security, Falcon relies on the fast Fourier transform for sampling and, therefore, must support floating-point arithmetic. This is a major disadvantage of resource-constrained hardware, where the gate count is paramount, as floating-point arithmetic will always be more costly to implement than either integer or fixed-point arithmetic.

Because of the complexity of Falcon, there are not many pure hardware implementations. A recently published design by Lee et al. targets low-end embedded devices by utilizing hardware/software co-design. Their implementation, which targets 28 nm and 45 nm technologies, integrates what Lee refers to as “Common Operation Blocks” (COBs), which break down the Falcon algorithm into manageable functions. The COBs are implemented in hardware, while functions that cannot be implemented in the COBs are calculated via software [21].

A high-level synthesis (HLS) approach was taken over the conventional register-transfer level (RTL) by Schmid et al. HLS allows for the coding of hardware in a C-like format, where a compiler can then generate a bitstream for an FPGA. This can be beneficial for a complex algorithm such as Falcon. In Schmid’s work, small modifications were made to the Falcon algorithm, such as unrolling recursive loops, to allow for an efficient hardware implementation. Their final design results in a 45k LUT/41k flip flop (FF) requirement, as well as 182 DSPs and 37 BRAMs, for a single signature. Further, key generation requires over 100k LUTs, 91K FFs, and over 1.2k DSPs. This large footprint shows that the underlying complexity of Falcon makes it non-optimal for resource-constrained devices [22].

2.3. SPHINCS+

SPHINCS+, the final of the three PQC signature algorithms, differs from the other two in that it is hash-based rather than lattice-based. Derived from the non-PQC secure algorithm SPHINCS-256 [23], SPHINCS+ combines two popular hash schemes: Winternitz one-time signatures (WOTS+) and a forest of random subsets (FORS). The security of these two algorithms is dependent on the underlying hash function, where SPHINCS+ was standardized for use with SHA-2, SHAKE-256, and Haraka.

A study by Berthet et al. aimed to produce a SPHINCS+ design that has a limited footprint for IoT devices. The linear nature of the SPHINCS+ algorithm allowed Berthet to leverage resource sharing, as each hash function for both FORS and WOTS must be computed sequentially. This limits the ability to parallelize the different subfunctions within the algorithm, making resource-sharing a key optimization. Their design allows for 256 bits of security with less than 9k LUTs, less than 6.5k FFs, and only 1 BRAM [24].

Another design by Amiet et al. approaches SPHINCS+ from the perspective of increasing the throughput. Their architecture supports all security levels of SPHINCS+, including both simple and robust variants. For 256-bit security in the Amiet design, there is a resource requirement of approximately 50k LUTs and 75k FFs, but with a signature time of 19.3 ms for the small-signature SPHINCS+ variant [25].

These two implementations show that SPHINCS+ can be designed to be both area-efficient and high-throughput. A separate design, implementing Ascon-Sign [26], a SPHINCS+ derivative algorithm by Magyari et al., attempts to lower resource usage further [27]. The Magyari design utilizes resource sharing, parallel hash functions to reduce run-time, and “pre-digests” to further reduce run-time. The primary difference between SPHINCS+ and Ascon-Sign is that the Ascon-Sign variant relies on the Ascon hash function. The Magyari implementation requires 6.5k LUTs and 5.9k FFs for their 128-bit implementation [28].

We see potential for balancing run-time and resource usage by utilizing principles from the above three implementations. Due to its low mathematical complexity, small key size, low area requirements, and quick run-time, SPHINCS+ is an ideal candidate for IoT digital signatures, provided further optimizations are made.

Among the three NIST-standardized PQC signature schemes, we find SPHINCS+ to be particularly well-suited for IoT environments where area and power consumption are primary constraints. Falcon relies heavily on floating-point arithmetic, which not only increases memory requirements for coefficient storage but also necessitates specialized floating-point units that raise both dynamic and static power. Dilithium, while integer-based, still depends on polynomial arithmetic over lattices and typically benefits from hardware accelerators such as DSPs, which add area and power overhead. In contrast, with SPHINCS+ being hash-based, its hardware building blocks largely reduce to FFs and LUTs, thereby avoiding the need for complex mathematical units. This makes SPHINCS+ an attractive target for low-power, resource-constrained devices, and motivates our focus on optimizing its area and power footprint.

3. Preliminaries

To provide context for the following sections, we describe a high-level overview of the SPHINCS+ algorithm and the SHAKE-256 extendable output function (XOF), as SHAKE-256 is the hash function used in our implementation. We also define the security parameters for SPHINCS+ and the impact on signature size and generation time.

3.1. SHAKE

The secure hashing algorithm (SHA) 3 standard includes SHA3-224, SHA3-256, SHA3-384, and SHA3-512, as well as two XOFs, SHAKE-128 and SHAKE-256. The number in the name of the hash algorithm refers to the bit-security level of each respective algorithm. The SHA3 family is based on the Keccak hash function. XOFs vary from other SHA3 algorithms, as their output can be chosen to meet the required output length for their designated function, as is necessary with SPHINCS+. For each function, the input plain-text is called the message m, and the output of the function is called the digest or hash value. Both are used interchangeably.

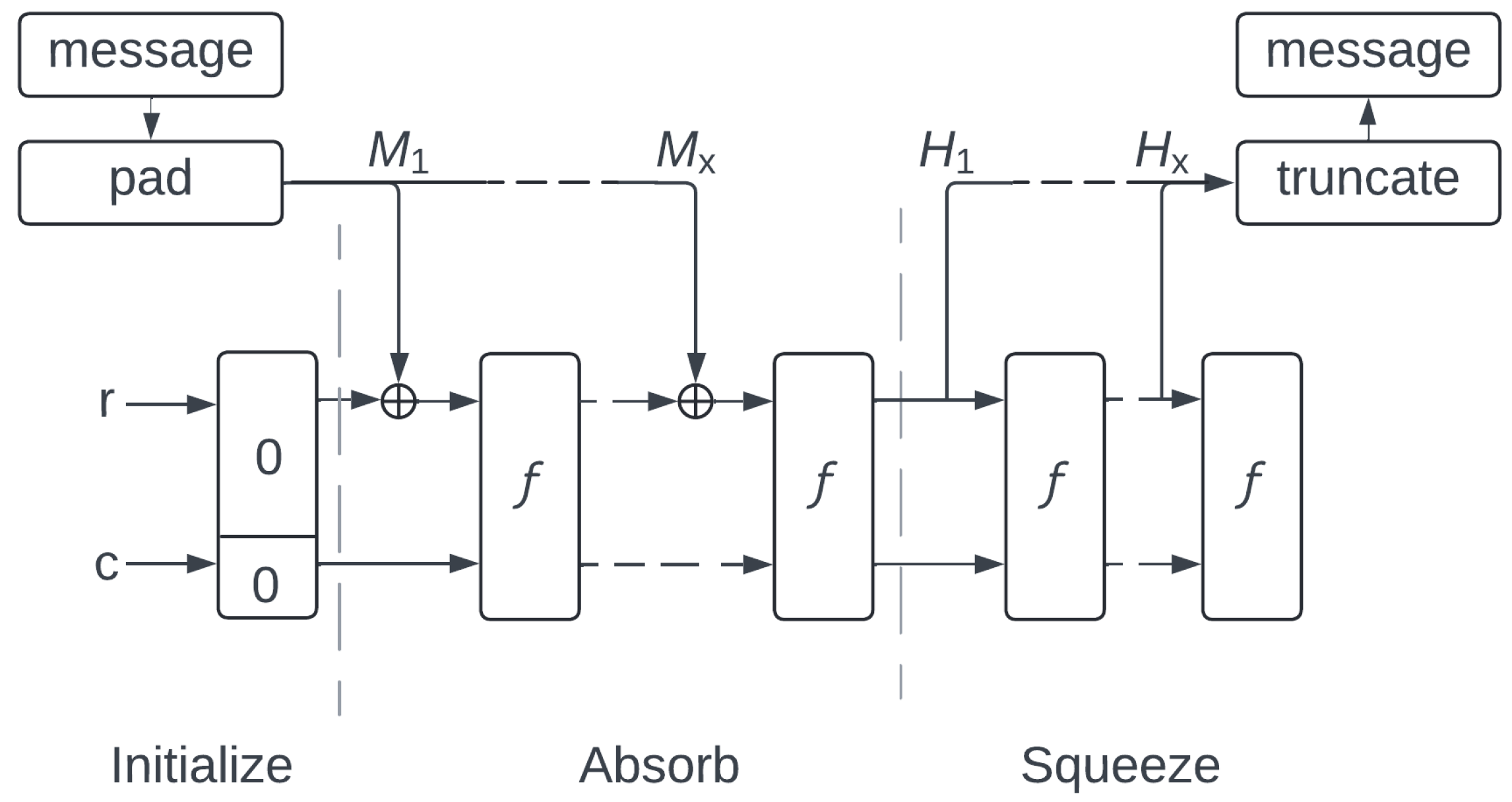
Keccak is an iterative sponge function, which refers to the ability to absorb fixed-length input strings and output a pre-determined, constrained-width digest. Each input rate of R bytes of the message is followed by a set number of permutations of internal functions, called step mappings. For Keccak, there are five step mappings, with the input of step n being the output of step $n-1$. The Keccak sponge, after permutating over the message, absorbs the next R bytes of input by XOR’ing the input with the output of the last permutation. The internal value of the hash, between each round, is called the state s of the function. This process is repeated until the entirety of the message is absorbed, at which time the sponge function will output the result of the hash by truncating the final state to the desired output length. All inputs are padded with a set bitstring so that they are equally divisible by R. An illustration of the sponge function is shown in Figure 1.

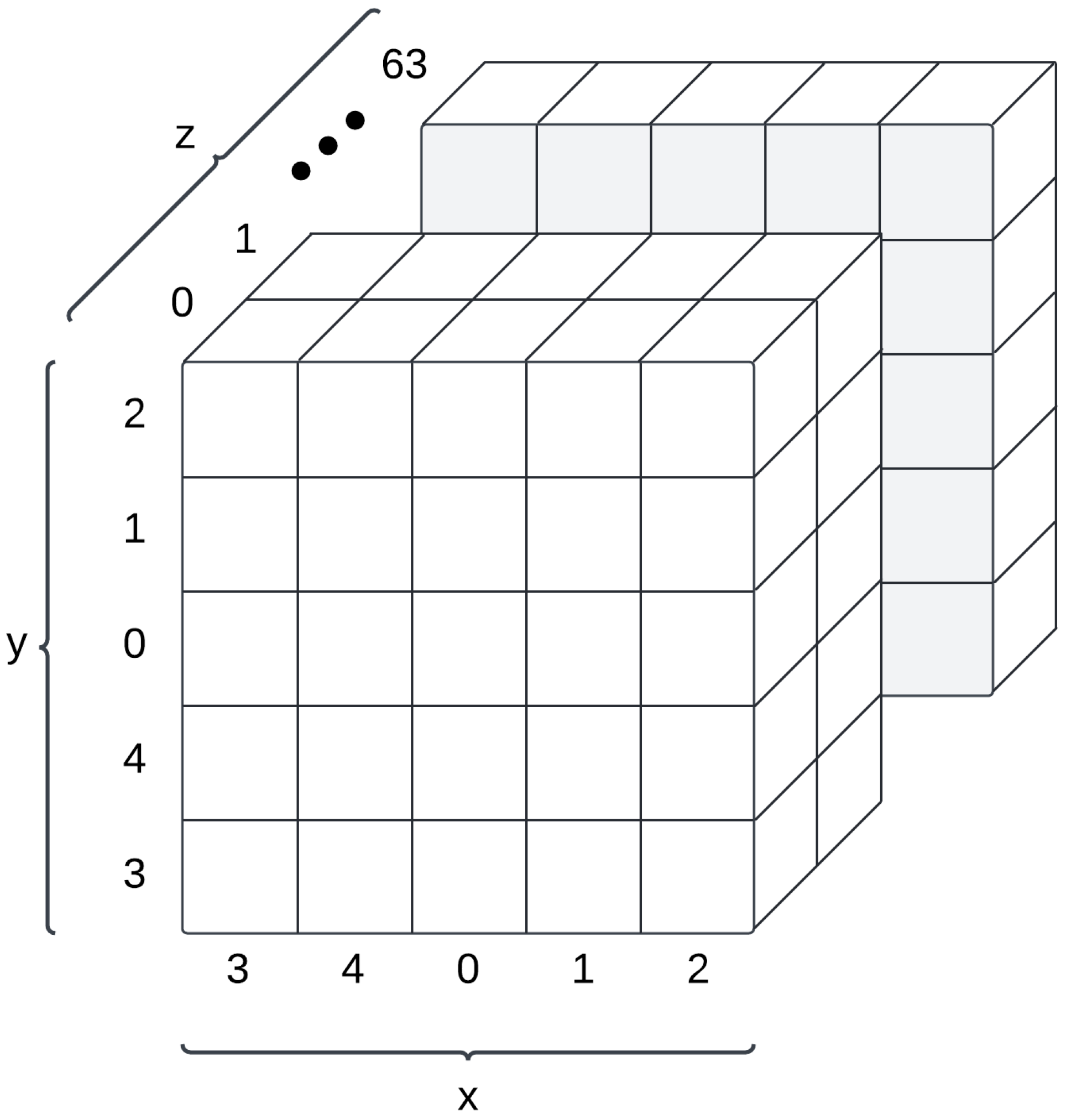
Keccak works by dividing the state, $r+c$, into a three-dimensional rectangular prism, where each bit represents a 3D coordinate in the prism. In the instance of SHAKE-256, the prism is five bits wide, five bits tall, and 64 bits deep. The depth of the prism forms 64-bit words, in which each bit within the word is a consecutive bit in the input message and corresponding state. This results in 25 64-bit words that describe the state with a series of x and y pairs. An illustration of the Keccak-256 state is shown in Figure 2. The location of a bit in the flattened array, from the most significant bit to the least significant bit, can be calculated as $64\times z+5\times y+x$.

The five-step functions within Keccak, shown in Figure 1 as f, ensure an even mixing of the bits within the state. The functions and their names are summarized below:

• Theta ($\theta$): Ensures diffusion within the state by adding parity bits from each column of the state matrix to every bit within the state.
• Rho ($\rho$): Rotates each 64-bit word by a position-dependent offset to introduce asymmetry into the state, further aiding diffusion.
• Pi ($\pi$): Rearranges the lanes within the state matrix with means to break the alignment between bits and distribute the data spatially.
• Chi ($\chi$): Applies a non-linear transformation to each row within the state matrix by utilizing a combination of XOR and AND operations. This introduces non-linearity to the matrix.
• Iota ($\iota$): The final step-function XORs a round-specific constant into a fixed position of the matrix. These values are defined by the SHA3 standard.

The full implementation of the SHAKE-256 standard is described in FIPS 202 [29].

3.2. SPHINCS+

SPHINCS+ is a stateless, hash-based digital signature algorithm. Out of the three standardized signature schemes from NIST, SPHINCS+ is the only one that does not rely on hard mathematical problems such as LWE or NTRU. The security for SPHINCS+ is derived from cryptographic hash functions and is provably secure against collision and preimage attacks. Further, its stateless design eliminates the risks associated with key reuse, a common vulnerability of stateful hash functions.

Within the NIST specification, SPHINCS+ has three defined security levels: 128, 192, and 256, which correlate with the defined PQC security levels 1, 3, and 5, respectively. Further, as the selected parameters for SPHINCS+ have a significant impact on run-time and signature size, there are two defined variants of SPHINCS+ with recommended parameters. The first of these, the “size” variant, focuses on minimizing the size of the signature output. Implementations of SPHINCS+ that focus on the size are designated with an “s”. The alternative is the “fast” variant, which prioritizes reducing the execution time. These SPHINCS+ designs are designated with an “f”. SPHINCS+ f variants have a larger signature, and SPHINCS+ s variants have a longer run-time.

The architecture of a SPHINCS+ algorithm is composed of a few different components. The first is a pseudorandom input derived from the message digest, which prevents replay attacks. The pseudorandom input is then fed into FORS. FORS is essentially a few-time signature scheme in which the message hash is encoded into multiple, small binary trees, where each index is signed by revealing an authentication path. In essence, FORS signs the message digest and is the mechanism that directly binds the message to the signature.

Following the FORS portion of the signature is the Merkle hypertree, which contains multiple layers built upon one another. The first layer of the hypertree is built on the output of the FORS process. At each subsequent layer in the tree is WOTS+, which is a one-time signature scheme based on iterated hashing. WOTS+ is used to authenticate nodes in the hypertree, linking the FORS output to the root public key in the signature. This method ensures that each layer of the tree can be authenticated securely by signing each underlying layer. Both WOTS+ and FORS are essential, as FORS enables compact message binding, while WOTS+ ensures secure authentication across multiple layers, which is necessary for PQC.

Contained within each portion of the SPHINCS+ signature, whether it be FORS, WOTS+, or a hyptertree layer, is a tweakable hash function. Given a secret key SK, a public key PK, and context about hash in the form of a 32-byte address, the tweakable hash function includes the message input m, as well as a variety of PK, SK, and address combinations. This allows the output of a hash to be unique for each input, given the current position of the algorithm, even if the input is the same. This is because the address and key combinations will be unique for each hash input within the algorithm.

The 32-byte address of a SPHINCS+ input includes data such as the hash function used (SHA3, SHA2, or Haraka), the tree type (WOTS or FORS), the layer, the node number within a tree, and chain addresses. This provides a systemic way to navigate the large structure of a SPHINCS+ iteration while allowing for scalability. This is essential, as the different security levels of SPHINCS+ require different parameters for the number of layers, the number of trees, and tree heights.

A SPHINCS+ implementation is defined by the following parameters:

• n: The security parameter in bytes. This also defines the key size, where each portion of the key is n bytes, as well as the signature element size.
• w: The Winternitz security parameter. For all NIST-approved implementations, this remains at 16. For any SPHINCS+ implementation, this must be from the set of 4, 16, or 256.
• h: The height of a hypertree within the WOTS+ scheme.
• d: The number of layers within a hypertree in the WOTS+ scheme.
• k: The number of trees in the FORS portion of the SPHINCS+ algorithm.
• t: The number of leaves in a FORS tree. For each increment of t, the size of the FORS tree doubles.
• a: $lo{g}_2\left(t\right)$. The width of the bottom-most layer in a FORS tree.

The recognized parameter sets for each SPHINCS+ recommendation are displayed in

Table 3. The recommended parameter sets for each NIST-recognized SPHINCS+ variant from [13].

Variant	n	h	d	log(t)	k	w
128s	16	63	7	12	14	16
192s	24	63	7	14	17	16
256s	32	64	8	14	22	16
128f	16	66	22	6	33	16
192f	24	66	22	8	33	16
256f	32	68	17	9	35	16

.

The entirety of the SPHINCS+ signature is derived from three key parts: the message “Randomness”, which is a pseudorandom digest derived from the message, a FORS signature, which signs the randomness, and a hypertree signature, which signs the FORS signature. The final size of the signature is shown in Equation (1). The variable $len$ is shown in Equation (2).

$$sig\text{\_}size=n+kn(a+1)+n(h+d\times len),$$

(1)

$$len=\lceil {\displaystyle \frac{8n}{lo{g}_2\left(w\right)}}\rceil +\lceil {\displaystyle \frac{\lceil \frac{8n(w-1)}{lo{g}_2\left(w\right)}\rceil }{lo{g}_2\left(w\right)}}\rceil .$$

(2)

4. Methods

Our SPHINCS+ implementation is designed to balance throughput and power consumption, with a higher focus being on a reduction in power. As mentioned in previous sections, there is both a need and a research gap for providing PQC signatures for resource- and power-constrained devices, specifically on the IoT edge.

Interestingly, to address power consumption, both active and static power must be acknowledged. Static power, which is the power consumed by the device while it is not actively computing a signature, can be eliminated or minimized by the design. This is possible by turning the module off when it is inactive, or clock-gating it if it is integrated into a larger design that must remain on. This is especially applicable to IoT devices, as they will likely not be constantly generating a signature. Rather, a better design practice would be to accumulate a large amount of data, sign the data as a single message, and then transmit them back to the data aggregator.

Therefore, for IoT applications, active power or the power consumed when the device is computing a signature must be prioritized over static power. This can be carried out using following three principles:

• Limit resource consumption, in turn, reducing static power. Each element, be it a DSP, LUT, or FF, will consume power whether it is actively switching or not.
• Reducing the switching activity of the circuit by removing redundant components and operations.
• Reducing the run-time so the circuit can be turned off following the completion of a generated signature.

Thus, a delicate balancing act must be performed between throughput, power, and area. This is best carried out by taking a broad approach to resource consumption and throughput by parameterizing the circuit and comparing the results against each other. To fulfill this need, we introduce multiple parameters for our SHAKE implementation, as well as multiple parameters for our SPHINCS+ architecture.

4.1. Hash Method Selection

From the three principles, it can be seen that throughput must also be taken into account, with means to reduce power consumption. A reduction in active power will be achieved by a faster circuit. Therefore, the selection of a hash algorithm with means to increase throughput (and, therefore, reduce power consumption) is of great importance. Even if a hash function requires a low amount of resources, if it has a long run-time, it can negatively impact the power requirements. As can be seen from previous SPHINCS+ implementations [24,25,28], the rate or how many bytes are absorbed per round of a hash function can significantly impact the speed of SPHINCS+. SPHINCS+ can call a single hash function billions of times for a single signature.

For example, let us assume an average message size of 128 bytes (key + address + two hash nodes) for a single hash message in a 256-bit SPHINCS+ scheme. For a small hash rate of 8 bytes, such as the case of Ascon-hash, we would have to perform 8 permutation rounds for every 8 bytes of input, as defined by the Ascon standard. This leads to 128 permutation rounds per message, which, when multiplied by the number of hash calls per signature, becomes the primary impact on run-time.

We kept this in mind when assessing the three hash functions certified to support SPHINCS+. Haraka and SHA-2 absorb 32 and 64 bytes, respectively; for their 256-bit variant. SHAKE, on the other hand, absorbs 136 bytes per round. This is wide enough to absorb the majority of hash messages within SPHINCS+ without having to iterate on only a partial message. For this reason, we determined that SHAKE-256 would be the ideal hash function for SPHINCS+ and power-constrained devices.

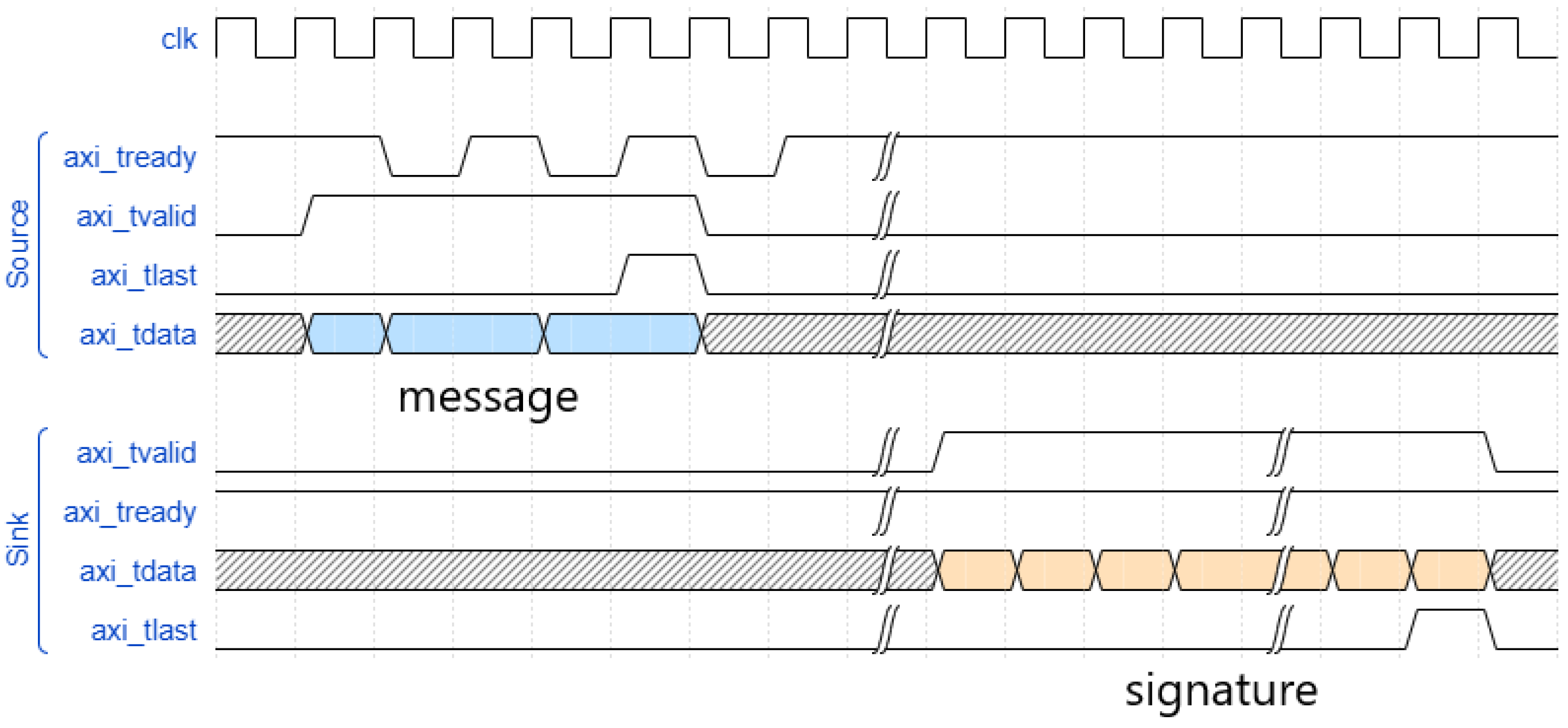
4.2. System Overview

Our full design was created with the motivation to support any form of binary input data. To uphold this desire, we built our design of the AXI-Stream standard. This allows data to be streamed in and out of the module, with a natively supported handshake feature. The upstream device asserts a valid signal, and the downstream device asserts a ready signal. When both signals are asserted, the data on the bus can be deemed by both the upstream and downstream devices to have been accepted. The system has a source and sink bus, where the sink accepts the message to be signed, and the source bus provides the signature. The handshake waveform for this bus is shown in Figure 3.

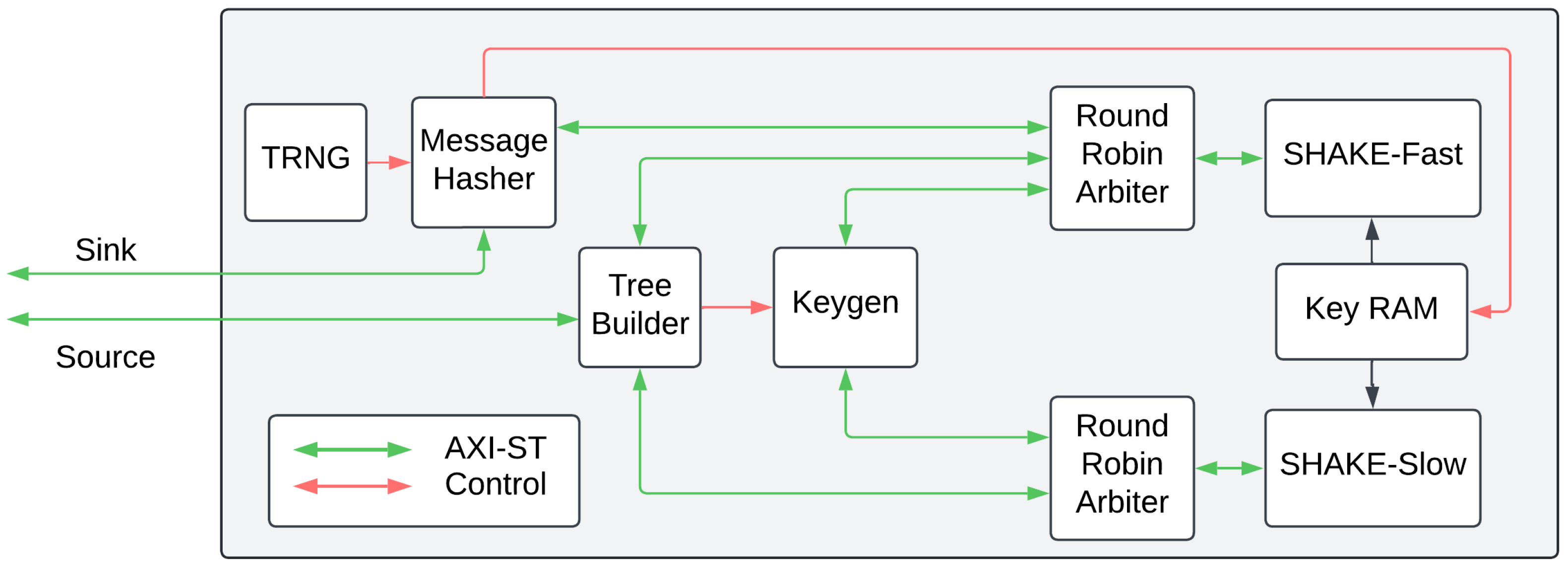
Within the system, we have six main components: a true random number generator, a module to hash the message, a tree-builder instance, a key generator, and the SHAKE instances. We cover a high-level overview of each instance within the following subsections. The full architecture is shown in Figure 4.

4.3. Entropy Source

The SPHINCS+ keys are generated via a sec_rand(n) function, where n is the security parameter in bytes, and in the context of sec_rand, indicates the number of bytes of the cryptographically random vector to be returned. As this function must agree with three different values of n to support the three security levels of SPHINCS+, we designed a random number generator (RNG) similar to the RNG used in [28]. This design allows us to capture two bytes of entropic data at a time, which can be used to fulfill the 16, 24, and 32 bytes required by the different security levels.

This entropy source is based on a unique type of ring oscillator that combines pseudorandom bit-stream (PRBS) designs with typical RNG designs. Classically, there are two types of recognized linear feedback shift registers (LFSRs) that can be used for PRBS generation. These include the Fibonacci and Galois implementations, both of which require strategically placed AND and XOR gates to ensure a unique pattern. We combine these two in our RNG by XORing the output from the two.

This, of course, would still result in a PRBS and would not be a true random number generator (TRNG). To remedy this, instead of utilizing basic registers for the bits within the LFSRs, we replace the one-bit registers with delay cells in the form of ring oscillators (ROs). ROs are one of the most common sources for entropy in hardware [30,31,32,33], and they have been consistently proven to be a quality entropy source. By integrating ROs into the LFSRs, we further increase the level of entropy.

4.4. Control Logic

Within the design of the algorithm, we implement three different controllers to efficiently pass hash nodes and the plain text message to the hash units. The first component is the message hasher (MH), which handles entropy sourcing for keys as well as calculating the message digest. At the beginning of the algorithm, to make the signature non-deterministic, SPHINCS+ defines a “message-random” to be generated with a user-defined number of entropy bits. The message-random, in the case of our design, is handled by the MH, as the MH’s primary goal is to calculate the digest, and this cannot be completed without the message-random.

Further, the MH has the additional function of taking the entropy from the TRNG and storing it in the key RAM. On a restart, the MH stores three n-byte wide keys, as defined by SPHINCS+, into the appropriate locations of the key RAM. These three vectors make up the SK.seed, SK.PRF, and PK.seed, as defined by SPHINCS+.

The next control module within the design is the KG. The KG is responsible for generating the keys and nodes used in the FORS and WOTS+ algorithms. This also includes the genchain function from SPHINCS+, which iteratively hashes over a node, as defined by the SPHINCS+ algorithm.

The final control module within our model is the tree builder (TB). As the KG module generates the nodes, the TB hashes them together to build the trees in the WOTS+ and FORS schemes. Further, as some of these nodes must be saved, the TB records the nodes from each layer of the hypertree and FORS trees, as defined by the search function in SPHINCS+. With respect to the signature, these nodes must be placed in order from the bottom-most layer to the top. As the search function does not necessarily find these nodes in order, the TB stores them in a BRAM module according to their layer number. For instance, the node to be saved at layer zero is saved at address zero, the layer one node is saved at address one, and so on. Once all nodes have been found, the TB outputs the data onto the AXI-St bus in order.

The MH is essential for the message-random, which constitutes the very beginning of a SPHINCS+ signature. Every other component, be it the TB, KG, or SHAKE modules, is used multiple times throughout the signature process, often operating in parallel. The TB acts as the primary arbiter between each of the modules by delegating which nodes are saved and which ones are hashed. This is different from the conventional SPHINCS+ paradigm, which is largely linear in nature. By not having separate modules for FORS and WOTS+ and instead, combining their functionality into shared components, we reduce the overall area of our design.

4.5. Hash Sharing

To efficiently handle intermediate hash data and prevent a reduction in data storage, we utilize two SHAKE hash modules, similar to how Ascon was handled in [27]. However, the two units are treated differently. One acts as the primary hash unit and is almost always acting on new data by constantly switching. This unit handles the brunt of the load and is referred to as SHAKE-fast in Figure 4.

For different parts of the algorithm, such as building WOTS+ nodes, multiple hash outputs must be further hashed together. This is especially relevant for the genchain function of SPHINCS+, where up to 16 hashes are computed and then hashed together. A slower module, designed for low area as opposed to high throughput, handles these hashes. As the hash digests are output by SHAKE-fast, they are captured and hashed together by SHAKE-slow.

Further, as each node requires keys, and to prevent the need for the control logic to manage keys per module, we offload the key integration to the SHAKE modules. The control units indicate the key type via a control signal, and the hash functions add it to the beginning or end of the message, depending on the key type indicated by the control bits. Since there are two hash units, we store the keys in a dual-port BRAM so the hash functions can operate separately from each other.

The last portion of the hash function is two round-robin arbiters (RRAs). The RRAs act as an AXI-passthrough that respond to the first valid control signal from the input control units. They are lightweight and can be viewed as individual AXI-based multiplexers.

4.6. Parametrization

With the means to evaluate our design for efficiency, power, and area, we integrate multiple parameters into the design. For our results, we iterate through each combination of parameters to deduce the optimal configuration for a given security parameter. The first of these configurable variables is the number of permutations per clock cycle (PPC). As each hash call requires multiple rounds of permutations, we can speed up the hash function by adding combinational logic to handle multiple permutations. As demonstrated in [28], the PPCs can be adjusted to effectively double or triple the operating frequency of a hash unit, while not affecting the frequency of the other control functions. This is essential, as the hash units are the most significant bottleneck within the design.

Individual controls for PPCs are provided for the SHAKE-slow and SHAKE-fast modules, allowing for the independent optimization of each module. As SHAKE-fast is constantly switching to efficiently produce a signature, and since SHAKE-slow is rarely operating and only acts to reduce memory utilization, we expect an increase in PPCs to only be beneficial for SHAKE-fast. Further, since SHAKE is more complicated than Ascon, we anticipate that we will only be able to fit two PPCs while still meeting timing. This is unlike the more lightweight Ascon-Sign algorithm, which was able to integrate three PPCs [27].

Furthermore, we experiment with two different instantiations of SHAKE. The first adds a rate-width register to the SHAKE input, and the second removes this register. For a smaller design that does not require billions of hashes, we would anticipate this to have a minimal impact. However, since SPHINCS+ is a lengthy algorithm, we expect to see differences in run-time and power consumption. For resource utilization, this register adds an extra 1088 bits worth of logic to the design. The benefit is that the control units can continue to input data into this register while the hash modules are permuting over the previously input data. Furthermore, the addition of this register will allow for tighter timing constraints, allowing the clock frequency to be increased. In turn, this will reduce the run-time of the algorithm. Similar to PPCs, we allow this tweak to be adjusted for the individual hash units.

4.7. Hash Units

As previously discussed, two major variables were experimented with within the design: permutations per clock cycle and the addition of an extra 1088-bit register to the input of the SHAKE hash units. This led to three major variations in the implementation, as there were two hash units per design. The first included an extra register for each hash unit, which we referred to as the SHAKE-register (SR) variation. The second removed the register from both hash units, which we referred to as the SHAKE-no-register (SNR) variation.

Preliminary results showed that the SNR unit operated faster than the SR unit; therefore, we decided to experiment with a mix of the two. This led to having an SNR function for the primary SHAKE-fast hash module and an SR for the secondary slower hash module. We call this implementation the SHAKE-hybrid (SH) unit.

4.8. Implementation

For each major variation, we tuned the number of PPCs. In order to meet a minimum 100 MHz clock frequency, we were only able to utilize a maximum of 2 PPCs, unlike the maximum of 3 PPCs in [27] that made up Ascon-Sign. This difference is likely due to the increased complexity, rate, and capacity of SHAKE over Ascon. Each variation in PPCs is referred to by PPCs for the primary unit x the PPCs for the secondary unit. For example, 2 × 1 means that SHAKE-fast has two PPCs and SHAKE-slow only has 1 PPC.

Further, as the throughput of the SPHINCS+ module is limited by the SHAKE-fast hash module, we do not experiment with the secondary unit that has more PPCs than the primary unit. This leads to three PPC combinations: 1 × 1, 2 × 1, and 2 × 2. We list the results for each variation in the SPHINCS+ small-signature in

Table 4. The power per signature (PPS) implementation results of the small-signature variants of SPHINS+, including the SHAKE implementation without an extra register (SNR), the SHAKE hybrid model (SH), and SHALE with a register model (SR): 1 × 1 PPCs are grouped into white rows, 2 × 1 PPCs are grouped into light blue rows, and 2 × 2 PPCs are grouped into blue rows.

Variant	FFs	LUTS	Key Gen. [ms]	Sig Gen. [ms]	Power [mw]	PPS [mw]
128s-SNR 1 × 1	6660	13,728	132	1011	364	368
128s-SH 1 × 1	7791	12,256	132	1011	352	356
128s-SR 1 × 1	8918	12,410	135	1033	357	369
128s-SNR 2 × 1	6674	14,255	97.9	749	735	551
128s-SH 2 × 1	7804	14,292	97.9	749	749	561
128s-SR 2 × 1	8892	14,988	101	770	873	672
128s-SNR 2 × 2	6660	18,233	97.9	749	773	579
128s-SH 2 × 2	7778	16,851	97.9	749	1242	930
128s-SR 2 × 2	8905	17,596	101	770	1380	1063
192s-SNR 1 × 1	7538	14,475	213	1943	375	729
192s-SH 1 × 1	8669	13,061	213	1943	359	698
192s-SR 1 × 1	9782	13,024	218	1981	345	683
192s-SNR 2 × 1	7551	15,066	163	1491	732	1091
192s-SH 2 × 1	8681	15,013	163	1491	744	1109
192s-SR 2 × 1	9756	15,584	167	1529	857	1310
192s-SNR 2 × 2	7538	18,992	163	1491	756	1127
192s-SH 2 × 2	8655	17,666	163	1491	1218	1816
192s-SR 2 × 2	9756	18,182	167	1529	1361	2081
256s-SNR 1 × 1	8449	14,920	154	1870	367	686
256s-SH 1 × 1	9537	13,534	154	1870	362	677
256s-SR 1 × 1	10,665	13,803	156	1902	368	700
256s-SNR 2 × 1	8407	16,250	121	1476	708	1045
256s-SH 2 × 1	9550	15,629	121	1476	741	1094
256s-SR 2 × 1	10,639	16,374	123	1509	850	1283
256s-SNR 2 × 2	8407	19,457	121	1475	963	1420
256s-SH 2 × 2	9538	18,231	121	1475	1256	1853
256s-SR 2 × 2	10,652	19,025	123	1508	1341	2022

and the results of each variation in SPHINCS+ fast variations in

Table 5. The power per signature (PPS) implementation results for the fast variants of SPHINS+, including the SHAKE implementation without an extra register (SNR), the SHAKE hybrid model (SH), and SHAKE with a register model (SR): 1 × 1 PPCs are grouped into white rows, 2 × 1 PPCs are grouped into light blue rows, and 2 × 2 PPCs are grouped into blue rows.

Variant	FFs	LUTS	Key Gen. [ms]	Sig Gen. [ms]	Power [mw]	PPS [mw]
128f-SNR 1 × 1	6713	13,728	2.1	51.6	363	18.7
128f-SH 1 × 1	7844	12,283	2.1	51.6	352	18.2
128f-SR 1 × 1	8969	12,276	2.1	53	357	18.7
128f-SNR 2 × 1	6727	14,280	1.5	38.2	706	27.0
128f-SH 2 × 1	7857	14,268	1.5	38.2	749	28.6
128f-SR 2 × 1	8943	14,883	1.6	39.3	859	33.8
128f-SNR 2 × 2	6713	18,217	1.5	38.2	796	30.4
128f-SH 2 × 2	7831	16,876	1.5	38.2	1239	47.3
128f-SR 2 × 2	8943	17,496	1.6	39.3	1349	53.0
192f-SNR 1 × 1	7587	14,424	3.3	91.9	373	34.3
192f-SH 1 × 1	8727	13,052	3.3	91.9	353	32.4
192f-SR 1 × 1	9833	13,174	3.4	94	357	34.3
192f-SNR 2 × 1	7600	15,080	2.6	70.5	693	48.9
192f-SH 2 × 1	8730	15,045	2.6	70.5	758	53.4
192f-SR 2 × 1	9807	15,756	2.6	72	870	62.6
192f-SNR 2 × 2	7587	18,948	2.6	70.4	756	53.2
192f-SH 2 × 2	8705	17,631	2.6	70.4	1238	87.2
192f-SR 2 × 2	9807	18,375	2.6	72	1339	96.4
256f-SNR 1 × 1	8464	15,004	9.6	201	366	73.6
256f-SH 1 × 1	9595	13,461	9.6	201	364	73.2
256f-SR 1 × 1	10,721	13,816	9.8	204	372	75.9
256f-SNR 2 × 1	8474	16,279	7.5	157	711	111.6
256f-SH 2 × 1	9610	15,610	7.5	157	737	115.7
256f-SR 2 × 1	10,695	16,394	7.7	161	858	138
256f-SNR 2 × 2	8466	19,527	7.5	157	969	152.1
256f-SH 2 × 2	9584	18,266	7.5	157	1207	189.5
256f-SR 2 × 2	10,708	19,053	7.7	161	1351	218

.

To generate these results, we ran a regression analysis through Vivado for both of our primary variables: PPC and the hash variant. This included iterating the two using a TCL script, with increasingly stringent timing requirements to maximize the possible clock frequency. For the comparison in Table 4 and Table 5, we used a comparison frequency of 100 MHz.

For the implementation results, we utilized a synthesis strategy targeting a highly optimized area and an implementation strategy of default power optimization. This allowed the synthesis process to reduce the LUT and FF count, while implementation focused on reducing power consumption. These two strategies were consistent throughout all runs of the different variations.

To time the model, we ran each variant through a simulation process, where a timer was run for the number of clock cycles for both signing time and key generation. The number of cycles for each run could then be multiplied by the minimum clock period that could be met by place and route to obtain the run-time for each of the modified algorithms.

While our evaluation relies on detailed post-synthesis and post-place-and-route simulations together with tool-generated power estimation, we acknowledge that board-level measurements provide additional validation. These simulation-based estimates incorporate real switching activity based on NIST test vectors.

In a similar study where we implemented an Ascon-based variant of SPHINCS+ on a physical FPGA, we observed strong agreement between the tool-reported power and timing and the actual measured results [27]. Therefore, we anticipated the results presented here to translate to hardware. In future work, we intend to extend this study with prototype implementations and a physical FPGA, enabling direct power and timing measurements under representative IoT workloads. Such results would complement our current findings and further strengthen the practical contributions of our design.

5. SPHINCS+ Modification

Our design, while implementing the classic SPHINCS+ outlined in the NIST revision, found an area for optimization. While SPHINCS+ was originally designed with software in mind, there is a shortcoming concerning hardware implementations. This is found in the generation of the pseudorandom string R. R is calculated as the PRF function, which equates to $R=SHAKE256(SK.prf|\left|OptRand\right|\left|M\right)$, where $SK.prf$ is part of the secret key, $OptRand$ is the random output from the TRNG, and M is the message. Further, the message digest within SPHINCS+ is calculated as $H_{msg}=SHAKE256\left(R\right||PK.seed||PK.Root|\left|M\right)$.

The primary issue with these two equations is that the plain-text message M must be passed in twice. The output of the signature is made non-deterministic by combining these two functions. This is a simple solution within software, as the message is stored in a plain-text byte array. However, in hardware, this means that the message must either be stored in a BRAM or passed into the SPHINCS+ signature generator twice. We can see this to be true by combining the two functions: $H_{msg}=SHAKE256\left(SHAKE256\right(SK.prf\left|\right|OptRand\left|\right|M\left)\right||PK.seed||PK.Root|\left|M\right)$.

We propose an amendment to the algorithm by instead passing R into the $H_{msg}$ function last, allowing us to run the two in parallel, without storing the message. The $H_{msg}$, after hashing the message plain-text, would then stall until the output of R is ready.

The benefit of this is two-fold: we do not have to store the message, removing the requirement for any BRAM within the entirety of the SPHINCS+ architecture. Further, this allows the length of the message to be unconstrained by hardware limitations, meaning that a message of arbitrary length can be input into SPHINCS+. The final $H_{msg}$ function is then $H_{msg}=SHAKE256(PK.seed||PK.Root|\left|M\right|\left|SHAKE256\right(SK.prf\left|\right|OptRand\left|\right|M\left)\right)$.

The NIST-standardized version of SPHINCS+, FIPS 205, only defines SHAKE and SHA2 as approved hash functions. For this reason, we only explore the security features of this amendment to SHA2 and SHAKE.

SHA2 relies on $H_{msg}$ being structured around an inner hash, and reordering $H_{msg}$ for this variant changes the Merkle–Damågard framing. Because of this, our modification may require more analysis to ensure security is not compromised when used with SHA2. For this reason, we limit our proposed change to the SHAKE variant of SPHINCS+.

To prove that our proposed amendment does not degrade the security of SPHINCS+, we first define a few key terms. First, it is stated that an encoding function, E, is a mapping from some set of structured inputs, x, to bit strings. In this particular case, $H_{msg}$ is the encoding function, and the structured inputs are $(R,PK,M)$. Second, we define an encoding function to be injective if $E\left(x_1\right)=E\left(x_2\right)$ when $x_1=x_2$ and $E\left(x_1\right)\ne E\left(x_2\right)$ when $x_1\ne x_2$.

Next, we define the random oracle model (ROM) as an idealized hash function that behaves like a perfectly random function. For every unique input string, the ROM outputs a random value that is uniformly distributed over the output space. SPHINCS+ proofs assume that the approved hash functions are modeled as a ROM. In practice, these random oracles are instantiated with SHAKE or SHA2.

If we define $PK$ as $PK.Seed\left|\right|PK.Root$, we can say that $H_{msg}$ is $E(R,PK,M)=R\left|\right|PK\left|\right|M$ in the standard SPHINCS+ specification, and $H_{msg}$ is $E^{\prime }(R,PK,M)=PK\left|\right|M\left|\right|R$ in our proposal. Since R and $PK$ are fixed-length fields and M is the remaining substring, we can therefore state that both E and $E^{\prime }$ are injective because no two different triples $(R,PK,M)$ map to the same encoded string. Therefore, under the ROM, the distribution of E is identical to the distribution under $E^{\prime }$. Because of this, the existing SPHINCS+ security reduction, as stated in the SPHINCS+ specification, remains unchanged, regardless of whether E or $E^{\prime }$ is used.

6. Discussion

Although our SPHINCS+ architecture was specifically designed to minimize power consumption per signature, the three major aspects of the design, including power, area, and throughput, are evaluated. Further, we evaluate the impact of both the hash modules used and the PPC of each hash unit.

6.1. Area

For area and resource consumption, there are four factors that must be evaluated across an FPGA design that does not rely on high-speed IP blocks: FFs, LUTs, BRAMs, and DSPs. As the SPHINCS+ design does not rely on arithmetic outside of addition, we would anticipate not using any DSPs. Further, our design limited the amount of memory usage by opting for a second hash function to store hash function outputs, rather than storing them in BRAM. We utilize a single BRAM to store the message, as the message must be input twice to the hash functions, according to the SPHINCS+ specifications.

The trait that has the most significant impact on LUTs, or combinational logic, would likely be PPC. As PPC increases, the combinational logic to handle the permutations within a clock cycle would have to increase linearly. Since PPC increases the strain on the place and route tools in relation to meeting timing specifications, we would anticipate PPC to have a minor impact on FFs as registers are duplicated across the design.

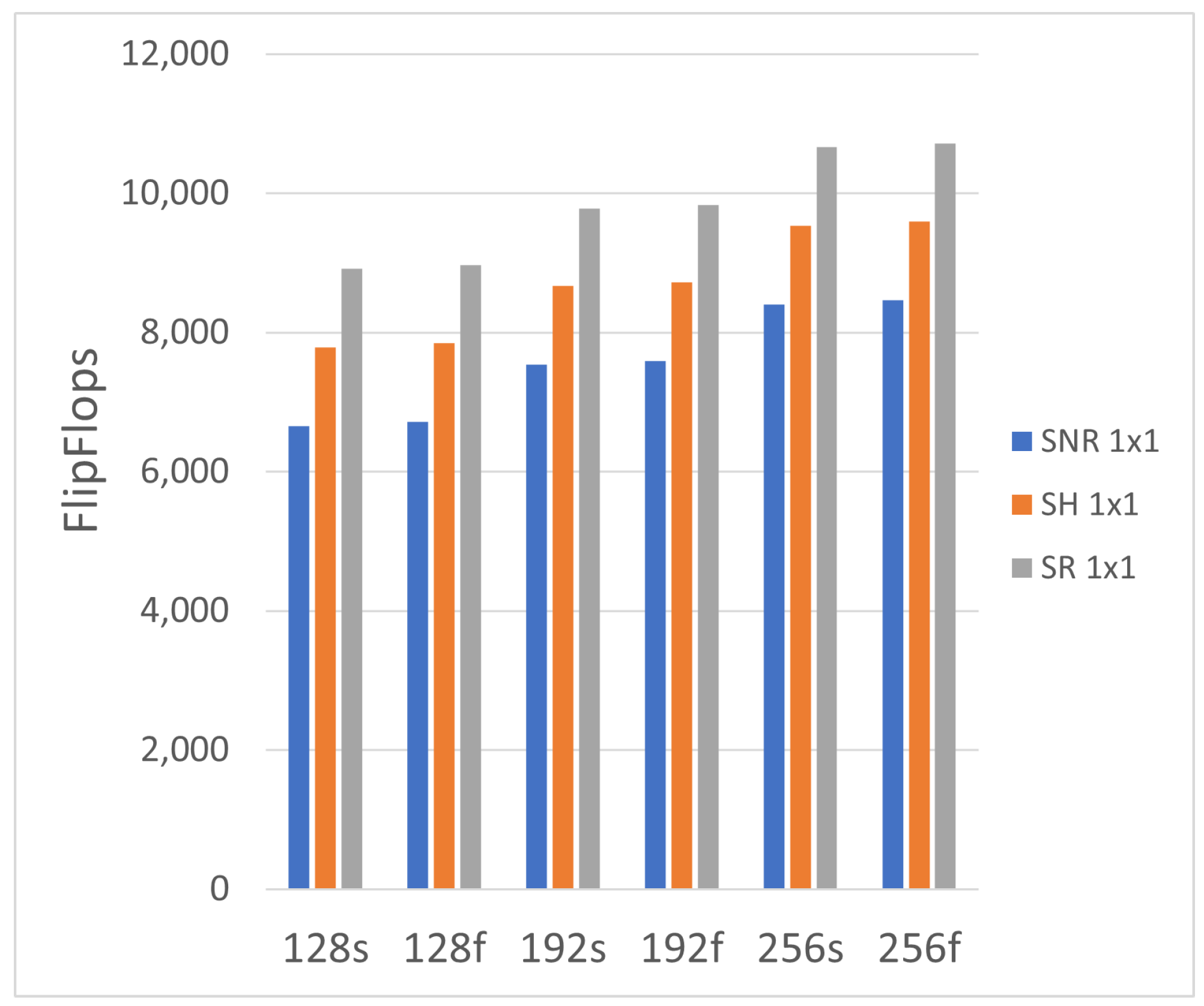
We first evaluate the difference in FFs between the three designs, as shown in Figure 5. One of our primary expectations was met: the number of FFs increased linearly with increasing security level. This was anticipated as each increment, from 128 to 192 to 256, requires eight additional bytes of hash digest per operation. This directly affects the message hash, key generation, key RAM, and tree generation modules in Figure 4.

Further, our other expectation was met. The SNR variant had the lowest amount of FF usage, while the SR variant had the highest. As SH is a mix of both units, the SH came in between, leveraging the registered input on the secondary unit, and no extra register on the primary hash unit.

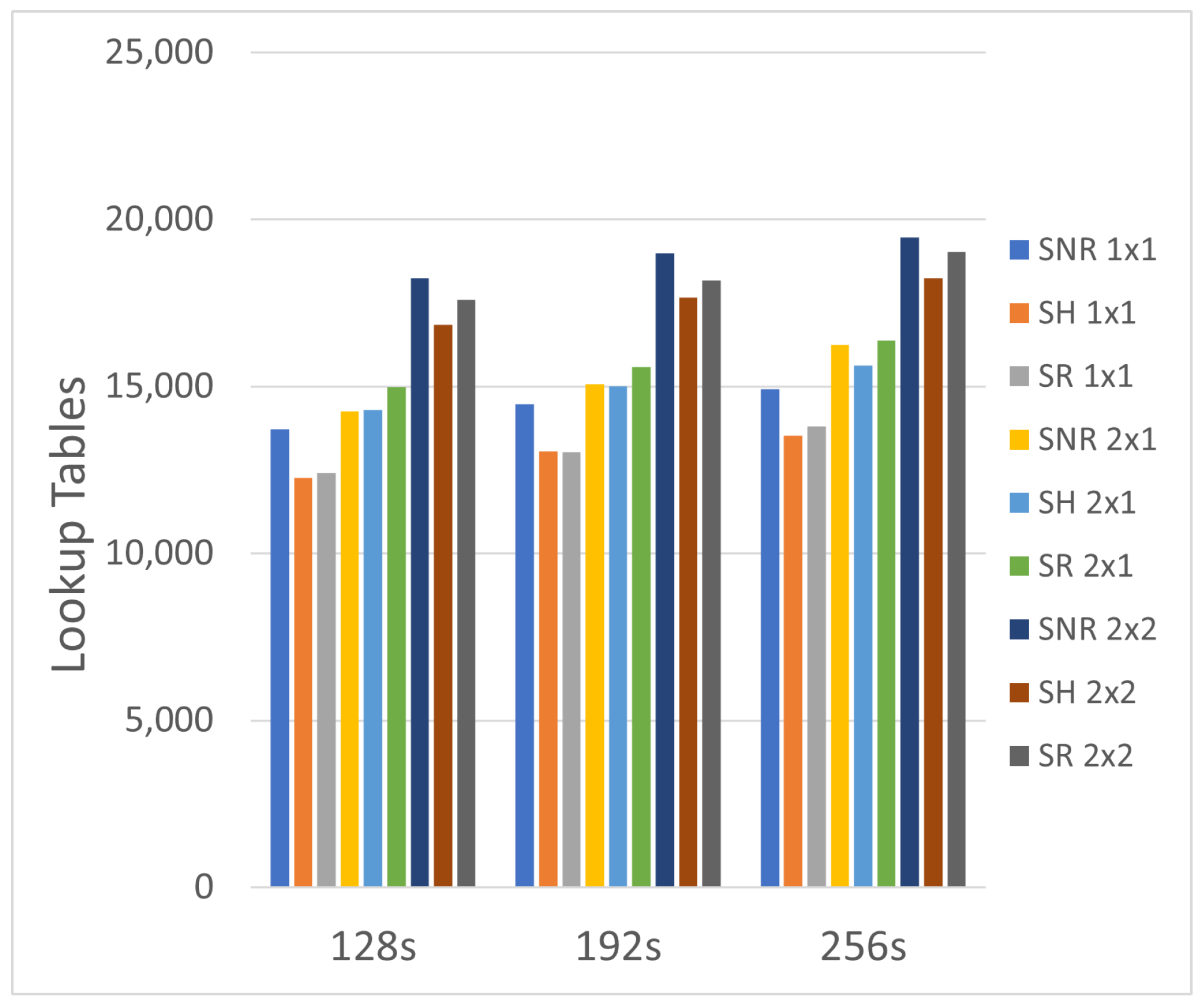
Looking at the LUTs, we see a positive correlation between the LUT count and PPC, as shown in Figure 6 and Figure 7. As mentioned previously, this is to be anticipated because an increase in PPC leads to an increase in combinational logic. This is one of the primary implementation factors that influences area, but will also directly reduce the run-time of an implementation, as we explore later. Interestingly, the SH variant has a marginally lower LUT count across the three SHAKE varieties, where we would expect it to be an average between the SNR and SR implementations. This difference in LUT count increases as the PPC increases, strengthening the linear correlation.

It can be deduced from Figure 5, Figure 6 and Figure 7 that if the primary priority of a design was to optimize for reduced area, a 1 × 1 approach with hybrid hash units would be the best model. This would have a balanced LUT and FF count, yielding the optimal area consumption.

6.2. Throughput

It is difficult to estimate which of the three SHAKE models would have the highest throughput, as the high hash rate of SHAKE may offset the benefits of registering the input. Initially, we believed that the register stage in SR would allow the control units to offload more data while working through their finite state machine, as data could continue to be loaded into the input register while the SHAKE unit is permutating on other data. However, the additional register stage may not be needed, and it may actually hinder throughput, as all data must pass through this input stage whether it is needed or not. The only way to be certain is to time the results of each SHAKE variant.

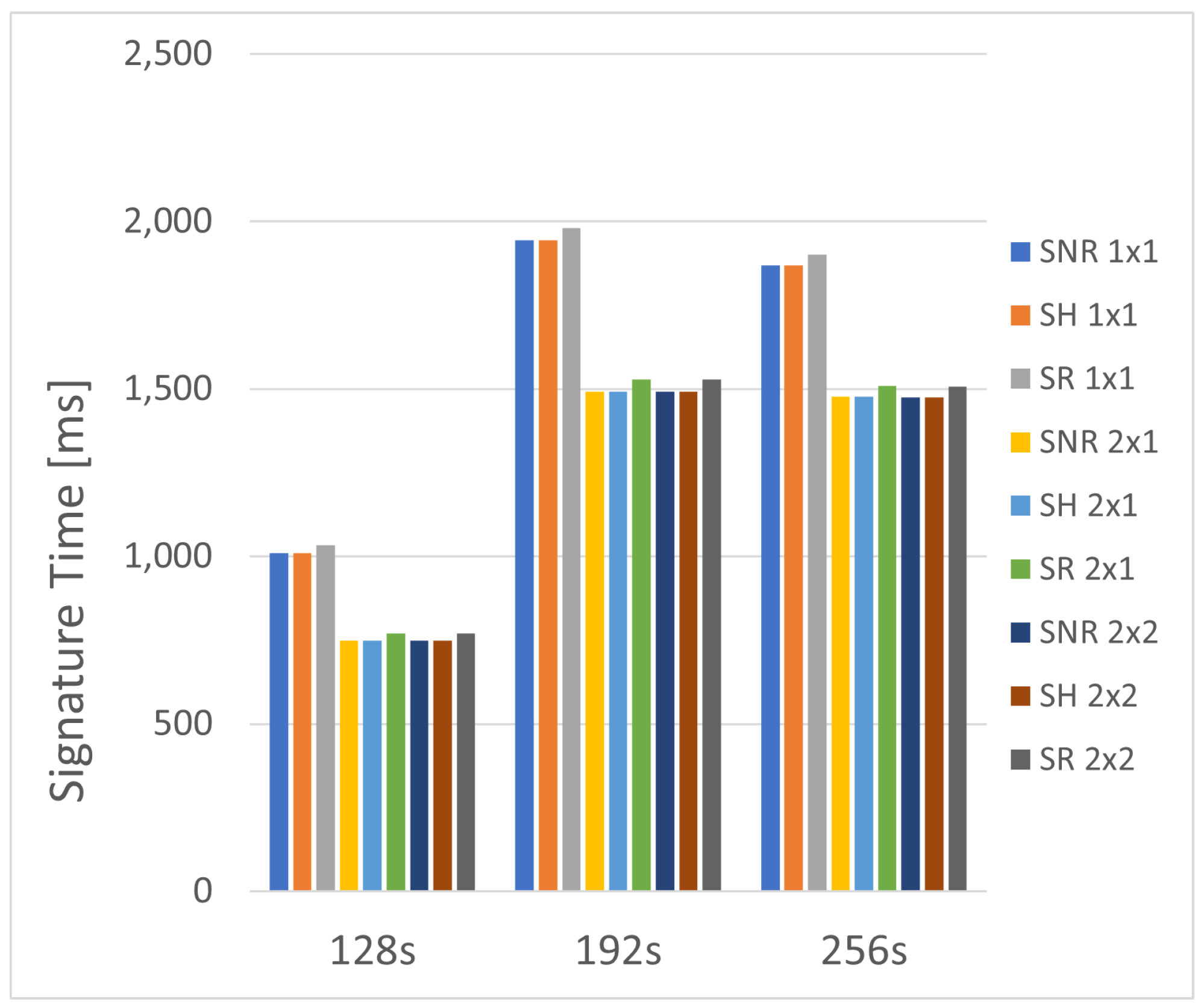
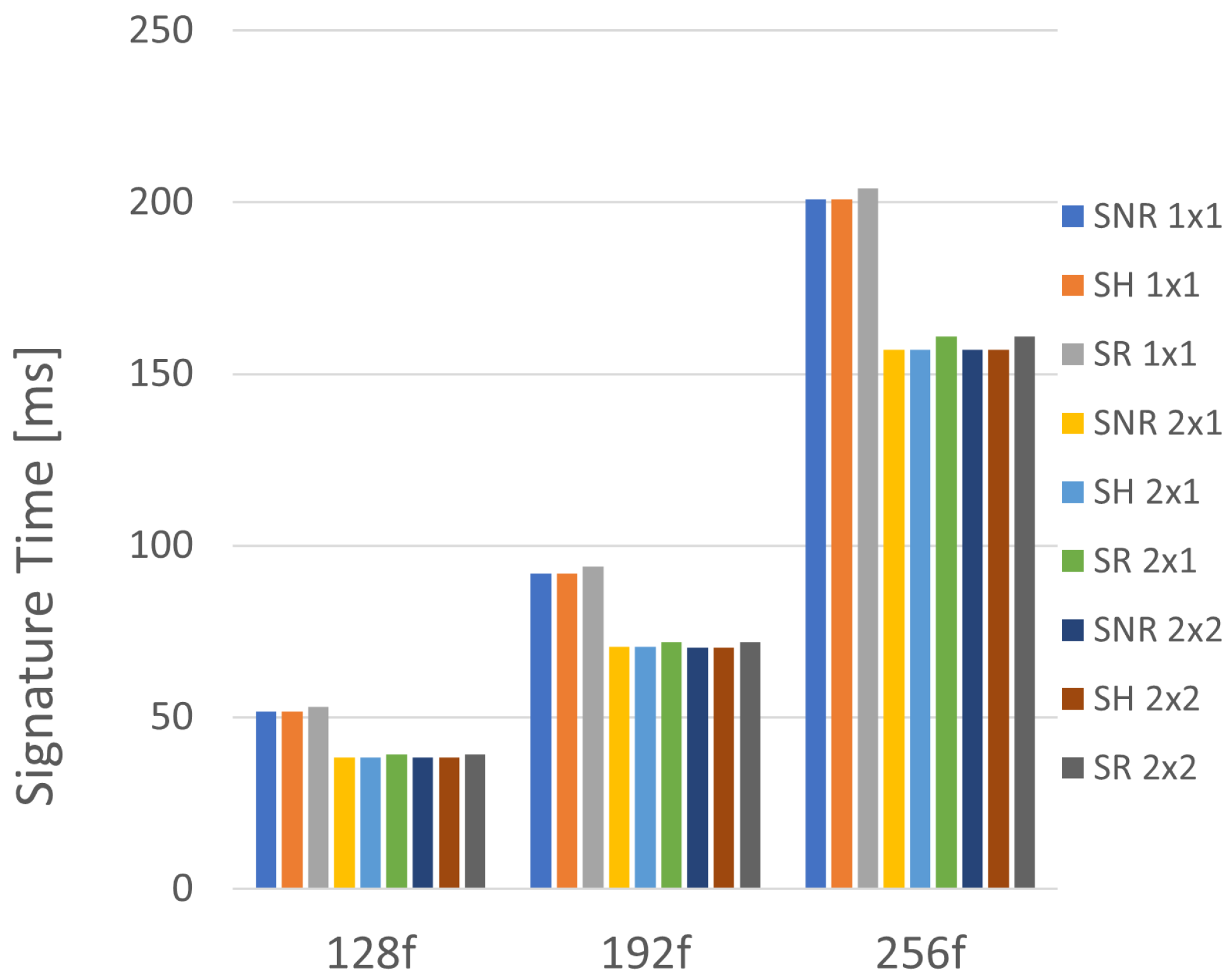
The run-time for each variant and PPC combination is shown in Figure 8 for the small-signature SPHINCS+ types, and Figure 9 for the fast models. While some models could meet faster timing requirements, all models in Figure 8 and Figure 9 are shown at a 100 MHz clock speed.

As expected, doubling the PPC in the primary unit results in a significant reduction in the signature generation time. Averaged between the three variants, a doubling of PPC on the primary hash unit shows an approximate 25% reduction in the time required to generate a signature. Despite this, increasing the PPC on the secondary unit has almost zero impact on the run-time. As shown in Table 4 and Table 5, only a couple of implementations see a decrease in the signature time by one millisecond. This is because the system throughput is restricted by the primary hashing unit, while the secondary unit is stalled under normal operation, waiting for input from the primary unit. Even if one were to prioritize the speed of the system, it would be difficult to justify the significant increase in area and power to save a millisecond of generation time. Therefore, one may opt for the 2 × 1 design to maximize throughput.

Further, as expected, the SH model was speed-limited by the primary hash unit, which was replicated from the SNR model. Therefore, these two variants had the same throughput, while the SH model benefited in power and area by reducing consumption via the secondary hash unit, which was borrowed from the SR model. Ultimately, the extra register had a slight negative impact on the system’s maximum throughput, as the rate of the SHAKE function made the extra 1088-bit register obsolete. While this is the case for a high-rate function such as SHAKE, it may not be the case for other functions such as the small rate Haraka or SHA2.

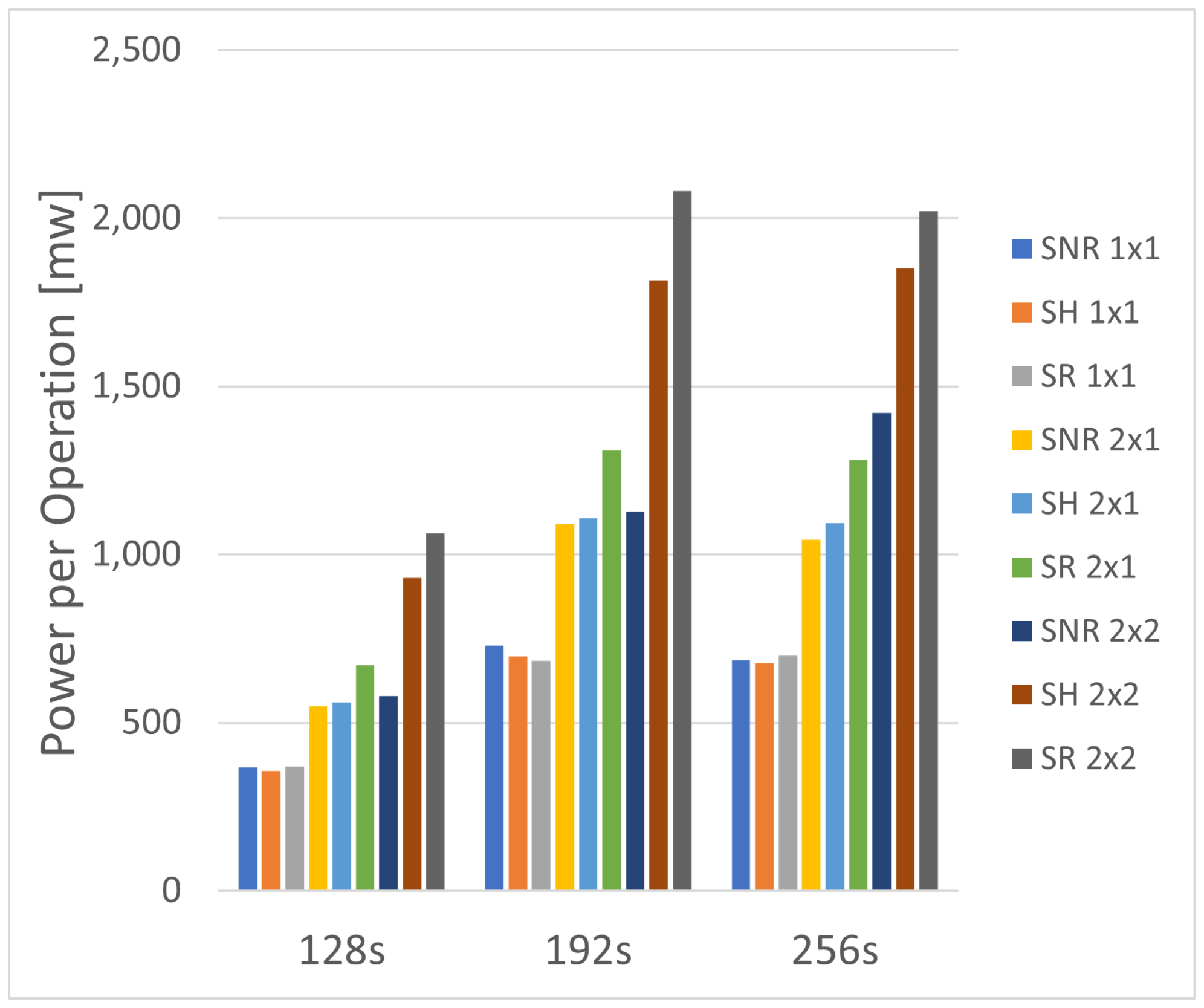
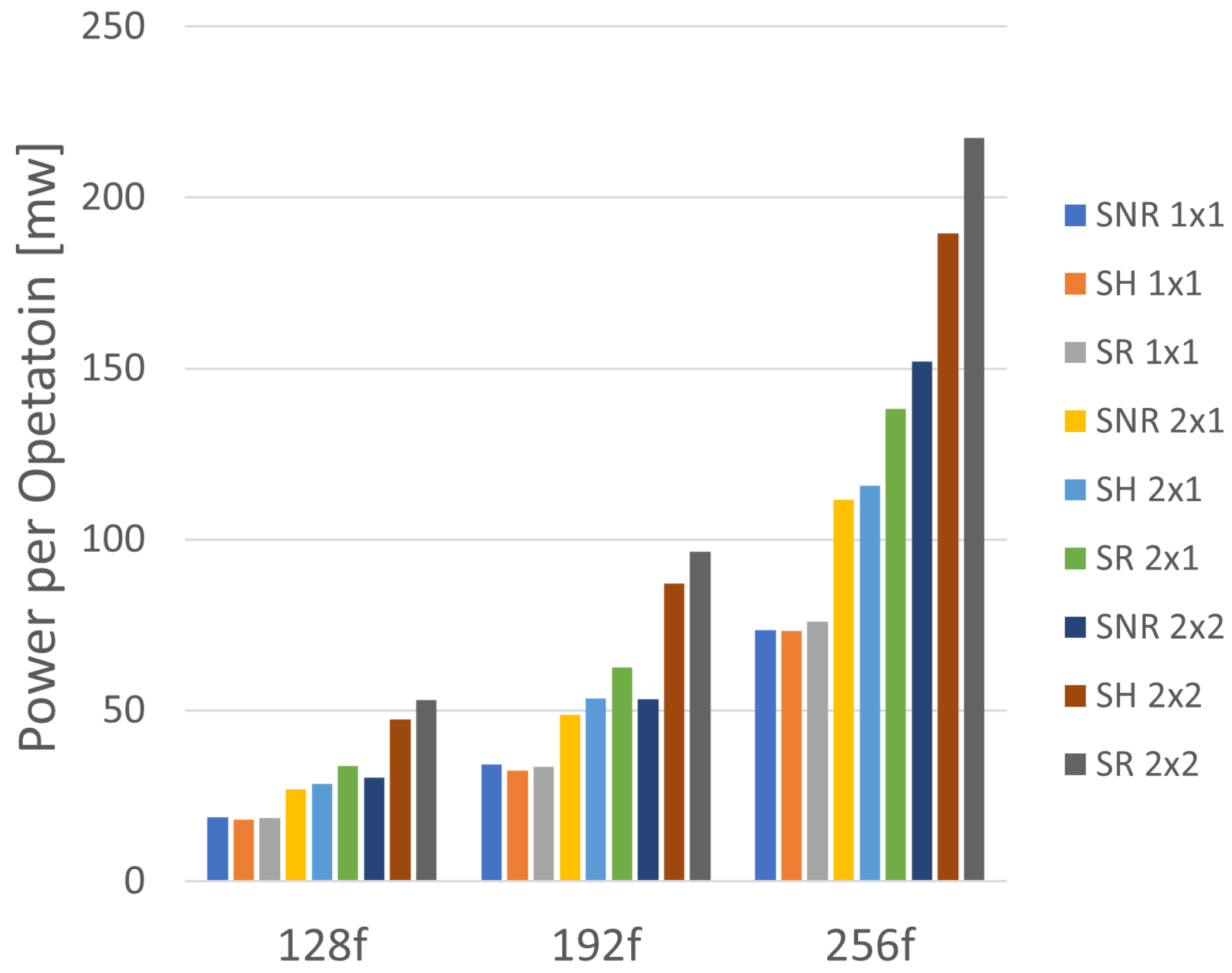
6.3. Power

Power estimations are difficult to project for different variations, but we would expect faster designs to have lower power per operation. As we learned in [28], the long run-time of the SPHINCS+ algorithm has a significant impact on power consumption. To provide a fair comparison across all variants, we evaluated the design at 100 MHz. The power consumption results are shown in Figure 10 for the small signature types of SPHINCS+, and Figure 11 for the fast types.

Further, the hybrid model balances the throughput of the SNR variant with the lower power area of the SR variant, resulting in the optimal model for power-constrained devices. We list the optimal combinations, combined with the maximum possible clock frequency, in

Table 6. The optimal combinations for each SPHINCS+ variant with respect to power consumption.

Scheme	Variant	Frequency [MHz]	E_Sign [mW]
SPHINCS+ 128s	SH 1 × 1	150	330
SPHINCS+ 192s	SR 1 × 1	150	639
SPHINCS+ 256s	SH 1 × 1	150	628
SPHINCS+ 128f	SNR 1 × 1	150	17.4
SPHINCS+ 192f	SH 1 × 1	150	30.1
SPHINCS+ 256f	SH 1 × 1	150	67.1

. When measuring the maximum clock frequency, the power consumption estimator from Vivado was run with the recommended parameters. For all variants, the 1 × 1 PPC combination proved to be optimal, with the SH model being the most consistent for minimal power consumption per operation.

Despite the reduced run-time for the increase in PPC, the doubling of PPC for the primary unit and secondary unit had a significant, nearly 20% increase in power per operation for each variant. The worst performance was on the 2 × 2 models, in which the secondary hash unit PPC impacted the resource count without reducing the run-time.

6.4. Design Comparison

To test the viability of our implementation, we compared our results against other PQC implementations, looking at both general designs and architectures targeting resource-constrained devices. This comparison is shown in

Table 7. A comparison of different FPGA-based PQC implementations, with a focus on area and power reduction. N/A: Not applicable.

	Variant	Level	Resources				Max Freq.	Sig. Time	Power	PPS
Scheme			LUT	FF	BRAM	DSP	MHz	ms	W	mW
SPHINCS+ 128s	SH 1 × 1	1	12 k	7.8 k	1	0	150	674	0.49	330
SPHINCS+ 192s	SR 1 × 1	3	13 k	9.8 k	1	0	150	1321	0.48	639
SPHINCS+ 256s	SH 1 × 1	5	14 k	9.5 k	1	0	150	1247	0.50	628
SPHINCS+ 128f	SNR 1 × 1	1	14 k	6.7 k	1	0	150	34.4	0.51	17
SPHINCS+ 192f	SH 1 × 1	3	13 k	8.7 k	1	0	150	61.3	0.49	30
SPHINCS+ 256f	SH 1 × 1	5	13 k	9.6 k	1	0	150	134	0.50	67
Ascon-Sign 128s [28]	1 × 1	N/A	6.5 k	5.9 k	1	0	150	1027	0.27	277
Ascon-Sign 128s [28]	2 × 1	N/A	7.4 k	5.9 k	1	0	150	548	0.33	180
SPHINCS+ 128s [24]	-	1	6.1 k	4.7 k	1	0	154	985	0.41	403
SPHINCS+ 128f [24]	-	3	6.1 k	4.9 k	1	0	156	64	0.40	26
SPHINCS+ 256s [24]	-	5	8.7 k	6.3 k	1	0	149	1735	0.47	815
SPHINCS+ 256f [24]	-	1	8.7 k	6.3 k	1	0	152	199	0.46	92
SPHINCS+ 128s [25]	-	3	48 k	73 k	11.5	0	500	12.4	9.7	120
SPHINCS+ 256s [25]	-	5	51 k	75 k	22.5	1	500	19.3	9.8	188
SPHINCS 256 [34]	-	N/A	19 k	38 k	36	0	525	1.53	5.0	7.60
Falcon 512 [22]	-	1	168 k	162 k	111	1.5 k	100	4.2	N/A	N/A
Falcon 1024 [22]	-	5	174 k	163 k	135	1.5 k	100	8.7	N/A	N/A
Falcon 512 [35]	-	1	80.5 k	47 k	45	220	185	0.086	N/A	N/A
Falcon 1024 [35]	-	5	80.5 k	47 k	85	220	185	1.73	N/A	N/A
Dilithium II [36]	-	2	54 k	28 k	29	16	256	0.117	N/A	N/A
Dilithium III [36]	-	3	54 k	28 k	29	16	256	0.193	N/A	N/A
Dilithium V [36]	-	5	54 k	28 k	29	16	116	0.475	N/A	N/A
Dilithium V [37]	-	5	14 k	6.8 k	35	4	163	0.699	N/A	N/A

. To compare our design against the other PQC algorithms, we chose the functions with optimal energy consumption, as that was the primary motivation behind our experimentation. Other SPHINCS+ implementations that we compared against focused on area reduction [24] and maximizing throughput [25].

We still believe that energy per signature is the primary aspect that should be considered for edge devices, as it will have the largest impact on battery life. Area consumption must be reasonable, as large devices will lead to high static power consumption but should not be the primary focus of the design. As expected, our design does not have the highest throughput when compared to implementations that do not consider power or area to be a constraint. Despite this, when compared against other SPHINCS+ implementations for resource-constrained devices, our power efficiency per operation showed up to a 23% reduction in the small signature variant of SPHINCS+ and a 35% reduction in power for the fast variant. This did not include large designs that have over 5W of operating power consumption.

Further, when compared to other resource-constrained designs, our implementation also runs faster, showing up to a 25% reduction in run-time. This may account for a significant portion of the power reduction, as our design shows increased resource consumption.

Our SHAKE-based SPHINCS+ implementation does not show improvements over Ascon-Sign. As Ascon-Sign is based on the lightweight hashing function Ascon, it would be infeasible for a typical hash function to show similar reductions in power and resource consumption. Ascon-Sign, however, is not certified by NIST as a PQC-safe algorithm. This highlights the gap between NIST certifications and the requirement of IoT nodes for a lightweight signature algorithm.

We also compare our work against multiple Dilithium and Falcon implementations in Table 7. Each of these works focuses primarily on signature time and does not include power consumption results. Therefore, we can only make comparisons for the area. As predicted in Section 2, each of the implementations requires DSPs to handle the mathematical complexities of the targeted algorithm. Further, among the Falcon designs, all but one of the Dilithium designs require significantly more resources than our SPHINCS+ implementation. Only one Dilithium design has comparable LUT and FF requirements. However, both Falcon and Dilithium implementations demonstrate a faster run-time. This is to be expected, as the NIST benchmarking for the approved algorithms consistently shows SPHINCS+ to be the slowest of the three algorithms.

7. Conclusions

In this work, we presented an optimized FPGA architecture for a SHAKE-based SPHINCS+ signature scheme targeting low-power IoT devices. Our design differs from prior work by introducing parallelized SHAKE modules, configurable PPC, and unified hardware modules that are reused throughout the entirety of signature generation, reducing area requirements. We also introduce a novel proposition to the SPHINCS+ algorithm in which a modification to the random oracle model removes the need for message storage, opening the possibility of arbitrarily long messages. Together, these optimizations reduce the energy per signature by 20–30%, while maintaining a modest area of 12–14k LUTs across all SPHINCS+ security levels.

Compared to existing SPHINCS+ FPGA implementations, our approach achieves significantly lower power per signature without relying on DSPs or large memory blocks, making it well-suited for resource-constrained IoT platforms. These results demonstrate that SPHINCS+, often considered too costly for power and area-limited hardware environments, can be engineered into a practical low-power PQC signature scheme. Future work includes extending the evaluation to physical FPGA prototypes and exploring lightweight ASIC projections for energy-critical applications.