Fairness-Based User Scheduling and Performance Optimization in Energy Harvesting Cognitive Network

Abstract

In this work we consider a cognitive radio network with a energy harvesting relay that facilitates coexistence between primary users and multiple secondary users (SU) and a secondary destination. We analyze the outage performance of this cognitive radio network that employs a decode-and-forward (DF) relay and harvests energy from the secondary user’s transmitted signal. Cumulative distribution function-based user scheduling is performed for equitable allocation of channels to each SU. We consider block Rayleigh fading channels and derive novel closed-form expressions for the outage probability and system throughput. Monte Carlo simulations are conducted to verify the accuracy of the outage expression. We also develop the expression for the outage probability at a high interference threshold and utilize it to examine the impact of the power splitting factor ($\alpha$) on overall performance. Our results demonstrate that through using an optimum power splitting factor the outage performance can be enhanced by nearly 2 dB.

1. Introduction

The next generation of wireless communication systems will have to accommodate about 100 billion connected devices, including cellular mobiles, cars, sensors, medical, and wearable devices, etc. [1]. Device-to-device communications (D2D), and vehicle-to-vehicle communications (V2V) will be possible due to the ultra-high data rate in 5G technology [2]. Fifth generation networks target efficient spectrum allocation and minimum interference for crowded networks. These dense networks increase the demand for radio resources, constraining the available spectrum leading to un-equitable resource allocation and degrading the quality of service (QoS). Cognitive Radio (CR) in 5G communication technology plays an important role of providing higher spectral efficiency, by accommodating the secondary users in the primary user (PU) frame without disrupting the present communication [3,4,5]. A cognitive network (CRN) can sense the environment and gather information such as power, frequency, and interference level. With this sensing ability, secondary users (SUs) can identify the vacant spectrum and utilize it for transmission. SUs can also adjust its parameters according to the sensed information to improve the QoS. PUs have priority to carry on its transmission as they co-exist with secondary users. CRN achieves spectral efficiency by permitting the secondary users to access the primary user’s spectrum using one of the three configurations—spectrum overlay, interweave, and spectrum underlay [6]. CRNs with cooperative relaying have been studied to enhance reliability as well as system capacity [7,8,9,10,11]. In [7], the authors consider a two-way cognitive radio network and perform joint power control and resource allocation. The authors in [8] investigated the multiple relay system where an optimal relay was selected for data transmission. The performance of underlay CRN has been investigated in terms of outage probability in [9] where a relay node can assist in both the primary and secondary transmission. The authors in [10,11] studied multiuser CRNs with multiple sources and destinations and analyzed the system outage probability performance. A stable power supply is obligatory for uninterrupted relay operation because wireless communication systems are powered using batteries that need to be charged or replaced on a regular basis. In this context, wireless energy harvesting (EH), which recharges batteries using energy gathered from ambient signals, is a potential method to extend the operational time of electronic communication devices [12,13]. While the above works did not consider EH technology, in recent years, many researchers have combined EH technology with CRNs and successfully constructed novel EH-based CRNs to achieve green communication. In [14], two notable energy harvesting receiver architectures—the power splitting (PS) receiver and the time switching (TS) receiver—are proposed and analyzed. In a PS receiver, a portion of the power from the received signal is utilized to generate energy, while the residual power is employed to retrieve data. A TS receiver allocates time to collect energy from the incoming signal and subsequently retrieves information from it. Based on PS, two functional receivers that simultaneously harvest RF energy and receive information are proposed in [15]. The RF energy harvesting relaying system improves the performance of CRN [16,17]. The optimization of the throughput of an EH-CRN was studied [18]. In [19], a cognitive relay network with an underlay architecture is proposed, featuring multiple primary user (PU) transceivers and a secondary network where the secondary source and relay can harvest energy from the primary network. The system performance metrics such as outage probability and throughput are derived. In [20,21], the outage performance of a decode-and-forward (DF) EH-cognitive relay network with multiple primary transmitters was studied. In [22] a novel galloping–flutter coupled nanogenerator (GFNG) is proposed that leverages the synergistic interaction between galloping and flutter to achieve high performance across broad wind speed bandwidth. This study offers new insights into designing high-performance aerodynamics-driven nanogenerators by harnessing multiple flow-induced vibrations (FIV) synergistic effects, broadening the potential for intelligent wind energy applications. In [23] the application of energy harvesting (EH) technology in Cognitive Industrial Internet of Things (CIIoT) is proposed which permits Secondary Users (SUs) to use the spectrum bands owned by Primary Users (PUs) opportunistically and can exacerbate the threat of security. While aforementioned work considered single secondary user (SU) scenarios, ref. [24] extended their study to focus on a multiuser EH-cognitive relay network where the best secondary user is selected by taking into consideration both the direct and relay link. In [25], the performance of a multiuser CRN with multiple primary transmitters was considered and an optimal SU was selected so as to maximize the received SNR at the secondary destination using maximal ratio combining. Their results indicate that both cooperative diversity and multiuser diversity are achieved. An energy harvesting overlay CRN with multiple randomly distributed SUs that assist the PU transmission is considered in [26]. Power allocation and time switching parameter are optimized to maximize the PU data rate. In [27], a EH-CRN with multiple PU, multiple relays, and a single SU and destination is considered. The best relay selection is performed and the outage performance is analyzed considering non-linear energy harvesting. Efficiently managing the allocation of resources and scheduling among multiple users is a crucial concern for preserving the capacity, energy efficiency, and fairness of a communication system. The authors in [28] analyze the outage probability in multiuser relaying system in the presence of interference, where optimal relay selection is performed based on the instantaneous channel state information (CSI). In [29], a multiuser spectrum-sharing CRN with multiple relays is investigated. The greedy scheduling strategy allocates radio resources to the user with the highest channel gain [30]. Nevertheless, in order to implement this scheduling method, it is imperative that instantaneous CSI is available at the transmitter. The utilization of an incremental relaying mechanism and a decentralized scheduling technique in [31] significantly enhances the efficiency of multiuser multi-relay networks. One of the major challenges in multiuser systems is related to fairness in resource allocation [32]. The aforementioned works did not consider cumulative distribution function (CDF)-based scheduling. In order to ensure fairness in the long-term average transmission rates among different links, the authors in [33] consider PF scheduling in CRN with spectrum underlay. In order to improve the fairness in channel access amongst multiple users in a wireless scenario, the authors in [34,35,36] proposed scheduling based on the cumulative distribution function (CDF). This approach ensures that users with better channel conditions are not consistently prioritized, resulting in improved fairness across the system. The authors in [37] analyzed proportional fairness (PF)-based scheduling and cumulative distribution (CDF)-based scheduling for ambient backscatter (AmBack) communication systems consisting of one RF source, multiple AmBack transmitters, and one AmBack receiver. The authors also derived an asymptotic expression to analyze multiuser diversity order, which is different from the other works that we have considered, since they focused only on EH-CRN with multiple secondary users and a CDF-based scheduling scheme for fairness in channel access. To the best of our knowledge, the performance of EH-CRN with a fairness-promoting scheduling scheme based on a user’s CDF has not been studied in the literature. The key contributions of this study are as follows:

• Novel expression for the outage probability (OP) of a CRN with an EH-relay and CDF-based user scheduling for fairness in channel access to the secondary users is obtained.
• An asymptotic expression for the OP is derived to study the effect of the power splitting factor on the system performance.
• We formulate the objective function for optimal power splitting factor, and, by using numerical methods, obtain the optimum value that minimizes the OP of the system.
• We also obtain the analytical expression for the throughput of the system.

The rest of this paper is organized as follows. In Section 2 we discuss the system model. In Section 3 we derive the expressions for the performance metrics. Section 4 illustrates the results and the findings of the study. Finally, in Section 5, we provide the conclusions.

2. System Model

We consider a multiuser EH-CRN comprising N secondary users $\left\{S{U}_n\right|n=1,2,\dots ,N\}$, a secondary energy harvesting decode-and-forward relay (R), a secondary destination (D), and a primary destination ($PD$), as depicted in Figure 1. The same spectrum as $PD$ is utilized by all SUs and a relay, keeping their transmit power to the extent that the primary destination’s interference stays below a certain threshold. The relay harvests RF energy from SU and employs power splitting to decode-and-forward the data to D with harvested energy. We assume that all secondary users are at non-identical distances from the relay. Further, all channel links in the network experience flat Rayleigh fading.

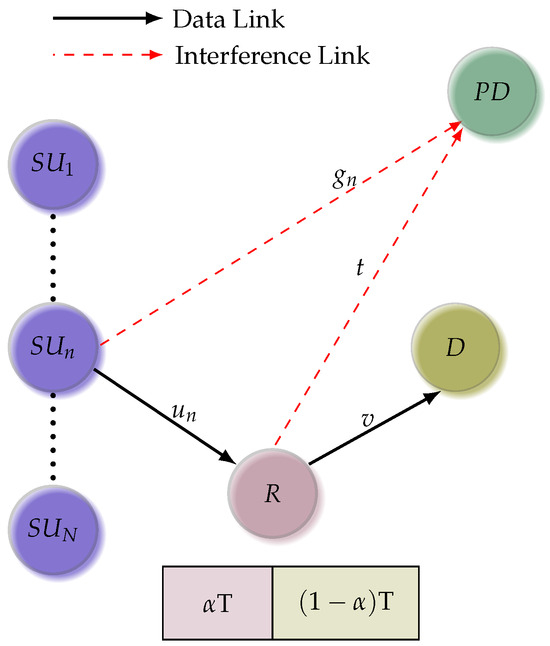
Figure 1. A multiuser cognitive network with energy harvesting relay.

In the first time slot of duration T, a secondary user $S{U}_n$ is selected for information and energy transmission. The unit energy message symbols x are transmitted by $S{U}_n$. The relay R acquires energy from the broadcast signal during the $\alpha T$ interval, decodes the information symbol, then forwards the information to the secondary destination D during the remaining $(1-\alpha )T$ interval. Here, $\alpha$ is the power splitting factor. The signal received at the relay R is mathematically given by the following:

$$y_{S{U}_n,R}=\sqrt{P_n}{h}_{S{U}_n,R}{x}_n+n_R$$

(1)

where $h_{S{U}_n,R}$ and the channel gain of nth $SU$ and R link, $P_n$ is the transmit power of $S{U}_n$, and $n_R\sim \mathcal{CN}(0,{\sigma }_R^2)$ is the additive white Gaussian noise (AWGN) at R. Since we are considering a cognitive network with underlay topology, the peak interference level at $PD$ should therefore be within the range of a specified threshold $I_p$. Therefore, the transmit power $P_n$ at $S{U}_n$ is given as follows:

$$P_n={\displaystyle \frac{I_P}{|h_{S{U}_n,PD}{|}^2}}$$

(2)

The harvested energy at relay R is given by the following:

$$E_{hr}=\eta \alpha P_n{\left|h_{S{U}_n,R}\right|}^{2}T$$

(3)

where $\eta$ represents the energy conversion efficiency coefficient of the energy harvester at R. The received signal at the relay is decoded and forwarded to the $PD$ in the interval $(1-\alpha )T$. The transmit power of the relay ($P_r$) is limited by the energy harvested ($E_{hr}$) and the peak interference power at $PD$. The received signal at the secondary destination (D) is mathematically given by the following:

$$y_{R,D}=\sqrt{P_r}{h}_{R,D}{x}_n+n_D$$

(4)

where, $h_{R,D}$ is the channel gain coefficient of R to D link, and $n_D\sim \mathcal{CN}(0,{\sigma }_D^2)$ is the AWGN noise at destination.

The relay transmit power $P_r$, under the peak interference constraint $I_P$ at $PD$, is given by the following:

$$P_r=\min \left[{\displaystyle \frac{\eta \alpha P_n{\left|h_{S{U}_n,R}\right|}^2}{(1-\alpha )}},{\displaystyle \frac{I_P}{|h_{R,PD}{|}^2}}\right]$$

(5)

Let, ${\tilde{I}}_P={\displaystyle \frac{I_P}{{\sigma }_R^2}}$, and $u_n={\left|h_{S{U}_n,R}\right|}^2$, $g_n={\left|h_{S{U}_n,PD}\right|}^2$, $v=|h_{R,D}{|}^2$, and $t=|h_{R,PD}{|}^2$, which are exponentially distributed with parameters ${\lambda }_{u_n}$, ${\lambda }_v$, ${\lambda }_{g_n}$, and ${\lambda }_t$ respectively. Using (1) and (4), the received signal-to-noise ratio (SNR) at the relay and destination denoted by ${\Gamma }_{S{U}_n,R}$ and ${\Gamma }_{R,D}$, respectively, (6) and (7) can be obtained as below:

$${\Gamma }_{S{U}_n,R}={\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}$$

(6)

$${\Gamma }_{R,D}=\min \left({\displaystyle \frac{{\tilde{I}}_P\eta \alpha v{u}_n}{g_n(1-\alpha )}},{\displaystyle \frac{{\tilde{I}}_{P}v}{t}}\right)$$

(7)

CDF-Based Scheduling

We consider that the channel gains of the nth secondary user ($S{U}_n$) to R link are i.ni.d. Therefore, in order to promote fairness in channel access to the user, CDF-based scheduling is performed before the start of transmission. The CDF-based scheduling allows precise control over the channel access to each user. Let $w_n$ be the channel access ratio of the nth user such that ${\sum }_{n=1}^N{w}_n=1$ and let $F_{u_n}\left(u_n\right)$ be the cumulative distribution function of the channel gain $u_n$ which is exponentially distributed with parameter ${\lambda }_{u_n}$. The nth secondary user is selected based on CDF-based scheduling as follows:

$$n^{*}=\underset{nϵ1,2\dots N}{\arg \max }{\left(F_{u_n}\left(x\right)\right)}^{{\displaystyle \frac{1}{w_n}}}.$$

(8)

A large value of $w_n$ signifies that the nth user will be scheduled more as compared to the other users for data transmission, and, by ensuring that $w_n={\displaystyle \frac{1}{N}}$, we can maintain fairness in channel access to all secondary users. CDF-based scheduling often requires frequent channel state information, which can introduce substantial signaling overhead—especially with many users and rapidly changing channels. However, the proportional fair scheduling also suffers from similar challenges in implementation.

3. Outage Probability

With $R_T$ denoting the target rate, and ${\gamma }_{th}=2^{2R_T}-1$ the target SNR, the outage probability (OP) with CDF-based user scheduling in (8) is given by:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_{out}& ={\displaystyle \sum _{n=1}^N}\mathrm{Prob}(\left(n^{*}=n\bigcap \min \left({\Gamma }_{S{U}_n,R},{\Gamma }_{R,D}\right)\right)<{\gamma }_{th})\hfill \\ \hfill & ={\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\Gamma }_{S{U}_n,R}<{\gamma }_{th}\right)+{\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\Gamma }_{S{U}_n,R}>{\gamma }_{th}\right)\mathrm{Prob}\left({\Gamma }_{R,D}<{\gamma }_{th}\right)\hfill \end{array}\end{array}$$

(9)

Substituting the values from (6) and (7) in (9), the expression for OP can be expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_{out}& ={\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}<{\gamma }_{th}\right)+{\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}>{\gamma }_{th}\right)\mathrm{Prob}\left(\min \left({\displaystyle \frac{{\tilde{I}}_P\eta \alpha v{u}_n}{g_n(1-\alpha )}},{\displaystyle \frac{{\tilde{I}}_{P}v}{t}}\right)<{\gamma }_{th}\right)\hfill \\ \hfill & =\underset{I_1}{\underbrace{{\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}<{\gamma }_{th}\right)}}+\underset{I_2}{\underbrace{{\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}>{\gamma }_{th},{\displaystyle \frac{{\tilde{I}}_P\eta \alpha v{u}_n}{g_n(1-\alpha )}}<{\gamma }_{th}\right)}}\hfill \\ \hfill & +\underset{I_3}{\underbrace{{\displaystyle \sum _{n=1}^N}{w}_n\mathrm{Prob}\left({\displaystyle \frac{{\tilde{I}}_P{u}_n}{g_n}}>{\gamma }_{th},{\displaystyle \frac{{\tilde{I}}_P\eta \alpha v{u}_n}{g_n(1-\alpha )}}>{\gamma }_{th},{\displaystyle \frac{{\tilde{I}}_{P}v}{t}}<{\gamma }_{th}\right)}}\hfill \end{array}\end{array}$$

(10)

After some involved mathematical manipulations (in Appendix A, Appendix B and Appendix C), and solving for $I_1$, $I_2$, $I_3$, the final equations for the outage probability (OP) can be expressed as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{P}_{out}=1+\sum _{n=1}^N\sum _{k=1}^{\infty }\sum _{m=1}^M\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right){\displaystyle \frac{{(-1)}^{k+m+1}{w}_n}{1+\frac{k\theta {\lambda }_{g_n}}{m{\lambda }_{u_n}}}}+\sum _{n=1}^N\sum _{k=1}^{\infty }\sum _{m=1}^M\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right){\displaystyle \frac{{(-1)}^{k+m+1}{w}_n}{{\lambda }_v}}\hfill \\ \times \left[{\displaystyle \frac{\theta k{\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_{u_n}}}\exp \left({\displaystyle \frac{\theta k{\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_{u_n}}}\right)\mathrm{Ei}\left(-{\displaystyle \frac{\theta k{\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_{u_n}{\lambda }_v}}\right)+{\lambda }_v-{\displaystyle \frac{{\lambda }_v}{1+\frac{\theta k{\lambda }_{g_n}}{m{\lambda }_{u_n}}}}\right]\hfill \\ +\left(\sum _{n=1}^N\sum _{k=1}^{\infty }\sum _{m=1}^M\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right){(-1)}^{k+m}{\displaystyle \frac{w_n}{1+\frac{k\theta {\lambda }_{g_n}}{m{\lambda }_{u_n}}}}\right)\times \left({\displaystyle \frac{1}{1+\frac{{\lambda }_v}{\theta {\lambda }_t}}}\exp \left(-\left({\displaystyle \frac{1}{\theta {\lambda }_t}}+{\displaystyle \frac{1}{{\lambda }_v}}\right)\left({\displaystyle \frac{(1-\alpha )}{\eta \alpha }}\right)\right)\right)\hfill \\ +\sum _{n=1}^N\sum _{k=1}^{\infty }\sum _{m=1}^M\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right){(-1)}^{k+m}{w}_n{\int }_0^{{\displaystyle \frac{(1-\alpha )}{\theta \eta \alpha }}}(1-\exp \left(-{\displaystyle \frac{\theta t}{{\lambda }_v}}\right)+{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\hfill \\ \exp \left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\right)\left[\mathrm{Ei}\left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\right)-\mathrm{Ei}\left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}+{\displaystyle \frac{\theta t}{{\lambda }_v}}\right)\right])f_t\left(t\right)dt\hfill \\ +\left(\sum _{n=1}^N\sum _{k=1}^{\infty }\sum _{m=1}^M\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{M}}\right){(-1)}^{k+m}{w}_n\right(1-\exp \left(-{\displaystyle \frac{(1-\alpha )}{\eta \alpha {\lambda }_v}}\right)+{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\hfill \\ \exp \left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\right)\left[\mathrm{Ei}\left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}\right)-\mathrm{Ei}\left(-{\displaystyle \frac{k\theta {\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_v{\lambda }_{u_n}}}+{\displaystyle \frac{(1-\alpha )}{\eta \alpha {\lambda }_v}}\right)\right]\left)\right)\hfill \\ \times \left(\exp \left[-{\displaystyle \frac{(1-\alpha )}{\eta \alpha \theta {\lambda }_t}}\right]\right)\hfill \end{array}\end{array}$$

(11)

3.1. Asymptotic Outage

The asymptotic expression for the OP as $I_P\to \infty$ is given by the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill P_{out}^{asym}& =1+{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \sum _{m=1}^M}\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right){(-1)}^{k+m+1}{w}_n\times \left(1-{\displaystyle \frac{k\theta {\lambda }_{g_n}}{m{\lambda }_{u_n}}}\right)+{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{k=1}^{\infty }}{\displaystyle \sum _{m=1}^M}\left({\displaystyle \genfrac{}{}{0pt}{}{\frac{1}{w_n}}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{M}{m}}\right)\hfill \\ \hfill & {(-1)}^{k+m+1}{w}_n\times [{\displaystyle \frac{\theta k{\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_{u_n}{\lambda }_v}}\ln \left({\displaystyle \frac{\theta k{\lambda }_{g_n}(1-\alpha )}{m\eta \alpha {\lambda }_{u_n}{\lambda }_v}}\right)+{\displaystyle \frac{\theta {\lambda }_t}{{\lambda }_v}}+\exp \left(-{\displaystyle \frac{(1-\alpha )}{\eta \alpha \theta {\lambda }_t}}\right)\hfill \end{array}\end{array}$$

(12)

The proof is presented in Appendix D.

3.2. Optimal Power Splitting Factor

To optimize power splitting factor $\alpha$ at the relay while minimizing OP in the context of CDF-based scheduling (12), the objective function can be mathematically represented as follows:

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill {\alpha }_{opt}& \hfill =& \underset{\alpha }{\arg \min }{P}_{out}^{asym},\hfill \\ & & \mathrm{subject}\mathrm{to}0<\alpha <1\hfill \end{array}\end{array}$$

(13)

Finding a closed-form equation for the optimal powers splitting factor might be challenging. Standard iterative root-finding procedures, such as the Bisection method, can be used to find a numerical solution. Increasing $\alpha$ generally boosts the amount of harvested energy at the secondary user or relay node, as more RF power is directed to the EH circuitry.

3.3. Throughput

In this section, we evaluate the throughput for a EH-cognitive network. The relay decodes the received information symbol x from $SU$ and transmits to D at a rate denoted by $R_T$, where

$$R_T={\displaystyle \frac{1}{2}}{\log }_2(1+{\gamma }_{th})$$

The throughput is expressed as follows:

$${\zeta }_T={\mathrm{R}}_T(1-P_{out}\left({\gamma }_{th}\right)),$$

where ${\zeta }_T$ is the rate of successful transmissions when ${\gamma }_{th}$ is satisfied at relay R. We use the expression derived in (11) to evaluate ${\zeta }_T$.

4. Simulation Results

In order to verify the accuracy of the analytical equations and examine the effects of several parameters on the system performance, including the number of users (N), power splitting factor ($\alpha$), and interference threshold ($I_P$), we provide the simulation results in this section of the paper. The Rayleigh flat fading is experienced by each link in the system. We consider a two-dimensional network layout in which the relay is positioned between the secondary users and the secondary destination, and the secondary nodes are situated along the X-axis. The distance between each secondary user and the relay to the primary destination is fixed at two, whereas the distance between the relay and secondary destination is assumed to be one. All the secondary users are placed at varying distances from the relay. We assume a path loss factor of 3 for the simulation and we set the channel gain of $SU$ to relay link as $u_n={(1-d)}^{-3}$, where d is the distance between $SU$ and D. The noise variance at R and D is set to 1. At the relay $\eta$, the energy harvester’s conversion efficiency is set to 0.7. Furthermore, ${\gamma }_{th}$, the SNR threshold, is set to 3. The simulation parameters are described in Table 1.

Table 1. Simulation parameters and description.

Parameter	Description	Value
$\alpha$	Power splitting factor	[0, 1]
$\beta$	Path loss exponent	3
$\eta$	Energy conversion efficiency	0.7
${\sigma }_R^2$	Noise variance at relay	1
${\sigma }_D^2$	Noise variance at destination	1

In Figure 2, for the system under consideration, we plot OP against the interference threshold ($I_P$), considering the number of secondary users $N=\{2,3,5\}$. We also consider an equal channel access ratio for each user, i.e., $w_n={\displaystyle \frac{1}{N}}$. Simulations are performed to verify the accuracy of the analytical expression for OP in (11) and the asymptotic expression for the OP (12). In the analytical expression (11), the infinite summation term can be truncated to those listed in the Table 2 to maintain the truncation precision. From Table 2, k = 2 terms have been used to obtain the results over a wide range of different parameters, and increasing the values beyond k = 2 does not have significant influence on performance metrics. Figure 2 shows that the asymptotic expression converges with the simulation at large values of $I_P$, while the analytical expression for the OP is close to the simulation result. The derived equations for OP are therefore validated.

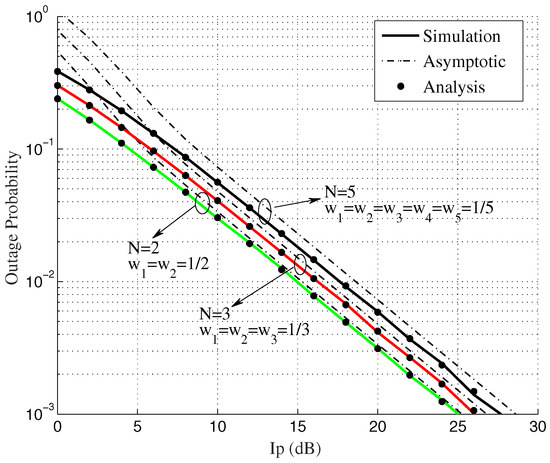
Figure 2. Outage probability v/s interference threshold for N = 2, 3, 5 and equal CAR.

Table 2. Truncation accuracy of summation limit.

Parameter	Truncation	${\mathit{P}}_{\mathit{out}}$
$I_P$ = 10 dB	k = 2	0.00939
	k = 5	0.00939
	k = 10	0.00939
	k = 50	0.00939
$I_P$ = 15 dB	k = 2	0.00298
	k = 5	0.00298
	k = 10	0.00298
	k = 50	0.00298
$I_P$ = 20 dB	k = 2	0.00094
	k = 5	0.00094
	k = 10	0.00094
	k = 50	0.00094

For estimating the number of terms to be included in the truncated series representation of outage probability in (11), the Knee Point Method is used. In Figure 3, we plot the outage probability as a function of number of terms (k) for varying interference thresholds, Ip = 10 dB, 15 dB, 20 dB. A knee point on a curve is the location where the curve changes most sharply from a steep to a slowly changing slope. We observe that increasing the value beyond k = 2 does not have significant influence on the accuracy of the outage probability performance.

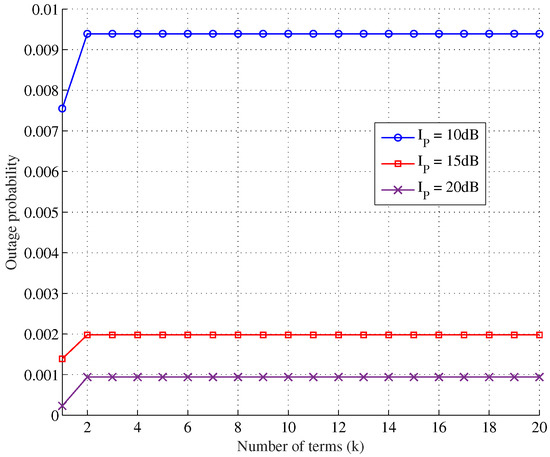
Figure 3. Outage probability v/s number of terms (k).

Figure 4 illustrates the effect of unequal channel access ratio on the system outage probability. We plot the OP versus interference threshold for the considered system, considering the number of secondary users $N=\{2,3,4\}$. We also consider unequal channel access ratio for each user, i.e., $w_n=(0.50007,0.49993),(0.4,0.3,0.3),(0.3,0.2333,0.2333,0.2333)$. Simulations are performed to verify the accuracy of the analytical expression for the OP in (11); the asymptotic expression for the OP (12). Figure 4 shows that the asymptotic expression converges with the simulation at large values of $I_P$, while the analytical expression for the OP is close to the simulation result. The derived equations for OP are therefore validated.

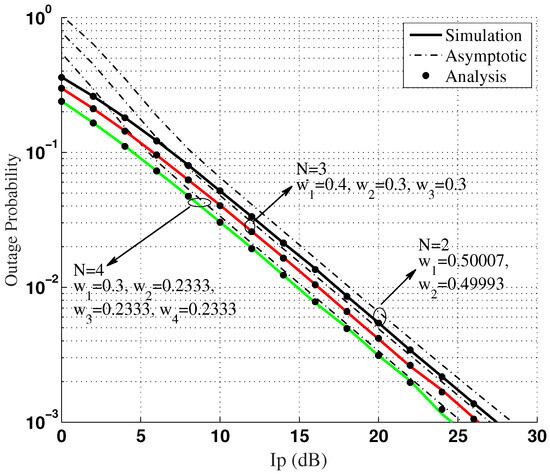
Figure 4. Outage probability v/s interference threshold for N = {2, 3, 4} and unequal CAR.

In Figure 5, we vary the power splitting factor $\alpha$∈{0,1} and plot the outage probability (OP) for varying interference thresholds, $I_p$ = 3 dB, 5 dB, 10 dB, 15 dB, considering N = 3, $w_1$ = $w_2$ = $w_3$ = 1/3 and d = 1. We see that, outage probability first decreases with increase in the power splitting factor $\alpha$. This is because for small values of $\alpha$, relay harvests insufficient energy for a reliable information transmission; therefore, the outage probability is high. As $\alpha$ goes on increasing, more power is available to the relay for successful transmission; however, the transmission time ($1-\alpha$)T is reduced and this leads to an increase in the outage probability as $\alpha \to 1$. In the figure the outage probability decreases and then increases as the $\alpha$ varies in the range (0, 1), indicating that there is an optimal value of power splitting factor ${\alpha }_{opt}$ obtained by solving (13) for which the outage performance is optimal. In the figure, the values of ${\alpha }_{opt}$ are obtained as {0.6, 0.64, 0.78, 0.88}, respectively, for $I_p$ = 3 dB, 5 dB, 10 dB, 15 dB. From the figure, $P_{out}$ = 0.02634 when $I_P$ = 15 dB and $\alpha$ = 0.5 and $P_{out}$ = 0.02197 when $I_P$ = 15 dB and ${\alpha }_{opt}$ = 0.9. Using ${\alpha }_{opt}$, a 2.1 dB improvement in the OP is obtained for N = 3 users and $I_P$ = 15 dB. Similarly, the OP improves by {2.3 dB, 2.4 dB, 3 dB} for N = 3 users and $I_P$ = {3 dB, 5 dB, 10 dB}.

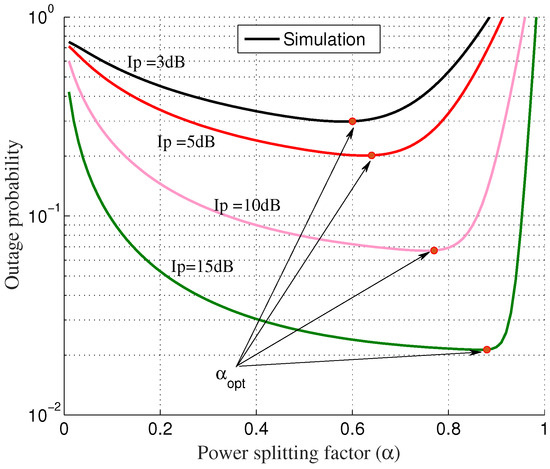
Figure 5. Outage probability v/s $\alpha$ for $I_P$ = {3 dB, 5 dB, 10 dB, 15 dB}.

In Figure 6 we plot the throughput as a function of $I_P$ for different values of d = {1, 1.2, 1.4, 1.6, 1.8, 2}). It can be seen that the throughput increases with $I_P$ and then attains a steady value. This is due to the fact that as $I_P$ increases relay can transmit at higher powers with acceptable interference at the primary destination. However, the OP of the considered system is dependent on two hops, and the second hop is the bottle-neck link leading to the convergence of the throughput values with increasing $I_P$.

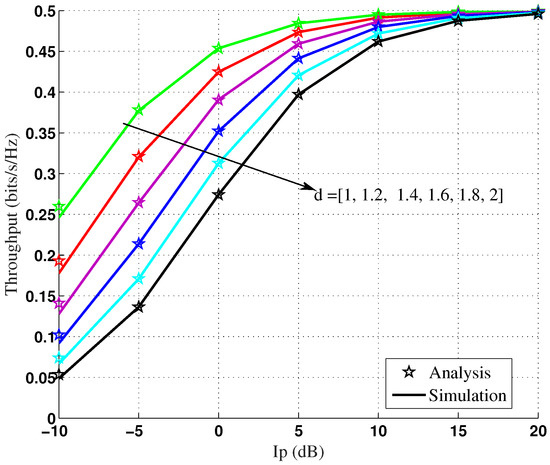
Figure 6. Throughput v/s $I_P$ for d = {1, 1.2,1.4,1.6, 1.8, 2}.

In Figure 7 we plot the throughput as a function of $I_P$ for different values of N = {2, 5, 10, 15}) for d = 1. The throughput increases as $I_P$ increases initially and attains study value. The reason is that as $I_P$ increases relay can transmit at higher powers with acceptable interference to the PD. However, by increasing the number of users N, the first hop SNR improves for lower values of $I_P$ as depicted in the figure and the throughput converges to steady value for a varying number of users. Also, throughput is calculated as the multiplication of the transmission rate and the probability of the non-outage event. With the increase in $I_P$, the allowed transmit power of relay will increase, which reduces outage probability and obtains a higher throughput.

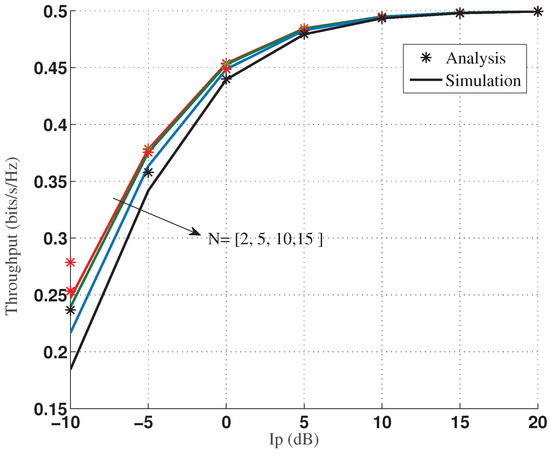
Figure 7. Throughput v/s $I_P$ for N = {2, 5, 10, 15}.

5. Conclusions

In this work, the outage analysis of a multiuser cognitive network with energy harvesting relay was investigated in the presence of co-channel interference. CDF-based scheduling was used to achieve fairness in user selection. It was observed that the derived analytical outage expression matches the simulation results over a wide range of parameters. We also obtained the asymptotic expression for the outage probability and optimized the power splitting factor. Our results revealed that optimum power splitting factor can improve the outage performance of the considered system by nearly 2 dB. The throughput of the system saturated as $I_p$ increases.