Abstract
Palmprint recognition is becoming more and more common in the fields of security authentication, mobile payment, and crime detection. Aiming at the problem of small sample size and low recognition rate of palmprint, a small-sample palmprint recognition method based on image expansion and Dynamic Model-Agnostic Meta-Learning (DMAML) is proposed. In terms of data augmentation, a multi-connected conditional generative network is designed for generating palmprints; the network is trained using a gradient-penalized hybrid loss function and a dual time-scale update rule to help the model converge stably, and the trained network is used to generate an expanded dataset of palmprints. On this basis, the palmprint feature extraction network is designed considering the frequency domain and residual inspiration to extract the palmprint feature information. The DMAML training method of the network is investigated, which establishes a multistep loss list for query ensemble loss in the inner loop. It dynamically adjusts the learning rate of the outer loop by using a combination of gradient preheating and a cosine annealing strategy in the outer loop. The experimental results show that the palmprint dataset expansion method in this paper can effectively improve the training efficiency of the palmprint recognition model, evaluated on the Tongji dataset in an N-way K-shot setting, our proposed method achieves an accuracy of 94.62% ± 0.06% in the 5-way 1-shot task and 87.52% ± 0.29% in the 10-way 1-shot task, significantly outperforming ProtoNets (90.57% ± 0.65% and 81.15% ± 0.50%, respectively). Under the 5-way 1-shot condition, there was a 4.05% improvement, and under the 10-way 1-shot condition, there was a 6.37% improvement, demonstrating the effectiveness of our method.
1. Introduction
In recent years, palmprint recognition has been an important biometric technique, and with the development of the technology, deep learning methods [1] that require a large number of training samples are also widely used for palmprint recognition [2]. However, existing publicly available palmprint datasets are usually small sample datasets with 5–20 samples [3], and collecting large-scale labeled data is very challenging due to confidentiality issues [4]. Training deep learning models using a small amount of labeled data can easily lead to overfitting, thus limiting their performance in practical applications [5]. How to achieve high-accuracy palmprint recognition under limited labeled data has become a hot issue in current research. At present, there are two main means to improve the accuracy of palmprint recognition: expanding the size of the dataset and applying small-sample learning methods.
Data augmentation techniques are commonly used to solve the data scarcity problem and alleviate the overfitting phenomenon of the model. Existing data augmentation techniques mainly include traditional data augmentation methods and deep learning-based image data augmentation methods. Traditional data augmentation methods increase the diversity of training data by performing operations such as rotating, scaling, translating, cropping, and flipping existing images [6,7]. However, these methods can only perform limited transformations based on the original data and cannot generate completely new image data. With the research and wide application of deep learning, some scholars have applied deep learning methods to the field of data expansion, which can be classified into adversarial training-based and generative model-based image data expansion methods according to the way of generating new samples. Adversarial training [8] generates new training samples by making small perturbations to the training data, while the generative adversarial network (GAN [9]) learns the distributional characteristics of the input data based on the training generative model and generates new images that are similar to the original images, thus increasing the number and diversity of training samples.
The goal of small sample learning is that the model obtains a certain generalization ability through a small amount of labeled data and acquires recognition ability through a small amount of fast fine-tuning when facing a new task. Existing small sample learning techniques mainly include transfer learning and meta-learning. Transfer learning refers to the learning task of acquiring the first few layers of a pre-trained network in other classification tasks and then fine-tuning the whole network on the target dataset to adapt to the small-sample dataset after obtaining enough a priori knowledge for the model. However, there are quantitative and distributional differences between the data and the model training [10] samples in real scenarios, and the model parameters may not be adequately tuned to the most appropriate state. Model-Agnostic Meta-Learning (MAML) [11] is a representative meta-learning algorithm that optimizes the initial parameters of the model during multi-task training, enabling the model to adapt quickly after receiving a small amount of new task data. The core idea of MAML is to learn through meta-training the generalized initial parameters of the model so that it can quickly adapt to new tasks after a small number of gradient updates, thus solving the data scarcity problem in few-sample learning. In the field of palmprint recognition, MAML can effectively utilize a small amount of labeled data to improve the generalization ability of the recognition model. However, palmprint images often contain complex background information, which may affect the recognition effect of the model. In order to effectively improve the accuracy of palm-print recognition under the condition of a small sample dataset, this paper conducts research from the perspective of data expansion and small sample learning at the same time. In terms of data expansion, a palmprint expansion method based on Multi-connection Conditions Generate Adversarial Networks (MCCGAN) is proposed. In terms of small-sample learning, introducing Model-Agnostic Meta-Learning into the field of palmprint recognition, designing Frequency-Domain Inception-RSE Palmprint Network (FDIR Net) considering frequency domain and residual inspiration, and a Dynamic Model-Agnostic Meta-learning method training method. The contributions of this paper are as follows:
- Aiming at the problem of the small sample size of palmprint data, MCCGAN is designed to expand the palmprint dataset.
- Aiming at the problem of low recognition rate of palmprint images with small samples, the MAML method is introduced and improved to enhance the fast adaptive learning capability of the feature extraction network on the small sample task.
2. Methods
2.1. MCCGAN-Based Palmprint Image Generation Model
Aiming at the difficulties in small sample palmprint recognition, this paper proposes a palmprint image generation model based on MCCGAN, which consists of a multi-connected palmprint generator (MC-G) and a multi-connected palmprint discriminator (MC-D). The palmprint training dataset images and random noise information are encoded and decoded using the generator to generate new palmprint images of the same class. The combination of real and generated data is judged using the discriminator, and the generator is utilized to expand the data for the small sample of palmprint images after adversarial training.
2.1.1. The Structure of MCCGAN
Palmprint has complex multilevel texture information; for this reason, this paper proposes a palmprint expansion method based on MCCGAN. The structure of MCCGAN is shown in Figure 1.
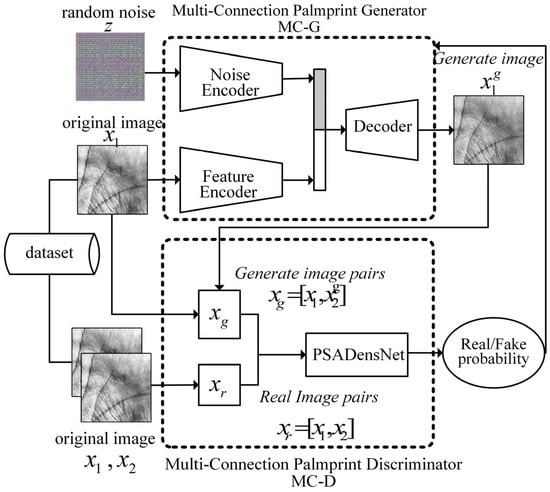
Figure 1.
The Structure of MCCGAN.
MCCGAN consists of two parts: a multi-connected palmprint generator (MC-G) and a multi-connected palmprint discriminator (MC-D). For the same category of palmprints , MC-G receives the original palmprint image and random noise z and outputs the generated palmprint image ; MC-D receives the generated sample pair consisting of one true and one false palmprint and the true sample pair consisting of two real palmprints. MC-D receives the generated sample pair, consisting of one true and one false palmprint, and the real sample pair consisting of two real palmprints, and outputs the probability of the sample pairs, which guides MC-G training.
The multi-connection palmprint generator is composed of U-Net [12] improved by Dense Connection (DC) [13] and Skip Connection (SC) [14], and its structure is shown in Figure 2.
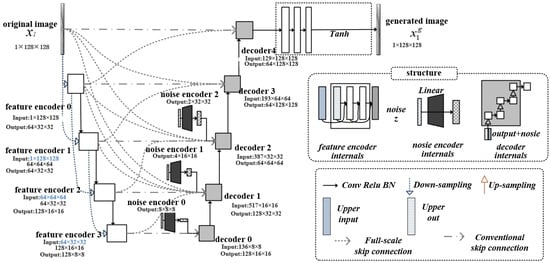
Figure 2.
The overall architecture of the Multi-connected palmprint generator.
MC-G mainly consists of a feature encoder, a noise encoder, a decoder, and an output module, and each component is described as follows:
- (1)
- The feature encoder is used to extract the palmprint () features and obtain different-scale feature maps. Among them, feature encoder 0 includes one convolutional layer with a 3 × 3 step size of 2, which performs preliminary feature encoding of the input palmprint image; feature encoders 1–3 firstly contain one convolutional layer with a 3 × 3 step size of 2 and one convolutional layer with a 3 × 3 step size of 1 internally, which achieves feature reuse and enhances the flow of gradients across the hierarchical levels through the dense concatenation operation of the input features of the upper level and the output features of the upper level; secondly, the feature encoding is performed by three 3 × 3 convolutions with a step size of 1 to accomplish the current layer feature extraction task, respectively.
- (2)
- The noise encoder is used to edit the noise (z) information of the input network by one linear layer to modify the random noise to match the size of the decoder input.
- (3)
- To complement the feature encoder, the decoder integrates multiple input sources and employs a series of upsampling operations to progressively restore spatial details from the encoded features. In addition to receiving features from the previous layer and noise, the decoder incorporates outputs from the U-Net encoder via full-size and regular skip connections, enabling effective gradient flow between the encoder and decoder to enhance training stability. Each decoder layer consists of an upsampling block, which includes a 3 × 3 transpose convolution with a stride of 2 to double the feature map resolution, followed by a 3 × 3 convolution with a stride of 1 to refine features, a ReLU activation for non-linearity, and batch normalization to stabilize training. This upsampling block is repeated three times, with each iteration processing the feature maps to produce higher-resolution outputs. The resulting decoder output aligns with the spatial dimensions of the corresponding encoder layer, facilitating tasks such as image reconstruction or semantic segmentation.
- (4)
- The output module is used to process the information from the network-generated data to produce a target image (), including three 3 × 3 convolutions + Relu activation + batch normalization operations with a step size of 1 and a hyperbolic tangent function (Tanh).
The multi-connected palmprint discriminator consists of DenseNet, which introduces the Pyramid Split Attention (PSA) [15] mechanism, and its structure is schematically shown in Figure 3, which mainly consists of the Pyramid Split Attention DenseBlock (PSADenseBlock), the transition block, and the output processing module.

Figure 3.
The architecture of a multi-connected palmprint discriminator.
- (1)
- The structure of PSADenseBlock is schematically shown in Figure 4, where Figure 4a shows the overall structure of the Pyramid Split Attention DenseBlock, which corresponds to the feature level extracted by MC-G, constructs a 4-layered dense network connection, and splices to obtain the inputs of the lth layer, = concat [, ,…,], the nonlinear transformation [16] function h(·) in DenseNet extracts features through a composite operation, consisting of batch normalization, ReLU activation, and a 3 × 3 convolution. To enhance the neural network’s ability to distinguish real and fake palmprint features, we integrate a Pyramid Split Attention (PSA) mechanism into this transformation, as illustrated in Figure 4b. The PSA module enhances channel-wise feature weighting by capturing multi-scale information through three steps: First, the input feature map is divided into S channel groups. Each group undergoes convolution with a kernel of size = 3 + 2 × ( − 1), where i is the group index, allowing the network to extract features at progressively larger scales. Second, the resulting feature maps from all groups are concatenated to form a unified feature representation, which is processed by a Squeeze-and-Excitation (SE) block to compute channel attention weights, emphasizing the most informative channels across scales. Finally, the attention weights for the S groups are normalized using a SoftMax function, as described in Equation (1), to produce a weighted combination of multi-scale features.
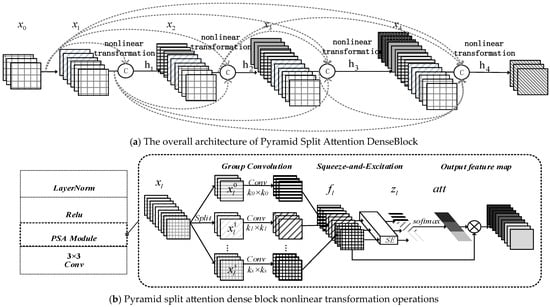 Figure 4. The architecture of Pyramid Split Attention DenseBlock.
Figure 4. The architecture of Pyramid Split Attention DenseBlock.
The weight and the corresponding feature map points are multiplied by ⊙, to get the weighted feature map.
- (2)
- The input of PSADenseBlock contains the feature maps of all previous layers stacked in the channel dimension, and the feature size is consistent within the module. In order to connect the PSADenseBlocks and control the complexity of the model, the Transition module is set up in the network to reduce the size of the feature maps. The Transition module connects two neighboring PSADenseBlocks, in which the features undergo the operation of “batch normalization + Relu activation + 1 × 1 convolution + 2 × 2 average pooling”, and the feature map obtained from the previous layer is compressed into .
- (3)
- The output processing includes the average pooling layer, linear layer, LeakyRelu activation layer, and linear layer, and after the output processing, the result of judging the authenticity of the image is output.
2.1.2. MCCGAN Network Training Method
Since the loss function of CGAN is mainly based on the Jensen-Shannon divergence to measure the difference between the real data distribution and the generated data distribution, the logarithmic operation may lead to the disappearance of the gradient when the performance difference between the generator and the discriminator is large, making the model training difficult. In order to improve the stability of MCCGAN training, this paper introduces the gradient penalization method described in WGAN-GP [17] into MCCGAN training, which constrains the gradient value of the network, and the improved loss function is shown in Equation (2).
where denotes the real palmprint data pair containing two palmprint images under the same label, () denotes its data distribution, denotes the generated palmprint data pair consisting of real palmprints and MC-G output palmprints, containing both real palmprint images and generated images of the same category, () denotes its data distribution, and construct a mixed sample by performing linear interpolation on and , as shown in Equation (3), denotes its data distribution, D(∙) denotes the MC-D output result.
μ is a random weight uniformly sampled from the interval [0, 1], ensuring that it lies on the line connecting the real sample and the generated sample. The gradient penalty term uses the L2 paradigm to measure the MC-D network output to ensure that it is uniformly smooth throughout the entire space, and λ denotes the gradient penalty coefficient, which is usually taken as λ = 10.
Traditional GANs simultaneously update the generator and discriminator during network training. However, in the initial stages of iteration, the quality of the palmprint images generated by MC-G is poor, and MC-D can easily learn the differences between them and real samples, resulting in very small or nearly zero gradient information obtained by MC-G, leading to the “vanishing gradient” phenomenon. To avoid this issue, the Two Time-Scale Update Rule (TTUR) is applied in MCCGAN to balance the training process of the generator and discriminator: Separate Adam optimizers are established for the MC-G and MC-D models. The learning rate for MC-G is set to 0.0001. Forward propagation is performed on 95% of the data, loss is calculated, and the gradients of the model parameters are computed. Based on the gradients and the optimizer’s rules, the parameters of the generator network are updated; The learning rate for MC-D is set to 0.0004. For each data set, forward propagation is performed, loss is calculated, and the gradients of the model parameters are computed. Based on the gradients and the optimizer’s rules, the parameters of MC-D are updated. As shown in Table 1.

Table 1.
Hyperparameter settings of MC-G and MC-D.
2.2. A Small Sample Palmprint Feature Learning Method Based on FDIR Network
2.2.1. Multi-Branch Parallel Feature Extraction Module
In neural networks, the learning goal of each layer is to learn the mapping of the input data [18], and when the number of network layers increases, the network becomes more difficult to train. He [19] proposed a Residual Network (ResNet), which guides the network to learn the difference between the input data and the desired output and mitigates problems such as gradient vanishing or gradient exploding. In this paper, we apply the residual connection to the Inception module [20], which can allow the network to pass the features of the original input directly, thus retaining more low-level feature information, which helps the transfer and fusion of multilevel features, and enhances the network’s ability to perceive features at different scales and different semantics of the image.
In this paper, the design of a parallel multi-branch residual feature extraction module is shown in Figure 5. For the feature map of the upper input layer, the following four sets of convolutional branches are used for feature extraction: a convolution operation with a kernel size of 1 × 1 and a step size of 1 outputs the feature data of the b1 channel; the output of the previous layer is average pooled and then passed through the convolutional kernel of 1 × 1, which outputs the feature data ; the output of the previous layer is feature-extracted by passing it through a convolution operation with a kernel size of 1 × 1 and a step size of 1 versus a kernel size of 5 × 5, a step size of 1, and a padding of 2. The output of the previous layer is feature-extracted, and the feature data of the b3 channel is outputted as ; the output of the previous layer is feature-extracted by passing it through a convolution operation with a kernel size of 1 × 1, a step size of 1 and a padding of 1, and a convolution operation with kernel size of 3 × 3, step size of 1, and padding of 1. The output of the previous layer is feature extracted, and the output of the b4 channel is feature data . The output of the four sets of branches is spliced by channel as in Equation (4) to output the feature data .
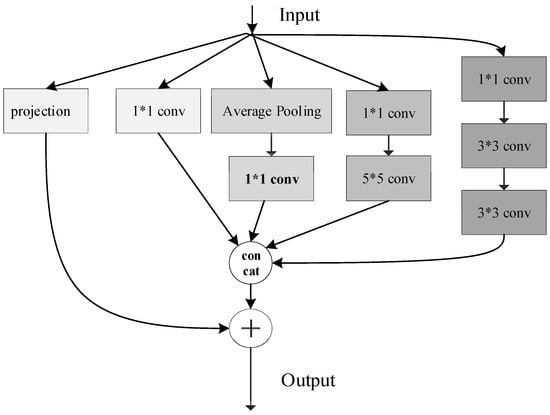
Figure 5.
Parallel Multi-Branch Residual Feature Extraction Module.
represents concatenation by channel.
The residual connection branch aligns to the feature data channel dimensions through the projection function , as in Equation (5).
Finally, splice and to get the output of the current module.
2.2.2. Considering the Channel Attention Mechanism in the Frequency Domain
Appearance, texture, and color similarity between palmprint data samples is high, and small samples have local subtle differences with frequency domain information variations. The attention mechanism can enhance the model’s performance [21] to focus on important features and suppress irrelevant information. Given that the attention mechanism is widely used in the field of computer vision, in order to capture the subtle feature changes and enhance the feature expression ability, the channel attention mechanism, which considers the frequency domain information, is introduced in the model construction, and the operation process is as follows:
Step 1. For the feature map output from the upper layer network is divided along the channel dimension, and for there is , and for each component, a Fast Fourier Transform (FFT) is applied to calculate the frequency components , as in Equation (6).
where are the corresponding 2D coordinates of and denotes the FFT basis function performed on the image.
Step 2. Combine the computed frequency domain , as in Equation (7).
cat(.) indicates splicing along the channel.
Step 3. Construct the correlation of feature channels by fully connected layers and activation functions, and output 1 × 1 × c feature weights, as in Equation (8).
Step 4. Normalize the weights, weight (1 × 1 × c) × (H × W × c) by channel-by-channel product and output the weighted feature , The process is shown in Figure 6.
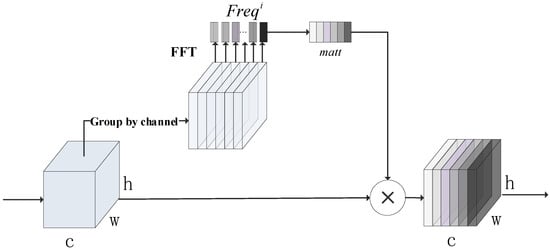
Figure 6.
Channel attention mechanism considering frequency domain information.
2.2.3. DMAML-Based Training Method for Small-Sample Learning Networks
- (1)
- Weighted multi-step loss parameter update method
In the backpropagation of MAML, only the last step of the specific feature extraction network is considered for the weights [22], while the previous multi-step updates are chosen to be optimized implicitly, leading to unstable training [23]. In order to preserve the influence of the inner loop query set on the meta-learner parameters, an annealed weighted summation of the query set loss after the support set parameter update is performed. The parameter updating process is described in detail below in conjunction with the formula.
Step 1. Randomly obtain the task from a set of tasks in the inner loop.
Step 2. Use the support set of the current task as the input to the small-sample palmprint feature extraction network to obtain the predicted probability that the observation sample belongs to the category c. Compute the cross-entropy loss according to Equation (9).
is the sign function (take 1 if the true category of sample is equal to c, and 0 otherwise); and n denotes the number of recognized categories.
Step 3. The inner loop parameter update using the cross-entropy loss according to Equation (10) is performed to obtain the new task-specific model parameters under the current task.
where denotes the loss gradient, and α is the inner loop learning rate, the initial network weight parameter .
Step 4. Input the query set the current task into the palmprint image recognition model , and calculate the query set cross-entropy loss .
Step 5. Calculate the weight w for the current query set loss according to Equation (11) and save to the list.
where in m in the formula represents the current number of update steps and represents the weight decay rate, select as the basic annealing function, as it decreases smoothly and is commonly used in optimization algorithms; Introduce the decay rate , adjusting the weight to to accelerate decay adaptation for small-sample tasks.
Step 6. The process of steps 2-step to 5 above is repeated, and the task is utilized to update the inner loop parameters M times. Wherein, the process of step 5 above is a data preparation action for the inner loop phase for subsequent outer loop parameter updates, i.e., generating a multi-step loss list.
Step 7. In the MAML outer loop, step 5 of the inner loop phase is utilized to generate the multi-step loss list for updating the outer loop meta-learner model weight parameters φ by means of the optimizer RMSprop, as in Equation (12).
where φ denotes the meta-learner model weight parameter, denotes the distribution of the set of tasks, is the query set test loss for the parameters in a particular sub-task, is the derivative of the loss function with respect to the parameters of the inner loop (of second order), and is the derivative of the loss function with respect to the parameters of the outer loop model (first order), and is the learning rate of the outer loop. In order to balance the model performance and computational efficiency, for the first tasks, the second-order derivatives are used to solve; for the other tasks, the first-order approximate derivatives are used.
- (2)
- Learning Rate Dynamic Adjustment Strategy
The outer loop learning rate of MAML determines the update speed and stability of the meta-learner parameters. When a smaller learning rate is used, the model is difficult to adapt to the changes in the training data, resulting in slower convergence of the training process and more iterative steps are required to achieve a reasonable level of performance; whereas, when a larger learning rate is used, the model is prone to overfitting on small-sample palmprint data, resulting in an unstable training process and divergence of the final model. In order to make the model converge faster and find suitable parameters stably, this paper combines progressive preheating and cosine annealing [24,25] to design a dynamic adjustment method for the learning rate of the outer loop. Specifically, the following steps are performed in a learning round.
Step 1. Set upper and lower bounds on the outer loop learning rate ].
Step 2. Apply Equation (13) to gradually increase the outer loop learning rate β through progressive warm-up rounds within the first learning round.
where is the number of iterative steps of the current training, is the total progressive warmup round iteration steps.
Step 3. Loop step 1 times to complete the learning rate warmup.
Step 4. Starting the cosine annealing phase from the current learning round, the outer loop learning rate β is dynamically updated according to Equation (14).
where is the total number of iterative steps trained in the current learning round, and the learning rate is restarted using cosine annealing hot restart whenever all the tasks in that learning round have been performed.
The pseudocode for training DMAML is as follows Algorithm 1:
| Algorithm 1 MAML with Weighted Multi-step Loss and Dynamic Learning Rate |
Require:
|
| 1: Initialize randomly. |
| 2: For each task do |
| 3: |
| 4: for to do |
| 5: Compute support loss: |
| 6: Update parameters: |
| 7: Compute query loss: |
| 8: Compute weight: |
| 9: Save to loss list |
| 10: |
| 11: end for |
| 12: Dynamic Learning Rate Adjustment: |
| 13: if then |
| 14: |
| 15: else |
| 16: |
| 17: end if |
| 18: |
| 19: if then |
| 20: Update |
| 21: else |
| 22: Update |
| 23: end if |
| 24: end for |
| 25: return |
3. Experiments and Analysis
Experimentation of this paper’s model with classical as well as state-of-the-art small-sample learning methods on three classical palmprint datasets.
3.1. Datasets and Data Preprocessing
The palmprint dataset data used in the experiments were obtained from the Hong Kong Polytechnic University (PolyU Palmprint Image Database), the Indian Institute of Technology (IIT Delhi Touchless Palmprint Database), and Tongji University (Tongji Palmprint Image Database).
To meet the requirements of the network architecture and palmprint recognition, we perform the following preprocessing on palmprint images: using the Python image processing library PIL to read the raw image dataset and generate data arrays, to achieve robust region localization across diverse palm print images while maintaining computational efficiency suitable for network input requirements, we select a keypoint detection-based method to crop a 128 × 128-pixel region of interest (ROI), specifically detecting key points in the palmprint images (the center of the palm and the positions of the finger creases), and cropping a 128 × 128 region centered on the palm that contains the primary texture features. We use the NumPy 2.2.3 2.7.1 to save the processed image data as an npy format file to accommodate subsequent network training.
3.2. Environment and Evaluation Metrics
The experiments are programmed in Python 3.7, the deep learning framework is Pytorch 2.7.1, the hardware GPU is NVIDIA GeForce RTX 2060, CUDA 11.6, the operating system is Windows 10 21H2, and the memory is 16 GB.
To verify the effectiveness of the data expansion algorithm proposed in this paper, a combination of qualitative and quantitative methods is used for evaluation. The quantitative metrics are Frechet Inception Distance (FID) [26], Structural Similarity Index Method (SSIM) [27], Peak Signal to Noise Ratio (PSNR) [28], and Inception Score (IS) [29]. Below is a brief introduction to these four indicators.
FID: The quality of the generated images is measured by comparing the distribution differences between real images and generated images in a high-dimensional feature space.
SSIM: Comparing the similarity of two images based on three aspects—brightness, contrast, and structural information—is a structure-based image quality evaluation method.
RSNR: Measures the reconstruction quality of an image, expressed as the ratio between the maximum signal value and noise. The unit is decibels (dB).
IS: Inception Score is a widely used metric for evaluating the performance of generative models, primarily measuring the quality and diversity of generated images. This metric evaluates the conditional probability distribution of generated images in category prediction and the marginal probability distribution by calculating the KL divergence between them.
3.3. Palmprint Expansion Comparison Experiment
To illustrate the state-of-the-art of the proposed method, subjective and objective comparisons are made using some open-source generative adversarial network data augmentation methods, all of which are supervised learning models that can constrain the classes of generated palmprints to meet the needs of the recognition experiments, including conditional generative networks (CGANs) [30], deep convolutional generative adversarial networks (DC-GAN) [31], Wasserstein generative adversarial network (WGAN) [32], conditional diffusion model (CDM) [33] and Few-shot image generation (FewshotGAN) [34].
Table 2 shows the comparison between the original dataset and the effect of each algorithm after data expansion. From Table 1, it can be seen that due to the small class of training samples in the PolyU palmprint dataset, other generative adversarial network models can hardly obtain the palmprint texture features, and the output image contains a large amount of irregular noise on the IIT-D dataset with more palm shadows; the DCGAN model mistakenly treats the unevenly illuminated portion as the palmprint feature information, which reduces the reasonableness of the generated image; on the more numerous but insufficiently illuminated On the Tongji dataset, most of the methods can obtain the image information, but the clarity of the generated image is limited. In contrast, the MCCGAN proposed in this paper can extract the palmprint feature information from the limited PolyU dataset. The generated image retains rich palmprint texture details, which can reasonably simulate the palm shadows generated during the palmprint acquisition process in the IIT-D dataset, and the generated image has clearer texture details.

Table 2.
Comparison of the results of the expansion experiments with different models.
Among table, represents that the larger the indicator value, the better the effect, while ↓ represents that the smaller the indicator value, the better the effect. The quantitative performance of each comparison algorithm in different datasets is shown in Table 3.

Table 3.
Quantitative comparison of expansion effects.
On the PolyU dataset, MCCGAN improves the FID metric by 10%, the SSIM value by 25%, and the PSNR metric by 0.7% compared to other generative algorithms. On the IITD dataset, MCCGAN improves the FID metric by 29%, the SSIM value reaches 0.748, and the PSNR metric improves by 13.2%. In the Tongji dataset, the FID value of MCCGAN is slightly inferior to that of WGAN, indicating that the difference between the distribution of the generated data and the real data distribution is larger than that of WGAN. Combined with Table 3, it can be seen that the visual effect of the image generated by MCCGAN is closer to the real situation of the palm prints than that of the WGAN-generated image, and the SSIM value reaches 0.580. The PSNR value is improved by 14.1%. It can be seen that MCCGAN has better structural similarity and less distortion than other expansion methods while maintaining better similarity in the distribution of the generated image data, and the quality of generation is more stable among different datasets. In terms of running time, the generator network in MCCGAN connects the bottom features to the top features through jump connections, which provides a faster information transfer and reconstruction path, helps to reduce information loss and blurring, and accelerates the speed of generating images.
3.4. Palmprint Expansion Ablation Experiment
To discuss the impact of generator structure design on image generation quality, ablation experiments were designed. Group 1 used a U-Net to construct the generator, Group 2 used a U-Net network with dense connections (U-Net + DC) to construct the generator, and Group 3 used a U-Net network with skip connections (U-Net + SC) to construct the generator, and Group 4 used a U-Net network with dense connections + skip connections (U-Net + DC + SC) to construct the generator. Each group of generators was set with 0–4 noise encoders for comparison, while other structural settings remained consistent with MCCGAN. The ablation experiment results are shown in Table 4.

Table 4.
Comparison of generator structure ablation experiment results.
As shown in Table 4, when four noise encoders are set, the FID value of the (2) U-Net + DC group is lower than that of the (1) group, while the IS, SSIM, and PSNR values improved. This indicates that the encoders effectively capture and utilize both low-level and high-level feature information from the image encoding process by receiving and leveraging the outputs of the first two layers through dense connections. This results in improvements in the distributional consistency, structural similarity, and reconstruction quality between the generated images and the real images.
The (3) U-Net + SC group showed a significant decrease in FID values compared to the (1) group when using 2 noise encoders, while SSIM and PSNR values improved significantly. This indicates that the decoder receives and utilizes the outputs from the previous layer and multiple feature encoders through skip connections, fully leveraging low-level and high-level semantic information during decoding and preserving more feature details during upsampling. The (4) U-Net + DC + SC group simultaneously improved the feature encoder and decoder, and when combined with three noise encoders, all four metrics achieved good results. This is because the model under this structure can more fully utilize low-level and high-level feature information and accurately reconstruct images through the combination of multiple encoders, thereby generating fingerprint images with small distribution differences from the original images, diverse categories, similar structures, and low distortion. In terms of runtime, increasing model complexity leads to longer runtime, but the increase is small and remains within an acceptable range.
To discuss the impact of the discriminator framework design on image generation quality, 0 to 3 sets of pyramid segmentation attention mechanisms were inserted into the nonlinear transformation of PSADenseBlock. Four experiments were designed, with other structural settings consistent with MCCGAN. The image generation experimental results are shown in Table 5.

Table 5.
Comparison of discriminator structure ablation experiment results.
From the comparison results, it can be seen that the pyramid-split attention module introduces a multi-scale attention mechanism for image features in the discriminator. As the number of pyramid-split attention modules increases, the distribution difference between the generated images and the real images decreases, and the FID score gradually decreases; Meanwhile, the IS score continues to rise, indicating that the pyramid segmentation attention module provides a more global feature representation and multi-scale perception capability, thereby improving the generated images in multiple aspects (such as category diversity and realism); The fluctuations in SSIM, PSNR, and runtime suggest that designing two PSA modules in the DensNetBlock is appropriate, as it can enhance the diversity and realism of the generated images while maintaining reasonable computational efficiency.
3.5. Small Sample Palmprint Recognition Experiment
In this section, the proposed FDIR Net and DMAML are compared with the current mainstream small-sample learning methods, including MatchingNets [35], ProtoNets [36], MAML, Reptile [37], and FETA [38], using the MCCGAN expanded dataset. The experiments use the image recognition accuracy in the N-way K-shot case as the evaluation index. The comparison of recognition accuracy is shown in Table 6 and Table 7.

Table 6.
IIT-D Small sample palmprint image recognition experiment.

Table 7.
Tongji Small sample palmprint image recognition experiment.
From the comparison of the results in Table 6 and Table 7, it can be seen that FDIR Net + DMAML can obtain a better recognition rate of palmprints with small samples under a variety of tasks, with the best recognition rate of 97.09% on the IIT-D dataset and 99.15% on the Tongji dataset and the range of fluctuation of the recognition rate is further reduced, and the model is more stable.
In order to test the palmprint verification performance of each model, each test sample and template are matched, and different matching similarity thresholds are taken to obtain the DET curves as shown in Figure 7 and Figure 8, and the equal error rates are obtained as shown in Figure 9 and Figure 10.
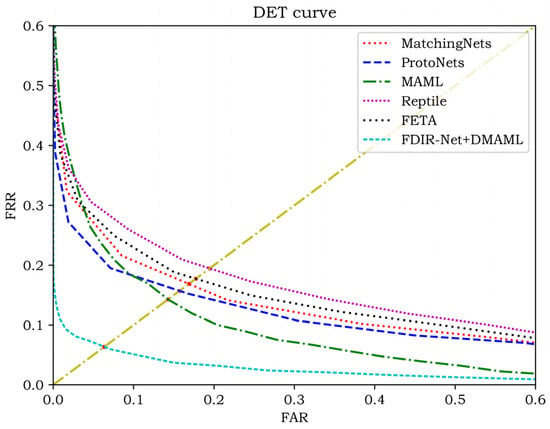
Figure 7.
DET curves for the IIT-D dataset.
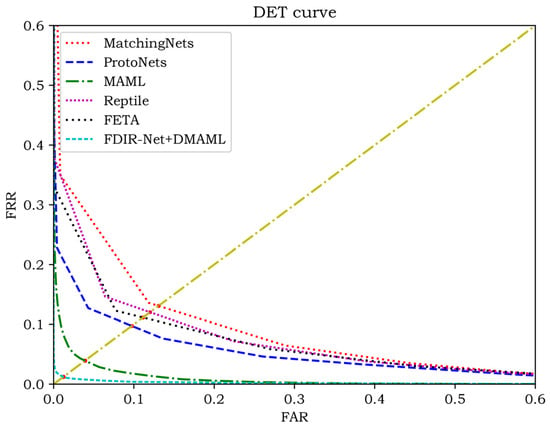
Figure 8.
DET curves for the Tongji dataset.
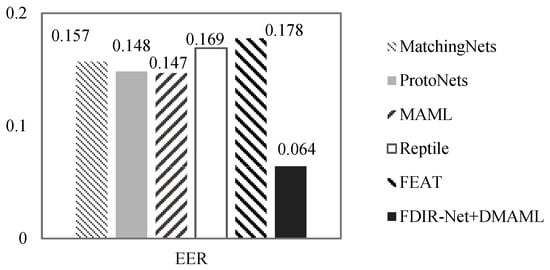
Figure 9.
Equal error rate for the IIT-D dataset.
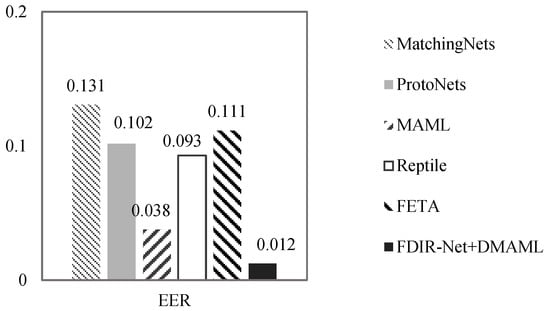
Figure 10.
Equal error rate for the Tongji dataset.
From the comparison of the experimental results, it can be seen that the DET curve of FDIR Net + DMAML is completely located below the other compared models, which indicates that the proposed model in this paper takes into account the security and ease of use of the recognition system.
4. Conclusions
In this paper, for the problem of the low recognition rate of a small sample palmprint, a small sample palmprint recognition method based on image expansion and DMAML is proposed. In terms of small-sample palmprint image expansion, the MCCGAN network is designed, which contains two parts of the network structure: the multi-connected palmprint generator encodes-decodes the palmprint training dataset images and random noise information to generate new palmprint images of the same category, the multi-connected palmprint discriminator judges the similarity between the real data and the generated data and guides the generator to improve the quality of the generated images. In the process of adversarial training, the loss function mixed with a gradient penalty is used to regularize the gradient to keep the training process stable and avoid gradient explosion or gradient disappearance. In terms of small-sample palmprint feature learning, the Inception multi-branch structure is used as the basis to design the feature extraction module combined with the ResNet residual idea, and at the same time, the channel attention mechanism considering the frequency domain is designed to enhance the network’s attention to the specific region of the palmprint image, so as to improve the model’s feature learning and representation ability. In order to meet the parameter update demand of MAML for this feature extraction network, the multi-step loss list of the inner loop is constructed, and the progressive preheating and cosine annealing are combined to design the dynamic adjustment method of the outer loop learning rate. Experiments show that the method proposed in this study can better generate high-quality palmprint images, expand the palmprint dataset, and perform well in terms of small-sample palmprint recognition accuracy, recognition efficiency, and model robustness. In future research work, the application of MCCGAN in the case of data imbalance will be considered to expand the application range of the expanded method and to combine many different modal information to enhance the model’s ability to understand and recognize palm texture and to realize multimodal palmprint recognition.
Author Contributions
Conceptualization, H.B. and Z.D.; methodology, X.Z. and H.B.; software, Y.L.; validation, H.B. and Y.L.; investigation, X.Z.; writing—original draft preparation, H.B. and Z.D.; writing—review and editing, X.Z. and K.Z.; visualization, Y.L.; supervision, X.Z.; project administration, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Major Program of Xiangjiang Laboratory (Grant No. 23XJ01001, Grant No. 22XJ01002).
Data Availability Statement
This study utilized publicly available palmprint datasets. The PolyU Palmprint Image Database can be accessed via: https://www4.comp.polyu.edu.hk/~csajaykr/IITD/Database_Palm.htm (accessed on 3 April 2025). The IIT Delhi Touchless Palmprint Database is available at: http://www4.comp.polyu.edu.hk/~csajaykr/IITD/Database_Palm.htm (accessed on 3 April 2025). The Tongji Palmprint Image Database can be obtained from: http://sse.tongji.edu.cn/linzhang/cr3dpalm/cr3dpalm.htm (accessed on 3 April 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| DMAML | Dynamic Model-Agnostic Meta-Learning |
| MAML | Model-Agnostic Meta-Learning |
| MCCGAN | Multi-connection Conditions Generate Adversarial Networks |
| FDIR Net | Frequency-Domain Inception-Rse Palmprint Network |
| MC-G | The generator of Multi-connection Conditions Generate Adversarial Networks |
| MC-D | The discriminator of Multi-connection Conditions Generate Adversarial Networks |
| PSA | Pyramid Split Attention |
| PSADenseBlock | Pyramid Split Attention DenseBlock |
References
- Zhou, X.; Liang, W.; Kevin, I. Deep-learning-enhanced human activity recognition for internet of healthcare things. IEEE Internet Things J. 2020, 7, 6429–6438. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, X.; Yu, L.; Shen, L.; Yu, S. Double bio-logically inspired transform network for robust palmprint recognition. Neurocomputing 2019, 337, 24–45. [Google Scholar] [CrossRef]
- Xue, Y.; Xue, M.; Liu, Y.; Bai, X. Palmprint Recognition Based on 2DGabor Wavelet and BDPCA. Comput. Eng. 2014, 40, 196–199. [Google Scholar]
- Fei, F.; Li, S.; Dai, H.; Hu, C.; Dou, W.; Ni, Q. A k-anony mity based schema for location privacy preservation. IEEE Trans. Sustain. Comput. 2017, 4, 156–167. [Google Scholar] [CrossRef]
- Zhenan, S.; Ran, H.; Liang, W. Overview of biometrics research. J. Image Graph. 2021, 26, 1254–1329. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Ma, X.; Hong, Z.; Fang, Q.; Guo, Y. Mask R-CNN and Data Augmentation and Transfer Learning. Chin. J. Biomed. Med. Eng. 2021, 40, 410–418. [Google Scholar]
- Ren, K.; Chang, L.; Wan, M.; Gu, G.; Chen, Q. An improved retinal vascular segmentation study based U-Net enhanced pretreatment. Laser J. 2022, 43, 192–196. [Google Scholar]
- Mao, X.; Shan, Y.; Li, F.; Chen, X.; Zhang, S. CLSpell: Contrastive learning with phonological and visual knowledge for Chinese spelling check. Neurocomputing 2023, 554, 126468. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, H.; Zhuang, S.; Zhan, X. Image Processing and Optimization Using Deep Learning-Based Generative Adversarial Networks (GANs). J. Artif. Intell. Gen. Sci. 2024, 5, 50–62. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Liang, W. CNN-RNN based intelligent recommendation for online medical pre-diagnosis support. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 18, 912–921. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. arXiv 2017, arXiv:1703.03400. [Google Scholar]
- Lv, P.; Wang, J.; Zhang, X.; Shi, C. Deep supervision and atrous inception-based U-Net combining CRF for automatic liver segmentation from CT. Sci. Rep. 2022, 12, 16995. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21 July 2017; pp. 4700–4708. [Google Scholar]
- Shi, C.; Cheng, Y.; Wang, J.; Wang, Y.; Mori, K.; Tamura, S. Low-rank and sparse decomposition based shape model and probabilistic atlas for automatic pathological organ segmentation. Med. Image Anal. 2017, 38, 30–49. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Lv, P.; Wang, H. SAR-U-Net: Squeeze and ex-citation block and atrous spatial pyramid pooling based residual U-Net for automatic liver segmentation in Computed Tomography. Comput. Methods Programs Biomed. 2021, 208, 106268. [Google Scholar] [CrossRef]
- Zhou, X.; Tian, J.; Wang, Z.; Yang, C.; Huang, T.; Xu, X. Nonlinear bilevel programming approach for decentralized supply chain using a hybrid state transition algorithm. Knowl. Based Syst. 2022, 240, 108119. [Google Scholar] [CrossRef]
- Gulrajan, I.; Ahmed, F.; Arjovsky, M. Improved Training of Wasserstein GANs. arXiv 2017, arXiv:1704.00028. [Google Scholar] [CrossRef]
- Liang, W.; Chen, X.; Huang, S.; Huang, G.; Yan, K.; Zhou, X. Federal learning edge network based sentiment analysis combating global COVID-19. Comput. Commun. 2023, 204, 33–42. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NE, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Liu, C.; Wang, Z. Efficient complex ISAR object recognition using adaptive deep relation learning. IET Comput. Vis. 2020, 14, 185–191. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, F.; Chen, J. Pythagorean fuzzy Bonferroni mean with weighted interaction operator and its application in fusion of online multidimensional ratings. Int. J. Comput. Intell. Syst. 2022, 15, 94. [Google Scholar] [CrossRef]
- Li, F.; Shan, Y.; Mao, X. Multi-task joint training model for machine reading comprehension. Neurocomputing 2022, 488, 66–77. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Y.; Chen, X. The new similarity measure and distance measure of a hesitant fuzzy linguistic term set based on a linguistic scale function. Symmetry 2018, 10, 367. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, K.; Dong, L. Stacked autoencoder-based deep reinforcement learning for online resource scheduling in large-scale MEC networks. IEEE Internet Things J. 2020, 7, 9278–9290. [Google Scholar] [CrossRef]
- Fréchet, M. Sur quelques points du calcul fonctionnel. Rend. Del Circ. Mat. Di Palermo 1906, 22, 1–72. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.R. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2014, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, J.; You, J. Peak signal-to-noise ratio revisited: Is simple beautiful? In Proceedings of the Fourth International Workshop on Quality of Multimedia Experience, Yarra Valley, Australia, 5–7 July 2012; pp. 37–38. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W. Improved techniques for training gans. In Proceedings of the Advances in neural information processing systems, NIPS 2016, Barcelona, Spain, 5–10 December 2016; pp. 2234–2242. [Google Scholar]
- Mirza, M.; Simon, O. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Gu, B.; Zhai, J. Few-shot image generation based on meta-learning and generative adversarial network. Signal Process. Image Commun. 2025, 137, 117307. [Google Scholar] [CrossRef]
- Vinyals, O.; Blundell, C.; Lillicrap, T. Matching Networks for One Shot Learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3637–3645. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical Networks for Few-shot Learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4080–4090. [Google Scholar]
- Nichol, A.; Achiam, J.; Schulman, J. On First-Order Meta-Learning Algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Maniparambil, M.; Mcguinness, K.; Connor, N. BaseTransformers: Attention over base data-points for One Shot Learning. In Proceedings of the 33rd British Machine Vision Conference, London, UK, 21–24 November 2022; pp. 1–14. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).