Abstract
Eye-written digit recognition presents a promising alternative communication method for individuals affected by amyotrophic lateral sclerosis. However, the development of robust models in this field is limited by the availability of datasets, due to the complex and unstable procedure of collecting eye-written samples. Previous work has proposed both conventional techniques and deep neural networks to classify eye-written digits, achieving moderate to high accuracy with variability across runs. In this study, we explore the potential of quantum machine learning by presenting a hybrid quantum–classical model that integrates a variational quantum circuit into a classical deep neural network architecture. While classical models already achieve strong performance, this work examines the potential of quantum-enhanced models to achieve such performance with fewer parameters and greater expressive capacity. To further improve robustness and stability, we employ an ensemble strategy that aggregates predictions from multiple trained instances of the hybrid model. This study serves as a proof-of-concept to evaluate the feasibility of incorporating a compact 4-qubit quantum circuit within a lightweight hybrid model. The proposed model achieves 98.52% accuracy with a standard deviation of 1.99, supporting the potential of combining quantum and classical computing for assistive communication technologies and encouraging further research in quantum biosignal interpretation and human–computer interaction.
1. Introduction
Human communication can be expressed through various modalities, including speech, gestures, writing, and facial expressions. However, individuals affected by neurodegenerative diseases, such as amyotrophic lateral sclerosis (ALS), gradually lose the ability to utilize these communication channels [1,2,3], ultimately limiting their ability to express intentions and interact with others. To address this issue, various assistive technologies that rely on residual eye movement as an input modality have been explored. These include camera-based systems that monitor eye gaze using optical or infrared sensors [4,5,6,7] and signal-based approaches such as electrooculography (EOG) [8].
While camera-based methods typically offer high angular precision, they are often costly and require complex setups with strict lighting and calibration requirements [9]. In contrast, EOG-based systems measure the potential difference between the cornea and retina using electrodes placed around the eyes, providing a more affordable and portable solution [8,10]. Despite their practicality, EOG signals are inherently noisy and exhibit limited spatial resolution, making the recognition of complex or fine-grained eye-written patterns particularly challenging [11].
To overcome these limitations, the concept of eye writing has been introduced. Eye writing refers to the intentional tracing of alphanumeric characters using eye movements, captured through EOG signals. Unlike traditional eye-tracking tasks that involve simple directional gestures, eye writing enables more expressive communication by allowing users to draw complete digits or letters with their eyes. A recent open dataset [11] has been made available, containing EOG recordings of eye-written characters from multiple subjects, which serve as benchmarks for evaluating recognition models.
Several existing works have been proposed for eye-written digit recognition to lay a foundation in the field. The heuristic method proposed by Tsai et al. achieved an accuracy of 75.55% for Arabic numbers and arithmetic symbols [12]. Chang et al. conducted a series of studies using classical pattern recognition methods, including dynamic time warping (DTW), dynamic positional warping (DPW), and their combinations with support vector machines (DTW-SVM and DPW-SVM), achieving recognition accuracies of 92.41%, 94.07%, 94.08%, and 95.74%, respectively [13]. To further improve performance, the authors later proposed a deep neural network (DNN) model [11], inspired by InceptionNet [14], which achieved an outstanding accuracy of 97.78%, outperforming all previously used conventional techniques. More recently, Bature et al. introduced the DCC-TCN model, which utilizes dilated causal convolutional layers and temporal convolutional networks to enhance temporal feature learning without an ensemble technique like DNN. This model achieved a recognition accuracy of 96.20% on a dataset that includes both Arabic numbers and alphabet characters [15].
In this study, we propose a hybrid quantum—classical model for eye-written digit recognition that combines classical preprocessing, such as feature encoding, with quantum layers projecting extracted features into a high-dimensional Hilbert space. This quantum feature mapping can improve class separability and generalization performance [16,17], and hybrid models have demonstrated versatility in applications including medical imaging [18], binary image classification [19], remote sensing [20], noise-resilient image recognition [21], and handwritten digit classification [22].
Although classical architectures such as DNN and DCC-TCN have achieved strong performance in eye-written digit recognition, QML offers a promising alternative with unique representational properties. To explore this potential, we extend the classical architecture proposed by Chang et al. [11] with a four-qubit variational quantum circuit [23,24], aiming to achieve comparable performance while introducing distinct learning characteristics from quantum feature spaces. This work serves as a proof-of-concept with particular relevance to assistive communication applications.
The structure of this paper is as follows. Section 2 describes the materials, including the dataset and preprocessing procedures. Section 3 details the architecture of the proposed hybrid model and the evaluation setup. Section 4 presents the evaluation results. Section 5 presents the discussion and limitations. Finally, Section 6 concludes the study and outlines directions for future research.
2. Materials
2.1. Dataset
This study was conducted using an open dataset from Chang et al. [11], which includes electrooculography (EOG) recordings collected over three trials from 18 healthy participants (5 females), with a mean age of 23.5 years and a standard deviation of 3.28. The recordings were obtained using four electrodes positioned around the eyes: one on each side and one above and below the right eye. Data were sampled at a rate of 2048 Hz. All participants had no known history of eye-related disorders.
The data collection process was structured around predefined Arabic numeral patterns, specifically designed to standardize both the starting point and trajectory of eye movements for each digit. During the experiment, participants were instructed to follow the guide patterns, as illustrated in Figure 1, by moving their eyes accordingly.
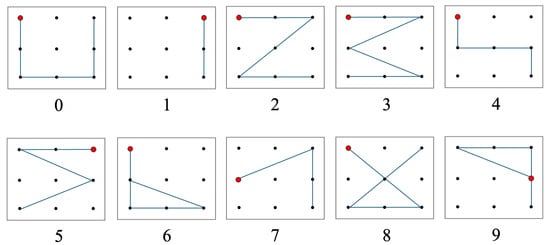
Figure 1.
Pattern designs of Arabic numerals, with red dots indicating the starting positions. Adapted from [11].
A total of 540 eye-written characters were recorded, with each participant writing the 10 Arabic numerals three times. Example recordings are shown in Figure 2. The resulting character shapes differ noticeably from the original pattern designs due to several factors: the recordings began when participants focused on the central point of a screen, and the signals included noise, artifacts, and distortions caused by unintentional errors during the eye-writing process. Additional details of the experimental configuration and procedures can be found in [11].
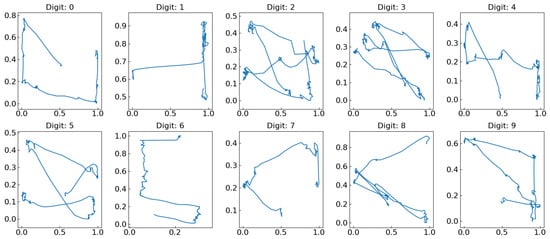
Figure 2.
Eye-written digit from 0 to 9, adapted from [11].
2.2. Preprocessing
The raw eye-written dataset was originally preprocessed by Chang et al. [11] using a four-stage procedure consisting of data resampling, saccade detection, resizing, and normalization, as illustrated in Figure 3 and Figure 4. The signals were initially downsampled from 2048 Hz to 64 Hz, which is sufficient for EOG analysis. In this study, we used the preprocessed data that incorporated a saccade detection technique, as an alternative to the MSDW-based eye-blink removal used in the original publication [11,25]. The saccade detection step helps reduce noise and smooth the eye movement trajectories by filtering out rapid, transient motions [26]. The signals had also been resized to a uniform length and normalized to fit within a 1 × 1 box in 2D space, preserving their original aspect ratio. Further details of the original preprocessing pipeline are available in [11].
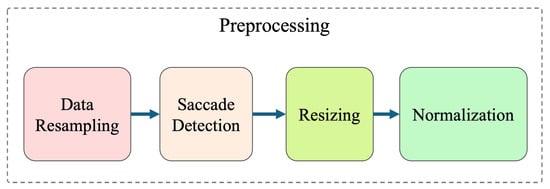
Figure 3.
Overview of the signal preprocessing pipeline, adapted from [11].
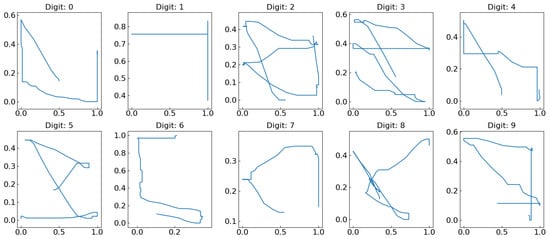
Figure 4.
Eye-written digit from 0 to 9 after preprocessing.
3. Proposed Method
3.1. Quantum Computing Overview
Quantum computing leverages the principles of quantum mechanics to process information in fundamentally new ways. Unlike classical bits that exist in binary states 0 or 1, quantum bits or qubits exist in a linear combination (superposition) of both states [27,28]:
Here, and are complex-valued probability amplitudes, and is the state vector of the qubit residing in a two-dimensional Hilbert space. The normalization condition ensures that the total probability is conserved, meaning the qubit must collapse to either state 0 or 1 when measured. This fundamental property allows quantum systems to encode and process information in a probabilistic and parallel fashion.
Quantum states are manipulated via reversible linear operations known as unitary gates. These quantum gates operate on one or more qubits and preserve the total probability of the quantum system. Some common single-qubit rotation gates include [28]:
These gates enable controlled rotation of the qubit’s state on the Bloch sphere, corresponding to different axes of quantum evolution.
In multi-qubit systems, entanglement—a uniquely quantum phenomenon—can be introduced using controlled gates such as the controlled- () gate:
Controlled gates conditionally apply operations based on the state of a control qubit and are essential for constructing entangled states and quantum circuits capable of performing non-classical computations.
3.2. Variational Quantum Circuit
Variational Quantum Circuits (VQCs) are a hybrid quantum–classical framework that leverages the expressive power of parameterized quantum circuits alongside classical optimization routines, and their generalization ability has been theoretically analyzed in several works. Schuld and Killoran [16] demonstrated that quantum circuits can act as feature maps that embed classical data into high-dimensional Hilbert spaces, enhancing class separability. Abbas et al. [29] provided generalization bounds for quantum neural networks using Rademacher complexity, revealing how circuit expressibility influences overfitting. Caro et al. [17] further demonstrated that quantum models can generalize effectively even with small training datasets under certain complexity constraints. VQCs are designed to be trainable, enabling them to learn task-specific representations through repeated evaluation and adjustment of gate parameters [23,30].
A typical VQC consists of three major components. First, a data encoding layer transforms classical input features into quantum states. Various encoding strategies can be employed, such as angle encoding, amplitude encoding, basis encoding, or more advanced methods like Hamiltonian encoding [31,32]. These techniques enable the mapping of real-valued vectors into quantum states suitable for computation. Next, the circuit includes a parameterized ansatz, which is a trainable quantum circuit composed of layers of unitary gates. The design and depth of the ansatz affect the expressive capacity of the VQC and are often selected to balance representation power and optimization efficiency. Finally, in the measurement stage, quantum observables such as Pauli-Z expectation values are measured to extract classical information from the quantum system. These outputs are passed to a classical optimizer, which updates the circuit parameters by minimizing a task-specific cost function. This iterative process forms the foundation of variational quantum learning algorithms [33]. An illustration of a typical VQC architecture, showing the data encoding, parameterized quantum layers, measurement, and classical optimization flow, is provided in Figure 5.
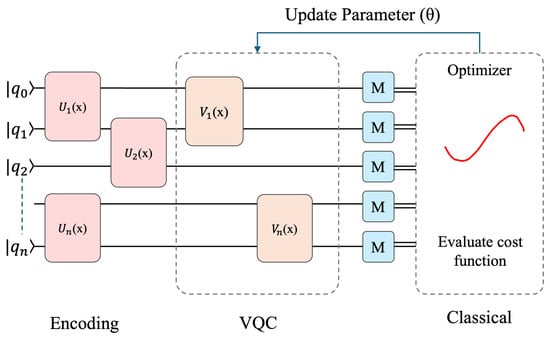
Figure 5.
Architecture of variational quantum circuit, adapted from [34].
While VQCs are broadly applicable across various domains, their suitability for EOG signals in eye writing stems from their strong capacity for modeling complex, nonlinear relationships in high-dimensional time-series data. EOG signals exhibit inherent noise, inter-subject variability, and subtle nonlinear temporal patterns that may not be easily captured by shallow classical models. The entanglement and interference properties of quantum circuits enable VQCs to represent intricate feature interactions with relatively fewer parameters compared to deep classical networks [24,29]. This makes them particularly effective in learning compressed and expressive representations from EOG signals. Although our study applies VQC specifically to eye-written EOG signals, the approach is not limited to this modality and could potentially be extended to other physiological signals such as EMG or EEG, where nonlinear dynamics and noise robustness are also critical.
3.3. Hybrid Quantum–Classical Architecture
The proposed hybrid quantum–classical model, illustrated in Figure 6, is designed to demonstrate the potential of QML in eye-written digit recognition by improving classification accuracy while utilizing fewer learnable parameters. The context will cover the overview of quantum computing, variational quantum circuits, and the hybrid quantum–classical architecture of our proposed model.
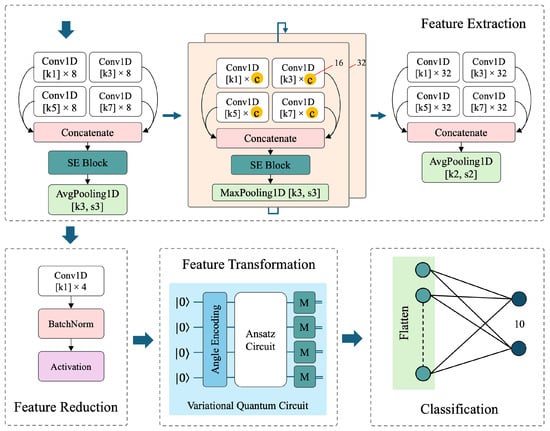
Figure 6.
Overall architecture of the proposed hybrid model, integrating VQC into a deep neural network. Kernel size (k), stride (s), and channels (c) are indicated for convolution and pooling layers.
The model processes 1D EOG signals collected during eye writing and progressively extracts and transforms relevant features through each module. These components work in a sequential pipeline: the extracted features are reduced for compactness, transformed via a variational quantum circuit, and finally classified into digit categories. The following subsections detail the structure and function of each module.
3.3.1. Feature Extraction Module
The feature extraction module is the first component of our proposed model and is adapted from the classical DNN architecture introduced by Chang et al. [11], which was originally designed for eye-written digit recognition. The architecture of classical DNN was inspired by the InceptionNet model [14], known for its ability to capture multi-scale features through parallel convolutional operations effectively.
As illustrated in Figure 6, our model utilizes four convolutional blocks, reflecting the structure of the classical DNN architecture proposed by Chang et al. [11]. Each block begins with four parallel 1D convolutional layers, each configured with a distinct kernel size (1, 3, 5, and 7). These kernel sizes are selected to extract features in varying receptive fields, allowing the model to simultaneously capture local and global patterns in the EOG signal data. After convolution, the outputs are concatenated to form a unified multi-scale representation. This design eliminates the need to select a single optimal kernel size manually and instead enables the model to learn model-relevant features at different scales.
Following the concatenation, a pooling operation is applied to reduce spatial resolution and enhance computational efficiency. In contrast to the original backbone, our hybrid model customizes this module in two essential ways. First, we replace the max pooling with the average pooling in the first and last convolutional blocks. Average pooling is known to preserve more contextual information and reduce sensitivity to outliers, which is particularly beneficial for smoothing noisy EOG signal features. Second, we integrate Squeeze-and-Excitation (SE) blocks [35,36], as illustrated in Figure 7, into the first three convolutional blocks. These attention mechanisms perform dynamic channel-wise feature recalibration by modeling interdependencies between feature channels. The SE blocks adaptively emphasize informative features and suppress less relevant ones, thus improving the discriminative capacity of the network. Together, these enhancements result in a robust and efficient feature extraction pipeline. The multi-scale convolutional layers ensure comprehensive representation learning, while the use of average pooling and SE attention blocks leads to better generalization and improved performance in downstream classification tasks.
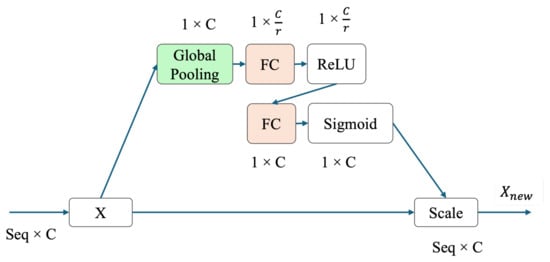
Figure 7.
Architecture of the Squeeze-and-Excitation (SE) block for one-dimensional input data, adapted from [35,36].
The feature extraction module employs a series of convolutional layers to capture local spatial patterns and hierarchical representations from input EOG data. Multiple kernel sizes are used to enhance feature diversity, followed by attention and pooling mechanisms to refine the extracted representations.
3.3.2. Feature Reduction Module
The feature reduction module serves as a bridge between the high-dimensional feature maps extracted by the convolutional layers and the quantum transformation stage. After the feature extraction module produces a rich set of multi-scale feature representations with 128 channels, this module compresses the features into a lower-dimensional latent space compatible with the quantum layer.
Specifically, the module includes a one-dimensional convolutional layer with a kernel size of 1, serving as a pointwise operation to reduce the number of channels from 128 to 4. This value corresponds to the number of qubits utilized in the subsequent variational quantum circuit. The transformation preserves spatial resolution while efficiently projecting the feature vector into the required dimensionality for quantum encoding.
Following the convolution, a batch normalization layer is applied to stabilize and accelerate the training by normalizing the intermediate feature distributions. Finally, a tanh activation function introduces non-linearity and bounds the output values to the range , which is essential for the next stage where features are embedded as rotation angles or amplitudes into the quantum circuit. This ensures that the input lies within a range suitable for quantum gate parameterization, especially for angle embedding strategies.
Overall, this module performs a critical dimensionality reduction that not only reduces computation but also ensures compatibility and smooth integration with the quantum processing pipeline.
3.3.3. Feature Transformation Module
The feature transformation module is the quantum component of the proposed hybrid architecture. In this module, classical features are first projected into a quantum Hilbert space through Angle Embedding, wherein each input feature is encoded as a rotation angle applied to a corresponding qubit. This embedding step allows classical data to be represented in a quantum state space.
After dimensionality reduction, the intermediate feature representation is reshaped to conform to a 4-qubit input layout, matching the requirements of the VQC. Following angle embedding, the reshaped features are processed through a parameterized ansatz circuit proposed by Sim et al. [24], as shown in Figure 8. This circuit is designed to provide a good trade-off between expressive capacity and computational feasibility, making it suitable for near-term quantum devices and simulators.
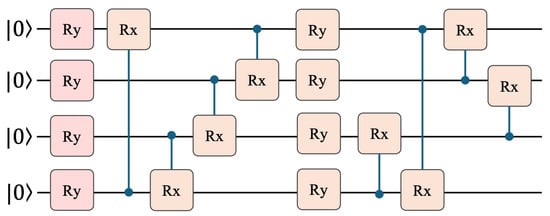
Figure 8.
Ansatz circuit 14 for variational quantum circuit, adapted from [24].
Once the quantum operations are applied, the resulting quantum state is measured using Pauli-Z observables. The measured expectation values, real-valued outputs, represent quantum-enhanced features. These features are subsequently flattened and passed to the classification head of the model, where they contribute to the final prediction.
3.3.4. Feature Classification Module
The feature classification module is the final component of the proposed hybrid model. It is responsible for mapping the quantum-transformed features from the feature transformation module to the target class space for eye-written digit recognition. After quantum transformation, the VQC produces a set of expectation values for each qubit, structured along a temporal or spatial sequence. These values are reshaped and flattened into a one-dimensional feature vector, making them compatible with standard fully connected layers for classical processing. To improve generalization and reduce the risk of overfitting, particularly in small datasets, a dropout layer with a rate of 0.5 is applied after flattening. This layer randomly deactivates a portion of the input units during training, preventing the model from relying too heavily on specific features. Next, a fully connected (linear) layer projects the flattened vector into a logit vector with dimensions corresponding to the number of digit classes (0 to 9). This layer learns to associate quantum-enhanced patterns with specific class labels. The output logits are passed through a softmax activation function to produce normalized probability scores, ensuring compatibility with the negative log-likelihood loss used during training.
Table 1 details the layer-wise structure of the proposed hybrid model, consisting of 118,530 trainable parameters, which is approximately 3.1% less compared to the classical DNN baseline [11].

Table 1.
Layer-wise configuration of the proposed model, including kernel size (k), padding (p), stride (s), output shape, and number of trainable parameters.
3.4. Ensemble Techniques
In deep learning, it is inevitable to observe variations in results due to inherent randomness, such as the initialization of weights and data shuffling. These factors can lead to different learning dynamics, even when using the same model architecture and configuration. To mitigate uncertainty, fixed random seeds were used during training. Additionally, an ensemble technique [37] was employed, following the approach applied in the DNN model by Chang et al. [11]. As illustrated in Figure 9, the network was trained 10 times on the same dataset, resulting in 10 models with different weight initializations. During inference, each input was passed through all 10 models to produce ten output vectors. The final prediction was obtained by computing the median across these outputs, element-wise. Specifically, for each position in the output vector, the median of the corresponding values from the 10 models was selected.
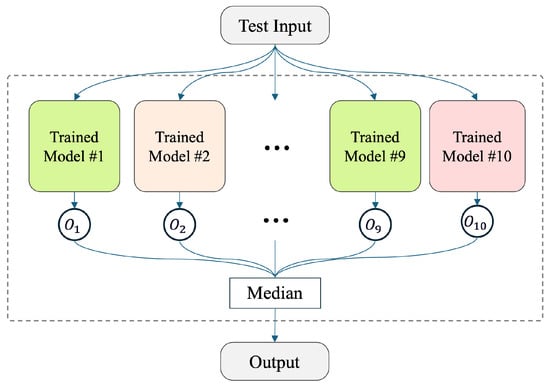
Figure 9.
Ensemble method, adapted from [11].
3.5. Evaluation
All our experiments were conducted on a local Ubuntu 24.04.1 LTS equipped with a 12th generation Intel Core i7-12700F processor (12 cores, 20 threads), 64 GB of RAM, and an NVIDIA GeForce RTX 3060 Ti GPU with 8 GB of VRAM. The system utilized CUDA 12.4 with the NVIDIA driver version 550.114.03. Python 3.12.3 scripts were executed within a virtual environment configured with PyTorch 2.4.0, ensuring performance with GPU acceleration.
Quantum components of the proposed hybrid models were executed using PennyLane 0.40.0’s default.qubit simulator backend, which is widely used in quantum machine learning studies due to its flexibility and accuracy in simulating gate-based quantum circuits.
To ensure robust evaluation across individuals, we employed a leave-one-subject-out (LOSO) cross-validation scheme [38]. Specifically, the model was trained 18 times, each time using data from 17 participants for training and testing on the remaining one. Furthermore, for each of the 18 LOSO folds, we trained the model 10 times with different initializations and averaged the predictions to form an ensemble. This ensemble strategy enhances stability and performance, while the LOSO setup guarantees subject independence by ensuring that the test data in each fold comes from a participant unseen during training. Overall, this approach addresses individual variability and signal noise, thereby improving the model’s generalization.
The proposed models were trained using the Adam optimizer for a total of 200 epochs. The initial learning rate was set to × and was scheduled to decay by a factor of 0.5 every 50 epochs to promote stable and efficient convergence.
To evaluate the model’s performance, we used four standard classification metrics: Accuracy, Precision, Recall, and F1-score, all derived from the confusion matrix. Let TP, TN, FP, and FN denote the numbers of true positives, true negatives, false positives, and false negatives, respectively. These metrics are computed as
Accuracy measures the overall proportion of correct predictions. Precision indicates the proportion of predicted positive cases that are actually positive. Recall refers to the proportion of actual positive cases correctly identified by the model. The F1-score, which is the harmonic mean of precision and recall, provides a balanced evaluation and is particularly useful when dealing with class imbalance.
4. Results
Figure 10 illustrates the training loss for the proposed model, where in each case the data from a single participant is used as the testing set. The blue curve represents the average loss across the 10 ensemble training runs, while the orange shaded region denotes the corresponding standard deviation. Variations in the magnitude of the standard deviation arise from differences in the training data and the random weight initialization used in each individual training run.
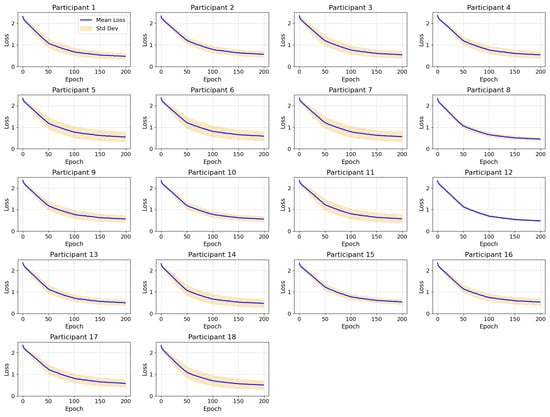
Figure 10.
Training loss per participant fold during 17:1 cross-validation. Blue lines represent the mean training loss across 10 ensemble runs. The orange bands indicate standard deviation.
The proposed hybrid model achieves an accuracy of 98.52%, surpassing the classical DNN, DCC-TCN, and other traditional pattern recognition methods (Table 2). Notably, the DCC-TCN model, despite being a single-model approach without ensemble techniques, achieved a strong accuracy of 96.20% on a more recent and diverse dataset that includes both numbers and alphabets, collected with improved signal acquisition infrastructure and more participants. Although these differences in dataset and setup should be taken into account, our hybrid model demonstrates superior performance and generalization within a standardized evaluation setting. Table 3 details the performance between individual trials, including error counts and accuracy metrics for both models. Although the classical DNN performs slightly better in the third trial, the proposed model yields higher accuracy in the first two trials and achieves the best overall accuracy.

Table 2.
Comparison of recognition accuracy for Arabic numeral eye-written digits across various methods.

Table 3.
Number of classification errors and accuracy values obtained by evaluating the collected data from each trial of all 18 participants using the DNN and the proposed model.
Table 4 presents the recognition accuracy of each participant, comparing the proposed method with traditional pattern recognition techniques and a classical deep neural network (DNN). The proposed hybrid model achieved an average accuracy of 98.52%, slightly outperforming the DNN baseline (97.96%) and exceeding the performance of dynamic time warping (DTW), dynamic positional warping (DPW), and their respective SVM-based variants. Notably, the proposed method yielded a standard deviation of 1.99, which is considerably lower than those of the other approaches, including the DNN (3.26). These results demonstrate that the proposed model not only improves overall accuracy but also delivers more consistent and generalizable performance across participants.

Table 4.
Recognition accuracy (%) for each participant across different classifiers.
Table 5 presents the performance in terms of digits of the proposed model in terms of precision, recall, and F1-score. The results indicate consistently high performance across all digits, with several classes achieving perfect scores. Even for digits with slightly lower metrics, the F1-scores remain above 97%, demonstrating the model’s robust and reliable performance in recognizing eye-written digits.

Table 5.
Recognition accuracy (%) of the proposed model for each digit.
Figure 11 shows the confusion matrix of the proposed hybrid model, indicating a total of eight misclassifications out of 540 samples. This result highlights the high accuracy of the model and its ability to correctly distinguish most eye-written digits in all classes.
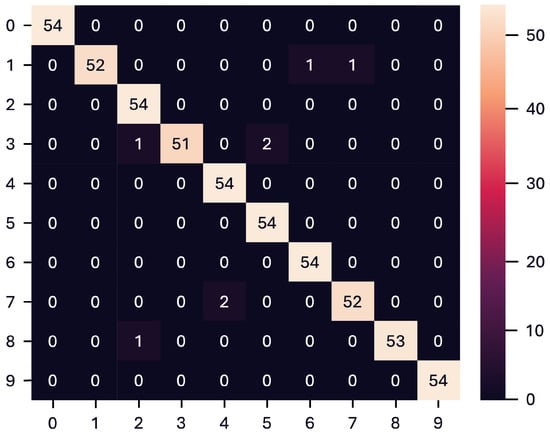
Figure 11.
Overall confusion matrix of the proposed hybrid model, showing 8 misclassifications.
Figure 12 presents the eight misclassified digits identified in the confusion matrix of Figure 11. These misclassifications are primarily attributed to the quality of the collected data, with some samples either lacking clarity or exhibiting patterns that significantly overlap with those of other digits.
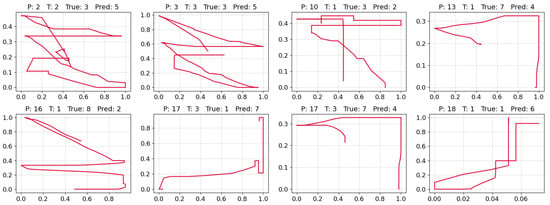
Figure 12.
Misclassified digit traces. “P” = participant, “T” = trial, “True” = actual label, “Pred” = predicted label.
5. Discussion
The strong performance of the proposed model can be attributed to the integration of key architectural modules. The feature extraction module combines convolutional layers with multiple inception and SE blocks to capture rich temporal–spatial features and enhance channel-wise attention. The feature reduction module compresses high-dimensional data for compatibility with the 4-qubit VQC, allowing efficient transformation with minimal information loss. The VQC introduces non-classical transformations that improve representation capacity, while the feature classification module, enhanced by ensemble learning, ensures robust decision making. Together, these components yield a high accuracy, low standard deviation across participants, and consistent performance across digit classes.
This study focused solely on the classification of eye-written digits using a single-modal input and a single-model approach. Incorporating additional sensing modalities could provide more comprehensive representations and potentially improve recognition accuracy, as demonstrated by previous multimodal studies in other domains [39,40,41]. Although multimodal fusion is beyond the scope of the current work, it remains a promising direction for future research in eye-written digit recognition. In addition, both our hybrid model and the classical DNN baseline still rely on ensemble techniques to improve prediction accuracy, highlighting the need for further advancements in single-model generalization. Although this work represents a proof-of-concept validation using offline data, future studies should also explore real-world deployment in practical assistive communication systems. Real-time validation was not feasible in the present study due to constraints in data availability and hardware infrastructure; however, we consider it an important avenue for future research.
6. Conclusions
In this study, we presented a hybrid quantum–classical model for eye-written digit recognition, building on a well-established classical architecture and extending it with an SE block and a variational quantum circuit. This proof-of-concept demonstrates the feasibility of integrating compact quantum components into biosignal classification pipelines. The proposed model achieved high accuracy, consistent performance across classes, and reduced variability compared to conventional deep neural networks, highlighting the potential of quantum-enhanced architectures for human–computer interaction and assistive communication tasks, particularly in low-data scenarios.
Future work will focus on validating the proposed approach in real-world assistive communication environments to further assess its practicality and robustness. Additional directions include exploring multimodal feature integration to enrich input representations and developing strategies to improve single-model generalization, thereby extending the applicability of the approach beyond its current single-modal scope.
Author Contributions
Conceptualization, K.P.; methodology, K.P.; software, K.P. and W.-D.C.; validation, T.K.; formal analysis, K.P.; investigation, K.P.; resources, W.-D.C. and Y.H.; data curation, W.-D.C.; writing—original draft preparation, K.P.; writing—review and editing, T.K., M.G., W.-D.C. and Y.H.; visualization, K.P.; supervision, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets and source code of this study are publicly available. The eye-written data can be accessed at https://github.com/EyeWriting/EyewritingNumber (accessed on 11 August 2025) by Chang et al. [11], while the resources of the quantum–classical hybrid model are available at https://github.com/povkimsay/qml-eye-written (accessed on 11 August 2025). All materials are provided to ensure reproducibility and to support further research.
Acknowledgments
This research was supported by the Pukyong National University Research Fund in 2024.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ALS | Amyotrophic Lateral Sclerosis |
| EOG | Electrooculography |
| DNN | Deep Neural Network |
| DPW | Dynamic Positional Warping |
| DTW | Dynamic Time Warping |
| SVM | Support Vector Machine |
| QML | Quantum Machine Learning |
| VQC | Variational Quantum Circuit |
| SE | Squeeze-and-Excitation |
| LOSO | Leave-One-Subject-Out |
References
- Kiernan, M.C.; Vucic, S.; Cheah, B.C.; Turner, M.R.; Eisen, A.; Hardiman, O.; Burrell, J.R.; Zoing, M.C. Amyotrophic lateral sclerosis. Lancet 2011, 377, 942–955. [Google Scholar] [CrossRef]
- Beukelman, D.; Fager, S.; Nordness, A. Communication support for people with ALS. Neurol. Res. Int. 2011, 2011, 714693. [Google Scholar] [CrossRef] [PubMed]
- Eshghi, M.; Yunusova, Y.; Connaghan, K.P.; Green, J.R. Rate of speech decline in individuals with amyotrophic lateral sclerosis. Sci. Rep. 2022, 12, 15713. [Google Scholar] [CrossRef] [PubMed]
- Dziemian, S.; Abbott, W.; Faisal, A. Gaze-based teleprosthetic enables intuitive continuous control of complex robot arm use: Writing & drawing. In Proceedings of the 6th IEEE International Conference on Biomedical Robotics and Biomechatronics, Singapore, 26–29 June 2016; pp. 1277–1282. [Google Scholar]
- Sáiz-Manzanares, M.; Pérez, I.; Rodríguez, A.; Arribas, S.; Almeida, L.; Martin, C. Analysis of the learning process through eye tracking technology and feature selection techniques. Appl. Sci. 2021, 11, 6157. [Google Scholar] [CrossRef]
- Scalera, L.; Seriani, S.; Gallina, P.; Lentini, M.; Gasparetto, A. Human–robot interaction through eye tracking for artistic drawing. Robotics 2021, 10, 54. [Google Scholar] [CrossRef]
- Wöhle, L.; Gebhard, M. Towards robust robot control in cartesian space using an infrastructureless head-and eye-gaze interface. Sensors 2021, 21, 1798. [Google Scholar] [CrossRef]
- Jang, S.T.; Kim, S.R.; Chang, W.D. Gaze tracking of four direction with low-price EOG measuring device. J. Korea Converg. Soc. 2018, 9, 53–60. [Google Scholar]
- Chang, W.D. Electrooculograms for Human–Computer Interaction: A Review. Sensors 2019, 19, 2690. [Google Scholar] [CrossRef]
- Acuña, O.V.; Aqueveque, P.; Pino, E.J. Eye-tracking capabilities of low-cost EOG system. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 610–613. [Google Scholar] [CrossRef]
- Chang, W.D.; Choi, J.H.; Shin, J. Recognition of eye-written characters using deep neural network. Appl. Sci. 2021, 11, 11036. [Google Scholar] [CrossRef]
- Tsai, J.Z.; Lee, C.K.; Wu, C.M.; Wu, J.J.; Kao, K.P. A feasibility study of an eye-writing system based on electro-oculography. J. Med. Biol. Eng. 2008, 28, 39–46. [Google Scholar]
- Chang, W.D.; Cha, H.S.; Kim, D.; Kim, S.; Im, C.H. Development of an electrooculogram-based eye-computer interface for communication of individuals with amyotrophic lateral sclerosis. J. Neuroeng. Rehabil. 2017, 14, 89. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar] [CrossRef]
- Bature, Z.A.; Abdullahi, S.B.; Chiracharit, W.; Chamnongthai, K. Translated Pattern-Based Eye-Writing Recognition Using Dilated Causal Convolution Network. IEEE Access 2024, 12, 59079–59092. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef]
- Caro, M.C.; Cerezo, M.; Sharma, K.; Sornborger, A.T.; Coles, P.J.; Cincio, L. Generalization in quantum machine learning from few training data. Nat. Commun. 2022, 13, 4919. [Google Scholar] [CrossRef]
- Wang, A.; Mao, D.; Li, X.; Li, T.; Li, L. HQNet: A hybrid quantum network for multi-class MRI brain classification via quantum computing. Expert Syst. Appl. 2025, 261, 125537. [Google Scholar] [CrossRef]
- Hafeez, M.A.; Munir, A.; Ullah, H. H-QNN: A Hybrid Quantum–Classical Neural Network for Improved Binary Image Classification. AI 2024, 5, 1462–1481. [Google Scholar] [CrossRef]
- Zhang, Z.; Mi, X.; Yang, J.; Wei, X.; Liu, Y.; Yan, J.; Liu, P.; Gu, X.; Yu, T. Remote Sensing Image Scene Classification in Hybrid Classical–Quantum Transferring CNN with Small Samples. Sensors 2023, 23, 8010. [Google Scholar] [CrossRef] [PubMed]
- Ji, N.; Bao, R.; Chen, Z.; Yu, Y.; Ma, H. Hybrid Quantum Neural Network Image Anti-Noise Classification Model Combined with Error Mitigation. Appl. Sci. 2024, 14, 1392. [Google Scholar] [CrossRef]
- Ranga, D.; Prajapat, S.; Akhtar, Z.; Kumar, P.; Vasilakos, A.V. Hybrid Quantum–Classical Neural Networks for Efficient MNIST Binary Image Classification. Mathematics 2024, 12, 3684. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Sim, S.; Johnson, P.D.; Aspuru-Guzik, A. Expressibility and Entangling Capability of Parameterized Quantum Circuits for Hybrid Quantum-Classical Algorithms. Adv. Quantum Technol. 2019, 2, 1900070. [Google Scholar] [CrossRef]
- Chang, W.D.; Cha, H.S.; Kim, K.; Im, C.H. Detection of eye blink artifacts from single prefrontal channel electroencephalogram. Comput. Methods Programs Biomed. 2016, 124, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Martens, T.J.; Van Cittert, E.H.; Bischof, W.F. Wavelet-based analysis of eye movements for psychophysiological research. J. Neurosci. Methods 2005, 142, 27–39. [Google Scholar] [CrossRef]
- Preskill, J. Lecture Notes for Physics 229: Quantum Information and Computation. 1998. Available online: https://preskill.caltech.edu/ph229/ (accessed on 11 August 2025).
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th anniversary ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Abbas, A.; Sutter, D.; Zoufal, C.; Lucchi, A.; Figalli, A.; Woerner, S. The power of quantum neural networks. Nat. Comput. Sci. 2021, 1, 403–409. [Google Scholar] [CrossRef]
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef]
- Ranga, D.; Rana, A.; Prajapat, S.; Kumar, P.; Kumar, K.; Vasilakos, A.V. Quantum Machine Learning: Exploring the Role of Data Encoding Techniques, Challenges, and Future Directions. Mathematics 2024, 12, 3318. [Google Scholar] [CrossRef]
- Rath, M.; Date, H. Quantum data encoding: A comparative analysis of classical-to-quantum mapping techniques and their impact on machine learning accuracy. EPJ Quantum Technol. 2024, 11, 72. [Google Scholar] [CrossRef]
- McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
- Sen, P.; Bhatia, A.; Bhangu, K.; Elbeltagi, A. Variational quantum classifiers through the lens of the Hessian. PLoS ONE 2022, 17, e0262346. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-excitation networks. arXiv 2019, arXiv:1709.01507. [Google Scholar]
- Chaudhary, K.; Bali, R. Easter2.0: Improving Convolutional Models for Handwritten Text Recognition. arXiv 2022, arXiv:2205.14879. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Individual Subject Prediction. Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. NeuroImage 2017, 145, 166–179. [Google Scholar] [CrossRef]
- Zhao, G.; Lin, Y.; Lu, Y.; Chen, Z.; Guo, W. Lightweight bilateral network of Mura detection on micro-OLED displays. Measurement 2025, 255, 117937. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.; Zhou, Z.; Zhang, B. Multi-task learning for hand heat trace time estimation and identity recognition. Expert Syst. Appl. 2024, 255, 124551. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.; Zhou, Z.; Zhang, B.; Xue, H. Deep soft threshold feature separation network for infrared handprint identity recognition and time estimation. Infrared Phys. Technol. 2024, 138, 105223. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).