MAFUZZ: Adaptive Gradient-Guided Fuzz Testing for Satellite Internet Ground Terminals

Abstract

With the proliferation of satellite internet systems, such as Starlink and OneWeb, ground terminals have become critical for ensuring end-user connectivity. However, the security of Satellite Internet Ground Terminals (SIGTs) remains underexplored. These Linux-based embedded systems are vulnerable to advanced attacks due to limited source code access and immature protection mechanisms. This paper presents MAFUZZ, an adaptive fuzzing framework guided by neural network gradients to uncover hidden vulnerabilities in SIGT binaries. MAFUZZ uses a lightweight machine learning model to identify input bytes that influence program behavior and applies gradient-based mutation accordingly. It also integrates an adaptive Havoc mechanism to enhance path diversity. We compare MAFUZZ with NEUZZ, a neural fuzzing tool that uses program smoothing to guide mutation through a static model. Our experiments on real-world Linux binaries show that MAFUZZ improves path coverage by an average of 17.4% over NEUZZ, demonstrating its effectiveness in vulnerability discovery and its practical value for securing satellite terminal software.

1. Introduction

Satellite internet has garnered significant global research attention, particularly regarding its security. Leading the industry are SpaceX’s Starlink, OneWeb, and Amazon’s Kuiper [1]. Notably, Starlink’s ground terminals have achieved widespread commercial deployment, with newer generations extending coverage to mobile platforms such as vehicles, ships, and aircraft.

While prior studies have focused extensively on inter-satellite laser links and satellite-to-ground microwave communications, the security of Satellite Internet Ground Terminals (SIGTs) remains underexplored. These terminals function as edge nodes within the satellite network, often built on Linux-based embedded platforms and exhibiting characteristics akin to Internet-of-Things (IoT) devices, such as constrained firmware, proprietary communication interfaces, and remote access capabilities. The existing literature in IoT security and firmware fuzzing has highlighted challenges such as closed-source binaries, incomplete verification, and inadequate input sanitization [2,3].

As illustrated in Figure 1, satellite internet communication architecture allows users to connect their personal computers or mobile devices wirelessly to SIGTs. These terminals upload user data to Low Earth Orbit (LEO) satellites, which then relay the data to ground gateways for internet access. Given their increasing ubiquity and external exposure, SIGTs are becoming attractive targets for attackers aiming to exploit vulnerabilities in embedded software, control protocols, and web-based management interfaces.

This paper aims to address this critical security gap by focusing on the automated vulnerability discovery of SIGT binary programs through adaptive gradient-guided fuzzing.

SIGTs in satellite internet systems play a vital role in linking user devices to communication satellites [4]. These terminals receive commands from user applications or web interfaces and employ proprietary phased array technology to locate and connect to Low Earth Orbit (LEO) satellites within their range, facilitating the upload and download of user data. As emerging IoT [5] devices and commercial routers [6,7], SIGTs face security challenges similar to those of existing terrestrial IoT devices [3]. Most SIGTs utilize embedded Linux systems. For instance, Starlink’s SIGTs share a similar internal structure with traditional Linux-embedded devices, utilizing binary programs on loopback and external ports for interactive functions. However, as early-stage IoT devices, many applications for these terminals remain immature, with their code security not thoroughly examined. Additionally, satellite internet providers typically offer interactive interfaces for user control and status monitoring of SIGTs. For example, Starlink provides applications and web management interfaces, which could be exploited by attackers for remote attacks, posing threats to user privacy and enabling malicious activities.

These practical concerns motivate the need for a proactive approach to binary-level vulnerability discovery in SIGTs.

Given this context, we have undertaken the following work on the security of SIGTs: We review past attack cases on Starlink’s SIGTs, analyzing the methods and principles behind these attacks [2,8]. We conduct an in-depth analysis of the hardware and software architecture of Starlink’s SIGTs [9]. This analysis aims to identify potential attack surfaces and construct a threat model. We address the challenges of acquiring binary program source code and the difficulties of reverse engineering and static analysis by proposing a fuzz testing method guided by neural network gradients. This method employs a neural network to approximate the relationship between seed inputs and program coverage, allowing it to compute input gradients and guide mutations toward paths that are more likely to trigger unexplored control-flow branches. We also designed an adaptive algorithm to automatically adjust the deterministic and havoc stages during the fuzz testing process. Our experimental results show that our method can achieve higher code coverage of the target binary programs in a shorter time [10,11].

2. Previous Attack Case Analysis

2.1. Fault Injection Attack

In the field of terminal security attack research, Lennert Wouters focused on exploring vulnerabilities in secure boot systems. He employed hardware attack techniques to design a custom circuit board called a modchip, which can temporarily disable decoupling capacitors used for power smoothing, inducing circuit faults. This allows for the circumvention of security protection mechanisms during the initialization process of the Linux bootloader. Once the security protection is bypassed, the modchip re-enables the decoupling capacitors, granting access to the underlying system of the Starlink’s SIGTs. The core principle of this attack is to temporarily short-circuit the terminal’s internal system, bypassing the security protection module during startup, thereby gaining access to the underlying system and allowing the execution of custom code on the Starlink system. Although this attack method is highly effective in achieving advanced malware injection, it is relatively difficult to implement because it requires complex physical hardware manipulation.

Notably, this type of physical-layer attack ultimately targets the software components of the system—particularly the bootloader, kernel, and initialization routines embedded in the firmware. These binaries are often closed-source and highly obfuscated, making static analysis challenging. Although such attacks are conducted at the hardware level, their ultimate objective is to compromise critical software binaries. This highlights the necessity of proactive vulnerability discovery mechanisms at the binary level. Our proposed framework, MAFUZZ, offers a dynamic and automated way to analyze these components. By applying adaptive gradient-guided fuzzing to the early boot stages, MAFUZZ enables the discovery of memory corruption, logic flaws, or unexpected state transitions that could be exploited during initialization. While MAFUZZ does not directly prevent physical intrusions, it strengthens firmware security by identifying software-layer vulnerabilities before they can be exploited by hardware-assisted attacks.

2.2. Remote Command Attack

In the realm of network security, researchers such as Joshua Smailes have conducted detailed analysis of the communication architecture employed by Starlink ground terminals [6,12]. Their investigations have revealed that both the front-end and back-end systems utilize Google Remote Procedure Call (gRPC) commands for interaction [13]. This approach facilitates high-performance and low-latency real-time communication. However, it also introduces vulnerabilities to potential tampering, allowing for the transmission of malicious commands. Furthermore, they noted the presence of the grpcurl command-line tool within the user’s web management interface, enabling users to issue arbitrary gRPC requests and interact with gRPC servers.

Based on the analysis, Joshua Smailes utilized the Wireshark tool to capture and extract gRPC commands encapsulated within HTTP packets. By analyzing the format of these commands, they constructed initial seeds and performed fuzz testing using the grpcurl command-line interface, successfully triggering remote command reception crashes on the target ground terminal. This attack method exploits design flaws in the Starlink user web management interface, particularly in the command handler’s input parsing logic.

Importantly, such command handlers are implemented as binary programs in the firmware and typically process external inputs without formal verification. These components are ideal candidates for fuzz testing to detect memory corruption, format string errors, and other parsing-related vulnerabilities. MAFUZZ provides an efficient solution for analyzing these closed-source gRPC handling binaries through gradient-guided seed mutation and adaptive exploration. By targeting this class of input-driven programs, MAFUZZ can help uncover critical flaws before they are exploited in remote command injection scenarios.

2.3. KA-SAT Attack

In the context of large-scale attacks on satellite networks, a significant cyberattack was launched by the Russian military intelligence agency (GRU) against ViaSat’s KA-SAT satellite network just hours before Russia’s invasion of Ukraine on 24 February 2022 [6]. This attack targeted critical communication equipment used by the Ukrainian Armed Forces—ViaSat SurfBeam 2 modems [14]. These modems were extensively utilized for tasks such as tactical communication, intelligence sharing, logistical support, and cyber defense. Their disruption severely degraded operational capabilities.

The attack unfolded in several phases: first, the attackers identified the KA-SAT network and its SurfBeam 2 modems [15], analyzed the configuration, and discovered a vulnerability in the VPN application setup. A Distributed Denial of Service (DDoS) attack followed, initially disrupting network availability. Then, leveraging the VPN vulnerability, the attackers gained unauthorized access to the management segment, from which they deployed the “AcidRain” malware [16] to remotely wipe device storage and disable modem functionality permanently.

While this attack does not originate from a fuzzing perspective, it highlights how firmware-level components—such as VPN clients, update agents, or configuration parsers—can serve as entry points for devastating exploits. These components are typically closed-source and embedded as binaries, making proactive vulnerability discovery difficult. MAFUZZ is designed to operate in exactly this context: as a binary-level fuzzing framework, it can dynamically explore and test such components to uncover input-handling flaws, unsafe state transitions, or logic errors. By applying MAFUZZ to SIGT firmware modules, it becomes possible to identify similar latent vulnerabilities before they are weaponized in attacks of this scale.

3. Threat Analysis and Model Construction

To effectively understand the attack surfaces of Satellite Internet Ground Terminals (SIGTs), it is essential to analyze the system from both physical and logical perspectives. Starlink SIGTs are composed of secure hardware modules, closed-source embedded firmware, and complex runtime communication interfaces. Each of these components may expose vulnerabilities that could be exploited for unauthorized access, command injection, or denial of service.

This section provides a comprehensive analysis of the Starlink ground terminal architecture from three dimensions—hardware, software, and runtime behavior—and constructs a corresponding threat model. This analysis directly supports the motivation for applying binary-level fuzzing, as many of the vulnerabilities identified reside in binary executables and cannot be detected through static inspection alone.

3.1. Starlink Terminal Hardware Structure Analysis

Similar to traditional Linux embedded devices, the internal hardware system of a STARLINK terminal is also built around a central System-on-Chip (SoC), which is responsible for storing all the files required for device operation and executing management programs. The specific core structure is illustrated in Figure 2.

Below, we detail the various components of the core structure:

• Microcontroller: A customized quad-core ARM Cortex-A53 processor, model STM GLLCCODGBF (STMicroelectronics, Geneva, Switzerland), responsible for executing program instructions from RAM or ROM.
• RAM: Consists of two DDR3 chips (e.g., Micron Technology Inc., Boise, ID, USA), each with a capacity of 4 Gbit, providing necessary memory support for system operation.
• Persistent storage: A 4 GB eMMC chip (e.g., Kingston Technology, Fountain Valley, CA, USA) is used to store all the files required for running the Linux system, which is also the primary target for attackers. Key files include the trusted firmware (TF-A), U-Boot bootloader, Linux kernel, and root filesystem.
• Security component: STSAFE-A110 (STMicroelectronics, Geneva, Switzerland), which provides identity authentication and secure data management services for local or remote hosts.

For attackers, the primary step towards executing malicious code injection or other threatening activities is to gain elevated access privileges to the target system. Only with these privileges can attackers modify internal files and steal sensitive information. However, compared to typical IoT-embedded devices, Starlink ground terminals have implemented stricter security measures.

As shown in Figure 3, a Starlink ground terminal incorporates a TF-A secure chain verification module into its system boot process. The boot process is initiated by the ROM inside the microcontroller, and upon receiving instructions the eMMC first activates the TF-A security module. Guided by the TF-A secure trust chain, U-Boot, the system kernel, and, finally, the root filesystem are sequentially started.

With the introduction of the trust chain, any modifications to the software in the memory are detected by the system. Therefore, if attackers want to achieve persistent modifications to the software, they must bypass the trust chain verification. An effective method is through fault injection, causing the initial signature check in the trust chain to fail, while simultaneously writing a patched firmware image that aims to skip subsequent verification steps. Once successfully written, attackers can enter the testing environment of the Starlink terminal through the USRT test interface.

Despite the existence of the TF-A secure chain and hardware-based verification, the system’s resilience still relies significantly on the STM STSAFE-A110 secure element. This component handles identity authentication, cryptographic key protection, and boot integrity validation, leveraging tamper-resistant hardware and elliptic-curve signature mechanisms [17].

However, fault injection attacks—such as voltage glitches—can interrupt the boot process before STSAFE-A110 completes its validation. To counter such hybrid physical–software threats, the system must integrate hardware and firmware defense measures. For example, TF-A or U-Boot can implement runtime integrity checks and challenge–response verification using secrets stored in the secure element.

These cooperative mechanisms substantially enhance an SIGT’s ability to detect and resist low-level intrusion attempts [18].

3.2. Starlink Terminal Runtime Structure Analysis

Starlink SIGTs, similar to common smart home IoT devices on the market, are equipped with corresponding mobile applications and web management interfaces. These external input interfaces undoubtedly provide potential avenues for attackers to remotely infiltrate the system. For traditional IoT devices, once an attacker obtains the terminal’s internal binary programs and uses static or dynamic analysis to discover software vulnerabilities, they can exploit these vulnerabilities remotely on the target terminal to steal sensitive information or gain elevated administrative privileges.

However, the internal programs of SIGTs are highly complex. Even if the external interfaces used as attack entry points are identified and the internal binary programs are obtained through reverse engineering, executing remote exploits remains challenging without a thorough understanding of the terminal’s runtime communication structure. This complexity arises because during the operation of the SIGT there are interactions with different access levels between the user terminal, the ground terminal’s internal processes, and the cloud servers. This results in varying user access permissions and access levels for different internal binary programs, making it more difficult to exploit vulnerabilities in these programs. Therefore, a deep understanding of the internal communication architecture during the terminal’s operation is crucial for carrying out remote network attacks.

As shown in Figure 4, the communication interaction architecture of a Starlink ground terminal mainly covers three levels: interaction between front-end applications and the internal processes of the terminal, interaction between remote servers and the internal processes of the terminal, and interaction among the internal processes of the terminal. Below is a detailed analysis of each interaction principle and its potential attack surfaces:

• Interaction between front-end applications and the internal processes of the terminal: Within the terminal, there are back-end processes that interact with front-end applications. These applications remotely send commands via the gRPC protocol, including requests for terminal status, telemetry data, factory resets, software updates, and terminal orientation control. If attackers identify the format of gRPC requests and exploit vulnerabilities via dynamic analysis (e.g., fuzz testing), they may remotely send malicious commands. Joshua Smailes et al. demonstrated this attack method on real terminals.
• Interaction between remote servers and the internal processes of the terminal: Starlink’s remote servers receive and respond to gRPC requests from terminal back-end processes. These servers interact with the terminal’s control, update, and telemetry processes. If attackers discover vulnerabilities in this server–terminal interaction, they may leverage the server as a proxy to deliver malicious commands to internal processes.
• Interaction among the internal processes of the terminal: These processes facilitate communication with front-end applications and satellites, mediated by the terminal control process. Internally, they exchange data via loopback ports using precompiled binary programs. Once communication interfaces are identified, attackers can focus on locating exploitable vulnerabilities in these binaries.

Figure 4. Starlink terminal communication architecture.

Figure 4. Starlink terminal communication architecture.

3.3. Threat Model Construction

Based on the preceding analysis of the Starlink ground terminal’s hardware, software, and communication architecture, we constructed a three-layer threat model encompassing the physical layer, the network/software layer, and the protocol/communication layer, as illustrated in Figure 5. This model reflects varying attacker capabilities, access levels, and technical complexity across different layers of the system.

Physical layer: Attackers with physical access can extract firmware from the eMMC storage, inject modified images with patched trust chains (e.g., TF-A), and use modchip-based fault injection to bypass secure boot verification [18]. This type of attack offers deep system control but requires high precision, specialized equipment, and close physical proximity—making it powerful but difficult to scale.

Network/software layer: Without hardware access, remote adversaries can exploit vulnerabilities exposed by front-end-back-end interfaces (e.g., gRPC) or use fuzzing techniques to generate malformed inputs that target back-end binaries. These attacks are scalable and automatable but are constrained by the closed-source nature of firmware and limited semantic feedback during testing [19]. Recent studies have shown that such vulnerabilities are prevalent in commercial satellite modem firmware, where over a dozen exploitable flaws were identified across real-world devices [20], highlighting the practical relevance of embedded binary fuzzing.

Protocol/communication layer: During runtime, dynamic behaviors such as satellite handovers introduce unique risks. Improper state synchronization—such as inconsistent session contexts or re-used authentication tokens—may result in session desynchronization or replay attacks [21,22]. Furthermore, satellite–ground and inter-satellite links are typically encrypted using application-layer or MAC-layer protocols. While encryption enhances security, it obscures program behavior from fuzzing tools, reducing both input observability and mutation effectiveness [9].

4. Fuzz

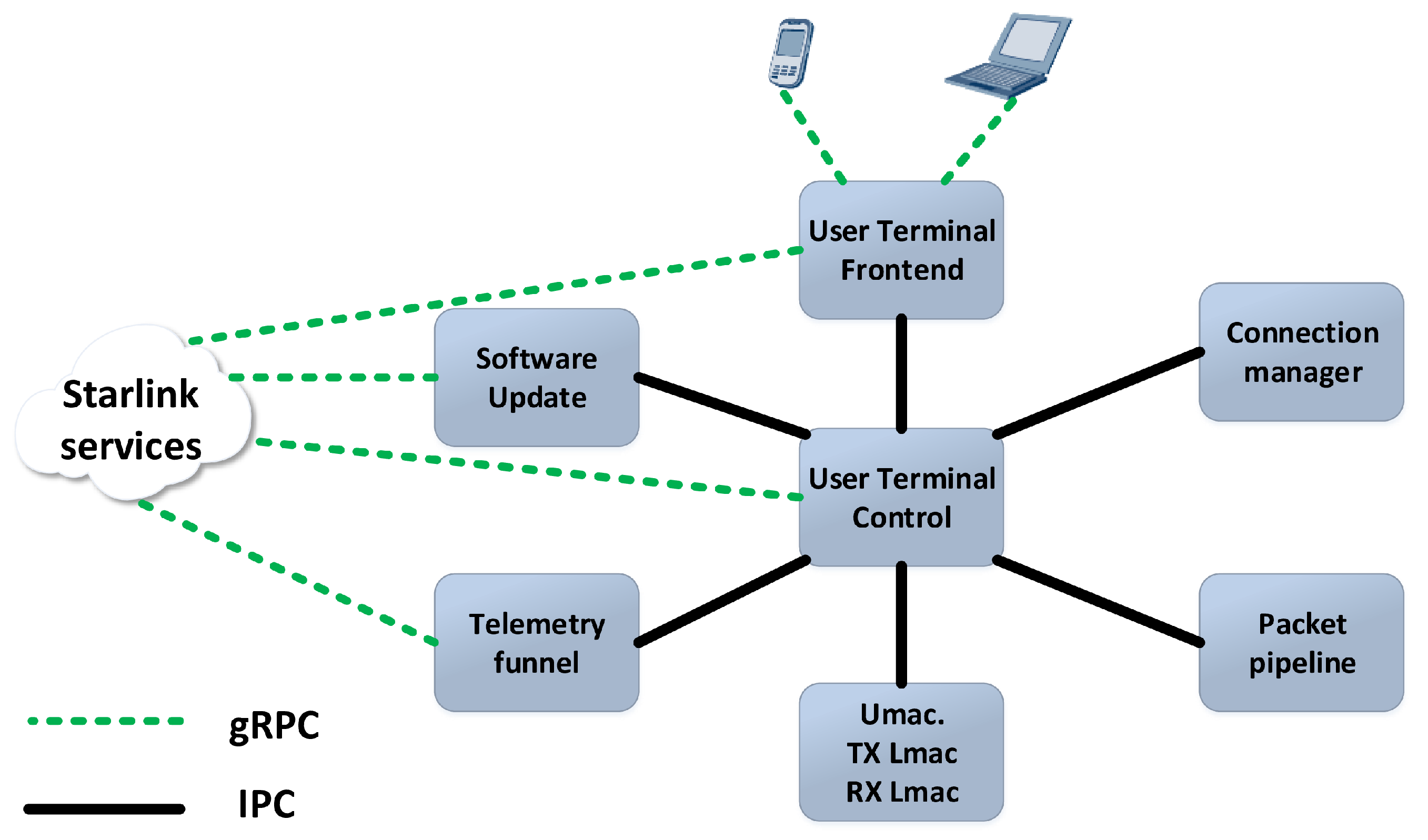
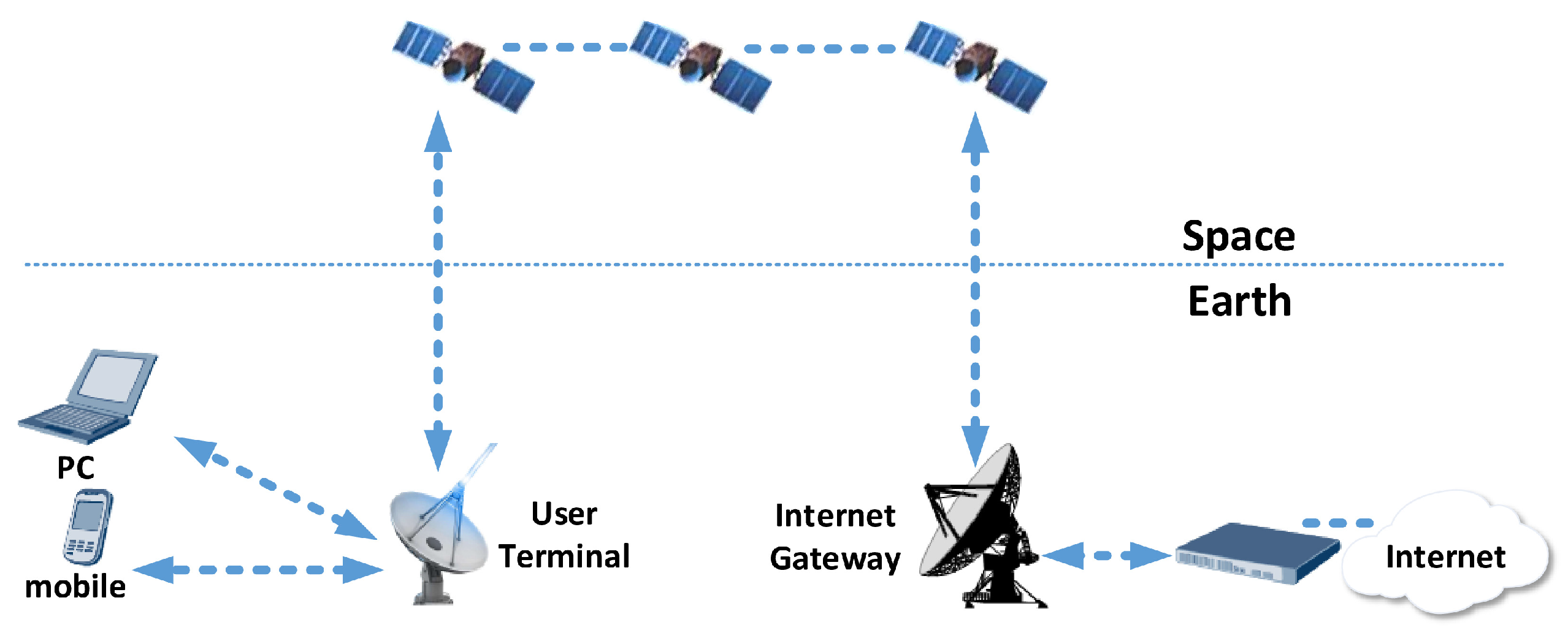
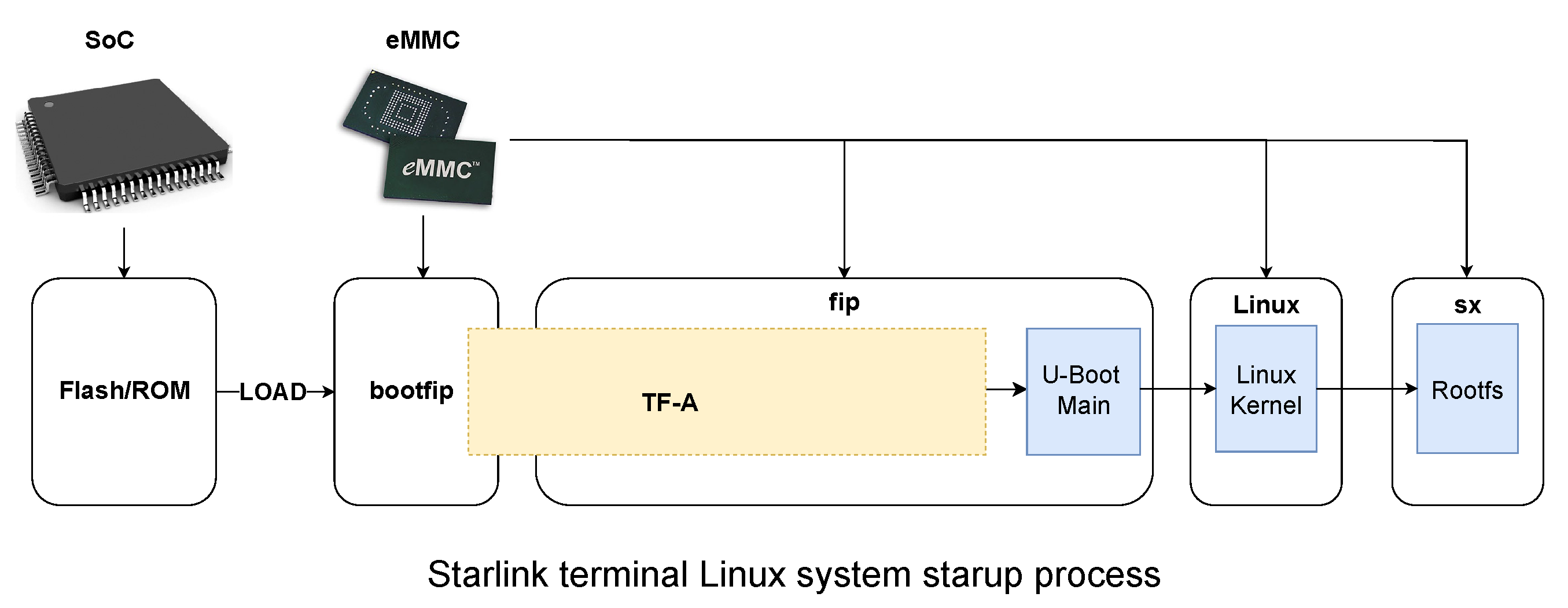
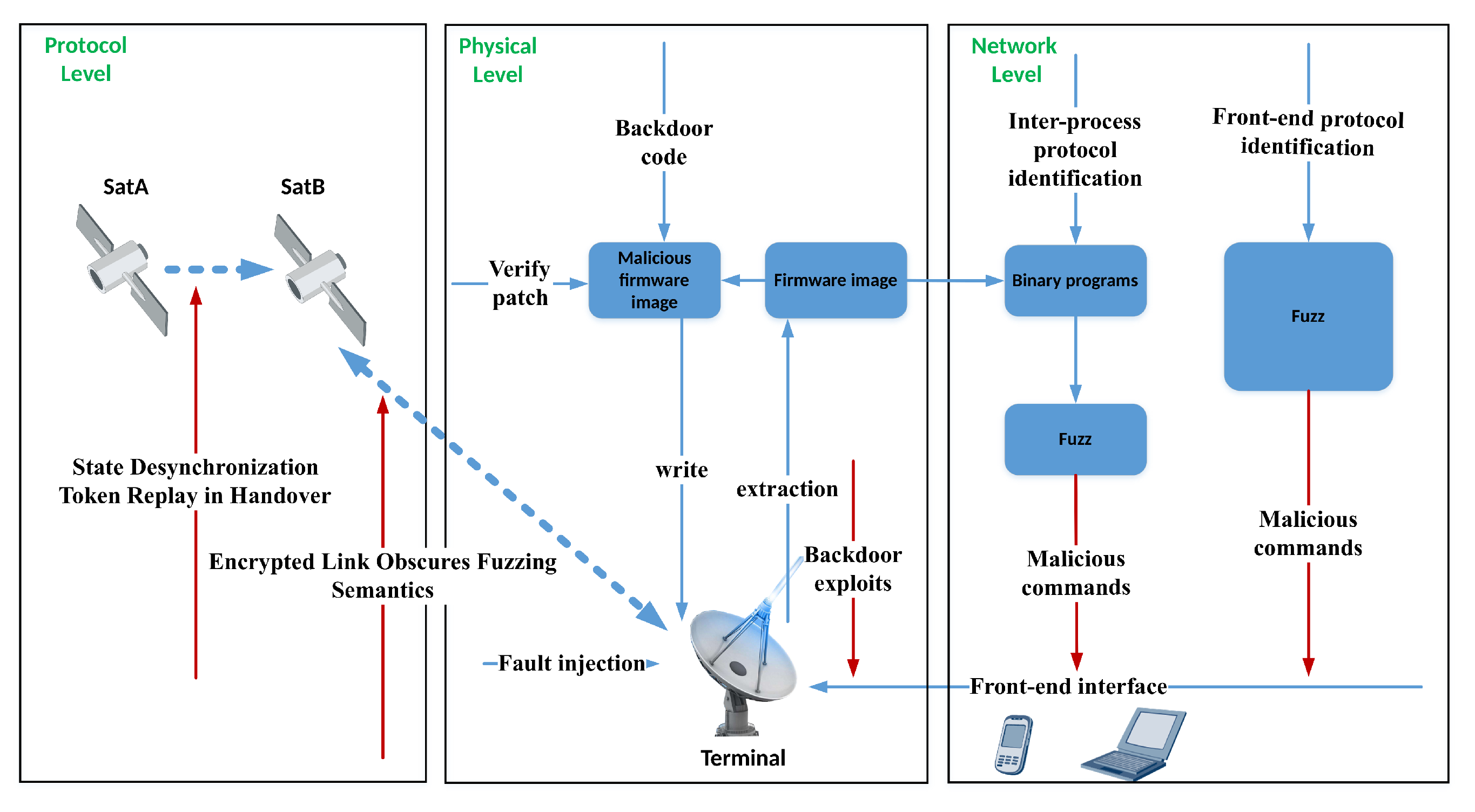
In this section, we will explore the principles of gradient-guided fuzz testing for efficiently discovering vulnerabilities in binary programs, and we will introduce our developed adaptive gradient-guided fuzz testing framework.

In summary, this threat model captures a spectrum of attack vectors: highly effective but hardware-dependent physical attacks, widely accessible but semantically opaque software attacks, and dynamic protocol-level threats that are both difficult to monitor and test. Collectively, these observations illustrate the unique challenges posed by SIGT systems—from physical tampering to protocol-level complexity. To address these issues, we introduce an adaptive fuzzing framework capable of dynamically navigating such deeply layered attack surfaces.

4.1. Gradient-Guided Fuzz Testing

Fuzz testing is a dynamic analysis vulnerability discovery technique that continuously sends mutated data to the target program to check if these inputs cause program errors or crashes [23]. Current mainstream binary fuzz testing tools, such as American fuzzy lop (AFL), adopt coverage-guided methods combined with the principles of evolutionary optimization algorithms, retaining only those inputs most likely to produce new code coverage to improve seed quality. However, evolutionary optimization algorithms tend to get stuck in local optima during the computation process [24], leading to a gradual decrease in efficiency in exploring new code paths. Gradient-guided optimization algorithms effectively address this issue [25].

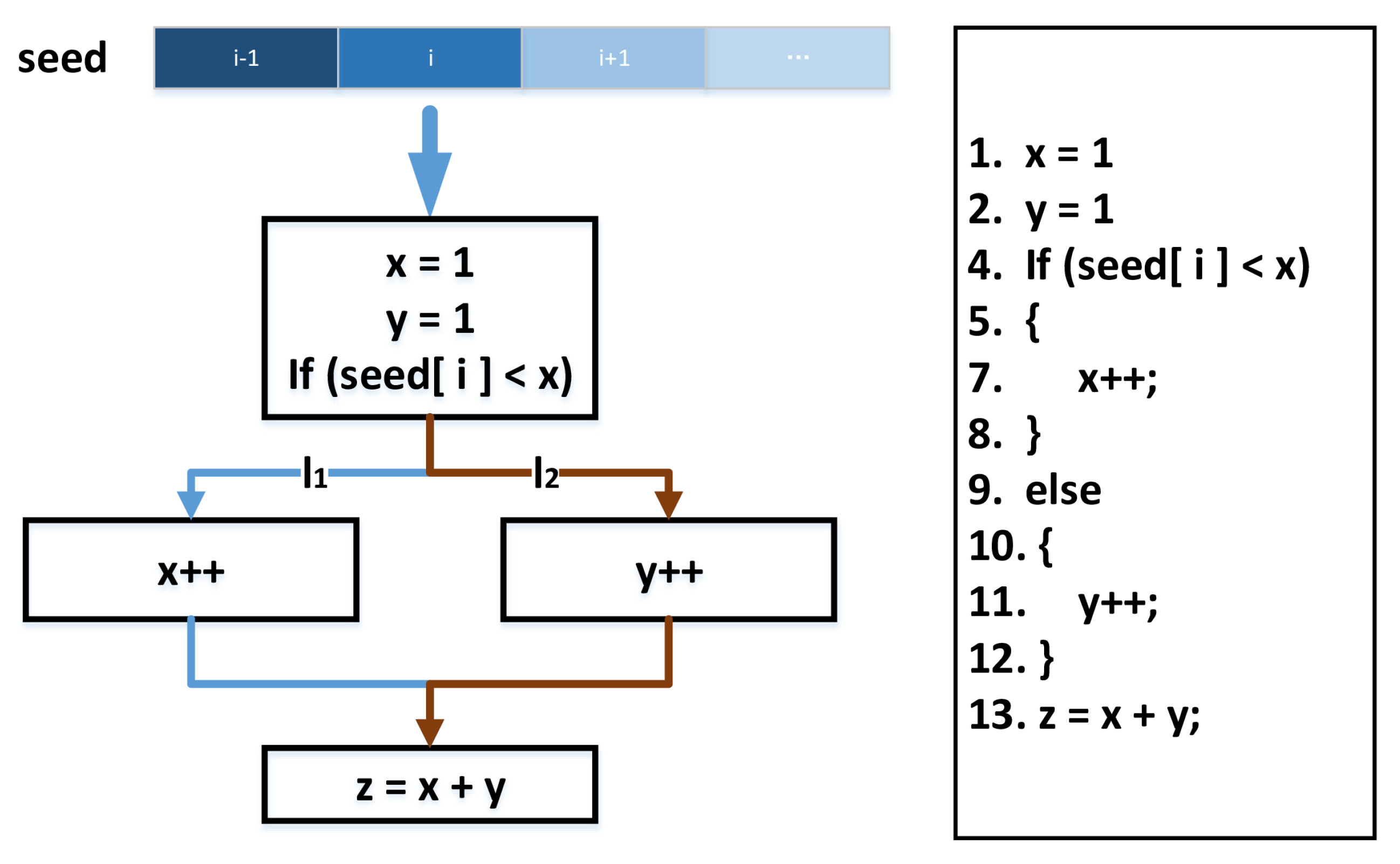
The principle of achieving efficient fuzz testing using gradient guidance is illustrated in Figure 6. For the seed provided as input to the target program, the ith byte typically corresponds to a reference point of a conditional branch statement in the program. Therefore, if we can identify, through gradient guidance, the byte in each seed most likely to change the branch statement and mutate it accordingly, we may explore the sibling path of the original branch. For example, in Figure 6, mutating the value of seed[i] to be greater than x can transition the seed exploration path from l1 to l2. The gradient-guided algorithm can meet this requirement by first constructing a surrogate function to establish the relationship between seed bytes and their coverage paths then utilizing this function to calculate the gradient corresponding to each byte, thereby identifying the most promising mutation bytes. However, due to the complexity of real-world programs, constructing a function that can smoothly represent the causal relationship mentioned above is highly challenging.

4.2. Neural Program Smoothing Fuzz Testing

Given the limitations of current gradient-guided methods in fuzzing programs, She et al. proposed a fuzz testing tool called NEUZZ based on neural program smoothing [26,27]. NEUZZ is a pioneering framework that integrates deep learning into fuzzing by modeling how input bytes affect code coverage. It trains a neural network to learn the mapping from inputs to edge coverage and uses gradient backpropagation to identify mutation positions. This method utilizes a neural network model [28] to learn the functional relationship between input seed bytes and output coverage edges. It takes the byte sequences of each initial seed as input and outputs a vector representation of the corresponding coverage bitmap. Through the neural network [29,30], it captures the implicit correlations between seed byte sequences and program branches, and it then performs gradient backpropagation to identify the input bytes most likely to influence control flow transitions [31]. Subsequent mutations are guided by the magnitude of these gradients, enabling targeted exploration of previously unreached paths.

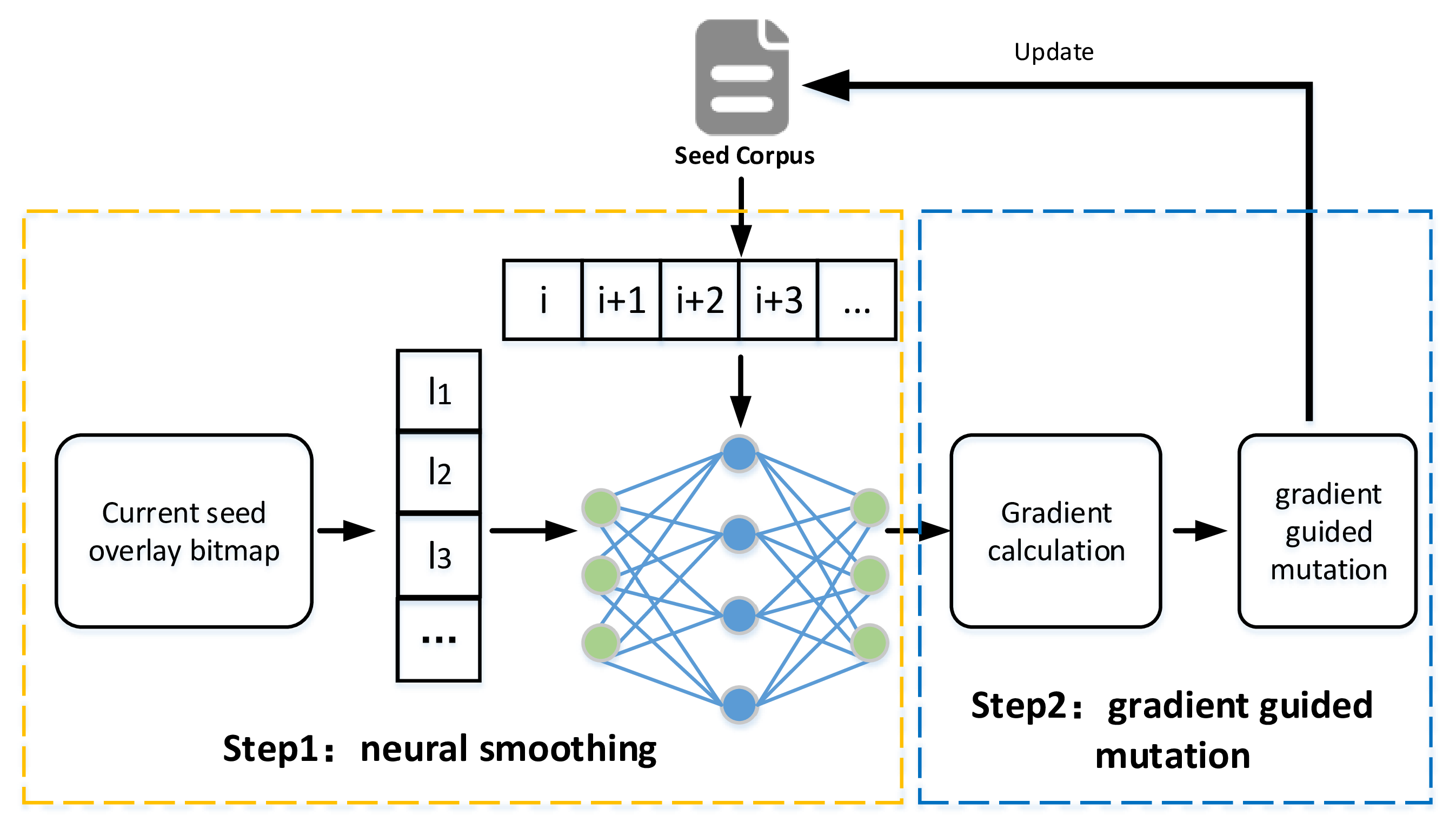
The specific process of NEUZZ is illustrated in Figure 7, and it can be divided into two stages: neural program smoothing and gradient-guided mutation. In the smoothing stage, NEUZZ constructs a mapping function between the seed byte positions and edge bitmap:

$$f:{\{i,i+1,i+2,i+3,\dots \}}^m\to {\{l_1,l_2,l_3,l_4,\dots \}}^n$$

(1)

All the initial seeds are first executed to collect the set of covered edges, defining the output bitmap’s dimensionality n. Each input seed is recorded as a byte sequence of length m, representing the input dimensionality. For any given execution, if an edge is triggered then the corresponding bit in the output vector is set to 1; otherwise, to 0. For example, a seed activating edge₁ but not edge₂ yields an output like $\{1,0,{\mathrm{edge}}_3,{\mathrm{edge}}_4,\dots \}$. The accumulated input–output pairs from all the seeds are then used to train the neural network. After training, gradient-based mutation is performed by computing the derivative of the output edge bitmap with respect to each input byte. These gradients serve as indicators of each byte’s mutation potential.

To implement the smoothing step, NEUZZ uses a fully connected feedforward neural network with a single hidden layer, typically consisting of 4096 neurons with ReLU activation. The output layer uses a sigmoid function to predict the edge activation probabilities. This lightweight design ensures both modeling capacity and computational efficiency.

The NEUZZ authors report that the neural network structure plays a secondary role compared to input diversity: experiments using deeper networks or wider hidden layers achieved only marginal improvements in coverage while significantly increasing training cost and risk of overfitting. Conversely, removing the hidden layer degraded performance, due to limited nonlinear modeling capacity. These findings indicate that a one-hidden-layer architecture is sufficient to approximate the mapping from seed bytes to coverage edges, offering a good trade-off between accuracy, generalization, and overhead in fuzzing scenarios [26].

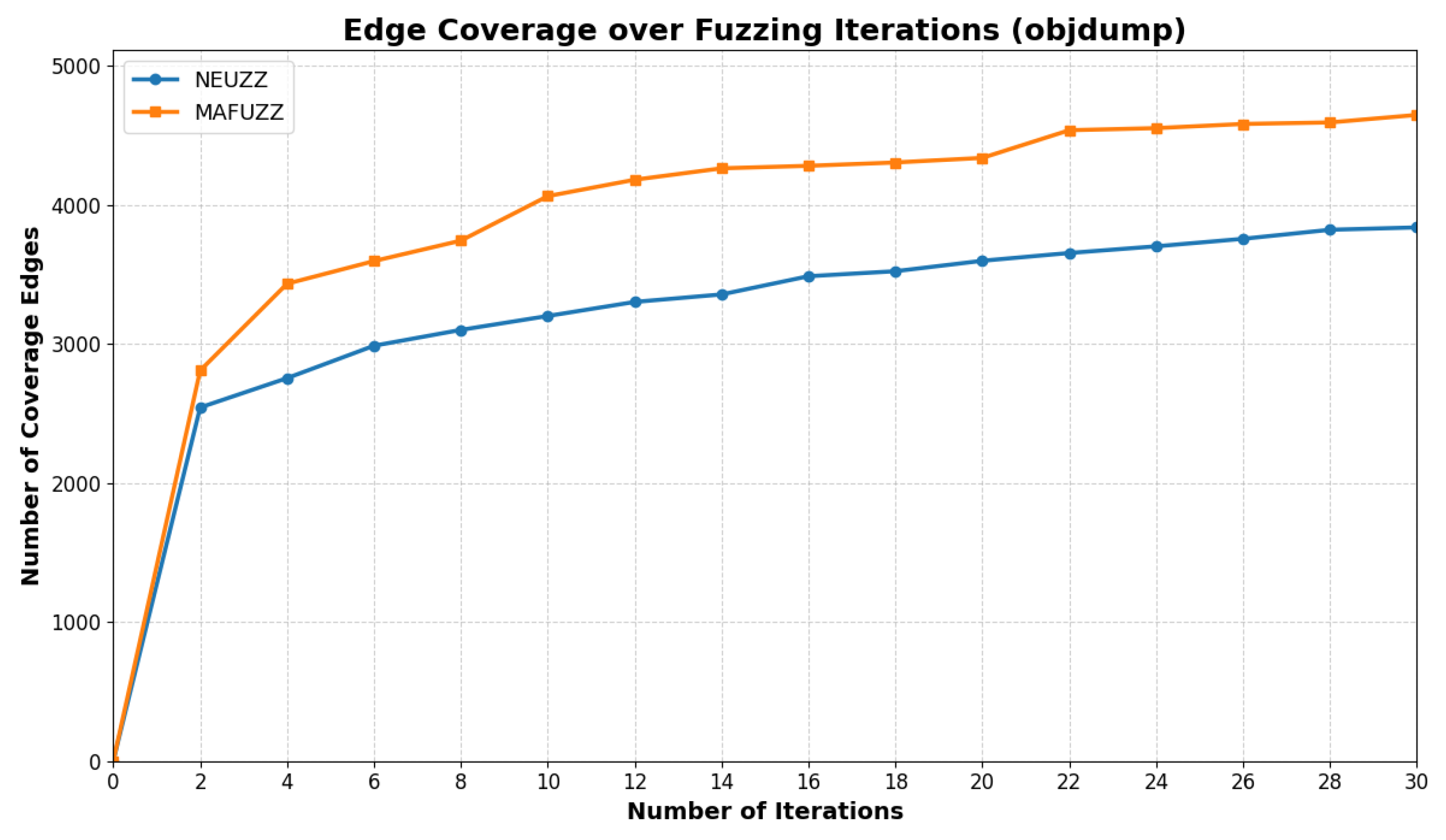
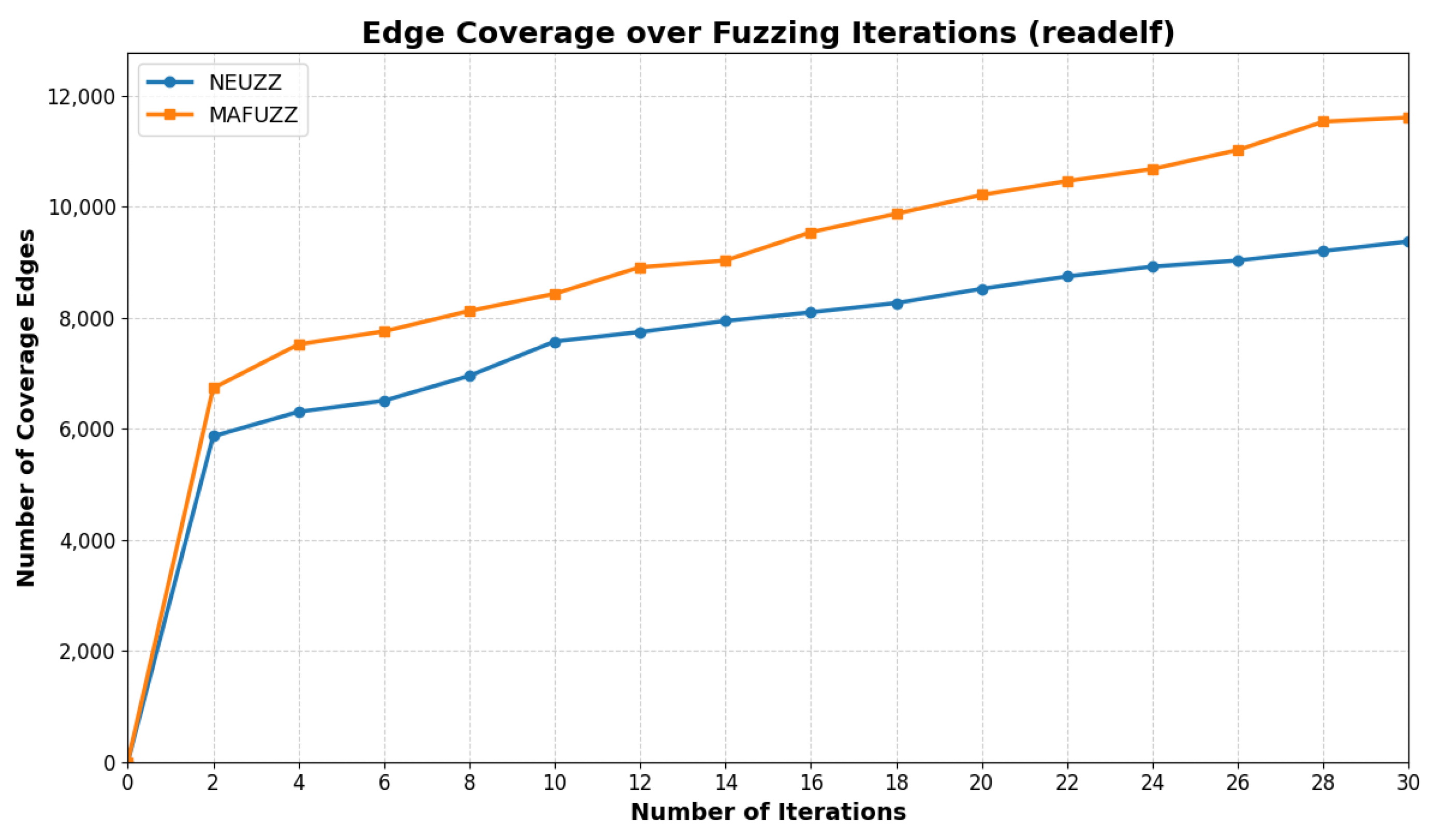
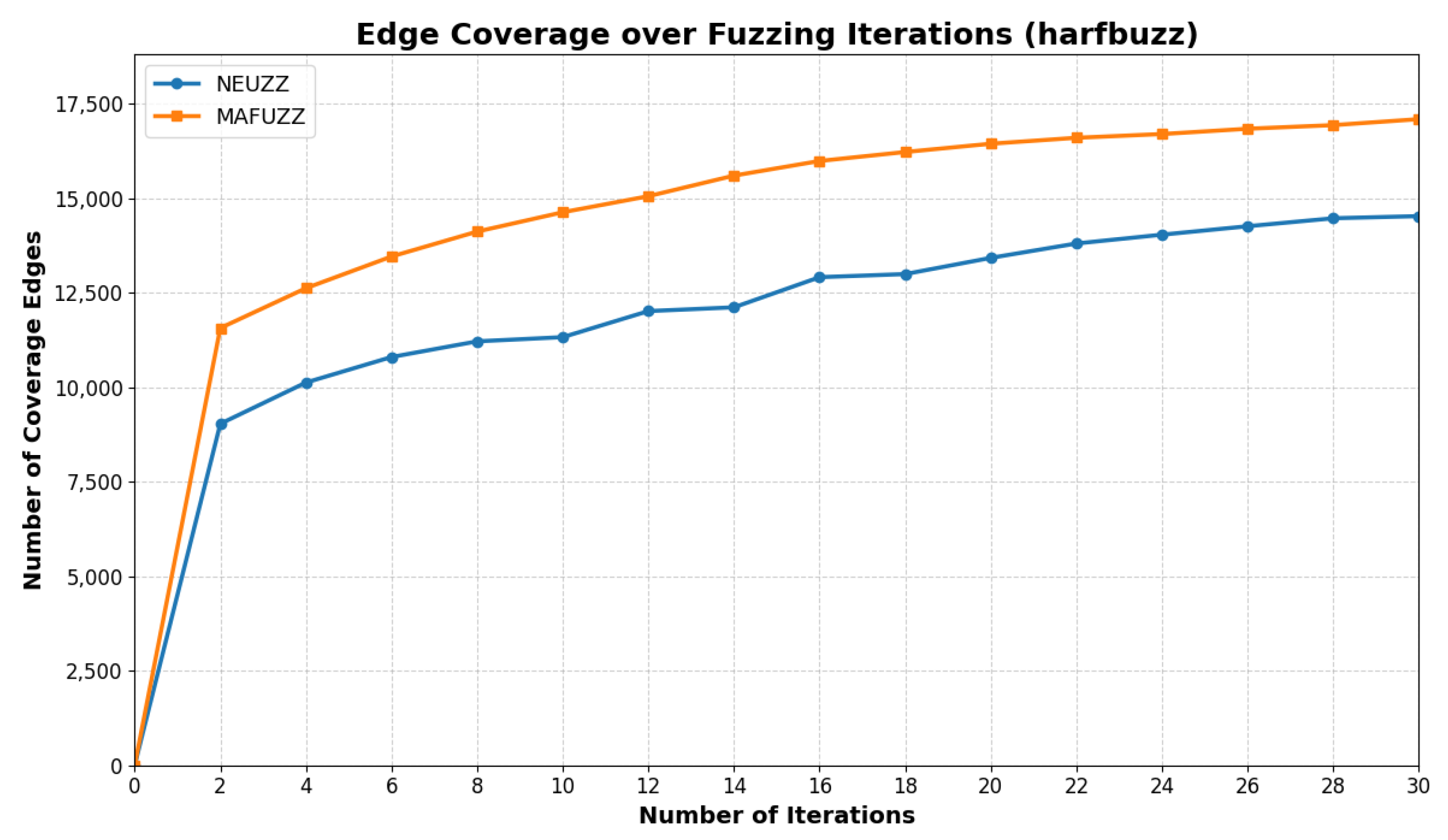
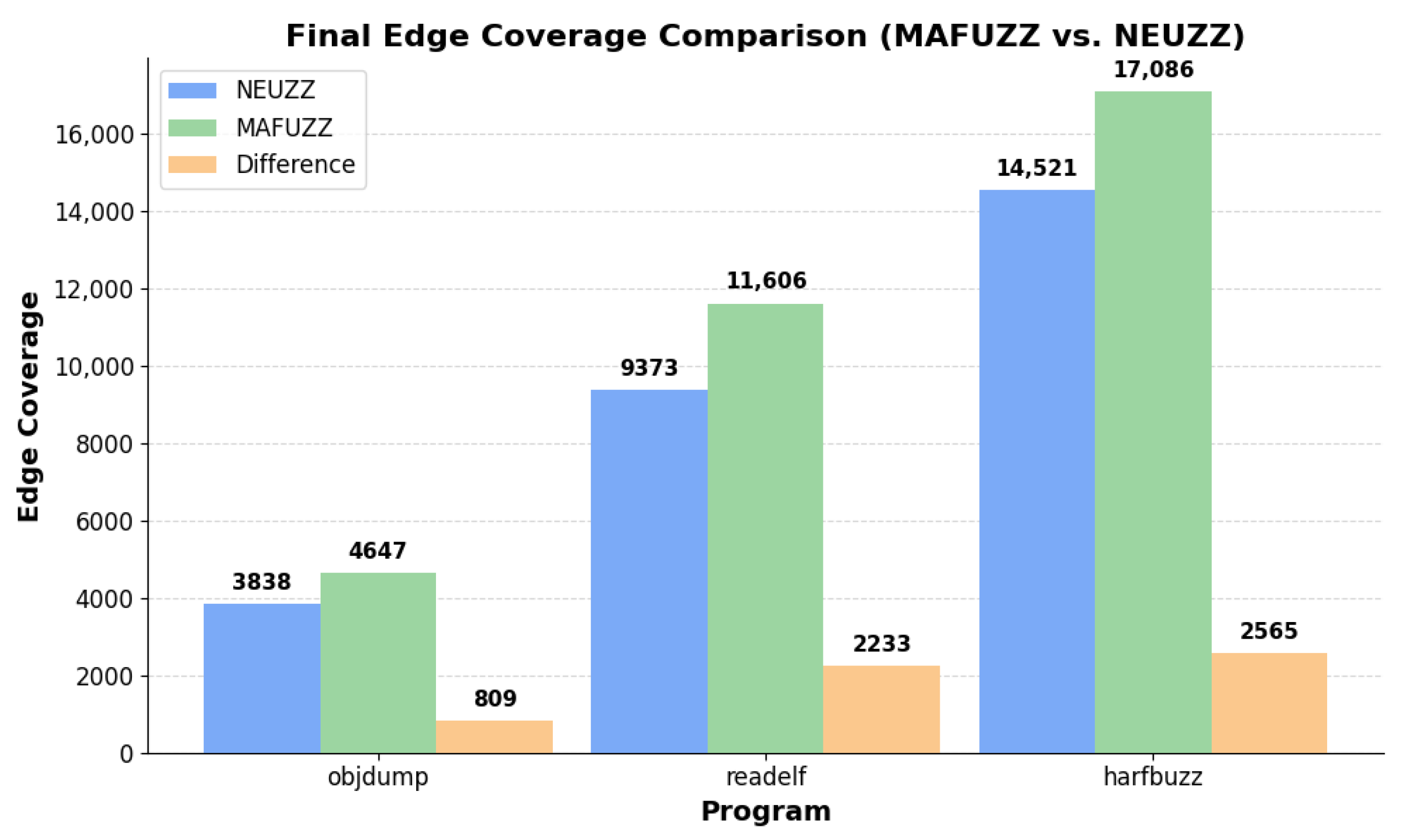
Experimental results demonstrate that NEUZZ achieves up to three times the edge coverage compared to traditional fuzzers like AFL over a 24 h run. It is particularly effective on large programs, where its learning-guided approach allows it to generalize internal branching logic and escape coverage plateaus. This advantage arises from the neural network’s ability to generalize over the collective edge-activation patterns of all seed inputs [32,33]. The quality and diversity of the initial seed set directly impact the model’s ability to capture complex branching behavior [34,35]. When the seed pool includes enough inputs to cover a broad range of sibling edge clusters, the neural model can guide mutations toward unexplored conditional branches more effectively. Conversely, a narrow seed distribution limits learning capacity and causes early saturation.

For Satellite Internet Ground Terminals (SIGTs), where binaries are large and obfuscated, NEUZZ’s gradient-based exploration framework offers significant advantages. Its learned model can navigate the deep and complex control-flow structures typical of SIGT binaries, triggering deeper paths and discovering subtle logic vulnerabilities. These properties make NEUZZ—and its successors, like MAFUZZ—particularly well-suited for security analysis in embedded and closed-source systems.

Building on NEUZZ, MAFUZZ retains the surrogate modeling framework using a single-layer feedforward neural network trained to approximate the mapping from seed byte sequences to coverage edge vectors. The model is optimized via standard backpropagation, and the gradient of the predicted coverage vector with respect to the input bytes is used to locate high-impact mutation positions.

Unlike conventional software, SIGT firmware often contains highly discrete control logic, such as hardcoded state machines and nested branches, which may introduce gradient discontinuities. To maintain the effectiveness of gradient-guided mutation in such scenarios, MAFUZZ restricts mutation to high-confidence bytes (i.e., those with large gradient magnitudes), reduces reliance on weak or noisy gradients, and emphasizes seed corpus diversity during training. This ensures that the model can generalize over discontinuous coverage landscapes and still provide meaningful directional guidance for mutation.

4.3. Baseline Justification and Tool Comparison

To justify the selection of NEUZZ as the main baseline for our fuzzing framework, we conducted independent comparative experiments between AFL and NEUZZ. All the evaluations were performed on three representative Linux binaries—objdump, readelf, and harfbuzz—using identical testing conditions: a 12 h runtime per target and a common initial seed corpus.

Table 1. Edge coverage comparison between AFL and NEUZZ under identical testing conditions.

Program	AFL	NEUZZ	NEUZZ Gain
objdump	426	3838	+9.0×
readelf	1420	9373	+6.6×
harfbuzz	7642	14,521	+1.9×

presents the observed edge coverage results.

The data show that NEUZZ significantly outperformed AFL across all the benchmarks. In particular, NEUZZ achieved up to 9.0× higher coverage on objdump and 6.6× on readelf, highlighting the benefit of its neural program smoothing and gradient-guided mutation strategy. These findings support the validity of NEUZZ as a robust baseline for evaluating further enhancements in our proposed framework.

4.4. Adaptive Gradient-Guided Fuzzing

While NEUZZ demonstrates strong performance in gradient-guided fuzzing, its reliance on a static neural program smoothing process limits its ability to discover new execution paths once the initial sibling edge clusters are exhausted. In particular, when the initial seed pool lacks diversity, the neural network can only guide mutations within a constrained edge space, leading to early saturation and coverage stagnation.

To address this limitation, we propose a novel adaptive gradient-guided fuzzing framework—MAFUZZ—that introduces two key enhancements to the traditional NEUZZ architecture: (1) integration of a Havoc mutation mode, and (2) a dynamic controller to adjust the balance between gradient-guided and random mutation strategies during fuzzing.

Hybrid mutation design. MAFUZZ extends the NEUZZ mutation pipeline by incorporating AFL-style Havoc mutation operations, such as random bit flips, byte insertions, and deletions. These random mutations enable the exploration of previously unreachable sibling edge clusters, complementing the precision of gradient-guided mutation. When the neural model becomes saturated, Havoc provides a mechanism to escape local minima by generating novel seed variants.

Adaptive mode regulation. Instead of statically applying both mutation strategies, MAFUZZ dynamically adjusts their usage during fuzzing based on real-time coverage feedback. After each round of seed execution, the algorithm analyzes the proportion of explored edges in sibling clusters and accordingly adjusts the number of gradient-guided and Havoc mutations for the next round. When the average saturation ratio is low, the controller favors gradient mutation for efficiency; when the ratio is high, it emphasizes Havoc to increase diversity.

Mutation control algorithm. The mutation strategy control algorithm lies at the heart of MAFUZZ’s adaptiveness. It evaluates the edge coverage status of the current seed pool and dynamically adjusts the balance between gradient-guided and Havoc mutation modes. The process consists of three stages, outlined as follows and corresponding to the structure of Algorithm 1:

Algorithm 1 Adaptive mutation pattern modulation

Input:  $program$, $seeds$ Output:  $guideNum$, $randNum$   1: for  $seed\left[i\right]\in seeds$ do   2:     Edge[i] ← SeedExecution(seeds[i])   3:     totalEdge[j] ← totalEdge[j] + Edge[i]   4: end for   5: correspRelation ← getEdgeRelation(program)   6: emptyArray ← correspRelation   7: for j in totalEdge do   8:     for $edge$ in correspRelation do   9:         if totalEdge[j] = edge then 10:             emptyArray[edge] ← 1 11:         end if 12:     end for 13:     for $i\in emptyArray$ do 14:         ratio[i] ←${\displaystyle \frac{num}{\mathrm{arrayLength}}}$ 15:         averageRatio ←${\displaystyle \frac{1}{n}}{\sum }_{i=0}^n\mathrm{ratio}\left[i\right]$ 16:     end for 17: end for 18: if $averageRatio\in [0,\mathrm{Threshold}]$ then 19:     guideNum ← guideNum(1 + averageRatio) 20:     randNum ← randNum(1 - averageRatio) 21: end if 22: if $averageRatio\in [\mathrm{Threshold},1]$ then 23:     guideNum ← guideNum(1 - averageRatio) 24:     randNum ← randNum(1 + averageRatio) 25: end if 26: return $guideNum$,$randNum$

• (1) Edge coverage aggregation (lines 1–4). Each seed in the seed pool is executed on the target binary, and the edges it triggers are recorded. These edges are aggregated into a global set, totalEdge, representing the complete set of coverage edges observed in the current round. This forms the empirical basis for evaluating exploration saturation.
• (2) Sibling edge cluster analysis (lines 5–12). Using static analysis (e.g., disassembling with objdump), the control flow graph (CFG) of the program is extracted. From this, all sibling edge clusters—sets of control-flow-related edges—are constructed as correspRelation. A zero-initialized structure emptyArray is created to match this layout.

The algorithm then flags each edge in totalEdge within its respective cluster. For each sibling cluster, the ratio of visited edges is computed. Averaging across all the clusters yields the global averageRatio, which quantifies the current round’s overall exploration depth.

• (3) Adaptive mutation adjustment (lines 13–20). Based on the calculated averageRatio and a predefined Threshold, the algorithm adjusts the number of gradient-guided (guideNum) and Havoc-based (randNum) mutations:
  • If averageRatio < Threshold, the seed pool is deemed underexplored. The algorithm increases guideNum and reduces randNum to exploit known edge clusters more efficiently.
  • If averageRatio ≥ Threshold, it shifts emphasis to exploration by increasing randNum and decreasing guideNum.

This feedback loop allows MAFUZZ to dynamically balance exploitation and exploration as fuzzing progresses, effectively improving coverage across structurally diverse programs.

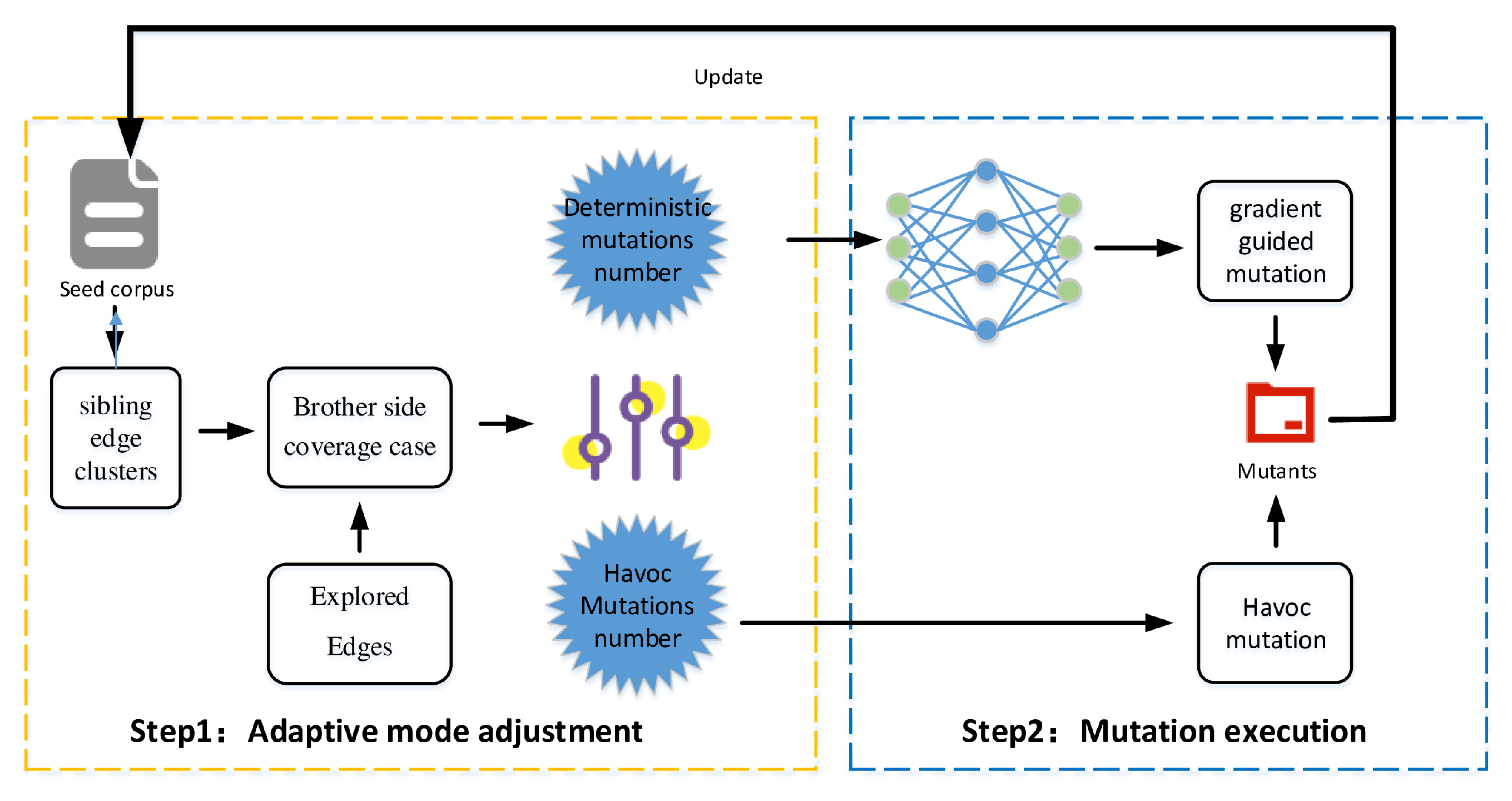
Figure 8 presents the architectural differences between NEUZZ and our proposed framework MAFUZZ. While retaining NEUZZ’s neural smoothing and gradient-guided mutation modules, MAFUZZ introduces two key enhancements. First, a Havoc mutation module is incorporated to explore novel edge clusters that are unreachable via gradient-guided paths. Second, an adaptive controller dynamically regulates the ratio of guided versus random mutations based on the saturation level of explored edge clusters in the seed pool. This closed-loop architecture improves fuzzing efficiency by balancing precision and diversity in input mutations.

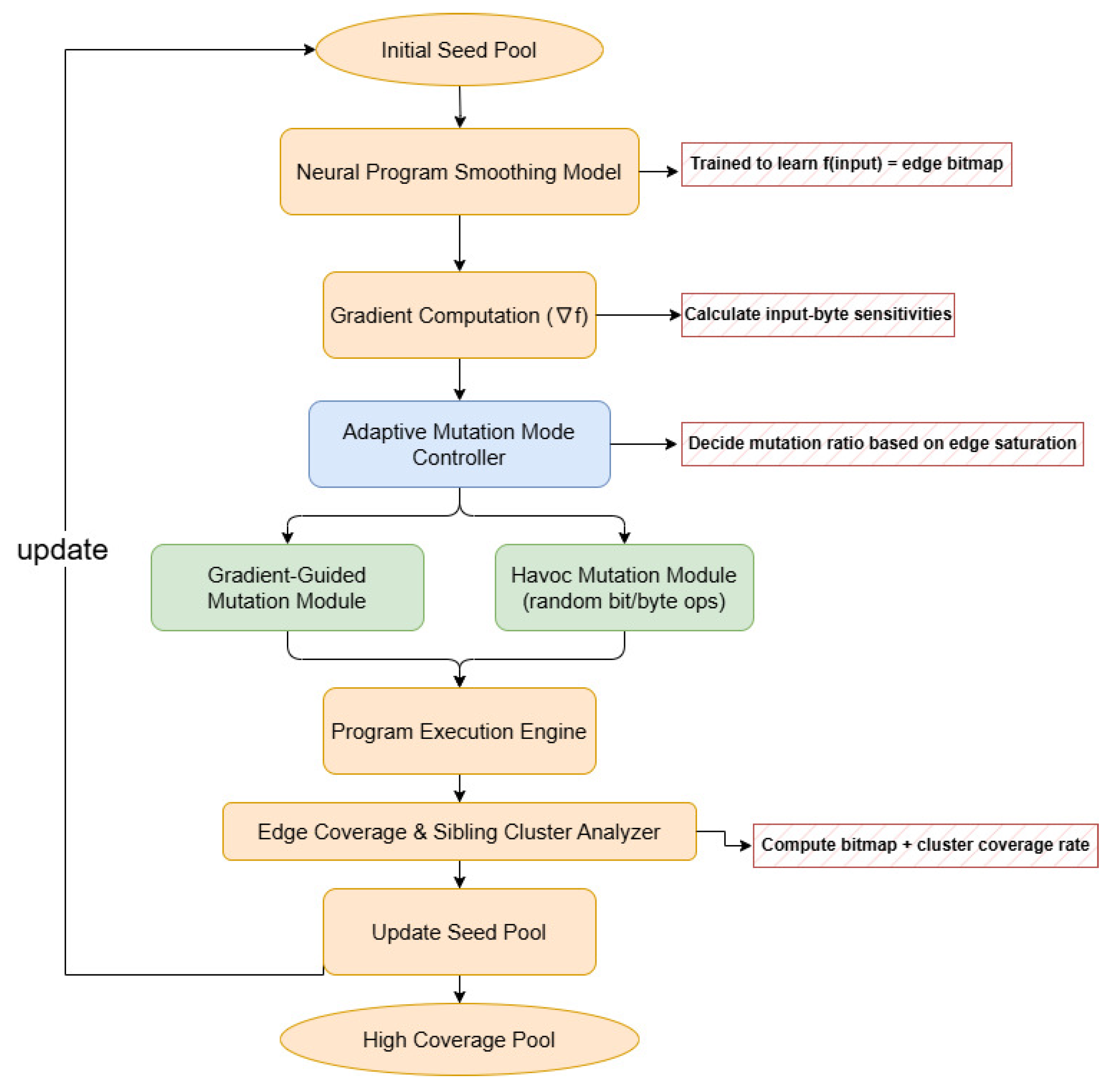
Framework overview. Figure 9 presents the overall workflow of MAFUZZ. Starting from an initial seed pool, inputs are processed by a neural smoothing model to estimate coverage gradients. An adaptive controller adjusts the ratio of gradient-guided and Havoc mutations based on coverage feedback (the two mutation types are applied sequentially, with gradient-guided mutation followed by Havoc). Mutated seeds are executed, and edge results are used to update the seed pool, forming a closed loop that continuously refines mutation strategies to improve path coverage.

Summary. In summary, MAFUZZ introduces a hybrid and adaptive mutation framework that combines the precision of gradient guidance with the exploratory strength of Havoc mutation. By dynamically regulating the two strategies according to the real-time saturation of edge clusters, MAFUZZ enhances the diversity and depth of seed mutation. This adaptive control significantly improves path coverage efficiency and robustness across different program complexities.

5. Experiment Validation

For this section, we conducted a two-part experimental study. The first part investigated the optimal threshold for adaptive mutation switching in our framework. The second part evaluated the fuzzing performance of MAFUZZ against NEUZZ under the selected threshold.

All our experiments were conducted on Ubuntu 18.04 (Canonical Ltd., London, UK) with an NVIDIA Tesla P4 GPU (NVIDIA Corporation, Santa Clara, CA, USA) for neural network acceleration. The targets included three widely used Linux binaries—objdump, readelf, and harfbuzz.

To ensure fair comparison, we first ran AFL on each target for 5 h to generate initial seed corpora. These seeds were re-used in both NEUZZ and MAFUZZ to eliminate variability and ensure identical initial conditions. The left table in

Table 2. Initial seed counts (left) and shared neural network training configuration (right).

Seed Corpus			NN Training Parameters
Program	Seeds		Parameter	Value
objdump	1586		Architecture	1 hidden layer (4096 ReLU)
readelf	1543		Learning rate	0.01
harfbuzz	1678		Epochs	50
			Loss function	Binary cross-entropy
			Optimizer	Adam
			Early stopping	Enabled

summarizes the number of seeds collected.

To avoid bias from model configuration, both tools used the same neural network architecture and training parameters. As shown in the right-hand column of Table 2, the network included one hidden layer with 4096 ReLU units, trained for 50 epochs using a learning rate of 0.01, binary cross-entropy loss, and early stopping.

5.1. Optimal Threshold Exploration

We hypothesized that fuzzing performance can be significantly improved if the adaptive mutation threshold is aligned with the structural characteristics of the target binary—specifically, its early-stage edge exploration capability. To evaluate this hypothesis, we measured the initial sibling edge cluster exploration rates ($R_0$) for each target program. This involved executing all AFL-generated seed inputs once and recording the number of distinct edge clusters triggered in each program. The observed exploration rates were: 0.371 for objdump, 0.517 for readelf, and 0.413 for harfbuzz.

Building on these measurements, we adopted a data-driven threshold selection strategy. Rather than applying fixed global values (e.g., 0.4, 0.5, 0.6) uniformly, we defined three program-specific thresholds:

• One slightly below the observed $R_0$ (to encourage early-stage exploration);
• The exact value of $R_0$ (as a baseline reference);
• One moderately above $R_0$ (to test conservative mutation control).

Table 3. Program-specific thresholds for adaptive mutation switching.

Program	Lower Threshold	Exploration Rate (${\mathit{R}}_{\mathbf{0}}$)	Higher Threshold
objdump	0.300	0.371	0.500
readelf	0.400	0.517	0.600
harfbuzz	0.300	0.413	0.500

summarizes the three threshold values selected for each program.

Each threshold configuration was tested under identical conditions: a 12 h fuzzing campaign with 30 iterations per configuration. Figure 10, Figure 11 and Figure 12 display the results. Each figure consists of two subplots: (a) shows the full coverage trajectory over time, while (b) provides a zoomed view of the final 10 iterations, highlighting subtle but impactful differences between the thresholds.

• Discussion. As illustrated in

  Table 4. Final edge coverage achieved under each threshold configuration. Bold values indicate the highest coverage achieved in each program.

  Program	Coverage @ Low	Coverage @ ${\mathit{R}}_0$	Coverage @ High	Optimal Threshold
  objdump	4625	4690	4544	0.371
  readelf	9831	11,732	9664	0.517
  harfbuzz	15,820	17,115	16,932	0.413

  , all three programs—objdump, harfbuzz, and readelf—achieved their highest edge coverage when the adaptive mutation threshold was set near the initial sibling edge cluster coverage rate ($R_0$) observed after the first round of seed execution. This outcome confirms our earlier hypothesis: aligning the mutation scheduling threshold with the early-stage edge exploration behavior of a program can significantly enhance fuzzing efficiency.

Specifically, objdump reached optimal coverage at a threshold of 0.371, harfbuzz peaked at 0.413, and the more structurally complex readelf achieved the highest coverage at its actual $R_0=0.517$. These results indicate that each binary benefits from a threshold tailored to its internal architecture and initial fuzzing dynamics, rather than from a uniform configuration.

5.2. Performance Comparison

To evaluate the effectiveness of our adaptive fuzzing framework MAFUZZ, we conducted comparative experiments against the gradient-guided fuzzing tool NEUZZ. We selected three representative Linux binary programs—readelf, objdump, and harfbuzz—that vary in size and complexity, to ensure that the evaluation covered a range of structural scenarios. All the experiments were performed under the same testbed, initial seed corpus, and a 12 h fuzzing window for each tool.

For MAFUZZ, the mutation switching threshold was customized for each program, based on its initial sibling edge cluster exploration rate ($R_0$), obtained by executing all AFL-generated seeds once. This threshold-aware configuration is designed to align mutation behavior with the early-stage structural features of the target program, thereby enhancing the balance between exploitation and exploration.

Each test configuration was repeated three times to ensure statistical reliability. During each run, we collected edge coverage at consistent intervals across 30 iterations. Figure 13, Figure 14 and Figure 15 present the averaged edge coverage curves. From the results, we observe that NEUZZ showed rapid initial growth but plateaued early, likely due to its fixed model-based mutation strategy. In contrast, MAFUZZ continued to accumulate coverage at the later stages by dynamically switching to Havoc-based mutations when gradient-guided exploration reached saturation.

Table 5. Comprehensive comparison of edge coverage between MAFUZZ and NEUZZ (12 h runtime, $n=3$).

Program	NEUZZ ($\mathsf{\mu }\pm \mathsf{\sigma }$)	MAFUZZ ($\mathsf{\mu }\pm \mathsf{\sigma }$)	Gain (#)	Gain (%)	p-Value
objdump	3,838.0 ± 15.9	4,646.7 ± 24.0	+809	+15.5%	$1.97\times {10}^{-5}$
readelf	9,373.0 ± 27.7	11,606.0 ± 60.0	+2,233	+19.2%	$2.75\times {10}^{-7}$
harfbuzz	14,521.0 ± 42.1	17,086.0 ± 32.6	+2,565	+17.6%	$4.88\times {10}^{-6}$

summarizes the final average coverage for both tools, the absolute and relative improvements of MAFUZZ, and p-values from independent-samples t-tests. The results show consistent performance gains on all three programs, with average improvements ranging from +15.5% to +19.2%. All differences are statistically significant ($p<0.001$), confirming that the observed gains were not due to chance.

• Discussion. As shown in Table 5 and Figure 16, MAFUZZ consistently delivered higher final edge coverage than NEUZZ across all the benchmarks. These results validate the design rationale of MAFUZZ: adaptive threshold-driven control enables effective switching between exploration and exploitation. When the seed space becomes saturated under gradient guidance, the system automatically increases the proportion of Havoc mutations, allowing the discovery of new sibling edge clusters that would otherwise be missed. This flexibility leads to deeper path exploration and better overall fuzzing effectiveness. The low standard deviations and statistically significant p-values ($p<0.001$) confirm the stability and reliability of these improvements.

5.3. Firmware Vulnerabilities and Mitigation Strategies in Satellite Terminals

MAFUZZ revealed several common binary flaws in satellite ground terminals:

• Memory overflows: from unchecked buffers or integer operations.
• Invalid state transitions: due to missing control logic.
• Unhandled errors: in malformed input processing.
• Unsafe command parsing: without format or field validation.

These issues affect back-end firmware modules directly and may lead to crashes, logic faults, or silent failures.

Table 6. Typical vulnerabilities and corresponding mitigation strategies.

Vulnerability in Satellite Terminal Firmware	Recommended Mitigation
Memory overflows	Enable stack canaries, ASLR; apply static analysis to prevent unsafe memory use.
Invalid state transitions	Use finite state machines (FSMs); validate state logic and log violations.
Unhandled input errors	Standardize error codes; add fallback paths and fault recovery handlers.
Unsafe command parsing	Define structured formats (e.g., TLV); validate type, length, and value constraints.

summarizes lightweight mitigation strategies tailored for embedded terminal systems.

6. Conclusions

In this paper, we conducted a comprehensive security analysis of Satellite Internet Ground Terminals (SIGTs), including real-world attack case studies, hardware/software architecture examination, and threat model construction. To address the identified vulnerabilities—especially those residing in closed-source binary firmware—we propose MAFUZZ, an adaptive gradient-guided fuzzing framework tailored to the characteristics of SIGT environments.

MAFUZZ integrates neural gradient mutation with a Havoc-style mutation strategy and adaptively balances the two, based on edge coverage feedback. This design enables it to effectively escape local plateaus and discover previously unreachable paths in complex embedded binaries.

Our experiments on three representative Linux binaries demonstrate that MAFUZZ consistently outperforms the state-of-the-art NEUZZ fuzzer. Specifically, MAFUZZ achieves an average path coverage improvement of +17.4%, with gains of +15.5% on objdump, +19.2% on readelf, and +17.6% on harfbuzz, as shown in Table 5. These results are statistically significant and validate the effectiveness of the adaptive mutation strategy, particularly in resource-constrained and semantically opaque environments such as SIGT firmware.

In future work, we plan to extend our framework to real-world satellite terminal firmware. This includes analyzing the runtime interaction data between the SIGT and its front-end interfaces and implementing targeted binary fuzzing based on observed protocol flows. We expect this work to further improve automated vulnerability discovery in satellite communication systems and contribute to the overall security of emerging space–ground infrastructure.