Two-Stage Power Delivery Architecture Using Hybrid Converters for Data Centers and Telecommunication Systems
Abstract
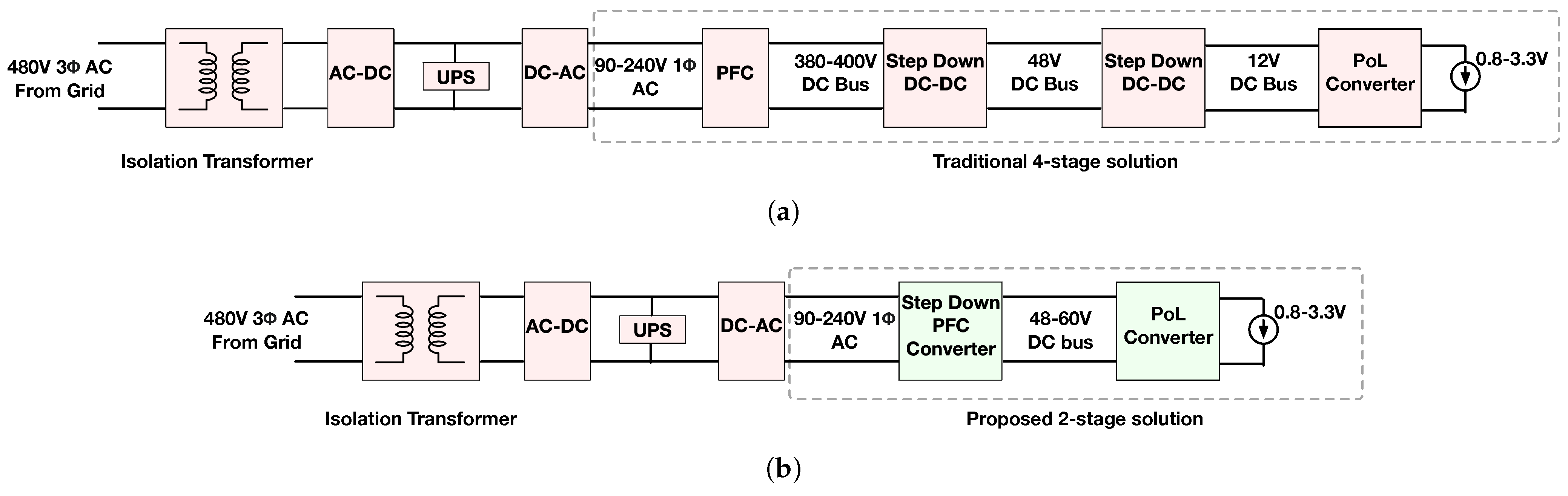
1. Introduction
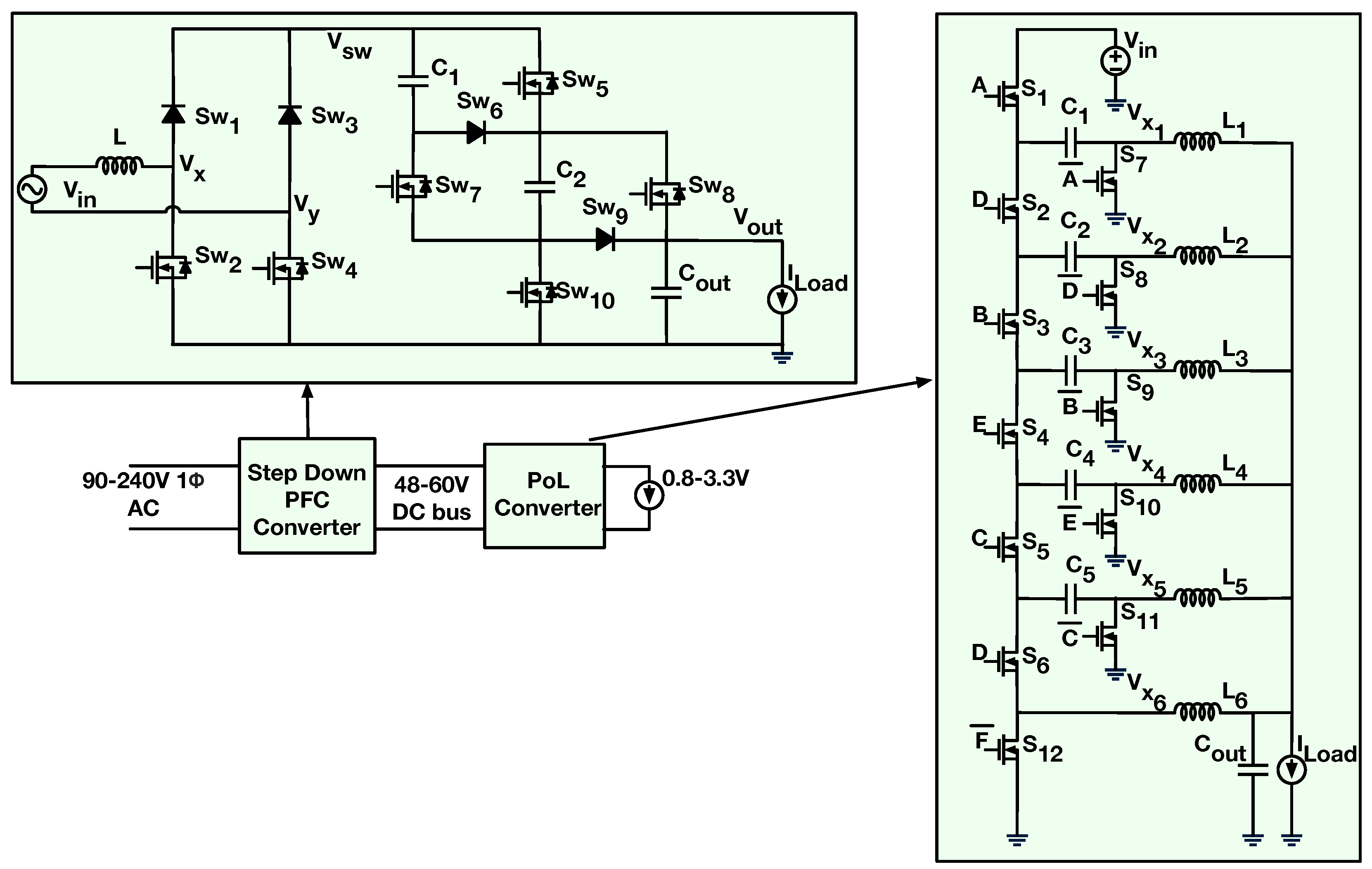
2. Step-Down PFC Converter
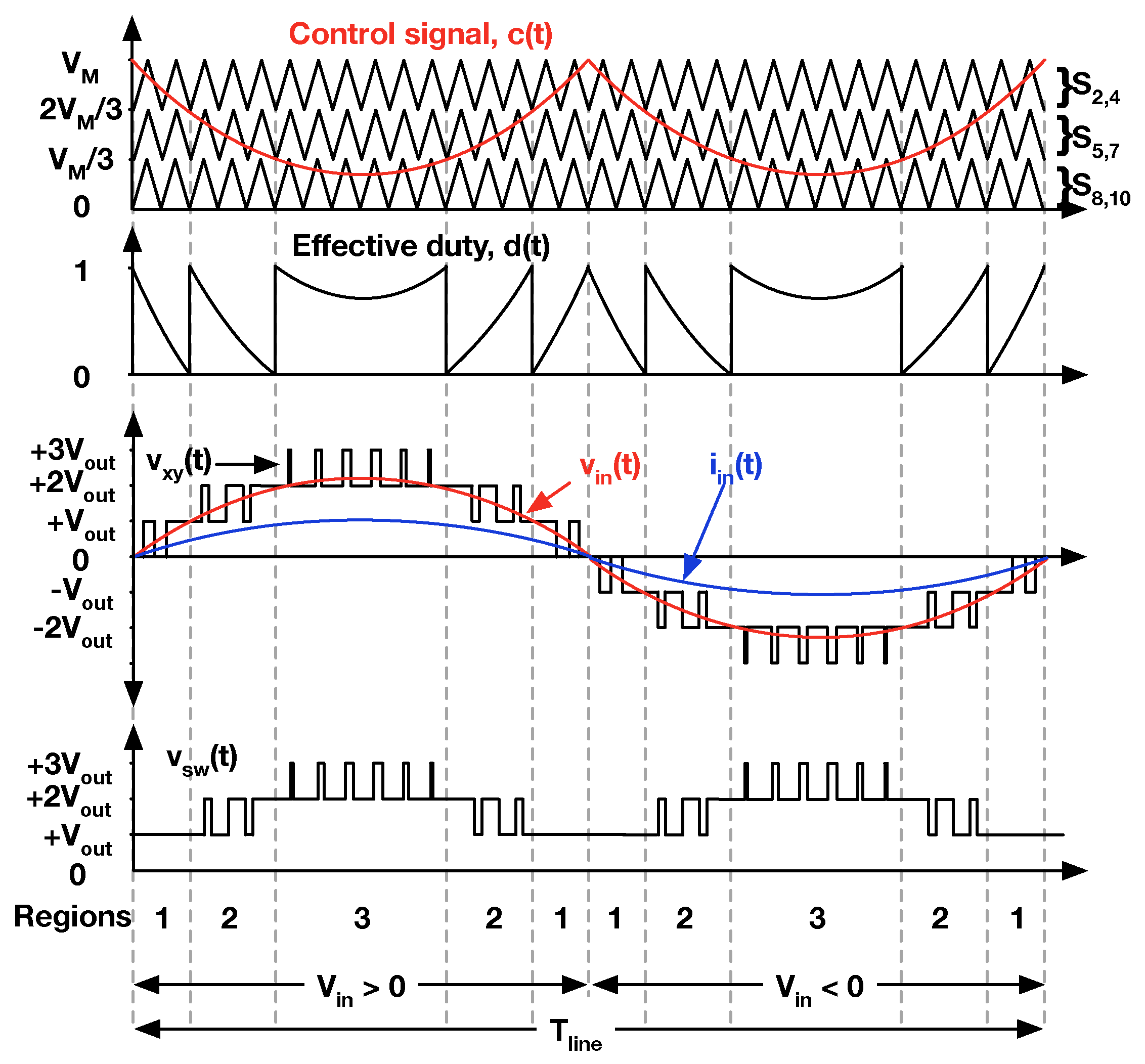
2.1. Topology and Operation
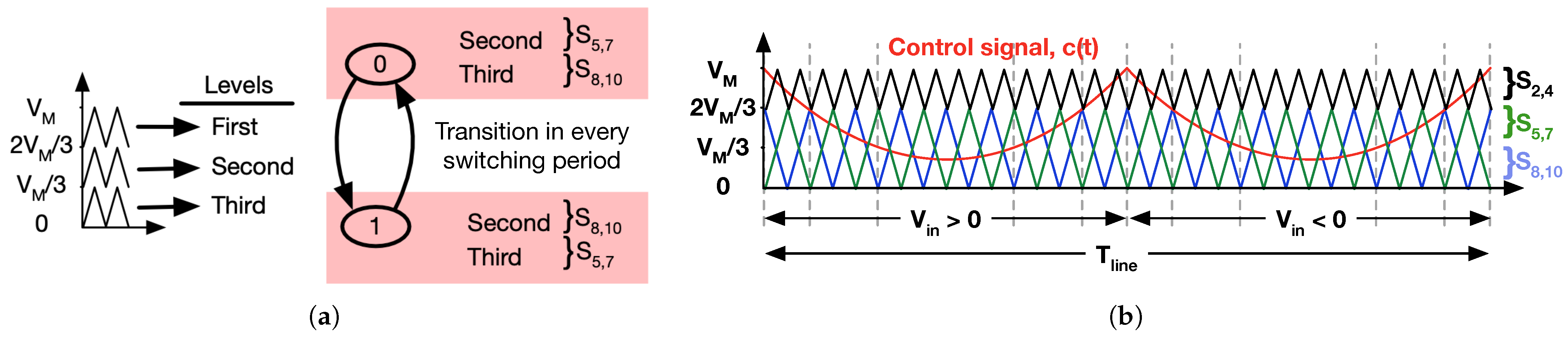
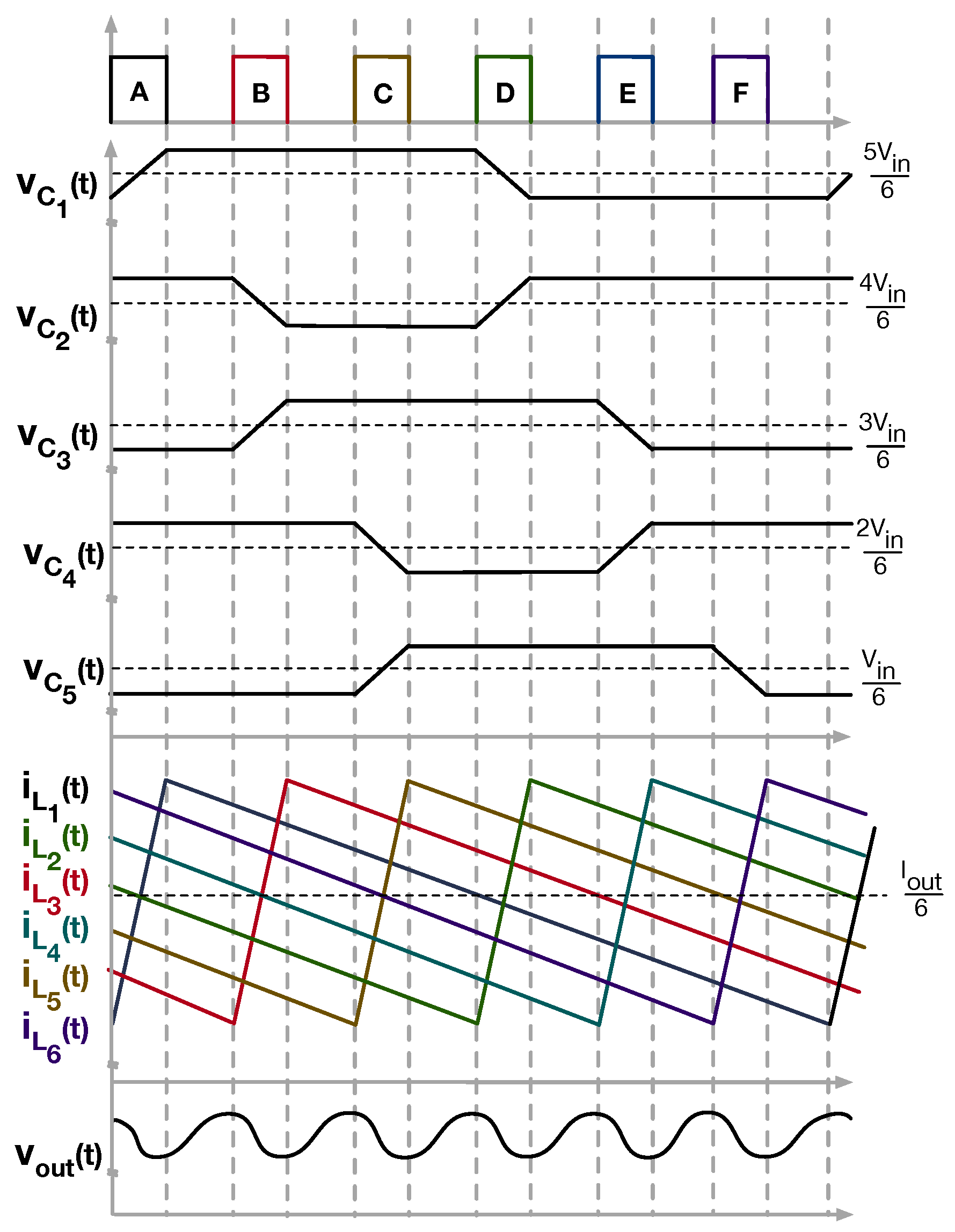
2.2. Modified Operation for Capacitor Balancing
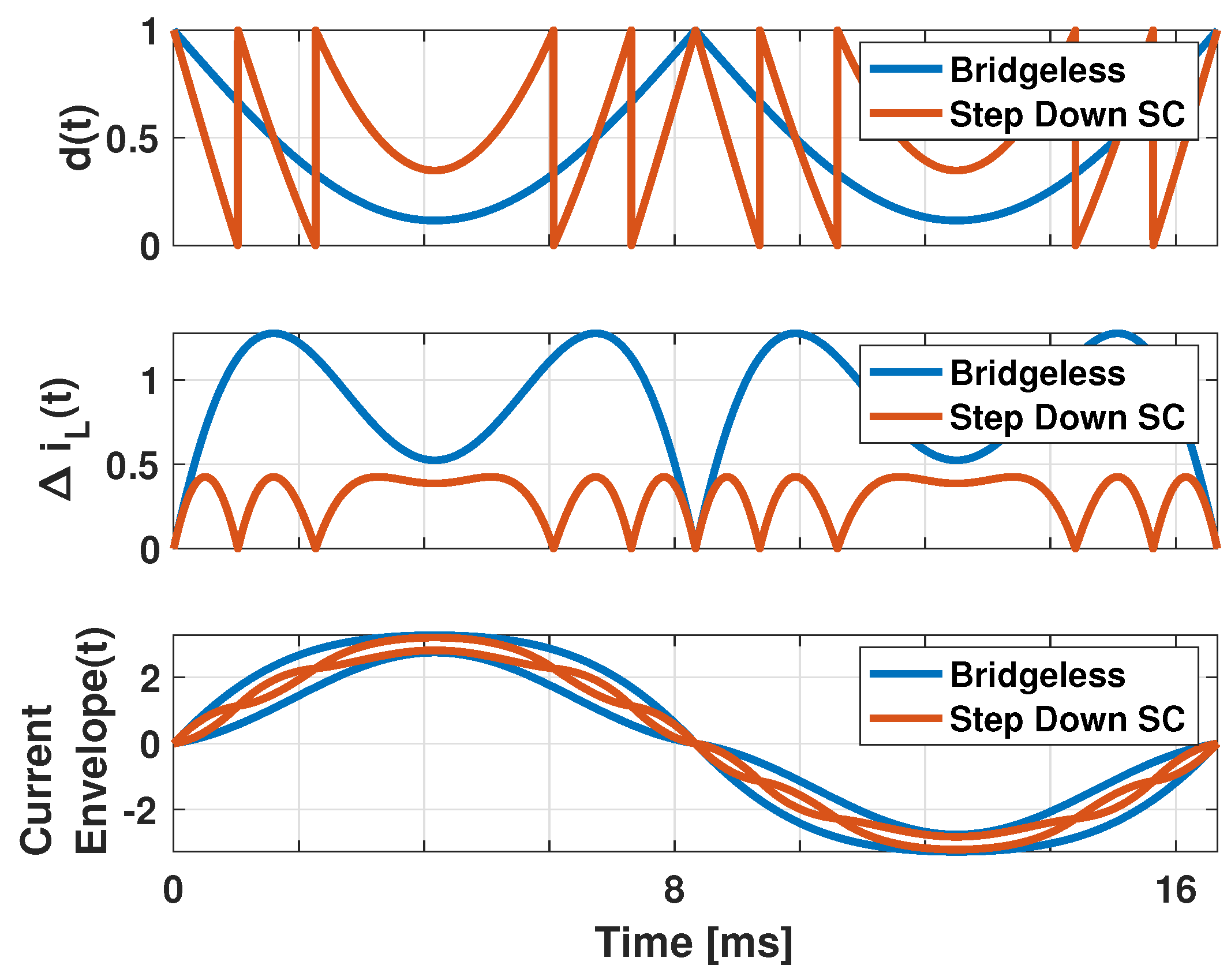
2.3. Advantage of the Proposed Converter: Reduced Inductor Current Ripple
2.4. Advantage of the Proposed PFC Converter: DC-Link Filtering with Distributed Low-Voltage Capacitors
2.5. Control and Sensing Circuits
3. Multi-Phase, Multi-Inductor Hybrid Converter
Multi-Inductor Converter with Multi-Phase Operation
4. Experimental Results
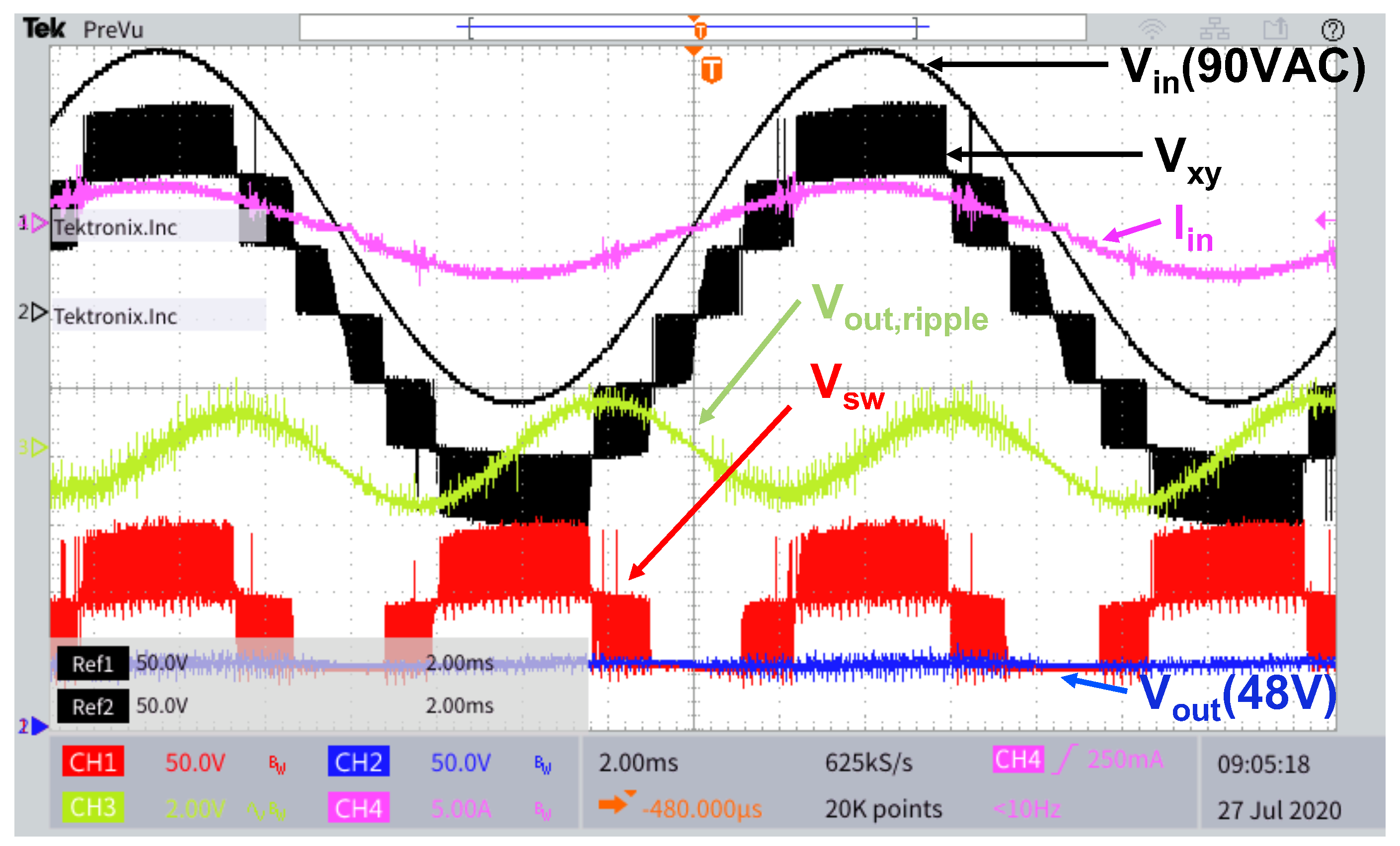
4.1. Step-Down PFC Converter
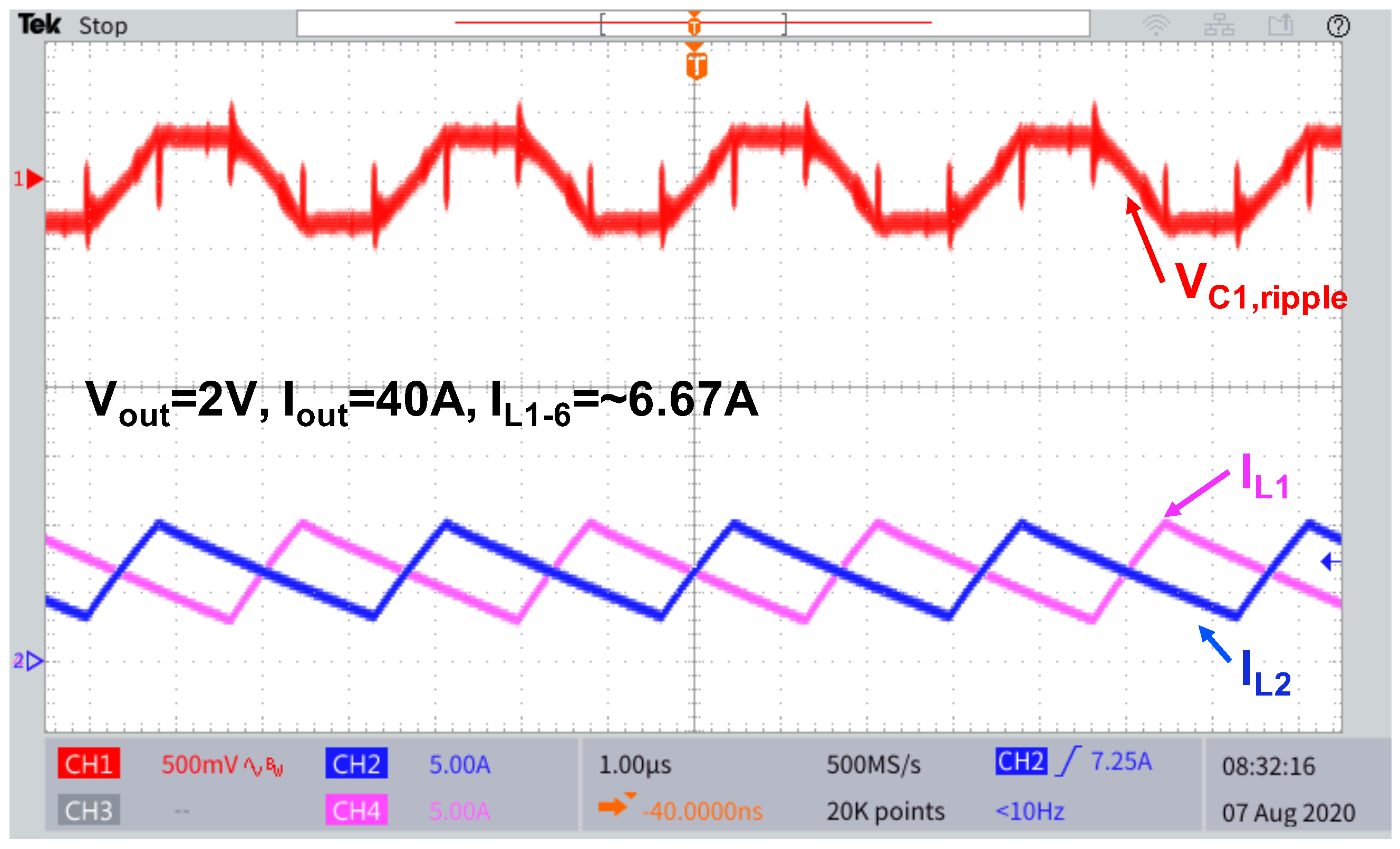
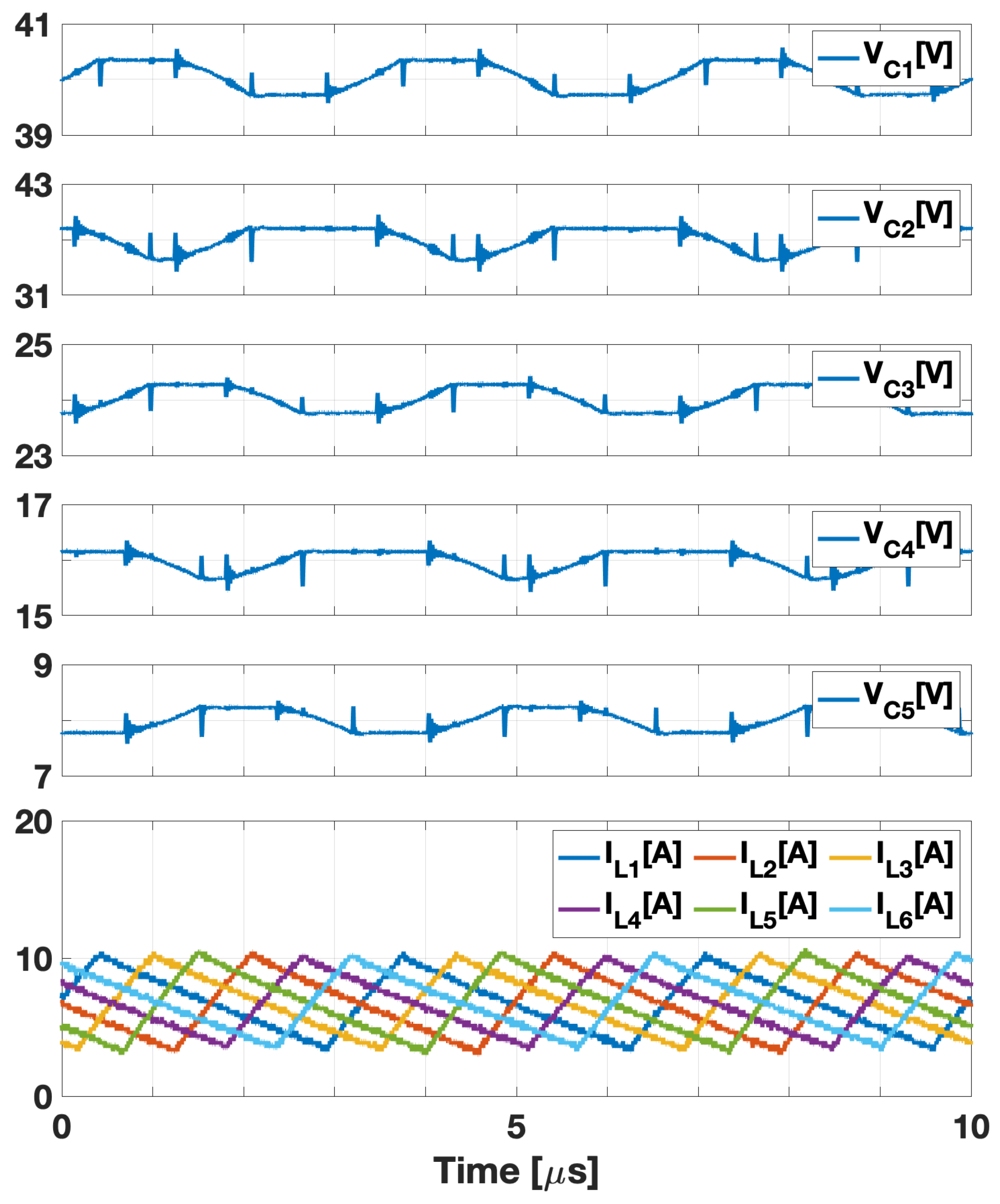
4.2. MP-MIH Converter
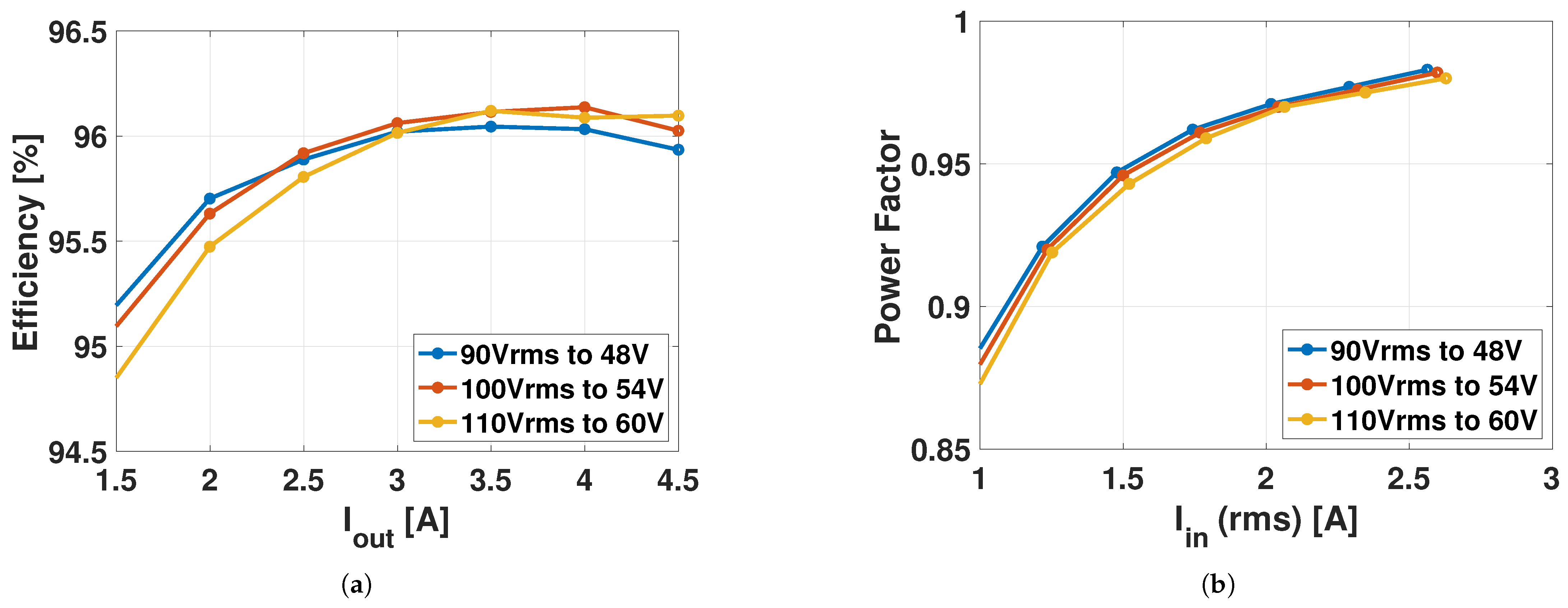
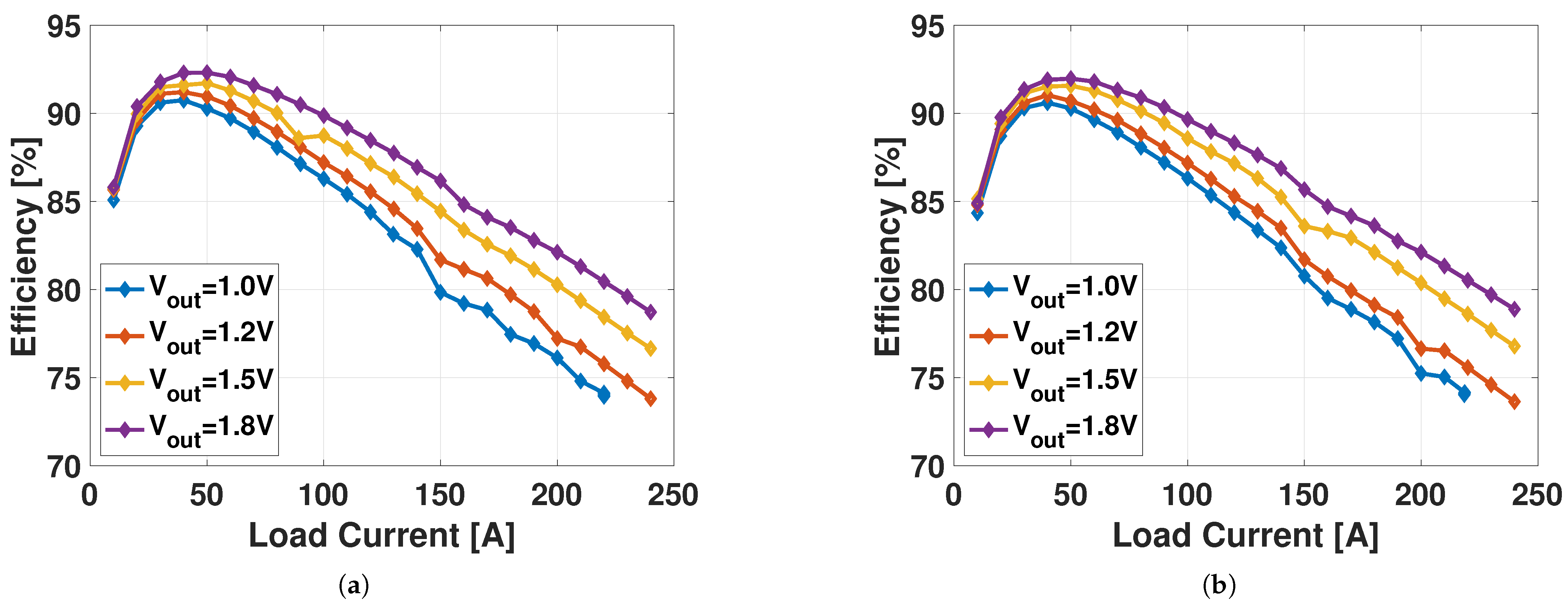
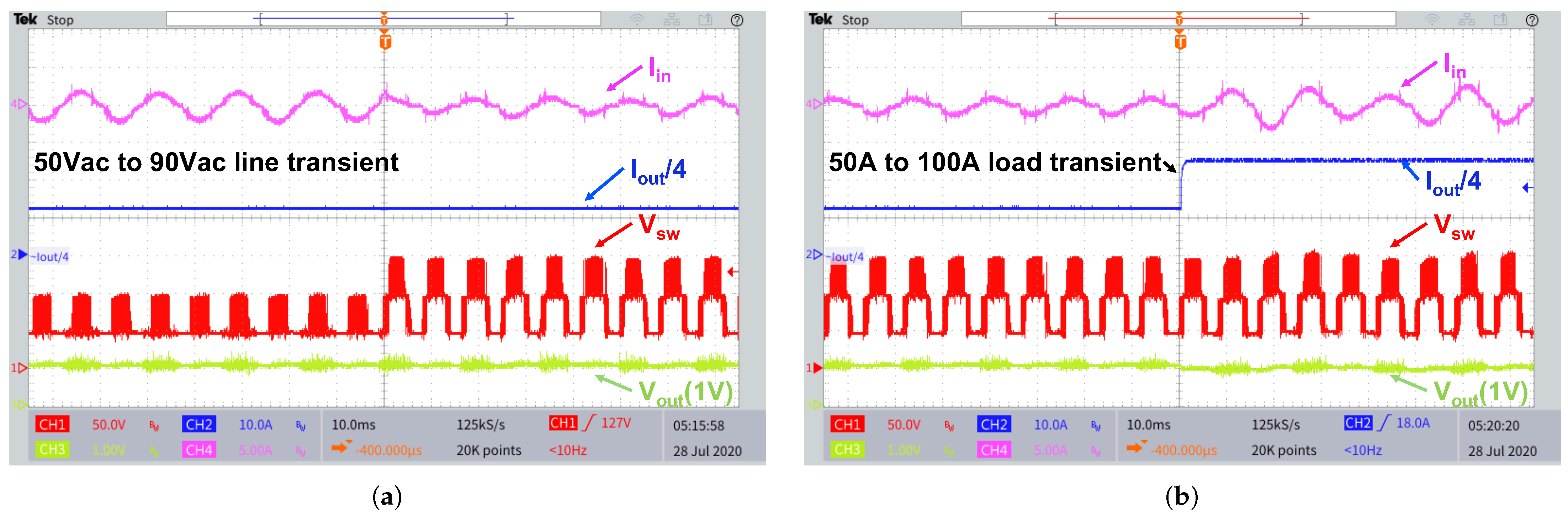
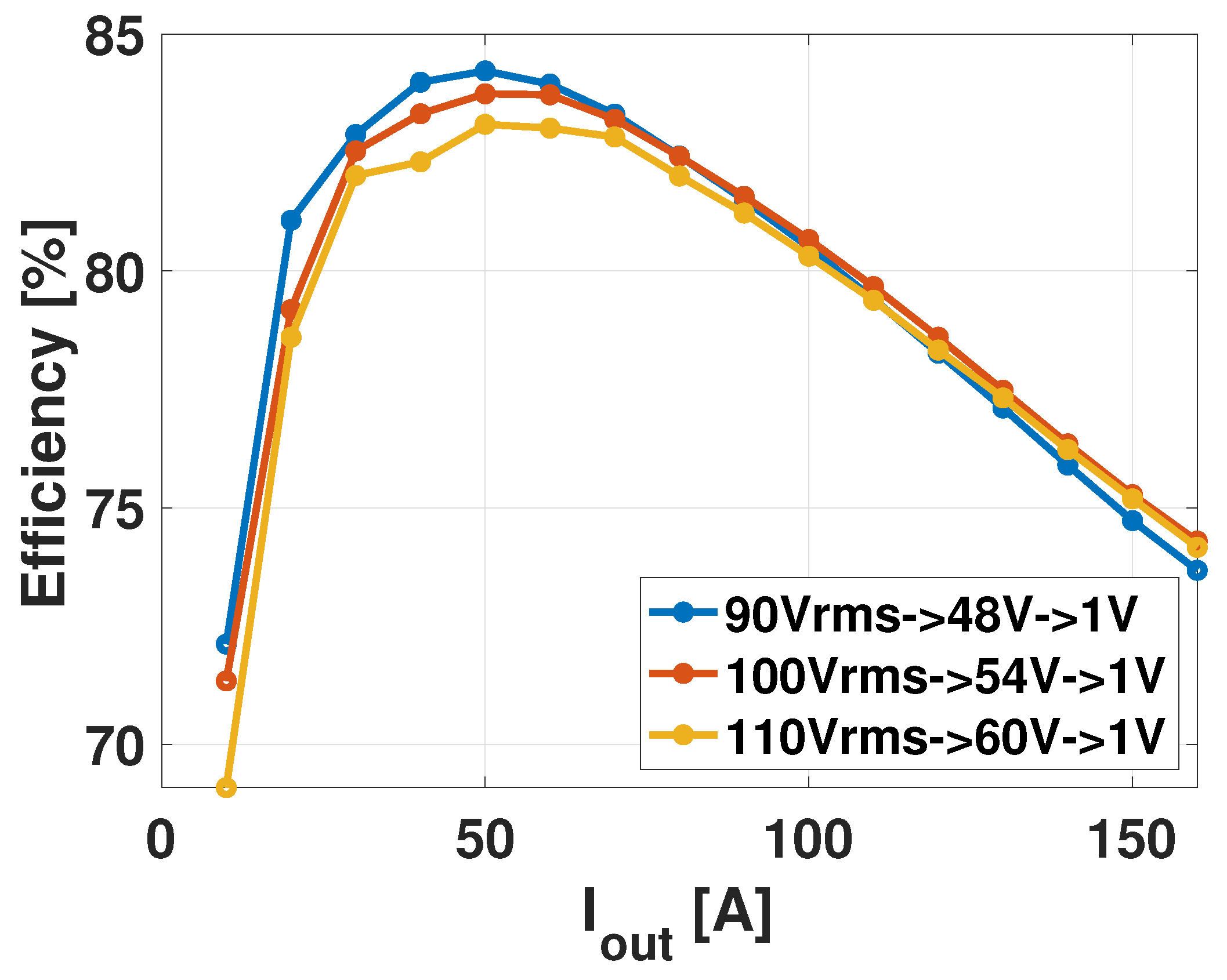
4.3. Full System Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pratt, A.; Kumar, P.; Bross, K.; Aldridge, T. Powering Compute Platforms in High Efficiency Data Centers; Technical Report; Intel Corporation: Santa Clara, CA, USA, 2006. [Google Scholar]
- Yeaman, P. Datacenter Power Delivery Architectures: Efficiency and Annual Operating Costs; Technical Report; Vicor Corporation: Andover, MA, USA, 2007. [Google Scholar]
- Cisco and/or Its Affiliates. Cisco Global Cloud Index: Forecast and Methodology, 2015–2020; Technical Report; 2016; Available online: https://www.cisco.com/c/dam/m/en_us/service-provider/ciscoknowledgenetwork/files/622_11_15-16-Cisco_GCI_CKN_2015-2020_AMER_EMEAR_NOV2016.pdf (accessed on 7 July 2025).
- Carson, S.; Lundvall, A. Ericsson Mobility Report June 2022; Technical Report; Ericsson: Stockholm, Sweden, 2022. [Google Scholar]
- Krein, P.T. Data center challenges and their power electronics. CPSS Trans. Power Electron. Appl. 2017, 1, 39–46. [Google Scholar] [CrossRef]
- Masanet, E.; Shehabi, A.; Lei, N.; Smith, S.; Koomey, J. Recalibrating global data center energy-use estimates. Science 2020, 6481, 984–986. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, D.M. AC-DC Converter Having an Improved Power Factor. U.S. Patent US4412277A, 25 October 1983. [Google Scholar]
- Chellappan, S. A Comparative Analysis of Topologies for a Bridgeless-Boost PFC Circuit. Tex. Instrum. Inc. Analog. Des. J. 2018, 3, 1–4. [Google Scholar]
- Erickson, R.W.; Maksimović, D. Pulse-Width Modulated Rectifiers. In Fundamentals of Power Electronics; Springer International Publishing: Boston, MA, USA, 2020; pp. 867–930. [Google Scholar]
- Hinago, Y.; Koizumi, H. A Switched-Capacitor Inverter Using Series/Parallel Conversion with Inductive Load. IEEE Trans. Ind. Electron. 2012, 59, 878–887. [Google Scholar] [CrossRef]
- Khan, M.N.H.; Forouzesh, M.; Siwakoti, Y.P.; Li, L.; Blaabjerg, F. Switched Capacitor Integrated (2n + 1)-Level Step-Up Single-Phase Inverter. IEEE Trans. Power Electron. 2020, 35, 8248–8260. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Siwakoti, Y.P.; Blaabjerg, F. A New Switched-Capacitor Five-Level Inverter Suitable for Transformerless Grid-Connected Applications. IEEE Trans. Power Electron. 2020, 35, 8140–8153. [Google Scholar] [CrossRef]
- Seo, G.S.; Le, H.P. S-Hybrid Step-Down DC–DC Converter—Analysis of Operation and Design Considerations. IEEE Trans. Ind. Electron. 2020, 67, 265–275. [Google Scholar] [CrossRef]
- Das, R.; Celikovic, J.; Abedinpour, S.; Mercer, M.; Maksimovic, D.; Le, H.P. Demystifying Capacitor Voltages and Inductor Currents in Hybrid Converters. In Proceedings of the 2019 20th Workshop on Control and Modeling for Power Electronics (COMPEL), Toronto, ON, Canada, 17–20 June 2019; pp. 1–8. [Google Scholar]
- Qin, S.; Lei, Y.; Barth, C.; Liu, W.C.; Pilawa-Podgurski, R.C.N. A High Power Density Series-Stacked Energy Buffer for Power Pulsation Decoupling in Single-Phase Converters. IEEE Trans. Power Electron. 2017, 32, 4905–4924. [Google Scholar] [CrossRef]
- Pervaiz, S.; Kumar, A.; Afridi, K.K. A Compact Electrolytic-Free Two-Stage Universal Input Offline LED Driver With Volume-Optimized SSC Energy Buffer. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1116–1130. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Current-Programmed Control. In Fundamentals of Power Electronics; Springer International Publishing: Boston, MA, USA, 2020; pp. 725–804. [Google Scholar]
- Corradini, L.; Maksimović, D.; Mattavelli, P.; Zane, R. Digital Control of High-Frequency Switched-Mode Power Converters: Corradini/Digital Control of High-Frequency Switched-Mode Power Converters; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Khatua, S.; Kastha, D.; Kapat, S. A New Single-Stage 48-V-Input VRM Topology Using an Isolated Stacked Half-Bridge Converter. IEEE Trans. Power Electron. 2020, 35, 11976–11987. [Google Scholar] [CrossRef]
- Kumar, A.; Pervaiz, S.; Afridi, K.K. High-Performance Single-Stage Isolated 48V-to-1.8V Point-of-Load Converter Utilizing Impedance Control Network and Distributed Transformer. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 3838–3843. [Google Scholar]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. 48-V Voltage Regulator Module With PCB Winding Matrix Transformer for Future Data Centers. IEEE Trans. Ind. Electron. 2017, 64, 9302–9310. [Google Scholar] [CrossRef]
- Abe, K.; Nishijima, K.; Harada, K.; Nakano, T.; Nabeshima, T.; Sato, T. A Novel Three-Phase Buck Converter with Bootstrap Driver Circuit. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1864–1871. [Google Scholar]
- Das, R.; Le, H.P. A Regulated 48V-to-1V/100A 90.9%-Efficient Hybrid Converter for POL Applications in Data Centers and Telecommunication Systems. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1997–2001. [Google Scholar]



| Components | Part Number |
|---|---|
| Sw1,3 | SBR10U200P5DICT-ND |
| Sw2,4 | BSC500N20NS3GATMA1CT-ND |
| Sw5,7,8,10 | BSC123N08NS3GATMA1 |
| Sw6,9 | SBRT20M80SP5-13 |
| C1,2 | 8xC5750X7S2A156M250KB |
| Cout | 8xC5750X7S2A156M250KB+ |
| 4xEKYB101ELL102MM40S | |
| L | IHLP6767GZER470M11 |
| Gate driver | UCC5350MCDR |
| Current Sensor | ACS716KLATR-6BB-NL-T |
| Frequency | 600 kHz |
| Components | Part Number |
|---|---|
| Sw1–6 | 2xEPC2015c |
| Sw7–12 | 2xEPC2023 |
| C1–5 | 4xCGA8M3X7S2A335M200KB |
| L1–6 | XAL1030-561ME |
| Gate Driver | LMG1210 |
| Frequency | 300 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, R.; Le, H.-P. Two-Stage Power Delivery Architecture Using Hybrid Converters for Data Centers and Telecommunication Systems. Electronics 2025, 14, 3169. https://doi.org/10.3390/electronics14163169
Das R, Le H-P. Two-Stage Power Delivery Architecture Using Hybrid Converters for Data Centers and Telecommunication Systems. Electronics. 2025; 14(16):3169. https://doi.org/10.3390/electronics14163169
Chicago/Turabian StyleDas, Ratul, and Hanh-Phuc Le. 2025. "Two-Stage Power Delivery Architecture Using Hybrid Converters for Data Centers and Telecommunication Systems" Electronics 14, no. 16: 3169. https://doi.org/10.3390/electronics14163169
APA StyleDas, R., & Le, H.-P. (2025). Two-Stage Power Delivery Architecture Using Hybrid Converters for Data Centers and Telecommunication Systems. Electronics, 14(16), 3169. https://doi.org/10.3390/electronics14163169







