GreenRP: Task-Aware Discharge-Resilient Routing for Sustainable Edge AI in Satellite Optical Networks
Abstract
1. Introduction
- Development of a comprehensive energy-efficient routing model that integrates satellite energy dynamics with operational strategies to optimize network longevity and performance in edge-AI-driven SONs;
- Introduction of a global traffic model that addresses spatial and temporal imbalances in traffic demands, incorporating load dormancy strategies to enhance edge AI sustainability;
- Proposal of a novel topology planning scheme leveraging payload dormancy to minimize energy consumption in large-scale satellite constellations;
- Design of the green task-aware routing planning (GreenRP) algorithm, validated through extensive simulations to optimize network performance and energy utilization.
2. Energy Efficiency Landscape
2.1. Energy Acquisition
2.2. Energy Consumption
2.3. Battery Life Calculation
2.4. Energy-Efficient Network Model
3. Energy Efficiency Problem Model for SONs
3.1. Global Traffic Model
3.2. Energy-Efficient Problem Model
3.3. GreenRP Algorithm
| Algorithm 1: Green Routing Planning (GreenRP) algorithm | |
|---|---|
| Input: Satellite_Network_Topology, Previous_Best_Topology | |
| Output: Final_Energy_Saving_Topology | |
| 1: | initialize Population_Size, Gene_Length, Best_Fitness ← ∞, No_Improve_Count ← 0; |
| 2: | Mean ← Previous_Best_Topology ? Count_Off_Links(Previous_Best_Topology): Gene_Length/2; |
| 3: | Population ← [GenerateGene(Gene_Length, NormalDistribution(Mean, σ)) for i in |
| 4: | 1..(0.75*Population_Size)] + [Copy(Previous_Best_Topology) for i in 1..(0.25*Population_Size)]; |
| 5: | for Iteration from 1 to Max_Iterations do |
| 6: | for each Gene IN Population do |
| 7: | Gene.Fitness ← w1 * Norm_Energy + w2 * Norm_Packet_Loss + w3 * Norm_Avg_Delay; |
| 8: | end for |
| 9: | Current_Best_Fitness ← Population.Best.Fitness; |
| 10: | if Current_Best_Fitness < Best_Fitness then |
| 11: | Best_Fitness ← Current_Best_Fitness; |
| 12: | No_Improve_Count ← 0; |
| 13: | else |
| 14: | No_Improve_Count ← No_Improve_Count + 1; |
| 15: | if No_Improve_Count ≥ 3 then break; |
| 16: | end if |
| 17: | while New_Population.SIZE < Population_Size do |
| 18: | Parent1, Parent2 ← SelectParents(Population); |
| 19: | Child1, Child2 ← (Random() < CrossoverProb) ? SinglePointCrossover: Copy; |
| 20: | New_Population.ADD(Mutate(Child1, MutationProb)); |
| 21: | New_Population.ADD(Mutate(Child2, MutationProb)); |
| 22: | end while |
| 23: | Population ← New_Population; |
| 24: | end for |
| 25: | Best_Gene ← Population.Best; |
| 26: | Path_Set ← { ShortestPathAlgorithm(Best_Gene, Pair).Links for Pair in Satellite_Regions.Pairs }; |
| 27: | for each Link in Path_Set do |
| 28: | Best_Gene[Link] ← 1; |
| 29: | end for |
| 30: | Final_Topology ← Best_Gen; |
| 31: | return Final_Topology. |
4. Performance Evaluation and Analysis
4.1. Simulation Setup
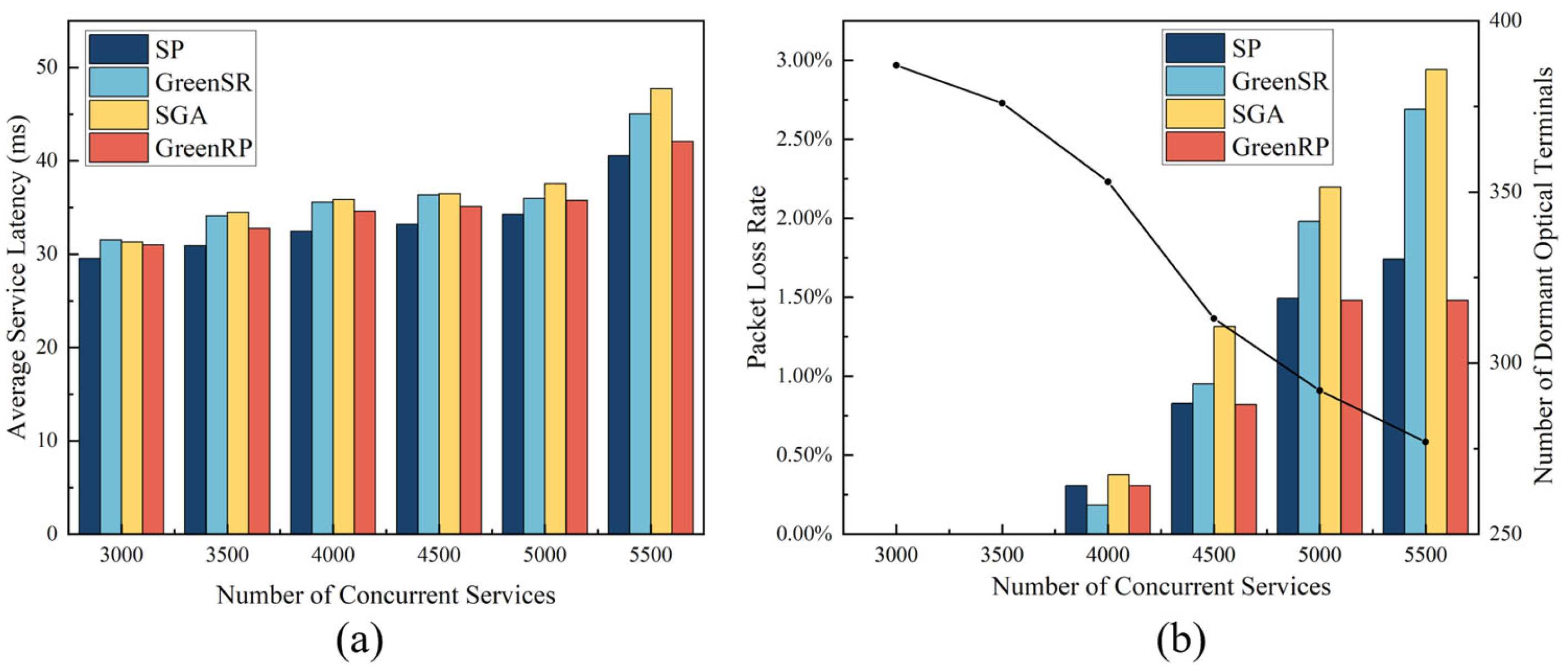
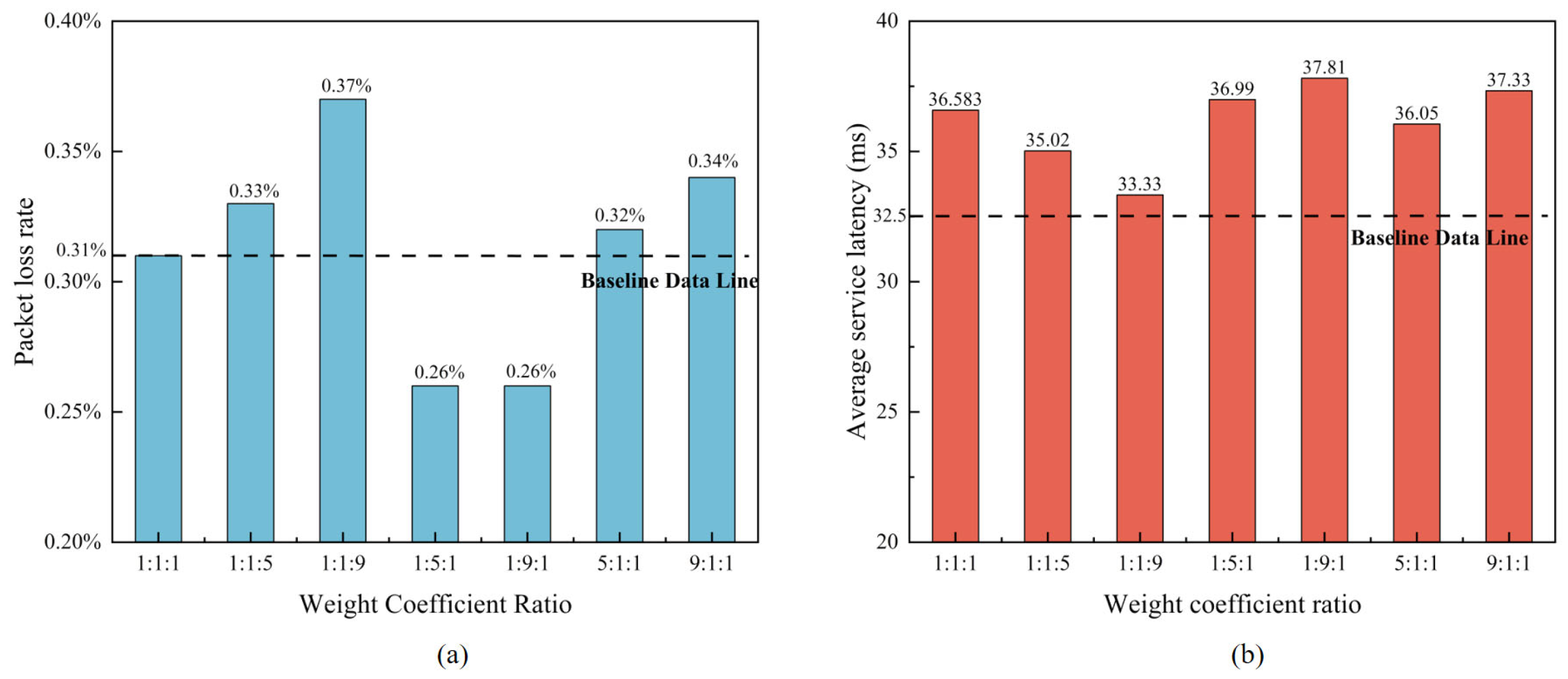
4.2. Comparison of Algorithm Performance Under Different Loads
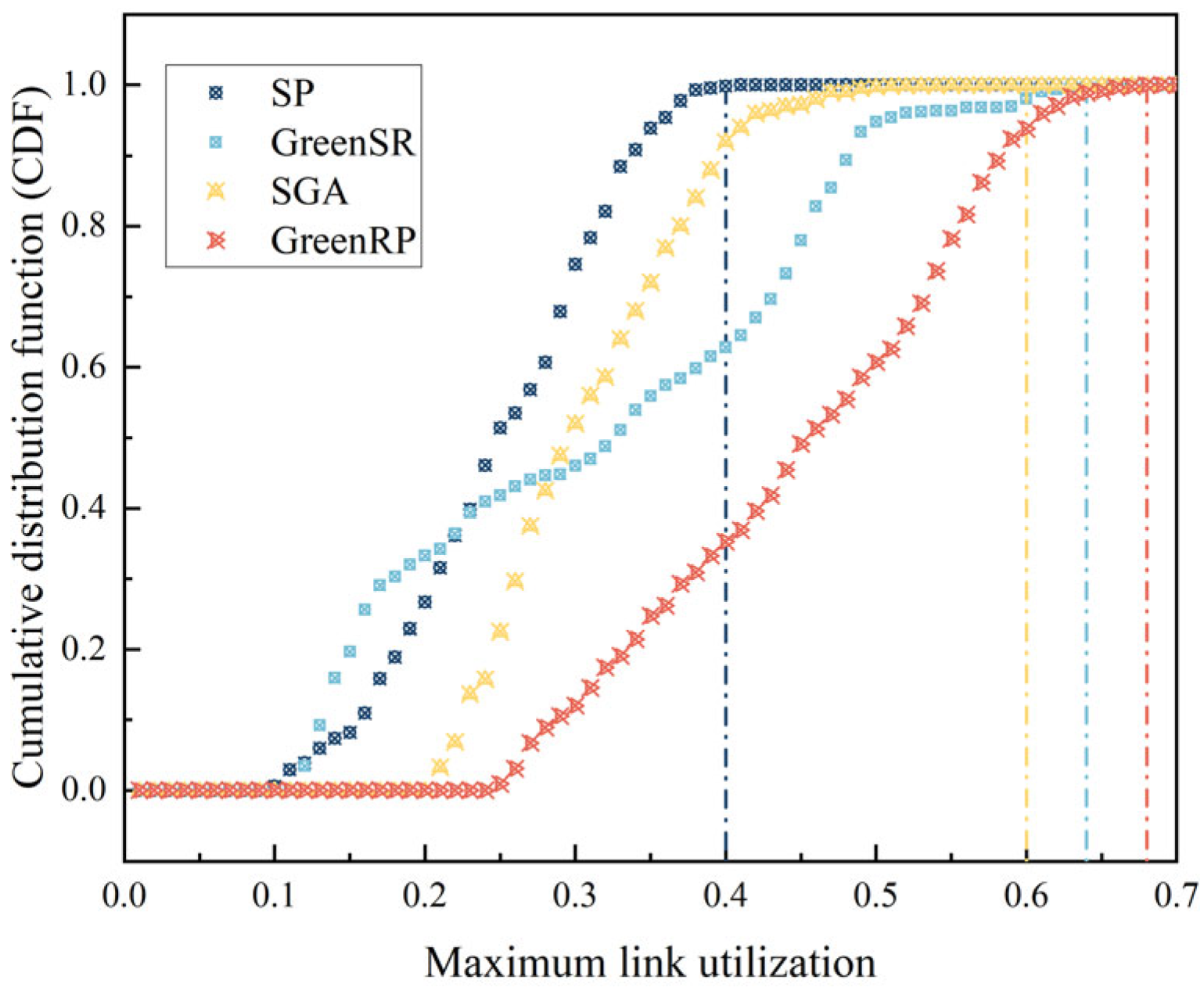
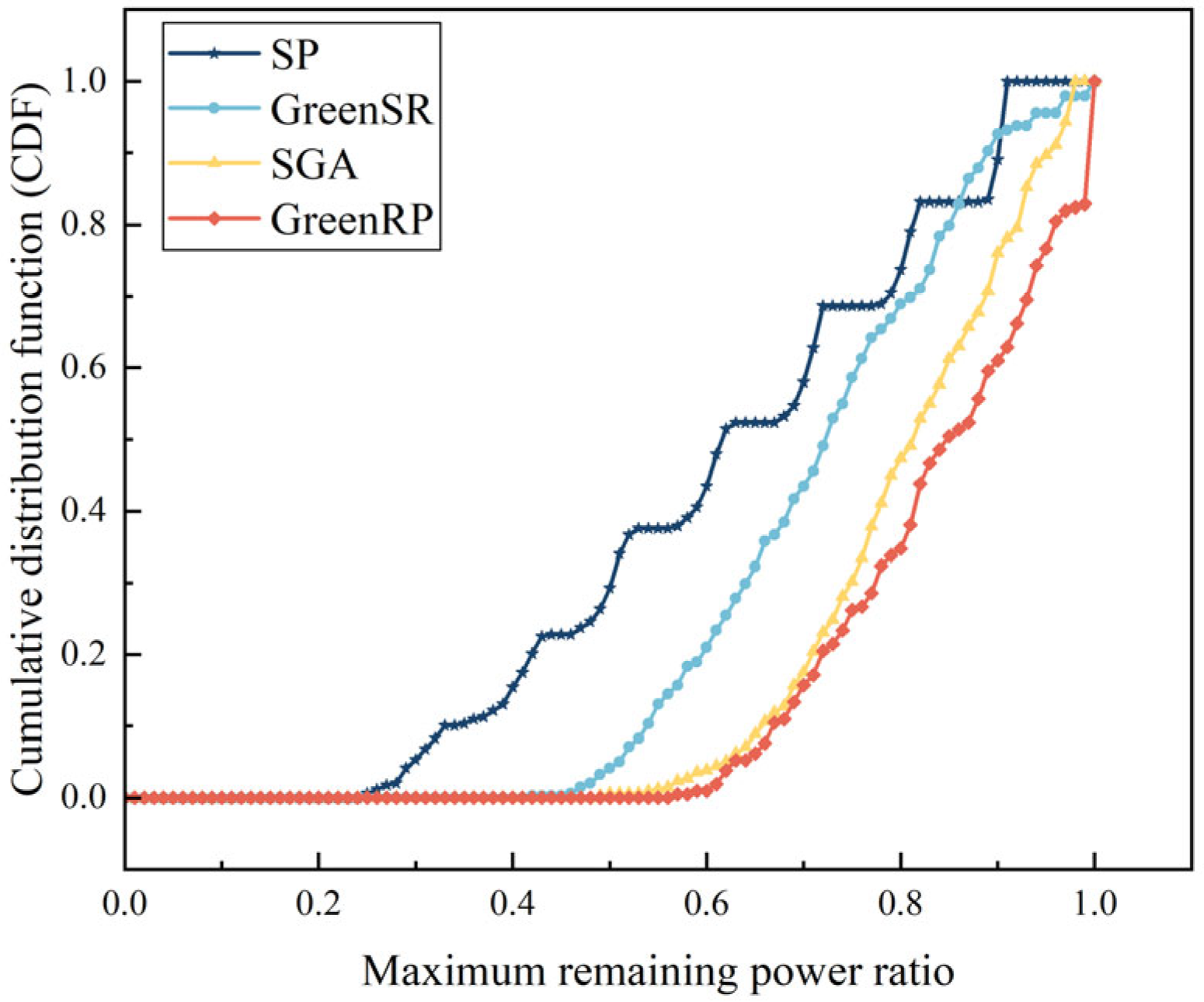
4.3. Comparison of Algorithm Performance Under Fixed Loads
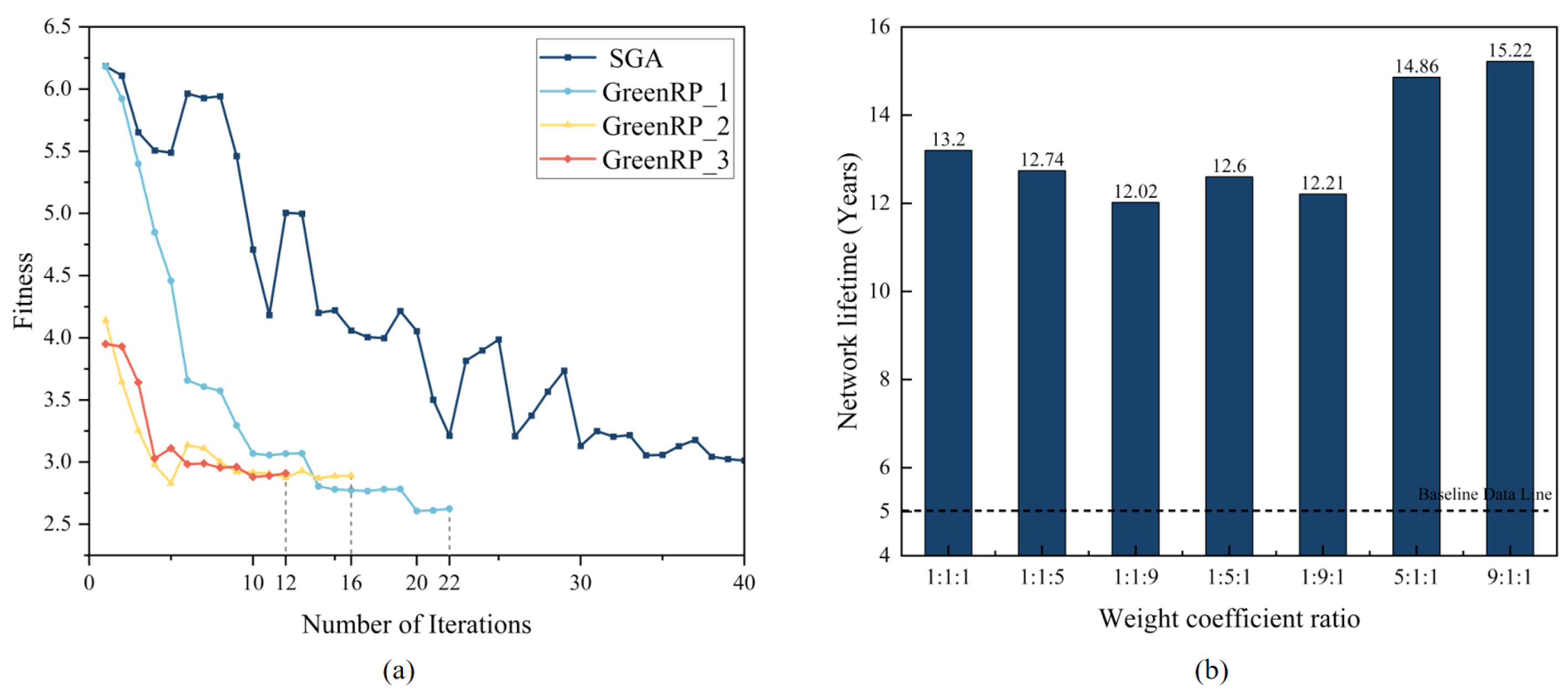
4.4. Performance Analysis of GreenRP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saeed, N.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Shamma, J.S.; Alouini, M.-S. Point-to-Point Communication in Integrated Satellite-Aerial 6G Networks: State-of-the-Art and Future Challenges. IEEE Open J. Commun. Soc. 2021, 2, 1505–1525. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, W.; Wan, P.; Liu, A.; Han, H.; Mu, J.; Liu, S.; Gu, W.; Huang, S.; Feng, Z. Building an Efficient Satellite Network Routing Scheme: Challenges and Opportunities. IEEE Commun. Stand. Mag. 2025, 9, 30–38. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Mohsin, M.; Ali, S.M.Z. Survey and technological analysis of laser and its defense applications. Def. Technol. 2021, 17, 583–592. [Google Scholar] [CrossRef]
- Kota, S.; Giambene, G. 6G Integrated Non-Terrestrial Networks: Emerging Technologies and Challenges. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Shaengchart, Y.; Kraiwanit, T. The Spacex Starlink Satellite Project: Business Strategies and Perspectives. Corp. Bus. Strategy Rev. 2024, 5, 30–37. [Google Scholar] [CrossRef]
- Ntontin, K.; Lagunas, E.; Querol, J.; ur Rehman, J.; Grotz, J.; Chatzinotas, S.; Ottersten, B. A vision, survey, and roadmap toward space communications in the 6G and beyond era. Proc. IEEE 2025, 1–37. [Google Scholar] [CrossRef]
- De Gaudenzi, R.; Ottersten, B.; Perez-Neira, A.; Yanikomeroglu, H.; Heyn, T.; Lichten, S.M. Guest Editorial Space Communications New Frontiers: From Near Earth to Deep Space. IEEE J. Sel. Areas Commun. 2024, 42, 1023–1028. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, G.; Huan, Z.; Zhang, Y.; Yuan, G.; Li, Q.; Ding, G.; Lv, Z.; Ni, W.; Shao, Y.; et al. Wireless laser power transmission: Recent progress and future challenges. Space Sol. Power Wirel. Transm. 2024, 1, 17–26. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, X.; Huang, K.; Zhang, Y.J.A.; Zhang, J. Green edge AI: A contemporary survey. Proc. IEEE 2024, 112, 880–911. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, T.; Liu, T.; Yao, L. Reliability Evaluation and In-Orbit Residual Life Prediction for Satellite Lithium-Ion Batteries. Math. Probl. Eng. 2018, 2018, 5918068. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Li, D.; Huang, S. Energy-efficient regeneration routing in satellite optical networks under translucent optical payload architectures. Opt. Express 2024, 32, 12368–12393. [Google Scholar] [CrossRef]
- Jing, Y.; Yang, Z.; Zhao, Y.; Wang, H.; Wang, W.; Rahman, S.; Zhang, J. Energy-efficient routing based on a genetic algorithm for satellite laser communication. Opt. Express 2023, 31, 8682–8695. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Q.; Ran, Y. Dynamic routing algorithm for maximizing battery life in LEO satellite networks. In Proceedings of the 2022 IEEE 8th International Conference on Computer and Communications (ICCC), Chengdu, China, 9–12 December 2022; pp. 671–676. [Google Scholar]
- Shi, K.; Li, H.; Suo, L. Temporal graph based energy-limited max-flow routing over satellite networks. In Proceedings of the 2021 IFIP Networking Conference (IFIP Networking), Espoo and Helsinki, Finland, 21–24 June 2021; pp. 1–3. [Google Scholar]
- Liu, J.; Zhao, B.; Xin, Q.; Su, J.; Ou, W. DRL-ER: An intelligent energy-aware routing protocol with guaranteed delay bounds in satellite mega-constellations. IEEE Trans. Netw. Sci. Eng. 2020, 8, 2872–2884. [Google Scholar] [CrossRef]
- Gupta, N.; Bitragunta, S. Green satellite communication link design, optimization, and performance analysis. In Proceedings of the 2020 IEEE 7th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Prayagraj, India, 27–29 November 2020; pp. 1–5. [Google Scholar]
- Tu, Z.; Zhou, H.; Li, K.; Li, M.; Tian, A. An energy-efficient topology design and DDoS attacks mitigation for green software-defined satellite network. IEEE Access 2020, 8, 211434–211450. [Google Scholar] [CrossRef]
- Tsuchida, H.; Kawamoto, Y.; Kato, N.; Kaneko, K.; Tani, S.; Hangai, M.; Aruga, H. Improvement of Battery Lifetime Based on Communication Resource Control in Low-Earth-Orbit Satellite Constellations. IEEE Trans. Emerg. Top. Comput. 2021, 10, 1388–1398. [Google Scholar] [CrossRef]
- Hussein, M.; Jakllari, G.; Paillassa, B. On routing for extending satellite service life in leo satellite networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2832–2837. [Google Scholar]
- Yang, Y.; Xu, M.; Wang, D.; Wang, Y. Towards energy-efficient routing in satellite networks. IEEE J. Sel. Areas Commun. 2016, 34, 3869–3886. [Google Scholar] [CrossRef]
- Chou, Y.C.; Ma, X.; Wang, F.; Ma, S.; Wong, S.H.; Liu, J. Towards Sustainable Multi-Tier Space Networking for LEO Satellite Constellations. In Proceedings of the 2022 IEEE/ACM 30th International Symposium on Quality of Service (IWQoS), Oslo, Norway, 10–12 June 2022; pp. 1–11. [Google Scholar]
- Yang, L.; Zhang, H.; Qi, Y.; Huang, Q. Available energy routing algorithm considering QoS requirements for LEO satellite network. Comput. Commun. 2024, 217, 87–96. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Li, D.; Zhao, C.; Huang, S. Green laser inter-satellite link planning in satellite optical networks: Trading off the battery lifetime and network throughput using numerical quantization. J. Opt. Commun. Netw. 2024, 16, 868–880. [Google Scholar] [CrossRef]
- Taherbaneh, M.; Ghafooifard, H.; Rezaie, A.H.; Rahimi, K. Evaluation end-of-life power generation of a satellite solar array. Energy Convers. Manag. 2011, 52, 2518–2525. [Google Scholar] [CrossRef]
- Liu, Z.; Tan, C.M.; Leng, F. A reliability-based design concept for lithium-ion battery pack in electric vehicles. Reliab. Eng. Syst. Saf. 2015, 134, 169–177. [Google Scholar] [CrossRef]
- Wierman, A.; Andrew, L.L.; Tang, A. Power-aware speed scaling in processor sharing systems: Optimality and robustness. Perform. Eval. 2012, 69, 601–622. [Google Scholar] [CrossRef]
- Zhu, Y. An analysis of influence of satellite design lifetime. Spacecr. Eng. 2007, 16, 9–18. [Google Scholar]
- INTERNET USAGE STATISTICS. The Internet Big Picture World Internet Users and 2023 Population Stats. Available online: https://www.internetworldstats.com/stats.htm (accessed on 1 December 2023).
- Liang, J.; Chaudhry, A.U.; Yanikomeroglu, H. Phasing Parameter Analysis for Satellite Collision Avoidance in Starlink and Kuiper Constellations. In Proceedings of the 2021 IEEE 4th 5G World Forum (5GWF), Montreal, QC, Canada, 13–15 October 2021; pp. 493–498. [Google Scholar]




| Parameter | Value |
|---|---|
| Orbital Altitude | 550 km, 570 km |
| Number of Orbits | 36, 18 |
| Satellites per Orbit | 22, 20 |
| Orbital Inclination | 53°, 70° |
| RAAN | 180° |
| Inter-Satellite Laser Link Bandwidth | 10 Gbps |
| Ground-to-Satellite Link Bandwidth | 8 Gbps |
| 100 W | |
| 150 W | |
| 1/1/1.5 W/Gbps | |
| 0.1 | |
| 1.4 | |
| 0.6 | |
| 40 | |
| Service Bandwidth | 50 MB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Du, D.; Zheng, K.; Cao, Y.; Zhao, L.; Zhao, Y.; Zhang, J. GreenRP: Task-Aware Discharge-Resilient Routing for Sustainable Edge AI in Satellite Optical Networks. Electronics 2025, 14, 3075. https://doi.org/10.3390/electronics14153075
Zhang H, Du D, Zheng K, Cao Y, Zhao L, Zhao Y, Zhang J. GreenRP: Task-Aware Discharge-Resilient Routing for Sustainable Edge AI in Satellite Optical Networks. Electronics. 2025; 14(15):3075. https://doi.org/10.3390/electronics14153075
Chicago/Turabian StyleZhang, Huibin, Dandan Du, Kunpeng Zheng, Yuan Cao, Lihan Zhao, Yongli Zhao, and Jie Zhang. 2025. "GreenRP: Task-Aware Discharge-Resilient Routing for Sustainable Edge AI in Satellite Optical Networks" Electronics 14, no. 15: 3075. https://doi.org/10.3390/electronics14153075
APA StyleZhang, H., Du, D., Zheng, K., Cao, Y., Zhao, L., Zhao, Y., & Zhang, J. (2025). GreenRP: Task-Aware Discharge-Resilient Routing for Sustainable Edge AI in Satellite Optical Networks. Electronics, 14(15), 3075. https://doi.org/10.3390/electronics14153075







