Multi-Feature AND–OR Mechanism for Explainable Modulation Recognition
Abstract
1. Introduction
- (1)
- Theoretical contribution: We first introduce symbolic feature interaction concepts to communication signal analysis. We develop an interpretable architecture based on modulation primitive decomposition, which resolves the feature coupling issue in traditional AMR models. We also present a unified theoretical framework that combines mathematical proofs with signal processing principles, reconciling interpretability with adversarial robustness.
- (2)
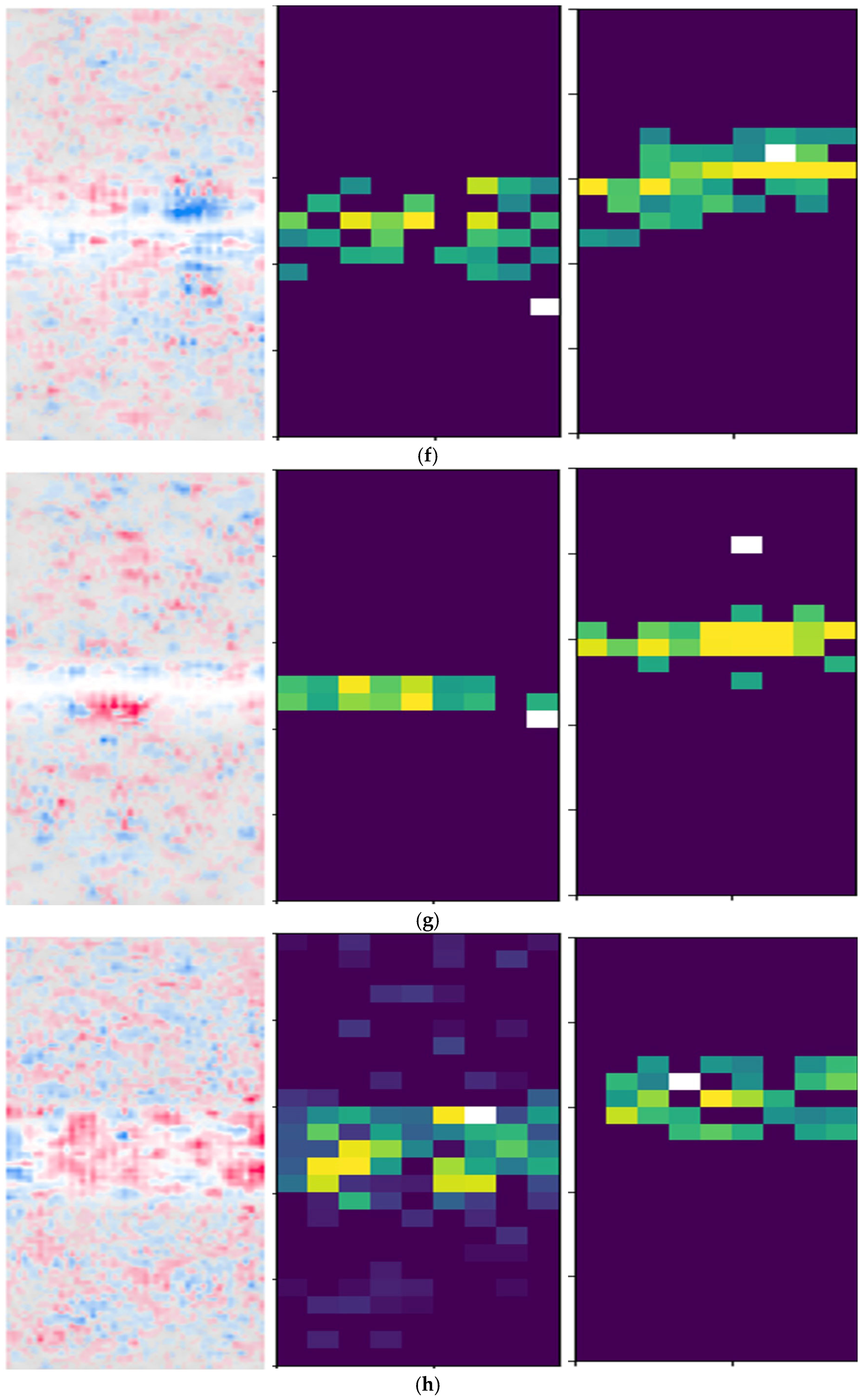
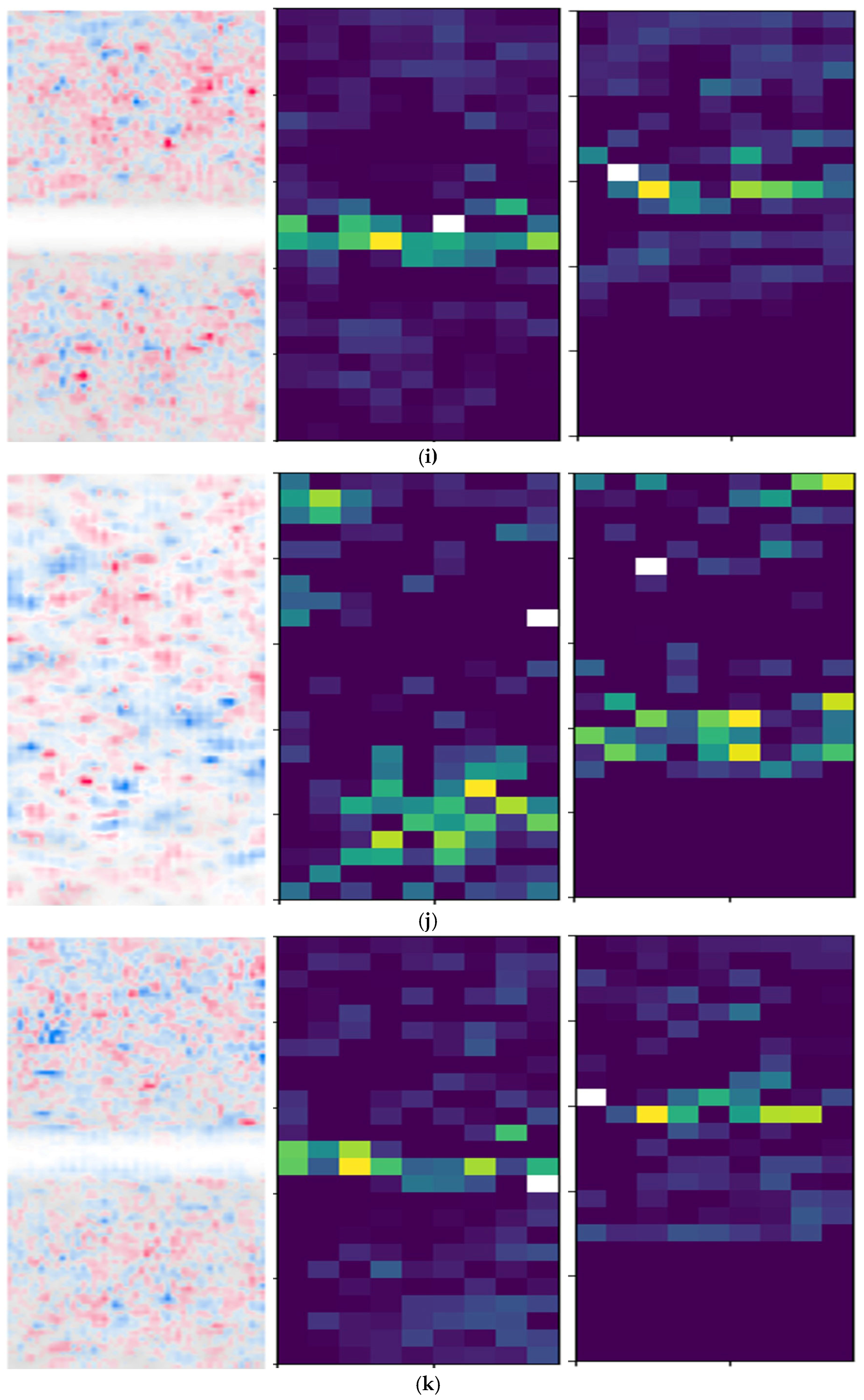
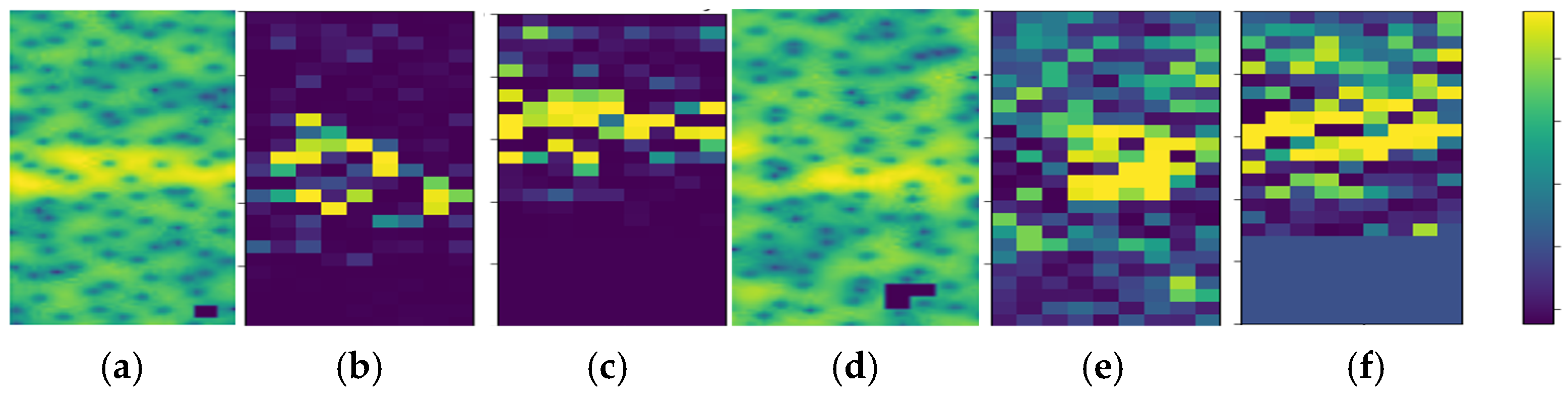
- Methodological advancement: A dual-branch XAI framework (feature extraction + interaction analysis) is developed, validated on a ResNet backbone. This architecture reveals explicit mappings between signal periodicity and modulation order in high-dimensional feature spaces, as evidenced by attention heatmaps localized to phase shift keying (PSK) phase jumps and quadrature amplitude modulation (QAM) constellation points. The symbolic interaction layer employs [1, 2, 4, 8]-order occlusion templates to quantify hierarchical feature dependencies, which are computed by evaluating Shapley interaction values (SIVs) under varying occlusion patterns.
- (3)
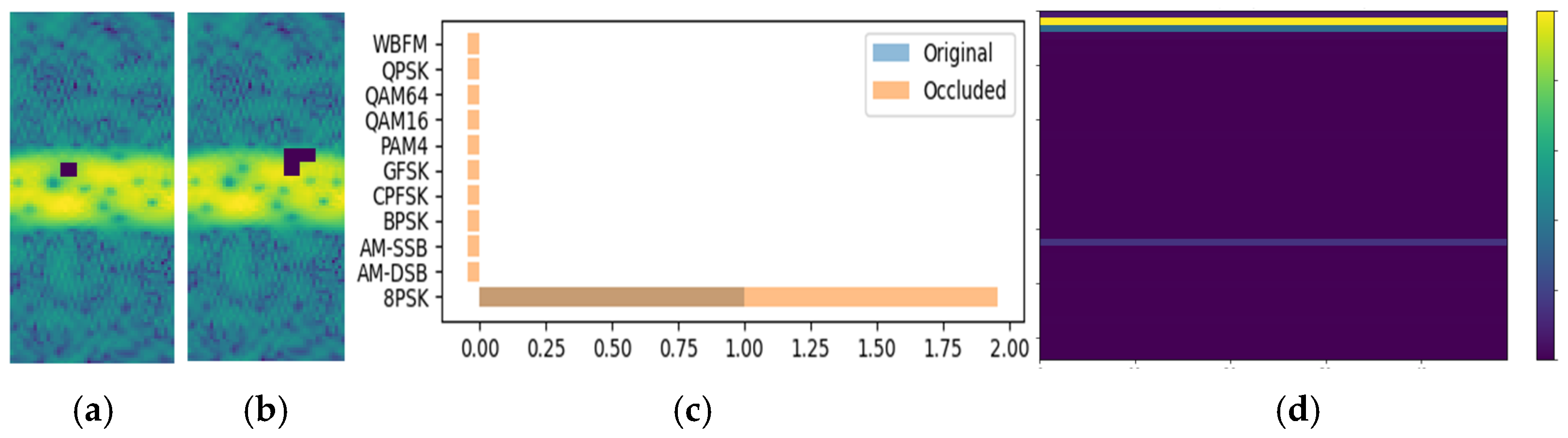
- Through responsibility attribution metrics, we implement modular adversarial verification to decouple input contributions. This enables quantitative evaluation of key elements (e.g., transient phases in 8PSK account for 65% of the decision weight) and establishes a certified benchmark for AMR systems under additive white Gaussian noise (AWGN) and selective fading channels. The methodology aligns with ablation testing principles, where critical modules are systematically disabled to validate robustness
2. Related Works
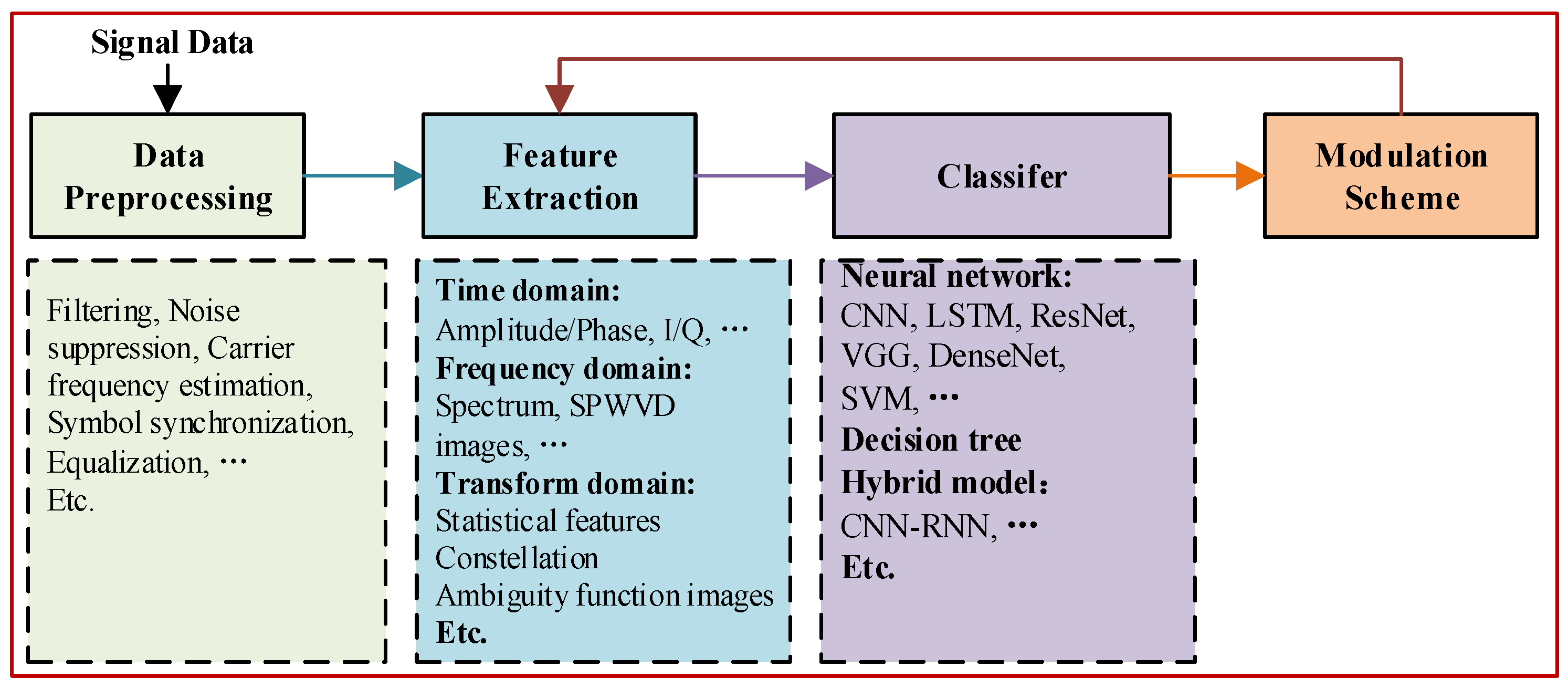
2.1. DL Models for AMR
2.2. XAI for AMR
3. Approach
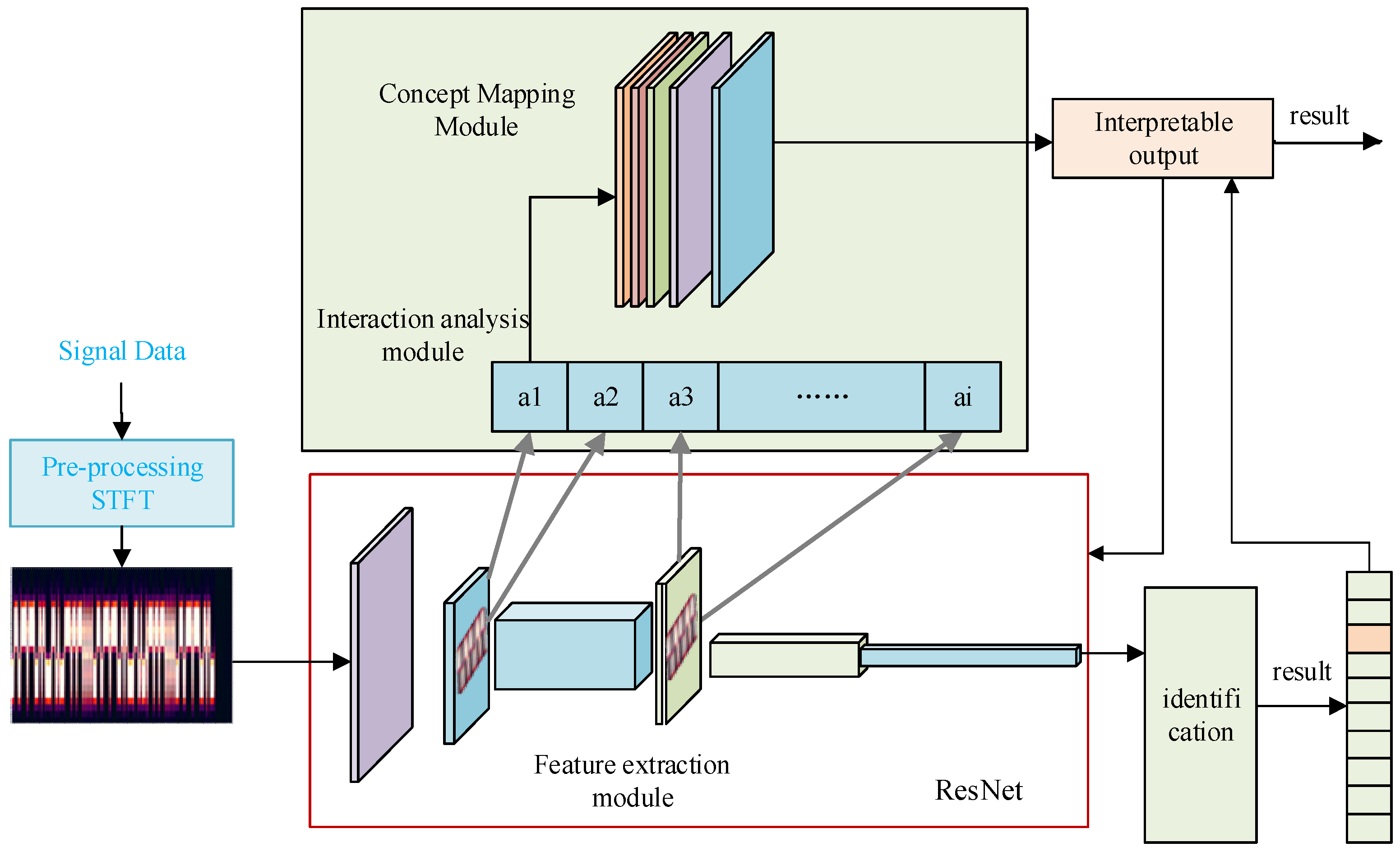
3.1. System Overview
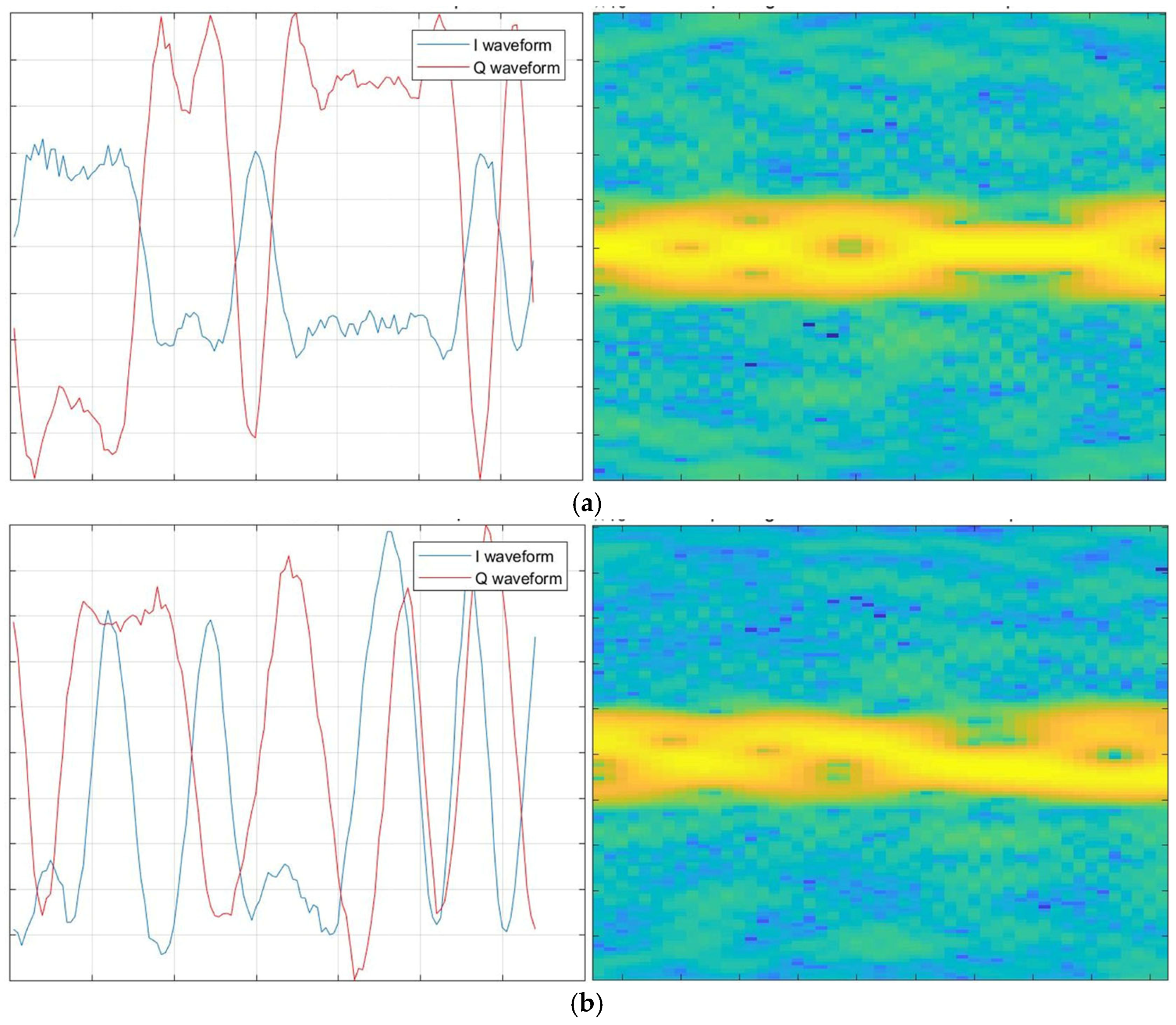
3.2. STFT+-Based Input Data Construction
3.3. Feature Extraction Module
3.4. Interactive Interpretability Theory
- (1)
- Quantifying knowledge concepts: Game-theoretic interactions measure the complexity and contribution of interactive concepts encoded in DNNs.
- (2)
- Exploring visual concept encoding: Prototypical visual concepts (e.g., edges, textures) are extracted by analyzing interaction patterns.
- (3)
- Optimizing Shapley value baselines: A unified framework compares 14 attribution methods by learning optimal baseline values for Shapley interactions.
- (4)
- Explaining the representation bottleneck: Theoretical analysis reveals that DNNs predominantly encode overly simple or complex interactions, failing to learn intermediate complexities—a phenomenon termed the “representation bottleneck”.
3.5. Concept Mapping Module
4. Experiments
4.1. Dataset and Experimental Setup
4.2. Evaluation Metrics
4.3. Adversarial Experiments
- Experiment 1: Multi-Order Feature Interaction Analysis
- Experiment 2: Robustness Under Varying SNRs
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | additive white Gaussian noise |
| AM-DSB | double-sideband amplitude modulation |
| AM-SSB | single-sideband amplitude modulation |
| AMR | automatic modulation recognition |
| BPSK | binary phase shift keying |
| CPFSK | continuous phase frequency shift keying |
| DNNs | deep neural networks |
| XAI | explainable AI |
| GFSK | Gauss frequency shift keying |
| Grad-CAM | gradient-weighted class activation mapping |
| LIME | local interpretable model-agnostic explanations |
| PAM4 | pulse amplitude modulation 4 |
| PSK | phase shift keying |
| QPSK | quadrature phase shift keying |
| QAM | quadrature amplitude modulation |
| SHAP | Shapley additive explanation |
| STFT | short-time Fourier transform |
| WBFM | wideband frequency modulation |
References
- Mitola, J.I. Cognitive Radio. An Integrated Agent Architecture for Software Defined Radio. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2000. [Google Scholar]
- Dobre, O.A.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y.; Zheng, F.C. Deep learning based automatic modulation recognition: Models, datasets, and challenges. Digit. Signal Process. 2022, 129, 103650. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Mi, J.-X.; Li, A.-D.; Zhou, L.-F. Review study of interpretation methods for future interpretable machine learning. IEEE Access 2020, 8, 191969–191985. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, H.; Yang, F.; Liu, N.; Deng, H.; Cai, H.; Wang, S.; Yin, D.; Du, M. Explainability for large language models: A survey. ACM Trans. Intell. Syst. Technol. 2024, 2, 1–38. [Google Scholar] [CrossRef]
- Li, X.; Xiong, H.; Li, X.; Wu, X.; Zhang, X.; Ji, L.; Bian, J.; Dou, D. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowl. Inf. Syst. 2022, 64, 3197–3234. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. Int. J. Comput. Vis. 2024, 129, 676–694. [Google Scholar]
- Lundberg, S.M. A Unified Approach to Interpreting Model Predictions Using SHAP Values. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 1223–1237. [Google Scholar]
- Zhang, Y.; Cho, K. Logic-Integrated Neural Networks for Protocol-Aware Signal Demodulation. IEEE Trans. Cogn. Commun. Netw. 2025, 10, 589–602. [Google Scholar]
- Shen, T.; Jin, R.; Huang, Y.; Liu, C.; Dong, W.; Guo, Z.; Wu, X.; Liu, Y.; Xiong, D. Large language model alignment: A survey. arXiv 2023, arXiv:2309.15025. [Google Scholar]
- Shen, H.; Zhang, Q.; Wang, L.; Chen, Y.; Liu, F.; Patel, V.; Gupta, R.; Kumar, S.; Li, X. Interpretability-Aware OFDM Symbol Detection via Gradient Refinement. IEEE Trans. Wirel. Commun. 2024, 23, 412–427. [Google Scholar]
- Tomašev, A.; Williams, B.; Almeida, J.; Rossi, M.; Nguyen, T.; Silva, C.; Kim, J.; Petrović, N.; Zhou, Y.; Fernández, S. Causal Attribution Challenges in SHAP-Based RF Systems. IEEE J. Sel. Areas Commun. 2025, 42, 832–845. [Google Scholar]
- Zhang, Q.; Zhao, R.; Ivanov, S.; Lee, K.; Müller, P.; Santos, A.; Wei, L.; Varshney, K.; Chen, H.; Sun, T. Logic-Based XAI Limitations in Adaptive Modulation Recognition. IEEE Trans. Aerosp. Electron. Syst. 2025, 60, 1453–1468. [Google Scholar]
- Snoap, J.; Popescu, D.; Spooner, C. Deep-Learning-Based Classifier with Custom Feature-Extraction Layers for Digitally Modulated Signals. IEEE Trans. Broadcast. 2024, 70, 763–773. [Google Scholar] [CrossRef]
- Ren, Q.; Gao, J.; Zhang, Q. Where We Have Arrived in Proving the Emergence of Sparse Interaction Primitives in DNNs. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- O’Shea, T.J.; West, N. Radio machine learning dataset generation with GNU radio. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 12–16 September 2016; Volume 1. [Google Scholar]
- Li, W.; Wang, X. Time series prediction method based on simplified LSTM neural network. J. Beijing Univ. Technol. 2021, 47, 480–488. [Google Scholar]
- Hochreiter, S.; Schmindhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tian, F.; Wang, L.; Xia, M. Signals recognition by CNN based on attention mechanism. Electronics 2022, 11, 2100. [Google Scholar] [CrossRef]
- O’Shea, T.; Corgan, J.; Clancy, T. Convolutional radio modulation recognition networks. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Aberdeen, UK, 2–5 September 2016; pp. 213–226. [Google Scholar]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Yang, D.; Liao, W.; Ren, X.; Ren, X.; Wang, Y. Power transformer fault diagnosis based on capsule network. High-Volt. Technol. 2021, 47, 415–425. [Google Scholar]
- Yi, Z.; Meng, H.; Gao, L.; He, Z.; Yang, M. Efficient convolutional dual-attention transformer for automatic modulation recognition. Appl. Intel. 2025, 55, 231. [Google Scholar] [CrossRef]
- Rashvand, N.; Witham, K.; Maldonado, G.; Katariya, V.; Prabhu, N.M.; Schirner, G.; Tabkhi, H. Enhancing automatic modulation recognition for iot applications using transformers. IoT 2024, 5, 212–226. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Fan, Y.; Wang, M.; Xu, Z.; Hou, S. A complex-valued convolutional fusion-type multi-stream spatiotemporal network for automatic modulation classification. Sci. Rep. 2024, 14, 22401. [Google Scholar] [CrossRef] [PubMed]
- Shen, D.; Mai, W. Automatic Modulation Recognition of Communication Signals Based on ResNet-Transformer Network; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Bhatti, S.G.; Taj, I.A.; Ullah, M.; Bhatti, A.I. Transformer-based models for intrapulse modulation recognition of radar waveforms. Eng. Appl. Artif. Intell. 2024, 136 Pt B, 108989. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You? Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Bau, D.; Zhu, J.; Strobelt, H.; Lapedriza, A.; Zhou, B.; Torralba, A. Understanding the role of individual units in a deep neural network. Proc. Natl. Acad. Sci. USA 2020, 117, 30071–30078. [Google Scholar] [CrossRef]
- Kim, B.; Wattenberg, M.; Gilmer, J.; Cai, C.; Wexler, J.; Viegas, F. Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (TCAV). In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 2668–2677. [Google Scholar]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Eng. Appl. Artif. Intell. 2025, 136 Pt B, 104–123. [Google Scholar]
- Zhang, Q.; Wu, Y.; Zhu, S. Interpretable convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Ren, J.; Li, M.; Chen, Q.; Deng, H.; Zhang, Q. Defining and quantifying the emergence of sparse concepts in DNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Li, M.; Zhang, Q. Does a neural network really encode symbolic concept? In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Zhou, H.; Zhang, H.; Deng, H.; Liu, D.; Shen, W.; Chan, S.; Zhang, Q. Explaining generalization power of a DNN using interactive concepts. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 17105–17113. [Google Scholar]
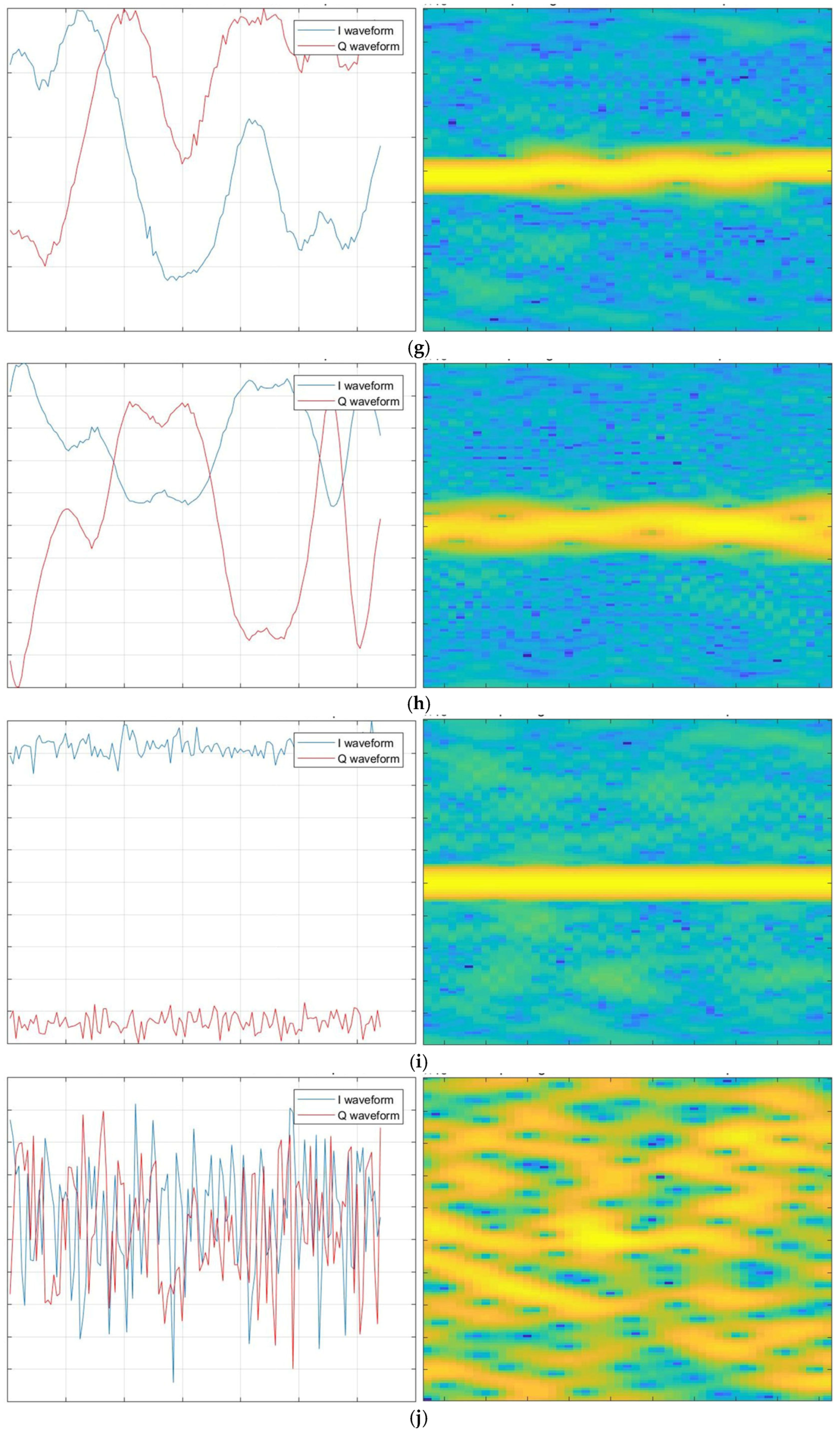
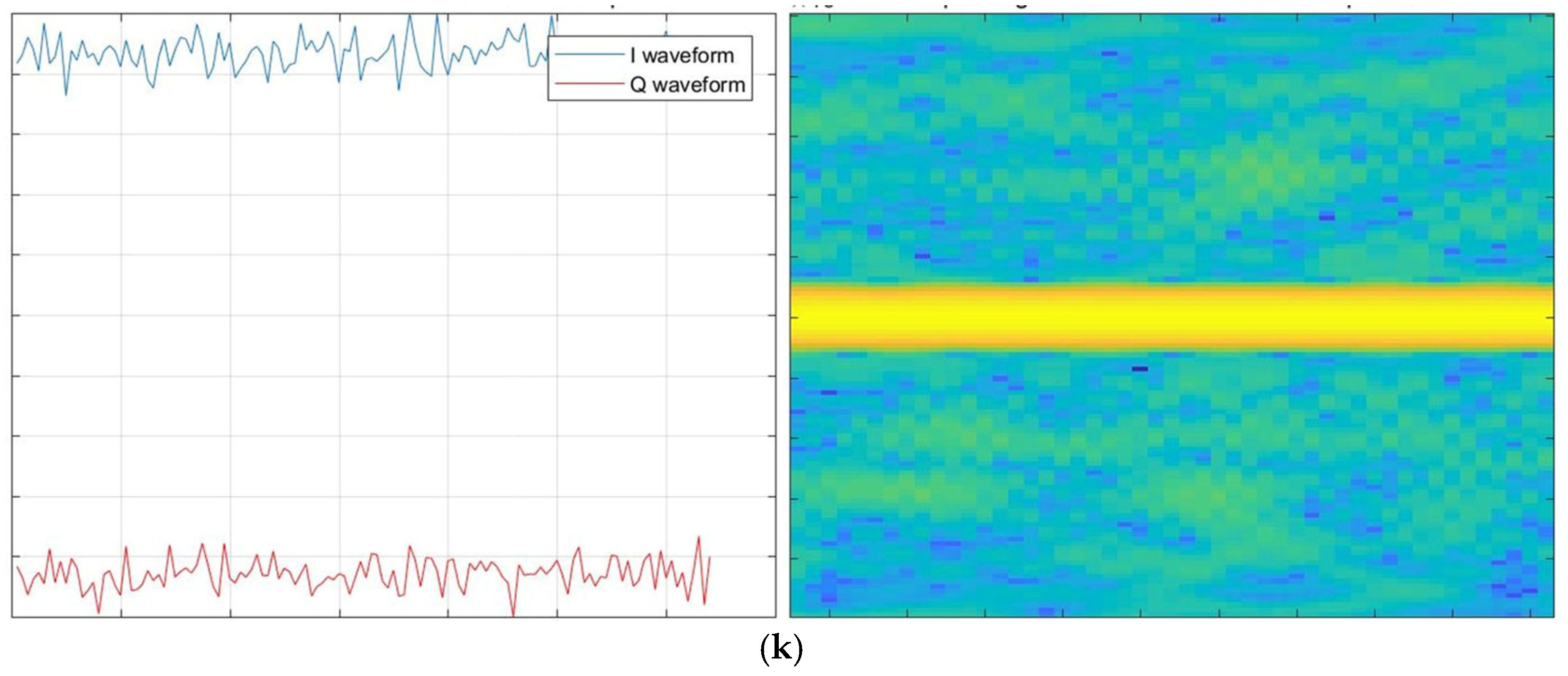
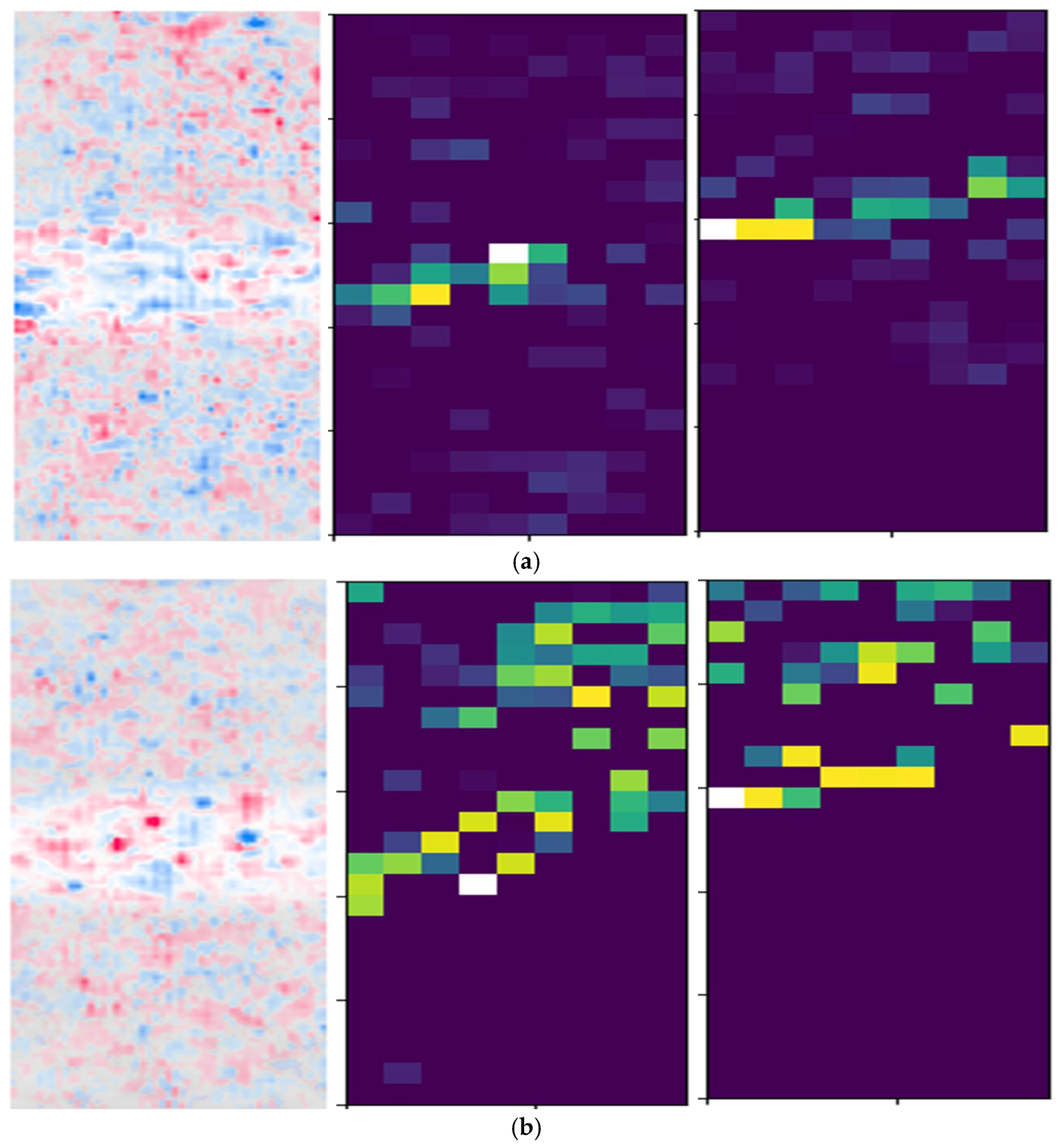
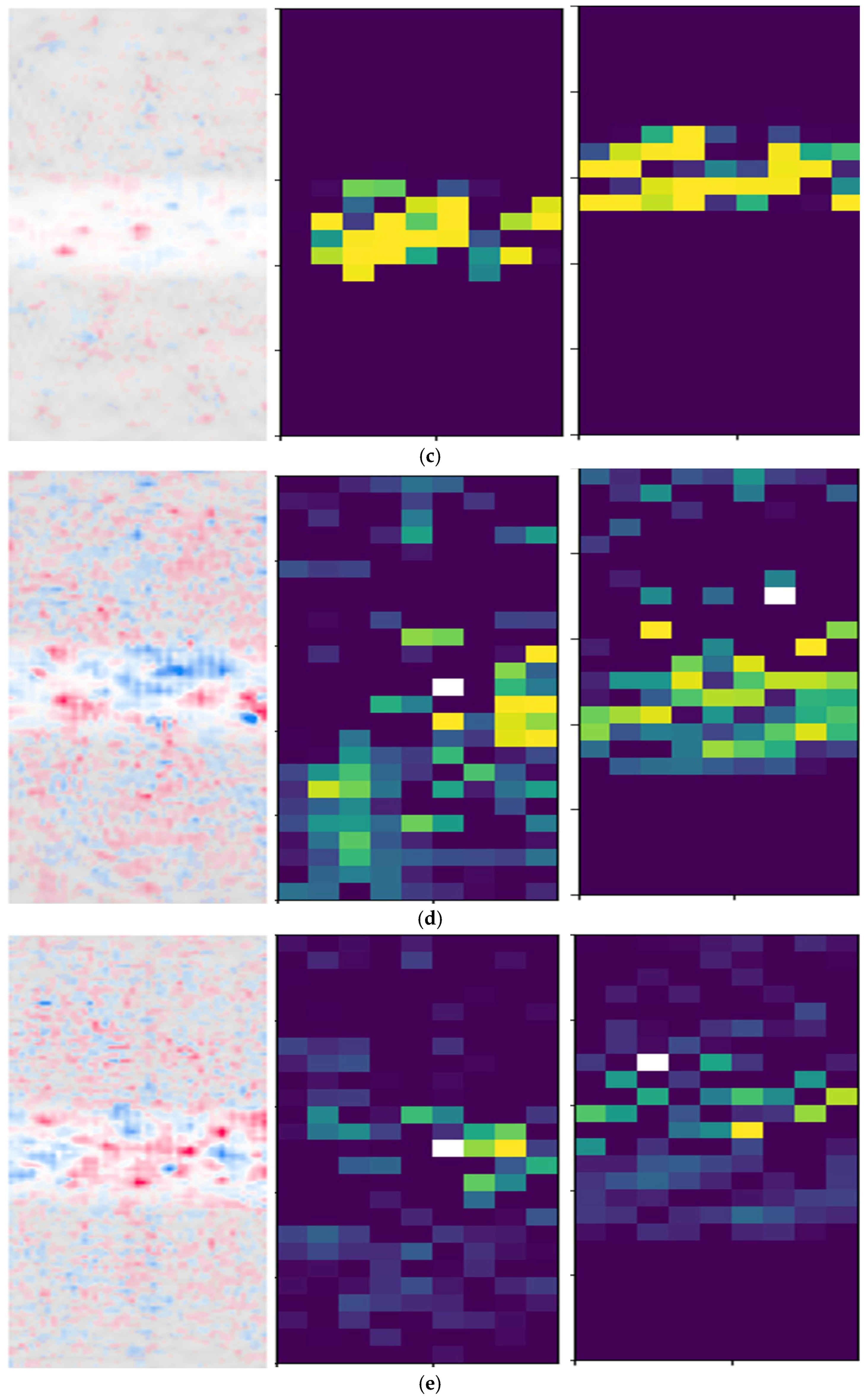
| Year | Authors | Model Type | Dataset(s) | Interpretability Technique | Main Metric | Limitations |
|---|---|---|---|---|---|---|
| 2016 | O’Shea et al. [22] | CNN | Synthetic I/Q | None | 80% Acc | Black-box feature fusion |
| 2018 | Rajendran et al. [23] | LSTM | RML 2016.10a | None | 82% Acc | No temporal interpretability |
| 2024 | Wang et al. [28] | Complex-valued CNN-RNN (CC-MSNet) | RML 2016.101 | Multi-stream visualization | Avg. 62.86–71.12% Acc | Unquantified stream contributions |
| 2025 | Yi et al. [26] | Dual-attention Transformer | RML 2018.01a | Gradient-guided attention maps | 92.4% Acc | Heuristic attention analysis without causality validation |
| 2024 | Bhatti et al. [30] | Spectral–temporal Transformer | Synthetic radar | Attention weight visualization | 93.6% Acc | No causality validation |
| 2024 | Ren et al. [17] | AND–OR interaction theoretical framework | Synthetic (occluded samples) | Symbolic interaction primitive analysis | Proved three emergence conditions | Limited empirical validation of interaction primitives |
| Parameter | Value |
|---|---|
| Modulation Classes | 8PSK, BPSK, CPFSK, GFSK, PAM4, 16QAM, 64QAM, QPSK, AM-DSB, AM-SSB, WBFM |
| SNR Range | −20 dB:2 dB:18 dB |
| Sample Length | 128 |
| Dataset Split | Training:Validation:Test = 6:2:2 |
| Optimizer | Adam |
| Batch Size | 32 |
| Max Epochs | 300 |
| Initial Learning Rate | 0.001 |
| Loss Function | ReLU |
| SNR | Stability (SIV) | Third-Order Occlusion Sensitivity (SIV) | Reliable Interaction Ratio (SIV) | Stability (Shapley) | Occlusion Sensitivity (Shapley) | Reliability Ratio (Shapley) |
|---|---|---|---|---|---|---|
| −6 | 0.338 | 0.884 | 0.740 | 0.462 | 0.948 | 0.605 |
| −2 | 0.275 | 0.838 | 0.783 | 0.392 | 0.948 | 0.716 |
| 0 | 0.308 | 0.789 | 0.822 | 0.212 | 0.927 | 0.672 |
| 2 | 0.198 | 0.718 | 0.851 | 0.193 | 0.916 | 0.739 |
| 6 | 0.108 | 0.637 | 0.864 | 0.13 | 0.887 | 0.716 |
| 10 | 0.095 | 0.445 | 0.870 | 0.111 | 0.762 | 0.759 |
| 14 | 0.077 | 0.347 | 0.884 | 0.095 | 0.667 | 0.785 |
| 18 | 0.069 | 0.191 | 0.953 | 0.091 | 0.502 | 0.825 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Sun, S.; Zhang, H.; Liu, Y.; Qiao, Q. Multi-Feature AND–OR Mechanism for Explainable Modulation Recognition. Electronics 2025, 14, 2356. https://doi.org/10.3390/electronics14122356
Wang X, Sun S, Zhang H, Liu Y, Qiao Q. Multi-Feature AND–OR Mechanism for Explainable Modulation Recognition. Electronics. 2025; 14(12):2356. https://doi.org/10.3390/electronics14122356
Chicago/Turabian StyleWang, Xiaoya, Songlin Sun, Haiying Zhang, Yuyang Liu, and Qiang Qiao. 2025. "Multi-Feature AND–OR Mechanism for Explainable Modulation Recognition" Electronics 14, no. 12: 2356. https://doi.org/10.3390/electronics14122356
APA StyleWang, X., Sun, S., Zhang, H., Liu, Y., & Qiao, Q. (2025). Multi-Feature AND–OR Mechanism for Explainable Modulation Recognition. Electronics, 14(12), 2356. https://doi.org/10.3390/electronics14122356






