Abstract
Today, numerous advanced options exist for analyzing and measuring magnetic hysteresis loops and core loss across a broad spectrum of applications. Most of these systems are compact and ready to use, fulfilling the measurement and data processing requirements for laminated iron cores according to the standards. However, modeling newly developed materials with complex structures or the high-frequency behavior of iron cores, and the computation of dynamic hysteresis properties’ temperature dependence, are still challenging problems in the field. Moreover, these standardized measurement tools are relatively expensive, and most of them represent a black box that impedes research and further development. This paper presents the development of a cheap and accessible measurement system that is explicitly designed for recording the hysteresis properties of 3D-printed iron cores. The paper presents a comprehensive overview of the design process, components, circuitry, and simulations integral to this project. The paper presents a completed circuit simulation conducted using LTspice and validation of the prototype’s measurement performance. The measurements obtained with the proposed system show good agreement with those of the reference setup, demonstrating its accuracy and practical applicability.
1. Introduction
A precise understanding of the magnetic properties of employed materials is necessary to design and develop electrical machines. One of the most essential magnetic parameters is magnetic permeability, which is typically represented by the B–H curve of the material, describing the complex, nonlinear relationship between magnetic flux density (B) and magnetic field strength (H) [1]. Accurate knowledge of this material property is essential for precisely modeling core losses and optimizing the performance of the designed machine [2]. However, accurately modeling magnetic hysteresis numerically remains challenging in many cases. For instance, creating accurate numerical models for high-frequency excitation-based applications and accurately predicting the temperature-dependent behavior of laminated magnetic steel-based applications remain challenging tasks [3,4].
For electrical machines, additive manufacturing provides increased design freedom, including the ability to create arbitrarily shaped geometries with rapid prototyping and reduced material waste. The various additive technologies enable the creation of distinct composites with unique magnetic properties. Depending on the selected energy source, it is possible to print metals, ceramics, or polymers with high structural integrity in the desired shape. Due to exceptionally high manufacturing precision, the thickness of the additively manufactured layers can be smaller than 20–30 [5,6,7]. Electrical machines have been constructed using FeCo, FeNi, and FeSi composites, which offer favorable magnetic properties. Among these, FeSi with 6.5 wt.% silicon content is the most advantageous for reducing magnetic losses; however, this material is also the most rigid and sensitive to mechanical stress. The high silicon content significantly increases the electrical resistivity of the alloy, thereby reducing eddy current losses and enhancing overall efficiency in alternating magnetic fields. This makes it especially suitable for high-performance applications despite the trade-off in mechanical workability [5,8,9,10].
Measurement and modeling over broad thermal ranges remain experimentally demanding [11,12]. Likewise, many hysteresis models exhibit limited applicability when applied across different materials or geometries, restricting their generalization and predictive capability in simulation-driven design workflows [13]. Magnetic hysteresis measurements are essential for characterizing the energy loss and magnetic behavior of materials under varying conditions. These measurements are typically categorized into three types: static, dynamic, and DC hysteresis [14]. DC hysteresis measurements involve the application of a steady-state magnetic field to observe the material’s magnetization characteristics, thereby eliminating the complexities introduced by alternating fields. This approach is fundamental for understanding the basic magnetization and demagnetization processes in materials. Static hysteresis measurements are conducted under slowly varying or constant magnetic fields, assessing the material’s response without significant influence from time-dependent effects. They are ideal for evaluating intrinsic magnetic properties, where dynamic factors such as eddy currents are negligible. Dynamic hysteresis measurements are performed under rapidly varying magnetic fields, capturing the material’s behavior when subjected to high-frequency excitations. Dynamic measurements are crucial for applications involving alternating currents, as they account for time-dependent phenomena such as eddy currents and magnetic relaxation, which can lead to increased energy losses.
Temperature has a significant impact on hysteresis behavior across all measurement types. Temperature variations can alter magnetic anisotropy, coercivity, and saturation magnetization, thereby affecting the shape and area of hysteresis loops. For instance, studies have shown that the coercivity of Nd–Fe–B alloy films exhibits complex temperature dependence, with notable changes observed as the temperature varies. Similarly, research on hard magnetic materials suggests that temperature variations affect hysteresis properties, underscoring the importance of considering thermal effects during magnetic characterization. Furthermore, investigations into amorphous metals have demonstrated that both coercive force and permeability can be temperature-dependent, thereby affecting the material’s magnetic performance [15,16].
An extensive literature search was conducted to identify potential circuit solutions for measuring the hysteresis of magnetic cores. It can be established that there is limited literature on custom-designed and developed electronic devices or methods, including those for measuring powdered iron cores [17]. There are simpler methods for investigating these properties, such as the so-called Epstein frame. This method is used to determine the magnetic properties of laminated iron cores. The advantages and technical implementation of this method are discussed in several papers [18,19,20,21]. However, it has the disadvantage that it can only be applied to low frequencies and laminated iron cores.
In [22], the authors presented a LabVIEW-based measurement system and hardware (DAQ card). The measurement is performed on a sample equipped with two coils. The current in the excitation coil is measured via a shunt resistor, which is used to calculate the magnetic field strength. Meanwhile, the voltage is measured across the second coil, used to calculate the magnitude of the magnetic induction [23]. Many recent papers have been published that advance the field of magnetic hysteresis measurements. In [24], several measurement techniques and modeling approaches are presented for accurately capturing hysteresis characteristics in ferromagnetic materials. Ref. [25] evaluates various magnetic characterization methods, discussing their reliability and validity in measuring the interaction fields of magnetic nanowires. While [26] discusses the complexities of magnetic hysteresis, it emphasizes the need for advanced analysis methods to understand and predict hysteresis behavior in magnetic alloys. Ref. [27] introduces a modeling approach that accounts for phase lag and amplitude attenuation to better represent frequency-dependent hysteresis behaviors in magnetic materials.
The goal of the paper is to present a low-cost, improved magnetic hysteresis measurement system tailored for characterizing 3D-printed magnetic cores [28], offering a simpler alternative to conventional complex setups. The design incorporates targeted circuit enhancements—such as improved amplifier stability, active current limiting with feedback, and an optimized frequency response—making it suitable for reliable B-H curve acquisition in research and prototyping environments. This work addresses the practical need for accessible instrumentation in the testing of novel magnetic materials. The structure of the paper is as follows: the first sub-section describes the industrial equipment available on the market. The second section presents the basic idea of the circuit we designed and built, along with the design requirements. The subsequent subsections describe, in detail, the design process for each circuit unit. The third section presents the simulation results of the proposed circuit in the LTspice environment. The fourth section provides a brief description of the PCB design and presents a 3D visualization of the circuit. In the last section, we present the laboratory measurement of the circuit, which includes a THD (Total Harmonic Distortion) test of the proposed circuit and a test of the magnetic hysteresis of a 3D-printed iron core using both a conventional measurement system and the measurement system presented in our paper. The measured results are analyzed and compared.
Industrial Equipment for Hysteresis Measurement of Magnetic Cores
Lots of high-accuracy professional industrial equipment is available for measuring laminated and other types of magnetic cores. The main disadvantages of this equipment are its high price and its black-box behavior, which is a significant issue, particularly in academic environments. These devices will be analyzed and investigated primarily from a technical perspective. The following is a non-exhaustive list of equipment available on the market.
The Eckel Robograph RE [29] is a high-precision hysteresisgraph designed for measuring hard magnetic materials, using a low-noise power amplifier to generate controlled magnetizing fields. It supports a sampling rate of up to 2000 Hz, and its redesigned yoke system delivers magnetizing fields up to 1 Tesla (T) while significantly reducing the system weight. Its signal conditioning and digital control ensure measurement repeatability better than 0.1%, compliant with IEC and ASTM standards.
The IWATSU SY-8218 is a high-speed B-H analyzer that uses a built-in current generator (power amplifier) to excite magnetic samples with sine or square waveforms from 10 Hz to 10 MHz. It supports excitation up to ±6 A and ±200 V, and automatically measures key magnetic parameters, including core loss, permeability, and coercivity, using the Cross Power Method. The system features an 8.4-inch TFT display, built-in demagnetization, and wide parameter control, making it ideal for the detailed magnetic characterization of ferrites, amorphous alloys, and laminated steels [30]. A similar hysteresis curve measurement device is the TD8220 [31].
Amplifier-based measurement systems, such as the Robograph RE, are well suited for quasi-static and low-frequency magnetic characterization but struggle with high-frequency performance due to their limited bandwidth and potential phase distortion. Their reliance on voltage-controlled excitation makes it harder to maintain stable magnetic field conditions at elevated frequencies, leading to inaccuracies in dynamic loss or permeability measurements. In contrast, current generator-based systems such as the IWATSU SY-8218 offer precise control over the excitation current, making them better suited for high-frequency or broadband analysis. However, these systems often operate as black boxes, limiting user control over waveform customization, timing, or synchronization with external systems. Additionally, their performance is sensitive to proper fixture calibration and can be less transparent when troubleshooting advanced or non-standard applications.
The REMAGRAPH® C is a precision hysteresisgraph developed by MAGNET-PHYSIK for measuring the quasi-static magnetic properties of soft magnetic materials. It supports a wide range of sample geometries, including Epstein frames, strips, rods, and toroidal cores, in compliance with IEC 60404 and ASTM standards. The system uses a voltage-controlled power amplifier to drive the magnetizing coil, providing stable excitation for accurate hysteresis loop acquisition. Unlike current generator-based systems, the excitation current depends on the sample’s impedance, requiring careful calibration to ensure reliable field control. The instrument achieves high precision through the use of low-noise analog signal conditioning, digitally compensated feedback loops, and a high-resolution fluxmeter for accurate B-field integration. Field strengths and flux densities can be measured with resolutions down to 0.01 A/m and 1 µT, respectively, depending on the coil design. Drift compensation, automatic demagnetization, and signal averaging techniques further improve measurement repeatability and long-term stability. With typical repeatability better than 0.1%, REMAGRAPH® C is widely used in industrial quality control and material certification workflows for electrical steels, ferrites, and soft magnetic alloys [32].
The OMICRON CMS 356 is a high-precision, voltage-controlled amplifier designed for applications such as protection relay testing, power system simulation, and the excitation of magnetic materials. It operates by amplifying low-level analog voltage signals (typically ±10 V) to produce high-output voltages or currents, depending on the connected load. As a voltage-controlled device, the output current is not fixed but varies with the load impedance, meaning that in magnetic measurements, the magnetizing current—and, thus, the magnetic field strength (H)—must be measured directly using an external current sensor (e.g., a shunt resistor). The amplifier offers excellent precision, with voltage and current accuracy typically better than %, and minimal phase error, making it suitable for highly sensitive or multi-phase systems. Its high fidelity and flexibility make it a powerful tool in experimental setups, although it requires careful calibration when precise magnetic field control is needed [33].
2. Requirements and Design of Electrical Circuit
To design the system, the initial parameters had to be defined. In our case, these were determined by the parameters of the 3D-printed magnetic cores, indirectly including the values of voltage, current, and frequency. These numerical values are given in Table 1. The 3D-printed iron cores we developed are best tested at low frequencies and typically under magnetic field strengths of a few thousand A/m to obtain full hysteresis loops. The choice of supply voltage was also influenced by the low operating frequency—through the inductive reactance—and the desired test current. The parameters presented in Table 1 largely depend on whether they are tailored specifically to the 3D-printed iron cores developed in this work or refer to a more general B-H hysteresis measurement setup.

Table 1.
Design parameters of the system.
It was also required to be mains-powered, have its own power supply, be platform-independent and have active electronic short-circuit protection (LED indicator).
The development of our circuit was fundamentally inspired by the schematic of a power amplifier-based measurement system published in [17]. While that design provided a solid foundation, we identified several limitations that required targeted improvements to enhance its overall performance. One significant issue in the original circuit was the parallel connection of four power transistors (TR1–TR4 in [17]), which led to inevitable current imbalances among the devices. To address this, we added individual emitter resistors to each transistor, promoting a more uniform distribution of the load current. In addition, we found the initial biasing of the differential amplifier—implemented using transistors TR9 and TR10 in [17]—to be suboptimal. We therefore modified the amplifier’s frequency response and incorporated a current-limiting circuit to improve its reliability and functionality. These enhancements were essential for achieving the performance required in our measurement system.
A block diagram of the proposed hysteresis measurement system is shown in Figure 1. The entire setup can be divided into two main parts: the power supply, which provides energy to the circuit, and the measurement system itself. The basic principle of operation is as follows: A sinusoidal voltage signal, with appropriate amplitude and frequency, is applied to the input of the amplifier via a signal generator. The amplifier then produces a test signal with the required characteristics, which is fed into the primary winding of the test sample. The induced voltage is measured on the secondary winding, while the current in the primary circuit is monitored using a LEM current sensor. A digital oscilloscope is used to acquire and process the measured signals. The following sections describe each subsystem in detail.
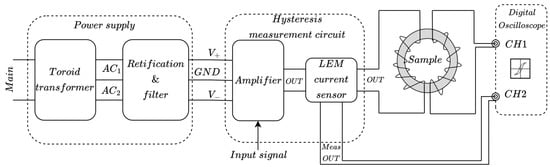
Figure 1.
A block scheme of hysteresis measurement system, including the power supply and the hysteresis measurement system.
2.1. Design of Power Supply
A key design requirement was that the measurement system should operate with its own dedicated mains power supply. In earlier prototypes, power was provided using a laboratory power supply unit (QPX600D) [34], which is suitable for a broad range of applications. However, this approach was ultimately deemed unsuitable due to the need for greater mobility and system integration. Consequently, the use of an external lab power supply was abandoned.
In the final design, the system is connected directly to the mains via a toroidal transformer (230 VAC, 50 Hz, as used in Hungary). The transformer’s power rating was selected based on the electrical requirements of the amplifier. The power supply unit delivers the necessary voltage and current levels for amplifier operation and functions as a fully independent subsystem within the overall measurement setup.
The key parameters of the selected toroid transformer are summarized in Table 2.

Table 2.
Parameters of the transformer (power supply).
The secondary side of the transformer had a symmetrical winding ( and ), to which the two Graetz bridges [35] and the filter capacitors are connected, which, together, formed a symmetrical power supply (, , ). Fuses were also used between the secondary winding and the Graetz bridge. In the selection of the bridge rectifiers, safety was a key consideration, as was the ability to connect to the heat sink. The rectified signal was filtered with 3 × 4700 capacitors; further, to reduce high-frequency noise, we implemented a 100 nF ceramic capacitor in the circuit. The value of the capacitances was chosen based on a simulation (LTspice) and previous tests. The circuit was also equipped with an appropriately sized heat sink.
The output of the circuit shows the following voltage symmetrically:
where is the stabilized output DC voltage, is the secondary AC voltage of the transformer, and is the forward voltage drop of the rectifier diode at 7 A and 125 °C (assuming the worst case situation) [35].
A circuit diagram of the designed power supply with the real components, created in Altium Designer, is shown in Figure 2.
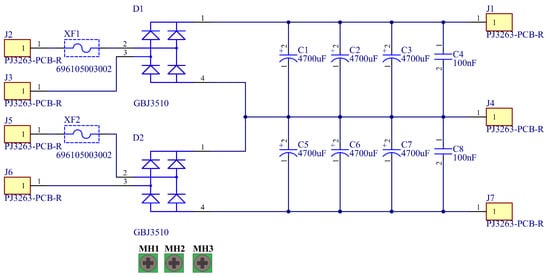
Figure 2.
A schematic of the symmetrical power supply, created in Altium Designer, including the electronic parts.
2.2. Design of Amplifier Circuit
A block diagram of the proposed circuit (Figure 3) shows the roles of the three main parts of the circuit. The first block is used to set the preamplification of the circuit between about one and ten times, the second block is used to compensate for the output offset error, and the third block is the main amplifier circuit, including the current measuring module.
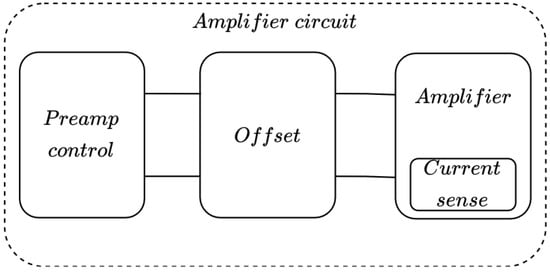
Figure 3.
A block scheme of the amplifier circuit, including the preamp, offset, and amplifier circuits.
The schematic of the circuit is based on a low-cost amplifier-based hysteresis measurement device, which was presented in [17].
A schematic of the control and offset adjustment circuit is shown in Figure 4. The control section (U4A) is a negative-feedback operational amplifier configuration, used to fine-tune the gain range of the system. The second section (U4B) implements offset compensation. Both functions are realized using a dual-operational amplifier housed in a single package. The NE5532 was selected for this purpose due to its favorable supply voltage range and stable gain characteristics [36]. The NE5532 operational amplifier is well suited for use in audio-frequency applications thanks to its low noise, low distortion, and wide supply voltage range.
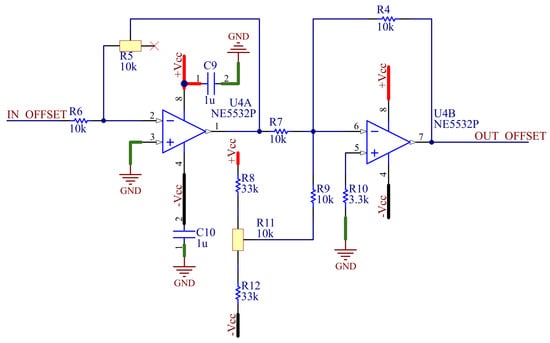
Figure 4.
Schematic of control device and offset, created in Altium Designer, built with operational amplifier.
The last unit is the amplifier itself, which includes the current measurement. A circuit diagram of the amplifier is shown in Figure 5.
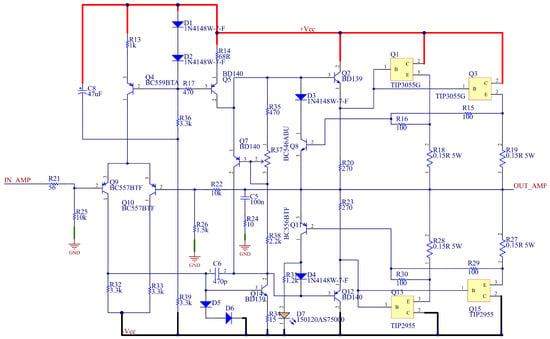
Figure 5.
Schematic of amplifier with current measurement, created in Altium Designer, including electronic parts.
The operation and structure of the main amplifier circuit are as follows: the input signal is processed by a differential amplifier constructed from PNP BJTs. Its stable operation is maintained by a current generator and current mirror formed of Q4, Q5, Q6, D1, D2, R13, R14, and R17. The steady-state current of the output transistors is set using Q7 and the VR1 potentiometer. Q7 is thermally coupled to the heat sink shared with the output transistors to ensure similar temperature behavior and maintain a stable bias point.
Q14 functions as the main amplification stage of the circuit. Q2 and Q12 act as drivers for the power transistors (Q1, Q3, Q13, Q15). The emitter resistors R18, R19, R27, and R28 are used to ensure equal current sharing among the parallel-connected power transistors.
Short-circuit protection is implemented using Q8, Q11, and resistors R15, R16, R29, and R30. This protection is triggered when the output current exceeds approximately 10 A, at which point the DS1 LED indicator lights up. To stabilize the amplifier’s response under reactive load conditions, a Zobel network composed of C5 and R24 is included.
The voltage gain of the amplifier can be adjusted using the resistors R22 and R26, as described below:
where is the voltage gain.
The choice of passive elements was based on the dissipation on them, which was determined by Ltspice-based simulation. For the encapsulation, the non-temperature-critical resistors were chosen to be 1206 in size to allow for hand soldering.The semiconductors were selected based on empirical and simulation data, taking into account the circuit on which this research is based. For example, the “classic 2N3055” TO3 package was abandoned and TO247 was chosen instead for heat sink mounting. Measuring the current is a critical point in the circuit. Based on previous experience and good technical characteristics, which include very good accuracy and linearity, low gain drift, a wide bandwidth, and a fast response time, the LEM family of sensors was chosen. Taking into account the value of the current to be measured, the LEM CASR15-NP type sensor was chosen for current measurement purposes. Its technical parameters are available in the datasheet of the device [37]. As shown in Figure 6, the current sensor operates with its own stabilized supply voltage, which is provided by an integrated voltage regulator of the type 7805. A low-pass Sallen-key-type filter with a cut-off frequency of 20 kHz was also designed for the output of the sensor. This is of course later modified by R1, R2, C3, and C4 if required. The operational amplifier of the low-pass filter does not require a separate stabilized power supply, since the supply voltage range of NE5532 is up to .
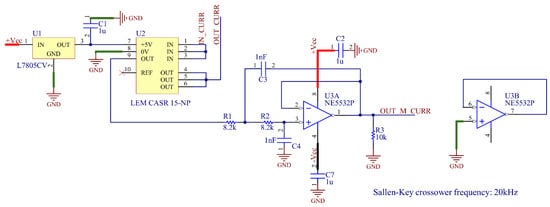
Figure 6.
A schematic of the current-sensing circuit, created in Altium Designer: the LEM sensor and the low-pass filter.
3. Simulation Results
In this chapter, we check that the circuit meets the technical requirements by carrying out the following:
- Gains verification;
- Current limiter verification;
- Frequency response verification (Bode plot).
A simulation circuit diagram is shown in Figure 7. In the circuit simulation, the following simplifications were applied: the load was represented by a simple resistor, and the input signal was replaced by an ideal voltage generator (V3) at the input of the amplifier. The simulation of all components was based on the realistic SPICE models obtained from the manufacturers’ websites.
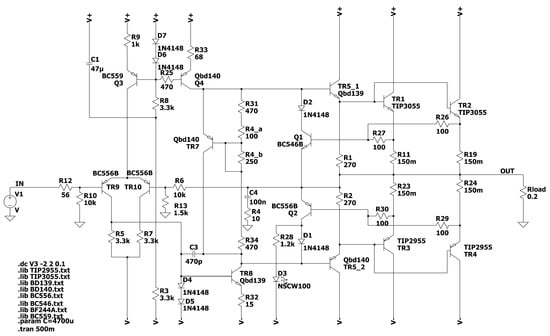
Figure 7.
Amplifier schematic in Ltspice, with components used in real applications.
The first test is a basic simulation test to check the operation of the circuit. As can be seen in Figure 8, the output voltage of the amplifier follows Equation (2): an excitation signal of 1 V results in an output voltage of 7.54 V.
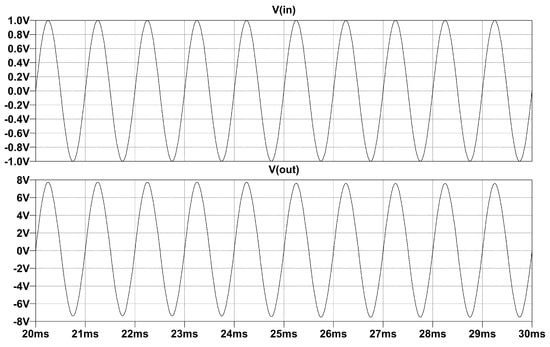
Figure 8.
Simulation results of gains verification test in Ltspice, along with input and output signals of amplifier.
The second test is very important, as the 3D-printed iron cores under testing operate in a higher frequency range (similar to powdered iron cores). Therefore, the circuit must operate correctly in all frequency ranges. To verify this, the frequency response of the amplifier was simulated (Bode diagram). The frequency response characteristics of the amplifier can be influenced by the value of capacitor C3, as shown in Figure 8.
The frequency range was set to extra wide for the simulation (1 kHz–100 kHz). The simulation results are shown in Figure 9. The results clearly show that the output voltage gain is close to the calculated and simulated values (, given here in dB (17.36 dB)). The gain is stable within the desired range.
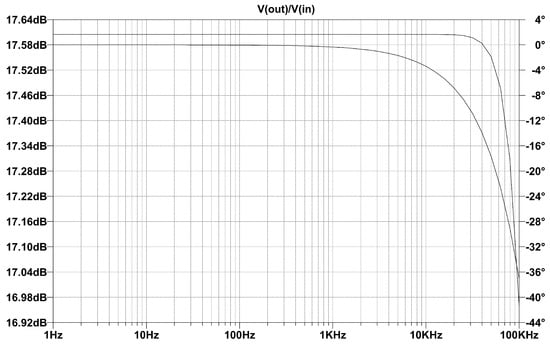
Figure 9.
Simulation results of frequency response (Bode-diagram) in Ltspice.
The third simulation demonstrates/validates the operation of electronic overcurrent protection. As shown before, the output current is limited at A. To demonstrate this, a DC simulation was run where the input excitation signal (V3) was varied between −2 V and 2 V and the load was chosen to be extremely low ( ) to achieve extreme load conditions. The simulation results in Figure 10 show that the protection circuit works properly, both in the positive and negative ranges: the output current is limited to ±10 A.
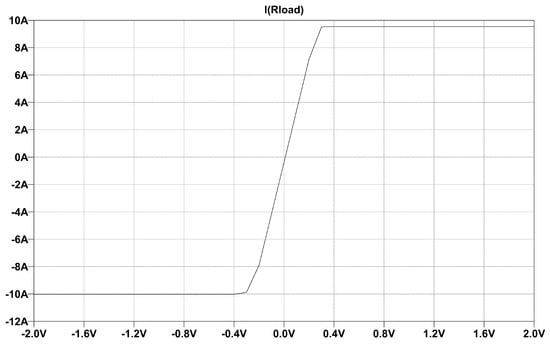
Figure 10.
Simulation results of current limiter in Ltspice.
These simulation results have also been used for other design purposes, which are not reported in detail to save space. These include different current and power losses, which can be used to modify the circuit subsections as required and to select the required heat sinks.
4. Printed Circuit Board Design
During the design process, the goal was to create a relatively inexpensive and modular system that can be used to automatically test and compare the characteristics of B-H curves in 3D-printed cores, which are manufactured by different technologies. The modularity of the system means that the power supply, the power amplification, and the measurement module are separated; therefore, each module of the proposed system can be developed further separately, or the proposed power amplifier can be used with other compatible labor devices, and the proposed experiments are reproducible. Also, taking into account manufacturability considerations, the PCB circuit was designed in two layers (top and bottom conductor layers) with special attention to the high-current parts. The circuit designs were created using Altium Designer software 26.5.2. The circuit layouts are not disclosed to save space. The 3D view of the designed printed circuit board (PCB) for the power amplifier circuit is shown in Figure 11. The proposed image was created in Altium Designer, and contains all of the used parts except the heat sink [38].

Figure 11.
A three-dimensional view of the realized hysteresis measurement circuit, created in Altium Designer.
The PCB designs were prepared in accordance with the following relevant standards of the Institute for Printed Circuits (IPC): IPC-2221, IPC-2251, IPC-2152, and IPC-2152. The assumptions from IPC-2221 [39] consider the minimum distances, trace widths, and mechanical tolerances to ensure the manufacturability and the reliability of the proposed design. The IPC-2251 [40] standard was followed to ensure the modularity and reusability of the PCB. The thermal dissipation rules were also considered for the trace width calculations according to IPC-2152 [41], while the proposed formulas and design rules from IPC-2141 [42]) were used to determine the signal fidelity.
5. Laboratory Test
5.1. Measurement Sample and Laboratory Setup
The proposed system’s benchmark was established by measuring 3D-printed toroidal cores, which were previously carefully analyzed and measured by a validated measurement system. The examined toroidal core is relatively small; its inner diameter is mm, outer diameter is mm, and height is mm. It is made from Fe-6.5 wt% Si powder, with a laser powder bed fusion-based 3D printing technology with an EOSINT M270 machine (EOS GmbH, Offenbach am Main, Germany). In the preparation stage, powder quality was assessed by the GB/T 19077-2016 standard [43] using the laser diffraction and scanning electron microscopy (SEM) techniques. A more detailed description of the manufacturing process and a description of the performed laboratory tests are published in [28,44]. The measurements were performed at room temperature and in a built state; no heat treatment was performed to improve its magnetic parameters. The sample was prepared in the same way as the previous measurements. A primary and a secondary wounding were placed on the toroidal core, with primary and secondary turns applied.
The manufactured PCB-based hysteresis measurement device with the necessary power supply, signal generator, and measurement device, which was an oscilloscope in our benchmark case, can be seen in Figure 12. The Keysight 33500B signal generator provided the sinusoidal control signal for the hysteresis measurement circuit, while the toroidal core-based power supply powered it. A Keysight DSOX2022A oscilloscope measured the signal of the LEM-type current sensor and the voltage of the sample secondary coil. To reduce measurement noise and increase the accuracy of the recorded measurements, a digital oscilloscope performed signal averaging over four complete memory recordings during the measurements.

Figure 12.
The measurement setup which was used for the benchmark used the proposed hysteresis measurement circuit. The different parts of the measurement setup are denoted as follows: 1. power supply, 2. the measured sample, 3. hysteresis measurement circuit, 4. digital oscilloscope, 5. signal generator.
5.2. Reference Measurements
To evaluate the performance of the proposed system, the measurements with the system were compared to those within a reference system, which used a voltage-controlled current generator to obtain the sinusoidal excitation current on the primary coil of the sample. The generator was controlled and the primary current, and the secondary voltage was measured using a National Instruments data acquisition card in a PC. The measurement control and data processing were performed using Labview. A more detailed description of the reference system can be found in [4,45].
Based on the measured current and voltage waveforms, the magnetic field density and field strength can be determined using Equations (3) and (4),
where A is the cross-sectional area of the toroidal sample, and is the effective path length of the magnetic field, and the definite integral was determined using the trapezoidal numerical integration rule,
with k being the discrete time index and the sampling period.
From the determined magnetic field density and field strength, the total loss due to the hysteresis of the toroid core can be calculated as
where V is the volume of the core, and f is the excitation frequency.
For the comparison, the sample was measured at a sinusoidal magnetic field strength of 4000 at 200 Hz. The primary current required to generate this field strength was calculated by rearranging Equation (3). This current reference was achieved by adjusting the amplitude of the system’s sinusoidal output voltage accordingly using a signal generator.
For the measurement, the output voltage offset was set as close to zero as possible using the R11 potentiometer shown in Figure 4. The acquired offset for the measurement was about 15 mV, which is negligible enough and can be compensated for during data processing in Matlab.
As an initial test for the measurement system, a purely ohmic resistor was used as the load, and the current and voltage were measured using a digital oscilloscope. It was found that there is about a 32 delay between them, which must be compensated for during the B-H curve measurement of the toroid sample.
The primary current and secondary voltage measured using the proposed and the reference systems can be seen in Figure 13a. In the Figure, the phase delay caused by the proposed system is compensated for.
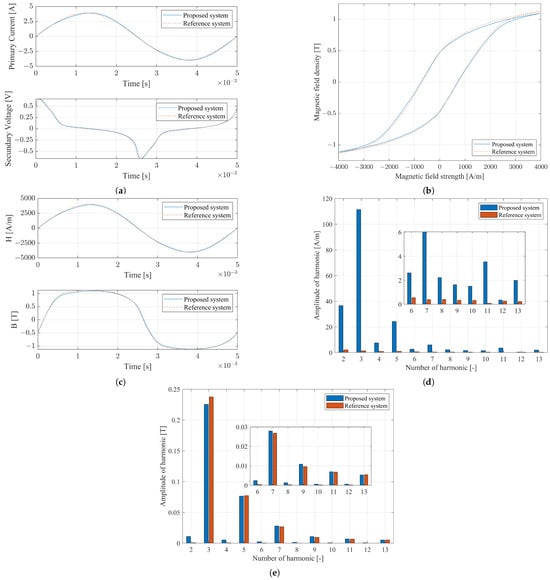
Figure 13.
(a) The measured current and voltage using the proposed and reference measurement systems. (b) The measured hysteresis curve using the proposed and reference measurement systems. (c) The measured magnetic field strength and magnetic field density with the proposed and reference measurement systems. (d) The harmonic content of the measured magnetic field strength. (e) The harmonic content of the measured magnetic field density.
A comparison of the measured hysteresis curve with that obtained using the reference system can be seen in Figure 13b). It can be observed that, with phase shift compensation, the measured hysteresis loop closely follows the reference curve. This indicates that the proposed system, when calibrated appropriately, can achieve a high degree of accuracy. Using Equation (6), the total magnetic loss in the sample was calculated from both systems. The measured loss with the proposed setup was mW, while the reference system yielded mW. Without phase compensation, however, the loss would increase significantly to mW. This overestimation highlights the critical role of correcting phase errors in voltage and current measurement, especially in systems where time alignment is not inherently guaranteed.
These results show that, after compensation, the loss measured with the proposed system deviates by less than from that of the reference system, which is considered accurate and based on a voltage-controlled current source architecture. Such a small deviation demonstrates the applicability of the presented low-cost system for practical B-H characterization tasks, and validates its performance compared to more complex commercial alternatives. Although not explicitly benchmarked against commercial hysteresisgraphs due to resource constraints, the measured accuracy falls within acceptable limits reported in the literature for laboratory-grade systems [28,45].
Figure 13c–e show the time-domain waveforms and harmonic content of the measured magnetic field strength and flux density. While the measured magnetic field strength using the proposed system slightly deviates from a pure sine wave due to the non-ideal behavior of the voltage-controlled voltage source under nonlinear loading, the fundamental characteristics are preserved. This deviation is quantified using the Total Harmonic Distortion (THD), which is for the proposed system and only for the reference system. This elevated THD arises from the limited linearity of the excitation circuit and the amplifier’s behavior at higher frequencies.
In contrast, the magnetic flux density—which directly integrates the measured voltage—shows very similar harmonic content between both systems, with THD values of and , respectively. This suggests that, despite the increased harmonic content in the magnetic field strength, the flux density—and, thus, the shape of the hysteresis loop—remains largely unaffected under the test conditions. However, at higher excitation amplitudes or frequencies, this nonlinearity could become more pronounced, potentially affecting the measured losses.
In summary, the proposed system demonstrates promising results in terms of hysteresis loop fidelity and loss calculation, aligning closely with a reference-grade setup. While some limitations remain, such as the sensitivity to phase shifts and excitation nonlinearity, the accuracy achieved places the system within the range of practical usability for laboratory and development purposes. With further refinements—such as implementing a voltage-controlled current source and improving component precision—the system has the potential to achieve commercial-grade performance for a fraction of the cost.
6. Conclusions
The aim of this research was to replace expensive and sometimes complicated hysteresis measurement systems with a low-cost and simple measurement system, without compromising the measurement results. To this end, the circuit, which is the basic subject of this paper, was improved in several ways: the paralleling of the output transistors was improved (emitter resistors), and the working point of the input differential amplifier was improved (current generator, filter capacitance etc.). The circuit was equipped with active current limiting (short-circuit protection), for which a feedback (LED) circuit was developed. The frequency response of the amplifier was also modified to fit our application. Apart from a few minor development mistakes, the circuit works perfectly. These errors include the fact that the operational amplifier circuits do not have a separate stabilized power supply (e.g., 7812, 7912) or their own elementary voltage stabilizer (e.g., Zener or TVS diode). This is a problem because the circuit is transformer-powered, so if the primary voltage is higher, the secondary voltage will be higher. This happened several times during testing (we obtained 242 V mains voltage instead of the rated 230VAC due to solar panels in the building). Another problem is that the offset and gain potentiometers are not precise, which makes them difficult to set accurately. It is advisable to replace them with better-quality ones in the future. During the development and testing, we made several observations. In the “classical” BH measurement, the excitation current of the test coil is kept constant. For a given circuit, the constant quantity is the output voltage of the amplifier, so the current is only indirectly affected. The supply voltage limits the measurement, which can cause problems, especially at higher frequencies. A solution to this may be to increase the supply voltage of the circuit and replace the necessary components. Another possible source of problems is that the sensitivity of the current sensor is 41.7 mV/A, which can make measurements difficult at low currents. Based on the experience gained in this study, a future goal could be to improve the presented circuit or to create a voltage-controlled current generator-like circuit while keeping the proposed circuit’s beneficial features.
Author Contributions
Conceptualization, T.O. and M.C.; methodology, T.O., T.H., and M.C.; software, T.H.; validation, T.H. and M.C.; formal analysis, T.O., T.H., and M.C.; investigation, T.O., T.H., and M.C.; resources, M.C.; data curation, T.H.; writing—original draft preparation, T.H. and M.C.; writing—review and editing, T.O.; visualization, T.H.; supervision, T.O.; project administration, T.O.; funding acquisition, T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research, Development, and Innovation Fund of Hungary—which was financed under the FK funding scheme. Project no. 147030.
Data Availability Statement
The original contributions presented in this study are included in the article material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hubert, A.; Schäfer, R. The Physics of Ferromagnetism; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Jiles, D. Review of magnetic hysteresis modeling. IEEE Trans. Magn. 2015, 51, 1–7. [Google Scholar]
- Jiang, D.; Burgos, R.; Wang, F.; Boroyevich, D. Temperature-dependent characteristics of SiC devices: Performance evaluation and loss calculation. IEEE Trans. Power Electron. 2011, 27, 1013–1024. [Google Scholar] [CrossRef]
- Kuczmann, M.; Orosz, T. Temperature-Dependent Ferromagnetic Loss Approximation of an Induction Machine Stator Core Material Based on Laboratory Test Measurements. Energies 2023, 16, 1116. [Google Scholar] [CrossRef]
- Orosz, T.; Horváth, T.; Tóth, B.; Kuczmann, M.; Kocsis, B. Iron loss calculation methods for numerical analysis of 3D-printed rotating machines: A review. Energies 2023, 16, 6547. [Google Scholar] [CrossRef]
- Sarap, M.; Kallaste, A.; Shams Ghahfarokhi, P.; Tiismus, H.; Vaimann, T. Utilization of additive manufacturing in the thermal design of electrical machines: A review. Machines 2022, 10, 251. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.S.; Podgornovs, A.; Kallaste, A.; Cardoso, A.J.M.; Belahcen, A.; Vaimann, T.; Tiismus, H.; Asad, B. Opportunities and challenges of utilizing additive manufacturing approaches in thermal management of electrical machines. IEEE Access 2021, 9, 36368–36381. [Google Scholar] [CrossRef]
- Liu, L.; Ge, T.; Ngo, K.D.; Mei, Y.; Lu, G.Q. Ferrite paste cured with ultraviolet light for additive manufacturing of magnetic components for power electronics. IEEE Magn. Lett. 2018, 9, 5102705. [Google Scholar] [CrossRef]
- Kokkinis, D.; Schaffner, M.; Studart, A.R. Multimaterial magnetically assisted 3D printing of composite materials. Nat. Commun. 2015, 6, 8643. [Google Scholar] [CrossRef]
- Kallaste, A.; Vaimann, T.; Rassãlkin, A. Additive design possibilities of electrical machines. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 November 2018; IEEE: Washington, DC, USA, 2018; pp. 1–5. [Google Scholar]
- Tiismus, H.; Kallaste, A.; Belahcen, A.; Tarraste, M.; Vaimann, T.; Rassõlkin, A.; Asad, B.; Ghahfarokhi, P.S. AC Magnetic Loss Reduction of SLM Processed Fe-Si for Additive Manufacturing of Electrical Machines. Energies 2021, 14, 1241. [Google Scholar] [CrossRef]
- Kallaste, A.; Tiismus, H.; Belahcen, A.; Rassõlkin, A.; Vaimann, T.; Arumägi, E. Frequency dependence of magnetic losses in Fe–Si alloy produced by additive manufacturing. J. Magn. Magn. Mater. 2021, 537, 168159. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Luginger, D.; Ebner, M.; Pirker, B.; Schrödl, M. Design optimization of electrical machines by finite-element-based surrogate models including magnetization characteristics. IEEE Trans. Ind. Electron. 2018, 65, 1575–1584. [Google Scholar] [CrossRef]
- Bertotti, G. Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Li, W.F.; Sepehri-Amin, H.; Sakuma, N.; Hono, K. Temperature dependence of coercivity in Nd–Fe–B alloy films. J. Magn. Magn. Mater. 2003, 266, 220–226. [Google Scholar]
- Ge, T.; Zhang, Z.; Zhao, Z.; Fu, Z. Temperature dependence of the magnetic properties of hard magnetic materials. J. Magn. Magn. Mater. 2001, 234, 350–356. [Google Scholar] [CrossRef]
- Munoz, V.; Martinez, M.C.; Such, V. Improved systems for the measurement of hysteresis loops: DC and AC characterisation. J. Phys. Sci. Instrum. 1987, 20, 861. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Jiang, Y. Effect of Cutting Stress on Magnetic Properties of Non-oriented Electrical Steel. In Proceedings of the 2023 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 27–29 October 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Nemeth, Z.; Kuczmann, M. Measuring and simulating magnetic characteristics using epstein frame. Pollack Period. Pollack Period. 2018, 13, 15–26. [Google Scholar] [CrossRef]
- Parent, G.; Penin, R.; Lecointe, J.P.; Brudny, J.F.; Belgrand, T. Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels. Sensors 2016, 16, 826. [Google Scholar] [CrossRef]
- Koprivica, B.; Milovanovic, A.; Brkovic, V. Electrical steel testing using modified Epstein frame. In Proceedings of the International Scientific Conference, Gabrovo, Bulgaria, 18–19 November 2016; pp. 18–19. [Google Scholar]
- Mohammadi Fathabad, S.; Shahri, F. BH hysteresis measurement system for thin soft magnetic materials. Measurement 2021, 172, 108896. [Google Scholar] [CrossRef]
- Guo, P.; Huang, W.; Feng, X.; Zhang, Z.; Liu, Y. Hysteresis Measurement and Generic Modeling of Magnetostrictive Materials Under High-Frequency Excitation and High-Intensity Bias Field. Measurement 2023, 210, 112572. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, X.; Zhao, Z.; Zou, X.; Xiao, Y.; Li, G. Measurement and modeling of hysteresis characteristics in ferromagnetic materials. AIP Adv. 2019, 9, 025111. [Google Scholar] [CrossRef]
- Kouhpanji, M.R.Z.; Stadler, B.J.H. Assessing the reliability and validity ranges of magnetic characterization methods. arXiv 2020, arXiv:2003.06911. [Google Scholar]
- Balakrishna, A.R. Rethinking hysteresis in magnetic materials. MRS Commun. 2024, 14, 835–845. [Google Scholar] [CrossRef]
- DeCamp, M.F.; Bhatt, S.; Hossain, M.T.; Wu, W.; Jungfleisch, M.B. Demonstration of high-throughput magnetic hysteresis measurements based on THz emission. J. Appl. Phys. 2023, 134, 233901. [Google Scholar] [CrossRef]
- Kocsis, B.; Orosz, T. Frequency- and Temperature-Dependent Uncertainties in Hysteresis Measurements of a 3D-Printed FeSi wt6.5% Material. Sensors 2024, 24, 2738. [Google Scholar] [CrossRef] [PubMed]
- Eckel Magnet Test Equipment. Robograph RE; Eckel Magnet Test Equipment: Berge, Germany, 2025. [Google Scholar]
- Iwatsu Electric Co., Ltd. B-H Analyzer SY-8218; Iwatsu Electric Co., Ltd.: Tokyo, Japan, 2025. [Google Scholar]
- Zhao, H.; Zhao, X.; Xu, S.; Liu, W. Energy Loss Prediction of Soft Magnetic Materials Based on Nonlinear Preisach Model. In Proceedings of the 2022 IEEE 20th Biennial Conference on Electromagnetic Field Computation (CEFC), Virtual, 24–26 October 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Magnet-Physik Dr. Steingroever GmbH. Remagraph® C; Magnet-Physik Dr. Steingroever GmbH: Cologne, Germany, 2023. [Google Scholar]
- Omicron Electronics GmbH. CMS 356 Voltage and Current Amplifier; Omicron Electronics GmbH: Klaus, Austria, 2023. [Google Scholar]
- Aim-TTi (Aim and Thurlby Thandar Instruments). QPX Series Power Supply Datasheet. 2018. Available online: https://www.aimtti.com/product-category/dc-power-supplies/aim-qpxseries (accessed on 14 May 2025).
- Diodes Incorporated GBJ3510-35A Glass Passivated Bridge Rectifier Datasheet. Product Number: GBJ3510. 2015. Available online: https://www.smc-diodes.com/propdf/GBJ35005-GBJ3510%20N1805%20REV.A.pdf (accessed on 14 May 2025).
- Texas Instruments NE5532, SA5532 Dual Low-Noise Operational Amplifiers Datasheet. Document No. SBOS137D. 2015. Available online: https://www.ti.com/lit/ds/symlink/ne5532.pdf (accessed on 14 May 2025).
- LEM International SA CASR Series Current Transducers Datasheet. CASR Series. 2017. Available online: https://www.lem.com/sites/default/files/products_datasheets/casr_series.pdf (accessed on 14 May 2025).
- Altium Limited. Electronic Design Automation (EDA) Software for PCB Design; Altium Designer; Altium Limited: San Diego, CA, USA, 2024. [Google Scholar]
- IPC-2221; Generic Standard on Printed Board Design. Technical Report IPC-2221; IPC—Association Connecting Electronics Industries: Bannockburn, IL, USA, 2003; Supersedes IPC-D-275.
- IPC-2251; Design Guide for Display and Interface Portability of Electronic Design. Technical Report IPC-2251; IPC—Association Connecting Electronics Industries: Bannockburn, IL, USA, 2003; Supplementary to IPC-2221 series.
- IPC-2152; Standard for Determining Current-Carrying Capacity in Printed Board Design. Technical Report IPC-2152; IPC—Association Connecting Electronics Industries: Bannockburn, IL, USA, 2009; Replaces IPC-2221 internal trace current guidelines.
- IPC-2141; Design Guide for High-Speed Controlled Impedance Circuit Boards. Technical Report IPC-2141; IPC—Association Connecting Electronics Industries: Bannockburn, IL, USA, 1996; Predecessor to IPC-2152 for impedance-related current carrying.
- GB/T 19077-2016; Particle Size Analysis—Laser Diffraction Methods. Chinese National Standard: Beijing, China, 2016.
- Kocsis, B.; Windisch, M.; Mészáros, I.; Károly Varga, L. 3D printing parameters optimization for Fe-6.5 wt%Si. J. Magn. Magn. Mater. 2024, 592, 171829. [Google Scholar] [CrossRef]
- Kuczmann, M. Fourier transform and controlling of flux in scalar hysteresis measurement. Phys. B Condens. Matter 2008, 403, 410–413. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).