Quantitative Analysis and Verification of Edge Computing Offloading Strategy Based on Probabilistic Model Checking

Abstract

Edge computing has become a key framework for meeting the demands of low latency and high reliability across various applications. To ensure efficient task execution in edge computing, many offloading strategies have been proposed; however, most lack quantitative analysis and formal verification to guarantee their correctness. This paper addresses this gap by presenting an integrated offloading strategy that combines delay-based, energy-efficient, and energy-delay trade-off approaches, enhancing both the clarity and verifiability of offloading methods. Furthermore, we apply probabilistic model checking using PRISM to rigorously analyze and validate the correctness of the proposed hybrid strategy. Our approach provides practical solutions and valuable insights, promoting the development of reliable and efficient offloading strategies for edge computing systems.

1. Introduction

Edge computing is an emerging computing paradigm aimed at fulfilling the demanding ultra-low latency needs of contemporary users. At the heart of this paradigm lies the offloading strategy, which plays a crucial role in edge computing systems. These offloading strategies are primarily classified into three categories: delay-based, energy-efficient, and energy-delay trade-off. Their purpose is to tackle the challenges posed by resource constraints in mobile devices and excessive energy consumption.

In the field of edge computing, the development of offloading strategies is pivotal in achieving low-latency and high-performance computing. As edge devices become increasingly heterogeneous and the network conditions vary, there is a growing demand for efficient decision-making processes to determine which computational tasks should be offloaded and where they should be executed. However, the complexity of this decision-making process, coupled with the inherent uncertainties in edge environments, underscores the need for a quantitative approach. In addition, the majority of current research efforts primarily focus on proposing the three aforementioned offloading strategies for different user scenarios. These strategies involve resource allocation algorithms and exploration algorithms to evaluate their impact on latency improvement or energy consumption reduction using various datasets. Although these existing schemes are clear and useful, they may not provide a complete picture. Quantitative analysis can complement this by offering empirical evidence and deeper insights into the system’s behavior. Furthermore, there is a notable lack of analysis regarding the correctness of the offloading strategy designs themselves. Fortunately, the application of quantitative analysis and verification through formal methods offers a means to assess the correctness of these strategies. Henceforth, in order to address these challenges, this research draws motivation from the recognition that probabilistic model checking provides a systematic means to analyze and validate edge computing offloading strategies [1]. In light of this, this paper introduces a verification method specifically designed for offloading strategies. The method abstracts the fundamental properties that an offloading strategy should adhere to, and employs probabilistic model checking for quantitative analysis and verification. By leveraging probabilistic models, we evaluate the correctness of edge computing offloading strategies, addressing uncertainties and risks in the design process. Our findings provide actionable guidance for designing and verifying offloading strategies in edge computing.

The key component of edge computing systems is the development of efficient and accurate offloading strategies. Researchers have proposed various offloading strategies tailored to different scenarios, such as single-user or multi-user, focusing on either delay reduction (delay-based offloading), energy consumption optimization (energy-efficient offloading), or a balance between the two (energy-delay trade-off). These strategies are typically evaluated through data comparison and performance analysis to assess their effectiveness and improvements in specific or multiple scenarios. However, a crucial aspect often overlooked in most research is the analysis and verification of the correctness of the designed strategies using mathematical logic. Most of the existing work revolves around proposing new strategies without conducting rigorous analysis. Therefore, it is essential to verify whether the designed offloading strategy is correct and aligns with the desired objectives of the designer. This verification serves as a prerequisite for performance analysis and further enhancements of offloading strategies.

An effective approach to designing a verification model for offloading strategies is to encompass the considerations of delay, energy consumption, and the balance between the two. This can be achieved by configuring the transmission cost parameters appropriately, allowing for quantitative analysis. In this paper, the investigation of correctness primarily focuses on the probabilistic nature of potential failures or issues within the strategy itself. Through comprehensive evaluation, quantitative analysis, and the application of the formal verification method, the success rate of the strategy can be determined from a mathematical statistical perspective. By utilizing probabilistic modeling techniques, the correctness of newly proposed strategies by researchers can be assessed effectively.

The main contributions of this paper are as follows:

• Proposing an integrated offloading strategy covering delay-based, energy-efficient, and energy-delay trade-off approaches to improve strategy clarity and verifiability.
• Modeling the integrated strategy probabilistically and verify its correctness via the PRISM model checker, demonstrating effectiveness.
• Offering technical guidance and insights for correctness verification and evaluation, advancing theoretical foundations for trustworthy edge computing offloading validation.

The structure of the rest of the paper is as follows. Section 2 provides an introduction to probabilistic model checking, along with an overview of the automated verification tools utilized in this paper. Additionally, it outlines the fundamental concepts and components of the offloading strategy. Section 3 focuses on modeling the offloading strategy, presenting a detailed framework that captures their essential characteristics and behaviors. Section 4 abstracts the key properties of offloading strategies and conducts quantitative analysis and verification using the methods of probabilistic model checking, aiming to assess the correctness of the strategies based on the established model framework. Section 5 then gives the related work, and Section 6 concludes the paper and gives the future work.

2. Background

In this section, we present the basic principles of the offloading strategy and provide an explanation of the probabilistic model checking approach employed in this paper.

2.1. Offloading Strategies

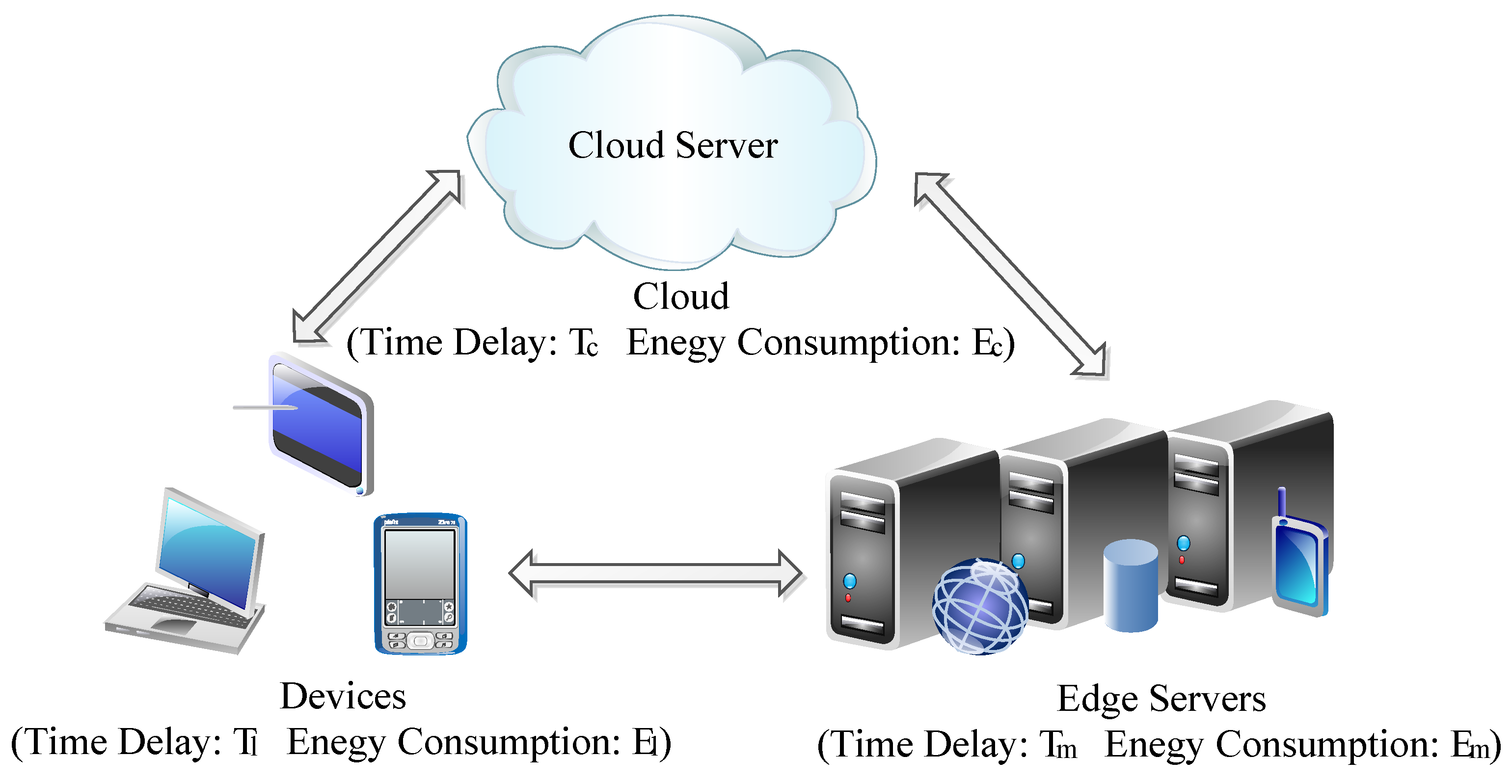
In this paper, edge computing is a distributed paradigm that processes data closer to its source to reduce latency and network congestion. The “edge” includes different levels such as local devices, nearby edge servers, and remote cloud servers. Accordingly, we categorize computation into three levels based on task location, including local (on-device processing), edge server (offloading to nearby nodes with moderate resources and low latency), and cloud server (offloading to remote data centers with high computing power but higher latency). These levels form the basis of our system model for analyzing delay, energy consumption, and offloading decisions. Figure 1 shows the workflow of offloading strategies in edge computing systems [2,3,4], where three different kinds of offloading strategies are outlined as summarized in

Table 1. The judgements of the delay and energy consumption in the offloading strategy.

Strategy Type	Notation	Offloading Decision
Delay-based	$min(T_l,T_m,T_c)=T_i$	$i=l$: local execution $i=m$: edge server offloading $i=c$: cloud server offloading
Energy-efficient	$min(E_l,E_m,E_c)=E_i$
Energy-delay trade-off	$C=\alpha ·T+(1-\alpha )·E$	User-defined

.

(1) Delay-based Offloading Strategy: This strategy focuses on minimizing the overall execution time delay. If the local execution delay $T_l$ is lower than the offloading execution delay $T_o$, which can be either the time delay in edge servers $T_m$ or the time delay in the cloud server $T_c$, the computation is performed locally. Conversely, if the offloading execution delay $T_o$ is lower, the computation is offloaded to either the edge servers or the cloud for faster execution.

(2) Energy-efficient Offloading Strategy: In this strategy, the primary consideration is minimizing energy consumption. If the energy consumption of local execution $E_l$ is lower than that of offloading execution $E_o$, where $E_o$ can be either the energy consumption in edge servers $E_m$ or the cloud server $E_c$, the computation is executed locally. Otherwise, if the energy consumption of offloading execution $E_o$ is lower, the computation is offloaded to either the edge servers or the cloud for more energy-efficient execution.

(3) Energy-delay Trade-off Offloading Strategy: This strategy dynamically adapts based on user requirements or specific scenarios, taking into account the trade-off between delay and energy consumption. The strategy evaluates the overall cost by considering both delay and energy consumption, represented as $C=\alpha T+(1-\alpha )E$ [5]. Note that when combining metrics with different units, such as energy consumption E (measured in, for example, Joules or Watts) and latency T (measured in milliseconds or seconds), it is important to ensure that the composite metric remains meaningful and interpretable. Hence, in the above formula, C is the composite metric that represents the combination of energy consumption E and latency T; $\alpha$ and $1-\alpha$ are weighting factors, denoting the relative importance of energy consumption and latency in the composite metric. Here, energy consumption refers to the energy used, measured in a standardized unit (Joules), to ensure unit consistency, while latency represents the time taken for data transmission or task execution, also measured in a standardized unit (seconds) to maintain unit consistency.

In brief, to address the issue of different units for energy consumption and latency, we adopt the standardized units for both metrics in the composite formula. This standardization ensures that the units are consistent, allowing for a meaningful combination of these two distinct metrics. The weighting factors, $\alpha$ and $1-\alpha$, are used to emphasize the relative importance of each metric in the composite metric, providing a clear and interpretable representation of the trade-off between energy consumption and latency. By standardizing the units and clearly defining the weighting factors, the composite metric C can effectively capture the trade-off between energy consumption and latency while maintaining unit consistency. As a result, this approach enables a more intuitive and interpretable assessment of system correctness. Furthermore, users can calculate the total cost to determine the most suitable offloading strategy for a given situation. Specifically, the weight coefficient $\alpha$ allows users to prioritize either minimizing delay or minimizing energy consumption, thereby striking a balance between the two objectives.

2.2. Probabilistic Model Checking

Probabilistic model checking is a formal verification technique that uses probabilistic models and statistical methods to rigorously analyze system behavior, performance, and reliability under uncertainty. By mathematically modeling state transitions and probabilistic events (e.g., data transmission delays or resource availability), it enables quantitative assessment of properties like correctness, security, and efficiency, helping identify design flaws early. This approach is particularly valuable in edge computing networks—such as IoT, smart grids, and vehicular systems—where real-time, safety-critical operations demand reliable evaluation of stochastic events (e.g., data loss or task delays). Combining quantitative analysis with probabilistic modeling ensures robust system design and risk mitigation in dynamic, uncertain environments.

In this paper, we leverage probabilistic model checking with PRISM [6,7] to quantitatively verify the correctness of offloading decisions in edge computing. PRISM supports multiple probabilistic models, including DTMC (discrete-time Markov chains with probabilistic transitions), MDP (extending DTMC with decision making), and CTMC (continuous-time variant with dense time modeling). Here, we give one of the probability formulas used in this paper as an example:

$$P=?[F\le T\varphi ]$$

This computes the probability that a given Linear Temporal Logic (LTL) property $\varphi$ holds eventually (denoted by F) within T time steps. Here, LTL is a formal logic for specifying and verifying temporal properties of system behaviors over future states.

3. Modeling the Integrated Offloading Strategy

In this section, we present the stateflow of the integrated offloading strategy, illustrate its automaton, and formalize the model in PRISM.

3.1. The Stateflow of the Integrated Offloading Strategy

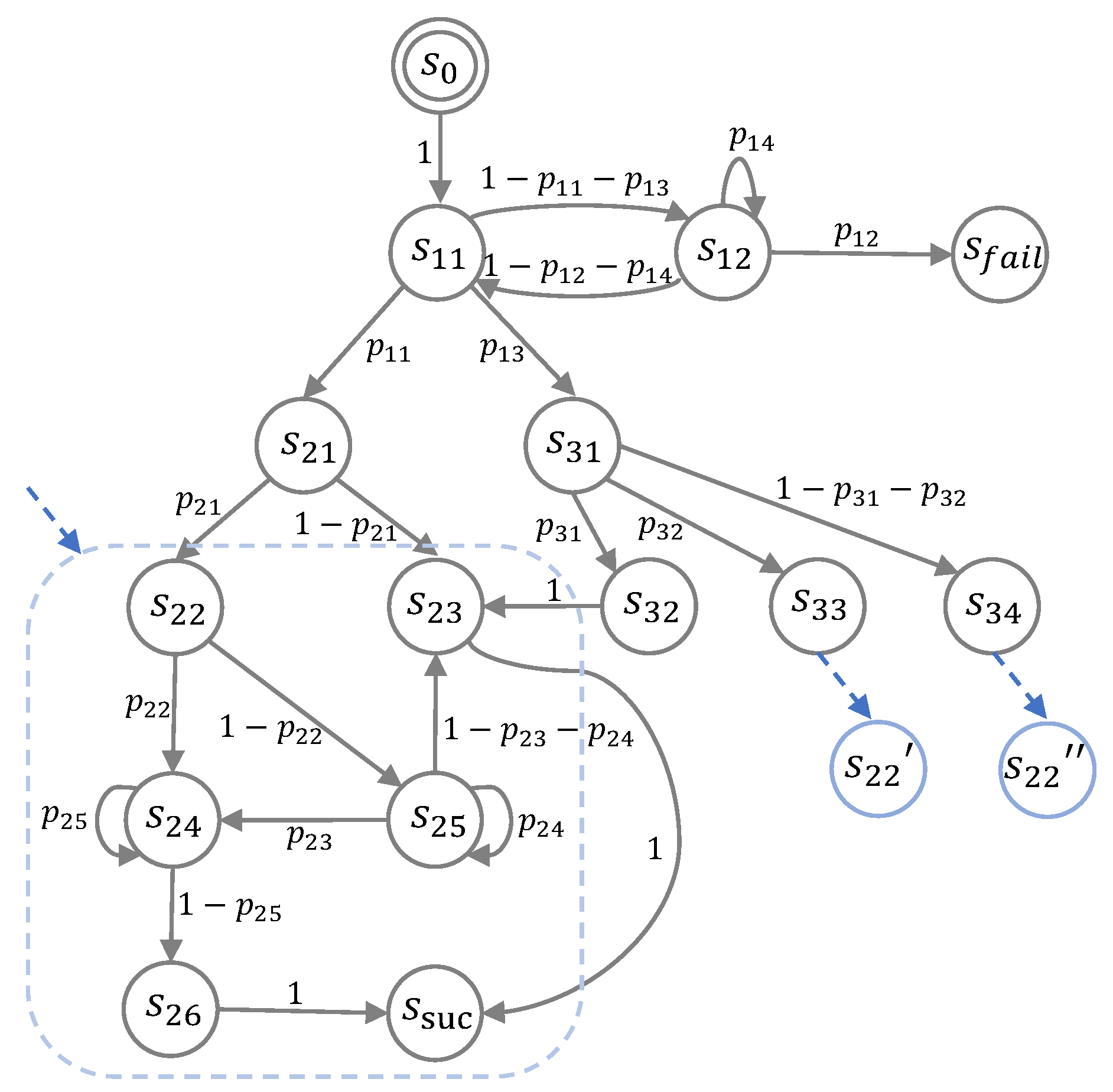
To enable quantitative analysis, we model the stateflow of three integrated offloading strategies (Figure 2), whose stages are as follows.

• Data integrity verification. Upon receiving a task submission, the strategy first verifies the success of the submission. If confirmed, it proceeds to the strategy selection phase. Otherwise, the system initiates a resubmission process. If the task fails after the maximum attempts, the offloading process is terminated.
• Strategy selection. The choice of offloading strategy depends on the coefficient $\alpha$ in the transmission cost. The two branches illustrated in Figure 2 correspond to distinct strategies based on the value of $\alpha$. Specifically, the left branch represents the delay-based and energy-efficient strategies when $\alpha$ is either 0 or 1, whereas the right branch corresponds to the energy-delay trade-off strategy applied when $\alpha$ takes any value between 0 and 1.

Detailed explanations for the left branch in Figure 2, which corresponds to the delay-based and energy-efficient offloading strategies outlined in Table 1, are as follows. When decisions are made based on either energy consumption or latency—that is, for the energy-efficient or delay-based offloading strategies—the key step is to determine the minimum transmission cost. If the minimum cost, $mi{n}_{c}ost$, matches the local execution cost $C_{local}$ shown in

Table 2. The metrics and descriptions in the offloading strategy.

Metrics	Notations	Explanations
Delay T	m	the quantity of computing resources
	$s_{local}$	the local execution speed
	$t_{local}$	the local execution time
	B	the current network bandwidth
	b	the current computation task size
	$s_{mec}$	the computation speed at edge server
	$t_{mec}$	the time required to offload and execute on edge server
	$s_{cloud}$	the computation speed at cloud server
	$t_{cloud}$	the time required to offload and execute on cloud
Consumption E	$P_{local}$	the power consumed by the mobile device during operation
	$P_{transmit}$	the transmission power during uploading
	$P_{connect}$	the power consumed by the mobile device to maintain connection with the network
	$E_{local}$	the energy consumption cost of local computing
	$E_{mec}$	the energy comsumption cost of edge computing
	$E_{cloud}$	the energy comsumption cost of cloud computing
Composite Metric C	$C_{local}$	the composite metric of the cost of local computing
	$C_{mec}$	the composite metric of the cost of edge computing
	$C_{cloud}$	the composite metric of the cost of cloud computing

, the task is executed locally and then completed. If $mi{n}_{c}ost$ corresponds to a remote option, the task is offloaded to either an edge server or a cloud server. At this point, it is necessary to check whether sufficient resources are available to process the task. If resources are adequate, data processing begins and the system continuously verifies whether the task has finished. If the task remains incomplete, processing continues until completion. However, if there are not enough resources, the task enters a waiting stage where resource availability is monitored. Once resources become sufficient, data processing resumes. If the waiting time exceeds the offloading latency benefit, the system switches promptly to local execution; otherwise, it continues to wait for resources.

Conversely, the right branch in Figure 2 corresponds to the energy-delay trade-off offloading strategy described in Table 1. This strategy balances energy consumption and delay based on the user’s choice. If the user opts for local execution, the strategy provides a smooth line chart illustrating the probability of success or failure depending on the selected coefficient $\alpha$. If offloading is chosen, a decision-making process similar to that used in the delay-based or energy-efficient strategies is applied, alongside a corresponding smooth probability chart related to the choice of $\alpha$. These charts are comparable to those presented in Figures 4–6 in Section 4.

To complement the stateflow diagram in Figure 2, Table 2 summarizes the key parameters adopted in our offloading strategy model. The core formulations are presented below [5]:

The local computation time is given by:

$$t_{\mathrm{local}}={\displaystyle \frac{m}{s_{\mathrm{local}}}}$$

(1)

The edge server computation time comprises both transmission and processing components:

$$t_{\mathrm{mec}}={\displaystyle \frac{b}{B}}+{\displaystyle \frac{m}{s_{\mathrm{mec}}}}$$

(2)

The offloading condition for latency optimization is:

$$m·\left({\displaystyle \frac{1}{s_{\mathrm{local}}}}-{\displaystyle \frac{1}{s_{\mathrm{mec}}}}\right)>{\displaystyle \frac{b}{B}}$$

(3)

Energy consumption models are defined as:

$$E_{\mathrm{local}}=P_{\mathrm{local}}·t_{\mathrm{local}}$$

(4)

$$E_{\mathrm{mec}}=P_{\mathrm{transmit}}·{\displaystyle \frac{b}{B}}+P_{\mathrm{connect}}·{\displaystyle \frac{m}{s_{\mathrm{mec}}}}$$

(5)

The composite cost functions for each computing mode are:

$$C_{\mathrm{local}}=\alpha ·t_{\mathrm{local}}+(1-\alpha )·E_{\mathrm{local}}$$

(6)

$$C_{\mathrm{mec}}=\alpha ·t_{\mathrm{mec}}+(1-\alpha )·E_{\mathrm{mec}}$$

(7)

$$C_{\mathrm{cloud}}=\alpha ·t_{\mathrm{cloud}}+(1-\alpha )·E_{\mathrm{cloud}}$$

(8)

The optimal strategy minimizes the cost:

$$C_{\min }=min(C_{\mathrm{local}},C_{\mathrm{mec}},C_{\mathrm{cloud}})$$

(9)

It is worth noting that the use of deterministic computation time or some other assumptions above are aimed at simplifying the modeling and analysis process to gain a clearer understanding of the fundamental workings of the edge computing strategy in this study. For instance, although computation time in real systems may often be stochastic or probabilistic, modeling them deterministically allows for initial assessments and performance analyses. This modeling approach contributes to an intuitive understanding.

3.2. The Automaton of the Offloading Strategies

In this subsection, we present the corresponding automaton in Figure 3 based on the stateflow discussed earlier in Figure 2. Figure 3 illustrates the automaton, where the cumulative sum of probability values between the subsequent nodes and the current node in each state is equal to 1. For instance, the state $s_{11}$ in the automaton represents a probability of $p_{11}$ entering the state $s_{21}$ of the energy-efficient or delay-based offloading strategy after the successful checking of data, which corresponds to $\alpha =0$ or 1, and a probability of $p_{13}$ entering the state $s_{31}$ of energy-delay trade-off, whose coefficient $\alpha$ belongs to $(0, 1)$. After passing through the probability branches mentioned above, if it is in the subsequent state of state $s_{21}$, the automaton continues to provide different probability branch scenarios. Specifically, there is a probability of $1-p_{21}$ transitioning to state $s_{23}$, where local computing is performed directly, and a probability of $p_{21}$ transitioning to state $s_{22}$, where data processing is offloaded to the edge or cloud server. To clarify, all conditional decisions depicted in Figure 2 can be converted into the probability branching model described earlier, while any repetitive structures can be translated into self-loops associated with states, such as $s_{12}$, $s_{24}$, and $s_{25}$.

The dashed blue boxes in Figure 3 represent the choices made based on resource adequacy when deciding whether to offload to the edge server or the cloud server, considering factors such as delay or energy consumption.

Table 3. The state name and its corresponding explanations in Figure 3.

State Name	Explanations
$s_0$	the start of the offloading strategy
$s_{11}$	checking data
$s_{12}$	resubmitting data
$s_{fail}$	strategy failing to execute
$s_{21}$	delay-based or energy-efficient
$s_{22}$	offload to edge or cloud server
$s_{22}$′	entering the same probability workflow as the edge server
$s_{22}$″	entering the same probability workflow as the cloud server
$s_{23}$	offloading to local
$s_{24}$	processing data
$s_{25}$	waiting to allocate resources
$s_{26}$	returning the results
$s_{31}$	energy-delay trade-off
$s_{32}$	choosing to offload to local
$s_{33}$	choosing to offload to edge server
$s_{34}$	choosing to offload to cloud server
$s_{suc}$	successful strategy execution

provides the names of the states and their corresponding explanations, as depicted in Figure 3. In Figure 3, to be specific, states $s_{22}^{\prime }$ and $s_{22}^{″}$ signify decisions related to offloading data to the edge server and the cloud server, respectively, balancing the trade-off between delay and energy consumption. The explanations for specific details within these two states closely resemble those for states $s_{22}$ and $s_{23}$. The selection process for offloading decisions, which hinges on factors like delay and energy consumption, remains uncertain depending on different probabilities.

Furthermore, in order to provide a clearer representation of the transition probability relationships and information between various states in the edge computing offloading probability model depicted in Figure 3, we give matrix q, where the specific probability values are determined by us. In the transition probability matrix q of the probability model, the rows and columns correspond to the states of the edge computing offloading strategy probability model and have been labeled within matrix q. For instance, what is meant by the entry in the first row and second column is that the probability value of transitioning from state $s_{11}$ to state $s_{12}$ equals $1-p_{11}-p_{13}$. For brevity, we have omitted the relationships between states $s_0$, $s_{31}$, $s_{32}$, $s_{33}$, $s_{34}$, and other states in matrix q, which are shown in Figure 3.

$$q=\begin{array}{cccc}\hspace{0.33em}\hspace{0.33em}& \hspace{0.33em}\hspace{0.33em}& \hspace{0.33em}\hspace{0.33em}\hspace{0.33em} s_{11}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{s}_{12}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} s_{21}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{s}_{22}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} s_{23} \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em} s_{24}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{s}_{25}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{s}_{26}\hspace{0.33em}\hspace{0.33em}{s}_{suc} \hspace{0.33em}{s}_{fail}& \\ \begin{array}{c}{s}_{11}\\ s_{12}\\ s_{21}\\ s_{22}\\ s_{23}\\ s_{24}\\ s_{25}\\ s_{26}\\ s_{suc}\\ s_{fail}\end{array}& (& \begin{array}{cccccccccc}0& 1-p_{11}-p_{13}& p_{11}& 0& 0& 0& 0& 0& 0& 0\\ 1-p_{12}-p_{14}& p_{14}& 0& 0& 0& 0& 0& 0& 0& p_{12}\\ 0& 0& 0& p_{21}& 1-p_{21}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& p_{22}& 1-p_{22}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& p_{25}& 0& 1-p_{25}& 0& 0\\ 0& 0& 0& 0& 1-p_{23}-p_{24}& p_{23}& p_{24}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}& )\end{array}$$

3.3. The Model in PRISM

In this section, we present the formal specification of our dynamic offloading model using the PRISM probabilistic model checker. The model is implemented as a Continuous-Time Markov Chain (CTMC) that captures the key components and decision processes involved in edge computing offloading. The PRISM model consists of several key components as below.

3.3.1. Constants and Parameters

The model begins with the declaration of various constants that represent system parameters and environmental conditions, which include parameters such as $step$ (state transition count), m (resource required for a computation task), $s\_local$, $s\_mec$, and $s\_cloud$ (execution speeds for local, edge server (mec), and cloud), $B\_mec$ and $B\_cloud$ (edge and cloud network bandwidth), b (task size), and various power-related parameters. Listing 1 gives the details.

3.3.2. Time and Energy Calculations

The model includes formulas for calculating execution time and energy consumption for different offloading locations related to Formulas (1)–(9) in Section 3.1. These formulas define the time ($t\_local$, $t\_mec$, $t\_cloud$) and energy consumption ($E\_local$, $E\_mec$, $E\_cloud$) required for task execution in different offloading scenarios. The formulas for calculating the cost ($C\_local$, $C\_mec$, $C\_cloud$), minimum cost ($min\_cost$), and maximum cost ($max\_cost$) are also defined. For brevity, here, we give several definitions in PRISM as an instance in Listing 2.

Listing 1: Main model constants and parameters.

Listing 2: Part of time and energy calculations.

3.3.3. State Variables and Transitions

The core of the model is defined in the DynamicOffload module, which contains the state variables and transition rules. It includes state variables like choice, s (representing different states), $task\_handling\_mec$, and $task\_handling\_cloud$ (number of tasks being handled in edge and cloud server), $t\_m$ and $t\_c$ (time waiting for edge and cloud server allocation), $submit\_times$ (number of task submissions), and various Boolean variables to track the success of different events. In addition, the model defines transitions between different states based on probabilistic choices and conditions. For example, it includes transitions for task submission, resubmission, local handling, offloading to the edge or cloud server, waiting for resource allocation, and returning results. Listing 3 shows core module and state transitions.

The proposed model formalizes a probabilistic state transition mechanism that governs the complete offloading lifecycle. The system evolves through distinct phases including task submission, potential resubmission, local/edge/cloud execution, resource allocation waiting periods, and result return procedures. Central to this framework are three core components: (1) strategy selection through optimization parameters $\alpha \in \{0,1\}$ for pure energy/delay minimization or $\alpha \in (0,1)$ for balanced trade-off, implemented via transition probabilities $\mathcal{P}=\{p_{11},\dots ,p_{32}\}$; (2) cost-aware offloading decisions that select between local ($\mathrm{choose}\_\mathrm{local}$), edge ($\mathrm{offload}\_\mathrm{mec}$), or cloud ($\mathrm{offload}\_\mathrm{cloud}$) execution based on minimum computed costs $\{C_{\mathrm{local}},C_{\mathrm{mec}},C_{\mathrm{cloud}}\}$; and (3) temporal control mechanisms incorporating maximum wait thresholds ($t_{\mathrm{mec}}^{\max }$, $t_{\mathrm{cloud}}^{\max }$) with fallback to local execution when exceeding $t_{\mathrm{wait}}$. State transitions are explicitly defined through success codes ${\mathcal{S}}^{+}=\{9_{\mathrm{local}},{19}_{\mathrm{mec}},{29}_{\mathrm{cloud}}\}$, failure state 11, and situational branching governed by $\mathrm{situation}\left(x\right)={\mathbb{I}}_{x\in \{0,1\}}+2·{\mathbb{I}}_{0<x<1}$ where $x=\alpha$. This integrated approach ensures adaptive decision making under dynamic environmental constraints while maintaining probabilistic guarantees throughout the offloading process.

Listing 3: Core module and state transitions.

3.3.4. Transition Probabilities

The model uses several probability values to govern the transitions between states, as shown in

Table 4. The name and value of the probability adopted in our model.

Probability Name	Probability Value
$p_{11}$	0.98
$p_{12}$	0.95
$p_{13}$	0.97
$p_{14}$	0.57
$p_{21}$	0.94
$p_{22}$	0.93
$p_{23}$	0.93
$p_{24}$	0.55
$p_{25}$	0.56
$p_{31}$	1/3
$p_{32}$	1/3

. These probabilities reflect the likelihood of different outcomes in the offloading process, such as successful task submission, resource allocation, and processing completion.

The complete model captures the dynamic nature of offloading decisions in edge computing environments, considering factors such as resource availability, network conditions, and energy-time trade-offs. The CTMC formulation allows for probabilistic analysis of different offloading strategies and their impact on system performance.

4. Quantitative Analysis and Verification

In this section, we first present the properties that need to be analyzed and verified, followed by a quantitative analysis and verification of the experimental parameters and results.

4.1. Property Specification

We formalize the following probabilistic properties to verify the correctness of our offloading decision strategy.

Overall success probability: This represents the probability that the entire strategy can eventually successfully handle the task within a given number of steps and within the specified range of submitted task times.

$$\begin{array}{cc}\hfill P=& ?[F\le step(handle\_suc=true\&\hfill \\ \hfill & submit\_times\le max\_submit\_times\left)\right]\hfill \end{array}$$

(10)

Overall failure probability: This depicts the probability that the entire strategy fails to process the task successfully within the specified number of steps and the number of submissions is within the specified range, even though all the conditions of the strategy are normal.

$$\begin{array}{cc}\hfill P=& ?[F\le step(s=11\&(handle\_suc=false)\&\hfill \\ \hfill & submit\_times\le max\_submit\_times\left)\right]\hfill \end{array}$$

(11)

Local processing success probability: This indicates the probability that the strategy chooses to offload to local devices and successfully processes the task within the specified number of steps.

$$\begin{array}{cc}\hfill P=& ?[F\le step(local\_handled\_suc=true\&\hfill \\ \hfill & submit\_times\le max\_submit\_times\left)\right]\hfill \end{array}$$

(12)

Edge server success probability: This describes the probability that the strategy chooses to offload to the edge server and successfully processes the task within the specified number of steps.

$$\begin{array}{cc}\hfill P=& ?[F\le step(mec\_handled\_suc=true\&\hfill \\ \hfill & submit\_times\le max\_submit\_times\left)\right]\hfill \end{array}$$

(13)

Cloud server success probability: This shows the probability that the strategy chooses to offload to the cloud server and successfully processes the task within the specified number of steps.

$$\begin{array}{cc}\hfill P=& ?[F\le step(cloud\_handled\_suc=true\&\hfill \\ \hfill & submit\_times\le max\_submit\_times\left)\right]\hfill \end{array}$$

(14)

Local processing ratio: This expresses the proportion of the probability of successful task processing by local devices to the probability of overall successful processing in the strategy.

$${\displaystyle \frac{\begin{array}{c}\hfill P=?[F\le step(local\_handled\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}{\begin{array}{c}\hfill P=?[F\le step(handle\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}}$$

(15)

Edge server ratio: This means the proportion of the probability of successful task processing by the edge server to the probability of overall successful processing in the strategy.

$${\displaystyle \frac{\begin{array}{c}\hfill P=?[F\le step(mec\_handled\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}{\begin{array}{c}\hfill P=?[F\le step(handle\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}}$$

(16)

Cloud server ratio: This outlines the proportion of the probability of successful task processing by the cloud server to the probability of overall successful processing in the strategy.

$${\displaystyle \frac{\begin{array}{c}\hfill P=?[F\le step(cloud\_handled\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}{\begin{array}{c}\hfill P=?[F\le step(handle\_suc=true\&\\ \hfill submit\_times\le max\_submit\_times\left)\right]\end{array}}}$$

(17)

4.2. Verification Results and Analysis

In this subsection, we analyze the properties discussed in the previous subsection to demonstrate the usability of the offloading strategies. Additionally, we discuss the curves depicted in the figures that represent the verification results.

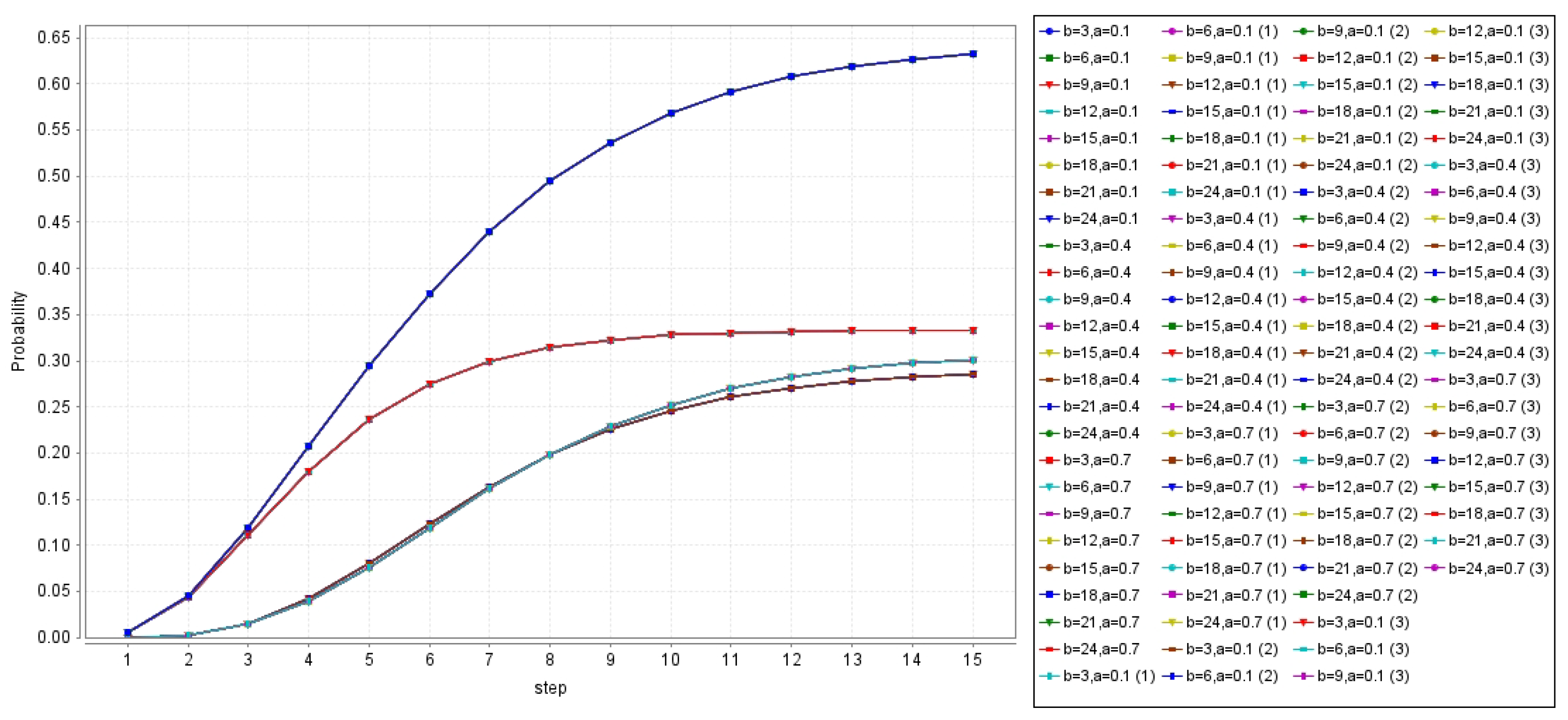
Figure 4 illustrates the overall success rate of strategies based on the delay-efficient or energy-efficient offloading strategy. The graph depicts the success rate of strategies completed at different time steps for different task sizes, where b takes the values of 3, 9, 15, and 21. Figure 5 presents the success rates of three different offloading objects, including local offloading, edge offloading, and cloud offloading.

Specifically, the analysis of the success rates of these strategies reveals that the success rate of different task sizes varies depending on the corresponding offloading strategy. It is evident that when other network factors such as bandwidth and computing power remain constant, local computing has the highest success rate but is more suitable for small tasks. In contrast, edge or cloud offloading is more suitable for medium to large tasks, but the overall success rate is lower due to factors such as data transmission delay.

Figure 6 shows the success rate data of strategies when users prefer to balance delay and energy consumption (energy-delay trade-off offloading strategy). It shows the success probabilities of overall computing, local computing, edge computing, and cloud computing. Compared to the overall graph based on delay and energy consumption strategies, the success rate of overall strategies has slightly decreased, mainly due to the potential impact of external environment parameters when balancing the strategies. To investigate the proportion of the three possible offloading computing methods in the overall success rate of strategies, we analyze the data and find that even with an increasing time step, the probability of successful local offloading is still greater than that of edge and cloud offloading shown in Figure 7. The overall curve can assist users in selecting a delay and energy consumption ratio based on the device’s battery level and the pending data task.

5. Related Work

Recent advances in edge computing offloading strategies have primarily evolved along two interrelated directions: algorithm-driven optimization and scenario-specific adaptation. In the domain of algorithmic optimization, various AI-based approaches have been proposed to enhance offloading performance in terms of latency, energy efficiency, and resource utilization. For instance, Wang et al. [8] introduced TPMOA, a deep reinforcement learning method for wireless VR systems, which integrates viewpoint prediction with multi-objective optimization to jointly reduce latency and energy consumption. Yang et al. [9] proposed KDECN, which combines an LSTM-based traffic demand predictor (TRDP) and a DRL-based resource allocator (L-CORA) to optimize dynamic edge network scheduling. Gong et al. [10] leveraged MOEA/D for multi-objective offloading across cloud–edge-end systems, while He et al. [11] formulated a KKT-based analytical solution derived from queueing models to support optimal offloading decisions under constrained conditions.

On the other hand, scenario-specific adaptation approaches have focused on addressing unique environmental and application constraints. Zhang et al. [12] proposed MILMST for infrastructure-less networks, which employs multi-agent imitation learning and Steiner tree-based migration to enhance offloading in the absence of fixed infrastructure. Li et al. [13] tackled high-mobility scenarios in MEC by integrating Lyapunov optimization with fully connected LSTM (FC-LSTM) scheduling to balance latency and energy consumption. Task dependency challenges have also been addressed: Li et al. [14] proposed a graph-based workflow partitioning method, achieving 7.8–9.5% energy savings, while Tang et al. [15] introduced a two-stage offloading strategy combining priority-based task grouping and game-theoretic scheduling for delay-sensitive IoT workloads.

In addition to performance-oriented offloading, recent research in edge and cloud computing optimization has extended toward system-level innovation, particularly in learning-driven resource management, formal verification, and quantum acceleration. For instance, Xu et al. [16] introduced CERACE, which applies prioritized deep Q-networks (P-DQN) for cost-efficient resource allocation, achieving a 30% cost reduction. Yang et al. [17] employed a hybrid heuristic and multi-agent DRL strategy for MEC caching to minimize latency. Similarly, Bo et al. [18] proposed MADSASPG, a MADRL-NOMA scheme for vehicular networks, reducing latency by 35% and energy consumption by 25%, while Su et al. [19] demonstrated that distributed edge control for HVAC systems can match centralized performance.

To improve the reliability of complex edge–cloud systems, formal verification techniques have been explored. Wunderlich et al. [20] extended classical temporal logics (LTL/CTL) by incorporating weight accumulations, enabling quantitative analysis in probabilistic model checking tools such as PRISM. Schneider et al. [21] adapted bounded model checking for imprecise probabilistic timed graph transition systems (IPTGTSs), enhancing verification under uncertainty in cyber–physical systems. Finally, at the frontier of computational acceleration, Jeon et al. [22] proposed QPMC, a quantum-enhanced probabilistic model checking framework that achieves quadratic speedup through quantum amplitude estimation, laying the groundwork for scalable verification of large-scale stochastic systems.

While existing research has made significant progress in optimizing edge offloading strategies, most efforts focus on performance improvement, with limited attention to the formal verification of correctness. To address this gap, this paper proposes a unified strategy that integrates three representative types of offloading strategies and employs probabilistic model checking to conduct quantitative analysis and correctness verification, aiming to provide theoretical guidance for the design and homologous evolution of offloading strategies.

6. Conclusions and Future Work

This paper presented a hybrid offloading strategy that combined delay-based, energy-efficient, and energy-delay trade-off approaches. These strategies were modeled using automata and analyzed with the PRISM model checker to verify various properties. Quantitative analysis showed that, within the energy-delay trade-off strategy, users could select the most appropriate approach based on the probability of successful offloading and their specific needs. Similarly, the success rates for energy-efficient and delay-based strategies were evaluated. This method has provided valuable guidance to ensure the correctness of the design and implementation of offloading strategies.

In future work, we will enhance the hybrid offloading strategy by incorporating network conditions, resource variability, and application demands, addressing current assumptions to better model real-world edge computing scenarios.