Abstract
Infrared video often encounters low resolution, which makes it difficult to perform the target detection and recognition task. Super-resolution (SR) is an effective technology to enhance the resolution of infrared video. However, the existing SR method of infrared image is basically a single image SR, which restricts the performance of SR due to ignoring the strong inter-frame correlation in video. We propose a self-supervised SR method for infrared video that can estimate the blur kernel and generate paired data from raw low-resolution infrared video itself, without the need for additional high-resolution videos for supervision. Furthermore, to overcome the limitations of optical flow prediction in handling complex motion, a deformable convolutional network is introduced to adaptively learn motion information to capture more accurate, tiny motion changes between adjacent images in an infrared video. Experimental results show that the proposed method can achieve an outstanding performance of restored image in both visual effect and quantitative metrics.
1. Introduction
Infrared imaging systems capture infrared radiation signals that are imperceptible to the human eye and convert them into visually recognizable image information through photoelectric conversion and processing. According to particularity and imaging mechanism of infrared radiation, infrared imaging technology has many advantages such as long imaging distance, strong anti-interference ability to penetrate smoke and haze, and working all weather, which have resulted in its extensive utilization across more application fields including power industry, construction industry, medical industry, petrochemical industry, port security, security and military. Despite rapid advancements in infrared imaging technology, infrared images often exhibit lower spatial resolution when compared to visible light images. SR restoration is an image processing technique for reconstructing high-resolution (HR) images from low-resolution (LR) images. In a traditional digital image, resolution is typically represented by the number of pixels in an image. Higher resolution implies more pixels, allowing for the display of greater detail and clarity. SR technology aims to recover missing details from LR images by utilizing information within the image or correlations between adjacent images. At present, the existing SR methods for infrared images are basically single-image SR (SISR), and most works on video SR are designed for video.
For SISR of infrared images, the methods based on neural networks have been explored by some researchers. An SISR technique based on multiscale saliency detection and residuals learned by a deep convolutional neural network (CNN) in the wavelet domain was proposed in [], in which the incorporation of multiscale salient regions in sub-band images helps to minimize blurring artifacts caused by downsampling effects. In order to achieve a lightweight network, an iterative error reconstruction network based on efficient dense connections for infrared image SR is designed in [], which achieves better performance using fewer parameters. Zewei He et al. [] presented a cascaded architecture of deep neural networks with multiple receptive fields to increase the spatial resolution of infrared images by a large scale factor, achieving improved reconstruction accuracy with significantly fewer parameters. Aiming at not depending on paired datasets, Jing Han et al. [] proposed a novel unsupervised infrared SR method based on the photoelectric characteristics of infrared images, establishing a fully unpaired generative adversarial framework to enrich image details without using high-resolution ground truth.
For the SR of visible light video, the goal of which is to infer the latent HR video from given LR frames. In recent years, people have gradually realized that inter-frame information has been overlooked in video SR. In fact, the information contained in the same object in adjacent frames of images has a tiny difference. If we can use information between adjacent frames to do SR restoration for video, it is definitely better than single-frame image SR theoretically. Therefore, restoration models based on the SR for static images [,,,,,], SR technology is expanding into the realm of video. In recent years, most methods of video SR are based on CNN. A video SR framework based on a CNN, which uses multiple LR frames as input to reconstruct one HR output frame, is introduced in []. Renjie Liao et al. [] propose a new direction for fast video super-resolution via an SR draft ensemble that considers contextual information provided from external data for super-resolution. Jose Caballero et al. [] introduce spatial-temporal sub-pixel convolution networks that effectively exploit temporal redundancies and improve reconstruction accuracy while maintaining real-time speed. Video SR typically extracts motion information, such as optical flow, to model interframe correlation, but it incurs high computational costs. Considering that recurrent neural networks can effectively model long-term correlation of video sequences, a fully convolutional recurrent neural network is proposed in [] to achieve super-resolution restoration with good performance for complex motion videos with low computational complexity. In order to address the challenges of aligning multiple frames with large motions and effectively fusing different frames with diverse motion and blur, EDvR [] devises a Pyramid, Cascading and Deformable (PCD) alignment module, in which frame alignment is done at feature level using deformable convolutions in a coarse-to-fine manner and a Temporal and Spatial Attention (TSA) fusion module, in which attention is applied both temporally and spatially to emphasize important features for subsequent restoration. TDAN [] overcomes artifacts in warped supporting frames caused by inaccurate flow and image-level warping strategy and adaptively aligns the reference frame and each supporting frame at the feature level without computing optical flow. Yi Xiao et al. [] propose to aggregate sharp information in severely degraded satellite videos with progressive temporal compensation, which exploits multiscale deformable convolution and deformable attention to explore sharper and cleaner clues by considering the blur level of pixels. Motion compensation and bidirectional residual convolutional network are combined in [] to model spatial and temporal non-linear mappings, which is the first time motion compensated frames are regarded as inputs of recurrent convolutional nets for video SR, and recurrent convolutional layers are utilized to reconstruct residual images rather than output images in video SR. A method is proposed in [] for high-quality and efficient video resolution upscaling tasks, which leverages spatial-temporal information to accurately divide video into chunks to keep the number of chunks and the model size to a minimum. The existing super-resolution methods usually impose optical flow between neighboring frames for temporal alignment. However, the estimation of accurate optical flow is hard and requires greater computation. GSTAN [] effectively incorporates spatial-temporal information in a hierarchical way to address this problem. An end-to-end spatial-temporal video super-resolution network, which is chiefly composed of cross-frame transformers instead of traditional convolutions and a multi-level residual reconstruction module, which can make full use of maximum similarity and similarity coefficient matrices obtained by cross-frame transformers, is proposed in [] to reconstruct high-resolution and frame-rate results from coarse to fine. To alleviate the problems of high computational costs and inefficient long-range information usage, a Bidirectional Recurrence Network (BRN) with an optical-flow-reuse strategy [] is proposed to better use temporal knowledge from long-range neighboring frames for high-efficiency reconstruction. Yuming Jiang et al. [] propose C2-Matching and design a dynamic aggregation module to address the potential misalignment issue between input images and reference images. Video SR methods usually require an accurate estimation of optical flow to wrap neighboring frames for temporal alignment, which is quite difficult. Therefore, an end-to-end deep convolutional network that dynamically generates spatially adaptive filters for alignment is proposed in [] to avoid generating explicit motion compensation and utilize spatial-temporal adaptive filters to achieve the operation of alignment. Furthermore, TCNet [] focuses on the temporal consistency of inter-frames and designs a spatial-temporal stability module to learn self-alignment from inter-frames to enhance the consistency of reconstructed videos. The aforementioned video SR methods based on CNN achieve significant performance. However, they are supervised learning approaches and depend on a dataset of HR-LR pairs to train a neural network, which is usually unavailable, especially in real-world applications. To address this problem, Haoran Bai et al. [] propose a self-supervised learning method to solve the blind video SR problem, which simultaneously estimates blur kernels and HR videos from LR videos and introduces an optical flow estimation module to exploit information from adjacent frames for better HR video restoration.
The abovementioned methods for video SR are primarily designed for visible light video. Except for a lack of color, infrared videos also have characteristics of unclear texture details and unsharp edges compared to visible light videos. Therefore, the method of SR for visible light video may not work well for infrared video. In this paper, we propose an SR method for infrared video, which introduces a self-supervised structure that enables the estimation of blur kernels and generation of paired data directly from original LR infrared videos without the need for additional HR video supervision. Furthermore, it incorporates a deformable convolution network to adaptively learn motion information, allowing for a more precise capture of subtle motion variations, which circumvents complex processes and potential estimation errors associated with optical flow estimation.
The main contributions of this paper are as follows:
- (1)
- We propose a self-supervised infrared video SR method. We estimate the potential HR infrared video only from low-quality LR infrared video data, rather than relying on datasets of high-low resolution video pairs, which are often not available in practical applications.
- (2)
- We employ a deformable convolutional network to directly learn alignment and motion information between adjacent infrared video frames. Deformable convolution allows for local deformations to be learned for each pixel, enabling convolutional kernels to adaptively correspond to the shape and structure of the target, which can better preserve fine-grained details in the image, especially in cases of small motion displacement, as is often encountered in infrared videos.
- (3)
- Experimental results demonstrate that this proposed method can obtain high-quality HR infrared videos and perform better than comparison methods. This proposed method can be applied in video SR of various infrared imaging systems, especially for infrared imaging systems used for weak and small target detection and recognition.
2. Proposed Method
This overall framework of the proposed infrared video SR method consists of two branches. The main branch is used for estimating the blur kernel and potential HR frames. It employs a deformable convolutional network to learn motion information between adjacent frames and align frames. The auxiliary branch utilizes auxiliary paired data, which is generated based on LR input frames, and estimates the blur kernel from the main branch to constrain the training of the deformable convolution network and the clear frame reconstruction network. As shown in Figure 1, this overall framework comprises several components, including Blur Kernel Estimation Network Nk, Deformable Convolution Alignment Network Nw (which includes Feature Extraction Network Ne), and Clear Frame Reconstruction Network Nr.
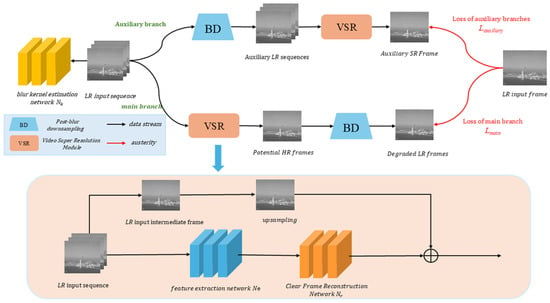
Figure 1.
The overall framework of the proposed method.
2.1. Blur Kernel Estimation Network Nk
The blur kernel Ki can be estimated from the LR input frames. The blur kernel estimation network is shown in Figure 2, which is a neural network that includes Residual Channel Attention Blocks (RCAB) [] modules and fully connected layers. RCAB combines the Channel Attention (CA) mechanism with the residual concept.
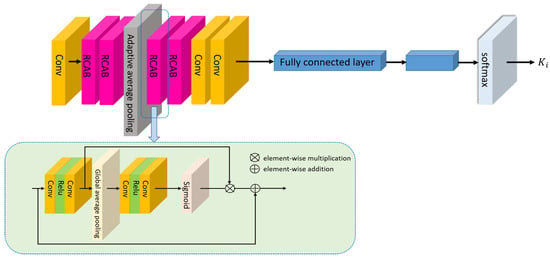
Figure 2.
Blur kernel estimation network Nk.
Each RCAB module maintains the same spatial resolution throughout. Specifically, it takes a feature map of shape (B,H,W,C) as input and processes it through two consecutive convolutional layers with a ReLU activation in between, followed by a CA mechanism. The CA mechanism first applies global average pooling along spatial dimensions, resulting in a tensor of shape (B,1,1,C), which captures global context for each channel. This pooled feature then passes through two convolutional layers with an intermediate ReLU and final sigmoid activation to produce channel-wise attention weights, also of shape (B,1,1,C). These weights are multiplied element-wise with the input feature map to produce an attention-modulated output (B,H,W,C), which is then added to the original input via a skip connection. As all intermediate feature maps maintain the same shape, no dimension adjustment is needed.
We clarify that in Figure 2, the skip connection is only used within the RCAB modules, where spatial dimensions remain unchanged, despite the use of pooling in the channel attention branch. The global average pooling only operates on spatial dimensions and compresses the feature map to (1,1) per channel without altering the feature dimensions required for residual addition. Therefore, all skip connections operate between tensors of identical shapes, ensuring compatibility throughout the network.
The blur kernel can be calculated by
where Nk represents the blur kernel estimation network, {Li−N, …, Li, …, Li+N} represents LR input frames, and C represents the concatenation operation performed sequentially.
2.2. Deformable Convolutional Alignment Network Nw
In video super-resolution restoration, effectively utilizing information from neighboring frames is a critical problem. It is common to use alignment methods to integrate information from adjacent frames. Many optical flow estimation networks, such as PWC-Net [], can accurately estimate optical flow between frames. Once frame-to-frame optical flow is available, a warp matrix can be constructed to compensate for the motion of objects in neighboring frames and align them with the reference frame []. Finally, aligned features are used for high-resolution frame restoration. In this paper, deformable convolution is employed to directly learn motion information, replacing the process of alignment based on optical flow calculations. Deformable convolution allows for local deformation at each pixel, enabling the convolution kernel to adaptively correspond to the shape and structure of the target, which can better preserve fine-grained details in the image, especially for infrared videos with small motion displacements. It avoids the complexity of optical flow estimation and the potential introduction of estimation errors. The deformable convolution alignment network is illustrated in Figure 3.
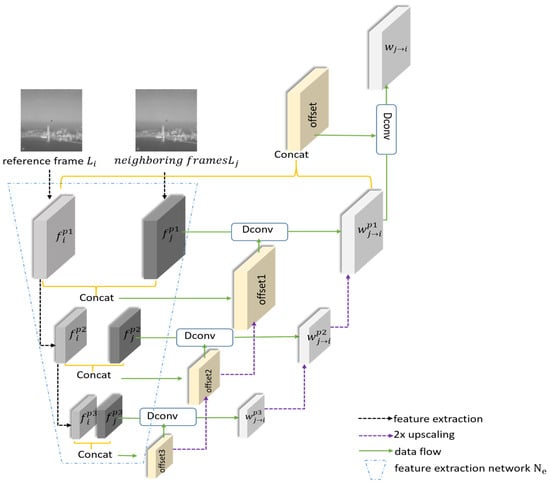
Figure 3.
Deformable Convolution Alignment Network Nw.
The features of LR input frames are initially extracted using a feature extraction network, as shown in Figure 4. Convolutional layers and five residual blocks are employed to extract features at scale p1 for each frame. Additionally, two convolutional layers are used to extract features at scales p2 and p3. This results in obtaining features at three different scales. The features at three scales can be calculated as follows:
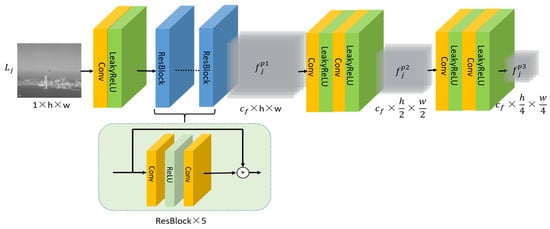
Figure 4.
Feature extraction network Ne.
Furthermore, utilizing deformable convolution and features at three different scales , we obtain the aligned feature of the LR input neighboring frames with reference frame. Specifically, at scale p3, we estimate offsets, which are denoted as offset3 using and , and the calculation formula is as follows:
where C represents the concatenation operation performed sequentially, Conv1 represents a general function composed of several convolution layers. The deformable convolution on offset3 and is used to obtain aligned features at p3 scale, which is given by:
where Conv2 represents a general function composed of several convolution layers, and Dconv represents deformable convolution.
and are concatenated and input together with the 2X up-sampled bilinear interpolation result with offset3 into a convolutional layer to obtain offset2. Then offset2 is convolved with using deformable convolution, followed by inputting aligned features at scale p3 into a convolution layer to obtain aligned features at scale p2. Similarly, the offset1 and aligned features can be obtained at scale p1. The calculation formulas are as follows:
Subsequently, and aligned features are concatenated at scale p1, and into a convolutional layer to obtain offset. Finally, offset is convolved with using deformable convolution to obtain the final aligned features . The calculation formulas are as follows:
The above operations are repeated to obtain aligned features of all neighboring frames towards the reference frame.
2.3. Clear Frame Reconstruction Network Nr
The clear frame reconstruction network is shown in Figure 5, in which aligned features are concatenated in sequence. Feature extraction is performed using a single convolutional layer and 20 residual blocks [], followed by up-sampling using the sub-pixel convolution method []. Finally, the potential HR frame is obtained by overlaying it with the LR input reference frame , which has been up-sampled using bicubic interpolation. is obtained by:
where represents LR input reference frame up-sampled by a factor of four using bicubic interpolation, C represents concatenation operation performed sequentially, represents clear frame reconstruction Network, and represents final reconstruction result.
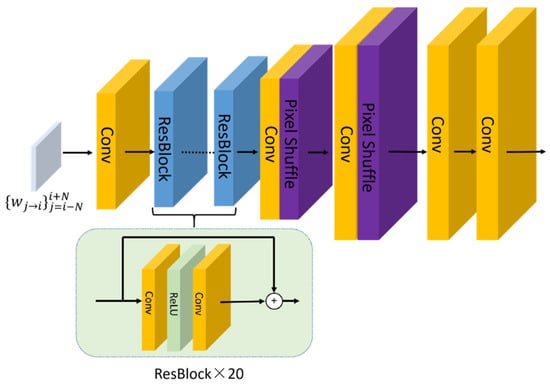
Figure 5.
Feature extraction network Nr.
2.4. Loss Function
The loss function L total consists of two parts: the main branch and the auxiliary branch loss .
where denotes D and represent down-sampling and blurring operations, respectively, is a potential HR frame, is an auxiliary LR sequence reference frame, is an LR input sequence reference frame, and have values equal to 1.
3. Experimental Results and Analysis
In the experiments, CPU used is an Intel Core i5-12490F @ 3.00 GHz with 32 GB of memory, and graphics processor is an NVIDIA RTX 3060. All deep learning experiments are implemented using the PyTorch framework. The installed packages in the environment include Python 3.10, NumPy 1.24.3, and OpenCV 4.7.0, etc. To accelerate training and computation, the platform utilizes CUDA 11.0 and CUDNN 8.0.3.
3.1. Datasets
The infrared video dataset used in this paper consists of two parts: one is obtained through an infrared dynamic scene simulation system, and the other is obtained through an infrared image capturing and processing system. The infrared dynamic scene simulation system can simulate various infrared images of infrared point targets and area targets. The infrared image capture and processing system can capture and process infrared targets and create images of them. The infrared images used in our experiments include 25 videos with infrared targets such as aircraft and missiles. Among these videos, 20 videos are used as training sets, while test sets are composed of the remaining 5 videos and a publicly available infrared video obtained from the Internet. When obtaining lower-resolution video image data for test sets, a bicubic down-sampling method is used. In the training phase, the initial learning rate is set to 2.5 × 10−5, and the optimizer used is Adam [] with parameter settings . The learning rate is reduced by half every 20 epochs, with a total of 60 epochs of training.
3.2. Results and Analysis
The performance of the proposed method is compared with traditional bicubic interpolation and a self-supervised video SR method in []. The analysis is conducted by quantifying results using subjective and objective evaluation metrics.
3.2.1. Subjective Results
The example frames extracted from the original infrared video are shown in Figure 6, in which the middle frame is used as a reference frame.

Figure 6.
Example frames of different infrared videos from the test set: (a) Missile. (b) Aircraft. (c) Car.
The LR example frames after performing down-sampling by a factor of 4× on the above original infrared frames are shown in Figure 7.

Figure 7.
4X down-sampled example frames of the original infrared video: (a) Missile. (b) Aircraft. (c) Car.
The SR reconstruction of middle frame of LR infrared frames in Figure 7 is performed using bicubic interpolation, method in [], and proposed method in this paper, respectively. The results of the SR reconstruction are shown in Figure 8.

Figure 8.
Comparison of SR reconstruction results using different methods.
From Figure 8, it can be seen that bicubic interpolation restoration is relatively blurry, with unclear edge details and an inability to present high-frequency details clearly. It performs the worst in subjective evaluation metrics. Although the method in [] has restored some high-frequency details compared to bicubic interpolation, it still suffers from unclear edge details and relatively blurry images. The images reconstructed by the proposed method in this paper are clearer compared to the other two methods.
From Figure 6, Figure 7 and Figure 8, it can be seen that the original images have strong noise. It shows that the original images have poor anti-noise ability, and even noise amplification occurs locally. At the same time, the outline of the target is also fuzzy. From Figure 6, Figure 7 and Figure 8, it can be seen that the Self-Supervised Super Resolution Restoration algorithm (SSRR) has a strong ability to suppress noise. From the restoration results, the background noise is filtered out. Overall restoration performance is good. It has a better restoration effect. The noise in the high-resolution restored image cannot be perceived from subjective observation.
3.2.2. Objective Results
The commonly used objective evaluation metrics, Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measurement (SSIM), are used to evaluate the reconstruction effects of each method. The PSNR is calculated by:
MSE is mean squared error, representing differences in pixel values at corresponding positions between two images, N is the total number of pixels, is the pixel value in the original image, is pixel value in SR reconstructed image, and MAX is the maximum pixel value of the image, which is typically set to 255. A higher PSNR value indicates that differences between the SR restored image and the original image are smaller, indicating better HR image quality. However, PSNR primarily focuses on the difference between pixels and is less sensitive to perceptual loss of details as perceived by human eyes.
SSIM not only considers the difference between pixels but also takes into account structural information and human perceptual characteristics of an image. Assuming that two input images are x and y, the calculation of SSIM is as follows:
where and represent means of x and y, and represent standard deviations of x and y, and represents covariance between x and y. and are constants to avoid division by zero, typically taken as small positive numbers. SSIM value ranges from 0 to 1, with values closer to 1 indicating a higher structural similarity between the SR reconstructed image and the original image, which indicates better HR image quality. For each video, the average PSNR and SSIM of all frames are calculated. The experimental results are shown in Table 1. The processing time of the proposed method is lower than that of the other method. The other methods are poor in noise suppression and edge detail retention, and the processing time is longer.

Table 1.
Quantitative comparison results of SR using different methods.
4. Conclusions
In this paper, we propose an infrared video SR method based on self-supervision and deformable convolution. It obtains a blur kernel from the LR input sequence itself and ultimately generates an image of the same size as the LR input sequence through the main branch and the auxiliary branch. A loss function is constructed between LR input frames to achieve self-supervision. In addition, deformable convolution is used to directly learn motion information, avoiding the complex process of optical flow estimation and potential estimation errors, which can better adapt to complex motion and deformation in infrared videos, providing a new direction for infrared video SR restoration methods. It can be found from experimental results that the proposed method in this paper can achieve satisfactory results without the need for paired HR-LR video datasets, and it is particularly effective in enhancing dim small targets, which has important practical significance for the detection and recognition of dim small targets. Although the proposed method achieves promising performance on infrared video super-resolution, there is still room for further improvement in terms of computational efficiency and generalization. In future work, we will explore lightweight backbone designs, such as employing depthwise separable convolutions or dynamic convolution modules, to reduce computational overhead. We also plan to incorporate model compression techniques, including pruning and quantization, to accelerate inference and reduce memory consumption. In addition, replacing the deformable alignment module with more efficient motion compensation strategies, such as attention-guided warping and object tracking [] may help strike a better balance between performance and speed. Finally, we intend to extend our framework to related video tasks, such as video denoising and temporal super-resolution, to evaluate its adaptability in broader scenarios.
Author Contributions
The main manuscript was written by J.C. The Self-Supervised Infrared Video Super-Resolution based on deformable convolution was designed by J.C., Y.Z. and M.C. Datasets were obtained from the infrared dynamic scene simulation system and infrared image capturing processing system by Y.W. and X.Y. The experiment process was carried out by M.C. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA28050102).
Data Availability Statement
Data are provided within the manuscript.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Liang, S.; Song, K.; Zhao, W.; Li, S.; Yan, Y. DASR: Dual-Attention Transformer for infrared image super-resolution. Infrared Phys. Technol. 2023, 133, 104837. [Google Scholar] [CrossRef]
- Hu, L.; Hu, L.; Chen, M.H. Edge-enhanced infrared image super-resolution reconstruction model under transformer. Sci. Rep. 2024, 14, 15585. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Zhang, B.; Zhou, J.; Lian, C.; Zhang, Q.; Yue, J. Gradient residual attention network for infrared image super-resolution. Opt. Lasers Eng. 2024, 175, 107998. [Google Scholar] [CrossRef]
- Liu, S.; Yan, K.; Qin, F.; Wang, C.; Ge, R.; Zhang, K.; Huang, J.; Peng, Y.; Cao, J. Infrared image super-resolution via lightweight information split network. In Proceedings of the International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; Springer Nature: Singapore, 2024; pp. 293–304. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on7 Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.-T.; Zhang, L. Second-order attention network for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11065–11074. [Google Scholar]
- Niu, B.; Wen, W.; Ren, W.; Zhang, X.; Yang, L.; Wang, S.; Zhang, K.; Cao, X.; Shen, H. Single image super-resolution via a holistic attention network. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XII 16. Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 191–207. [Google Scholar]
- Kappeler, A.; Yoo, S.; Dai, Q.; Katsaggelos, A.K. Video super-resolution with convolutional neural networks. IEEE Trans. Comput. Imaging 2016, 2, 109–122. [Google Scholar] [CrossRef]
- Liao, R.; Tao, X.; Li, R.; Ma, Z.; Jia, J. Video super-resolution via deep draft-ensemble learning. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 531–539. [Google Scholar]
- Caballero, J.; Ledig, C.; Aitken, A.; Acosta, A.; Totz, J.; Wang, Z.; Shi, W. Real-time video super-resolution with spatio-temporal networks and motion compensation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4778–4787. [Google Scholar]
- Huang, Y.; Wang, W.; Wang, L. Video super-resolution via bidirectional recurrent convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1015–1028. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chan, K.C.; Yu, K.; Dong, C.; Change Loy, C. Edvr: Video restoration with enhanced deformable convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Tian, Y.; Zhang, Y.; Fu, Y.; Xu, C. Tdan: Temporally-deformable alignment network for video super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3360–3369. [Google Scholar]
- Pan, J.; Bai, H.; Dong, J.; Zhang, J.; Tang, J. Deep blind video super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4811–4820. [Google Scholar]
- Li, D.; Liu, Y.; Wang, Z. Video super-resolution using motion compensation and residual bidirectional recurrent convolutional network. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 1642–1646. [Google Scholar]
- Li, G.; Ji, J.; Qin, M.; Niu, W.; Ren, B.; Afghah, F.; Guo, L.; Ma, X. Towards high-quality and efficient video super-resolution via spatial-temporal data overfitting. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 10259–10269. [Google Scholar]
- Lu, M.; Zhang, P. Grouped spatio-temporal alignment network for video super-resolution. IEEE Signal Process. Lett. 2022, 29, 2193–2197. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, M.; Ji, C.; Sui, X.; Bai, J. Cross-frame transformer-based spatio-temporal video super-resolution. IEEE Trans. Broadcast. 2022, 68, 359–369. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Zhu, H.; Chen, Z. Optical flow reusing for high-efficiency space-time video super resolution. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 2116–2128. [Google Scholar] [CrossRef]
- Jiang, Y.; Chan, K.C.K.; Wang, X.; Loy, C.C.; Liu, Z. Reference-based image and video super-resolution via C2-matching. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 8874–8887. [Google Scholar]
- Wen, W.; Ren, W.; Shi, Y.; Nie, Y.; Zhang, J.; Cao, X. Video super-resolution via a spatio-temporal alignment network. IEEE Trans. Image Process. 2022, 31, 1761–1773. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Jin, S.; Yao, C.; Lin, C.; Zhao, Y. Temporal consistency learning of inter-frames for video super-resolution. IEEE Trans. Circuits Syst. Video Technol. 2022, 33, 1507–1520. [Google Scholar] [CrossRef]
- Bai, H.; Pan, J. Self-supervised deep blind video super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4641–4653. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Yang, X.; Liu, M.Y.; Kautz, J. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8934–8943. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Real, Z.W. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Kingma, D.P.; Ba, J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ma, S.; Khader, A.; Xiao, L. Complementary features-aware attentive multi-adapter network for hyperspectral object tracking. In Proceedings of the Fourteenth International Conference on Graphics and Image Processing (ICGIP 2022), Nanjing, China, 21–23 October 2022; SPIE: San Francisco, CA, USA, 2023; pp. 686–695. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).