Abstract
The development of Vehicle AD Hoc Networks (VANETs) has significantly enhanced the efficiency of intelligent transportation systems. Through real-time communication between vehicles and roadside units (RSUs), the immediate sharing of traffic information has been achieved. However, challenges such as network congestion, data privacy, and low computing efficiency still exist. Data privacy is at risk of leakage due to the sensitivity of vehicle information, especially in a resource-constrained vehicle environment, where computing efficiency becomes a bottleneck restricting the development of VANETs. To address these challenges, this paper proposes a certificateless aggregated signcryption scheme based on edge computing. This scheme integrates online/offline encryption (OOE) technology and a pseudonym mechanism. It not only solves the problem of key escrow, generating part of the private key through collaboration between the user and the Key Generation Center (KGC), but also uses pseudonyms to protect the real identities of the vehicle and RSU, effectively preventing privacy leakage. This scheme eliminates bilinear pairing operations, significantly improves efficiency, and supports conditional traceability and revocation of malicious vehicles while maintaining anonymity. The completeness analysis shows that under the assumptions of calculating the Diffie–Hellman (CDH) and elliptic curve discrete logarithm problem (ECDLP), this scheme can meet the requirements of IND-CCA2 confidentiality and EUF-CMA non-forgeability. The performance evaluation further confirmed that, compared with the existing schemes, this scheme performed well in both computing and communication costs and was highly suitable for the resource-constrained VANET environment.
1. Introduction
In modern society, with the increasing number of vehicles and the increasingly serious traffic problems, intelligent transportation has become a hot topic. VANETs are an important technology to realize intelligent transportation, which not only ensures the safety of the people in the vehicle but also greatly improves people’s travel experience and provides more intelligent services for the vehicle [1]. Through real-time information exchange, VANETs provide more accurate data support for traffic management. Therefore, the development of VANETs plays a crucial role in advancing intelligent transportation systems [2]. As an extension of the Internet of Things in the transportation field, VANETs can significantly improve vehicle management efficiency and optimize route planning [3]. VANETs mainly connect vehicles to the Internet and realize vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communication through the linkage of on-board devices and sensors. In the framework of VANETs, on-board units (OBUs), as wireless communication devices, enable vehicles to acquire and share real-time data [4]. In addition, RSUs act as roadside network nodes to efficiently exchange data with vehicles through protocols such as 5G-V2X to improve traffic efficiency and prevent accidents [5]. The reliability and security of the entire system is the responsibility of a trusted authority (TA), which generates and manages the identity information and key of the vehicle and RSU and tracks the malicious vehicle, providing security for the entire system.
Although VANETs provide great convenience for people’s travel, with the continuous development of VANETs, the challenges facing them are gradually emerging; for example, a large number of data transmissions may cause network congestion and data privacy and security issues are also concerned. In order to deal with the problem of network congestion, edge computing technology comes into being. Edge computing pushes computing and storage functions to the edge of the network so that data can be stored, calculated, and analyzed at the edge nodes, and the calculated data can be further sent to the central server(CS) for computing and storage, effectively reducing the delay and bandwidth requirements of data transmission [6,7]. Therefore, it is necessary to apply edge computing in the field of the Internet of Vehicles.
Combining the advantages of certificateless signcryption and aggregation, many schemes for certificateless aggregate signcryption (CLAS) have been proposed [8,9,10,11,12,13,14]. However, these schemes are not secure enough, and there are still some security loopholes that cause privacy to be inadequately protected, and the communication overhead and efficiency need to be improved. Recently, some schemes [14,15,16] have proposed the combination of CLAS and OOE, which can ensure message confidentiality while reducing communication costs. After doing a lot of work on the security and privacy requirements of VANETS, we found that these schemes could not meet the privacy protection needs of users, so it is necessary to design an efficient and secure VANET certificateless online/offline aggregate signature encryption scheme.
1.1. Our Contributions
- This paper proposed a certificateless aggregate signature encryption protocol with conditional traceability in edge computing environments. This protocol does not need expensive bilinear pairing operations and can be used for V2I communication in vehicle networking with higher computational efficiency. When a vehicle communicates with an edge node (i.e., RSU), the authentication, confidentiality, integrity, and non-repudiation of the message are realized.
- In our protocol, a pseudonym mechanism is implemented to protect the privacy of vehicles and RSUs, effectively hiding the true identity of vehicles and RSUs. And we can track malicious vehicles under the condition of ensuring the anonymity of vehicles and achieve conditional traceability. If a malicious vehicle sends a false message, TRA can revoke the vehicle from the system based on the false name in the signature.
- Our protocol meets the security required for the design of VANETs, providing confidentiality, unforgeability, authentication, integrity, anonymity, non-repudiation, conditional traceability, revocability, and unlinkability. And our protocol can effectively protect against potential attacks, such as replay attacks, impersonation attacks, modification attacks, man-in-the-middle attacks, Ephemeral Secret Leakage (ESL) attacks, and full chosen-key attacks.
1.2. Organization
The rest of this article is arranged as follows. We introduce the related work in the Section 2. Section 3 provides the system model, scheme definition, security and attack model, design objectives, and ECC. Section 4 describes the specific content of our proposal. Section 5 and Section 6 give the security analysis and performance analysis of the scheme. Finally, Section 7 summarizes this paper.
2. Related Works
2.1. Certificateless Aggregate Signature Encryption
In traditional public key systems, the public key authentication of devices is achieved through Public Key Infrastructure (PKI). In VANETs, the rapid increase in the number of devices leads to a high overhead for storing PKI certificates and is not suitable for on-board units (OBUs) with limited computing and storage capacity [17]. To address the certificate management issues in PKI, Shamir [18] proposed the concept of Identity-Based Cryptography (IBC) in 1984. The principle of IBC is to use the user’s identity information (such as ID number, email, age, etc.) as the public key and apply to a trusted third party for the corresponding private key, namely the Key Generation Center (PKG). Since the private key in IBC is generated by the PKG, there is a key escrow problem. To solve the key escrow problem, Al-Riyami and Paterson [19] proposed the first certificateless signature (CLAS) scheme. In CLAS, the Key Generation Center (KGC) first sends a partial private key to the user. By combining the partial private key with a private key value determined by the user themselves, the user can generate a complete private key. Therefore, the KGC cannot access the user’s private key. In 2007, Castro and Dahab [20] introduced aggregate signatures and proposed the first certificateless aggregate signature scheme, which combined the advantages of certificateless encryption and aggregate signatures. In 2015, Horng et al. [21] proposed a certificateless aggregate signature scheme suitable for communication between vehicles and infrastructure in the Internet of Vehicles. This scheme uses pseudonyms to achieve conditional privacy protection. Li et al. [22] proved in the following year that Horng et al.’s scheme [21] did not achieve complete aggregation and was insecure against Type II attackers. In 2020, Mei et al. [12] proposed a certificateless aggregate signature scheme with conditional privacy protection in the Internet of Vehicles using bilinear pairings. However, due to the high cost of cryptographic operations using bilinear pairings, these schemes are not suitable for resource-limited environments. To reduce computational costs and time, Cui et al. [9] proposed a certificateless aggregate signature scheme without pairings, using elliptic curve encryption operations to improve computational efficiency. However, Xie et al. [14] found that the scheme in [9] was not proven to be existentially unforgeable against adversary . The scheme in [14] redesigned a certificateless aggregate signature scheme without pairings, introducing an edge computing architecture to perform signature verification and aggregation closer to the edge layer of the end user and proved that it was existentially unforgeable against adversary . In summary, although these certificateless aggregate signature schemes have improved computational efficiency and reduced computational costs, they still have vulnerabilities, lack tracking and revocation mechanisms, and are susceptible to replay attacks, malicious vehicle attacks, transient key leakage attacks, and complete key selection attacks. Therefore, a certificateless aggregate signature protocol with conditional traceability based on edge computing is proposed.
2.2. Online/Offline Encryption Technology
To enhance efficiency on resource-constrained devices, Even et al. [23] proposed a scheme to reduce computational overhead in digital signature processes by dividing the signing procedure into online/offline phases. The first phase (offline) is executed prior to message acquisition, while the second phase (online) occurs when message transmission is required. In 2008, Guo et al. [24] introduced an identity-based online/offline encryption (IBOOE) scheme where the offline phase operates without recipient identities or encrypted messages. This enables efficient completion of the online phase once recipient identities and messages become available. However, the ciphertext size in the scheme in [24] was excessively large, rendering it impractical for resource-limited devices. To address this issue, Lai et al. [25] achieved the shortest ciphertext size in both offline and online phases, demonstrating optimal performance during offline computations. Subsequently, Chen et al. [26] presented a certificateless signature scheme integrated with online/offline encryption technologies, requiring only one-point multiplication for resource-constrained edge devices in cloud–edge collaborative architectures, while verification demands only one bilinear pairing. In 2023, Ali et al. [5] proposed a heterogeneous online/offline signcryption scheme that eliminates the need for bilinear pairings, thereby reducing computational costs. Collectively, such OOE technologies have seen widespread adoption across diverse domains, including industrial networks, cloud computing, and VANETs, significantly improving encryption efficiency. However, security challenges persist in these schemes. By integrating TPD into physical devices, our proposed solution ensures security during both offline/online encryption phases while effectively mitigating ESL attacks.
2.3. Edge Computing Architecture
In recent years, the proliferation of internet-connected smart devices has brought significant data generation challenges in VANETs. Edge computing has gained increasing popularity and deployment across various latency-sensitive application domains, including VANETs [27]. As a technology enabling computation at the network edge, edge computing performs processing in proximity to data sources [28]. This architecture reduces data transmission latency and bandwidth demands by pushing computing and storage resources to the network periphery, thereby enhancing system responsiveness and efficiency.
In VANETs, edge computing applications are particularly critical. The massive volumes of data generated by vehicles require real-time processing and analysis to ensure traffic safety and efficiency. Traditional data centers are insufficient to handle the storage demands at this scale. Instead, CS can serve as a computing and storage platform for massive data in the Internet of Vehicles, enabling efficient data sharing between users and vehicles through centralized remote processing and storage. Edge computing nodes, such as RSUs, can process these data locally without transmitting all information to remote cloud servers. This not only mitigates network congestion but also lowers data transmission latency, enabling vehicles to respond more rapidly to traffic conditions [29]. Beyond improving data processing speed and efficiency, edge computing in VANETs enhances system security and privacy protection. By processing data at edge nodes, sensitive data transmission is minimized, reducing data leakage risks [30]. Furthermore, given the prevalence of resource-constrained devices in VANETs, cloud-collaborative frameworks provide specialized services that further optimize resource utilization and computational efficiency [31]. In 2023, Xie et al. [14] utilized edge computing to process data at the network edge, reducing the transmission of sensitive data and lowering the risk of leakage. Moreover, they employed a pseudonym mechanism to hide the true identities of vehicles, further protecting user privacy. In 2024, Han et al. [32] utilized edge computing to avoid the single-point-of-failure problem of CS, enhancing the robustness and reliability of the system.
3. Preliminaries
We introduce the system model, scheme definition, security and attack model, design objectives, and ECC in this section.
3.1. System Model
The network model of the VANET in this scheme is composed of vehicle, RSU, KGC, and TRA equipped with edge computing equipment. The structure is shown in Figure 1.
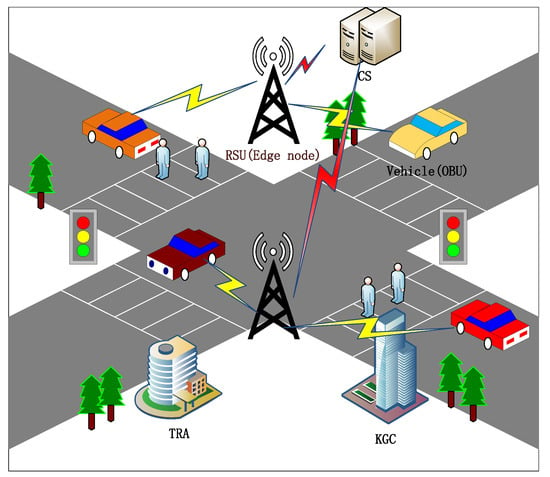
Figure 1.
System model.
- Vehicle: Each vehicle is equipped with OBUs, and each OBU is equipped with TPD. The OBU collects real-time traffic data and encrypts the information to communicate wirelessly with a nearby RSU. And the energy required for each signature encryption operation of the OBU is consistent. TPD protects the OBU’s encryption process, as well as securely storing sensitive data and the vehicle’s public and private keys.
- RSU: It is a roadside infrastructure that communicates with vehicles in range and verifies the traffic-related information received. RSU is equipped with edge computing equipment, which extends more powerful computing power to the edge of the network and can process large amounts of data intelligently and efficiently.
- KGC: It is part of a reliable TA and has powerful computing and storage capabilities. It is responsible for generating and publishing system parameters, registration of RSU and vehicle, and generation of partial private keys. Together with TRA, it is responsible for managing the entire system of VANETs. In this model, it is assumed that KGC is a semi-trusted institution.
- TRA: It is part of TA and is responsible for establishing and saving anonymity for vehicles and RSUs. If anonymous identity lapses or malicious vehicles appear, it will track and revocate them from the system, thus ensuring the security of the system. In this model, it is assumed that TRA is a completely reliable institution.
- CS: In this model, CS serves only as a data center to receive messages sent by edge nodes and store them for future reference.
3.2. Scheme Definition
In this section, we describe the algorithmic flow of the scheme structure.
- Setup: Given a security parameter , KGC generates the master private key a and the system public parameter .
- Anonymization: Given , TRA interacts with a user (such as a vehicle) with a real identity to generate a anonymous identity .
- Partial Private Key: Given , KGC generates a partial private key for that user.
- Public/Private Key: The user sets its full private key and public key .
- Offline Signcryption: Given a vehicle’s private key and a RSU’s public key , an offline ciphertext is obtained.
- Online Signcryption: Given , the vehicle’s anonymous identity and the RSU’s anonymous identity output the ultimate ciphertext .
- Unsigncryption: Given the ciphertext , RSU performs this operation to obtain plaintext and verifies it.
3.3. Security Model
To protect V2I communication, we define the security model of this scheme. According to the attacker’s behavior, we consider the following types of attackers.
(1) Type 1 attack (Public-Key Replacement Attack): The attacker possesses the target user’s private key and can replace the user’s public key at will but cannot access the KGC’s master private key a.
(2) Type 2 attack (Malicious KGC Attack): The attacker possesses the KGC’s master private key a and can generate the user’s partial private key but cannot know the user’s private key .
Game-1: This game is played between the challenger C and the adversary .
Setup: First, C inputs the security parameter 1, generates the master private key a and the system public parameters , and sends to . Additionally, C performs the public/private key operation to obtain and sends to .
Phase 1: In this phase, can make the following queries to C:
Partial Private Key Query: sends to C, C performs the partial private key operation to obtain the partial private key and sends it to .
Private Key Query: sends to C, C invokes the private key operation to obtain the private key and sends it to .
Public Key Query: sends to C, C invokes the public key operation to obtain the public key and sends it to .
Public Key Replacement Query: submits the public key to C, C replaces with in the list .
Signcryption Query: C performs the offline signcryption and online signcryption operations to generate and sends it to .
Unsigncryption Query: C performs the unsigncryption operation to generate M or ⊥ and sends it to .
Challenge: generates two messages and of the same length and marks them with the identity information , then sends them to the challenger C. C performs the partial private key and private key operations to obtain the sender’s complete private key and sends it to . C selects and obtains through the offline signcryption and online signcryption operations. Finally, C sends to .
Phase 2: In this phase, repeats the same queries as in phase 1. However, it cannot request the unsigncryption query operation on (, , ) to obtain the corresponding message.
Guess: outputs ; if , it indicates that the game is won.
Definition 1.
If no adversary can win Game 1 with a non-negligible advantage, the proposed scheme can achieve security.
Game-2: This game is played between the challenger C and the adversary .
Setup: First, C inputs the security parameter 1, generates the master private key a and the system public parameters , and sends params to . Additionally, C performs the public/private key operation to obtain and sends to .
Phase 1: At this stage, can make the following queries:
Partial Private Key Query: sends to C, and C performs the partial private key operation to obtain the partial private key and sends it to .
Private Key Query: sends to C, and C invokes the private key operation to obtain the private key and sends it to .
Public Key Query: sends to C, and C invokes the public key operation to obtain the public key and sends it to .
Signcryption Query: C performs the offline signcryption and online signcryption operations to generate and sends it to .
Unsigncryption Query: C performs the unsigncryption operation to generate M or ⊥ and sends it to .
Forgery: forges a signature , corresponding to the message and the sender identity , satisfying the following conditions:
(1) has not been queried in the partial private key query of Phase 1 (i.e., has not obtained );
(2) has not been generated in the signcryption query of Phase 1.
Guess: C verifies the validity of . If passes the verification and is valid, succeeds in the forgery.
Definition 2.
If no polynomial-time adversary can win Game 2 with a non-negligible advantage (i.e., successfully forge a valid ciphertext), then the scheme satisfies security.
3.4. Elliptic Curve Cryptography
Let be a finite field defined by a large prime number p, where . Over the finite field , an elliptic curve E consists of all points satisfying the equation , where , and the discriminant condition holds. Additionally, a point at infinity O is included. All points on the elliptic curve E, together with the point at infinity O, form a group , known as the elliptic curve group. An addition operation is defined in the group such that for any two points , there exists a unique point with . The addition operation satisfies associativity, commutativity, and the existence of an identity element O (i.e., for any , we obtain ).
Elliptic Curve Discrete Logarithm Problem (ECDLP): Given two points P and Q in the elliptic curve group , where (x is some unknown integer), the ECDLP is to find this integer x. In ECC, it is assumed that this problem is computationally infeasible, meaning no efficient algorithm can solve it in probabilistic polynomial time (PPT).
4. Proposed Scheme
In Section 4, we describe the construction of our scheme in detail. Our scheme consists of six algorithms, and the flow of our scheme is shown in Figure 2. For ease of reading, the symbols used in this protocol are defined in Table 1.
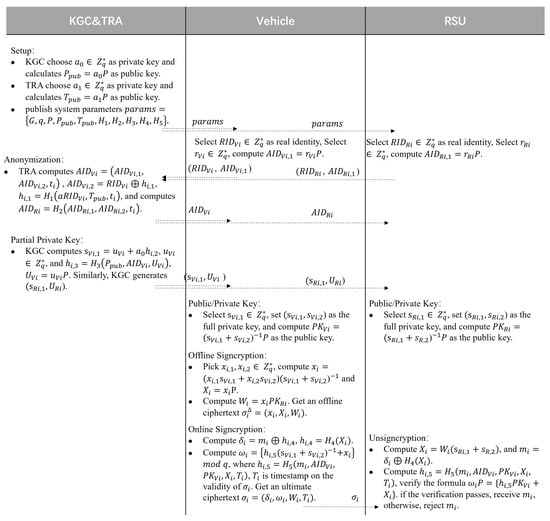
Figure 2.
Process of our scheme.

Table 1.
Notations with definition.
4.1. Setup
This algorithm takes a security parameter as input. It generates a group of an elliptic curve with prime order q, where P is the generator of . Next, the KGC and TRA execute the following steps:
(1) KGC randomly selects a parameter as master private key and calculates master public key .
(2) TRA randomly selects a parameter as master private key and calculates master public key .
(3) Select four hash functions , , , and .
(4) KGC and The TRA store and , respectively, and publish the system parameter .
4.2. Anonymization
TRA invokes this algorithm to generate the anonymous identity of vehicle and RSU. The algorithm is executed as follows:
(1) A vehicle with real identity randomly selects , computes , and sends to the TRA.
(2) TRA checks the validity of and computes , where and is the anonymous identity’s validity period. The vehicle’s anonymous identity is .
(3) TRA stores in the local database, then sends to the KGC and the vehicle. Similarly, TRA generates and sends to the KGC and RSU.
4.3. Partial Private Key
In this phase, the KGC generates the partial private key of vehicle and RSU, and the KGC executes the following operations:
(1) KGC receives sent by the vehicle and retrieves in the local list; if exists and is valid, KGC proceeds to the next step.
(2) KGC selects and computes . Then, KGC calculates as partial secret key, where .
(3) KGC sends the to the vehicle secretly. Similarly, KGC generates and sends it to the RSU.
4.4. Public/Private Key
The vehicle is calculated to obtain the full key at this stage, and it executes the following operations:
(1) The vehicle receives and checks the equation , where . If not, the vehicle rejects it; otherwise, the vehicle accepts the and proceeds to the next step.
(2) The vehicle randomly selects as its secret value, and then the full private key is set as .
(3) The vehicle calculates as the public key.
(4) Similarly, the RSU generates as the full private key and sets its public key as .
4.5. Offline Signcryption
The vehicle whose anonymous identity is obtains the public key of the RSU and performs the following operations:
(1) Pick at random.
(2) Compute , and .
(3) Compute .
(4) Obtain an offline ciphertext .
4.6. Online Signcryption
In this phase, the vehicle gives , the offline signcryption , and its anonymous identity , public key , and private key . The vehicle computes the following algorithm:
(1) Compute , where .
(2) Compute , where .
(3) Obtain an ultimate ciphertext . The vehicle sends to a nearby RSU where is the timestamp on the validity of .
4.7. Unsigncryption
When the RSU receives the ciphertext from the vehicle, it first checks the freshness of . If or is invalid, is rejected. Otherwise, the RSU gives ciphertext , the vehicle’s anonymous identity , public key , and the RSU’s private key , and the verification process is executed below:
(1) Compute .
(2) Recover by calculating .
(3) Compute and verify the formula , Then, receive if the verification passes; otherwise, reject .
4.8. Aggregate Unsigncryption
This algorithm has the functions of ciphertext aggregation and batch verification, which can significantly improve the efficiency. If is valid, the RSU receives multiple ciphertexts sent by multiple vehicles and provides . This algorithm works as follows:
(1) The RSU selects a small random integer set and calculates , where and is a small integer (e.g., ). and outputs aggregate ciphertext .
(2) Similarly, compute and recover by calculating . Then, compute .
(3) Compute . If the above equations hold, accept the messages . If not, reject it.
5. Security Analysis
In Section 5, we give formal security analysis and informal security analysis of our scheme and prove the security of the security model in the VANETs.
5.1. Formal Security Analysis
(1) Correctness: The next steps are to verify the validity of the aggregated signcryption.
Firstly, we calculate
Secondly,
Then,
(2) Confidentiality: Our scheme achieves security under the Computational Diffie–Hellman (CDH) assumption.
Theorem 1.
If there is an opponent that can break our in PPT with a non-negligible advantage ε, then there is a challenger that can solve the CDH problem in polynomial time with a non-negligible advantage . Here, is the number of private key extraction queries, is the number of signcryption queries, and e is the base of the natural logarithm.
Proof.
Suppose has a CDH problem instance and intends to compute . constructs a simulation scheme and interacts with . Assuming that the hash function is a random oracle under the control of , its value is uniformly random and unpredictable unless the corresponding hash query is made.
- : performs the setup operation to obtain ( is and is not accessible) and , and then publishes .
- :-Public key queries: When receives an identity from , first checks whether an item . If so, returns . Otherwise, generates a new according to and stores it in and returns it to .- queries: When receives queries from , first checks whether list exists items , if so, returns to ; otherwise generates a new for in and returns it to .- queries: When receives an query from , first checks the list for the presence of items , and if so, returns to . Otherwise, will generate a new in for and return it to .- queries: When receives queries from , first checks the list for the existence of items , and if so, returns to ; otherwise, generates a new in for and returns it to .- queries: When receives queries from , first checks the list for the existence of items , and if so, returns to ; otherwise, generates a new for in and returns it to .- queries: When receives an query from , first checks the list for the presence of items , and if so, returns to ; otherwise, generates a new for in and returns it to .-Partial private key queries: When receives an anonymous identity from , performs the partial private key operation to calculate the partial private key and returns it to .-Private key queries: When receives one from , performs the private key operation to obtain and returns it to . Otherwise, run the public key query to generate the private key.-Public key replacement queries: submits public key to , which replaces with in list .-Signcryption queries: When requests signcryption message m, simulates offline signcryption and online signcryption operations to generate the ciphertext and returns it to .-Unsigncryption queries: generates m or ⊥ by simulating the unsigncryption operation and sends it to .
- : selects two equal-length messages, , and specifies the target identity . randomly selects to generate the challenge ciphertext and return it to .
- : can repeat the query of , but it is forbidden to initiate a decryption query for the challenge ciphertext . If this rule is violated, terminates the interaction immediately.
- : outputs guess value . If , then wins.
□
fails if has already performed a private key query in response to and . The event in which does not make such a query is represented by x, and its probability is . The event that does not stop executing at is denoted by with probability . The event that does not stop execution at Challenge is denoted by with probability . Therefore, the probability that does not stop executing throughout the simulation is . Knowing , it can be found that when is large enough, will be infinitely close to (e represents the base of the natural logarithm). Therefore, the probability that does not stop executing during the entire simulation is .
If attacks the confidentiality of our scheme with a non-negligible advantage , can construct a solution to the CDH problem from ’s interactive record. Through the above analysis, we can obtain that the advantage of is .
(3) Unforgeability: Our scheme implements security under the ECDLP.
Theorem 2.
If there is an opponent who can break our in PPT with a non-negligible advantage ε, then there is a challenger who can solve the ECDLP in polynomial time with a non-negligible advantage . Here, is the number of private key extraction queries, is the number of signcryption queries, and e is the base of the natural logarithm.
Proof.
Suppose has an ECDLP instance , and intends to compute . constructs a simulation scheme and interacts with . Assuming that the hash function is a random oracle under control, its value is uniformly random and unpredictable unless the corresponding hash query is made.
- : performs the setup operation to obtain ( is and is not accessible) and , and then publishes .
- :-Queries: Perform the same queries, public key queries, partial private key queries, private key queries, and public key replacement queries as in .-Signcryption queries: submits message m and anonymous to request signcryption of m. queries whether exists. If does not exist, perform related operations to generate and save and corresponding to . The offline signcryption and online signcryption operations are simulated to generate the ciphertext and return it to .-Unsigncryption queries: submits signature and anonymous identity to request the signcryption of . searches the public key corresponding to and simulates the unsigncryption operation to obtain m or ⊥ and sends it to .
- : randomly selects , , calculates , then calculates , , chooses to prove that . Return to . If solves the ECDLP, the private key b can be calculated; otherwise, the ECDLP is not solved.
□
fails if has already performed a private key query in response to . The event in which does not make such a query is represented by x, and its probability is . The event that does not stop executing at is denoted by with probability . The event that does not stop execution at challenge is denoted by with probability . Therefore, the probability that does not stop executing throughout the simulation is . Knowing , it can be found that when is large enough, will be infinitely close to (e represents the base of the natural logarithm). Therefore, the probability that does not stop executing during the entire simulation is .
From the above analysis, it can be seen that the probability of not stopping execution in the whole process is , and can attack the unforgeability of the improved scheme with a non-negligible probability . Then, can obtain a solution to the ECDLP in PPT with probability .
5.2. Informal Security Analysis
The security requirements met by our scheme are as follows:
(1) Confidentiality and unforgeability: Formal security analysis confirms that our scheme achieves confidentiality and unforgeability.
(2) Authentication and integrity: According to ’s proof of the existence of unforgeability, our scheme is secure against Type I and Type II attackers who cannot forge a valid signature.
(3) Anonymity: Anonymous identity is used to hide the real identity, where , . represents the timestamp of , ensuring the validity of . The attacker would have to obtain if they wanted to obtain the real identity . However, is the key chosen by the TRA. According to the ECDLP, no attacker can extract from Tpub in PPT. Therefore, our scheme ensures anonymity.
(4) Non-repudiation: If the vehicle attempts to deny the transmission, the TRA can verify that the message was indeed sent by the vehicle by verifying the legitimacy of the signature. Because of the uniqueness and confidentiality of the private key, the signer cannot deny its signcryption behavior, thus ensuring non-repudiation.
(5) Conditional traceability and revocability: If the anonymous identity is used to send malicious messages, the TRA can search the corresponding anonymous identity in the database, find the real identity bound to it, and revoke the registration of the malicious vehicle to achieve conditional traceability and revocability.
(6) Unlinkability: In the anonymization phase, TRA randomly selects to generate anonymous identity. In addition, the vehicle randomly selects and computes the resulting to generate the signature. Due to the randomness of , and , neither different anonymous identities nor different signatures of the same vehicle can be linked by the attacker in the PPT.
(7) Resist attacks: In addition to the above security features, our scheme resists the following common attacks.
Replay attacks: There are two timestamps in our scheme; is included in the anonymous identity AIDVi and is included in the signature . When a message/signature pair is received, the verifier can detect the playback of the message by verifying the freshness of the timestamp.
Impersonation attacks: In order to launch a impersonation attack, the attacker should generate a valid signature. However, according to , an attacker cannot generate valid message/signature pairs in PPT because neither of them can solve the ECDLP. Therefore, our scheme can successfully resist impersonation attacks.
Modification attacks: According to the security analysis of our scheme described above, any modification of the message/signature pair can be detected by checking whether the formula holds, so our scheme can successfully resist modification attacks.
Man-in-the-middle attacks: Our scheme implements authentication based on ECDLP security, making it impossible for any third party to forge a valid signature between the message signer and the verifier, so our scheme is resistant to this attack.
ESL attacks: If the temporary keys and of the offline phase are compromised, the attacker cannot calculate unless the attacker breaks the CDH problem. According to the confidentiality proof of , our scheme successfully defends against ESL attacks.
Full chosen-key attack: Our scheme uses a simplified small index testing technique in the aggregation process [33]. Using the above techniques, we add small random integer sets in the aggregate unsigncryption phase. Due to the randomness of , any modification to a single signature can be detected by the verifier (a strict proof can be found in [33]). Therefore, our scheme successfully resists the full chosen-key attack.
6. Performance Analysis
In Section 6, we analyze the performance of the protocol in terms of computational cost and communication overhead. We chose four signcryption schemes [26,34,35,36] to compare with our scheme to prove the effectiveness of our scheme. Therefore, in the comparison experiment phase, we choose the elliptic curve , where q is 160 primes, p is 512 primes, is the addition group of order q, and P is the generator of . The simulation uses two core Intel Core i5 processors clocked at 2.5 GHz, 4 GB of RAM, and a Linux operating system.
6.1. Computational Overhead Comparison
To calculate the computational cost of each scheme, we conducted experiments on the time cost of the main cryptographic operations. Each cryptographic operation was run 1000 times, and the average value was taken as the final time cost. The cryptographic operations involved in our scheme and those in the schemes [26,34,35,36] are as follows: (1) represents scalar multiplication in ; (2) represents a hash function mapping to the string ; (3) represents a hash function mapping to the string ; (4) represents symmetric bilinear pairing; (5) represents exponentiation in the multiplicative group. We list the running times of these cryptographic operations in Table 2. Based on the above values, the computational costs of the five schemes are given in Table 3, assuming that each vehicle only sends one message to the RSU and n is the number of vehicles, so the number of ciphertexts is also n. In the performance analysis, if the scheme adopts the OOE technology, we only focus on the online signcryption operation cost rather than the complete offline–online signcryption operation cost. The reason is as follows: in the real application environment, since the precomputation in the offline stage does not involve real-time messages, the computation process in this stage can be carried out during idle periods. In other words, this study focuses on the real-time message processing stage.

Table 2.
Execution time of primary operations.

Table 3.
Computational overhead for each scheme.
In our scheme, the complex scalar multiplication operation is run in the offline stage, and only simple hash function operations are run in the online stage. This division of labor reduces the burden on vehicles in real-time computation, thereby improving communication efficiency. In contrast, scheme [34] only uses one scalar multiplication in the offline stage, resulting in additional scalar multiplications in the online stage. Therefore, the online stage cost of our scheme is much smaller than that of the scheme in [34]. Thus, the precomputation in the offline stage is of practical significance. Taking the transmission of a sensitive message as an example, the computational costs of signcryption and decryption in these comparison schemes are shown in Figure 3 and Figure 4.
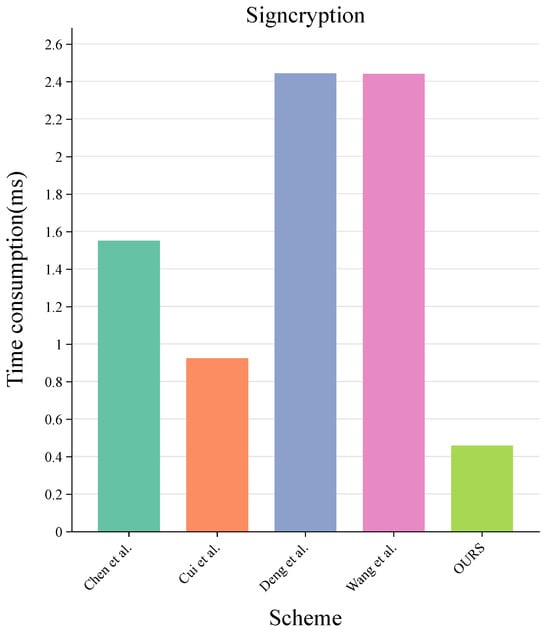
Figure 3.
Comparison of computation cost in signcryption [26,34,35,36].
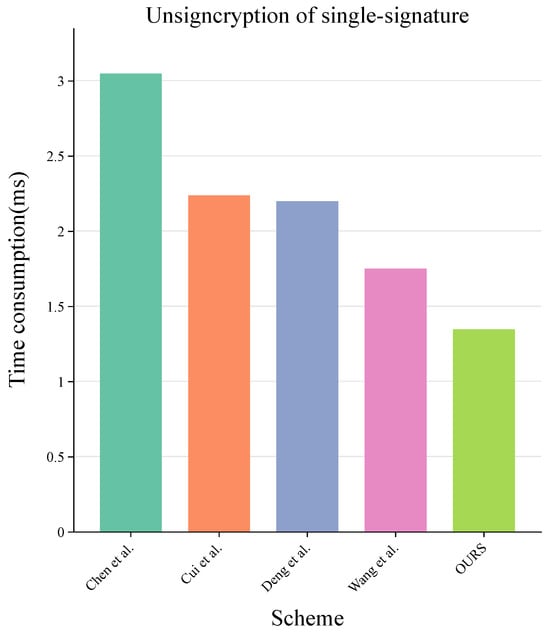
Figure 4.
Comparison of computation cost in unsigncryption of single signature [26,34,35,36].
For the scheme in [26], one symmetric bilinear pairing, two scalar multiplications, two hash functions mapping to the string , and one hash function mapping to the string are implemented in the signcryption phase. Four symmetric bilinear pairings, one scalar multiplication, three hash functions mapping to the string , and one hash function mapping to the string are implemented in the unsigncryption phase. For the scheme in [34], two scalar multiplications, three hash functions mapping to the string , and one hash function mapping to the string are implemented in the signcryption phase. Five scalar multiplications, two hash functions mapping to the string , and one hash function mapping to the string are implemented in the unsigncryption phase. For the scheme in [35], one symmetric bilinear pairing, four scalar multiplications, four hash functions mapping to the string , and one hash function mapping to the string are implemented in the signcryption phase. Two scalar multiplications, two symmetric bilinear pairing, three hash functions mapping to the string , and one hash function mapping to the string are implemented in the unsigncryption phase. For the scheme in [36], one symmetric bilinear pairing, four scalar multiplications, three hash functions mapping to the string , and one hash function mapping to the string are implemented in the signcryption phase. Two symmetric bilinear pairings, one scalar multiplication, three hash functions mapping to the string , and one hash function mapping to the string are implemented in the unsigncryption phase. For our scheme, in the signcryption phase, two scalar multiplications, one hash function mapping to the string , and one hash function mapping to the string are implemented. In the unsigncryption phase, three scalar multiplications, one hash function mapping to the string , and one hash function mapping to the string are implemented. Based on the analysis above, it can be observed from Figure 3 and Figure 4 that our scheme demonstrates significantly lower computational overhead during the signcryption phase compared to other schemes. Furthermore, in the decryption phase, our scheme achieves the smallest computational cost, and this is accomplished without employing symmetric bilinear pairings.
According to the DSRC specification, each vehicle must broadcast a basic safety message every 300 ms [37]. Assuming that there are usually 100 vehicles within the communication range of the RSU, approximately 350 messages are generated per second. To enhance the rationality of the analysis, our evaluation should include the computational cost of 350 signcryption operations. As shown in Figure 5, and with the increase in the number of messages, the signcryption efficiency of our scheme is superior to that of the schemes in [26,34,35,36].
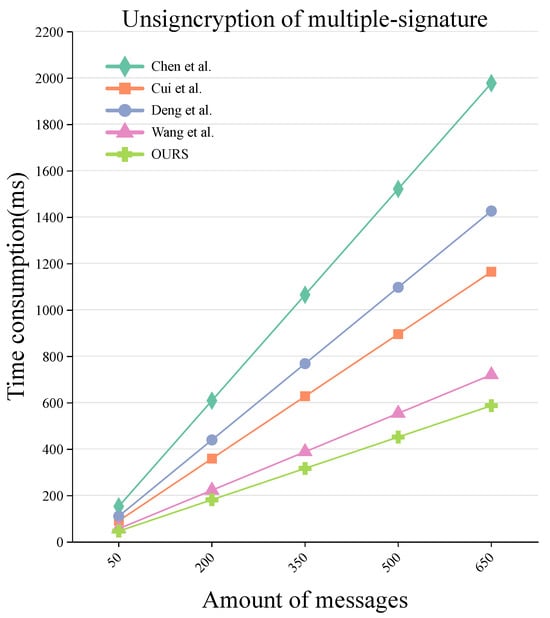
Figure 5.
Comparison of computation cost in unsigncryption of multiple signatures [26,34,35,36].
We used omnet++ to conduct a real simulation of the time delay of this scheme, including the signcryption time, communication delay, and unsigncryption time. By making corresponding adjustments to the number of vehicles, when the number of vehicles was 20, the corresponding average communication delay was 13.9 ms. When the number of vehicles was 40, the corresponding average communication delay was 15.1 ms. When the number of vehicles was 60, the corresponding average communication delay was 16.6 ms. When the number of vehicles was 80, the corresponding average communication delay was 14.2 ms. When the number of vehicles was 100, the corresponding average communication delay was 14.6 ms. Figure 6 shows part of the simulation model based on 20 vehicles in the experiment. In Figure 6, our scheme defines the effective communication range of the RSU as 1 km and the speed of the vehicle as 30 m/s.
Figure 6.
Part of the simulation model.
6.2. Communication/Storage Cost
Suppose that the element in G has size and the message size is . Given that the primary communication overhead depends on ciphertext size, Table 4 presents a comparative analysis of the communication costs for the five schemes. The storage cost depends primarily on the size of the public/private key pair for both the sender and receiver, as well as the size of the signcryption itself. As shown in Table 4, we have reduced computing costs without increasing communication costs.

Table 4.
Computational overhead for each scheme.
7. Conclusions
In order to meet the complex security requirements of VANETs, we propose a certificateless aggregated signcryption scheme based on edge computing. The scheme eliminates the dependence on expensive bilinear pairing operations and improves computational efficiency through online/offline encryption technology, making it suitable for resource-constrained environments. By adopting pseudonym mechanisms and conditional traceability, the protocol ensures strong privacy protections while enabling the identification and revocation of malicious vehicles. The security analysis shows that the scheme satisfies the confidentiality of and unforgerability of under CDH and ECDLP assumptions and can effectively resist common attacks, such as replay attacks, impersonation attacks, modification attacks, man-in-the-middle attacks, ESL attacks, and full chosen-key attacks. The performance analysis further verifies the advantages of the proposed scheme in terms of computation and communication overhead compared with the existing schemes and realizes faster signature encryption and de-signature encryption processes. This scheme still requires the KGC and TRA to generate and distribute some private keys and anonymous identities. This process increases the management cost of the system and potential security risks. The future research direction focuses on studying more lightweight key management and distribution mechanisms to reduce the burden of the KGC and TRA while improving the security and reliability of the system. In addition, in the work of reducing communication costs, we will shorten the length of the ciphertext without affecting the effect.
Author Contributions
Conceptualization, W.Z. and X.X.; methodology, W.Z.; software, W.Z.; validation, Q.G. and X.X.; formal analysis, Q.G.; investigation, X.X.; resources, W.Z.; data curation, X.X.; writing—original draft preparation, Q.G.; writing—review and editing, W.Z.; visualization, X.X.; supervision, W.Z.; project administration, Q.G.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Guangxi Science and Technology Major Project (grant number Guike AA23062035-2), the Guangxi Science and Technology Base and Talent Special Project (grant number Guike AD24010060).
Data Availability Statement
The anonymized data used in this study are available upon request from the corresponding author.
Acknowledgments
We thank the anonymous reviewers for their comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, Y.; Cao, L.; Qiao, Z.; Xia, Z.; Yang, B.; Zhang, M.; Zhang, W. An Efficient Identity Authentication Scheme with Dynamic Anonymity for VANETs. IEEE Internet Things J. 2023, 10, 10052–10065. [Google Scholar] [CrossRef]
- Wang, L.L.; Gui, J.S.; Deng, X.H.; Zeng, F.; Kuang, Z.F. Routing Algorithm Based on Vehicle Position Analysis for Internet of Vehicles. IEEE Internet Things J. 2020, 7, 11701–11712. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, X.; Zhang, N.; Tian, Y.; Ma, X.; Ma, J. Three-factor authentication protocol using physical unclonable function for IoV. Comput. Commun. 2021, 173, 45–55. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Xu, B.; Huang, X. An Efficient Identity-Based Conditional Privacy-Preserving Authentication Scheme for Vehicular Ad Hoc Networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2681–2691. [Google Scholar] [CrossRef]
- Ali, I.; Chen, Y.; Li, J.; Wakeel, A.; Pan, C.; Ullah, N. Efficient Offline/Online Heterogeneous-Aggregated Signcryption Protocol for Edge Computing-Based Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14506–14519. [Google Scholar] [CrossRef]
- Peng, C.; Chen, J.; Obaidat, M.S.; Vijayakumar, P.; He, D. Efficient and Provably Secure Multireceiver Signcryption Scheme for Multicast Communication in Edge Computing. IEEE Internet Things J. 2020, 7, 6056–6068. [Google Scholar] [CrossRef]
- Jia, X.; He, D.; Kumar, N.; Choo, K.K.R. A Provably Secure and Efficient Identity-Based Anonymous Authentication Scheme for Mobile Edge Computing. IEEE Syst. J. 2020, 14, 560–571. [Google Scholar] [CrossRef]
- Kumar, P.; Sharma, V. On the security of certificateless aggregate signature scheme in vehicular ad hoc networks. In Proceedings of the Soft Computing: Theories and Applications: Proceedings of SoCTA 2016; Springer: Singapore, 2018; Volume 1, pp. 715–722. [Google Scholar]
- Cui, J.; Zhang, J.; Zhong, H.; Shi, R.; Xu, Y. An efficient certificateless aggregate signature without pairings for vehicular ad hoc networks. Inf. Sci. 2018, 451, 1–15. [Google Scholar] [CrossRef]
- Kamil, I.A.; Ogundoyin, S.O. An improved certificateless aggregate signature scheme without bilinear pairings for vehicular ad hoc networks. J. Inf. Secur. Appl. 2019, 44, 184–200. [Google Scholar] [CrossRef]
- Thumbur, G.; Rao, G.S.; Reddy, P.V.; Gayathri, N.; Reddy, D.K.; Padmavathamma, M. Efficient and secure certificateless aggregate signature-based authentication scheme for vehicular ad hoc networks. IEEE Internet Things J. 2020, 8, 1908–1920. [Google Scholar] [CrossRef]
- Mei, Q.; Xiong, H.; Chen, J.; Yang, M.; Kumari, S.; Khan, M.K. Efficient certificateless aggregate signature with conditional privacy preservation in IoV. IEEE Syst. J. 2020, 15, 245–256. [Google Scholar] [CrossRef]
- Dai, C.; Xu, Z. Pairing-Free Certificateless Aggregate Signcryption Scheme for Vehicular Sensor Networks. IEEE Internet Things J. 2022, 10, 5063–5072. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, Y.; Ali, I.; Pan, C.; Li, F.; He, W. Efficient and Secure Certificateless Signcryption without Pairing for Edge Computing-Based Internet of Vehicles. IEEE Trans. Veh. Technol. 2022, 72, 5642–5653. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, C.; Chen, G.; Jin, Y.; Zong, H. A heterogeneous online/offline signcryption scheme for Internet of Vehicles. Veh. Commun. 2023, 43, 100635. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, X.; Bao, Y.; Cao, Y.; Wen, J. Efficient and Provably Secure Offline/Online Heterogeneous Signcryption Scheme for VANETs. IEEE Internet Things J. 2024, 11, 41248–41260. [Google Scholar] [CrossRef]
- Ogundoyin, S.O. An autonomous lightweight conditional privacy-preserving authentication scheme with provable security for vehicular ad-hoc networks. Int. J. Comput. Appl. 2020, 42, 196–211. [Google Scholar] [CrossRef]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the Advances in Cryptology: Proceedings of CRYPTO 84 4; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2003; pp. 452–473. [Google Scholar]
- Castro, R.; Dahab, R. Efficient certificateless signatures suitable for aggregation. Cryptol. ePrint Arch. 2007, 2007, 453–478. [Google Scholar]
- Horng, S.J.; Tzeng, S.F.; Huang, P.H.; Wang, X.; Li, T.; Khan, M.K. An efficient certificateless aggregate signature with conditional privacy-preserving for vehicular sensor networks. Inf. Sci. 2015, 317, 48–66. [Google Scholar] [CrossRef]
- Li, J.; Yuan, H.; Zhang, Y. Cryptanalysis and improvement of certificateless aggregate signature with conditional privacy-preserving for vehicular sensor networks. Cryptol. ePrint Arch. 2016. Available online: https://eprint.iacr.org/2016/692 (accessed on 7 February 2023).
- Even, S.; Goldreich, O.; Micali, S. On-line/off-line digital signatures. J. Cryptol. 1996, 9, 35–67. [Google Scholar] [CrossRef]
- Guo, F.; Mu, Y.; Chen, Z. Identity-based online/offline encryption. In Proceedings of the Financial Cryptography and Data Security: 12th International Conference, FC 2008, Cozumel, Mexico, 28–31 January 2008; Revised Selected Papers 12. Springer: Berlin/Heidelberg, Germany, 2008; pp. 247–261. [Google Scholar]
- Lai, J.; Mu, Y.; Guo, F. Efficient identity-based online/offline encryption and signcryption with short ciphertext. Int. J. Inf. Secur. 2017, 16, 299–311. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Wen, M.; Zhang, K.; Chen, K. Efficient certificateless online/offline signcryption scheme for edge IoT devices. IEEE Internet Things J. 2021, 9, 8967–8979. [Google Scholar] [CrossRef]
- Miao, D.; Liu, L.; Xu, R.; Panneerselvam, J.; Wu, Y.; Xu, W. An efficient indexing model for the fog layer of industrial internet of things. IEEE Trans. Ind. Informatics 2018, 14, 4487–4496. [Google Scholar] [CrossRef]
- Fan, K.; Pan, Q.; Wang, J.; Liu, T.; Li, H.; Yang, Y. Cross-domain based data sharing scheme in cooperative edge computing. In Proceedings of the 2018 IEEE International Conference on Edge Computing (EDGE), San Francisco, CA, USA, 2–7 July 2018; pp. 87–92. [Google Scholar]
- Hou, X.; Li, Y.; Chen, M.; Wu, D.; Jin, D.; Chen, S. Vehicular fog computing: A viewpoint of vehicles as the infrastructures. IEEE Trans. Veh. Technol. 2016, 65, 3860–3873. [Google Scholar] [CrossRef]
- Roman, R.; Lopez, J.; Mambo, M. Mobile edge computing, fog et al.: A survey and analysis of security threats and challenges. Future Gener. Comput. Syst. 2018, 78, 680–698. [Google Scholar] [CrossRef]
- Ning, Z.; Zhang, K.; Wang, X.; Guo, L.; Hu, X.; Huang, J.; Hu, B.; Kwok, R.Y. Intelligent edge computing in internet of vehicles: A joint computation offloading and caching solution. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2212–2225. [Google Scholar] [CrossRef]
- Yang, W.; Cao, P.; Zhang, F. A secure pairing-free certificateless online/offline signcryption scheme with batch verification for edge computing-based VANETs. IEEE Trans. Veh. Technol. 2024, 74, 1570–1583. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Song, B.; Choi, D.; Jin, S.H.; Cho, H.S.; Lee, M.K. Simplified small exponent test for batch verification. Theor. Comput. Sci. 2017, 662, 48–58. [Google Scholar] [CrossRef]
- Cui, M.; Han, D.; Wang, J. An efficient and safe road condition monitoring authentication scheme based on fog computing. IEEE Internet Things J. 2019, 6, 9076–9084. [Google Scholar] [CrossRef]
- Deng, L. Anonymous certificateless multi-receiver encryption scheme for smart community management systems. Soft Comput. 2020, 24, 281–292. [Google Scholar] [CrossRef]
- Deng, L.; Wang, B.; Gao, Y.; Chen, Z.; Li, S. Certificateless anonymous signcryption scheme with provable security in the standard model suitable for healthcare wireless sensor networks. IEEE Internet Things J. 2023, 10, 15953–15965. [Google Scholar] [CrossRef]
- Han, Y.; Song, W.; Zhou, Z.; Wang, H.; Yuan, B. eCLAS: An efficient pairing-free certificateless aggregate signature for secure VANET communication. IEEE Syst. J. 2021, 16, 1637–1648. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).