A Novel Mathematical Approach for Inductor-Current Expressions Definition in Multilevel Dual-Active-Bridge Converters

Abstract

The study of multilevel dual-active-bridge (DAB) converters has garnered significant attention in recent years thanks to their advantages with respect to the conventional two-level (2L) DAB; namely, its greater performance and its capability to operate at higher voltage. The analysis of the converter high-frequency inductor current ($i_{\mathrm{L}}$) is crucial, for instance, to compute its root mean square (RMS) value, required to estimate the conduction losses in the converter. The mathematical expression of $i_{\mathrm{L}}$ is piecewise and multiple variations, i.e., modes, exist depending on the modulation parameter values. This increases the complexity of converter performance analytical study. Thus, a more practical and generalizable expression of $i_{\mathrm{L}}$ current is desirable. This paper proposes novel compact analytic expressions for the instantaneous and RMS inductor current in the 2L-NL DAB converter, leveraging binary functions to define the piecewise intervals and to identify the mode as a function of the modulation parameter values. The proposed method paves the way for more simple and computationally efficient DAB performance optimization software tools that allow exploring any given converter structures and modulation strategies.

1. Introduction

Dual-active-bridge (DAB) dc-dc converters have become popular in industrial applications due to their great efficiency and power density. As the demand for high-performance power conversion continues to rise, DAB converter topologies have emerged as an attractive solution, particularly in systems that require both bidirectional power flow and galvanic isolation [1,2]. Moreover, the introduction of multilevel (ML) converter-leg topologies in the DAB offer several performance gains [3,4]. For instance, for the same semiconductor device voltage rating, ML topologies allow increasing the dc-port voltages and the converter power rating, compared to conventional two-level (2L) topologies. On the other hand, for the same dc-port voltage, they allow reducing the converter conduction and switching losses by using lower-voltage-rated semiconductor devices with better performance figures and cost benefit ratios. Additionally, ML topologies open the door to advanced modulation techniques that leverage the additional degree of freedom offered by the ML ac-voltage waveforms to further improve the converter performance [5,6,7]. ML DAB converters have a wide range of applications, such as solid-state transformers [8,9], high-power battery storage systems [10,11], electric vehicles fast-charging stations [12,13] or low-voltage dc distribution systems [14,15,16,17]. They may also be applicable to lower power applications, given their comparable better performance as a trade-off of cost and complexity.

The performance analysis of ML DAB converters requires an accurate study of the current flowing through its high-frequency inductor ($i_{\mathrm{L}}$). For instance, it allows determining the root mean square (RMS) current flowing through the power semiconductor devices and passive components and thus computing their conduction losses. Therefore, an accurate expression for $i_{\mathrm{L}}$ in the form of a piecewise expression is necessary for the analysis of the converter [7,14,18,19].

However, the piecewise-defined nature of $i_{\mathrm{L}}$ presents a challenge for its study. When any of the DAB ac-voltage waveforms presents more than two voltage levels, different piecewise expressions for $i_{\mathrm{L}}$ arise (known as “modes” or “cases” in the literature), each one valid for different intervals of the modulation parameters, i.e., the phase shift and voltage waveform duty cycles. The number of $i_{\mathrm{L}}$ expressions increases as the number of levels in the ac-voltage waveform increases, for instance, when ML converter leg topologies are employed in the DAB. Thus, ML DAB performance analysis through the analytical study of the $i_{\mathrm{L}}$ piecewise expressions becomes complex and laborious.

To address this challenge, this paper proposes a generalized and compact mathematical function that provides the DAB $i_{\mathrm{L}}$ piecewise expression, employing binary indicator functions to define the piecewise intervals and to identify the mode as a function of the modulation parameter values. The proposed expression is valid for any DAB featuring a two-level square-wave ac voltage on one side and a staircase-wave ac voltage with any number of levels on the other side, i.e., a 2L-NL ML DAB converter. With the proposed generalized function, the paper also provides the generalized function for the DAB inductor RMS current.

The rest of the paper is organized as follows: First, Section 2 derives the proposed generalized function that provides the compact expressions for $i_{\mathrm{L}}$ instantaneous and RMS values for a 2L-NL DAB converter. The generalization to N levels is accomplished by following an inductive process, first analyzing the 2L-3L DAB and 2L-4L DAB cases and finally inferring the generalized function. Then, Section 3 validates the proposed function by comparing numerically and graphically $i_{\mathrm{L}}$ for multiple modulation parameter values against the results obtained through Fourier analysis of the current. Section 4 performs a comparison of the computational time required to obtain $i_{\mathrm{L}}$ instantaneous and RMS values using the compact expressions and through Fourier analysis. Finally, Section 5 discusses the implications of the proposed method and outlines future research work.

2. Derivation of the Generalized Inductor Current Expression

Let us consider the ideal lossless ML DAB converter shown in Figure 1, featuring two 2L converter legs in side a and two NL NPC converter legs in side b, that is, a single-phase 2L-NL DAB converter. Such a converter is capable of synthesizing an ac-voltage waveform with two voltage levels in side a ($v_{\mathrm{a}}$) and $2N-1$ voltage levels in side b ($v_{\mathrm{b}}$), as shown in Figure 2a and Figure 2b, respectively. Parameters $V_{\mathrm{a}}$ and $V_{\mathrm{b}}$ are the dc-link voltages of sides a and b of the converter, respectively. Let us consider that the capacitance in the converter dc port is large enough such that $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$ are constant over each waveform step interval. Let us also consider a modulation where $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$ present quarter-wave symmetry and that it works in steady-state operation. As shown in Figure 2, a total of N modulation angles are used, which are defined as the phase shift between $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$, $\phi$, and the angles controlling the dwell times of the voltage pulses in $v_{\mathrm{b}}$, {${\alpha }_1$, ${\alpha }_2$, ..., ${\alpha }_M$}, where $M=N-1$ and

$$0\le \phi \le {\displaystyle \frac{\pi }{2}}$$

(1)

$$0\le {\alpha }_1\le ...\le {\alpha }_M\le \pi .$$

(2)

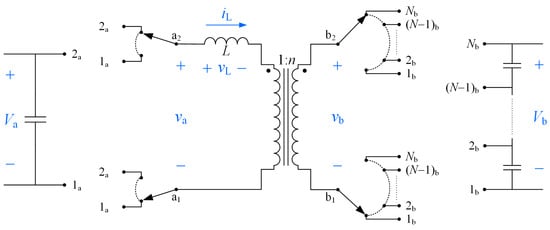
Figure 1. Topology of the considered ML DAB converter. Neutral-point-clamped (NPC) converter legs are considered, represented as single-pole double-throw switches in side a and as single-pole multiple-throw switches in side b. Relevant electrical variables are shown in blue.

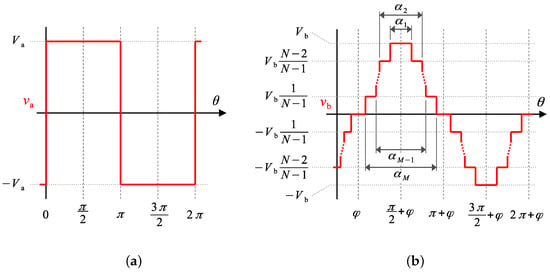
Figure 2. Synthesized ac-voltage waveforms and modulation parameters in the considered 2L-NL DAB. (a) a-side voltage ($v_{\mathrm{a}}$). (b) b-side voltage ($v_{\mathrm{b}}$) and its modulation parameters.

It should be noted that other ML converter-leg topologies could be considered, such as flying-capacitor [20] or modular-ML [21] topologies.

2.1. 2L-3L DAB Instantaneous Current Compact Expression

The voltage across the series inductor in the DAB converter, $v_{\mathrm{L}}$, is

$$v_{\mathrm{L}}=v_{\mathrm{a}}-{\displaystyle \frac{v_{\mathrm{b}}}{n}},$$

(3)

where n is the inverse of the converter transformer turns ratio. Then, the slope of the current through the inductor, $i_{\mathrm{L}}$, is

$${\displaystyle \frac{d{i}_{\mathrm{L}}}{dt}}={\displaystyle \frac{v_{\mathrm{a}}-v_{\mathrm{b}}/n}{L}},$$

(4)

where L is the equivalent inductance given by the series connection of the transformer leakage inductance and an external series inductor. Given the stepped nature of voltages $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$, the mathematical expression of $i_{\mathrm{L}}$ is piecewise-defined, where each segment of the piecewise current shape is delimited by the instants when $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$ feature a rising or falling edge (switching instants). Figure 3 shows three examples of $v_{\mathrm{a}}$, $v_{\mathrm{b}}$, and $i_{\mathrm{L}}$. This figure reveals that, for a given $V_{\mathrm{a}}$, $V_{\mathrm{b}}$, n, and L, the sequence of slope values present in $i_{\mathrm{L}}$ within a switching period ($\theta \in \left[0,2\pi \right]$) depends on the specific values of the modulation parameters. For instance, in the $i_{\mathrm{L}}$ waveform shown in Figure 3a, the first interval ($\left[0,{\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_2}{2}}\right]$) has a slope ${\displaystyle \frac{d{i}_{\mathrm{L}}}{dt}}={\displaystyle \frac{V_{\mathrm{a}}}{L}}$, the second interval ($\left[{\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_2}{2}},{\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_1}{2}}\right]$) has ${\displaystyle \frac{d{i}_{\mathrm{L}}}{dt}}={\displaystyle \frac{V_{\mathrm{a}}-V_{\mathrm{b}}/\left(2n\right)}{L}}$ and so on. However, in Figure 3b, the first interval ($\left[0,\phi -{\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}}\right]$) has a slope ${\displaystyle \frac{d{i}_{\mathrm{L}}}{dt}}={\displaystyle \frac{V_{\mathrm{a}}+V_{\mathrm{b}}/\left(2n\right)}{L}}$, the second interval ($\left[\phi -{\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}},\phi +{\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_2}{2}}\right]$) has a slope ${\displaystyle \frac{d{i}_{\mathrm{L}}}{dt}}={\displaystyle \frac{V_{\mathrm{a}}}{L}}$, and so on. From Figure 3, it can be inferred that different piecewise expressions for $i_{\mathrm{L}}$ exist depending on the position of the $v_{\mathrm{b}}$ switching instants with respect to those of $v_{\mathrm{a}}$; i.e., different modes exist.

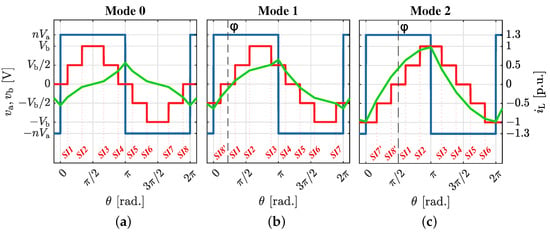
Figure 3. ac-voltages $v_{\mathrm{a}}$ (blue waveform) and $v_{\mathrm{b}}$ (red) and current $i_{\mathrm{L}}$ (green) for different modes in the 2L-3L DAB converter. All current values are divided by the peak current in Mode 2. Switching angles are $\{{\alpha }_1,{\alpha }_2\}=\{{\displaystyle \frac{\pi }{3}},{\displaystyle \frac{7\pi }{9}}\}$ (a) Mode 0, with $\phi =0$. (b) Mode 1, with $\phi ={\displaystyle \frac{2\pi }{9}}$. (c) Mode 2, with $\phi ={\displaystyle \frac{\pi }{2}}$.

In the 2L-3L DAB three different modes arise, referred to as Mode 0, Mode 1, and Mode 2 (c.f. Figure 3). One can identify each mode with

$$\left\{\begin{array}{c}{\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_1}{2}}+\phi <2\pi \left\{\begin{array}{c}{\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}}+\phi <2\pi \mathrm{Mode}0\hfill \\ {\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}}+\phi \ge 2\pi \mathrm{Mode}1\hfill \end{array}\right.\hfill \\ {\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_1}{2}}+\phi \ge 2\pi \mathrm{Mode}2\hfill \end{array}\right..$$

(5)

Based on Equation (5), let us define the binary function $K_j$ associated to ${\alpha }_j,j\in \{1,2\}$ as

$$K_j(\phi ,{\alpha }_j)=⌊{\displaystyle \frac{{\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_j}{2}}+\phi }{2\pi }}⌋,$$

(6)

to allow for an automatic detection of each mode for a given set of modulation parameter values. The values of $K_1$ and $K_2$ for each mode in the 2L-3L converter are

$$\begin{array}{c}\hfill \mathrm{Mode}0\left\{\begin{array}{c}{K}_1=0\hfill \\ K_2=0\hfill \end{array}\right.\end{array}\begin{array}{c}\hfill \mathrm{Mode}1\left\{\begin{array}{c}{K}_1=0\hfill \\ K_2=1\hfill \end{array}\right.\end{array}\begin{array}{c}\hfill \mathrm{Mode}2\left\{\begin{array}{c}{K}_1=1\hfill \\ K_2=1\hfill \end{array}\right.\end{array}.$$

(7)

Let us now define $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$ over the whole switching period by means of the indicator function $\mathbb{1}{\left(\theta \right)}_{[{\theta }_0,{\theta }_1]}$ and the binary function $K_j\left(\phi ,{\alpha }_j\right)$ defined previously, such that

$$v_{\mathrm{a}}\left(\theta \right)=V_{\mathrm{a}}·\mathbb{1}{\left(\theta \right)}_{[0,\pi ]}-V_{\mathrm{a}}·\mathbb{1}{\left(\theta \right)}_{[\pi ,2\pi ]},$$

(8)

$$\begin{array}{cc}\hfill v_{\mathrm{b}}(\theta ;\phi ,{\alpha }_1,{\alpha }_2)& ={\displaystyle \frac{V_{\mathrm{b}}}{2}}·\mathbb{1}{\left(\theta \right)}_{[SI1,SI2]\bigcup [SI3,SI4]}+V_{\mathrm{b}}·\mathbb{1}{\left(\theta \right)}_{[SI2,SI3]}-{\displaystyle \frac{V_{\mathrm{b}}}{2}}·\mathbb{1}{\left(\theta \right)}_{[SI5,SI6]}\hfill \\ \hfill & +(1-K_2)\left(-V_{\mathrm{b}}·\mathbb{1}{\left(\theta \right)}_{[SI6,SI7]}-{\displaystyle \frac{V_{\mathrm{b}}}{2}}·\mathbb{1}{\left(\theta \right)}_{[SI7,SI8]}\right)\hfill \\ \hfill & +K_2(1-K_1)\left(-V_{\mathrm{b}}·\mathbb{1}{\left(\theta \right)}_{[SI6,SI7]}-{\displaystyle \frac{V_{\mathrm{b}}}{2}}·\mathbb{1}{\left(\theta \right)}_{[SI7,2\pi ]\bigcup [0,SI{8}^{\prime }]}\right)\hfill \\ \hfill & +K_1\left(-V_{\mathrm{b}}·\mathbb{1}{\left(\theta \right)}_{[SI6,2\pi ]\bigcup [0,SI{7}^{\prime }]}-{\displaystyle \frac{V_{\mathrm{b}}}{2}}·\mathbb{1}{\left(\theta \right)}_{[SI{7}^{\prime },SI{8}^{\prime }]}\right),\hfill \end{array}$$

(9)

where $\mathbb{1}{\left(\theta \right)}_{[{\theta }_0,{\theta }_1]}=1$ when $\theta \in [{\theta }_0,{\theta }_1]$ and $\mathbb{1}{\left(\theta \right)}_{[{\theta }_0,{\theta }_1]}=0$ otherwise, and

$$\left\{\begin{array}{c}SI1={\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_2}{2}}+\phi \hfill \\ SI2={\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_1}{2}}+\phi \hfill \\ SI3={\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_1}{2}}+\phi \hfill \\ SI4={\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}}+\phi \hfill \\ SI5={\displaystyle \frac{3\pi }{2}}-{\displaystyle \frac{{\alpha }_2}{2}}+\phi \hfill \\ SI6={\displaystyle \frac{3\pi }{2}}-{\displaystyle \frac{{\alpha }_1}{2}}+\phi \hfill \\ SI7={\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_1}{2}}+\phi \hfill \\ SI8={\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_2}{2}}+\phi \hfill \\ SI{7}^{\prime }=SI7-2\pi \hfill \\ SI{8}^{\prime }=SI8-2\pi \hfill \end{array}\right.$$

(10)

correspond to the switching instants of $v_{\mathrm{b}}$ as depicted in Figure 3.

The instantaneous current through the series inductance is

$$i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,{\alpha }_2)={\displaystyle \frac{1}{2\pi fL}}{\int }_0^{\theta }\left(v_{\mathrm{a}}\left(x\right)-{\displaystyle \frac{v_{\mathrm{b}}(x;\phi ,{\alpha }_1,{\alpha }_2)}{n}}\right)·dx+i_{\mathrm{L}}\left(0\right),$$

(11)

where f is the converter switching frequency. Let us separate the integral terms in Equation (11) into two terms, such as

$$i_{\mathrm{L}}\left(\theta \right)={\displaystyle \frac{1}{2\pi fL}}\left({\int }_0^{\theta }{v}_{\mathrm{a}}\left(x\right)·dx-{\int }_0^{\theta }{\displaystyle \frac{v_{\mathrm{b}}\left(x\right)}{n}}·dx\right)+i_{\mathrm{L}}\left(0\right).$$

(12)

Let us also define the integral of an indicator function using the min function, such as

$${\int }_0^{\theta }\mathbb{1}{\left(x\right)}_{[{\theta }_0,{\theta }_1]}dx=min\{\theta ,{\theta }_1\}-min\{\theta ,{\theta }_0\}\forall \theta ,{\theta }_0,{\theta }_1\in [0,2\pi ].$$

(13)

The expressions of $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$ can now be substituted into Equation (12) to obtain the compact $i_{\mathrm{L}}$ expression. On the one hand, the ${\int }_0^{\theta }{v}_{\mathrm{a}}\left(x\right)·dx$ term in Equation (12) is solved as

$$\begin{array}{cc}\hfill {\int }_0^{\theta }{v}_{\mathrm{a}}\left(x\right)·dx& ={\int }_0^{\theta }\left(V_{\mathrm{a}}·\mathbb{1}{\left(x\right)}_{[0,\pi ]}-V_{\mathrm{a}}·\mathbb{1}{\left(x\right)}_{[\pi ,2\pi ]}\right)dx\hfill \\ \hfill & =-V_{\mathrm{a}}\theta +2V_{\mathrm{a}}min\{\theta ,\pi \}.\hfill \end{array}$$

(14)

On the other hand, solving ${\int }_0^{\theta }{\displaystyle \frac{v_{\mathrm{b}}\left(x\right)}{n}}·dx$ involves integrating both $\mathbb{1}{\left(x\right)}_{[{\theta }_0,{\theta }_1]}$ and $K_j$ functions. Since the value of $K_j$ does not depend on the variable of integration ($\theta$), it is treated as a constant parameter, facilitating the resolution of the integral. The result is simplified by grouping the common factors of the expression, and

$${\int }_0^{\theta }{\displaystyle \frac{v_{\mathrm{b}}\left(x\right)}{n}}·dx={\displaystyle \frac{{\gamma }_2}{n}}{V}_{\mathrm{b}}·\theta +{\displaystyle \frac{V_{\mathrm{b}}}{4\pi nfL}}(A_1-B_1+A_2-B_2),$$

(15)

solution is obtained, where ${\gamma }_2$, $A_j$ and $B_j$ are defined as

$${\gamma }_2(\phi ,{\alpha }_1,{\alpha }_2)={\displaystyle \frac{K_1+K_2}{2}},$$

(16)

$$\begin{array}{cc}\hfill A_j(\theta ;\phi ,{\alpha }_j)& =min\left\{\theta ,{\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_j}{2}}+\phi \right\}-min\left\{\theta ,{\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_j}{2}}+\phi \right\}\hfill \\ \hfill B_j(\theta ;\phi ,{\alpha }_j)& =min\left\{\theta ,{\displaystyle \frac{3\pi }{2}}-{\displaystyle \frac{{\alpha }_j}{2}}+\phi \right\}-min\left\{\theta ,{\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_j}{2}}+\phi -2\pi K_j\right\}\hfill \end{array}.$$

(17)

Then, from Equations (12), (14), and (15),

$$\begin{array}{cc}\hfill i_{\mathrm{L}}\left(\theta \right)& ={\displaystyle \frac{1}{2\pi fL}}\left[\left({\displaystyle \frac{{\gamma }_2}{n}}{V}_{\mathrm{b}}-V_{\mathrm{a}}\right)\theta +2V_{\mathrm{a}}min\{\theta ,\pi \}\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{4\pi nfL}}(A_1-B_1+A_2-B_2)+i_{\mathrm{L}}\left(0\right)\hfill \end{array}$$

(18)

is obtained.

In the DAB converter, the average value for the inductor current over a switching period is zero, i.e., ${\int }_0^{2\pi }{i}_{\mathrm{L}}\left(\theta \right)·d\theta =0$. Then,

$$i_{\mathrm{L}}\left(0\right)=-{\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }(i_{\mathrm{L}}\left(\theta \right)-i_{\mathrm{L}}\left(0\right))·d\theta .$$

(19)

Solving $i_{\mathrm{L}}\left(0\right)$ in Equation (19) and substituting it into Equation (18), the compact analytic expression for $i_{\mathrm{L}}$ in a 2L-3L DAB converter is obtained, such as

$$\begin{array}{cc}\hfill i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,{\alpha }_2)& ={\displaystyle \frac{1}{2\pi fL}}\left[{\displaystyle \frac{{\gamma }_2}{n}}{V}_{\mathrm{b}}(\theta -\pi )-V_{\mathrm{a}}\left({\displaystyle \frac{\pi }{2}}+\theta \right)+2V_{\mathrm{a}}min\{\theta ,\pi \}\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{8\pi nfL}}\left[2A_1-2B_1+{\alpha }_1+K_1(3\pi -{\alpha }_1-2\phi )\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{8\pi nfL}}\left[2A_2-2B_2+{\alpha }_2+K_2(3\pi -{\alpha }_2-2\phi )\right].\hfill \end{array}$$

(20)

Note that Equation (20) transitions smoothly between consecutive modes; i.e., the expression for $i_{\mathrm{L}}$ is the same when the boundary condition is met. For example, the boundary between Mode 0 to Mode 1 is defined by ${\displaystyle \frac{3\pi }{2}}+{\displaystyle \frac{{\alpha }_M}{2}}+\phi =2\pi$. Imposing this condition to Equation (20) on Mode 0 and on Mode 1 results in the same mathematical expression.

2.2. Generalized Current Compact Expression of a 2L-NL DAB

Defining the compact analytical expression for the instantaneous current through the series inductor in a 2L-3L DAB enables us to generalize $i_{\mathrm{L}}\left(\theta \right)$ for a 2L-NL DAB using an inductive process.

First, the compact analytical expression for $i_{\mathrm{L}}\left(\theta \right)$ in a 2L-4L DAB is derived following the methodology employed for the 2L-3L converter, such as

$$\begin{array}{cc}\hfill i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3)& ={\displaystyle \frac{1}{2\pi fL}}\left[{\displaystyle \frac{{\gamma }_3}{n}}{V}_{\mathrm{b}}(\theta -\pi )-V_{\mathrm{a}}\left({\displaystyle \frac{\pi }{2}}+\theta \right)+2V_{\mathrm{a}}min\{\theta ,\pi \}\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{12\pi nfL}}\left[2A_1-2B_1+{\alpha }_1+K_1(3\pi -{\alpha }_1-2\phi )\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{12\pi nfL}}\left[2A_2-2B_2+{\alpha }_2+K_2(3\pi -{\alpha }_2-2\phi )\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{12\pi nfL}}\left[2A_3-2B_3+{\alpha }_3+K_3(3\pi -{\alpha }_3-2\phi )\right]\hfill \end{array},$$

(21)

where ${\gamma }_3$ is defined as

$${\gamma }_3(\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3)={\displaystyle \frac{K_1+K_2+K_3}{3}}.$$

(22)

Equations (20) and (21) let us define the structure of the expression for $i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,\cdots ,{\alpha }_M)$, with the number of levels at side b of the converter, N, and the number of modulation angles controlling the amplitude of the pulses of $v_{\mathrm{b}}$, M, treated as parameters. Then, the generalized compact expression for $i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,\cdots ,{\alpha }_M)$ in a 2L-NL DAB is defined as

$$\begin{array}{cc}\hfill i_{\mathrm{L}}(\theta ;\phi ,{\alpha }_1,\cdots ,{\alpha }_M)& ={\displaystyle \frac{1}{2\pi fL}}\left[{\displaystyle \frac{{\gamma }_M}{n}}{V}_{\mathrm{b}}(\theta -\pi )-V_{\mathrm{a}}\left({\displaystyle \frac{\pi }{2}}+\theta \right)+2V_{\mathrm{a}}min\{\theta ,\pi \}\right]\hfill \\ \hfill & +{\displaystyle \frac{V_{\mathrm{b}}}{4\pi nMfL}}\sum _{j=1}^M\left[2A_j-2B_j+{\alpha }_j+K_j(3\pi -{\alpha }_j-2\phi )\right],\hfill \end{array}$$

(23)

where ${\gamma }_M$ is

$${\gamma }_M(\phi ,{\alpha }_1,\cdots ,{\alpha }_M)={\displaystyle \frac{{\sum }_{j=1}^M{K}_j}{M}}.$$

(24)

2.3. RMS Expression

The RMS expression for the inductor current in a 2L-NL DAB is defined as

$$I_{\mathrm{L},\mathrm{RMS}}=\sqrt{{\displaystyle \frac{1}{2\pi }}{\int }_0^{2\pi }{i}_{\mathrm{L}}^2\left(\theta \right)d\theta }.$$

(25)

Then, from Equations (23) and (25), the generalized compact expression for $I_{\mathrm{L},\mathrm{RMS}}$ is obtained using the MATLAB R2023b Symbolic Math Toolbox, resulting in

$$\begin{array}{cc}\hfill I_{\mathrm{L},\mathrm{RMS}}& ={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}fL}}\left[{\displaystyle \frac{2{\pi }^3}{3}}{\displaystyle \frac{{\gamma }_M^2}{n^2}}{V}_{\mathrm{b}}^2+{\displaystyle \frac{1}{6}}{\pi }^3{V}_{\mathrm{a}}^2+2{\displaystyle \frac{V_{\mathrm{b}}^2}{M^2{n}^2}}\sum _{1\le i<j\le M}{P}_{i,j}\right.\hfill \\ \hfill & {\left.+{\displaystyle \frac{1}{M}}\sum _{j=1}^M\left({\displaystyle \frac{2V_{\mathrm{b}}^2}{n^2}}{\gamma }_M{U}_j+{\displaystyle \frac{2V_{\mathrm{b}}}{n}}{V}_{\mathrm{a}}{W}_j+{\displaystyle \frac{V_{\mathrm{b}}^2}{M{n}^2}}{P}_{j,j}\right)\right]}^{1/2}\hfill \end{array}$$

(26)

where

$$\begin{array}{cc}\hfill U_j& =-\pi {\alpha }_j\phi -K_j\left({\displaystyle \frac{\pi }{12}}(5{\pi }^2+6\pi {\alpha }_j+12\pi \phi -3{\alpha }_j^2-12{\alpha }_j\phi -12{\phi }^2)\right),\hfill \\ \hfill W_j& ={\displaystyle \frac{{\alpha }_j}{12}}(-3{\pi }^2+{\alpha }_j^2+12{\phi }^2)-K_j{\displaystyle \frac{1}{12}}{({\alpha }_j-\pi +2\phi )}^3,\hfill \\ \hfill P_{i,j}& =-{\displaystyle \frac{{\alpha }_i}{12}}\left({\alpha }_i^2+3{\alpha }_j^2-6\pi {\alpha }_j\right)+K_j\pi {\alpha }_i\phi \hfill \\ \hfill & +K_i\left({\displaystyle \frac{19{\pi }^3}{6}}-{\displaystyle \frac{{\pi }^2{\alpha }_i}{2}}+{\displaystyle \frac{{\pi }^2{\alpha }_j}{2}}-{\displaystyle \frac{\pi {\alpha }_i^2}{4}}-\pi {\alpha }_i\phi -{\displaystyle \frac{\pi {\alpha }_j^2}{4}}-2\pi {\phi }^2+{\displaystyle \frac{{\alpha }_i^3}{48}}-{\displaystyle \frac{{\alpha }_i^2{\alpha }_j}{16}}+{\displaystyle \frac{{\alpha }_i{\alpha }_j^2}{16}}-{\displaystyle \frac{{\alpha }_j^3}{48}}\right)\hfill \\ \hfill & +K_i{K}_j\left(-3{\pi }^3+{\pi }^2{\alpha }_i+2\phi {\pi }^2-{\displaystyle \frac{{\alpha }_i^3}{48}}+{\displaystyle \frac{{\alpha }_i^2{\alpha }_j}{16}}-{\displaystyle \frac{{\alpha }_i{\alpha }_j^2}{16}}+{\displaystyle \frac{{\alpha }_j^3}{48}}\right).\hfill \end{array}$$

(27)

3. Numerical Verification

To verify the proposed DAB inductor current compact expression, the results obtained with the proposed approach are compared with reference results; i.e., results obtained through Fourier analysis up to the $2000\mathrm{th}$ harmonic. Then, this section presents the instantaneous and RMS current expressions derived from the Fourier analysis, the numerical verification of the compact analytic expressions for the 2L-3L DAB, and the 2L-4L DAB.

The MATLAB code implementing the functions to compute the inductor-current instantaneous and RMS values with the proposed compact approach are provided as Supplementary Files.

3.1. 2L-NL DAB Instantaneous and RMS Current Expressions Through Fourier Analysis

The expressions for the ac voltage waveforms in a 2L-NL DAB (Figure 2) obtained through Fourier analysis are

$$v_{\mathrm{a}}=\sum _h\left[\left|\right|{\mathbf{V}}_{\mathrm{a},h}\left|\right|sin\left(h\theta +arg\left({\mathbf{V}}_{\mathrm{a},h}\right)\right)\right]$$

(28)

$$v_{\mathrm{b}}=\sum _h\left[\left|\right|{\mathbf{V}}_{\mathrm{b},h}\left|\right|sin\left(h\theta +arg\left({\mathbf{V}}_{\mathrm{b},h}\right)\right)\right],$$

(29)

where h is the harmonic index and ${\mathbf{V}}_{\mathrm{a},h}$ and ${\mathbf{V}}_{\mathrm{b},h}$ are the $h\mathrm{th}$-harmonic voltage phasors,

$$\begin{array}{cc}\hfill {\mathbf{V}}_{\mathrm{a},h}& =V_{\mathrm{a},h}\hfill \\ \hfill {\mathbf{V}}_{\mathrm{b},h}& =V_{\mathrm{b},h}\left(cos\left(h\phi \right)-i·sin\left(h\phi \right)\right)\hfill \\ \hfill V_{\mathrm{a},h}& ={\displaystyle \frac{2V_{\mathrm{a}}}{\pi h}}\left[1-cos\left(h\pi \right)\right]\hfill \\ \hfill V_{\mathrm{b},h}& ={\displaystyle \frac{2V_{\mathrm{b}}}{(N-1)\pi h}}\sum _{j=1}^M\left[cos\left(h\left({\displaystyle \frac{\pi }{2}}-{\displaystyle \frac{{\alpha }_j}{2}}\right)\right)-cos\left(h\left({\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{{\alpha }_j}{2}}\right)\right)\right]\hfill \end{array},$$

(30)

and $V_{\mathrm{a},h}$ and $V_{\mathrm{b},h}$ are the amplitudes of the $v_{\mathrm{a}}$ and $v_{\mathrm{b}}$$h\mathrm{th}$ harmonic, respectively. Then, from Equations (3) and (4), the $h\mathrm{th}$-harmonic component of the inductor-current phasor is defined as

$${\mathbf{I}}_{\mathrm{L},h}={\displaystyle \frac{{\mathbf{V}}_{\mathrm{a},h}-{\mathbf{V}}_{\mathrm{b},h}/n}{i·\left(2\pi hfL\right)}}.$$

(31)

Then, the expression for the instantaneous current through the series inductor obtained through Fourier analysis is defined as

$$i_{\mathrm{L}}\left(\theta \right)=\sum _h\left[\left|\right|{\mathbf{I}}_{\mathrm{L},h}\left|\right|sin\left(h\theta +arg\left({\mathbf{I}}_{\mathrm{L},h}\right)\right)\right],$$

(32)

and its RMS value is obtained from

$$I_{\mathrm{L},\mathrm{RMS}}=\sqrt{{\displaystyle \frac{1}{2}}{\sum }_h\left|\right|{\mathbf{I}}_{\mathrm{L},h}{\left|\right|}^2}.$$

(33)

3.2. Numerical Verification for the 2L-3L DAB

Table 1 and Table 2 provide a comparison of the $i_{\mathrm{L}}$ and $I_{\mathrm{L},\mathrm{RMS}}$ per-unit (p.u.) values for the 2L-3L DAB as obtained from the compact analytical expressions (Equation (23) and Equation (26), respectively) and from the Fourier analysis (Equation (32) and Equation (33), respectively). The Table 1 results are obtained for three distinct operation points, defined by the modulation angles $\phi$, ${\alpha }_1$, and ${\alpha }_2$, and at five arbitrary values of $\theta$. The values of the modulation angles have been selected such that each operation point corresponds to a specific mode (Mode 0, Mode 1, and Mode 2, defined in Section 2.1). The Table 2 results are obtained for the same modulation angles as Table 1. The instantaneous and RMS current values obtained using the analytical expression and the Fourier approximation are found to be equal at all three operating points. Furthermore, Figure 4 provides a visual comparison of the $i_{\mathrm{L}}$ waveform obtained using the analytic expression and the Fourier approximation (same operation points as Table 1). As shown, both waveforms are identical throughout the entire switching cycle.

Table 1. Numerical comparison of $i_{\mathrm{L}}\left(\theta \right)$ using the compact analytical expression ($i_{\mathrm{L},\mathrm{Comp}}$) and the Fourier approximation ($i_{\mathrm{L},\mathrm{Fourier}}$). All current values are divided by the peak current in Figure 4c.

	Mode 0: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{5}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi }\}$		Mode 1: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{5}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 2: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=$ $\{\frac{1}{3}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$
$\mathit{\theta }$ [rad]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]
0	$-1.00$	$-1.00$	$-0.79$	$-0.79$	$-1$	$-1$
1	$-0.05$	$-0.05$	$0.19$	$0.19$	$0.35$	$0.35$
2	$0.50$	$0.50$	$0.50$	$0.50$	$0.99$	$0.99$
3	$0.86$	$0.86$	$0.72$	$0.72$	1	1
4	$0.18$	$0.18$	$-0.12$	$-0.12$	$-0.22$	$-0.22$

Table 2. Numerical comparison of $I_{\mathrm{L},\mathrm{RMS}}$ using the compact analytical expression ($i_{\mathrm{L},\mathrm{Comp}}$) and the Fourier approximation ($i_{\mathrm{L},\mathrm{Fourier}}$). All current values are divided by the peak current in Figure 4c.

Mode 0: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=\{\frac{1}{6}\mathit{\pi },\frac{5}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi }\}$		Mode 1: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=\{\frac{1}{6}\mathit{\pi },\frac{5}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 2: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2\}=\{\frac{1}{3}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$
${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]
$0.55$	$0.55$	$0.47$	$0.47$	$0.78$	$0.78$

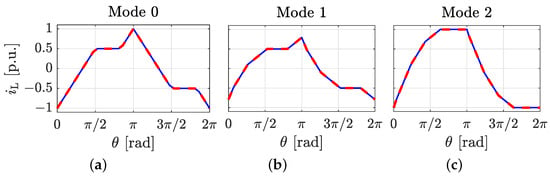
Figure 4. Waveform of $i_{\mathrm{L}}\left(\theta \right)$ obtained using the compact analytic expression (solid blue line) and the Fourier approximation (dashed red line) at three different operation points. All current values are divided by the peak current in (c). (a) Mode 0, with $\{\phi ,{\alpha }_1,{\alpha }_2\}=\left\{{\displaystyle \frac{1}{6}}\pi ,{\displaystyle \frac{5}{18}}\pi ,{\displaystyle \frac{7}{18}}\pi \right\}$. (b) Mode 1, with $\{\phi ,{\alpha }_1,{\alpha }_2\}=\left\{{\displaystyle \frac{1}{6}}\pi ,{\displaystyle \frac{5}{18}}\pi ,{\displaystyle \frac{29}{36}}\pi \right\}$. (c) Mode 2, with $\{\phi ,{\alpha }_1,{\alpha }_2\}=\left\{{\displaystyle \frac{1}{3}}\pi ,{\displaystyle \frac{7}{18}}\pi ,{\displaystyle \frac{29}{36}}\pi \right\}$.

3.3. Numerical Verification for the 2L-4L DAB

For the purpose of validating the presented compact analytical expressions for the instantaneous and RMS inductor currents, the same verification conducted in Section 3.2 is performed for a 2L-4L DAB. Table 3 and Table 4 provide a comparison of the $i_{\mathrm{L}}$ and $I_{\mathrm{L},\mathrm{RMS}}$ p.u. values for the 2L-4L DAB as obtained from the compact analytical expressions and from the Fourier analysis.

Table 3. Numerical comparison of $i_{\mathrm{L}}\left(\theta \right)$ using the compact analytical expression ($i_{\mathrm{L},\mathrm{Comp}}$) and the Fourier approximation ($i_{\mathrm{L},\mathrm{Fourier}}$). All current values are divided by the peak current in Figure 5a.

	Mode 0: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{1}{18}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi }\}$		Mode 1: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 2: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{3}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 3: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{3}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{20}{36}\mathit{\pi },\frac{30}{36}\mathit{\pi }\}$
$\mathit{\theta }$ [rad]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{Fourier}}$ [p.u.]
0	$-1$	$-1$	$-0.74$	$-0.74$	$-0.90$	$-0.90$	$-0.86$	$-0.86$
1	$-0.18$	$-0.18$	$0.09$	$0.09$	$0.14$	$0.14$	$0.29$	$0.29$
2	$0.43$	$0.43$	$0.43$	$0.43$	$0.78$	$0.78$	$0.86$	$0.86$
3	$0.88$	$0.88$	$0.66$	$0.66$	$0.87$	$0.87$	$0.86$	$0.86$
4	$0.30$	$0.30$	$-0.02$	$-0.02$	$-0.02$	$-0.02$	$-0.18$	$-0.18$

Table 4. Numerical comparison of $I_{\mathrm{L},\mathrm{RMS}}$ using the compact analytical expression ($i_{\mathrm{L},\mathrm{Comp}}$) and the Fourier approximation ($i_{\mathrm{L},\mathrm{Fourier}}$). All current values are divided by the peak current in Figure 5a.

Mode 0: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{1}{18}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi }\}$		Mode 1: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{6}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 2: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{3}\mathit{\pi },\frac{4}{18}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{29}{36}\mathit{\pi }\}$		Mode 3: $\{\mathit{\phi },{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,{\mathit{\alpha }}_3\}=$ $\{\frac{1}{3}\mathit{\pi },\frac{7}{18}\mathit{\pi },\frac{20}{36}\mathit{\pi },\frac{30}{36}\mathit{\pi }\}$
${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Comp}}$ [p.u.]	${\mathit{i}}_{\mathbf{L},\mathbf{RMS},\mathbf{Fourier}}$ [p.u.]
0.55	0.55	0.42	0.42	0.65	0.65	0.67	0.67

In a 2L-4L DAB converter, four modes arise. The Table 3 and Table 4 results are obtained for four distinct operation points, each operation point corresponding to a specific mode. As can be seen from both tables, the instantaneous and RMS current values obtained using the analytical expression and the Fourier approximation are equal at all four operating points. Furthermore, the visual comparison of the $i_{\mathrm{L}}$ waveform in Figure 5 shows that the analytic expression yields the same results as the Fourier approximation throughout the entire switching cycle for all four operation points (same operation points as Table 3). These results consequently validate the analytical expressions presented in this document.

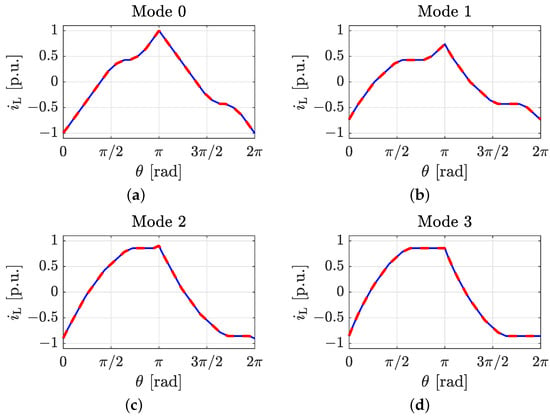
Figure 5. Waveform of $i_{\mathrm{L}}\left(\theta \right)$ obtained using the compact analytic expression (solid blue line) and the Fourier approximation (dashed red line) at three different operation points. All current values are divided by the peak current in (a). (a) Mode 0, with $\{\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3\}=\left\{{\displaystyle \frac{1}{6}}\pi ,{\displaystyle \frac{1}{18}}\pi ,{\displaystyle \frac{4}{18}}\pi ,{\displaystyle \frac{7}{18}}\pi \right\}$. (b) Mode 1, with $\{\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3\}=\left\{{\displaystyle \frac{1}{6}}\pi ,{\displaystyle \frac{4}{18}}\pi ,{\displaystyle \frac{7}{18}}\pi ,{\displaystyle \frac{29}{36}}\pi \right\}$. (c) Mode 2, with $\{\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3\}=\left\{{\displaystyle \frac{1}{3}}\pi ,{\displaystyle \frac{4}{18}}\pi ,{\displaystyle \frac{7}{18}}\pi ,{\displaystyle \frac{29}{36}}\pi \right\}$. (d) Mode 3, with $\{\phi ,{\alpha }_1,{\alpha }_2,{\alpha }_3\}=\left\{{\displaystyle \frac{1}{3}}\pi ,{\displaystyle \frac{7}{18}}\pi ,{\displaystyle \frac{20}{36}}\pi ,{\displaystyle \frac{30}{36}}\pi \right\}$.

4. Comparative Computational Time Analysis

When developing software tools for the performance optimization of DAB converters, computational time becomes a critical factor, as multiple mathematical expressions must be evaluated a significant number of times to evaluate the converter performance for different operation points and modulation parameter values. In that sense, the expression of the inductor current is crucial, as its RMS value determines the conduction losses of the converter and the instantaneous value determines the power-semiconductor switching losses and the inductor magnetic-field peak value. Therefore, minimizing the computational time required to obtain these magnitudes is essential for developing a faster and more effective optimization tool.

A comparative analysis is conducted on the computational time required to obtain the instantaneous current and its RMS value, using both the compact analytical expressions and the Fourier analysis up to the 63rd harmonic. In performance studies using Fourier analysis, the number of harmonics determines the trade-off between calculation precision and computational time. In the present study, the maximum harmonic index has been selected such that the maximum error in the computation of the instantaneous current is less than 0.01 p.u.

The expressions for the instantaneous current from the proposed compact expressions (Equation (23)) and from the Fourier analysis (Equation (32)) are executed using MATLAB for 100 equally distributed values of $\theta$ in the range $[0,2\pi ]$. The current at each instant is computed 1000 times, resulting in a total of 100,000 executions. The expressions for the RMS current from the compact expressions (Equation (26)) and from the Fourier analysis (Equation (33)) are executed for 100 randomly generated operation points, defined by the values of the modulation angles. The RMS current for each operation point is computed 1000 times, also resulting in 100,000 executions. The computational time for each execution is measured, and the median computational time required for both currents and methods is obtained.

Table 5 shows the results of this analysis for 3, 4, 5, and 6 levels at side b of the converter. The results show a substantial reduction in computational time when using the compact analytical expression. The analysis reveals that, on average, employing the compact analytical expression allows to reduce by 34.6 times the computational time to obtain the instantaneous value for the inductor current. Furthermore, the computation of the RMS value is, on average, 2.9 times faster when using the compact analytical expression. The results obtained in the comparative computational time analysis then support the advantages of the proposed analytical approach.

Table 5. Median time to compute the instantaneous and RMS current using the proposed compact expressions and the Fourier approximation for $N=\{3,4,5,6\}$.

	$\mathit{N}=3$	$\mathit{N}=4$	$\mathit{N}=5$	$\mathit{N}=6$
$t_{\mathrm{iL},\mathrm{Fourier}}\left[\mu s\right]$	14.9	15.8	16.9	21.6
$t_{\mathrm{iL},\mathrm{Comp}}\left[\mu s\right]$	0.5	0.5	0.5	0.5
$t_{\mathrm{iLRMS},\mathrm{Fourier}}\left[\mu s\right]$	14.0	14.7	15.6	20.4
$t_{\mathrm{iLRMS},\mathrm{Comp}}\left[\mu s\right]$	4.2	5.0	6.0	7.8

5. Discussion

The compact analytical expression for inductor current in ML DAB converters proposed in this paper significantly simplifies performance analysis. By using binary indicator functions, the piecewise nature of the current expression is generalized, allowing for efficient calculation of both instantaneous and RMS values for any arbitrary value of the modulation parameters and any given number of converter voltage levels. This generalization makes the performance analysis versatile and reduces the complexity associated with conventional methods.

The validation results, which agree with results from Fourier analysis, confirm the accuracy of the proposed method across different operating points. Furthermore, as shown in [5,15,18], the DAB inductor current waveforms obtained from an ideal lossless model and from experimental tests are very similar, and thus, the proposed method provides a fair trade-off between simplicity in the expressions and reproducibility of the real current and voltage waveforms. Moreover, the proposed method significantly reduces the computational time required to determine the inductor current in ML converters compared to the Fourier approximation.

These findings align with previous efforts in the field aimed at optimizing multilevel DAB converter topologies to enhance efficiency and reduce power losses, as seen in [5,6,7]. The method paves the way for optimization software tools that allow exploring multiple DAB converter structures and modulation strategies, without requiring ad hoc current expressions for each current mode. Applications like electric vehicles and renewable energy systems might benefit greatly from these tools.

Further work could explore applying this approach to DAB converter configurations with any arbitrary number of levels per side [22] and featuring other modulation techniques [23]. Furthermore, future work includes deriving generalized expressions for the soft-switching-region boundaries in different ML DAB converter topologies and modulation techniques [24,25]. Finally, the same approach can be extended to other converters with piecewise-defined inductor currents, such as the buck, boost, flyback, and resonant dc-dc converters.