Efficient FPGA Binary Neural Network Architecture for Image Super-Resolution

Abstract

Super-resolution systems refer to computer-based systems designed to enhance the quality of images or video by producing high-resolution renditions from low-resolution counterparts using computational algorithms and technologies. Various methods and techniques have been used in development of super-resolution systems. The development of Convolution Neural Networks (CNNs) and the Deep Learning (DL) methods have outperformed traditional methods. However, as models become increasingly deeper with wider receptive fields, the number of parameters significantly increases. While this often results in better performance, it renders these models impractical for real-life scenarios such as smartphones or other mobile systems. Currently, most proposed methods with higher perceptual quality demand a substantial amount of time to process a single image, even on powerful hardware like NVIDIA GPUs. Such computationally expensive models are not cost-effective for real-world application scenarios. Optimization is needed to reduce the computational costs and memory requirements to enhance their suitability for less powerful hardware configurations. In this work, we propose an efficient binary neural network architecture, ResBinESPCN, designed for image super-resolution. In our design, we improved the energy efficiency of the architecture through algorithmic and hardware-level optimizations. These optimizations not only enhance computational efficiency and reduce memory consumption but also achieve effective image super-resolution in resource-constrained environments. Our experimental validation highlights the effectiveness of this network structure and includes ablation studies on models with varying data bit widths. Hardware analysis substantiates the efficiency and real-time capabilities of this model. Additionally, deploying the model on FPGA using FINN demonstrates its low hardware resource usage and low power consumption.

1. Introduction

Over the past decade, CNN-based methods have demonstrated outstanding performance across various tasks. Among these, the restoration of high-resolution (HR) images or videos from low-resolution (LR) counterparts has garnered significant attention. Referred to as Single Image Super-Resolution (SISR), this task holds direct applicability in various domains including satellite imaging [1,2], medical imaging [3,4], surveillance [5,6] and biometric information identification [6,7,8]. Fundamentally, SISR involves a mapping process from the LR space to the HR space; however, the LR space is given, and there typically exist numerous solutions in the HR space. Consequently, identifying the correct solution from this one-to-many mapping is a challenging task.

To address this problem, recently many researchers have utilized the efficient data learning capabilities of CNNs to identify the optimal solution within the mapping from LR to HR space. Dong et al. [9] were pioneers in introducing deep learning to the realm of image super-resolution reconstruction. They utilized a three-layer convolutional neural network to understand the mapping between low-resolution and high-resolution images. An overview of the SRCNN model structure is shown in Figure 1.

This marked the onset of the deep learning revolution in the field of super-resolution reconstruction, and their network model was termed Super-Resolution Convolutional Neural Network (SRCNN) [9]. SRCNN used an interpolation method to initially upsample the low-resolution images before restoration through the model.

Before the introduction of the SRCNN method, the traditional methods, such as interpolation and reconstruction methods [10,11], were widely used in image super-resolution applications. By adopting the pioneering CNN-based algorithm SRCNN and comparing it with traditional methods, several advantages of the CNN-based method can be observed.

Firstly, compared to traditional methods, the CNN-based methods extract a considerable number of features from the inputs. The quantity of features, also indicative of the number of parameters, can be adjusted based on the number of filters used during feature extraction. Having a substantial number of parameters for feature extraction allows the model the flexibility to optimize these values, with the aim of closely approximating the relationship between the reconstructed output and the actual output. This differs from interpolation-based methods, which rely on neighboring values and compute the value at a specific point only.

Secondly, the CNN-based method exhibits good generalizability and flexibility. During each iteration of model training, the loss difference between the reconstructed output and actual output is computed and fed back into the model network to fine-tune parameter values. The ultimate goal of parameter fine-tuning is to minimize loss in model predictions. However, in interpolation and reconstruction methods, the output is calculated based on a certain parameter, typically fixed for specific scenarios, requiring separate designs for numerous scenarios.

However, Shi et al. [12] argued that pre-scaling using nearest-neighbor interpolation inherently affects performance. They believe in learning how to perform upsampling from the samples themselves. Based on this principle, they introduced ESPCN [12]. This model, which is based on not performing an upsampling process on the given low-resolution images before inputting them into the neural network, introduced a sub-pixel convolutional layer to indirectly achieve the image’s upsampling process. The structure overview is depicted in Figure 2. This approach significantly reduced the computational load of SRCNN, enhancing the reconstruction efficiency.

On the other hand, Kim et al. [13] analyzed the limitations of the SRCNN and proposed the Very Deep Super-Resolution (VDSR) model. They highlighted three limitations of SRCNN:

• When the convolutional kernel size remains constant, a model with insufficient depth leads to a limited receptive field in the generated images. A deeper model inherently brings about a larger receptive field, allowing the network to utilize more contextual information, thus capturing a more comprehensive global mapping.
• Slow convergence during model training.
• The model is limited to handle only a single scale of image super-resolution.

To address these limitations, three solutions were proposed:

• The deeper model can gain larger receptive fields to capture broader image contextual information.
• The model adopted residual learning with higher learning rates to expedite convergence. However, employing higher learning rates could lead to the problem of vanishing or exploding gradients; thus, they implemented moderate gradient clipping to mitigate these gradient issues.
• The neural network was capable of handling image super-resolution for various scales.

Ultimately, the results indicated that VDSR, with a deeper network compared to SRCNN, achieved superior performance, faster convergence, and could be applied to multi-scale super-resolution.

In addition to the three models we discussed above, in recent years, many researchers have made remarkable progress by improving SR deep learning models from various perspectives [14,15,16,17,18].

Kim et al. [15] proposed a super-resolution network architecture named Deep Recursive Convolutional Network (DRCN) that deepens the model using a recursive structure. DRCN enhances the image reconstruction performance by recursively extracting multi-level feature information across multiple layers. The recursive structure of DRCN shares model parameters and a common reconstruction layer, thereby controlling the overall number of model parameters. To address the gradient vanishing and exploding issues caused by recursion, the author introduced recursive supervision. This method directly involves each recursive step in the loss function to provide additional supervision. Additionally, to counterbalance excessive information loss during recursion and merge low-level and high-level information while preserving the original input data, skip connections were implemented. Furthermore, the author controlled the depth of recursion by introducing different weights for learning at various recursion levels at the end, serving as an attention mechanism. Figure 3 demonstrates the overview structure of DRCN.

The authors [17] introduced the Deep Recursive Residual Network (DRRN) to achieve better performance while requiring fewer parameters compared to models like VDSR, DRCN. To some extent, DRRN can be considered an improved version of DRCN. It retains the DRCN concept of global skip connections and recursive blocks to enhance model depth while limiting the number of parameters, incorporating the idea of local skip connections from ResNet [19]. There are two main differences between DRRN and DRCN: First, not all convolutional layers share the same weight in DRRN. Instead, DRRN consists of several residual units forming recursive blocks where weights are shared within these units. Second, DRRN liberates itself from the burden of gradient vanishing or exploding by designing recursive blocks with a multi-path structure, allowing for easier training. Additionally, it improves performance solely by increasing convolutional depth without adding parameters. Figure 4 demonstrates the overview recursive blocks structure of DRRN.

Unlike DRCN and DRRN, Zhang et al. [20] summarize and analyze the advantages and disadvantages of ResNet and DenseNet and combine them to propose a new structure ResidualDenseNet (RDN). In RDN, each layer is connected to every other layer in a feed-forward manner. This dense connectivity facilitates the flow of feature maps, enabling the model to effectively capture and reuse features from various stages of processing. Furthermore, residual learning facilitates the model’s ability to focus on learning the differences and details required for super-resolution.

Basically, even though these models have made remarkable strides in SR, their computational and storage demands are exceedingly complex and burdensome for hardware systems, making real-time processing unachievable on resource-limited devices. In order to mitigate the extremely high hardware requirements, the researchers have also produced outstanding results in model structure [21,22,23] and model quantization [24,25,26].

Of the various methods that make CNN lightweight or hardware-friendly, Binary Neural Networks (BNNs) are considered the most hardware-friendly and are capable of improving real-time performance. By mapping full-precision data to binary values {−1, 1} [27], BNNs reduce the number of bits required for storing data, significantly alleviating memory pressure.

Moreover, because of the characteristics of binary values, matrix multiplication can be replaced by XNOR-popcount operations, thus conserving a substantial amount of computational resources. Over the past few years, many researchers have demonstrated the advantages of BNN for implementation on resources-limited hardware and applied it across various domains with exceptionally high real-time requirements [28,29,30,31]. While BNNs significantly reduce hardware strain, they inevitably introduce some issues for performance of neural networks, notably information loss resulting from binarization. Over the past few years, numerous researchers have been committed to resolving this problem. The majority of these solutions can be categorized into the following research directions: the structure of neural networks [32,33,34,35,36,37] and improvements in binarization rules [32,38,39,40,41,42].

The introduction of the Binary Neural Network (BNN) by Courbariaux et al. [27] marked a significant milestone in DL, by utilizing binary representations for weight and activation, and leading the way for the Binary Neural Network concept. Although binary neural networks (BNNs) greatly save storage and computational resources through the binarization of weights and activations, the inevitable loss of a considerable amount of information due to binarization leads to a sharp decline in performance. Hence, subsequent research efforts aimed to address information loss arising from binarization. Rastegari et al. [32] innovatively introduced scaling factors computed via L1-norm during weight binarization to mitigate quantization errors and improve model performance. They simplified computation by substituting convolutions with XNOR-bitcount, substantially reducing matrix computation costs. This pioneering introduction of scaling factors opened avenues for potential research. XNOR-Net++ [38] further refined this concept by incorporating learnable scaling factors for distinct vector dimensions, reducing computational complexity through optimized calculations. However, later observations underscored the issue that scaling factors inevitably increase hardware demands. Despite IR-Net [40] utilizing a hardware-friendly integer scaling factor, the method necessitates data normalization before binarization, inevitably leading to increased computational complexity in the end.

In recent years, researchers have not only discovered that scaling factors can reduce information loss but also found that well-designed model architecture can effectively mitigate information loss compared to alternative models. Liu et al. [33] enhance the information of feature map by a full-precision shortcut. Research by Bethge, J et al. [36] confirmed the effectiveness of full-precision shortcuts and highlighted that binarizing shortcuts leads to irreversible information loss. Afterward, the Binarized Ghost Module (BGM) [34] and IE-Net [37] enhanced the model’s ability to capture information from inputs through multi-branch convolution blocks to varying degrees.

However, while existing works significantly enhance the performance of BNNs, such as the introduction of scaling factors, improving activation functions and multi-branch convolution, most improvements tend to increase the computational and storage burdens on the hardware. Therefore, for scenarios with limited hardware resources, the introduction of improvements might result in a trade-off that outweighs the benefits. As mentioned above, with the advancement of Super-Resolution (SR) and binarization techniques and optimizations in algorithmic complexity and memory requirements, barriers between SR algorithms and constraints related to hardware limitations in real-time applications are gradually diminishing.

The authors [43] proposed a specialized BNN architecture tailored for super-resolution. This approach only binarized the convolutional filters within the residual blocks and employed trainable weights for each binarized filter. In experiments, their proposed binarization strategy reduces the model size of SRResNet [44] by 80% and increases the inference speed by a factor of five. This work underscores the potential of employing BNNs for super-resolution tasks as an efficient alternative to traditional neural network architectures. Xin et al. [45] designed a Bit-Accumulation Mechanism (BAM) that approximates full-precision convolutions through value accumulation schemes, gradually refining the quantization precision along the direction of model inference. They also proposed an efficient model architecture called Binary Super-Resolution Network (BSRN) based on BAM to reduce computational complexity and parameters. In their experiments, they implemented their BAM into VDSR and SRResNet to prove effectiveness of their method and also have a comparison with BSRN.

The authors [26] introduced a novel approach called Binary Super-Resolution (BSR) using Mixed Binary Representation (MBR) to achieve higher pixel-level accuracy. This study introduces an innovative framework that combines binary and non-binary representations within the super-resolution architecture to enhance the quality of generated high-resolution images. By employing a mixed-precision approach, selectively using binary and non-binary representations in different parts of the network, the proposed method aims to preserve more detailed information, thus enhancing the fidelity of the images.

With regard to hardware, it is noteworthy that FPGAs stand out due to their exceptional parallel computing capabilities and high programmability. It is based on these considerations that we propose ResBinESPCN, two super-resolution networks designed for deployment on FPGA.

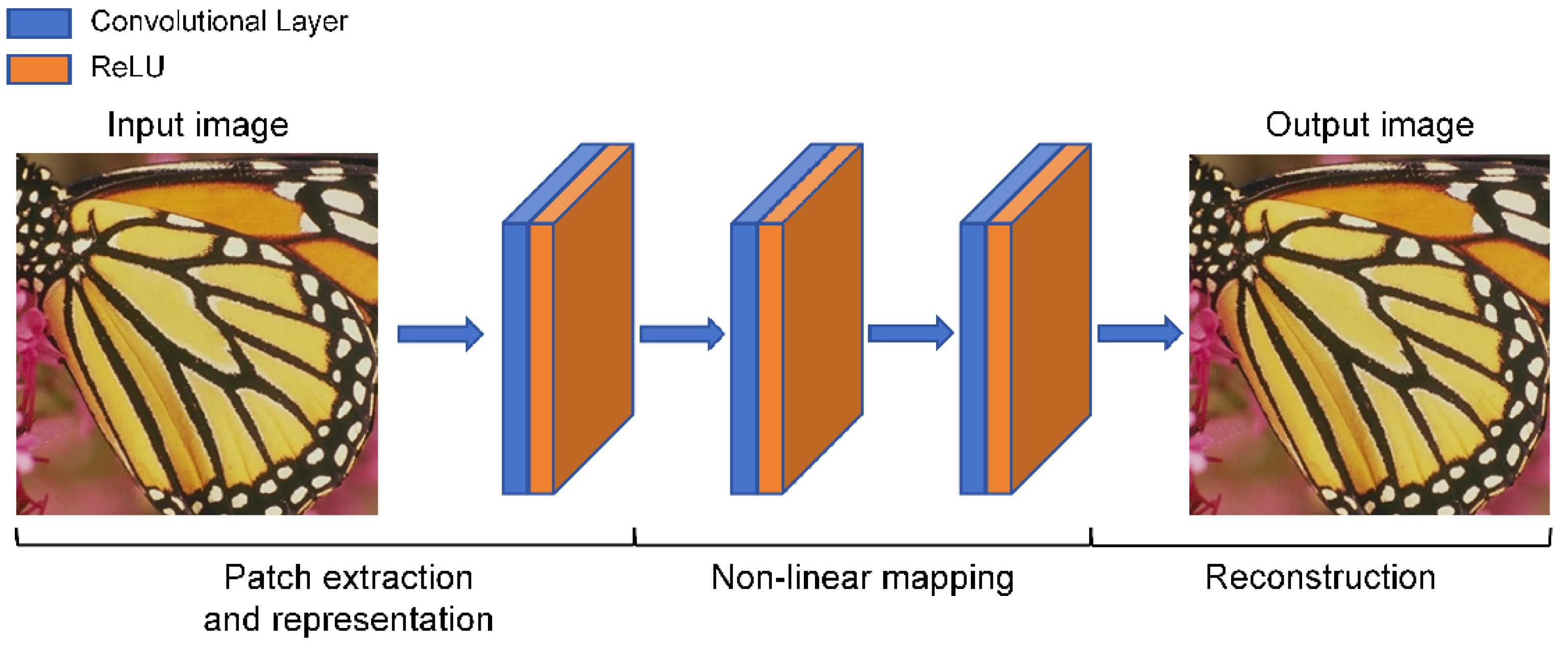
2. Binary Neural Network for Super-Resolution

For resource-constrained devices, models should not have an excessive number of parameters or overly complex computation demands, as this could burden the hardware significantly. However, as discussed above, most CNN-based methods nowadays unavoidably strain the hardware while enhancing performance. To provide a more intuitive understanding of the impact of various CNN-based methods on hardware consumption, we conducted a preliminary computation complexity and model size analysis on SRCNN, ESPCN, DRRN, and RDN, as shown in

Table 1. Hardware cost analysis with scaling factor 3.

Model	Input Shape	BOPs/MAC $(\times {10}^9)$	Total Number of Bits for Layer Parameters $(\times {10}^5)$	Estimated Total Size (MB)
SRCNN	Bicubic (1, 1, 255, 255)	590.42	18.30	50.95
ESPCN	LR (1, 1, 85, 85)	167.38	7.23	6.19
DRRN	Bicubic (1, 1, 255, 255)	51,271	236	3397.83
RDN	LR (1, 1, 85, 85)	160,590	713.46	670.5

.

Table 1 reveals that ESPCN manages to sustain a relatively compact model size and lightweight computational requirements, while demonstrating impressive model performance. This underscores ESPCN suitability as an excellent framework for our network architecture design.

Furthermore, limited-resource devices also often struggle to accommodate full-precision DNNs. Hence, quantization of parameters and activations becomes inevitable within DNNs. BNNs are widely regarded as the most hardware-friendly networks, offering advantages for improving real-time performance. Through (1), BNNs have the capability to convert full-precision weights and activation values into binary values {−1, 1}, significantly reducing the hardware burden [27].

$$sign(x)=\left\{\begin{array}{ll}-1,\hfill & if\hspace{1em}x\le 0\hfill \\ 1,\hfill & if\hspace{1em}x>0\hfill \end{array}\right.$$

(1)

And as we discussed above the multiplication in BNNs can be replaced by XNOR-popcount operation. The operation can be expressed as

$$X*W\approx sign(X)⊛sign(W)=X_b⊛W_b$$

(2)

where $W$ and $X$ denote inputs and weights of convolutional layer respectively. $*$ denotes the convolution operation. ⊛ presents the XNOR-Popcount operation. A key consideration is that, despite the advantages in storage and computational speed presented by BNNs, it is essential to acknowledge the inevitable decline in model performance due to the inadequate information representation of binary values. This issue can be alleviated through well-designed network structures. However, determining whether an architecture can enhance the performance of the neural networks requires extensive experiments. Fortunately, Bethge, J et al. [36] have summarized several BNNs structural design guidelines to assist researchers in devising suitable BNN architectures quickly [36]. In summary, the guidelines for designing BNN structures specific to SR can be summarized as follows:

• The fundamental principle of the design of BNN structures should prioritize the utmost preservation of information.
• As much as possible, bottleneck structures should be avoided. Bottleneck structures, characterized by reducing channel numbers and then increasing them, may result in irreversible information loss within BNNs.
• The downsampling layer should keep full precision to avoid mass loss of information by decreased number of channels.
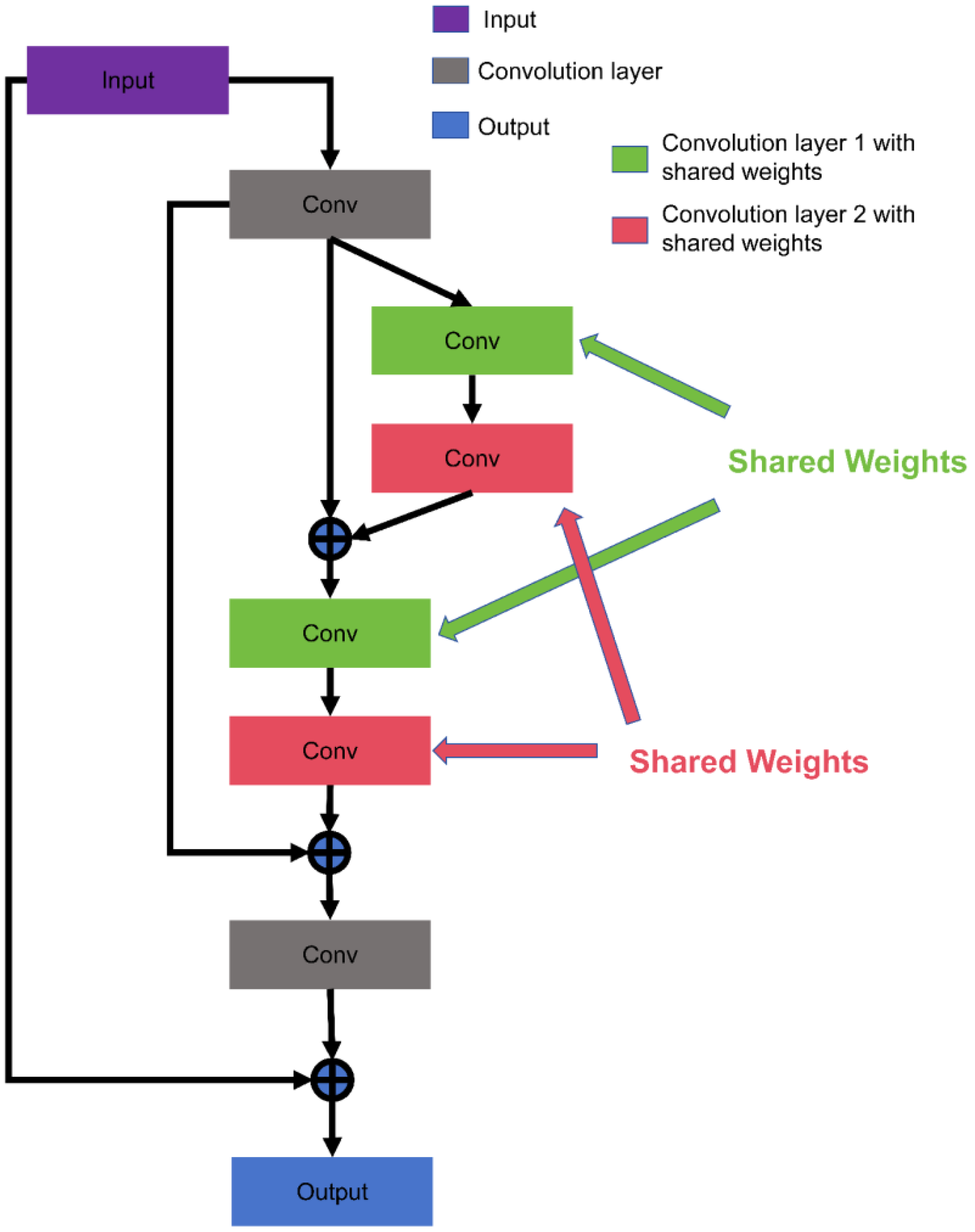
• The shortcut structure can preserve information significantly.

Following the aforementioned guidelines, and based on ESPCN, we propose the end-to-end model ResBinESPCN, the overview of whose model structure is illustrated in Figure 5.

In our design, aiming to maximize information preservation while minimizing hardware computational burden, we quantized the input layer and downsampling layers into W8A2. Here, W8 represents Int8 data type for weights, while A2 represents ternary data types for activations. The quantified input layer and downsampling layers can be expressed as:

$$Y=(Q_{Int8}(W)*Q_T(x))=W_{Int8}*X_T$$

(3)

where $Q_{Int8}$ and $Q_T$ denotes the 8-bit integer data type and ternary data type quantizer.

In addition, leveraging both design guidelines and the experimental outcomes from VDSR, we added additional shortcut connections into the model to mitigate the information loss caused by binarization.

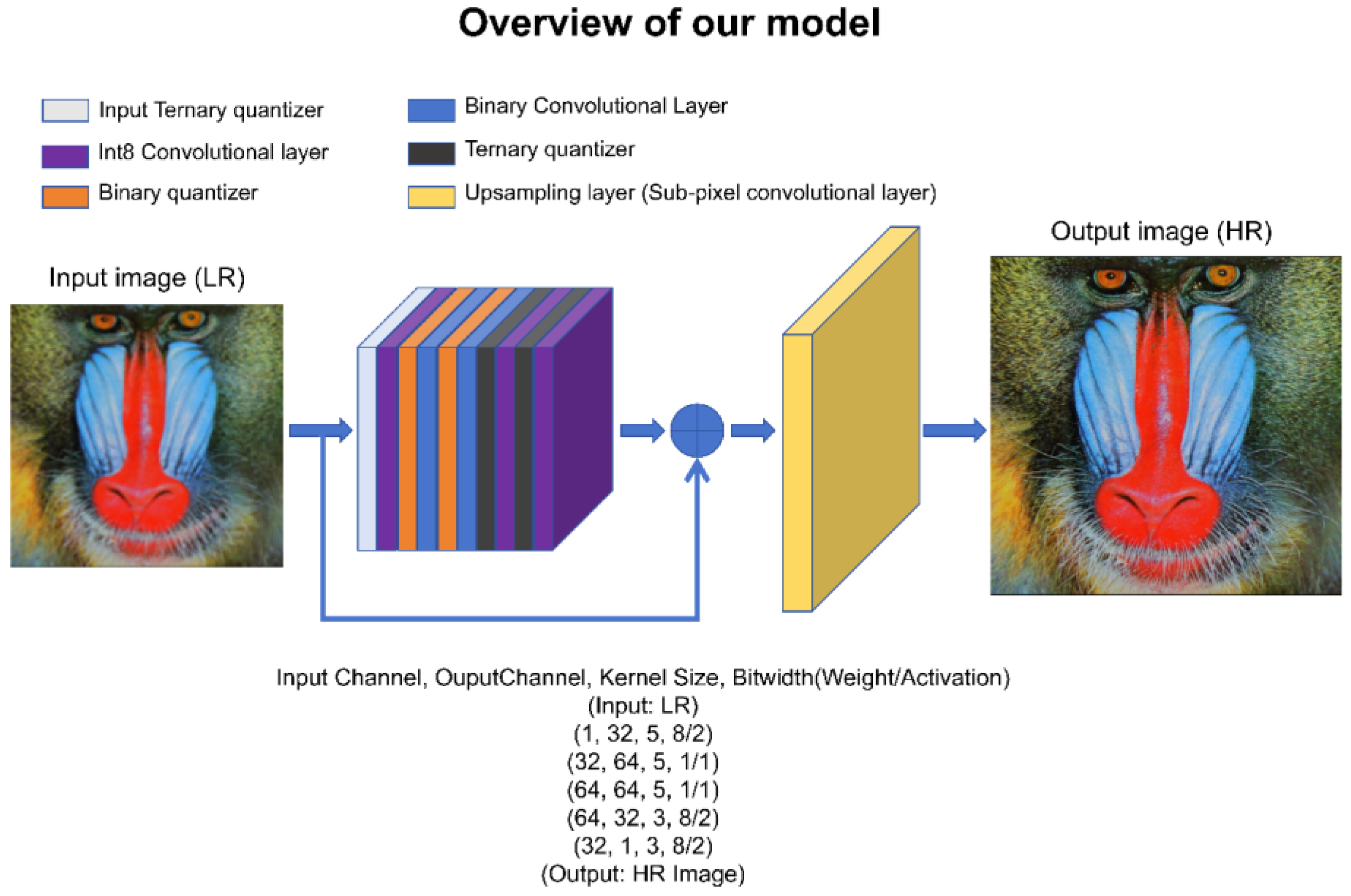
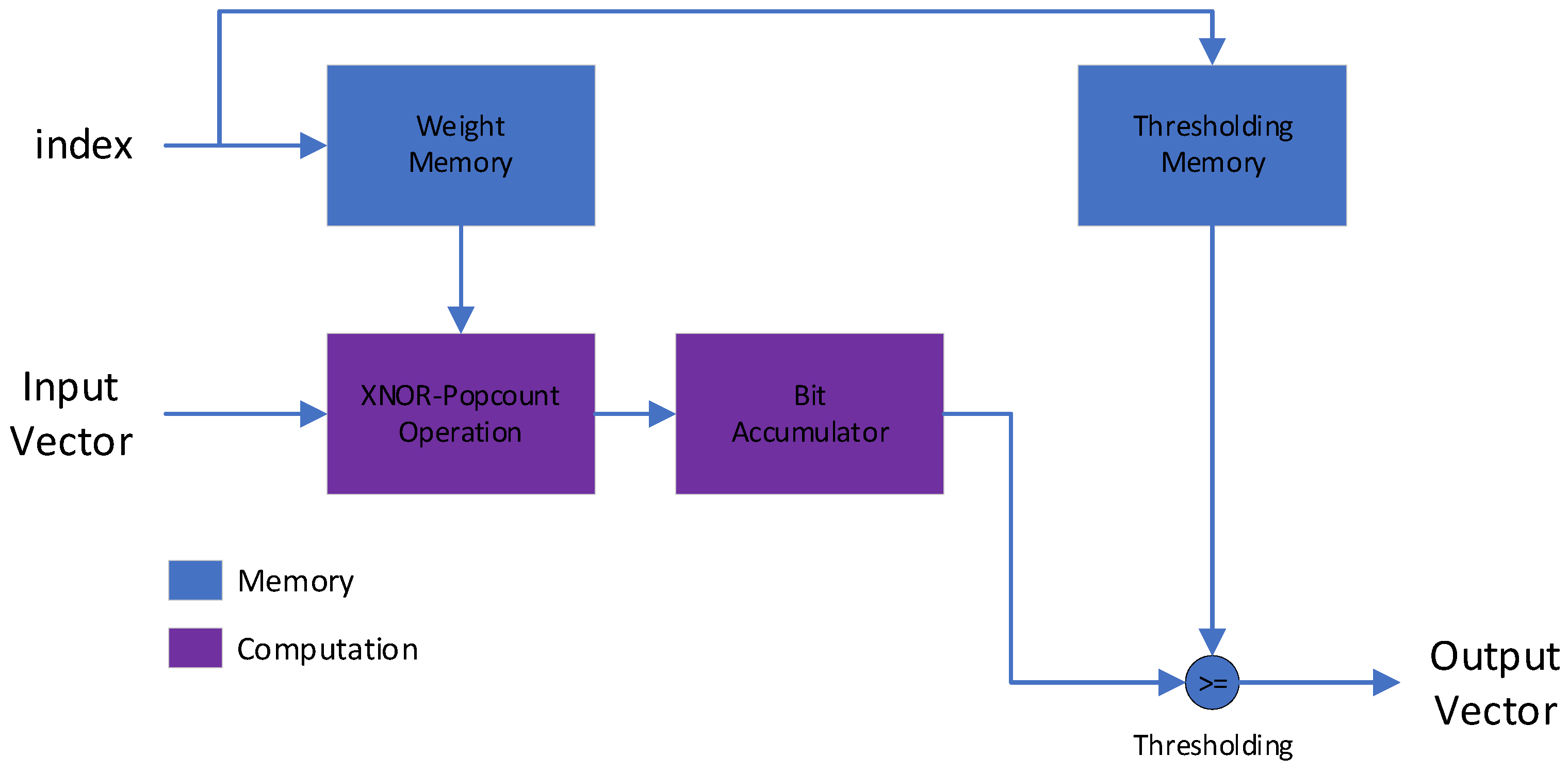
3. FPGA Implementation

As discussed above, the high parallelism offered by FPGA platforms presents an attractive option for accelerating the SR algorithmic process. Before going into the details of FPGA deployment, it is essential to understand some of the hardware resources of the FPGA platform, including the LUT, FF and BRAM.

Lookup Tables (LUTs) are fundamental components of Configurable Logic Blocks (CLBs) within FPGAs. These tables store information similar to truth tables and are programmable, enabling them to implement any combinational logic function with a specific number of inputs.

BRAM (Block RAM) refers to dedicated memory blocks available within FPGAs used to store a significant volume of data. Its memory capacity is relatively larger compared to distributed RAM within CLBs. In FPGA-based designs, BRAM is typically employed for tasks such as data buffering, coefficient storage, caching, and other memory-intensive operations. They offer faster access speeds compared to external memory, making them highly suitable for applications requiring rapid data access.

Flip-Flops (FF) are basic memory elements used to store a single bit of data. FF are used for sequential logic and to store state information in digital circuits, playing an essential role in constructing complex digital circuits.

However, in terms of development, FPGA circuit programming demands a substantial amount of specialized knowledge, which might not be readily available. For instance, programmers need to be familiar with Hardware Description Languages (HDL) or Verilog. The lack of experienced programmers can lead to challenges in reliably adopting FPGA and underutilizing its computational capabilities. To streamline the entire design process, in our approach, we deployed ResBinESPCN using FINN [46,47].

FINN, which was developed by Xilinx, supports various Xilinx FPGA boards and is specifically designed for Quantized Neural Networks (QNNs). Its primary function is to generate custom dataflow architectures for each neural network. Additionally, Xilinx has developed the quantization-aware training toolkit Brevitas, based on PyTorch, for FINN. FINN achieves automatic conversion from computational flow that is represented by ONNX models to hardware designs, breaking down barriers between software and hardware design. To achieve high flexibility, Xilinx also provides the finn-hlslib library which offers highly customizable HLS templates for data types such as inputs, weights, and outputs.

Additionally, FINN has undergone extensive optimization for Quantized Neural Networks (QNNs), including different dataflow architectures and specially designed computational units. Their proposed computational unit, the Matrix-Vector-Threshold Unit (MVTU), cleverly converts all multiplications and function mappings in the neural networks into more hardware-friendly additions and thresholding through skillful structural design. The datapath of MVTU is shown in Figure 6.

Due to the nature of parallel computing, the higher levels of parallelism also produce higher resource costs. Therefore, FINN can control the level of parallelism for each layer in the neural network through adjusting the number of Processing Elements (PEs) and Single Instruction Multiple Data (SIMD) units to adapt to different levels of FPGA platforms.

4. Results

In our experiments, we used the Z7P hardware experimental platform. Z7P is a development board that uses Xilinx components from the same series as ZCU104 (xczu7ev-ffvc1156-2-i). The detailed hardware resources are shown in

Table 2. Hardware Resources.

	Z7P (XCZU7EV-2FFVC1156-MPSoC)
System Logic Units	504 K
DSPs	1728
LUTs	230.4 K
LUTRAM	101.76 K
FF	460.8 K
Block Ram (BRAM)	312

.

In terms of model training, to ensure fairness in the ablation experiments, all models are trained on a publicly available benchmark dataset, the Timofte dataset [48], consisting of 91 images for training purposes. For testing, the Set5 [49] and Set14 [50] datasets, which provide 5 and 14 images, respectively, were used. Additionally, the Berkeley segmentation dataset, comprising 100 images, was used for model evaluation. For parameter initialization, we use Kaiming initialization [51] to initialize the parameters of convolution layers.

To demonstrate the performance improvement brought about by shortcuts and to showcase the performance differences between downsampling layers with different precision, three models were trained for comparison purposes. These models include: BinESPCN, which is without shortcut structures and with activation of downsampling layers using binary precision; ResBinESPCN-A1, which has an added shortcut structure based on BinESPCN; and ResBinESPCN-A2, which uses the downsampling layer with ternary precision. We also trained the original ESPCN on the same dataset as our baseline model.

Table 3. The mean PSNR of various methods evaluated on different datasets.

Dataset	Scale	Bicubic	ESPCN	BinESPCN	ResBinESPCN-A1	ResBinESPCN-A2	VDSR BAM	SRResNet BAM	BSRN
Set5	3	30.46	32.29	25.20	27.30	29.82	32.52	33.33	-
Set14		27.59	28.90	24.28	25.60	27.33	29.17	29.63	-
BSDS100		27.26	28.16	24.37	25.53	27.03	-	-	-
Set5	4	28.48	28.80	23.80	26.00	28.11	30.31	31.24	31.35
Set14		25.92	26.16	22.69	24.46	25.78	27.46	27.97	28.04
BSDS100		26.02	26.21	22.99	24.73	25.87	-	-	-

presents the performance comparison.

Compared to ESPCN, the BinESPCN model suffers from severe overall information loss due to the absence of a shortcut structure, resulting in a sharp decline in model performance. However, with the introduction of the shortcut structure in ResBinESPCN, the model performance presents a certain degree of improvement. This enhancement is attributed to the fact that the shortcut structure assists the model with binary data type in preserving a greater amount of information. A preliminary hardware resource consumption analysis is given in

Table 4. Hardware cost on FPGA with scaling factor 3.

Model	Parameters	MACs $(\times {10}^9)$	BOPs/MACs $(\times {10}^9)$	Total Number of Bits for Layer Outputs $(\times {10}^5)$	Total Number of Bits for Layer Parameters $(\times {10}^5)$
ESPCN	23 K	0.163	167.38	242.76	7.23
VDSR_BAM	668 K	616.9	-	-	-
SRResNet BAM	1547 K	127.9	-	-	-
BSRN	1216 K	85	-	-	-
BinESPCN	349 K	1.2433	3.50	464.71	3.01
ResBinESPCN-A1	349 K	1.2435	3.53	464.71	3.01
ResBinESPCN-A2	349 K	1.2435	36.38	464.71	3.01

, with the aim of visualizing the difference in computational and memory resources after quantization.

BOPs/MACs means total bit operations (BOPs) normalized to Multiply-Accumulate operations (MACs). This would represent the total number of bit-level operations executed for all MAC operations within a neural network layer, a network, or an entire model. It is obtained by summing up the BOPS for each MAC operation across the network or layer. A lower BOPS per MAC (BOPs/MAC) value indicates that fewer bit-level operations are required to perform a single MAC operation. This implies greater computational efficiency, as fewer operations are needed to achieve the same computation. In hardware implementations, a lower total number of BOPS normalized to MACs translates to reduced computational complexity and potentially lower resource requirements. This is advantageous for deploying neural network models on resource-constrained devices or specialized hardware accelerators. Furthermore, Lower BOPS per MAC values or fewer total BOPS normalized to MACs often correlate with faster processing times. Fewer bit-level operations mean quicker computations, resulting in faster inference or training speeds for neural network models.

Based on Table 3 and Table 4, the introduction of the shortcut structure did not impose a substantial computational burden on the hardware. Simultaneously, it contributed to a certain improvement in the model performance. Moreover, the introduction of downsampling with ternary data type further improved the model performance. However, the utilization of ternary data types added complexity to the model’s computations. Nonetheless, compared to the baseline model, ResBinESPCN-A2 reduced the number of BOPs/MAC by approximately ten times. Additionally, concerning memory efficiency, our model showcased significant progress through reducing memory consumption by nearly two times. Compared to VDSR, SRResNet with BAM, and BSRN, the drawbacks of a lightweight model structure are evident in terms of underperformance. Nonetheless, our model performs well in terms of reducing the number of parameters and hardware resource consumption, making it still potentially useful for practical applications in resource-constrained environments. This trade-off also means that our approach is perhaps slightly less effective in handling complex image details. Overall, our approach finds a balance between performance and computational efficiency, providing a viable solution for specific application scenarios.

To visualize the model performance, Figure 7, Figure 8 and Figure 9 display three different HR images. We also zoomed in on the images to facilitate the observation of changes in image details.

FINN offers the flexibility to control the parallelism of computations by adjusting the quantity of PEs and SIMD, leading to a myriad of potential configurations. To streamline the experimental process, we broadly categorized the parallelism into three levels: low, medium, and high. Low denotes the minimal level of parallelism within the constraints provided by FINN, while high signifies the maximum. Medium stands as an intermediate point between low and high parallelism levels.

Table 5. Hardware cost on FPGA.

Board	Model	Parallelism	LUT (Utilization)	LUTRAM	FF	BRAM	BUFG	Power (W)
Z7P	ResBinESPCN-A2	Low	21,685 (9.41%)	4752 (4.67%)	24,653 (5.35%)	14 (4.49%)	2 (0.37%)	3.545
		Medium	44,255 (19.21%)	7372 (7.24%)	45,144 (9.8%)	87 (27.88%)	9 (1.65%)	4.207
		High	64,015 (27.78%)	12,736 (12.52%)	70,154 (15.55%)	58 (18.59%)	11 (2.02%)	4.452

and Figure 10 present the FPGA hardware costs for deploying ResBinESPCN-A2. From the results, it can be seen that the computational resources and energy consumption of the hardware increase as the degree of parallelism increases.

5. Conclusions

This paper proposed an end-to-end super-resolution deep learning model named ResBinESPCN, based on Binary Neural Networks (BNNs). The model accelerates computations and reduces memory consumption by data binarization and by using low bit-width data types. Moreover, the introduction of the shortcut structure has also brought about a notable improvement in reconstruction quality. ResBinESPCN exhibits strong model performance while maintaining high-speed execution and a relatively smaller model size. With regard to the hardware, deploying deep learning models on FPGA using FINN has streamlined the complex deployment process. Additionally, FINN’s flexibility in controlling parallelism allows for different levels of parallel computation based on the computational and storage resources of various hardware platforms, which is beneficial for large-scale system deployments such as heterogeneous IoT sensor networks and distributed computing systems. Additionally, closed-circuit television (CCTV) is a critical component of today’s security systems for monitoring various locations. Our method can be effortlessly integrated into wireless multimedia sensors such as RGB cameras, without significant hardware costs. In the field of biometric information recognition, our model also demonstrates promise. It significantly enhances details in shape and structural textures, potentially boosting recognition capabilities in related applications by effectively preserving the global structure. Take, for example, the images shown in Figure 7. In the aforementioned applications, owing to its lightweight design, our model can be deployed at the edge, achieving the task of image super-resolution locally. This enables the effective protection of user data privacy while ensuring relatively rapid responsiveness.

6. Future Work

Although BNNs significantly reduce hardware burdens, the information loss incurred by binarization is often intolerable. This implies that, while introducing methods like scaling factors, specially designed activation functions, or multi-branch convolutions in the proposed model, may lead to some performance improvements, most existing approaches aimed at mitigating information loss due to binarization are not inherently hardware-friendly. However, in environments where hardware conditions are relatively lenient and stringent model performance is required, sacrificing some hardware resources to enhance model performance, such as introducing scaling factors or increasing depth of model, might be acceptable. In future work, we believe it is crucial to focus on a co-design approach involving both software and hardware to devise an efficient method that is hardware-friendly and capable of extracting input information effectively.