Set Restabilization of Perturbed Boolean Control Networks

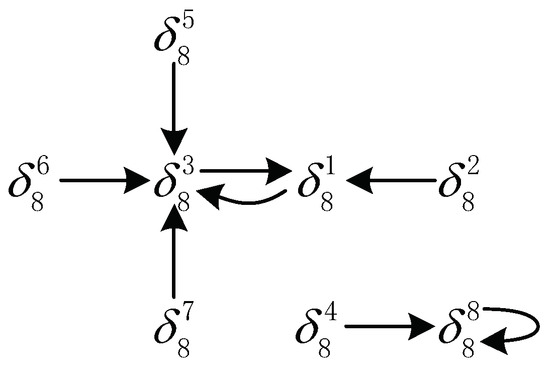
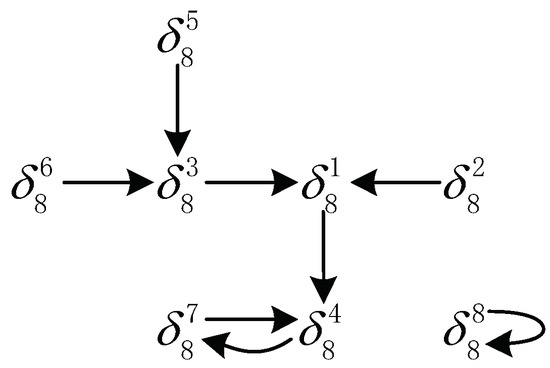
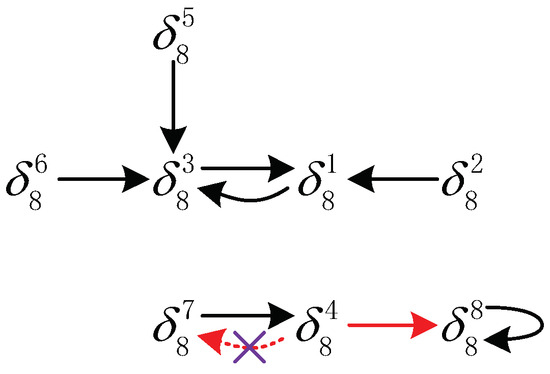
Abstract

This paper develops a parameter tuning method for solving the set restabilization problem of perturbed Boolean control networks (BCNs). First, the absorbable attractor, which we previously proposed, is recalled. Based on the relationship between attractors, a necessary and sufficient restabilizability criterion is derived. This criterion is used to check whether a perturbed BCN can be stabilized to the original target set by modifying the least number of parameters to the old controller. Furthermore, a constructive method for fine-tuning the old controller is provided if the criterion condition derived above is satisfied. Compared with the existing relevant results, ours have clear advantages, since they can address the set restabilization problem of BCNs subject to multi-column function perturbations, which has not been solved yet. Finally, two examples are employed to show the effectiveness and advantages of our results.

1. Introduction

The Boolean network (BN), proposed by Kauffman in 1969, is a simple logical dynamic system. It is commonly used to study genetic regulatory networks [1], cryptography [2], games [3], and so on. A BN consists of a set of nodes, each with two states. These nodes are connected with each other through logical rules. In addition, a BN with external inputs is called a Boolean control network (BCN). It should also be investigated as in control theory, because the goal of systems biology is to design therapy strategies in the treatment of some diseases, for example, cancer. To achieve the goal, gene intervention was proposed, whose main idea is to perturb some genes and then facilitates the gene regulatory network to evolve to a set of desired states from an unhealthy state. BNs and BCNs may seem simple, but they possess complex dynamic characteristics. Many problems related to practical biology can be effectively studied in such a Boolean form [4], which prompts researchers to explore BNs and BCNs.

In the past two decades, there has been a lot of research on BNs and BCNs. The stability and stabilization of BCNs has always been a research hotspot. For example, Cheng et al. gave basic definitions for the stability of BNs and the stabilization of BCNs in [5], and provided stability criteria and stabilization design methods. Li et al. pioneered a design method for state feedback controller of BCNs in [6]. Tian et al. proposed a design method with relatively low complexity for open control in [7]. The output feedback stabilization of BCNs was studied in [8], and a specific controller design method was provided. The simultaneous stabilization for a set of BCNs was investigated in [9]. Lin et al. discussed the stabilization of constrained BCNs [10]. These results are all about how to design a controller to stabilize a BCN to a fixed point. Later, some scholars directed their attention to set stability and set stabilization of BCNs [11,12,13,14,15,16], since in some cases, the interest lies in whether a BCN can be stabilized to a given target set, rather than a single point. A typical application of set stabilization is the synchronization design of a collection of interconnected systems; see Examples 1, 2, and 3 in [11].

On the other hand, the actual system is inevitably disturbed by its surrounding environment. This may lead to changes in the structural parameters of the system. In particular, the impact of immeasurable variables or gene mutation on the gene regulatory network cannot be ignored. So the robustness of BCNs is particularly important, and many excellent research results have been reported, for example, refs. [17,18,19,20,21,22,23,24,25,26,27,28,29]. Most of these results are about the influence of perturbations on BNs [17,18,19,20,21,22,23,24,25] and robust stabilization of perturbed BCNs [20,26,27,28,29]. It is worth pointing out that the designed controllers are robust, but the robustness is limited. In other words, when some sensitive parameters in a BCN change slightly, the perturbed BCN may become unstable if it is still under the old controller. The simplest solution to this problem is to redesign the controller. However, a completely new controller can easily cause serious oscillation at the beginning of the system response. Therefore, it is significant to investigate how to deal with the restabilization problem of perturbed systems. Unfortunately, there are few papers in this respect. Recently, Li et al. have proposed an effective algorithm in [30] to modify the old state feedback controller, such that the unstable closed-loop system, due to disturbances, can be stabilized back to the original state. The pity is that the algorithm, as the authors said, can only deal with the single column function perturbation problem, but cannot solve the perturbation problem of multiple columns. Hou et al. developed a fine-tuning method in [31] to solve the multi-column function perturbation problem. Regrettably, it cannot be directly applied to the set restabilization problem. The above information is summarized in Table 1.

Table 1. Summary of research on the stability and stabilization of perturbed BCNs.

References	Research Contents	Existing Problems
[17,18,19,20,21,22,23,24,25]	They studied the influence of perturbations on BNs.	They have not investigated how to ensure the stability of perturbed BCNs.
[20,26,27,28,29]	They designed various robust controllers for the stabilization of perturbed BCNs.	When some sensitive parameters change slightly, the perturbed BCN may become unstable. For this case, they have not studied how to adjust the parameters to restabilize the perturbed BCN to its original state or target set.
[30]	It proposed a parameter adjustment algorithm that can deal with the single column perturbation problem of BCNs.	It cannot solve the restabilization problem of BCNs subject to multi-column function perturbations.
[31]	It developed a parameter adjustment method that can handle the multi-column function perturbation problem of BCNs.	It cannot be directly used to solve the set restabilization problem of perturbed BCNs.

Under the background, this paper tries to investigate the set restabilization of BCNs subjected to multi-column function perturbations. The main contributions are summarized as follows:

• An algorithm for calculating absorbable attractors is provided, where absorbable attractors play a key role in our method.
• For the perturbed BCNs, a method is developed to solve the set restabilization problem of BCNs subject to multi-column function perturbations, which has not been settled yet. This method has a wider scope of application, since most results in the existing literature are mainly about restabilization to a singleton, which is a special case of set restabilization.

The remaining part of our paper is arranged as follows. Some preliminary knowledge is introduced in Section 2. The main results are provided in Section 3. These results include some concepts, a set restabilizability criterion, and three algorithms. Section 4 gives two illustrative examples, and Section 5 offers a conclusion.

2. Materials and Methods

For the sake of convenience, some symbol explanations are given first.

• $\mathbb{D}:=\{0,1\}$.
• ${\Delta }_n$ represents the set $\{{\delta }_n^i\mid i=1,2,\cdots ,n\}$, where ${\delta }_n^i$ denotes the ith column of the $n\times n$ identity matrix.
• ${\delta }_n[i_1,i_2,\cdots ,i_s]$ stands for the matrix $[{\delta }_n^{i_1}{\delta }_n^{i_2}\cdots {\delta }_n^{i_s}]$, called a logical matrix.
• $Co{l}_i\left(L\right)$ and $Ro{w}_i\left(L\right)$ express the ith column and ith row of a matrix L, respectively.
• ${\mathbb{L}}_{m\times n}$ (${\mathbb{M}}_{m\times n}$) is the set of $m\times n$ logical (real) matrices.
• ${\mathbb{B}}_{m\times n}$ is the set of $m\times n$ matrices with all entries in $\mathbb{D}$.

The semi-tensor product (STP) is the main mathematical tool. We recall its definition and a basic property [32].

• For two matrices $A\in {\mathbb{M}}_{m\times n}$ and $B\in {\mathbb{M}}_{p\times q}$, the STP of A and B is

  $$A⋉B:=(A\otimes I_{{\displaystyle \frac{r}{n}}})(B\otimes I_{{\displaystyle \frac{r}{p}}}),$$

  where r is the least common multiple of n and p; ⊗ is the Kronecker product of matrices.
• The $2^{2n}\times 2^n$ logical matrix

  $${\Phi }_n={\delta }_{2^{2n}}[1,2^n+2,2·2^n+3,\cdots ,(2^n-2)2^n+2^n-1,2^{2n}],$$

  called a power-reducing matrix, satisfies ${\delta }_{2^n}^i⋉{\delta }_{2^n}^i={\Phi }_n{\delta }_{2^n}^i$.

Remark 1. 

The STP is a natural extension of ordinary matrix multiplication, since it has the same basic properties as the ordinary matrix multiplication. In particular, STP is the ordinary matrix multiplication when $n=p$. The operational symbol ⋉ is usually omitted for simplicity in this paper.

As we know, all entries of a Boolean matrix are in $\mathbb{D}$. Now, Boolean addition ⊕ and Boolean product ⊙ of two Boolean matrices $A=\left(a_{ij}\right)\in {\mathbb{B}}_{m\times n}$ and $B=\left(b_{ij}\right)\in {\mathbb{B}}_{p\times q}$ are recalled.

• When $m=p$ and $n=q$, $A\oplus B=(a_{ij}\vee b_{ij})\in {\mathbb{B}}_{m\times n}$.
• When $n=p$, $A\odot B=\left(c_{ij}\right)\in {\mathbb{B}}_{m\times q}$, where $c_{ij}={\vee }_{k=1}^n(a_{ik}\wedge b_{kj})$.

Consider a BCN

$$\left\{\begin{array}{c}{x}_1(t+1)=f_1(u_1\left(t\right),\cdots ,u_m\left(t\right),x_1\left(t\right),\cdots ,x_n\left(t\right))\hfill \\ x_2(t+1)=f_2(u_1\left(t\right),\cdots ,u_m\left(t\right),x_1\left(t\right),\cdots ,x_n\left(t\right))\hfill \\ \cdots \hfill \\ x_n(t+1)=f_n(u_1\left(t\right),\cdots ,u_m\left(t\right),x_1\left(t\right),\cdots ,x_n\left(t\right)),\hfill \end{array}\right.$$

(1)

and a state feedback controller

$$\left\{\begin{array}{c}{u}_1\left(t\right)=g_1(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right))\hfill \\ u_2\left(t\right)=g_2(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right))\hfill \\ \cdots \hfill \\ u_m\left(t\right)=g_m(x_1\left(t\right),x_2\left(t\right),\cdots ,x_n\left(t\right)),\hfill \end{array}\right.$$

(2)

where $x_i\in \mathbb{D}$, $i=1,2,\cdots ,n$ are state variables; $u_j\in \mathbb{D}$, $j=1,2,\cdots ,m$ are control inputs; $f_i:{\mathbb{D}}^n\times {\mathbb{D}}^m\to \mathbb{D}$ and $g_j:{\mathbb{D}}^n\to \mathbb{D}$ are logical functions.

We replace 1 and 0 with ${\delta }_2^1$ and ${\delta }_2^2$, respectively. The symbols $x_i\left(t\right)$ and $u_j\left(t\right)$ are also used to represent the vector forms of corresponding logical variables, if no confusion arises. Define $x\left(t\right)={⋉}_{i=1}^n{x}_i\left(t\right)\in {\Delta }_{2^n}$ and $u\left(t\right)={⋉}_{j=1}^m{u}_j\left(t\right)\in {\Delta }_{2^m}$. According to STP techniques [32], it is easy to obtain the algebraic form of (1)–(2):

$$\begin{array}{ccc}\hfill x(t+1)& =& Lu\left(t\right)x\left(t\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill u\left(t\right)& =& Gx\left(t\right),\hfill \end{array}$$

(4)

where $L\in {\mathbb{L}}_{2^n\times 2^{n+m}}$ and $G\in {\mathbb{L}}_{2^m\times 2^n}$ are called the structure matrix of (3) and state feedback matrix of (4), respectively. Due to the equivalence between (1)–(2) and (3)–(4), we only study (3)–(4) to highlight our method hereafter.

Substituting (4) into (3), we obtain the closed-loop system

$$\begin{array}{cc}\hfill x(t+1)=& LGx\left(t\right)x\left(t\right)\hfill \\ \hfill =& LG{\Phi }_{n}x\left(t\right)\hfill \\ \hfill =& \overline{L}x\left(t\right),\hfill \end{array}$$

(5)

where $\overline{L}$ is the structure matrix of (5).

Definition 1. 

For a given target set $\mathfrak{M}$, BCN (3) is said to be stabilized to $\mathfrak{M}$ by the state feedback controller (4), if for any initial state $x_0\in {\Delta }_{2^n}$, there is an integer T, such that the state $x(t,x_0)$ of (5) satisfies $x(t,x_0)\in \mathfrak{M},\forall t\ge T.$

Definition 2 

([11]). A set $\mathfrak{M}$ is an invariant subset of the closed-loop system (5), if for any initial state $x_0\in \mathfrak{M}$, we have $x(t,x_0)\in \mathfrak{M},t\ge 0$. And the union of all of the invariant subsets contained in $\mathfrak{M}$ is called the largest invariant subset contained in $\mathfrak{M}$, denoted by $I(\mathfrak{M};L,G)$.

Definition 3 

([11]). A set $\mathfrak{M}$ is a control invariant subset of BCN (3), if for any initial state $x_0\in \mathfrak{M}$, there is a control sequence $u\left(t\right)$, such that $x(t,x_0,u\left(t\right))\in \mathfrak{M},t\ge 0$. And the union of all of the control invariant subsets contained in $\mathfrak{M}$ is called the largest control invariant subset contained in $\mathfrak{M}$, denoted by $I_c(\mathfrak{M};L)$.

Remark 2. 

As we know, the union of (control) invariant subsets is still a (control) invariant subset. So $I(\mathfrak{M};L,G)$ ($I_c(\mathfrak{M};L)$) is also a (control) invariant subset. From Lemma 4 of [11], BCN (3) is $\mathfrak{M}$-stabilizable if and only if it is $I_c(\mathfrak{M};L)$-stabilizable. Refer to [11] for more about the largest invariant subset and the largest control invariant subset.

When BCN (1) is seriously perturbed, there may be a logical function with a bit error or multiple bit errors in its truth table. Correspondingly, we call this phenomenon a one-bit function perturbation and a multibit function perturbation, respectively. These bit perturbations lead to changes in the columns of the structure matrix L. Such column changes are called column perturbations. Specifically, if only one column changes, we call it a single column function perturbation; otherwise, it is said to be a multi-column function perturbation.

Example 1. 

Consider the following BCN:

$$\left\{\begin{array}{c}{x}_1(t+1)=x_1\left(t\right)\vee x_2\left(t\right)\hfill \\ x_2(t+1)=u\left(t\right)\wedge x_1\left(t\right)\wedge x_2\left(t\right),\hfill \end{array}\right.$$

(6)

whose truth table is shown in Table 2. Assume that BCN (6) is perturbed, which causes $f_1(1,0,0)$ to change from 0 to 1 (this is a one-bit function perturbation). Correspondingly, $Co{l}_4\left(L\right)$ changes from ${\delta }_4^4$ to ${\delta }_4^2$ (it is a single column function perturbation). If the value 0 of $f_2(1,1,0)$ also changes and turns into 1 (accordingly, $Co{l}_2\left(L\right)$ changes from ${\delta }_4^2$ to ${\delta }_4^1$), then BCN (6) suffers from a multi-bit perturbation.

Table 2. Truth table of logical functions $f_1$ and $f_2$ in (6).

$\mathit{u},{\mathit{x}}_1,{\mathit{x}}_2$	1, 1, 1	1, 1, 0	1, 0, 1	1, 0, 0	0, 1, 1	0, 1, 0	0, 0, 1	0, 0, 0
$f_1$	1	1	1	0	1	1	1	0
$f_2$	1	0	0	0	0	0	0	0

The target set is always denoted by $\mathfrak{M}$ in this paper. It is assumed that BCN (3) is stabilized to $\mathfrak{M}$ by an appropriate controller (4). That is, the closed-loop system (5) is $\mathfrak{M}$-stable. If BCN (1) is seriously disturbed and its structure matrix L changes into another matrix $L^{\ast }$, then BCN (3) becomes

$$x(t+1)=L^{\ast }u\left(t\right)x\left(t\right),$$

(7)

and the closed-loop system (5) turns into

$$x(t+1)=L^{\ast }G{\Phi }_{n}x\left(t\right).$$

(8)

At this time, the perturbed closed-loop system (8) may no longer be $\mathfrak{M}$-stable. In practical engineering, in order to avoid large oscillations in the system response, engineers usually tune parameters of the old controller as little as possible, rather than redesign a new controller to stabilize the perturbed system back to the original target set. The adjustment process is called parameter fine-tuning.

Our main purpose is to develop a method which can be used to check whether the perturbed and unstable closed-loop system (8) can be stabilized back to the original target set $\mathfrak{M}$, through a fine-tuning technique. In addition, a specific parameter fine-tuning technique should be proposed.

3. Results

When the perturbed closed-loop system (8) is not stable within $\mathfrak{M}$, we analyze its $\mathfrak{M}$-restabilization from the following two problems.

• $Problem 1$. How do we tune the old controller when $I(\mathfrak{M};L^{\ast },G)\ne I_c(\mathfrak{M};L^{\ast })$?
• $Problem 2$. How do we tune the old controller when there are attractors not contained in the target set $\mathfrak{M}$?

Remark 3. 

As we know, $I(\mathfrak{M};L^{\ast },G)\subseteq I_c(\mathfrak{M};L^{\ast })$. So if $I(\mathfrak{M};L^{\ast },G)\ne I_c(\mathfrak{M};L^{\ast })$, then $I(\mathfrak{M};L^{\ast },G)\subset I_c(\mathfrak{M};L^{\ast })$. The purpose of handling Problem 1 is just to increase the likelihood of solving Problem 2, since Problem 2 is the main issue we need to solve in $\mathfrak{M}$-restabilization of the perturbed system (8).

3.1. Modification for the Largest Invariant Subset

For the perturbed BCN (7), as we mentioned earlier, $\mathfrak{M}$-stabilizability is equivalent to $I_c(\mathfrak{M};L^{\ast })$-stabilizability. Therefore, if BCN (7) is $\mathfrak{M}$-stabilizable, the largest control invariant subset $I_c(\mathfrak{M};L^{\ast })$ must be nonempty.

Assumption 1. 

For BCN (7), the largest control invariant subset $I_c(\mathfrak{M};L^{\ast })$ is nonempty.

Under Assumption 1, we use Proposition 2 given in [11] to calculate $I_c(\mathfrak{M};L^{\ast })$ of BCN (7). Now we further provide an algorithm to implement $I_c(\mathfrak{M};L^{\ast })$ as the largest invariant subset of the closed-loop system by modifying columns of G.

Remark 4. 

For any state ${\delta }_{2^n}^i$ in $I_c(\mathfrak{M};L^{\ast })$, there may be several different control signals u, such that the next state of BCN (7) is still in $I_c(\mathfrak{M};L^{\ast })$, namely $L^{\ast }u{\delta }_{2^n}^i\in I_c(\mathfrak{M};L^{\ast })$. In this case, we adopt the principle of modifying the parameters as little as possible, which can be seen from Step 1 of Algorithm 1. Specifically, if the control signal $u=G{\delta }_{2^n}^i$, given by the old controller (7), is one of the above feasible control signals, we keep the ith column of G unchanged. In this way, while implementing $I_c(\mathfrak{M};L^{\ast })$ as the largest invariant subset of the new closed-loop system, we minimize the number of parameter modifications of G.

Algorithm 1 The feedback matrix G can be modified by the following steps to make $I_c(\mathfrak{M};L^{\ast })$ equal to the largest invariant subset of the new closed-loop system.

Step 1 For any ${\delta }_{2^n}^i\in I_c(\mathfrak{M};L^{\ast })$, check whether $L^{\ast }G{\Phi }_n{\delta }_{2^n}^i\in I_c(\mathfrak{M};L^{\ast })$. If yes, the column vector $Co{l}_i\left(G\right)$ remains unchanged. Else, go to Step 2. Step 2 Find a constant control $u={\delta }_{2^m}^{{\mu }_i}$ satisfying $L^{\ast }{\delta }_{2^m}^{{\mu }_i}{\delta }_{2^n}^i\in I_c(\mathfrak{M};L^{\ast })$, and then set $Co{l}_i\left(G\right)={\delta }_{2^m}^{{\mu }_i}$.

3.2. Modification for Unstable Attractors

Let the feedback matrix G be modified into $G^{\ast }$ by Algorithm 1. Then, the old controller (4) changes into

$$u\left(t\right)=G^{\ast }x\left(t\right),$$

(9)

and the closed-loop system (8) becomes

$$x(t+1)=L^{\ast }{G}^{\ast }{\Phi }_{n}x\left(t\right),$$

(10)

whose largest invariant subset $I(\mathfrak{M};L^{\ast },G^{\ast })$ is equal to $I_c(\mathfrak{M};L^{\ast })$.

The closed-loop system (10) is still not stable within $\mathfrak{M}$, since the system (10) has attractors not included in $\mathfrak{M}$. Let all such attractors be given as follows:

$${\mathcal{X}}_1,{\mathcal{X}}_2,\cdots ,{\mathcal{X}}_p,$$

(11)

where

$${\mathcal{X}}_i:{\delta }_{2^n}^{i_1}\to {\delta }_{2^n}^{i_2}\to \cdots \to {\delta }_{2^n}^{i_{q_i}}\to {\delta }_{2^n}^{i_1},i=1,2,\cdots ,p.$$

For any ${\mathcal{X}}_i$, we define its attraction domain as

$$R\left({\mathcal{X}}_i\right)=\left\{x\right|\mathrm{There}\mathrm{exists}\mathrm{a}\mathrm{positive}\mathrm{integer}r\le 2^n-1,\mathrm{such}\mathrm{that}{\left(L^{\ast }{G}^{\ast }{\Phi }_n\right)}^{r}x\in {\mathcal{X}}_i\}.$$

Before giving our main theorem, an important concept is recalled.

Definition 4 

([31]). 1. Assume that ${\mathcal{X}}_i$ and ${\mathcal{X}}_j$ are attractors of the closed-loop system (10). If there is a state ${\delta }_{2^n}^k\in {\mathcal{X}}_i$ and an integer ${\alpha }_k$ satisfying $1\le {\alpha }_k\le 2^m$, such that $Co{l}_{({\alpha }_k-1)2^n+k}\left(L^{\ast }\right)\in R\left({\mathcal{X}}_j\right)$, then ${\mathcal{X}}_i$ is said to be an absorbable attractor of ${\mathcal{X}}_j$ by one step, and we denote it as ${\mathcal{X}}_i\in {\mathbb{A}}_1\left({\mathcal{X}}_j\right)$.

2. Let ${\mathcal{X}}_i$ and ${\mathcal{X}}_j$ be two attractors of (10), where ${\mathcal{X}}_i\notin {\mathbb{A}}_{s-1}\left({\mathcal{X}}_j\right)$. If there is a different attractor ${\mathcal{X}}_r$ satisfying ${\mathcal{X}}_r\in {\mathbb{A}}_{s-1}\left({\mathcal{X}}_j\right)$, such that ${\mathcal{X}}_i\in {\mathbb{A}}_1\left({\mathcal{X}}_r\right)$, then ${\mathcal{X}}_i$ is said to be an absorbable attractor of ${\mathcal{X}}_j$ by s steps, and we denote it as ${\mathcal{X}}_i\in {\mathbb{A}}_s\left({\mathcal{X}}_j\right)$. When the number of steps s does not need to be emphasized, ${\mathcal{X}}_i\in {\mathbb{A}}_s\left({\mathcal{X}}_j\right)$ is usually written as ${\mathcal{X}}_i\in \mathbb{A}\left({\mathcal{X}}_j\right)$, and ${\mathcal{X}}_i$ is simply called an absorbable attractor of ${\mathcal{X}}_j$. For consistency of notation, we define ${\mathbb{A}}_0\left({\mathcal{X}}_j\right)={\mathcal{X}}_j$.

Remark 5. 

According to item 1 of Definition 4, we know that for any attractor ${\mathcal{X}}_i$, if ${\mathcal{X}}_i\in {\mathbb{A}}_1\left({\mathcal{X}}_j\right)$, then ${\mathcal{X}}_i$ can be broken and $R\left({\mathcal{X}}_i\right)$, including ${\mathcal{X}}_i$, becomes a new part of $R\left({\mathcal{X}}_j\right)$ by replacing $Co{l}_k\left(G^{\ast }\right)$ with ${\delta }_{2^m}^{{\alpha }_k}$. Similarly, for any ${\mathcal{X}}_i\in {\mathbb{A}}_s\left({\mathcal{X}}_j\right)$, the attractor ${\mathcal{X}}_i$ can be cut off and $R\left({\mathcal{X}}_i\right)$ becomes a part of $R\left({\mathcal{X}}_j\right)$ by modifying s columns of $G^{\ast }$.

In the following, we give a method for checking whether an attractor ${\mathcal{X}}_i$ is absorbable into another attractor $\mathcal{X}$. For convenience, let

$$L^{\ast }={\delta }_{2^n}[l_1,l_2,\cdots ,l_{2^{n+m}}],G^{\ast }={\delta }_{2^m}[p_1,p_2,\cdots ,p_{2^n}].$$

(12)

We first split $L^{\ast }$ into $2^m$ pieces

$$L^{\ast }=[L_1^{\ast }{L}_2^{\ast }\cdots L_{2^m}^{\ast }],$$

(13)

where $L_j^{\ast }={\delta }_{2^n}[l_{(j-1)2^n+1},l_{(j-1)2^n+2},\cdots ,l_{(j-1)2^n+2^n}]\in {\mathbb{L}}_{2^n\times 2^n}$, $j=1,2,\cdots ,2^m$.

Compute

$$H={\oplus }_{i=1}^{2^m}{L}_i^{\ast }.$$

(14)

Next, for any set $\mathcal{X}\subseteq {\Delta }_{2^n}$, we define a $2^n$-dimensional Boolean vector V. Specifically, if ${\delta }_{2^n}^k\in \mathcal{X}$, then the kth element of V is 1; else, it is 0.

Proposition 1. 

Let $V_i$ and $V_{R\left(\mathcal{X}\right)}$ be two vector representations corresponding to attractor ${\mathcal{X}}_i$ and attraction domain $R\left(\mathcal{X}\right)$, respectively, where $\mathcal{X}$ is also an attractor of system (10). ${\mathcal{X}}_i\in {\mathbb{A}}_1\left(\mathcal{X}\right)$ if and only if $0_{2^n}\ne H\odot V_i\le V_{R\left(\mathcal{X}\right)}$.

Proof. 

$0_{2^n}\ne H\odot V_i\le V_{R\left(\mathcal{X}\right)}$, if and only if there must exist an element at the same position in $H\odot V_i$ and $V_{R\left(\mathcal{X}\right)}$, both equal to 1. We let $Ro{w}_j(H\odot V_i)=Ro{w}_j\left(V_{R\left(\mathcal{X}\right)}\right)=1$. Then, equivalently, there is a block in $L^{\ast }$, say $L_s^{\ast }$, such that $Ro{w}_j(L_s^{\ast }\odot V_i)=1$. In other words, there is a positive integer k, such that $Co{l}_k\left(Ro{w}_j\left(L_s^{\ast }\right)\right)=Ro{w}_k\left(V_i\right)=1$, which shows that the state ${\delta }_{2^n}^k$ and integer ${\alpha }_k=s$ satisfy item 1 of Definition 4. Therefore, ${\mathcal{X}}_i\in {\mathbb{A}}_1\left(\mathcal{X}\right)$.    □

It is easy to compute ${\mathbb{A}}_1\left(\mathcal{X}\right)$ by directly using Proposition 1. Now we present an algorithm for calculating ${\mathbb{A}}_s\left(\mathcal{X}\right)$.

From Remark 5, it is easy to find that if ${\mathcal{X}}_i\in \mathbb{A}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$ holds for all attractors ${\mathcal{X}}_i$, then the system (10) can be stabilized to $I(\mathfrak{M};L^{\ast },G^{\ast })$ (of course, also to the original target subset $\mathfrak{M}$) through the appropriate modification to $G^{\ast }$, where $\mathbb{A}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$ can be calculated by using Algorithm 2. Based on this discovery, we give the main theorem.

Algorithm 2 Let all attractors that are not contained in $\mathfrak{M}$ be given in (11). Assume that ${\mathbb{A}}_p\left(\mathcal{X}\right)$, $p=1,2,\cdots ,s-1$ have been obtained. Then, ${\mathbb{A}}_s\left(\mathcal{X}\right)$ can be calculated by the following steps.

Step 1  Check whether there is an attractor that is not in any ${\mathbb{A}}_p\left(\mathcal{X}\right)$, $p=1,2,\cdots ,s-1$. If yes, denote $W_{s-1}={\bigcup }_{{\mathcal{X}}_i\in {\bigcup }_{p=1}^{s-1}{\mathbb{A}}_p\left(\mathcal{X}\right)}R\left({\mathcal{X}}_i\right)$, and go to Step 2. Else, stop, and there is no ${\mathbb{A}}_s\left(\mathcal{X}\right)$. Step 2  Replace $R\left(\mathcal{X}\right)$ with $R\left(\mathcal{X}\right)\bigcup W_{s-1}$. For any ${\mathcal{X}}_i$ that is not in ${\bigcup }_{p=1}^{s-1}{\mathbb{A}}_p\left(\mathcal{X}\right)$, check whether ${\mathcal{X}}_i\in {\mathbb{A}}_1\left(\mathcal{X}\right)$ holds by using Proposition 1. If yes, then ${\mathcal{X}}_i\in {\mathbb{A}}_s\left(\mathcal{X}\right)$. Set $s=s+1$, and go back to Step 1.

Theorem 1. 

Assume that the system (10) has p attractors not included in $\mathfrak{M}$, and these attractors are given in (11). The system (10) can be stabilized to $\mathfrak{M}$ by making modifications to p columns of $G^{\ast }$, if and only if

$${\mathcal{X}}_i\in {\mathbb{A}}_p\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right),i=1,2,\cdots ,p,$$

(15)

where $I(\mathfrak{M};L^{\ast },G^{\ast })$ is the largest invariant subset of (10) in $\mathfrak{M}$. Moreover, if (15) holds, p is the minimum number of columns to be modified to stabilize (10) to $\mathfrak{M}$.

Proof. 

(Necessity) We prove it by using reduction to absurdity. It is assumed that (15) is not true. In other words, there is an attractor ${\mathcal{X}}_i$ that does not belong to $\mathbb{A}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$.

We know that the system (10) can be stabilized to $\mathfrak{M}$ by modifying $G^{\ast }$. Denote the modification result of $G^{\ast }$ by $G^{\ast \ast }$. Then, (10) becomes

$$x(t+1)=L^{\ast }{G}^{\ast \ast }{\Phi }_{n}x\left(t\right),$$

(16)

which is $\mathfrak{M}$-stable.

From Lemma 3 of [11], the closed-loop system (16) is also $I(\mathfrak{M};L^{\ast },G^{\ast \ast })$-stable. Now let us take a state $x_0$ from ${\mathcal{X}}_i$ as the initial state. According to Definition 1, there must be a positive integer T, such that

$$x(t,x_0)\in I(\mathfrak{M};L^{\ast },G^{\ast \ast }),t\ge T,$$

(17)

where $x(t,x_0)={\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^t{x}_0$.

It is noted that

$$I(\mathfrak{M};L^{\ast },G^{\ast \ast })\subseteq I_c(\mathfrak{M};L^{\ast }).$$

(18)

and

$$I_c(\mathfrak{M};L^{\ast })=I(\mathfrak{M};L^{\ast },G^{\ast })\subseteq R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right).$$

(19)

Combining (17), (18), and (19), we have

$$x(t,x_0)\in R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right),t\ge T.$$

It implies ${\mathcal{X}}_i\in {\mathbb{A}}_k\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, where k is a nonnegative integer and satisfies $k\le T$. This contradicts our assumption.

(Sufficiency) First, we split $L^{\ast }$ into $2^n$ pieces as (12) and (13). From (12) and (13), it is easy to obtain

$$L^{\ast }{G}^{\ast }=[L_{p_1}^{\ast }{L}_{p_2}^{\ast }\cdots L_{p_{2^n}}^{\ast }]$$

and

$$L^{\ast }{G}^{\ast }{\Phi }_n={\delta }_{2^n}[l_{(p_1-1)2^n+1},l_{(p_2-1)2^n+2},\cdots ,l_{(p_{2^n}-1)2^n+2^n}].$$

For any ${\mathcal{X}}_i\in {\mathbb{A}}_s\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, $i=1,2,\cdots ,p$, we consider it in two cases. When $s=1$, from item 1 of Definition 4, there exists a state ${\delta }_{2^n}^k\in {\mathcal{X}}_i$ and an integer ${\alpha }_k$ satisfying $1\le {\alpha }_k\le 2^m$, such that $Co{l}_{({\alpha }_k-1)2^n+k}\left(L^{\ast }\right)\in R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$. Then, ${\mathcal{X}}_i$ is broken by replacing $Co{l}_k\left(G^{\ast }\right)$ with ${\delta }_{2^m}^{{\alpha }_k}$, and $R\left({\mathcal{X}}_i\right)$, including ${\mathcal{X}}_i$, becomes a new part of $R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$.

When $s\ne 1$, according to item 2 of Definition 4, there is a different attractor ${\mathcal{X}}_r$ satisfying ${\mathcal{X}}_r\in {\mathbb{A}}_{s-1}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, such that ${\mathcal{X}}_i\in {\mathbb{A}}_1\left({\mathcal{X}}_r\right)$. Then, there exists a state ${\delta }_{2^n}^j\in {\mathcal{X}}_i$ and an integer ${\alpha }_j$ satisfying $1\le {\alpha }_j\le 2^m$, such that $Co{l}_{({\alpha }_j-1)2^n+j}\left(L^{\ast }\right)\in R\left({\mathcal{X}}_r\right)$. We replace $Co{l}_j\left(G^{\ast }\right)$ with ${\delta }_{2^m}^{{\alpha }_j}$.

In this way, we let the feedback matrix $G^{\ast }$ be finally modified into $G^{\ast \ast }$. Then, the closed-loop system (10) turns into

$$x(t+1)=L^{\ast }{G}^{\ast \ast }{\Phi }_{n}x\left(t\right).$$

(20)

We denote the largest invariant subset of (20) in $\mathfrak{M}$ by $I(\mathfrak{M};L^{\ast },G^{\ast \ast })$. It is easy to find that

$$I(\mathfrak{M};L^{\ast },G^{\ast \ast })=I(\mathfrak{M};L^{\ast },G^{\ast })=I_c(\mathfrak{M};L^{\ast }).$$

Next, we show that the closed-loop system (20) is $\mathfrak{M}$-stable. We take any point $x_0$ as the initial state. If $x_0\in R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, the conclusion is a direct result. Otherwise, let $x_0\in R\left({\mathcal{X}}_i\right)$ and ${\mathcal{X}}_i\in {\mathbb{A}}_s\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$. According to the design method of $G^{\ast \ast }$, there is a state ${\delta }_{2^n}^j\in {\mathcal{X}}_i$, such that $L^{\ast }{G}^{\ast \ast }{\Phi }_n{\delta }_{2^n}^j\ne L^{\ast }{G}^{\ast }{\Phi }_n{\delta }_{2^n}^j$ and

$$L^{\ast }{G}^{\ast \ast }{\Phi }_n{\delta }_{2^n}^j\in R\left({\mathcal{X}}_r\right),$$

(21)

where ${\mathcal{X}}_r\in {\mathbb{A}}_{s-1}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$ is a different attractor. Then, the front part of the state trajectory of (20) is

$$\begin{array}{cc}\hfill x_0\to L^{\ast }{G}^{\ast \ast }{\Phi }_n{x}_0\to {\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^2{x}_0\to \cdots & \to {\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^{t_0}{x}_0={\delta }_{2^n}^j\hfill \\ & \to L^{\ast }{G}^{\ast \ast }{\Phi }_n{\delta }_{2^n}^j\in R\left({\mathcal{X}}_r\right),\hfill \end{array}$$

where ${\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^k{x}_0={\left(L^{\ast }{G}^{\ast }{\Phi }_n\right)}^k{x}_0$, $k=1,2,\cdots ,t_0$.

In the following, we use mathematical induction to prove that for the above s, the closed-loop system (20) is convergent to $I(\mathfrak{M};L^{\ast },G^{\ast })$.

When $s=1$, from the analysis provided above, the state trajectory of (20) must be convergent to $I(\mathfrak{M};L^{\ast },G^{\ast })$. Assume that it is true for the case of $s=\lambda$. Let us consider the case of $s=\lambda +1$, namely ${\mathcal{X}}_i\in {\mathbb{A}}_{\lambda +1}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$.

From (21), we obtain

$${\delta }_{2^n}^j\to L^{\ast }{G}^{\ast \ast }{\Phi }_n{\delta }_{2^n}^j\to {\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^2{\delta }_{2^n}^j\to \cdots \to {\left(L^{\ast }{G}^{\ast \ast }{\Phi }_n\right)}^{t_1}{\delta }_{2^n}^j\in {\mathcal{X}}_r,$$

where ${\mathcal{X}}_r$ is a distinct attractor satisfying ${\mathcal{X}}_r\in {\mathbb{A}}_{\lambda }\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$. It follows that the state trajectory of (20) is convergent to $I(\mathfrak{M};L^{\ast },G^{\ast })$ in accordance with the assumption. Then, the system (20) is $I(\mathfrak{M};L^{\ast },G^{\ast })$-stable, equivalently $\mathfrak{M}$-stable.

Finally, every attractor in (11) has to be broken to ensure the convergence of the state trajectory to $I(\mathfrak{M};L^{\ast },G^{\ast })$. Hence, the number of modified columns in $G^{\ast }$ is no less than p. It implies that p is the minimum number of columns to be modified.    □

Remark 6. 

1. Under Assumption 1, $\mathfrak{M}$-stabilizability of the perturbed system (8) is equivalent to that of the system (10), so Theorem 1 provides a necessary and sufficient criterion for $\mathfrak{M}$-stabilizability of (8).

2. The proof process of Sufficiency in Theorem 1 provides a constructive method for tuning the controller (9). And when the condition (15) is met, only the minimum number of columns in $G^{\ast }$ need to be modified.

3. The purpose of modifying $I(\mathfrak{M};L^{\ast },G)$ into $I(\mathfrak{M};L^{\ast },G^{\ast })$ is to increase the possibility of solving Problem 2, since $R\left(I(\mathfrak{M};L^{\ast },G)\right)\subseteq R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$. In other words, if those attractors of the perturbed closed-loop system (8), not included in $\mathfrak{M}$, all belong to $\mathbb{A}\left(I(\mathfrak{M};L^{\ast },G)\right)$, then we can use our fine-tuning method to directly modify G without calculating the largest invariant subset $I(M$; $L^{\ast }$, G).

4. Theorem 1 has a wider scope of application. As we know, most results at present are mainly about restabilization to a single state. However, such a restabilization problem is a special case of the set restabilization (specifically, when the target set is a singleton). In addition, Theorem 1 is not only applicable to single column function perturbation problem of BCNs, but also to the multi-column function perturbation problem that has not been settled yet in [30].

5. Since the dimension of system (5) is $2^n$, Theorem 1 is of exponential complexity. To some extent, it limits the application of this method in large-scale systems.

3.3. Parameter Adjustment Algorithm

Combining the results of Section 3.1 and Section 3.2 together, we provide an algorithm for fine tuning the parameters of the old state feedback matrix G in (8).

Remark 7. 

1. It can be determined in Steps 1 and 2 whether the perturbed system (8) can be restabilized to $\mathfrak{M}$. The specific fine-tuning process for parameters is implemented in Step 3.

2. As analyzed in Remark 4, the number of parameters that need to be modified is as little as possible in handling Problem 1. In addition, Theorem 1 shows that as long as condition (15) is met, we only need to modify the least number of columns in $G^{\ast }$. Therefore, our method always follows the principle of minimizing the number of modified columns in G.

In order to better understand Algorithm 3, a flowchart is provided in Figure 1. Through Algorithm 3, the matrix $G^{\ast }$ is modified into $G^{\ast \ast }$. Then, we obtain the final new controller

$$u\left(t\right)=G^{\ast \ast }x\left(t\right),$$

(22)

which can stabilize the perturbed BCN (7) within $\mathfrak{M}$.

Algorithm 3 The closed-loop system (5) is $\mathfrak{M}$-stable. Assume that BCN (3) is perturbed, its structure matrix L becomes $L^{\ast }$, and the new closed-loop system (8) has p attractors that are not contained in $\mathfrak{M}$ and are given as in (11). Then, under Assumption A1, the problem of fine-tuning the old controller can be solved to restabilize BCN (8) to $\mathfrak{M}$ by the following steps.

Step 1  Compute $I_c(\mathfrak{M};L^{\ast })$ of the perturbed BCN (7) and $I(\mathfrak{M};L^{\ast },G)$ of the perturbed closed-loop system (8). Check whether $I_c(\mathfrak{M};L^{\ast })=I(\mathfrak{M};L^{\ast },G)$ holds. If yes, denote G by $G^{\ast }$ and go to Step 2. Else, modify the old controller (4) according to Algorithm 1, and then obtain a new controller (9). Go to Step 2. Step 2  Check whether condition (15) is satisfied. If yes, go to Step 3. Else, the system (8) cannot be stabilized to $\mathfrak{M}$ by using our method. Step 3  For any attractor ${\mathcal{X}}_i\in {\mathbb{A}}_s\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, find an attractor ${\mathcal{X}}_r\in {\mathbb{A}}_{s-1}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$, and search for a state ${\delta }_{2^n}^j\in {\mathcal{X}}_i$ and an integer ${\alpha }_j$, such that they satisfy $Co{l}_{({\alpha }_j-1)2^n+j}\left(L^{\ast }\right)\in R\left({\mathcal{X}}_r\right)$. Replace $Co{l}_j\left(G^{\ast }\right)$ with ${\delta }_{2^m}^{{\alpha }_j}$.

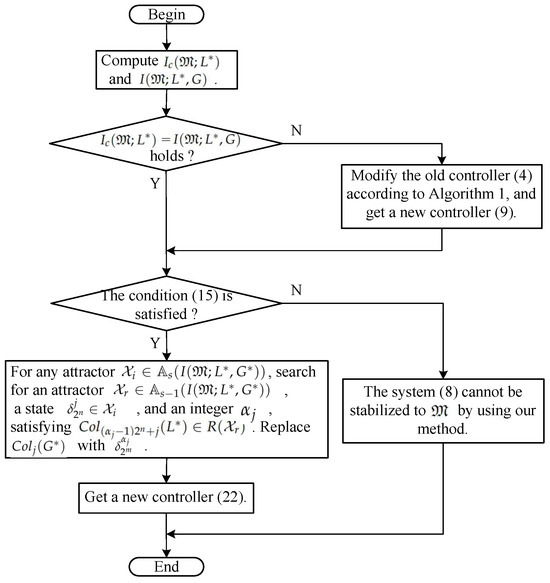
Figure 1. Flowchart of Algorithm 3.

4. Discussion

In the following, we demonstrate how to deal with the set restabilization problem of a perturbed BCN through two examples.

Example 2. 

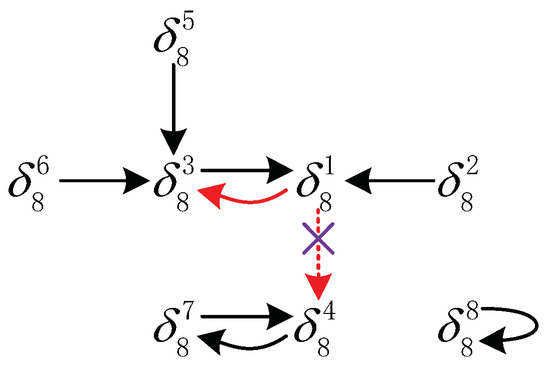
Consider a simplified model of the lac operon in Escherichia coli, whose stabilization problem has been discussed in [9,12,33].

$$\left\{\begin{array}{c}{x}_1(t+1)=(x_2\left(t\right)\vee x_3\left(t\right))\wedge \neg u_1\left(t\right)\hfill \\ x_2(t+1)=x_1\left(t\right)\wedge \neg u_1\left(t\right)\wedge u_2\left(t\right)\hfill \\ x_3(t+1)=((u_3\left(t\right)\wedge x_1\left(t\right))\vee u_2\left(t\right))\wedge \neg u_1\left(t\right),\hfill \end{array}\right.$$

(23)

where the state variables $x_1$, $x_2$, and $x_3$ stand for lac mRNA, lactose in high concentrations, and lactose in medium concentrations, respectively; the inputs $u_1$, $u_2$, and $u_3$ represent extracellular glucose, high extracellular lactose, and medium extracellular lactose, respectively.

We utilize the vector form of logical variables to set $x\left(t\right)=x_1\left(t\right)x_2\left(t\right)x_3\left(t\right)$ and $u\left(t\right)=u_1\left(t\right)u_2\left(t\right)u_3\left(t\right)$. Then, it is easy to obtain the algebraic form of BCN (23):

$$x(t+1)=Lu\left(t\right)x\left(t\right),$$

(24)

where

$$\begin{array}{cc}L={\delta }_8[\hfill & 8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,\hfill \\ & 1,1,1,5,3,3,3,7,1,1,1,5,3,3,3,7,3,3,3,7,4,4,4,8,4,4,4,8,4,4,4,8].\hfill \end{array}$$

Just like in [12], the target set is taken as

$$\mathfrak{M}=\{{\delta }_8^1,{\delta }_8^3,{\delta }_8^8\}.$$

For a given state feedback controller, for example,

$$\begin{array}{cc}\hfill u\left(t\right)=& {\delta }_8[7,6,5,8,5,6,5,2]x\left(t\right)\hfill \\ \hfill =& Gx\left(t\right),\hfill \end{array}$$

(25)

we substitute (25) in (24), and then obtain

$$\begin{array}{cc}\hfill x(t+1)=& LGx\left(t\right)x\left(t\right)\hfill \\ \hfill =& LG{\Phi }_{3}x\left(t\right)\hfill \\ \hfill =& {\delta }_8[3,1,1,8,3,3,3,8]x\left(t\right).\hfill \end{array}$$

(26)

The state transition diagram of (26) is given in Figure 2. Obviously, the closed-loop system (26) is $\mathfrak{M}$-stable.

Figure 2. State transition diagram of BCN (24) with the controller (25).

Now, let us suppose that the BCN (24) is perturbed. And the 39th, 49th, 57th, and 60th columns of L are changed into ${\delta }_8^4$, ${\delta }_8^4$, ${\delta }_8^3$, and ${\delta }_8^7$, respectively. Then, (24) becomes

$$x(t+1)=L^{\ast }u\left(t\right)x\left(t\right),$$

(27)

where

$$\begin{array}{cc}{L}^{\ast }={\delta }_8[\hfill & 8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,\hfill \\ & 1,1,1,5,3,3,4,7,1,1,1,5,3,3,3,7,4,3,3,7,4,4,4,8,3,4,4,7,4,4,4,8].\hfill \end{array}$$

Correspondingly, the closed-loop system (26) turns into

$$\begin{array}{cc}\hfill x(t+1)=& L^{\ast }G{\Phi }_{3}x\left(t\right)\hfill \\ \hfill =& {\delta }_8[4,1,1,7,3,3,4,8]x\left(t\right).\hfill \end{array}$$

(28)

We plot the state transition diagram of the perturbed closed-loop system (28) in Figure 3. From this figure, we find that there is an attractor

$${\mathcal{X}}_1:{\delta }_8^4\to {\delta }_8^7\to {\delta }_8^4,$$

which is not contained in $\mathfrak{M}$. Therefore, the perturbed BCN (27) is not $\mathfrak{M}$-stable if still under the old controller (25).

Figure 3. State transition diagram of the perturbed BCN (27) with the old controller (25).

In the following, we use Algorithm 3 to deal with the $\mathfrak{M}$-restabilization problem of (27). First, through calculation, we have

$$I(\mathfrak{M};L^{\ast },G)=\left\{{\delta }_8^8\right\},I_c(\mathfrak{M};L^{\ast })=\{{\delta }_8^1,{\delta }_8^3,{\delta }_8^8\}.$$

Obviously, $I(\mathfrak{M};L^{\ast },G)\ne I_c(\mathfrak{M};L^{\ast })$. So we need to tune the controller (25) to implement $I_c(\mathfrak{M};L^{\ast })$ as the largest invariant subset of the closed-loop system. We divide $L^{\ast }$ into eight blocks

$$L^{\ast }=\left[L_1^{\ast }{L}_2^{\ast }{L}_3^{\ast }{L}_4^{\ast }{L}_5^{\ast }{L}_6^{\ast }{L}_7^{\ast }{L}_8^{\ast }\right],$$

where $L_i^{\ast }\in {\mathbb{L}}_{8\times 8}$, $i=1,2,\cdots ,8$.

Because

$$L^{\ast }G{\Phi }_3{\delta }_8^1={\delta }_8^4\notin I_c(\mathfrak{M};L^{\ast })$$

and

$$L^{\ast }{\delta }_8^8{\delta }_8^1=L_8^{\ast }{\delta }_8^1=Co{l}_1\left(L_8^{\ast }\right)={\delta }_8^3\in I_c(\mathfrak{M};L^{\ast }),$$

we set

$$Co{l}_1\left(G\right)={\delta }_8^8.$$

That is to say, the first column of G should be modified from ${\delta }_8^7$ to ${\delta }_8^8$. Then, we obtain a new controller

$$\begin{array}{cc}\hfill u\left(t\right)=& {\delta }_8[8,6,5,8,5,6,5,2]x\left(t\right)\hfill \\ \hfill =& G^{\ast }x\left(t\right).\hfill \end{array}$$

(29)

Putting (29) into (27), we have

$$\begin{array}{cc}\hfill x(t+1)=& L^{\ast }{G}^{\ast }{\Phi }_{3}x\left(t\right)\hfill \\ \hfill =& {\delta }_8[3,1,1,7,3,3,4,8]x\left(t\right).\hfill \end{array}$$

It is directly verified that the largest invariant subset $I(\mathfrak{M};L^{\ast },G^{\ast })$ equals $I_c(\mathfrak{M};L^{\ast })$. Figure 4 is its state transition diagram.

Figure 4. State transition diagram of the perturbed BCN (27) with a controller (29) modified for the first time.

Similarly, due to

$$L^{\ast }{\delta }_8^1{\delta }_8^4=L_1^{\ast }{\delta }_8^4=Co{l}_4\left(L_1^{\ast }\right)={\delta }_8^8\in R\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right),$$

then ${\mathcal{X}}_1\in \mathbb{A}\left(I(\mathfrak{M};L^{\ast },G^{\ast })\right)$. It implies that the condition (15) is satisfied. Furthermore, according to Algorithm 3, we modify the fourth column of $G^{\ast }$ to ${\delta }_8^1$. So the final controller is

$$\begin{array}{cc}\hfill u\left(t\right)=& {\delta }_8[8,6,5,1,5,6,5,2]x\left(t\right)\hfill \\ \hfill =& G^{\ast \ast }x\left(t\right).\hfill \end{array}$$

(30)

Substituting (30) in (27), we have

$$\begin{array}{cc}\hfill x(t+1)=& L^{\ast }{G}^{\ast \ast }{\Phi }_{3}x\left(t\right)\hfill \\ \hfill =& {\delta }_8[3,1,1,8,3,3,4,8]x\left(t\right).\hfill \end{array}$$

(31)

The state transition diagram of the new closed-loop system (31) is plotted in Figure 5. It is easy to see that the system (31) is $\mathfrak{M}$-stable.

Figure 5. State transition diagram of the perturbed BCN (27) under the final controller (30).

Remark 8. 

Example 2 shows how to fine-tune the old controller to realize $\mathfrak{M}$-stabilization of the BCN (27) subject to a multi-column function perturbation. It is noted that such a set restabilization problem has not been solved in the current literature.

Example 3. 

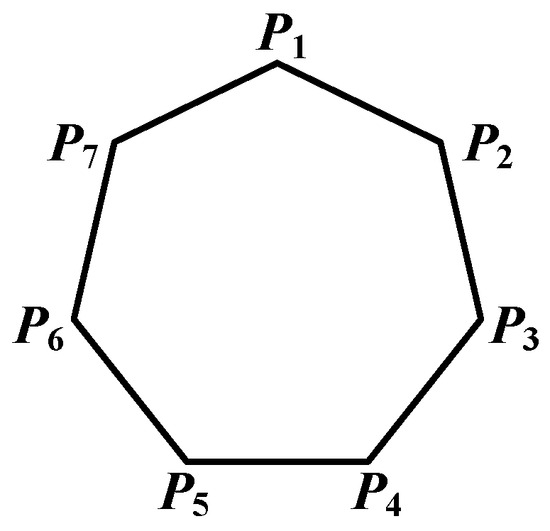
Consider a networked evolutionary game, which has seven players $\mathfrak{N}=\{P_1,P_2,P_3,P_4,P_5,P_6,P_7\}$. The network graph is shown in Figure 6. The fundamental game is the Prisoner’s Dilemma [20] and its payoff bimatrix is given in Table 3. The strategy updating rule adopts unconditional imitation with fixed priority [3]. Each player chooses strategy “defect” or “cooperate”, denoted by 1 and 2, respectively. In this model, $P_1$ and $P_2$ are two pseudo-players with the same aim of achieving cooperation among all players.

Figure 6. Network graph.

Table 3. Payoff bimatrix for Prisoner’s Dilemma.

${\mathit{P}}_{\mathit{i}}\mathit{\setminus }{\mathit{P}}_{\mathit{j}}$	1	2
1	$(1,1)$	$(9,0)$
2	$(0,9)$	$(6,6)$

We denote the strategies of $P_1$ and $P_2$ at time step t by $u_1\left(t\right)$ and $u_2\left(t\right)$, respectively, and express the strategy of $P_i$ as $x_i\left(t\right)$, $i=3,4,5,6,7$. Using the techniques provided in [3], we can obtain the algebraic form of the above model:

$$x(t+1)=Lu\left(t\right)x\left(t\right),$$

(32)

where $L\in {\mathbb{L}}_{32\times 128}$ and

$$\begin{array}{cc}\hfill L={\delta }_{2^5}[& 1,4,8,4,15,16,7,8,29,32,32,32,13,16,15,16,25,28,32,32,31,32,32,32,25,\hfill \\ & 32,32,32,29,32,31,32,29,32,32,32,17,20,32,32,31,32,32,32,17,20,24,20,\hfill \\ & 31,32,32,32,29,32,32,32,25,32,32,32,29,32,32,32,2,2,8,7,16,16,8,8,30,\hfill \\ & 32,32,32,32,32,32,32,26,26,32,32,32,32,32,32,26,32,32,32,32,32,32,32,\hfill \\ & 1,2,8,4,32,32,32,32,29,32,32,32,32,32,32,32,17,18,32,32,32,32,32,32,25,\hfill \\ & 32,32,32,32,32,32,32].\hfill \end{array}$$

It is easy to verify that the system (32) is stabilized to ${\delta }_{32}^{32}$ by the following controller:

$$u\left(t\right)=Gx\left(t\right),$$

(33)

where

$$G={\delta }_4[2,2,2,2,4,4,4,4,1,4,4,4,4,4,4,4,2,2,2,2,2,2,2,2,3,1,3,3,3,3,3,3].$$

It is assumed that $Co{l}_6\left(L\right)$ and $Co{l}_{49}\left(L\right)$ are perturbed to ${\delta }_{32}^{15}$ and ${\delta }_{32}^{17}$, respectively. That is, the structure matrix L changes into

$$\begin{array}{cc}\hfill L^{\ast }={\delta }_{2^5}[& 1,4,8,4,15,15,7,8,29,32,32,32,13,16,15,16,25,28,32,32,31,32,32,32,25,32\hfill \\ & 32,32,29,32,31,32,29,32,32,32,17,20,32,32,31,32,32,32,17,20,24,20,17,32,\hfill \\ & 32,32,29,32,32,32,25,32,32,32,29,32,32,32,2,2,8,7,16,16,8,8,30,32,32,32,\hfill \\ & 32,32,32,32,26,26,32,32,32,32,32,32,26,32,32,32,32,32,32,32,1,2,8,4,32,\hfill \\ & 32,32,32,29,32,32,32,32,32,32,32,17,18,32,32,32,32,32,32,25,32,32,32,32,\hfill \\ & 32,32,32].\hfill \end{array}$$

Correspondingly, (32) becomes

$$x(t+1)=L^{\ast }u\left(t\right)x\left(t\right),$$

(34)

and the perturbed closed-loop system is

$$\begin{array}{cc}\hfill x(t+1)=& L^{\ast }Gx\left(t\right)x\left(t\right)\hfill \\ \hfill =& {\widehat{L}}^{\ast }x\left(t\right).\hfill \end{array}$$

(35)

where ${\widehat{L}}^{\ast }\in {\mathbb{L}}_{32\times 32}$ and

$$\begin{array}{cc}\hfill {\widehat{L}}^{\ast }={\delta }_{2^5}[& 29,32,32,32,32,32,32,32,29,32,32,32,32,32,32,32,\hfill \\ & 17,32,32,32,29,32,32,32,26,32,32,32,32,32,32,32].\hfill \end{array}$$

The target set here is a singleton (“cooperate”. cooperate”. cooperate”. cooperate”. cooperate”. cooperate”. cooperate”), whose algebraic form is $\mathfrak{M}=\left\{{\delta }_{32}^{32}\right\}$. Since the closed-loop system (35) has two fixed points ${\mathcal{X}}_1={\delta }_{32}^{17}$ and ${\mathcal{X}}_2={\delta }_{32}^{32}$, then the perturbed networked evolutionary game (34) is unstable if still under the old controller (33).

In the following, we use our method to fine-tune the old controller (33). It is noted that $I(\mathfrak{M};L^{\ast },G)=\mathfrak{M}$. For the fixed point ${\mathcal{X}}_1$, we have

$$L^{\ast }{\delta }_4^3{\delta }_{32}^{17}={\delta }_{32}^{26}\in R\left(I(\mathfrak{M};L^{\ast },G)\right),$$

then ${\mathcal{X}}_1\in \mathbb{A}\left(I(\mathfrak{M};L^{\ast },G)\right)$, satisfying the condition (15). From Algorithm 3, the 17th column of G is modified to ${\delta }_4^3$. So we obtain a new controller:

$$u\left(t\right)={\delta }_4[2,2,2,2,4,4,4,4,1,4,4,4,4,4,4,4,3,2,2,2,2,2,2,2,3,1,3,3,3,3,3,3]x\left(t\right).$$

(36)

It is verified directly that the perturbed networked evolutionary game (34) is stabilized to ${\delta }_{32}^{32}$ by the controller (36).

Remark 9. 

In Example 3, the perturbation occurring on $Co{l}_{49}\left(L\right)$ is actually what causes the instability in system (35). The old controller (33) is robust to the perturbation occurring on $Co{l}_6\left(L\right)$. That is, if only $Co{l}_6\left(L\right)$ experiences the aforementioned perturbation, the disturbed system remains stable at ${\delta }_{32}^{32}$ under the old controller.

5. Conclusions

This paper has proposed a fine-tuning technique to restabilize perturbed BCNs to their target set. A restabilizability criterion was derived and a parameter tuning algorithm was developed. Compared with the existing results, ours have obvious advantages. They are not only applicable to the multi-column function perturbation problem, but can also address the set restabilization of perturbed BCNs, which is a more general stabilization problem.

However, as analyzed in item 5 of Remark 6, Theorem 1 is of exponential complexity, which is the weakness of our method. Seeking a way to effectively reduce the computational complexity of this method is our future research work. One possible solution is to refer to the aggregation algorithm. Firstly, consider and calculate the connected subnetworks separately, and then integrate the parameter tuning problem of the entire network through coupling relationships.