Differential–Linear Approximations of CHAM

Abstract

CHAM is a family of lightweight block ciphers designed for resource-constrained environments like IoT devices and embedded systems, which require low power consumption and high performance. Despite numerous cryptanalytic evaluations, the security of CHAM remains robust. Differential–linear cryptanalysis, a method that combines two of the strongest attack methods on block ciphers—differential cryptanalysis and linear cryptanalysis—has been successfully applied to many block ciphers. This study introduces the first concrete differential–linear approximations of CHAM, marking a significant advancement in the cryptanalysis of this cipher family. Utilizing a Boolean satisfiability problem framework, we present a 46-round differential–linear approximation of CHAM-64/128 with a correlation of $2^{-31.08}$ and a 58-round approximation for CHAM-128/128 and CHAM-128/256 with correlations of $2^{-58.86}$ and $2^{-59.08}$, respectively. These findings significantly exceed the designers’ expectations for differential–linear approximations using CHAM. Furthermore, the 46-round differential–linear approximation of CHAM-64/128 is the best distinguisher of CHAM-64/128 to date in a single-key attack model. Notably, our findings do not threaten the security of CHAM but provide deeper insights into its cryptanalytic resistance.

1. Introduction

CHAM is a family of lightweight block ciphers designed for resource-constrained environments, such as Internet of Things (IoT) devices, embedded systems, and other applications where both low power consumption and high performance are crucial. It was introduced by Koo et al. [1] and further revised by Roh et al. [2] to increase the numbers of rounds (note that only the numbers of rounds were changed, without changing the other structures). CHAM is based on a four-branch generalized Feistel structure and consists of ARX operations (modular addition ${\displaystyle ⊞}$, bitwise rotation ${\displaystyle ⋘}$, and bitwise XOR ${\displaystyle \oplus }$). There are three ciphers, CHAM-64/128, CHAM-128/128, and CHAM-128/256, where the first number denotes the block size in bits and the second number denotes the key size in bits. For example, CHAM-64/128 has a 64-bit block size and a 128-bit key size, while CHAM-128/256 features a 128-bit block and a 256-bit key. Notably, CHAM is one of the ciphers that can be implemented with the smallest hardware area.

Several cryptanalytic results using CHAM have been published, including differential cryptanalysis [3,4], linear cryptanalysis [5], integral cryptanalysis [6], meet-in-the-middle type attacks [7,8], and impossible differential cryptanalysis [9]. Despite these analyses, the security of CHAM remains unthreatened due to its sufficient security margin.

Two important statistical techniques in the cryptanalysis of block ciphers are differential cryptanalysis, introduced by Biham and Shamir [10], and linear cryptanalysis, introduced by Matsui [11]. These techniques have been used to mount the best-known attacks on numerous block ciphers [12,13,14,15]. Consequently, resistance to these two cryptanalytic techniques, particularly the non-existence of high-probability differential characteristics or high-bias linear approximations spanning many rounds of the cipher, has become a crucial criterion in block cipher design.

The initial step in differential cryptanalysis is to search for high-probability differential characteristics, while in linear cryptanalysis, it is to search for high-correlation linear approximations. Over the last decade, a major focus has been on developing efficient methods to automatically search for these distinguishers (differential characteristics and linear approximations) [14,16,17,18,19,20]. Notable works in this area have significantly expanded the search space that can be explored within a practical time, thereby increasing our confidence in a cipher’s resistance against differential cryptanalysis and linear cryptanalysis.

For some block ciphers, it is relatively easy to find high-probability differential characteristics and high-correlation linear approximations within a few rounds. However, as the number of rounds increases, the effectiveness of both differential and linear cryptanalysis decreases. While it might seem that preventing long differential characteristics and linear approximations would suffice to make a block cipher immune to these attacks, short characteristics and approximations can also be exploited to break the cipher. The first cryptanalytic technique to demonstrate this was differential–linear cryptanalysis, introduced by Langford and Hellman in 1994 [21]. This technique combines differential cryptanalysis and linear cryptanalysis, leveraging their individual strengths over a few rounds to mount more effective attacks over many rounds. Differential–linear cryptanalysis has been used to evaluate the security of many block ciphers, including IDEA [22], COCONUT98 [23], Serpent [24,25], CTC2 [25], ICEPOLE [26,27], Chaskey [28,29], ChaCha [29], LEA [30], SPECK [30], and others. However, no concrete differential–linear approximations for CHAM have been reported until now. Currently, the only information we have is the expectation set by the designers of CHAM that differential–linear approximations would not exist beyond a certain number of rounds.

In differential–linear cryptanalysis, a crucial initial step is identifying differential–linear approximations (denoted by ${\Delta }_{\mathrm{in}}\to {\gamma }_{\mathrm{out}}$) with high correlations. The development of automated searches for these approximations has remained virtually stagnant for nearly 20 years. Researchers typically identify differential–linear approximations using a three-stage process: (1) experimentally verifying short differential–linear approximations, denoted by ${\Delta }_m\to {\gamma }_m$; (2) searching for short differential characteristics (denoted by ${\Delta }_{\mathrm{in}}\to {\Delta }_m$) and linear approximations (denoted by ${\gamma }_m\to {\gamma }_{\mathrm{out}}$); and (3) concatenating these three short distinguishers (differential characteristics and linear approximations) into a long differential–linear approximation ${\Delta }_{\mathrm{in}}\to {\Delta }_m\to {\gamma }_m\to {\gamma }_{\mathrm{out}}$. Due to the lack of an efficient method for searching for the short differential–linear approximations of ${\Delta }_m\to {\gamma }_m$, the practical search space for a difference ${\Delta }_m$ is severely constrained to linear masks, ${\gamma }_m$, with a Hamming weight of 1 or 2. This persistent limitation weakens confidence in a cipher’s resistance to differential–linear cryptanalysis.

Recently, two methods have been proposed to automatically find the differential–linear approximation of the ARX cipher. One is based on mixed-integer linear programming (MILP) and mixed-integer quadratic constraint programming (MIQCP) techniques [31], and the other is based on a Boolean satisfiability problem [30]. The primary objective of this study is to provide the first concrete differential–linear approximations of CHAM, one of the ARX ciphers, by utilizing the latter framework.

1.1. Our Contributions

This paper gives the first concrete differential–linear approximations of CHAM. To the best of our knowledge, the security analysis of CHAM against differential–linear cryptanalysis has only been provided by its designers. However, they did not present concrete differential–linear approximations. They only provided upper bounds on the maximum numbers of rounds for which they expected differential–linear approximations to exist. This was achieved by using the known maximum probabilities of the differential characteristics and the known maximum correlations of the linear characteristics for short rounds. Furthermore, their analysis did not consider the differential–linear connectivity table (DLCT) and focused solely on the direct combination of differential characteristics and linear approximations.

Specifically, we present a 46-round differential–linear approximation with a correlation of $2^{-31.08}$ for CHAM-64/128. This differential–linear approximation demonstrates that a differential–linear approximation can indeed cover significantly more rounds than anticipated by the designers of CHAM. Additionally, this approximation serves as a distinguisher for the longest rounds within the single-key attack model. The previous best distinguisher in the single-key model was the 40-round differential [7]. If we take the multi-key model into account, the 47-round related-key differential characteristic is the best distinguisher [2].

Furthermore, we introduce a 58-round differential–linear approximation with correlations of $2^{-58.86}$ and $2^{-59.08}$ for CHAM-128/128 and CHAM-128/256, respectively. Although this does not serve as a distinguisher for the longest rounds, it nevertheless illustrates that a differential–linear approximation can span more rounds than anticipated by the designers of CHAM. Note that the best distinguisher in the single-key model is the 67-round differential [2].

Table 1 provides a summary of our differential–linear approximation results compared to existing distinguishers for CHAM.

Table 1. Summary of distinguishers of CHAM.

Cipher	Type	Round	Refs.
CHAM-64/128	Differential characteristic	38	[4]
	Differential	40	[7]
	Related-key differential characteristic	47	[2]
	Linear approximation	34	[1,5]
	Integral distinguisher	21	[6]
	Impossible differential 1	22	[9]
	Differential–linear approximation 2	35	[2]
	Differential–linear approximation	46	This paper
	Differential characteristic	63	[3]
	Differential	67	[2]
CHAM-128/128	Linear approximation	40	[1]
CHAM-128/256	Integral distinguisher	19	[6]
	Differential–linear approximation 2	45	[1]
	Differential–linear approximation	58	this paper

¹ under $2^{127}$ weak keys. ² Only the estimated number of rounds is given. No concrete differential–linear approximation is given.

1.2. Paper Organization

The outline of the paper is as follows. In Section 2, we provide basic definitions and notations, introduce differential–linear approximations, Boolean satisfiability problems, and SAT solvers, and describe CHAM. We review the method proposed by Chen et al. for searching for differential–linear approximations of ARX block ciphers in Section 3. Section 4 presents our results: the first differential–linear approximations of CHAM. Finally, Section 5 concludes this paper and proposes further studies.

2. Preliminaries

2.1. Basic Definitions and Notations

Given a vector $x\in {\mathbb{F}}_2^n$, $x\left[j\right]$ denotes the j-th bit of x, where $x\left[0\right]$ is the least significant bit. Let us denote as $\left[i\right]$ the vector $y\in {\mathbb{F}}_2^n$, such that $y\left[i\right]=1$ and $y\left[j\right]=0$ for $j\ne i$ and $0\le j<n$. Let $[i_1,i_2,\cdots ,i_t]$ denote $\left[i_1\right]\oplus \left[i_2\right]\oplus \cdots \oplus \left[i_t\right]$, where $0\le i_1,i_2,\cdots ,i_t<n$, and $t\le n$. The inner product of two vectors x and y in ${\mathbb{F}}_2^n$ is defined as $⟨x,y⟩={\sum }_{i=0}^{n-1}x\left[i\right]y\left[i\right]$.

The correlation of a Boolean function $g:{\mathbb{F}}_2^n\to {\mathbb{F}}_2$ over a set $S\subseteq {\mathbb{F}}_2^n$ is defined as follows:

$$\underset{x\in S}{\mathrm{Cor}}\left[g\left(x\right)\right]={\displaystyle \frac{\left|\right\{x\in S\left|g\right(x)=0\}|-|\{x\in S|g\left(x\right)=1\left\}\right|}{\left|S\right|}}.$$

(1)

For a vectorial Boolean function $f:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$, a set $S\subseteq {\mathbb{F}}_2^n$, an n-bit input mask ${\gamma }_{\mathrm{in}}$, and an m-bit output mask ${\gamma }_{\mathrm{out}}$, the (linear) correlation of f with respect to the set and the mask pair, denoted by ${\mathrm{Cor}}_{x\in S}[f\left(x\right);{\gamma }_{\mathrm{in}},{\gamma }_{\mathrm{out}}]$, is defined to be the correlation of a Boolean function $x\mapsto ⟨{\gamma }_{\mathrm{in}},x⟩\oplus ⟨{\gamma }_{\mathrm{out}},f\left(x\right)⟩$ over the set S as follows:

$$\underset{x\in S}{\mathrm{Cor}}[f\left(x\right);{\gamma }_{\mathrm{in}},{\gamma }_{\mathrm{out}}]={\displaystyle \frac{|\{x\in S|⟨{\gamma }_{\mathrm{in}},x⟩\oplus ⟨{\gamma }_{\mathrm{out}},f\left(x\right)⟩=0\}|-|\{x\in S|⟨{\gamma }_{\mathrm{in}},x⟩\oplus ⟨{\gamma }_{\mathrm{out}},f\left(x\right)⟩=1\}|}{\left|S\right|}}.$$

(2)

We call the pair $\left({\gamma }_{\mathrm{in}},{\gamma }_{\mathrm{out}}\right)$ the linear approximation of f over S. When $S={\mathbb{F}}_2^n$, we call it the linear approximation of f.

Example 1.

Let $f:{\mathbb{F}}_2^4\to {\mathbb{F}}_2^4$ be a vectorial Boolean function. The function f maps the input x to an output $f\left(x\right)$, as given in hexadecimal notation in Table 2. (The function f is the 4-bit to 4-bit S-box of PRESENT [32].) Let ${\gamma }_{\mathrm{in}}=(1,0,0,1)$ and ${\gamma }_{\mathrm{out}}=(0,0,0,1)$. Then, the linear correlation of f with respect to the set ${\mathbb{F}}_2^4$ and the mask pair $\left({\gamma }_{\mathrm{in}},{\gamma }_{\mathrm{out}}\right)$ is as follows:

$$\underset{x\in {\mathbb{F}}_2^4}{\mathrm{Cor}}[f\left(x\right);{\gamma }_{\mathrm{in}},{\gamma }_{\mathrm{out}}]={\displaystyle \frac{12-4}{16}}=2^{-1}.$$

(3)

Table 2. The vectorial Boolean function f.

x	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
f(x)	C	5	6	B	9	0	A	D	3	E	F	8	4	7	1	2

2.2. Differential–Linear Approximation

The initial approach developed by Langford and Hellman [21] involved splitting the targeted cipher E into two sub-ciphers, $E_1$ and $E_2$, such that $E=E_2\circ E_1$, and combining a differential characteristic for $E_1$ with a linear approximation for $E_2$ to form an attack on the entire cipher E. Thanks to the differential–linear connectivity table concept introduced by Bar-On et al. [27], the differential–linear attack strategy has evolved to divide the cipher E into three sub-ciphers, $E_1$, $E_m$, and $E_2$, such that $E=E_2\circ E_m\circ E_1$ instead of two (Figure 1).

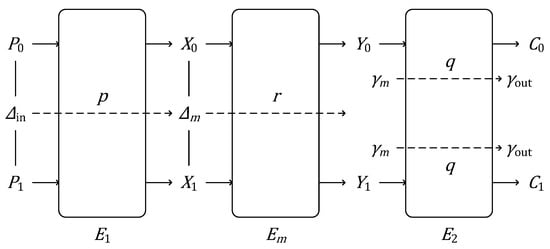
Figure 1. The structure of a differential–linear approximation.

Suppose that the differential characteristic for $E_1$, ${\Delta }_{\mathrm{in}}\stackrel{E_1}{\to }{\Delta }_m$, holds with a probability p, the linear approximation for $E_2$, ${\gamma }_m\stackrel{E_2}{\to }{\gamma }_{\mathrm{out}}$, has a correlation of q, and the differential–linear approximation for $E_m$, ${\Delta }_m\stackrel{E_m}{\to }{\gamma }_m$, has a correlation of r:

$$\begin{array}{c}\underset{x\in {\mathbb{F}}_2^n}{\mathrm{Pr}}[E_1\left(x\right)\oplus E_1\left(x\oplus {\Delta }_{\mathrm{in}}\right)={\Delta }_m]=p,\\ \underset{x\in {\mathbb{F}}_2^n}{\mathrm{Cor}}[E_2\left(x\right);{\gamma }_m,{\gamma }_{\mathrm{out}}]=q,\\ \underset{x\in S}{\mathrm{Cor}}[⟨{\gamma }_m,E_m\left(x\right)⟩\oplus ⟨{\gamma }_m,E_m\left(x\oplus {\Delta }_m\right)⟩]=r,\end{array}$$

(4)

where S represents the set of samples used to calculate the correlation. Note that when $E_m$ involves round keys, the correlation r is estimated using N samples and M random keys. This is achieved by computing an empirical value with a random key and repeating the process M times. The final value of r is determined as the median (or mean) of the M obtained values [27,30,33]. Subsequently, the total correlation of the differential–linear approximation ${\Delta }_{\mathrm{in}}\stackrel{E}{\to }{\gamma }_{\mathrm{out}}$ is estimated as follows:

$$\underset{x\in {\mathbb{F}}_2^n}{\mathrm{Cor}}[⟨{\gamma }_{\mathrm{out}},E\left(x\right)⟩\oplus ⟨{\gamma }_{\mathrm{out}},E\left(x\oplus {\Delta }_{\mathrm{in}}\right)⟩]=pr{q}^2.$$

(5)

2.3. Boolean Satisfiability Problem and SAT Solver

The Boolean satisfiability problem involves determining whether a given Boolean formula can be satisfied by any interpretation. In other words, it aims to ascertain if the variables in the formula can be assigned values of TRUE or FALSE in a consistent manner that results in the formula being evaluated as TRUE. If such an assignment is possible, the formula is said to be satisfiable. Conversely, if no such assignment exists, the formula is unsatisfiable, indicating that the formula is evaluated as FALSE for all potential variable assignments.

Example 2.

Consider the Boolean formula $(P\vee \neg Q)\wedge (Q\vee \neg R)\wedge (R\vee \neg P)$. To determine if this formula is satisfiable, we can construct the following truth table (see Table 3). The formula is satisfiable because there are combinations of P, Q, and R (specifically, $(0,0,0)$ and $(1,1,1)$) that make the formula true.

Table 3. The truth table of $(P\vee \neg Q)\wedge (Q\vee \neg R)\wedge (R\vee \neg P)$.

P	Q	R	$\mathit{P}\vee \neg \mathit{Q}$	$\mathit{Q}\vee \neg \mathit{R}$	$\mathit{R}\vee \neg \mathit{P}$	Formula
0	0	0	1	1	1	1
0	0	1	1	0	1	0
0	1	0	0	1	1	0
0	1	1	0	1	1	0
1	0	0	1	1	0	0
1	0	1	1	0	1	0
1	1	0	1	1	0	0
1	1	1	1	1	1	1

The Boolean satisfiability problem is known to fall into the category of NP-complete problems, which means that currently, only algorithms with exponential worst-case complexity can solve it. Despite this complexity, there is ongoing research and development aimed at creating efficient and scalable algorithms to address it.

In this paper, we use two well-known SAT solvers, CryptoMiniSat by M. Soos et al. [34] and CaDiCaL by Biere [35], to search for differential–linear approximations of CHAM. CryptoMiniSat is recognized for its efficiency, scalability, and suitability for cryptographic applications. It supports multi-threaded operations and XOR clauses, making it highly versatile. On the other hand, CaDiCaL is designed with simplicity, performance, and lightweight architecture in mind, excelling in situations where these attributes are paramount. Both solvers bring unique strengths to the table, contributing to the continuous efforts to develop robust solutions for the Boolean satisfiability problem.

2.4. The Block Cipher CHAM

CHAM, consisting of ARX operations (modular addition ${\displaystyle ⊞}$, bitwise rotation ${\displaystyle ⋘}$, and bitwise XOR ${\displaystyle \oplus }$), is a family of block ciphers with a four-branch generalized Feistel structure. Each cipher in this family is denoted as CHAM-n/k, where n represents the block size in bits and k represents the key size in bits. Table 4 lists the ciphers in this family and their parameters. Here, w denotes the bit length of a branch (word) and $Nr$ represents the number of rounds.

Table 4. The block cipher CHAM parameters.

Cipher	n	k	w	$\mathit{Nr}$
CHAM-64/128	64	128	16	88
CHAM-128/128	128	128	32	112
CHAM-128/256	128	256	32	120

By applying $Nr$ iterations of the key-dependent round function, CHAM-n/k encrypts an n-bit plaintext of four w-bit words to an n-bit ciphertext of four w-bit words. For a round key $r{k}_i\in \mathrm{GF}{\left(2\right)}^w$, the i-th round function of CHAM is defined as follows:

$$\begin{array}{c}{f}_{r{k}_i}^{\left(i\right)}:\mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w⟶\mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w\times \mathrm{GF}{\left(2\right)}^w\\ f_{r{k}_i}^{\left(i\right)}\left(x_i,y_i,z_i,w_i\right)=\left(y_i,z_i,w_i,\left((x_i\oplus i)⊞\left(\left(y_i⋘{\alpha }_i\right)\oplus r{k}_i\right)\right)⋘{\beta }_i\right),\end{array}$$

(6)

where ${\alpha }_i=1$ and ${\beta }_i=8$ when i is even and ${\alpha }_i=8$ and ${\beta }_i=1$ when i is odd. The round function of CHAM is depicted in Figure 2.

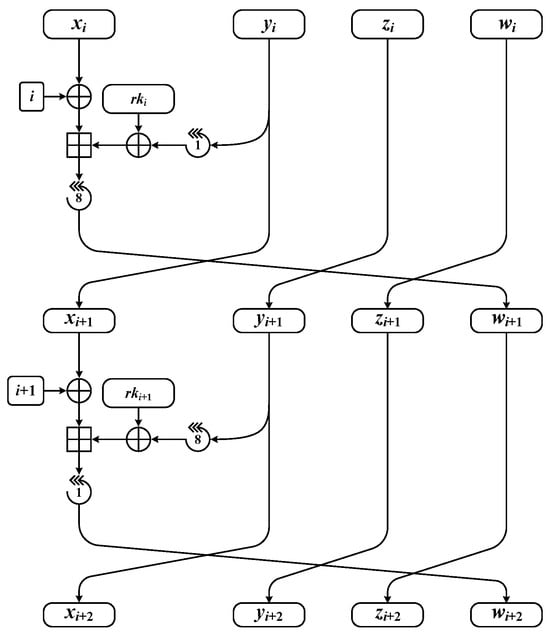
Figure 2. The round function of CHAM.

The CHAM key schedules generate round keys $r{k}_i$ for a given key of $k/w$ w-bit words $K=\left(k_0,k_1,\cdots ,k_{k/w-1}\right)$. The round keys are generated by the following:

$$r{k}_i=\left\{\begin{array}{cc}{k}_j\oplus \left(k_j⋘1\right)\oplus \left(k_j⋘8\right),\hfill & \mathrm{if}0\le j<k/w,\hfill \\ k_{j\oplus 1}\oplus \left(k_{j\oplus 1}⋘1\right)\oplus \left(k_{j\oplus 1}⋘11\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(7)

where $j=i\mathrm{mod}2k/w$. The value $r{k}_i$ is the i-th round key for $0\le i<Nr$.

3. Searching for Differential–Linear Approximations

In this section, we briefly review the method proposed by Chen et al. for finding differential–linear approximations of block ciphers [30]. The core idea of Chen et al.’s method involves generating new differential–linear approximations by XORing known approximations, aiming to create approximations with high correlations. Their motivation is based on an intuitive understanding of correlations, leading to the conclusion that combining high-correlation approximations is likely to result in another effective approximation. Although this hypothesis relies on an assumption of independence that may not always be valid, it has been supported by experimental results.

We first introduce two concepts, strong unbalanced bit and weak unbalanced bit.

Definition 1

([30]). Consider an n-bit block cipher, an n-bit difference Δ, and a threshold c. The i-th ciphertext bit, where $0\le i<n$, is called a strong unbalanced bit if the absolute correlation of the differential–linear approximation $\Delta \to \gamma$ exceeds c, where $\gamma =\left[i\right]$. If this condition is not met, the bit is called a weak unbalanced bit.

Suppose that two sub-ciphers, $E_m$ and $E_2$ and a difference ${\Delta }_m$ are given. Based on the heuristic conclusion, a meet-in-the-middle search algorithm to search for differential–linear approximations ${\Delta }_m\stackrel{E_m}{\to }{\gamma }_m\stackrel{E_2}{\to }{\gamma }_{\mathrm{out}}$ is proposed. The algorithm works as follows. We first search for a set of strong unbalanced bits, ${\mathcal{B}}_{\mathcal{S}}$, for a sub-cipher $E_m$, a difference ${\Delta }_m$, and a threshold. Next, we search for linear approximations $\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)$ of a sub-cipher $E_2$ under the conditions that ${\gamma }_m\left[i\right]=0$ if $i\notin {\mathcal{B}}_{\mathcal{S}}$ for $0\le i<n$. Finally, for each returned linear approximation $\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)$ of $E_2$, we compute the experimental correlation of the differential–linear approximation. We add the approximation to a list if the correlation is greater than or equal to the threshold. See Algorithm 1 for the detailed steps.

Algorithm 1 [30] Searching for ${\Delta }_m\stackrel{E_m}{\to }{\gamma }_m\stackrel{E_2}{\to }{\gamma }_{\mathrm{out}}$ using the meet-in-the-middle method

Require:  a difference ${\Delta }_m$, a threshold c, a sample size N Ensure:  a set $\mathcal{P}$ of linear mask tuples $\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)$   1: $\mathcal{P}\leftarrow \varphi$ and ${\mathcal{B}}_{\mathcal{S}}\leftarrow \varphi$   2: Generate N random plaintexts $P_i$ ($1\le i\le N$).   3: Collect N pseudo-ciphertext pairs $\left(E_m\left(P_i\right),E_m\left(P_i\oplus {\Delta }_m\right)\right)$ ($1\le i\le N$).   4: for $0\le i<n$  do   5:     ${\gamma }_m\leftarrow \left[i\right]$   6:     Compute the correlation $\mathbf{Cor}$ of ${\Delta }_m\to {\gamma }_m$ over the N pseudo-ciphertext pairs.   7:     if $\left|\mathbf{Cor}\right|\ge c$ then   8:         ${\mathcal{B}}_{\mathcal{S}}\leftarrow {\mathcal{B}}_{\mathcal{S}}\cup \left\{i\right\}$.   9:     end if  10: end for  11: for $0\le i<n$ and $i\notin {\mathcal{B}}_{\mathcal{S}}$ do  12:     Add a condition ${\gamma }_m\left[i\right]=0$ to $\mathbf{Model}\left(\right)$. ▹$\mathbf{Model}\left(\right)$ is the automatic search model of linear approximations ${\gamma }_m\to {\gamma }_{\mathrm{out}}$  13: end for  14: Collect linear mask tuples $\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)$ by running $\mathbf{Model}\left(\right)$.  15: for each returned tuple $\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)$ do  16:     Compute the correlation $\mathbf{Cor}$ of ${\Delta }_m\to {\gamma }_m$ over N pseudo-ciphertext pairs.  17:     if $\left|\mathbf{Cor}\right|\ge c$ then  18:         $\mathcal{P}\leftarrow \mathcal{P}\cup \left\{\left({\gamma }_m,{\gamma }_{\mathrm{out}}\right)\right\}$.  19:     end if  20: end for

4. Differential–Linear Approximations of CHAM

This section presents the first differential–linear approximations of CHAM. We will denote $r_1$, $r_m$, and $r_2$ as the numbers of rounds covered by $E_1$, $E_m$, and $E_2$, respectively. We first search for a differential–linear approximation ${\Delta }_m\stackrel{E_m}{\to }{\gamma }_m$ and a linear approximation ${\gamma }_m\stackrel{E_2}{\to }{\gamma }_{\mathrm{out}}$ using Algorithm 1. Following this, we prepend a differential characteristic ${\Delta }_{\mathrm{in}}\stackrel{E_1}{\to }{\Delta }_m$. Given the computational infeasibility of testing all the differences ${\Delta }_m\in {\mathbb{F}}_2^n$, we confine our investigation to cases where ${\Delta }_m$ takes the form $\left[i\right]$ for $0\le i<n$ (1-bit differences) or $[i,i+1]$ for $0\le i<n-1$ (2-bit differences).

4.1. Differential–Linear Approximation of CHAM-64/128

This subsection presents the first differential–linear approximation of CHAM-64/128. A 46-round differential–linear approximation of CHAM-64/128 with a correlation of $2^{-31.08}$ is found using Algorithm 1 by setting $r_m=26$, $r_2=14$, and $c=2^{-7}$ (see Table 5). This approximation is composed of the following:

Table 5. A 46-round differential–linear approximation of CHAM-64/128.

$\left({\mathit{r}}_1,{\mathit{r}}_{\mathit{m}},{\mathit{r}}_2\right)$	${\mathit{\Delta }}_{\mathbf{in}}\to {\mathit{\Delta }}_{\mathit{m}}\to {\mathit{\gamma }}_{\mathit{m}}\to {\mathit{\gamma }}_{\mathbf{out}}$	Correlation
$\left(6,26,14\right)$	$\left(\mathtt{8120}\mathtt{2090}\mathtt{8020}\mathtt{4000}\right)$→	$2^{-31.08}$
	$\left(\mathtt{2000}\mathtt{0000}\mathtt{0000}\mathtt{0000}\right)$→
	$\left(\mathtt{0001}\mathtt{8000}\mathtt{0400}\mathtt{0201}\right)$→
	$\left(\mathtt{0106}\mathtt{0400}\mathtt{0200}\mathtt{0002}\right)$

• A six-round differential characteristic with an output difference of $\left(\mathtt{2000}\mathtt{0000}\mathtt{0000}\mathtt{0000}\right)$ and a probability of $2^{-10}$ (note that this is optimal, as there is no six-round differential characteristic with a higher probability for this output difference; see Table 6);
  Table 6. An optimal 6-round differential characteristic of CHAM-64/128 with an output difference of $\left(\mathtt{2000}\mathtt{0000}\mathtt{0000}\mathtt{0000}\right)$.

  Round	Difference	Prob.	Round	Difference	Prob.
  0	$\left(\mathtt{8120}\mathtt{2090}\mathtt{8020}\mathtt{4000}\right)$		4	$\left(\mathtt{0040}\mathtt{0020}\mathtt{2000}\mathtt{0000}\right)$	$2^{-1}$
  1	$\left(\mathtt{2090}\mathtt{8020}\mathtt{4000}\mathtt{0040}\right)$	$2^{-3}$	5	$\left(\mathtt{0020}\mathtt{2000}\mathtt{0000}\mathtt{0000}\right)$	$2^{-1}$
  2	$\left(\mathtt{8020}\mathtt{4000}\mathtt{0040}\mathtt{0020}\right)$	$2^{-3}$	6	$\left(\mathtt{2000}\mathtt{0000}\mathtt{0000}\mathtt{0000}\right)$	$2^{-1}$
  3	$\left(\mathtt{4000}\mathtt{0040}\mathtt{0020}\mathtt{2000}\right)$	$2^{-1}$

• A 26-round differential–linear approximation with a correlation of $2^{-11.08}$. This value is the median of 200 experimental correlations, each derived from $2^{24}$ plaintext–ciphertext pairs. (The average and standard deviation of the 200 correlations are $2^{-10.59}$ and $2^{-10.72}$, respectively. The 95% and 99% confidence intervals are $\left(2^{-10.79},2^{-10.42}\right)$, and $\left(2^{-10.85},2^{-10.37}\right)$, respectively.)
• A 14-round linear approximation with a correlation of $2^{-5}$ (Note that this is also optimal, as there is no 14-round linear approximation with a higher correlation; see Table 7).
  Table 7. An optimal 14-round linear approximation of CHAM-64/128 with a correlation of $2^{-5}$.

  Round	Linear Mask	Cor.	Round	Linear Mask	Cor.
  0	$\left(\mathtt{0001}\mathtt{8000}\mathtt{0400}\mathtt{0201}\right)$		8	$\left(\mathtt{0000}\mathtt{0000}\mathtt{0400}\mathtt{0000}\right)$	1
  1	$\left(\mathtt{0000}\mathtt{0400}\mathtt{0201}\mathtt{0100}\right)$	1	9	$\left(\mathtt{0000}\mathtt{0400}\mathtt{0000}\mathtt{0000}\right)$	1
  2	$\left(\mathtt{0400}\mathtt{0201}\mathtt{0100}\mathtt{0000}\right)$	1	10	$\left(\mathtt{0400}\mathtt{0000}\mathtt{0000}\mathtt{0000}\right)$	1
  3	$\left(\mathtt{0001}\mathtt{0100}\mathtt{0000}\mathtt{0006}\right)$	$2^{-1}$	11	$\left(\mathtt{0200}\mathtt{0000}\mathtt{0000}\mathtt{0006}\right)$	$2^{-1}$
  4	$\left(\mathtt{0000}\mathtt{0000}\mathtt{0006}\mathtt{0002}\right)$	1	12	$\left(\mathtt{0003}\mathtt{0000}\mathtt{0006}\mathtt{0400}\right)$	$2^{-1}$
  5	$\left(\mathtt{0000}\mathtt{0006}\mathtt{0002}\mathtt{0000}\right)$	1	13	$\left(\mathtt{0001}\mathtt{0006}\mathtt{0400}\mathtt{0200}\right)$	$2^{-1}$
  6	$\left(\mathtt{0006}\mathtt{0002}\mathtt{0000}\mathtt{0000}\right)$	1	14	$\left(\mathtt{0106}\mathtt{0400}\mathtt{0200}\mathtt{0002}\right)$	1
  7	$\left(\mathtt{0000}\mathtt{0000}\mathtt{0000}\mathtt{0400}\right)$	$2^{-1}$

This approximation represents the most effective distinguisher for CHAM-64/128 found to date in a single-key attack model, significantly exceeding the designers’ expectations for differential–linear approximations of CHAM-64/128.

As mentioned earlier, for each 1-bit and 2-bit difference, the set of strong unbalanced bits for the 26-round $E_m$ is determined using the threshold $2^{-7}$ and $2^{28}$ pseudo plaintext–ciphertext pairs. These results are summarized in Table A1 provided in Appendix A.

4.2. Differential–Linear Approximation of CHAM-128/128 and CHAM-128/256

This subsection presents the first differential–linear approximation of CHAM-128/128 and CHAM-128/256. A 58-round differential–linear approximation with correlations of $2^{-58.86}$ for CHAM-128/128 and $2^{-59.08}$ for CHAM-128/256 is found using Algorithm 1 by setting $r_m=32$, $r_2=16$, and $c=2^{-8}$ (see Table 8). This approximation is composed of the following:

Table 8. A 58-round differential–linear approximation of CHAM-128/128 and CHAM-128/256.

$\left({\mathit{r}}_1,{\mathit{r}}_{\mathit{m}},{\mathit{r}}_2\right)$	${\mathit{\Delta }}_{\mathbf{in}}\to {\mathit{\Delta }}_{\mathit{m}}\to {\mathit{\gamma }}_{\mathit{m}}\to {\mathit{\gamma }}_{\mathbf{out}}$	Correlation
$\left(10,32,16\right)$	$\left(\mathtt{00100104}\mathtt{04082082}\mathtt{80000820}\mathtt{40000000}\right)$→
	$\left(\mathtt{08000000}\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\right)$→	$2^{-58.86}$
	$\left(\mathtt{00040000}\mathtt{c}\mathtt{1020000}\mathtt{00800000}\mathtt{00008000}\right)$→	$2^{-59.08}$
	$\left(\mathtt{01040000}\mathtt{00000600}\mathtt{00000200}\mathtt{00000002}\right)$

• A 10-round differential characteristic with an output difference of $\left(\mathtt{08000000}\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\right)$ and a probability of $2^{-26}$ (Note that this is optimal, as there is no 10-round differential characteristic with a higher probability for this output difference. See Table 9);
  Table 9. An optimal 10-round differential characteristic of CHAM-128/128 and CHAM-128/256 with an output difference of $\left(\mathtt{08000000}\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\right)$.

  Round	Difference	Prob.	Round	Difference	Prob.
  0	$\left(\mathtt{00100104}\mathtt{04082082}\mathtt{80000820}\mathtt{40000000}\right)$		6	$\left(\mathtt{00082000}\mathtt{00001000}\mathtt{00000010}\mathtt{00000008}\right)$	$2^{-3}$
  1	$\left(\mathtt{04082082}\mathtt{80000820}\mathtt{40000000}\mathtt{00400008}\right)$	$2^{-5}$	7	$\left(\mathtt{00001000}\mathtt{00000010}\mathtt{00000008}\mathtt{08000000}\right)$	$2^{-2}$
  2	$\left(\mathtt{80000820}\mathtt{40000000}\mathtt{00400008}\mathtt{08200004}\right)$	$2^{-6}$	8	$\left(\mathtt{00000010}\mathtt{00000008}\mathtt{08000000}\mathtt{00000000}\right)$	$2^{-1}$
  3	$\left(\mathtt{40000000}\mathtt{00400008}\mathtt{08200004}\mathtt{00082000}\right)$	$2^{-2}$	9	$\left(\mathtt{00000008}\mathtt{08000000}\mathtt{00000000}\mathtt{00000000}\right)$	$2^{-1}$
  4	$\left(\mathtt{00400008}\mathtt{08200004}\mathtt{00082000}\mathtt{00001000}\right)$	$2^{-2}$	10	$\left(\mathtt{08000000}\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\right)$	$2^{-1}$
  5	$\left(\mathtt{08200004}\mathtt{00082000}\mathtt{00001000}\mathtt{00000010}\right)$	$2^{-3}$

• A 32-round differential–linear approximation with correlations of $2^{-14.86}$ for CHAM-128/128 and $2^{-15.08}$ for CHAM-128/256 (These values are the medians of 100 experimental correlations, each derived from $2^{28}$ plaintext–ciphertext pairs. (For CHAM-128/128, the average and standard deviation of the 100 correlations are $2^{-13.75}$ and $2^{-13.86}$, respectively. The 95% and 99% confidence intervals are $\left(2^{-14.04},2^{-13.51}\right)$, and $\left(2^{-14.14},2^{-13.44}\right)$, respectively. For CHAM-128/256, the average and standard deviation of the 100 correlations are $2^{-14.03}$ and $2^{-14.34}$, respectively. The 95% and 99% confidence intervals are $\left(2^{-14.28},2^{-13.82}\right)$, and $\left(2^{-14.37},2^{-13.76}\right)$, respectively).
• A 16-round linear approximation with a correlation of $2^{-9}$ (note that this is also optimal, as there is no 16-round linear approximation with a higher correlation; see Table 10).
  Table 10. An optimal 16-round linear approximation of CHAM-128/128 and CHAM-128/256 with a correlation of $2^{-9}$.

  Round	Linear Mask	Cor.	Round	Linear Mask	Cor.
  0	$\left(\mathtt{00040000}\mathtt{c1020000}\mathtt{00800000}\mathtt{00008000}\right)$		9	$\left(\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\mathtt{00000600}\right)$	$2^{-1}$
  1	$\left(\mathtt{c1000000}\mathtt{00800000}\mathtt{00008000}\mathtt{06000000}\right)$	$2^{-1}$	10	$\left(\mathtt{00000000}\mathtt{00000000}\mathtt{00000600}\mathtt{00000000}\right)$	1
  2	$\left(\mathtt{00018000}\mathtt{00008000}\mathtt{06000000}\mathtt{02000001}\right)$	$2^{-2}$	11	$\left(\mathtt{00000000}\mathtt{00000600}\mathtt{00000000}\mathtt{00000000}\right)$	1
  3	$\left(\mathtt{00000000}\mathtt{06000000}\mathtt{02000001}\mathtt{01000000}\right)$	$2^{-1}$	12	$\left(\mathtt{00000600}\mathtt{00000000}\mathtt{00000000}\mathtt{00000000}\right)$	1
  4	$\left(\mathtt{06000000}\mathtt{02000001}\mathtt{01000000}\mathtt{00000000}\right)$	1	13	$\left(\mathtt{00000200}\mathtt{00000000}\mathtt{00000000}\mathtt{00040000}\right)$	$2^{-1}$
  5	$\left(\mathtt{00000001}\mathtt{01000000}\mathtt{00000000}\mathtt{00000004}\right)$	$2^{-1}$	14	$\left(\mathtt{00000002}\mathtt{00000000}\mathtt{00040000}\mathtt{00000600}\right)$	$2^{-1}$
  6	$\left(\mathtt{00000000}\mathtt{00000000}\mathtt{00000004}\mathtt{00000002}\right)$	1	15	$\left(\mathtt{00000001}\mathtt{00040000}\mathtt{00000600}\mathtt{00000200}\right)$	$2^{-1}$
  7	$\left(\mathtt{00000000}\mathtt{00000004}\mathtt{00000002}\mathtt{00000000}\right)$	1	16	$\left(\mathtt{01040000}\mathtt{00000600}\mathtt{00000200}\mathtt{00000002}\right)$	1
  8	$\left(\mathtt{00000004}\mathtt{00000002}\mathtt{00000000}\mathtt{00000000}\right)$	1

Although this approximation is not the best distinguisher for CHAM-128/128 and CHAM-128/256, it stands as the first concrete differential–linear approximation. Remarkably, it surpasses the designers’ expectations for differential–linear approximations of CHAM-128/128 and CHAM-128/256.

As mentioned earlier, for each 1-bit and 2-bit difference, the set of strong unbalanced bits for the 32-round $E_m$ is determined using the threshold $2^{-8}$ and $2^{28}$ pseudo plaintext–ciphertext pairs. These results are summarized in Table A2 and Table A3 provided in Appendix A.

5. Conclusions

In this work, we presented the first concrete differential–linear approximations of CHAM. We found a 46-round differential–linear approximation of CHAM-64/128 with a correlation of $2^{-31.08}$ and a 58-round approximation for CHAM-128/128 and CHAM-128/256 with correlations of $2^{-58.86}$ and $2^{-59.08}$, respectively. These are not only the first known concrete differential–linear approximations of CHAM, but they also have much longer rounds than the designers anticipated. Despite these findings, CHAM remains secure due to its sufficient security margin.

Further research is needed to better understand the differential–linear approximations and differential–linear cryptanalysis of ARX-based block ciphers, including CHAM. We anticipate that the following studies are necessary:

• mounting differential–linear attacks on CHAM using known differential–linear approximations,
• calculating more exact correlations of the differential–linear approximations, and
• developing more efficient and effective methods for finding differential–linear approximations.