Self-HCL: Self-Supervised Multitask Learning with Hybrid Contrastive Learning Strategy for Multimodal Sentiment Analysis
Abstract
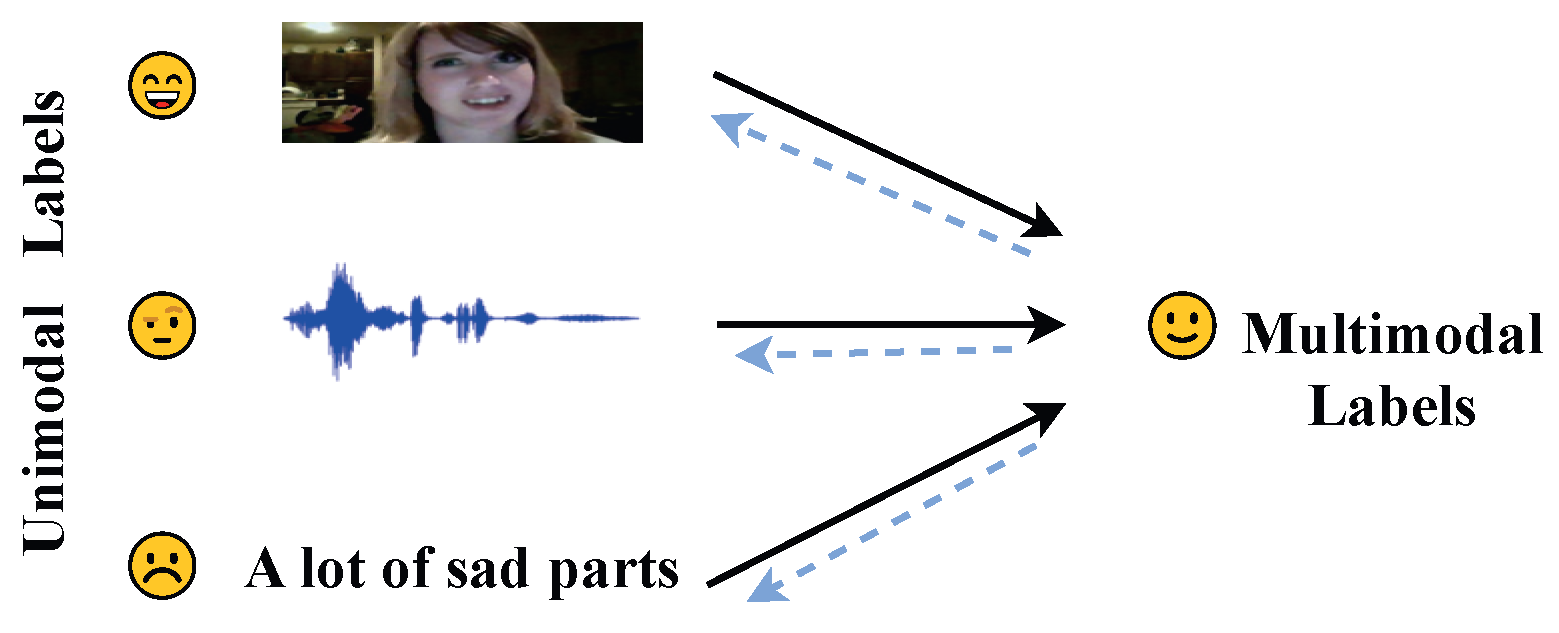
1. Introduction
- We construct a novel MSA framework called Self-HCL, which improves the identification of salient features in the absence of unimodal annotation using the UFEM and optimizes the features by combining the gating mechanism with element multiplication, which effectively improves the representation learning of unimodal features.
- A hybrid contrastive learning strategy is designed for the purpose of deep exploration of the fused multimodal features and the inherent relationship between each single modal feature and emotional labels.
- We propose an improved ULGM, which reveals the deep relationship between different modalities and optimizes the spatial distribution of modal features by constructing a new unsupervised contrastive learning space, thus achieving the stable generation of unimodal labels within a short training cycle.
2. Related Work
2.1. Multimodal Sentiment Analysis
2.2. Multitask Learning
2.3. Contrastive Learning
2.4. ULGM
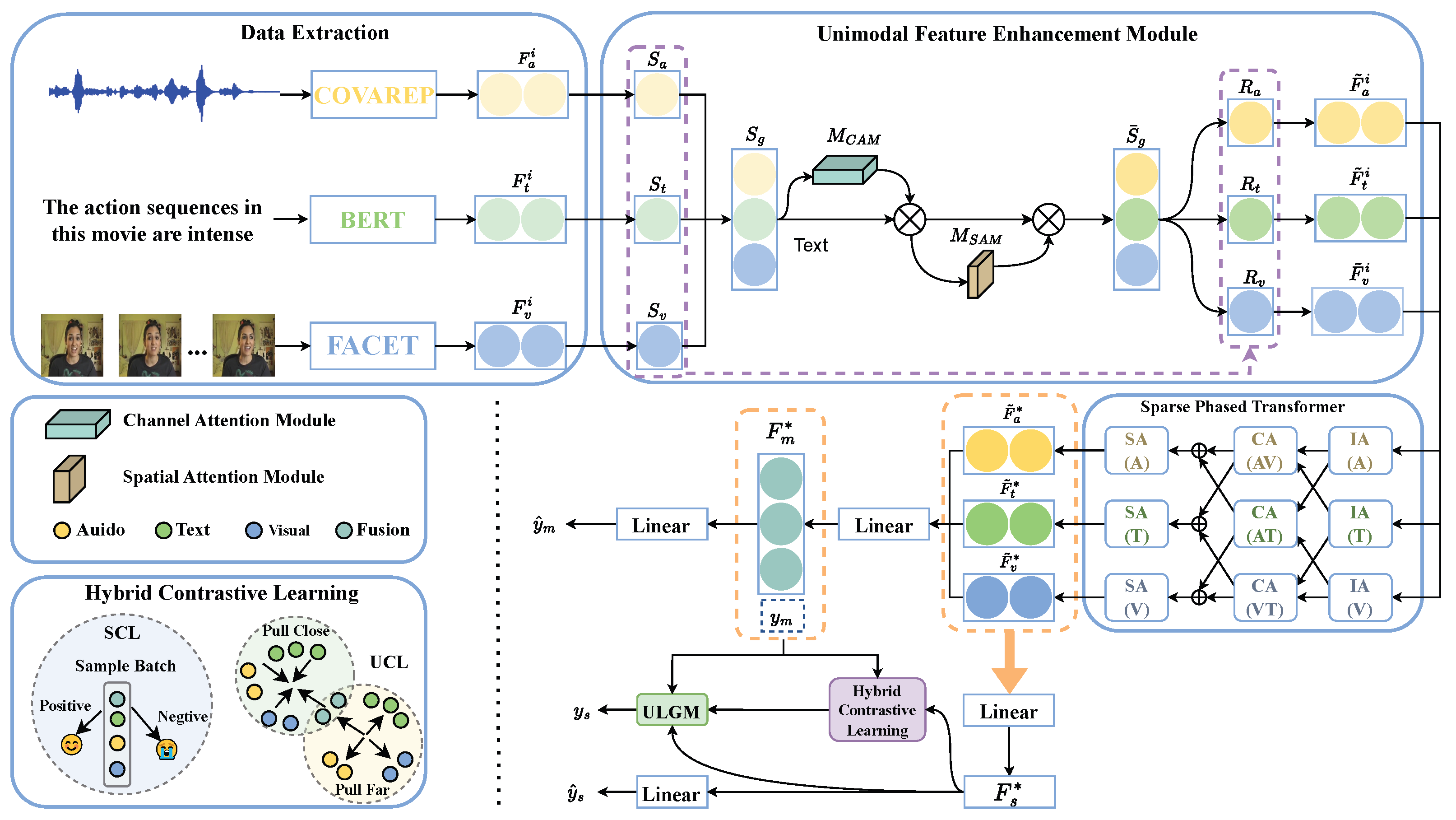
3. Approach
3.1. Problem Definition
3.2. Overall Architecture
3.3. Multimodal Task
3.4. Unimodal Task
3.5. Hybrid Contrastive Learning
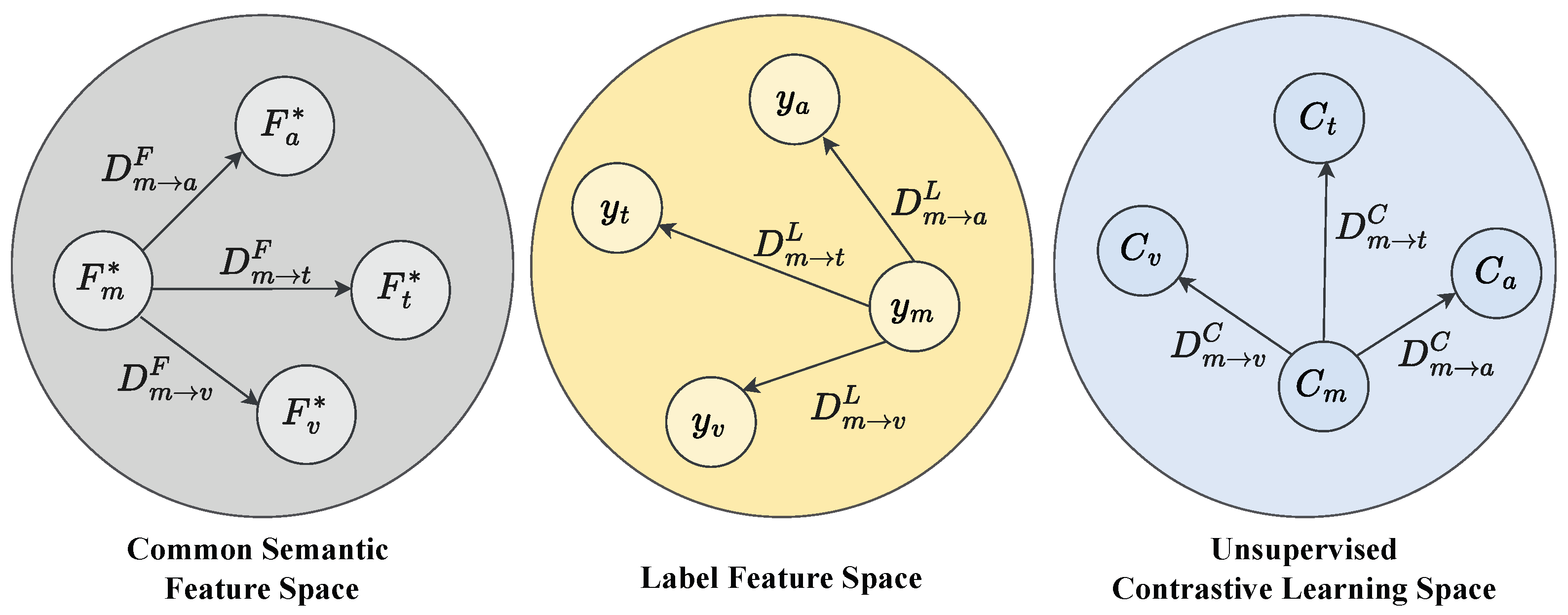
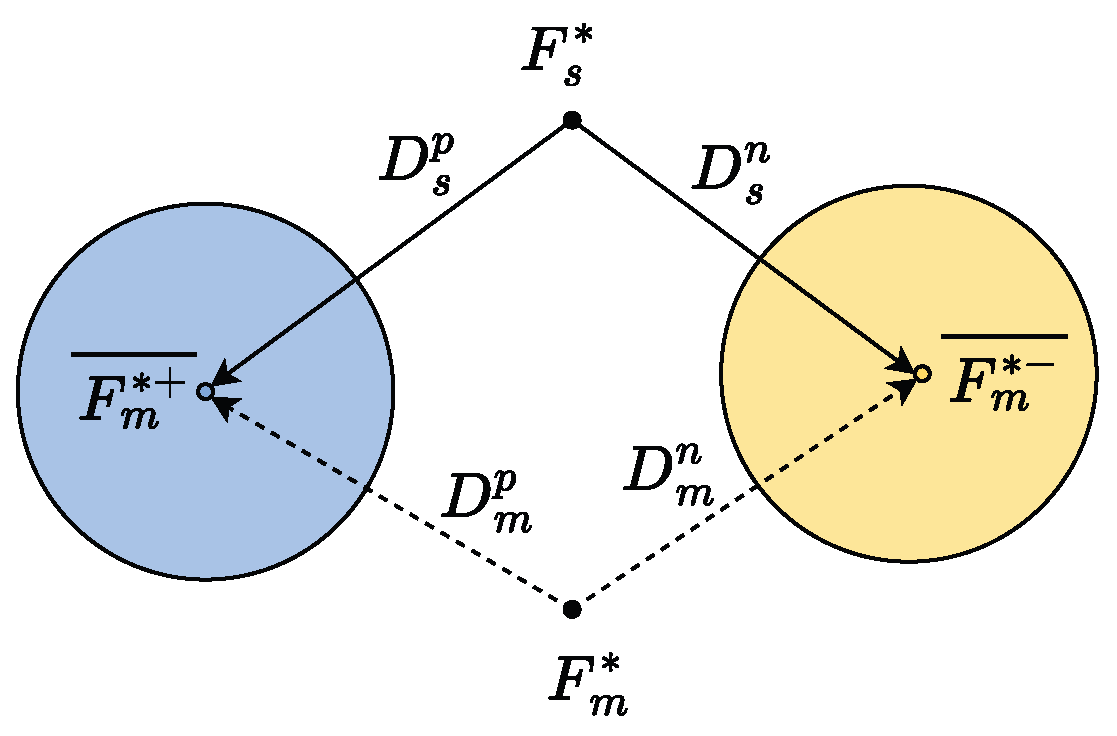
3.6. ULGM
3.7. Objective Function for Training
4. Experimental Settings
4.1. Datasets
4.2. Baselines
- TFN [6]: The Tensor Fusion Network (TFN) applies a subnetwork for modality embedding, along with tensor fusion, to understand both the intra- and intermodality dynamics.
- LMF [16]: Low-Rank Multimodal Fusion (LMF) carries out the fusion of multiple modalities by utilizing low-rank tensors, thus enhancing computational efficiency.
- RAVEN [33]: The Recurrent Attended Variation Embedding Network (RAVEN) captures the detailed structure of nonverbal subword sequences and adapts word representations in response to nonverbal signals.
- MulT [4]: The Multimodal Transformer (MulT) employs a crossmodal transformer with crossmodal attention to facilitate modality translation.
- MISA [5]: The Modality-Invariant and -Specific Representations (MISA) projects features into two separate spaces with specific constraints and performs fusion on these features.
- MAG-BERT [34]: The Multimodal Adaptation Gate for BERT (MAG-BERT) designs an alignment gate and inserts that into a vanilla BERT model to refine the fusion process.
- Self-MM [9]: Learning Modality-Specific Representations with Self-Supervised Multitask Learning (Self-MM) assigns each modality a unimodal training task with automatically generated labels, thus aiming to adjust the gradient backpropagation.
- MMIM [10]. Multimodal InfoMax (MMIM) uses the first implementation of the InfoMax principle on an MSA task, where the fusion representation is learned by maximizing its mutual information with unimodal representations.
- SUGRM [11]: The Self-Supervised Unimodal Label Generation Model (SUGRM) leverages recalibrated information to produce unimodal annotations by adaptively tuning features, thus postulating that the distance between two representations in a shared space should correspondingly reflect the distance between their associated labels in the label space.
4.3. Implementation Details
5. Results and Analysis
5.1. Quantitative Results
5.2. Ablation Study
- Employ w/o UCL: Remove only unsupervised contrastive learning from Self-HCL while leaving the rest unchanged.
- Employ w/o SCL: Remove only supervised contrastive learning from Self-HCL while keeping the remaining parts unaltered.
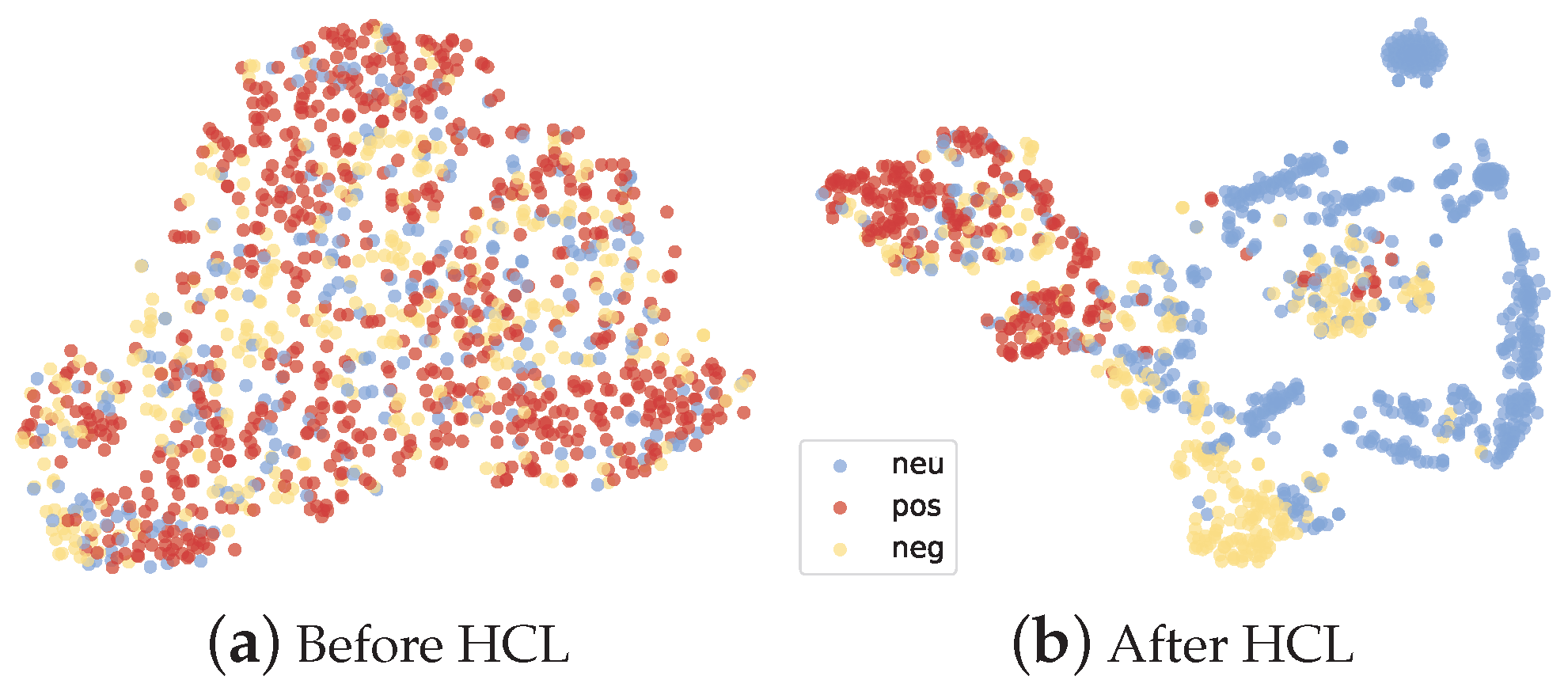
5.3. Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Grossberg, S. Recurrent neural networks. Scholarpedia 2013, 8, 1888. [Google Scholar] [CrossRef]
- Ranaldi, L.; Pucci, G. Knowing knowledge: Epistemological study of knowledge in transformers. Appl. Sci. 2023, 13, 677. [Google Scholar] [CrossRef]
- Tsai, Y.H.H.; Bai, S.; Liang, P.P.; Kolter, J.Z.; Morency, L.P.; Salakhutdinov, R. Multimodal transformer for unaligned multimodal language sequences. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; Volume 2019, p. 6558. [Google Scholar]
- Hazarika, D.; Zimmermann, R.; Poria, S. Misa: Modality-invariant and-specific representations for multimodal sentiment analysis. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1122–1131. [Google Scholar]
- Zadeh, A.; Chen, M.; Poria, S.; Cambria, E.; Morency, L.P. Tensor Fusion Network for Multimodal Sentiment Analysis. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017. [Google Scholar]
- Zadeh, A.; Liang, P.P.; Mazumder, N.; Poria, S.; Cambria, E.; Morency, L.P. Memory fusion network for multi-view sequential learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Poria, S.; Hazarika, D.; Majumder, N.; Mihalcea, R. Beneath the tip of the iceberg: Current challenges and new directions in sentiment analysis research. IEEE Trans. Affect. Comput. 2020, 14, 108–132. [Google Scholar] [CrossRef]
- Yu, W.; Xu, H.; Yuan, Z.; Wu, J. Learning modality-specific representations with self-supervised multi-task learning for multimodal sentiment analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 10790–10797. [Google Scholar]
- Han, W.; Chen, H.; Poria, S. Improving multimodal fusion with hierarchical mutual information maximization for multimodal sentiment analysis. arXiv 2021, arXiv:2109.00412. [Google Scholar]
- Hwang, Y.; Kim, J.H. Self-supervised unimodal label generation strategy using recalibrated modality representations for multimodal sentiment analysis. In Proceedings of the Findings of the Association for Computational Linguistics: EACL 2023, Dubrovnik, Croatia, 2–6 May 2023; pp. 35–46. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Cheng, J.; Fostiropoulos, I.; Boehm, B.; Soleymani, M. Multimodal phased transformer for sentiment analysis. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, Punta Cana, Dominican Republic, 7–11 November 2021; pp. 2447–2458. [Google Scholar]
- Belghazi, M.I.; Baratin, A.; Rajeshwar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, D. Mutual information neural estimation. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 531–540. [Google Scholar]
- Kaur, R.; Kautish, S. Multimodal sentiment analysis: A survey and comparison. In Research Anthology on Implementing Sentiment Analysis across Multiple Disciplines; IGI Global: Hershey, PA, USA, 2022; pp. 1846–1870. [Google Scholar]
- Liu, Z.; Shen, Y.; Lakshminarasimhan, V.B.; Liang, P.P.; Zadeh, A.; Morency, L.P. Efficient low-rank multimodal fusion with modality-specific factors. arXiv 2018, arXiv:1806.00064. [Google Scholar]
- Liang, P.P.; Liu, Z.; Zadeh, A.; Morency, L.P. Multimodal language analysis with recurrent multistage fusion. arXiv 2018, arXiv:1808.03920. [Google Scholar]
- Pham, H.; Liang, P.P.; Manzini, T.; Morency, L.P.; Póczos, B. Found in translation: Learning robust joint representations by cyclic translations between modalities. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 6892–6899. [Google Scholar]
- Sun, Z.; Sarma, P.; Sethares, W.; Liang, Y. Learning relationships between text, audio, and video via deep canonical correlation for multimodal language analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 8992–8999. [Google Scholar]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Yang, B.; Wu, L.; Zhu, J.; Shao, B.; Lin, X.; Liu, T.Y. Multimodal sentiment analysis with two-phase multi-task learning. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 2015–2024. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Dhanush, S.; Ekbal, A.; Bhattacharyya, P. Sentiment and emotion help sarcasm? A multi-task learning framework for multi-modal sarcasm, sentiment and emotion analysis. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 4351–4360. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 18661–18673. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Degottex, G.; Kane, J.; Drugman, T.; Raitio, T.; Scherer, S. COVAREP—A collaborative voice analysis repository for speech technologies. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 960–964. [Google Scholar]
- iMotions. Facet iMotions Biometric Research Platform, 2013. Available online: https://imotions.com/products/imotions-lab/modules/fea-facial-expression-analysis/ (accessed on 16 July 2024).
- Rakhlin, A. Convolutional neural networks for sentence classification. GitHub 2016, 6, 25. [Google Scholar]
- Zadeh, A.; Zellers, R.; Pincus, E.; Morency, L.P. Mosi: Multimodal corpus of sentiment intensity and subjectivity analysis in online opinion videos. arXiv 2016, arXiv:1606.06259. [Google Scholar]
- Zadeh, A.B.; Liang, P.P.; Poria, S.; Cambria, E.; Morency, L.P. Multimodal language analysis in the wild: Cmu-mosei dataset and interpretable dynamic fusion graph. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, Melbourne, Australia, 15–20 July 2018; Volume 1, pp. 2236–2246. [Google Scholar]
- Wang, Y.; Shen, Y.; Liu, Z.; Liang, P.P.; Zadeh, A.; Morency, L.P. Words can shift: Dynamically adjusting word representations using nonverbal behaviors. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7216–7223. [Google Scholar]
- Rahman, W.; Hasan, M.K.; Lee, S.; Zadeh, A.; Mao, C.; Morency, L.P.; Hoque, E. Integrating multimodal information in large pretrained transformers. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; Volume 2020, p. 2359. [Google Scholar]
- Hinton, G.E.; Roweis, S. Stochastic neighbor embedding. Adv. Neural Inf. Process. Syst. 2002, 15, 857–864. [Google Scholar] [CrossRef]
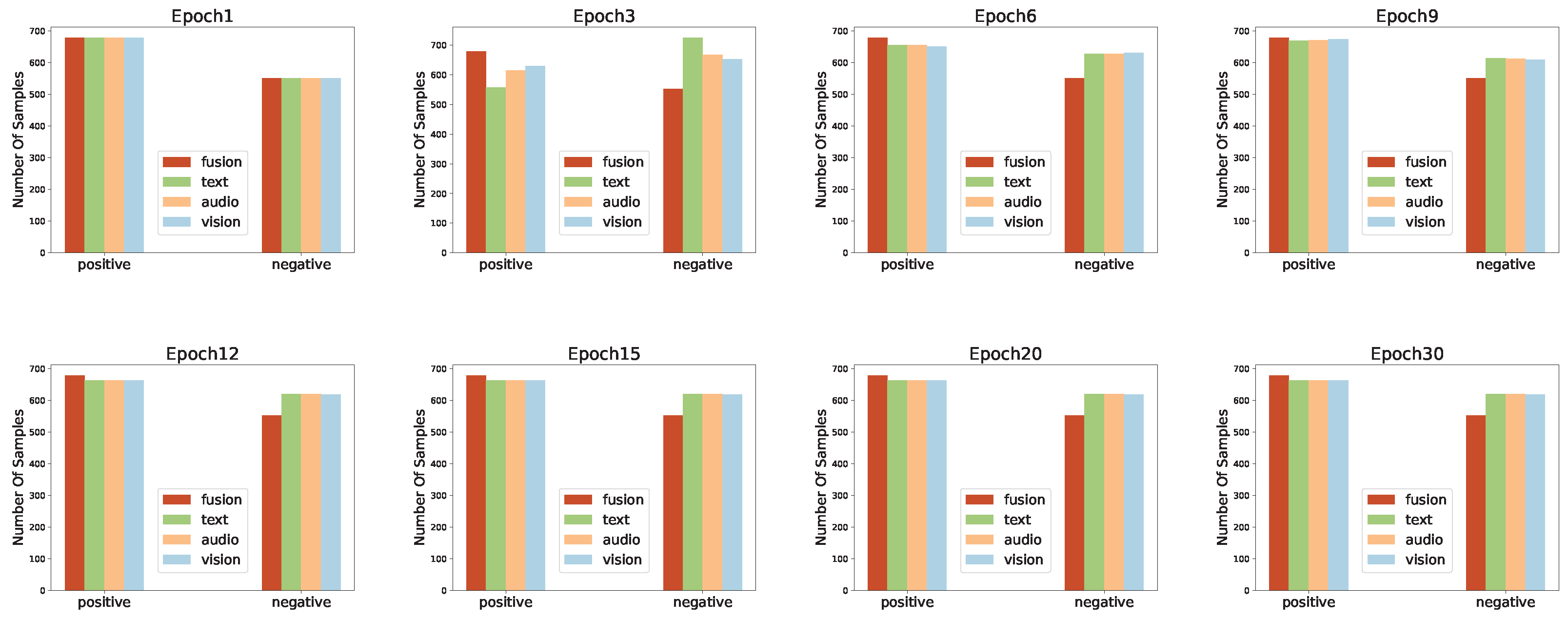
| Dataset | Train | Valid | Test | Total |
|---|---|---|---|---|
| CMU-MOSI | 1284 | 229 | 686 | 2199 |
| CMU-MOSEI | 16,326 | 1871 | 4659 | 22,856 |
| Hyperparameter | CMU-MOSI | CMU-MOSEI |
|---|---|---|
| Early Stop | 8 | 8 |
| Batch Size | 32 | 32 |
| LR for BERT | 5 | 5 |
| LR for Others | 1 | 1 |
| Encoder Layer | 4 | 4 |
| Num Heads | 8 | 4 |
| Output Dropout | 0.3 | 0.1 |
| Attn Dropout | 0.3 | 0.1 |
| Model | CMU-MOSI | CMU-MOSEI | Data State | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc-2 | F1-Score | MAE | Corr | Acc-2 | F1-Score | MAE | Corr | ||
| TFN † | -/80.8 | -/80.7 | 0.970 | 0.698 | -/82.5 | -/82.1 | 0.593 | 0.700 | Unaligned |
| LMF † | -/82.5 | -/82.4 | 0.917 | 0.695 | -/82.0 | -/82.1 | 0.623 | 0.677 | Unaligned |
| RAVEN ‡ | -/78.0 | -/76.6 | 0.915 | 0.691 | -/79.1 | -/79.5 | 0.614 | 0.662 | Aligned |
| MulT † | 81.5/84.1 | 80.6/83.9 | 0.861 | 0.711 | -/82.5 | -/82.3 | 0.580 | 0.703 | Aligned |
| MISA † | 80.79/82.10 | 80.77/82.03 | 0.804 | 0.764 | 82.59/84.23 | 82.67/83.97 | 0.568 | 0.724 | Aligned |
| MAG-BERT ‡ | 82.5/84.0 | 82.4/84.0 | 0.778 | 0.766 | 81.3/84.8 | 81.7/84.7 | 0.567 | 0.742 | Aligned |
| Self-MM | 84.00/85.98 | 84.42/85.95 | 0.713 | 0.798 | 82.81/85.17 | 82.53/85.30 | 0.530 | 0.765 | Unaligned |
| MMIM | 84.14/86.06 | 84.00/85.98 | 0.700 | 0.800 | 82.24/85.97 | 82.66/85.94 | 0.526 | 0.772 | Unaligned |
| SUGRM | 84.4/86.3 | 84.3/86.3 | 0.703 | 0.800 | 83.7/84.4 | 83.6/84.0 | 0.544 | 0.748 | Unaligned |
| Self-MM * | 82.60/84.67 | 82.52/84.66 | 0.726 | 0.786 | 82.51/84.99 | 82.57/85.02 | 0.535 | 0.769 | Unaligned |
| MMIM * | 82.94/84.91 | 82.81/84.84 | 0.707 | 0.785 | 82.89/85.34 | 82.75/85.48 | 0.552 | 0.768 | Unaligned |
| SUGRM * | 82.36/83.99 | 82.35/84.04 | 0.727 | 0.776 | 82.85/83.81 | 82.94/83.83 | 0.542 | 0.742 | Unaligned |
| Ours * | 83.14/84.91 | 83.17/84.96 | 0.711 | 0.788 | 83.12/85.91 | 83.19/85.93 | 0.531 | 0.775 | Unaligned |
| CMU-MOSI | CMU-MOSEI | |||||||
|---|---|---|---|---|---|---|---|---|
| Task | Acc-2 | F1-Score | MAE | Corr | Acc-2 | F1-Score | MAE | Corr |
| M | 81.78/83.73 | 81.80/83.91 | 0.729 | 0.775 | 82.19/84.15 | 82.70/84.42 | 0.548 | 0.757 |
| M, T | 82.13/83.93 | 82.07/83.99 | 0.737 | 0.783 | 82.40/84.70 | 82.42/84.15 | 0.538 | 0.758 |
| M, A | 82.20/84.06 | 82.19/84.13 | 0.748 | 0.772 | 82.70/84.77 | 82.90/84.60 | 0.543 | 0.762 |
| M, V | 81.47/84.23 | 82.51/84.06 | 0.742 | 0.769 | 82.23/83.52 | 82.36/83.73 | 0.546 | 0.751 |
| M, A, V | 82.99/84.77 | 82.55/84.56 | 0.722 | 0.782 | 82.23/84.23 | 82.68/85.29 | 0.544 | 0.761 |
| M, A, T | 83.02/84.92 | 83.21/84.95 | 0.728 | 0.783 | 83.20/85.43 | 83.07/85.51 | 0.543 | 0.762 |
| M, V, T | 82.92/85.08 | 82.72/84.86 | 0.718 | 0.775 | 82.23/85.23 | 82.68/86.10 | 0.529 | 0.757 |
| M, T, A, V | 83.14/84.91 | 83.17/84.96 | 0.711 | 0.788 | 83.12/85.91 | 83.19/85.93 | 0.531 | 0.775 |
| CMU-MOSI | CMU-MOSEI | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Module | Acc-2 | F1-Score | MAE | Corr | Acc-2 | F1-Score | MAE | Corr |
| SUGRM | MRM | 82.36/83.99 | 82.35/84.04 | 0.727 | 0.776 | 82.85/83.81 | 82.94/83.83 | 0.542 | 0.742 |
| UFEM | 82.47/84.23 | 82.45/84.27 | 0.723 | 0.779 | 83.02/84.23 | 83.11/84.43 | 0.538 | 0.756 | |
| Ours | MRM | 82.84/84.52 | 82.93/84.47 | 0.718 | 0.780 | 82.94/85.63 | 82.96/85.71 | 0.536 | 0.762 |
| UFEM | 83.14/84.91 | 83.17/84.96 | 0.711 | 0.788 | 83.12/85.91 | 83.19/85.93 | 0.531 | 0.775 |
| CMU-MOSI | CMU-MOSEI | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Acc-2 | F1-Score | MAE | Corr | Acc-2 | F1-Score | MAE | Corr |
| w/o UCL | 82.55/84.26 | 82.60/84.25 | 0.728 | 0.769 | 82.62/85.45 | 82.60/85.38 | 0.558 | 0.759 |
| w/o SCL | 82.78/84.23 | 82.86/84.57 | 0.722 | 0.773 | 82.87/85.68 | 82.86/85.68 | 0.546 | 0.762 |
| Ours | 83.14/84.91 | 83.17/84.96 | 0.711 | 0.788 | 83.12/85.91 | 83.19/85.93 | 0.531 | 0.775 |
| CMU-MOSI | CMU-MOSEI | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Acc-2 | F1-Score | MAE | Corr | Acc-2 | F1-Score | MAE | Corr |
| 82.49/84.30 | 82.58/84.33 | 0.727 | 0.768 | 82.50/85.47 | 82.66/85.58 | 0.552 | 0.760 | |
| 83.14/84.91 | 83.17/84.96 | 0.711 | 0.788 | 83.12/85.91 | 83.19/85.93 | 0.531 | 0.775 |
| Example | Annotation | Self-MM | SUGRM | Ours |
|---|---|---|---|---|
Save your money wait till it comes out on rental. | −2.0 | −2.0 | −1.9 | −2.0 |
And I liked the first movie. I thought the first movie was really good. | 1.5 | 1.6 | 1.5 | 1.5 |
And I guess normally Shrek is for adults. | 0.0 | 0.1 | 0.1 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Fu, J.; Xue, H.; Xu, Z. Self-HCL: Self-Supervised Multitask Learning with Hybrid Contrastive Learning Strategy for Multimodal Sentiment Analysis. Electronics 2024, 13, 2835. https://doi.org/10.3390/electronics13142835
Fu Y, Fu J, Xue H, Xu Z. Self-HCL: Self-Supervised Multitask Learning with Hybrid Contrastive Learning Strategy for Multimodal Sentiment Analysis. Electronics. 2024; 13(14):2835. https://doi.org/10.3390/electronics13142835
Chicago/Turabian StyleFu, Youjia, Junsong Fu, Huixia Xue, and Zihao Xu. 2024. "Self-HCL: Self-Supervised Multitask Learning with Hybrid Contrastive Learning Strategy for Multimodal Sentiment Analysis" Electronics 13, no. 14: 2835. https://doi.org/10.3390/electronics13142835
APA StyleFu, Y., Fu, J., Xue, H., & Xu, Z. (2024). Self-HCL: Self-Supervised Multitask Learning with Hybrid Contrastive Learning Strategy for Multimodal Sentiment Analysis. Electronics, 13(14), 2835. https://doi.org/10.3390/electronics13142835






