Hardware Acceleration and Approximation of CNN Computations: Case Study on an Integer Version of LeNet

Abstract

AI systems have an increasing sprawling impact in many application areas. Embedded systems built on AI have strong conflictual implementation constraints, including high computation speed, low power consumption, high energy efficiency, strong robustness and low cost. Neural Networks (NNs) used by these systems are intrinsically partially tolerant to computation disturbances. As a consequence, they are an interesting target for approximate computing seeking reduced resources, lower power consumption and faster computation. Also, the large number of computations required by a single inference makes hardware acceleration almost unavoidable to globally meet the design constraints. The reported study, based on an integer version of LeNet, shows the possible gains when coupling approximation and hardware acceleration. The main conclusions can be leveraged when considering other types of NNs. The first one is that several approximation types that look very similar can exhibit very different trade-offs between accuracy loss and hardware optimizations, so the selected approximation has to be carefully chosen. Also, a strong approximation leading to the best hardware can also lead to the best accuracy. This is the case here when selecting the ApxFA5 adder approximation defined in the literature. Finally, combining hardware acceleration and approximate operators in a coherent manner also increases the global gains.

1. Introduction

Artificial Intelligence (AI) applications exist today spanning through all areas, including natural language processing, computer vision, speech recognition, robotics, autonomous vehicles, aeronautics, spacecraft, biology, healthcare, malware classification and security, but also supply chain management, manufacturing, education, recruitment, marketing, financial services, agriculture and many others. Applications are so varied that all papers in the literature focus on a given application subset. However, as a common point, Machine Learning (ML) and Deep Learning (DL) systems manipulate large amounts of data and require high computational capability, often centralized in cloud-based services. Nevertheless, the rapidly increasing number of devices that are producing and collecting data in Internet of Things (IoT) applications raises the need for applying AI computation on the edge for performance and energy efficiency. In this context of Edge AI, many resources have to be developed, both hardware and software [1].

We focus in this paper on applications such as computer vision and pattern recognition, widely used in many embedded systems. However, the general approach and the global conclusions could be applied in many other cases. We seek systems with strong implementation constraints in terms of hardware resources, power, energy, cost and also dependability. Such systems increasingly run ML or DL models for edge AI even with strong requirements for reliability in harsh environments, e.g., avionics and space [2,3], or in safety-critical applications, e.g., autonomous vehicles. We will not directly address the dependability aspects in this paper. However, optimizations leading to more efficient hardware and software implementations can also help in reaching a better dependability level for the final system. The presented case study is therefore chosen to be well suited to this kind of application, especially when implemented using field programmable gate arrays (FPGAs) with hard or soft microprocessor (CPU) cores.

We will also focus in this paper on inference only. Training the model is assumed to have been performed before it is used in the embedded system. However, even inference requires heavy computations. Real-time constraints that are necessary in some applications still increase the difficulty of running the AI models on resource-constrained equipment. In order to reach the required computation speed as well as meet the resource and power constraints, hardware acceleration is most often unavoidable. In consequence, many works have addressed this aspect for various AI models, using different number representations and different architectures for the underlying neural networks (NNs) [1,3,4,5]. For the type of systems we target, floating point or even fixed point computations are not optimal in terms of resources, computation load and power or energy consumption. We will therefore focus our study on models using integer computations and accelerators built around integer operators.

Another approach to achieve higher computation speed is to increase the hardware clock frequency, at least when it is feasible within the power budget. One possibility is to reduce the critical path in the operators thanks to the approximate (AxC) or inexact computation paradigm [6,7]. In fact, AxC is often considered as able to simultaneously improve computation speed, resource usage, power consumption and energy efficiency, at the expense of some loss in accuracy of outputs. NNs, being brain-inspired architectures, have some inherent fault tolerance capabilities, partly because they contain more neurons than are actually required for a given task. In spite of some similarities with brain characteristics, the analogy of biological neural networks cannot lead to the assumption of a very high fault tolerance level by relying only on the intrinsic masking ability [8,9,10]; the actual level of robustness clearly depends on the hardware design decisions. As already mentioned, we will not discuss further this attribute in this paper, but regardless, the inherent capability of these networks to tolerate some discrepancies during computations makes them particularly attractive in the context of approximate computing. The use of approximations can even result in more dependable systems, as discussed in [11]. This approach can be applied at all levels, from the ML definition and implementation in the global system down to the design of circuit subblocks. It can also target the weight format and values, or the computations during inference. In our case, we will consider approximated operations at circuit level and focus more specifically in this study on approximated additions.

In the sequel, we will show the benefits of combining hardware acceleration and approximate computing on an example of a convolutional neural network (CNN) using integer computations. We will also discuss the need for a cautious selection of the approximations in order to achieve the best gains while preserving good accuracy of the results.

The remainder of this paper is structured as follows: Section 2 gives more details on related works, emphasizing previous works leveraged during our study. Section 3 details the analysis of the LeNet software, describes the decisions made for the accelerated implementation and summarizes the results. Section 4 reports on the accuracy achievable with the selected set of adder approximations, for both non-uniform and uniform implementations. Finally, Section 5 draws conclusions based on a global discussion and provides some perspectives.

2. Related Works and Case Study Definition

We will focus here on previous works directly used during our study. This covers the three aspects mentioned in the introduction: (1) the CNN chosen as the target application, (2) the hardware/software embedded system used as the implementation target with hardware acceleration of the AI computations and (3) the type of approximations used during inferences.

2.1. Target Network and Data Set

Since we focus for this case study on applications such as computer vision and pattern recognition, a natural choice was to consider LeNet as a reference model. This network was initially proposed in [12] and named after Yann LeCun, who was at that time a researcher at AT&T Bell Labs. It is one of the first published CNNs, having captured wide attention for its performance on computer vision tasks and especially handwritten character recognition, achieving an error rate of less than 1% per digit. It was eventually adapted to recognize digits for processing deposits in ATMs and was still in use recently [13].

As illustrated in Figure 1, LeNet is composed of six hidden layers and a final output layer. Layers C1, C3 and C5 are convolutions. The pooling layers S2 and S4 are sums of four inputs, multiplied by a trainable weight coefficient, with a trainable offset and results output through the sigmoid function. The F6 layer is a fully connected layer, calculating the dot product between the input vector and the weight vector, plus an offset, and the result is output through the sigmoid function. Lastly, the output layer, finalizing the handwritten character recognition, is also a densely connected layer but with Gaussian connections; the results are directly output without an activation function.

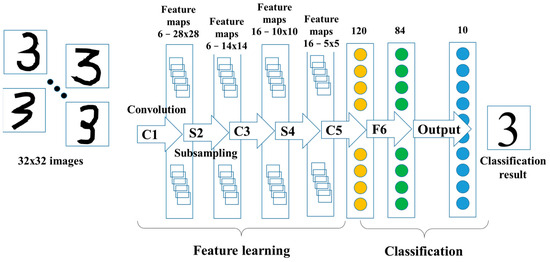
Figure 1. Architecture of LeNet-5, a CNN used for digit recognition.

For our purpose, we looked for a version of LeNet avoiding the costly floating point computations performed in TensorFlow or GPU implementations. We also wanted to avoid fixed point computations. We therefore relied on a version using only integer computations and that is publicly available at [14].

In this version, the seven layers of the network are adapted with respect to the original implementation. In particular, tanh and sigmoid activations are rarely used nowadays due to saturation problems and complex computations. They are most often replaced by ReLU (Rectified Linear Unit). Also, the post-training quantization from [15] is used to achieve a weight offset that is null after training. The computations in the layers, without mentioning the differences in dataset sizes, can then be summarized as follows.

C1—convolutional with output through ReLU (negative results are forced to 0, all results are on 8 bits with values above 255 forced to 255);

S2—downsampling with MaxPool (activation already applied on the output of C1);

C3—as C1;

S4—as S2, followed by reshaping;

C5—full connection with ReLU;

F6—full connection with ReLU;

Output—ReLU followed by Argmax (Gaussian connections are not useful for inference only).

In practice, C5, F6 and Output are three similar layers that use the “dense” function we will refer to in the following. C1 and C3 use “conv2d”.

In this study, we only consider the inference computations performed by a pre-trained network. The set of weights is stored in a file for the software version of the network, or in a memory when implemented as an embedded system. The network was trained using the MNIST database (Modified National Institute of Standards and Technology database) containing binary images of handwritten digits. This collection has a training set of 60,000 examples and a test set of 10,000 examples. It was used for all our experiments.

2.2. Hardware Setup: Target Embedded System

The goal of this study was to evaluate the global effect of acceleration and approximation in the context of edge AI implemented in an embedded system. This system should also be able to run other functions, so it cannot be reduced to a dedicated AI accelerator. We therefore targeted a general-purpose processor associated with a hardware accelerator well suited for the main operations performed in AI systems, i.e., matrix multiplication and accumulation.

Such an accelerator was recently proposed, designed with the same global objectives and targeting critical applications such as in aerospace [16,17,18]. The accelerator can be associated with one general-purpose CPU from Frontgrade Gaisler, i.e., Leon3 or NOEL-V. It is available at [19] with all the necessary support for software development exploiting the custom instructions that control the accelerator functions. We decided for our study to select this accelerator, called Sparrow, and the Leon3 CPU core. Compilations were made with the adapted version of GCC, using assembly instructions for the accelerated parts of the LeNet software.

Sparrow is activated by custom instructions dedicated to parallel computations based on the SIMD (Single Instruction Multiple Data) paradigm. The most important features of the SIMD architecture of Sparrow, leveraged during our study, are summarized in Figure 2. Two 32-bit operand registers are used to store four pairs of 8-bit data. A first computation stage allows computing a given operation on the four pairs in parallel. The available operations include integer multiplication. The four results are stored in 16-bit registers. A second computation stage allows reduction, including accumulation with a final result on 32 bits. More details are given in [16].

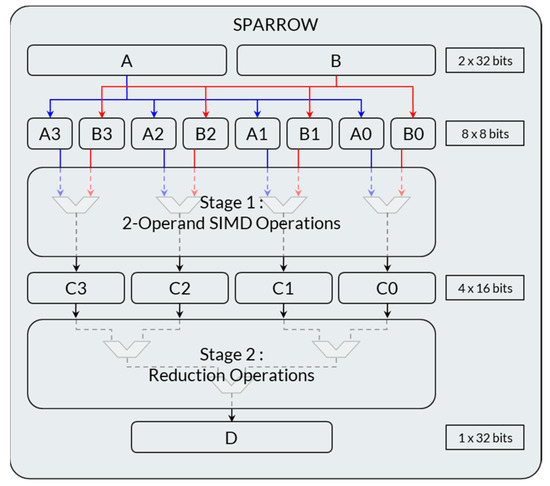
Figure 2. Simplified architecture of Sparrow.

2.3. Selected Approximation Alternatives

As illustrated in [20], approximations can be performed at algorithm level or at circuit level, combined with error compensation and accuracy recovery techniques. In our case, we use the weights obtained during the training without further modification or retraining and we apply approximations at circuit level during the computations by modifying arithmetic operators. Since no retraining is performed, the approximation method must be chosen to directly satisfy an acceptable accuracy level. For the reported case study, we focused on adders that perform one of the two main operations in the selected network and are the most straightforward to efficiently modify at the hardware level. Previous works also considered, for example, approximate multipliers, as in [21] where such operators were implemented in ASICs for Depthwise Separable CNNs, but this was left in our case for future work, especially because multipliers optimized at the layout level in FPGA fabrics are often more efficient than multiplier architectures eventually implemented using general logic primitives and inefficient routing.

Various approaches to approximate additions have been proposed for more or less complex adder architectures (e.g., [22]). The main constraints in our case were to use flexible architectures that allow easy changes to the level of approximation and to ensure compatibility with efficient implementations in soft cores, which can be synthesized either on ASIC standard cell libraries or onto FPGAs. In the latter case, efficient structures generally exist in the fabric to implement fast carry propagation. In consequence, simple adders are in general more efficient than more complex adder architectures with irregular and/or complex connections that eventually require using the general-purpose interconnection resources when routing critical paths. In consequence, we focused on adders implemented with architectures very close to the simple Ripple Carry architecture, in order to reach a good trade-off between hardware complexity/flexibility/power/energy efficiency and computation speed.

The main selected hardware architecture is represented in Figure 3a and corresponds basically to a Ripple Carry Adder with n serially connected 1-bit adders (“Full Adders” or FAs). In the exact version, all FAs implement the reference addition truth tables of the 1-bit sum and the output carry as recalled in column FA of Table 1. In an approximate version, the k Least Significant Bits (LSBs) are computed with an approximate FA (ApxFA) defined by slightly modified truth tables. The n-bit operator is therefore made of a k-bit fully approximate adder, connected in series with a (n-k)-bit exact adder. For our work, we considered as ApxFA the five alternatives presented in [23] and recalled for completeness in Table 1. This table also compares the published evaluations about area and power characteristics for the six FAs.

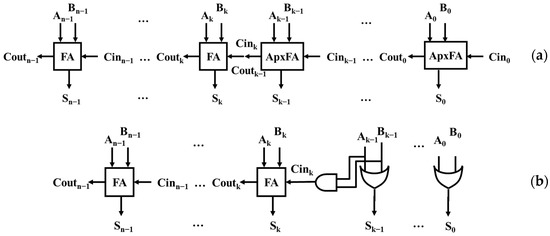
Figure 3. Architectures of studied approximate adders: (a) k-bit approximate Ripple Carry Adder; (b) k-bit Lower-part OR Adder (LOA).

Table 1. Full adder truth tables and implementation characteristic examples for accurate and studied approximated 1-bit additions (reproduced from [23]). Red bold characters indicate the approximated values, i.e., those modified with respect to exact computations performed with FA.

Inputs	FA	ApxFA1	ApxFA2	ApxFA3	ApxFA4	ApxFA5
A B Cin	Sum Cout	Sum Cout	Sum Cout	Sum Cout	Sum Cout	Sum Cout
0 0 0	0   0	0   0	1   0	1   0	0   0	0   0
0 0 1	1   0	1   0	1   0	1   0	1   0	0   0
0 1 0	1   0	0   1	1   0	0   1	0   0	1   0
0 1 1	0   1	0   1	0   1	0   1	1   0	1   0
1 0 0	1   0	0   0	1   0	1   0	0   1	0   1
1 0 1	0   1	0   1	0   1	0   1	0   1	0   1
1 1 0	0   1	0   1	0   1	0   1	0   1	1   1
1 1 1	1   1	1   1	0   1	0   1	1   1	1   1
Area (GE)	4.41	4.23	1.94	1.59	1.76	0
Power (nW)	1130	771	294	198	416	0

We also included in our study a well-known approximate adder called LOA for Lower-part OR Adder, introduced in [24] and represented in Figure 3b. This bio-inspired structure, as presented by the authors, may be thought to be relevant in the context of neural networks and was applied in the implementation of a face-recognition three-layer network in [24]. In this version of approximate adder, a small modification of the carry propagation chain consists in adding an extra AND gate to generate the input carry of the (n-k)-bit exact adder subblock. Since there is no carry propagation within the LSBs, this architecture does not modify the use of the optimized interconnection resources in an FPGA.

Another design decision is between the choice of uniform or non-uniform approximation. Uniform approximation employs only a single type of approximate unit. For our case, it means only one type of addition approximation is used, and all approximations are made with the same number of approximated bits. The main advantage is to simplify the hardware design and the use of the implemented operators. With non-uniform approximation, several types of approximations are used depending on the on-going operation, and/or the number of approximated bits can change from one operation to the other. This may allow tuning the approximation to each operation’s intrinsic tolerance. However, this implies the use of more resources in an operator to configure it for the selected approximated function and select the right number of bits at each operation. A consequence is that this hinders most of the advantages of the hardware-implemented approximation since the configuration resources (e.g., multiplexers) imply more area, more power and energy consumption and in most cases an increased critical path, resulting in increased computation time. In the following, we will discuss the two possibilities for our case study.

3. Accelerated LeNet Implementation

3.1. Analysis of LeNet Source Code

Both acceleration and approximation require identifying in the code the operations that can be targeted for optimizations. Operations that must be sequential cannot be targeted for SIMD execution. Some operations must also have exact results to guarantee correct network behavior during execution.

The main operations in our targeted software are integer additions and multiplications. Among all the additions performed when running an inference, some correspond to loop index computations. These additions cannot be parallelized and would completely disturb the control flow if approximated. Our optimizations must therefore focus on additions and multiplications performed on the data manipulated by the AI model (object data and weights) but leave the control operations unchanged.

Integer data multiplications can be found in matrix multiplications performed during the convolutions. Integer data additions can be found in both matrix multiplications and offset computations.

We eventually found four different additions that are potentially interesting for our purposes. They correspond to inner-loop data computations and can be individually selected for accelerated or approximated computing. Each of them is used in several layers in the network, as summarized in Table 2. The Additions numbered 1 and 3 are in the inner loops of matrix multiplications and have a much larger number of occurrences than the Additions numbered 2 and 4, which are in offset computations. In the following, these four additions will be written with a capital letter (i.e., Additions) to distinguish them to all other additions performed during the inferences.

Table 2. Data Additions in LeNet data flow: position and number of occurrences.

Layer	Addition to Approximate	Number of Occurrences
C1—conv2d function	Addition 1	117,600
	Addition 2	4704
C3—conv2d function	Addition 1	240,000
	Addition 2	1600
C5—dense function	Addition 3 Addition 4	48,000 120
F6—dense function	Addition 3 Addition 4	10,080 84
Output—dense function	Addition 3 Addition 4	840 10

In the target architecture, the most frequent operations are the most interesting to assign to the SIMD accelerator. The main focus for speed improvement is therefore on Additions 1 and 3 in the conv2d and dense functions. Data manipulations during MaxPool or reshaping are not pertinent for optimizations.

In our target embedded system, we therefore decided to assign Additions 1 and 3 and the associated multiplications to the Sparrow accelerator. All other operations are performed using the Arithmetic and Logic Unit (ALU) of the general-purpose processor.

3.2. Accelerated Version of the Software: Modifications and Results

The architecture of Sparrow allows performing four operations in parallel in its first pipeline stage (including multiplications and subtractions) and additions in the second pipeline stage. The number of loop iterations must therefore be a multiple of four, or the loop must be modified with some padding or loop transformations.

In the dense function, the inner loop directly has a number of iterations that is a multiple of four. The global operation performed can be decomposed into a subtraction, a multiplication and an addition. The 8-bit data used for subtractions and multiplications are concatenated into 32-bit words and the operations are then performed using the custom Sparrow instructions, inserted as assembly instructions in the LeNet C code.

One problem here is the list of operations available in the original version of Sparrow. Multiplications can be performed on several data types, whether signed or unsigned (integer or natural), but for LeNet, multiplications must be made between a signed and an unsigned integer. We therefore slightly modified the Sparrow description, available open-source, to slightly change the behavior of one Sparrow operation. With this modification, the dense function was accelerated using two SIMD instructions in the inner loop. Let us mention that in the future this modification may have to be revisited in order to maintain upward compatibility with other applications using Sparrow.

In the case of conv2d calls, the transformation to SIMD instructions is more tricky. In the first call, iterations can be limited to parameters equal to one or five and in the second call the inner loop has six iterations. It was therefore necessary to deeply modify the loop imbrications. Finally, five operations in the loops were replaced by two SIMD instructions.

During this transformation, another important point had to be taken into account. The implementation of our system is on a SoC FPGA, and 8-bit data are stored in internal memory blocks called BRAMs, with 32-bit words. In order to read four 8-bit pieces of data in one memory access, all pieces must be in the same word. When five pieces of data are required as in an inner loop of the first call, they cannot all be in the same word, and furthermore, the group of useful pieces of data for one computation is not always split in the same way between two memory words. Making the computation regular requires aligning the data tables in a specific way, with lines of four pieces of data and adapted to the loop transformations. Some paddings with zeros were also necessary. These zeros allow both alignment and masking of extra computations performed by the SIMD instructions but not present in the reference application program.

The results obtained after all these transformations are summarized in Table 3. Both versions of the software (with and without use of the SIMD instructions) were compiled with the –O3 GCC optimization with Leon3 as a target. About 1,250,000 basic operations were replaced by 420,000 SIMD operations. As shown in Table 3, this resulted in a 3.8× acceleration factor with a small size increase in the two main memory sections. The Text section contains the instructions. The Data section contains data that are initialized at the beginning of the program, such as weights. The system validation becomes also much more tractable, with a 4.8× gain in simulation time using GHDL on a standard PC: 25 ms for simulating a single LeNet inference using SIMD instructions instead of 95 ms for simulating an inference with only standard operations on the general-purpose processor.

Table 3. Comparison of LeNet implementations: characteristics of the accelerated version compared to the original version.

Characteristic	Difference from the Original Software
Memory size—Text section	+2.7%
Memory size—Data section	+5.4%
Execution time	−73.7%
Simulation time	−79.2%

4. Selection of Approximations and Impacts

4.1. Impact of the Approximations on the Network Accuracy: Results for Individual Additions

As detailed in Section 3.1, control-related additions must be differentiated from data-related additions. Control-related additions cannot be approximated without disastrous control flow modifications. We therefore focus here on the additions previously numbered 1 to 4. The approximated additions in the convolutional layers are thus only the additions performing accumulations in the second stage of Sparrow, shown in Figure 2; multiplications are left unchanged and computed in the first stage of Sparrow.

The impact of the approximations was first analyzed on the software implementation of the network. For this purpose, a configurable addition function was written and used as replacement of the standard C addition in the four selected places. This function allowed us to quantify the accuracy loss with respect to each type of approximation and to the number of approximated bits for each individual Addition. The results are summarized in Figure 4 and Figure 5. They were obtained after inference with the whole set of 10,000 test images in the MNIST database.

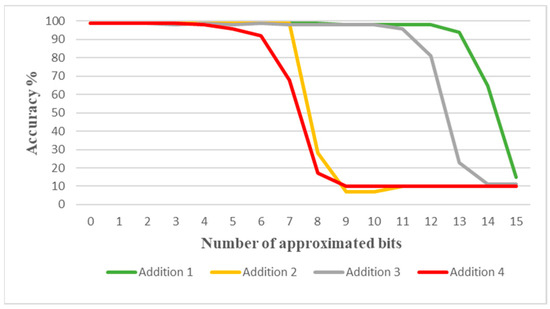
Figure 4. Effect of LOA approximation on individual LeNet Additions (10,000 images).

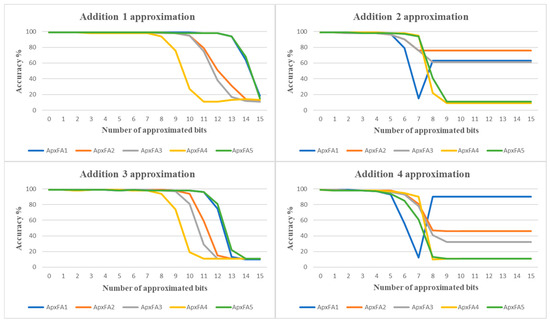
Figure 5. Effect of ApxFA approximations on individual LeNet Additions (10,000 images).

Starting with the LOA approximation, Figure 4 shows the evolution of the network accuracy as a function of the number of approximated bits in each individual Addition among the four selected targets. Without approximation, the accuracy is 99%. Addition 4 and Addition 2 are the two most sensitive operations with respect to the number of approximated bits, with a quick decrease in the accuracy around 8 approximated bits out of 16. Addition 1 is very robust, with little impact on accuracy until 13 approximated bits.

With LOA, it clearly appears that computations on offsets are more critical in terms of approximation than computations in matrix multiplications. This trend is confirmed for the five other approximation types, as shown in Figure 5. Also, in the case of offsets, a saturation phenomenon appears, sometimes after some trend inversion in terms of accuracy loss as exhibited with ApxFA1. Addition 1 remains the less sensitive operation with respect to the recognition accuracy.

Table 4 summarizes the type of approximation inducing the fastest significant decrease in accuracy for each Addition. A threshold of 97% accuracy was arbitrarily selected. As an example, when increasing the number of approximated bits for Addition 1, ApxFA4 is the first type of approximation leading to an accuracy under 97% (in that case, 94%) for 8 approximated bits. With the same number of approximated bits, all the other types of approximation maintain an accuracy of at least 97%.

Table 4. Worst approximation type and minimum number of approximated bits leading to an accuracy under 97% for each individual LeNet Addition (10,000 images).

Approximated Operation	Number of Bits	Type of Approximation	Accuracy
Addition 1	8	ApxFA4	94%
Addition 2	5	ApxFA2 or ApxFA3	96%
Addition 3	8	ApxFA4	94%
Addition 4	5	ApxFA1	93%

Table 5 lists in a similar way the approximation leading to the latest decrease in accuracy under 97%. As an example, when increasing the number of approximated bits for Addition 2, LOA is the last type of approximation leading to an accuracy over 97% (in that case, 99%) for 7 approximated bits. With the same number of approximated bits, all the other types of approximation have an accuracy under 97%, and with 8 approximated bits the accuracy with LOA goes under 97% (in that case, a sharp drop down to 28%).

Table 5. Best approximation type and maximum number of approximated bits leading to an accuracy at least equal to 97% for each individual LeNet Addition (10,000 images).

Approximated Operation	Number of Bits	Type of Approximation	Accuracy
Addition 1	12	ApxFA1 or ApxFA5 or LOA	98%
Addition 2	7	LOA	99%
Addition 3	10	ApxFA1 or ApxFA5 or LOA	98%
Addition 4	5	ApxFA2	98%

As shown in these tables, the worst and best approximation types often differ from one Addition target to another; however, similar results are observed for the two Additions involved in matrix multiplications. From these results, approximations ApxFA4 and then ApxFA3 are not suited to our application target. LOA, and then ApxFA1 or ApxFA5, are the most efficient for one single approximated Addition.

Even when the same approximation type can be chosen for several Additions, the best number of bits is not the same for all. This could lead to favoring non-uniform approximation. However, as mentioned in Section 2.3, modifying the type of approximation or just the number of approximated bits for the different computation phases during an inference would imply implementing a configurable operator. Such a configuration capability would lead to a more complex operator with higher area, higher power consumption and increased critical path. All this would be opposite to the main objectives of using approximate computing. In order to reach the best profit from approximation, another approach is to determine the best solution for the global inference computation. The best trade-off has to be reached choosing the same approximation type and the same number of approximated bits for all the approximated additions.

4.2. Impact of the Approximations on the Network Accuracy: Results for Global Approximations

Figure 6 shows the impact of LOA approximation applied to all four selected additions with the same number of approximated bits. With only 6 bits, the accuracy falls down to 93% (96% with 5 bits). This is basically the result obtained with the most sensitive Addition alone (Addition 4).

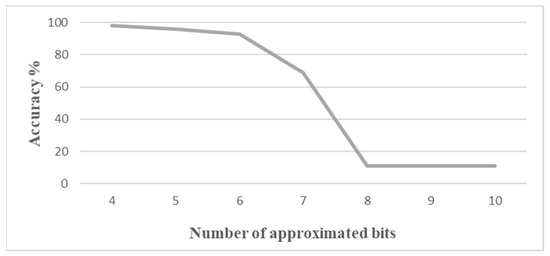
Figure 6. Accuracy vs. number of approximated bits for all four Additions computed with the same approximated LOA adder.

Since the Additions computing offsets have a higher sensitivity to approximation, it is interesting to analyze the accuracy decrease when only Addition 1 and Addition 3 are approximated. The result with LOA is shown in Figure 7. In that case, with 10 approximated bits, the accuracy is still at 98%, and it goes down to 96% with 11 bits.

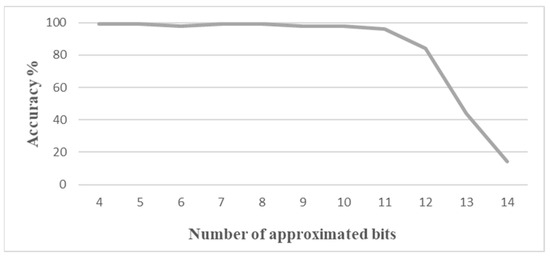
Figure 7. Accuracy vs. number of approximated bits for Addition 1 and Addition 3 computed with the same approximated LOA adder, with Addition 2 and Addition 4 being computed without approximation.

The same analyses can be made for the five other approximation types. Results are summarized in Figure 8a for the four additions being approximated and in Figure 8b when only Addition 1 and Addition 3 are approximated.

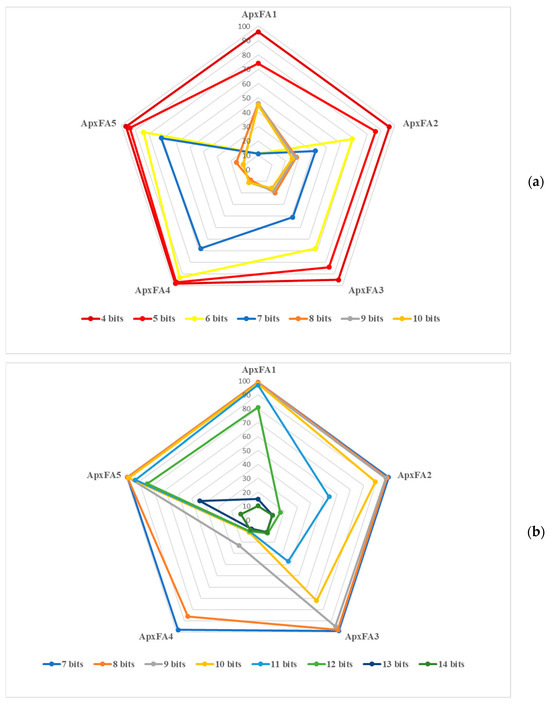
Figure 8. Accuracy vs. approximation type and number of approximated bits (a) for all four Additions with the same approximated adder and (b) for Addition 1 and Addition 3 with the same approximated adder, and Addition 2 and Addition 4 with exact computation.

As in the case of LOA, targeting approximation for the four Additions results in a limited approximation feasibility with 97% accuracy reached from only 5 bits with ApxFA4 and fewer bits for the other approximation types.

Restricting approximations to Addition 1 and Addition 3 clearly leads to better opportunities since several approximation types allow 98% accuracy with 10 approximated bits (ApxFA1, ApxFA5 and LOA). With 11 approximated bits, ApxFA1, ApxFA5 and LOA allow, respectively, 97%, 93% and 96% accuracy.

5. Discussion

The results presented in Section 4 support the choice of restricting approximations to a subset of the Additions. Approximating Addition 2 and Addition 4 is too limiting in the case of uniform approximation, and the use of non-uniform approximation would completely hinder the potential advantages of approximate computing when taking into account the required hardware modifications.

These results also have to be put in perspective with the study on acceleration. The conclusion was to accelerate multiplications and the same subset of additions. The two types of optimizations go therefore in the same direction, towards a separation between SIMD approximated additions and standard exact additions. The first ones can be assigned in our system to the Sparrow accelerator with an approximate adder and the others can be executed by the standard ALU of the general-purpose processor, with all operations related to control flow.

Another interesting point is about the type of approximations that are the most efficient for our case study. Looking at the truth tables for ApxFA5, one could notice that Sum = B and Cout = A. This means that for the k approximated bits, the output bit is equal to one operand bit and there is no carry propagation. The global n-bit approximate adder is therefore just an (n-k)-bit exact adder. The single carry propagation is the connection of one operand bit to the input carry of the exact adder. This also explains the null cost indicated in Table 1 for a 1-bit ApxFA5 cell. In the case of LOA, the approximate adder is made of k OR gates and an AND gate, so the hardware cost is higher but there is again no carry propagation. The critical path can, however, be larger than with the ApxFA5 version since the AND gate is added before the input carry of the exact adder. The penalty depends on the exact implementation of the FA cell. In the case of ApxFA1, a real carry propagation occurs in the approximate part, so the computation will be noticeably slower. Also, ApxFA1 is the most costly alternative in terms of area and power among those considered in this study, as shown in Table 1. It is therefore more efficient from a hardware point of view to select ApxFA5 or LOA, even with a slightly smaller value of k if required to achieve the specified accuracy.

Following this analysis, uniform approximation is therefore performed in our case study for Addition 1 and Addition 3 in the SIMD version using ApxFA5, in the Sparrow accelerator equipped with a simplified non-configurable adder with approximation on 10 bits to maintain an accuracy over 97% (98% in this case). In practice, this means that the 16-bit adders are replaced by 6-bit adders connected to the MSBs of the operands and another bit used as input carry; the other outputs are directly connected to operand inputs. The modifications in Sparrow are therefore quite straightforward to make in this case. The gain in area for each 16-bit adder is 10/16, i.e., 62.5%, and the gains obtained for each addition in terms of power and computation speed are similar.

If an accuracy of 96% is considered sufficient for the application, LOA could be selected with 11 approximated bits. However, the 11 OR gates and the AND gate would be more costly than one FA both in terms of power and area. Moreover, the propagation time through the AND gate would roughly lead to the same critical path as with an additional carry propagation in one FA, and would even probably be larger if implemented in an FPGA, with a Configurable Logic Block used to implement the AND function and then routed to the input carry of the exact adder.

For completeness, we must mention that the gains in terms of power are not limited to the approximate adders. In fact, combining SIMD acceleration and approximation leads to more global power savings. In a standard execution of the initial software on the general-purpose microprocessor, each addition would use three 32-bit registers and the 32-bit ALU, resulting in power consumption also in all the register cells that are not really useful for the computations. The SIMD acceleration avoids this waste, since all bits in registers become meaningful. Of course, the exact gain could only be quantified taking into account all modifications in the system (hardware structures, application code, memory accesses, …) and the characteristics of the target implementation technology.

Conclusions for this case study, and in particular the comparison between the approximation types, cannot be considered as universal. However, an interesting outcome is that a strong approximation, very efficient in terms of hardware optimization, can also be very efficient in terms of computation accuracy. This study also shows that several approximation types that look very similar can exhibit very different trade-offs between accuracy loss and hardware optimizations. Combining hardware acceleration and approximate operators in a coherent manner also increases the global gains. All these findings can be leveraged when implementing neural networks, not limited to the type of network considered in this case study.

Perspectives of this work include from one side the approximation of the multiplications in the context of the hardware accelerator and on another side analyzing the impact of both acceleration and approximation on the robustness of the resulting system when operating in harsh environments and/or safety-critical applications.

In this case study, the critical path limiting the main clock frequency of the whole system is not related to the adders modified with the approximations. In consequence, the speed improvement due to approximate computation cannot really be exploited. Another perspective would be to revisit the architecture of the accelerator in order to perform several successive operations in one cycle, taking advantage of the reduced carry chains to further accelerate SIMD operations.