A Nonparametric Regression-Based Multi-Scale Gradient Correlation Filtering Method for Infrared Small Target Detection

Abstract

Infrared small target detection, especially under low SCR conditions and complex backgrounds, is still a challenging research task. Considering the scale change caused by small targets rapidly moving, in this paper, a nonparametric regression-based multi-scale gradient correlation filtering (MGCF) detection method is proposed. First, a nonparametric regression method is applied to calculate the gradient of each point. Then, based on the unique gradient characteristics of small targets, a multi-scale gradient correlation (MGC) template is designed to distinguish small targets from clutter. After that, a multi-scale gradient correlation filtering method is proposed to enhance the target intensity and suppress clutter. At last, based on the obtained filtering response, an adaptive threshold segmentation method is adopted to extract real small targets. Experimental results demonstrate that the proposed method can fully improve the signal-to-clutter ratio (SCR) of small targets under different complex backgrounds. Moreover, compared with other baseline methods, the proposed method exhibits excellent detection performance.

1. Introduction

With the development of infrared imaging technology, infrared imaging guidance has become a main guidance mode in the precision guidance system. The infrared im-aging guidance technology uses the thermal radiation difference between the target and the background to image and detect, which can accurately capture the target.

In order to find the target as soon as possible, it is required that the seeker can detect the target when it is far away from the target. At a long distance, the target lacks clear features, such as shape and texture, and only occupies few pixels in the image. At the same time, due to the interference of clutter in the background and the limitation of hardware imaging conditions, the field of view is filled with a lot of noise. These factors make it difficult to accurately detect small targets. Therefore, infrared small target detection under complex backgrounds is still a highly challenging research topic.

Among the existing infrared small target detection algorithms, a detection method based on local contrast measurement (LCM) [1] has attracted increasingly more attention. The LCM method is used for detection based on the infrared radiation difference between the small target and the background, which can achieve a good detection performance in scenes with simple backgrounds. However, when the scene where the located target is complex and changeable, and there is a large amount of clutter with drastic grayscale changes in the background, the local contrast of the target will become unclear, which can easily lead to false detection.

To overcome this problem, a detection method based on an infrared gradient vector field (IGVF) [2] was proposed. Although the contrast of the target and the contrast of the clutter might be similar under complex backgrounds, the gradient performance of the two was obviously different. The IGVF adopted the gradient of the target rather than the contrast to detect small targets, which performs well under complex and changeable scenes.

Based on the unique gradient characteristics of the small target, a novel detection method named multi-scale gradient correlation filtering (MGCF) is proposed in this paper. The contributions of the proposed MGCF method can be summarized as:

• A nonparametric regression method is proposed to calculate the IGVF.
• A multi-scale gradient correlation (MGC) template is designed and a multi-scale gradient correlation filtering method is proposed to discriminate between the small target and clutter.
• The proposed method exhibits excellent small target detection performance, especially in low SCR and dense cloud scenes.

The remaining sections are organized as follows. In Section 2, some classical and new infrared small target detection methods are presented. In Section 3, the proposed MGCF method is introduced in detail. In Section 4, a large number of detection results and comparison experiments are shown in detail. Finally, the conclusion is presented in Section 5.

2. Related Work

Over the past few decades, a variety of detection methods have been proposed. In the early years, researchers mainly used traditional filtering methods and morphological methods to detect small targets, such as Max-mean filter, Max-median filter, and [3] the Top-Hat method [4]. Max-mean and Max-median filters used a fixed window to traverse the image, and then selected the mean or median value in each window as the response of the point. The Top-Hat method detected the target based on the erosion and expansion operation, which can improve the target intensity and suppress background noise. Based on the Top-Hat method, Deng et al. [5] proposed an improved Top-Hat detection method. This method proposed a ring-structured window and adopted local information entropy for weighting. Morphological methods are easy to implement and fast in detection. However, the morphological method depends too much on the shape and size of the structural window, and some information of small targets are unknown in practical applications. Therefore, the morphological method has certain limitations when used.

Zhang et al. [6] proposed a first-order directional derivative (FODD) filter. The FODD filter was built based on the facet model, which distinguished the small target from clutters by calculating the first derivative of each point in multiple directions and searching for zeros-crossings. Lu et al. [7] also used the facet model to calculate the directional derivative of each point, and used the directional derivative as the regional contrast information to improve the intensity of the target. Chen et al. [8] first extracted the suspected target area, and then combined gradient and contrast information to further distinguish the small target. Wu et al. [9] designed an irregular window template to replace the rectangular window template for filtering. In addition, local intensities and gradient were applied to constrain candidate small targets. Aiming at the gray distribution of the background edge in maritime images of the sea surface, Zhang et al. [10] designed a candidate target descriptor and directional sub-bands to distinguish the sea level from the small target. Nie et al. [11] proposed a multiscale local homogeneity measure (MLHM) method. The MLHM method integrated the homogeneity feature of the target region and the heterogeneity feature of the background region to improve the image SCR, and designed a multi-scale measurement method for detection.

Apart from spatial filtering methods, researchers have proposed a series of background estimation detection methods. The background estimation method first estimates the background based on the designed algorithm, and then the foreground can be obtained by subtracting the background from the original image. Finally, the small target is extracted from the foreground image. Song et al. [12] proposed a patch propagation filter (PPF) method. The PPF method designed a propagation-filter-based background estimation method, which can well preserve the structure information of complex backgrounds, such as clouds. Gao et al. [13] proposed an infrared patch-image (IPI) model. The IPI model believed that the background image was mainly composed of large areas of similar grayscale elements, such as clouds and sea surface. The foreground image was mainly composed of small targets and noise. Therefore, the foreground and the background could be regarded as a sparse matrix and a low-rank matrix with linear correlation, respectively. The IPI model first traversed through the entire image with a fixed window, then vectored the image patches at each location into a column, and employed the robust principal component analysis (RPCA) method to extract the foreground and background images. In order to overcome the interference caused by strong edges, Dai et al. [14] used the partial sum of singular values and non-negative terms to constrain the background and foreground matrices, and employed an inexact augmented Lagrange algorithm to solve. Li et al. [15] proposed a multi-scale window IPI (MW-IPI) model. The MW-IPI model performed multi-scale decomposition on the original image. Multiple windows of different sizes were used to acquire image patches of different scales, which could improve the ability of the model to distinguish strong edges. Zhu et al. [16] proposed a target-aware method. In this method, information entropy was added to the objective function to constrain the foreground image. Rawat et al. [17,18,19] proposed a series of low-rank decomposition-based detection methods. These methods improved the constraint term of the objective and solution method of the approximation, which further improved the detection ability of small targets under complex backgrounds.

Since the IPI model will destroy the structural information between pixels when vectoring image patches, Zhang et al. [20] proposed an image-patch tensor (IPT) model. The IPT model transformed the two-dimensional small target detection problem into a three-dimensional tensor space, stacked image patches at different positions into a three-dimensional tensor block, and employed the Tensor-RPCA technology to optimize a low-rank background tensor and a sparse foreground tensor for detection. Luo et al. [21] proposed a tensor-based detection method, which decomposed the background and the target in the spatial-temporal domain. Then, a novel tensor rank and an approximation method were designed to estimate the background image and target image.

Inspired by the Human Visual System (HVS), Chen et al. [1] proposed an LCM method. The HVS believed that the part of an image which received the most attention from the human eye was not the brightest part of the image, but the part with the strongest contrast. Therefore, the LCM method improved the target intensity and suppressed the background clutter by measuring the local contrast of the image, and then employed an adaptive threshold to extract the target. On the basis of the LCM method, an improved LCM (ILCM) [22] method was proposed. The ILCM method improved the measurement method of local contrast, which improved the detection accuracy and detection speed. Shi et al. [23] proposed a High-Boost-Based Multiscale LCM (HB-MLCM) method. The HB-MLCM method first designed a high boost filter to increase the intensity of high-frequency signals where small targets were likely to appear. Then, a novel multi-scale LCM method was proposed to extract real targets. Yi et al. [24] proposed a target detection method guided by the visual saliency (TDGS) method. The TDGS method adopted a coarse-to-fine detection strategy. First, a saliency model was constructed to suppress background clutter. Then, an adaptive LCM method was designed to detect small targets. Han et al. [25] proposed a Weighted Strengthened LCM (WSLCM) method. The WSLCM method first used the Gaussian filter and background estimation method to calculate the strengthened LCM, and then defined a weight function to further enhance the contrast of the target. Li et al. [26] proposed a Strengthened Robust LCM (SRLCM) method. The SRLCM method combined the sparse low-rank theory with the LCM algorithm, which achieved a better detection performance under irregular backgrounds. Qin et al. [27] first extracted several suspected targets based on LCM, and then adopted random walker theory to separate the real small targets. Du et al. [28] proposed a multi-scale target edge diffusion (M-TED) detection method. The M-TED detection method adopted the transition region to measure the local contrast, and proposed a multi-scale edge diffusion strategy to further improve the contrast of the target response map. He et al. [29] proposed a novel high-boost filter to distinguish non-homogeneous backgrounds. Then, a local Weber contrast measurement was applied to enhance target intensity.

3. The Proposed MGCF Method

In the following section, the proposed MGCF detection method is described in detail. We first introduce a novel IGVF construction method. Then, the designed multi-scale gradient correlation template and filtering method are described. Finally, an adaptive threshold segmentation method is adopted for extracting real targets.

3.1. IGVF Construction Method Based on Nonparametric Regression

We adopt a nonparametric regression method [30] to construct the IGVF. Different from directly using adjacent points or a fixed parameter model for calculation, the nonparametric regression method does not rely on any prior information, so it does not need to pre-assume various model parameters. For complex infrared backgrounds or noisy scenes, the fixed parameters in the parametric model cannot guarantee a comprehensive assumption for the background. Therefore, in the proposed method, a data-driven nonparametric regression method is employed to calculate the gradient at each point.

The nonparametric regression model of a 2D image can be expressed as:

$$m_i=f\left({\mathrm{p}}_i\right)+{\epsilon }_i, i=1,2,\dots ,N$$

(1)

where ${\mathrm{p}}_i$ is a vector represented as ${\mathrm{p}}_i={\left[x_i,y_i\right]}^T$, $\left(x_i,y_i\right)$ is the coordinates of the sample pixel. $m_i$ represents the intensity of this pixel. $f\left({\mathrm{p}}_i\right)$ is a nonparametric regression function, which represents the estimated value of the intensity at this point. ${\epsilon }_i$ is random error, usually represented by Gaussian noise with zero mean. $N$ indicates the number of sample pixels used by the regression model.

To estimate the value of the regression function at any pixel $\mathrm{p}$, if $\mathrm{p}$ is near the sample ${\mathrm{p}}_i$, we have the following multi-variate Taylor expansion:

$$f\left({\mathrm{p}}_i\right)\approx f\left(\mathrm{p}\right)+{\left\{\nabla f\left(\mathrm{p}\right)\right\}}^T\left({\mathrm{p}}_i-\mathrm{p}\right)+\frac{1}{2}{\left({\mathrm{p}}_i-\mathrm{p}\right)}^T\left\{\mathscr{H}f\left(\mathrm{p}\right)\right\}\left({\mathrm{p}}_i-\mathrm{p}\right)+\dots$$

(2)

where $\nabla$ and $\mathscr{H}$ represent the $\left(2\times 1\right)$ gradient operator and the $\left(2\times 2\right)$ Hessian operator, respectively. In our method, the regression function is extended to a second-order expansion. After deduction, (2) can be expressed as:

$$f\left({\mathrm{p}}_i\right)\approx {\beta }_0+{\beta }_1^T\left({\mathrm{p}}_i-\mathrm{p}\right)+{\beta }_2^{T}vech\left\{\left({\mathrm{p}}_i-\mathrm{p}\right){\left({\mathrm{p}}_i-\mathrm{p}\right)}^T\right\}+\cdots$$

(3)

where $vech(\cdot )$ is a half-vectorized operator. For example, for a symmetric matrix $\left[\begin{array}{cc}a& b\\ b& d\end{array}\right]$:

$$vech\left(\left[\begin{array}{cc}a& b\\ b& d\end{array}\right]\right)={\left[\begin{array}{ccc}a& b& d\end{array}\right]}^T$$

(4)

By comparing (2) and (3), it can be found that:

$${\beta }_0=f\left(\mathrm{p}\right)$$

(5)

$${\beta }_1=\nabla f\left(\mathrm{p}\right)={\left[\frac{\partial f\left(\mathrm{p}\right)}{\partial x},\frac{\partial f\left(\mathrm{p}\right)}{\partial y}\right]}^T$$

(6)

$${\beta }_2=\frac{1}{2}{\left[\frac{{\partial }^{2}f\left(\mathrm{p}\right)}{\partial x^2},\frac{{\partial }^{2}f\left(\mathrm{p}\right)}{\partial xy},\frac{{\partial }^{2}f\left(\mathrm{p}\right)}{\partial y^2}\right]}^T$$

(7)

That is, ${\beta }_1$ is the gradient we want. If interested, ${\beta }_0$ and ${\beta }_2$, i.e., the gray intensity and the second derivative of the pixel, can also be obtained.

Through the least squares technique, $\left\{{\beta }_n\right\}$ can be solved by the following optimization method:

$$\underset{\left\{{\beta }_n\right\}}{\min }{\displaystyle \sum _{i=1}^N[m_i-}{\beta }_0-{\beta }_1^T\left({\mathrm{p}}_i-\mathrm{p}\right){-{\beta }_2^{T}vech\left\{\left({\mathrm{p}}_i-\mathrm{p}\right){\left({\mathrm{p}}_i-\mathrm{p}\right)}^T\right\}-\cdots ]}^2\cdot Ker\left({\mathrm{p}}_i-\mathrm{p}\right)$$

(8)

where $Ker(\cdot )$ is a 2D weight function. It can assign different weights according to the distance between the sample pixel and the estimated pixel. After a series of derivations, the matrix form of the local gradient to be estimated can be expressed as:

$${\stackrel{\wedge }{\beta }}_1=\stackrel{\wedge }{\nabla f}\left(\mathrm{p}\right){=\mathrm{e}}_1^T{\left({\mathrm{P}}_{\mathrm{p}}^T{\mathrm{W}}_{\mathrm{p}}{\mathrm{P}}_{\mathrm{p}}\right)}^{-1}{\mathrm{P}}_{\mathrm{p}}^T{\mathrm{W}}_{\mathrm{p}}\mathrm{m}$$

(9)

$${\mathrm{W}}_{\mathrm{p}}=\mathrm{diag}\left[Ker\left({\mathrm{p}}_1-\mathrm{p}\right),Ker\left({\mathrm{p}}_2-\mathrm{p}\right),\cdots ,Ker\left({\mathrm{p}}_N-\mathrm{p}\right)\right]$$

(10)

$${\mathrm{P}}_{\mathrm{p}}=\left[\begin{array}{cccc}1& {\left({\mathrm{p}}_1-\mathrm{p}\right)}^T& vech\left\{\left({\mathrm{p}}_1-\mathrm{p}\right){\left({\mathrm{p}}_1-\mathrm{p}\right)}^T\right\}& \cdots \\ 1& {\left({\mathrm{p}}_2-\mathrm{p}\right)}^T& vech\left\{\left({\mathrm{p}}_2-\mathrm{p}\right){\left({\mathrm{p}}_2-\mathrm{z}\right)}^T\right\}& \cdots \\ ⋮& ⋮& ⋮& ⋮\\ 1& {\left({\mathrm{p}}_N-\mathrm{p}\right)}^T& vech\left\{\left({\mathrm{p}}_N-\mathrm{p}\right){\left({\mathrm{p}}_N-\mathrm{p}\right)}^T\right\}& \cdots \end{array}\right]$$

(11)

$$\mathrm{m}={\left[m_1,m_2,\cdots ,m_N\right]}^T$$

(12)

$${\mathrm{e}}_1={\left(0,1,1,0,0,0\right)}^T$$

(13)

In our method, the multi-variate Taylor expansion is extended to second order. So, the size of ${\mathrm{W}}_{\mathrm{p}}$ is $N\times N$, the size of ${\mathrm{P}}_{\mathrm{p}}$ is $N\times 6$, and the size of $\mathrm{m}$ is $N\times 1$.

We employ a $5\times 5$ neighborhood to compute the gradient of the center point. That is, the gradient of each point is estimated by 24 points in its $5\times 5$ neighborhood. After the calculation of (9), the IGVF can be obtained.

Figure 1 shows several image patches of an infrared image and their IGVF patches. In IGVF, the gradient of each point is described as an arrow, where the length of the arrow indicates the gradient modulus, and the direction of the arrow indicates the gradient direction. The gradient modulus and direction can be written as:

$$M\left(\mathrm{p}\right)=\sqrt{{\left(\frac{\partial f\left(\mathrm{p}\right)}{\partial x}\right)}^2+{\left(\frac{\partial f\left(\mathrm{p}\right)}{\partial y}\right)}^2}$$

(14)

$$D\left(\mathrm{p}\right)=\arctan \left(\frac{\partial f\left(\mathrm{p}\right)}{\partial y}/\frac{\partial f\left(\mathrm{p}\right)}{\partial x}\right)$$

(15)

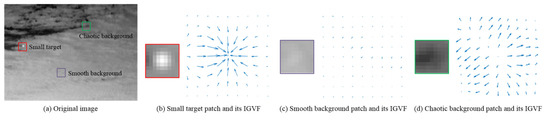
Figure 1. Several patches of an infrared image.

Because the range of the arctangent function is $-{90}^{\circ }–{90}^{\circ }$. In our method, in order to ensure the integrity of the gradient direction, we modify the range of $D\left(\mathrm{p}\right)$ to $-{180}^{\circ }–{180}^{\circ }$.

As can be seen from Figure 1, the IGVF of different image patches have completely different characteristics. In Figure 1b of the small target patch, when the sunlight is behind the imaging system, it can be seen that the length of the arrow at the small target is very long, which means that the modulus of the gradient at this point is large. In addition, all arrows are pointing towards the center. However, the background IGVF patch does not have this obvious characteristic. For example, for the IGVF patch with the smooth background in Figure 1c, since the region is relatively flat, the gradient modulus in this region is very small. That is, the arrow length in the IGVF is very short, and the arrow direction is disordered. In the IGVF with the chaotic background of Figure 1d, although the length of the arrow is long, the directions of the arrows are chaotic and lack a clear pattern.

Based on the above analysis, we believe that the IGVF patch of the small target has a unique gradient characteristic. That is, the gradient modulus at the target is very large, and the gradient directions all point towards the center. However, the gradient of background clutter and chaotic noise does not have a clear pattern. For the chaotic background patch in Figure 1d, the intensity of the background patch drastically changes and the contrast is obvious. If the LCM-based method is applied to detect small targets, it is easy to misdetect this patch as a small target area, resulting in a detection failure. However, the gradient of the chaotic background patch is significantly different from that of the small target. Therefore, in our method, we detect small targets based on their unique gradient characteristics.

3.2. The Proposed MGCF Method

Considering the scale changes caused by small targets are fast moving, different from the gradient correlation template proposed in [31], we designed a multi-scale gradient correlation (MGC) template, as shown in Figure 2. The MGC template consists of angles. In order to simulate the characteristic that the gradients of small targets all point towards the center, each angle in the MGC template also points towards the center. At the same time, to ensure computational efficiency in multi-scale calculation, the designed template omits the angles of some points, and only retains the angles in the horizontal, vertical, diagonal, and anti-diagonal directions, as shown in Figure 2a. Meanwhile, the angle at the center of the template is manually set to 0. In our method, the proposed MGC template contains five scales from $3\times 3$ to $11\times 11$. Figure 2b shows the arrow description of the MGC template. Each angle in the template is described as an arrow.

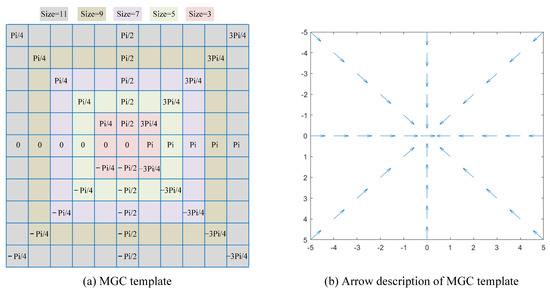
Figure 2. The MGC template.

By comparing the MGC template with the IGVF patch of the small target, it can be found that the points in both all point towards the center. To take full advantage of this gradient characteristic, we propose a multi-scale gradient correlation measurement method for detecting small targets. By sliding the designed MGC template through the IGVF, the multi-scale gradient correlation response at each point can be measured. The MGC measurement is defined as:

$$\begin{array}{ll}G{C}_s\left(x,y\right)=& \mathrm{IGVF}\otimes \mathrm{MGC} \mathrm{template}\\ & ={\displaystyle \sum _{u=-\left(s-1/2\right)}^{\left(s-1/2\right)}{\displaystyle \sum _{v=-\left(s-1/2\right)}^{\left(s-1/2\right)}DC\left(x+u,y+v\right)}}·{\mathrm{avg}}_s\left(x,y\right)·{\min }_s\left(x,y\right)\\ & ={\displaystyle \sum _{u=-\left(s-1/2\right)}^{\left(s-1/2\right)}{\displaystyle \sum _{v=-\left(s-1/2\right)}^{\left(s-1/2\right)}\cos \{abs[D\left(x+u,y+v\right)}}\\ & \hspace{1em}\hspace{1em}-{\mathrm{MGC}}_s \mathrm{template}\left(u,v\right)]\}·{\mathrm{avg}}_s\left(x,y\right)·{\min }_s\left(x,y\right)\end{array}$$

(16)

and

$${\mathrm{avg}}_s\left(x,y\right)=\frac{1}{s^2}{\displaystyle \sum _{i=x-\left(s-1/2\right)}^{x+\left(s-1/2\right)}{\displaystyle \sum _{j=y-\left(s-1/2\right)}^{y+\left(s-1/2\right)}M\left(i,j\right)}}$$

(17)

where $\otimes$ is the MGC operator, $s$ represents the scale of the MGC template. ${\min }_s\left(x,y\right)$ represents the minimum value of the gradient modulus within the scale window. When the MGC template slides to a new IGVF patch, the directional correlation (DC) of this scale window is first calculated. The DC is obtained by calculating the cosine difference between the directions of the IGVF patch and the corresponding points on the MGC template. If the DC of a position is larger, it indicates that the gradient distribution of this region is close to the MGC template, and there is a higher possibility of small targets in this region. Then, the GC response at one scale can be calculated as the product of the DC response with the mean and minimum of the gradient modulus in the corresponding scale window. Calculating with the mean and minimum of the modulus can reduce the disturbance of sharp noises in the window. Finally, in order to cope with the scale change of small targets, the maximum of GC under multiple scales is taken as the final response of this point, which is:

$$GC\left(x,y\right)=\underset{s}{\max }G{C}_s\left(x,y\right),\hspace{1em}s=3,5,7,9,11$$

(18)

The scale where the maximum value located is the scale of the small target.

Figure 3 presents an original image and its filtered MGC map. In Figure 3a, the cloud of the original image is changeable, the clutter is dense, and the background violently fluctuates. After the MGC filtering, the target intensity has been significantly enhanced, and the background has been fully suppressed. Although the intensity of some clutter is also increased after filtering, the intensity of the clutter is far lower than that of the small target. If an appropriate segmentation threshold is selected, the small target can be well extracted.

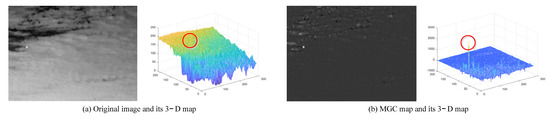
Figure 3. The original image and its MGCF map.

3.3. Small Target Extraction Based on the Adaptive Threshold

Based on the obtained MGCF map, it can be believed that the point with greater intensity of the MGCF map is more likely to have a small target. Therefore, an adaptive threshold is adopted for extracting the small target based on the MGCF map. The adaptive threshold $T{h}_{extr}$ is expressed as:

$$T{h}_{extr}=\lambda \cdot Ma{x}_{MGC}$$

(19)

where $Ma{x}_{MGC}$ is the maximum value in the MGCF map, and the range of $\lambda$ is $\left[0.5-0.8\right]$. After the threshold segmentation, the points in the MGC map with an intensity higher than the adaptive threshold are identified as small targets. The detection framework of the proposed MGCF method is shown in Figure 4. In addition, the complete detection steps of the proposed MGCF method are described as:

Figure 4. Detection framework of the proposed MGCF method.

• Step 1: Calculate the IGVF map based on a nonparametric regression method, according to (1)–(13).
• Step 2: Calculate the module map and direction map according to (14)–(15).
• Step 3: Calculate the gradient correlation based on the designed MGC template with the IGVF map in a fix scale, according to (16)–(17). After that, a GC map within a fix scale is obtained.
• Step 4: Find the maximum value of gradient correlation response under multiple scales, according to (18).
• Step 5: Set an adaptive threshold on the MGC map to extract the infrared small target, according to (19).

4. Experimental Results and Analysis

In this section, several ways are adopted to evaluate the proposed MGCF method. We first present the main results of the proposed MGCF method in a variety of different scenes. Then, some objective evaluation metrics are adopted to compare with other excellent baseline methods. All the experiments were implemented in MATLAB 2020b with a 3.00 GHz Intel i7 processor and a 8 GB random memory. In addition, $Ker(\cdot )$ is set as a Gaussian radial basis function with a standard deviation of 0.5.

4.1. Main Results of the Proposed MGCF Method

We employed six different complex scenes for evaluating the proposed method, as shown in the first column in Figure 5. For sequence 1, the cloud is complex and the clutter is changeable. There are many small blocks in the background with intensity characteristics similar to small targets. For sequence 2, the clouds are dense, and the small target is hidden at the boundary between the clouds and the sky. For sequence 3, the signal intensity of the small target is weak, and it is easy to mistake the small target as the cloud background. For sequence 4, there are two small targets with inconsistent intensities. For sequence 5 and sequence 6, multi-scale small targets rapidly move in the cloud. In addition, the resolution of the first three images is $290\times 212$, and the resolution of the fourth image is $314\times 230$, and the resolution of the last two images is $290\times 212$.

Figure 5. The experimental results of the proposed MGCF method under different backgrounds.

Figure 5 presents the main experimental results of the proposed MGCF method under different backgrounds. In Figure 5, the first and second columns show the original images and their 3D maps, respectively. The third column shows the IGVF maps obtained based on the nonparametric regression method. The fourth and fifth columns show the MGCF response maps filtered by the proposed MGCF method and their 3D maps, respectively. The last column shows the detection results.

By comparing the original images and the MGCF maps, it can be found that after the MGCF filtering, the target intensity has been fully enhanced, and the clutter has been significantly suppressed. Especially in scenes with changeable cloud, such as sequence 1 and sequence 2 of Figure 5, the chaotic clouds are obviously suppressed. In addition, by observing the 3D map of the original image in sequence 3 of Figure 5, it can be found that the intensity of the small target is even lower than the surrounding backgrounds. However, after MGCF filtering, the target intensity has been fully enhanced. Although there is still a small amount of clutter interference remaining on the obtained MGCF map, the intensity of clutter is far weaker than the small target. Therefore, as long as an appropriate threshold is adopted, the real small target can be accurately extracted, as shown in the detection results of the last row in Figure 5.

4.2. Evaluation Metrics and Comparison

To objectively evaluate the detection performance of the proposed method, we employ six excellent baseline small target detection algorithms for comparison, including LCM [1], ILCM [22], MLHM [11], HB-MLCM [23], TDGS [24], and PPF [12]. The first five methods are template-filtered-based methods, and the last PPF method is based on background estimation. Meanwhile, two objective evaluation metrics, SCR gain (SCRG) [32] and background suppression factor (BSF) [32], are adopted to compare the detection performance. SCRG and BSF are defined as:

$$SCRG=\frac{{\left(\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}_{out}}{{\left(\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}_{in}}$$

(20)

$$BSF=\frac{C_{in}}{C_{out}}$$

(21)

where $S$ represents the intensity of the target signal and $C$ represents the standard deviation of the clutter. $in$ and $out$ represent the original image and the response map after operation. A higher $SCRG$ score indicates that the method has a better ability to improve the target intensity. A higher $BSF$ score reflects a better performance of the method to suppress background clutter and noise.

Table 1 and Table 2 display the SCRG and BSF scores of all methods under different backgrounds, respectively. It can be found from the comparison of SCRG scores in Table 1 that the proposed MGCF method achieves the highest SCRG scores in the other five sequences, except in sequence 3. It proves the effectiveness of the proposed method in improving the signal intensity of small targets. Furthermore, in the comparison of BSF scores, it can be found that under the four complex backgrounds, the BSF scores of the proposed MGCF method is the highest among all of the methods. This demonstrates the excellent ability of the proposed method to suppress clutter and noise.

Table 1. The comparisons of SCRG under different backgrounds.

	Sequence 1	Sequence 2	Sequence 3	Sequence 4	Sequence 5	Sequence 6
LCM	2.8866	4.1496	1.5281	3.7841	7.5133	2.5293
ILCM	3.9644	11.9253	2.7618	27.6793	11.7564	7.8480
MLHM	6.2763	13.8237	5.2146	28.0575	15.3286	11.0568
HB-MLCM	5.8175	14.2563	6.5174	29.6812	14.1477	13.0805
TDGS	6.5844	16.8215	11.2475	34.0754	16.5291	16.3574
PPF	7.0428	14.4267	15.3578	35.4496	16.8865	15.7144
Proposed	7.5254	18.1034	13.6565	37.2877	18.2110	17.1263

Table 2. The comparisons of BSF under different backgrounds.

	Sequence 1	Sequence 2	Sequence 3	Sequence 4	Sequence 5	Sequence 6
LCM	1.2467	1.1236	1.0659	0.8021	3.9277	0.9947
ILCM	1.9097	2.9447	1.8618	5.8491	5.0080	3.0302
MLHM	2.1193	4.5275	5.2364	7.7593	6.2163	4.1969
HB-MLCM	1.9842	4.3168	2.3187	8.8269	6.8497	5.3782
TDGS	2.4748	9.2534	3.5882	15.0752	7.3351	5.0860
PPF	2.1387	9.5821	4.6638	14.6297	8.0568	5.8293
Proposed	2.6641	11.0911	6.6090	18.4273	8.4615	6.2692

In addition, the receiver operator characteristic (ROC) curve is employed to evaluate the detection performance of different methods. The ROC curve reflects the relationship between the detection rate and the false alarm rate. If a detection method can quickly reach a high detection rate at a low false alarm rate, it indicates that the detection performance of this method is excellent. By continuously adjusting the segmentation threshold of the algorithm, a ROC curve can be obtained. The above six sequences are used for evaluation. Where sequence 1 contains 117 images with 117 targets, sequence 2 contains 131 images with 131 targets, sequence 3 contains 145 images with 145 targets, sequence 4 contains 86 images with 172 targets, sequence 5 contains 121 images with 104 targets, and sequence 6 contains 104 images with 104 targets. Figure 6 shows the comparison of ROC curves of all methods under different backgrounds, where the red curve represents the proposed method. As can be seen from Figure 6, the proposed method can quickly achieve a high detection rate at a low false alarm rate in all four scenes. The area enclosed under the ROC curve of the proposed method is the largest, which indicates that the proposed method achieves the best detection performance.

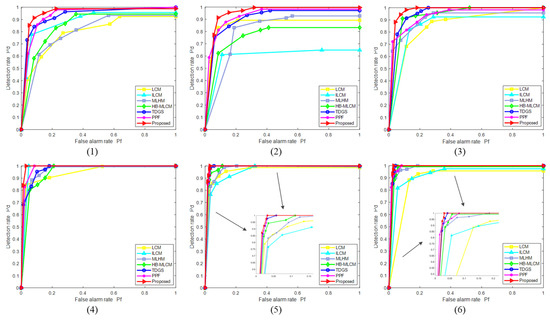
Figure 6. The comparisons of ROC curves.

Furthermore, Figure 7 shows some detection results of the proposed method for detecting multi-scale small targets in sequences 5 and 6. The images in the first row shows the detection results of sequence 5, and the images in the second row shows the detection results of sequence 6. As can be clearly seen in Figure 7, the proposed method can accurately find small targets with different scales.

Figure 7. Detection results of two multi-scale small target sequences.

5. Conclusions

In this paper, a novel method based on nonparametric regression and multi-scale gradient correlation filtering for small target detection is proposed. For accurate estimation under complex and changeable backgrounds, a nonparametric regression method is first employed to compute the gradient of each point. Then, considering the unique gradient properties and scale change characteristics of small targets, a multi-scale gradient correlation template is designed, and a multi-scale filtering method is proposed to distinguish targets from backgrounds. Finally, an adaptive threshold is adopted to extract small targets. The experimental results show that the proposed method can fully improve the intensity of the small target and suppress clutter no matter the complex background. In addition, in the comparison of ROC curves, the proposed method achieves the best detection performance in all backgrounds, which demonstrates that the proposed method has excellent detection ability under complex backgrounds.