Document Image Restore via SPADE-Based Super-Resolution Network

Abstract

With the development of deep learning technology, various structures and research methods for the super-resolution restoration of natural images and document images have been introduced. In particular, a number of recent studies have been conducted and developed in image restoration using generative adversarial networks. Super-resolution restoration is an ill-posed problem because of some complex restraints, such as many high-resolution images being restored for the same low-resolution image, as well as difficulty in restoring noises such as edges, light smudging, and blurring. In this study, we applied super-resolution restoration to text images using the spatially adaptive denormalization (SPADE) structure, different from previous methods. This paper used SPADE for document image restoration to solve previous problems such as edge unclearness, hardness to catch features of texts, and the image color transition. As a result of this study, it can be confirmed that the edge of the character and the ambiguous stroke are restored more clearly when contrasting with the other previously suggested methods. Additionally, the proposed method’s PSNR and SSIM scores are 8% and 15% higher compared to the previous methods.

1. Introduction

Ultra-resolution, which restores and extracts low-resolution images as high-resolution images, is a field where many studies are conducted due to its high utilization in society as a whole. Only simple photo images were restored in the past, but the area gradually expanded to be used in fields such as text and video. Meanwhile, the digitization of many documents covered by banks, securities, insurance, and public affairs includes characters in video being restored and is sensitive to distortion, loss, and noise caused by transmission tasks such as faxes and scans. Therefore, super-resolution restoration technology can help restore the noise lost in the process to almost the same quality as the original document.

The super-resolution restoration problem is an ill-posed problem that is prematurely difficult to contrast with the original image because it shows various results, as shown in Figure 1, depending on the degree and method of restoration of the low-resolution image. However, with the development of deep learning structures such as convolutional neural networks (CNN) and the recent use of generative adversarial networks (GAN), we have tried to solve them by declaring mapping functions by combining low-resolution and high-resolution images in pairs [1,2,3,4,5,6,7,8]. Furthermore, we conducted research on strings [9,10]. The above study used a function to replace the mean square error loss, and the concept of perceptual loss was also introduced to optimize the model by identifying features such as the overall texture of the photographic images, rather than pixels [2]. Through this development process, the quality of images was significantly improved [11].

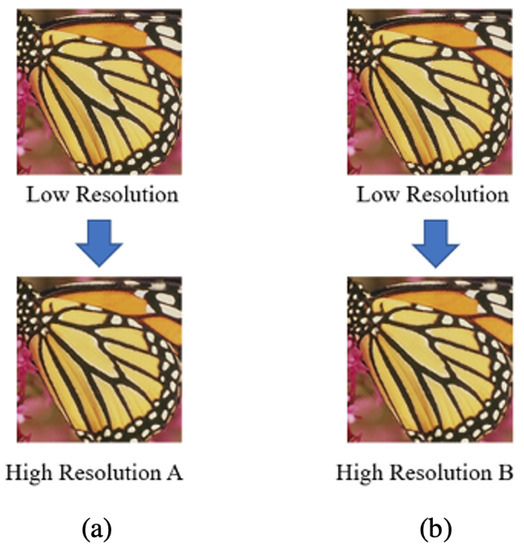
Figure 1. Restored Images: (a) High-Resolution A restored from the same low-resolution image used to make High-Resolution B; (b) High-Resolution B restored from the same low-resolution image used to make High-Resolution A. Both A and B were restored from the same low-resolution image; however, High-Resolution A and B are not the exactly same image.

However, although this theoretical development significantly improved the quality of the image, restoration of edges and detailed features still tended to be difficult. In particular, unlike photographs, the distinction between strokes may be ambiguous, and the distinction between edges and main parts is also a problem that needs to be considered more carefully in characters that are difficult to distinguish [3]. This is because there is a possibility that the phrase in the restored high-resolution image for the low-resolution image of the same single character is different from the existing original. Therefore, in the case of restoring the character, detailed restoration is required, compared to the edge problem of the single image described above [10].

This paper attempts to apply the super-resolution restoration technique using deep neural networks to characters. Existing methods include converting the original high-resolution images into low-resolution images to utilize adversarial generative networks that have recently made significant progress and to restore them to high resolution using deep convolutional neural networks [12,13]. The two representative methods for the super-resolution problem use convolutional neural networks, and the previous work mentioned they achieved possibilities to restore document images [12]. Additionally, with the advancement of deep learning processes, researches have tried to use generative adversarial networks for solving document restoration problems [13]. However, for these two methods, we were able to confirm the loss of character feature information, especially during the restoration of edges and the characterization of characters’ important parts [14,15]. Therefore, it is necessary to restore images to high resolution while preserving this information.

In this paper, spatial adaptive denormalization is applied to text images [1]. Unlike other methods, this combines the input images into a hierarchical pyramid structure in each layer of the decoder, providing spatial information so that various characteristics can be learned in the zoom generator. Therefore, in the conventional method, it is fairly simple to restore the flat texture of an edge that is easily missed [1]. The proposed method has some novelty compared to the previous work because spatial adaptive denormalization is not a method currently used for image super-resolution problems. This method was designed for generating new natural images using some features and shapes from the original. However, this paper grafts spatial adaptive denormalization onto the super-resolution restoring problem, and achieves an advancement in efficiency.

2. Related Works

In previous studies, super-resolution restoration usually tends to focus on simple photographs. Several prior studies on documents have also been conducted, but shortcomings have been presented in each method. In addition, unlike the super-resolution restoration of simple photos, where various prior studies have been conducted and sufficient datasets exist, the super-resolution restoration of characters is difficult to prepare without a dataset first. Therefore, previous studies had no choice but to use their own datasets [9,10,15] and as a result, it is difficult to say that their results are enough to claim that they achieved learning various languages. All previous studies had to learn only languages and fonts limited to self-produced datasets, and the number of them is relatively small [9,10,15].

2.1. Super-Resolution Convolutional Neural Network

Among the studies that initially attempted to restore documents to ultra-resolution, studies using CNN showed advanced values in Peak Signal-to-Noise Ratio (PSNR) compared to the previously used bicubic interpolation [9]. SRCNN applied a simple CNN structure to the field of super-resolution, showing performance beyond all traditional techniques and becoming the beginning of subsequent super-resolution techniques [16]. As shown in Figure 1, the super-resolution restoration problem is an ill-posed problem in which the answer is not determined. Consequently, conventional state-of-the-art (SOTA) techniques have sought to determine the correct answer to some degree of high-resolution images through prior knowledge. First, there is an example-based method that builds a pre-learning function that maps low-resolution image and high-resolution image patch pairs. The second is a method of preprocessing a low-resolution image in advance in a sparse coding-based method, performing an encoding process with a sparse coefficient and restoring it through a high-resolution dictionary. In contrast, by relating the super-resolution problem to CNN, we directly designed a CNN structure that learns low-resolution and high-resolution images by passing end-to-end mapping, as shown in Figure 2 [9].

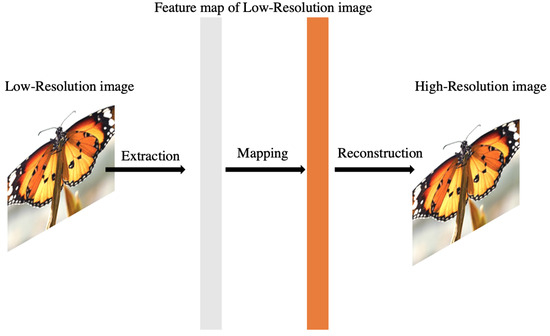
Figure 2. Structure of Super-Resolution Convolutional Neural Network: the first convolutional layer of the SRCNN extracts a set of feature maps. The second layer maps these feature maps nonlinearly as high-resolution patch representations. The last layer combines the predictions within a spatial neighborhood to produce the final high-resolution image [16].

This method has the advantage of processing all prior knowledge within the convolutional layer, as illustrated in Figure 3, and the weight of the model itself is light, so there is no significant difference in time consumption. In addition, it was found that the performance of PSNR indicators was higher than that of the limited dataset [9].

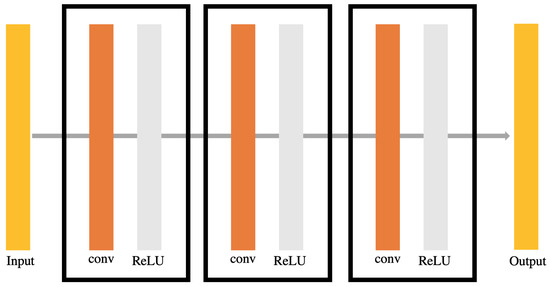
Figure 3. The Structure of SRCNN: Whereas Figure 2 mentioned what function each layer performs in an SRCNN structure, more specifically, this structure uses ReLU as its activation function [16].

2.2. Super-Resolution Generative Adversarial Network

It is clear that the aforementioned SRCNN has made progress in the field of super resolution, but the problem of whether it is possible to restore more detailed texture is still presented [2]. Although loss function is important in solving the super-resolution problem, it is limited to complementing parts such as high textured detail because the previously used mean squared error (MSE) method lacks visual satisfaction in high-frequency detail, and both MSE and PSNR are defined based on the pixel-wise differences in images [2]. Figure 4 shows the structure of GAN that supplements this. The significance of this previous study is to propose a permanent loss function including adversarial loss and content loss, where adversarial loss is related to the training of the discriminator network, with the structure shown below in Figure 4. Therefore, the super-resolution GAN, with this structure, can recover the heavily down-sampled image [2].

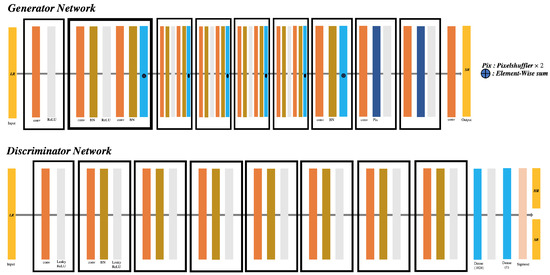
Figure 4. Architecture of SRGAN: The SRGAN structure consists of a Discriminator model and a Generator model. Each of them have own kernel size and number of feature maps and strides [2].

It is true that SRGAN exhibits superior super-resolution performance to SRCNN, but there are still challenging constraints in capturing detailed textures. In addition, there is a problem in that the color of the image changes relatively due to the processing of the edge portion, or the overall image quality appears to be impaired [1]. In the process of restoring documents to super-resolution, not just photographs, it is important to restore detailed edges and find features.

3. The Proposed Method

3.1. Single Image Super Resolution

The super-resolution restoration of a single image restores a high-resolution image with a new image, and the result may not be unique. For instance, the original image is defined in Figure 5, and it is made into a low-resolution image through down-sampling and noise addition. Thereafter, a model recovers it to a high-resolution original image. In this paper, we used the bicubic interpolation, which is representatively adapted in the low-resolution generation.

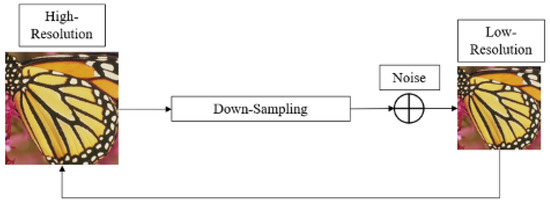
Figure 5. Single image super-resolution structure.

3.2. Super-Resolution of Low-Resolution Images

To restore high-resolution images from low-resolution images, we used the domain mapping of two pair-defined images. By defining the domain $\alpha$ and high-resolution domain of low-resolution images, we attempted to restore single image super-resolution through image conversion between low-resolution domains.

$$\begin{array}{c}\hfill F^{*}\left(\alpha \right)=N\left(\beta \right)\end{array}$$

(1)

In Equation (1), $F^{*}\left(\alpha \right)$ is the function of mapping a high-resolution output image from a low-resolution input image, which means image conversion from a low-resolution domain to a high-resolution domain. Furthermore, $N(·)$ is the neural network proposed in this paper, consisting of conditional adversarial generation networks.

3.3. Spatially Adaptive Denormalization Network

As a network for converting high-resolution images from low-resolution images, high-resolution images are estimated from low-resolution input images through a conditional adversarial generation network.

First of all, a typical adversarial generation network consists of a generator G that receives data distribution and generates data close to reality, and a discriminator D that determines whether the input data are real or made from the generative model G, all of which is nonlinearly mapped. Accordingly, the objective function $L_{GAN}(G,D)$ is expressed by the following equation.

$$\begin{array}{c}\hfill L_{GAN}(G,D)=mi{n}_{G}ma{x}_{D}V(D,G)=E_x\left[logD\left(x\right)\right]+E_y\left[log(1-D(G\left(z\right)\left)\right)\right]\end{array}$$

(2)

In Equation (2), x means data and z means any noise variable. The purpose of discriminator D is to determine whether the input data are original or generated by generator G, so it can label the data accurately. The purpose of generator G is to increase the probability that determinator D will make a mistake, i.e., the probability that D is either determined to be the original data or the data generated by G. These two networks, G and D, are learned with different goals through adversarial learning.

Conditional adversarial generation networks can create conditional generation models with the condition of additional information y at generator G and discriminator D. In this case, y may be a class label or other distribution of data, and y may be additionally added to the input layers of G and D. In generator G, noise z and condition y are combined, and in discriminator D, data x and condition y are entered as the inputs. This is expressed by the formula as follows.

$$\begin{array}{c}\hfill L_{CGAN}(G,D)=mi{n}_{G}ma{x}_{D}V(D,G)=E_x\left[logD\left(x\right|y)\right]+E_y\left[log(1-D(G\left(z\right|y\left)\right))\right]\end{array}$$

(3)

A conditional adversarial generation network is constructed from condition y data paired with data x. Unlike the adversarial generation network, noise z and condition y are the inputs of generator G, and the paired condition y with the data x are the inputs of discriminator D. This allows generator G of the conditional adversarial generation network to create images that match a pair of data x and condition y, and discriminator D must determine whether the input and output images are correctly made in pairs that satisfy the condition. That is, the conditional adversarial generation network may acquire an image satisfying the corresponding condition.

Based on this, we have designed a conditional adversarial generation network for super-resolution restoration from a single image. Accordingly, the objective function is expressed by the following equation.

$$\begin{array}{c}\hfill L_{our}(G,D)=E_x\left[logD\left(H\right|L)\right]+E_z\left[log(1-D(G\left(z\right|L\left)\right))\right]\end{array}$$

(4)

In Equation (4), L means an input low-resolution image and H means a high-resolution image corresponding thereto. Therefore, the proposed objective function allows us to learn a function $F^{*}$ that maps the input low-resolution image L to the corresponding high-resolution image H via a conditional adversarial generation network.

3.4. Document Single Image Super-Resolution via Spatially Adaptive Denormalization

Through the conditional adversarial generation network proposed in Section 2.2, the orientation of the output can be adjusted by the input. In the structure of the conditional adversarial generation network, the convergence rate of learning was accelerated using a batch normalization layer. In deep neural networks, batch normalization layers are generally important and the presence or absence of this batch normalization can cause a large difference in performance. In this case, the batch normalization layer is the process of calculating the average and variance of the characteristic vectors of the previous hidden layer and then normalizing them. However, when generator G must contain complex structural features and high-frequency components, such as super-resolution restoration, this batch normalization rather adversely affects high-resolution image generation. In this paper, we rely on a single input low-resolution image for learning. This results in spatial loss and loss of important high-frequency components contained in the input low-resolution image through the batch normalization process, which eventually fails to draw correct inference. To solve this problem, spatially adaptive denormalization [14] is utilized. Based on this, important components of low-resolution images are preserved and spatial loss is minimized.

As shown in Figure 6, if the characteristic space from generator G is H, the spatial adaptive denormalization technique S can be expressed in the form of an element-wise product or element agreement of $\gamma$ and $\beta$. This is expressed as a formula, as follows.

$$\begin{array}{c}\hfill S(L,T)=\gamma \left(L\right){\times }_{element}\frac{(T-{\mu }_T)}{{\sigma }_T}{+}_{element}\beta \left(L\right)\end{array}$$

(5)

${\mu }_T$ and ${\sigma }_T$ are the mean and standard deviation considering all the elements of each characteristic space channel, and ${\times }_{element}\frac{T-{\mu }_T}{{\sigma }_T}$ and ${+}_{element}\beta \left(L\right)$ represent the product of each element and the sum of each element, respectively. Here, the product of each element and the sum of each element are calculated for each element in each channel. Since T, $\gamma$, and $\beta$ are tensors with the same channel depth, the product of each element and the sum of each element are possible. In addition, as shown in the figure, the spatial adaptive non-normalization technique normalizes the characteristic space T and then combines the information of the characteristic space of the input low-resolution image into the product of each element and the sum of each element, respectively. As previously explained, spatial feature information and high-frequency information are lost due to the general batch normalization process, and through this technique, features with various spatial characteristics can be reflected in the decoder. This is similar to analyzing images over different sizes, such as image pyramid shapes, and identifying features of each size. Through this, the process can take the form of a hierarchical structure, which means that both structural features in a wide range of images and detailed features in a narrow range of images can be restored in super-resolution. Figure 7 presents the overall network structure of the proposed method. In the entire network, low-resolution images are converted into input, the encoder into original size input, and the decoder into hierarchical image size, as mentioned above and used as input. After that, the high-resolution image generated by the discriminator and the original high-resolution image are used to determine whether it is real or fake.

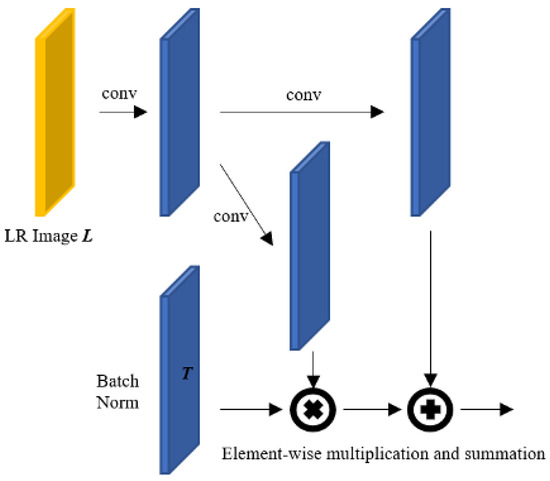
Figure 6. Spatially adaptive denormalization structure for single image super-resolution: From the low-resolution image L and the batch normalization layer T, through the convolution steps and element-wise multiplication and summation, the process obtains the final result to input into G and D.

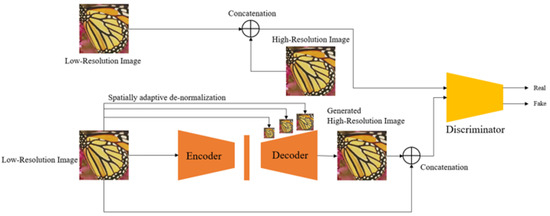
Figure 7. The overall structure of single image super-resolution via spatially adaptive denormalization: The proposed SPADE-GAN structure is differentiated from ordinary super-resolution methods in the decoder because it uses hierarchical image inputs to obtain feature maps. With this new method, the discriminator D compares the fake image and the real image.

4. Experiments and Results

The PC environment used in this paper consisted of an Intel Core i9 CPU and a GTX 1080Ti 16 GB GPU. Both the proposed method and the comparison method were implemented in the Pytorch environment. Before conducting the experiment with text images, we used the DIV2K dataset [17] as a data set for pre-training, released in 2017 in CVPR’s “New Trends in Image Restoration and Enhancement Workshop”, and selected and compared SRNN [9] and SRGAN [2]. For the comparison between the existing method and the method used in this paper, 800 pairs of data were used as a training set, 100 pairs were used as a validation set, and 100 pairs were used as a test set. A total of 300 epochs were conducted for training, and the learning rate was adjusted using the Adam method as the optimization method. Additionally, for the uniform training and testing environment, for the comparison algorithms, this study chose comparison algorithms consisting of similar hyper-parameters, such as loss function and the depth of the architecture of each algorithm. Then, during the pre-training, all of the other hyper-parameters were maintained for uniform testing environments. However, in the case of this dataset, there were no photos of documents or characters, so an additional 500 pairs of self-produced datasets were attached to conduct learning. Besides this paper, many previous works have also mentioned the lack of document image datasets. To solve this problem, a dataset was composed with various types of document images, such as scanned documents and camera-taken pictures. A total of 300 pairs of training sets and 150 pairs of validation and training sets were pre-trained on a total of 500 pairs of datasets. In addition, in the case of OCR, which is the main purpose of text super-resolution restoration, there is no significant difference in efficiency in documents with image quality between 300 and 600 dpi. However, for documents between 75 and 100 dpi, its efficiency drops sharply [9,10,15]. Therefore, the main target for the super-resolution restoration of document images that have undergone a process such as scanning is documents of 75 dpi or less. In this paper, after setting the original image of the same document image, the resolution was lowered to 72 dpi to generate a low-resolution image, and then a comparative analysis was performed. The Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) were used as objective indicators for performance identification. These two indicators are typically used to determine the similarity of images, PSNR comparing the size between image pixels and SSIM determining the structural similarity of images.

Figure 8 shows the results of the ultra-high-resolution restoration technique of the document image through each method. In the case of high-resolution images restored with SRCNN, it was difficult to accurately identify the characters after relatively high-resolution restoration, as they showed a spreading appearance. The results of high-resolution restoration through SRGAN allowed natural edge restoration and stroke separation compared to SRCNN. However, not only did the color of the image change due to the formation of a grid on the edge [1], but the overall image quality also appeared to be degraded [2]. On the other hand, we show that the method presented in this paper uses a conditional adversarial generation network to show superior image quality problems and fine edge planning restoration to preserve characteristic space features in both images and characters. In addition to the results in Figure 8, Table 1 summarizes the quantitatively judged PSNR and SSIM indicators, showing that the quantitative indicators are high in the order presented in this paper, i.e., SRGAN to SRCNN. In particular, the commonly used quantitative indicators in SRCNN and SRGAN show similar patterns, but it can be seen that the method presented in this paper shows the highest figure. This means that the method presented in this paper represents the best quality super-resolution image, even as a quantitative indicator outside of the visible area. Through Table 2, the learning time for each structure can also be confirmed. As previously described, the advantage of SRCNN is that learning was possible in a relatively short time [15]. However, it can be confirmed that the method presented in this paper is slightly faster in the same dataset and PC environment. This paper shows that our method is more efficient with less weight in the learning environment.

Figure 8. Comparison for each method: (a) The ground-truth low-resolution image. (b) Restored low-resolution image with SRCNN algorithm. (c) Restored low-resolution image with SRGAN. (d) Restored low-resolution image with proposed architecture. As mentioned in Section 4, restored images using SRCNN present unclear edges and contain some blur effects. With SRGAN, the edges of the text present more clearly than with SRCNN; however, the result’s color changed. Finally, the results from the proposed method present more clear edge texture and image color, and have not changed compared to previous works.

Table 1. Results of each model: Compared to ordinary methods using SRGAN [9] and SRCNN in previous works [15], the proposed method has higher scores both in PSNR and SSIM.

	SRCNN	SRGAN	Ours
PSNR [dB]	26.25	26.98	28.32
SSIM	0.7145	0.7319	0.8217

Table 2. Speed of each model: In the same environment, the proposed method has high-quality speed compared to ordinary methods.

	SRCNN	SRGAN	Ours
Time [min]	90	70	78

5. Conclusions

In this paper, we proposed a technique for restoring ultra-high-resolution images through spatial adaptive denormalization from a single image. We connected the existing ultra-high-resolution problems with low-resolution and high-resolution domain conversions to solve them, and used convolutional neural networks and adversarial generation networks. In addition, spatial adaptive denormalization techniques were applied to prevent spatial information loss and image feature loss caused by a structure using a batch normalization layer. As a result, we achieved ultra-high-resolution restoration that preserves detailed textures and edges within the document image, which showed higher performance figures qualitatively and quantitatively than conventional methods. Additionally, this paper showed that this proposed method can be adapted not only for the natural image, but also for document images. However, since the detailed texture and edge restoration still do not match the original high-resolution image, we will analyze the hierarchical information of the input image and upgrade and apply it to further enhance the performance index. For future works, it is better to attempt this proposed method for the taken notes. Finally, as the results showed, there are still some missed points in some details based on several fonts and texts in different languages; this could be one of the most significant limitations of this proposed method, and more advanced methods should solve this through several methods, such as more detailed hierarchical inputs and more feature maps, and adapting to several fonts.