Resource Allocation of Multiple Base Stations for Throughput Enhancement in UAV Relay Networks

Abstract

An unmanned aerial vehicle (UAV), with the advantages of mobility and easy deployment, serves as a relay node in wireless networks, which are known as UAV relay networks (URNs), to support user equipment that is out of service range ($U_o$) or does not have a direct communication link from/to the base station (BS) due to severe blockage. Furthermore, URNs have become crucial for delivering temporary communication services in emergency states or in disaster areas where the infrastructure is destroyed. The literature has explored single transmissions from one BS to a UAV to establish a wireless backhaul link in the URN; however, there exists a possibility of $U_o$ outages due to severe interference from an adjacent BS, causing an overall throughput degradation of user equipment (UE) in the URN. In this paper, to improve the signal-to-interference-plus-noise ratio (SINR) of a wireless backhaul link, avoid an outage of $U_o$, and guarantee a reliable relay transmission, simultaneous transmissions from multiple BSs (e.g., macrocell BSs (mBSs) and small cell BSs (sBSs)) is considered. An outage probability is analyzed, and an optimal transmit time allocation algorithm is proposed to maximize the throughput of the UE and guarantee a reliable relay transmission. Simulation results demonstrate that simultaneous transmissions from multiple BSs in the URN leads to higher throughput and reliable transmission without an $U_o$ outage compared to a single transmission in the URN from a single BS (e.g., mBS or sBS), and the optimization of transmit time allocation is essential in the URN.

1. Introduction

With the rapid advances in unmanned aerial vehicle (UAV) technologies, UAVs have been utilized in a wide range of applications, such as military, public safety, and civil applications [1,2,3,4,5,6,7]. Specifically, considerable attention has been paid to enhancing the network capacity, utilizing the UAV as an aerial node, which forms the UAV network. The UAV base station (BS) is considered a key technology to satisfy the service requirement of the fifth generation (5G) and beyond networks [8,9,10,11]. The UAV relay node, which forms the UAV relay network (URN), can provide an extra communication link to the remote user equipment (UE) [12,13]. The demand for UAV networks is growing, hence, the research studies have improved the performances of UAV networks.

UAV networks possess unique features, such as high aerial node mobility, dynamic topology, intermittent links, and power constraints [1]. These features are quite different from those in mobile ad hoc networks (MANETs) and vehicular ad hoc networks (VANETs); therefore, protocols for UAV networks need to be developed, considering the unique features of UAV networks. Even though UAV networks have different features from MANETs and VANETs, they have been applied to support them. Ref. [14] examined the integration of UAV networks with vehicle networks in VANETs to aid in the routing process and the detection of malicious vehicles. The proposed routing protocol achieves gains of 16% and 7% in packet delivery ratio and malicious vehicle detection, respectively, cooperating with UAV networks. In addition, UAV networks can play an important role in realizing safer autonomous vehicles by sharing traffic or accident information quickly with vehicles within a monitoring range [15,16]. Another unique feature of UAV networks is the strong air-to-ground and air-to-air line-of-sight(LOS) channel link. Ref. [17] provided a comprehensive survey of the design of UAV channel characteristics with field measurements and a statistical channel model. Empirical, deterministic, stochastic, and geometry-based stochastic modeling approaches are summarized with their pros and cons.

The deployment and trajectory of UAVs have emerged as significant research areas in the construction of UAV networks since they determine the channel conditions between a ground node and a UAV or between UAVs. Ref. [13] summarized research studies on UAV deployment and trajectory when a UAV served as an aerial BS, a relay station (RS), or an aggregator. The deployment of UAV BS and RS aims to maximize the coverage area, overall throughput, and spectral efficiency, and minimize the transmit delay and power. When the UAV is applied as an aggregator to collect data from or to disseminate information to devices or sensors, minimizing energy consumption and mission completion time is crucial to extending the network lifetime due to the power constraints on the UAV. Machine learning (ML) frameworks are integrated into UAV deployment and trajectory to satisfy the target performances of applications. In [18], the authors proposed the echo state network (ESN)-based prediction algorithm and multi-agent Q-learning-based placement algorithm for the joint optimization of UAV deployment and power control. The authors in [19] introduced Q-learning to maximize the sum rate, and the proposed algorithm can learn the network topology for unknown environments to improve the performance of the network.

Due to the inherent nature of wireless communications, UAV networks are prone to security threats. Ref. [20] provided a systematic survey for secure communication in IoT-based UAV networks. IoT-based UAV networks consist of interconnected UAVs, which are equipped with sensors. Physical and logical attacks are defined, and solutions based on encryption, blockchain, and software-defined networking (SDN) are summarized. The physical attacks, and the threats that degrade the quality-of-service (QoS) in UAV networks or disable reliable transmission, are of considerable concern. Ref. [21] investigated the physical layer security to bolster secure transmission in satellite networks, which share their downlink spectra with terrestrial cellular networks. Hybrid zero-forcing and partial zero-forcing beamforming schemes are proposed to maximize the instantaneous rate of terrestrial cellular users while satisfying the interference probability constraint of satellite users. Ref. [22] proposed hybrid beamforming at the BS and digital beamforming at satellites to maximize the achievable secrecy-energy efficiency of a satellite–terrestrial integrated network, which shares the millimeter-wave spectral resource with a cellular network. In [23], the authors exploited the effects of an aerial intelligent-reflecting surface (IRS) to improve the communication security. An IRS is transported by a UAV, and the deployment and phase shift of aerial IRS aimed at maximizing the secrecy rate is accomplished by successive convex approximation (SCA) and Riemannian manifold optimization (RMO) methods, respectively. Satellite communications share similarities with UAV networks, as both operate under constraints on limited power at UAVs and satellites and leverage a strong LOS link. In this sense, security techniques proposed in [21,22,23] can be adapted for robust transmission in UAV networks. In addition, the authors in [24] introduced a reconfigurable intelligent surface (RIS) to boost the received signal power, and proposed joint beamforming and optimization for RIS-aided hybrid satellite–terrestrial relay networks to minimize the total transmit power at both the satellite and BS, while guaranteeing the required rate of users. This can serve as a potential technique to improve the signal power in UAV relay networks in the future.

As mentioned above, there has been research on the construction of UAV networks, UAV deployment, performance enhancement, and reliable and secure transmission because UAV networks ensure unique features over MANETs and VANETs and have the potential to provide robust solutions for problems that current networks are facing. Furthermore, URN can provide many advantages. Compared to the terrestrial relay network, URN is more cost-effective and much easier to be deployed, and can extend the service range of the ground BS with less transmit power, guaranteeing a reliable relay transmission with a strong air-to-ground LOS link. In addition, the mobility of the UAV can improve the performance of URN via the UAV position adjustment to achieve higher throughput and enhance the signal-to-interference-plus-noise ratio (SINR) of a wireless backhaul link. Such advantages allow the URN to support temporary communication services where tremendous data transmissions are suddenly required or emergency communication links are needed due to infrastructure destruction or natural disasters [2]. However, studies on URN are less frequently conducted compared to the UAV BS case, due to its limited capacity to support users with seamless wireless connectivity [13].

In the URNs, the SINR enhancement of a wireless backhaul link is the key to guaranteeing a reliable relay link to isolated user equipment $\left(U_o\right)$ without throughput degradation of another UE in the URN. Several studies have focused on achieving a stronger backhaul link in the URN by focusing on optimal UAV placement and resource allocation [25,26,27,28,29,30,31]. In [25], the resource allocation of the transmission power, bandwidth and transmission rate, and the position of the UAV relay node are jointly investigated to maximize the system throughput. The formulated problem is transferred to a monotonic optimization problem to achieve the optimal global solution. Ref. [26] considered a cellular-to-UAV and an air-to-ground path loss model for the wireless backhaul link and downlink scenario, respectively, to solve the problem of the efficient placement of an aerial relay node for the overall throughput maximization. Ref. [27] cooperatively optimized the UAV trajectory and relay power allocation to maximize the minimum achievable information rate for the communication link between two ground users. Ref. [28] utilized multiple UAVs and proposed a UAV deployment algorithm to provide seamless relay connectivity to a remote user and maximize the average data rate of the user in the URN. In [29], an orthogonal transmission at the BS with a decode and forward (DF) relay scheme was considered to optimize the throughput of $U_o$, but without considering that of other UE. Ref. [29] introduced non-orthogonal transmission at the BS in the URN, which could effectively extend the service range of the BS, and increase the throughput capacity compared to the orthogonal transmission. Ref. [30] applied non-orthogonal transmission to URN and proposed optimal resource management of transmit power and time at BS and UAV to maximize the throughput of the UE within a BS service range and simultaneously guarantee seamless relay transmission to $U_o$. Ref. [31] proposed UAV deployment and the time allocation algorithm for fast and optimal UAV deployment. It first determines the minimum required transmission time slots between ground BS and UAV and between UAV and a remote user to ensure a robust wireless backhaul and access link.

Studies in [25,26,27,28,29,30,31] considered a single transmission from a single BS to set up a wireless backhaul link without considering an adjacent BS. However, due to interference from a nearby BS, an outage of $U_o$ can occur because it cannot have a strong relay link, which results in the throughput degradation of other UE in the URN. Motivated by this issue and the importance of the SINR enhancement to guarantee a reliable relay link in the URN, this paper investigates simultaneous transmissions from multiple BSs to improve the wireless backhaul link, utilizing the swift mobility of the UAV. If there is a small cell BS (sBS) capable of providing a communication link to the UAV, when the UAV is inside the macrocell BS (mBS) coverage, the UAV, due to its fast mobility, can move into the region where it can receive signals from both mBS and sBS. This is a very useful way to utilize UAV in the URN practically; however, the performance enhancement should be analyzed. The main contributions of this paper can be summarized as follows:

• This paper defines simultaneous transmissions from multiple BSs to UAV relay nodes to improve the SINR of a wireless backhaul link. Most of the research studies consider a single transmission from a single BS, which has a limit on the capacity of the wireless backhaul link, thereby degrading the performance of the URN. The fast mobility of the UAV is the most powerful function to use; hence, the deployment of UAVs within the region where it can receive a signal from multiple BSs is a simple concept but a practical way in the real world.
• To demonstrate the improvement of the SINR of a wireless backhaul link and guarantee a reliable relay transmission to $U_o$, an outage probability of $U_o$ is first derived mathematically to prove a seamless transmission to $U_o$. When an outage occurs, the throughput of $U_m$ becomes worse, which decreases the overall performance of URN. This paper proves that $U_o$ does not experience an outage, and the performance improvement of $U_m$ is achieved by the proposed method.
• To further enhance the throughput of $U_m$ and extend the UAV operation range, the optimal time allocation algorithm for the adaptive time allocation parameter $\lambda$ is proposed, utilizing a bisection method, which guarantees the optimality in the worst case when the length of uncertainty interval is smaller than the predetermined tolerance.

The rest of this paper is organized as follows. Section 2 explains the different system models of URNs and analyzes the outage probabilities. In Section 5, we formulate the optimization problem and propose an optimal time allocation algorithm. Section 6 demonstrates the superior performances of simultaneous transmissions in the URN from simulations, and our conclusion is drawn in Section 7.

2. System Model

We consider two-hop downlink relay networks, where an $U_o$ cannot have a direct transmission link from the nearby mBS and sBS due to severe blockages or under an emergency state, as shown in Figure 1. A relay transmission in the URN consists of two time slots, as shown in Figure 2. In the first time slot, the transmission from mBS or sBS is considered, where mBS uses a non-orthogonal transmission to transmit a superposition-coded signal to the UE in the macrocell ($U_m$) and UAV simultaneously, or sBS utilizes orthogonal transmission to transmit the data to UAV, respectively. It is well known that a non-orthogonal transmission at mBS in the URN achieves superior performance in terms of the overall throughput of the UE in the macrocell over an orthogonal transmission [30]. sBS supports mBS when the wireless backhaul link cannot provide a reliable relay link to $U_m$ and sBS has extra time resources. Therefore, we assume that sBS utilizes orthogonal transmission to maximize the throughput enhancement. In the second time slot, UAV forwards the received data in the first time slot to $U_o$. It is assumed that the channel condition between mBS and $U_m$ is better than that between mBS and UAV in general, because UAV remains closer to $U_o$ to set a strong LOS air-to-ground link.

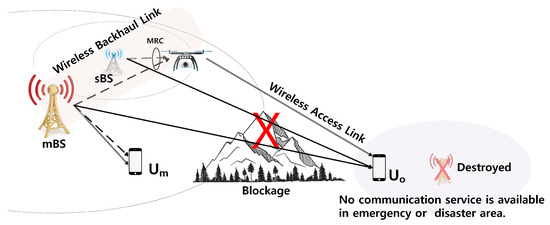
Figure 1. System model: multiple BSs in the URN.

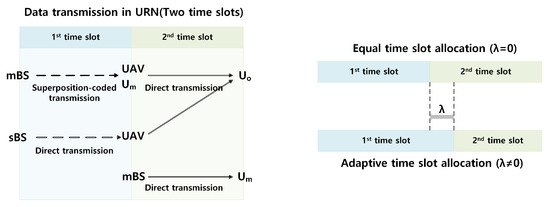
Figure 2. Time slot allocation by the adaptive parameter of $\lambda$.

2.1. Signal-to-Interference-Plus-Noise Ratio (SINR)

Simultaneous transmissions from mBS and sBS can guarantee a seamless relay transmission to $U_o$ and maximize the throughput of the UE in the URN, with the placement of UAV in a region where the UAV can receive signals from both mBS and sBS. Therefore, the SINR of a wireless backhaul link can be improved for a reliable relay transmission. Due to the non-orthogonal transmission in the power domain, mBS uses the transmit power of $P_{mBS}$, where $P_{mBS,U_m}^{1^{st}}$ and $P_{mBS,UAV}^{1^{st}}$ are transmit powers allocated to the mBS-to-$U_m$ link and mBS-to-UAV link in the first time slot, respectively. On the other hand, sBS transmits a signal with a maximum power of $P_{sBS}$ to a scheduled node (e.g., UAV).

If the relay transmission originates from mBS, both $U_m$ and the UAV receive a superposition-coded signal, but $U_m$ can remove the interference from the BS-UAV link by using the successive interference cancellation [32]. This is due to the channel condition that the BS-to-$U_m$ link has a better channel condition than the BS-to-UAV link. On the other hand, the UAV receives interference from the BS-to-$U_m$ link. Since sBS acts as an interference source to the relay transmission, both $U_m$ and UAV receive interference from it. In another case, where relay transmission originates from sBS, the UAV receives forwarding data from sBS and interference from mBS. In summary, the received SINRs at the UAV for mBS-to-UAV and sBS-to-UAV links and the received SINR at $U_m$ in the first time slot are given by

$$\begin{array}{cc}\hfill SIN{R}_{mBS,UAV}^{1^{st}}& =\frac{P_{mBS,UAV}^{1^{st}}{g}_{mBS,UAV}}{P_{sBS}{g}_{sBS,UAV}+P_{mBS,U_m}^{1^{st}}{g}_{mBS,UAV}+{\sigma }_{UAV}^2},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill SIN{R}_{sBS,UAV}^{1^{st}}& =\frac{P_{sBS}{g}_{sBS,UAV}}{(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})g_{mBS,UAV}+{\sigma }_{UAV}^2}=\frac{P_{sBS}{g}_{sBS,UAV}}{P_{mBS}{g}_{mBS,UAV}+{\sigma }_{UAV}^2},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill SIN{R}_{mBS,U_m}^{1^{st}}& =\frac{P_{mBS,U_m}^{1^{st}}{g}_{mBS,U_m}}{P_{sBS}{g}_{sBS,U_m}+{\sigma }_{U_m}^2},\hfill \end{array}$$

(3)

where $g_{tx,rx}\triangleq h_{tx,rx}·l_{tx,rx}$ denotes the channel gain, $h_{tx,rx}$ denotes the small-scale fading coefficient, $l_{tx,rx}=d_{tx,rx}^{-pathloss}$ denotes the path loss-dependent large-scale fading coefficient, and $d_{tx,rx}$ denotes the distance between the transmitter (tx) and receiver (rx), respectively. ${\sigma }_i^2$ denotes the variance of the additive white Gaussian noise (AWGN) at node i. Note that $U_m$ receives its own data from mBS; hence, (3) is consistent, regardless of the relay transmission source.

In the second time slot, the UAV forwards the received signal from mBS or sBS in the first time slot to $U_o$ with a transmit power of $P_{UAV}$, and $U_m$ receives a signal with the power of $P_{mBS,U_m}^{2^{nd}}(=P_{mBS})$ from mBS. Both $U_o$ and $U_m$ receive interference from sBS. The received SINRs at $U_o$ and $U_m$ in the second time slot are expressed as follows:

$$\begin{array}{cc}\hfill SIN{R}_{UAV,U_o}^{2^{nd}}& =\frac{P_{UAV}{g}_{UAV,U_o}}{P_{mBS,U_m}^{2^{nd}}{g}_{mBS,U_o}+P_{sBS}{g}_{sBS,U_o}+{\sigma }_{U_o}^2},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill SIN{R}_{mBS,U_m}^{2^{nd}}& =\frac{P_{mBS,U_m}^{2^{nd}}{g}_{mBS,U_m}}{P_{sBS}{g}_{sBS,U_m}+P_{UAV}{g}_{UAV,U_m}+{\sigma }_{U_m}^2}.\hfill \end{array}$$

(5)

2.2. Throughput

The data rate in the bps/Hz of $U_m$, $R_{U_m}$, and that of $U_o$, $R_{U_o}$, can be calculated by the Shannon formula [33], as

$$\begin{array}{cc}\hfill R_{U_m}& =\frac{(1+\lambda )}{2}{R}_{mBS,U_m}^{1^{st}}+\frac{(1-\lambda )}{2}{R}_{mBS,U_m}^{2^{nd}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill R_{U_o}& =min\left(\frac{(1+\lambda )}{2}{R}_{xBS,UAV}^{1^{st}},\frac{(1-\lambda )}{2}{R}_{UAV,U_o}^{2^{nd}}\right),\hfill \end{array}$$

(7)

where $R_{mBS,U_m}^{1^{st}}={log}_2(1+SIN{R}_{mBS,U_m}^{1^{st}})$, $R_{mBS,U_m}^{2^{nd}}={log}_2(1+SIN{R}_{mBS,U_m}^{2^{nd}})$ and $R_{UAV,U_o}^{2^{nd}}={log}_2(1+SIN{R}_{UAV,U_o}^{2^{nd}})$. $R_{xBS,UAV}^{1^{st}}={log}_2(1+SIN{R}_{mBS,UAV}^{1^{st}})$ if data are transmitted from mBS to UAV, otherwise, $R_{xBS,UAV}^{1^{st}}={log}_2(1+SIN{R}_{sBS,UAV}^{1^{st}})$. The maximal ratio combining (MRC) [33] is applied to the calculation of $R_{xBS,UAV}^{1^{st}}$. Moreover, (7) adheres to the fact that the data rate of the access link cannot exceed that of the wireless backhaul link. $\lambda$$(-1\le \lambda \le 1)$ is the adaptive time allocation parameter, which determines the length of each time slot, as depicted in Figure 2.

2.3. Outage Probability

To guarantee the seamless relay transmission to $U_o$, the outage probability of $U_o$, where $R_{U_o}$ is less than the minimum required data rate $\eta$, can be defined and expanded as follows:

$$\begin{array}{}\mathrm{(8a)}& \hfill P_{out}\left(R_{U_o}\right|\eta )& =prob\left(R_{U_o}\le \eta \right)\hfill \mathrm{(8b)}& \hfill & =1-prob\left(R_{U_o}^{\left(1\right)}\ge \eta ,R_{U_o}^{\left(2\right)}\ge \eta \right)\hfill \mathrm{(8c)}& \hfill & \stackrel{\left(a\right)}{=}1-prob\left(R_{U_o}^{\left(1\right)}\ge \eta \right)prob\left(R_{U_o}^{\left(2\right)}\ge \eta \right),\hfill \end{array}$$

where $R_{U_o}^{\left(1\right)}=\frac{(1+\lambda )}{2}{R}_{xBS,UAV}^{1^{st}}$, $R_{U_o}^{\left(2\right)}=\frac{(1-\lambda )}{2}{R}_{UAV,U_o}^{2^{nd}}$ from (7), and $\left(a\right)$ in (8c) follows the independence of two events.

3. Simultaneous Transmissions from Multiple Base Stations in the URN (Multi-BSs-URN)

We assume that mBS and sBS can transmit the same data to the UAV in the first time slot. Therefore, the SINR of a wireless backhaul link can be improved by simultaneous transmissions from both mBS and sBS when UAV moves inside mBS and sBS service ranges. When UAV receives signals from both BSs, the MRC is applied; hence, $R_{xBS,UAV}^{1^{st}}$ can be obtained as $R_{(mBS+sBS),UAV}^{1^{st}}={log}_2(1+SIN{R}_{mBS,UAV}^{1^{st}}+SIN{R}_{sBS,UAV}^{1^{st}})$. Based on the positions of mBS, sBS, UAV, and $U_m$, two channel conditions can be assumed: (1) the channel condition between mBS and $U_m$ is better than that between mBS and UAV (i.e., $g_{mBS,U_m}>g_{mBS,UAV}$), and (2) the channel condition between sBS and UAV is better than that between mBS and UAV (i.e., $g_{sBS,U_{UAV}}>g_{mBS,UAV}$). Therefore, $SIN{R}_{mBS,UAV}^{1^{st}}$ with $P_{sBS}=0$ is used to calculate $R_{(mBS+sBS),UAV}^{1^{st}}$ since UAV can eliminate interference from the sBS-to-UAV link when decoding data from the mBS-to-UAV link. In the second time slot, no transmission from sBS is assumed; therefore, $P_{sBS}=0$ is in the denominators of (4) and (5). With the conditions that $P_{sBS}=0$ in the denominator of (1),

$$\begin{array}{cc}\hfill & prob\left(R_{U_o}^{\left(1\right)}\ge \eta \right)\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill & =prob(\frac{P_{mBS,UAV}^{1^{st}}{g}_{mBS,UAV}}{P_{mBS,U_m}^{1^{st}}{g}_{mBS,UAV}+{\sigma }_{UAV}^2}+\frac{P_{sBS}{g}_{sBS,UAV}}{P_{mBS}{g}_{mBS,UAV}+{\sigma }_{UAV}^2}\ge 2^{{\omega }^{+}}-1)\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill & =E_{h_{mBS,UAV}}\left[prob\left(h_{sBS,UAV}\ge {\psi }^{B{S}_{(m+s)}}\left(h_{mBS,UAV}\right)\right)\right]\hfill \end{array}$$

(9c)

$$\begin{array}{cc}\hfill & \stackrel{\left(a\right)}{=}{E}_{h_{mBS,UAV}}\left[1-\frac{\gamma \left(k_{sBS,UAV},k_{sBS,UAV}{\psi }^{B{S}_{(m+s)}}\left(h_{mBS,UAV}\right)\right)}{\Gamma \left(k_{sBS,UAV}\right)}\right]\hfill \end{array}$$

(9d)

$$\begin{array}{cc}\hfill & \stackrel{\left(b\right)}{=}1-\underset{0}{\overset{x_{max}}{\int }}\frac{\gamma \left(k_{sBS,UAV},k_{sBS,UAV}{\psi }^{B{S}_{(m+s)}}\left(x\right)\right)}{\Gamma \left(k_{sBS,UAV}\right)}{f}_{h_{mBS,UAV}}\left(x\right)dx,\hfill \end{array}$$

(9e)

where

$$\begin{array}{cc}\hfill & {\omega }^{+}=\frac{2\eta }{1+\lambda },\hfill \\ \hfill & {\psi }^{B{S}_{(m+s)}}\left(h_{mBS,UAV}\right)=\frac{(2^{{\omega }^{+}}-1){\sigma }_{UAV}^4-A_1{h}_{mBS,UAV}^2-A_3{h}_{mBS,UAV}}{A_2{h}_{mBS,UAV}+A_4},\hfill \\ \hfill & A_1=\left(P_{mBS,UAV}^{1^{st}}-\left(2^{{\omega }^{+}}-1\right)P_{mBS,U_m}^{1^{st}}\right)(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})l_{mBS,UAV}^2,\hfill \\ \hfill & A_2=P_{mBS,U_m}^{1^{st}}{P}_{sBS}{l}_{mBS,UAV}{l}_{sBS,UAV},\hfill \\ \hfill & A_3={\sigma }_{UAV}^2{l}_{mBS,UAV}\left(P_{mBS,UAV}^{1^{st}}-\left(2^{{\omega }^{+}}-1\right)(P_{mBS,U_m}^{1^{st}}+P_{mBS})\right),\hfill \\ \hfill & A_4=P_{sBS}{\sigma }_{UAV}^2{l}_{sBS,UAV},\hfill \\ \hfill & f_{h_{mBS,UAV}}\left(x\right)=\frac{{k_{mBS,UAV}}^{k_{mBS,UAV}}}{\Gamma \left(k_{mBS,UAV}\right)}{x}^{(k_{mBS,UAV}-1)}{e}^{-k_{mBS,UAV}x},x\ge 0,\hfill \end{array}$$

$\left(a\right)$ in (9d) takes the expectation with respect to $h_{mBS,UAV}$, and $\left(b\right)$ in (9e) follows that $h_{mBS,UAV}$ has a $Gamma(k_{mBS,UAV},1/k_{mBS,UAV})$ with a gamma function $\Gamma \left(t\right)=\underset{0}{\overset{\infty }{\int }}{z}^{t-1}{e}^{-z}dz$, and a lower incomplete gamma function $\gamma (s,x)=\underset{0}{\overset{x}{\int }}{z}^{s-1}{e}^{-z}dz$. The integral in (9e) should guarantee ${\psi }^{B{S}_{(m+s)}}\left(x\right)\ge 0$; therefore, the integral interval needs to be selected carefully. Based on the fact that ${\psi }^{B{S}_{(m+s)}}\left(0\right)\ge 0$, $A_2\ge 0$, and $A_4\ge 0$, it guarantees that ${\psi }^{B{S}_{(m+s)}}\left(x\right)\ge 0$, $\forall x\ge 0$ if $A_1<0$. Otherwise, ${\psi }^{B{S}_{(m+s)}}\left(x\right)\ge 0$, only with a proper upper limit of $x_{max}$,

$$x_{max}=\left\{\begin{array}{cc}\frac{-A_3+\sqrt{{A_3}^2+4A_1\left(2^{{\omega }^{+}}-1\right){\sigma }_{UAV}^4}}{2A_1},\hfill & \mathrm{if}{A}_1\ge 0,\hfill \\ \infty ,\hfill & \mathrm{if}{A}_1<0.\hfill \end{array}\right.$$

(10)

The second probability $prob\left(R_{U_o}^{\left(2\right)}\ge \eta \right)$ in (8c) can be expanded as

$$\begin{array}{cc}\hfill & prob\left(R_{U_o}^{\left(2\right)}\ge \eta \right)\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill & =prob\left((1-\lambda )R_{UAV,U_o}^{2^{nd}}\ge \eta \right)\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill & =prob(\frac{P_{UAV}{g}_{UAV,U_o}}{P_{mBS,U_m}^{2^{nd}}{g}_{mBS,U_o}+P_{sBS}{g}_{sBS,U_o}+{\sigma }_{U_o}^2}\ge 2^{{\omega }^{-}}-1)\hfill \end{array}$$

(11c)

$$\begin{array}{cc}\hfill & \stackrel{\left(a\right)}{=}{E}_{h_{UAV,U_o}}{E}_{h_{sBS,U_o}}\left[P(h_{mBS,U_o}\le B_1{h}_{UAV,U_o}-B_2{h}_{sBS,U_o}-B_3)\right]\hfill \end{array}$$

(11d)

$$\begin{array}{cc}\hfill & \stackrel{\left(b\right)}{=}1-E_{h_{UAV,U_o}}{E}_{h_{sBS,U_o}}\left[e^{-B_1{h}_{UAV,U_o}+B_2{h}_{sBS,U_o}+B_3}\right]\hfill \end{array}$$

(11e)

$$\begin{array}{cc}\hfill & =1-E_{h_{UAV,U_o}}\left[e^{-B_1{h}_{UAV,U_o}}\right]E_{h_{sBS,U_o}}\left[e^{B_2{h}_{sBS,U_o}}\right]e^{B_3}\hfill \end{array}$$

(11f)

$$\begin{array}{cc}\hfill & \stackrel{\left(c\right)}{=}1-{\left(\frac{k_{UAV,U_o}}{k_{UAV,U_o}+B_1}\right)}^{k_{UAV,U_o}}\frac{1}{1-B_2}{e}^{B_3},\hfill \end{array}$$

(11g)

where

$$\begin{array}{cc}\hfill & {\omega }^{-}=\frac{2\eta }{1-\lambda },\hfill \\ \hfill & B_1=\frac{l_{UAV,U_o}{P}_{UAV}}{(2^{{\omega }^{-}}-1)l_{mBS,U_o}(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})},\hfill \\ \hfill & B_2=\frac{l_{sBS,U_o}{P}_{sBS}}{l_{mBS,U_o}(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})},\hfill \\ \hfill & B_3=\frac{{\sigma }_{U_o}^2}{l_{mBS,U_o}(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})},\hfill \end{array}$$

$\left(a\right)$ in (11d) takes the expectations with respect to $h_{UAV,U_o}$, $h_{sBS,U_o}$; $\left(b\right)$ in (11e) follows a cumulative distribution function (CDF) of exponential distribution because $h_{mBS,U_o}$ has a exponential distribution of $exp\left(1\right)$. $\left(c\right)$ in (11g) follows a moment-generating function (MGF) of a gamma distribution, $h_{UAV,U_o}Gamma(k_{UAV,U_o},1/k_{UAV,U_o})$ and an exponential distribution $h_{mBS,U_o}exp\left(1\right)$.

4. Comparison: Single Transmission from the Single Base Station in the URN

Simultaneous transmissions from multiple BSs (i.e., mBS and sBS) to UAVs can guarantee a seamless relay transmission to $U_o$ and maximize the throughput of the UE in the URN with the placement of the UAV to a region where the UAV can receive signals from both. To prove the throughput enhancement of simultaneous transmissions in the URN, we consider a single transmission from a single BS (i.e., mBS or sBS) in the URN. It can also provide data to $U_o$; however, interference from an adjacent BS exists, thereby resulting in the outage of $U_o$ and the performance degradation of other UE in the URN. In addition, an outage can occur depending on the SINRs of wireless backhaul and access links during two time slots, which are dependent on the position of the UAV.

4.1. mBS-Based URN (mBS-URN)

The UAV receives a signal via a wireless backhaul link in the first time slot only from mBS, even when the UAV is within an sBS service range. This is an equivalent model considered in [30]; however, with interference from the sBS. Because it does not receive a signal from sBS, $SIN{R}_{S,UAV}^{1^{st}}=0$ in (2).

With the condition that $SIN{R}_{S,UAV}^{1^{st}}=0$,

$$\begin{array}{cc}\hfill & prob\left(R_{U_o}^{\left(1\right)}\ge \eta \right)\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill & =prob(\frac{P_{mBS,UAV}^{1^{st}}{g}_{mBS,UAV}}{P_{sBS}{g}_{sBS,UAV}+P_{mBS,U_m}^{1^{st}}{g}_{mBS,UAV}+{\sigma }_{UAV}^2}\ge 2^{{\omega }^{+}}-1)\hfill \end{array}$$

(12b)

$$\begin{array}{cc}\hfill & \stackrel{\left(a\right)}{=}{E}_{h_{mBS,UAV}}\left[\frac{\gamma \left(k_{sBS,UAV},k_{sBS,UAV}{\psi }^{mBS-URN}\left(h_{mBS,UAV}\right)\right)}{\Gamma \left(k_{sBS,UAV}\right)}\right]\hfill \end{array}$$

(12c)

$$\begin{array}{cc}\hfill & \stackrel{\left(b\right)}{=}\underset{x_{min}}{\overset{\infty }{\int }}\frac{\gamma \left(k_{sBS,UAV},k_{sBS,UAV}{\psi }^{mBS-URN}\left(x\right)\right)}{\Gamma \left(k_{sBS,UAV}\right)}{f}_{h_{mBS,UAV}}\left(x\right)dx,\hfill \end{array}$$

(12d)

where

$$\begin{array}{cc}\hfill & x_{min}={\left({\psi }^{mBS-URN}\right)}^{-1}\left(0\right),\hfill \\ \hfill & {\psi }^{mBS-URN}\left(h_{mBS,UAV}\right)=\frac{\left(P_{mBS,UAV}^{1^{st}}-\left(2^{{\omega }^{+}}-1\right)P_{mBS,U_m}^{1^{st}}\right)}{\left(2^{{\omega }^{+}}-1\right)P_{sBS}}\frac{l_{mBS,UAV}}{l_{sBS,UAV}}{h}_{mBS,UAV}-\frac{{\sigma }_{UAV}^2}{l_{sBS,UAV}{P}_{sBS}},\hfill \\ \hfill & f_{h_{mBS,UAV}}\left(x\right)=\frac{{k_{mBS,UAV}}^{k_{mBS,UAV}}}{\Gamma \left(k_{mBS,UAV}\right)}{x}^{k_{mBS,UAV}-1}{e}^{-k_{mBS,UAV}x},x\ge 0,\hfill \end{array}$$

and ${\left({\psi }^{mBS-URN}\right)}^{-1}$ is an inverse function of ${\psi }^{mBS-URN}$. $\left(a\right)$ in (12c) takes the expectation with respect to $h_{mBS,UAV}$; $\left(b\right)$ in (12d) follows that $h_{mBS,UAV}$ has a $Gamma(k_{mBS,UAV},$$1/k_{mBS,UAV})$ with a gamma function $\Gamma \left(t\right)=\underset{0}{\overset{\infty }{\int }}{z}^{t-1}{e}^{-z}dz$ and a lower incomplete gamma function $\gamma (s,x)=\underset{0}{\overset{x}{\int }}{z}^{s-1}{e}^{-z}dz$.

4.2. sBS-Based URN (sBS-URN)

URN with a wireless backhaul link only from sBS is considered for the performance comparison. The sBS-UAV link receives interference from mBS transmissions. mBS transmits only to $U_m$ in both time slots; therefore, $SIN{R}_{mBS,UAV}^{1^{st}}$ in (1) is equal to 0, $P_{mBS,U_m}^{1^{st}}=P_{mBS}$ in (2) and (3) because $P_{mBS,UAV}^{1^{st}}=0$.

With the conditions that $SIN{R}_{mBS,UAV}^{1^{st}}=0$, $P_{mBS,U_m}^{1^{st}}=P_{mBS}$ and $P_{mBS,UAV}^{1^{st}}=0$,

$$\begin{array}{cc}\hfill & prob\left(R_{U_o}^{\left(1\right)}\ge \eta \right)\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill & =prob(\frac{P_{sBS}{g}_{sBS,UAV}}{(P_{mBS,U_m}^{1^{st}}+P_{mBS,UAV}^{1^{st}})g_{mBS,UAV}+{\sigma }_{UAV}^2}\ge 2^{{\omega }^{+}}-1)\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill & \stackrel{\left(a\right)}{=}{E}_{h_{sBS,UAV}}\left[\frac{\gamma \left(k_{mBS,UAV},k_{mBS,UAV}{\psi }^{sBS-URN}\left(h_{sBS,UAV}\right)\right)}{\Gamma \left(k_{mBS,UAV}\right)}\right]\hfill \end{array}$$

(13c)

$$\begin{array}{cc}\hfill & \stackrel{\left(b\right)}{=}\underset{x_{min}}{\overset{\infty }{\int }}\frac{\gamma \left(k_{mBS,UAV},k_{mBS,UAV}{\psi }^{sBS-URN}\left(x\right)\right)}{\Gamma \left(k_{mBS,UAV}\right)}{f}_{h_{sBS,UAV}}\left(x\right)dx,\hfill \end{array}$$

(13d)

where

$$\begin{array}{cc}\hfill & x_{min}={\left({\psi }^{sBS-URN}\right)}^{-1}\left(0\right),\hfill \\ \hfill & {\psi }^{sBS-URN}\left(h_{sBS,UAV}\right)=\frac{P_{sBS}}{\left(2^{{\omega }^{+}}-1\right)P_{mBS}}\frac{l_{sBS,UAV}}{l_{mBS,UAV}}{h}_{sBS,UAV}-\frac{{\sigma }_{UAV}^2}{l_{mBS,UAV}{P}_{mBS}},\hfill \\ \hfill & f_{h_{sBS,UAV}}\left(x\right)=\frac{{k_{sBS,UAV}}^{k_{sBS,UAV}}}{\Gamma \left(k_{sBS,UAV}\right)}{x}^{k_{sBS,UAV}-1}{e}^{-k_{sBS,UAV}x},x\ge 0,\hfill \end{array}$$

and ${\left({\psi }^{sBS-URN}\right)}^{-1}$ is an inverse function of ${\psi }^{sBS-URN}$. $\left(a\right)$ in (13c) takes the expectation with respect to $h_{sBS,UAV}$, and $\left(b\right)$ in (13d) follows that $h_{sBS,UAV}$ has a $Gamma(k_{sBS,UAV},$$1/k_{sBS,UAV})$.

5. Optimization Problem and Algorithm

5.1. Problem Formulation: Throughput Maximization

The optimal time allocation to maximize the data rate of $U_m$, while guaranteeing the minimum outage requirement $\epsilon$ of $U_o$, can be obtained by solving the following problem.

$$\begin{array}{cccc}\hfill & \underset{\lambda }{max}\hfill & \hfill & R_{U_m}\hfill \end{array}$$

(14a)

$$\begin{array}{cccc}\hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & P_{out}\left(R_{U_o}\right|\eta )\le \epsilon \hfill \end{array}$$

(14b)

$$\begin{array}{cccc}\hfill & \hfill & & -1\le \lambda \le 1.\hfill \end{array}$$

(14c)

The optimal time allocation for the adaptive parameter $\lambda$ can be achieved by a one-dimensional searching method, such as a bisection method [34]. Similar to the bisection method, an optimal time allocation algorithm is carried out in two steps. First, it determines an initial time allocation ${\lambda }_i$ and a search interval $[a,b]$ between $-1$ and 1. Second, with ${\lambda }_i$ and $[a,b]$ found in the first step, an optimal time allocation ${\lambda }_{opt}$ is defined, such that it maximizes $R_{U_m}$ while guaranteeing an outage probability constraint in (14a). Details are in Algorithms 1 and 2 for each step, respectively.

Algorithm 1 Initialize ${\lambda }_i$ and $[a,b]$
Inputs: $a=-1,b=1$
1:	Calculate ${\lambda }_i=\frac{(a+b)}{2}$
2:	Check the validity of ${\lambda }_i$ by (14b)
3:	if $\lambda$ is valid then
4:	Save ${\lambda }_i$ and $[a,b]$
5:	Break
6:	else
7:	$b={\lambda }_i$ if $R_{(mBS+sBS),UAV}^{1^{st}}>R_{UAV,U_o}^{2^{nd}}$
8:	$a={\lambda }_i$ otherwise
9:	end if
10:	Go to line 1

5.2. Optimal Time Allocation Algorithm

As explained in Section 5.1, outcomes of Algorithm 1, ${\lambda }_i$ and a search interval [a, b], are used as the input to Algorithm 2. Algorithm 1 works as follows. If ${\lambda }_i$ is invalid (i.e., an outage occurs at $U_o$ for a given ${\lambda }_i$), and ${\lambda }_i$ should be decreased or increased until the outage requirement of $R_{U_o}$ in (14a) is satisfied. If $R_{(mBS+sBS),UAV}^{1^{st}}>R_{UAV,U_o}^{2^{nd}}$, ${\lambda }_i$ needs to be decreased to increase $R_{UAV,U_o}^{2^{nd}}$ in $R_{U_o}$ from (7), the next ${\lambda }_i$ needs to be updated within an interval $[a,{\lambda }_i]$. Otherwise, ${\lambda }_i$ should be increased and updated in an interval $[{\lambda }_i,b]$.

Algorithm 2 Optimal time allocation Algorithm
Initialization
Inputs: ${\lambda }_i,[a,b],\tau$.
Initialization: $\lambda ={\lambda }_i$, and go to the line2.
Phase1: Update a search interval.
1:	Check the validity of $\lambda$ by (14b)
2:	if $\lambda$ is valid then
3:	$a=\lambda$ if $R_{mBS,U_m}^{1^{st}}>R_{mBS,U_m}^{2^{nd}}$
4:	$b=\lambda$ otherwise
5:	else
6:	$b=\lambda$ if $R_{mBS,U_m}^{1^{st}}>R_{mBS,U_m}^{2^{nd}}$
7:	$a=\lambda$ otherwise
8:	end if
Phase2: Update $\lambda$.
9:	if  $b-a<\tau$then
10:	Save $\lambda$ as ${\lambda }_{opt}$ and break.
11:	else
12:	$\lambda =\frac{a+b}{2}$
13:	end if
14:	Go to line 1

With an initial ${\lambda }_i$ and a search interval $[a,b]$, Algorithm 1 determines ${\lambda }_{opt}$ based on $R_{mBS,U_m}^{1^{st}}$ and $R_{mBS,U_m}^{2^{nd}}$ in (6). When $R_{mBS,U_m}^{1^{st}}>R_{mBS,U_m}^{2^{nd}}$, maximizing $R_{U_m}$ in (14a) is the same as increasing $\lambda$; hence, $\lambda$ should be updated from $[\lambda ,b]$ for a valid $\lambda$ or from $[a,\lambda ]$ for an invalid $\lambda$ in the next step. On the other hand, when $R_{mBS,U_m}^{1^{st}}<R_{mBS,U_m}^{2^{nd}}$, maximizing $R_{U_m}$ in (14a) is the same as decreasing $\lambda$; therefore, a search interval needs to be changed to $[a,\lambda ]$ for a valid $\lambda$, and $[\lambda ,b]$ for an invalid $\lambda$ to update $\lambda$. ${\lambda }_{opt}$ can be determined when the length of the uncertainty interval $(b-a)$ is smaller than the predetermined value of $\tau$.

The complexity of the optimal time allocation algorithm is equal to $O\left(lo{g}_2(2/\tau )\right)$. It is well-known that the bisection method has a complexity of $O\left(lo{g}_2(W/TOR)\right)$, where W is the width of the initial interval and $TOR$ is the desired tolerance or precision (e.g., $\tau$ in this paper). The number of iterations $n_i$ where the bisection method converges to a root to achieve a required tolerance is upper-bounded as $n_i\leqq n_{i,1/2}\equiv \lceil lo{g}_2(W/TOR)\rceil$. In addition, the bisection method is optimal in that it guarantees a root in the worst case, which has an absolute error of $TOR$ within $n_{i,1/2}$ iterations [35,36].

6. Numerical Results

In this section, we present the simulation results to demonstrate that multi-BSs-URN achieves a higher throughput of $U_m$ without an outage of $U_o$ over mBS-URN or sBS-URN. In addition, it is demonstrated that an optimal time allocation ${\lambda }_{opt}$ extends the operation range of UAV compared to an equal time allocation (i.e., $\lambda =0$, denoted as ${\lambda }_0$ in Figure 3 and Figure 4) and achieves a larger throughput gain.

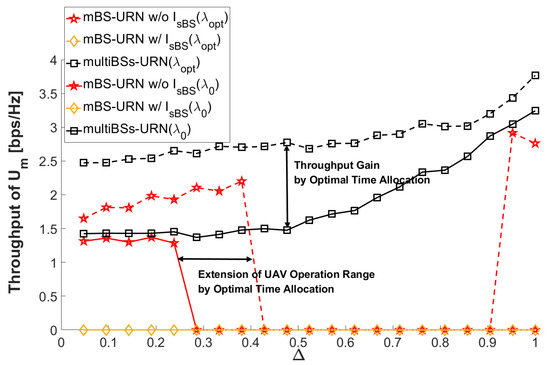
Figure 3. Throughput comparison of multi-BSs-URN and mBS-URN.

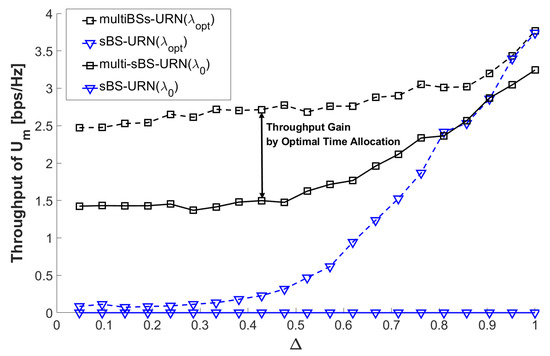
Figure 4. Throughput comparison of multi-BSs-URN and sBS-URN.

The following are assumed for simulations. $U_m$ and $U_o$ are located inside and outside the mBS coverage, respectively; therefore, $U_o$ cannot have a direct link from mBS. sBS is in the middle between $U_m$ and $U_o$, and the distance between sBS and $U_o$ is large, so that there is no direct link between them. UAV moves from $U_m$ to $U_o$, and a relative distance $\Delta$ is defined as $\Delta =\frac{d_{U_m,UAV}}{d_{U_m,U_o}}$. A large $\Delta$ indicates that the UAV stays close to $U_o$, while a small $\Delta$ means that the UAV stays close to $U_m$. An equal power allocation at mBS is assumed in the first time slot, so that $P_{mBS,U_m}^{1^{st}}=P_{mBS,UAV}^{1^{st}}=15$ [dBm], $P_M=30$ [dBm], $P_S=P_{UAV}=25$ [dBm], path loss $=3$, the height of UAV $=70$ [m], $\eta =0.1$ [bps/Hz], $ϵ=0.1$, and $\tau =0.01$.

Figure 3 demonstrates the superior performance of multi-BSs-URN over mBS-URN for both ${\lambda }_{opt}$ and ${\lambda }_0$. The multi-BSs-URN achieves a higher throughput within an entire operation range of UAV without an outage of $U_o$. For comparison, two mBS-URNs are considered; mBS-URN with or without interference from sBS (i.e., mBS-URN w/ I${}_{sBS}$ and mBS-URN w/o I${}_{sBS}$, respectively, in Figure 3). In mBS-URN w/ I${}_{sBS}$, an outage of $U_o$ always occurs for both ${\lambda }_{opt}$ and ${\lambda }_0$, thereby resulting in the throughput degradation of $U_m$ within the operation range of UAV. Even in mBS-URN w/o I${}_{sBS}$, an outage of $U_o$ occurs when $0.4\le \Delta \le 0.9$ for ${\lambda }_{opt}$, and $\Delta \ge 0.25$ for ${\lambda }_0$. This is because a time allocation for two time slots is not enough for reliable relay transmission to $U_o$. When $\Delta \ge 0.9$ for ${\lambda }_{opt}$, $U_m$ achieves high throughput because UAV remains very close to $U_o$ and a small amount of time is needed to set up an access link. Even though mBS-URN suffers from an outage without interference from sBS, it can extend the valid operation range of the UAV from $0\le \Delta \le 0.25$ to $0\le \Delta \le 0.4$ and $\Delta \ge 0.9$ with an optimal ${\lambda }_{opt}$. Figure 4 compares the throughput of multi-BSs-URN with that of sBS-URN. Without a time allocation, sBS-URN suffers from an outage of $U_o$ for an entire operation range of the UAV. For an optimal ${\lambda }_{opt}$, the throughput of $U_m$ is very low when $0\le \Delta \le 0.5$ due to the severe interference from mBS. However, it increases as $\Delta$ increases because the UAV receives less interference when it approaches $U_o$.

Simulation results in Figure 3 and Figure 4 demonstrate that simultaneous transmissions from mBS and sBS can achieve higher throughput over a single transmission from mBS or sBS without an outage of $U_o$, thereby guaranteeing a reliable relay link to $U_o$. Furthermore, the optimal time allocation can provide additional throughput gain and extend the UAV operation range. Therefore, simultaneous transmissions from multiple BSs in the URN with optimal time allocations are essential for the throughput maximization of URN and stable relay transmission to $U_o$.

7. Conclusions

The mobility of UAVs is a powerful function and a simple way to enhance the SINR of a wireless backhaul link in the URN. Simultaneous transmissions from mBS and sBS in the URN with an optimal time allocation is proposed to maximize the throughput of the UE and guarantee a seamless relay transmission without an outage of $U_o$. The outage probability of $U_o$ is analyzed, and an optimal time allocation algorithm is presented. Simulation results demonstrate that simultaneous transmissions from mBS and sBS perform better than a single transmission from mBS or sBS with respect to the overall throughput, and the optimal time allocation is necessary for throughput maximization and the extension of the operation range.