Support Vector Machine Chains with a Novel Tournament Voting

Abstract

Support vector machine (SVM) algorithms have been widely used for classification in many different areas. However, the use of a single SVM classifier is limited by the advantages and disadvantages of the algorithm. This paper proposes a novel method, called support vector machine chains (SVMC), which involves chaining together multiple SVM classifiers in a special structure, such that each learner is constructed by decrementing one feature at each stage. This paper also proposes a new voting mechanism, called tournament voting, in which the outputs of classifiers compete in groups, the common result in each group gradually moves to the next round, and, at the last round, the winning class label is assigned as the final prediction. Experiments were conducted on 14 real-world benchmark datasets. The experimental results showed that SVMC (88.11%) achieved higher accuracy than SVM (86.71%) on average thanks to the feature selection, sampling, and chain structure combined with multiple models. Furthermore, the proposed tournament voting demonstrated higher performance than the standard majority voting in terms of accuracy. The results also showed that the proposed SVMC method outperformed the state-of-the-art methods with a 6.88% improvement in average accuracy.

1. Introduction

Machine learning (ML) involves developing algorithms that are able to emulate human intelligence. In ML, the adaptation of processes such as data preprocessing, feature engineering, algorithm selection, and parameter setting directly affects the performance of the predictive model. It is expected that ML models will be effective even with small-sized datasets gathered from various industries. Labeling data manually, protecting privacy, and processing imbalanced, insufficient, high-dimensional, incomplete, or noisy datasets are difficulties associated with machine learning. For this reason, research studies seeking to develop effective ML models and increase their performance are currently ongoing.

Support vector machine (SVM) is one of the most popular ML methods due to its impressive characteristics, including high generalization ability, efficiency in high dimensions, and easy implementation [1]. SVM is a supervised machine learning technique that usually performs well in many different areas, such as health [2,3] psychology [4] neuroscience [5], marketing [6], biometry [7], robotics [8], food [9], the environment [10,11], and agriculture [12].

Although SVM is effective in many situations, it has some shortcomings that reduce its classification ability. The use of a single model is insufficient when compared to the performance of ensemble models. There are essentially two reasons that ensemble learning (EL) is preferred over a single model: performance and robustness. Parallel or sequential trials increase the performance compared to a single model. Furthermore, the failure of one classifier can be rectified by the successes of other classifiers. In EL, the main focus is on training multiple models and combining the results from these models. Homogeneous ensembles can be created using the same ML algorithm or heterogeneous ensembles using different algorithms. The power of different models can be utilized by applying the SVM method to different subsets of the dataset. Based on this motivation, in this study, we propose a novel ensemble learning approach that uses SVM as a base learner.

Majority voting (MV) is the most frequently used method when combining the results of classifiers in an ensemble. In the classification problem, the class label with the majority vote is the final prediction, while, in the regression problem, the results from the models are averaged. A problem related to majority voting is that it ignores the fact that some learners that lie in the minority may produce more accurate outputs, since it does not explicitly address diversity [13].

To overcome these limitations, this paper proposes a novel voting mechanism, called tournament voting, in which the results of classifiers compete in groups at each stage and the process is repeated until one winner remains. It also introduces the support vector machine chains (SVMC) method, which builds a series of learners in a special structure and integrates their outputs via the tournament voting mechanism so as to achieve better prediction performance than a single SVM learner.

The remainder of the article is organized as follows. In Section 2, studies on ensemble learning are explained. Section 3 describes two novel concepts proposed in this paper: SMVC and tournament voting. In Section 4, experimental studies and a discussion of the findings are presented. In addition, in this section, our results are compared with the results of state-of-the-art studies. Finally, Section 5 provides a few final observations and future directions.

2. Related Work

Ensemble learning (EL) is an approach whereby multiple models are trained and the results of the models are combined to obtain the final result [14]. The goal of ensemble learning is to achieve better performance with a collection of models compared to any individual model. This includes deciding both how to build models and how best to combine the prediction results from ensemble elements. EL is sensitive to preprocessing steps and parameter tuning, as with individual models, as it is a collection of basic learners. In this context, when current studies in the field of ensemble learning are examined, it is apparent that they generally focus on feature selection, instance sampling, or voting methods since these play important roles in the final value estimation.

The ensemble learning model can be supported by active learning. For example, in a study conducted in 2022 [15], an ensemble learning model based on active learning was developed for heterogeneous data analysis using different feature extraction methods. The researchers trained the model with datasets from five different fields and compared them with traditional machine learning models. In another study [16], feature selection techniques were emphasized since they are a significant issue, and a hybrid model was proposed using bagging, boosting, and stacking ensemble learning approaches. The authors selected the most important features with the linear discriminant analysis (LDA), principal component analysis (PCA), and isomap techniques. They tested the successes of these alternative feature selection methods on the performance of the model on the datasets. They used the majority voting technique for the outcome estimation of the hybrid model. While working with the features obtained by feature extraction, it can also been seen that feature selection is performed using different metrics. As an example, in a study [17], features were selected according to the F-Score. The authors proposed a new ensemble learning algorithm, called the F-Score Subspace Method (FsBoost), by emphasizing the importance of feature selection. They tested two versions of their proposed method. In the first version, k-nearest neighbors (kNN), SVM, and probabilistic neural networks (PNN) were run on homogeneous ensemble groups for each feature selection. After this, the result was then obtained by ensemble members. In the second version, heterogeneous ensemble groups were created. The result from each heterogeneous group was once again assessed for the final result. Thus, it was possible to observe how the stages of feature selection and ensemble creation affected the success of the study.

Another important criterion that increases the success rate in ensemble learning is how to combine the results of the models. A study [18] addressed this issue and proposed that the true positive rate could be used as a weight value and combined with a cost-sensitive probability value to guide community learning on a class basis. The focus was on the combination strategy that was combined with a weighted voting mechanism. In another study combining the results by giving weights to the models [19], a deep learning method was used as a basic learner, instead of classical machine learning methods. The final class label was assigned as the category that obtained the maximum number of votes from these learners. To demonstrate the success of the proposed ensemble, a comparison was made with the transfer learning model and convolutional neural network model.

Parameter tuning is an effective way to increase the success of an ensemble. Shahhosseini et al. [20] proposed an optimization-based method that found the optimal weights and the optimal hyperparameter set (GEMITH) for each classifier in the ensemble. Their algorithm selected a set of combinations from the input hyperparameter sets of a basic learner using Bayesian search. For each combination, the optimal objective value and ensemble weights were found using estimates from the hold-out sets of cross-validation. Another study [21] emphasized that the issue of combining models should be addressed more carefully, especially in studies with unbalanced datasets. It reported that the curse of correlation caused correct predictions to be often overridden by incorrect ones when deciding the final outcome in ensemble learning. Therefore, solutions were sought for the “correlation curse” and imbalanced classification problems. They proposed the Ranked-Based Chain-Mode Ensemble (RBCM) algorithm as a solution to these problems. They divided the dataset into three separate subsets: training, sorting, and test sets. Base learners were trained with the training set, validated with the sorting set, and evaluated with the test set according to their precision values. The group with low precision on a class basis was selected, and, if none of the models in this group could tag the incoming sample, the other class label was assigned; in this way, the result was reached.

When current ensemble learning studies are examined, it is seen that the generation of the training sets from the original dataset directly affects the success rate. Bagging, which is one of the ensemble learning techniques, randomly selects samples when creating the training sets. The same sample may be selected more than once, or it may not be selected at all. In order to improve the random selection stage and make predictions with high accuracy, Tuysuzoglu and Birant [22] proposed a new approach, called enhanced bagging (eBagging). In their approach, the training set is created by giving a higher possibility of selection to the samples that are misclassified and difficult to classify by the initial learner. Their results showed that the proposed eBagging technique reduced the disadvantages of the classical bagging method. Similarly, sample selection for the creation of the training sets is very important, especially in studies with unbalanced datasets. Random over-sampling and random under-sampling methods are frequently used methods to select equal numbers of samples from minority and majority classes in unbalanced datasets. In a study [10] that analyzed an unbalanced dataset, a hybrid sampling method was tested, in which the minority class was reproduced by over-sampling, and, after this, the samples in the majority class were down-sampled. Ensemble models and traditional machine learning models were tested with the training sets with and without preprocessing (balanced and unbalanced forms). The study clearly showed that the models were sensitive to this imbalance and the over-sampling method produced better results overall. Another work [23] focused on the same problem. Automatic credit scoring work also usually has an unbalanced dataset. To deal with this, the Bagging Supervised Autoencoder Classifier (BSAC) method was proposed. In their method, firstly, the subsets of balanced data were randomly generated from unbalanced training data. After this, each subset was given to the algorithm as a training set. The estimates of the base classifiers were finally reduced to a single class label by majority voting. The proposed model used an autoencoder network as a base learner to embed the underlying information of heterogeneous data into a lower-dimensional space and reduce the adverse impacts of class imbalance. Compared to the classical ensemble and machine learning models, the results showed that the proposed model achieved a higher success rate.

Our method differs from the previous works in many aspects. First, a general structure is created that covers all the stages of feature selection, sample selection, and model assembly. Second, the information carrier of the features is considered one-by-one, instead of random feature selection methods or metrics that can be used as threshold values. Third, this study proposes a new voting mechanism, called tournament voting, in which the results of classifiers compete in groups at each stage and the process is repeated until one winner remains.

3. Proposed Method

3.1. Support Vector Machine Chains (SVMC)

This paper proposes a novel method, support vector machine chains (SVMC), which has a structure in which a set of models are trained by reducing the attributes at each stage. The predictions of each learner in the chain are aggregated using a novel voting mechanism (tournament voting). The proposed voting mechanism is executed through the division of the results of classifiers by the tournament size, and then a selection approach is used based on the class labels in the groups for further processes; it gradually moves on to the next round, and, at the end of the tournament rounds, the winning class label is assigned as the final prediction.

Figure 1 shows a general overview of the proposed SVMC method. First, the relationships between the features and the target are revealed using mutual information. All features are listed from the most informative to the least. At each stage, the feature with the lowest value is eliminated and the model to be trained with the remaining attributes is added to the chain. In other words, a Mutual Information-Based Feature Elimination method is performed to reduce attributes iteratively. In order to increase the speed and improve the performance in high-dimensional datasets, m features to m/2 features in descending order are evaluated when creating an ensemble. Each classifier is built on a bootstrapped training set. For a given query instance in the test set, each classifier provides a vote to a class. After this, tournament voting is used to combine the results. The results from the models are divided into groups of the desired number and compete among themselves. The label that emerges successfully from each group is grouped again in the next level and this process is repeated until only one finalist remains.

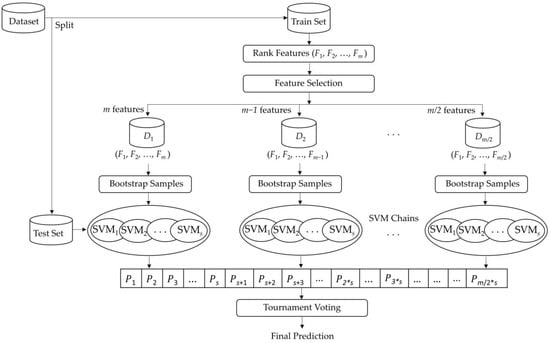
Figure 1. The general overview of the proposed SVMC method.

Majority voting (MV) is a simple and straightforward method for classification problems as it selects the class with the most votes. However, it has some drawbacks. A class label supported by many learners does not necessarily mean that it is the correct answer because the learners’ ability highly determines the quality of the final output. This paper proposes a novel voting mechanism, called tournament voting.

In the proposed tournament voting method, the results of the models compete in groups. The label that moves up from each group is the dominant class label in the group. Labels for all groups are promoted to the next round according to their dominance and continue to be evaluated according to their dominance in the following rounds.

An example of tournament voting is illustrated in Figure 2. In this example, the predicted values coming from the classifiers are gradually evaluated in groups of three. There are three class labels: “0”, “1”, and “2”. The dominant class label in each group is determined as the winner. For example, the winner of the first group [1 0 0] in the first round is determined as label “0” and fed to the next round to compete again with the results of other groups. In the figure, the winners of groups are shown below the round. In the first round, there are 9 groups, and the winners of these groups are [0 0 1 2 0 2 0 1 0], respectively. These winners compete once again in the second round. The winner of a group is the class label that achieves the highest number of votes from each classifier in the group. Therefore, the winners of the groups in the second round are “0”, “2”, and “0”, respectively. This voting continues until a single result is achieved. In the last round, the class label “0” is handled as the final prediction.

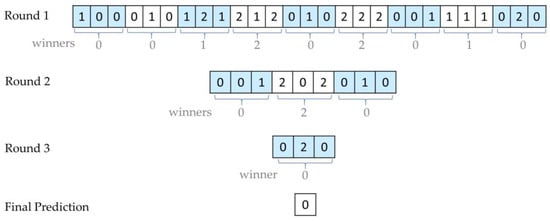
Figure 2. An example illustrating tournament voting.

Suppose that we run the same example with majority voting. The label “0” has 10 votes, the label “1” has 10 votes, and the label “2” has 7 votes. In such equality situations, majority voting will assign the first label that it sees as the final label and return the label “1” as a result. As can be seen, the result of majority voting is different from the result obtained by tournament voting.

3.2. Formal Description

Suppose a dataset D with n instances such that $D={\left\{\left(x_i,y_i\right)\right\}}_{i=1}^n$, where $x_i \in X$ denotes the input vector, $y_i\in Y=\left\{c_1,c_2, \dots , c_r\right\}$ is the class label associated with instance $x_i$, and $r$ is the number of class labels. Let $F=\left\{f_1, f_2, \dots , f_m\right\}$ be the set of features; each instance is a point in the m-dimensional feature space. The importance score of each feature F is calculated by the mutual information measure.

Mutual Information-Based Feature Elimination is an effective approach that selects a subset of features $S$ that shares the highest MI with $Y$, i.e., $\underset{S⸦F}{\max }I\left(S ;Y\right)$. Mutual information (MI) is a measure used to rank and evaluate the features of data with respect to their relevance to the target class variable. The information (I) between two variables X and Y is defined as the extent to which knowing Y reduces the uncertainty about X, as given in Equation (1).

$$I\left(X ; Y\right)=H\left(X\right)-H(X | Y)$$

(1)

where $I\left(X ; Y\right)$ is the mutual information for the variables X and Y, $H\left(X\right)$ is the entropy for X, and $H(X | Y)$ is the conditional entropy for X given Y. MI is always greater than or equal to zero, $I\left(X ; Y\right)\ge 0$, with a higher value indicating a stronger link between these two variables. If the computed result is zero, the variables are considered independent. The measure is symmetrical, i.e.,$I\left(X ; Y\right)=I\left(Y ; X\right)$. A conventional choice of entropy is Shannon entropy with the logarithmic information gain with a probability mass function (p), as given in Equation (2).

$$I\left(X ; Y\right)={\displaystyle \sum }_{x\in X}{\displaystyle \sum }_{y\in Y}p\left(x,y\right){log}_2\frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}$$

(2)

After the ranking process, features are arranged from the highest to the lowest based on the amount of discriminative information that they carry, i.e., they are ranked as follows: $\left(F_1, F_2,\dots , F_m\right).$ Afterward, the algorithm generates a collection of datasets $\left\{D_1, D_2,\dots , D_{m/2}\right\}$ from the original data such that the first one $\left(D_1\right)$ is composed of instances with m features $\left(F_1, F_2,\dots , F_m\right)$, the second one $\left(D_2\right)$ includes instances with m-1 features $\left(F_1, F_2,\dots , F_{m-1}\right)$, and so on, until the final dataset $\left(D_{m/2}\right)$ involves instances with m/2 features $\left(F_1, F_2,\dots , F_{m/2}\right)$. The main idea behind this approach is that higher classification accuracy can be achieved with features of higher importance. After this, a collection of training sets is created from $D_i$with the bootstrap resampling technique and each one is used to train an individual SVM learner $L_i$. In this way, an ensemble is created of s classifiers such that $\{SV{M}_1, SV{M}_2, \dots , SV{M}_s\}$. The same process is repeated m/2 times with each dataset $D_i$, $i=1,2,\dots ,m/2$, to build SVM chains.

Definition 1. 

SVM chains are a collection of SVM models that have been trained on bootstrap samples drawn from the datasets, which are generated by removing one feature in each iteration based on the mutual information values.

Given a new data tuple to classify, each classifier in the SVM chain independently votes for a specific class, and, therefore, a set of predictions $\left(P_1, P_2,\dots , P_{m/2\ast s}\right)$is obtained. Afterward, a novel voting mechanism, called tournament voting, is used to combine the predictions and determine the final output.

Definition 2. 

Tournament voting is a meta-algorithm that divides the predictions of classifiers into groups, which compete among themselves, by identifying the class with the highest number of votes in the groups, and the winners proceed to the next round until only one finalist remains.

Algorithm 1 presents the pseudocode of the proposed SVMC approach. In the first loop, mutual information values are calculated for each attribute $f_i$, where $i=1,2,\dots ,m$. According to the MI values, attributes are arranged in decreasing order such that $\left(F_1, F_2, \dots , F_m\right)$. In the outer loop, the algorithm generates a dataset $D_i$ from the original data $D={\left\{\left(x_i,y_i\right)\right\}}_{i=1}^n$ by removing the feature with the lowest MI value in each iteration. In the inner loop, a collection of training sets is created from $D_i$ with the bootstrap resampling technique and each one is used to train an individual SVM learner $L_{ij}$. Here, an ensemble is created of s learners. When the same process is repeated $m/2$ times, a total of $m/2\ast s$ learners are trained to build SVM chains. For each tuple x in the test set $T$, a prediction is made by each classifier in the SVM chain separately, and, therefore, a set of predictions $\left(P_1, P_2,\dots , P_{m/2\ast s}\right)$ is obtained. Finally, the tournament voting method is used to combine the predictions and determine the ultimate output. All predicted class labels are stored in a single list, named C.

Algorithm 1: Support Vector Machine Chains (SVMC).

Inputs:  D: dataset $D={\left\{\left(x_i,y_i\right)\right\}}_{i=1}^n$   m: number of features  s: chain size  T: test set Outputs:  C: the predicted class labels

Begin   for $i=1$ to $m$      Calculate mutual information ($MI$) for feature $f_i$   end for   $\left(F_1, F_2,\dots , F_m\right)=$ Sort features in descending order according to $MI$ scores   for $i=1$ to $m/2$      $D_i$ = $D$ with features $\left(F_1, F_2,\dots , F_{m-i+1}\right)$      for $j=1$ to $s$ $D_{ij}$ = Generate a new set from $D_i$ with bootstrapping $L_{ij}$ = SVM($D_{ij}$)      end for   end for   $P=\varnothing$     C $=\varnothing$   foreach $x$ in $T$       for $i=1$ to $m/2$        for $j=1$ to $s$         $P$.Add $(L_{ij}\left(x\right))$        end for       end for       $C$.Add($TournamentVoting\left(P\right)$)   end for End Algorithm

Algorithm 2 presents the pseudocode of the proposed tournament voting method. The predicted class labels in array $P={\left\{P_i\right\}}_{i=1}^{m/2\ast s}$ are the input of the algorithm. It gradually splits them into groups with a size of $t$ and the candidates in the groups compete. The recursively structured algorithm continues to process the labels in groups until only one class label $c$ is left. The dominant label (i.e., the most common label or the mode of class labels) advances to the next round as the winner and the competition continues until only one final label $c$ remains.

Algorithm 2: Tournament Voting.

Inputs:   P: array of predicted class labels   t: the number of candidates in the group Output:   c: final class label

Begin     if length($P$) = 1       c = $P$[0]       return c     else       Divide $P$ into $groups$ with the size of $t$       $P=\varnothing$       for $candidates$ in $groups$       $winner$ = mode $\left(candidates\right)$       $P$.Add($winner$)       end for       return $TournamentVoting\left(P\right)$     endif End Algorithm

We can summarize the advantages of the SVMC method as follows:

• Since SVMC is an ensemble-learning-based method, it tends to produce a better success rate than a single SVM model. Although some models make incorrect predictions, other models in the ensemble are predisposed to correct these errors.
• Most significantly, the rank-based feature elimination strategy in SVMC makes the data less redundant, thus reducing the possibility of decision making based on unimportant and irrelevant features.
• The proposed tournament voting aims to achieve correct outcomes by excluding incorrect answers in local groups. It benefits from the strengths of a group of classifiers while overcoming the weaknesses of one classifier in the group.
• The SVMC handles feature selection, sampling, and model fusion on its own. During the construction of chain classifiers, various subspaces of the dataset are assessed along with sample and feature selection. Therefore, it benefits from the advantages of providing diversity.
• Many application domains, such as bioinformatics and text mining, usually have many input features, often of several hundreds, where many of them include only a small amount of information. In the analysis of such high-dimensional data, feature selection based on their importance can provide higher accuracy than using all features or choosing features randomly.
• Another advantage of SVMC is its implementation simplicity. The algorithm is essentially an enhanced ensemble learning algorithm that involves chaining together multiple SVM classifiers in a special structure.
• If it is required, SVMC can be easily parallelized. It is suitable for distributed and parallel environments.

4. Experimental Studies

In the experiments in this research, the proposed SVMC approach was applied to 14 commonly used and publicly available datasets to demonstrate its classification ability. The application was implemented in the Python programming language. SVM learners were built with default parameters. In the verification step, 10-fold cross-validation was applied to evaluate the stability of the models. The proposed method was compared with the state-of-the-art methods in terms of the accuracy, precision, recall, and F-measure metrics, as given in Equations (3) to (6), respectively.

Accuracy is a widely used criterion to evaluate the performance of a model in the classification task. It is calculated by determining the counts of true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).

$$Accuracy= \frac{TP+TN}{TP+TN+FP+FN}$$

(3)

Precision shows how many of the examples that we classify as correct are actually correct. It is particularly crucial in research where false positive estimations are costly. In such cases, the precision value is examined in model selection.

$$Precision= \frac{TP}{TP+FP}$$

(4)

Recall shows how many of the samples that should be positively predicted are correctly estimated by the model. It is the preferred metric when the cost of false negative predictions is high.

$$Recall= \frac{TP}{TP+FN}$$

(5)

The F-measure is the harmonic average of the precision and recall values. For datasets that are not evenly distributed, it allows the evaluation of both states and provides a more accurate direction for model selection than accuracy.

$$F-measure= 2\ast \frac{Precision\ast Recall}{Precision+Recall}$$

(6)

4.1. Dataset Description

The proposed SVMC method was tested in 14 different real-world datasets, which are available in the UCI Machine Learning Repository [24]. Table 1 shows the characteristics of the experimental datasets. The datasets are suitable for both binary and multiclass classification. In addition to datasets with only categorical features or numeric features, some datasets have features that include both types. The datasets come from different domains, including health, marketing, animal science, and the environment.

Table 1. Characteristics of experimental datasets (#: The number of elements, √: available).

No.	Dataset	#Class	#Feature	#Instance	Categoric	Numeric
1	Breast Cancer	2	30	569		√
2	Dermatology	6	34	366	√	√
3	Diabetes	2	9	768		√
4	Ecoli	4	8	336		√
5	Hepatitis	2	20	155	√	√
6	Horse Colic Surgical	2	28	300	√	√
7	Ionosphere	2	35	355	√	√
8	Iris	3	5	150		√
9	Lenses	3	5	24	√
10	Mammographic Mass	2	6	961		√
11	Spectf Heart	2	45	349		√
12	User Knowledge	5	6	403		√
13	Wholesale Channel	2	8	440	√	√
14	Wine	3	14	178		√

4.2. Experimental Results

The superiority of the proposed SVMC method over the traditional SVM method was demonstrated on various datasets. In order to assess the model’s effectiveness in a variety of ways, tests were specifically performed on different types of datasets, containing categorical, numerical, or mixed values and having binary or multi-class labels. As seen in Table 2, SVMC outperformed SVM in terms of accuracy in 13 of 14 datasets, which are marked by bullet points. For example, SVMC (89.16%) achieved better classification performance than SVM (86.80%) on the hepatitis dataset. The proposed method obtained the highest improvement (10%) compared to the conventional SVM method on the lenses dataset. On average, SVMC demonstrated higher classification ability than SVM. Similar improvements were also obtained in terms of the precision and recall measures.

Table 2. Comparison of the proposed SVMC method with the standard SVM method (●: higher accuracy).

Dataset	SVM			SVMC (Proposed)
	Accuracy (%)	Precision	Recall	Accuracy (%)	Precision	Recall
Breast Cancer	91.37	0.9209	0.9137	91.55 ●	0.9225	0.9155
Dermatology	97.76	0.9814	0.9776	98.30 ●	0.9863	0.9830
Diabetes	77.59	0.7920	0.8912	77.99 ●	0.7912	0.9008
Ecoli	87.21	0.8728	0.8721	87.80 ●	0.8773	0.8780
Hepatitis	86.80	0.8781	0.9750	89.16 ●	0.9001	0.9750
Horse Colic Surgical	85.66	0.8584	0.9337	85.00	0.8562	0.9215
Ionosphere	93.18	0.9640	0.8437	94.60 ●	0.9663	0.8859
Iris	96.00	0.9698	0.9600	96.66 ●	0.9748	0.9666
Lenses	60.00	0.4861	0.6000	70.00 ●	0.6944	0.7000
Mammographic Mass	80.43	0.8268	0.8040	81.06 ●	0.8319	0.8118
Spectf Heart	82.52	0.6628	0.7069	83.11 ●	0.6678	0.6877
User Knowledge	88.57	0.8912	0.8857	89.81 ●	0.8950	0.8981
Wholesale Channel	89.09	0.9103	0.9295	90.22 ●	0.9164	0.9387
Wine	97.71	0.9829	0.9771	98.30 ●	0.9862	0.9830
Average	86.71	0.8570	0.8764	88.11	0.8762	0.8890

As some of the datasets were imbalanced according to the target classes, the F-measure values were also assessed. The F-measure values obtained by the SVM and SVMC methods are visually represented in Figure 3. As can be seen, SVMC outperformed SVM in terms of the F-measure in 12 of 14 datasets. For example, SVMC (0.9663) achieved better performance than SVM (0.8976) on the ionosphere dataset. SVMC increased the performance of the model since it applied a special feature selection and sampling strategy to build a chain structure. Another reason is that the final result was reached by tournament voting, rather than majority voting.

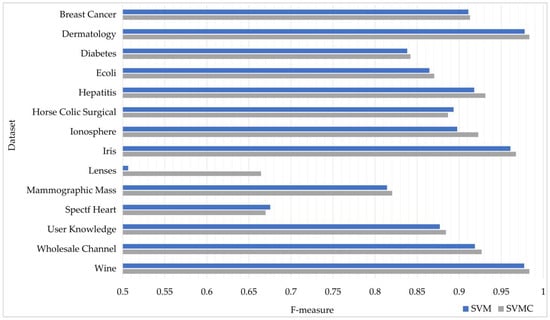
Figure 3. Comparison of SVM and SVMC in terms of F-measure.

To demonstrate the efficiency of the proposed voting technique, SVMC was conducted with both tournament voting (TV) and majority voting (MV). In TV, the predictions of the classifiers in the ensemble compete in groups, whereas MV delivers the result with the most votes out of all the outcomes returned from the classifiers. Table 3 presents the accuracy, precision, and recall values obtained by both techniques. According to Table 3, SVMC with TV achieved equal or higher performance compared to SVMC with MV on all the datasets, where the results are marked by bullet points. For example, TV (83.11%) demonstrated higher classification ability over MV (82.53%) on the spectf heart dataset.

Table 3. Comparison of the proposed tournament voting with the majority voting.

Dataset	SVMC (Majority Voting)			SVMC (Tournament Voting) (Proposed)
	Accuracy (%)	Precision	Recall	Accuracy (%)	Precision	Recall
Breast Cancer	91.55	0.9225	0.9155	91.55 ●	0.9225	0.9155
Dermatology	98.03	0.9837	0.9803	98.30 ●	0.9863	0.9830
Diabetes	77.73	0.7886	0.9003	77.99 ●	0.7912	0.9008
Ecoli	87.50	0.8755	0.8750	87.80 ●	0.8773	0.8780
Hepatitis	89.16	0.9001	0.9750	89.16 ●	0.9001	0.9750
Horse Colic Surgical	84.66	0.8523	0.9209	85.00 ●	0.8562	0.9215
Ionosphere	94.03	0.9652	0.8643	94.60 ●	0.9663	0.8859
Iris	96.66	0.9748	0.9666	96.66 ●	0.9748	0.9666
Lenses	70.00	0.6944	0.7000	70.00 ●	0.6944	0.7000
Mammographic Mass	80.64	0.8271	0.8099	81.06 ●	0.8319	0.8118
Spectf Heart	82.53	0.6533	0.6961	83.11 ●	0.6678	0.6877
User Knowledge	89.81	0.8896	0.8981	89.81 ●	0.8950	0.8981
Wholesale Channel	90.00	0.9107	0.9424	90.22 ●	0.9164	0.9387
Wine	98.30	0.9862	0.9830	98.30 ●	0.9862	0.9830
Average	87.90	0.8731	0.8877	88.11	0.8762	0.8890

The F-measure values obtained by the majority voting and tournament voting techniques are visually displayed in Figure 4. For example, TV (0.9663) demonstrated better performance than MV (0.9103) on the ionosphere dataset. As can be observed, TV usually achieved higher F-measure values than MV. This is because grouping the results and analyzing them locally decreases the disadvantage that can occur in the event of equal votes, as opposed to returning the value that is most prevalent among all outcomes as the final result.

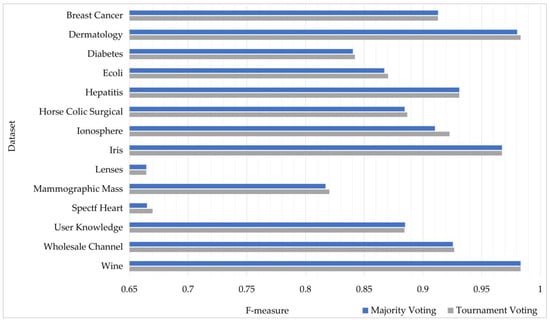
Figure 4. Comparison of tournament voting and majority voting in terms of F-measure.

The results of this study were compared with those of state-of-the-art studies that used the same datasets. The research was organized according to the datasets and the findings are shown in Table 4.

The effectiveness of our method was experimentally verified by comparing the accuracy values of other methods on the same datasets. When we compared it with the decision-tree-based studies, it was observed that the C5.0, conditional inference tree (CTree), recursive partitioning tree (RPART), traditional tree, and Boolean sensing-based tree (BSNSING) methods obtained the maximum of 80.80% accuracy on the hepatitis dataset [25], whereas the SVMC method achieved 89.16% accuracy. Similar improvements were also demonstrated for other datasets.

When we compared it with ensemble learning techniques such as random forest (RF) and AdaBoost, our method also outperformed them in terms of accuracy. For instance, SVMC (87.80%) demonstrated its superiority over the classifier ensemble approach based on reduce-error pruning (CEREP) (82.42%), progressive-subspace ensemble learning (PSEL) (83.42%), and the classifier ensemble approach based on complementarity measure pruning (CECMP) (82.82%) methods [26] on the ecoli dataset.

When we compared it with the variations of k-nearest neighbor (KNN), such as center-based nearest neighbor (CNN) and k-nearest centroid neighborhood (K-NCN), the SVMC method achieved higher accuracy on the datasets. For instance, in the spectf heart dataset, 79.47%, 79.77%, and 76.05% accuracy rates were obtained with the k-min–max sum (K-MMS), k-min ranking sum (K-MRS) [27], and interval valued k-nearest neighbor (IV-KNN) [28] methods, respectively, while an 83.11% accuracy rate was obtained with SVMC. Similarly, SVMC (98.30%) outperformed the k-nearest neighbor learning with graph neural networks (KNNGNN) method (94.78%) [29] on the wine dataset.

In some studies, genetic algorithm and gene expression programming (GEP) methods were used for the classification task, which offered the opportunity to evaluate our method from different perspectives. For instance, on the ionosphere dataset, SVMC (94.60%) demonstrated a stronger classification ability over the adaptive reference-point-based non-dominated sorting with GEP (AR-NSGEP) method (87.35%) [30], generational genetic algorithm (GGA) (90.85%), steady state genetic algorithm (SSGA) (91.04%), and cross-generational elitist selection (CHC) method (90.63%) [31].

Table 4. Comparison of the proposed method with the state-of-the-art methods on the same datasets.

Ref.	Year	Method	Accuracy (%)
			Dermatology	Ecoli	Hepatitis	Ionosphere	Iris	Spectf Heart	Wine
[25]	2022	C5.0	94.90	-	75.95	89.20	93.40	-	92.00
		CTree	93.40		79.10	90.50	94.10		89.70
		RPART	92.80		78.90	87.00	93.00		88.90
		Tree	92.30		80.80	87.40	93.60		92.10
		BSNSING	91.50		79.80	85.90	94.50		91.10
[29]	2021	Uniform KNN	-	81.47	-	81.92	91.14	-	89.65
		Weighted KNN		82.97		82.10	92.34		91.39
		KNNGNN		81.51		91.62	94.27		94.78
[32]	2018	SVM	-	60.41	-	-	90.66	-	85.39
		KNN		54.16			84.66		79.77
		C4.5		55.65			92.66		41.01
		CBCC-IM-EUC		83.78			94.66		97.15
[33]	2018	C4.5	94.10	82.83	79.22	89.74	94.73	-	93.20
		CC4.5	94.07	82.95	77.63	88.95	94.73		92.98
		AdaptiveCC4.5	93.96	81.72	80.62	88.27	94.13		92.47
[30]	2018	AR-NSGEP	95.41	71.10	87.23	87.35	96.53	-	94.60
[31]	2016	No TSS	96.62	78.00	86.08	89.17	93.33	79.49	96.08
		GGA	97.30	80.92	87.64	90.85	96.52	83.10	97.07
		CHC	93.29	78.89	83.59	90.63	92.67	76.44	96.67
		SSGA	97.42	80.42	88.33	91.04	94.00	82.31	96.88
[26]	2016	PSEL	97.51	83.42	-	93.62	94.87	81.06	96.96
		Random Subspace	96.98	84.38		93.36	94.67	79.40	96.33
		Random Forest	97.37	85.30		93.53	95.13	81.12	97.69
		MultiBoostAB	50.25	64.59		91.20	95.20	80.83	91.91
		AdaBoostM1	50.25	64.59		92.37	95.33	80.15	91.35
		Bagging	96.09	83.06		92.20	94.60	80.72	95.05
		CECMP	94.81	82.82		91.45	93.73	79.85	91.40
		CEREP	95.06	82.42		89.94	93.67	78.76	91.46
		RTBoost	92.55	77.11		88.38	94.20	73.74	92.86
[28]	2015	IV-KNN	-	82.76	84.67	84.32	94.67	76.05	96.60
[34]	2015	PMC	98.00	76.19	87.10	93.73	96.00	72.51	97.55
		KNN	96.90	80.67	82.51	85.18	94.00	68.18	95.49
		CNN	95.78	67.89	82.33	89.17	92.67	64.07	96.63
[35]	2015	eW KNN	-	-	-	-	92.77	-	96.12
		dW KNN					95.40		96.75
		dW-ABC KNN					94.11		97.04
[27]	2011	NN	85.68	-	-	85.24	95.20	72.81	71.57
		K-NN	85.68			83.71	94.80	79.10	67.39
		K-MRS	85.68			83.71	95.20	79.77	68.75
		K-MMS	85.08			84.90	94.53	79.47	69.63
		K-NCN	89.89			92.25	96.27	79.32	71.22
Average			90.69	76.86	82.44	88.82	93.97	77.65	89.33	Overall Average	85.68
SVMC (proposed method)			98.30	87.80	89.16	94.60	96.66	83.11	98.30	Overall Average	92.56

Table 4. Comparison of the proposed method with the state-of-the-art methods on the same datasets.

Ref.	Year	Method	Accuracy (%)
			Dermatology	Ecoli	Hepatitis	Ionosphere	Iris	Spectf Heart	Wine
[25]	2022	C5.0	94.90	-	75.95	89.20	93.40	-	92.00
		CTree	93.40		79.10	90.50	94.10		89.70
		RPART	92.80		78.90	87.00	93.00		88.90
		Tree	92.30		80.80	87.40	93.60		92.10
		BSNSING	91.50		79.80	85.90	94.50		91.10
[29]	2021	Uniform KNN	-	81.47	-	81.92	91.14	-	89.65
		Weighted KNN		82.97		82.10	92.34		91.39
		KNNGNN		81.51		91.62	94.27		94.78
[32]	2018	SVM	-	60.41	-	-	90.66	-	85.39
		KNN		54.16			84.66		79.77
		C4.5		55.65			92.66		41.01
		CBCC-IM-EUC		83.78			94.66		97.15
[33]	2018	C4.5	94.10	82.83	79.22	89.74	94.73	-	93.20
		CC4.5	94.07	82.95	77.63	88.95	94.73		92.98
		AdaptiveCC4.5	93.96	81.72	80.62	88.27	94.13		92.47
[30]	2018	AR-NSGEP	95.41	71.10	87.23	87.35	96.53	-	94.60
[31]	2016	No TSS	96.62	78.00	86.08	89.17	93.33	79.49	96.08
		GGA	97.30	80.92	87.64	90.85	96.52	83.10	97.07
		CHC	93.29	78.89	83.59	90.63	92.67	76.44	96.67
		SSGA	97.42	80.42	88.33	91.04	94.00	82.31	96.88
[26]	2016	PSEL	97.51	83.42	-	93.62	94.87	81.06	96.96
		Random Subspace	96.98	84.38		93.36	94.67	79.40	96.33
		Random Forest	97.37	85.30		93.53	95.13	81.12	97.69
		MultiBoostAB	50.25	64.59		91.20	95.20	80.83	91.91
		AdaBoostM1	50.25	64.59		92.37	95.33	80.15	91.35
		Bagging	96.09	83.06		92.20	94.60	80.72	95.05
		CECMP	94.81	82.82		91.45	93.73	79.85	91.40
		CEREP	95.06	82.42		89.94	93.67	78.76	91.46
		RTBoost	92.55	77.11		88.38	94.20	73.74	92.86
[28]	2015	IV-KNN	-	82.76	84.67	84.32	94.67	76.05	96.60
[34]	2015	PMC	98.00	76.19	87.10	93.73	96.00	72.51	97.55
		KNN	96.90	80.67	82.51	85.18	94.00	68.18	95.49
		CNN	95.78	67.89	82.33	89.17	92.67	64.07	96.63
[35]	2015	eW KNN	-	-	-	-	92.77	-	96.12
		dW KNN					95.40		96.75
		dW-ABC KNN					94.11		97.04
[27]	2011	NN	85.68	-	-	85.24	95.20	72.81	71.57
		K-NN	85.68			83.71	94.80	79.10	67.39
		K-MRS	85.68			83.71	95.20	79.77	68.75
		K-MMS	85.08			84.90	94.53	79.47	69.63
		K-NCN	89.89			92.25	96.27	79.32	71.22
Average			90.69	76.86	82.44	88.82	93.97	77.65	89.33	Overall Average	85.68
SVMC (proposed method)			98.30	87.80	89.16	94.60	96.66	83.11	98.30	Overall Average	92.56

According to Table 4, the overall average accuracy reported in the state-of-the-art studies on the seven datasets was 85.68%, while the proposed method obtained average accuracy of 92.56%. When we take into account the difference between these values, it is clear that our method achieved an average of a 6.88% accuracy improvement compared to its counterparts. The highest improvement (11%) was recorded in the ecoli dataset. As a result, the SVMC method, which includes specific feature selection, sampling, and aggregating processes at the same time, outperformed the methods used in the previous studies on the same datasets.

5. Conclusions and Future Work

The SVMC method is proposed in this paper, in which multiple SVM models are built with bootstrapped samples and features, assessed according to mutual information values in each iteration. The proposed method differs from the conventional machine learning methods with its special chain structure that includes feature selection in a specific manner, sample selection, and model fusion all at once. The predictions of the models on a given new data are combined using a novel voting mechanism, called tournament voting. In this voting process, class labels compete against one another within and between groups until only one finalist is left.

The main contributions of this study are highlighted as follows:

• It proposes a novel method, called support vector machine chains (SVMC), that has a structure in which the training SVM model is included in the chain by reducing the attributes in the dataset by one at each iteration.
• It proposes a novel voting mechanism, called tournament voting, in which the outputs of classifiers compete in groups, the common result in each group gradually moves to the next round, and, in the last round, the winning class label is assigned as the final prediction.
• The results of the experiments showed the superiority of SVMC (88.11%) over SVM (86.71%) in terms of average accuracy on the same datasets.
• The proposed tournament voting achieved higher accuracy than the standard majority voting in terms of the accuracy, recall, precision, and F-measure metrics when they were tested and compared on 14 well-known benchmark datasets.
• The proposed method outperformed the state-of-the-art methods, with a 6.88% improvement in average accuracy.

One limitation is that the developed version of the SVMC method is suitable for the classification task only. Research and development is necessary to create a version that works for the regression task. In the future, this situation will be addressed.