Optimal Deployment in Moving Target Defense against Coordinated Cyber–Physical Attacks via Game Theory
Abstract
1. Introduction
- We summarize the essence of MTD against CCPAs. When abiding by the essence and considering the practical constraints, an initial protected transmission line set is obtained;
- Based on a game model presented in Ref. [11], we compute a Nash equilibrium (NE) Minimax robust solution. To acquire the true solution, some real load profiles from New York State are used. This is the first time that the NE robust solution has been analyzed from the perspective of the attacker. Relying on the solution, those lines that are most likely to be tripped form a new protected transmission line set. Due to the game’s characteristics, the new protected transmission line set reflects the smart attacker’s sense of action;
- On the basis of the new protected transmission lines, we design a more comprehensive algorithm fueled by a metric developed in Ref. [11] for achieving the ultimately intelligent deployment of D-FACTS devices.
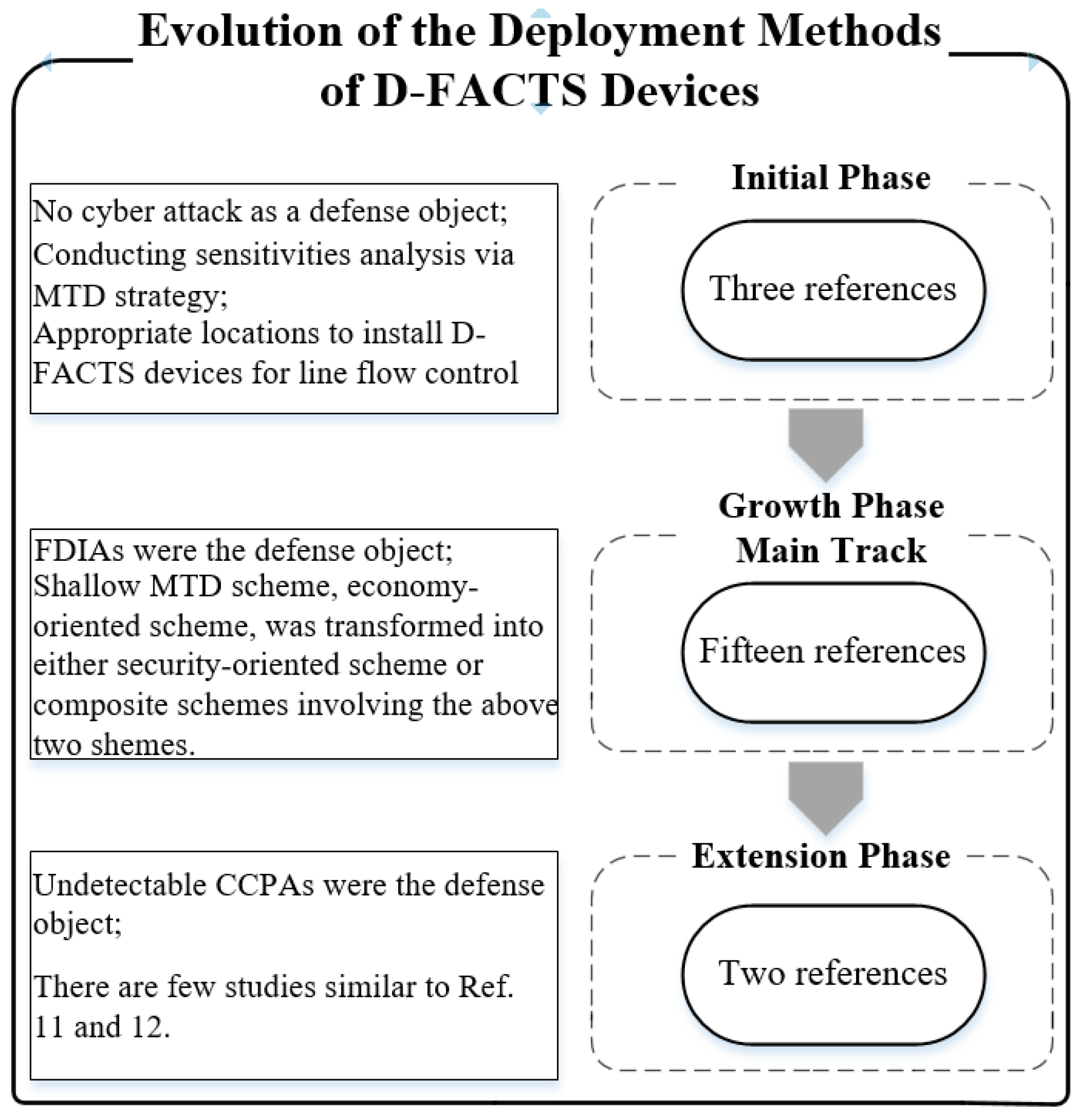
2. Related Works
- Limitations of Existing Works
- Main Innovations in our Work:
3. Theory Analysis
3.1. State Estimation and Bad Data Detection
3.2. Coordinated Cyber–Physical Attacks
3.2.1. Undetectable FDIAs
3.2.2. CCPA
3.2.3. Knowledge Required to Launch a CCPA
3.3. Preliminary Moving Target Defense and Accurate Limitation of the Protected Lines
3.3.1. Preliminary of MTD
3.3.2. Practical Constraints
3.3.3. Protected Transmission Lines’ Accurate Reconstruction via Game Theory [39]
Zero-Sum Game Formulation [40]
NE Solution and Machine Learning to Solve the Game
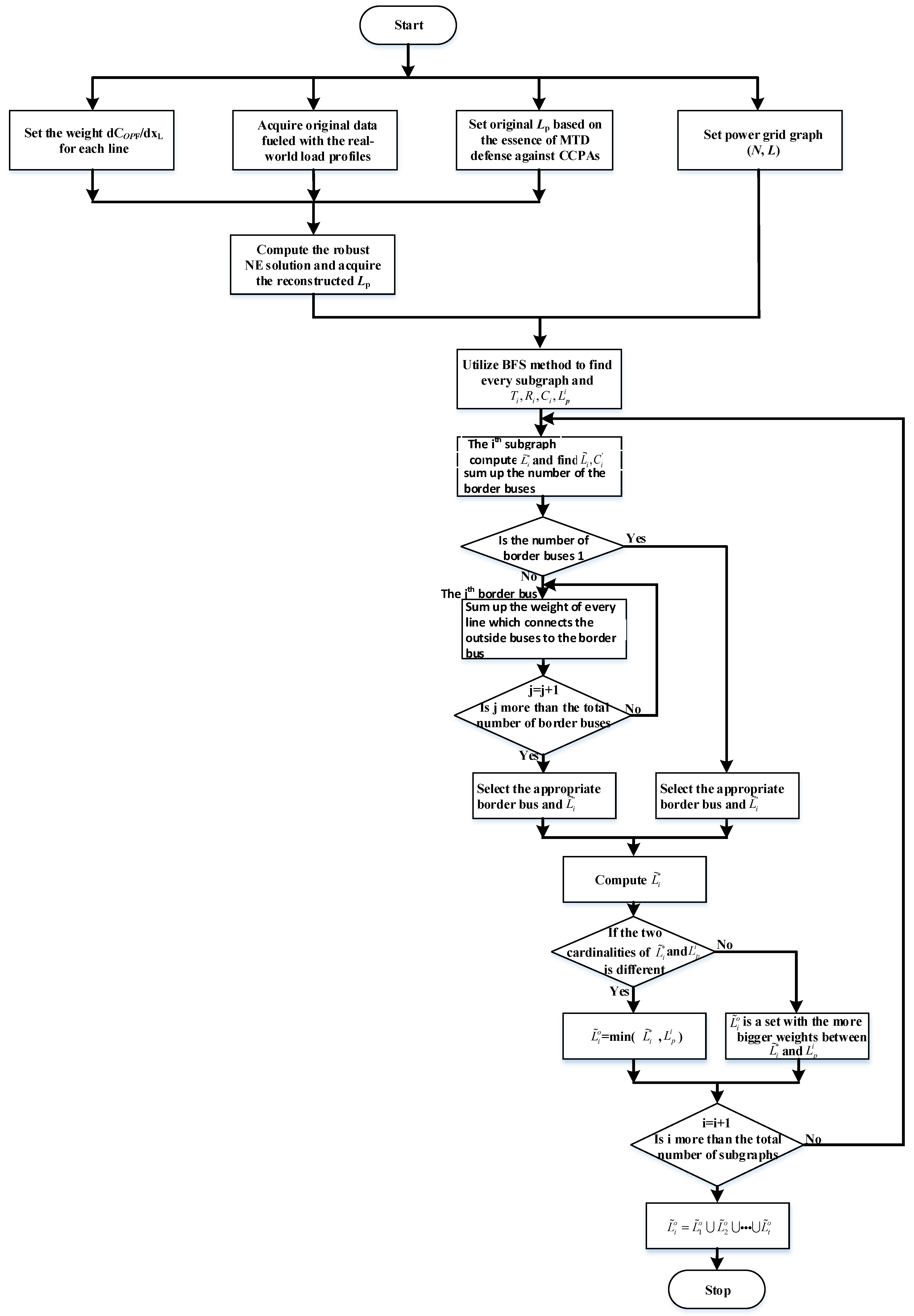
4. Proposed Methodology
4.1. MTD against CCPAs
4.2. Deployment of D-FACTS Devices
| Algorithm 1: Minimizing the number of used D-FACTS devices |
| Input: Power grid graph Output: 1 Set the weight of link as ; 2 Based on the specific set through injecting the real-world load profiles from New York State, compute the robust NE solution; 3 From the attacker’s angle, implement to reconstruct the set through selecting several maximal actions used by the attacker; 4 Based on the new set , construct the subgraph according to and ; 5 Use the breath-first search (BFS) to find the connected subgraph of , and find the spanning tree the remaining transmission lines , the cut lines , and the protected transmission lines , for each subgraph ; 6 for each do 7 Compute ; 8 Find the set of outside transmission lines incident to and the set of cut lines in ; Sum up the number of the border buses of which has the greatest number of transmission lines incident to the outside buses; 9 if the number of border buses is equal to one 10 the set of transmission lines that connect the outside buses to the border bus are denoted as ; 11 else 12 for each of the border buses do 13 Sum up the weight of every transmission line which connects the outside buses to a border bus; 14 end for 15 Select the appropriate border bus corresponding to the least sum of weights, and the set of transmission lines that connect the border bus to the outside buses are denoted as ; 16 end if 17 Compute ; 18 if the two cardinalities of and are different 19 Calculate the minimum set ; 20 else 21 Select a set with the bigger sum of weights between and and the selected set is ; 22 end if 23 end for 24 Compute ; |
5. Simulation
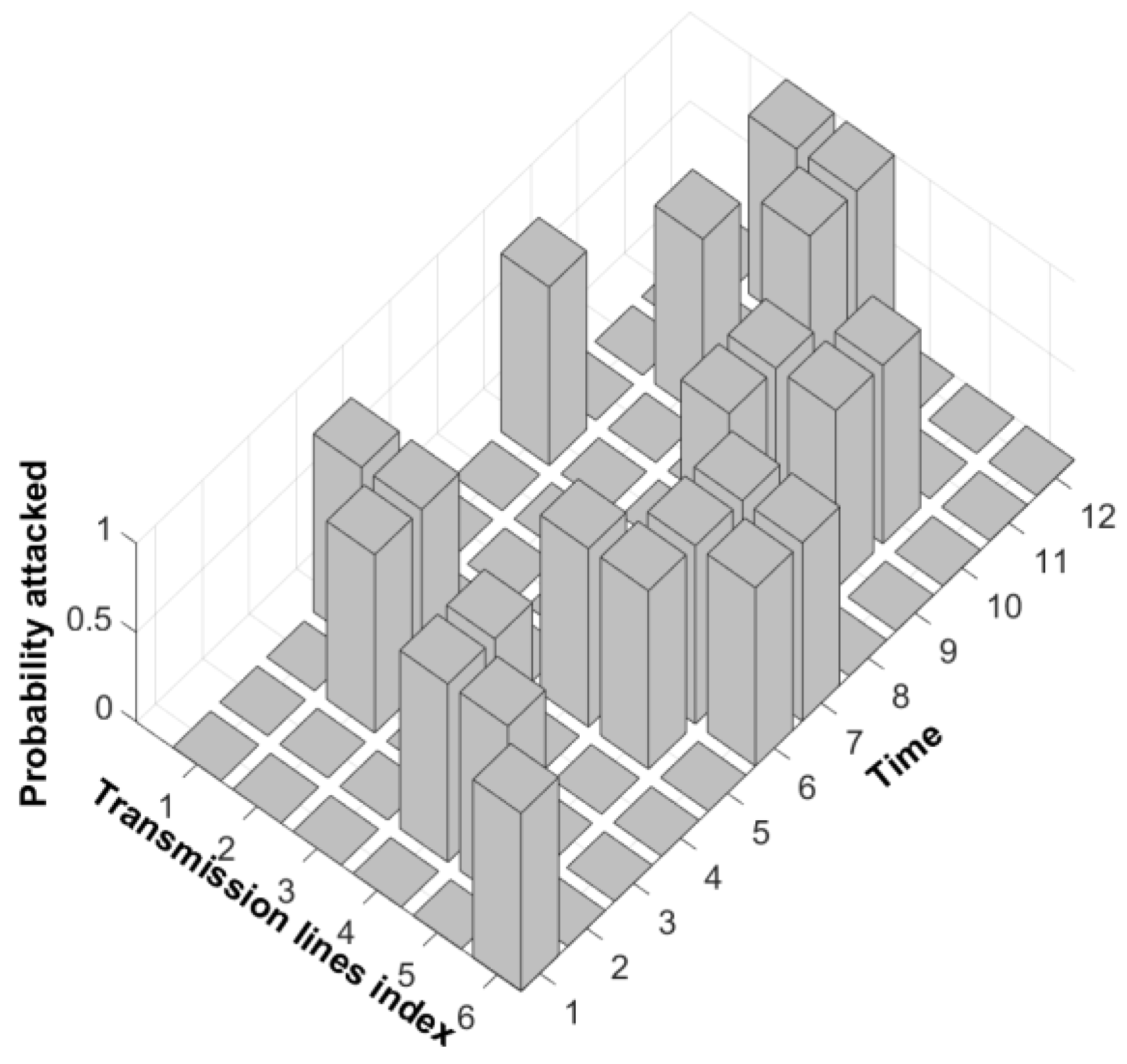
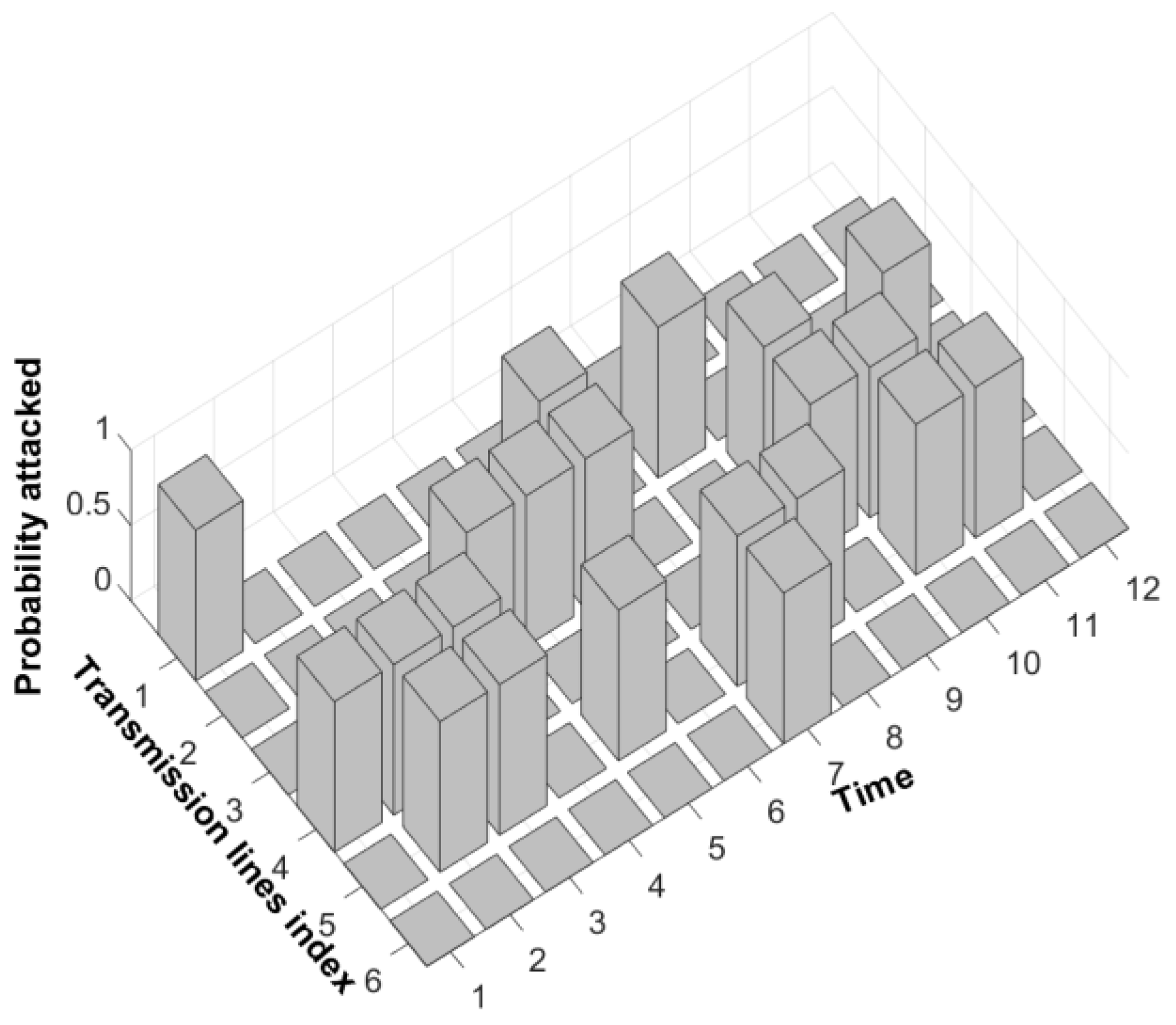
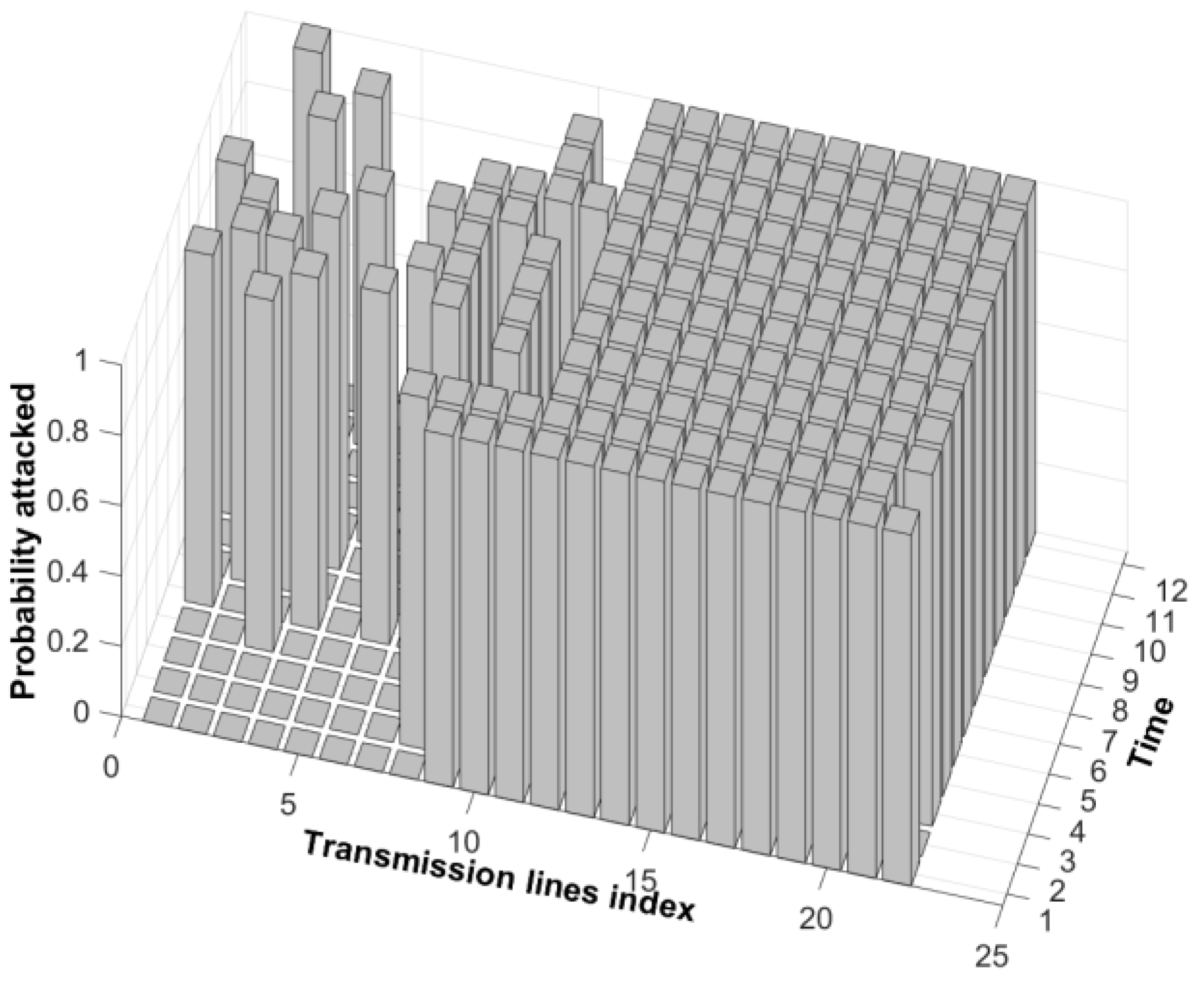
5.1. Reconstruction of the Specific Protected Transmission Lines
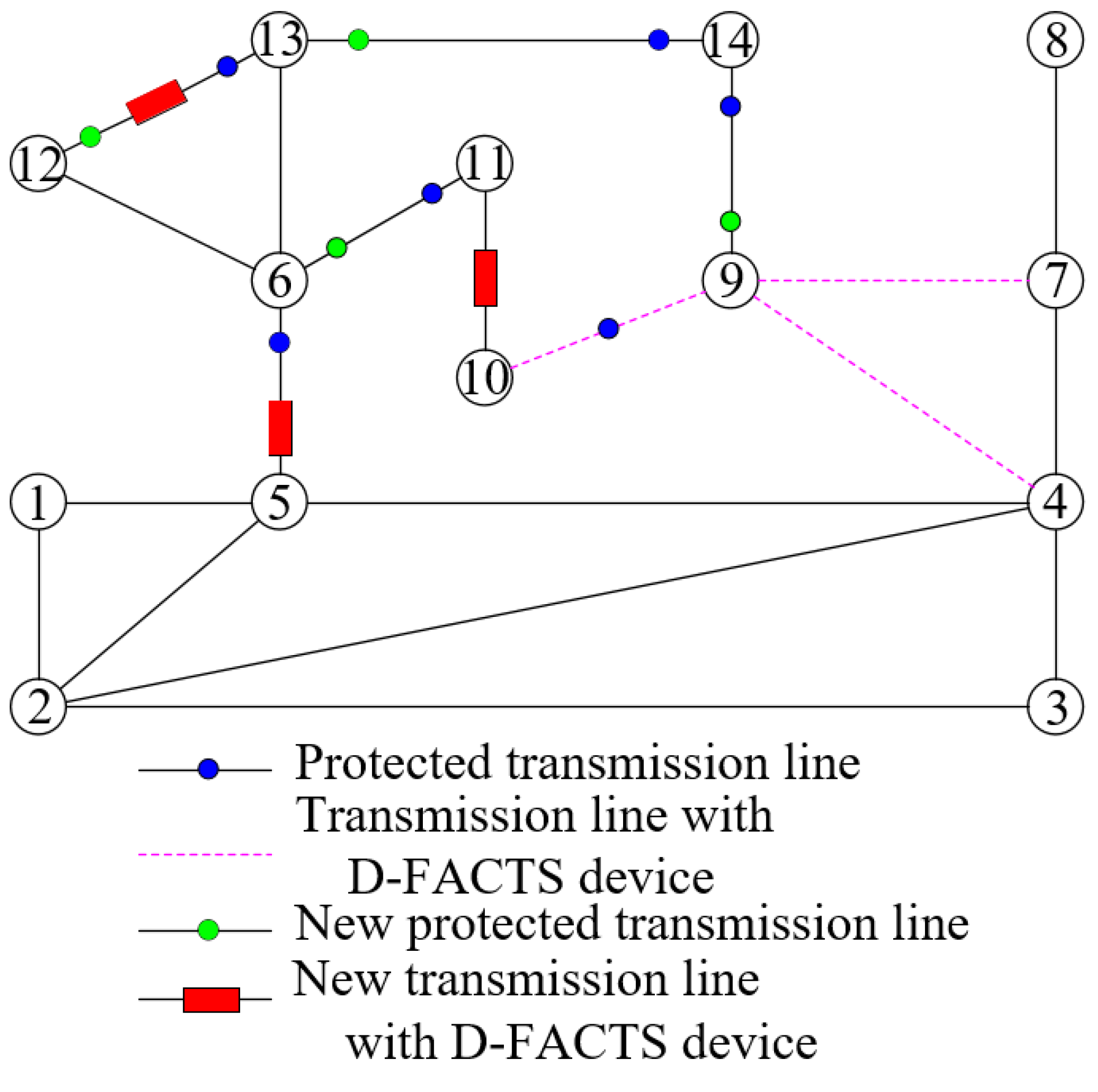
5.1.1. New Lp Reconstructed for the IEEE 14-Bus System
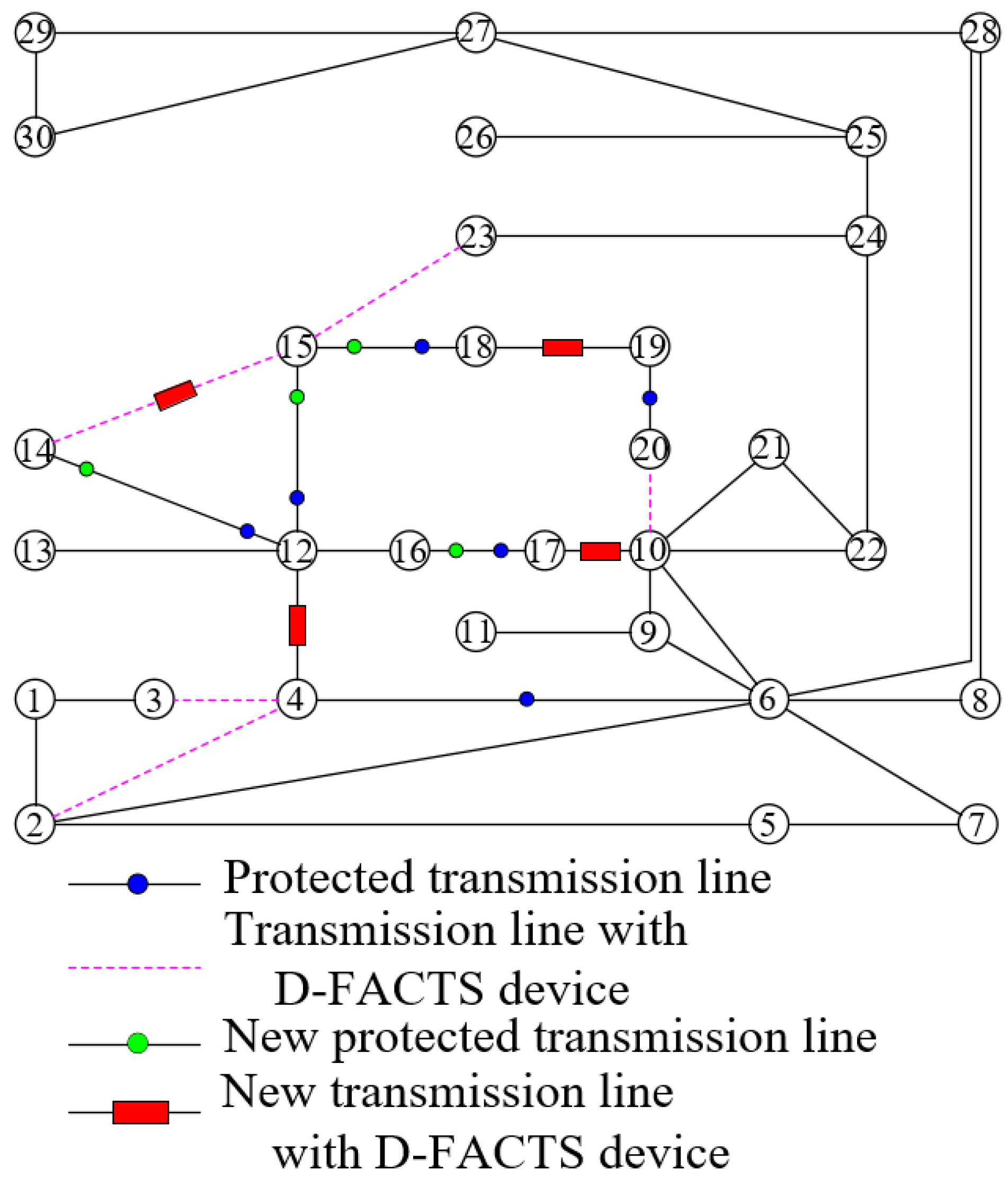
5.1.2. New Lp Reconstructed for the IEEE 30-Bus System
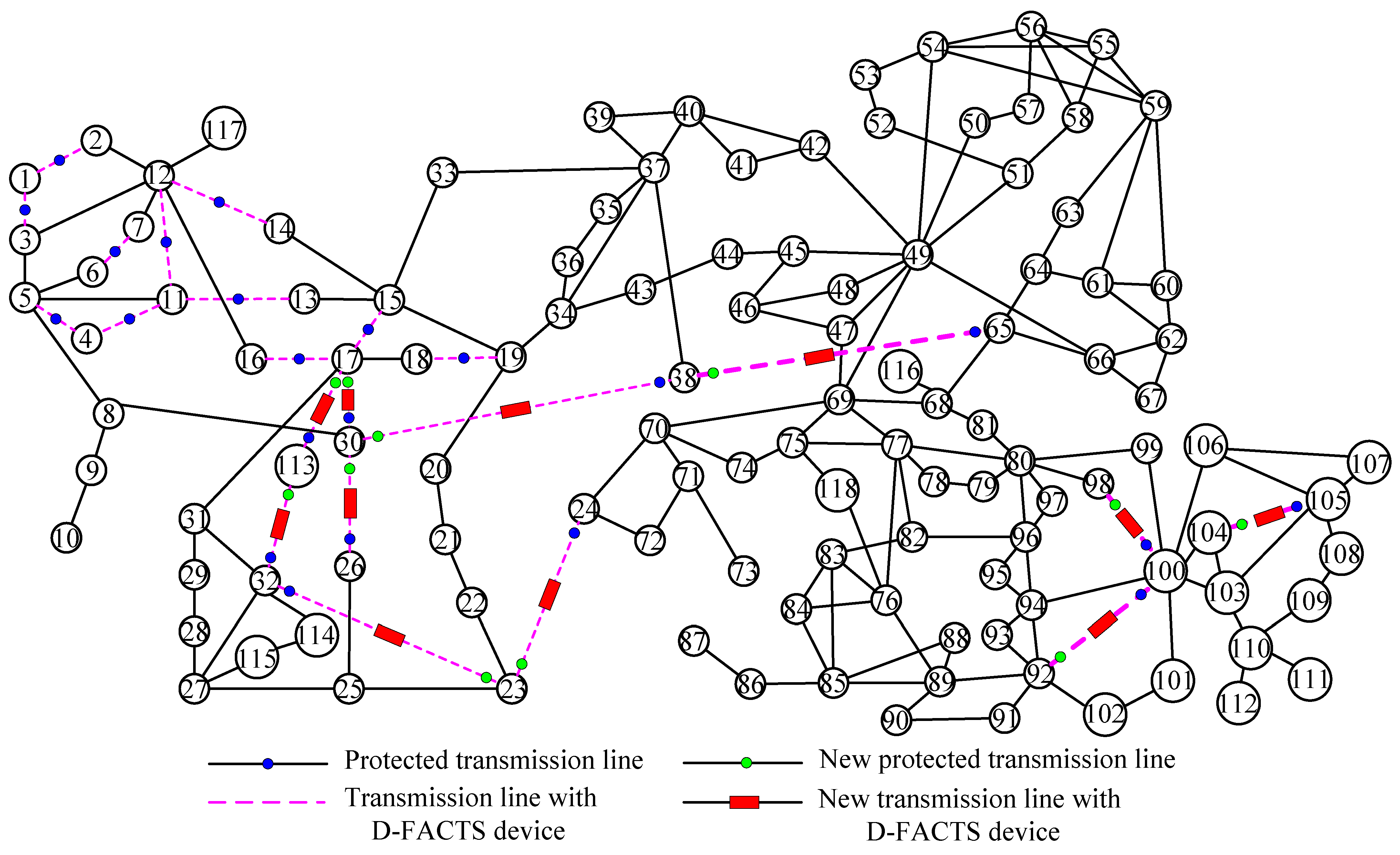
5.1.3. New Lp Reconstructed for the IEEE 118-Bus System
5.1.4. Analysis of the Results of the New Lp Reconstructed
5.2. Optimal Deployment of D-FACTS Devices and Analysis of the Results
6. Discussion
6.1. Research Motivation
6.2. Research Value
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CPS | Cyber–physical system |
| SG | Smart grid |
| FDIAs | False data injection attacks |
| CCPAs | Coordinated cyber–physical attacks |
| PMUs | Phasor measurement units |
| ML | Machine learning |
| MTD | Moving target defense |
| D-FACTS | Distributed flexible AC transmission system |
| NE | Nash equilibrium |
| SE | State estimation |
| OPF | Optimal power flow |
| SPA | Smallest principal angle |
| WLS | Weighted least squares |
| BDD | Bad data detection |
| EXP3 | Exploration and exploitation |
| BFS | Breath-first search |
| Graph representing the topology of the system | |
| Set of the buses in the system | |
| Set of the lines in the system | |
| i, j | Bus index |
| Susceptance of the line between buses i and j | |
| Vector of all measurements | |
| H | Measurement matrix |
| Measurement error vector | |
| θ | Voltage phase angles vector |
| Voltage phase angle at bus i | |
| Hk | The kth row of H |
| r | Measurement residual vector |
| τ | Threshold of BDD system |
| A | Reduced branch-bus incidence matrix |
| D | Diagonal branch susceptance matrix |
| a | Attack vector |
| Compromised vector of all measurements | |
| ap | Physical attack vector |
| Measurement matrix after a physical attack | |
| Voltage phase angles vector after a physical attack | |
| Measurement difference matrix between post-attack and pre-attack |
References
- Lydia, M.; Kumar, G.E.P.; Selvakumar, A.I. Securing the cyber-physical system: A review. Cyber-Physical Syst. 2022, 1–31. [Google Scholar] [CrossRef]
- Shetu, S.F.; Saifuzzaman, M.; Moon, N.N.; Nur, F.N. A survey of botnet in cyber security. In Proceedings of the ICCT, Jaipur, India, 28–29 September 2019; pp. 174–177. [Google Scholar]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grids. In Proceedings of the 16th of ACM Conference on Computer and Communications Security, Chicago, IL, USA, 9–13 November 2009. [Google Scholar]
- E-ISAC. Analysis of the Cyber Attack on the Ukrainian Power Grid; DUC Tech. Rep. 5; Electricity Information Sharing and Analysis Center: Washington, DC, USA, 2016; Available online: https://ics.sans.org/media/E-ISACsANSUkraineDUC5.pdf (accessed on 18 March 2016).
- Li, Z.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Bilevel model for analyzing coordinated cyber-physical attacks on power systems. IEEE Trans. Smart Grid 2016, 7, 2260–2272. [Google Scholar] [CrossRef]
- Deng, R.; Zhuang, P.; Liang, H. CCPA: Coordinated cyber-physical attacks and countermeasures in smart grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Shepard, D.P.; Humphreys, T.E.; Fansler, A.A. Evaluation of the vulnerability of phasor measurement units to GPS spoofing attacks. Int. J. Crit. Infrastruct. Prot. 2012, 5, 146–153. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Vural, F.T.Y.; Kulkarni, S.R.; Poor, H.V. Machine learning methods for attack detection in the smart grid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1773–1786. [Google Scholar] [CrossRef]
- He, Y.; Mendis, G.J.; Wei, J. Real-time detection of false data injection attacks in smart grid: A deep learning-based intelligent mechanism. IEEE Trans. Smart Grid 2017, 8, 2505–2526. [Google Scholar] [CrossRef]
- Sayghe, A.; Anubi, O.M.; Konstantinou, C. Adversarial examples on power systems state estimate. In Proceedings of the IEEE Power Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 1–5 February 2020. [Google Scholar]
- Lakshminarayana, S.; Belmega, E.V.; Poor, H.V. Moving-target defense against cyber-physical attacks in power grids via game theory. IEEE Trans. Smart Grid 2021, 12, 5244–5257. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, Y.; Deng, R.; Ma, J. A double-benefit moving target defense against cyber-physical attacks in smart grid. IEEE Internet Things J. 2022, 9, 17912–17925. [Google Scholar] [CrossRef]
- Morrow, K.L.; Heine, E.; Rogers, K.M.; Bobba, R.B.; Overbye, T.J. Topology perturbation for detecting malicious data injection. In Proceedings of the Hawaii ICSS, Maui, HI, USA, 4–7 February 2012. [Google Scholar]
- Davis, K.R.; Morrow, K.L.; Bobba, R.; Heine, E. Power flow cyberattacks and perturbation-based defense. In Proceedings of the IEEE SmartGridComm, Taiwan, China, 5–8 November 2012. [Google Scholar]
- Esmalifalak, M.; Shi, G.; Han, Z.; Song, L. Bad data injection attack and defense in electricity market using game theory study. IEEE Trans. Smart Grid 2013, 4, 160–169. [Google Scholar] [CrossRef]
- Sanjab, A.; Saad, W. Data injection attacks on smart grids with multiple adversaries: A game-theoretic perspective. IEEE Trans. Smart Grid 2016, 7, 2038–2049. [Google Scholar] [CrossRef]
- Habibi, M.R.; Baghaee, H.R.; Dragičević, T.; Blaabjerg, F. False data injection cyber-attacks mitigation in parallel DC/DC converters based on artificial neural networks. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 717–721. [Google Scholar] [CrossRef]
- Rahman, M.A.; Al-Shaer, E.; Bobba, R.B. Moving target defense for hardening the security of the power system state estimation. In Proceedings of the ACM MTD, Scottsdale, AZ, USA, 3 November 2014. [Google Scholar]
- Yang, Q.; Li, D.; Yu, W.; Liu, Y.; An, D.; Yang, X.; Lin, J. Toward data integrity attacks against optimal power flow in smart gird. IEEE Internet Things J. 2017, 4, 1726–1738. [Google Scholar] [CrossRef]
- Liu, C.; Wu, J.; Long, C.; Kundur, D. Reactance perturbation for detecting and identifying fdi attacks in power system state estimation. IEEE J. Sel. Top. Signal Process. 2018, 12, 763–776. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Yau, D.K. Cost-benefit analysis of moving target defense in power grids. IEEE Trans. Power Syst. 2021, 36, 1152–1163. [Google Scholar] [CrossRef]
- Tian, J.; Tan, R.; Guan, X.; Liu, T. Enhanced hidden moving target defense in smart grids. IEEE Trans. Smart Grid 2019, 10, 2208–2223. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chen, J. Analysis of moving target defense against false data injection attacks on power grid. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2320–2335. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Optimal D-FACTS placement in moving target defense against false data injection attacks. IEEE Trans. Smart Grid 2020, 11, 4345–4357. [Google Scholar] [CrossRef]
- Soltan, S.; Yannakakis, M.; Zussman, G. Joint cyber and physical attacks on power grids: Graph theoretical approaches for information recovery. In Proceedings of the ACM SIGMETRICS, Portland, OR, USA, 15–19 June 2015. [Google Scholar]
- Zhang, Z.; Deng, R.; Cheng, P.; Chow, M.-Y. Strategic protection against FDI attacks with moving target defense in power grids. IEEE Trans. Control Netw. Syst. 2022, 9, 245–256. [Google Scholar] [CrossRef]
- Divan, D.; Johal, H. Distributed FACTS—A new concept for realizing grid power flow control. IEEE Trans. Power Electron. 2007, 22, 2253–2260. [Google Scholar] [CrossRef]
- Rogers, K.M.; Overbye, T.J. Some applications of distributed flexible AC transmission system (D-FACTS) devices in power systems. In Proceedings of the 2008 40th North American Power Symposium, Calgary, AB, Canada, 28–30 September 2008. [Google Scholar]
- Rogers, K.M.; Overbye, T.J. Power flow control with distributed flexible AC transmission system (D-FACTS) devices. In Proceedings of the 41st North American Power Symposium, Starkville, MS, USA, 4–6 October 2009. [Google Scholar]
- Li, B.; Xiao, G.; Lu, R.; Deng, R.; Bao, H. Data injection attacks on power grid state estimation using D-FACTS devices. IEEE Trans. Ind. Inform. 2020, 16, 854–864. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Optimal planning and operation of hidden moving target defense for maximal detection effectiveness. IEEE Trans. Smart Grid 2021, 12, 4447–4459. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Systematic planning of moving target defense for maximizing detection effectiveness against false data injection attacks in smart grid. IET Cyber-Phys. Syst. Theory Appl. 2021, 6, 151–163. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, C.; Zhang, Z.; Deng, R. Explicit analysis on effectiveness and hiddenness of moving target defense in AC power systems. IEEE Trans. Power Syst. 2022, 37, 4732–4746. [Google Scholar] [CrossRef]
- Wang, J.; Tian, J.; Liu, Y.; Yang, D.; Liu, T. MMTD: Multi-stage moving target defense for security-enhanced D-FACTS operation. IEEE Internet Things J. 2023, 1. [Google Scholar] [CrossRef]
- Xu, W.; Jaimoukha, I.M.; Teng, F. Robust moving target defense against false data injection attacks in power grids. IEEE Trans. Inf. Forensics Secur. 2023, 18, 29–40. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chow, M.-Y. Security enhancement of power system state estimation with an effective and low-cost moving target defense. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3066–3081. [Google Scholar] [CrossRef]
- Chen, Y.; Lakshminarayana, S.; Teng, F. Localization of coordinated cyber-physical attacks in power grids using moving target defense and deep learning. In Proceedings of the IEEE SmartGridComm, Singapore, 25–28 October 2022. [Google Scholar]
- Biswas, R.S.; Pal, A.; Werho, T.; Vittal, V. A graph theoretic approach to power system vulnerability identification. IEEE Trans. Power Syst. 2021, 36, 923–935. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Saha, T.K.; Nizami, S.; Alam, M.R.; Smith, D.B.; Poor, H.V. A survey of cyber-physical systems from a game-theoretic perspective. IEEE Access 2023, 11, 9799–9834. [Google Scholar] [CrossRef]
- Etesami, S.R.; Başar, T. Dynamic games in cyber-physical security: An overview. Dyn. Games Appl. 2019, 9, 884–913. [Google Scholar] [CrossRef]
- NYISO Load Data. 2020. Available online: https://www.nyiso.com/load-data (accessed on 7 June 2020).

| Author | Publication Year | Subject Investigated | Main Contributions | Limitations |
|---|---|---|---|---|
| Kate L. Morrow et al. [13] | 2012 | FDIA | A ‘probing’ approach for detecting FDIAs based on perturbing the power system by changing the impedance on a set of chosen lines was proposed. | How to deploy the D-FACTS was not mentioned. |
| Katherine R. Davis et al. [14] | 2012 | FDIA | A proactive defense strategy that was capable of detecting FDIAs was introduced. | There was not enough discussion about the proposed approach’s detection capability against FDIAs. |
| Mohammad Esmalifalak et al. [15] | 2013 | FDIA | A two-person zero-sum strategic game was formulated to find the Nash equilibrium and maximize the attacker’s and defender’s profits. | The simulation experiment was only conducted in a PJM-5-BUS test system, which was slightly less convincing. |
| Anibal Sanjab et al. [16] | 2016 | FDIA | 1. A Stackelberg game was proposed in which the defender acted as a leader that could anticipate the actions of the adversaries. Simultaneously, a distributed learning algorithm was presented for solving the game solution; 2. A hybrid game was considered in which the defender could not anticipate the action of the adversaries. Simultaneously, a search-based algorithm was presented for finding the equilibrium of this hybrid game. | The simulation experiment was only conducted on the IEEE 30-bus test system, which was slightly less convincing. |
| Mohammad Reza Habibi et al. [17] | 2021 | FDIA | An effective and proper strategy based on an artificial-neural-network-based reference tracking application was introduced to remove the FDIAs in the DC microgrid. | The training data should be large enough to support the neural network performance. In this paper, the amount of data used for the neural networks was unclear. In addition, the DC microgrids were constructed by parallel DC/DC converters in this paper; other types of microgrids were not considered. |
| Mohammad Ashiqur Rahman et al. [18] | 2014 | FDIA MTD | An MTD mechanism to secure state estimation was proposed, and a formal MTD design to ensure its effectiveness in detecting FDIAs was presented | How to deploy the D-FACTS was not mentioned. |
| Qingyu Yang et al. [19] | 2017 | FDIA | 1. The equality constraints and the physical property of the transmission line in the OPF process were investigated to determine the lowest number of target nodes attacked; 2. The problem of finding the critical attack vector to increase the minimum fuel cost as an objective of OPF was formalized; 3. Two types of defense schemes were proposed to defend against the FDIA. | The attacker needed comprehensive information on the power grid, such as the system topology, all nodal load active powers, and power flow limits on each transmission line, when an FDIA was successfully launched. |
| Chensheng Liu et al. [20] | 2018 | FDIA MTD | 1. The FDIA detection conditions under a noiseless setting that were practical to apply and that relate the probability of FDIA detection to the rank of a composite matrix were derived; 2. A secure reactance perturbation optimization problem was formulated, and an associated algorithm for solving the perturbation settings was proposed. | The scientific research achievements were limited to the premise of the system full column rank. If the system was a non-full column rank, the relevant issues were not addressed. |
| Subhash Lakshminarayana et al. [21] | 2021 | FDIA MTD | 1. Formal design criteria to select MTD reactance perturbations that were truly effective were presented; 2. The important trade-offs between the MTD’s detection capability and its associated required cost were characterized. | A metric, denoted as the smallest principal angle (SPA), was proposed for characterizing MTD effectiveness against FDIAs. However, there was not enough discussion about the SPA. In particular, the SPA’s calculation was fuzzy. |
| Jue Tian et al. [22] | 2019 | FDIA MTD | A hidden MTD approach that could not be detected by the attackers was proposed. | No limitations were found. |
| Zhenyong Zhang et al. [23] | 2020 | FDIA MTD | The conditions for thwarting all FDIAs via an MTD strategy were proposed. | No limitations were found. |
| Bo Liu et al. [24] | 2020 | FDIA MTD | 1. The D-FACTS placement algorithms by using the minimum number of D-FACTS devices to achieve the maximum MTD effectiveness were designed; 2. A novel MTD-based ACOPF model was proposed to find a trade-off between the system loss and the MTD effectiveness. | The presented algorithm to acquire the D-FACTS placement for the incomplete MTD seems too complicated. When applied in practice, it can be simplified. |
| Zhenyong Zhang et al. [26] | 2022 | FDIA MTD | The correlation between MTD design and FDI detection was revealed, and the MTD’s performance was optimized in terms of detecting FDIAs. | No limitations were found. |
| Ruilong Deng et al. [6] | 2017 | CCPA | Two potential CCPAs, namely replay and optimized CCPAs, were presented, and countermeasures were proposed to detect them based on the analytical results. | The method of detecting optimized CCPAs was slightly complicated and confusing. |
| Subhash Lakshminarayana et al. [11] | 2021 | CCPA MTD | 1. Sufficient conditions for disrupting the construction of CCPAs were presented; 2. A novel metric was developed, which was devoted to finding the optimal deployment of D-FACTS devices; 3. To minimize the defense cost, a zero-sum game was formulated to identify the best subset of links to perturb against a strategic attacker. | The presented sufficient conditions were not comprehensive. When formulating the game model, the practical constraints were not considered, which affected the game solution’s efficiency. |
| Zhenyong Zhang et al. [12] | 2022 | CCPA MTD | 1. More comprehensive sufficient conditions for disrupting the construction of CCPAs were presented; 2. On the basis of considering the practical constraints, an algorithm for minimizing the number of used D-FACTS devices was designed. | The presented conditions could also be further summarized. The proposed algorithm was not comprehensive. |
| Indexes of the Literature | The Type of Attack | Specific Deployment Method of D-FACTS Devices | MTD Categories |
|---|---|---|---|
| Ref. [27] | - | The devices can be incrementally deployed as needed, providing a precedented level of scalability [27]. | Economy-oriented scheme |
| Ref. [28] | - | The best k lines were chosen corresponding to the k sensitivities in power loss to impedance (PLI), which are the furthest from zero [28]. | Economy-oriented scheme |
| Ref. [29] | - | Relying with line impedance sensitivities, the result of placing D-FACTS devices for line flow control was achieved. | Economy-oriented scheme |
| Ref. [13] | FDIAs | The placement was primarily based on sensitivity analysis [13]. | Economy-oriented scheme |
| Ref. [18] | FDIAs | Originally, in an arbitrary set of D-FACTS deployed lines, L was selected. Then, based on the judgment results of whether L can satisfy the system security and MTD criteria, L was finally confirmed. | Economy-oriented scheme |
| Ref. [20] | FDIAs | Due to the MTD detection efficiency against FDIAs being closely correlated with the composite matrix rank, following this principle, the deployment was properly implemented. | Security-oriented scheme |
| Ref. [22] | FDIAs | To defend against a class of highly structured FDIAs, all critical sets were covered by MTD, which means enhanced MTD was accomplished. | Security-oriented scheme |
| Ref. [23] | FDIAs | With the aim of minimizing the dimension of the stealthy attack space and maximizing the number of covered buses, two algorithms were adopted. Based on the obtained results, eventually, deployment was acquired. | Security-oriented scheme |
| Ref. [24] | FDIAs | D-FACTS placement algorithms for both complete and incomplete MTDs were designed, which achieved the maximum rank of the composite matrix with the minimum number of D-FACTS devices; Additionally, the concept of power loss sensitivity was leveraged into the proposed algorithms to account for the economic benefits. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [30] | FDIAs | D-FACTS devices deployed on a branch were able to detect the existence of effective FDIAs targeted on either end bus(es) (with degrees both larger than 1) of this branch if and only if the injected phase angle difference between the two end buses is larger than a tolerance threshold [30]. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [21] | FDIAs | In the paper, the trade-off between the MTD’s detection capability and its cost was mainly concerned. But no specific deployment method was depicted. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [31] | FDIAs | A depth-first-search-based D-FACTS placement algorithm was proposed to guarantee the hiddenness of MTD while maximizing the rank of its composite matrix [31]. | Security-oriented scheme |
| Ref. [32] | FDIAs | Initially, the power loss to impedance sensitivity (PLIS) to each line as its weight was calculated and assigned. After two algorithms were simulated, the deployment solution was obtained. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [33] | FDIAs | To balance the trade-off between effectiveness and hiddenness, the design of explicit residual-based MTD was accomplished. Howeverno specific deployment approach was proviede. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [26] | FDIAs | A heuristic algorithm to compute a near-optimal solution for the deployment of D-FACTS devices was developed. | Security-oriented scheme |
| Ref. [34] | FDIAs | In an MTD perturbation cycle, during the initial time, a security-oriented MTD scheme was implemented, and an economy-oriented MTD scheme was followed at the reset of time, so a multi-stage MTD was conducted. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [35] | FDIAs | A new D-FACTS devices placement algorithm, which could reach all necessary buses with the smallest number of D-FACTS devices, was proposed. | Security-oriented scheme |
| Ref. [36] | FDIAs | An efficient algorithm to minimize the number of required D-FACTS devices for protecting a specific set of buses was proposed. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [11] | CCPAs | A sufficient condition for destroying the construction of undetectable was presented. Based on the condition, a random assignment of D-FACTS devices was given. When adjusting the load profiles in the power grid and applying a zero-sum game model, a specific deployment of D-FACTS devices was acquired through computing the NE robust solution of the game. | Combination of economy-oriented scheme and security-oriented scheme |
| Ref. [12] | CCPAs | Due to the practical constraints, the protected transmission lines were specific, and the number of deployed D-FACTS devices was limited. In this context, an algorithm seeking optimal deployment was proposed. | Combination of economy-oriented scheme and security-oriented scheme |
| Original Lp | New Lp | Standard Power System |
|---|---|---|
| {10, 11, 16, 17, 19, 20} | {11, 17, 19, 20} | IEEE 14-bus power system |
| {7, 17, 18, 21, 22, 24} | {17, 18, 21, 22} | IEEE 30-bus power system |
| {1, 2, 3, 6, 10, 12, 16, 17, 21, 22, 24, 30, 36, 38, 41, 54, 93, 147, 151, 161, 171, 172} | {30, 36, 38, 41, 54, 93, 147, 151, 161, 171, 172} | IEEE 118-bus power system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, Q. Optimal Deployment in Moving Target Defense against Coordinated Cyber–Physical Attacks via Game Theory. Electronics 2023, 12, 2484. https://doi.org/10.3390/electronics12112484
Yu J, Li Q. Optimal Deployment in Moving Target Defense against Coordinated Cyber–Physical Attacks via Game Theory. Electronics. 2023; 12(11):2484. https://doi.org/10.3390/electronics12112484
Chicago/Turabian StyleYu, Jian, and Qiang Li. 2023. "Optimal Deployment in Moving Target Defense against Coordinated Cyber–Physical Attacks via Game Theory" Electronics 12, no. 11: 2484. https://doi.org/10.3390/electronics12112484
APA StyleYu, J., & Li, Q. (2023). Optimal Deployment in Moving Target Defense against Coordinated Cyber–Physical Attacks via Game Theory. Electronics, 12(11), 2484. https://doi.org/10.3390/electronics12112484







