Efficient MIMO Signal Predistortion for Secrecy-Enhancing

Abstract

Massive machine type communications or internet of things (IoT) over wireless systems have invoked attention in terms of security problems, especially for multi-input multi-output (MIMO) schemes. In this paper, we propose efficient physical layer security (PLS) enhancing methods for space-time block coding (STBC), as well as spatial multiplexing (SM) schemes. The proposed methods pre-distort the transmit signals by using the phase information of the legitimate MIMO channel, and, as a result, the illegal eavesdropper cannot extract any information. The proposed predistortion for the STBC schemes is done so that the channel matrix at the receiver is a real-valued one, which results in full-rate and full-diversity gain for more than two transmit antennae. Therefore, compared to the conventional schemes, the proposed scheme eventually leads to the higher performance gain and lower detection complexity in addition to the high security protection. By extending the principle of the proposed method for STBC, a predistortion scheme is also proposed for SM by using the phase information of the column space of the channel matrix. The simulation results investigated in this paper reveal that the proposed methods can achieve enhanced error rate performances, as well as high security protection.

1. Introduction

The multi-input multi-output (MIMO) scheme is one of the most representative technologies in modern wireless communication systems, including wireless LAN as well as 4G to beyond 5G systems. To date, most of the physical layer technologies for MIMO systems have prioritized performance and capacity issues over security protection. However, dramatically increasing traffic demands, especially of machine-type communications, require more secure communication for privacy protection. Therefore, a number of studies have emphasized the importance of physical layer security (PLS) schemes for modern wireless communication systems [1,2], and there have been many proposals concentrating on the signal design for MIMO systems [3,4,5,6,7,8,9,10,11].

Techniques to add artificial noise (AN) have been considered as an effective means to protect the legitimate channel [3,4,5,6,7,8]. A typical design principle of AN is to make it orthogonal to the legitimate channel, so that it can be null to the legitimate receiver, while serving as interference to the illegal receiver [3]. Then, this idea of adding AN was applied to spatial modulation and space time block coding (STBC) schemes in [4,5,6,7,8], respectively, for PLS. However, adding AN obviously requires additional energy, which decreases the energy efficiency. Because of this, a recent study proposed the idea of adding artificial interference (AI), which can be considered as the channel dependent re-distribution of signal power, and this, therefore, accomplishes security protection without requiring any additional energy [9]. All of these ideas of adding AN or AI utilize the addition or re-distribution of channel-dependent power at the transmitter, which results in a seriously high peak-to-average power ratio (PAPR) problem.

To avoid the high PAPR problem, ideas that involve distorting the phase of the complex signal have been proposed [10,11]. For example, a phase rotation method has been applied to the STBC schemes to enhance secrecy [10], but the randomness of the phase distortion to the eavesdropper is only guaranteed by the additional secret key exchange between the legitimate transmitter and receiver. Meanwhile, a phase rotation technique was applied to the spatial modulation scheme to increase secrecy performance without risking any PAPR problem [11]. In these schemes, the secrecy protection capability is limited by the number of antennae and the modulation order employed.

In this paper, we propose novel secrecy enhancing methods for MIMO schemes. We consider that full-rate orthogonal STBC (O-STBC) schemes exist for instances employing more than two transmit antennae when real-numbered signals are used [12]. The proposed scheme first forms a full-rate non-orthogonal STBC encoding matrix, and then applies signal distortion for PLS in such a way as to make the channel matrix at the receiver fully orthogonal. Therefore, we can have a full-rate encoding matrix at the transmitter and a fully orthogonal channel matrix at the receiver. In addition to high secrecy protection, this leads to high performance gain due to higher diversity gain than the conventional methods. By extending this to the spatial multiplexing (SM) MIMO scheme, we design a new predistortion scheme.

The main contributions of this paper compared to the conventional schemes can be summarized as follows:

• Compared to the conventional AN or AI-aided schemes [3,4,5,6,7,8,9], the proposed methods distort the phase of the transmit signal, and they therefore avoid the PAPR problem and do not require additional energy for AN.
• Compared to the conventional phase-distortion based schemes [10,11], the proposed methods do not require an additional secret key exchange and have no limit on the secrecy protection capability.
• Compared to the conventional STBC schemes [12,13,14,15], the proposed scheme not only provides better bit error rate (BER) performance at the same rate (or can achieve the same performance at a higher rate), but it can also achieve high security protection. In addition, the complexity of the detection process can be reduced due to the use of the real-numbered channel matrix.

This paper is organized as follows. Following this introduction, Section 2 reviews the related works. After presenting the concept of PLS schemes with AN and AI, the concept of O-STBC for real-numbered signals is introduced. Section 3 describes the proposed scheme. Section 4 presents the simulation results and discussions, and finally, Section 5 draws the conclusion.

Notation: Bold lower and upper case letters represent vectors and matrices, respectively. ${\mathbf{A}}^T$ and ${\mathbf{A}}^H$ represent the transpose and Hermitian transpose of a matrix $\mathbf{A}$, respectively. For a column vector, a, diag(a) returns a square diagonal matrix with the elements of vector a on the main diagonal. For a modulated signal, x denotes a real-numbered signal while z denotes a complex-numbered signal. $\left|\right|z\left|\right|$ and $z^{*}$ denote the absolute value and conjugate of a complex number z, respectively.

2. Related Works

2.1. Adding AN to STBC MIMO Schemes for Secrecy Enhancing

We consider a multi-input-single-output (MISO) wiretap channel, which includes a transmitter Alice with $N_T$ transmit antennae, a legitimate receiver Bob, and a passive eavesdropper Eve. Let $\mathbf{h}={\left[\begin{array}{cccc}{h}_1& h_2& \dots & h_{N_T}\end{array}\right]}^T$ and $\mathbf{g}={\left[\begin{array}{cccc}{g}_1& g_2& \dots & g_{N_T}\end{array}\right]}^T$ respectively denote the channel state information (CSI) vectors of Bob and Eve, where $h_k$ and $g_k$ represent the complex channel gains for the k-th transmit antenna from Alice to Bob and Eve, respectively. The perfect CSI is assumed to be available at both Bob and Eve, but Alice only shares the CSI with Bob. It is also assumed that the channel states of $h_k$ and $g_k$ are independent of each other. For the purpose of employing AN [7], the $2\times 1$ Alamouti scheme is adopted with the following encoding matrix, ${\mathbf{Z}}_{\mathrm{A}}$ [13],

$${\mathbf{Z}}_{\mathrm{A}}=\left[\begin{array}{cc}{z}_1& z_2\\ -{z_2}^{*}& {z_1}^{*}\end{array}\right],$$

(1)

where $z_1$ and $z_2$ are the signals transmitted during the two symbol periods. Prior to transmission, Alice adds the following AN, $\mathbf{W}$, to ${\mathbf{Z}}_{\mathrm{A}}$:

$$\mathbf{W}=\left[\begin{array}{cc}{\alpha }_{11}\nu & {\alpha }_{12}\nu \\ -{\left({\alpha }_{21}\nu \right)}^{*}& {\left({\alpha }_{22}\nu \right)}^{*}\end{array}\right],$$

(2)

where $\nu$ is the complex Gaussian AN with zero-mean and unit variance and ${\alpha }_{ik}$s are the coefficients of the $\nu$ for the i-th time slot at the k-th antenna, which are designed to be nulled at Bob. Therefore, one of the possible coefficients sets can be ${\alpha }_{11}=h_2$, ${\alpha }_{12}=-h_1$, ${\alpha }_{21}={h_2}^{*}$, and ${\alpha }_{22}={h_1}^{*}$ [7].

Then, Alice transmits $({\mathbf{Z}}_{\mathrm{A}}+\mathbf{W})$ and the received signal vectors at Bob and Eve during the two symbol periods, ${\mathbf{y}}_{\mathrm{b}}$ and ${\mathbf{y}}_{\mathrm{e}}$ can, respectively, be expressed by:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{\mathrm{b}}& =({\mathbf{Z}}_{\mathrm{A}}+\mathbf{W})\mathbf{h}+{\mathbf{n}}_{\mathrm{b}},\hfill \\ \hfill & ={\mathbf{Z}}_{\mathrm{A}}\mathbf{h}+{\mathbf{n}}_{\mathrm{b}},\hfill \\ \hfill {\mathbf{y}}_{\mathrm{e}}& =({\mathbf{Z}}_{\mathrm{A}}+\mathbf{W})\mathbf{g}+{\mathbf{n}}_{\mathrm{e}},\hfill \end{array}$$

(3)

where ${\mathbf{n}}_{\mathrm{b}}$ and ${\mathbf{n}}_{\mathrm{e}}$ are additive white Gaussian noise (AWGN) vectors at Bob and Eve, respectively. Since the AN is designed to be nulled out at Bob, Bob received ${\mathbf{y}}_{\mathrm{b}}$ as if Alice transmitted without any AN. Meanwhile, since the channel gains $h_k$ and $g_k$ are independent of each other, Eve cannot retrieve any signal due to uncancelled $\mathbf{W}$.

Because this method requires additional energy for AN, a new method was proposed that does not require any additional energy for secrecy protection. The idea of this proposed method is to utilize the quasi-orthogonal STBC (QO-STBC) scheme with linear detection capability, called linear decoding QO-STBC (LD-QO-STBC) [15], and to re-allocate the signal power across the transmission time and antennae [9].

2.2. O-STBC for Real-Numbered Signals

Even though the full-rate O-STBC scheme for complex-numbered signals only exists for the two transmit antennae system [13], it is well known that it can be designed for more than two transmit antennae for real-numbered signals, such as pulse-amplitude modulation (PAM) [12]. The encoding matrices of the full-rate O-STBC schemes for p time periods and $N_T$ transmit antennae, ${\mathbf{X}}_{N_T}$ of size $p\times N_T$, can be found in the literature [12]; here we provide the following examples for $N_T=4$ and 8:

$${\mathbf{X}}_4=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ -x_2& x_1& -x_4& x_3\\ -x_3& x_4& x_1& -x_2\\ -x_4& -x_3& x_2& x_1\end{array}\right],$$

(4)

$${\mathbf{X}}_8=\left[\begin{array}{cccccccc}{x}_1& x_2& x_3& x_4& x_5& x_6& x_7& x_8\\ -x_2& x_1& x_4& -x_3& x_6& -x_5& -x_8& x_7\\ -x_3& -x_4& x_1& x_2& x_7& x_8& -x_5& -x_6\\ -x_4& x_3& -x_2& x_1& x_8& -x_7& x_6& -x_5\\ -x_5& -x_6& -x_7& -x_8& x_1& x_2& x_3& x_4\\ -x_6& x_5& -x_8& x_7& -x_2& x_1& -x_4& x_3\\ -x_7& x_8& x_5& -x_6& -x_3& x_4& x_1& -x_2\\ -x_8& -x_7& x_6& x_5& -x_4& -x_3& x_2& x_1\end{array}\right],$$

(5)

where $x_1,\dots ,x_p$ are real-numbered signals. It is clear that the ${\mathbf{X}}_{N_T}$s in (4) and (5) are orthogonal matrices. In addition, they achieve the full rate, i.e., $R=1$, because they are constituted by the transmit signal vector $\mathbf{x}=\left[\begin{array}{c}{x}_1,\dots ,x_p\end{array}\right]$ with p symbols over p time periods. Therefore, they can offer the full-diversity of $N_T$ due to the orthogonality as well as full-rate [12].

Assuming the signal vector $\mathbf{x}$ is transmitted using ${\mathbf{X}}_{N_T}$ via $N_T$ transmit antennae, the received signal vector can be expressed as:

$$\mathbf{y}={\mathbf{X}}_{N_T}\mathbf{h}+\mathbf{n},$$

(6)

where $h_k$ is the complex channel gain from the k-th transmit antenna to the receiver and $\mathbf{n}$ is an AWGN vector. Then, the above (6) can be equivalently expressed by:

$$\mathbf{y}={\mathbf{H}}_{\mathrm{C},N_T}\mathbf{x}+\mathbf{n},$$

(7)

where ${\mathbf{H}}_{\mathrm{C},N_T}$ is a complex-numbered channel matrix and is therefore not an orthogonal matrix. For example, the ${\mathbf{H}}_{\mathrm{C},4}$ corresponding to the encoding matrix, ${\mathbf{X}}_4$ of (4) can be given by:

$${\mathbf{H}}_{\mathrm{C},4}=\left[\begin{array}{cccc}{h}_1& h_2& h_3& h_4\\ h_2& -h_1& h_4& -h_3\\ h_3& -h_4& -h_1& h_2\\ h_4& h_3& -h_2& -h_1\end{array}\right].$$

(8)

Even though the above ${\mathbf{H}}_{\mathrm{C},N_T}$ with complex elements does not have full-orthogonality, a linear decoding can be performed for real number signal detection as follows:

$$\begin{array}{cc}\hfill \widehat{\mathbf{x}}& =\frac{1}{{\sum }_{k=1}^{N_T}{\left|\right|h_k\left|\right|}^2}{\mathbf{H}}_{\mathrm{C},N_T}^H\mathbf{y}\hfill \\ \hfill & =\frac{1}{{\sum }_{k=1}^{N_T}{\left|\right|h_k\left|\right|}^2}({\mathbf{H}}_{\mathrm{C},N_T}^H{\mathbf{H}}_{\mathrm{C},N_T}\mathbf{x}+{\mathbf{H}}_{\mathrm{C},N_T}^H\mathbf{n}),\hfill \end{array}$$

(9)

where $\widehat{\mathbf{x}}$ is the estimated result of $\mathbf{x}$. This is because the diagonal elements of the Gram matrix, ${\mathbf{H}}_{\mathrm{C},N_T}^H{\mathbf{H}}_{\mathrm{C},N_T}$, are pure real numbers, while the off-diagonal elements are pure imaginary numbers which do not affect the real number signal detection.

3. The Proposed Methods

3.1. Secrecy Enhancement for STBC Schemes

Motivated by the fact that a full-rate O-STBC scheme can be achieved for real-numbered signal transmission through the use of more than two transmit antennae [12], we propose an efficient PLS scheme for STBC.

In the proposed scheme, we first form a non-orthogonal full-rate encoding matrix for complex-numbered signals by inserting complex signals into ${\mathbf{X}}_{N_T}$. Then, the proposed scheme transforms the encoding matrix using a phase distortion matrix which represents the null space of the phase of the channel gain. During the transmission, the channel phase will be nulled out, and eventually only the amplitude component of the channel gain will arrive at the receiver. Therefore, we can have a full orthogonal real-numbered channel matrix at the receiver. Even though the encoding matrix with complex numbered signals is not orthogonal, the proposed scheme can achieve performance equivalent to that of the scheme with full-rate and full-diversity. It can also achieve high secrecy protection.

Here, we detail the operational principle of the proposed scheme. At the transmitter, Alice first generates a complex signal vector $\mathbf{z}={\left[\begin{array}{c}{z}_1,\dots ,z_p\end{array}\right]}^T$ for p time periods and constructs a non-orthogonal encoding matrix ${\mathbf{Z}}_{N_T}$ by inserting complex signals into ${\mathbf{X}}_{N_T}$. For example, the following ${\mathbf{Z}}_4$ can be found for a system with four transmit antennae.

$$\begin{array}{c}\hfill {\mathbf{Z}}_4=\left[\begin{array}{cccc}{z}_1& z_2& z_3& z_4\\ -z_2& z_1& -z_4& z_3\\ -z_3& z_4& z_1& -z_2\\ -z_4& -z_3& z_2& z_1\end{array}\right]\end{array}.$$

(10)

Note that ${\mathbf{Z}}_{N_T}$ keeps full-rate but is not orthogonal.

Next, the transmitting signals are predistorted so as to null out the phase of the channel gain. To this end, we form a phase-distorting vector, $\mathbf{p}$, as follows:

$$\mathbf{p}={\left[\begin{array}{cccc}{e}^{-j\angle h_1}& e^{-j\angle h_2}& \dots & e^{-j\angle h_{N_T}}\end{array}\right]}^T,$$

(11)

where $\angle h_k$ represents the phase of $h_k$. The next step is to determine the encoding matrix with the predistortion capability, ${\mathbf{Z}}_{N_T}^{\prime }$, as follows:

$$\begin{array}{cc}\hfill & {\mathbf{Z}}_{N_T}^{\prime }={\mathbf{Z}}_{N_T}\mathrm{diag}\left(\mathbf{p}\right)\hfill \\ \hfill & =\left[\begin{array}{cccc}{\mathbf{z}}_1& {\mathbf{z}}_2& \dots & {\mathbf{z}}_{N_T}\end{array}\right]\left[\begin{array}{cccc}{e}^{-j\angle h_1}& 0& \dots & 0\\ 0& e^{-j\angle h_2}& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & e^{-j\angle h_{N_T}}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}{e}^{-j\angle h_1}{\mathbf{z}}_1& e^{-j\angle h_2}{\mathbf{z}}_2& \dots & e^{-j\angle N_T}{\mathbf{z}}_{N_T}\end{array}\right],\hfill \end{array}$$

(12)

where ${\mathbf{z}}_k$ is the k-th column vector of ${\mathbf{Z}}_{N_T}$. Note that multiplying $e^{-j\angle h_k}$ to ${\mathbf{z}}_k$ will lead to nulling of the phase of the complex channel gain for ${\mathbf{z}}_k$ at Bob.

Finally, the received signal vector at Bob for p time periods can be represented by:

$$\begin{array}{cc}\hfill & {\mathbf{y}}_{\mathrm{b}}={\mathbf{Z}}_{N_T}^{\prime }\mathbf{h}+{\mathbf{n}}_{\mathrm{b}}\hfill \\ \hfill & =\left[\begin{array}{cccc}{e}^{-j\angle h_1}{\mathbf{z}}_1& e^{-j\angle h_2}{\mathbf{z}}_2& \dots & e^{-j\angle N_T}{\mathbf{z}}_{N_T}\end{array}\right]\left[\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{b}}\hfill \\ \hfill & =\left[\begin{array}{c}\left|\right|h_1\left|\right|{\mathbf{z}}_1+\left|\right|h_2\left|\right|{\mathbf{z}}_2+\dots +\left|\right|h_{N_T}\left|\right|{\mathbf{z}}_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{b}},\hfill \end{array}$$

(13)

because $h_k=\left|\right|h_k\left|\right|e^{j\angle h_k}$ and $\left|\right|h_k\left|\right|e^{j\angle h_k}{e}^{-j\angle h_k}{\mathbf{z}}_k=\left|\right|h_k\left|\right|{\mathbf{z}}_k$. Further, ${\mathbf{y}}_{\mathrm{b}}$ can be equivalently expressed by using a channel matrix as follows:

$${\mathbf{y}}_{\mathrm{b}}={\mathbf{H}}_{R,N_T}\mathbf{z}+{\mathbf{n}}_{\mathrm{b}},$$

(14)

where the channel matrix ${\mathbf{H}}_{R,N_T}$ results in a real-numbered orthogonal matrix. For example, when we apply the ${\mathbf{Z}}_4$ of (10), the corresponding ${\mathbf{H}}_{R,4}$ results in:

$${\mathbf{H}}_{R,4}=\left[\begin{array}{cccc}\left|\right|h_1\left|\right|& \left|\right|h_2\left|\right|& \left|\right|h_3\left|\right|& \left|\right|h_4\left|\right|\\ \left|\right|h_2\left|\right|& -\left|\right|h_1\left|\right|& \left|\right|h_4\left|\right|& -\left|\right|h_3\left|\right|\\ \left|\right|h_3\left|\right|& -\left|\right|h_4\left|\right|& -\left|\right|h_1\left|\right|& \left|\right|h_2\left|\right|\\ \left|\right|h_4\left|\right|& \left|\right|h_3\left|\right|& -\left|\right|h_2\left|\right|& -\left|\right|h_1\left|\right|\end{array}\right].$$

(15)

Because the ${\mathbf{H}}_{R,N_T}$ is a real-numbered matrix and has full-orthogonality, the complex signal detection at Bob can be easily performed by multiplying the transpose of ${\mathbf{H}}_{R,N_T}$. This will eliminate any complex inversion operation of the matrix, and it will lead to the following simple real-numbered matrix multiplication to obtain the recovered signal at Bob, ${\widehat{\mathbf{z}}}_{\mathrm{b}}$:

$$\begin{array}{cc}\hfill {\widehat{\mathbf{z}}}_{\mathrm{b}}& =\frac{1}{{\sum }_{k=1}^{N_T}{\left|\right|h_k\left|\right|}^2}{\mathbf{H}}_{R,N_T}^T{\mathbf{y}}_{\mathrm{b}},\hfill \\ \hfill & =\frac{1}{{\sum }_{k=1}^{N_T}{\left|\right|h_k\left|\right|}^2}({\mathbf{H}}_{R,N_T}^T{\mathbf{H}}_{R,N_T}\mathbf{z}+{\mathbf{H}}_{R,N_T}^T{\mathbf{n}}_{\mathrm{b}}).\hfill \end{array}$$

(16)

Note that the Gram matrix in (16), ${\mathbf{H}}_{R,N_T}^T{\mathbf{H}}_{R,N_T}$, is a diagonal matrix, and thus there is no interference term for signal detection.

On the other hand, the received signal at Eve can be represented by:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{\mathrm{e}}& ={\mathbf{Z}}_{N_T}^{\prime }\mathbf{g}+{\mathbf{n}}_{\mathrm{e}}\hfill \\ \hfill & =\left[\begin{array}{cccc}{e}^{-j\angle h_1}{\mathbf{z}}_1& e^{-j\angle h_2}{\mathbf{z}}_2& \dots & e^{-j\angle N_T}{\mathbf{z}}_{N_T}\end{array}\right]\left[\begin{array}{c}{g}_1\\ g_2\\ ⋮\\ g_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{e}}\hfill \\ \hfill & =\left[\begin{array}{c}{g}_1{e}^{-j\angle h_1}{\mathbf{z}}_1+\dots +g_{N_T}{e}^{-j\angle h_{N_T}}{\mathbf{z}}_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{e}}.\hfill \end{array}$$

(17)

Because ${\mathbf{Z}}_{N_T}^{\prime }$ contains distortion factors that cannot be nulled out at Eve, the non-diagonal Gram matrix of Eve results in signal detection that cannot be performed properly. Although we have shown the example of a $4\times 1$ system, the proposed idea can be applied to ${\mathbf{Z}}_{N_T}$ obtained from ${\mathbf{X}}_{N_T}$ for systems with more than two transmit antennae.

3.2. Secrecy Enhancement for Spatial Multiplexing

We consider a wiretap SM MIMO system with $N_T$ transmit antennae at Alice as well as $N_R$ receive antennae at Bob and Eve, respectively. In this system, Alice transmits spatially multiplexed $N_T\times 1$ complex signal vector $\mathbf{z}={\left[\begin{array}{cccc}{z}_1& z_2& \dots & z_{N_T}\end{array}\right]}^T$ via the $N_T$ antennae for each time period. Then, $\mathbf{z}$ is transmitted through the $N_R\times N_T$ channel matrices of $\mathbf{H}=\left[\begin{array}{cccc}{\mathbf{h}}_1& {\mathbf{h}}_2& \dots & {\mathbf{h}}_{N_T}\end{array}\right]$ and $\mathbf{G}=\left[\begin{array}{cccc}{\mathbf{g}}_1& {\mathbf{g}}_2& \dots & {\mathbf{g}}_{N_T}\end{array}\right]$ at Bob and Eve, respectively, where ${\mathbf{h}}_k$ and ${\mathbf{g}}_k$ respectively denote the k-th column vectors of $\mathbf{H}$ and $\mathbf{G}$. We propose a new PLS scheme for this environment.

By considering that the k-th signal component of $\mathbf{z}$, $z_k$ will be transmitted through ${\mathbf{h}}_k$ to Bob, the proposed PLS scheme applies phase distortion to $z_k$ by using the sum of the channel phases of ${\mathbf{h}}_k$. For this purpose, the phase distorting vector, $\mathbf{q}$, is first found as follows:

$$\mathbf{q}={\left[\begin{array}{cccc}{\theta }_1& {\theta }_2& \dots & {\theta }_{N_T}\end{array}\right]}^T,$$

(18)

where

$${\theta }_k=e^{\left(-j{\sum }_{i=1}^{N_R}\angle h_{ik}\right)},$$

(19)

and $h_{ik}$ and $\angle h_{ik}$ are the complex channel gain from the k-th transmit antenna to the i-th receive antenna and its phase, respectively.

Next, the pre-distorted signal vector at Alice, ${\mathbf{z}}^{\prime }$, can be found as follows:

$$\begin{array}{cc}\hfill {\mathbf{z}}^{\prime }& =\mathrm{diag}\left(\mathbf{z}\right)\mathbf{q}\hfill \\ \hfill & =\left[\begin{array}{cccc}{z}_1& 0& \dots & 0\\ 0& z_2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & z_{N_T}\end{array}\right]\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\\ {\theta }_{N_T}\end{array}\right]\hfill \\ \hfill & ={\left[\begin{array}{cccc}{\theta }_1{z}_1& {\theta }_2{z}_2& \dots & {\theta }_{N_T}{z}_{N_T}\end{array}\right]}^T.\hfill \end{array}$$

(20)

Then, the received signal at Bob can be represented by:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{\mathrm{b}}& =\mathbf{H}{\mathbf{z}}^{\prime }+{\mathbf{n}}_{\mathrm{b}}\hfill \\ \hfill & =\left[\begin{array}{cccc}{\mathbf{h}}_1& {\mathbf{h}}_2& \dots & {\mathbf{h}}_{N_T}\end{array}\right]\left[\begin{array}{c}{\theta }_1{z}_1\\ {\theta }_2{z}_2\\ ⋮\\ {\theta }_{N_T}{z}_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{b}}\hfill \\ \hfill & =\left[\begin{array}{c}{\theta }_1{z}_1{\mathbf{h}}_1+\dots +{\theta }_{N_T}{z}_{N_T}{\mathbf{h}}_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{b}}\hfill \\ \hfill & ={\mathbf{H}}^{\prime }\mathbf{z}+{\mathbf{n}}_{\mathrm{b}},\hfill \end{array}$$

(21)

where the resulting channel matrix can be represented by:

$${\mathbf{H}}^{\prime }=\left[\begin{array}{cccc}{\theta }_1{\mathbf{h}}_1& {\theta }_2{\mathbf{h}}_2& \dots & {\theta }_{N_T}{\mathbf{h}}_{N_T}\end{array}\right].$$

(22)

Therefore, the signal detection can be achieved by using various well known detection methods, as follows:

$${\widehat{\mathbf{z}}}_{\mathrm{b}}=\mathbf{F}{\mathbf{y}}_{\mathrm{b}},$$

(23)

where $\mathbf{F}$ is a detection matrix, e.g., $\mathbf{F}={\left({\mathbf{H}}^{\prime H}{\mathbf{H}}^{\prime }\right)}^{-1}{\mathbf{H}}^{\prime H}$ for zero forcing (ZF) detection and $\mathbf{F}={({\mathbf{H}}^{\prime H}{\mathbf{H}}^{\prime }+{\sigma }^2\mathbf{I})}^{-1}{\mathbf{H}}^{\prime H}$ for minimum mean square error (MMSE) detection, where ${\sigma }^2$ is the noise variance and $\mathbf{I}$ is the $N_T\times N_T$ identity matrix. On the other hand, the received signal at Eve is represented by:

$$\begin{array}{cc}\hfill {\mathbf{y}}_{\mathrm{e}}& =\mathbf{G}{\mathbf{z}}^{\prime }+{\mathbf{n}}_{\mathrm{e}}\hfill \\ \hfill & =\left[\begin{array}{c}{\theta }_1{z}_1{\mathbf{g}}_1+\dots +{\theta }_{N_T}{z}_{N_T}{\mathbf{g}}_{N_T}\end{array}\right]+{\mathbf{n}}_{\mathrm{e}}.\hfill \end{array}$$

(24)

As in the previous case for STBC schemes, ${\mathbf{z}}^{\prime }$ contains $\mathbf{H}$-dependent distortion, and as a result, Eve cannot retrieve any information on the signal.

4. Simulation Results

We estimate the performance simulation results of the proposed schemes over a Rayleigh fading environment in comparison to the conventional STBC and SM schemes. In the simulations, we assume that the power of the modulation symbols was normalized to one. Figure 1 shows a comparison of the signal constellation change in the QPSK modulation scheme, when PLS schemes are applied for STBC schemes. If AN or AI is used to enhance secrecy [7,9], the amplitude of the signal varies greatly, which will lead to a high PAPR problem at the transmitter. On the other hand, due to its phase distortion characteristics, the proposed scheme maintains constant amplitude value, and it will therefore not suffer from a high PAPR problem.

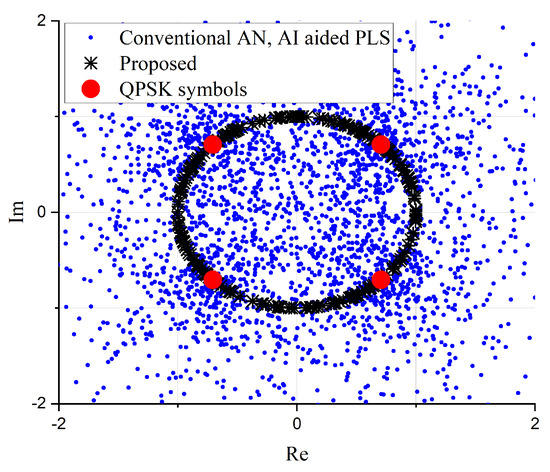
Figure 1. Signal constellation comparison at the transmitter.

Figure 2 shows the BER performance comparison for various STBC schemes with QPSK modulation. Without any secrecy enhancing schemes, Bob and Eve are expected to achieve exactly the same BER performance. The conventional secrecy enhancing scheme with the Alamouti scheme can achieve excellent security protection by making the BER at Eve so bad that it is almost impossible for Eve to extract information [7]. However, this scheme involves sacrificing a power loss of 3 dB for AN to obtain high secrecy protection from Eve. We also note that these AN (or AI)-aided PLS schemes involve a trade-off between the power allocated to AN (or AI) and secrecy protection.

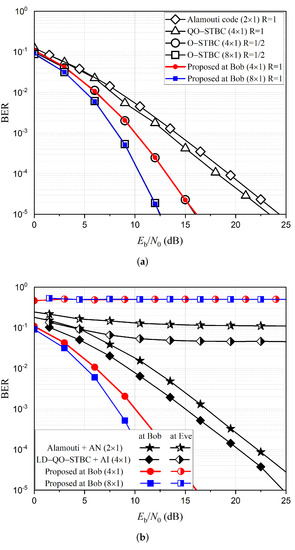
Figure 2. BER performance comparison for various STBC schemes. (a) without PLS. (b) with PLS.

On the other hand, the proposed scheme maintains high secrecy protection, and it also achieves BER performance comparable to that of the conventional full-rate or full-diversity scheme without any additional power allocation. The BER performance of the proposed $4\times 1$ scheme shows exactly the same performance as the half rate $4\times 1$ O-STBC scheme, indicating that it achieves full diversity, even with $R=1$. In addition, the BER performance at Eve with the proposed scheme shows that the proposed scheme does not allow any information leakage to Eve.

To evaluate the performance of the SM schemes, we use the 4 × 4 MIMO systems with QPSK and 16-QAM, respectively. Figure 3 shows the BER performance comparison with the ZF and MMSE detection schemes. As in the previous case, the conventional schemes without any secrecy enhancing capability lead to the same BER performance at Bob and Eve. The BER performance of the proposed scheme at Bob shows exactly the same performance as the conventional schemes, while the BER performance at Eve is highly deteriorated, indicating that it is almost impossible for Eve to properly extract information.

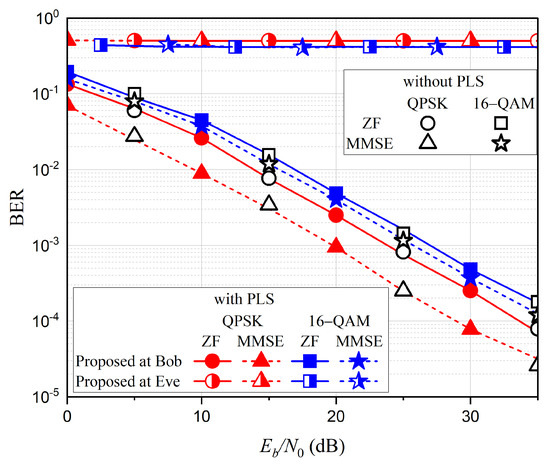
Figure 3. BER performance comparison for various SM schemes.

We also investigate the influence of channel estimation error on BER performance. At this time, signals are transmitted through the channel with $h=\sqrt{1-{\rho }^2}\widehat{h}+\sqrt{{\rho }^2}e$, where $\widehat{h}$ is an estimated channel gain, e is the estimation error, and ${\rho }^2$ is the variance of estimation error [16]. Figure 4 shows the BER performance changes for various STBC schemes according to ${\rho }^2$. As can be seen in the figure, as ${\rho }^2$ increases, the proposed method for rate one STBC shows worse performance than the conventional O-STBC scheme with rate 1/2. This is because the phase distortion cannot be perfectly nulled out at the receiver in the proposed scheme, which results in a non-orthogonal channel matrix. Nevertheless, the proposed scheme still shows better performance than the conventional QO-STBC scheme with the same rate, and it also provides high security protection. On the other hand, Figure 5 shows the proposed method for SM achieves the same performance behavior as the conventional schemes. The results confirm that the proposed methods are not particularly vulnerable to channel estimation error relative to other conventional methods.

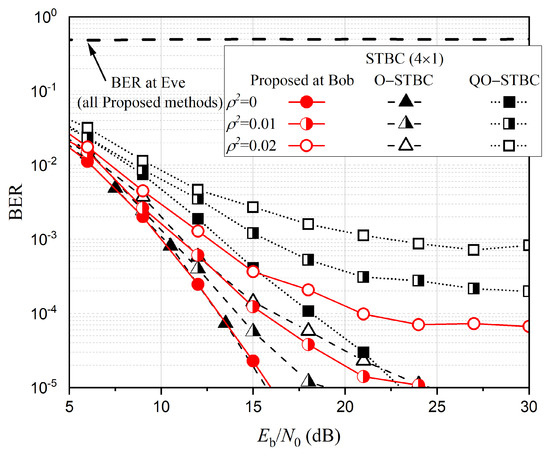
Figure 4. BER performance comparison of various STBC schemes with channel estimation error.

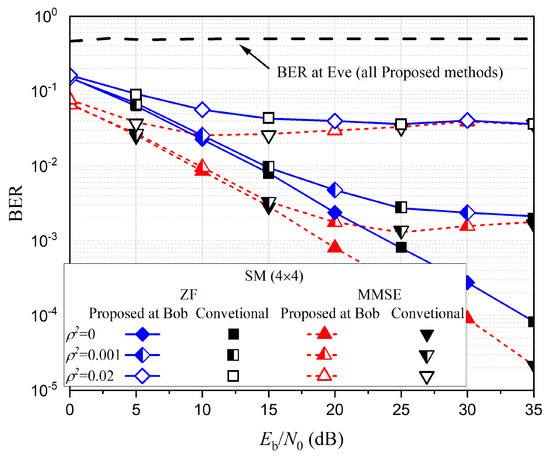
Figure 5. BER performance comparison of various SM schemes with channel estimation error.

To compare a security capability of PLS schemes, the secrecy capacity has usually been investigated in the previous studies [3,9,17]. Here we first present the equations for the secrecy capacities of the proposed and conventional PLS schemes. The secrecy capacity $C_s$ can be defined as follows:

$$C_s=C_B-C_E,$$

(25)

where $C_B$ and $C_E$ are the capacities at Bob and Eve, respectively. For conventional AN (or AI)-aided schemes [7,9], the capacity at Bob, $C_{A,B}$ can be represented as:

$$C_{A,B}={\log }_2\left(1+\frac{{\left|\right|{\mathbf{Z}}_{\mathrm{A}}\mathbf{h}\left|\right|}^2/N_T}{{{\sigma }_{\mathrm{b}}}^2}\right),$$

(26)

where ${{\sigma }_{\mathrm{b}}}^2$ represents the variance of AWGN at Bob. On the other hand, Eve suffers from the noise effect of uncanceled $\mathbf{W}$ as well as AWGN, that is,

$${\mathbf{y}}_{\mathrm{e}}=\underset{\mathrm{Signal}}{\underbrace{{\mathbf{Z}}_{\mathrm{A}}\mathbf{g}}}+\underset{\mathrm{AN}}{\underbrace{\mathbf{W}\mathbf{g}}}+\underset{\mathrm{AWGN}}{\underbrace{{\mathbf{n}}_{\mathrm{e}}}},$$

(27)

and thus, $\mathbf{W}\mathbf{g}$ should be treated as noise in addition to AWGN. The capacity at Eve for AN (or AI)-aided schemes, $C_{A,E}$, can be estimated as follows:

$$C_{A,E}={\log }_2\left(1+\frac{{\left|\right|{\mathbf{Z}}_{\mathrm{A}}\mathbf{g}\left|\right|}^2/N_T}{{\left|\right|\mathbf{Wg}\left|\right|}^2/N_T+{{\sigma }_{\mathrm{e}}}^2}\right),$$

(28)

where ${{\sigma }_{\mathrm{e}}}^2$ represents the variance of AWGN at Eve.

In the case of the proposed method, the detector at Eve cannot discriminate signal components inside ${\mathbf{y}}_{\mathrm{e}}$ in (17), since the signal is distorted by unknown phase information at Alice. That is,

$${\mathbf{y}}_{\mathrm{e}}=\underset{\mathrm{Noise\; to\; Eve}}{\underbrace{\left[\begin{array}{c}{g}_1{e}^{-j\angle h_1}{\mathbf{z}}_1+\dots +g_{N_T}{e}^{-j\angle h_{N_T}}{\mathbf{z}}_{N_T}\end{array}\right]}}+\underset{\mathrm{AWGN}}{\underbrace{{\mathbf{n}}_{\mathrm{e}}}},$$

(29)

and thus there is no pure signal component inside ${\mathbf{y}}_{\mathrm{e}}$. Therefore, the capacities at Bob and Eve for the proposed method can be represented as follows:

$$\begin{array}{cc}\hfill C_{P,B}& ={\log }_2\left(1+\frac{{\left|\right|{\mathbf{Z}}_{N_T}^{\prime }\mathbf{h}\left|\right|}^2/N_T}{{{\sigma }_{\mathrm{b}}}^2}\right),\hfill \\ \hfill C_{P,E}& ={\log }_2\left(1+\frac{0}{{\left|\right|{\mathbf{Z}}_{N_T}^{\prime }\mathbf{g}\left|\right|}^2/N_T+{{\sigma }_{\mathrm{e}}}^2}\right).\hfill \end{array}$$

(30)

This eventually leads to $C_{P,E}$ of 0, and this can be confirmed from the BER simulation results shown in Figure 2b. The result shows that BER at Eve is 0.5 regardless of signal to noise ratio (SNR) values, showing no information leakage to Eve.

We evaluate the capacities of various PLS schemes by using the above derived equations, and Figure 6 presents the capacity comparisons of PLS schemes at Bob and Eve. Since the proposed method does not consume any additional power for PLS, the capacity of the proposed method at Bob accomplishes the highest, while the capacity of the proposed method at Eve is the lowest that is always zero. The capacity of the existing AN method at Bob shows about 3 dB power loss compared to the proposed method because of the power consumption for AN. On the other hand, the existing AI method barely consumes extra energy, and thus it achieves almost the same capacity as the proposed method at Bob. Nevertheless, Eve also can accomplish better capacity performance with the AI method since the energy consumed for AI is much less than that for AN. This can also be confirmed in Figure 2b, where the BER performance of the AI method is better than that of AN, at Eve.

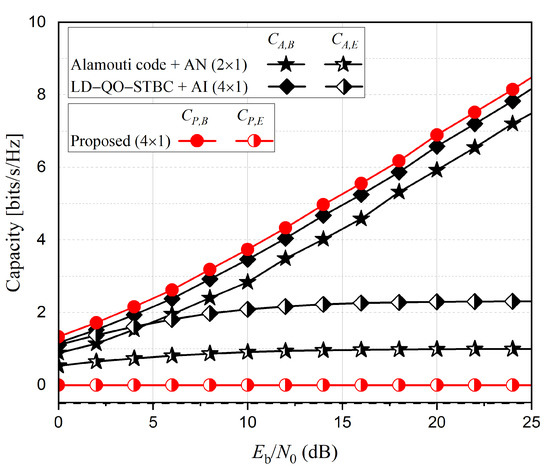
Figure 6. Capacity comparison of various PLS schemes at Bob and Eve.

Figure 7 shows the secrecy capacity comparison of the proposed and AN (or AI)-aided PLS schemes. It reveals that the secrecy capacity of the proposed method shows the best performance due to the best and worst capacities at Bob and Eve, respectively, as shown in Figure 6. On the other hand, the conventional AN scheme should sacrifice secrecy capacity due to additional power consumption. We note that the AN method achieves better secrecy capacity than the AI method. This is because the difference in capacities between Bob and Eve is smaller in the AI method compared to that in the AN method.

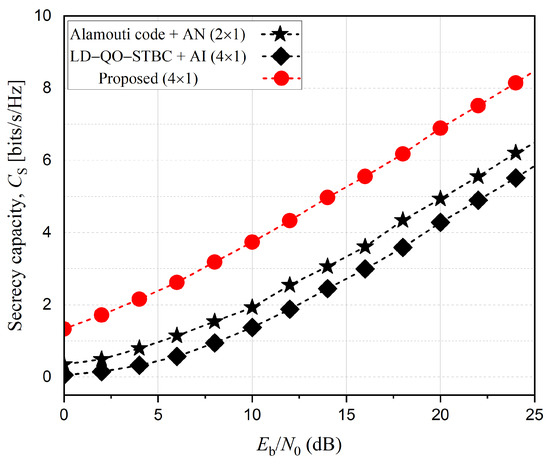
Figure 7. Secrecy capacity comparison of various PLS schemes.

5. Conclusions and Discussion

This paper proposed efficient PLS schemes for STBC and SM-based MIMO systems. Compared to the conventional AN-based PLS scheme, the proposed schemes neither require additional power nor have a PAPR problem, because they distort the phase of the complex signals. The performance simulation results showed that, in addition to high security protection, the proposed scheme for the STBC-based MIMO system achieves BER performance approximating those of the conventional schemes with full rate or full orthogonality. The proposed scheme for the SM-based MIMO system also showed almost no information leakage to the illegal eavesdropper.

The proposed scheme requires accurate CSI at both the transmitter and the receiver, which may not be the common assumption for the STBC-based MIMO systems. The future work should focus on other alternative methods which do not require CSI at the transmitter, by considering STBC as a transmit diversity technique. In addition, we investigated the effect of CSI estimation error by using a commonly used model, but the estimation error accumulation effect may impact further on the performance of the proposed SM-based MIMO scheme. Hence, future work should focus on detailed investigation on the effect of imperfect channel information, leading to more efficient PLS schemes.