Realization of an Electronically Tunable Resistor-Less Floating Inductance Simulator Using VCII

Abstract

In this paper, a new implementation of an electronically tunable resistor-less floating inductance simulator using a second-generation voltage conveyor (VCII) is presented. The proposed circuit is resistor-free (benefiting from the intrinsic resistors at the Y terminals of the employed VCIIs) and composed of three VCIIs and a single grounded capacitor. Using a control current (I_con), the value of impedance at the Y terminal of the VCII is varied, whereby the value of the simulated inductance is tuned. The proposed circuit is designed at a transistor level using 0.18 µm TSMC CMOS parameters and ±0.9 V supply voltage. PSpice simulations are carried out to confirm the effectiveness of the proposed circuit. For a range of Icon from 0 µA to 50 µA, the value of the simulated L can be varied from −576 µH to −324 µH and from +316 µH to +576 µH for negative and positive simulators, respectively, in the frequency range of 100 kHz–3 MHz. Favorably, the value of the series resistance remains below 76 Ω. Simulation results show an error value below 4.8% and power consumption variation is from 1.64 mW to 1.92 mW. Moreover, application of the proposed circuit as a standard band-pass RLC filter is also included.

1. Introduction

In the integrated circuit technology, the use of inductors, especially with large values, is impractical, mainly due to the large-occupied area. Accordingly, instead of bulky physical inductors, simulated inductors are used to overcome this problem. In this approach, active building blocks (ABBs) along with capacitors and resistors are used to synthesize the equivalent of inductors in a specified frequency range. More importantly, unlike physical inductors which suffer from a limited adjustment range of 15% [1], the value of simulated inductors can be easily adjusted. For those with electronic tuning capability, it is possible to adjust the value of simulated inductors electronically through a control current or voltage which is considered advantageous for providing full integration. Floating and grounded simulated inductors find wide applications in the design of filters and oscillators as well as in the cancellation of unavoidable parasitic capacitances [1,2,3,4]. The industry’s recent trend toward integration and miniaturization has made the inductance simulator design a popular research topic.

A survey of recent literature reveals that various approaches are used in the realization of floating inductors [5,6,7,8,9,10,11,12,13,14,15]. In [5], a digitally tunable floating inductor using two current differential amplifiers (CDAs), two resistors and an array of five floating capacitors, each one connected to a switch, is reported. The value of the achieved inductor is changed by controlling the bits applied to the switches. The main drawback of this approach is the large number of floating capacitors used in the implementation and the need for digital controlling. Another approach based on four second-generation current conveyors (CCIIs), one grounded capacitor, two grounded resistors and an array of ten floating resistors, each one connected to a switch, is reported in [6] for a digitally programmable floating inductance. The equivalent value of the resistor array is changed by controlling the bits applied to the switches; therefore, the value of the achieved simulated inductor is defined. Compared to the digitally programmable floating inductor of [5], the circuit of [6] does not employ floating capacitors. However, its operation depends on the matching between two resistors connected to the Y and X terminals of the first CCII. Moreover, to precisely define the value of the achieved inductor, the value of the resistors connected to switches must be trimmed carefully. The solution reported in [7] utilizes three current differencing transconductance amplifiers (CDTAs) and one grounded capacitor. Electronic tunability is achieved by changing the transconductance of the used ABBs through increasing the bias current, which results in high power consumption. In [8], only one differential voltage current conveyor transconductance amplifier (DVCCTA) is used as ABB. Electronic tuning is performed through increasing the bias current, which sacrifices power consumption and the quality of the achieved inductor. The latter occurs because, by increasing the bias current, the value of the parasitic resistors connected in parallel to the simulated inductor are reduced, which limits its overall performance. In [9], one dual output differential difference current conveyor (DO-DDCC), two resistors and one grounded capacitor are used to design a floating inductor simulator. Unfortunately, the achieved inductance lacks electronic tuning capability, and its operation relies on the matching between the used resistors. The topology reported in [10] utilizes one differential voltage current conveyor (DVCC), one current controlled current conveyor (CCCII), one grounded resistor and one floating capacitor. Using the electronic controlling capability of CCCII, the achieved inductor is electronically tunable. However, as the bias current is increased to change the value of the achieved inductor, power consumption is increased accordingly. In addition, the topology is not desirable from an integration point of view due to the used floating capacitor. In [11], an attempt is made to design a floating inductor simulator using active building blocks only, which utilizes one current controlled conveyor transconductance amplifier (CCCTA) and one operational amplifier (OA). Although it is claimed that the proposed topology is capacitor free, its operation relies on the compensation capacitor used in the internal structure of OA. In addition, the circuit suffers from high power consumption and limited frequency range due to the limited frequency performance of OA. In [12], two differential voltage-to-current converters, two resistors and one capacitor are used. In [13], another topology using two differential difference current conveyors, two resistors and one grounded capacitor is introduced. The circuit reported in [14] employs two modified current feedback operational amplifiers (MCFOAs), two resistors and one grounded capacitor. The main weakness of [12,13,14] is the lack of electronic tunability. In [15], a different topology based on CCII±, one dual output transconductance amplifier (DO-OTA), one resistor and one floating capacitor is used. It is electronically tunable, but it employs a floating capacitor. In addition, as the bias current of DO-OTA is increased to tune the value of the simulated capacitor, the value of the parasitic parallel resistors is reduced, which causes the quality of the simulated inductor to deteriorate.

Recently, a new active building block called a second-generation voltage conveyor (VCII) [16,17,18,19,20], which is the dual circuit of well-known CCII, has been employed in the design of grounded impedance simulators [21,22]. Comparison shows that the simulated grounded capacitors and inductors using VCII exhibit many advantages, namely, simpler realizations, reduced error, reduced parasitics, lower power consumption, etc., over simulated grounded impedances utilized by other ABBs. From the reported results in [21,22], the use of VCII in realizing impedance simulators looks quite promising. In this paper, we aim to employ VCII in realizing a floating inductor simulator. The proposed topology is resistor-less and uses three VCIIs and one grounded capacitor. Instead of passive resistors, the internal resistors at the Y terminals of the used ABBs are used. The proposed topology has the capability to simulate both positive and negative inductors. The value of the simulated inductor is easily adjusted by a control current which is used to change the value of the Y terminal impedance of the used VCIIs. To provide low voltage operation, the bias current is increased only in the input section of VCII and the bias current in the other sections remains constant. Therefore, by increasing the control current, the parallel parasitic resistors associated with the simulated inductor will not experience any reduction, thereby resulting in high performance. The circuit enjoys a simple resistor-free realization made of 52 transistors in total. The reduced error, low parasitic elements and high adjustable range are other features of the proposed floating inductor simulator. To investigate the effect of VCII parasitics and non-idealities on the performance of the simulated floating inductor, a complete non-ideal analysis is performed. Spice simulation results are also reported. The application of the proposed floating inductor simulator as an RLC band-pass filter is also given. The organization of this paper is as follows. In Section 2, the proposed topology is introduced. In Section 3, non-ideal analyses are reported. In Section 4, the CMOS implementation of the active blocks is discussed. Simulation results are given in Section 5. Finally, Section 6 includes the conclusion.

2. The Proposed VCII Based Floating Inductance Simulator

The proposed VCII-based floating capacitor simulator is shown in Figure 1. It is composed of one VCII^±, one VCII⁺, one VCII⁻ and a grounded capacitor. The operation of VCII⁺ and VCII⁻ is expressed by the matrix Equation (1) as follows:

$$\left[\begin{array}{c}{I}_X\\ V_Z\\ V_Y\end{array}\right]=\left[\begin{array}{ccc}\pm \beta & \frac{1}{r_x}+s{C}_x& 0\\ 0& \alpha & r_z\\ r_y& 0& 0\end{array}\right]\left[\begin{array}{c}{I}_Y\\ V_X\\ I_Z\end{array}\right]$$

(1)

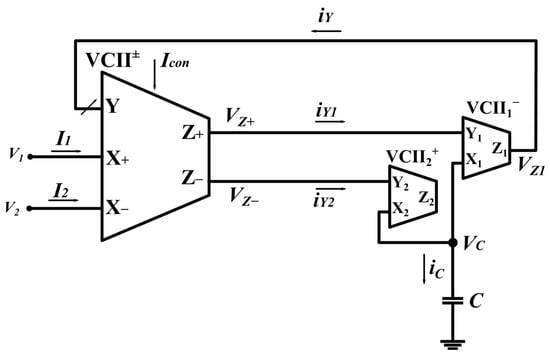
Figure 1. The proposed floating positive capacitance simulator.

In (1), β is the current gain between the Y and X terminals while α is the voltage gain between then X and Z terminals. Here, +β and −β indicate VCII⁺ and VCII⁻, respectively. In the ideal case, the values of β and α are unity. The parameters r_x, r_z and r_Y are parasitic impedances at the X, Z and Y terminals, respectively. In the ideal case, r_x and r_z are infinite and zero, respectively, while C_x (with ideal value of zero) represents the parasitic capacitance at the X terminal. To eliminate the need for passive resistors, we take advantage of the parasitic impedance at the Y terminals of VCII⁺ and VCII^-. For the used VCIIs, the value of r_Y is designed at a constant non-zero value, while the value of r_Y in VCII^± is varied using a control current resulting in electronic tunability for the simulated inductor. This property is shown as a small arrow on the Y terminal of VCII^±. The performance of VCII^± with electronically variable impedance at the Y terminal is shown in the matrix (2):

$$\left[\begin{array}{c}{I}_{X+}\\ I_{X-}\\ V_{Z+}\\ V_{Z-}\\ V_Y\end{array}\right]=\left[\begin{array}{ccccc}{\beta }_{+}& \frac{1}{r_{x+}}+s{C}_{x+}& 0& 0& 0\\ -{\beta }_{-}& 0& \frac{1}{r_{x-}}+s{C}_{x-}& 0& 0\\ 0& {\alpha }_{+}& 0& r_{z+}& 0\\ 0& 0& {\alpha }_{-}& 0& r_{z-}\\ r_Y& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{I}_Y\\ V_{X+}\\ V_{X-}\\ I_{Z+}\\ I_{Z-}\end{array}\right]$$

(2)

In (2), the current gain between Y and X+ are shown by β+ while the one between Y and X− are shown by −β₋ with ideal values of unity. The voltage gain between the X+ and Z+ terminals is shown by α+ and the voltage gain between the X− and Z− terminals is shown by α− with ideal values of unity. Here, r_x+, r_x−, r_z+ and r_z− are parasitic impedances at the X+, X−, Z+ and Z− terminals, respectively, with ideal values of infinite, infinite, zero and zero, respectively. The parasitic resistor r_Y is designed at a non-zero value which can be electronically varied through I_con. In (1) and (2), the parasitic capacitors at the X terminals are shown by C_x+ and C_x− which have ideal values of zero.

In the ideal case analysis, the values of β and α are assumed to be unitary. The parasitic impedances at the X and Z ports are assumed as infinite and zero, respectively. The values of the Y port impedances are shown by r_Y1, r_Y2 and r_Y for VCII⁻₁, VCII⁺₂ and VCII^±, respectively.

By these assumptions, the operation of the proposed circuit of Figure 1 can be analyzed as follows. Using (2) for V_Z+ and V_Z− we have:

$$V_{Z+}=V_1, V_{Z-}=V_2$$

(3)

where V₁ and V₂ are input voltages. At the Y terminals of VCII⁻₁ and VCII⁺₂, proportional currents are produced through r_Y1 and r_Y2 as:

$$i_{Y1}=\frac{V_{z+}}{r_{Y1}}=\frac{V_1}{r_{Y1}}$$

(4)

$$i_{Y2}=\frac{V_{z-}}{r_{Y2}}=\frac{V_2}{r_{Y2}}$$

(5)

Using (1), (4) and (5), the current produced at C is found as:

$$i_C=\frac{V_1}{r_{Y1}}-\frac{V_2}{r_{Y2}}$$

(6)

By assuming r_Y1 = r_Y2 = r, from (6), V_C is found as:

$$V_C=\frac{V_1-V_2}{sCr}$$

(7)

From (2), V_C is transferred to the Z₁ terminal where it is converted to a proportional current through the Y terminal impedance of VCII^± as:

$$i_Y=\frac{V_1-V_2}{sCr{r}_Y}$$

(8)

where r_Y is the electronically variable impedance at the Y terminal of VCII^±. From (8), the value of the simulated inductor is found as:

$$L_{eq}=Cr{r}_Y$$

(9)

To achieve negative impedance values, we need to change the connection of the Z terminals of VCII^± and the Y terminals of VCII⁻₁ and VCII⁺₂, as shown in Figure 2. Similarly, it can be shown that the simulated inductor of Figure 2 is:

$$L_{eq}=-Cr{r}_Y$$

(10)

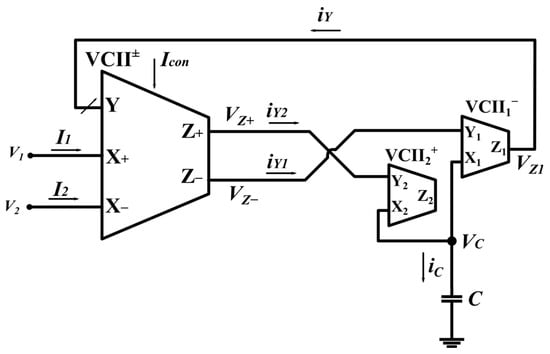
Figure 2. The proposed floating negative inductor simulator.

3. Non-Ideal Analysis

Figure 3 shows the proposed inductor simulator topology in which all parasitic elements of the used ABBs are shown. A complete non-ideal analysis of the proposed circuit can be performed as follows.

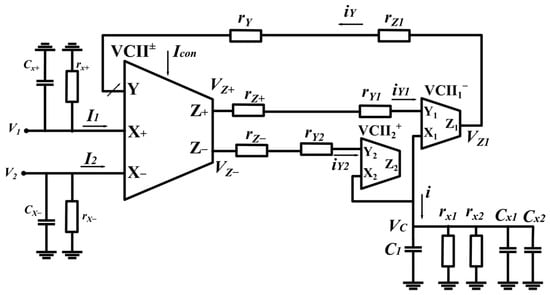
Figure 3. The floating inductor simulator with parasitic elements.

Using (1) and performing a simple analysis using the Kirchhoff current and voltage laws (KCL, KVL) i_Y1 and i_Y2 are found as:

$$i_{Y1}=\frac{V_{z+}}{r_{z+}+r_{Y1}}=\frac{{\alpha }^{+}{V}_1}{r_{z+}+r_{Y1}}$$

(11)

$$i_{Y2}=\frac{V_{z-}}{r_{z-}+r_{Y2}}=\frac{{\alpha }^{-}{V}_2}{r_{z-}+r_{Y2}}$$

(12)

Again using (1) and performing a KCL analysis, V_C is found as:

$$V_C=[{\beta }_1{i}_{Y1}-{\beta }_2{i}_{Y2}]\frac{r_{eq}}{1+s{C}_{eq}{r}_{eq}}$$

(13)

where:

$$r_{eq}={\left(\frac{1}{r_{x1}}+\frac{1}{r_{x2}}\right)}^{-1}$$

(14)

$$C_{eq}=C_{x1}+C_{x2}+C_1$$

(15)

Inserting (11) and (12) into (13) results in:

$$V_C=\frac{r_{eq}}{1+s{C}_{eq}{r}_{eq}}\left[\frac{{\beta }_1{\alpha }^{+}{V}_1}{r_{z+}+r_{Y1}}-\frac{{\beta }_2{\alpha }^{-}{V}_2}{r_{z-}+r_{Y2}}\right]$$

(16)

Using (1), (2) and (16), i_Y is found as:

$$i_Y=\frac{{\alpha }_1{r}_{eq}}{1+s{C}_{eq}{r}_{eq}}\left[\frac{{\beta }_1{\alpha }^{+}{V}_1}{r_{z+}+r_{Y1}}-\frac{{\beta }_2{\alpha }^{-}{V}_2}{r_{z-}+r_{Y2}}\right]$$

(17)

From the matrix equation of (2), by ignoring the effect of r_x+ and r_x−, I₁ and I₂ are:

$$I_1=\frac{{\alpha }_1{r}_{eq}{\beta }^{+}}{\left(1+s{C}_{eq}{r}_{eq}\right)\left(r_{z1}+r_Y\right)}\left[\frac{{\beta }_1{\alpha }^{+}{V}_1}{r_{z+}+r_{Y1}}-\frac{{\beta }_2{\alpha }^{-}{V}_2}{r_{z-}+r_{Y2}}\right]$$

(18)

$$I_2=-\frac{{\alpha }_1{r}_{eq}{\beta }^{-}}{\left(1+s{C}_{eq}{r}_{eq}\right)\left(r_{z1}+r_Y\right)}\left[\frac{{\beta }_1{\alpha }^{+}{V}_1}{r_{z+}+r_{Y1}}-\frac{{\beta }_2{\alpha }^{-}{V}_2}{r_{z-}+r_{Y2}}\right]$$

(19)

Assuming (r_Z+ + r_Y1) = (r_Z− + r_Y2) = r′ and (r_Z1 + r_Y) = r″, (18) and (19) become:

$$I_1=\frac{{\alpha }_1{r}_{eq}{\beta }^{+}}{\left(1+s{C}_{eq}{r}_{eq}\right)r^{ʹ}{r}^{ʹʹ}}\left[{\beta }_1{\alpha }^{+}{V}_1-{\beta }_2{\alpha }^{-}{V}_2\right]$$

(20)

$$I_2=-\frac{{\alpha }_1{r}_{eq}{\beta }^{-}}{\left(1+s{C}_{eq}{r}_{eq}\right)r^{ʹ}{r}^{ʹʹ}}\left[{\beta }_1{\alpha }^{+}{V}_1-{\beta }_2{\alpha }^{-}{V}_2\right]$$

(21)

By defining the voltage gain and current gain parameters of the used VCII as:

$${\beta }_1=1\pm \epsilon$$

(22)

$${\beta }_2=1\mp \epsilon$$

(23)

$${\alpha }^{+}=1\pm {\epsilon }^{ʹ}$$

(24)

$${\alpha }^{-}=1\mp {\epsilon }^{ʹ}$$

(25)

$${\beta }^{+}=1\pm {\epsilon }^{ʹʹ}$$

(26)

$${\beta }^{\mp }=1\mp {\epsilon }^{ʹʹ}$$

(27)

where ε << 1, ε′ << 1 and ε″ << 1 are gain errors, and inserting (22)–(27) into (20) and (21) and simplifying the results gives:

$$I_1\approx \frac{{\alpha }_1{r}_{eq}{\beta }^{+}}{\left(1+s{C}_{eq}{r}_{eq}\right)r^{ʹ}{r}^{ʹʹ}}\left[1-\left(\pm \epsilon \pm {\epsilon }^{ʹ}\pm {\epsilon }^{ʹʹ}\right)\right]\left(V_1-V_2\right)$$

(28)

$$I_2\approx -\frac{{\alpha }_1{r}_{eq}{\beta }^{-}}{\left(1+s{C}_{eq}{r}_{eq}\right)r^{ʹ}{r}^{ʹʹ}}\left[1-\left(\pm \epsilon \pm {\epsilon }^{ʹ}\pm {\epsilon }^{ʹʹ}\right)\right]\left(V_1-V_2\right)$$

(29)

From (28), (29) L_eq and its series impedance R_seri are found as:

$$L_{eq}\approx C_{eq}{r}^{ʹ}r$$

(30)

$$R_{seri}=\frac{r^{ʹ}{r}^{ʹʹ}}{r_{eq}}$$

(31)

As can be seen from (30), the value of L_eq can be varied by r_Y. From (14) and (31), it is also deduced that as the value of r_eq is much larger than r_Y1, r_Y2 and r_Y, the value of R_seri is low. The equivalent circuit of the proposed capacitor simulator is shown in Figure 4, where L_eq is the proposed electronically tunable equivalent floating inductor. r_x and C_x are the parasitic parallel resistance and capacitance and R_seri is the parasitic series resistance of the simulated inductor. Similar analysis can be performed for the negative inductance simulator which is not repeated here.

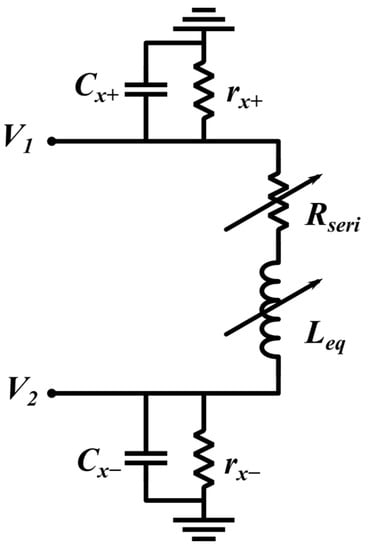
Figure 4. The equivalent circuit of the proposed floating L simulator.

4. CMOS Implementation of VCII

A simple realization of the internal structure of VCII^± is shown in Figure 5a. The input section at the Y port is composed of transistors M₁ and M₂, I_con, I_B1 and I_B2. Transistor M₂ is used in common gate structure and the bias voltage at its gate is provided by diode connected transistor M₁. The impedance at the Y terminal is:

$$r_Y=\frac{1}{g{m}_{M2}}$$

(32)

where gm_M2 (with usual meaning of symbols) is:

$$g{m}_{M2}=\sqrt{\mu C_0\frac{W_{M2}}{L_{M2}}\left(I_{con}+I_{B1}\right)}$$

(33)

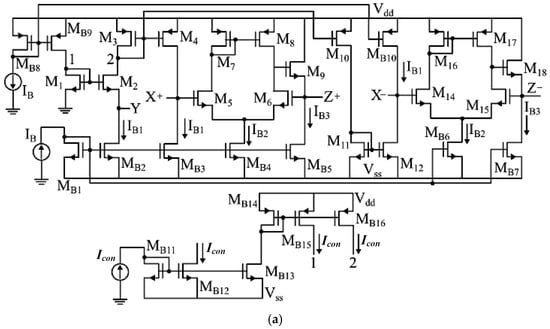
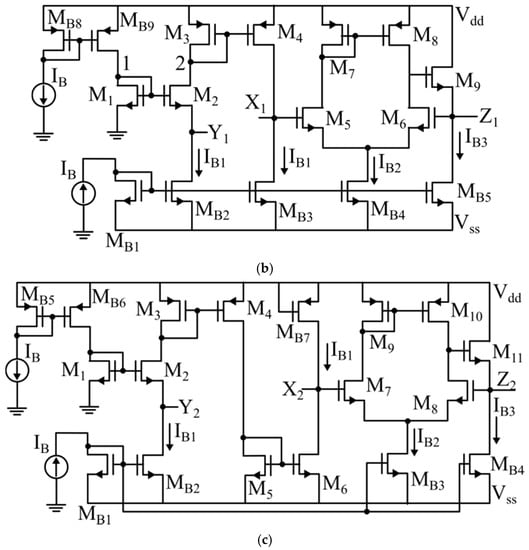
Figure 5. CMOS implementation of (a) electronically controllable VCII^±, (b) VCII⁺ and (c) VCII⁻.

From (33), by increasing the value of I_con, the value of gm_M2 will be increased and according to (32), the value of r_Y will be reduced. To reduce power consumption, I_con is added to the drain of M₂ to keep the bias current at other branches constant. To set the zero-offset voltage at Y port, I_con is also added to the drain of M₁. This is performed by transistors M_B11-M_B16.

The input current applied to the Y terminal is transferred to the X+ terminal through a simple current mirror made of M₃ and M₄. On the other hand, the input current at the Y terminal is transferred to the X− terminal by transistors M₃, M₄, M₁₀–M₁₂. The voltage produced at the X+ terminal is transferred to the Z+ terminal through a voltage buffer made of M₅–M₉. Similarly, the voltage produced at the X− terminal is transferred to the Z− terminal through a voltage buffer of M₁₄–M₁₈. Transistors M_Bi for i = 1–10 are used for biasing. A simple analysis gives the parasitic elements at the X+, X− Z+ and Z− terminals as:

$$r_{X+}=r{o}_{M4}\Vert r{o}_{MB3}$$

(34)

$$C_{X+}=Cd{s}_{M4}+Cd{g}_{M4}+Cd{s}_{MB3}+Cd{g}_{MB3}$$

(35)

$$r_{X-}=r{o}_{M12}\Vert r{o}_{MB10}$$

(36)

$$C_{X-}=Cd{s}_{M12}+Cd{g}_{M12}+Cd{s}_{MB10}+Cd{g}_{MB10}$$

(37)

$$r_{Z+}=\frac{1}{g{m}_{M9}g{m}_{M5(}r{o}_{M8}\Vert r{o}_{M6})}$$

(38)

$$r_{Z-}=\frac{1}{g{m}_{M18}g{m}_{M14(}r{o}_{M15}\Vert r{o}_{M17})}$$

(39)

where for ith transistor, ro_Mi is the drain-source impedance, gm_Mi is the transconductance and ro_MBi is the drain source impedance and Cds_Mi and Cdg_Mi are the drain-source capacitance and drain-gate capacitance of the related transistor.

The implementation of the VCII⁺ and the VCII⁻ are shown in Figure 5b,c, respectively. Here, transistor M₂ is configured in a common gate structure and the diode connected transistor M₁ provides proper biasing at the gate of M₁. A simple current mirror made of M₃ and M₄ in Figure 5b, and current mirrors made of M₃ and M₄, and M₅ and M₆ in Figure 5c, are used to transfer the Y port input current to the X ports. The voltage produced at the X ports is transferred to the Z ports by a voltage buffer made of M₅–M₉ in Figure 5b and M₇–M₁₁ in Figure 5c.

Parasitic elements are found as:

$$r_{Y1}=r_{Y2}=\frac{1}{g{m}_{M2}}={\left[\sqrt{\mu C_0\frac{W_{M2}}{L_{M2}}{I}_{B1}}\right]}^{-1}$$

(40)

$$r_{Z1}=\frac{1}{g{m}_{M9}g{m}_{M5}\left(r{o}_{M8}\Vert r{o}_{M6}\right)}$$

(41)

$$r_{Z2}=\frac{1}{g{m}_{M11}g{m}_{M7}\left(r{o}_{M10}\Vert r{o}_{M8}\right)}$$

(42)

$$r_{X1}=r{o}_{M4}\Vert r{o}_{MB3}$$

(43)

$$r_{X2}=r{o}_{M6}\Vert r{o}_{MB7}$$

(44)

$$C_{X1}=Cd{s}_{M4}+Cd{g}_{M4}+Cd{s}_{MB3}+Cd{g}_{MB3}$$

(45)

$$C_{X2}=Cd{s}_{M6}+Cd{g}_{M6}+Cd{s}_{MB7}+Cd{g}_{MB7}$$

(46)

5. Simulation Results

PSpice simulations of the proposed floating inductors of Figure 1 and Figure 2 based on 0.18 μm CMOS technology and supply voltage of ±0.9 V are performed. The aspect ratios for the used PMOS and NMOS transistors are 9 µm/0.9 µm and 27 µm/0.9 µm, respectively. The values of the bias currents are I_B = I_B1 = I_B2 = I_B3 = 20 µA. All bias currents are realized by simple current mirrors. The performance parameters and parasitic elements of the used ABBs are reported in Table 1.

Table 1. The simulated characteristics of VCII^±, VCII⁺ and VCII⁻.

VCII±			VCII−	VCII+
rY	Icon = 0 µA	3.43 kΩ	3.43 kΩ	3.43 kΩ
	Icon = 25 µA	2.18 kΩ
	Icon = 50 µA	1.8 kΩ
rX		rx+ = 240 kΩ, rx− = 244 kΩ	240 kΩ	250 kΩ
rz		rz− = rz+ = 48 Ω	48 Ω	48 Ω
α		α+ = α− = 0.981	0.981	0.981
β	Icon = 0 µA	β+ = 1.007, β− = 1.04	1.042	1.002
	Icon = 25 µA	β+ = 0.988, β− = 1.03
	Icon = 50 µA	β+ = 0.999, β− = 1.023
Cx		Cx+ = 48 fF, Cx− = 64 fF	74 fF	37 fF
Power dissipation		0.352–0.625 mW	0.242 mW	0.201 mW

For C₁ = 50 pF, Figure 6 shows the phase and magnitude frequency response of the proposed floating inductor for I_con = 0 µA, I_con = 25 µA and I_con = 50 µA. The proposed circuit frequency range is from 100 kHz to 3 MHz.

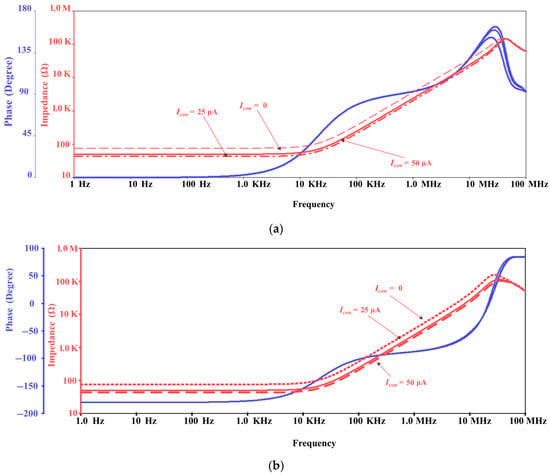
Figure 6. Frequency response of magnitude and phase for the proposed (a) positive and (b) negative floating inductor simulator.

Table 2 shows the value of the achieved inductance for different values of I_con for both theoretical and simulated values. As can be seen, the error for L_eq remains below 4.8%. Fortunately, the maximum value of R_seri remains at 76 Ω.

Table 2. Deviation between theoretical and ideal values at different control currents.

	Icon	Calc. Rseri	Sim. Rseri	Calc. Leq	Sim. Leq	% of Error in Leq
Negative simulator	0	97 Ω	76 Ω	588 µH	−576 µH	−2%
	25 µA	61 Ω	50.2 Ω	374 µH	−382 µH	2.1%
	50 µA	51 Ω	43 Ω	309 µH	−324 µH	4.8%
Positive simulator	0	97 Ω	76 Ω	588 µH	576 µH	−2%
	25 µA	61 Ω	49 Ω	374 µH	366 µH	−2.9%
	50 µA	51 Ω	42 Ω	309 µH	316 µH	2.3%

To test the time domain response of the proposed inductor simulator, a sinusoidal input voltage with a peak-to-peak value of 80 mV and frequency of 1 MHz is used as the input signal to the simulated inductor. The output signal phase is 93.6° and −86.4° for positive and negative types, respectively. The resulting outputs are shown in Figure 7.

Figure 7. Time domain response of the proposed (a) positive and (b) negative floating inductors.

The functionality of the proposed floating inductor is tested on a standard RLC band-pass filter for C₁ = 50 pF, R_L = 10 kΩ shown in Figure 8. Figure 9 shows the frequency response of the RLC band-pass filter for both the ideal and the simulated inductance. The simulated value of f₀ is 1.04 MHz, 1.39 MHz and 2.39 MHz for I_con = 0 µA, I_con = 25 µA and I_con = 50 µA, respectively.

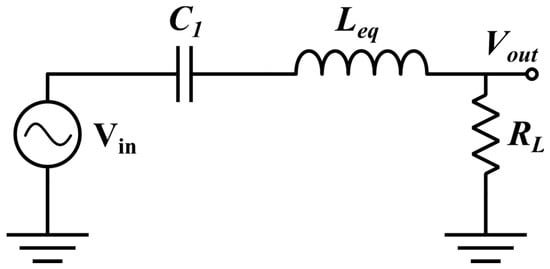
Figure 8. Application of simulated Floating L as a RLC band-pass filter.

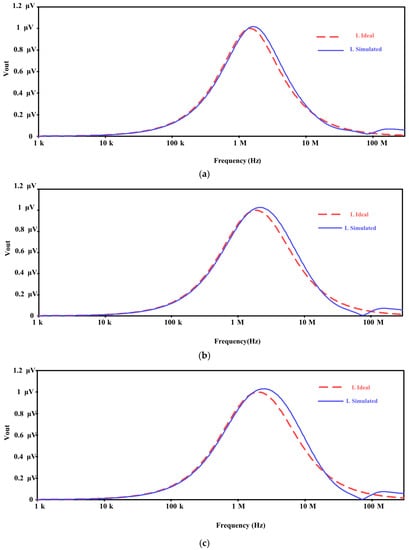
Figure 9. Frequency response of the RLC band-pass filter for different values of I_con (a) 0 µA (b) 25 µA and (c) 50 µA.

The robustness of the design was tested as well. In particular, Table 3, Table 4 and Table 5 show the PVT variations of the VCII^±, VCII⁺ and VCII⁻ ABBs, respectively, while in Table 6, the same variations are tested for the actual equivalent inductor value. Simulations have been reported at different I_con levels. Results show that, regardless of the conditions, values always remain within 3% of the nominal ones reported along the manuscript concerning the ABBs parameters, while they remain within 11% when it comes to the equivalent inductor value.

Table 3. PVT simulation results for VCII^±.

Parameter		P				V (Vdd-Vss)		T (°C)
		FF	SF	FS	SS	±0.99 V	±0.81 V	−20	25	80
rY (Ω)	Icon = 0 µA	3.36 k	3.41 k	3.416 k	3.5 k	3.395 k	3.462 k	2.985 k	3.45 k	3.944 k
	Icon = 25 µA	2.21 k	2.16 k	2.168 k	2.2 k	2.18 k	2.22 k	1.87 k	2.16 k	2.52 k
	Icon = 50 µA	1.75 k	1.78 k	1.79 k	1.81 k	1.76 k	1.86 k	1.52 k	1.77 k	2.11 k
[rX+, rX−] kΩ		[238, 205]	[243, 132]	[240, 243]	[245, 242]	[225, 242]	[242, 248]	[200.1, 200]	[242, 239]	[249, 287.4]
rZ+ = rz− (Ω)		45	47.6	45	49	51	54	54	47.6	50.2
α+ = α−		0.981	0.980	0.990	0.980	0.982	0.978	0.980	0.981	0.980
β+, β−	Icon = 0 µA	1.01, 1.047	1.01, 1.046	0.993, 1.029	1.004, 1.026	1.009, 1.057	1.011, 1.065	1.018, 1.066	1.01, 1.047	1.005, 1.03
	Icon = 25 µA	1, 1.038	1, 1.036	1, 1.0368	0.999, 1.035	1.006, 1.046	1.056, 1.006	1.006, 1.055	1, 1.037	0.995, 1.021
	Icon = 50 µA	0.993, 1.031	0.993, 1.029	0.993, 0.980	0.992, 1.028	0.999, 1.049	0.997, 1.009	0.999, 1.047	0.993, 1.03	0.988, 1.015
Cx+, Cx− (fF)		49, 80	59, 81	61, 77	58, 64	59, 119	34, 60	92, 94	61, 77	68, 81
Power Dissipation (µW)		313–583	353–625	317–605	313–625	332–657	313–553	356–630	353–625	350–620

Table 4. PVT simulation results for VCII⁺.

Parameter	P				V (Vdd-Vss)		T (°C)
	FF	SF	FS	SS	±0.99 V	±0.81 V	−20	25	80
rY	3.38 kΩ	3.43 kΩ	3.44 kΩ	3.49 kΩ	3.4 kΩ	3.5 kΩ	3 kΩ	3.4 kΩ	4 kΩ
rX	250 kΩ	250 kΩ	250.3 kΩ	252.6 kΩ	250 kΩ	251 kΩ	205 kΩ	249 kΩ	302 kΩ
rZ	46 Ω	47 Ω	47.1 Ω	48.4 Ω	50 Ω	88 Ω	43 Ω	54 Ω	72 Ω
α	0.981	0.981	0.984	0.983	0.986	0.978	0.980	0.973	0.974
β	1.0026	1.0023	1.0023	0.9966	1.008	0.996	1.008	0.996	0.993
cx	32 fF	41 fF	38 fF	38.1 fF	32 fF	37 fF	37 fF	39 fF	40 fF
Power dissipation	202 µW	203 µW	202 µW	201 µW	224 µW	186 µW	204 µW	203 µW	202 µW

Table 5. PVT simulation results for VCII⁻.

Parameter	P				V (Vdd-Vss)		T (°C)
	FF	SF	FS	SS	±0.99 V	±0.81 V	−20	25	80
rY	3.36 kΩ	3.41 kΩ	3.41 kΩ	3.46 kΩ	3.39 kΩ	3.46 kΩ	2.97 kΩ	3.4 kΩ	3.94 kΩ
rX (kΩ)	211 kΩ	212 k Ω	212.5 kΩ	214 kΩ	199 kΩ	223 kΩ	178.44 kΩ	206.3 kΩ	252 kΩ
rZ (Ω)	46.5 Ω	47.7 Ω	47.6 Ω	49 Ω	46.2 Ω	52.5 Ω	42 Ω	46 Ω	54 Ω
α	0.981	0.980	0.984	0.980	0.986	0.976	0.980	0.980	0.980
β	1.048	1.046	1.046	1.045	1.0665	1.027	1.066	1.047	1.038
cx	110 fF	112 fF	115 fF	110 fF	119 fF	130 fF	107 fF	113 fF	115 fF
Power dissipation	190 µW	200 µW	190 µW	190 µW	228 µW	187 µW	191 µW	190 µW	189 µW

Table 6. PVT simulation results for the achieved L_eq at different control currents.

		+Leq (µH)									−Leq (µH)
		Icon = 0 µA			Icon = 25 µA			Icon = 50 µA			Icon = 0 µA			Icon = 25 µA			Icon = 50 µA
		S. 1	C. 2	E 3 (%)	S.	C.	E (%)	S.	C.	E (%)	S.	C.	E (%)	S.	C.	E (%)	S.	C.	E (%)
P	FF	538	580	−7.2	360	382	−5.7	309	311	−0.6	539	583	−7.5	361	378	−4.5	310	312	−0.64
	SF	571	597	−4.3	379	341	+11	323	316	+2.2	573	601	−4.6	378	384	−1.5	324	318	+1.9
	FS	571	597	−4.3	379	342	+11	324	323	+0.3	572	603	−5.1	378	386	−2	323	320	+1
	SS	605	622	−2.7	396	389	+1.8	338	320	+5.6	606	628	−3.5	396	400	−1	338	329	+2.7
V (V)	±0.99	523	591	−11.5	362	383	−5.4	317	314	+1	484	591	−11.5	362	390	−7.1	317	312	+1.6
	±0.81	566	606	−6	385	392	−1.8	338	318	+6.2	563	624	−9.8	385	404	−4.7	338	340	−0.6
T (°C)	−20	428	458	−6.5	307	289	+6.2	234	236	−0.8	423	462	−8.4	307	292	+5.2	234	239	−2
	25	568	602	−5.6	356	380	−6.3	308	313	−1.6	569	603	−5.6	357	380	−6	306	313	−1
	80	877	797	+10	483	513	−5.8	423	432	−2	879	810	+8	483	521	−7.3	423	438	+3.4

¹ simulation, ² Calculation, ³ Error.

Monte Carlo simulations have been performed and reported in Table 7 as well. They have been conducted emulating a 1% mismatch in the β parameter with an overall of 50 runs. As can be seen, the spread between minimum and maximum value increases as the control current reduces. This is expected and depends on the fact that the error from the mirroring action of the current mirrors is more relevant at a low bias current. It could be mitigated, for instance, using cascaded structures if the voltage swing is not a strong issue.

Table 7. Monte Carlo for 1% mismatch in β and 50 runs.

		+Leq (µH)				−Leq (µH)
		Max	Min	Mean	Typical	Max	Min	Mean	Typical
Icon	0 µA	1221	453	672	576	1710	459	749	576
	25 µA	580	362	427	366	529	359	416	389
	50 µA	500	316	355	316	431	315	349	324

A comparison between the proposed circuit and other previously reported ones is presented in Table 8. As can be seen, compared to other works, the proposed circuit provides full integration as it is resistor-free and uses only one grounded capacitor. Although the circuit reported in [11] is also resistor-free, it includes a floating compensation capacitor inside the used OA. Moreover, the proposed floating inductor can provide both positive (+L) and negative (−L) inductance values. Although the circuits reported in [5,6] are electronically tunable, the large number of capacitors and resistors which their values must trim is their weakness. The circuits reported in [7,8,10,11] are electronically tunable but they can provide only +L. The circuits reported in [9,12,13,14,15] are not electronically tunable.

Table 8. Comparison between proposed circuit and other reported works.

Ref.	Frequency Range	+L/−L	Vdd-Vss	Tuning	#R	#Float. C	ABB
[5]	NA	+L	NA	Digital		5	2CDA
[6]	NA	+L	±1.5 V	Digital	10	0	4CCII
[7]	1 Hz–1 MHz	+L	±2.5 V	Yes		0	3CDTA
[8]	100 kHz–10 MHz	+L	±2 V	Yes	1	0	1DVCCTA
[9]	10 kHz–400 kHz	+L	±1.5 V	No	2	0	1DO DDCC
[10]	NA	+L	±1.25 V	Yes	1	1	1DVCC 1CCCII 1 1Gm 1CCCII 2
[11]	NA	+L	±5 V	Yes	0	0	1CCCCTA OA
[12]	1 kHz–10 MHz	+L	±0.75 V	No	2	0	2DTVC
[13]	<10 MHz	+L	±0.75 V	No	2	0	2DDCC
[14]	10 kHz–10 MHz	+L	±1.5 V	No	2	0	2MCFOA
[15]	NA	+L	NA	No	1	1	1CCII± 1DO OTA
this	0.1–3 MHz	L±	±0.9 V	Yes	0	0	1VCII± 1VCII+ VCII−

¹ Topology one; ² Topology two.

6. Conclusions

In this paper, we present a new topology for implementing either a positive or negative floating inductor multiplier. One VCII^±, one VCII⁺, one VCII⁻ and a single grounded capacitor are used. Instead of passive resistors, intrinsic resistors at the Y terminals of VCIIs are used. The value of the simulated inductor is tunable by a control current. The circuit enjoys low voltage and low power operation, reduced series resistance and offers fewer errors compared to other works. Non-ideal analysis is given by taking into account the non-ideal gains and parasitic impedances of the active elements that are used. The proposed circuit enjoys a simple implementation and is free from any restricting matching requirements. The application of the proposed circuit as a standard RLC filter is also given to verify its functionality.