Adaptive Non-Singular Fast Terminal Sliding Mode Trajectory Tracking Control for Robot Manipulators

Abstract

In order to improve the efficiency of human–robot interaction (HRI), it is necessary to carry out research on precise control of the manipulator. In this paper, an adaptive non-singular fast terminal sliding mode control scheme is proposed for robot manipulators to solve the trajectory tracking problem with model uncertainty and external disturbances. At first, a novel non-singular fast terminal sliding mode surface is proposed, and by introducing an auxiliary function, the singularity problem caused by the inverse of the error-related matrix could be avoided in the controller design process. Then, the controller is developed by using Lyapunov synthesis. A robust adaptive strategy is used to deal with lumped uncertainty, with an adaptive update law designed to compensate for the upper bound of lumped uncertainty whose upper bound is prior unknown. Finally, a two-link robot manipulators as a simulation example is given to illustrate the effectiveness of the proposed scheme. Compared with other similar algorithms, the proposed adaptive non-singular fast terminal sliding mode control scheme has higher efficiency and smaller computational complexity for the reason that no piecewise continuous function is needed to be constructed during the controller design.

1. Introduction

Robot manipulators play an important role in human–robot interaction (HRI). So far, they have been widely applied in the manufacturing industry, medical treatment, cargo handling, space exploration and so on to improve automation and efficiency. In the dynamics of robot manipulators, there exist complicated inherent characteristics, such as load variation, hysteresis, friction and coupling, which make the control issues challenging and nontrivial. In order to achieve the accurate control objective of positioning tracking, some feedback control strategies have been proposed in the past decades, such as decentralized control [1], feedback linearization [2], PID control [3], iterative learning control [4], $H_{\infty }$ control [5], robust control [6], neural network control [7] and sliding mode control (SMC) [8].

SMC has many advantages, e.g., fast response and strong robustness to the variety of system parameters and external disturbances. Additionally, SMC is convenient in physical implementation for free of online system identification. Based on the above merits, SMC algorithms for robot manipulator have been reported in many works in the literature [8,9,10,11,12]. Specifically, Zhang et al. investigated the trajectory tracking control based on smooth second-order sliding mode for robot manipulators [8]. Zhao et al. studied the sliding mode control for a two-joint coupling nonlinear system based on extended state observer [9]. In [10], Baek et al. presented a new adaptive SMC scheme that uses the time-delay estimation technique and applied the scheme to robot manipulators. In [11], Van et al. developed an adaptive fuzzy fault tolerant SMC strategy for robot manipulators. In [12], Tran et al. investigated the backstepping adaptive sliding mode control for an electrohydraulic elastic manipulator in the presence of the matched and unmatched uncertainties. The SMC algorithms given in literature [8,9,10,11,12] can ensure that the tracking error asymptotically converges to zero or its neighborhood.

Unlike these traditional SMC schemes, terminal SMC aims at converging to zero within a finite time, which motivates people to research and develop terminal SMC schemes for practical applications [13]. The potential singularity is an obstacle for applying terminal SMC theoretical algorithms into industrial applications because the singularity means that the value of the control input is infinite. In order to overcome the singularity problem, some nonsingular terminal SMC strategies have been proposed in the literature [14,15,16,17]. In [14], a robust nonsingular terminal SMC method was proposed for rigid manipulator systems with unmodeled dynamics and external disturbances. The further investigation of [14] was reported in [15], where a novel terminal SMC approach was developed to improve the convergence speed and tracking accuracy. In [16], an integral nonsingular terminal sliding mode surface was constructed for the SMC design of manipulators with unmodeled dynamics and unknown external disturbances. In [17], a second-order fast nonsingular terminal SMC approach was proposed for robotic systems with external disturbances and inertial uncertainties, which can make the tracking error quickly converge to zero, with the chattering phenomena of control signal avoided. So far, the most popular strategy to deal with singularity problems is to construct piecewise continuous sliding mode surfaces [14,15,16,17]. However, this solution have two flaws. First, it is not an easy job to construct a piecewise continuous sliding mode surface. Second, the online computation load is very large while such a control system runs.

Based on the above analysis, we obtain the following consequent conclusions: (1) It is worthwhile to investigate the terminal SMC scheme free of constructing piecewise continuous sliding mode surface. (2) It is necessary to study how to lighten the online calculation burden of closed-loop systems and reduce the analysis difficulty of finite-time stability during controller design.

In this paper, an adaptive nonsingular fast terminal SMC (ANSFTSMC) approach is proposed for a class of robot manipulators with internal uncertainties and external disturbances such that the tracking error can converge to the neighborhood of the origin during a finite time. The main contributions are as follows. First, a new terminal sliding surface is designed to avoid the occurrence of singularity problem. Second, during control law design, an auxiliary function method is developed to overcome the singular problem caused by matrix inversion. Compared with the traditional piecewise continuous function methods, the auxiliary function method can reduce the design difficulty and the burden computation. Third, robust adaptive method is used to design feedback term to compensate for the sum of uncertainties, whose upper bound need not be prior known.

The remainder of this paper is organized as follows. The problem formulation is presented in Section 2. The construction of a nonsingular fast terminal sliding mode surface, the detailed design process of controller and stability analysis are introduced in Section 3. The simulation results are shown in Section 4. Finally, Section 5 concludes this work.

2. Problem Formulation

Consider an n degrees-of-freedom rigid manipulator, whose dynamic equation is expressed by [17]

$$\begin{array}{c}\hfill M\left(\mathit{q}\right)\ddot{\mathit{q}}+C(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+\mathit{G}\left(\mathit{q}\right)=\mathit{\tau }+\mathit{d}\end{array}$$

(1)

where $\mathit{q}=[q_1,$$q_2,\cdots ,$$q_n{]}^T\in {\mathbb{R}}^n$ is the vector of joint angular position, $M\left(\mathit{q}\right)\in {\mathbb{R}}^{n\times n}$ is a symmetric positive definite inertia matrix, $C(\mathit{q},\dot{\mathit{q}})\in {\mathbb{R}}^n$ represents the vector of centripetal and Coriolis torques, $\mathit{G}\left(\mathit{q}\right)\in {\mathbb{R}}^n$ is the gravitational force, $\mathit{\tau }\in {\mathbb{R}}^n$ is the input torque, and $\mathit{d}={[d_1,d_2,\cdots ,d_n]}^T\in {\mathbb{R}}^n$ represents the sum of external disturbances and unmodeled dynamics.

Due to modeling errors, physical parameter perturbations and other factors, there exist some unmodeled dynamics in robot manipulator systems as follows:

$$\left\{\begin{array}{l}M\left(\mathit{q}\right)=M_0\left(\mathit{q}\right)+\mathsf{\Delta }M\left(\mathit{q}\right)\hfill \\ C(\mathit{q},\dot{\mathit{q}})=C_0(\mathit{q},\dot{\mathit{q}})+\mathsf{\Delta }C(\mathit{q},\dot{\mathit{q}})\hfill \\ \mathit{G}\left(\mathit{q}\right)={\mathit{G}}_0\left(\mathit{q}\right)+\mathsf{\Delta }\mathit{G}\left(\mathit{q}\right)\hfill \end{array}\right.$$

(2)

where $M_0\left(\mathit{q}\right)$, $C_0(\mathit{q},\dot{\mathit{q}})$ and ${\mathit{G}}_0\left(\mathit{q}\right)$ are the nominal components of robot manipulator systems; $\mathsf{\Delta }M\left(\mathit{q}\right),\mathsf{\Delta }C(\mathit{q},\dot{\mathit{q}}),\mathsf{\Delta }\mathit{G}\left(\mathit{q}\right)$ are uncertainties.

Combining (2) with (1) leads to

$$\begin{array}{c}\hfill M_0\left(\mathit{q}\right)\ddot{\mathit{q}}+C_0(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+{\mathit{G}}_0\left(\mathit{q}\right)=\mathit{\tau }+{\mathit{d}}_{\mathsf{\Sigma }}\end{array}$$

(3)

where ${\mathit{d}}_{\mathsf{\Sigma }}=\mathit{d}-\mathsf{\Delta }M\left(\mathit{q}\right)\ddot{\mathit{q}}-\mathsf{\Delta }C(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}-\mathsf{\Delta }\mathit{G}\left(\mathit{q}\right)$. Let ${\mathit{x}}_1=\mathit{q},{\mathit{x}}_2=\dot{\mathit{q}}$. Then, (3) may be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\mathit{x}}}_1={\mathit{x}}_2\hfill \\ {\dot{\mathit{x}}}_2=M_0^{-1}\left({\mathit{x}}_1\right)\left. [{\mathit{d}}_{\mathsf{\Sigma }}+\mathit{\tau }-C_0({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2-{\mathit{G}}_0\left({\mathit{x}}_1\right)\right]\hfill \end{array}\right.\end{array}$$

(4)

Let us define ${\mathit{e}}_1$ and ${\mathit{e}}_2$ as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathit{e}}_1=\hfill & {[e_{11},e_{12},\cdots ,e_{1n}]}^T={\mathit{x}}_1-{\mathit{x}}_d,\hfill \\ {\mathit{e}}_2=\hfill & {[e_{21},e_{22},\cdots ,e_{2n}]}^T={\dot{\mathit{x}}}_1-{\dot{\mathit{x}}}_d,\hfill \end{array}\right.\end{array}$$

(5)

where ${\mathit{x}}_d={\mathit{q}}_d={[q_{1d},q_{2d},\cdots ,q_{nd}]}^T$ is the reference trajectory. From (4) and (5), we can obtain the error dynamic equation as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\mathit{e}}}_1={\mathit{e}}_2\hfill \\ {\dot{\mathit{e}}}_2=\mathit{F}+\mathit{D}+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau },\hfill \end{array}\right.\end{array}$$

(6)

where $\mathit{F}=-M_0^{-1}\left({\mathit{x}}_1\right)(C_0({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2+{\mathit{G}}_0\left({\mathit{x}}_1\right))-{\ddot{\mathit{x}}}_d$, $\mathit{D}=M_0^{-1}\left({\mathit{x}}_1\right)d_{\mathsf{\Sigma }}$.

Based on the above system descriptions, the following lemmas and assumptions are given in this article.

Lemma 1 

([18]). For a given system $\dot{x}=f\left(x\right)$, if there exists a continuous non-negative function $V\left(x\right)$ and scalars $\alpha >0,$ $\beta >0,$ $0<\gamma <1$ and $0<\eta <+\infty$ such that $\dot{V}\left(x\right)\le -\alpha V-\beta V^{\gamma }+\eta$ holds, then the system $\dot{x}=f\left(x\right)$ is finite-time stable, that is, x converges to a small residual set $\left\{\underset{t\to T}{lim}x\mid V\left(x\right)\le \min \left\{\left(\frac{\eta }{(1-\mu )\alpha }\right),{\left(\frac{\eta }{(1-\mu )\beta }\right)}^{\frac{1}{\gamma }}\right\}\right\}$ in a finite time, where $0<\mu <1$,

$$\begin{array}{cc}\hfill T\le & max\{t_0+\frac{1}{\mu \alpha (1-\gamma )}\ln \frac{\mu \alpha V^{1-\gamma }\left(t_0\right)+\beta }{\beta },\hfill \\ \hfill & t_0+\frac{1}{\alpha (1-\gamma )}\ln \frac{\mu \alpha V^{1-\gamma }\left(t_0\right)+\mu \beta }{\mu \beta }\}.\hfill \end{array}$$

(7)

Here, $t_0$ indicates the initial time of control system operation.

Lemma 2 

([19]). For $\varphi \in \mathbb{R},\phi \in \mathbb{R}$, and any constants $p>0,q>0,m>0$, the following inequality holds:

$$\begin{array}{c}\hfill {\left|\varphi \right|}^p{\left|\phi \right|}^q\le \frac{p}{p+q}{m\left|\varphi \right|}^{p+q}+\frac{q}{p+q}{m}^{-\frac{p}{q}}{\left|\phi \right|}^{p+q}\end{array}$$

(8)

Lemma 3 

([20]). For any positive number $x_i$, $i=1,2,...,n$, there exists a constant r, which satisfies

$$\begin{array}{c}\hfill \sum _{i=1}^n{x}_i^r\ge {\left(\sum _{i=1}^n{x}_i\right)}^r,0<r<1.\end{array}$$

(9)

Assumption 1 

([14]). The sum of uncertainties $\mathit{D}$ meets the following inequality:

$$\begin{array}{c}\hfill \parallel \mathit{D}\parallel \le b_1+b_2\left|\right|{\mathit{x}}_1\left|\right|+b_3\left|\right|{\dot{\mathit{x}}}_1{\left|\right|}^2={\mathit{b}}^T\mathbf{\Phi },\end{array}$$

(10)

where $\mathit{b}={[b_1,b_2,b_3]}^T$, $\mathsf{\Phi }=[1,||{\mathit{x}}_1\left|\right|,\left|\right|{\dot{\mathit{x}}}_1{\left|\right|]}^T$. Here, $b_i$ is a positive constant for i = 1, 2, 3; the operator $\parallel ·\parallel$ means taking the Euclidean norm for ·.

The control objective of this paper is to design an adaptive nonsingular fast terminal sliding mode controller $\mathit{\tau }$ for the system (4) to make the joint position of the manipulator ${\mathit{x}}_1$ track the reference trajectory ${\mathit{x}}_d$ in a finite time. In addition, by constructing a nonsingular terminal sliding surface and auxiliary function, the singularity problem is avoided during the controller design.

3. Main Results

3.1. Design of Nonsingular Fast Terminal Sliding Surface and Control Law

On the basis of (6), we construct a novel nonsingular fast terminal sliding surface as

$$\begin{array}{c}\hfill S_i=e_{1i}+\frac{k_{2}a}{2a-1}·{\mathrm{sig}}^{2-\frac{1}{a}}(e_{2i}+k_1{e}_{1i}),i=1,...,n\end{array}$$

(11)

where $k_1>0,k_2>0,a>1$ and ${\mathrm{sig}}^{2-\frac{1}{a}}(e_{2i}+k_1{e}_{1i})={|e_{2i}+k_1{e}_{1i}|}^{2-\frac{1}{a}}\mathrm{sgn}(e_{2i}+k_1{e}_{1i})$, with $\mathrm{sgn}(·)$ being a symbolic function operator.

When $S_i=0$, it follows from (11) that

$$\begin{array}{c}\hfill {\dot{e}}_{1i}=-k_1{e}_{1i}-{\overline{k}}_2{\mathrm{sig}}^{\overline{a}}{e}_{1i},\end{array}$$

(12)

where ${\overline{k}}_2={\left(\frac{2a-1}{k_{2}a}\right)}^{\frac{a}{2a-1}},\overline{a}=\frac{a}{2a-1}$. Let us define

$$\begin{array}{c}\hfill V_1=\frac{1}{2}\sum _{i=1}^n{e}_{1i}^2.\end{array}$$

(13)

Taking the derivative of $V_1$ with respect to time yields

$$\begin{array}{c}\hfill \begin{array}{ccc}{\dot{V}}_1\hfill & =\hfill & {\displaystyle \sum _{i=1}^n}{e}_{1i}{\dot{e}}_{1i}\hfill \\ \hfill & =\hfill & -{\overline{k}}_1{\displaystyle \sum _{i=1}^n}{e}_{1i}^2-{\overline{k}}_2{\displaystyle \sum _{i=1}^n}{\left|e_i\right|}^{1+\overline{a}}\hfill \\ \hfill & \le \hfill & -2{\overline{k}}_1{V}_1-{\overline{k}}_2{2}^{\frac{1+\overline{a}}{2}}{V}_1^{\frac{1+\overline{a}}{2}},\hfill \end{array}\end{array}$$

(14)

where $0<\frac{1+\overline{a}}{2}<1$. By Lemma 1, it follows from (13) that the tracking error $e_{1i}$ can converge to 0 within a finite time $T_1$.

Let $\mathit{S}={[S_1,...,S_n]}^T$. Differentiating $\mathit{S}$ leads to

$$\begin{array}{c}\hfill \dot{\mathit{S}}={\mathit{e}}_2+h({\dot{\mathit{e}}}_2+k_1{\dot{\mathit{e}}}_1).\end{array}$$

(15)

where $h=\mathrm{diag}(h_1,...,h_n)$, $h_i=k_2{|e_{2i}+k_1{e}_{1i}|}^{1-\frac{1}{a}}\ge 0$, $i=1,2,\cdots ,n$. Define an auxiliary variable $\mathbf{\Psi }={[{\mathsf{\Psi }}_1,...,{\mathsf{\Psi }}_n]}^T$. For $i=1,2,\cdots ,n$,

$$\begin{array}{c}\hfill {\mathsf{\Psi }}_i=\frac{1}{k_2}{\mathrm{sig}}^{\frac{1}{a}}(e_{2i}+k_1{e}_{1i})+\frac{k_{1}a}{2a-1}(e_{2i}+k_1{e}_{1i}).\end{array}$$

(16)

According to (11) and the definition of h and $\mathsf{\Psi }$, we can deduce that

$$\begin{array}{c}\hfill h\mathbf{\Psi }={\mathit{e}}_2+k_1\mathit{S}.\end{array}$$

(17)

It follows from (15) and (17) that

$$\begin{array}{cc}\hfill \dot{\mathit{S}}=& h\left(\mathit{F}+\mathit{D}+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau }+k_1{\mathit{e}}_2\right)\hfill \\ \hfill =& h\left(\mathit{F}+\mathit{D}+\mathbf{\Psi }+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau }+k_1{\mathit{e}}_2\right)-k_1\mathit{S}\hfill \\ \hfill =& h\left(\mathit{F}+\mathbf{\Psi }+k_1{\mathit{e}}_2+\mathit{D}+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau }\right)-k_1\mathit{S}\hfill \end{array}$$

(18)

Remark 1. 

The singularity problem may happen while the following traditional sliding mode surface (19) is used:

$$\begin{array}{c}\hfill S_i={\dot{e}}_{1i}+{\alpha }_1{e}_{1i}+{\alpha }_2{\mathrm{sig}}^{\beta }{e}_{1i},{\alpha }_1>0,{\alpha }_2>0,0<\beta <1.\end{array}$$

(19)

Differentiating (11) leads to

$$\begin{array}{c}\hfill {\dot{S}}_i={\dot{e}}_{1i}+k_2{|e_{2i}+k_1{e}_{1i}|}^{1-\frac{1}{a}}({\dot{e}}_{2i}+k_1{\dot{e}}_{1i}),\end{array}$$

(20)

in which $0<1-\frac{1}{a}<1$ holds such that the singularity problem can be directly avoided by constructing the novel sliding mode surface (11).

Remark 2. 

If adopting the solution given in (21), then the singularity problem happens for performing matrix inversion $h^{-1}{\mathit{e}}_2$. We adopt an auxiliary function method (18) to solve this problem, rather than the traditional piecewise continuous function construction method. Compared to the traditional piecewise continuous function method, the computational complexity and finite-time stability analysis difficulty of the auxiliary function method can be reduced.

$$\begin{array}{cc}\hfill \dot{\mathit{S}}=& {\mathit{e}}_2+h\left(\mathit{F}+\mathit{D}+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau }+k_1{\mathit{e}}_2\right)\hfill \\ \hfill =& h\left(\mathit{F}+h^{-1}{\mathit{e}}_2+\mathit{D}+M_0^{-1}\left({\mathit{x}}_1\right)\mathit{\tau }+k_1{\mathit{e}}_2\right).\hfill \end{array}$$

(21)

Based on (18), we define the nonsingular fast terminal SMC law as

$$\begin{array}{c}\hfill \mathit{\tau }=-M_0\left. [{\mathit{F}}^{\ast }+{\lambda }_1\mathit{S}+{\lambda }_2{\mathrm{sig}}^{\gamma }\mathit{S}+{\widehat{\mathit{b}}}^T\mathbf{\Phi }\mathrm{sgn}\left({\mathit{S}}^{T}h\right)\right]\end{array}$$

(22)

and the adaptive law as

$$\begin{array}{c}\hfill \dot{\widehat{\mathit{b}}}=\eta \left(\right||\overline{\mathit{S}}\left|\right|\mathsf{\Phi }-m\widehat{\mathit{b}}),\end{array}$$

(23)

where ${\mathit{F}}^{\ast }={[F_1^{\ast },...,F_n^{\ast }]}^T=\mathit{F}+\mathbf{\Psi }+k_1{\mathit{e}}_2$, ${\mathrm{sig}}^{\gamma }\mathit{S}$=$[{\mathrm{sig}}^{\gamma }{S}_1,$$...,{\mathrm{sig}}^{\gamma }{S}_n{]}^T$, $\mathrm{sgn}\left({\mathit{S}}^{T}h\right)$$={[\mathrm{sgn}\left(S_1{h}_1\right),...,\mathrm{sgn}\left(S_n{h}_n\right)]}^T$,

$\overline{\mathit{S}}={\left({\mathit{S}}^{T}h\right)}^T=h\mathit{S}$, ${\lambda }_1>0,{\lambda }_2>0,0<\gamma <1$, $\eta >0,m>0$, ${\widehat{b}}_i\left(0\right)>0$, $i=1,2,3$. The control diagram of the designed SMC scheme is shown in Figure 1.

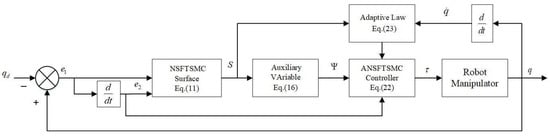
Figure 1. Control diagram of the designed SMC scheme.

3.2. Stability Analysis

The finite-time stability of the robot manipulator (6) in both the reaching phase and the sliding phase is established by the following theorem.

Theorem 1. 

Consider the robot manipulator (6) with nonsingular sliding mode surface (11), auxiliary variable (14), finite-time controller (22) and update law (23). The system tracking error can converge to the neighborhood of the origin in finite time.

Proof of Theorem 1. 

Let us define a Lyapunov function as

$$\begin{array}{c}\hfill V_2=\frac{1}{2}{\mathit{S}}^T\mathit{S}+\frac{1}{2\eta }{\tilde{\mathit{b}}}^T\tilde{\mathit{b}},\end{array}$$

(24)

where $\tilde{\mathit{b}}=\mathit{b}-\widehat{\mathit{b}}$. Differentiating (24) leads to

$$\begin{array}{c}\hfill {\dot{V}}_2={\mathit{S}}^T\dot{\mathit{S}}-\frac{1}{\eta }{\tilde{\mathit{b}}}^T\dot{\widehat{\mathit{b}}}.\end{array}$$

(25)

Substituting (18) and (22) into (24) yields

$$\begin{array}{cc}\hfill {\dot{V}}_2=& {\mathit{S}}^{T}h\left({\mathit{F}}^{\ast }+\mathit{D}+M_0^{-1}\mathit{\tau }\right)-k_1\sum _{i=1}^n{S}_i^2-\frac{1}{\eta }{\tilde{\mathit{b}}}^T\dot{\widehat{\mathit{b}}}\hfill \\ \hfill =& {\mathit{S}}^{T}h\left. [-{\lambda }_1\mathit{S}-{\lambda }_2{\mathrm{sig}}^{\gamma }\mathit{S}-{\widehat{\mathit{b}}}^T\mathbf{\Phi }\mathrm{sgn}\left({\mathit{S}}^{T}h\right)+\mathit{D}\right]\hfill \\ \hfill & -k_1\sum _{i=1}^n{S}_i^2-\frac{1}{\eta }{\tilde{\mathit{b}}}^T\dot{\widehat{\mathit{b}}}\hfill \\ \hfill \le & -k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i|S_i{|}^{1+\gamma }+\left|\right|\overline{\mathit{S}}\left|\right|{\tilde{\mathit{b}}}^T\mathbf{\Phi }-\frac{1}{\eta }{\tilde{\mathit{b}}}^T\dot{\widehat{\mathit{b}}}\hfill \\ \hfill =& -k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i{\left|S_i\right|}^{1+\gamma }+{\tilde{\mathit{b}}}^T\left(\left|\right|\overline{\mathit{S}}\left|\right|\mathbf{\Phi }-\frac{1}{\eta }\dot{\widehat{\mathit{b}}}\right)\hfill \end{array}$$

(26)

Substituting (23) into (26), we have

$$\begin{array}{c}\hfill {\dot{V}}_2=-k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i{\left|S_i\right|}^{1+\gamma }+m\tilde{\mathit{b}}\widehat{\mathit{b}}\end{array}$$

(27)

According to Young’s inequality, the following inequality holds:

$$\begin{array}{c}\hfill m\tilde{\mathit{b}}\widehat{\mathit{b}}\le -\frac{3m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{4}+\frac{{m\left|\right|\mathit{b}\left|\right|}^2}{4}.\end{array}$$

(28)

Combining (28) with (27), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i{\left|S_i\right|}^{1+\gamma }-\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}\hfill \\ \hfill & -\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{4}+\frac{{m\left|\right|\mathit{b}\left|\right|}^2}{4}\hfill \\ \hfill =& -k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i{\left|S_i\right|}^{1+\gamma }-\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}+\hfill \\ \hfill & {\left(\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}\right)}^{\frac{1+\gamma }{2}}-{\left(\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}\right)}^{\frac{1+\gamma }{2}}-\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{4}\hfill \\ \hfill & +\frac{{m\left|\right|\mathit{b}\left|\right|}^2}{4}.\hfill \end{array}$$

(29)

Let $\varphi =1,\phi =\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2},p=1-\overline{\gamma },q=\overline{\gamma },\omega =1$ and $\overline{\gamma }=\frac{1+\gamma }{2}$. By Lemma 2, we obtain

$$\begin{array}{c}\hfill {\left(\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}\right)}^{\overline{\gamma }}\le \mathsf{\Theta }\left(\overline{\gamma }\right)+\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2},\end{array}$$

(30)

where $\mathsf{\Theta }\left(\overline{\gamma }\right)=1-\overline{\gamma }$.

Substituting (30) into (29) leads to

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -k_1\sum _{i=1}^n{S}_i^2-{\lambda }_2\sum _{i=1}^n{h}_i{\left|S_i\right|}^{1+\gamma }-\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{4}+\hfill \\ \hfill & -{\left(\frac{m\left|\right|\tilde{\mathit{b}}{\left|\right|}^2}{2}\right)}^{\overline{\gamma }}+\frac{{m\left|\right|\mathit{b}\left|\right|}^2}{4}+\mathsf{\Theta }\left(\overline{\gamma }\right).\hfill \end{array}$$

(31)

By Lemma 3, it follows from (31) that

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -{\mu }_{1}V-{\mu }_2{V}^{\overline{\gamma }}+\delta \hfill \end{array}$$

(32)

where $\delta =\frac{{m\left|\right|\mathit{b}\left|\right|}^2}{4}+\mathsf{\Theta }\left(\overline{\gamma }\right)$, ${\mu }_1=\min \{k_1,\frac{m\eta }{2}\}$, ${\mu }_2=\min \{2^{\overline{\gamma }}{\lambda }_2{h}_i,{\left(m\eta \right)}^{\overline{\gamma }}\}$.

Then, by Lemma 1, the system (6) is finite-time stable with the convergence region

$$\begin{array}{cc}\hfill \mathsf{\Delta }=& \{\underset{t\to T_r}{lim}\mathit{S}\mid V_2\le \min \{(\frac{\delta }{(1-\kappa ){\mu }_1}),\hfill \\ \hfill & {(\frac{\delta }{(1-\kappa ){\mu }_2})}^{\frac{1}{\overline{\gamma }}}\}\},\hfill \end{array}$$

(33)

where $0<\kappa <1$,

$$\begin{array}{cc}\hfill T_r\le & max\{t_0+\frac{1}{\kappa {\mu }_1(1-\overline{\gamma })}\ln \frac{\kappa {\mu }_1{V}_2^{1-\overline{\gamma }}\left(t_0\right)+{\mu }_2}{{\mu }_2},\hfill \\ \hfill & t_0+\frac{1}{{\mu }_1(1-\overline{\gamma })}\ln \frac{\kappa {\mu }_1{V}_2^{1-\overline{\gamma }}\left(t_0\right)+\kappa {\mu }_2}{\kappa {\mu }_2}\}.\hfill \end{array}$$

(34)

When $S_i$ converges to the region $|S_i|\le \mathsf{\Delta }$, $i=1,...,n$, it follows from (11) that

$$\begin{array}{cc}\hfill S_i=& e_{1i}+\frac{k_{2}a}{2a-1}·{\mathrm{sig}}^{2-\frac{1}{a}}(e_{2i}+k_1{e}_{1i})\hfill \\ \hfill =& {\vartheta }_i,\left|{\vartheta }_i\right|<\mathsf{\Delta },\hfill \end{array}$$

(35)

which means both

$$\begin{array}{c}\hfill {\dot{e}}_{1i}+e_{1i}\left(k_1-\frac{{\vartheta }_i}{e_{1i}}\right)+{\overline{k}}_2{\mathrm{sig}}^{\overline{a}}{e}_{1i}=0\end{array}$$

(36)

and

$$\begin{array}{c}\hfill {\dot{e}}_{1i}+k_1{e}_{1i}+{\mathrm{sig}}^{{\overline{a}}_1}{e}_{1i}\left({\overline{k}}_2-\frac{{\vartheta }_i}{{\mathrm{sig}}^{\overline{a}}{e}_{1i}}\right)=0\end{array}$$

(37)

hold.

From (36), we can see that $e_{1i}$ converges if $k_1-\frac{{\vartheta }_i}{e_{1i}}>0$. From (37), we can see that $e_{1i}$ converges if ${\overline{k}}_2-\frac{{\vartheta }_i}{{\mathrm{sig}}^{\overline{a}}{e}_{1i}}>0$. Hence, $e_{1i}$ will converge to the region

$$\begin{array}{c}\hfill |e_{1i}|\le \min \left\{\frac{\mathsf{\Delta }}{k_1},{\left(\frac{\mathsf{\Delta }}{{\overline{k}}_2}\right)}^{\frac{1}{\overline{a}}}\right\}\end{array}$$

(38)

within the finite time $T_1+T_r$. □

Remark 3. 

In order to avoid the chattering phenomenon, (22) may be modified by replacing the signum function with a hyperbolic tangent function as follows:

$$\begin{array}{c}\hfill \mathit{\tau }=-M_0\left. [{\mathit{F}}^{\ast }+{\lambda }_1\mathit{S}+{\lambda }_2{\mathrm{sig}}^{\gamma }\mathit{S}+{\widehat{b}}^T\mathbf{\Phi }\tanh \left({\mathit{S}}^{T}h\right)\right]\end{array}$$

(39)

where $\tanh \left({\mathit{S}}^{T}h\right)={[\tanh \left(S_1{h}_1\right),...,\tanh \left(S_n{h}_n\right)]}^T$.

Remark 4. 

Based on Assumption 1, the robust adaptive approach is used to deal with uncertainties in this work. Additionally, these uncertainties may be approximated by adaptive neural networks and adaptive fuzzy systems [21].

4. Simulation

Consider a two-joint rigid robot manipulator [17] shown in Figure 2.

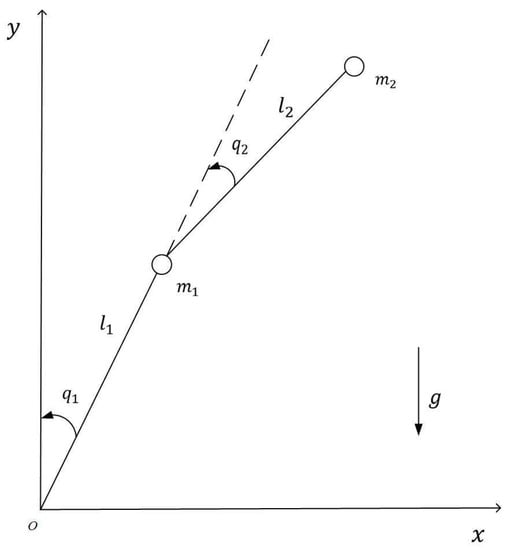
Figure 2. Configuration of a two-link robot manipulator.

The dynamic of robot manipulator in (1) and (2) by Lagrangian equation is represented as

$$\begin{array}{c}M\left(q\right)=\left. [\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right],C(q,\dot{q})=\left. [\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}\right],\hfill \\ G\left(q\right)=\left. [\begin{array}{cc}{g}_1,& g_2\end{array}\right],\hfill \end{array}$$

(40)

where $q={[q_1,q_2]}^T$, $m_{11}=(m_1+m_2)l_1^2+m_2{l}_2^2+2m_2{l}_1{l}_{2}cos\left(q_2\right)+J_1,m_{12}=m_2{l}_2^2+m_2{l}_1{l}_{2}cos\left(q_2\right),m_{21}=m_2{l}_2^2+m_2{l}_1{l}_{2}cos\left(q_2\right),m_{22}=m_2{l}_2^2+J_2$, $c_{11}=-m_2{l}_1{l}_{2}sin\left(q_2\right){\dot{q}}_2$, $c_{12}=-m_2{l}_1{l}_{2}sin\left(q_2\right)({\dot{q}}_1+{\dot{q}}_2),c_{21}=m_2{l}_1{l}_{2}sin\left(q_2\right){\dot{q}}_1,c_{22}=0$, $g_1=(m_1+m_2)l_{1}gcos\left(q_1\right)+m_2{l}_{2}gcos(q_1+q_2)$ and $g_2=m_2{l}_{2}gcos(q_1+q_2)$. Table 1 shows the physical attributes of the manipulator used for the simulation analysis.

Table 1. Physical parameters of the two-link robot manipulator.

Symbol	Definition	Value
$l_1$	Length of link 1	1.0 m
$l_2$	Length of link 2	0.8 m
$m_{10}$	Nominal mass of joint 1	0.4 kg
$m_{20}$	Nominal mass of joint 2	1.2 kg
$m_1$	Mass of joint 1	0.5 kg
$m_2$	Mass of joint 2	1.5 kg
$J_1$	Moment of inertia of link 1	5 kg.${\mathrm{m}}^2$
$J_2$	Moment of inertia of link 2	5 kg.${\mathrm{m}}^2$
g	Gravitational constant	9.8 $\mathrm{m}/{\mathrm{s}}^2$

The reference position trajectories are $q_{1d}=1.25-1.4{\mathrm{e}}^{-t}+0.35{\mathrm{e}}^{-4t}$ rad and $q_{2d}=1.25+{\mathrm{e}}^{-t}-0.25{\mathrm{e}}^{-4t}$ rad. $d_1\left(t\right)=2sin\left(t\right)+0.5sin\left(200\pi t\right)$$\mathrm{N}·\mathrm{m}$, $d_2\left(t\right)=cos\left(2t\right)+0.5sin\left(200\pi t\right)$$\mathrm{N}·\mathrm{m}$. The initial states of the robot manipulator are set as follows: $q_1\left(0\right)=1$ $\mathrm{rad}$, $q_2\left(0\right)=0.5$ $\mathrm{rad}$, ${\dot{q}}_1\left(0\right)=0$ $\mathrm{rad}$ and ${\dot{q}}_2\left(0\right)=0$ $\mathrm{rad}/\mathrm{s}$.

The ANSFTSMC approach proposed in this paper (including nonsingular fast terminal sliding surface (11), control law (22) and adaptive law (23)) is applied for simulation, where the parameters are set as $k_1=2.5,k_2=2,a=\frac{5}{3},{\lambda }_1=1,{\lambda }_2=1,\gamma =\frac{3}{5},\eta =0.1$, $m=0.001$. The angular positions of joints 1 and 2 in are illustrated in Figure 3 and Figure 4, respectively. The angular position error signals and angular velocity error signals of two joints are shown in Figure 5 and Figure 6, respectively. It is observed from Figure 3, Figure 4, Figure 5 and Figure 6 that favorable trajectory tracking responses are obtained by using the proposed control law. Figure 7 exhibits the control torques, which shows that the input signals are continuous and chattering-free. Figure 8 displays the parameter estimation. We can see that ${\widehat{b}}_1,{\widehat{b}}_2$ and ${\widehat{b}}_3$ can converge to corresponding constants over time, respectively, which indicates good compensation for the uncertainties in robot manipulators.

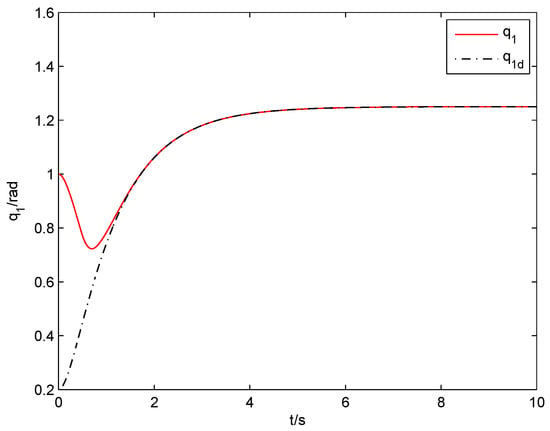
Figure 3. Trajectory tracking response of joint-1 (ANSFTSMC).

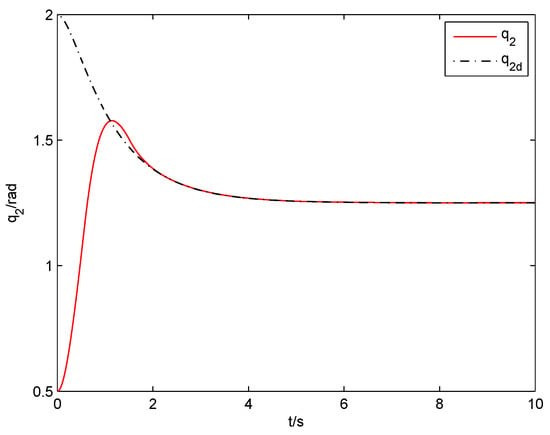
Figure 4. Trajectory tracking response of joint-2 (ANSFTSMC).

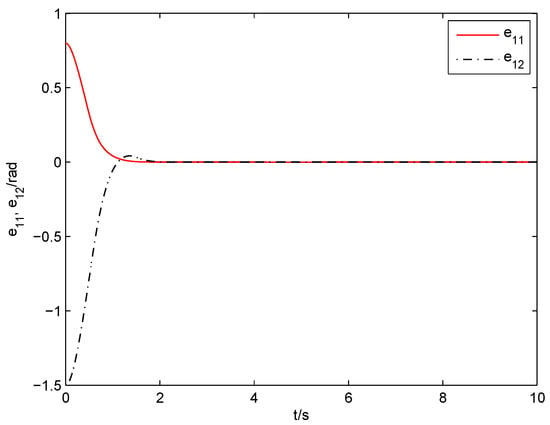
Figure 5. Position errors of joint-1 and joint-2 (ANSFTSMC).

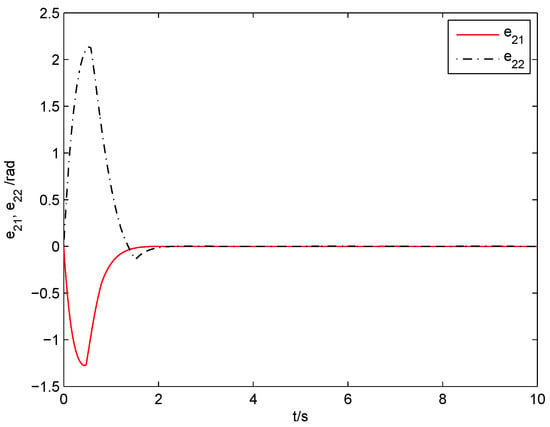
Figure 6. Velocity errors of joint-1 and joint-2 (ANSFTSMC).

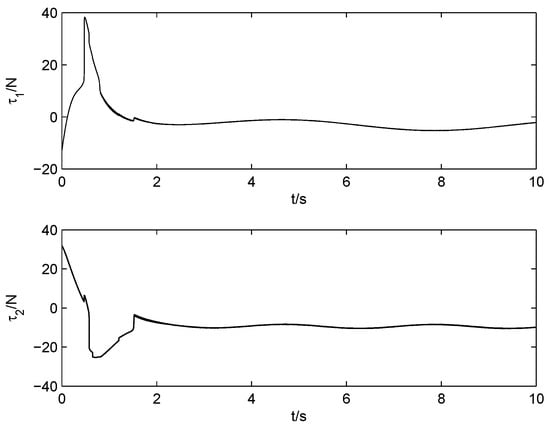
Figure 7. Control torques of joint-1 and joint-2 (ANSFTSMC).

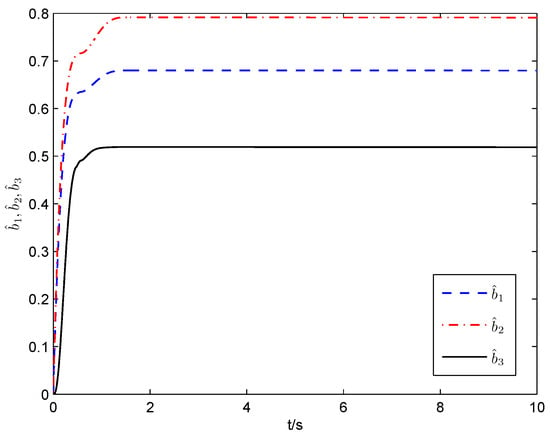
Figure 8. Parameter estimation (ANSFTSMC).

Remark 5. 

In Section 3, the design parameters are theoretically required to meet $k_1>0$, $k_2>0$, $a>1$, ${\lambda }_1>0,{\lambda }_2>0,0<\gamma <1$, $\eta >0,m>0$. In the practical application, we recommend to set their values as follows: $0.5\le k_1\le 5$, $0.5\le k_2\le 5$, $1.1\le a\le 2$, $0.5\le {\lambda }_1\le 5$, $0.5\le {\lambda }_2\le 5$, $0.1\le \gamma \le 0.9$, $0.02\le \eta \le 0.2$, $0.00005\le m\le 0.1$.

In order to verify the effectiveness of the proposed control approach, two comparisons will be carried out.

Comparison A: The following sliding surface and the nonsingular terminal SMC (NSTSMC) law proposed in [14] are introduced for comparison as follows:

$$\begin{array}{cc}\hfill {\mathit{S}}_L=& {\mathit{e}}_1+{\mathit{C}}_1{\dot{\mathit{e}}}_1^{{\mu }_2/{\mu }_1}\hfill \\ \hfill \mathit{\tau }=& {\mathit{\tau }}_0+{\mathit{u}}_0+{\mathit{u}}_1,\hfill \end{array}$$

(41)

where

$$\begin{array}{cc}\hfill {\mathit{\tau }}_0=& {\mathit{C}}_0(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+{\mathit{g}}_0\left(\mathit{q}\right)+M_0\left(\mathit{q}\right){\ddot{\mathit{q}}}_d,\hfill \\ \hfill {\mathit{u}}_0=& -\frac{{\mu }_1}{{\mu }_2}{M}_0\left(\mathit{q}\right){\mathit{C}}_1^{-1}{\dot{\mathit{e}}}_1^{2-{\mu }_2/{\mu }_1},\hfill \\ \hfill {\mathit{u}}_1=& -\frac{{\mu }_1}{{\mu }_2}\frac{{\left[{\mathit{s}}_L^T{\mathit{C}}_1\mathrm{diag}\left({\dot{\mathit{e}}}_1^{{\mu }_2/{\mu }_1-1}\right)M_0^{-1}\left(\mathit{q}\right)\right]}^T}{\parallel {\mathit{s}}_L^T{\mathit{C}}_1\mathrm{diag}\left({\dot{\mathit{e}}}_1^{{\mu }_2/{\mu }_1-1}\right)M_0^{-1}\left(\mathit{q}\right)\parallel }.\hfill \end{array}$$

(42)

The design parameters of (41) and (42) are chosen as ${\mathit{C}}_1=\mathrm{diag}[2.5,2.5],{\mu }_1=3$ and ${\mu }_2=5$, respectively. The simulation results are shown in Figure 9, Figure 10, Figure 11 and Figure 12. From them, we can see that the convergence speed of the proposed ANSFTSMC approach is faster than that of the NSTSMC algorithm.

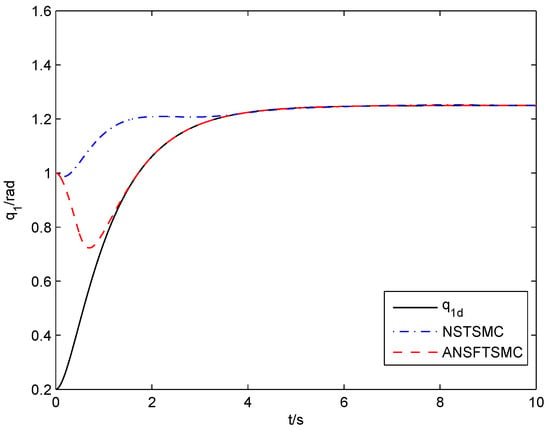
Figure 9. Trajectory tracking response of joint-1 (NSTSMC, ANSFTSMC).

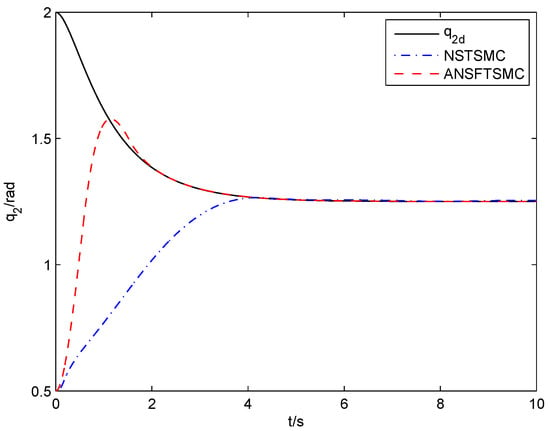
Figure 10. Trajectory tracking response of joint-2 (NSTSMC, ANSFTSMC).

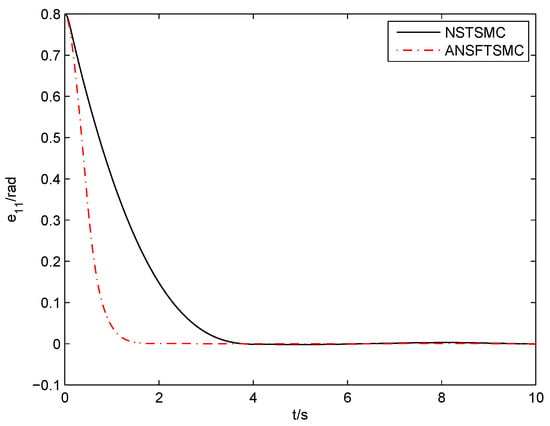
Figure 11. Position error of joint-1 (NSTSMC, ANSFTSMC).

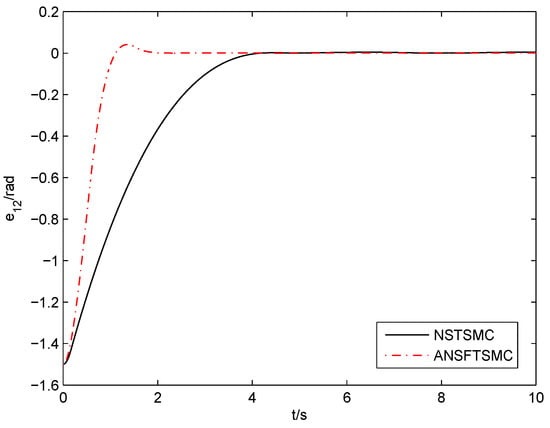
Figure 12. Position error of joint-2 (NSTSMC, ANSFTSMC).

Comparison B: The following sliding surface and nonsingular fast terminal SMC (NSFTSMC) algorithm are designed in light of the literature [22] as

$$\begin{array}{cc}\hfill {\mathit{S}}_{\mathsf{\Sigma }}=& {\mathit{e}}_1+{\mathrm{sign}}^{{\mathsf{\Gamma }}_1}\left({\mathit{e}}_1\right)+{\mathrm{sign}}^{{\mathsf{\Gamma }}_2}\left({\mathit{e}}_2\right),\hfill \\ \hfill \mathit{\tau }=& -M_0[{\varsigma }_2{\mathit{S}}_{\mathsf{\Sigma }}+(\rho +{\varsigma }_1)\frac{{\mathit{S}}_{\mathsf{\Sigma }}}{\parallel {\mathit{S}}_{\mathsf{\Sigma }}\parallel +\delta }+\mathit{F}+{\mathsf{\Gamma }}_2^{-1}(I_2+\hfill \\ \hfill & {\mathsf{\Gamma }}_1\mathrm{diag}\left(\right|{\mathit{e}}_1{|}^{{\mathsf{\Gamma }}_1-I_2}\left)\right){\mathrm{sign}}^{2I_2-{\mathsf{\Gamma }}_2}\left({\mathit{e}}_2\right)],\hfill \end{array}$$

(43)

where ${\varsigma }_1=1,{\varsigma }_2=2,\delta =0.01,{\mathit{S}}_{\mathsf{\Sigma }}={\mathit{e}}_1+{\mathrm{sign}}^{{\mathsf{\Gamma }}_1}\left({\mathit{e}}_1\right)+{\mathrm{sign}}^{{\mathsf{\Gamma }}_2}\left({\mathit{e}}_2\right)$, $\mathit{F}=-M_0^{-1}\left(\mathit{q}\right)(C_0(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+{\mathit{G}}_0\left(\mathit{q}\right))-{\ddot{\mathit{q}}}_d$,

$$\begin{array}{cc}\hfill \rho =& \parallel M_0^{-1}\parallel (b_0+b_1\parallel \mathit{q}\parallel +b_2\parallel \dot{\mathit{q}}\parallel ),\hfill \\ \hfill b_0=& 2,b_1=0.5,b_2=0.3,\hfill \end{array}$$

(44)

$${\mathsf{\Gamma }}_1=\left. [\begin{array}{cc}2& 0\\ 0& 2\end{array}\right],{\mathsf{\Gamma }}_2=\left. [\begin{array}{cc}\frac{5}{3}& 0\\ 0& \frac{5}{3}\end{array}\right],I_2=\left. [\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$$

(45)

As shown in Figure 13 and Figure 14, the system angular position states track the desired reference signals quickly in the cases of NSFTSMC and ANSFTSMC, respectively. However, the ANSFTSMC system is better than NSFTSMC in convergence speed and stable precision, which can also be verified by Figure 15 and Figure 16. In the controller deign of NSFTSMC, $b_0,b_1$ and $b_2$ are assumed to be known (see (44)), which is required in the controller design of ANSFTSMC. Note that if the design parameter $\delta$ is set close to zero, then the chattering phenomenon will happen. Figure 17 and Figure 18 show the control input for the case of $\delta =0.01$ and $\delta =0$, respectively.

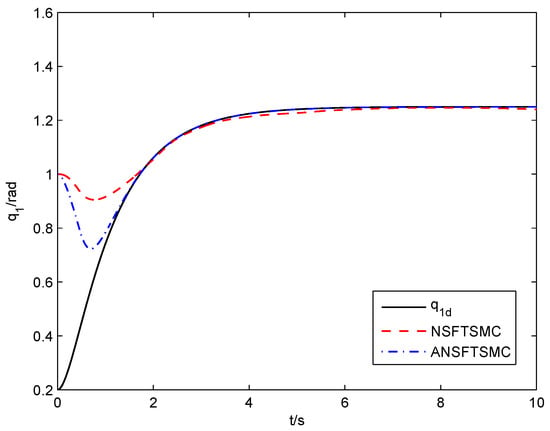
Figure 13. Trajectory tracking response of joint-1 (NSFTSMC, ANSFTSMC).

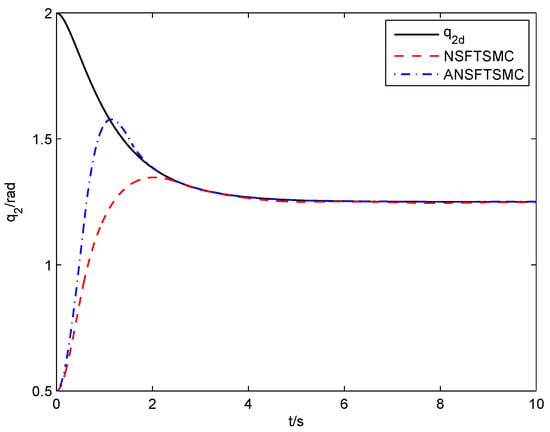
Figure 14. Trajectory tracking response of joint-2 (NSFTSMC, ANSFTSMC).

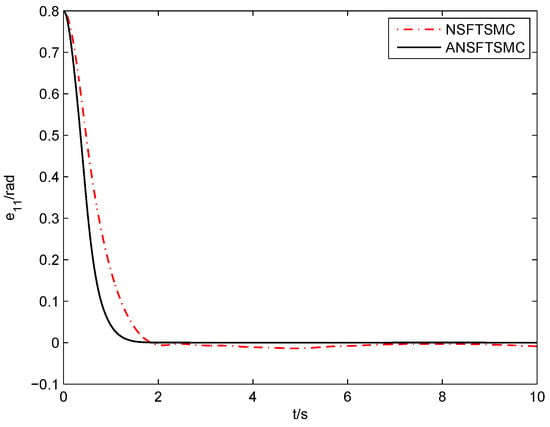
Figure 15. Position error of joint-1 (NSFTSMC, ANSFTSMC).

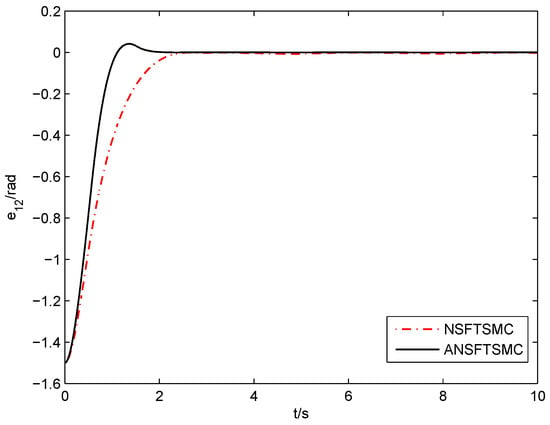
Figure 16. Position error of joint-2 (NSFTSMC, ANSFTSMC).

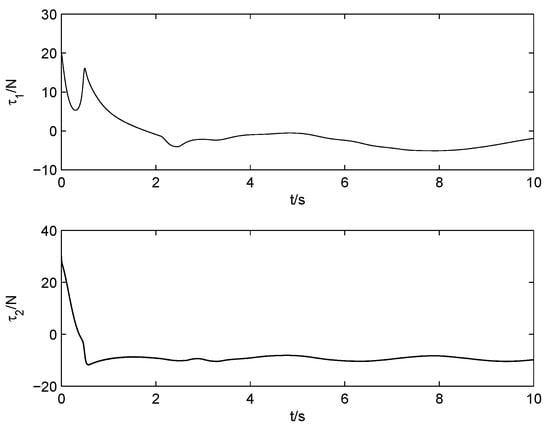
Figure 17. Control torques of joint-1 and joint-2 (NSFTSMC, $\delta =0.01$).

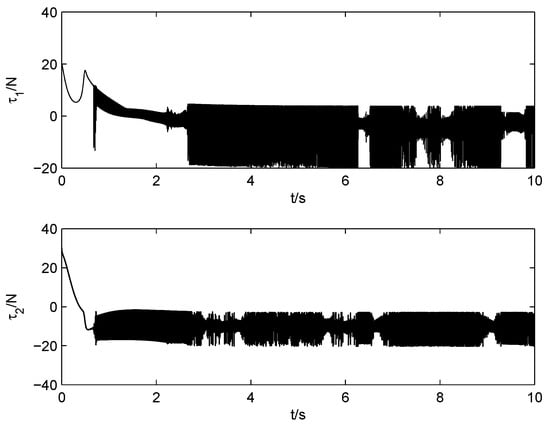
Figure 18. Control torques of joint-1 and joint-2 (NSFTSMC, $\delta =0$).

5. Conclusions

In this paper, an ANSFTSMC approach is proposed for robot manipulators with internal uncertainties and external disturbances to achieve a fast and high-precision trajectory tracking. We design a novel nonsingular fast terminal sliding surface and auxiliary function to avoid the singularity problem caused by the inverse matrix operation during the controller design, where the traditional piecewise continuous function approach is replaced by the auxiliary function approach to reduce the design difficulty and the burden computation. By designing an adaptive updating law, the total uncertainties, whose upper bound are unknown, in the system are compensated for. The system tracking error can converge to the neighborhood of the origin in finite time, and all the signals of the closed-loop system are guaranteed to be bounded. In future studies, we will attempt to develop an adaptive fuzzy nonsingular terminal SMC approach for robot manipulators.