Feature Subset Selection Hybrid Deep Belief Network Based Cybersecurity Intrusion Detection Model

Abstract

Intrusion detection system (IDS) has played a significant role in modern network security. A key component for constructing an effective IDS is the identification of essential features and network traffic data preprocessing to design effective classification model. This paper presents a Feature Subset Selection Hybrid Deep Belief Network based Cybersecurity Intrusion Detection (FSHDBN-CID) model. The presented FSHDBN-CID model mainly concentrates on the recognition of intrusions to accomplish cybersecurity in the network. In the presented FSHDBN-CID model, different levels of data preprocessing can be performed to transform the raw data into compatible format. For feature selection purposes, jaya optimization algorithm (JOA) is utilized which in turn reduces the computation complexity. In addition, the presented FSHDBN-CID model exploits HDBN model for classification purposes. At last, chicken swarm optimization (CSO) technique can be implemented as a hyperparameter optimizer for the HDBN method. In order to investigate the enhanced performance of the presented FSHDBN-CID method, a wide range of experiments was performed. The comparative study pointed out the improvements of the FSHDBN-CID model over other models with an accuracy of 99.57%.

1. Introduction

Cybersecurity incident as a ubiquitous threat to enterprises, organizations, and governments, seems to be increasing in scale, severity, frequency, and sophistication [1]. Natural disasters like earthquakes, hurricanes, and floods, and human-made disasters (i.e., financial crashes and military nuclear accidents), cybersecurity events that include extreme events result in unintended significance or even disastrous damages [2]. A cybersecurity incident is described as an event by which an intruder uses a tool for implementing action that uses a susceptibility on an objective and makes an unauthorized result that would satisfy the intention of the attackers. A network security mechanism has a computer security system and a network security system [3]. All these systems involve intrusion detection systems (IDS), firewalls, and antivirus software. IDSs will be helpful in identifying, determining, and discovering unauthorized system behavior like modification, use, copying, and destruction. Security breaches involve internal intrusions and external intrusions [4]. There were 2 predominant kinds of network analysis for IDSs they are hybrid and misuse-based, otherwise called signature-based, anomaly-based. Misuse-based detecting approaches aim at detecting renowned assaults through the signatures of such attacks; they were utilized for known kinds of assaults without making a great number of false alarms [5]. However, administrators should manually update the signatures and database rules. New (zero-day) assaults could not be detected related to misused technologies [6].

In General, an IDS can be overwhelmed with a massive amount of data and have redundant and irrelevant features will make a long-term issue in network traffic classifications [7]. One main limitation of recent IDS technologies was the necessity to sort out false alarms and the system being overwhelmed with data; it is because of additional and irrelevant features in datasets that diminish the speed of detection [8]. Feature selection can be defined as the preprocessing technique, which could efficiently solve the IDS issue through the selection of appropriate features and eradicating of irrelevant and redundant features [9]. The benefits of feature selection have limitations of required storage, space data understanding, reduction of processing cost, and data reduction. Advancing computational security methods for analyzing various cyber incident paradigms and simultaneously forecasting the threats by utilizing cybersecurity data is employed for framing a data-driven intellectual IDS [10]. Therefore, the knowledge of AI, specifically ML approaches could learn from security data well.

This paper presents a Feature Subset Selection Hybrid Deep Belief Network based Cybersecurity Intrusion Detection (FSHDBN-CID) model. The presented FSHDBN-CID model mainly concentrates on the recognition of intrusions to accomplish cybersecurity in the network. In the presented FSHDBN-CID model, different levels of data preprocessing can be performed to transform the raw data into compatible format. For feature selection purposes, jaya optimization algorithm (JOA) is utilized which in turn reduces the computation complexity. In addition, the presented FSHDBN-CID model exploits the HDBN model for classification purposes. At last, the chicken swarm optimization (CSO) technique can be applied as a hyperparameter optimizer for the HDBN method. In order to investigate the enhanced performance of the presented FSHDBN-CID method, a wide range of experiments was performed. In summary, the contributions of the paper is given as follows.

• A new FSHDBN-CID technique is developed for intrusion detection process. To the best of our knowledge, the proposed FSHDBN-CID technique never existed in the literature.
• Design a new JOA based feature selection technique to improve detection accuracy and reduce high dimensionality problem.
• Develop a new CSO-HDBN model in which the hyperparameter tuning of the HDBN take place using the CSO algorithm.

The rest of the paper is organized as follows. Section 2 offers a brief survey of existing intrusion detection techniques and Section 3 introduces the proposed model. Next, Section 4 provides experimental validation and Section 5 concludes the work.

2. Related Works

Li et al. [11] present an innovative federated DL technique, termed DeepFed, for detecting cyber threats toward industrial CPSs. Particularly, the authors primarily devise an innovative DL-related ID for industrial CPSs, by using a GRU and a CNN. Secondly, the authors formulate a federated learning structure, enabling several industrial CPSs for collectively build a complete ID method in a privacy-preserving way. Additionally, a Paillier cryptosystem-related secure transmission protocol can be crafted for preserving the privacy and security of model variables. Wu et al. [12] introduce a new network ID method using CNNs. The authors employ CNN for selecting traffic features from raw data mechanically, and the authors establish cost function weight coefficients of every class related to its numbers for solving the imbalanced dataset issue. The method not just minimizes the false alarm rates (FARs) and enhances the class accuracy by having small numbers. For reducing the calculating cost further, the authors transform the raw traffic vector formats into image formats.

Al-Abassi et al. [13] devise a DL method for constructing novel balanced representations of the imbalanced dataset. The novel representations were nourished into an ensemble DL attack detection method exactly devised for an ICS atmosphere. The presented attack detection method uses DT and DNN techniques for detecting cyber-attacks from the new representations. Akgun et al. [14] modelled an IDS that involves preprocessing process and a DL technique for detecting DDoS assaults. For this purpose, various methods related to LSTM, DNN, and CNN were assessed with regard to real-time performance and detection performance. Haider et al. [15] devise in this article an ID technique related to a Real-Time Sequential Deep Extreme Learning Machine Cybersecurity IDS (RTS-DELM-CSIDS) security method. This presented approach primarily regulates the rating of security aspects contributes to its importance and formulates an ID structure that concentrates on the indispensable features.

Zhang et al. [16] introduce an effectual network ID technique related to DL approaches. The presented technique uses a DAE including a weighted loss function for selecting features that regulate a limited number of significant features for ID for reducing feature dimensionality. The data selected was after classified by a compact multilayer perceptron (MLPs) for ID. In [17], the authors study the practicality of adversarial samples in the field of network IDS (NIDS). To be specific, the authors inspect how adversarial samples affect the DNN performance well-trained for detecting abnormal performances in the black-box method. The authors establish that the adversary could produce effectual adversarial samples towards DNN classifier well-trained for NIDS even if internal data of the target method can be separated from the adversary.

Though several IDS models are available in the literature, it is still needed to enhance the detection rate and reduce false alarms. Because of continual deepening of the DL models, the number of parameters of DL models also increases quickly which results in model overfitting. At the same time, different hyperparameters have a significant impact on the efficiency of the DL model. As the trial and error method for hyperparameter tuning is a tiresome and erroneous process, metaheuristic algorithms can be applied. Therefore, in this work, we employ the CSO algorithm for the parameter selection of the DBN model.

Machine learning models have become vital for intrusion detection [18]. The process of selecting significant features in the dataset have an important role on increasing the model’s performance and reducing the training process, especially that intrusion detection datasets suffer from high dimensionality. Therefore, choosing relevant features is a crucial step for creating relevant intrusion detection models. The study in [19] have relied on Information Gain and Gain Ration measures to select the top 50% ranked features using, subsequently, intersection and union operations. The selected features from each measure were fed to a JRip rule-based classifier to select the final subset of features. The study is focused on intrusion detection for data generated by IoT devices. The KDD Cup 1999 public dataset was employed to assess the suggested approach and the IoT-BoT dataset was used to validate it. The results show that the proposed method outperformed the state-of-the-art models by improving the accuracy and detection rate and reducing the false alarm rate. In terms of accuracy, detection rate, and false alarm rate, the IoT-Bot-based model achieved 99.9993%, 99.5798%, 0.000004194 respectively while the KDD Cup 1999-based model achieved 99.9920% accuracy.

The authors of [20] considered the intrusion detection as an optimization problem and attempted to improve the detection by decreasing the false positive rate and increasing the performance speed using improved krill swarm algorithm based on linear nearest neighbor lasso step (LNNLS-KH) that reduces the features of NSL-KDD and CICIDS2017 public datasets. The step following the feature selection process was applying K-nearest neighbor classifier to detect intrusion. The results showed that the prosed model was able to reduce the features up to 40% while improving the detection of intrusion by 10.03% and 5.39% copared to other feature selection algorithms. Although the selection process was time consuming compared to some linear feature selection methods, the time of intrusion detection was decreased by 12.41% and 4.03% on NSL-KDD and CICIDS2017 datasets respectively.

3. The Proposed Model

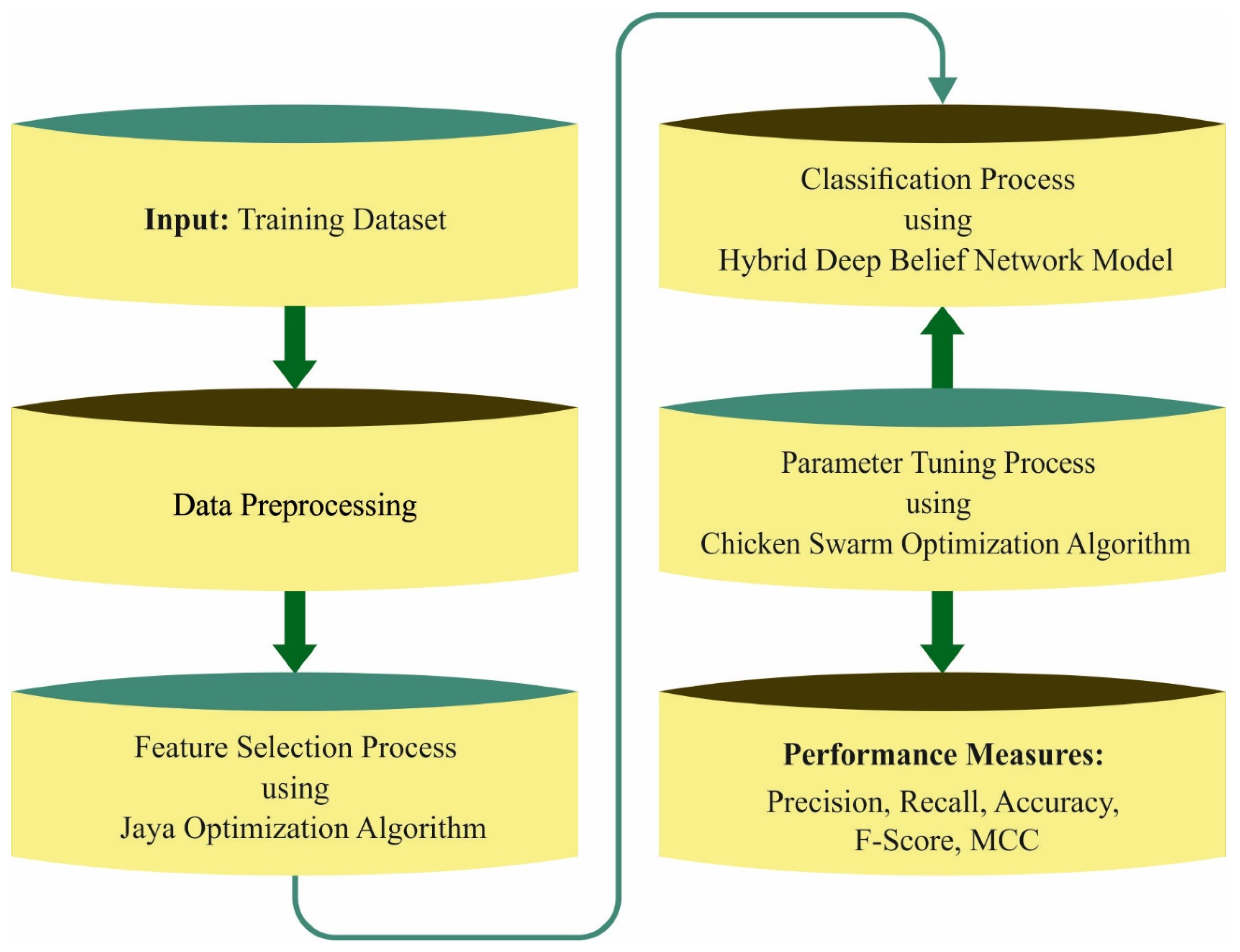
In this paper, an effective FSHDBN-CID technique has been developed for intrusion detection. The presented FSHDBN-CID model mainly concentrates on the recognition of intrusions to accomplish cybersecurity in the network. Figure 1 showcases the overall process flow of FSHDBN-CID technique. The presented FSHDBN-CID model initially preprocesses the network traffic data to make it compatible for further processing. Next, the preprocessed data is passed into the JOA based feature subset selection technique for effectively choosing the features. Then, the HDBN based intrusion detection technique is employed to detect intrusions and and CSO based hyperparameter optimization process take place.

3.1. Data Pre-Processing

In the presented FSHDBN-CID model, different levels of data preprocessing are performed to transform the raw data into a compatible format.

Data processing includes 3 major steps [21]:

• Data transfer: detection method requires every input record in a form of vectors of real numbers. Thus, symbolic features in the data are converted to numeric values.
• Data discretization: the main purpose was to limit the constant values to the limited sets. Discretized data will cause a superior categorization. Many features in the dataset were continuous. The technique of discretization can be utilized in this paper

  $$Normalize{d}_{-}X=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$$

  (1)
• Data normalization: every feature in data contains distinct data limitations; thus, they were normalized into a particular range of [0, 1].

3.2. Feature Selection Using JOA

For feature selection purposes, the JOA is utilized which in turn reduces the computation complexity. Rao developed the JOA in [22] to manage constraint and unconstraint optimization approaches; it is considerably easier for implementing those approaches since it only has single stage. Jaya means (“victory” in Sanskrit). This technique makes use of a population based metaheuristic that has swarm intelligence and evolutionary features; it is found in the behaviors of “survival of fittest” concept. “The search technique of the presented approach aims to get closer to success by finding the better global solution and avoid failure by evading the worst choice”. In study algorithm, the property of the evolutionary algorithm and swarm-based intelligence are integrated.

Assume that objective function $\psi \left(x\right)$ should be maximized or minimized based on the problem. Consider that $d$ number of design parameters and $n$ number of candidate solutions as (population size, $k=1, 2\dots , n)$ for $t$ iteration. Consider the better candidate acquires the better values of $\psi \left(x\right)$ $(\psi (x{)}_{best})$ in every candidate solution, and the worst candidate obtains the worst values of $\psi \left(x\right)$ ($\psi {(x)}_{worst}$) in every candidate solution. When the value of jth parameter for k-th candidate during the t-th iteration is $X_{\left(j,k,t\right)}$, then these values are upgraded in the following [23]:

$$X_{\left(j,k,t\right)}^{\prime }=X_{\left(j,k,t\right)}+q_{\left(1,j,t\right)}\left(X_{\left(j,best,t\right)}-\left|X_{\left(j,k,t\right)}\right|\right)-q_{\left(2,j,t\right)}\left(X_{\left(j,worst,t\right)}-\left|X_{\left(j,k,t\right)}\right|\right)$$

(2)

In Equation (9), the value of parameter $j$ for the better candidate denotes $X_{\left(j,best,t\right)}$ whereas the value of parameter $j$ for the worst candidate represent $X_{\left(j,worst,t\right)}.$ $X_{\left(j,k,t\right)}^{\prime }$ indicates the upgrades values of $X_{\left(j,k,t\right)}$, and $q_{\left(1,j,t\right)}$ and $q_{\left(2,j,t\right)}$ signifies two random values within [0, 1] for j-th parameter during the t-th iteration. The term $q_{\left(1,j,t\right)}(X_{\left(j,best,t\right)}-|X_{\left(j,k,t\right)})$ shows the solution’s tendency to get closer to the better solution, while the term $“q_{\left(2,j,t\right)}(X_{\left(j,worst,t\right)}-|X_{\left(j,k,t\right)})”$ shows the solution’s tendency for avoiding the worst. When $X_{\left(j,k,t\right)}^{\prime }$ produces superior function values, it is accepted. At the end of all the iterations, each satisfactory function value is used and kept as the input for upcoming iterations.

The fitness function (FF) of the JOA will consider the number of selected features and the classifier accuracy; it would maximize the classifier accuracy and reduces the size set of the selected features. Thus, the following FF can be utilized for evaluating individual solutions, as displayed in Equation (3).

$$Fitness=\alpha \ast ErrorRate+\left(1-\alpha \right)\ast \frac{\#SF}{\#All\_F}$$

(3)

whereas $ErrorRate$ specifies the classifier error rate utilizing the features which are selected. ErrorRate can be computed as the percentage of inaccurate classified to count of classifications made, indicated as a value among 0 and 1. (ErrorRate was the complement of the classifier accuracy), $\#SF$ was the selected features count and $\#All\_F$ was the total number of features in the actual dataset. $\alpha$ was utilized to control the significance of subset length and classification quality. In this experiment, $\alpha$ can be set to 0.9.

3.3. Intrusion Detection

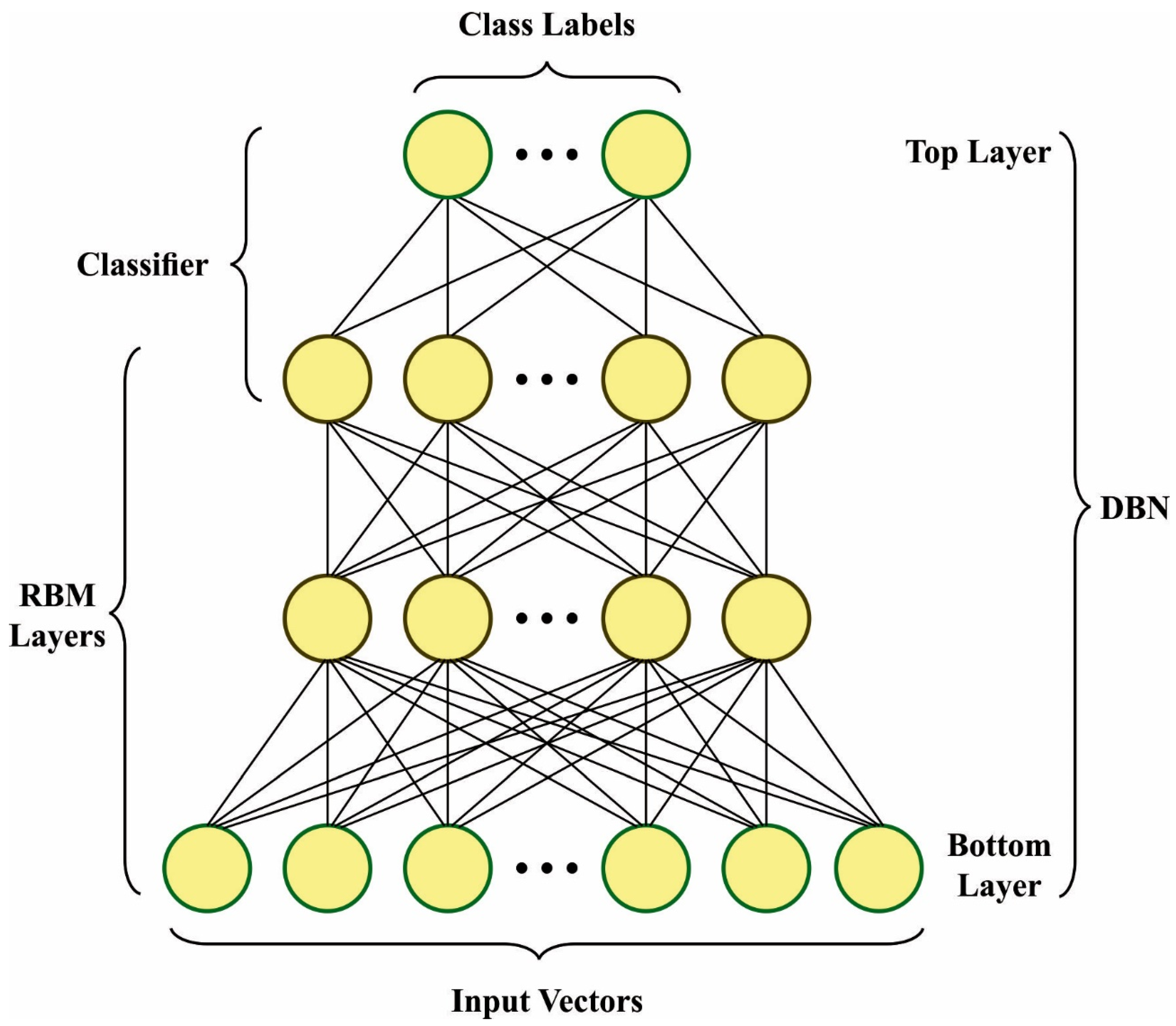
In the presented FSHDBN-CID model, the HDBN model is applied for classification purposes. The DNN model comprises 4 layers of pretrained RBM and output layers (Softmax Regression) [24]. Parameter should be anticipated by training model beforehand utilizing DBN to classify and represent assaults. The training of DBN can be classified into pretraining for presentation and fine-tuning for classifications. Simultaneously, the resultant DBN was transferred to the input of Softmax Regression and included in the DBN that comprises stacked RBM. Initially, the DBN is trained for reconfiguring untagged trained datasets, and consequently implemented unsupervised. Emodel [.] and Edata [.] were expectations of probabilities.

$$\frac{\partial \log P\left(x\right)}{\partial W_{ij}}=E_{data}\left[h_j{x}_i\right]-E_{model}\left[h_j{x}_i\right]$$

(4)

$$\frac{\partial \log P\left(x\right)}{\partial a_i}=E_{data}\left[x_i\right]-E_{model}\left[x_i\right]$$

(5)

$$\frac{\partial \log P\left(x\right)}{\partial b_j}=E_{data}\left[h_j\right]-E_{model}\left[h_j\right]$$

(6)

In this work, three algorithms (Equations (4)–(6)) first included in conventional DBN network, the second term couldn’t be directly attained. Since it was the probability in distribution that could be studied using the DBN. Gibb’s sampling is used for calculating these probabilities. However, this technique can be time-consuming and could be used in real-time. For finding a better solution, the contrastive divergence (CD) technique is used, fast-learning algorithm. Firstly, a training instance was utilized to finish the start of the Markov chain. Then, samples can be attained afterward the $k$ steps of Gibb’s sampling. This technique is named CD-k. Note that the performance of CD can be satisfactory if $k=1$. Figure 2 depicts the infrastructure of DBN.

In this work, to train stacked RBM layer-wise for creating the DBN, $b$, and $W$ parameters are upgraded based on the CD-1.

$$\begin{array}{c}{W}^{t+1}=W^t+\epsilon (P(\frac{h}{x^{(0)}})[x^{(0)}{]}^T-P(\frac{h}{x^{(1)}})[x^{(1)}{]}^T) a^{t+1}=a^t+\epsilon (x^{\left(0\right)}-x^{\left(1\right)})\\ b^{t+1}=b^t+\epsilon \left(P\left(\frac{h}{x^{\left(0\right)}}\right)-P\left(\frac{h}{x^{\left(1\right)}}\right)\right)\end{array}$$

(7)

Form the equation, $\in$ signifies learning rate, $t$ denotes time steps. The visible variable can be denoted as $h=\left\{h\right\}$ and the hidden variable as $x=\left\{x_m\right\}$. Now, $M$ and $N$ nodes are in the visible and hidden layers. The weight of feature vector is initiated randomly within the network by sampling in CD approach.

The steps for executing greedy layer-wise training mechanisms for all the layers of the DBN are given below.

During initial RBM training, the data suitable to $W_1$ parameter is considered as input $x.W_1$ will be frozen and applied to the trained RBM $h_1$ as $Q(\frac{h_1}{v})=P(\frac{h_2}{h_1} , W_2)$ for training of RBM and the following binary feature layer. $W_2$, that determines 2-layered features, was frozen, and the dataset essential for training the binary feature at 3 layers was attained from $h_2$ as $(\frac{h_2}{h_1})=P(\frac{h_2}{h_1} , W_2)$. This procedure repeats continuously across each layer. LR is utilized in conventional binary classification. However, the study preferred Softmax since there exist various classifications in the DBN.

As the training set $\{(z_{(1)}^i,y_{(1)}),$ $(z_{(2)}^i,y_{(2)})$, $(z_{(m)}^i,y_{(m)})\},$ $m$ indicates the number of samples in the training set and $(z_{(1)}^i, z_{(m)}^i)$ shows the hidden vector of top RBM. The Softmax function ϕ in output layer, $j=0,\dots ,$ $k$ for all the classes, the conditional probability of $P(y=j|z^{\left(i\right)})$ is evaluated by the following equation.

$$P(y=j|z^{(i)})={\varphi }_{softma{x}^{ }}(z^{(i)})=\frac{e^{z^{(i)}}}{{{\displaystyle \sum }}_j^k{e}^{z_k^{(i)}}}$$

(8)

In Equation (8), $z_{\left(i\right)}\in R^{n+1}$ shows the topmost secret vector and it is given in the following:

$$z=w_0{x}_0+w_1{x}_1+\dots +w_m{x}_m={\displaystyle \sum }_{l=0}^m{w}_l{x}_l=w^{T_X}$$

(9)

3.4. Hyperparameter Tuning

To optimally adjust the hyperparameters related to the HDBN model, the CSO algorithm is utilized in this work. The CSO simulates the behavior and the movement of chicken swarm, the CSO is discussed in the following [25]: In CSO there exist several groups, and all the groups comprising of chicks, dominant rooster, and some hens. Chicks, Roosters, and hens in the group are defined based on their fitness values. Chicks are the chicken that has worst fitness value. Whereas roosters (group head) are the chicken that has better fitness values. Most of the chickens would be the hens and they arbitrarily choose which group to stay in. Indeed, the mother-child relationship between the chicks and the hens is randomly carried out. The mother-child and dominance relationships in a group remain unchanged and upgraded (G) time step. The movement of chicken is given as follows:

(1) The rooster position update equation can be given in the following:

$$X_{i,j}^{t+1}=X_{i,j}^t\ast \left(1+randn\left(0, {\sigma }^2\right)\right)$$

(10)

where

$${\sigma }^2=\{\begin{array}{ll}1\hfill & if{f}_i\le f_k\hfill \\ exp\left(\frac{f_k-f_i}{\left|f_i+\epsilon \right|}\right)\hfill & Otherwise\hfill \end{array}$$

whereas $k\in \left[1, N_r\right],$ $k\ne i$ and $N_r$ indicates the number of chosen roosters. $X_{i,j}$ characterizes the location of $i$-$\mathrm{th}$ rooster number in $j$-$\mathrm{th}$ dimension during $t$ and $t+1$ iteration, $randn$ $\left(O, {\sigma }^2\right)$ generates Gaussian random value with mean $0$ and variance ${\sigma }^2,$ $\epsilon$ represents a constant with lower values, and $f_i$ shows the fitness value for the respective rooster $i$.

(2) The equation that is utilized for the hen location upgrade is shown below:

$$X_{i,j}^{t+1}=X_{i,j}^t+S_{1}randn\left(X_{r_1,j}^t-X_{i,j}^t\right)+S_{2}randn\left(X_{r_2,j}^t-X_{i,j}^t\right)$$

(11)

whereas,

$$S_1=exp\left(\frac{f_i-f{r}_1}{\left|f_i\right|+ϵ}\right)$$

(12)

and

$$S_1= exp \left(f_{r_2}-f_i\right)$$

(13)

From the expression, $r_1,$ $r_2\in \left[1, \dots , N\right], r_1\ne r_2$ indicates the index of rooster, whereas $r_2$ indicates a chicken from the swarm that is hen or rooster and a uniform random value can be produced using $randn$.

(3) The equation utilized for chick position update is shown below:

$$X_{i,j}^{t+1}=X_{i,j}^t+FL\left(X_{m,j}^t-X_{i,j}^t\right), FL\in \left[0,2\right]$$

(14)

whereas, $X_{m,j}^t$ indicates the location of $i$-$\mathrm{th}$ chick’s mother. The CSO algorithm will derive a fitness function (FF) for achieving enhanced classifier outcomes; it would determine a positive value for denoting superior performance of the candidate solutions. In this article, the reduced classifier error rate can be taken as the FF, as specified in Equation (15).

$$\begin{array}{c}fitness\left(x_i\right)=ClassifierErrorRate\left(x_i\right)\\ =\frac{number of misclassified samples}{Total number of samples} \ast 100\end{array}$$

(15)

4. Experimental Validation

The proposed model is simulated using Python 3.6.5 tool on PC i5-8600k, GeForce 1050 Ti 4 GB, 16 GB RAM, 250 GB SSD, and 1 TB HDD. The performance validation of the FSHDBN-CID method is tested using the IDS dataset. The dataset comprises 125,973 samples under five class labels as depicted in

Table 1. Dataset details.

Attack Type	Description	No. of Samples
Dos	Denial of service attack	45,927
R2l	Unauthorized access from a remote host	995
Probe	Port monitoring or scanning	11,656
U2r	Unauthorized local super user privileged access	52
Normal	Not an Attack	67,343
Total Number of Samples		125,973

.

The confusion matrices formed by the FSHDBN-CID method on cybersecurity intrusion detection are shown in Figure 3. The figure implied that the FSHDBN-CID model has attained effectual detection efficiency under distinct training (TR) and testing (TS) data. For instance, on 60% of TR data, the FSHDBN-CID model has identified 27,320 samples into DoS class, 547 samples into R2l class, 6982 samples into Probe class, 0 samples into U2r class, and 39,913 samples into normal class. Moreover, on 40% of TS data, the FSHDBN-CID technique has identified 18,111 samples into DoS class, 388 samples into R2l class, 4519 samples into Probe class, 0 samples into U2r class, and 26,815 samples into normal class. Furthermore, on 70% of TR data, the FSHDBN-CID approach has identified 31,480 samples into DoS class, 455 samples into R2l class, 7712 samples into Probe class, 2 samples into U2r class, and 46,641 samples into normal class.

Table 2. Result analysis of FSHDBN-CID algorithm with distinct class labels under 60:40 of TR and TS datasets.

Labels	Accuracy	Precision	Recall	F-Score	MCC
Training Phase (60%)
Dos	99.35	99.34	98.88	99.11	98.60
R2l	99.59	67.03	93.19	77.98	78.85
Probe	99.64	97.46	98.76	98.10	97.91
U2r	99.96	00.00	00.00	00.00	00.00
Normal	99.28	99.53	99.12	99.32	98.56
Average	99.57	72.67	77.99	74.90	74.78
Testing Phase (40%)
Dos	99.37	99.29	98.98	99.14	98.64
R2l	99.59	67.48	95.10	78.94	79.92
Probe	99.61	97.16	98.54	97.85	97.63
U2r	99.95	00.00	00.00	00.00	00.00
Normal	99.27	99.60	99.04	99.32	98.53
Average	99.56	72.71	78.33	75.05	74.95

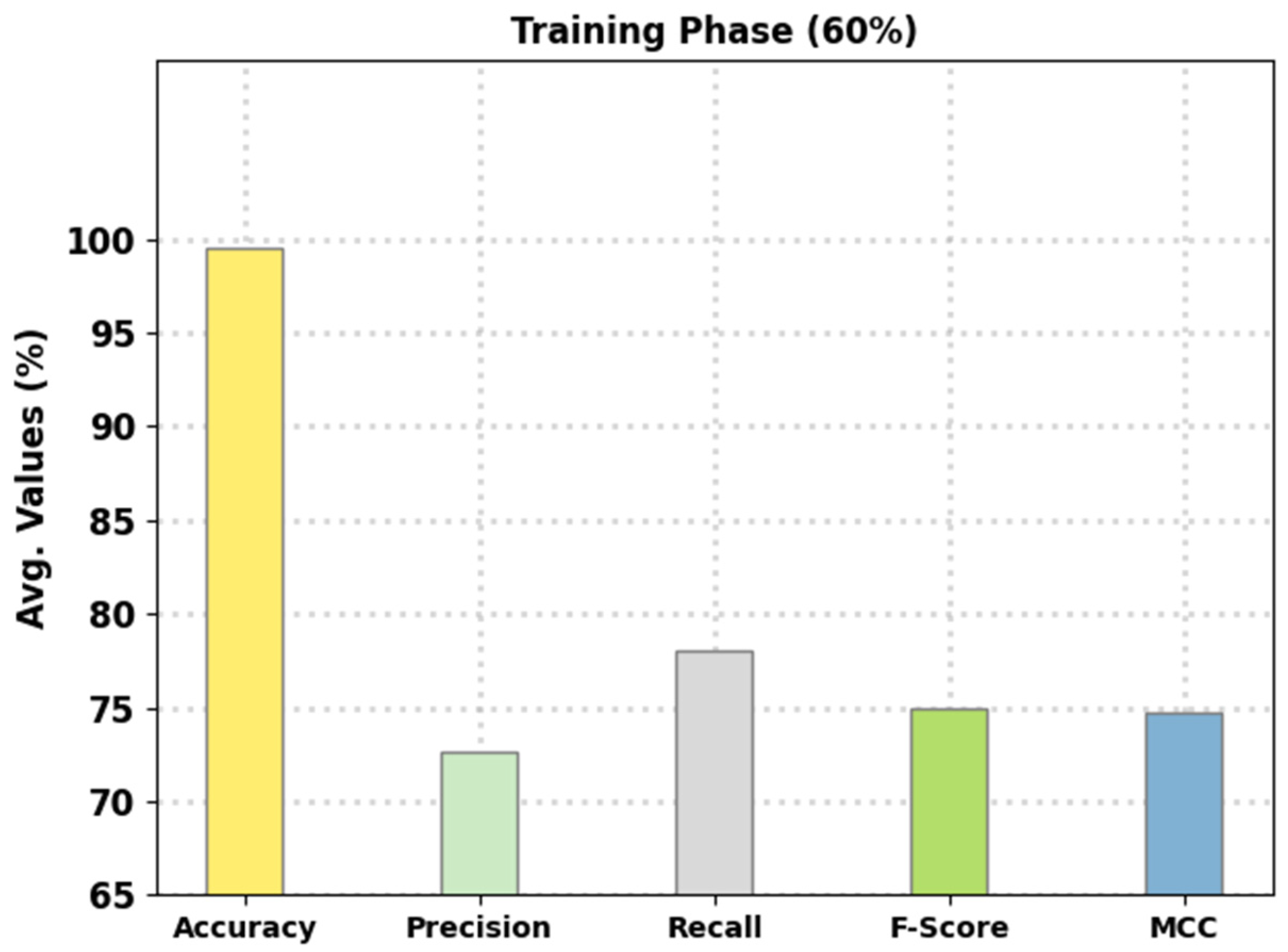
provides an overall intrusion detection outcome of the FSHDBN-CID model on 60% of TR data and 40% of TS data. Figure 4 reports the intrusion classification performance of the presented FSHDBN-CID method on 60% of TR data. The experimental outcomes inferred that the FSHDBN-CID model has shown enhanced results under both aspects. For instance, on DoS class, the FSHDBN-CID model has offered $acc{u}_y$ of 99.35%, $pre{c}_n$ of 99.34%, $rec{a}_l$ of 98.88%, $F_{score}$ of 99.11%, and MCC of 98.60%. Simultaneously, on Probe class, the FSHDBN-CID technique has presented $acc{u}_y$ of 99.64%, $pre{c}_n$ of 97.46%, $rec{a}_l$ of 98.76%, $F_{score}$ of 98.10%, and MCC of 97.91%. Concurrently, on Normal class, the FSHDBN-CID technique has rendered $acc{u}_y$ of 99.28%, $pre{c}_n$ of 99.53%, $rec{a}_l$ of 99.12%, $F_{score}$ of 99.32%, and MCC of 98.56%.

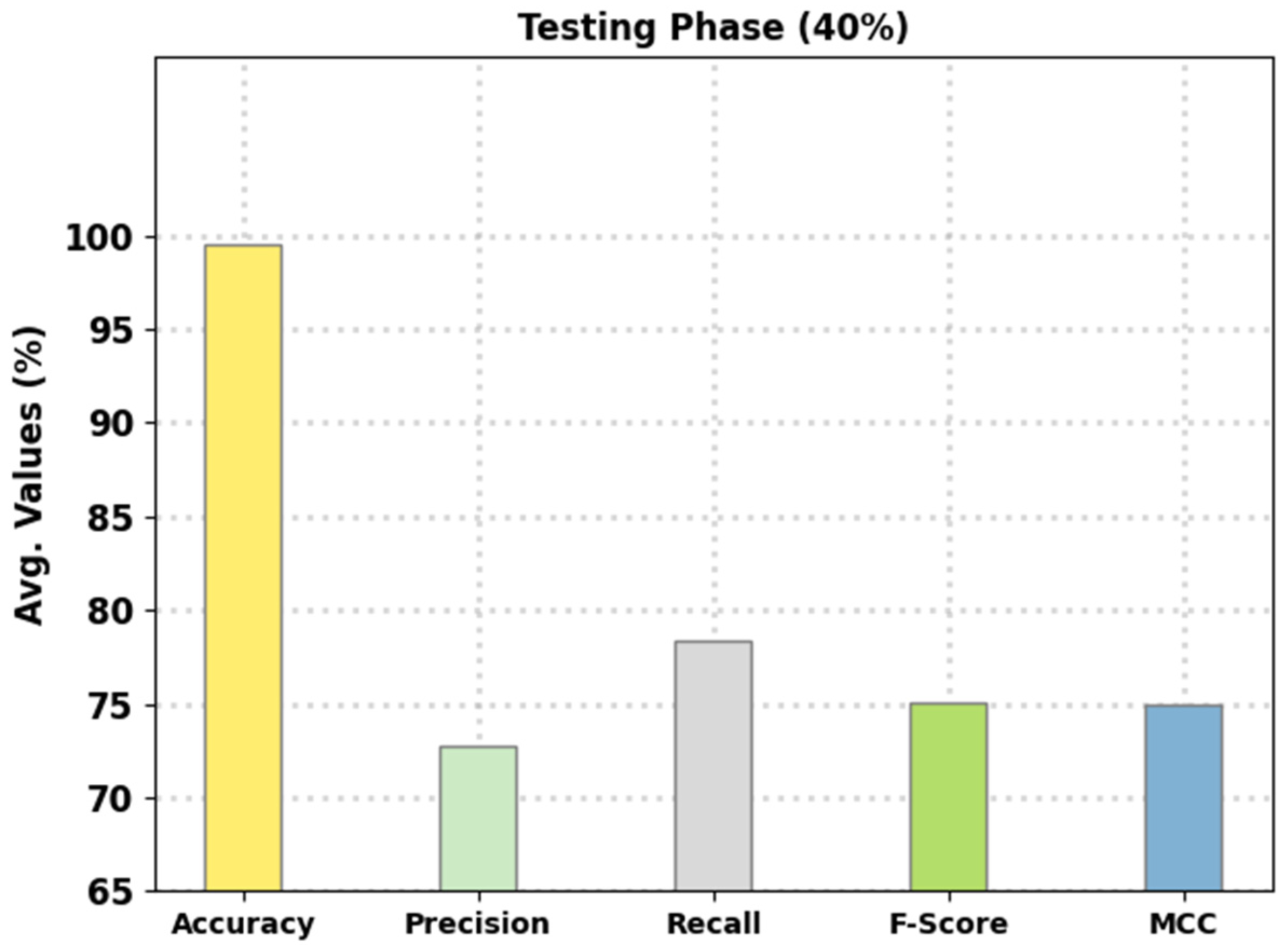
Figure 5 reports the intrusion classification performance of the presented FSHDBN-CID technique on 40% of TS data. The experimental outcomes exhibited the FSHDBN-CID approach have depicted enhanced consequences under both aspects. For instance, in DoS class, the FSHDBN-CID method has presented $acc{u}_y$ of 99.37%, $pre{c}_n$ of 99.29%, $rec{a}_l$ of 98.98%, $F_{score}$ of 99.14%, and MCC of 98.64%. Concurrently, on Probe class, the FSHDBN-CID technique has granted $acc{u}_y$ of 99.61%, $pre{c}_n$ of 97.16%, $rec{a}_l$ of 98.54%, $F_{score}$ of 97.85%, and MCC of 97.63%. Concurrently, on Normal class, the FSHDBN-CID method has presented $acc{u}_y$ of 99.27%, $pre{c}_n$ of 99.60%, $rec{a}_l$ of 99.04%, $F_{score}$ of 99.32%, and MCC of 98.53%.

Table 3. Result analysis of FSHDBN-CID algorithm with distinct class labels under 70:30 of TR and TS datasets.

Labels	Accuracy	Precision	Recall	F-Score	MCC
Training Phase (70%)
Dos	98.38	97.55	98.00	97.78	96.50
R2l	99.51	70.65	65.00	67.71	67.52
Probe	99.19	96.32	94.87	95.59	95.15
U2r	99.96	100.00	06.06	11.43	24.61
Normal	98.67	98.69	98.82	98.76	97.32
Average	99.14	92.64	72.55	74.25	76.22
Testing Phase (30%)
Dos	98.30	97.52	97.84	97.68	96.35
R2l	99.60	76.89	68.81	72.63	72.54
Probe	99.16	95.91	95.07	95.49	95.03
U2r	99.95	00.00	00.00	00.00	00.00
Normal	98.59	98.59	98.76	98.68	97.16
Average	99.12	73.78	72.10	72.89	72.21

portrays the complete intrusion detection outcomes of the FSHDBN-CID technique on 70% of TR data and 30% of TS data. The experimental results denoted the FSHDBN-CID approach has displayed enhanced results under both aspects. For example, on DoS class, the FSHDBN-CID method has presented $acc{u}_y$ of 98.38%, $pre{c}_n$ of 97.55%, $rec{a}_l$ of 98%, $F_{score}$ of 97.78%, and MCC of 96.50%. At the same time, on Probe class, the FSHDBN-CID algorithm has granted $acc{u}_y$ of 99.19%, $pre{c}_n$ of 96.32%, $rec{a}_l$ of 94.87%, $F_{score}$ of 95.59%, and MCC of 95.15%. Parallelly, on Normal class, the FSHDBN-CID approach has exhibited $acc{u}_y$ of 98.67%, $pre{c}_n$ of 98.69%, $rec{a}_l$ of 98.82%, $F_{score}$ of 98.76%, and MCC of 97.32.

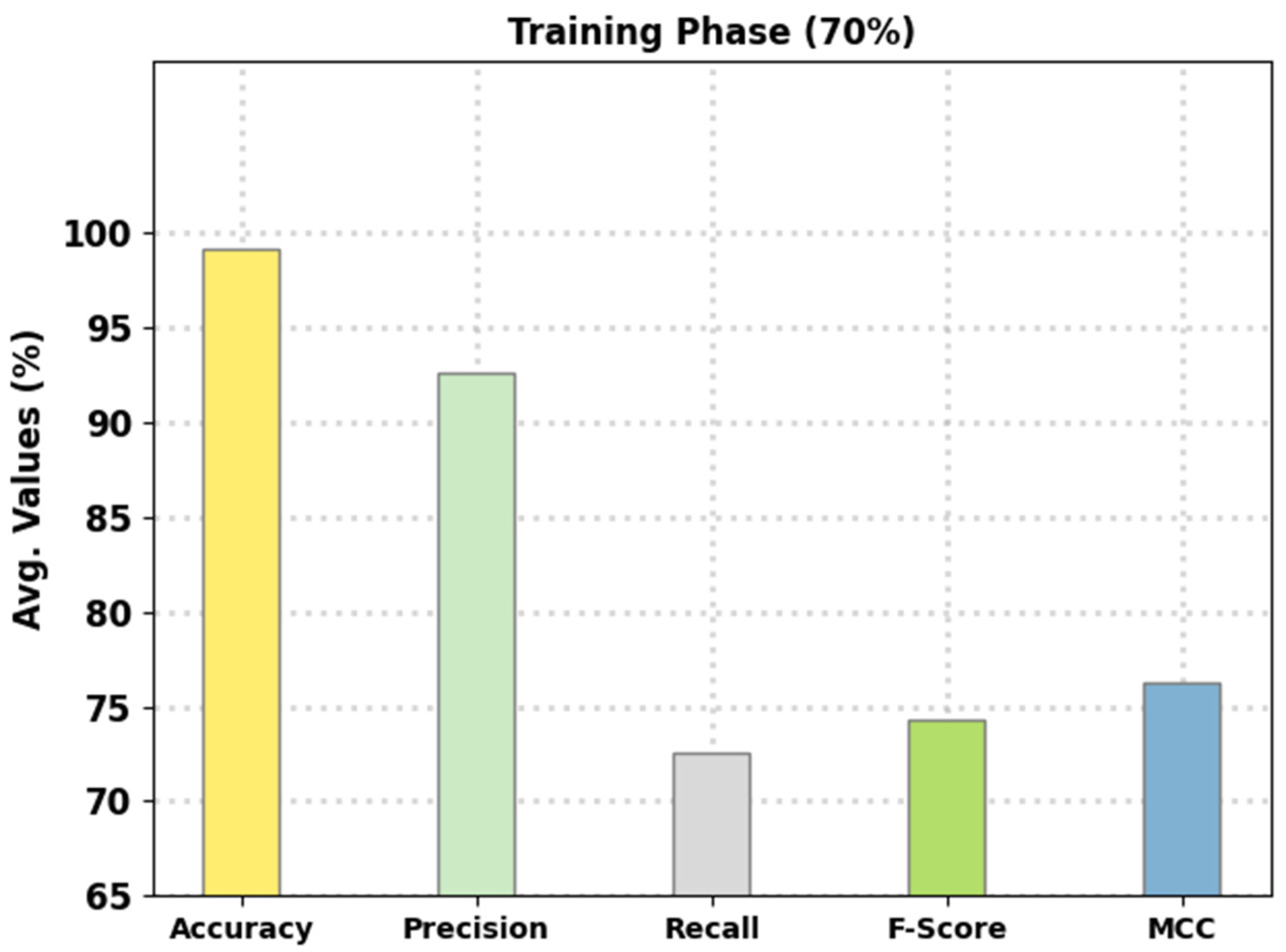
Figure 6 signifies the average intrusion classification performance of the presented FSHDBN-CID method on 70% of TR data. The figure indicated that the FSHDBN-CID model has reached an enhanced average $acc{u}_y$ of 99.14%.

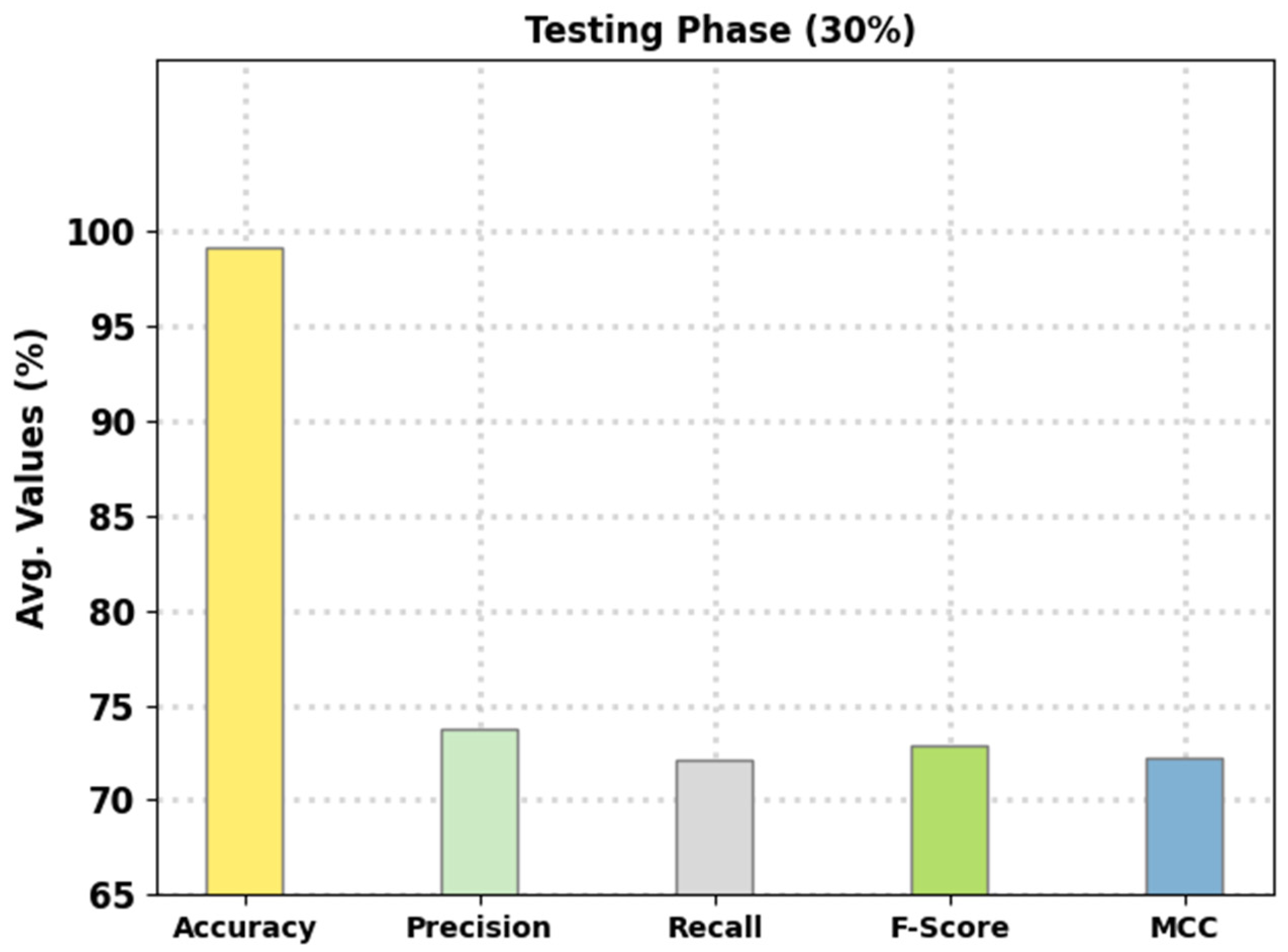
Figure 7 reports the intrusion classification performance of the presented FSHDBN-CID algorithm on 30% of TS data. The experimental outcomes denoted the FSHDBN-CID approach has exhibited enhanced results under both aspects. For example, on DoS class, the FSHDBN-CID technique has displayed $acc{u}_y$ of 98.30%, $pre{c}_n$ of 97.52%, $rec{a}_l$ of 97.84%, $F_{score}$ of 97.68%, and MCC of 96.35%. At the same time, on Probe class, the FSHDBN-CID algorithm has granted $acc{u}_y$ of 99.16%, $pre{c}_n$ of 95.91%, $rec{a}_l$ of 95.07%, $F_{score}$ of 95.49%, and MCC of 95.03%. Parallelly, on Normal class, the FSHDBN-CID approach has shown $acc{u}_y$ of 98.59%, $pre{c}_n$ of 98.59%, $rec{a}_l$ of 98.76%, $F_{score}$ of 98.68%, and MCC of 97.16%.

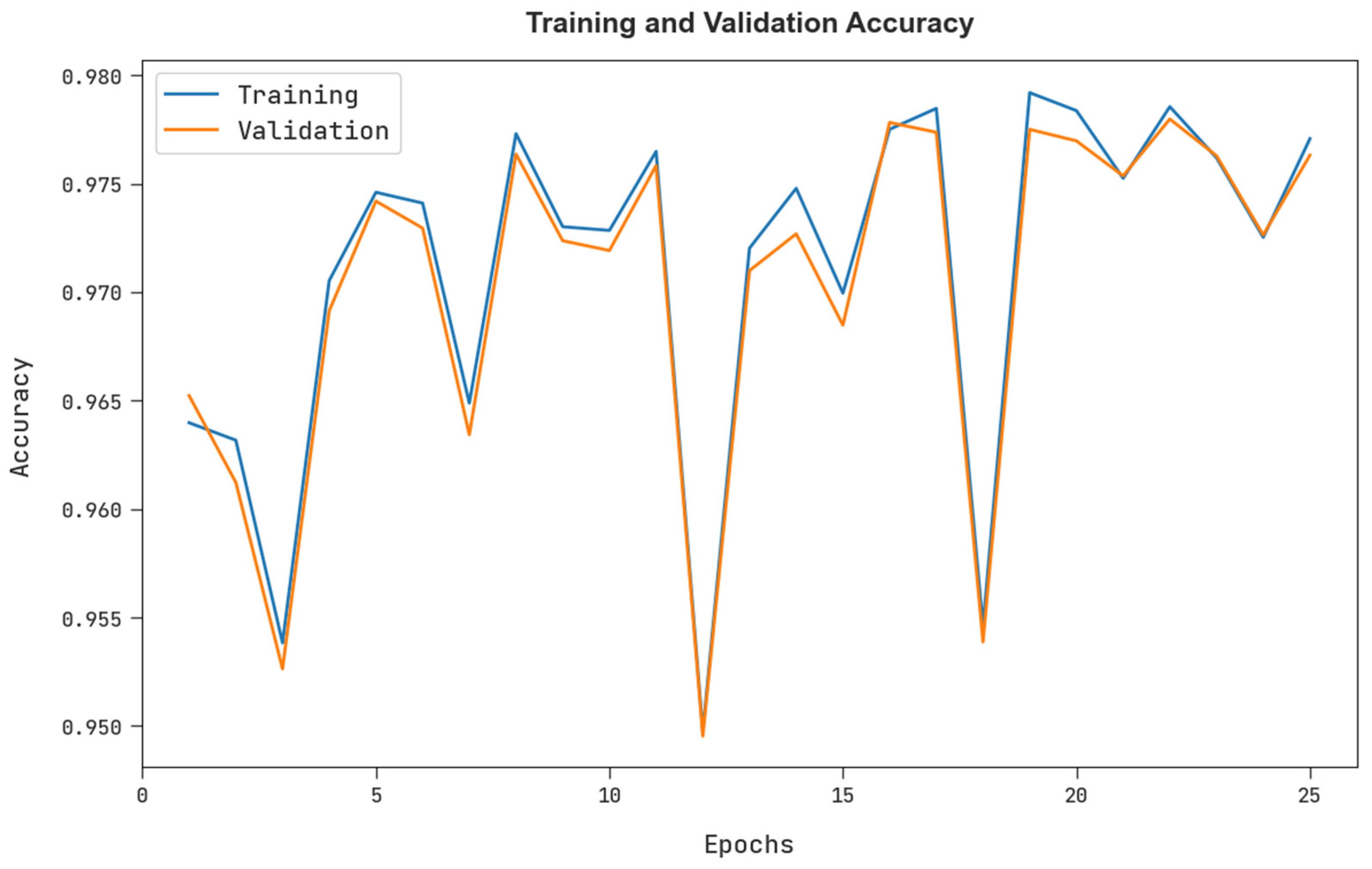
The training accuracy (TRA) and validation accuracy (VLA) gained by the FSHDBN-CID approach under test dataset is exemplified in Figure 8. The experimental result specified the FSHDBN-CID approach has achieved maximal values of TRA and VLA. seemingly the VLA is greater than TRA.

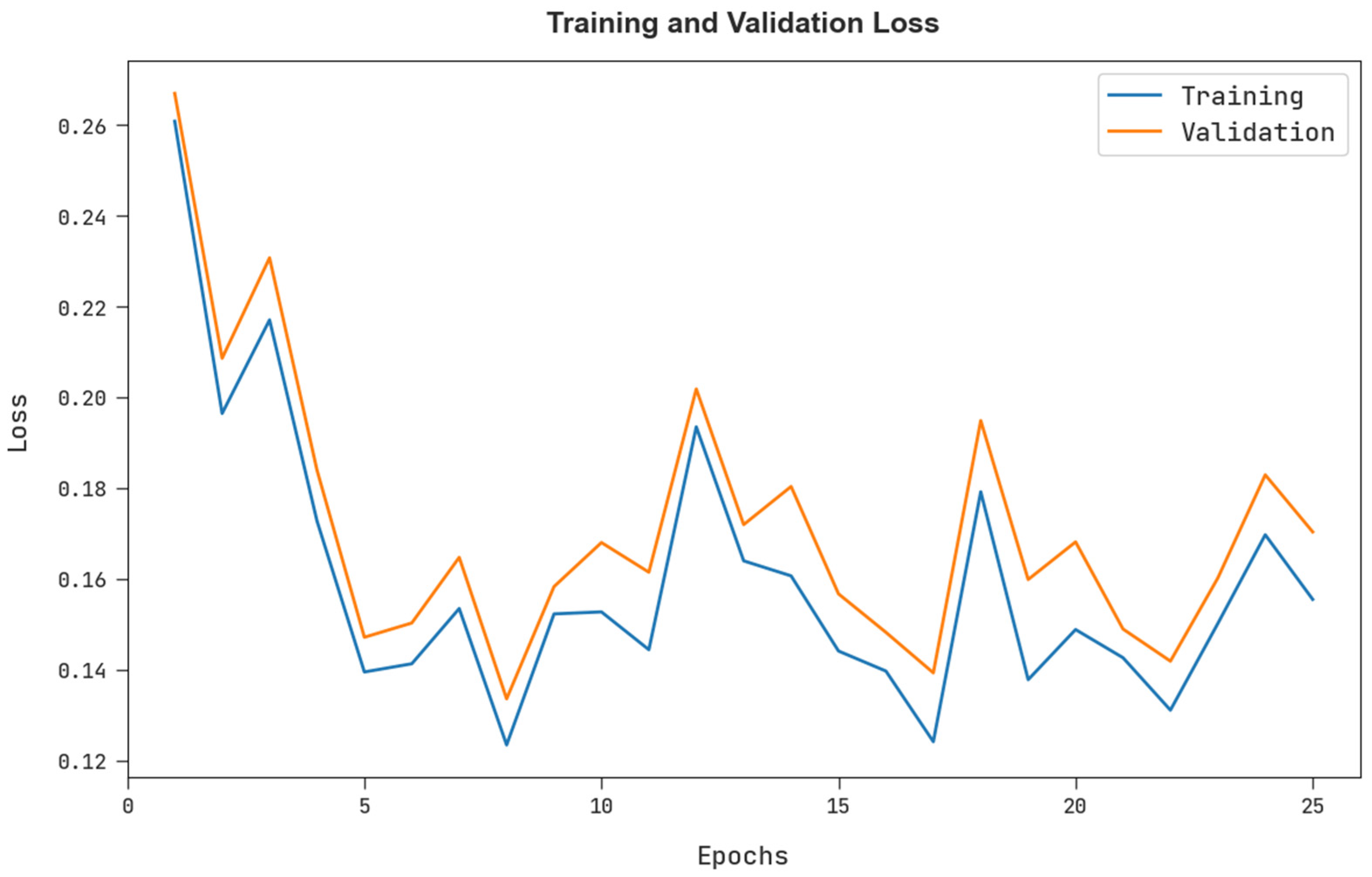
The training loss (TRL) and validation loss (VLL) obtained by the FSHDBN-CID method under test dataset are shown in Figure 9. The experimental outcome represents the FSHDBN-CID approach has exhibited minimal values of TRL and VLL. Particularly, the VLL is lesser than TRL.

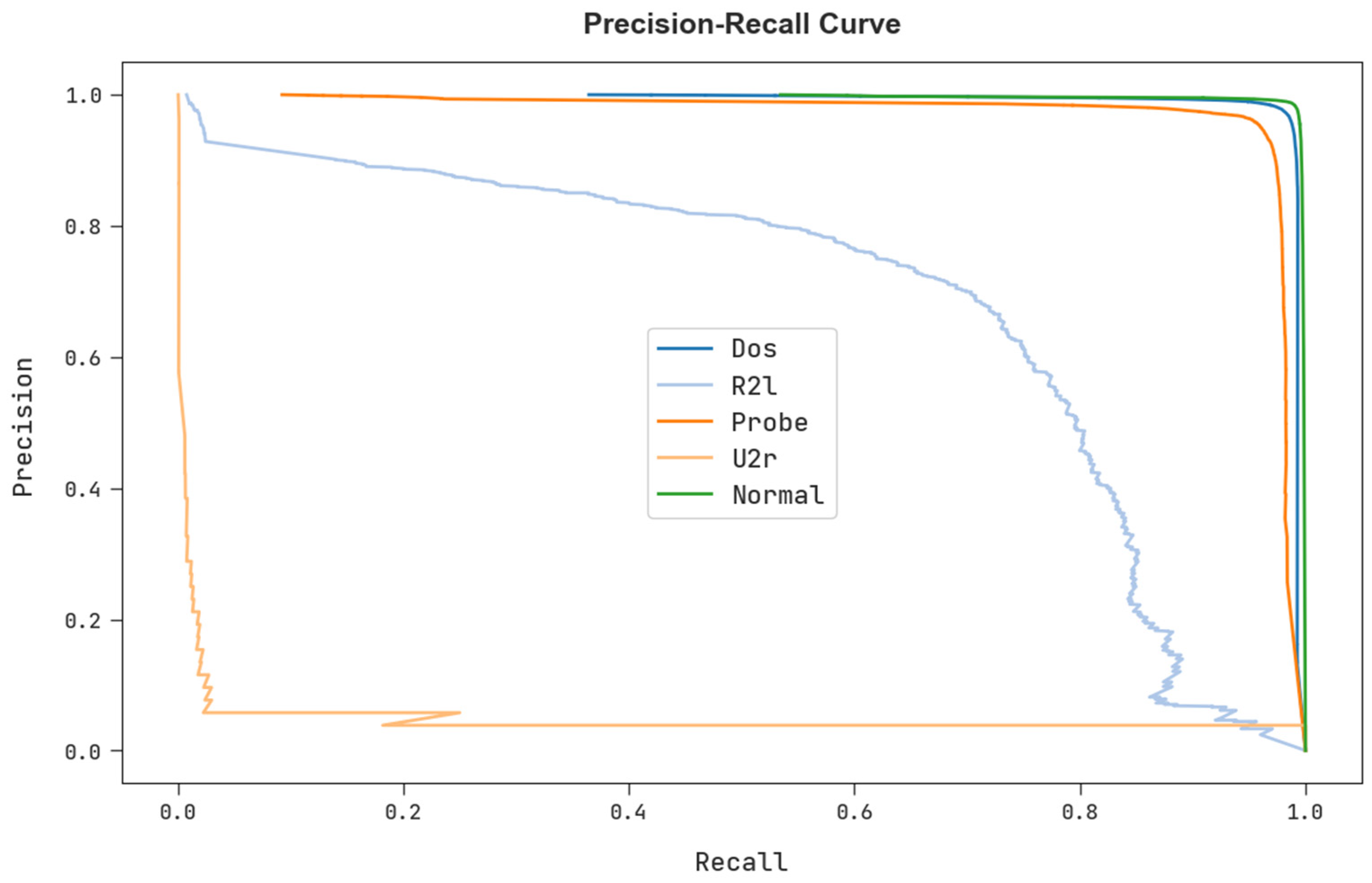
A clear precision-recall study of the FSHDBN-CID technique under test dataset is described in Figure 10. The figure specified the FSHDBN-CID algorithm has resulted in enhanced values of precision-recall values in every class label.

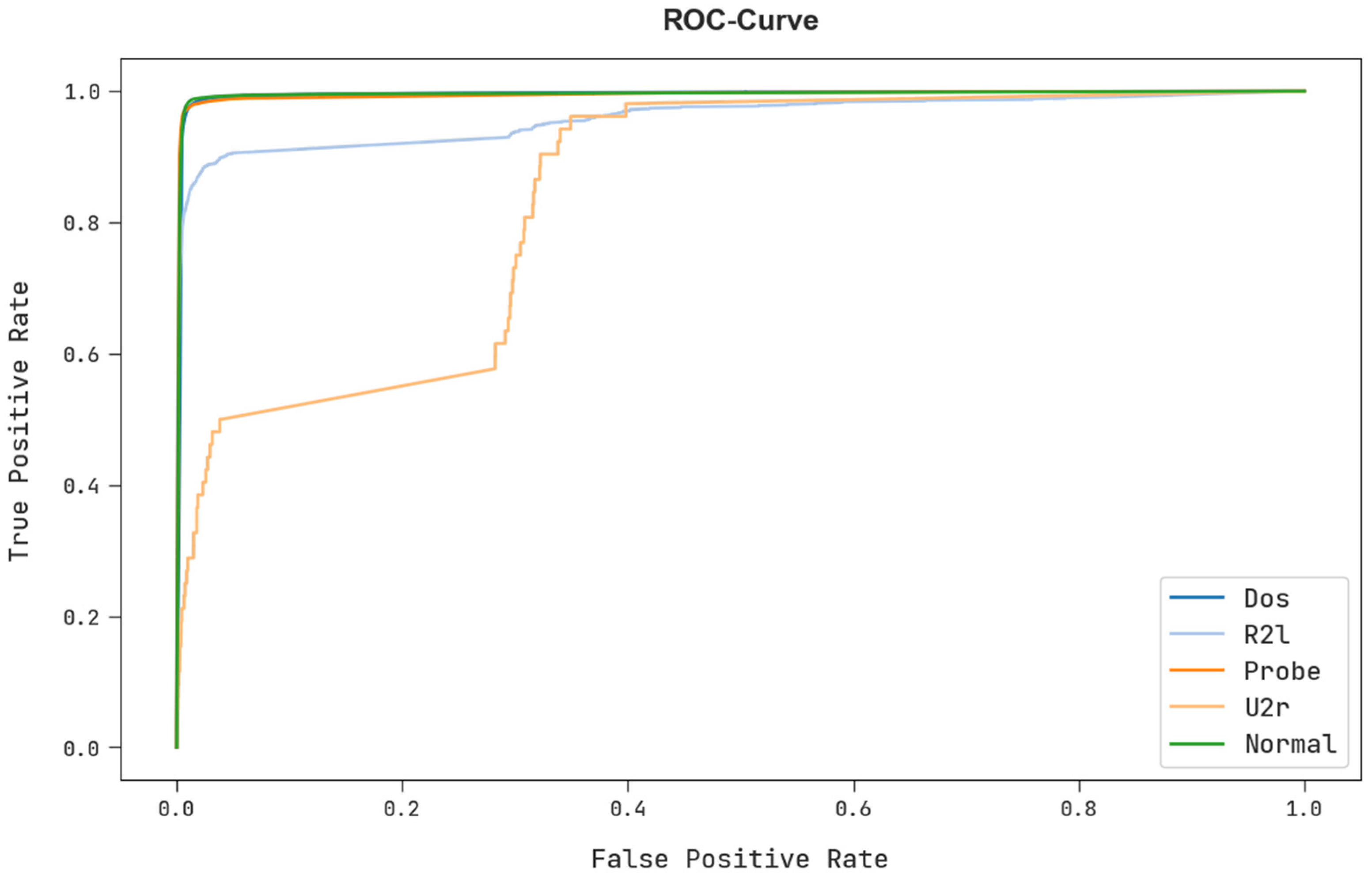
A brief ROC examination of the FSHDBN-CID technique under test dataset is shown in Figure 11. The results exhibited the FSHDBN-CID method has revealed its capability in classifying different classes in test dataset.

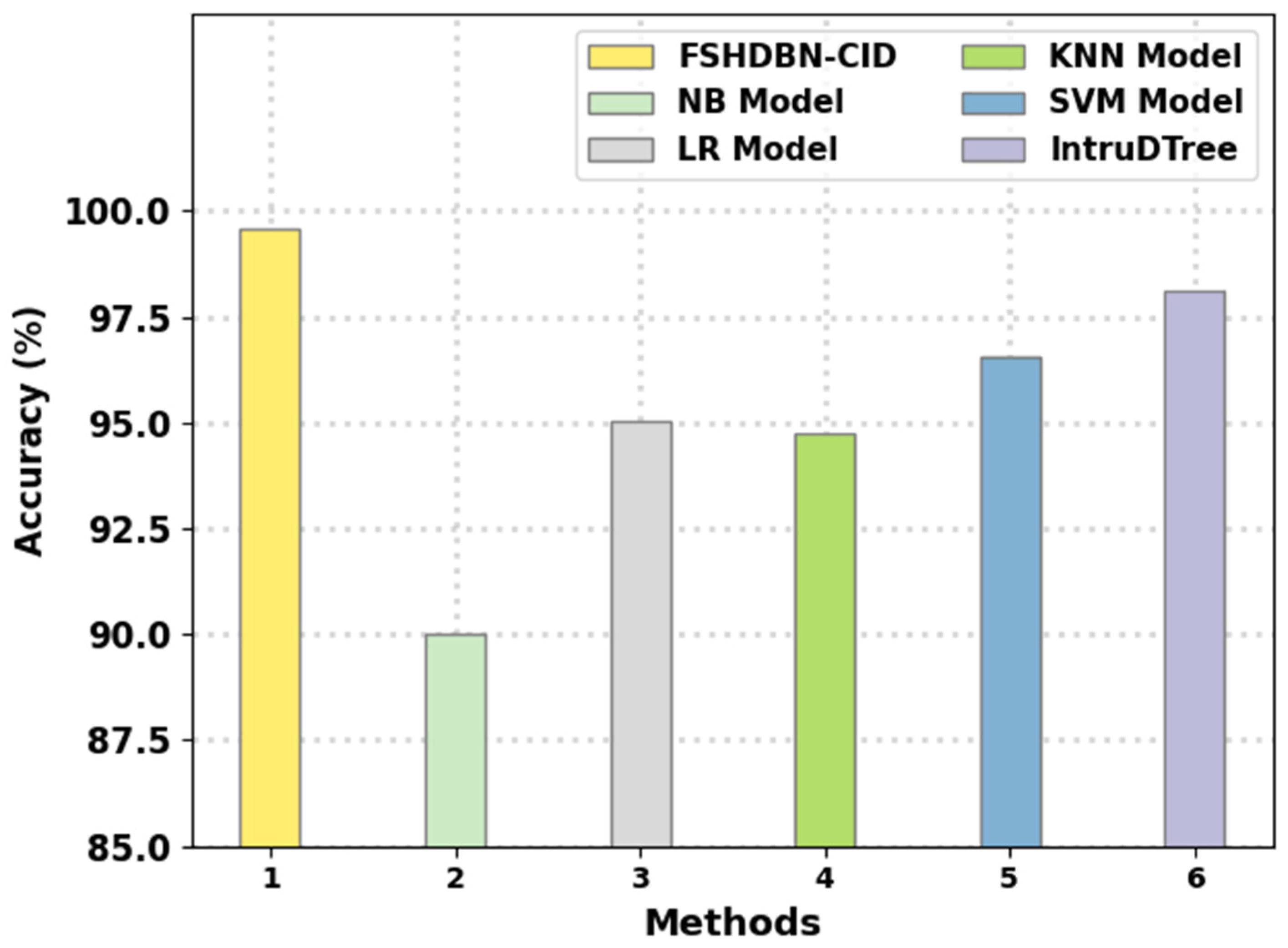
Finally, a comparison study of the FSHDBN-CID method with other IDS methods is given in

Table 4. Comparative analysis of FSHDBN-CID approach with existing methodologies.

Methods	Accuracy
FSHDBN-CID	99.57
NB Model	90.03
LR Model	95.03
KNN Model	94.73
SVM Model	96.56
IntruDTree	98.13

and Figure 12 [1]. The results indicated that the NB model has shown poor performance with minimal $acc{u}_y$ of 90.03%. Next, the KNN model has attained moderately improved $acc{u}_y$ of 94.73% whereas the LR and SVM models have reached reasonable $acc{u}_y$ of 95.03% and 96.56%, respectively. Though the IntruDTree method has resulted in near optimal $acc{u}_y$ of 98.13%, the FSHDBN-CID model has shown maximum $acc{u}_y$ of 99.57%. Therefore, the presented FSHDBN-CID model is found to be effective in accomplishing cybersecurity.

5. Conclusions

In this paper, an effective FSHDBN-CID technique has been developed for intrusion detection. The presented FSHDBN-CID model mainly concentrates on the recognition of intrusions to accomplish cybersecurity in the network. In the presented FSHDBN-CID model, different levels of data preprocessing will be performed to transform the raw data into a compatible format. For feature selection purposes, the JOA is utilized which in turn reduces the computation complexity. In addition, the presented FSHDBN-CID model exploits the HDBN model for classification purposes. Lastly, the CSO algorithm can be applied as a hyperparameter optimizer for the HDBN method. In order to investigate the enhanced performance of the presented FSHDBN-CID method, a wide range of experiments was performed. The comparison study pointed out the improvements of the FSHDBN-CID model over other models. Therefore, the proposed model can be employed for cyberattack detection in real time environments such as finance, e-commerce, education, etc. As a part of the future scope, the improved performance of the FSHDBN-CID model will be improvised using the outlier detection and data clustering algorithms.