Virtual Synchronous Generator Using an Intelligent Controller for Virtual Inertia Estimation

Abstract

Virtual synchronous generators (VSGs) with inertia characteristics are generally adopted for the control of distributed generators (DGs) in order to mimic a synchronous generator. However, since the amount of virtual inertia in VSG control is usually constant and given by trial and error, the real power and frequency oscillations of a battery energy storage system (BESS) occurring under load variation result in the degradation of the control performance of the DG. Thus, in this study, a novel virtual inertia estimation methodology is proposed to estimate suitable values of virtual inertia for VSGs and to suppress the real power output and frequency oscillations of the DG under load variation. In addition, to improve the function of the proposed virtual inertia estimator and the transient responses of the real power output and frequency of the DG, an online-trained Petri probabilistic wavelet fuzzy neural network (PPWFNN) controller is proposed to replace the proportional integral (PI) controller. The network structure and the online learning algorithm using backpropagation (BP) of the proposed PPWFNN are represented in detail. Finally, on the basis of the experimental results, it can be concluded that superior performance in terms of real power output and frequency response under load variation can be achieved by using the proposed virtual inertia estimator and the intelligent PPWFNN controller.

1. Introduction

In recent years, the percentage of distributed generators (DGs) based on renewable energy sources has been significantly increasing [1,2] due to the increased awareness of environmental pollution. However, a serious issue arises with respect to the stability of the power system. In general, conventional synchronous generators (SGs) are adopted to stabilize the frequency of the power grid [3,4]. By means of absorbing or delivering the kinetic energy stored in the rotor of SG, the frequency response of the power grid can be smoothed owing to the inertial response [3,4]. Moreover, a large amount of kinetic energy can also be delivered to the utility grid in cases of a sudden disturbance or fault [5,6]. However, since inverter-based DGs lack inertia and are without grid-forming capability, the stability of the power grid is threatened [7,8]. Thus, in order to overcome the drawbacks of inverter-based DGs, various algorithms for virtual synchronous generators (VSGs) have recently been proposed [9,10]. The main principle of the VSG’s control is the adoption of the well-known swing equation for SG based on droop control [11,12]. Hence, the VSG control imitates the basic characteristics of the SG, including the inertia and the droop mechanism, so that rotating inertia can be emulated in inverter-based DGs. The VSG possesses the ability to provide grid support and to improve the stability of frequency and power flow. Furthermore, the VSG control can also perform in an islanded operation mode, naturally guaranteeing load sharing [13], which is similar to traditional SGs [7,8]. Hence, there have been many studies focusing on VSG control, as reviewed in [14,15]. In [13], a new algorithm based on a finite-control-set model-predictive-control scheme and a corrective VSG control was proposed to suppress the distorted current waveform. In addition, an improved synchronization stability method that adopts the frequency difference between the power grid and VSG for reactive power control was researched in [14]. A fuzzy-secondary-controller-based VSG for grid-connected inverters of DGs was proposed in [15] to regulate the voltage and frequency of microgrid systems.

The frequency and power output oscillations under sudden disturbances, which are inherent characteristics of real SGs as well as VSGs, can be introduced by the swing equation [16,17]. In general, since conventional SGs possess considerable overload capability, this is not a serious issue for SGs. However, the inverter-based DGs adopt VSG control without overload capability in order to ride though large fluctuations [16]. Deterioration, as well as serious frequency and power flow oscillations, will result in damage to the equipment during sudden disturbances. Although the oscillations during disturbances can be mitigated by adjusting the parameters of the swing equation, such as the damping factor and the virtual inertia, the low moment of the inertia results in a deterioration in frequency stability and can cause large frequency oscillations during disturbances [15]. Moreover, since the swing equation of the VSG control is nonlinear and it is difficult to obtain the proper parameters, the parameters of the swing equation are generally constants and are given by trial and error [18]. In other words, the characeristics of the VSG can be changed by means of adjusting the damping factor and the virtual inertia of the swing equation [17].

In the past decade, in many studies, wavelet fuzzy neural networks (WFNNs) have been proposed to solve the system identification, signal processing, time-series prediction, regression and control issues [19,20]. Since WFNNs integrate a fuzzy neural network (FNN) with wavelet transform theory, they possess the ability of FNN to deal with complex nonlinear systems and parallel computation, and the capabilities of wavelet transform theory for quick convergence, fault tolerance, high accuracy and approximation [21,22]. In [22], a robust WFNN identifier was investigated to improve the function of the micro permanent magnet synchronous motor drive. In [23], a self-learning WFNN controller was adopted to regulate the dc-link voltage of the induction generator system for wind power applications. Moreover, the probabilistic neural network (PNN) was first proposed as a data classifier by Specht in 1990 [24,25]. The main principle of the PNN is the adoption of a Bayes classification rule along with probability density function estimation as a pattern layer for each training sample [26,27]. The PNN possesses classification capability and is good at processing high-dimensional data [28]. Furthermore, the PNN has been widely adopted in the area of nonlinear mapping, pattern recognition, approximation and fault diagnosis [27,29]. In addition, Petri net (PN) is a powerful mathematical and graphical tool for solving deadlocks in flexible manufacturing systems and discrete event systems owing to the ability to cope with conflicts and concurrences [30,31]. Thus, in accordance with the above merits of WFNN, PNN and PN, a new online-trained Petri probabilistic wavelet fuzzy neural network (PPWFNN) controller is proposed for the first time in this study.

To suppress the real power output and frequency oscillations of a battery energy storage system (BESS) using VSG control under load variation, a novel virtual inertia estimator is proposed for the first time to estimate suitable values of virtual inertia for the VSG control, and verified in islanded operation. Moreover, to improve the performance of the proposed virtual inertia estimator and the transient responses of the real power output and frequency of the BESS, an online-trained PPWFNN controller using real power error as input is proposed to take the place of the proportional integral (PI) controller. The operating principles of the proposed virtual inertia estimator for VSG control are introduced in Section 2. The network structure and online learning based on the backpropagation (BP) algorithm of the proposed PPWFNN controller are described in Section 3. Moreover, the feasibility and effectiveness of the proposed virtual inertia estimator and PPWFNN controller for the BESS using VSG under various load variation conditions are manifested in Section 4. Finally, some conclusions are expressed in Section 5.

The novelty and major contributions of this study can be described as follows:

• The successful development of a virtual inertia estimator for VSG control.
• The successful development of the proposed online-trained PPWFNN controller.
• The successful implementation of a BESS using the proposed virtual inertia estimator and PPWFNN controller for the inertia estimator of the VSG control under load variation.

2. Operating Theory of Proposed Virtual Inertia Estimator for VSG Control

In this study, a BESS operated in islanded mode is investigated by using the proposed virtual inertia estimator and PPWFNN intelligent controller. A block diagram of the BESS is represented in Figure 1. The BESS is equipped with a varying load, regarded as sudden disturbances, in order to certify the performance of the proposed algorithms. The detailed operating theories of the BESS using the proposed virtual inertia estimation methodology are described in the following.

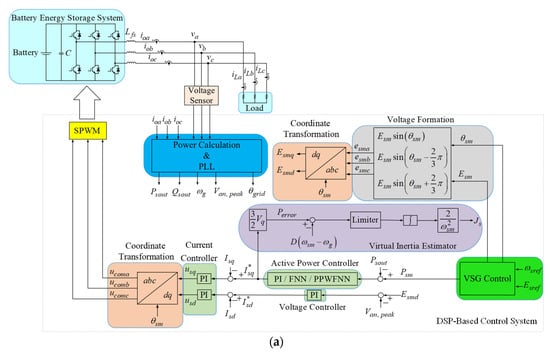
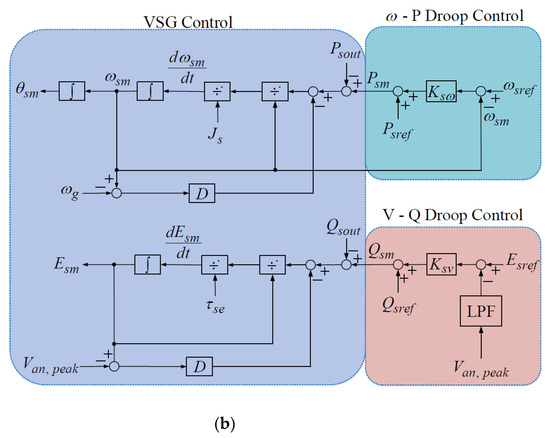
Figure 1. Block diagram of BESS. (a) Control block of BESS using proposed virtual inertia estimator and PPWFNN intelligent controller; (b) control block of VSG based on droop control.

2.1. Control Algorithm of VSG

The control block of the BESS using the proposed virtual inertia estimator and PPWFNN intelligent controller is shown in Figure 1a. The BESS is performed in islanded mode and VSG control is adopted to imitate the basic characteristics of the SG, including the inertia and the droop mechanism, so that the rotating inertia can be emulated in the BESS. The control block of the VSG based on droop control is provided in Figure 1b. In general, VSG control adopts the well-known swing equations of the SG based on angular frequency–real power $\omega \text{-}P$ and voltage–reactive power $V\text{-}Q$ droop control. In this study, the designed characteristics of $\omega \text{-}P$ and $V\text{-}Q$ droop control are illustrated in Figure 2a,b, and given as follows [15,16]:

$$P_{sm}=P_{sref}+K_{s\omega }({\omega }_{sref}-{\omega }_{sm})$$

(1)

$$Q_{sm}=Q_{sref}+K_{sv}(E_{sref}-V_{an,peak})$$

(2)

where $P_{sm}^{}$ is the virtual shaft real power of the VSG; $P_{sref}^{}$ is the set value of real power; $K_{s\omega }^{}$ is the droop coefficient; is the reference angular frequency; ${\omega }_{sm}^{}$ is the virtual rotor angular frequency of the VSG; $Q_{sm}^{}$ is the virtual shaft reactive power of the VSG; $Q_{sref}^{}$ is the set value of reactive power; $K_{sv}^{}$ is the droop coefficient; $E_{sref}^{}$ is the reference voltage; $V_{an,peak}^{}$ is the voltage output of the VSG. Moreover, the swing equation for the VSG control shown in Figure 1b is described as [15,16]:

$$P_{sm}-P_{sout}=J_s{\omega }_{sm}\frac{d{\omega }_{sm}}{dt}+D({\omega }_{sm}-{\omega }_g)$$

(3)

where $P_{sout}^{}$ is the actual real power output; $J_s^{}$ is the virtual inertia; $D$ is the virtual damping factor; ${\omega }_g^{}$ is the output angular frequency. According to Equation (3), if the virtual damping factor $D$ and the virtual inertia $J_s^{}$ are set to zero, the swing Equation (3) is equal to the $\omega \text{-}P$ droop control shown in Equation (1). In other words, the $\omega \text{-}P$ droop control is the special case of the VSG control and without the inertial characteristic [6,16]. Furthermore, Equation (3) can be rewritten as follows, and is shown in Figure 1b:

$${\theta }_{sm}={\displaystyle \int {\omega }_{sm}=}{\displaystyle \int \left\{{\displaystyle \int \frac{1}{J_s{\omega }_{sm}}\left[\left(P_{sm}-P_{sout}\right)-D({\omega }_{sm}-{\omega }_g)\right]dt}\right\}}dt$$

(4)

where ${\theta }_{sm}^{}$ is the virtual rotor angle. In addition, a similar control concept can be applied to the $V\text{-}Q$ droop control as follows [9]:

$$Q_{sm}-Q_{sout}={\tau }_{se}{E}_{sm}\frac{d{E}_{sm}}{dt}+D(E_{sm}-V_{an,peak})$$

(5)

where $Q_{sout}^{}$ is the actual reactive power output; ${\tau }_{se}^{}$ is a time constant; $E_{sm}^{}$ is the amplitude of virtual internal electromotive force of the VSG. Equation (5) can be rewritten as follows, and is also shown inFigure 1b:

$$E_{sm}={\displaystyle \int \frac{1}{{\tau }_{se}{E}_{sm}}\left[\left(Q_{sm}-Q_{sout}\right)-D(E_{sm}-V_{an, peak})\right]dt}$$

(6)

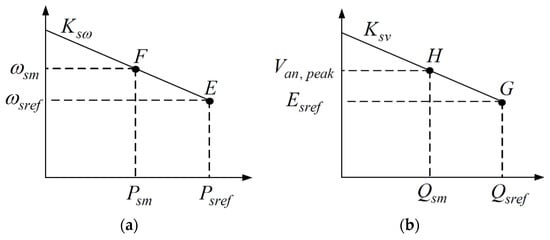
Figure 2. Droop control. (a) $\omega \text{-}P$ droop; (b) $V\text{-}Q$ droop.

The virtual rotor angle ${\theta }_{sm}^{}$ and the amplitude of virtual internal electromotive force $E_{sm}^{}$ of the VSG are sent to the voltage formation shown in Figure 1a to obtain the three-phase induced electromotive force $e_{sma}^{},\hspace{0.17em}{e}_{smb}^{},\hspace{0.17em}{e}_{smc}^{}$. Furthermore, the dq-axis induced electromotive forces $E_{smd}$ and $E_{smq}$ are obtained using $abc/dq$ coordinate transformation.

2.2. Proposed Virtual Inertia Estimator for VSG

In Figure 1a, the three-phase output voltages $v_a,\hspace{0.17em}{v}_b,\hspace{0.17em}{v}_c$ and output currents $i_{oa},\hspace{0.17em}{i}_{ob},\hspace{0.17em}{i}_{oc}$ of the BESS are detected and sent to the power calculation and phase-lock-loop (PLL) unit to compute the actual real power output $P_{sout}^{}$, the reactive power output $Q_{sout}^{}$, the output angular frequency ${\omega }_g^{}$, and the voltage output $V_{an,peak}^{}$. Then, the tracking error between the virtual shaft real power $P_{sm}^{}$ and the actual real power output $P_{sout}^{}$ is sent to the real power controller, namely the traditional PI or FNN or the proposed PPWFNN intelligent controller, to obtain the q-axis current command $I_{sq}^{*}$. In this study, the main principle of the proposed virtual inertia estimation methodology is obtained and derived as follows, according to Equation (3):

$$J_s=\frac{2}{{\omega }_{sm}^2}{\displaystyle \int \left[(P_{sm}-P_{sout})-D({\omega }_{sm}-{\omega }_g)\right]dt}$$

(7)

Hence, the product of the value 3/2, the q-axis current command $I_{sq}^{*}$ and the q-axis voltage $V_q^{}$ obtained by the three-phase output voltages $v_a,\hspace{0.17em}{v}_b,\hspace{0.17em}{v}_c$ with the $abc/dq$ coordinate transformation is equal to the real power error $P_{error}^{}$ [1,2]. Since the real power error $P_{error}^{}$ is also equivalent to the value $P_{sm}^{}-P_{sout}^{}$, the estimated virtual inertia in Equation (7) can be rewritten based on the real power error $P_{error}^{}$ as follows:

$$J_s=\frac{2}{{\omega }_{sm}^2}{\displaystyle \int \left[P_{error}-D({\omega }_{sm}-{\omega }_g)\right]dt}$$

(8)

Therefore, by means of the q-axis current command $I_{sq}^{*}$ regulated by the PI or FNN or the proposed PPWFNN controller, the suitable virtual inertia of the VSG control can be estimated to suppress the real power output and frequency oscillations of the BESS using VSG control under the load variation according to Equation (8). Moreover, the d-axis induced electromotive force $E_{smd}$ is compared to the voltage output $V_{an,peak}^{}$ and regulated by the PI controller to obtain the d-axis current command $I_{sd}^{*}$. The dq-axis current commands $I_{sd}^{*}$ and $I_{sq}^{*}$ are compared to the dq-axis current $I_{sd}^{}$ and $I_{sq}^{}$ obtained by the output currents $i_{oa},\hspace{0.17em}{i}_{ob},\hspace{0.17em}{i}_{oc}$ of the BESS with the $abc/dq$ coordinate transformation. Finally, the control signals $u_{coma},\hspace{0.17em}{u}_{comb},\hspace{0.17em}{u}_{comc}$ for the sinusoidal pulse width modulation (SPWM) switching signals are obtained by means of $dq/abc$ coordinate transformation.

3. Online-Trained PPWFNN Controller

To increase the performance of the proposed virtual inertia estimator, an online-trained PPWFNN controller is proposed to take the place of the PI controller to regulate the q-axis current command $I_{sq}^{*}$ of the BESS using VSG control under load variation. The proposed PPWFNN controller is made up of an input layer, a membership layer, a Petri layer, a probabilistic layer, a wavelet layer, a rule layer, and an output layer. The network structure of the proposed PPWFNN is provided in Figure 3. The network structure, online learning algorithm and convergence analysis of the proposed PPWFNN controller are introduced in detail in the following.

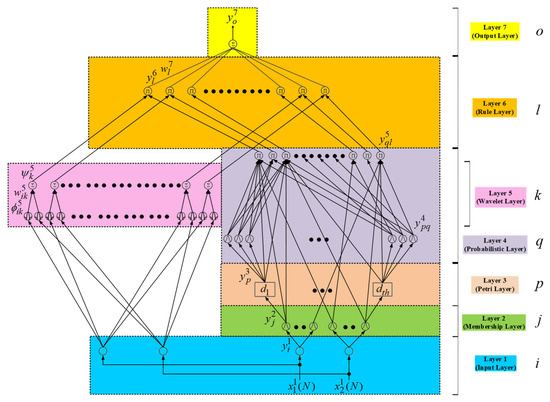
Figure 3. Network structure of proposed PPWFNN controller.

3.1. Network Structure

Layer 1 (Input Layer): The input and output of the node are depicted as follows:

$$ne{t}_i^1(N)=x_i^1\left(N\right)$$

(9)

$$y_i^1(N)=f_i^1(ne{t}_i^1(N))=ne{t}_i^1(N), i=1,2$$

(10)

where N expresses the Nth iteration; $x_1^1(N)=e$; $x_2^1(N)=\dot{e}$. The input variables of the proposed PPWFNN controller are the tracking error $x_1^1(N)=e$ between the virtual shaft real power $P_{sm}^{}$ and the actual real power output $P_{sout}^{}$, namely $e=P_{sm}^{}(t)-P_{sout}^{}(t)$, and its derivative $x_2^1(N)=\dot{e}$ for the proposed virtual inertia estimator of the BESS using VSG control under load variation.

Layer 2 (Membership Layer): To implement the membership function, the Gaussian function is adopted in each node to carry out the fuzzification operation. For the jth node,

$$ne{t}_j^2(N)=-\frac{{(y_i^1-m_{ij}^2)}^2}{{({\sigma }_{ij}^2)}^2}$$

(11)

$$y_j^2(N)=f_j^2(ne{t}_j^2(N))=\exp (ne{t}_j^2(N)) j=1,2,\dots ,6$$

(12)

where ${\sigma }_{ij}^2$ and $m_{ij}^2$ are the standard deviation and the mean of the Gaussian function, respectively, in the jth term input linguistic variable $y_i^1(N)$ to the node of membership layer.

Layer 3 (Petri Layer): The main purpose of the Petri layer is to take advantage of the competition law to choose the proper fired nodes [2] for the generation of tokens. When the tokens are generated in input position, the transitions are in enable state. Thereupon, the transition is unfired or fired in accordance with Equations (13) and (14).

$$t_p^3(N)=\{\begin{array}{l}1, y_j^2(N)\ge d_{th}\\ 0, y_j^2(N)<d_{th}\end{array} , th=1,\dots ,6$$

(13)

$$d_{th}=\frac{\alpha \exp (-\beta F)}{1+\exp (-\beta F)}$$

(14)

where $t_p^3(N)$ is the transition; $\alpha$ and $\beta$ are positive constants and are set as 1.3 and 0.06; $d_{th}^{}$ is the dynamic threshold value and is modulated by the function as follows [2,23]:

$$F=\frac{1}{2}\left[x_1^1\left(N\right)+x_2^1\left(N\right)\right]$$

(15)

When the transition is fired, the token is moved from its input position to the output position. Moreover, when the transition is unfired, the token remains in the input position. Consequently, the output and input of the Petri layer can be described as follows:

$$ne{t}_p^3(N)=y_j^2(N)t_p^3(N)$$

(16)

$$y_p^3(N)=f_p^3(ne{t}_p^3(N))=ne{t}_p^3(N),p=1,\dots ,6$$

(17)

Layer 4 (Probabilistic Layer): A general Gaussian function is used for the receptive field function, expressed as:

$$ne{t}_{pq}^4(N)=-\frac{{(y_p^3(N)-m_{pq})}^2}{{({\sigma }_{pq})}^2}$$

(18)

$$y_{pq}^4\left(N\right)=f_{pq}^4(ne{t}_{pq}^4(N))=\exp (ne{t}_{pq}^4(N)), \hspace{0.17em}q=1,\hspace{0.17em}2,\hspace{0.17em}3$$

(19)

where ${\sigma }_{pq}^{}$ and $m_{pq}^{}$ represent the normal deviation and the mean, respectively; $y_{pq}^4\left(N\right)$ is the output of this layer.

Layer 5 (Wavelet Layer): The wavelet function is carried out and introduced as follows:

$$\begin{array}{l}{\varphi }_{ik}^5(N)=\frac{1}{\sqrt{\left|{\sigma }_{ik}^5\right|}}\left[1-\frac{{(x_i^1(N)-m_{ik}^5)}^2}{{({\sigma }_{ik}^5)}^2}\right]\exp \left[-\frac{{(x_i^1(N)-m_{ik}^5)}^2}{2{({\sigma }_{ik}^5)}^2}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} i=1,2; k=1,2,\dots ,9\end{array}$$

(20)

$$ne{t}_k^5(N)={\displaystyle \sum w_{ik}^5}{\varphi }_{ik}^5(N)$$

(21)

$${\psi }_k^5(N)=f_k^5(ne{t}_k^5(N))=ne{t}_k^5(N)$$

(22)

where ${\varphi }_{ik}^5(N)$ is ith in the kth term wavelet output to the node of wavelet sum layer; $w_{ik}^5$ is the wavelet weight of the units in the wavelet function layer; ${\psi }_k^5(N)$ is the kth term wavelet function output to the node of the wavelet layer.

Layer 6 (Rule Layer): The signal propagation of the rule layer performs the $\prod$ operation, which multiplies the input signals and the outputs the resulting product. The relationship of the input and output of the rule layer is expressed in the following:

$$y_{ql}^5\left(N\right)=\prod y_j^2{y}_p^3{y}_{pq}^4$$

(23)

$$ne{t}_l^6(N)=\prod y_{ql}^5{\psi }_k^5$$

(24)

$$y_l^6(N)=f_l^6(ne{t}_l^6(N))=ne{t}_l^6(N), l=1,2,\dots ,9$$

(25)

where $y_j^2$, $y_p^3$ and ${\psi }_k^5$ are the jth, pth and kth inputs to the node of the ruler layer; $y_{pq}^4$ is the output of the probabilistic layer.

Layer 7 (Output Layer): The $\sum$ operation, which calculates the overall outputs as the summation of all input signals, is implemented, and can be depicted as follows:

$$ne{t}_o^7(N)={\displaystyle \sum _{l=1}^9{w}_l^7{y}_l^6(N)},o=1$$

(26)

$$y_o^7(N)=f_o^7(ne{t}_o^7(N))=ne{t}_o^7(N)$$

(27)

where $w_l^7$ is the connective weight between the rule layer and the output layer; $y_o^7(N)$ is the output of the proposed PPWFNN controller, which is equal to the q-axis current command $I_{sq}^{*}$ shown in Figure 1a for the regulation of the real power output and the virtual inertia estimator of the BESS.

3.2. Online Learning

In this study, by means of the supervised gradient descent method, the proposed PPWFNN controller possesses online learning capability. The online-trained PPWFNN controller derives an error function with regard to the variables of the network by using the chain rule algorithm. The error function $E(N)$ is depicted as:

$$E(N)=\frac{1}{2}{\left(P_{sm}-P_{sout}\right)}^2=\frac{1}{2}{e}^2$$

(28)

The process of the learning algorithm of the proposed PPWFNN controller is expressed in detail as follows:

Output Layer: The propagated error term can be depicted as:

$${\delta }_o^7=-\frac{\partial E}{\partial y_o^7(N)}=-\frac{\partial E}{\partial P_{sout}}\frac{\partial P_{sout}}{\partial y_o^7(N)}$$

(29)

Through the chain rule, the connected weight can be updated and computed as follows:

$$\Delta w_l^7=-{\eta }_1\frac{\partial E}{\partial w_l^7}=-{\eta }_1\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial w_l^7}={\eta }_1{\delta }_o^7{y}_l^6$$

(30)

where ${\eta }_1^{}$ is the learning rate. Then, the connected weight $w_l^7$ is updated as:

$$w_l^7(N+1)=w_l^7(N)+\Delta w_l^7$$

(31)

Rule Layer: In the rule layer, the error terms to be propagated are introduced as:

$${\delta }_l^6=-\frac{\partial E}{\partial y_l^6(N)}=-\left[\frac{\partial E}{\partial y_o^7(N)}\right]\frac{\partial y_o^7(N)}{\partial y_l^6}={\delta }_o^7{w}_l^7$$

(32)

Wavelet Layer: Two error terms of the wavelet layer to be propagated are computed as follows:

$${\delta }_{ql}^5=-\frac{\partial E}{\partial y_{ql}^5(N)}=-\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\right]\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}={\delta }_l^6{\psi }_k^5$$

(33)

$${\delta }_{ik}^5=-\frac{\partial E}{\partial {\psi }_k^5}=-\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\right]\frac{\partial y_l^6(N)}{\partial {\psi }_k^5(N)}={\delta }_l^6{y}_{ql}^5$$

(34)

The updates of the connected weight $\Delta w_{ik}^5$ are calculated using the chain rule:

$$\Delta w_{ik}^5=-{\eta }_2\frac{\partial E}{\partial w_{ik}^5}=-{\eta }_2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial {\psi }_k^5(N)}\right]\frac{\partial {\psi }_k^5(N)}{\partial w_{ik}^5(N)}={\eta }_2{\delta }_{ik}^5{\varphi }_{ik}^5$$

(35)

where ${\eta }_2^{}$ is learning rate. Hence, the connective weight $w_{ik}^5$ can be updated in accordance with the following equation:

$$w_{ik}^5(N+1)=w_{ik}^5(N)+\Delta w_{ik}^5$$

(36)

Membership Layer: The error term to be propagated and computed is given as:

$${\delta }_j^2=-\frac{\partial E}{\partial y_j^2}=-\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\right]\frac{\partial y_{ql}^5(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}={\displaystyle \sum _{}{\delta }_{ql}^5}{y}_{ql}^5{y}_j^2$$

(37)

Moreover, the updated amounts of the standard deviation $\Delta {\sigma }_{ij}^2$ and the mean $\Delta m_{ij}^2$ of the membership function, respectively, are obtained according to the chain rule as follows:

$$\begin{array}{l}\Delta m_{ij}^2=-{\eta }_3\frac{\partial E}{\partial m_{ij}^2}\\ \hspace{0.17em}=-{\eta }_3\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\right]\frac{\partial ne{t}_j^2(N)}{\partial m_{ij}^2(N)}\\ \hspace{0.17em}={\eta }_3{\delta }_j^2\frac{2(y_i^1-m_{ij}^2)}{{({\sigma }_{ij}^2)}^2}\end{array}$$

(38)

$$\begin{array}{l}\Delta {\sigma }_{ij}^2=-{\eta }_4\frac{\partial E}{\partial {\sigma }_{ij}^2}\\ =-{\eta }_4\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\right]\frac{\partial ne{t}_j^2(N)}{\partial {\sigma }_{ij}^2(N)}\\ ={\eta }_4{\delta }_j^2\frac{2{(y_i^1-m_{ij}^2)}^2}{{({\sigma }_{ij}^2)}^3}\end{array}$$

(39)

where ${\eta }_3^{}$ and ${\eta }_4^{}$ are the learning rates of the mean and standard deviation, respectively. Then, the updated standard deviation ${\sigma }_{ij}^2$ and mean $m_{ij}^2$ of the membership function are obtained as follows:

$$m_{ij}^2(N+1)=m_{ij}^2(N)+\Delta m_{ij}^2$$

(40)

$${\sigma }_{ij}^2(N+1)={\sigma }_{ij}^2(N)+\Delta {\sigma }_{ij}^2$$

(41)

Owing to uncertainties such as external disturbance and parameter variation in the dynamic of the BESS, the correct computation of the Jacobian of the BESS, $\partial P_{sout}/\partial y_o^7(N)$, cannot be achieved. Consequently, to solve this issue and to increase the online learning rate of the network parameter, the delta adaptation law is used in the following [1,2].

$${\delta }_o^7\cong (P_{sm}^{}-P_{sout})+({\dot{P}}_{sm}^{}-{\dot{P}}_{sout})=e+\dot{e}$$

(42)

The main objective of the proposed PPWFNN controller is to online train the parameters shown in Equations (31), (36), (40) and (41) for the q-axis current command $I_{sq}^{*}$ of the BESS to achieve the minimum real power error $P_{error}^{}$ and obtain the optimum virtual inertia $J_s^{}$ of the VSG control under load variation. Hence, a suitable virtual inertia of the VSG control can be obtained to suppress the real power output and frequency oscillations of DG under load variation.

3.3. Convergence Analysis

In this study, to effectively train the proposed PPWFNN intelligent controller, the varied learning rates [32,33] are derived. The objective of the convergence analysis is to derive the specific learning rate coefficient for the network parameter that guarantees the convergence of the q-axis current command $I_{sq}^{*}$ of the BESS using VSG control by the analysis of the discrete-type Lyapunov function.

Regarding the error function in Equation (28) as a discrete-type Lyapunov function, the variation of the Lyapunov function is depicted as:

$$\Delta E(N)=E(N+1)-E(N)$$

(43)

Subsequently, the linearized model [33] of the error equation is expressed, via Equations (30), (35), (38) and (39), by

$$\begin{array}{l}E(N+1)=E(N)+\Delta E(N)\\ \approx E(N)+{\displaystyle \sum _{l=1}^9\left[\frac{\partial E(N)}{\partial w_l^7}\Delta w_l^7\right]}+{\displaystyle \sum _{k=1}^9{\displaystyle \sum _{i=1}^2\left[\frac{\partial E(N)}{\partial w_{ik}^5}\Delta w_{ik}^5\right]}}+{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E(N)}{\partial m_{ij}^2}\Delta m_{ij}^2+\frac{\partial E(N)}{\partial {\sigma }_{ij}^2}\Delta {\sigma }_{ij}^2\right]}}\\ =\frac{1}{4}E(N)-{\eta }_1{{\displaystyle \sum _{l=1}^9\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial w_l^7(N)}\right]}}^2\\ +\frac{1}{4}E(N)-{\eta }_2{\displaystyle \sum _{k=1}^9{{\displaystyle \sum _{i=1}^2\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial {\psi }_k^5(N)}\frac{\partial {\psi }_k^5(N)}{\partial w_{ik}^5(N)}\right]}}^2}\\ +\frac{1}{4}E(N)-{\eta }_3{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial m_{ij}^2(N)}\right]}}}^2\\ +\frac{1}{4}E(N)-{\eta }_4{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial {\sigma }_{ij}^2(N)}\right]}}}^2\end{array}$$

(44)

where $\Delta w_l^7$, $\Delta w_{ik}^5$, $\Delta m_{ij}^2$ and $\Delta {\sigma }_{ij}^2$ depict the change of connective weights in the output layer and wavelet layer, and the change in the mean and the standard deviation of the Gaussian function in the membership layer, respectively. If the learning rate parameters of the proposed PPWFNN are designed as:

$${\eta }_1=\frac{E(N)}{4\left[{{\displaystyle \sum _{l=1}^9\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial w_l^7(N)}\right]}}^2+\epsilon \right]}$$

(45)

$${\eta }_2=\frac{E(N)}{4\left[{\displaystyle \sum _{k=1}^9{{\displaystyle \sum _{i=1}^2\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial {\psi }_k^5(N)}\frac{\partial {\psi }_k^5(N)}{\partial w_{ik}^5(N)}\right]}}^2}+\epsilon \right]}$$

(46)

$${\eta }_3=\frac{E(N)}{4\left[{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial m_{ij}^2(N)}\right]}}}^2+\epsilon \right]}$$

(47)

$${\eta }_4=\frac{E(N)}{4\left[{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial {\sigma }_{ij}^2(N)}\right]}}}^2+\epsilon \right]}$$

(48)

where $\epsilon$ is a positive constant, Equation (44) can be redescribed as:

$$\begin{array}{l}E(N+1)\approx \epsilon ({\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4)\\ \approx \frac{E(N)\epsilon }{4\left[{{\displaystyle \sum _{l=1}^9\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial w_l^7(N)}\right]}}^2+\epsilon \right]}\\ +\frac{E(N)\epsilon }{4\left[{\displaystyle \sum _{k=1}^9{{\displaystyle \sum _{i=1}^2\left[\frac{\partial E(N)}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial {\psi }_k^5(N)}\frac{\partial {\psi }_k^5(N)}{\partial w_{ik}^5(N)}\right]}}^2}+\epsilon \right]}\\ +\frac{E(N)\epsilon }{4\left[{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial m_{ij}^2(N)}\right]}}}^2+\epsilon \right]}\\ +\frac{E(N)\epsilon }{4\left[{{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{i=1}^2\left[\frac{\partial E}{\partial y_o^7(N)}\frac{\partial y_o^7(N)}{\partial y_l^6(N)}\frac{\partial y_l^6(N)}{\partial y_{ql}^5(N)}\frac{\partial y_{ql}^5(N)}{\partial y_{pq}^4(N)}\frac{\partial y_{pq}^4(N)}{\partial y_p^3(N)}\frac{\partial y_p^3(N)}{\partial y_j^2(N)}\frac{\partial y_j^2(N)}{\partial ne{t}_j^2(N)}\frac{\partial ne{t}_j^2(N)}{\partial {\sigma }_{ij}^2(N)}\right]}}}^2+\epsilon \right]}\\ <\frac{E(N)}{4}+\frac{E(N)}{4}+\frac{E(N)}{4}+\frac{E(N)}{4}=E(N)\end{array}$$

(49)

In accordance with Equations (28) and (49), the convergence of the proposed PPWFNN control can be guaranteed. Thereupon, the intelligent control of the q-axis current of the BESS using VSG for real power control will gradually converge to the real power command.

4. Experimental Results

To verify the effectiveness of the proposed virtual inertia estimator and the online-trained PPWFNN controller for the suitable virtual inertia of the VSG control under load variation, a BESS using VSG control was designed and implemented using the digital signal processor (DSP) control platform. The designed BESS using VSG control was operated in islanding mode. Moreover, the block diagram and photo of the BESS are presented in Figure 4a,b, respectively. In Figure 4a, the three-phase output voltages $v_a,\hspace{0.17em}{v}_b,\hspace{0.17em}{v}_c$ and output currents $i_{oa},\hspace{0.17em}{i}_{ob},\hspace{0.17em}{i}_{oc}$ of the BESS are detected and sent to the peripheral circuit for the control algorithms, including the power calculation, PLL, VSG, the proposed virtual inertia estimator, and the PPWFNN controller. The control algorithms of the BESS are implemented by the DSP TMS320F28335 with a sampling time of 1 ms. A switching frequency of 16 kHz was adopted in the control platform. In addition, the droop coefficients $K_{s\omega }^{}$ and $K_{sv}^{}$ were set to be 500 W/(rad/s) and 20 Var/V, respectively. The virtual damping factor $D$ was set to be 0.01. The parameters of the PI controller for the q-axis current command $I_{sq}^{*}$ were obtained by trial and error to achieve superior control performance. The resulting parameters were $K_P=1.5, K_I=0.01$.

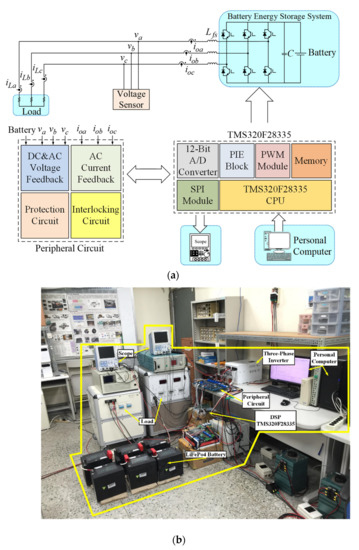
Figure 4. BESS using VSG control. (a) Block diagram of DSP-based BESS; (b) photo of experimental setup.

Owing to the unsuitable virtual inertia of the VSG control, the real power output and frequency oscillations of the BESS occurring under load variation resulted in deterioration of the control performance of the BESS. Consequently, to prove the effectiveness of the BESS using the proposed virtual inertia estimator and PPWFNN controller, two test cases were designed for the experiment, as follows: (1) Case 1: BESS using VSG control with different values of moment of virtual inertia under load variation; and (2) Case 2: BESS using the proposed virtual inertia estimator under load variation. Moreover, in order to compare the control performance of the proposed PPWFNN controller, the experimental results obtained using PI and FNN controllers for the control of the q-axis current command $I_{sq}^{*}$ with the proposed virtual inertia estimator in case 2 are demonstrated in this study.

In case 1, the characteristics and performance of the BESS using VSG control with different values of moment of virtual inertia $J_s^{}$ under load variation were demonstrated. In this scenario, different values of virtual inertia of $J_s^{}$= 0 ${\mathrm{kgm}}^2$, 0.002713 ${\mathrm{kgm}}^2$, 0.00407 ${\mathrm{kgm}}^2$ and 0.0407 ${\mathrm{kgm}}^2$ were adopted. The load was changed from 1 kW to 2 kW at 0.5 s. The experimental results of the BESS using VSG control with $J_s^{}$= 0 ${\mathrm{kgm}}^2$ are illustrated in Figure 5a–c. The responses of the real power output $P_{sout}^{}$ and the reactive power output $Q_{sout}^{}$ of the BESS are shown in Figure 5a. The responses of the line-to-line voltage $v_{ab}^{}$ and the output current $i_{oa}$ of the BESS are shown in Figure 5b. The response of the virtual rotor frequency $f_{sm}^{}$ of VSG control is provided in Figure 5c. According to the experimental results, shown in Figure 5a–c, since the virtual inertia $J_s^{}$= 0 ${\mathrm{kgm}}^2$ was adopted in the VSG control of the BESS, the characteristics of the BESS using VSG control were similar to the BESS using droop control under load variation [6]. Hence, the real power output $P_{sout}^{}$, output current $i_{oa}$, and virtual rotor frequency $f_{sm}^{}$ respond rapidly. Moreover, the experimental results of the BESS using VSG control with $J_s^{}$ = 0.002713 ${\mathrm{kgm}}^2$ are provided in Figure 6a–c. The responses of the real power output $P_{sout}^{}$ and the reactive power output $Q_{sout}^{}$ of the BESS are shown in Figure 6a. The responses of the line-to-line voltage $v_{ab}^{}$ and the output current $i_{oa}$ of the BESS are shown in Figure 6b. The responses of the virtual rotor frequency $f_{sm}^{}$ of the VSG control and the virtual inertia $J_s^{}$ are provided in Figure 6c. From the experimental results as shown in Figure 6, although a virtual inertia of $J_s^{}$ = 0.002713 ${\mathrm{kgm}}^2$ was adopted in the VSG control, the oscillation phenomena of the real power output $P_{sout}^{}$, output current $i_{oa}$, and virtual rotor frequency $f_{sm}^{}$ seriously deteriorate the control performance of the BESS under load variation owing to the low moment of virtual inertia [15]. Furthermore, the experimental results of the BESS using VSG control with $J_s^{}$ = 0.00407 ${\mathrm{kgm}}^2$ and $J_s^{}$ = 0.0407 ${\mathrm{kgm}}^2$ are represented in Figure 7 and Figure 8, respectively. In accordance with the experimental results shown in Figure 7 and Figure 8, the larger the moment of virtual inertia $J_s^{}$, the more sluggish the response of the oscillations of real power output $P_{sout}^{}$, output current $i_{oa}$, and virtual rotor frequency $f_{sm}^{}$. Therefore, from the experimental results shown in Figure 5, Figure 6, Figure 7 and Figure 8, when the amount of virtual inertia in the VSG is unsuitable, oscillations in the real power output and frequency of the BESS will occur under load variation.

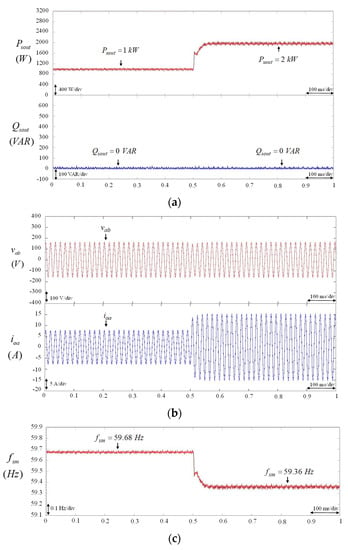
Figure 5. BESS using VSG control with constant virtual inertia $J_s^{}$ = 0 ${\mathrm{kgm}}^2$. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) response of virtual rotor frequency $f_{sm}^{}$ of VSG control.

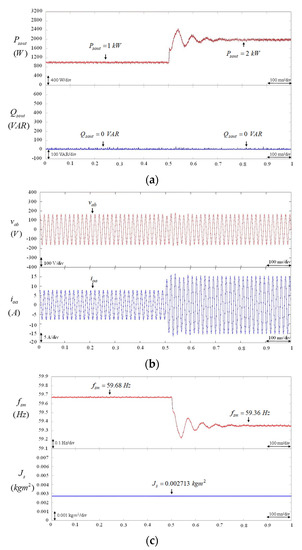
Figure 6. BESS using VSG control with constant virtual inertia $J_s^{}$ = 0.002713 ${\mathrm{kgm}}^2$. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS. (b) Responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS. (c) Responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and virtual inertia $J_s^{}$.

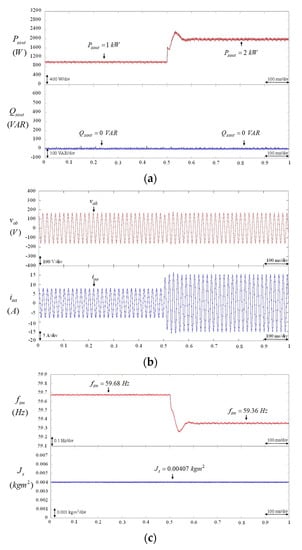
Figure 7. BESS using VSG control with constant virtual inertia $J_s^{}$ = 0.00407 ${\mathrm{kgm}}^2$. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) Responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) Responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and virtual inertia $J_s^{}$.

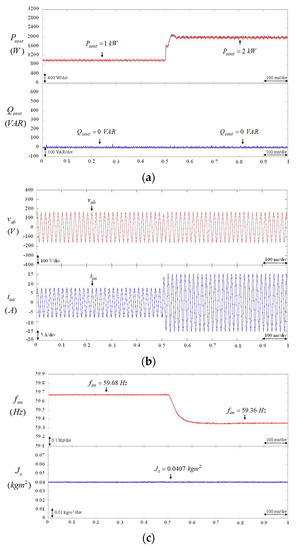
Figure 8. BESS using VSG control with constant virtual inertia $J_s^{}$ = 0.0407 ${\mathrm{kgm}}^2$. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) Responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) Responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and virtual inertia $J_s^{}$.

To overcome the above drawback and to suppress the real power output and frequency oscillations of the BESS using VSG control under load variation, the experimental results of the BESS using the proposed virtual inertia estimator with the PI, FNN, and the proposed PPWFNN controllers, respectively, for the control of the q-axis current command $I_{sq}^{*}$ were tested in case 2. In this case, the load was changed from 0.25 kW to 2 kW and then changed to 1 kW. First, the experimental results of the PI-controlled BESS using the proposed virtual inertia estimator are provided in Figure 9. The responses of the real power output $P_{sout}^{}$ and the reactive power output $Q_{sout}^{}$ of the BESS are shown in Figure 9a. The responses of the line-to-line voltage $v_{ab}^{}$ and the output current $i_{oa}$ of the BESS are presented in Figure 9b. The responses of the virtual rotor frequency $f_{sm}^{}$ of the VSG control and the estimated virtual inertia $J_s^{}$ are provided in Figure 9c. From the experimental results, when the load changes at 1.5 s and 3.5 s, the proposed virtual inertia estimator can effectively estimate the virtual inertia $J_s^{}$, as shown in Figure 9c. Although the oscillation phenomena of the real power output $P_{sout}^{}$, output current $i_{oa}$, and virtual rotor frequency $f_{sm}^{}$ of the BESS using VSG control can be reduced, as shown in Figure 9a–c, the deteriorated transient responses of the power output $P_{sout}^{}$ and frequency $f_{sm}^{}$ are still obvious at 1.5 s and 3.5 s owing to the poor robustness of the control property of the PI controller. Then, the experimental results of the FNN-controlled BESS using the proposed virtual inertia estimator are provided in Figure 10. The responses of the real power output $P_{sout}^{}$ and the reactive power output $Q_{sout}^{}$ of the BESS are illustrated in Figure 10a. The responses of the line-to-line voltage $v_{ab}^{}$ and the output current $i_{oa}$ of the BESS are presented in Figure 10b. The responses of the virtual rotor frequency $f_{sm}^{}$ of VSG control and the estimated virtual inertia $J_s^{}$ are shown in Figure 10c. According to the experimental results of the FNN-controlled BESS, the proposed virtual inertia estimator can effectively estimate the suitable virtual inertia $J_s^{}$, as shown in Figure 10c under load variation. Moreover, as a result of estimating a suitable value of virtual inertia $J_s^{}$, the transient responses of the real power output $P_{sout}^{}$, the output current $i_{oa}$, and the frequency $f_{sm}^{}$ of the BESS using VSG control can be improved at 1.5 s and 3.5 s, as shown in Figure 10b,c. In addition, the experimental results of the proposed PPWFNN-controlled BESS using the proposed virtual inertia estimator are given in Figure 11. The responses of the real power output $P_{sout}^{}$ and the reactive power output $Q_{sout}^{}$ of the BESS are presented in Figure 11a. The responses of the line-to-line voltage $v_{ab}^{}$ and the output current $i_{oa}$ of the BESS are provided in Figure 11b. The responses of the virtual rotor frequency $f_{sm}^{}$ of VSG control and the estimated virtual inertia $J_s^{}$ are shown in Figure 11c. Since the proposed PPWFNN controller incorporates the merits of WFNN, PNN and PN, compared to the experimental results using PI- and FNN-controlled BESSs, the proposed PPWFNN-controlled BESS with the virtual inertia estimator can provide more effective estimation of the virtual inertia $J_s^{}$ under load variation. Furthermore, the oscillation phenomena of the real power output $P_{sout}^{}$, output current $i_{oa}$, and virtual rotor frequency $f_{sm}^{}$ of the proposed PPWFNN-controlled BESS using VSG control were much reduced at 1.5 s and 3.5 s, as shown in Figure 11a–c. In addition, the maximum real power and frequency error of PI-, FNN-, and the proposed PPWFNN-controlled BESSs using the proposed virtual inertia estimator under different load variation conditions are provided in Table 1. According to the experimental results and Table 1, the transient responses of the power output $P_{sout}^{}$ and the virtual rotor frequency $f_{sm}^{}$ of the proposed PPWFNN-controlled BESS are superior to the PI- and FNN-controlled BESSs owing to the powerful control ability of the proposed PPWFNN controller. Therefore, the feasibility and the effectiveness of the proposed virtual inertia estimator with the PPWFNN controller for VSG control are confirmed.

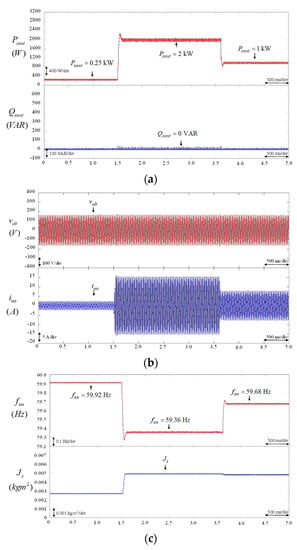
Figure 9. PI-controlled BESS using proposed virtual inertia estimator. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) Responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) Responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and estimated virtual inertia $J_s^{}$.

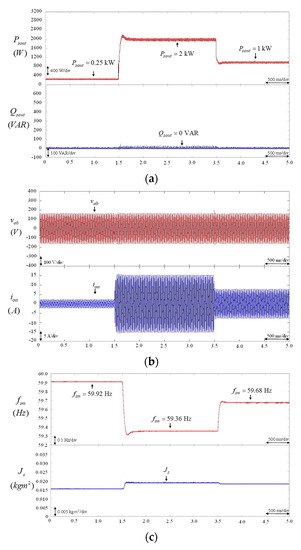
Figure 10. FNN-controlled BESS using proposed virtual inertia estimator. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and estimated virtual inertia $J_s^{}$.

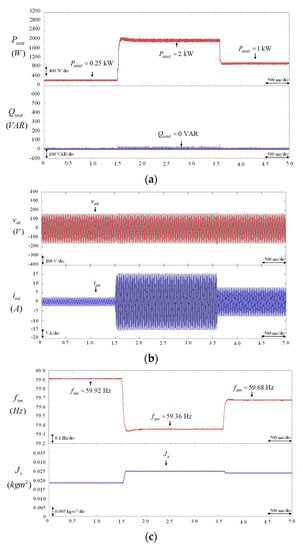
Figure 11. PPWFNN-controlled BESS using proposed virtual inertia estimator. (a) Responses of real power output $P_{sout}^{}$ and reactive power output $Q_{sout}^{}$ of BESS; (b) responses of line-to-line voltage $v_{ab}^{}$ and output current $i_{oa}$ of BESS; (c) responses of virtual rotor frequency $f_{sm}^{}$ of VSG control and estimated virtual inertia $J_s^{}$.

Table 1. Maximum real power error and frequency error of PI-, FNN- and proposed PPWFNN-controlled BESSs using proposed virtual inertia estimator under load variation.

Test Condition	Controller	Active Power Error		Frequency Error
		0.25 kW→2 kW	2 kW→1 kW	0.25 kW→2 kW	2 kW→1 kW
Case 2	PI	320 W	187 W	0.073 Hz	0.027 Hz
	FNN	186 W	74 W	0.044 Hz	0.016 Hz
	PPWFNN	106 W	44 W	0.022 Hz	0.007 Hz

In this study, the compute or training time of the “C” program in the TMS320F28335 32-bit floating-point DSP with 150 MHz can be obtained by the clock tool of Texas Instruments (TI) Code Composer Studio (CCS) v6 program editing interface. The total operation cycles and total execution time of the PI-, FNN- and the proposed PPWFNN-controlled BESSs are compared in Table 2. The total operation cycles and total execution time for the proposed PPWFNN are 8700 cycles and 58 us, respectively. In consequence, the total execution time of BESS using the proposed PPWFNN controller is still less than 1 ms, which is the sampling interval of the control loop.

Table 2. Compute time of PI-, FNN- and proposed PPWFNN-controlled BESSs.

Controller	Total Operation Cycles	Execution Time
PI	173	1.153 us
FNN	2477	16.513 us
PPWFNN	8700	58 us

5. Conclusions

Since the amount of virtual inertia of the VSG control is usually constant and given by trial and error, the real power output and frequency oscillations of BESS using VSG control usually occur under abrupt disturbances owing to unsuitable virtual inertia. In this study, to overcome this problem, a virtual inertia estimation methodology was successfully developed and implemented to estimate a suitable virtual inertia for VSG control and to suppress the real power output and frequency oscillations of the BESS under load variation. Moreover, in order to improve the performance of the proposed virtual inertia estimator and the transient response of the real power output and frequency of the BESS, an online-trained PPWFNN controller was proposed to replace the conventional PI controller for the regulation of the q-axis current command $I_{sq}^{*}$. Furthermore, the feasibility and the effectiveness of the BESS using the proposed virtual inertia estimator and PPWFNN controller were verified by experimental results. According to the experimental results, the proposed PPWFNN-controlled BESS with the virtual inertia estimator was able to effectively estimate suitable virtual inertia under various load variation conditions. Thus, the transient responses of the power output and frequency of the proposed PPWFNN-controlled BESS were better than the PI- and FNN-controlled BESSs owing to the powerful control capability of the proposed PPWFNN.

The major contributions of this study are: (i) the successful development of a virtual inertia estimator for VSG control; (ii) the successful development of the proposed online-trained PPWFNN controller; (iii) the successful implementation of a BESS using the proposed virtual inertia estimator and PPWFNN controller for the inertia estimator of the VSG control under load variation.