Optimization of Antireflection Coating Design Using PC1D Simulation for c − Si Solar Cell Application

Abstract

Minimizing the photon losses by depositing an anti-reflection layer can increase the conversion efficiency of the solar cells. In this paper, the impact of anti-reflection coating $\left(ARC\right)$ for enhancing the efficiency of silicon solar cells is presented. Initially, the refractive indices and reflectance of various $ARC$ materials were computed numerically using the $OPAL2$ calculator. After which, the reflectance of ${\mathrm{SiO}}_2,{\mathrm{TiO}}_2,{\mathrm{SiN}}_x$ with different refractive indices $\left(n\right)$ were used for analyzing the performance of a silicon solar cells coated with these materials using $PC1D$ simulator. ${SiN}_x$ and ${\mathrm{TiO}}_2$ as single-layer anti-reflection coating $\left(SLARC\right)$ yielded a short circuit current density ($J_{sc}$) of $38.4$ $\mathrm{mA}/{\mathrm{cm}}^2$ and $38.09\mathrm{mA}/{\mathrm{cm}}^2$ respectively. Highest efficiency of $20.7\%$ was obtained for the ${SiN}_x$ ARC layer with $n=2.15$. With Double-layer anti-reflection coating $\left(DLARC\right)$, the $J_{sc}$ improved by ∼0.5 $\mathrm{mA}/{\mathrm{cm}}^2$ for ${\mathrm{SiO}}_2/{\mathrm{SiN}}_x$ layer and hence the efficiency by $0.3\%$. Blue loss reduces significantly for the $DLARC$ compared with $SLARC$ and hence increase in $J_{sc}$ by 1 $\mathrm{mA}/{\mathrm{cm}}^2$ is observed. The $J_{sc}$ values obtained is in good agreement with the reflectance values of the $ARC$ layers. The solar cell with $DLARC$ obtained from the study showed that improved conversion efficiency of $21.1\%$ is obtained. Finally, it is essential to understand that the key parameters identified in this simulation study concerning the $DLARC$ fabrication will make experimental validation faster and cheaper.

1. Introduction

With the substantial technological advancements, the potential for high conversion efficiency of crystalline silicon $(c-Si)$ solar cells. Photovoltaic $\left(PV\right)$ market dominated by crystalline silicon $(c-Si)$ solar cells [1] by larger than $90\%$ worldwide. The efficiency of $24.4\%$ has been reached with $c-Si$ based modules and is continuously escalating both in the research and in the commercial market. Theoretically, the bandgap, long radiative recombination lifetimes, Auger recombination of the generated carriers restrict the conversion efficiency to about $29\%$ [2,3,4]. It is mandatory to reduce the various losses (optical, carrier, and electrical loss) in $c-Si$ solar cell to achieve the maximum conversion efficiency [5]. One of the key issues of the contemporary PV industry is reducing the optical losses which make up about $4\%$ efficiency loss in $c-Si$ solar cells [6]. An approach to reduce the optical loss is to use an ARC at the front surface, which reduces the reflection losses and enhances the $J_{sc}$ consequently, improving the conversion efficiency. Several researchers employed various ARCs that might be used to increase the efficiency of the solar cell. Thin films such as ${\mathrm{TiO}}_2,{\mathrm{SiO}}_2,{\mathrm{SiN}}_x$, ${\mathrm{Al}}_2{\mathrm{O}}_3$ etc., were used as $ARC$ layers [7,8,9,10,11]. ${\mathrm{TiO}}_2$ was a commonly used $ARC$ on the front surface, owing to its versatility and inexpensive [7]. Though ${\mathrm{TiO}}_2$ coatings possess better optical properties (high refractive index, low absorption coefficient) in the visible region, the passivation properties in addition to the optical properties made the $PV$ manufacturers shift to plasma-enhanced chemical vapour deposited $\left(PECVD\right)$ ${\mathrm{SiN}}_x$. In the recent study by various researchers, ${\mathrm{TiO}}_2$ films demonstrated the potential of delivering the exceptional passivation on boron-doped $\left(p^{+}\right)$ emitters [12,13,14]. ${\mathrm{TiO}}_2$ is the ideal $ARC$ material for the encapsulated cell as its $n=\sim$2.1 at the wavelength of $630\mathrm{nm}$. In the earlier days of solar cell fabrication, ${\mathrm{TiO}}_2$ was considered only for $ARC$ purposes. Later researchers found that ${\mathrm{SiO}}_2$/${\mathrm{SiN}}_x$ layers provided both surface passivation as well as $ARC$ layers. Hence the solar cell industry utilizes the ${\mathrm{SiO}}_2$/${\mathrm{SiN}}_x$ layers. However recent research found the passivation properties especially provided better surface passivation with $p^{+}$ surfaces. However, the change in its crystalline phase at higher temperatures hinders the application of ${\mathrm{TiO}}_2$ in conventional commercial solar cells fabrication, which requires high-temperature metallisation firing. Hence it might be considered. Thus, optimizing the ${\mathrm{TiO}}_2$ film with a trade-off between optical and passivation properties will be valuable for the $PV$ industry.

However, the single-layer $ARC$s $\left(SLARC\right)$ employed in silicon solar cells still instigate substantial optical reflectance loss in a wide-ranging of the solar spectrum. Thus, high-efficiency solar cells utilize double-layer ARCs $\left(DLARC\right)$ which improves the carrier collection by reducing the reflectance in the visible and in the near-IR range [15,16,17,18]. The $DLARC$ (${\mathrm{SiO}}_2/{\mathrm{TiO}}_2$ or ${\mathrm{SiO}}_2$) is a favorable design to enhance the efficiency owing to its benefits in both antireflection and surface passivation properties. Doshi et.al. optimized the $ARC$ film thickness and their refractive indices and utilized the ${\mathrm{SiO}}_2$/${\mathrm{SiN}}_x$ $DLARC$ for their simulation [15]. With ${\mathrm{SiO}}_2$/${\mathrm{SiN}}_x$ $DLARC$ layer, Lennie et al. obtained an efficiency of $4.56\%$ [16] using Silvaco ATLAS simulation. Similar work with $PC1D$ simulation can be found elsewhere [17,18,19]. $PC1D$ is the most commercially accessible software utilized by several groups to simulate solar cells with unique $ARC$ layers [20]. In most of the $ARC$ simulation studies, the maximum conversion efficiency of 3–13% only has been achieved [16,17,18,19].

In the present study, we employed the $SLARC$ and $DLARC$ on the actual industrial solar cell with a surface area of $244.32$ ${\mathrm{cm}}^2$. Similarly, we analyzed the $ARC$ loss for each $ARC$ layer, to find the most optimum $ARC$ specification that can be employed for solar cell application. For $DLARC$, varying the thickness of the ${\mathrm{SiO}}_2$ and its capping layer was one of the most novel concepts explored in this manuscript. This simulation-based approach highlighted in this manuscript plays a vital role in identifying the most optimal configuration of the $ARC$ layers for achieving increased efficiency of silicon solar cells. The simulation approach highly reduces the time and cost involved in testing the different combinations of $DLARC$ layers and helps in identifying the optimal configuration of the $ARC$ layers. ${\mathrm{SiN}}_x$ with different refractive indices were chosen as a capping layer when experimentally testing the $DLARC$ layer. Mono-crystalline silicon solar cells were simulated using $PC1D$. The simulated device results were validated by comparing the solar cell fabricated with identical device parameters. This study offers a better insight into solar cell performance.

2. Simulation of $c-Si$ Solar Cell

To simulate the $c-Si$ solar cell behaviour $PC1D$ software package is used in this study. The mathematical modelling tool used a more detailed silicon solar cell model as shown in Figure 1. To increase the conversion accuracy of solar cells we need an accurate solar cell modelling tool. After studying each layer’s physical and electrical parameters of the $c-Si$ solar cell the $PC1D$ tool helps in studying the impact of various parameters considered in the fabrication of the solar cells. In this study, the actual device configuration for simulating and optimizing the anti-reflection coating $\left(ARC\right)$ layer of solar cell is evaluated using $PC1D$ simulation and the optimized configuration for achieving higher accuracy is obtained. Using numerical modelling tools such as $PC1D$ to optimize the $ARC$ layer configurations reduces the cost, time, and effort required to analyze the impact of the change in the design of the solar cells.

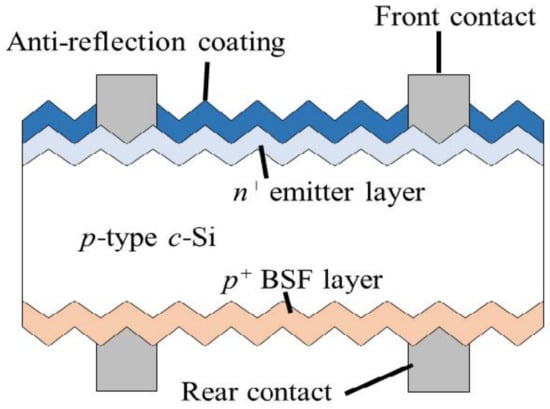
Figure 1. Silicon solar cell structure used for this study.

In the $PC1D$ simulation tool, crystalline Si ($c-Si$) solar cell device simulations are carried out using the following numerical equations representing the quasi-one-dimensional transportation of electrons and holes of a semiconductor material (Solar cells). Equations (1)–(7) gives us a clear cut idea of creating a model of a silicon cell and optimizing various process parameters including the $ARC$ coating layer properties [21].

$$\begin{array}{c}\hfill J_n={\mu }_n·n·▽E_{Fn}\end{array}$$

(1)

$$\begin{array}{c}\hfill J_p={\mu }_p·p·▽E_{Fp}\end{array}$$

(2)

The current densities of the electrons and the holes are represented as $J_n$ and $J_p$ respectively and they are numerically formulated as indicated in Equations (1) and (2). In which, the parameters n and p are the electron and hole density, ${\mu }_n$ and ${\mu }_p$ is the mobility of the electron and holes. The $▽E_{Fn}$ and $▽E_{Fp}$ are the diffusion coefficients that represents the difference in electron and hole quasi-Fermi energies $E_{Fn}$ and $E_{Fp}$.

$$\begin{array}{c}\hfill \frac{\partial n}{\partial t}=\frac{▽·J_n}{q}+G_L-U_n\end{array}$$

(3)

$$\begin{array}{c}\hfill \frac{\partial p}{\partial t}=\frac{▽·J_p}{q}+G_L-U_p\end{array}$$

(4)

$$\begin{array}{c}\hfill {\Delta }^2\varphi =\frac{q}{ϵ}\left(n-p+N_{acc}^{-}-N_{don}^{+}\right)\end{array}$$

(5)

Equations (3) and (4) are derived from the law of conservation of charge or the continuity equation. where $G_L$ and $U_n$ are generation rate and recombination rate. Equation (5) represents Poisson’s equation for solving the electrostatic field problems. where $N_{acc}^{-}$ and $N_{don}^{+}$ are acceptor and donor doping concentrations.

$$\begin{array}{c}\hfill n=N_C{F}_{1/2}\left(\frac{q\psi +V_n-q{\varphi }_{n,i}+ln\left(n_{i,0}/N_C\right)}{k_{B}T}\right)\end{array}$$

(6)

$$\begin{array}{c}\hfill p=N_V{F}_{1/2}\left(\frac{-q\psi +V_p-q{\varphi }_{p,i}+ln\left(n_{i,0}/N_V\right)}{k_{B}T}\right)\end{array}$$

(7)

Here $N_c$ and $N_v$ are the effective density of states in the conduction and valence bands. To describe the type of material used, Fermi-Dirac statistics directly related to the band edges and $N_c$ and $N_v$ carrier densities are expressed in the Equations (7) and (8). The finite element approach is used to solve the three basic equations that assist in simulating the solar cell behaviours using the $PC1D$ modelling tool. Many other process parameters are optimized using the $PC1D$ simulation tool in the literature, but the proposed research aims to optimise the design process characteristics of the $ARC$ layer used in the fabrication of the $c-Si$ solar cells. Finally, the efficiency of $c-Si$ solar cells is calculated using the following equations.

$$\eta =\frac{P_{max}}{I_{\mathrm{in}}}=\frac{J_{\mathrm{mpp}}{V}_{\mathrm{mpp}}}{I_{\mathrm{in}}}=\frac{J_{\mathrm{SC}}{V}_{\mathrm{OC}}FF}{I_{\mathrm{in}}}$$

(8)

where, $\eta$ represents the efficiency of the solar cell which is calculated using $P_{max}$, $I_{\mathrm{in}}$, $J_{\mathrm{mpp}}$, $V_{\mathrm{mpp}}$, $J_{\mathrm{SC}}$, $V_{\mathrm{OC}}$ and $FF$ that indicates the maximum power, incident power, current at maximum power point, voltage at maximum power point, saturation current density, Open circuit voltage and fill factor.

In this present study, we have considered p-type wafer with resistivity of 1 $\mathsf{\Omega }-\mathrm{cm}$ (doping of $\left.1.5\times {10}^{16}{\mathrm{cm}}^3\right)$, device area of $244.32{\mathrm{cm}}^2$, front surface textured with 3 $\mathsf{\mu }\mathrm{m}$ depth. The $n^{+}$ emitter and $p^{+}$ back surface field was formed with doping concentration of $1\times {10}^{20}{\mathrm{cm}}^{-3}$ and $3\times {10}^{18}{\mathrm{cm}}^{-3}$ respectively. Bulk lifetime of 100 $\mathsf{\mu }\mathrm{s}$ and front and rear surface recombination velocity of 10,000 $\mathrm{cm}/\mathrm{s}$ were considered for solar cell simulation by PC1D. Numerous simulations were performed to study the impact of different parameters on the solar cell device performance. Base resistance $(0.015$ $\mathsf{\Omega })$, internal conductance $(0.3$ S), light intensity (0.1 $\left.\mathrm{W}/{\mathrm{cm}}^2\right)$ were kept constant during simulation. $AM1.5G$ spectrum was used in this modelling.

3. Results and Discussion

The refractive index as a function of wavelength defines the characteristics of an $ARC$ layer [22]. Figure 2 shows the wavelength dependent refractive indices of the $ARC$ layers such as ${\mathrm{TiO}}_2$ [14], ${\mathrm{MgF}}_2$ [23], ${\mathrm{SiO}}_2$ [24], ${SiN}_x$ [9] thin films determined using the spectroscopic ellipsometer. The inset of Figure 2 shows the refractive index corresponding to each $ARC$ layer. The refractive index values of the ${\mathrm{TiO}}_2,{\mathrm{MgF}}_2,{\mathrm{SiO}}_2,{SiN}_x-A,B$ and C at $600\mathrm{nm}$ were about $2.28$$2.34,1.36,1.46,1.99,2.15$, and $2.17$ respectively.

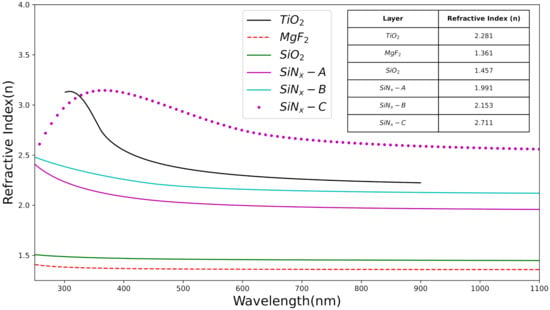
Figure 2. Refractive indices of various $ARC$ layers.

Reflectance spectra as a function of wavelength feed significant insights that can be used for investigating the optical properties of the $ARC$, textured surface, and internal reflectance at the rear surface of the solar cell device. An optimal $ARC$ film for $c-Si$ solar cells should possess (i) low optical losses and (ii) provide good surface passivation. Reflectance spectra exhibit characteristic minima that are defined by the following equation:

$$t=\frac{{\lambda }_0}{4n}$$

(9)

where t represents the thickness of the $ARC$, ${\lambda }_0$ represents the characteristic minimum wavelength, and n represents the index of refraction. For each $ARC$ layer with a different refractive index, the thickness of the $ARC$ layer was varied from 70–100 $\mathrm{nm}$ to keep the optical thickness of the film constant. Figure 3 shows the measured reflectance of the different $ARC$ layers coated on the textured surface. These reflectance values were measured using $OPAL2$ software. The $OPAL2$ simulator was also used to optimise the layer thickness of the single/double-layer $ARC$ coatings. The reflectance values were measured at the wavelength of $630\mathrm{nm}$. The reflectance of $ARC$ layers such as ${\mathrm{TiO}}_2, {\mathrm{MgF}}_2, {\mathrm{SiO}}_2, {SiN}_x-A, {SiN}_x-B$ and ${\mathrm{SiN}}_x-C$ are $0.29\%,0.46\%,4.18\%,0.88\%,0.045\%$, $0.08\%$ and $1.55\%$ respectively. Overall, the lowest reflectance value is for ${Sin}_{x-A}(n=1.99)$ and ${Sin}_x-B(n=2.15)$ $ARC$ layer, closely followed by ${\mathrm{TiO}}_2(n=1.99)$. Similar behaviour is observed in the case of saturation current density $\left(J_{sc}\right)$. Table 1 represents the $I-V$ parameters as well as the calculated blue loss and $ARC$ loss with different $SLARC$ layers $J_{sc}$ of $38.37$ $\mathrm{mA}/{\mathrm{cm}}^2, 38.4\mathrm{mA}/{\mathrm{cm}}^2$ was obtained for ${SiN}_x-A(n=1.99)$ and ${SiN}_x-B(n=2.15)$ $ARC$ layer and $38.16\mathrm{mA}/{\mathrm{cm}}^2$ and $38.09\mathrm{mA}/{\mathrm{cm}}^2$ for ${\mathrm{TiO}}_2(n=1.99)$ respectively. The $J_{sc}$ values obtained is in good agreement with the reflectance values of the $ARC$ layers. Highest efficiency of $20.7\%$ was obtained for the ${SiN}_x$ $ARC$ layer with $n=1.99$ and $2.15$. Current is one of the easiest factor that can be improved with substantial margin. Thus it is significant to enumerate systematically the source of $J_{sc}$ loss, breaking them into (i) optical losses and (ii) collection losses. The optical loss is due to metal shading, reflection and parasitic absorption and the collection losses arises due to imperfect emitter collection. By investigating the losses, it gives a clear representation of possible improvement areas which helps the PV manufacturers to predict and plan the strategies on the cell and module level fabrication for the future. Despite the well-known fact that the Mg-based $ARC$ material is considered as the highly impactful material its associated drawback in terms of the $J_{\mathrm{SC}}$ loss was highlighted and alternative materials $J_{\mathrm{SC}}$ loss was evaluated and a detailed overview of the results was presented in Table 2.

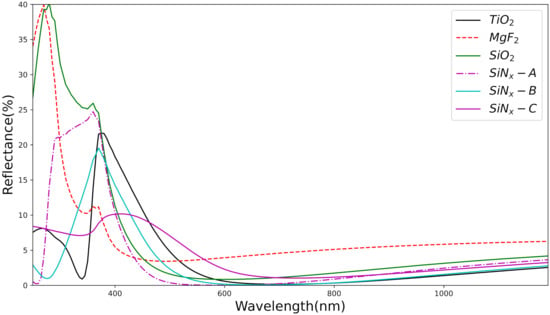
Figure 3. Reflectance spectra as a function of wavelength for some optimised single-layer anti-reflection coating.

Table 1. $I-V$ parameters and ARC loss calculation based on the different SLARC layers.

$\mathit{ARC}$ Layer	${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)	${\mathit{V}}_{\mathit{oc}}$ (mV)	$\mathit{FF}$ $(\%)$	Eff (%)	Blue Loss (%)	ARC Loss [%]	Unshaded ${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)
${\mathrm{TiO}}_2$	38.16	654.2	82.42	20.58	0.17	1.74	39.35
${\mathrm{MgF}}_2$	37.27	653.5	82.45	20.08	0.17	1.81	39.29
${\mathrm{SiO}}_2$	38.0	653.9	82.43	20.48	0.17	1.34	39.75
${SiN}_x-A$	38.37	654.1	82.42	20.69	0.17	0.90	40.18
${SiN}_x-B$	38.4	654.3	82.42	20.71	0.17	1.25	39.83
${SiN}_x-C$	37.79	653.7	82.43	20.37	0.17	1.95	39.13

Table 2. $I-V$ parameters of the different $DLARC$ layers.

$\mathit{ARC}$ Layer	${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)	${\mathit{V}}_{\mathit{oc}}$ (mV)	$\mathit{FF}$ $(\%)$	Eff (%)	Blue Loss (%)	ARC Loss [%]	Unshaded ${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)
${\mathrm{SiO}}_2-{\mathrm{TiO}}_2$	30.84	648.6	82.59	16.52	0.13	10.39	30.83
${\mathrm{SiO}}_2-{\mathrm{MgF}}_2$	37.75	653.9	82.43	20.35	0.13	2.52	38.65
${\mathrm{SiO}}_2-{SiN}_x-A$	33.16	650.5	82.54	17.8	0.13	8.70	32.50
${\mathrm{SiO}}_2-{SiN}_x-B$	31.87	649.4	82.57	17.09	0.13	9.48	31.72
${\mathrm{SiO}}_2-{SiN}_x-C$	29.48	647.4	82.61	15.76	0.13	8.91	32.30

To explain the variation in the $J_{sc}$ with different $ARC$ layers, the ARC loss was calculated by considering the $AM1.5G$ photon flux spectrum [25] and internal quantum efficiency of the solar cell.

$$J_{sc}=q\int I_{AM1.5}\left(\lambda \right)[1-R\left(\lambda \right)]·IQE\left(\lambda \right)d\lambda$$

(10)

where q is the elementary charge, lam $1.5\left(\lambda \right)$ denotes the photon flux of the standard air mass solar spectrum between 300 to $1100\mathrm{nm},\mathrm{R}\left(\lambda \right)$ is the reflectance and $\mathrm{IQE}\left(\lambda \right)$ is the internal quantum efficiency as a function of wavelength.

Reflection loss lead to a reduction of $2\mathrm{mA}/{\mathrm{cm}}^2$ in $J_{sc}$ for ${\mathrm{TiO}}_2,{\mathrm{MgF}}_2$ layers, $1.5\mathrm{mA}/{\mathrm{cm}}^2$ for thermal ${\mathrm{SiO}}_2,1.07,1.42$ and $2.12\mathrm{mA}/{\mathrm{cm}}^2$ for ${SiN}_x$ layers with different refractive indices, thus decreasing the efficiency with respective ARC layers. The front metal coverage is not considered while calculating the $J_{sc}$ values and hence, the variation. By considering the metal coverage area (4–7%), the calculated unshaded $J_{sc}$ values is in good agreement with the measured $J_{sc}$.

This $ARC$ loss may be reduced by tuning the $ARC$ optical properties (e.g., refraction index and thickness), as well as through improved front surface texturing for better light-trapping. In general, the optical properties of the $ARC$ materials are modified by replacing them with an alternate material to be used as the $ARC$ material. One other alternate way of reducing the $ARC$ loss is by optimizing the refractive indices of the $ARC$ layer. In this study, ${\mathrm{SiN}}_x$ layers have been used with different refractive indices from n = 1.99; 2.15 and 2.711 to analyse the impact of the material used as the $ARC$ in the manuscript. From Table 1 it is inferred that the $ARC$ loss was higher for the ${\mathrm{SiN}}_x$ layers with the highest refractive indices, and it reduces significantly with a reduction in the refractive indices. The blue loss is the combined effect of $ARC$ absorption, imperfect emitter collection, and front surface recombination. $ARC$-related blue loss may be reduced to a certain extent by tuning the $ARC$ optical properties. Optimizing the emitter doping profile and junction depth can also help reduce emitter recombination losses. Front surface recombination can be reduced by improved front surface passivation.

For further reduction in the reflectance, we considered the $DLARC$. Figure 4 depicts the reflectance spectra of various $DLARC$ layers. The ${\mathrm{SiO}}_2$ layer was capped with ${\mathrm{MgF}}_2,{\mathrm{TiO}}_2$ and ${\mathrm{SiN}}_x$ layers. The thickness of the ${\mathrm{SiO}}_2$ layer and the capping layers were fixed as $100\mathrm{nm}$ and $80\mathrm{nm}$ respectively. The reflectance was higher for all the $DLARC$ layers and hence poor $J_{sc}$ values which are depicted in Table 2. The high reflectance values for all the $DLARC$ layers are attributed to the unequal optical thickness of the $DLARC$ layer. The necessary and sufficient refractive index condition for a $DLARC$ with equal optical thickness to give zero reflectance is [26]:

$$\frac{n_1}{n_2}=\sqrt{\frac{n_0}{n_s}}$$

(11)

where $n_0$ is the admittance of the surrounding medium.

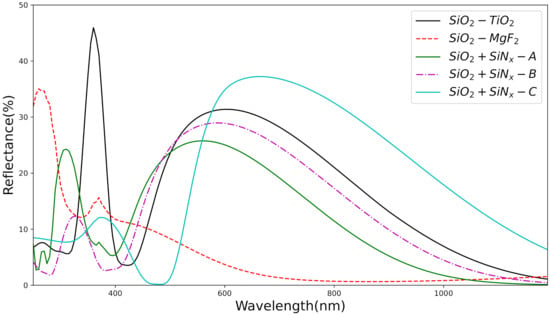
Figure 4. Reflectance spectra as a function of wavelength for some double-layer anti-reflection coating.

Based on Equation (11) the optical thickness of the $DLARC$ layers was optimized to obtain a minimum reflectance. Figure 5 shows the reflectance spectra of the $DLARC$ layers. The inset of Figure 6 shows the thickness variation for both ${\mathrm{SiO}}_2$ and the capping layer. The ${\mathrm{SiO}}_2$ layer capped with ${\mathrm{MgF}}_2$ and ${SiN}_{x-C}(n=2.71)$ showed a reflectance of $2.2\%$ whereas for the ${\mathrm{TiO}}_2,{SiN}_x-A$ and ${SiN}_x-B$ layers the reflectance was $0.34\%,0.11\%$ and $0.19\%$ respectively with the thickness of ∼60–70 $\mathrm{nm}$. From the optimized reflectance curves, we can observe that when the reflectivity is substantially mitigated at the front surface, the gain in efficiency of the solar cell. Table 3 represents the $I-V$ parameters as well as the calculated blue loss and $ARC$ loss with optimized $DLARC$ layers. With $DLARC$, the $J_{sc}$ improved by ∼0.5 $\mathrm{mA}/{\mathrm{cm}}^2$ when the ${\mathrm{SiO}}_2$ was capped with ${\mathrm{SiN}}_x$ layer and hence the efficiency by $0.3\%$. It can be observed that the blue loss reduces significantly for the $DLARC$ compared with $SLARC$. This reduction can be attributed to the effective passivation provided by the ${\mathrm{SiO}}_2$ layer. With $DLARC$, the reflection loss reduced by $50\%$ i.e., ∼1 $\mathrm{mA}/{\mathrm{cm}}^2$ in $J_{sc}$ compared with $SLARC$.

Table 3. $I-V$ parameters and $ARC$ loss calculation based on the optimized $DLARC$ layers.

$\mathit{ARC}$ Layer	${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)	${\mathit{V}}_{\mathit{oc}}$ (mV)	$\mathit{FF}$ $(\%)$	Eff (%)	Blue Loss (%)	ARC Loss [%]	Unshaded ${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)
${\mathrm{SiO}}_2-{\mathrm{TiO}}_2$	38.29	654.2	82.42	20.65	0.13	1.03	40.13
${\mathrm{SiO}}_2-{\mathrm{MgF}}_2$	38.11	654.1	82.43	20.55	0.13	1.42	39.74
${\mathrm{SiO}}_2-{SiN}_x-A$	38.41	654.3	82.42	20.72	0.13	0.83	40.34
${\mathrm{SiO}}_2-{SiN}_x-B$	38.52	654.4	82.42	20.78	0.13	0.67	40.49
${\mathrm{SiO}}_2-{SiN}_x-C$	38.16	654.1	82.42	20.57	0.13	1.03	40.13

Table 3. $I-V$ parameters and $ARC$ loss calculation based on the optimized $DLARC$ layers.

$\mathit{ARC}$ Layer	${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)	${\mathit{V}}_{\mathit{oc}}$ (mV)	$\mathit{FF}$ $(\%)$	Eff (%)	Blue Loss (%)	ARC Loss [%]	Unshaded ${\mathit{J}}_{\mathit{sc}}$ (mA/cm2)
${\mathrm{SiO}}_2-{\mathrm{TiO}}_2$	38.29	654.2	82.42	20.65	0.13	1.03	40.13
${\mathrm{SiO}}_2-{\mathrm{MgF}}_2$	38.11	654.1	82.43	20.55	0.13	1.42	39.74
${\mathrm{SiO}}_2-{SiN}_x-A$	38.41	654.3	82.42	20.72	0.13	0.83	40.34
${\mathrm{SiO}}_2-{SiN}_x-B$	38.52	654.4	82.42	20.78	0.13	0.67	40.49
${\mathrm{SiO}}_2-{SiN}_x-C$	38.16	654.1	82.42	20.57	0.13	1.03	40.13

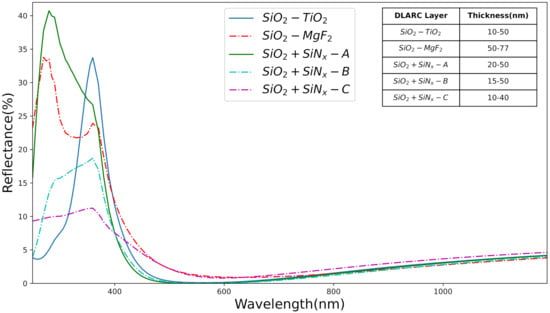
Figure 5. Reflectance spectra as a function of wavelength with optimized thickness of double-layer anti-reflection coating.

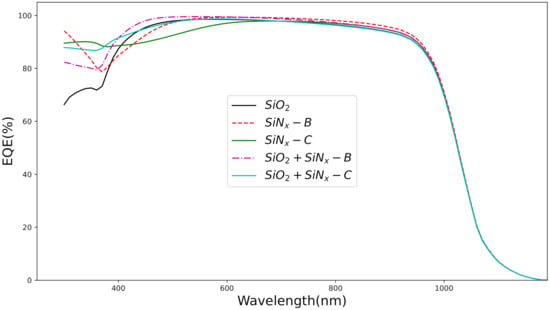
Figure 6. $EQE$ measurement carried on selected $ARC$ layers.

Figure 6 depicts the $\mathrm{EQE}$ obtained on the selected ARC layers. $SLARC$ of ${\mathrm{SiO}}_2$ layer showed a better blue response compared with ${\mathrm{SiN}}_x-B$ layers. However, the increase in $J_{sc}$ for the ${SiN}_x-B$ layers is due to the better response i.e., more absorption in the long-wavelength region. From Figure 6 it is obvious that with the utilization of the $DLARC$ layer, the carrier collection has improved significantly in the short wavelength range leading to the best conversion efficiency and $J_{sc}$. This enhancement in $\mathrm{EQE}$ is attributed to the decrease in reflection with $DLARC$. It is sufficient to say, this effective collection of carriers reduce the recombination at the interface, and hence the overall $\mathrm{EQE}$ is enhanced [10].

To validate the simulation data, a simulated device with identical parameters was compared to the measurements of actual solar cells in real application conditions. The industrial silicon solar cell was fabricated with both $SLARC$ and $DLARC$. $55\mathrm{nm}$ thick ${\mathrm{SiO}}_x$ layer with the refractive index of $2.05$ was used as $SLARC$ layer. ${\mathrm{SiO}}_2$ with $15\mathrm{nm}$ thick and ${\mathrm{SiN}}_x$ with $70\mathrm{nm}$ thick were used as $DLARC$ layer. The monocrystalline silicon solar cell showed the conversion efficiency of $20.8\%$ and $21.1\%$ shown in the inset of Figure 7. $\mathrm{EQE}$ spectra indicate that the efficiency improvement for a solar cell with the $DLARC$ compared to the $SLARC$. This improvement at the short wavelength region is vital and it’s attributed mainly to the role of the $DLARC$. Thus, the ${\mathrm{SiO}}_2/{\mathrm{SiN}}_x$ stacked layers reduce the reflection of high energy photons. In addition, the $ARC$ layers provide better passivation thus enhancing the overall $\mathrm{EQE}$ by reducing the surface recombination at the interface. The efficiency of the solar cell using the optimized $ARC$ layer settings is compared with the results obtained from the literature and presented in Table 4. The result indicated that the identified $ARC$ layer configuration outperforms the previously identified $SLARC$ and $DLARC$ layers highlighted in the literature.

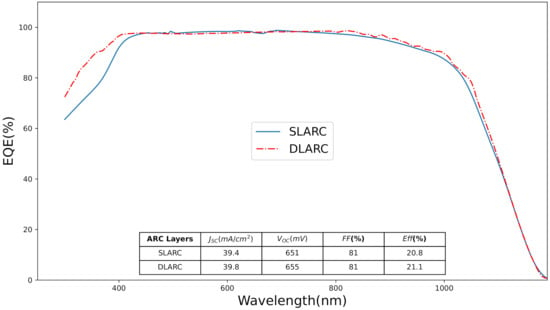
Figure 7. EQE measurement carried on single and double layer $ARC$ layers. Inset shows the IV results obtained with the solar cell measurement.

Table 4. Comparison of the $I-V$ results obtained with different $ARC$ layers.

Layer Type		Eff (%)	Reference
$SLARC$	${\mathrm{SiO}}_2$	18.3	[27]
	${\mathrm{SiN}}_x$	19.6	[18]
	${\mathrm{SiN}}_x$	20.35	[17]
	${\mathrm{SiN}}_x$	20.8	This article
$DLARC$	${\mathrm{SiO}}_2/{\mathrm{SiN}}_x$	4.56	[18]
	${\mathrm{SiN}}_x/{\mathrm{SiN}}_x$	17.8	[28]
	${\mathrm{SiO}}_2/{\mathrm{SiO}}_x$${\mathrm{N}}_y$	18.59	[27]
	${\mathrm{SiO}}_2/{\mathrm{SiN}}_x$	18.62	[29]
	${\mathrm{SiN}}_x/{\mathrm{SiN}}_x$	20.22	[19]
	${\mathrm{SiN}}_x/{\mathrm{SiN}}_x$	20.67	[17]
	${\mathrm{SiN}}_x/{\mathrm{SiN}}_x$	21.1	This Article

4. Conclusions

The impact of different anti-reflective coating layers on improving the efficiency of silicon solar cells has been studied in this manuscript. Initially, $OPAL2$ simulator was used to compute the refractive indices and reflectance of ${\mathrm{SiO}}_2$, ${\mathrm{TiO}}_2$ and ${\mathrm{SiN}}_x$ as $ARC$ materials. The calculated reflectance value of the $ARC$ material was later used in analyzing its performance on the silicon solar cells using $PC1D$ software. The impact of the ARC as single and double-layered $ARC$ was studied in this research and results indicated that the ${SiN}_x$ and ${\mathrm{TiO}}_2$ as $SLARC$ yielded a $J_{sc}$ of $38.4\mathrm{mA}/{\mathrm{cm}}^2$ and $38.09\mathrm{mA}/{\mathrm{cm}}^2$ respectively. Highest efficiency of $20.7\%$ was obtained for the ${SiN}_x$ $ARC$ layer with $n=2.15.$ ${\mathrm{SiO}}_2$ layer capped with ${\mathrm{TiO}}_2$, and ${SiN}_x$ layers showed the lowest reflectance of $0.34\%$ and $0.11\%$ respectively. ${\mathrm{SiO}}_2/{\mathrm{SiN}}_x$ $DLARC$ layer increases the $J_{sc}$ by $0.5\mathrm{mA}/{\mathrm{cm}}^2$; thereby by increasing the efficiency by $0.3\%$. The increase in $J_{sc}$ by $1\mathrm{mA}/{\mathrm{cm}}^2$ for $DLARC$ is attributed to significant reduction in blue loss compared with $SLARC$.

Therefore, it is clear from the observation that the use of $DLARC$ over $SLARC$ will be advocated considering the impact of increased efficiency and reduced blue loss. This enhancement in $\mathrm{EQE}$ for the $DLARC$ is attributed to the decrease in reflection as well as a decrease in recombination at the interface. The $J_{sc}$ values obtained is in good agreement with the reflectance values of the $ARC$ layers. Further research insights would be targeted towards experimentally evaluating the simulation results on the impact of identified $ARC$ layers with silicon solar cell efficiency. The simulation approach highlighted in this manuscript has a bigger advantage in terms of reducing the cost and time required for identifying the best-suited combination of ARC layers that can be considered for the silicon solar cells with $DLARC$ finally resulting in higher efficiency. Future research can be benefited from the methodology used in the simulation study to identify the impact of new materials in $DLARC$ or $SLARC$ fabrication or to identify the optimized parameters required for the fabrication of the silicon solar cells.