Abstract
With a target to maximize the throughput, a fast link rate adaptation algorithm for IEEE 802.11a/b/g/n/ac is proposed, which is basically preamble based and can adaptively compensate for the discrepancy between transmitter and receiver radio frequency performances by exploiting the acknowledgment signal. The target system is a 1 × 1 wireless local area network chip with no null data packet or sounding. The algorithm can be supplemented by automatic rate fallback at the initial phase to further expedite rate adaptation. The target system receives wireless channel coefficients and previous packet information, translates them to amended signal-to-noise ratios, and then, via the mean mutual information, selects the modulation and coding scheme with the maximum throughput. Extensive simulation and wireless tests are carried out to demonstrate the validity of the proposed adaptive preamble-based link adaptation in comparison with both the popular automatic rate fallback and ideal link adaptation. The throughput gain of the proposed link adaptation over automatic rate fallback is demonstrated over various packet transmission intervals and Doppler frequencies. The throughput gain of the proposed algorithm over ARF is 46% (15%) for a 1-tap (3-tap) channel over 10 m–250 m (16 m–160 m) normalized Doppler frequencies. Assuming a 3-tap channel and 30 m–50 m normalized Doppler frequencies, the throughput of the proposed algorithm is about 31 Mbps, nearly the same as that of ideal link adaptation, whereas the throughput of ARF is about 24 Mbps, leading to a 30% throughput gain of the proposed algorithm over ARF. The firmware is implemented in C and on Xilinx Zynq 7020 (Xilinx, San Jose, CA, USA) for wireless tests.
1. Introduction
The wireless channel features variations over time in the temporal domain and across frequency in the spectral domain are characterized by delay spread and Doppler spread, respectively, giving rise to frequency selectivity and time selectivity, respectively. Both the physical layer (PHY) and the data link layer or the medium access control (MAC) sublayer of the air interface (or access mode) should be designed in consideration of this wireless channel. In other words, signal transmission techniques should be effectively adjusted according to the varying channel quality or channel status.
For instance, the access point (AP) in wireless local area networks (WLANs) may send a known signal to the station and subsequently the station can send to the AP a feedback signal with channel state information that recommends which signal transmission techniques are adequate for the channel. Taking this feedback into account, the AP may choose effective transmission techniques with which to send data to the station. This is known as closed-loop link adaptation. As another way, the station sends a known signal to the AP (via the uplink) and from the quality of this signal, the AP predicts the status of the downlink channel, assuming channel reciprocity. This is known as open-loop link adaptation.
Closed-loop link adaptation assumes perfect channel knowledge available at the transmitter from either receiver feedback or channel sounding, incurring high computational complexity and communication overhead. A link adaptation algorithm where the receiver feedback is considered through the acknowledgment (ACK) of the transmitted data is a closed-loop link adaptation algorithm [1]. On the other hand, open-loop link adaptation utilizes only the transmitter’s statistics and can maintain seamless interoperability and coexistence with legacy WLAN devices [2,3]. In a target system that is based on the time division duplex (TDD), the wireless channel holds channel reciprocity for a relatively short time and accordingly open-loop link adaptation is an amenable choice in IEEE 802.11 with multi-user multi-input multi-output (MIMO). When the AP senses that the wireless channel condition is good or the signal-to-noise ratio (SNR) level is high, it will switch to another modulation and coding scheme (MCS) available in the WLAN which offers a higher data rate or enhanced throughput [4].
One of the most widely used basic link rate adaptation algorithm is automatic rate fallback (ARF) [5] which is based on statistical count of frames. After first ACK miss, the retransmission is still performed at the same rate but after second ACK miss, the second retry and subsequent transmission attempts are performed at the fallback rate. When the No. of successively received good ACKs reaches 10, the rate is upgraded. However, if the first transmission fails right after the rate upgrade, the rate is immediately decreased. A drawback of ARF is that if the channel changes quickly, the rate in ARF cannot be adapted effectively. Another statistical-count-based link adaptation algorithm called dynamic link adaptation [6] employs a success counter and a failure counter such that it increases the rate when the success counter reaches the threshold value S and decreases the rate when the failure counter reaches the threshold value F. If the channel changes very slowly, the number of retransmission attempts in both ARF and dynamic link adaptation increases. To address these two problems with ARF, adaptive ARF [7] was proposed such that if the first transmission fails right after the rate upgrade, not only the rate is immediately switched back to the previous rate but also the success threshold is doubled. On the other hand, if the rate is decreased owing to two consecutive fails, the success threshold is set to the initial value, 10.
More variant algorithms exist as the statistical-count-based link adaptation using frame-based measurement. The Onoe algorithm [8] is less sensitive to individual packet failure than the ARF algorithm by means of employing averaged credits as another condition to increase the rate. Fast-responsive link adaptation [9] decreases the rate in the same manner as ARF but tries to increase the rate more frequently if the transmission duration of the current rate is sufficiently long. The SampleRate algorithm [10] sends data at the rate that has the smallest predicted average packet transmission time. Loss-differentiating ARF [11] entails a new control frame, NAK [12], in IEEE 802.11, which indicates a channel error to the transmitter. Fail count increases only when a NAK is received whereas if no ACK, a collision is deemed to have occurred. Collision-aware rate adaptation [13] handles the inability of ARF to differentiate collisions from channel errors by adopting request-to-send probing and/or clear-channel-assessment detection. The robust rate adaptation algorithm [14] estimates the packet loss ratio during a given time window of observation and increases (decreases) the rate if this ratio is lower (higher) than a given lower (upper) threshold. In addition, to suppress collision losses, an adaptive request-to-send filter is employed. The drawback of the algorithm in [14] is that the algorithm may tend to be too aggressive for static stations and too conservative for moving stations. Stochastic automata rate adaptation [15] is based on stochastic learning automata that can estimate the probabilistic packet success rate. Sequential hypothesis testing-based rate control [16] is also a statistical-count-based link adaptation algorithm.
Another category for link adaptation, as opposed to statistical-count-based link adaptation, is SNR-measurement-based or PHY-measurement-based link adaptation, an example of which is receiver-based AutoRate [17]. This algorithm allows the receiver to select the appropriate rate for the data packet during the request-to-send and clear-to-send packet exchange. Link adaptation methods based on a multitude of link quality metrics [18,19,20,21,22,23,24,25] are other examples of PHY-measurement-based link adaptation. The effective goodput (which is the expected data payload length delivered divided by the expected transmission time spent on the frame delivery) is computed in [20] and the best set of PHY modes that maximizes this goodput is found. Exponential effective SNR of the orthogonal frequency division multiplexing (OFDM) system is proposed as a link quality metric in [21]. To estimate the packet error rate (PER), lookup tables of PER vs. SNR in the additive white Gaussian noise (AWGN) channel for all PHY modes are constructed first and then the average SNRs of all subcarriers are estimated. Subsequently, the effective SNR is calculated and the PER is found from the lookup table at this effective SNR. The motivation of [22] is that if the SNR distance from the AWGN PER curve is known (by means of a PER indicator), the PER of a specific frequency selective channel can be predicted accordingly. On the other hand, it is proved in [23] that the exponential effective SNR has a slightly better performance than the PER indicator in [22]. Ref. [24] calculates the PER, starting with the per-subcarrier post detection SNR from the channel matrix and then the bit error rate forms the effective SNR. It is proved in [25] that among the three link quality metrics, namely, the instantaneous SNR, the exponential effective SNR, and Shannon capacity, the exponential effective SNR usage shows the best performance. Yet another link quality metric exists, which provides better PER estimation accuracy than the exponential effective SNR, in case of fast link adaptation. This metric [26] is based on mutual information, which will be explained in Section 2.
Some more variant algorithms exist as the PHY-measurement-based link adaptation [27,28]. RSSI-based link adaptation [29,30], which does not require feedback from the receiver, is based on the measured received signal strength of received frames and the number of retransmission attempts, in order to determine the channel and receiver conditions. Hybrid automatic rate control [31] uses both SNR-based and statistic-based algorithms. In this approach, a signal-strength-indicator-to-rate lookup table is employed such that the three signal-strength-indicator thresholds of the table are dynamically adjusted at the end of each time window, according to the frame error rate. Opportunistic rate adaptation is used in [32,33] and distributed cooperative rate adaptation is used in [34].
To summarize, the problems in ARF-like algorithms include:
- No consideration of fails due to collision;
- Non-optimal rate selection (due to the rate fallback only in successive fails);
- Meaningless periodic rate upgrade in slow channel variations;
- Obscure number of consecutive transmission successes or fails before a rate change.
On the other hand, the problems in PHY-measurement-based algorithms include:
- A large SNR variation in case of a short-term measurement;
- Weakness with mobile clients in case of a long-term measurement for smoothening.
The system considered in this paper for fast link rate adaptation is a 1 × 1 WLAN chip having one transmitter (TX) antenna and one receiver (RX) antenna. In a certain system that allows null data packet transmission, the RX can utilize a null data packet (NDP) from the TX to decide an MCS feedback which will be sent to the TX. However, since the target system considered in this paper is a 1 × 1 WLAN chip, an NDP is not sent. Many APs in WLANs do not support sounding and accordingly an algorithm that does not use a sounding PHY protocol data unit is considered in this paper. As a consequence, in our target system, no MCS feedback is assumed from the RX. The proposed fast link rate adaptation algorithm in this paper is based on the preamble (instead of NDP or sounding). The target system in the proposed algorithm receives wireless channel coefficients (namely, channel state information or CSI, from PHY measurements) and previous packet information (ACKs), translates them to amended signal-to-noise ratios, and then, via the mean mutual information, selects the MCS with the maximum throughput. The proposed algorithm can be applied to IEEE 802.11a/b/g/n/ac WLAN systems.
The paper is organized as follows. The basics of the link rate adaptation algorithm is addressed in Section 2, followed by the link adaptation firmware in Section 3 that deals with the overall flow of the proposed link adaptation and the functions in detail that constitute the proposed firmware. Analysis and optimization of the operating speed of the proposed link adaptation are covered in Section 4 and the link adaptation performance measurements and wireless tests are depicted in Section 5, followed by discussion and conclusion with an appendix.
2. Link Adaptation Algorithm Basics
The target system supposed in the paper is made up of one TX antenna and one RX antenna, as drawn in Figure 1. The system supports IEEE 802.11a, 11b, 11g, 11n, and 11ac WLAN standards in the AP and the non-AP modes, and leverages an open-loop type link adaptation (LA) in which the RX of the station (STA) does not support MCS feedback. The goal of the link rate adaptation implementation in this paper, based on adaptive modulation and coding, is to select an MCS that can achieve the maximum throughput.
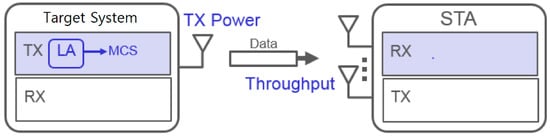
Figure 1.
Target system.
In comparison, with ideal link adaptation, the RX estimates the SNR and accordingly selects an MCS that enables the maximum available throughput and feeds this MCS back to the TX via a control wrapper, which is a closed-loop type link adaptation, as drawn in Figure 2. Assuming the feedback delay is negligible, this type of link adaptation with MCS feedback can predict the link most accurately and swiftly.
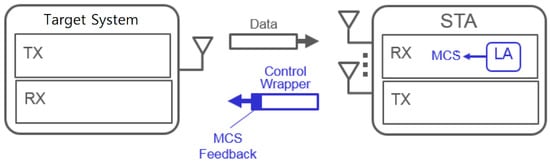
Figure 2.
Ideal link adaptation.
In case the MCS feedback of the RX being not available, illustrated in Figure 3, an acknowledgment (ACK) success or fail (S/F) of the data frame sent by the TX can be leveraged by the target system for link adaptation. However, it takes long for this method to obtain the channel information. Another method is to utilize the preamble [35] in the frames (ACK frame, beacon frame, etc.,) received by the RX. It has the upside of acquiring the channel information swiftly and has the downside of degrading the performance in the event that the channel information is inaccurate.
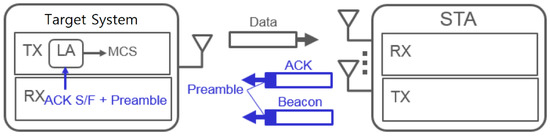
Figure 3.
Link adaptation in case of no modulation and coding scheme (MCS) feedback from the receiver (RX) antenna.
One of the most well-known and widely used traditional link adaptation algorithm is ARF. In ARF, the MCS value steps up by 1 (upgrade or UG) if ten consecutive ACKs are received whereas the MCS value steps down by 1 (downgrade or DG) if two consecutive no ACKs (namely, two consecutive failures to receive ACK) occur or if a no ACK is received immediately after the MCS value steps up by 1. Table 1 shows the modulation scheme and the throughput for each of the MCS values or indices, along with the code rate (R). Each throughput value in the parenthesis indicates the throughput value when two streams are used instead of a single stream. Table 1 is specified for 20 MHz channels and 600 ns guard intervals in WLAN standards. Figure 4 shows the simulation results that compare ARF with ILA or ideal link adaptation. ARF, since it selects an MCS according to its qualifications described above even if the channel is in favorable conditions, has its MCS altered at a slow pace, as opposed to ILA which has its MCS altered fast accordingly as the channel varies, since it selects an MCS that achieves maximum throughput according to the channel condition. With ARF, packet numbers 12 and 25 correspond to the case when a no ACK comes in immediately after the MCS value is upgraded, at which an ARF function called probing comes into play, whose role is to one step downgrade the MCS value. In this case, ARF probing interprets a no ACK directly after an upgrade in MCS occurs as an erroneous decision.

Table 1.
Modulation and throughput for each of the modulation and coding scheme (MCS) values.
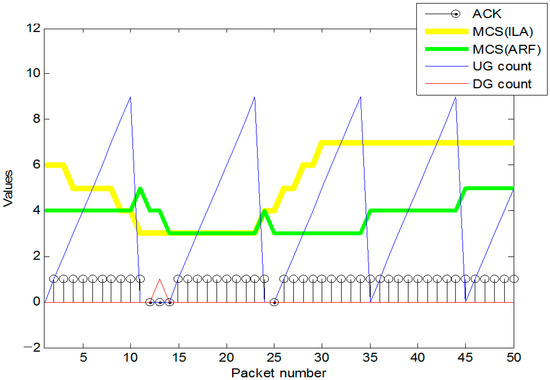
Figure 4.
Automatic rate fallback (ARF) simulation results.
On the other hand, preamble-based link adaptation (PBLA), categorized as PHY-measurement-based link adaptation, utilizes the preambles in the received frames such as ACK frames, beacon frames, and so forth. Rate adaptation based on the received packet SNR measurement may be highly erroneous under certain scenarios like mobile multipath channels. Thus, from the SNR concerning the received channel, mutual information (MI) is calculated per modulation scheme and subsequently the mean MI or MMI is obtained by taking the average of MI over the channel subcarriers in the OFDM [26]. Then, the packet error rate (PER) is obtained from the MMI and finally the throughput is calculated from the PER. Through this procedure the throughput is obtained for each of the MCS and among all the MCS values, the MCS with the maximum throughput is selected. As mentioned in Section 1, the MMI-based link quality metric is known to be more accurate than the exponential effective SNR.
More specifically, conversion of the SNR to the MI and conversion of the MMI to the PER are explained as follows. MI is the probability that one bit is transmitted successfully, namely, the expectation value of the number of bits that are delivered successfully. MMI is the mean MI over all the subcarriers. PER is the probability that the packet is transmitted unsuccessfully and hence the lower the PER the better the likelihood of successful transmission. SNRk,i that is the SNR of the i-th subcarrier of the k-th packet is computed with Equation (1).
where Hk,i is the channel coefficient of the i-th subcarrier of the k-th packet and N0 is the noise power spectral density (PSD). MI vs. SNR has the same shape for the same modulation scheme, as plotted in Figure 5. MI per symbol can be calculated from the SNR by using cubic polynomials, which is specified in Appendix A.
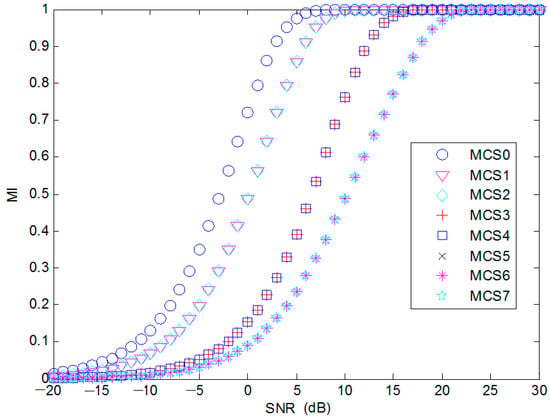
Figure 5.
Signal-to-noise ratio (SNR)-to-mutual information (MI) conversion for MCS 0–7.
Figure 6 is obtained from Monte Carlo simulations under the additive white Gaussian noise (AWGN) environment, from which the PER is acquired and the throughput can be expressed in terms of the PER as in Equation (2).
where TPMCS is the expected value of the data rate or throughput for each MCS value in Table 1, PERMCS is the expected value of the PER, and RMCS is the peak data rate or throughput listed in Table 1. Under fading channel environments, the PERMCS varies as the channel condition varies, and hence TPMCS also varies.
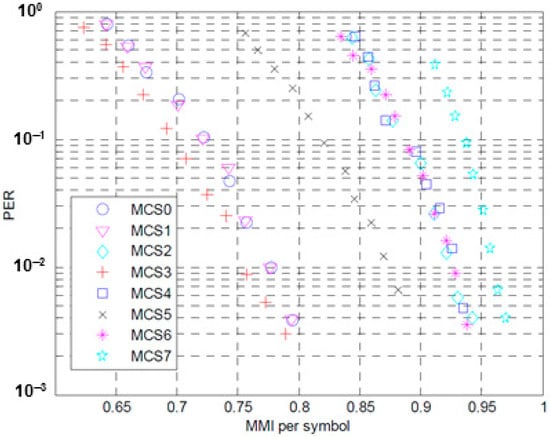
Figure 6.
Mean mutual information (MMI)-to- packet error rate (PER) conversion for MCS 0–7.
In this paper, an adaptive preamble-based link adaptation (adaptive PBLA or APBLA) algorithm is proposed, which is outlined in the following. If a difference exists between the MMI-to-PER table (Figure 6) in PBLA and the actual RX performance (owing to the mismatch between uplink SNR and downlink SNR), then performance degradation will occur. The right half of Figure 7 shows the MMI-to-PER table used in PBLA while the left half of Figure 7 shows the result after the curves for MCS values are shifted randomly and independently of each other, in order to model the actual RX performance. If PBLA is adopted for link adaptation, the right half of Figure 7 is put to use to determine the MCS value. If the actual RX is assumed to have the MMI-to-PER relationship shown on the left half of Figure 7, then, in this case, PBLA will be unable to carry out correct link adaptation. Besides, if the channel coefficients experience separate scaling procedures, the channel quality will be falsely predicted and hence PBLA will scarcely select the MCS value with the maximum throughput.
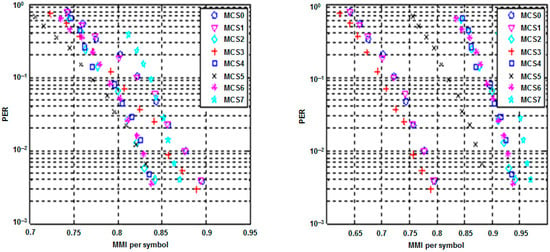
Figure 7.
Randomly shifted (left) and standard (right) MMI-to-PER tables.
To cope with the case that the actual RX performance is different than the performance PBLA assumes, the adaptive PBLA or APBLA algorithm takes advantage of the ACK information of the previous packets to amend the channel SNR. If ACKs have frequently occurred, the channel condition is regarded as better than what the table predicts whereas if ACKs have not occurred often, the channel condition is counted as worse than that expected by the table. Thus when many ACKs have occurred, the channel SNR is incremented and conversely when ACKs have not occurred many times, the channel SNR is decremented. More specifically, the SNR offset value renewed every packet on the basis of the ACKs of the previous packets and this renewed SNR offset is applied to each subcarrier SNR, whereby the discrepancy between the actual RX and the PBLA internal model is overcome.
3. The Link Adaptation Firmware
The firmware for the proposed link adaptation, APBLA, consists of the coef2snr function, the offset_update function, the snr2thr function, the snr2mi_bpsk, snr2mi_qpsk, snr2mi_16qm, and snr2mi_64qm functions, the mmi2thr function, and the interp function, as shown in Figure 8. In the first place, the overall flow of the link adaptation firmware is explained. Subsequently, the details of each function in the firmware are accounted for in detail. The firmware is implemented in the C programming language.
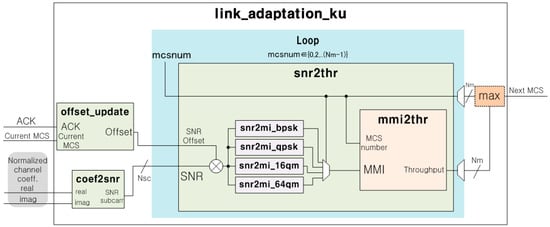
Figure 8.
Overall structure of the proposed link adaptation.
3.1. Overall Flow
The wrapper function is named link_adaptation_ku which is shown in Figure 8. The inputs to this function are the integer data type PHY_Mode (the mode used in the PHY that is 0 for legacy, 1 for high throughput or HT, and 2 for very high throughput or VHT) (not shown in Figure 8 for brevity), the integer data type mcsin (the MCS index for the previous packet), the integer data type ack (the ACK for the previous packet), and the pointer to short data types nch_coef_real and nch_coef_imag (the real and imaginary parts of the channel information or normalized channel coefficients per subcarrier). This wrapper function determines the MCS value of the next packet and returns this value. It may be subdivided into two parts—one part that executes the PBLA algorithm and the other part that runs the remaining algorithms.
If a mismatch occurs between the uplink and the downlink SNRs, stemming from the disagreement between the TX and the RX radio frequency (RF) performances, then PBLA will not run correctly. By contrast, the proposed algorithm, APBLA, by means of amending the channel SNR through the SNR offset, gets around this problem. APBLA multiplies the channel SNR by the SNR offset and this product is fed to the next firmware functions, as shown in Figure 8. The SNR offset grows or drops according to whether the ACK of the previous packet is 1 or 0.
In Equation (3), Offsetk means the SNR offset of the k-th packet and SNRAPBLAk,i means the amended SNR of the i-th subcarrier of the k-th packet. Equations (4) and (5) show the way the SNR offset is updated according to ACK or NACK. (NACK frames are not actually transmitted over the air in IEEE 802.11 but a NACK signal is sent by the driver internally when an ACK is not received over the air. Thus, we denote no ACK as NACK, hereafter.)
In case of ACK,
In case of NACK,
here, StepACK is the ACK update step which is multiplied to the SNR offset in case of ACK while StepNACK is the NACK update step which is multiplied to the SNR offset in case of NACK. The update steps vary when channel conditions vary, which is detailed in Section 3.3 on the offset_update function.
The APBLA algorithm compensates for the mismatch of the channel SNRs but if this mismatch is much too large it takes some time to compensate. Thus, on initiation of the overall function (link_adaptation_ku), ARF can be employed at the beginning. In this ARF phase, the MCS is determined and output by ARF and at the same time the computation is executed to determine the SNR offset (from the MCS obtained by running PBLA) before APBLA sets in. The SNR offset in the ARF phase is updated once every 200 packets whereas before reaching the packet count of 200, the temporary SNR offset is (internally) updated every packet, by Equation (6). The SNR offset is updated every 200 packets by substituting the corresponding temporary SNR offset and then the SNR offset is applied to PBLA for 200 packets.
where OffsetTMPk+1 is the temporary SNR offset, MCSARFk is the MCS determined by ARF, and MCSPBLAk is the MCS determined by PBLA. Specifically, the update step of the temporary SNR offset is determined by the difference between the MCS value recommended by PBLA and the MCS value recommended by ARF. In this paper, the update step is chosen such that the value is proportional to the difference between the two MCS values and, through extensive simulation, the proportionality constant is determined at 0.995405 empirically. The ARF phase terminates and the APBLA phase is initiated on the condition that the variation of the SNR offset for the following 200 packets is below 35% of the SNR offset 200 packets before, which is expressed in Equation (7). This 35% is associated with the time point where the mismatch of the channel SNR is compensated for such that APBLA exhibits better performance over ARF. In this paper, the percentage value is empirically set after extensive simulation so that the throughput of APBLA is maximized.
What is meant by meeting this condition is that over the past 200 packets the difference between the MCS determined by PBLA and that determined by ARF is not significant and hence the channel SNR mismatch is not considerable. Thus if the condition above is satisfied, the APBLA phase sets in to conduct fine mismatch compensation.
In the APBLA phase, the MCS is decided by means of APBLA. This algorithm introduced in Section 2 can be represented by the state diagram shown in Figure 9. A0 state is defined as the state when the SNR offset is incremented and the APBLA algorithm is executed to determine the MCS. N0 state is defined as the state when the SNR offset is decremented and the APBLA algorithm is executed to determine the MCS.
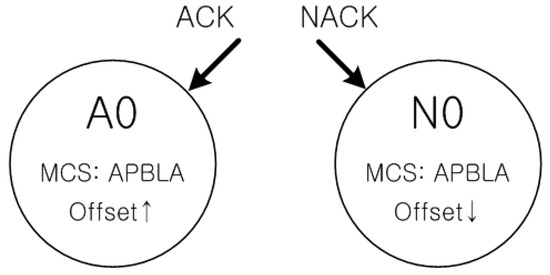
Figure 9.
State diagram of the basic adaptive preamble-based link adaptation (APBLA).
With the basic APBLA the MCS is determined always through the APBLA algorithm as shown above and simply two cases exist, namely, in case of ACK, the SNR offset steps up and in case of NACK, the SNR offset steps down. However, in reality, with the current target system in case a NACK occurs, no channel coefficients are received for link adaptation. Accordingly, an MCS-determining mechanism is needed when a no ACK or NACK occurs and a link adaptation mechanism is proposed as a state diagram in Figure 10. In A0 state, the SNR offset is increased and APBLA is conducted to decide the MCS. In N0 state, the MCS is maintained. In N1 state, both the SNR offset is decreased and the MCS index is stepped down by one. In N2 state, the MCS is maintained. In N3 state, the MCS value is stepped down by one. Regardless of the current state, if an ACK occurs, then the state transitions to A0 state. Additionally, if the current MCS value is 0 when the MCS value is to be decremented, the current MCS value is held unchanged as 0. For instance, if the current MCS value is 1, the state is A0, and thereafter four consecutive NACKs come in, then basically state transitions occur to N0 through N2 to N3, reflecting in principle an MCS index drop by two steps and an SNR offset drop by one step. However, when the MCS value is 0, no way exists to lower the MCS anymore and hence the value stays at 0. The SNR offset step-up or step-down is implemented in the form of multiplying the existing SNR offset by the update step as explained earlier in this subsection.

Figure 10.
Proposed state diagram of the action according to acknowledgment (ACK) or no acknowledgment (NACK) of the previous packet.
The reason the current form of APBLA behaves as such is elaborated as follows. When an actual test was carried out under a wireless test environment, the channel SNR varied too quickly and hence despite the correct prediction of APBLA based on the channel SNR at that time, NACKs were received too frequently. As a provision against this problem, the SNR offset is not reduced for a NACK immediately after an ACK. Furthermore, the SNR offset decrement is executed only once even for consecutive NACKs since the SNR offset is to be updated only once for each APBLA action. Thus, if consecutive NACKs occur, then N2 and N3 states are repeated over and again and the MCS drop takes place once every two NACKs.
If an ACK occurs with the previous packet in the APBLA phase, the state enters A0 state and the MCS is determined according to the proposed APBLA algorithm which will be executed as follows. First, as was drawn in Figure 8, by using the coef2snr function, the channel information is converted to the SNR per subcarrier. Second, by means of the repetitive statement (i.e., the loop construct) in the snr2thr function the expected values of the throughput are calculated for all the MCS values apropos of the current subcarrier SNR. Among these MCS values, the value with the highest expected throughput value is opted for as the optimal MCS value that is returned. The offset_update function renews the SNR offset value in accordance with ACKs or NACKs of the previous packets. These component functions, shown in Figure 8, are explained in depth in the following subsections.
3.2. Function coef2snr
The inputs to the coef2snr function are the real pointer to short data type (the real part of the channel information per subcarrier), the image pointer to short data type (the imaginary part of the channel information per subcarrier), and the snr_subcarr pointer to float data type (the SNR value per subcarrier). The coef2snr function receives the channel information as the input and calculates the subcarrier SNR. The operation that governs this function is Equation (8).
where the sqscale constant is the square of the scale value in order to match the channel information that is input as an integer to the original magnitude. The function terminates after the calculated result is stored in order at the address of the subcarrier SNR array.
3.3. Function Offset_Update
The inputs to the offset_update function are the mcsin integer data type (the MCS index applied to the previous packet), the ack integer data type (the ACK concerning the previous packet), and the snr_offset pointer to float data type (the SNR offset value per MCS). The function offset_update, as explained in Section 3.1, references the ACK of the previous packet and accordingly renews the SNR offset. If the previous transmission has succeeded, the SNR offset is multiplied by the ACK_OFFSET value (A0 state in Figure 10), whereas if the previous transmission has failed, the offset is multiplied by the NACK_OFFSET value. In state A0, if two NACKs occur in sequence, NACK_OFFSET is multiplied (N1 state). The update step of the SNR offset is not constant but varies according to a given condition. More specifically, if the channel SNR compensation by the SNR offset is not enough, update steps with a large step up or a large step down are made use of to rapidly compensate for the channel SNR. In this case the SNR offset update step is set to 0.015 dB in case of an ACK and 0.15 dB in case of a NACK. After it is decided that the channel SNR mismatch compensation is nearly attained, update steps with a small step up and a small step down are exploited to finely tune the channel SNR mismatch, in which case the SNR offset update step is set to 0.005 dB with an ACK and 0.05 dB with a NACK. How the values of the SNR offset update step are determined is explained as follows. If the update step is chosen too small, the adaptation is unable to keep track of the channel variation or unable to compensate for the error in the MMI-to-PER mapping table whereas if chosen too large, much deviation from the mapping table will arise. Generally, the update step may well be chosen smaller in case of slow fading and larger in case of fast fading, which is demonstrated in Table 2 in Section 6 later on. In this paper, the SNR offset values for ACK and NACK are determined empirically to achieve the balance mentioned above, from a multitude of wireless tests.

Table 2.
Performance comparison table.
If the SNR offset value does not oscillate around a specific value but continually increases or decreases, it is decided that the channel SNR mismatch compensation is not sufficient. On the contrary, the channel SNR mismatch compensation being almost reached is judged from the SNR offset value fluctuating around a specific value.
In Equations (9) and (10), Offsetk is the SNR offset up to the k-th packet, Mk is the mean SNR offset up to the k-th packet, and Dk is the mean variation (or deviation) of the SNR offset up to the k-th packet. Equations (9) and (10) represent IIR filters to take on averages, which are to filter out the SNR variations caused by AWGN observed in wireless tests. As is well-known, the sum of the coefficients is set to be unity, e.g., 0.95 + 0.05 = 1 and 0.9 + 0.1 = 1, where each of the coefficients, 0.05 and 0.1, that is attached to the new sample, is the forgetting factor of the IIR filter, which decides the magnitude of the average window of the filter. For instance, if the forgetting factor is 0.05 (0.1), the magnitude of the average window is 20 (10) samples wide. In this paper, the forgetting factors are determined from AWGN and Doppler identified in wireless tests.
Since Mk and Dk denote the average SNR offset and the average variation of the SNR offset, respectively, inequality Equation (11) is the condition that discerns whether the channel SNR mismatch compensation is enough or not. If the value that relates Mk and Dk in Equation (11), 0.02 in our case, is set too large, then the update step will be diminished too early before the SNR offset value oscillates around a specific value. On the other hand, if the value is set too small, then the update step will be reduced too late after the SNR offset value oscillates unnoticed. In this paper, the value, 0.02, is empirically determined to maximize the throughput in the wireless tests. If the SNR offset fluctuates around a constant value, Equation (11) may be satisfied and hence in this case it is decided that the compensation is almost fulfilled and thereafter the SNR offset is finely tuned by means of small update steps. If Equation (11) is not met, it is deemed that the compensation is not satisfactory and on this occasion the update steps are bumped up to compensate for the SNR offset rapidly.
3.4. Function snr2thr
The inputs that are fed to the snr2thr function are the mcsnum integer data type (the MCS index loop variable for which the throughput is to be computed), the snr_subcarr pointer to float data type (the SNR per subcarrier), and the snr_offset pointer to float data type (the SNR offset value for each MCS). The snr2thr function receives the MCS index loop variable and the array of subcarrier SNRs and calculates the MMI by summing up the MI of subcarriers as to the current MCS loop variable. More specifically, through the conditional statement the MCS values are distinguished according to the modulation schemes. Then, each MI computation function corresponding to the distinguished modulation scheme is decided as follows. As displayed in Figure 8, in case of BPSK (MCS 0), the snr2mi_bpsk function is selected, and in case of QPSK (MCS 1 and 2), the snr2mi_qpsk function is selected. For 16-QAM (MCS 3 and 4), the snr2mi_16qm function is picked up and for 64-QAM (MCS 5–7), the snr2mi_64qm function is chosen. The procedure of computing the MI value from the corresponding function is reiterated over all the subcarriers and the MI values are summed up. The total sum of the MI values are multiplied by the inverse of the number of subcarriers, yielding the MMI, which is input to the mmi2thr function to obtain the expected value of the throughput. This throughput value is the output of the snr2thr function.
3.5. Functions snr2mi_bpsk, snr2mi_qpsk, snr2mi_16qm, and snr2mi_64qm
The input to the snr2mi_bpsk function is the snr float data type that is the SNR loop variable per subcarrier, for which the MI is to be calculated. The snr2mi_bpsk function receives the subcarrier SNR loop variable and computes the MI. To apply the BPSK SNR-to-MI table, particularly at which location the current subcarrier SNR lies in the SNR axis of the table is detected by using conditional statements. Here, a linear interpolation function, interp, is employed to compute a more accurate MI value from the SNR lying between two given entries on the SNR axis of the table. The interp function is briefly explained in Section 3.7. The SNR-to-MI tables according to the modulation schemes are shown in Figure 11.
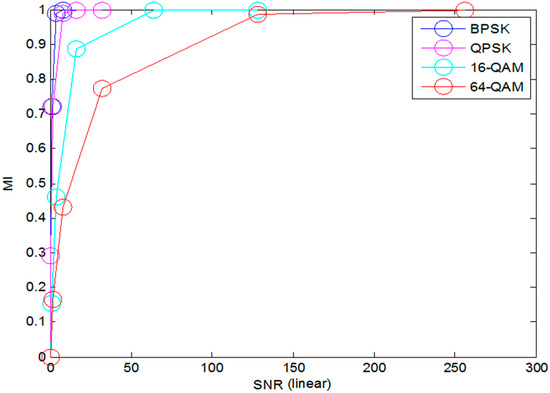
Figure 11.
SNR-to-MI tables for modulation schemes.
In a similar fashion, the input to the snr2mi_qpsk function is the SNR loop variable per subcarrier, for which the MI is calculated. This function computes the MI from the single subcarrier SNR and the only difference from the snr2mi_bpsk is that a QPSK SNR-to-MI table is applied rather than the BPSK SNR-to-MI table. The simple linear interpolation function interp is employed here as well. How the MI value for each modulation scheme was obtained from the SNR is provided in Appendix A in equations. Likewise, the snr2mi_16qm function and the snr2mi_64qm function are constructed to behave as desired.
3.6. Function mmi2thr
The inputs to the mmi2thr function are the mcsnum integer data type (the MCS index loop variable for which the throughput is obtained) and the mmi float data type (the MMI as regards the MCS being calculated). The mmi2thr function receives the MCS index and MMI and computes the expected value of the throughput. More specifically, first, in order to apply the MMI-to-throughput table, the location of the current MMI input value on the MMI axis is identified by using conditional statements. Then, linear interpolation (the interp function) is employed to estimate the throughput value at an MMI value between two predetermined MMI points on the x axis, and this throughput value is returned. The MMI-to-throughput tables for MCS 0–7 are plotted in Figure 12.
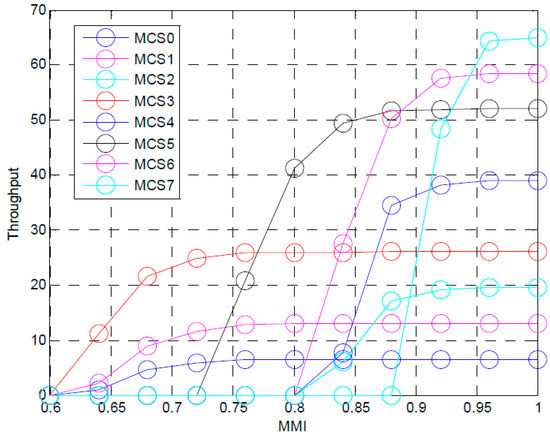
Figure 12.
MMI-to-throughput tables for modulation schemes.
3.7. Function Interp
The inputs to the interp function are the y1 float data type (the y-axis value of table variable 1), the y2 float data type (the y-axis value of the table variable 2), the dx_inv float data type (the inverse of the interval between the x-axis values of table variable 1 and table variable 2), and the a float data type (the difference between the x-axis value of the input and the x-axis value of table variable 1). The interp function conducts linear interpolation and the related operation is shown in Equation (12) with an example drawn in Figure 13.
where dx_inv corresponds to the inverse of x2 − x1 and a corresponds to x3 − x1.
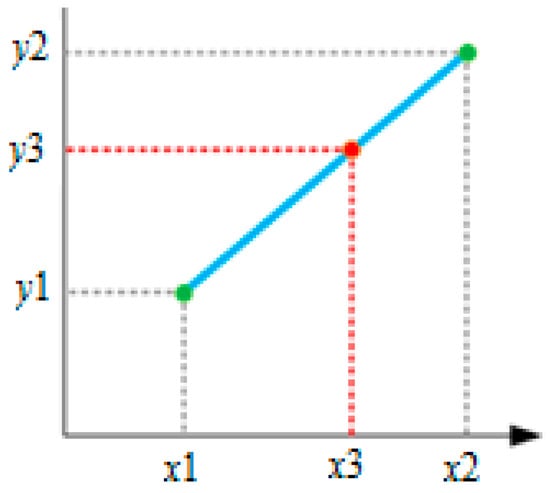
Figure 13.
Linear interpolation.
4. Operating Speed of the Link Adaptation
4.1. Execution Time Breakdown and Analysis
Figure 14 shows the analysis of the internal functions of the firmware after repeating APBLA before optimization. The experiments are made with the Xilinx Zynq 7020 programmable SoC chip that includes an embedded ARM Cortex A9 core running at 667 MHz. The timer (individual) column is obtained by measuring the execution time of each internal function in the APBLA firmware by using platform-provided library functions. The timer (overall) column is obtained by algebraically estimating the execution time according to the number of function calls of the internal functions after measuring the execution time of the overall APBLA. The measured values for the two means, timer (individual) and timer (overall), are generally similar to each other.
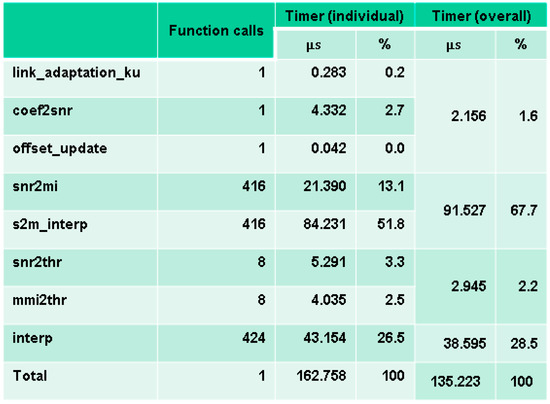
Figure 14.
Execution time per packet for each function.
It is conjectured that although the experimental environment (e.g., performance of the microprocessor unit, clock frequency, etc.,) of the SoC platform may be different than the actual operating environment of link adaptation, the ratio of each function affecting the overall execution time in the platform case will be similar to that in the actual link adaptation case. The snr2mi_interp function occupies about half of the overall execution time and the interp function with the snr2mi function is the next culprit concerning the latency. Thus, these three functions are the targets for optimization as far as the link adaptation firmware speed enhancement is concerned.
4.2. Execution Time Optimization
When the main time-consuming functions, snr2mi and interpolation functions, were compared with the other functions in the firmware, little difference was found in terms of the number of additions and multiplications but the number of conditional statements and repetitive statements was much larger with the snr2mi and interpolation functions.
In case of the snr2mi function, this function was executed once per subcarrier and the conditional statement execution regarding modulation scheme selection also occurred every subcarrier. Therefore, the firmware has been modified and optimized such that the conditional statement execution is not reiterated by the number of subcarriers but occurs for only the MCS indices, leading to a much smaller number of conditional statements executed. To achieve this, the snr2mi_interp function is made to exist for each of the four modulation schemes and within each modulation scheme, the function execution is reiterated by the number of subcarriers to obtain the MI.
The snr2mi_interp function as well has repetitive statements (the for loops) other than conditional statements. The repetitive statement execution is reiterated by the size of the table and hence the reiteration count is a fixed number. Therefore, the repetitive statements are removed and only the conditional statements are left for the sake of execution time saving. Whenever the aforementioned two optimized functions that contribute to reducing the execution time are executed, the interp functions are called, and hence in proportion to the number of executions of the interp function, the execution time is reduced by a large amount.
The execution time and ratio (in percentage) of each internal function and the total execution time before and after the optimization are listed in Figure 15. It is shown that the ratio of the execution time of each function is not altered a lot but the total execution time after optimization shrunk to less than a half of the execution time before optimization.
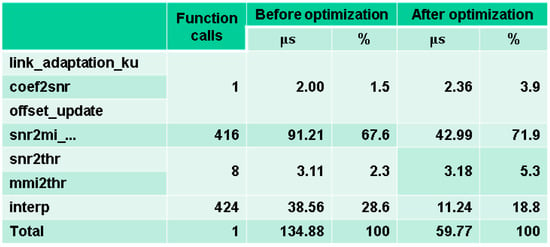
Figure 15.
Execution time and ratio of each function before and after optimization.
5. Performance Measurements and Wireless Tests of the Link Adaptation
5.1. Simulation
To identify the conditions for which the throughput gain of APBLA over ARF is guaranteed, simulation in a MATLAB environment is carried out according to packet transmission intervals and Doppler frequencies. The simulation environment to identify the throughput gain interval of APBLA relative to ARF is set up as drawn in Figure 16. Channel coefficients are first generated in MATLAB and sent to the TX as is whereas they are sent to the RX with an SNR error. The reason for this is to express the SNR difference that stems from the RF gain mismatch between the uplink and the downlink channels. Through the MMI table error the disagreement is considered between the RX performance assumed by APBLA and the actual performance. In summary, by means of the SNR error and the MMI table error, the simulation environment is made closely akin to the actual test environment. In case of ARF, link adaptation is applied every packet whereas in case of APBLA, link adaptation is applied every 1 ms when the packet transmission interval is less than 1 ms and it is applied every packet when the interval is longer than 1 ms. For example, if the transmission interval is 0.1 ARFms, ARF is applied every packet but APBLA is applied once every ten applications of ARF, in view of the operating speed of ARF and APBLA. During the time when APBLA is not applied, the MCS value of the most recently applied point in time is taken and sustained until the next applied time point.
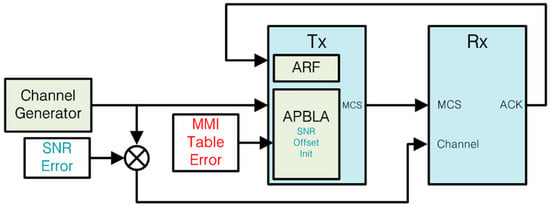
Figure 16.
Simulation setup to identify the throughput gain of APBLA vs. ARF.
Figure 17 plots the simulation results of the gain of APBLA against ARF. The x-axis is the normalized Doppler frequency. For instance, if the packet transmission interval is 1 ms and Doppler frequency is 1 Hz, the normalized Doppler frequency is 1 m, which is defined the product of the packet transmission interval and Doppler frequency. The y-axis is the throughput that is measured from ACKs stochastically produced with respect to the calculated PER in the RX model. The blue line is for ARF, the grey line for ILA, and the red line for APBLA. Here, ILA means the link adaptation model where the most ideal MCS is selected according to the received channel information. As the channel information is acquired from the preamble of the previous packet, 1 packet delay is reflected in any events. Three-tap Rayleigh fading is assumed as to MCS 0–7 in IEEE 802.11n. Also, the MMI table errors corresponding to the left half of Figure 7 are considered. From Figure 17, it is identified that when the normalized Doppler frequency increases, the throughput for ARF is heavily aggravated. On the other hand, the throughput for APBLA only modestly deteriorates as the normalized Doppler frequency grows. When the throughput gain of APBLA over ARF is maximized or equivalent when the normalized Doppler frequency is 50 m (say, when the packet transmission interval is 10 ms for a 5 Hz Doppler frequency), the ARF throughput is 24 Mbps and the APBLA throughput is 31 Mbps, yielding a throughput gain of around 30% for APBLA against ARF.
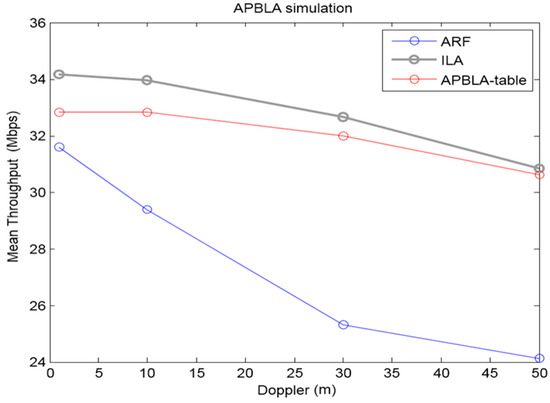
Figure 17.
APBLA vs. ARF throughput simulation results.
To identify the conditions to obtain the throughput gain of APBLA over ARF in terms of Doppler frequency and the transmission interval, simulation is carried out with the MMI table errors maximized as in the left half of Figure 18 and also with the worst case of no compensation assumed (in practice, the MMI table errors will be smaller, which can be partly compensated for by the SNR offsets, and hence the actual throughput gain is predicted to be larger). Except for the MMI table errors considered, the simulation environment is identical to that for obtaining Figure 17. One-tap and three-tap Rayleigh fading is assumed. Figure 18 represents the MMI-to-throughput tables with (left) and without (right) the MMI table errors. Since the curves on the left half of Figure 18 are shifted right or left individually, it is hard to compensate for the errors even with the SNR offsets, in which case the impact of the MMI table errors will be severe. Hereafter, the simulation environment is set up assuming that the MCS is determined by using the left half of Figure 18.
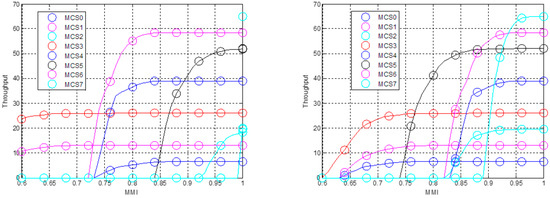
Figure 18.
Shifted (left) and standard (right) MMI-to-throughput tables.
The throughput gain of APBLA versus ARF for a 1-tap channel is plotted in Figure 19 as a function of the ARF packet transmission interval. As Doppler frequency grows from 2.5 Hz to 10 Hz, the throughput gain curves are shifted left, from which it follows that the APBLA-vs-ARF throughput gain for a 1-tap channel is up to 46% over 10 m–250 m of the normalized Doppler frequency (which is the product of Doppler frequency and the packet transmission interval).
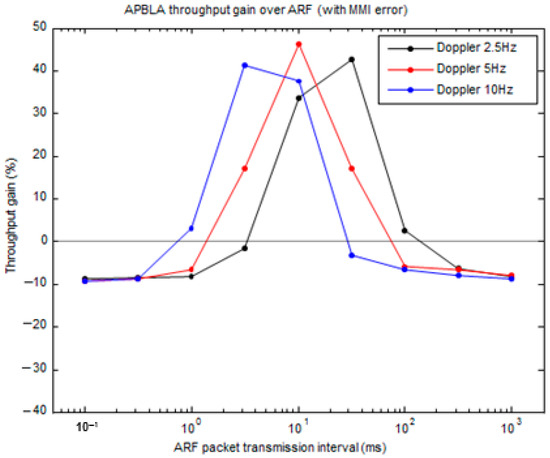
Figure 19.
Throughput gain of APBLA relative to ARF as a function of the packet transmission interval over some Doppler frequencies (1-tap channel).
The throughput gain of APBLA relative to ARF is plotted in Figure 20 for a 3-tap channel (where it is assumed that the first three taps have a uniform power-delay profile) as a function of the ARF packet transmission interval. The gain has significantly reduced and the range that the gain can be acquired has also reduced, compared with that for the 1-tap channel, but the general property that the throughput gain is limited to a specific range of the normalized Doppler frequency is maintained. Similarly to the 1-tap channel case, as Doppler frequency grows, the range where the gain of APBLA over ARF occurs is shifted to the left. The gain of APBLA over ARF for a 3-tap channel manifests itself up to 15% over 16 m–160 m of the normalized Doppler frequency.
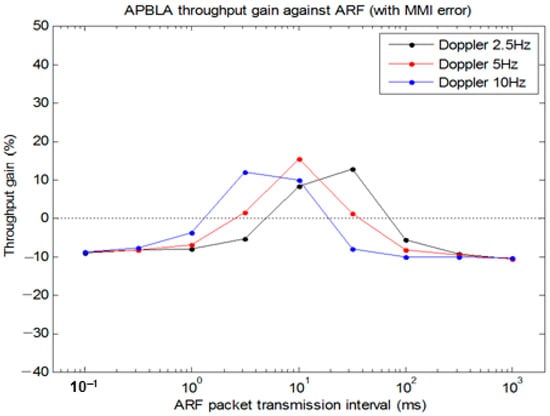
Figure 20.
Throughput gain of APBLA relative to ARF as a function of the packet transmission interval over some Doppler frequencies (3-tap channel).
In turn, given that the packet transmission interval is fixed and Doppler frequency is varied, the throughput gain of APBLA against ARF is plotted in Figure 21, which exhibits to what degree the transmission interval should be, according to Doppler frequency, when a throughput gain is expected. To summarize, with a 1-tap (3-tap) channel, the throughput gain of APBLA vs. ARF is at its maximum of 46% (15%) when the normalized Doppler frequency range is about 10 m–250 m (16 m–160 m). When the packet transmission interval is less than 1 ms, the throughput gain of APBLA over ARF can be expected only if Doppler frequency is over 100 Hz–1000 Hz. The throughput gain of APBLA relative to ARF can be maximized if the normalized Doppler frequency is about 50 m and the packet transmission interval is greater than 1 ms.
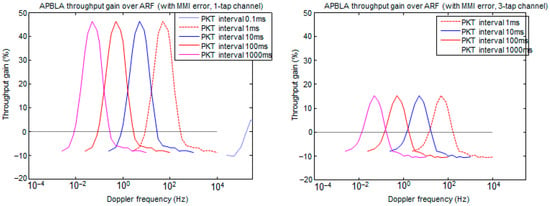
Figure 21.
Throughput gain of APBLA vs. ARF as a function of Doppler frequency over various packet transmission intervals, assuming a 1-tap channel (left) and a 3-tap channel (right).
5.2. Wireless Tests
Figure 22 shows the parameters used in the wireless tests (T0–T5) of the link adaptation firmware which includes the three algorithms, ARF, APBLA, and ARF + APBLA (i.e., initially ARF to compensate for the SNR mismatch and later converted to APBLA). An initial value of −20 dB is given as the SNR offset to compensate for the SNR mismatch due to the RF gain difference between the uplink and the downlink, in view of the channel coefficients that the firmware receives. The update step (NACK) column denotes to which extent the SNR offset is updated whenever a NACK is assumed to have occurred. On the other hand, whenever an ACK has occurred, the update step is set to a positive value with a magnitude of one tenth the update step value for a NACK. The coarse and fine update step values in case of NACK and ACK were explained previously in Section 3.3. The SNR offset and the update step values are needed in APBLA and not in ARF.
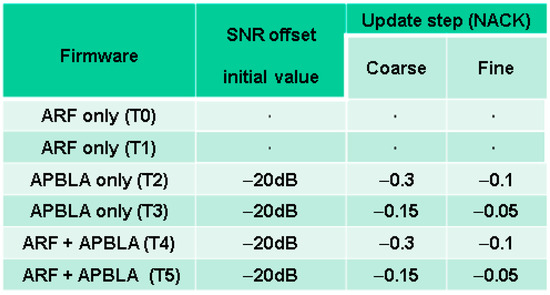
Figure 22.
Firmware and parameters used for the wireless tests.
The SNR offset variation with time when APBLA is applied in the T3 test environment is plotted in Figure 23. For the first 2k packets NACKs occur heavily and hence the SNR offset drops rapidly from −20 dB to −40 dB. Then as the SNR offset approaches near the expected value, one of the two means, coarse tuning and fine tuning, is selected and the update step is altered accordingly. Most of the wireless tests have the SNR offset reach the −45 dB to −40 dB range. The throughput measurement thereafter is conducted in the 2k-th to 10k-th packet range in which the SNR offset is relatively stabilized.
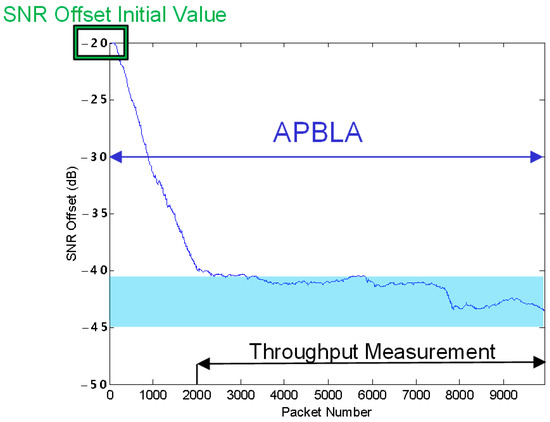
Figure 23.
SNR offset variation over time in case of APBLA only (test T3).
Figure 24 displays how the SNR offset varies with time in the T5 test environment, in which ARF is initially applied to amend the SNR offset and subsequently the algorithm is converted to APBLA. The first 5k packets are taken to be applied to ARF in this test. Compared with APBLA in Figure 23, ARF + APBLA has its SNR offset converge to the expected range more quickly.
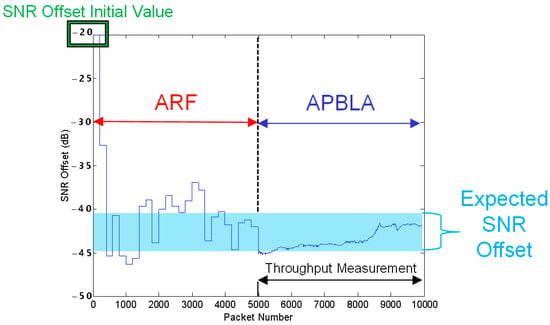
Figure 24.
SNR offset variation with time for ARF + APBLA (test T5).
Measurement results are analyzed by exploiting the channel information from the wireless tests. In Figure 25, the channel quality (left) and MCS variations (right) with time are plotted in the T1 test environment (ARF only). The MCS selected by ARF goes up and down repeatedly and quickly and hence it is inferred that the width of the channel variation will be large, which may also be identified in the left half of Figure 25 that shows the channel quality variation over time.
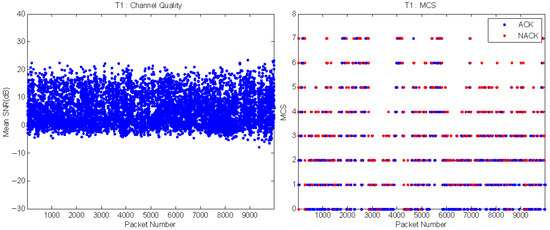
Figure 25.
T1 channel quality and ARF MCS variations as a function of time.
In Figure 26, the channel quality (left) and MCS variations (right) with time are plotted in the T5 test environment (ARF + APBLA) where initially ARF is applied to amend the SNR offset and subsequently APBLA substitutes ARF. It is shown that during the ARF period, a host of NACKs occur and ARF lowers the MCS index at a fast pace. The first 5k packets are used to amend the SNR offset and then APBLA supplants ARF, leading to stabilized MCS selection. Then, as the channel quality improves, higher MCS indices are selected. The channel quality fluctuation in this test case is not uniform, which adversely impacts the MCS selection by APBLA.
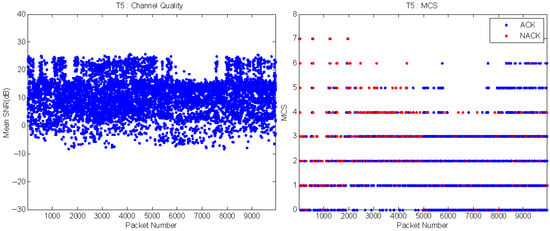
Figure 26.
T5 channel quality and (ARF + APBLA) MCS variations as a function of time.
6. Discussion and Conclusions
Link adaptation or rate adaptation is still under active research in various fields. An enhanced outer-loop link adaptation algorithm based on cyclic redundancy code and CSI is proposed [36], coding and modulation formats are adjusted according to the state of the optical link [37], rate is adapted in spatial modulation [38], adaptive modulation and coding is applied in a cognitive radio [39], link is adaptively adjusted in mobile satellite links [40], and link is adapted in 5G cellular networks and LTE Advanced [41,42,43]. In [44], MIMO mode, channel bonding, and frame aggregation level are adjusted together with modulation coding scheme in a holistic manner.
As was demonstrated from the wireless tests in Section 5, the proposed firmware achieves fast link rate adaptation, when compared with ARF and ideal link adaptation, and is amenable to potential upgrades and changes in a flexible and swift manner. The throughput gain of the proposed algorithm over ARF is 46% (15%) for a 1-tap (3-tap) channel over 10 m–250 m (16 m–160 m) normalized Doppler frequencies. For a 3-tap channel and 30 m–50 m normalized Doppler frequencies, the throughput of the proposed algorithm is about 31 Mbps, all but the same as that of ideal link adaptation, whereas the throughput of ARF is about 24 Mbps, leading to a 30% throughput gain of the proposed algorithm over ARF.
Table 2 lists the simulated results of APBLA, PBLA, and ARF, together with theoretical maximum rates, in the presence of MMI-to-PER mapping table errors. The theoretical maximum rate means the data rate of ILA, namely, the throughput achieved when the optimal MCS is always selected with respect to a given channel and hence no LA can achieve a better throughput than this throughput. PBLA is similar to FLA in [26] in its operating principle and since the mapping table is fixed, the error is not overcome and the throughput shows a large degradation, which is much inferior to that with ARF. Slow fading (at 1 m of normalized Doppler) is the optimal environment for ARF whereas fast fading (at over 5 m) is the optimal environment for APBLA, which is consistent with the remarks in other literatures. APBLA always accomplishes more than 94% of the theoretical maximum rate, irrespective of Doppler, on condition that the ACK offset is set appropriately. If the offset is set overly small, LA is unable to follow the channel variation or unable to compensate for the mapping table error whereas if set overly large, deviation from the mapping table will be severe. As is shown, the ACK offset is generally set small for slow fading and large for fast fading.
LA techniques to date are compared with one another in Table 3, in terms of performance and complexity. The LA inputs may be ACK/NACK or CSI but in some cases the cyclic redundancy code (CRC) or the log-likelihood ratio (LLR). Lots of means exist to quantify the channel quality, called link quality metrics (LQMs), but among them, MI calculated from subcarrier SNRs is generally known to be the most accurate LQM especially in coded MIMO-OFDM. The mapping table used by the LQM needs some compensation to reflect the discrepancy between two individual receivers (since different receivers will exhibit different PERs under the same MMI) or between uplink and downlink SNRs. If the mapping is adaptive rather than fixed, then the corresponding LA will be more robust to the mapping table error. Moreover, the LA with adaptive mapping can keep track of the channel variation more favorably. Most of the techniques in Table 3 are based on fixed mapping, leading to considerable performance degradations, similar to the degradation with PBLA in Table 2. Since ARF in [5] and SampleRate in [10] do not compute a separate LQM, the computational complexity is considerably low but both of them are vulnerable to fast fading owing to the fact that the optimal MCS is found by means of trial and error on the ACK/NACK basis. For example, [45] showed that SampleRate in [10] achieved a much lower throughput than the LA based on the effective SNR LQM. The proposed LA algorithm in our paper is based on the most accurate LQM, subcarrier SNR—MI, and also based on the adaptive mapping such that the algorithm is robust to mapping table errors and channel variations. Furthermore, it can attain above 94% of the theoretical max rate under fast fading as well, as was previously underscored in Table 2.

Table 3.
Comparison of this work and selected other works.
The proposed algorithm, APBLA, is associated with rate adjustment through the modulation and coding scheme. Power control and antenna selection in MIMO are not associated since the target system assumed is a 1 × 1 wireless local area network chip with no null data packet or sounding.
A fast link adaptation algorithm to maximize the throughput with preamble-based MMI calculation supplemented by the ACK mechanism to adaptively adjust the SNR offset is proposed, simulated, implemented, and tested in this paper. As additional remarks, the requirements imposed on the RF chain to guarantee the throughput gain of APBLA compared with ARF are that the RX RF chain should exhibit little RF gain variation from packet to packet, and also the SNR mismatch from the RF gain mismatch between the TX RF and the RX RF should be all but time invariant, albeit this mismatch between TX and RX can be compensated for by means of the SNR offset employed by APBLA.
Author Contributions
Conceptualization, C.S.P.; data curation, S.P.; formal analysis, S.P.; funding acquisition, C.S.P.; investigation, S.P.; methodology, S.P.; project administration, C.S.P.; resources, S.P.; software, C.S.P.; supervision, S.P.; validation, C.S.P.; visualization, C.S.P.; writing—original draft preparation, C.S.P.; writing—review and editing, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by Konkuk University in 2018.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The SNR-to-MI equations, IM(γ), as a function of SNR γ, mentioned in Section 2 and Section 3.5, are listed in Table A1. IM is the MI per symbol. The equations are different for different modulation schemes and are expressed in terms of J(x), listed in Table A2, depending on the condition of x. The coefficients which constitute J(x) are listed in Table A3.

Table A1.
SNR-to-MI equations in terms of J(x).
Table A1.
SNR-to-MI equations in terms of J(x).
| Modulation | IM(γ) |
|---|---|
| BPSK | J() |
| QPSK | J() |
| 16-QAM | 0.5 J() + 0.25 J() + 0.25 J(0.9316) |
| 64-QAM | 0.333 J() + 0.333 J() + 0.333 J(0.4765) |

Table A2.
J(x) used in IM(γ).
Table A2.
J(x) used in IM(γ).
| J(x) | Condition |
|---|---|
| a1x3 + b1x2 + c1x | 0 < x < 1.6363 |
| 1 − exp(a2x3 + b2x2 + c2x + d2) | 1.63633 ≤ x < ∞ |

Table A3.
Coefficient values of J(x).
Table A3.
Coefficient values of J(x).
| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| a1 | −0.0421061 | c1 | −0.00640081 |
| a2 | 0.00181491 | c2 | −0.08220540 |
| b1 | 0.209252 | d2 | −0.08220540 |
| b2 | −0.142675 | - | - |
References
- Karmakar, R.; Chattopadhyay, S.; Chakraborty, S. Dynamic link adaptation for high throughput wireless access networks. In Proceedings of the IEEE International Conference Advanced Networks and Telecommunication Systems, Kolkata, India, 15–18 December 2015. [Google Scholar]
- Xia, Q.; Hamdi, M.; Ben Letaief, K. Open-Loop Link Adaptation for Next-Generation IEEE 802.11n Wireless Networks. IEEE Trans. Veh. Technol. 2009, 58, 3713–3725. [Google Scholar]
- Xia, Q.; Pu, J.; Hamdi, M.; Ben Letaief, K. Practical and efficient open-loop rate/link adaptation algorithm for high-speed IEEE 802.11n WLANs. In Proceedings of the 2009 IEEE Symposium on Computers and Communications, Sousse, Tunisia, 5–8 July 2009; pp. 661–666. [Google Scholar] [CrossRef]
- Zhu, H.J.; Kidston, D. The Impact of Link Adaptation on Wifi 802.11N. In Proceedings of the 2016 IEEE International Conference on Networking, Architecture and Storage (NAS), Long Beach, CA, USA, 8–10 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Kamerman, A.; Monteban, L. WaveLAN-II: A high-performance wireless LAN for the unlicensed band. Bell. Labs Tech. J. 1997, 2, 118–133. [Google Scholar] [CrossRef]
- Chevillat, P.; Jelitto, J.; Barreto, A.N.; Truong, H. A dynamic link adaptation algorithm for IEEE 802.11 a wireless LANs. In Proceedings of the IEEE International Conference on Communications, Anchorage, AK, USA, 11–15 May 2003; pp. 1141–1145. [Google Scholar]
- Lacage, M.; Manshaei, M.H.; Turletti, T. IEEE 802.11 rate adaptation: A practical approach. In Proceedings of the Seventh ACM International Symposium Modeling, Analysis and Simulation of Wireless and Mobile Systems, Venice, Italy, 4–6 October 2004. [Google Scholar]
- Onoe Rate Control. Available online: http://sourceforge.net/projects/madwifi (accessed on 5 October 2019).
- Qiao, D.; Choi, S. Fast-responsive link adaptation for IEEE 802.11 WLANs. In Proceedings of the IEEE International Conference on Communications, Seoul, Korea, 16–20 May 2005; pp. 3583–3588. [Google Scholar]
- Bicket, J. Bit-Rate Selection in Wireless Networks. Master’s Thesis, MIT, Cambridge, MA, USA, 2005. [Google Scholar]
- Pang, Q.; Leung, V.C.M.; Liew, S.C. A rate adaptation algorithm for IEEE 802.11 WLANs based on MAC-layer loss differentiation. In Proceedings of the 2nd International Conference on Broadband Networks, Boston, MA, USA, 7 October 2005; pp. 709–717. [Google Scholar]
- Pocovi, G.; Pedersen, K.I.; Mogensen, P. Joint link adaptation and scheduling for 5G ultra-reliable low-latency communications. IEEE Access 2018, 6, 28912–28922. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.; Choi, S.; Qiao, D. CARA: Collision-Aware Rate Adaptation for IEEE 802.11 WLANs. In Proceedings of the IEEE INFOCOM 2006, 25th IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006; pp. 1–11. [Google Scholar]
- Wong, S.H.Y.; Lu, S.; Yang, H.; Bharghavan, V. Robust rate adaptation for 802.11 wireless networks. In Proceedings of the 12th Annual International Conference on Mobile Systems, Applications, and Services, Los Angeles, CA, USA, 12–16 September 2006; pp. 146–157. [Google Scholar]
- Joshi, T.; Ahuja, D.; Singh, D.; Agrawal, D. SARA: Stochastic Automata Rate Adaptation for IEEE 802.11 Networks. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 1579–1590. [Google Scholar] [CrossRef]
- Rong, Y.; Teymorian, A.Y.; Ma, L.; Cheng, X.; Choi, H.-A. A novel rate adaptation scheme for 802.11 networks. IEEE Trans. Wirel. Commun. 2009, 8, 862–870. [Google Scholar] [CrossRef]
- Holland, G.; Vaidya, N.; Bahl, P. A rate-adaptive MAC protocol for multi-Hop wireless networks. In Proceedings of the 7th Annual International Conference on Mobile Computing and Networking—MobiCom ′01, Rome, Italy, 16–21 July 2001; pp. 236–251. [Google Scholar]
- Simoens, S.; Bartolome, D. Optimum performance of link adaptation in HIPERLAN/2 system. In Proceedings of the IEEE VTS 53rd Vehicular Technology Conference, Rhodes, Greece, 6–9 May 2001; pp. 1129–1133. [Google Scholar]
- Qiao, D.; Choi, S. Goodput enhancement of IEEE 802.11a wireless LAN via link adaptation. In Proceedings of the ICC 2001 IEEE International Conference on Communications, Conference Record (Cat. No.01CH37240), Washington, DC, USA, 11–14 June 2001; Volume 7, pp. 1995–2000. [Google Scholar]
- Qiao, D.; Choi, S.; Shin, K. Goodput analysis and link adaptation for IEEE 802.11a wireless LANs. IEEE Trans. Mob. Comput. 2002, 1, 278–292. [Google Scholar] [CrossRef]
- Ericsson. System-Level Evaluation of OFDM—Further Considerations; Technical Report, 3GPP TSG-RAN WG1; Ericsson: Lisbon, Portugal, 2003. [Google Scholar]
- Lampe, M.; Giebel, T.; Rohling, H.; Zirwas, W. PER-prediction for PHY mode selection in OFDM communication systems. In Proceedings of the GLOBECOM ’03. IEEE Global Telecommunications Conference (IEEE Cat. No.03CH37489), San Francisco, CA, USA, 1–5 December 2003; pp. 25–29. [Google Scholar]
- Blankenship, Y.; Sartori, P.; Classon, B.; Desai, V.; Baum, K. Link error prediction methods for multicarrier systems. In Proceedings of the IEEE 60th Vehicular Technology Conference, Los Angeles, CA, USA, 26–29 September 2004; pp. 4175–4179. [Google Scholar]
- Bjerke, B.A.; Ketchum, J.; Walton, R.; Nanda, S.; Medvedev, I.; Wallace, M.; Howard, S. Packet Error Probability Prediction for System Level Simulations of MIMO-OFDM Based 802.11n WLANs. In Proceedings of the IEEE International Conference on Communications, Seoul, Korea, 16–20 May 2005; pp. 2538–2542. [Google Scholar]
- Simoens, S.; Rouquette-Léveil, S.; Sartori, P.; Blankenship, Y.; Classon, B. Error prediction for adaptive modulation and coding in multiple-antenna OFDM systems. Signal Process. 2006, 86, 1911–1919. [Google Scholar] [CrossRef]
- Jensen, T.L.; Kant, S.; Wehinger, J.; Fleury, B.H. Fast Link Adaptation for MIMO OFDM. IEEE Trans. Veh. Technol. 2010, 59, 3766–3778. [Google Scholar] [CrossRef]
- Peng, F.; Zhang, J.; Ryan, W.E. Adaptive Modulation and Coding for IEEE 802.11n. In Proceedings of the 2007 IEEE Wireless Communications and Networking Conference, Washington, DC, USA, 26–30 November 2007; pp. 656–661. [Google Scholar]
- Tan, P.H.; Wu, Y.; Sun, S. Link adaptation based on adaptive modulation and coding for multiple-antenna OFDM system. IEEE J. Sel. Areas Commun. 2008, 26, 1599–1606. [Google Scholar] [CrossRef]
- del Prado Pavon, J.; Choi, S. Link adaptation strategy for IEEE 802.11 WLAN via received signal strength measurement. In Proceedings of the IEEE International Conference on Communications, Anchorage, AK, USA, 11–15 May 2003; pp. 1108–1113. [Google Scholar]
- Huang, T.; Li, S.; Lu, X.; Gao, S. An Interference-Aware Rate and Channel Adaptation Scheme for Dense IEEE 802.11n Networks. Wirel. Commun. Mob. Comput. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Haratcherev, I.; Langendoen, K.; Lagendijk, R.; Sips, H. Hybrid rate control for IEEE 802.11. In Proceedings of the Second International Workshop on RESTful Design—WS-REST ′11, Philadelphia, PA, USA, 1 October 2004. [Google Scholar]
- Wang, J.; Zhai, H.; Fang, Y.; Yuang, M.C. Opportunistic media access control and rate adaptation for wireless ad hoc networks. In Proceedings of the 2004 IEEE International Conference on Communications (IEEE Cat. No.04CH37577), College Park, MD, USA, 20–24 June 2004; Volume 1, pp. 154–158. [Google Scholar]
- Sadeghi, B.; Kanodia, V.; Sabharwal, A.; Knightly, E.W. OAR: An Opportunistic Auto-Rate Media Access Protocol for Ad Hoc Networks. Wirel. Netw. 2005, 11, 39–53. [Google Scholar] [CrossRef]
- Wang, K.; Yang, F.; Zhang, Q.; Wu, D.O.; Xu, Y. Distributed cooperative rate adaptation for energy efficiency in IEEE 802.11-based multi-hop networks. In Proceedings of the 3rd International Conference on Intelligent Information, Pasadena, CA, USA, 18–20 December 2006; Volume 56, pp. 888–898. [Google Scholar]
- Choi, J.-Y.; Jo, H.-S.; Mun, C.; Yook, J.-G. Preamble-Based Adaptive Channel Estimation for IEEE 802.11p. Sensors 2019, 19, 2971. [Google Scholar] [CrossRef]
- Casado, F.B. Enhanced Link Adaptation Techniques for Cellular Networks. Ph.D. Thesis, University of Malaga, Malaga, Spain, 2017. [Google Scholar]
- Jaiswal, A.; Jain, V.K.; Kar, S. Adaptive coding and modulation (ACM) technique for performance enhancement of FSO Link. In Proceedings of the 2016 IEEE First International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2016; pp. 53–57. [Google Scholar]
- Bindu, P.; Jibukumar, M.G. Rate adaptation in generalised spatial modulation with RCPC codes. In Proceedings of the 6th Edition of International Conference on Wireless Networks & Embedded Systems, Rajpura, India, 16–17 November 2018; pp. 126–130. [Google Scholar]
- Hwang, J.; Saki, H.; Shikh-Bahaei, M. Adaptive modulation and coding and cooperative ARQ in a cognitive radio system. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics, Udupi, India, 13–16 September 2017; pp. 310–315. [Google Scholar]
- Rico-Alvariño, A.; Arnau, J.; Mosquera, C. Link adaptation in mobile satellite links: Schemes for different degrees of CSI knowledge. Int. J. Satell. Commun. Netw. 2015, 34, 679–694. [Google Scholar] [CrossRef]
- Shariatmadari, H.; Li, Z.; Uusitalo, M.A.; Iraji, S.; Jantti, R. Link adaptation design for ultra-reliable communications. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Wang, J.; Han, Y.; Li, X.; Jin, S. Design and Implementation of a 5G NR-based Link-adaptive System. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9–11 August 2020; pp. 196–201. [Google Scholar]
- Ku, G.; Walsh, J.M. Resource Allocation and Link Adaptation in LTE and LTE Advanced: A Tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1605–1633. [Google Scholar] [CrossRef]
- Kriara, L.; Marina, M.K. SampleLite: A hybrid approach to 802.11n link adaptation. ACM SIGCOMM Comput. Commun. Rev. 2015, 45, 5–13. [Google Scholar] [CrossRef]
- Halperin, D.; Hu, W.; Sheth, A.; Wetherall, D. Predictable 802.11 packet delivery from wireless channel measurements. ACM SIGCOMM Comput. Commun. Rev. 2010, 40, 159–170. [Google Scholar] [CrossRef]
- Vutukuru, M.; Balakrishnan, H.; Jamieson, K. Cross-layer wireless bit rate adaptation. ACM SIGCOMM Comput. Commun. Rev. 2009, 39, 3–14. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).