Abstract
The Wuppertal Institute developed, in the early 1990s, an input-oriented lifecycle-wide resource accounting method, the “Material Input per Service-Unit” concept (MIPS), today also referred to as “Material Footprint”. The official handbook applicable to products, services, and processes describes a MS Excel-based sequential approach for calculating MIPS. Today’s computing power, available to every researcher, and access to software and databases dedicated to lifecycle analysis make calculating MIPS using matrix inversion possible. This also opens up possibilities for enhancing MIPS-models programmatically: parameterizing the foreground and background systems, batch modeling for producing time series, and computational algorithms enhancing interpretation. The article provides (1) an overview of the methods and tools used for calculating MIPS from its origins to today, and (2) demonstrates some of the programmatically enhanced capabilities offered to MIPS-practitioners.
1. Introduction
The Wuppertal Institute (WI) developed, in the early 1990s, an input-oriented life cycle-wide resource accounting method, the “Material Input Per Service-unit” concept (MIPS) [1,2], today also referred to as “Material Footprint”. Simultaneously, the concept of Life Cycle Inventory (LCI), around since the 1960s, enjoyed significant penetration in both academia and industry [3], and evolved towards Life Cycle Impact Assessment (LCIA). The CML LCA-guide [4] introduced the midpoint characterization of LCIs, while the Eco-indicators 95 and 99 were endpoint characterization approaches. The MIPS concept was not another characterization method, rather a more comprehensive compilation of the inputs throughout the life cycle of a product system.
A MIPS value is a proxy for the environmental impact caused by the whole life cycle of a product relative to the service it provides. A MIPS value is the sum (in mass unit) of all resources (“material” in the MIPS concept) extracted from nature along the life cycle of one service-unit of the studied product. Material inputs are classified in biotic raw material, abiotic raw material, water, air, and earth movement in agriculture and silviculture.
Material input indicators represent the “cumulative primary materials demand” (by analogy to cumulative primary energy demand) and as such are “generic environmental pressure indicators” [5]. It means that they cannot substitute for substance-specific potential impact indicators usually obtained from LCA midpoint impact categories. However, considering that not all direct and indirect impacts resulting from human activities are understood, let alone modelled, material input indicators do provide complementary information. Undesired environmental consequences of human activities result in essence from the extraction of primary materials and the amount of said extraction determines the future flows that will, sooner or later, return to the environment. The rationale for material input indicators, therefore, is that there is a plausible link between increasing extraction of primary materials and increasing risk of direct and indirect detrimental consequences [5].
Over the years, the WI prepared so-called material intensity (MIT) factors for many materials, energy and transport services and made them publicly available through its website [6]. The purpose was to simplify and harmonize MIPS calculations, as these MIT factors can be reused in MIPS studies of complex products. The preparation of MIT factors, however, is cost intensive and keeping them up-to-date has proven too big a challenge for the traditional MIPS calculation method.
The MIPS concept is largely comparable to the input-side of a LCI in traditional LCA. Therefore, using LCA databases seems a promising way to streamline the calculation of MIT factors and MIPS values. There are, however, also noticeable differences between MIPS and ISO LCA. First, a MIPS-abiotic value is not simply the sum of the categories “resource, in ground” of a traditional LCI. A MIPS-abiotic value includes the total used and unused resource extraction. For example, an LCI would account for some metal input, while a MIPS would include the extracted ore (run-of-mine, i.e., used extraction) and the overburden (unused extraction). Other conceptual differences exist regarding allocation and cut-off criteria. We take these compatibility aspects into account when looking into the possibility of calculating MIPS using LCA databases.
This paper proposes to adopt modern inventory problem solving techniques to streamline the production of MIT factors and more complex MIPS. MIPS and LCA practitioners, alike, will find concrete options for calculating (abiotic) material input indicators using well established LCA software and databases. It allows MIPS and LCA analysts to extend their customary material input indicators and LCA potential impact indicators, respectively, with complementary indicators, while using a unified set of tools. Section 2 presents an overview of methods and tools historically used to calculate MIPS and expands these with the ecoinvent LCA database [7] and matrix calculations enabling analytical algorithms, dynamic modelling, and hybridization with input-output frameworks. In Section 3, we apply these “new” methods and discuss how they enhance MIPS calculations and could be further developed.
2. Methodology
2.1. Sequential MIPS
Historically MIPS was developed as a sequential inventory method comparable to the early days of LCI. All inputs from nature at each step of the process chain of the modelled product are inventoried and summed up in five categories (biotic raw material, abiotic raw material, water, air, and earth movement). The main advantage of the sequential approach is that it is in principle simple and does not require complex or costly software tools.
2.1.2. Spreadsheet-Based Calculation Tool
After the MIPS concept had matured in the 1990s, a handbook was released in the early 2000s, together with a spreadsheet calculation tool and first MIT data [8]. We briefly recall here this simple, though still popular, methodology.
A MIPS study starts by defining a product system (cradle-to-product boundaries) delivering a particular service, which includes the use and end-of-life phases of said product (cradle-to-grave boundaries). The next steps consist in representing the process chain, compiling data, and expressing total material input (MI) per mass unit of product (material intensity MIT) and/or per unit of service (MIPS).
For doing so, the MIPS spreadsheet calculation tool [9] consists of two forms: the compilation sheet and the calculation sheet. In the former, the modeller needs to input data about each process in the process chain of the modelled product system. Such data include in- and output flows (type, quantity, unit), sources, reference year, and region. Input flows are sorted out between “natural inputs” and “pre-treated/processed inputs”. Each category hosts two further levels of classification. The “natural inputs” in particular consist of “abiotic raw materials”, “biotic raw materials”, “earth movings/movements”, “water”, and “air”, which are the final material input categories of a MIPS study. “Pre-treated inputs” include electricity, transport, infrastructure, pre-products, etc.
All inputs listed in the compilation sheet are then entered in the calculation sheet scaled for one mass unit (or another physical unit, e.g., energy) of the modeled product. Natural inputs such as metals, unused extraction, biomass, etc., are added together in their respective MI categories. Pre-treated inputs (e.g. electricity, cold rolled steel, etc.) are multiplied with existing MIT factors [10], thus, augmenting these flows with their own ecological rucksacks. If MIT factors do not exist for certain important pre-treated flows, separate life cycle modelling using the same MIPS methodology is necessary. The resulting material inputs are added up with the natural inputs into the five MI categories. This finally delivers MIT values from the cradle to the modelled product, expressed in mass of moved nature by unit of mass of product.
For a cradle-to-grave approach, additional processes and material inputs involved in the use and end-of-life phases have to be drawn up on the compilation sheet. MIPS values expressed in mass of moved nature by unit of performed service are then calculated using the calculation sheet as described above.
2.1.3. Features of GaBi LCA Software
The spreadsheet calculation tool is targeted at an audience without access to dedicated software. Some of the MIT values on MIPS-online, however, were generated at the WI using specific features of the LCA software GaBi [11]. This alternative is briefly described here for the first time. Note that this approach is less automated than the custom midpoint characterization method described in Section 2.2 but allows for a control over regional differentiation not available when using a characterization method with an LCA database.
GaBi has an aggregation function that automatically adds up (without characterization factors) the elementary flows of an LCI into predefined categories. We, therefore, define new categories of elementary flows in GaBi following the classification and hierarchization used in the MIPS spreadsheet calculation tool. We create for instance a category “abiotic raw materials” consisting of the sub-categories “minerals”, “energy carrier”, “unused extraction”, and “soil excavation”. GaBi will automatically add up all elementary flows marked “minerals” together and present the result along with the detailed LCI. GaBi will, similarly, deliver an aggregated result for “abiotic materials”. MIPS values can therefore be read directly from the LCI result page in GaBi.
For this method to work, however, the relevant elementary flows must occur in the product system model and be labeled properly. The ecoinvent database or the built-in GaBi database provides no unused extraction flows, for instance. Such flows must be entered by hand along the modeled process chain, wherever they might occur. The associated cost is a limitation of this method.
Manually inputting material flows such as “unused extraction” has, however, advantages over using a rigid characterization method that would automatically associate a given unused extraction to a given elementary flow. Regional and other differences can be accounted for at the level of the extraction process and associated elementary flows.
2.2. Matrix Formulation
An inventory problem (LCI or MI inventory) can be written as a system of linear equations. First described in [12], and further explicated in [13], this method utilizes an n × n technology matrix A where any given column represents a process and the elements in this column are the inflows and outflows of commodities necessary for the execution of this process. The inventory problem is then expressed as follows (see illustration in Supplementary Material S1 and S2):
where f is an n × 1 arbitrary vector representing the service unit, A is the n × n technology matrix, and B is an m × n environmental intervention matrix. Any given row of B represents an elementary flow (natural resource, pollutant, etc.) and each element in this row corresponds to the amount extracted from or emitted to the environment by the corresponding process in column. q is an m × 1 vector representing the inventory of elementary flows from and to the environment activated by the service unit.
q = B ⋅ A−1 ⋅ f
If the matrix A respects certain conditions, such as being mono-functional (each process column produces only one output flow, which is achieved by allocation procedure) and normalized (the elements in each column are normalized for one unit of output of the corresponding process), Suh and Heijungs [14] show that the inverse of matrix A has a power series form:
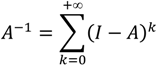
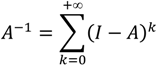
Replacing Equation (2) in Equation (1), it appears that each (I − A)k matrix represents the contribution of the kth tier down the process chain starting from the service unit vector. When the equality in Equation (2) is verified, the inventory problem can be solved with the holistic approach using matrix inversion (infinite process chain) and further analyzed using tools based on the power series expansion approach (e.g., structural path analysis, accumulative structural path analysis) [14,15]. LCA software usually implements the matrix inversion in the background and proposes such analytical tools (e.g., Sankey diagrams). The LCA or MIPS analyst can also program his/her own matrix inversion and analytical tools with numerical computation software. The necessary conditions on matrix A (also including waste streams having to be expressed as inputs of waste treatment processes and not as outputs) are met in existing commercial LCA databases such as ecoinvent.
In LCA studies, Equation (1) gives the LCI (vector q), which in turn is characterized into a life cycle impact assessment (LCIA), as follows (see illustration in Supplementary Material S1 and S2):
where C is a p × m characterization matrix. Any given row in C represents a characterization method and each element in this row is a weight (characterization factor) applied to the corresponding elementary flow (resource extraction, emission, etc.) in column. r is a p × 1 vector representing the life cycle assessment results for p environmental impact categories associated with one service unit.
r = C ⋅ q
2.3. LCA Databases
MIPS was purposely not developed as a LCI characterization method, while LCA databases were developed with midpoint and endpoint interpretation in mind. We show here, however, that MIPS calculations and today’s LCA databases can be seamlessly integrated using custom characterization methods. We use the ecoinvent database version 2.2 [7].
First, we define five midpoint categories after the five MI categories in the MIPS concept. Note that those are not “impact categories” in the usual LCIA sense. Second, we establish characterization factors (MIT factors) to convert LCI results into the five MI categories. Third, the new MI characterization method can be imported into the software of your choice and used together with ecoinvent 2.2.
We detail below how the second step is or can be implemented. In the rest of the article, we focus on abiotic materials.
2.3.1. Abiotic Raw Materials (MI Abiotic)
An ecoinvent-based LCI lists abiotic materials extracted from nature as “elementary flows” in the category “resource, in ground”. These elementary flows do not account, however, for all material flows required in a MIPS calculation: used and unused extractions are missing. Table 1 explains these terminology differences between LCI and MIPS in the case of metals. It shows how the latter, although similar in many ways to LCA, is also related to macro-level economy-wide material flow accounting.
We propose to generate characterization factors that would convert ecoinvent’s elementary flows of the category “resource, in ground” into material input flows including used and unused extraction. Table 2 shows how such MI abiotic characterization factors are constructed. We identified four cases A, B, C, and D detailed below.

Table 1.
MIPS and LCA terminologies for material flows in the case of metal mining, after [16].
| Description of the material | Common terminology | MFA/MIPS terminology | Ecoinvent LCI terminology |
|---|---|---|---|
| Material removed to get access to reserve, i.e., metal containing ores | Overburden, interburden | Unused extraction | N.A. |
| The metal containing material | Run of mine, gross ore, crude ore | Used extraction | N.A. |
| The pure metal | Net ore or metal content | Metal component of used extraction | Elementary flow |

Table 2.
Construction of selected MI abiotic characterization factors for the “midpoint impact category” MI abiotic.
| Elementary flows in ecoinvent 2.2 | Allocation factor [%] | Allocated used extraction [kg/kg elementary flow] | Unused extraction coeff. [kg/kg used extraction] | MI abiotic factor [kg/kg elementary flow] | ||
|---|---|---|---|---|---|---|
| Case | Unit | |||||
| A | Granite, in ground | [kg] | 100 | 1.00 | 0.01* (world average) | 1.01 = 1.00 × (1 + 0.01) |
| B | Nickel, 1.98% in silicates, 1.04% in crude ore, in ground | [kg] | 100 | 96.15 = 1/0.0104 | 0.60** (world average) | 153.75 = 96.15 × (1 + 0.60) |
| C | Silver, Ag 4.6E−5%, Au 1.3E−4%, in ore, in ground | [kg] | 0.26 = 4.6E−5/(4.6E−5 + 1.3E−4) | 568,181.82 = 0.26*1/4.6E−7 | 1.25 (Peru) | 1,278,409.09 = 568,181.82 × (1 + 1.25) |
| C | Copper, Cu 0.38%, Au 9.7E−4%, Ag 9.7E−4%, Zn 0.63%, Pb 0.014%, in ore, in ground | [kg] | 0.37 = 0.38/(0.38 + 2 × 9.7E−4 + 0.63 + 0.014) | 97.47 = 0.37 × 1/0.0038 | 2*** (Sweden) | 292.41 = 97.47 × (1 + 2) |
| D | Cadmium, 0.30% in sulfide, Cd 0.18%, Pb, Zn, Ag, In, in ground | [kg] | 0 (Cd is always a by-product) | 1.00 (by-product’s own mass) | N.A. | 1.00 (by-product’s own mass) |
Notes: * [17,18]; ** [19];*** Personal communication of U.S. Bureau of Mines to Dr. H. Schütz in the context of [20].
The column “unused extraction coefficient” in Table 2 corresponds to intensities expressed in kilogram unused extraction per kilogram of used extraction. The Wuppertal Institute gathered and compiled this data from a number of sources. For this beta version of the MI abiotic characterization factors, we use world averages unless the corresponding elementary flow in ecoinvent is an input to one extraction process only whose description clearly indicates a geographical reference. For example the elementary flow “Silver, Ag 4.6E−5%, Au 1.3E−4%, in ore, in ground” is an input to one process only in the ecoinvent database, “Silver, from combined gold-silver production, at refinery/PE/kg”. We therefore use an unused extraction coefficient specific to Peru.
Case A: Non-Metallic Minerals
Materials corresponding to case A in Table 2 are non-metallic minerals for which “it may generally be assumed that the difference between run-of-mine production and reported production (of commercial grade material) is not relevant” [16] (p. 34). The ecoinvent elementary flow is therefore considered equal to the used extraction. The MI abiotic characterization factor is obtained by augmenting the elementary flow with the amount of unused extraction associated with it. For example, the extraction of 1 kg granite induces 0.01 kg unused extraction on average in the world.
Cases B, C, and D below deal with materials (mostly metals) for which net and gross ore (see Table 1) do differ significantly.
Case B: Single-Metal Metallic Ores
Materials belonging to case B are metals mined alone. Used extraction (gross ore) can be estimated directly as the inverse of metal concentration in ore, about which ecoinvent provides information in the description of the elementary flows (e.g. 1.04% nickel concentration in crude ore). The unused extraction coefficient then applies to the calculated used extraction. The MI abiotic characterization factor is the sum of used and unused extraction associated with one kilogram of elementary flow.
Case C: Multiple-Metals Metallic Ores
We are in presence of “coupled production” [16] when an ore is exploited for more than one metal of economic value. For the metals in case C, we assume that the additional metals listed in the description of the ecoinvent elementary flow are co-products for which the extraction process is also operated. We therefore allocate used extraction to the elementary flow according to its mass share, following the allocation procedure prescribed in the MIPS methodology [2,8]. Ecoinvent usually uses allocation based on the value of the metal co-products but always corrects the metal elementary flows to respect the mass balance. Therefore metal elementary flows are unaffected by ecoinvent’s allocation choices and can be used directly for calculating used and unused extraction. As in case B, the unused extraction coefficient—which is identical for all co-products from one mine and independent of the allocation method (see Supplementary Material S3)—then applies to the calculated used extraction. The MI abiotic characterization factor is the sum of used and unused extraction associated with one kilogram of elementary flow.
Case D: By-Products
The MIPS handbook defines by-products as “products which are also marketable, but for which the process in not mainly operated, perhaps because the market price is too low, or because they accumulate as surplus” [8] (p.28). Neither used nor unused extraction is allocated to such products which are accounted for by their own mass only, hence the MI abiotic characterization factor equal to one.
2.3.2. Biotic Raw Materials (MI Biotic)
In the MIPS concept, biotic material inputs from nature cover plant biomass from cultivation and biomass from uncultivated areas (plants, animals, etc.), observing that domesticated animals are part of the technosphere but the fodder they receive, for example, is not [2,8]. Ecoinvent has a different approach: elementary input flows associated with biomass production are traced back to CO2 binding from the atmosphere [21]. The one elementary flow “Carbon dioxide, in air” (see Table 3) is an input to all biomass products modeled in ecoinvent but in quantities depending on the C-content of the biomass dry matter, this parameter in turn depending on the composition of the biomass. It is therefore not possible to establish one characterization factor that would convert the elementary flow “Carbon dioxide, in air” into the mass of the corresponding biomass product. A way to solve this issue would be to drop the characterization method approach. Instead, the mass of the biomass product binding CO2 from the atmosphere (i.e., one step up in the process chain of the ecoinvent-based model) would be computed into the MI biotic value.
Wood is considered elementary flows in ecoinvent (see Table 3). Wood elementary flows are expressed in volume unit. Therefore, converting such flows into mass flows would require accounting for the water content of the wood, which drastically impacts its density. Data on water content is available from ecoinvent’s meta information [22].
The approaches delineated above are not pursued in this article. Further efforts are needed for integrating ecoinvent data and MI biotic calculation.

Table 3.
Elementary flows in ecoinvent related to biotic raw material extraction.
| Elementary flows in ecoinvent 2.2 | Unit |
|---|---|
| Wood, hard, standing | [m3] |
| Wood, primary forest, standing | [m3] |
| Wood, soft, standing | [m3] |
| Wood, unspecified, standing | [m3] |
| Carbon dioxide, in air | [kg] |
2.3.3. Water (MI Water)
Any LCI generated with ecoinvent 2.2 contains nine elementary flows related to water extracted from nature and either stored or used. A ReCiPe midpoint impact category uses water depletion potential (WDP) characterization factors on five of them to build a freshwater depletion indicator. Since the ReCiPe method focuses on potential freshwater water shortages it is restricted to elementary flows where freshwater “is lost from an area” rather than “consumed, but also released very close to the point of consumption” [23]. In the MIPS concept, the MI water category encompasses all processing and cooling water from surface, ground, and deep ground water sources [2,8]. Table 4 lists the MIT water factors that we use in combination with ecoinvent elementary flows and shows the differences with WDP factors.

Table 4.
Comparison of characterization factors for ReCiPe midpoint impact category freshwater depletion and MI water category.
| Elementary flows in ecoinvent 2.2 | Unit | Water depletion, GLO (H) [m3/m3] | MIT water factor [kg/m3] |
|---|---|---|---|
| Volume occupied, reservoir | [m3] | 0 | 0 |
| Water, cooling, unspecified natural origin | [m3] | 0 | 1000 |
| Water, lake | [m3] | 1 | 1000 |
| Water, river | [m3] | 1 | 1000 |
| Water, salt, ocean | [m3] | 0 | 1025 |
| Water, salt, sole | [m3] | 0 | 1007–1200 |
| Water, turbine use, unspecified natural origin | [m3] | 0 | 0 |
| Water, unspecified natural origin | [m3] | 1 | 1000 |
| Water, well, in ground | [m3] | 1 | 1000 |
2.3.4. Earth Movement in Agriculture and Silviculture (MI Soil)
The moved soil category is defined as mechanical earth movement or erosion [2,8]. There is no corresponding elementary flow in ecoinvent. One way around this problem would be to expand the ecoinvent list of elementary flows with “Moved soil, in ground” and introduce estimates for this flow into the relevant ecoinvent processes. We leave this for future developments.
2.3.5. Air (MI Air)
Air inputs in the MIPS concept encompass combustion, and chemical and physical transformation processes [2,8]. For processes where combustion is the dominant contributor, one could use a characterization factor that would convert LCI CO2 emissions into air inputs, using the stoichiometry of the combustion equation and an average composition of air. This approach, however, would not be suitable for calcination processes (e.g., cement production, calcinated lime) and for chemical processes that use air as an input (e.g., formaldehyde production by catalytic oxidation of methanol with atmospheric oxygen). We leave these aspects for future developments.
2.3.6. Import MIT Characterization Factors into LCA Software
A beta version of the MIT abiotic characterization factors in EcoSpold format is available from Supplementary Material S3. It should be noted that this is a beta release, fit for testing but not for production as bugs may remain. Future versions will be made available through the WI website.
The EcoSpoldImpact xml file can be imported into the LCA software of your choice after you have imported the ecoinvent database and, optionally, other impact assessment methods. This approach has been tested with the software openLCA [24] and version 2.2 of the ecoinvent database.
2.3.7. Import MIT Characterization Factors into Numerical Computation Software
For those, like the authors, who prefer importing the ecoinvent database into numerical computation software (we use Scilab [25]) and program LCI and LCIA calculations from there, a beta version (same restrictions as above apply) of the MIT abiotic characterization factors is available as a text file from Supplementary Material S3. When importing ecoinvent 2.2 into Scilab, one works with the following matrices:
- Technology matrix (A) of processes × processes;
- Intervention matrix (B) of elementary flows × processes;
- Characterization matrix (C) of impact categories × elementary flows.
Importing the beta MIT abiotic characterization factors requires the following steps:
- Add an empty row to the characterization matrix C;
- Fill this new row with the MIT abiotic characterization factors in the columns corresponding to the elementary flows of the category “Resource, in ground”.
2.4. Enhancing Algorithms
What follows in Section 2.4.1 to Section 2.4.3 is a rather technical description of algorithms operating on the matrix representation of life cycle inventory problems. Established LCA software usually do apply the matrix inversion approach for producing LCI and LCIA results, even though the LCA analyst using them is not necessarily aware of what is happening in the background. Therefore, readers unfamiliar with the details of the LCI matrix formulation as presented in [12,13,14] may skip Section 2.4.1 to Section 2.4.3.
2.4.1. Structural Path Analysis and Accumulative Structural Path Analysis
Calculating MIPS using large LCA databases, as demonstrated in the previous sections, can both simplify the modeling exercise and complexify the modeled process chains. Analytical tools are needed to assess the contributions of the thousands processes interrelated in feedback loops to the life cycle impact of a product system. Structural path analysis and accumulative structural path analysis are such methods [14,26,27,28]. Expanding on such approaches, Bourgault et al. [15] describe a computationally efficient algorithm combining the matrix inversion and sequential approaches that identifies processes contributing more than a user-defined threshold to any given environmental impact category.
Bourgault’s algorithm provides detailed useful information but stops at the process level. The elementary flows activated by a given process are not further disaggregated. In the case of MI abiotic it can become critical to know which of the abiotic raw materials extracted from nature by a given process contribute most to this process’ MI abiotic category.
The following list presents Bourgault’s algorithm augmented with our own algorithm (steps 7 to 9). The disaggregation now goes all the way down to the elementary flows, subject to the user-defined threshold:
- Pre-calculation: direct C ∙ B and total C ∙ B ∙ A−1 MI abiotic for one unit of each process in the technology matrix A (“total” means life cycle-wide here);
- Build a final demand vector (f) to model the product system;
- Use the results of step 1 to calculate the reference total MI abiotic associated with the product system defined in step 2: C ∙ B ∙ A−1 ∙ f;
- Choose a disaggregation criterion (e.g., 5%), contribution threshold to MI abiotic under which processes are not further disaggregated;
- For each element in the final demand vector (or in the vectors built in step 10 after the first round), store relevant information (e.g., process name, parent process name, disaggregation path length, etc.), and scale the direct and total MI abiotic results calculated in step 1 with the demand level defined in step 2 (or step 10 after the first round);
- Divide each of the total MI abiotic results obtained in step 5 by the reference calculated in step 3. Each resulting relative contribution to total MI abiotic of the product system is compared to the disaggregation criterion. If the contribution is smaller than the disaggregation criterion, this branch of the process chain is flagged and will not be further disaggregated;
- Divide each of the direct MI abiotic results obtained in step 5 by the reference calculated in step 3. Each resulting relative contribution to total MI abiotic of the product system is compared to the disaggregation criterion. If the contribution is higher than the disaggregation criterion, go to step 8, otherwise jump to step 10;
- If the direct contribution of a given process to the total MI abiotic of the product system is higher than the disaggregation criterion, we want to find out which elementary flows contribute the most. Each non-zero element in the corresponding process column of the intervention matrix B is first scaled with the demand level defined in step 2 (or step 10 after the first round). This result is then converted into an MI abiotic value by multiplication with the MI abiotic characterization factor from matrix C corresponding to this elementary flow;
- Divide the MI abiotic results from each of the elementary flows obtained in step 8 by the reference calculated in step 3. Store the result. The resulting relative contributions to total MI abiotic of the product system can be compared to the disaggregation criterion but, whatever the ratio, no further disaggregation is possible because we have already reached the elementary flow level;
- All processes that have been tested in steps 5 to 9, and not flagged in step 6, are to be disaggregated one level deeper down the process chain. A vector is created for each of these now “parent processes”, gathering the flows from their “children processes”. The flows are scaled according to the corresponding coefficient of the technology matrix A and the demand of the parent process. Take these vectors and go back to step 5;
We have implemented this extended algorithm in Scilab with ecoinvent 2.2 and show an application in Section 3.1.
2.4.2. Dynamic MIPS
LCA and MIPS usually are static, meaning that the matrices A, B, and C and the vector f have point value coefficients (although vintages should be documented) without further possibility to let them vary over time. Dynamic LCA (DLCA) and dynamic MIPS (DMIPS) are approaches where Equation (3) becomes:
Where f(t) is a service unit vector varying over time. For example, in a mobility study where the service unit is a certain amount of person-kilometers per month, the structure of vector f may be varied accounting for changes over time in the shares of different transport modes. Technology matrix A(t) may reflect some of the developments occurring in production processes, such as efficiency improvements, input substitutions, dynamic background systems (e.g., changing energy mix). Intervention matrix B(t) may incorporate the effects over time of emission control efforts, resource efficiency strategies, etc. Characterization matrix C(t) may represent variations over time in the physical models underlying the characterization factors. In DMIPS, C(t) would account for such things as changes in metal concentration in ore and in the ratio used over unused extraction. Coefficients in A(t), B(t), C(t), and f(t) are not necessarily explicit functions of time but at least some are expressed as time series (e.g., as scenario results).
r(t) = C(t) ∙ B(t) ∙ A−1(t) ∙ f(t)
Existing DLCA studies have used LCA software and large LCA databases (e.g., Umberto and IFEU database in [29]), thus making possible to parameterize production processes and whole background systems. However, such a parameterization is tedious work in traditional LCA software—designed for static studies—thus limiting the possibility to create time series (two data points, 2010 and 2030, in [29]). Other studies have relied on fewer data (e.g., already published inventories) and thus limited parameterization to the foreground system (e.g., wafer thickness and PV efficiency in Zhai and Williams’ [30] dynamic hybrid LCA of multicrystalline silicon PV systems). A recent study [31] used ecoinvent and produced long time series of DLCA results by varying the four variables in Equation (4). The matrices and vectors were stored in Microsoft Excel and the matrix calculations performed with VBA macros. Collinge et al. [31] do not detail the algorithm used to introduce A, B, C, and f coefficients’ time series into the calculations. Moreover it is not clear whether MS Excel is a computationally efficient solution for storing and inverting long time series of potentially large sparse matrices.
We propose here a simple algorithm that LCA and MIPS analysts using numerical calculation software (e.g., Scilab) can easily implement, in particular with large LCA databases (e.g., ecoinvent, expanded or not with own process models). As prerequisite, we assume that the following matrices have been imported into the numerical calculation software of choice:
- Technology matrix A and corresponding matrix of meta-data A_meta containing at least a list of the processes in matrix A with a unique ID and their position in matrix A (i.e., row or column number, which should be the same);
- Intervention matrix B and corresponding matrix of meta-data B_meta containing at least a list of the elementary flows in matrix B with a unique ID and their row number in matrix B;
- Characterization matrix C and corresponding matrix of meta-data C_meta containing at least a list of the impact categories in matrix C with a unique ID and their row number in matrix C.
The algorithm then consists of the following steps:
Preparation:
- In the numerical calculation software, replicate the matrices A, B, and C, and vector f to cover each time step of the time series and rename the replicates accordingly (e.g., A_2020 for matrix A(t) in year 2020);
- Write a routine to automatically export spreadsheets as separate text files. Although numerical calculation software have read/write functions for usual spreadsheet programs such as Microsoft Excel, compatibility issues may arise. Using dedicated read/write functions for text files helps avoiding such issues;
For dynamic technology and intervention matrices A(t) and B(t):
- 3.
- Create a spreadsheet for each process that should be dynamic. The first row after the headers should contain at least the unique ID of this output process. Each subsequent row corresponds to an intermediary input or elementary flow that should be modified in matrix A or B, respectively. Flows that do not vary need not be listed. Each row should contain a code identifying the type of flow, the flow unique ID, and time series of the quantities needed for one unit of output process;
- 4.
- Save the spreadsheets as text files (see step 2);
- 5.
- Read each text file into the numerical calculation software. Start by matching the unique ID of the output process with the meta-data in matrix A_meta, which gives its column number (cj) in matrices A and B;
- 6.
- Then read each subsequent row. If it refers to an intermediary input, match its unique ID with the meta-data in matrix A_meta. If it refers to an elementary flow, match its unique ID with the meta-data in matrix B_meta. In both cases it also gives the row number (ri) in matrix A or B of the process or elementary flow, respectively, that should be modified. For each time step t of the time series, replace the value at the coordinate (ri; cj) of the corresponding matrix A(t) or B(t) (replicates generated in step 1) with the quantity stored in the text file;
For a dynamic characterization matrix C(t):
- 7.
- Create a spreadsheet for each characterization method that should be dynamic. The first row after the headers should contain at least the unique ID of the impact category. Each subsequent row corresponds to an elementary flow whose characterization factor should be modified in matrix C. Factors that do not vary need not be listed. Each row should contain the flow unique ID and time series of the characterization factor;
- 8.
- Save the spreadsheets as text files (see step 2);
- 9.
- Read each text file into the numerical calculation software. Start by matching the unique ID of the characterization method with the meta-data in matrix C_meta, which gives its row number (ri) in matrix C;
- 10.
- Then read each subsequent row. Match each unique ID with the meta-data in matrix B_meta. It gives the column number (cj) in matrix C of the elementary flow whose characterization factor should be modified. For each time step t of the time series, replace the value at the coordinate (ri; cj) of the corresponding matrix C(t) (replicates generated in step 1) with the quantity stored in the text file;
For a dynamic functional unit vector f(t):
- 11.
- Create a spreadsheet for the functional unit vector. The first row after the headers should contain a code that identifies it as a functional unit vector. Subsequent rows should contain the unique ID of each process making up the functional unit with time series of the quantities needed for one functional unit;
- 12.
- Save the spreadsheet as text file (see step 2);
- 13.
- Read the text file into the numerical calculation software;
- 14.
- Match each row’s unique ID with the meta-data in matrix A_meta. It gives the row number (ri) in vector f of the process whose quantity should be modified. For each time step t of the time series, replace the value at the coordinate (ri) of the corresponding vector f(t) (replicates generated in step 1) with the quantity stored in the text file;
Calculation:
- 15.
- Compute Equation (4) for each time step of the time series, save and export the results.
We have implemented this algorithm for a dynamic technology matrix A(t) in Scilab with ecoinvent 2.2 and show an application in Section 3.2.
2.4.3. Hybrid MIPS
Life cycle assessment evolved from a process-based approach to hybrid LCA, which is now considered state-of-the-art [32,33,34,35,36]. Hybrid LCA embeds the studied product system into input-ouput accounts, thus greatly improving the completeness of the system representation and reducing the problem of truncation [37]. Suh and Huppes [13] describe three hybrid approaches: tiered analysis, IO-based hybrid analysis, and integrated hybrid analysis.
In tiered analysis IO-based LCI or LCIA results are simply added to process-based LCI or LCIA results. The part of the model using input-ouput typically corresponds to inputs (such as services) in the upstream process-chain that are not explicitly modeled in the process-based approach.
IO-based hybrid analysis is a tiered analysis where the use and end-of-life phases of the product system are modeled process-based, while the entire upstream process-chain is modeled with a disaggregated input-output table. Industries in the original input-ouput table are disaggregated iteratively and so are the environmental extensions, until the production phase of the product system can be modeled accurately and comprehensively.
Integrated hybrid analysis builds an expanded technology matrix in four blocks, with the process-based technology matrix A in the top left corner and the input-ouput table in the bottom right corner. Equation (1) becomes Equation (5) [13]. Both blocks are then linked with the matrices X and Y. Block-matrix X represents upstream inputs into the product system not modeled process-based but included via the input-output system. Block-matrix Y represents flows from the process-based system to the input-output system.
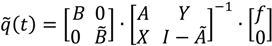
Each of these approaches can be used to produce hybrid MIPS. It requires, however, to use input-ouput tables with environmental extensions that include both used and unused material extraction, or to generate such extensions.
In Section 3.3, we present a simple application of a tiered hybrid MIPS using Scilab, ecoinvent 2.2, and the World Input Output Database.
3. Results and Discussion
What follows offers simple but eloquent example applications of how the algorithms described in Section 2.4.1 to Section 2.4.3 can enhance MIPS calculations. Readers who skipped those sections may skim through the technical details related to linear algebra in the following. LCA software users with access to ecoinvent 2.2 can easily reproduce the results presented in Section 3.2 after importing the EcoSpoldImpact file available from the Supplementary Material.
3.1. Application of Structural Path Analysis
When testing MIPS calculation with ecoinvent and MI abiotic characterization factors, we needed a procedure to locate potential sources of error. When an ecoinvent-based MIPS result looked suspicious compared to existing MIPS data, we ran a structural path analysis to identify the processes and elementary flows contributing most the MIPS result. We then had valuable information on possible sources for the discrepancy: difference in the modeling of the process chain, problem with some of the MI abiotic characterization factors, etc.
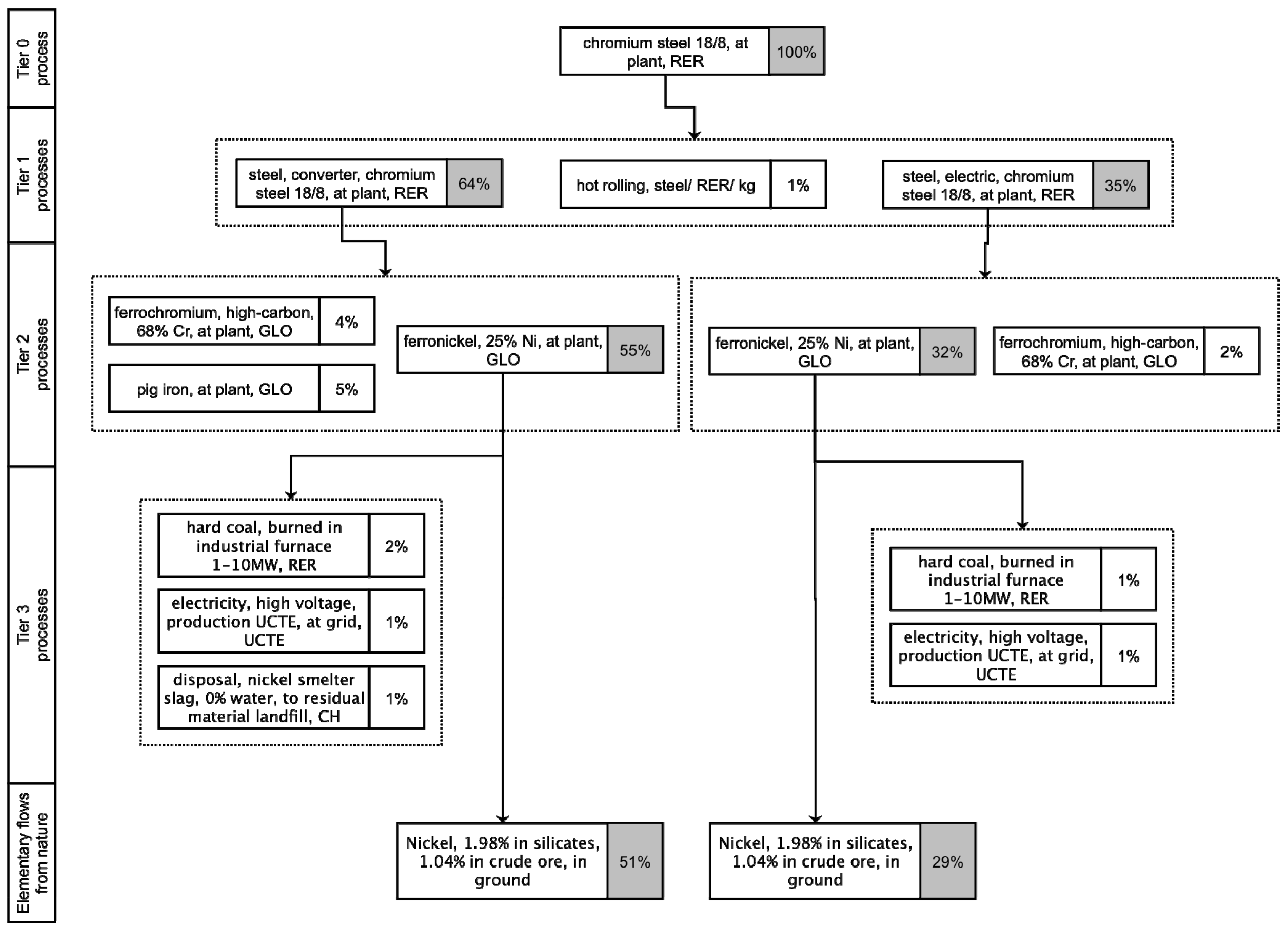
The situation described above occurred when calculating the MI abiotic of stainless steel using ecoinvent 2.2’s process “Chromium steel 18/8, at plant, RER”. A value of 107 kg abiotic material extracted per kg of produced stainless steel came out. The WI MIT table provides a value around 15 kg/kg for a comparable product. Part of the difference can be related to different shares of primary vs. secondary materials, different energy background systems, etc., but there was possibly something else.
We therefore ran the MI abiotic of ecoinvent’s “Chromium steel, 18/8, at plant, RER” through a structural path analysis as described in Section 2.4.1. Processes contributing 5% or more to the overall MI abiotic were further disaggregated. The result of the disaggregation is shown in Figure 1. Processes contributing at least 1% of MI abiotic are shown. The disaggregation algorithm went three levels down the process chain (tier 3) and also examined some elementary flows. It appears that 80% of the MI abiotic indicator for stainless steel results from inputs of the elementary flow “Nickel, 1.98% in silicates, 1.04% in crude ore, in ground” into the process “Ferronickel, 25% Ni, at plant, GLO”.
After looking into ecoinvent’s documentation [38], we applied a simple correction to the elementary flow inputs of the process “Ferronickel, 25% Ni, at plant, GLO”. The rationale for the correction is described in the Supplementary Material S4. The correction drastically changes the MI abiotic value of stainless steel, now at 45 kg/kg down from 107 kg/kg. The new value is still higher than past MIPS calculations have shown, but the difference is in a range not incompatible with differences due to background system modeling, cut-off criteria, etc. The correction noticeably has no impact on impact categories such as climate change and terrestrial acidification, which may partly explain why the issue went unnoticed so far (see Table S1 in Supplementary Material). All results shown in the rest of the article use ecoinvent 2.2 with “Ferronickel, 25% Ni, at plant, GLO” corrected.
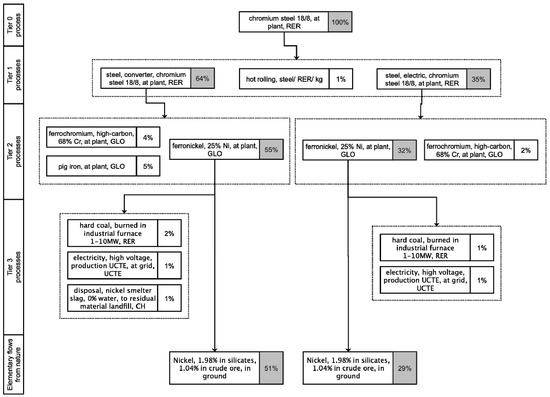
Figure 1.
Structural path analysis for MI abiotic of stainless steel calculated with ecoinvent 2.2 (% of MI abiotic of “chromium steel 18/8, at plant, RER”).
Figure 1.
Structural path analysis for MI abiotic of stainless steel calculated with ecoinvent 2.2 (% of MI abiotic of “chromium steel 18/8, at plant, RER”).
3.2. Application of Midpoint MI Abiotic Characterization Method
With the ecoinvent matrices (technology A, intervention B, characterization C) imported into Scilab and matrix C expanded with MI abiotic characterization factors, one can easily calculate MI abiotic values for all ecoinvent 2.2 processes. It takes no more than a few minutes to invert matrix A with the computing power about any researcher has access to today.
The MI abiotic results obtained are abiotic MIT values because they are expressed in kg per unit of product (“process” in ecoinvent terminology) expressed in kg or kWh, etc. without reference to a service-unit. We selected some MIT values from the table available on MIPS online. Criteria for selection were robustness/variability of the MIT values and relevance of the material as input into more complex products. We picked up a total of 23 materials from seven categories: metals (5), basic materials (3), energy and fuels (2), chemicals (4), plastics (4), construction materials (3), and others (2). We then screened the ecoinvent-based MIT values (over 4000 in total) and isolated processes with matching descriptions. If several ecoinvent processes corresponded to one MIPS online material description, we then selected a representative with matching geographical specifications.
Figure 2 shows on a logarithmic scale how the MIT values from MIPS online (black diamonds on the graph) and the ecoinvent-based MIT values compare (see Supplementary Material S5 for the detail of the data used). For plastics, glass, and cardboard the ecoinvent representative (white diamond) matches very closely the corresponding MIPS online material. Basic materials also show close results, apart from “soda” (MIT value higher by a factor 1.9 in MIPS online). However, the geographical reference is different for this material: Germany for MIPS online, Europe for ecoinvent. The background systems are therefore sure to have been modeled quite differently. The selected chemicals and construction materials also have different geographical references (Germany for MIPS online, Europe or world for ecoinvent). The ratio between MIPS online and ecoinvent, however, is sometimes higher, sometimes lower than 1, which indicates that other parameters have an influence. The unused extraction intensity of raw materials is probably a prominent one.
The MIPS online MIT values have in most cases out-of-date energy systems in the background. The German electricity mix, however, has been updated to 2008. Its MIT value is close to that of the corresponding ecoinvent process (vintage 2005).
The MIPS online table has over ten abiotic MIT values (not shown on Figure 2) for different qualities of hard coal from different countries with an order of magnitude between the lowest (1.47 kg/kg, for one sort of German hard coal) and highest (15.32 kg/kg, Canada). We have chosen the world average value (5.06 kg/kg) for Figure 2, which is lower but comparable to the ecoinvent representative we have chosen (7.52 kg/kg for hard coal mix, at regional storage—i.e., it includes some more transport—for countries in the Union for the Co-ordination of Transmission of Electricity—UCTE). It is important to note here that there is only one type of “hard coal, in ground” in ecoinvent’s elementary flows, and consequently only one characterization factor. This is a drawback of the approach with characterization factors but the comparison here shows that the approximation is acceptable. If coal inputs play a decisive part in the product system modeled it is then recommended to re-model the coal supply chain as well, introducing a specific elementary flow (e.g., “hard coal, Germany, in ground”) and its corresponding characterization factor.
The abiotic MIT values for metals depicted in Figure 2 show some differences between MIPS online and ecoinvent. However, there are often in ecoinvent several different processes producing one given metal. The MIT abiotic of such alternative processes (“+” on the graph)—i.e., that we did not choose as representatives—can span quite a range. The MIT abiotic of primary gold and copper (world) are respectively twice and three times higher based on ecoinvent than on MIPS online. Those values are, however, well within the overall range including the other ecoinvent gold and copper processes. The MIT value for the ecoinvent process “gold, at refinery, South Africa” (one of the largest producers) matches perfectly the value from MIPS online. The WI has further unpublished MIT abiotic results for copper mining that nicely fit with the range obtained from ecoinvent.
This heterogeneity is not surprising considering all the parameters that can influence the final MIT abiotic. Such parameters include metal concentration in ore, which in turn influences the processing technologies that differ regarding energy intensity, recovery yields, etc. For example, in steel production, the ecoinvent-based MIT values are consistently higher than MIPS online. Ecoinvent uses the elementary flow “iron, 25% in crude ore” as basis for all steel products. The MIPS online value takes into account, however, that many steel production processes now rely on high-grade iron ore to increase efficiency, which reduces abiotic MIT.
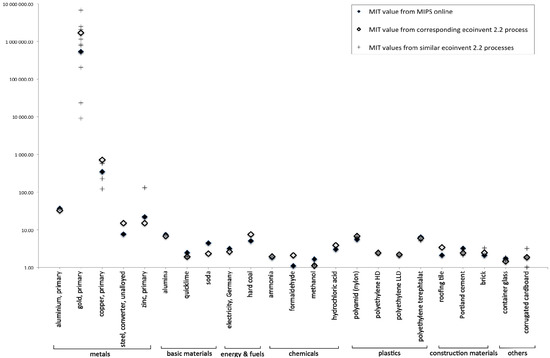
Figure 2.
Comparison between MIT values from MIPS online and values calculated with our MI characterization method applied to ecoinvent 2.2 (MIT values in kg/kg, except for electricity in kg/kWh; logarithmic scale).
Figure 2.
Comparison between MIT values from MIPS online and values calculated with our MI characterization method applied to ecoinvent 2.2 (MIT values in kg/kg, except for electricity in kg/kWh; logarithmic scale).
This first evaluation of abiotic MIT values calculated with a custom midpoint characterization method shows very promising results. We did not expect perfect matches between MIPS online and ecoinvent-based values but at least values within a reasonable range from one another, accounting for differences in background systems, regional specifications, etc. This is the case. The combination of the matrix formulation of the inventory problem, a large LCA database, and reliable MI abiotic characterization factors opens up new possibilities for calculating MIPS.
3.3. Application of Dynamic MIPS
We present here a simple application of dynamic MIPS. The underlying equation is the following simplification of Equation (4):
r(t) = C ∙ B ∙ A−1(t) ∙ f
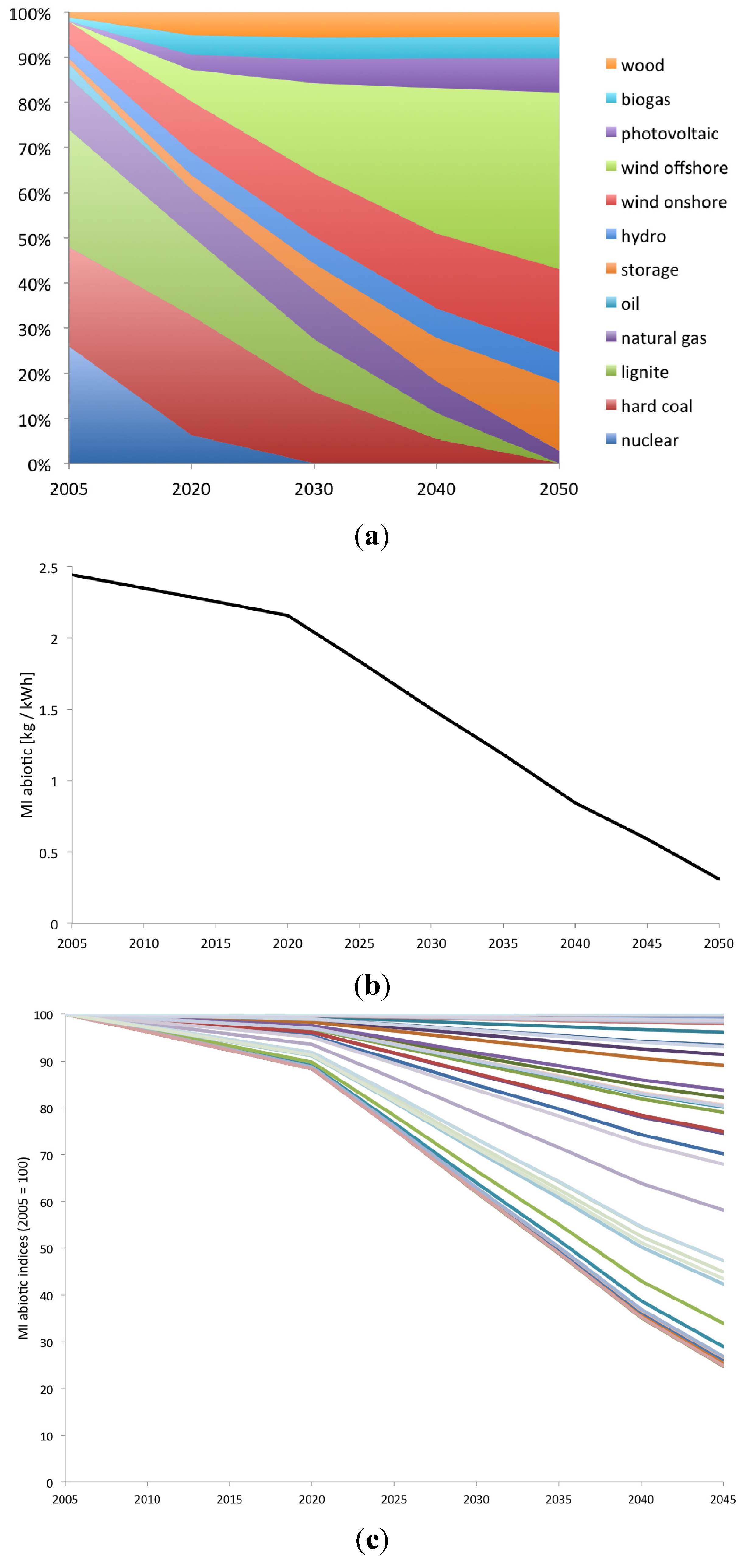
We build instances of the dynamic technology matrix A(t) in five-year time steps for the period 2005 to 2050. We modify the ecoinvent 2.2 process “electricity mix, DE, kWh” using the scenario “Innovation without CCS” developed for WWF Germany [39]. According to this scenario, nuclear energy and fossil energy carriers except natural gas are phased out in Germany until 2050. The scenario provides time series of net power generation detailed by technology (see Figure 3a). The original ecoinvent process “electricity mix, DE, kWh” includes power imports from neighboring countries. For the sake of simplification, we use the net power data and model all power generation as domestic production. This is equivalent to assume that export countries use the same technologies as Germany. We choose existing ecoinvent processes to model the different energy technologies in the German mix. The WWF scenario includes geothermal energy for which there is no ecoinvent process. We distributed the contribution of geothermal energy over the other non-biomass renewable energy technologies according to their sizes in the scenario. The WWF scenario has one item “biomass” that we have split between biogas and wood according to their respective shares in the original ecoinvent dataset. The result is a text file (presented in Supplementary Material S6) listing the contributions of each power technology over the time series. We imported the file into Scilab along with the ecoinvent 2.2 database and the MI abiotic characterization method and processed it as described in the algorithm in Section 2.4.2 (see illustration in Supplementary Material S6).
Figure 3b shows that the life cycle-wide abiotic material intensity of power generation in Germany decreases by 87% (from 2.4 kg/kWh to 0.3 kg/kWh) in this scenario. It is mainly due to the phase out of power generation from lignite and hard coal whose abiotic rucksacks outweigh that of renewable energies. However, this should not be over-interpreted given the limitations of the model (e.g., expansion of power networks, power storage, etc., are missing). In this simplistic model, only the German energy mix is dynamic. No efficiency gain is assumed in the power or any other sector. Despite the limited dynamics, the life cycle MI abiotic value of any ecoinvent process is affected if it requires German electricity at some point in its supply chains. Figure 3c illustrates this with MI abiotic values from the 107 ecoinvent processes that report Germany as region of reference.
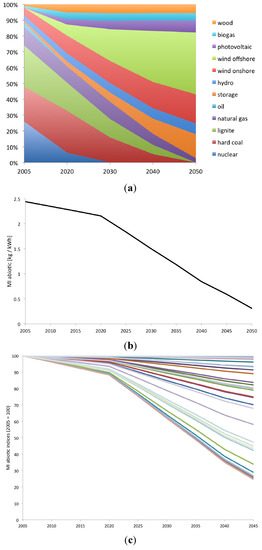
Figure 3.
(a) Scenario of net power generation in Germany 2005–2050, adapted from the scenario “Innovation without CCS” in [39]; (b) Resulting MI abiotic time series for the process “electricity mix, DE” (in kg/kWh); (c) Impact of the scenario on the life cycle-wide MI abiotic value of ecoinvent processes with Germany as region of reference (indices 2005 = 100).
Figure 3.
(a) Scenario of net power generation in Germany 2005–2050, adapted from the scenario “Innovation without CCS” in [39]; (b) Resulting MI abiotic time series for the process “electricity mix, DE” (in kg/kWh); (c) Impact of the scenario on the life cycle-wide MI abiotic value of ecoinvent processes with Germany as region of reference (indices 2005 = 100).
3.4. Application of Tiered Hybrid MIPS-IOA
We present here a simple application of tiered hybrid MIPS analysis. We extend a process-based wind power plant model with an environmentally extended input-output model. The general equation is as follows:
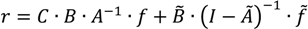
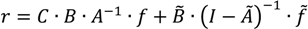
The term C ∙ B ∙ A−1 ∙ f corresponds to Equation (3). The technology matrix A and intervention matrix B are from ecoinvent 2.2. The ferronickel process in matrix A has been modified as described in Section 3.1. Matrix C is a characterization matrix extended with the MI abiotic characterization method presented in Section 2.2.
The term 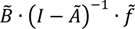 is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension
is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension 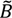 is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD.
is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD.
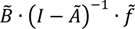 is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension
is the input-output-based extension to the process-based model. The input-output table à is the coefficient matrix built from the 2009 world input-output table “WIOT 2009” [40] of the World Input-Output Database (WIOD) [41]. The environmental extension 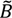 is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD.
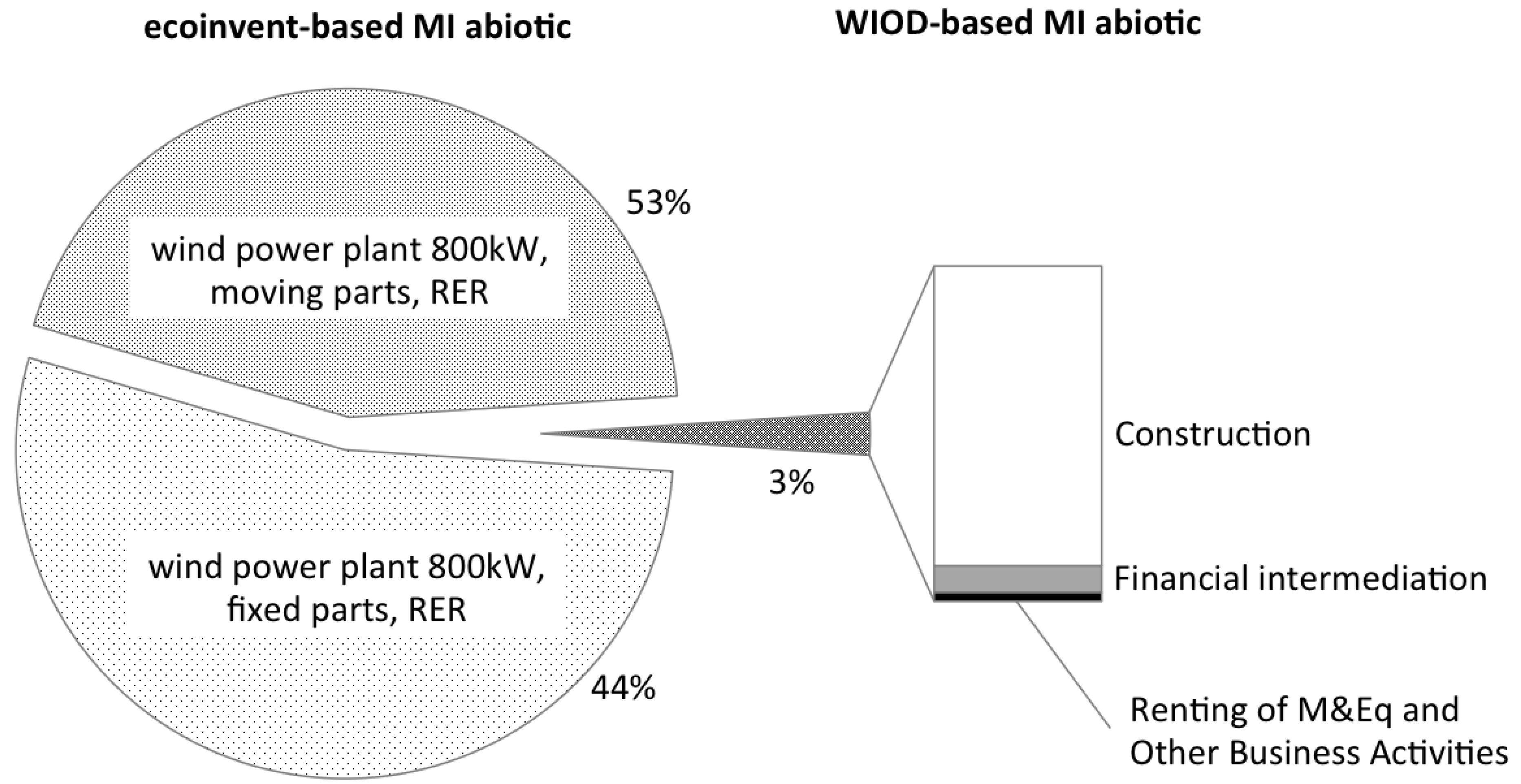
is the coefficient matrix built from the material use accounts for all countries [42] also available from WIOD.Our overall functional unit is “one wind power plant 800 kW, Europe”. The process-based functional unit vector f pulls two processes from ecoinvent 2.2: “wind power plant 800 kW, fixed parts, RER, unit” and “wind power plant 800 kW, moving parts, RER, unit”. This ecoinvent model covers the processing, transport, and disposal of the materials required for the fixed (tower and base) and moving (rotor, nacelle, electric parts) components of the wind turbine, the energy requirements for the installation itself, and the connection to the grid [43]. The industry-based functional unit vector 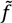 contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.
contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.
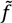 contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.
contains demand (in USD) for three industries chosen to represent the parts of the supply chain that are not included in the ecoinvent model. The US National Renewable Energy Laboratory (NREL) provides a detailed breakdown of the cost of a wind turbine on a USD/kW basis [44] and Table 5 shows which items of the breakdown are matched with WIOD industries.The input-output-based tier represents about 3% of the modeled total abiotic material requirement for an 800 kW wind turbine (Figure 4). The construction industry contributes by far the highest share among the three upstream services added to the supply chain. This could be an indication that the analysis of technologies requiring roads and civil works (e.g., installed away from human settlements) could be enhanced with input-ouput analysis since cost data for this kind of input is more readily available and easier to handle than dedicated process-based models. The tiered hybrid MIPS analysis application presented here should not be over-interpreted, however: it has an illustrative purpose only. Several aspects should be made consistent in a real-world case study: the ecoinvent process is representative of technology in Europe until the year 2002, at the latest; the NREL cost breakdown represents the situation in the US in 2010, which we combined with German industries in the 2009 WIOD world input-output table. For a state-of-the-art hybrid LCA of wind energy, see for example Wiedemann et al. [45] who apply both Input-Output-based Hybrid LCA and Integrated Hybrid LCA to wind power in the UK, describing for the first time a fully integrated hybrid system in a biregional supply and use framework.

Table 5.
Breakdown of land-based wind turbine cost by [44] and modeling of each component with process-sum or input-output approaches.
| Components of installed capital costs | NREL cost modeling [$/kW] | included in ecoinvent model | included in IOA model + WIOD industry |
|---|---|---|---|
| Direct capital cost | |||
| Turbine | 1212 | yes | no |
| Foundations | 57 | yes | no |
| Electrical interface and connections | 154 | yes | no |
| Indirect capital costs | |||
| Turbine transportation | 40 | yes | no |
| Roads and civil work | 85 | no | yes—Construction |
| Turbine assembly and installation | 59 | yes | no |
| Engineering and permits | 24 | no | yes—Renting of M&Eq and Other Business Activities |
| Soft costs | |||
| Contingencies | 100 | no | no |
| Market price adjustment | 362 | no | no |
| Financing cost | 63 | no | yes—Financial Intermediation |
Figure 4.
Tiered hybrid IOA-MIPS of an 800 kW wind turbine; the process-based part uses ecoinvent 2.2 with the MI abiotic characterization method; the input-output part uses WIOD tables and environmental extensions.
Figure 4.
Tiered hybrid IOA-MIPS of an 800 kW wind turbine; the process-based part uses ecoinvent 2.2 with the MI abiotic characterization method; the input-output part uses WIOD tables and environmental extensions.
3.5. Discussion
Abiotic MIT values can be calculated using ecoinvent 2.2 and abiotic characterization factors. The results we obtain are of the same order of magnitude than existing MIT results. Some of the discrepancies that still exist are the result of several inhomogeneities in the modeling: cut-off criteria, background systems, allocation procedures, year, and region of reference. In certain cases the reason can be pinpointed very precisely. For example, the ecoinvent iron/steel processes use lower grade ores compared to existing MIPS studies. This may stem from the fact that current LCA studies are often aimed at life cycle outputs (e.g., emissions) or, when looking into life cycle inputs, do not account for used and unused extraction. In the latter case, whether modeling, for example, life cycle iron use, or implementing the midpoint characterization method Abiotic Depletion Potential, only the existing “net ore” elementary flows are required. Since used and unused extraction quantities are closely linked to ore quality and mining techniques, extraction processes are usually more differentiated in MIPS studies.
A closer integration of MIPS concepts into LCA databases such as ecoinvent could help overcome this issue. New elementary flows labelled “used extraction” and “unused extraction” would be introduced. Some of the existing ecoinvent extraction processes could be duplicated and modeled with different used and unused extractions (and possibly other changes regarding e.g., energy intensity) to represent the extraction of different types of ores. The MI abiotic characterization method would then simply add up the used and unused extraction elementary flows, leaving out the traditional “net ore” elementary flows, thus avoiding double counting.
Future-oriented MIPS analyses can be tackled with dynamic MIPS. Forecasts of technological change in the foreground and background systems are used to alter the technology matrix A and intervention matrix B. To keep the added complexity manageable, processes both contributing significantly to the MIPS results and expected to vary substantially over time should be focused on [46]. We focused in this paper on abiotic MI, MIT, and MIPS values. Possible variations of used and unused extraction in the mining industry are critical for future-oriented MIPS studies. Therefore, MI abiotic characterization factors in matrix C should be dynamic too. First, used and unused extraction of certain minerals may represent a considerable share of a given MIPS result. Second, variations at these levels can also induce large changes in reagent, energy and water requirements in subsequent processing steps. Quantifying such future changes is difficult and specific data scarce. But certain trends are clear and should be accounted for. Mudd [47] produced an authoritative study on Australian mining industry. He found strong evidence that “ore grades are in gradual but permanent decline”, “solid waste burden (waste rock/overburden and tailings) per unit mineral is increasing”, and metallurgically “more complex ores are now being developed” (with the suspicion that this leads to “a gradual increase in reagent, energy and water requirements as well as pollutant release problems”) [47] (pp. 126 and 127). Because of its impact on mine economics, mine infrastructure, and the environment unused extraction (“waste rock”) is deemed “a fundamentally strategic and critical issue facing the mining sector in Australia, as well as worldwide” [47] (p. 120). This statement supports both the relevance of an indicator such as MIPS that accounts for such flows and the necessity of a dynamic approach to MIPS that would account for changes over time.
Hybrid MIPS analyses can be conducted today and represent the same improvement over regular MIPS as hybrid LCA over regular LCA: limit truncation errors [26] and embed product systems within the macro-economic system [37]. A limitation to hybrid MIPS is the availability of physical environmental accounts dealing with material flows and compatible with existing input-output tables. The World Input-Output Database (see Section 3.4) proposes time series (1995–2009) of trade-linked input-output tables (30 countries and rest-of-the-world; 35 industries) augmented with environmental accounts that include extraction of five biotic and seven abiotic materials, each declined in used and unused extraction. The EXIOBASE [48] provides a multi-regional environmentally extended input-output table for one reference year (2000), covering 43 countries and the rest-of-the-world, 129 industry sectors and products, and the used and unused extraction of 23 biotic and 25 abiotic materials. Five-yearly (latest in 2008) symmetric input-output tables (64 activities/products) are available from Eurostat [49] for the European Member States. The physical flow accounts provided by Eurostat [50] cover the domestic used extraction and imports of 24 biotic and 29 abiotic materials but are not readily usable as environmental extensions. The European Environmental Agency [51] published an input-output analysis of European production and consumption using environmental extensions that include both used and unused extraction, thus potentially adapted for hybrid MIPS too. These extensions were generated by combining Eurostat’s used material flow accounts and Wuppertal Institute’s data on associated unused extraction.
4. Conclusions
This article has attempted to provide a complete picture of historical MIPS calculation methods and extend it with modern inventory problem solving techniques based on matrix inversion. The matrix formulation is a powerful one. It allows one to rather simply use whole LCA databases and implement algorithms for in-depth result analysis, dynamic modeling, and hybridization with IOA. We have demonstrated how a custom midpoint characterization method can be applied to the ecoinvent database for calculating abiotic MIT and MIPS.
We conclude that it is viable to use ecoinvent data combined with abiotic MI characterization factors and that this approach can be extended to other MI categories. We advocate a closer integration of the MIPS concept in LCA databases such as ecoinvent, which would benefit both ISO LCA and MIPS analysts. New elementary flows would cover “used extraction” and “unused extraction”. Extracting processes modeled in the technology matrix would be more differentiated (e.g., regarding ore types). We also conclude that MIPS calculations based on matrix inversion opens up a new range of applications towards dynamic and hybrid studies, which places MIPS at a similar level of development as its well-established LCA counterpart.
Acknowledgments
The authors thank and acknowledge Helmut Schütz (Wuppertal Institute) for compiling and providing the data on unused extraction necessary for generating the MI abiotic characterization factors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schmidt-Bleek, F. Wieviel Umwelt braucht der Mensch? MIPS—Das Maß für ökologisches Wirtschaften, 1st ed.; Birkhäuser Verlag: Basel, Switzerland, 1993. [Google Scholar]
- Schmidt-Bleek, F. Das MIPS-Konzept, 1st ed.; Droemer-Knaur-Verlag: Munich, Germany, 1998. [Google Scholar]
- Vigon, B.W.; Tolle, D.A.; Cornaby, B.W.; Latham, H.C.; Harrison, C.L.; Boguski, T.L. Life Cycle Assessment: Inventory Guidelines and Principles; EPA/600/R-92/245; U.S. Environmental Protection Agency: Washington, DC, USA, 1993. [Google Scholar]
- Guinée, J.B.; Gorrée, M.; Heijungs, R.; Huppes, G.; Kleijn, R.; de Koning, A.; van Oers, L.; Wegener Sleeswijk, A.; Suh, S.; Udo de Haes, H.A.; et al. I: LCA in perspective. IIa: Guide. IIb: Operational annex. III: Scientific background. In Handbook on Life Cycle Assessment. Operational Guide to the ISO Standards; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2002. [Google Scholar]
- Bringezu, S.; Schütz, H.; Moll, S. Rationale for and interpretation of economy-wide materials flow analysis and derived indicators. J. Ind. Ecol. 2003, 7, 43–64. [Google Scholar] [CrossRef]
- MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/en/projects/topics-online/mips/ (accessed on 23 July 2013).
- Frischknecht, R.; Jungbluth, N.; Althaus, H.J.; Doka, G.; Dones, R.; Heck, T.; Hellweg, S.; Hischier, R.; Nemecek, T.; Rebitzer, G.; et al. Overview and Methodology—Data v2.0 (2007); ecoinvent Report No. 1; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- Ritthoff, M.; Rohn, H.; Liedtke, C. Calculating MIPS—Resource Productivity of Products and Services; Wuppertal Spezial 27e; Wuppertal Institute for Climate, Environment and Energy: Wuppertal, Germany, 2002. [Google Scholar]
- MIPS Calculation Sheet. MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/uploads/tx_wupperinst/MIPS_calculation-sheet.xls (accessed on 23 July 2013).
- Material Intensity Factors. MIPS Online. Wuppertal Institute for Climate, Environment and Energy. Available online: http://wupperinst.org/uploads/tx_wupperinst/MIT_2011.pdf (accessed on 23 July 2013).
- GaBi Software Homepage. Available online: http://www.gabi-software.com/international/index/ (accessed on 23 July 2013).
- Heijungs, R. A generic method for the identification of options for cleaner products. Ecol. Econ. 1994, 10, 69–81. [Google Scholar] [CrossRef]
- Suh, S.; Huppes, G. Methods for life cycle inventory of a product. J. Clean. Prod. 2005, 13, 687–697. [Google Scholar] [CrossRef]
- Suh, S.; Heijungs, R. Power series expansion and structural analysis for life cycle assessment. Int. J. Life Cycle Assess. 2007, 12, 381–390. [Google Scholar]
- Bourgault, G.; Lesage, P.; Samson, R. Systematic disaggregation: A hybrid LCI computation algorithm enhancing interpretation phase in LCA. Int. J. Life Cycle Assess. 2012, 17, 774–786. [Google Scholar] [CrossRef]
- Weisz, H.; Krausmann, F.; Eisenmenger, N.; Schütz, H.; Haas, W.; Schaffartzik, A. Economy—Wide Material Flow Accounting—“A Compilation Guide”; Eurostat: Luxembourg, 2007. [Google Scholar]
- WRI Materials Flows Database. Available online: http://www.wri.org/publication/material-flow-accounts#database (accessed on 23 July 2013).
- Wernick, I.K.; Irwin, F.H. Material Flows Accounts—A Tool for Making Environmental Policy; WRI Report; World Resource Institute: Washington, DC, USA, 2005. [Google Scholar]
- Bundesanstalt für Geowissenschaften und Rohstoffe (BGR). Nickel—Geologisches Jahrbuch; Spezial Heft No. 7; BGR: Hannover, Germany, 1999. [Google Scholar]
- Adriaanse, A.; Bringezu, S.; Hammond, A.; Moriguchi, Y.; Rodenburg, E.; Rogich, D.; Schütz, H. Resource Flows : The Material Basis of Industrial Economies; World Resource Institute: Washington, DC, USA, 1997. [Google Scholar]
- Nemecek, T.; Kägi, T. Life Cycle Inventories of Agricultural Production Systems—Data v2.0 (2007); Ecoinvent Report No. 15; Swiss Centre for Life Cycle Inventories: Zürich, Switzerland, 2007. [Google Scholar]
- Werner, F.; Althaus, H.J.; Künniger, T.; Richter, K.; Jungbluth, N. Life Cycle Inventories of Wood as Fuels and Construction Material—Data v2.0 (2007); Ecoinvent Report No. 9; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- Goedkoop, M.; Heijungs, R.; Huijbregts, M.; de Schryver, A.; Struijs, J.; van Zelm, R. ReCiPe 2008—A Life Cycle Impact Assessment Method Which Comprises Harmonised Category Indicators at the Midpoint and the Endpoint Level—Report I: Characterisation; Ministry of Housing, Spatial Planning and Environment (VROM): The Hague, The Netherlands, 2009. [Google Scholar]
- OpenLCA Home Page. Available online: http://www.openlca.org (accessed on 23 July 2013).
- Scilab Home Page. Available online: http://www.scilab.org (accessed on 23 July 2013).
- Lenzen, M. A guide for compiling inventories in hybrid life-cycle assessments: Some Australian results. J. Clean. Prod. 2002, 10, 545–572. [Google Scholar] [CrossRef]
- Peters, G.P.; Hertwich, E.G. Structural analysis of international trade: Environmental impacts of Norway. Econ. Sys. Res. 2006, 18, 155–181. [Google Scholar] [CrossRef]
- Defourny, J.; Thorbecke, E. Structural path analysis and multiplier decomposition within a social accounting matrix framework. Econ. J. 1984, 94, 111–136. [Google Scholar] [CrossRef]
- Pehnt, M. Dynamic life cycle assessment (LCA) of renewable energy technologies. Renew. Energy 2006, 31, 55–71. [Google Scholar] [CrossRef]
- Zhai, P.; Williams, E.D. Dynamic hybrid life cycle assessment of energy and carbon of multicrystalline silicon photovoltaic systems. Environ. Sci. Technol. 2010, 44, 7950–7955. [Google Scholar] [CrossRef]
- Collinge, W.O.; Landis, A.E.; Jones, A.K.; Schaefer, L.A.; Bilec, M.M. Dynamic life cycle assessment: Framework and application to an institutional building. Int. J. Life Cycle Assess. 2013, 18, 538–552. [Google Scholar] [CrossRef]
- Suh, S. Input-output and hybrid life cycle assessment. Int. J. Life Cycle Assess. 2003, 8, 257. [Google Scholar] [CrossRef]
- Suh, S.; Lenzen, M.; Treloar, G.J.; Hondo, H.; Horvath, A.; Huppes, G.; Jolliet, O.; Klann, U.; Krewitt, W.; Moriguchi, Y.; et al. System boundary selection in life-cycle inventories using hybrid approaches. Environ. Sci. Technol. 2004, 38, 657–664. [Google Scholar] [CrossRef]
- Suh, S.; Nakamura, S. Five years in the area of input-output and hybrid LCA. Int. J. Life Cycle Assess. 2007, 12, 351–352. [Google Scholar]
- Finnveden, G.; Hauschild, M.Z.; Ekvall, T.; Guinée, J.; Heijungs, R.; Hellweg, S.; Koehler, A.; Pennington, D.; Suh, S. Recent developments in life cycle assessment. J. Environ. Manag. 2009, 91, 1–21. [Google Scholar] [CrossRef]
- Rowley, H.; Lundie, S.; Peters, G. A hybrid life cycle assessment model for comparison with conventional methodologies in Australia. Int. J. Life Cycle Assess. 2009, 14, 508–516. [Google Scholar] [CrossRef]
- Suh, S. Functions, commodities and environmental impacts in an ecological-economic model. Ecol. Econ. 2004, 48, 451–467. [Google Scholar] [CrossRef]
- Classen, M.; Althaus, H.J.; Blaser, S.; Scharnhorst, W.; Tuchschmid, M.; Jungbluth, N.; Emmenegger, M.F. Life Cycle Inventories of Metals—Data v2.0 (2007); Ecoinvent Report No. 10; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2007. [Google Scholar]
- World Wide Fund for Nature (WWF). Modell Deutschland—Klimaschutz bis 2050: Vom Ziel her denken; Final Report; WWF Germany: Berlin, Germany, 2009. [Google Scholar]
- The WIOD-Database. World input-output tables and international supply and use tables. Available online: http://www.wiod.org/protected3/data/wiot_analytic/wiot09_row_apr12.xlsx (accessed on 23 July 2013).
- Timmer, M.; Erumban, A.A.; Gouma, R.; Los, B.; Temurshoev, U.; de Vries, G.J.; Arto, I.; Andreoni, V.; Genty, A.; Neuwahl, F.; et al. The World Input-Output Database (WIOD): Contents, Sources and Methods; University of Groningen: Groningen, The Netherlands, 2012. [Google Scholar]
- Materials use-All countries; Environmental Accounts; The WIOD-Database. Available online: http://www.wiod.org/protected3/data/materials/mat_may12.zip (accessed on 23 July 2013).
- Burger, P.; Bauer, C. Teil XIII—Windkraft—Data v2.0 (2007); Ecoinvent Report No. 6-XIII; Swiss Centre for Life Cycle Inventories: Villigen, Switzerland, 2007. [Google Scholar]
- Tegen, S.; Hand, M.; Maples, B.; Lantz, E.; Schwabe, P.; Smith, A. 2010 Cost of Wind Energy Review; Technical Report NREL/TP-5000-52920; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Wiedemann, T.O.; Suh, S.; Kuishuang, F.; Lenzen, M.; Acquaye, A.; Scott, K.; Barrett, J.R. Application of hybrid life cycle approaches to emerging energy technologies—The case of wind power in the UK. Environ. Sci. Technol. 2011, 45, 5900–5907. [Google Scholar] [CrossRef]
- Williams, E.D.; Weber, C.L.; Hawkins, T.R. Hybrid framework for managing uncertainty in life cycle inventories. J. Ind. Ecol. 2009, 13, 928–944. [Google Scholar] [CrossRef]
- Mudd, G.M. The Sustainability of Mining in Australia: Key Production Trends and Their Environmental Implications for the Future; Research Report No. RR5; Department of Civil Engineering, Monash University and Mineral Policy Institute: Melbourne, Australia, 2009. [Google Scholar]
- Exiobase Homepage. Available online: http://www.exiobase.eu (accessed on 23 July 2013).
- Access workbooks by country; ESA 95 Supply Use and Input-Output tables; Eurostat. Available online: http://epp.eurostat.ec.europa.eu/portal/page/portal/esa95_supply_use_input_tables/data/workbooks (accessed on 23 July 2013).
- Material flow accounts. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=env_ac_mfa&lang=en (accessed on 23 July 2013).
- Watson, D.; Acosta Fernandez, J.; Wittmer, D.; Gravgard Pedersen, O. Environmental Pressures from European Consumption and Production : A Study in Integrated Environmental and Economic Analysis; EEA Technical Report No. 2/2013; European Environment Agency: Copenhagen, Denmark, 2013. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
